Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 May 16;9(22):19278–19286. doi: 10.1021/acsami.7b02739

Defect Dominated Charge Transport and Fermi Level Pinning in MoS2/Metal Contacts

Pantelis Bampoulis †,‡,*, Rik van Bremen †, Qirong Yao †, Bene Poelsema †, Harold J W Zandvliet †, Kai Sotthewes †,*
PMCID: PMC5465510  PMID: 28508628

Abstract

graphic file with name am-2017-027399_0002.jpg

Understanding the electronic contact between molybdenum disulfide (MoS2) and metal electrodes is vital for the realization of future MoS2-based electronic devices. Natural MoS2 has the drawback of a high density of both metal and sulfur defects and impurities. We present evidence that subsurface metal-like defects with a density of ∼1011 cm–2 induce negative ionization of the outermost S atom complex. We investigate with high-spatial-resolution surface characterization techniques the effect of these defects on the local conductance of MoS2. Using metal nanocontacts (contact area < 6 nm2), we find that subsurface metal-like defects (and not S-vacancies) drastically decrease the metal/MoS2 Schottky barrier height as compared to that in the pristine regions. The magnitude of this decrease depends on the contact metal. The decrease of the Schottky barrier height is attributed to strong Fermi level pinning at the defects. Indeed, this is demonstrated in the measured pinning factor, which is equal to ∼0.1 at defect locations and ∼0.3 at pristine regions. Our findings are in good agreement with the theoretically predicted values. These defects provide low-resistance conduction paths in MoS2-based nanodevices and will play a prominent role as the device junction contact area decreases in size.

Keywords: MoS2, defects, conductive AFM, metal/MoS2 junction, Schottky barrier, Fermi level pinning, transition metal dichalcogenides, 2D semiconductor

1. Introduction

Shortly after the isolation of graphene, an sp2 hybridized carbon layer,1−3 a wealth of other two-dimensional (2D) materials appeared on stage. One of the most promising and widely used materials is MoS2.4,5 MoS2 belongs to the family of materials known as transition metal dichalcogenides (TMDCs). TMDCs (and consequently MoS2) consist of a transition metal layer (e.g., Mo, W) sandwiched between two covalently bonded chalcogen layers (e.g., S, Se, Te). The trilayers are weakly bonded to each other via van der Waals forces. TMDCs exhibit a variety of electronic properties that depend on the composition (transition metal and chalcogen) of the crystal.5,6 For instance, MoS2 in its bulk form is a semiconductor with an indirect gap of 1.3 eV. Its band gap is tunable with thickness, and it has been shown to increase up to 1.8 eV in its monolayer manifestation due to quantum confinement.7,8 Furthermore, a transition from an indirect bulk band gap to a direct band gap occurs for monolayer MoS2.9 A highly informative and comprehensive review covering recent developments on MoS2 and other transition-metal dichalcogenides has been compiled by McDonnell and Wallace.10

MoS2 is a promising candidate for future (opto-)electronic devices.8,11−15 Radisavljevic et al.8 demonstrated that a monolayer MoS2-based field-effect transistor exhibits high current on/off ratios (108) at room temperature. Interestingly, they demonstrated that Au contacts on n-type MoS2 can be considered ohmic, despite the high work function of Au. Various metal/MoS2 contacts display a low Schottky barrier height.8,16,17 This is surprising because, in principle, the Schottky barrier height should strongly depend on the metal work function. This behavior was attributed to a strong Fermi level pinning effect.16

Fermi level pinning results from interface states that are formed at the interface between a metal and a semiconductor.18 The strength of the Fermi level pinning increases as the number of gap states at the interface increases.18 The observed strong Fermi level pinning at the MoS2/metal contact was attributed to the presence of S-vacancies.19−21 This was based on the lower formation energy of the S-vacancies compared to that of the Mo-vacancies19 and impurities. S-vacancies are indeed found to dominate in transition electron microscopy (TEM) images.22 In addition to S-vacancies, MoS2 has been shown to contain a substantial amount of other structural and metal-like defects.23,24

Intrinsic metal-like defects were reported to result in parallel conduction paths and were held responsible for large variations in the contact resistance and doping of MoS2.20 McDonnell et al.20 have demonstrated that defects dope the MoS2 surface. n-Type behavior was associated with sulfur deficiency, whereas p-type behavior was attributed to a sulfur-rich environment. Several other studies have used scanning tunneling microscopy (STM) and TEM to determine the structural and electronic properties of these defects.19,21−23,25−32 These studies have provided valuable information on the physical mechanisms that govern charge transport in MoS2-based junctions and have pointed toward properties that could impact the underlying mechanism. In addition to investigations of the metal/MoS2 junction using large metal contacts,8,16,17 nanoscopic metal/MoS2 contacts have been recently obtained by conductive AFM (C-AFM) measurements. In C-AFM, the tip can act as the metal electrode at the MoS2/metal contact.33−35 For instance, Giannazzo et al.34,35 recorded I(V) characteristics of the (Pt coated) tip/MoS2 contact and observed local variations in the Schottky barrier height. By comparing simultaneously recorded C-AFM images and I(V) curves one can, in principle, obtain information on the mechanisms that govern charge transport with high spatial resolution and link this behavior to the presence of defects and impurities.36 Unfortunately, such a comparison is still missing from the literature, and C-AFM has yet to realize its full potential. This is of particular importance in nanoelectronics because nanoscale variations in the electrical conductance of MoS2/metal contacts are expected to play a crucial role in defining device characteristics and performance.37−40 Therefore, a thorough investigation of the influence of nanoscopic defects on the behavior of metal/MoS2 contacts as well as a quantitative understanding of the underlying physics is highly desirable.

In this work, we perform high-spatial-resolution C-AFM, lateral force microscopy (LFM), and STM measurements on freshly cleaved natural MoS2 to understand the transport mechanism of the metal/MoS2 junctions and the influence of defects. We show that subsurface metal-like defects induce a negative ionization of the outermost S complex and dominate the charge transport at the MoS2/metal interface. The conductance of these defective regions is measured to be orders of magnitude larger than that in the pristine regions. Note here that the pristine regions should contain S-vacancies due to their high density.20,24 Spatially resolved maps of the Schottky barrier height reveal a decrease of the Schottky barrier height at the defects, where the magnitude of the decrease depends on the metal contact. We explain these results in terms of Fermi level pinning. The defects display a much stronger Fermi level pinning, the pinning factor is at least 3 times smaller compared to that of the pristine regions. Our results are in line with a recent theory61,66 on Fermi level pinning and provide improved insight into the physics governing the charge transport through MoS2/metal contacts.

2. Results and Discussion

2.1. Characterization of MoS2 Defects

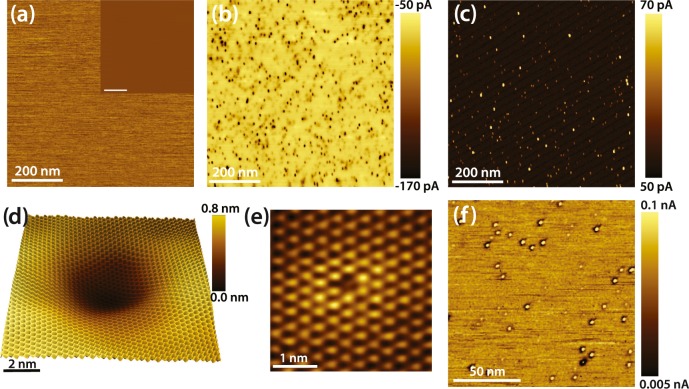
Topographic AFM and lateral force images reveal a smooth and defect-free MoS2 surface, see Figure 1a and its inset. However, this claim cannot be made for the simultaneously recorded C-AFM images when a positive sample bias (SB) is applied, using a boron-doped diamond tip. C-AFM has been previously demonstrated to be able to provide detailed information on the nanoscopic conductance of 2D materials.36,41Figure 1b reveals an inhomogeneous surface covered with dark circular depressions (with radii ranging from 3 to 4 nm), where higher negative currents are recorded as compared to those of the pristine surroundings. The density of the features varies between 1010 cm–2 and 1011 cm–2, as measured at different samples and at different locations. The features display a contrast reversal when switching from positive to negative SB (see Figure 1c), wherein both cases higher currents are measured at these locations. The measured currents are somewhat smaller when a negative SB is applied. Interestingly, these features display higher current values at all SBs, indicative of a lower local contact resistance. On the basis of the absence of contrast in the topographic and LFM images and in line with STM images recorded on the same sample, we conclude that the observed features are electronic in nature, and they are induced by subsurface defects or impurities. A high resolution STM image is shown in Figure 1d, and it clearly demonstrates that the features are indeed superimposed on the atomically resolved MoS2 lattice. We note that large-scale STM images (an example is shown in the Supporting Information) reveal an average defect density of (0.8 ± 0.3) × 1011 cm–2, which is similar to the defect density extracted from C-AFM images. Additionally, S-vacancies, similar to the one shown in Figure 1e, are found with a higher density across the surface, (0.7 ± 0.4) × 1013 cm–2, in line with previous reported values (density of (1.2 ± 0.4) × 1013 cm–2).20,26 The S-vacancies show a minor influence (∼1 nm in radius) on their surroundings and thus excludes them from being the cause of the dark/bright round features that extend for over 5 nm, found in both the C-AFM and STM measurements.

Figure 1.

Figure 1

Open in a new tab

(a) LFM image of the freshly cleaved MoS2 surface (650 × 650 nm2). Inset: the corresponding topography and (b) the simultaneously recorded C-AFM image, SB is +0.5 V. (c) C-AFM image recorded at −0.5 V. (d) STM topography image (10 × 10 nm2) of a dark circular depression recorded at −1.8 V and 0.4 nA. A low-pass filter has been applied. (e) STM image (3.6 × 3.6 nm2) of a S-vacancy in the outermost sulfur layer. Set point −2.2 V, 1.4 nA. (f) C-AFM image (120 × 120 nm2) recorded at −0.9 V.

Interestingly, at higher negative SBs (SB < −0.9 V) a dark ring is observed around the bright defects in the C-AFM images, as can be seen in Figure 1f. Similar behavior was previously reported for defects created by Ar ion bombardment: The origin of this behavior was ascribed to a negative ionization of the S atom complex (the sulfur atoms at the vicinity of the defect) at the defect site.30 However, in this study, the MoS2 surface was not irradiated by ions. The defects that are found must be intrinsic for natural MoS2 because the samples have not gone through any treatment prior to scanning. Indeed, as has been previously reported, the surface of natural MoS2 suffers from a high density of dark defects.23 The electron-depleted zone (dark ring) observed in both the STM and AFM images is caused by Coulomb repulsion around the negatively ionized S atoms or impurities. The electron-depleted region appears dark in both the STM and AFM images owing to local band bending or a screening effect.30,42 Therefore, based on Figure 1d–f, we argue that the ionization of the S complex occurs due to metal-like defects or impurities located below the outermost S layer. Both Mo-vacancies and antisite (Mo-substitutional) defects occur subsurface without a structural modification of the top S-layer.22,26,27,43 These defects can act as donors or acceptors at different locations near the surface. The dark defects measured in both C-AFM and STM show strong similarities to structures observed in other TMDCs when impurity atoms, such as Re, Na, and Li, are present in the crystal.23,44,45 It has also been suggested that the presence of dark defects could be induced by subsurface S vacancies.46 This is at variance with our measurements because of the 2 orders of magnitude difference in density between S-vacancies and dark defects. In addition, a previous study on WSe2 showed that one can map subsurface Se-vacancies by dI/dV mapping of the surface. Their results revealed a clear difference between subsurface Se-vacancies and dark defects.47 This suggests that subsurface Se-vacancies (or S-vacancies in the case of MoS2) cannot be the cause of the large dark features. Therefore, we suggest that the dark features are induced most probably from Mo-vacancies or antisites. These defects will hereby be referred to as metal-like defects.

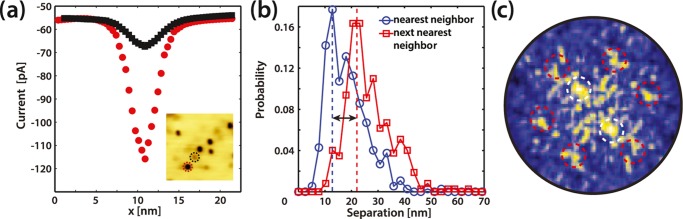
Supporting evidence that the defects located in the Mo-plane are obtained by C-AFM. First, from images similar to Figures 1b,c, we can see that even though the defects are dark depressions at positive SB and bright protrusions at negative SB, they have distinct current values that fall into two categories. For example, when a SB of 0.5 V is applied, the vast majority of defects fall into two categories: defects with current amplitudes of ∼−100 pA, and defects with current amplitudes of ∼−65 pA, see Figure 2a. We interpret this result as follows: The first category reflects defects in the first MoS2 trilayer, whereas the second category is caused by defects in the second MoS2 trilayer. These results suggest that the conductance of MoS2 can be influenced by defects located in the first two trilayers. Subsurface defects and impurities corresponding to different surface layers have also been identified and characterized in conventional semiconductors.48−51 Additional information regarding the nature of the defects has been obtained by measuring the separation distance between neighboring defects that fall in the same subcategory, that is, the first trilayer. The histograms of the probability distribution of the nearest neighbor and the next nearest neighbor separation distance, as measured from Figure 1b, show skewed distributions (as shown in Figure 2b). The separation distance between the nearest neighboring defects is measured to be larger than 8 nm, hinting at a repulsive interaction between defects. The histogram of the next-nearest neighbor shows a shift of the peak of the distribution equal to √3 × nn, where nn refers to the peak of the nearest neighbor distribution probability. This is an indication of a dominant sixfold symmetry. FFT performed on Figure 1b by only considering the center of each defect reveal a hexagonal symmetry (shown by the red circles in Figure 2c), with a periodicity equal to the median (∼19 nm) of the nearest neighbor distance of the probability distribution. This behavior suggests that the defects are formed in the same plane and strongly repel each other, resulting in the formation of a close-packed arrangement. Because the MoS2 surface is not fully packed by defects, our conclusion is only applicable to regions with a high defect density. The FFT reveals also two strong peaks with a larger periodicity (∼38 nm), marked with white circles in Figure 2c. The observation of the two additional strong spots within the hexagonal FFT pattern is indicative of the presence of a one-dimensional striped phase that is superimposed on the hexagonal ordering of the defects, see Supporting Information. To summarize, the above observations indicate that defects (or impurities) of the same charge located in Mo planes (hereby referred to as metal-like defects) of the first and second (and possibly deeper) MoS2 trilayers strongly influence the conductance of MoS2.

Figure 2.

Figure 2

Open in a new tab

(a) Current cross sections recorded with C-AFM at dark depressions induced by defects within the first (red) and second (black) trilayer, respectively. Inset: C-AFM image indicating the defects where the cross sections were taken (40 × 40 nm2), SB is 0.5 V. (b) A histogram of the probability distribution of the separation distance between nearest neighbor defects measured from Figure 1b. The median is ∼19 nm, and the minimum separation distance is ∼8 nm. (c) The FFT spectra is created from Figure 1b by only considering the centers of the darker circular depressions. The FFT reveals a hexagonal symmetry (red circles) with a periodicity of ∼19 nm. Besides, two somewhat stronger features are observed (white circles) indicative of a linear arrangement of the defects.

2.2. Spatially Resolved Schottky Barrier Height of the MoS2 Surface

To obtain quantitative information on the electron transport at the metal/MoS2 interface, we have performed C-AFM measurements using a highly doped diamond tip with a work function of ∼5.1 eV and an electron affinity of ∼0.02 eV.52 In contrast to STM measurements, where a tunneling gap exists between the tip and the sample, in C-AFM measurements, the tip is always in physical contact with the sample. When the metal tip is in physical contact with the 2D semiconductor, a Schottky barrier (ϕB) is formed. According to the Schottky–Mott rule, the Schottky barrier height is given by the difference between the work function of the metal (ϕM) and the electron affinity of the semiconductor (χ)

2.2. 1

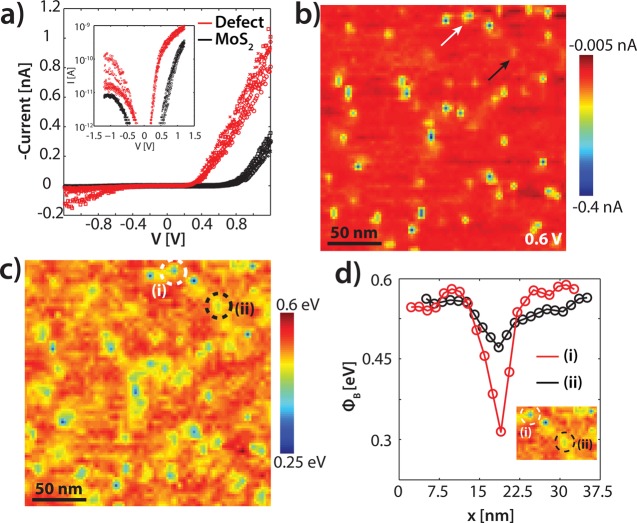
The measured conductance depends on the contact between the tip and the substrate. I(V) curves recorded on the MoS2 surface, see Figure 3a, exhibit nonlinear behavior, which is characteristic for a metal/semiconductor junction. A clear difference is observed between the I(V) curves recorded on a pristine region and a defect. Especially at the forward bias regime (SB > 0) of the spectrum, a much higher current is measured at the same voltage for the defects compared to that of the pristine MoS2 surface. This is in line with the C-AFM images shown in Figure 1. The advantage of using a sharp AFM tip as the metal electrode in the metal-semiconductor junction is the ability to record individual I(V) curves at every point of the surface with high spatial resolution. We have recorded I(V) curves in a 128 × 128 grid. From these I(V) curves, it is possible to make a current map at any voltage. Figure 3b shows an example of a spatially resolved current map at 0.6 V (200 × 200 nm2). A clear difference is observed between the subsurface metal-like defects and the pristine MoS2 regions. The defects occur as dark features, that is, higher negative currents are measured corresponding to a higher conductance. To explain the observed differences in the current map, the Schottky barrier height is extracted from all of the individual I(V) curves. Carrier transport across a Schottky barrier can be described by using the thermionic emission model, wherein the thermionic emission current I and the saturation current I0 are given by

2.2. 2

and

2.2. 3

where V is the applied bias voltage, T is the temperature (in this study equal to room temperature), q is the electron charge, kB is the Boltzmann constant, A* is the Richardson constant 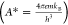Inline graphic, and η is the ideality factor. A is the junction area, that is, the tip contact area, calculated to be ∼3 nm2 for the diamond tip under a load of ∼20 nN. The calculation is based on the method described in ref (40). We note here that a careful selection of the tip load is essential to establish a stable and constant contact area across different regions of the scanning area. The induced pressure should be kept at a minimum to avoid any strain induced effects53−55 or even irreversibly damaging the surface. High-resolution LFM images recorded before and after such measurements reveal no apparent differences, suggesting that the surface remains undamaged (see Supporting Information). The ideality factor is obtained from

2.2. 4

and the Schottky barrier height (ϕB) is given by

2.2. 5

Figure 3.

Figure 3

Open in a new tab

(a) I(V) curves recorded with a doped diamond tip on the pristine MoS2 surface (red) and on a defect (black). The different symbols represent different measurements. Inset: The corresponding semi logarithmic I(V) curves. (b) A spatially resolved current map (200 × 200 nm2) obtained via 128 × 128 grid I(V) curves, recorded from −1.2 to 1.2 V. The map corresponds to a voltage of 0.6 V. The white arrow indicates a metal-like defect located at the first trilayer, whereas the black arrow a metal-like defect located at the second trilayer. (c) The extracted Schottky barrier height (ϕB) map of the surface obtained by the I(V) curves in (a). Significant variations are observed that are induced by subsurface defects. (d) Cross sections of the ϕB taken above subsurface defects of the first (red) and second (black) MoS2 trilayers indicated with dashed white and black circles in the inset. Inset: the corresponding ϕB map.

By applying the above mentioned equations on the recorded I(V) curves, we find that the Schottky barrier height for electron injection (hereby referred to as Schottky barrier height) of the pristine regions is ∼0.53 eV. The ideality factor, η, which is typically used to assess the deviation of the current transport from ideal thermal emission, has a value that varies between 2 and 4. We note that the fitting of the curves was performed within the range 0.5–1.1 V, to avoid a contribution from the MoS2 substrate resistance.56 Furthermore, in our experimental structure, we have used a second large electrode (see Supporting Information) to close the electrical circuit. The large contact (graphite electrode) and the nanocontact (AFM tip) to the MoS2 are typically described as two Schottky diodes connected (reversely) in series.57 Because the tip-MoS2 contact area is much smaller than the macroscopic contact (7–8 orders of magnitude), the current blocked by the macroscopic contact is negligible35,58 for the forward bias regime, and the tip/MoS2 contact dominates the charge transport. Therefore, even though our setup is, in principle, a metal–semiconductor–metal system, it can effectively be described as a metal–semiconductor junction, justifying the use of the above equations.

Figure 3c shows a spatially resolved ϕB map, in which every point represents the measured Schottky barrier height. Large inhomogeneities in the barrier height are observed. Interestingly, the ϕB remains approximately constant at the pristine locations, whereas directly above the metal-like defects (bright features in Figure 3b), a decrease of the barrier height of approximately 30–50% is measured. A cross section of the spatially resolved ϕB map is shown in Figure 3d. The cross section (red curve) on top of a defect (see the inset of Figure 3d) shows a decrease of the Schottky barrier height by almost 40%. The corresponding ideality factor at the defects is measured to be slightly larger at ∼5–6.

A closer look at Figure 3b,c reveals features showing up as a third contrast with respect to the environment, which is indicated by the black arrow in Figure 3b and marked with a black dashed circle in Figure 3c. In line with the C-AFM images of Figure 1, we attribute this faint contrast to Mo-plane based defects located in the second MoS2 trilayer. The cross section in Figure 3d (black curve) shows that the Schottky barrier height decreases by approximately 10–15%, a value much lower than the decrease (∼40%) induced by defects located in the outermost trilayer. Therefore, defects located in the second trilayer have a smaller influence on the Schottky barrier height created between the metal tip and the MoS2 surface. The effect is expected to vanish for defects located in deeper trilayers.

2.3. Fermi Level Pinning and the Role of Defects

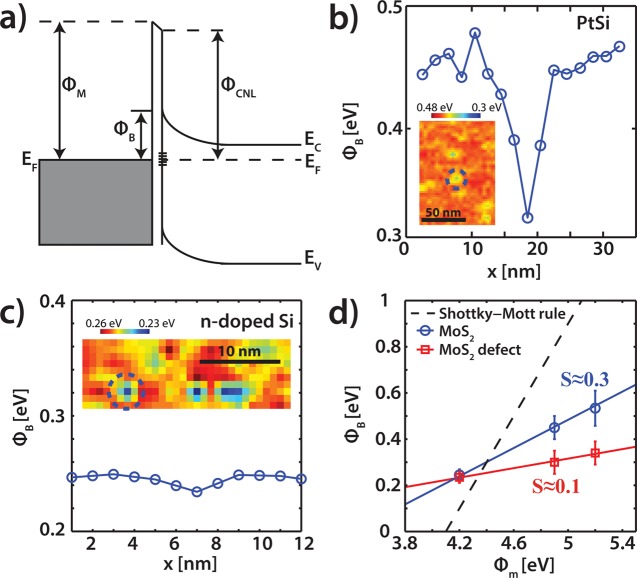
The predicted Schottky barrier height based on the Schottky–Mott rule (eq 1) is 1 eV (based on ϕM = 5.1 eV52 and χMoS2 = 4.1 eV59,60), whereas the measured Schottky barrier height is ∼0.53 eV at the pristine MoS2 surface. Recent experimental20,61 and theoretical studies60,62,63 have found a similar discrepancy. According to these studies, the Fermi level is partly pinned as a result of two interface effects: first, due to a metal work function modification resulting from a dipole formation at the interface, and second, by the introduction of gap states due to the weaker Mo–S bonding induced by interface metal–S interactions at the interface.62 To introduce Fermi level pinning into the Schottky–Mott rule, a pinning factor (S) and a charge neutrality level (ϕCNL) are added to eq 1(61,64,65)

2.3. 6

S is defined as S = dϕB/dϕM and can vary from 1 for an unpinned interface to 0 for a strongly pinned interface. b is the y-intercept of the ϕB versus ϕM graph, which is related to the ϕCNL as

2.3. 7

here, ϕCNL is the energy at which the interface is electroneutral (see Figure 4a). In the case of S = 1, the Schottky–Mott limit is recovered (see eq 1), whereas for S = 0, the Schottky barrier height is independent of the metal work function, that is, ϕB = ϕCNL – χ.

Figure 4.

Figure 4

Open in a new tab

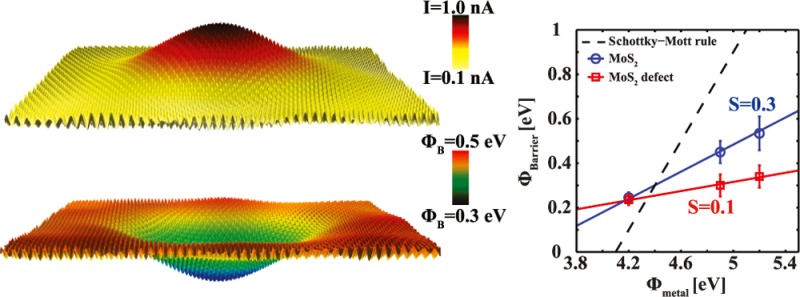
(a) Schematic of a metal–semiconductor junction with a Schottky barrier including Fermi level pinning. (b) Cross section of the spatially resolved ϕB map above a first trilayer subsurface defect, recorded with a PtSi tip. Inset: the corresponding ϕB map. (c) Cross section of the ϕB map for a subsurface defect recorded with a n-doped Si tip. Inset: the corresponding ϕB map. (d) Schottky barrier height for the pristine MoS2 (blue) and the defects (red) for various work functions of the tip (ϕM). The pinning factor S and the charge neutrality level (ϕCNL) are extracted using eq 6. The dotted line is the standard Schottky–Mott rule (see eq 1).

To experimentally characterize the pinning factor, S, and the charge neutrality level, (ϕCNL), the dependence of the Schottky barrier height on the work function of the metal tip should be defined. Therefore, the measurements were repeated with two other AFM tips, a PtSi (ϕM ≈ 4.9 eV, contact area 5.7 nm2) and a highly n-type doped Si (ϕM ≈ 4.1–4.2 eV, contact area 1.5 nm2). For the PtSi tips, we have obtained similar results as with the diamond tips. Figure 4b shows a cross section of a spatially resolved work function map, wherein the map is shown in the inset. The measured ϕB on the pristine MoS2 surface is ∼0.45 eV, which is lower than the barrier found with the doped diamond tip this is attributed to the lower ϕM of the PtSi tip. A decrease of approximately 25–35% is observed at the locations of the defects. However, when the same experiment is repeated with n-doped silicon tips (ϕM ≈ 4.1 eV), only a very small difference is observed between the Schottky barrier heights of the pristine MoS2 and the defects, see for example, the cross section of Figure 4c and the spatially resolved Schottky barrier height map (see inset of Figure 4c). Moreover, in both cases, defects corresponding to the second trilayer do not show any visible change of the Schottky barrier height, in contrast to the observations made with the diamond tips. The latter is expected because even the defects that are located in the first trilayer display a smaller decrease of the Schottky barrier height.

The Schottky barrier heights extracted from the different experiments are plotted as a function of the metal tip work function in Figure 4d. The pinning factor and charge neutrality level are extracted using eqs 6 and 7. The obtained values for S are ∼0.3 and ∼0.1 for the pristine MoS2 surface and the metal-like defects, respectively, whereas the ϕCNL is equal to 4.34 and 4.4 eV. The observed pinning factor of the pristine surface is equal to the theoretically predicted value61,63,66 but is significantly larger than the pinning factor found in other experimental works (S ∼ 0.1).16,61,67 However, the measured pinning factor that corresponds to defect sites matches well with previous experimentally obtained values.16,61,67 We argue that the strong Fermi level pinning and the unexpectedly low Schottky barrier height observed in previous studies,16,20,61,68 wherein large metal contacts are used are a direct consequence of the presence of metal-like defects and in particular of subsurface defects located in the outermost Mo-plane of the MoS2 trilayer. The fact that the pinning factor of the pristine MoS2 surface matches very well with the expected theoretical value, despite the presence of S-vacancies that are found at a high density in our MoS2 samples (as well as in the literature), is surprising. In these theoretical studies S-vacancies are neglected, whereas our samples suffer from a high density of S-vacancies. As we have shown, these vacancies do not induce any significant changes in their surroundings, which is in sharp contrast to the subsurface metal-like defects.

Initially, the low Schottky barrier height and the strong Fermi level pinning observed in previous studies were attributed to the presence of such S-vacancies. If this was true, we should have observed a pinning factor equal to ∼0.1 across the whole surface because of the high density of S-vacancies ((0.8 ± 0.3) × 1013 cm–2). In contrast, however, the pinning factor is measured to be ∼0.3 on the surface away from the bright/dark subsurface defects. It is clear that the low pinning factor found in previous studies originates from the presence of subsurface defects. As we have shown in the previous section, these defects are located at the Mo-plane of the first (and to some extent the second) trilayer. It is therefore apparent that not S-vacancies of the top S-layer but rather subsurface (Mo-plane located) defects dominate the charge transport and are responsible for the measured low Schottky barriers. Note also that even though a clear difference is observed between the Fermi level pinning strength of the pristine and the defected MoS2, the charge neutrality levels are almost equal. In both cases, the Fermi level pinning occurs just below the conduction band (<0.25 eV from the conduction band). This suggests that the pinning energy level is only slightly affected by the defect, despite the expected different band structure. The precise origin of the observed subsurface defects is currently unknown, and further studies need to be undertaken. It is known that a Mo-vacancy, or a Mo-replacement, or other intrinsic structural defects and impurities in MoS2, can act as donors or acceptors at different locations at or near the surface.22−24,27,32,69

The low Schottky barrier height induced by the subsurface defects can have a tremendous impact even at junctions with large contact areas because the junction current will be dominated by the current going through the defects, owing to the lower contact resistance. Indeed, McDonnell et al.20 found in their calculations that the currents of defected MoS2 surfaces were several orders of magnitude higher than those for pristine surfaces. The effect was sizable even when considering very low (0.3%) defect concentrations.20 Furthermore, we would like to stress that these findings could also be of particular interest in nanoscale electronics, wherein the junction contact area is of the order of a few nanometers. Large conductance variations induced by metal-like subsurface MoS2 defects must be expected to play a prominent role in device characteristics and predictability, in addition to the known impact of surface reactions with the contact metal.70,71

3. Conclusions

In summary, we have studied, at the nanometer scale, the underlying mechanisms that dominate the charge transport at the MoS2/metal interface using C-AFM and STM. We have explained the charge transport in terms of thermionic emission. Spatially resolved Schottky barrier height maps reveal a substantial conductivity difference between MoS2 with and without subsurface metal-like defects that depend on the tip’s work function. High work function tips show large spatial variations that amount to ∼40%, whereas for low work function tips the differences vanish. These observations are attributed to Fermi level pinning, which is the strongest at defect locations. We have also been able to determine the pinning factors and the charge neutrality levels for both the pristine surface and defects. The pinning factor is measured to be ∼0.3 for the pristine surface and ∼0.1 for locations where metal-like defects are found. The pristine surface pinning factor is equal to the theoretically predicted value.61,63,66 Subsurface defects have a lower pinning factor of ∼0.1 (thus stronger Fermi level pinning), which concurs well with experimental values obtained in previous studies wherein large metal contacts where used.16,61,67 Our findings show that the charge transport at the MoS2/metal interface is dominated by subsurface defects that provide alternative low resistance conduction paths. Therefore, considerable attention needs to be paid to control the concentration and nature of defects. This provides alternative routes for surface functionalization for device applications.

4. Methods

In this study, we use natural MoS2 samples obtained from HQ graphene (Groningen, The Netherlands). The MoS2 samples were mechanically cleaved and subsequently inserted into the AFM environmental chamber. To avoid any discrepancies in the data induced by water contamination, the AFM measurements were performed in a N2 environment by continuously purging with N2 gas. The samples were imaged in contact mode with an Agilent 5100 (Agilent) AFM using conductive AFM probes. LFM images can be obtained simultaneously with topographic images by recording the lateral torsion/deflection of the cantilever. For current imaging, the conductive tip is grounded and a bias voltage is applied at the MoS2 substrate. We have performed experiments with highly boron-doped diamond tips (AD-E-0.5-SS; Adama Innovations Ltd., resistivity: 0.003–0.005 Ω cm), PtSi tips (PtSi-Cont, Nanosensors), and highly n-doped silicon tips (Hi’Res-C14/Cr-Au, MikroMasch, resistivity: 0.01–0.025 Ω cm). The nominal spring constant of the diamond tips is 0.5 N/m, for the PtSi tips it is 0.3 N/m, and it is 5 N/m for the n-type Si tips. The resonance frequency is 30, 15, and 160 kHz for the diamond, PtSi, and n-type Si tips, respectively. STM and scanning tunneling spectroscopy investigations were performed with an ultra-high vacuum scanning tunneling microscope (Omicron) with chemically etched W tips. The base pressure of the ultrahigh vacuum system was maintained below 10–10 mbar.

Acknowledgments

The authors would like to thank Dr. E.S. Kooij for fruitful discussions. P.B. would like to thank the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO, STW 11431) for financial support. R.V.B. and H.J.W.Z. thank the Stichting voor Fundamenteel Onderzoek der Materie (FOM, FV157 14TWDO07) for financial support.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.7b02739.

  • SI-1, experimental configuration; SI-2, water adsorption and desorption; SI-3, comparison between metal-like defects and sulfur vacancies measured by STM and AFM; SI-4, nondestructive measurements; SI-5, inverse FFT and striped phase (PDF)

The authors declare no competing financial interest.

Supplementary Material

am7b02739_si_001.pdf (2.1MB, pdf)

References

  1. Novoselov K.; Jiang D.; Schedin F.; Booth T.; Khotkevich V.; Morozov S.; Geim A. Two-Dimensional Atomic Crystals. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 10451–10453. 10.1073/pnas.0502848102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Novoselov K. S.; Geim A.; Morozov S.; Jiang D.; Katsnelson M.; Grigorieva I.; Dubonos S.; Firsov A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. 10.1038/nature04233. [DOI] [PubMed] [Google Scholar]
  3. Novoselov K. S.; Geim A.; Morozov S.; Jiang D.; Zhang Y.; Dubonos S.; Grigorieva I.; Firsov A. Electric Field in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  4. Xu M.; Liang T.; Shi M.; Chen H. Graphene-like Two-Dimensional Materials. Chem. Rev. 2013, 113, 3766–3798. 10.1021/cr300263a. [DOI] [PubMed] [Google Scholar]
  5. Wang Q. H.; Kalantar-Zadeh K.; Kis A.; Coleman J. N.; Strano M. S. Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. 10.1038/nnano.2012.193. [DOI] [PubMed] [Google Scholar]
  6. Duan X.; Wang C.; Pan A.; Yu R.; Duan X. Two-Dimensional Transition Metal Dichalcogenides as Atomically Thin Semiconductors: Opportunities and Challenges. Chem. Soc. Rev. 2015, 44, 8859–8876. 10.1039/C5CS00507H. [DOI] [PubMed] [Google Scholar]
  7. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  8. Radisavljevic B.; Radenovic A.; Brivio J.; Giacometti V.; Kis A. Single-Layer MoS2 Transistors. Nat. Nanotechnol. 2011, 6, 147–150. 10.1038/nnano.2010.279. [DOI] [PubMed] [Google Scholar]
  9. Splendiani A.; Sun L.; Zhang Y.; Li T.; Kim J.; Chim C.-Y.; Galli G.; Wang F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. 10.1021/nl903868w. [DOI] [PubMed] [Google Scholar]
  10. McDonnell S. J.; Wallace R. M. Atomically-Thin Layered Films for Device Applications Based upon 2D TMDC Materials. Thin Solid Films 2016, 616, 482–501. 10.1016/j.tsf.2016.08.068. [DOI] [Google Scholar]
  11. Radisavljevic B.; Whitwick M. B.; Kis A. Integrated Circuits and Logic Operations Based on Single-Layer MoS2. ACS Nano 2011, 5, 9934–9938. 10.1021/nn203715c. [DOI] [PubMed] [Google Scholar]
  12. Wang H.; Yu L.; Lee Y.-H.; Shi Y.; Hsu A.; Chin M. L.; Li L.-J.; Dubey M.; Kong J.; Palacios T. Integrated Circuits Based on Bilayer MoS2 Transistors. Nano Lett. 2012, 12, 4674–4680. 10.1021/nl302015v. [DOI] [PubMed] [Google Scholar]
  13. Lee H. S.; Min S.-W.; Chang Y.-G.; Park M. K.; Nam T.; Kim H.; Kim J. H.; Ryu S.; Im S. MoS2 Nanosheet Phototransistors with Thickness-Modulated Optical Energy Gap. Nano Lett. 2012, 12, 3695–3700. 10.1021/nl301485q. [DOI] [PubMed] [Google Scholar]
  14. Lopez-Sanchez O.; Lembke D.; Kayci M.; Radenovic A.; Kis A. Ultrasensitive Photodetectors Based on Monolayer MoS2. Nat. Nanotechnol. 2013, 8, 497–501. 10.1038/nnano.2013.100. [DOI] [PubMed] [Google Scholar]
  15. Yin Z.; Li H.; Li H.; Jiang L.; Shi Y.; Sun Y.; Lu G.; Zhang Q.; Chen X.; Zhang H. Single-Layer MoS2 Phototransistors. ACS Nano 2012, 6, 74–80. 10.1021/nn2024557. [DOI] [PubMed] [Google Scholar]
  16. Das S.; Chen H.-Y.; Penumatcha A. V.; Appenzeller J. High Performance Multilayer MoS2 Transistors with Scandium Contacts. Nano Lett. 2013, 13, 100–105. 10.1021/nl303583v. [DOI] [PubMed] [Google Scholar]
  17. Liu H.; Neal A. T.; Ye P. D. Channel Length Scaling of MoS2 MOSFETs. ACS Nano 2012, 6, 8563–8569. 10.1021/nn303513c. [DOI] [PubMed] [Google Scholar]
  18. Cowley A.; Sze S. Surface States and Barrier Height of Metal-Semiconductor Systems. J. Appl. Phys. 1965, 36, 3212–3220. 10.1063/1.1702952. [DOI] [Google Scholar]
  19. Liu D.; Guo Y.; Fang L.; Robertson J. Sulfur Vacancies in Monolayer MoS2 and its Electrical Contacts. Appl. Phys. Lett. 2013, 103, 183113 10.1063/1.4824893. [DOI] [Google Scholar]
  20. McDonnell S.; Addou R.; Buie C.; Wallace R. M.; Hinkle C. L. Defect-Dominated Doping and Contact Resistance in MoS2. ACS Nano 2014, 8, 2880–2888. 10.1021/nn500044q. [DOI] [PubMed] [Google Scholar]
  21. Guo Y.; Liu D.; Robertson J. Chalcogen Vacancies in Monolayer Transition Metal Dichalcogenides and Fermi Level Pinning at Contacts. Appl. Phys. Lett. 2015, 106, 173106 10.1063/1.4919524. [DOI] [Google Scholar]
  22. Zhou W.; Zou X.; Najmaei S.; Liu Z.; Shi Y.; Kong J.; Lou J.; Ajayan P. M.; Yakobson B. I.; Idrobo J.-C. Intrinsic Structural Defects in Monolayer Molybdenum Disulfide. Nano Lett. 2013, 13, 2615–2622. 10.1021/nl4007479. [DOI] [PubMed] [Google Scholar]
  23. Addou R.; Colombo L.; Wallace R. M. Surface Defects on Natural MoS2. ACS Appl. Mater. Interfaces 2015, 7, 11921–11929. 10.1021/acsami.5b01778. [DOI] [PubMed] [Google Scholar]
  24. Addou R.; McDonnell S.; Barrera D.; Guo Z.; Azcatl A.; Wang J.; Zhu H.; Hinkle C. L.; Quevedo-Lopez M.; Alshareef H. N.; Colombo L.; Hsu J. W. P.; Wallace R. M. Impurities and Electronic Property Variations of Natural MoS2 Crystal Surfaces. ACS Nano 2015, 9, 9124–9133. 10.1021/acsnano.5b03309. [DOI] [PubMed] [Google Scholar]
  25. Jeong H. Y.; Lee S. Y.; Ly T. H.; Han G. H.; Kim H.; Nam H.; Jiong Z.; Shin B. G.; Yun S. J.; Kim J.; Kim U. J.; Hwang S.; Lee Y. H. Visualizing Point Defects in Transition-Metal Dichalcogenides using Optical Microscopy. ACS Nano 2016, 10, 770–777. 10.1021/acsnano.5b05854. [DOI] [PubMed] [Google Scholar]
  26. Hong J.; et al. Exploring Atomic Defects in Molybdenum Disulphide Monolayers. Nat. Commun. 2015, 6, 6293 10.1038/ncomms7293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Santosh K.; Longo R. C.; Addou R.; Wallace R. M.; Cho K. Impact of Intrinsic Atomic Defects on the Electronic Structure of MoS2 Monolayers. Nanotechnology 2014, 25, 375703 10.1088/0957-4484/25/37/375703. [DOI] [PubMed] [Google Scholar]
  28. Komsa H.-P.; Krasheninnikov A. V. Native Defects in Bulk and Monolayer MoS2 from First Principles. Phys. Rev. B 2015, 91, 125304 10.1103/PhysRevB.91.125304. [DOI] [Google Scholar]
  29. Noh J.-Y.; Kim H.; Kim Y.-S. Stability and Electronic Structures of Native Defects in Single-Layer MoS2. Phys. Rev. B 2014, 89, 205417 10.1103/PhysRevB.89.205417. [DOI] [Google Scholar]
  30. Sengoku N.; Ogawa K. Investigations of Electronic Structures of Defects Introduced by Ar Ion Bombardments on MoS2 by Scanning Tunneling Microscopy. Jpn. J. Appl. Phys. 1995, 34, 3363. 10.1143/JJAP.34.3363. [DOI] [Google Scholar]
  31. Liu X.; Balla I.; Bergeron H.; Hersam M. C. Point Defects and Grain Boundaries in Rotationally Commensurate MoS2 on Epitaxial Graphene. J. Phys. Chem. C 2016, 120, 20798–20805. 10.1021/acs.jpcc.6b02073. [DOI] [Google Scholar]
  32. Addou R.; Wallace R. M. Surface Analysis of WSe2 Crystals: Spatial and Electronic Variability. ACS Appl. Mater. Interfaces 2016, 8, 26400–26406. 10.1021/acsami.6b08847. [DOI] [PubMed] [Google Scholar]
  33. Fu D.; Zhou J.; Tongay S.; Liu K.; Fan W.; King Liu T.-J.; Wu J. Mechanically Modulated Tunneling Resistance in Monolayer MoS2. Appl. Phys. Lett. 2013, 103, 183105 10.1063/1.4827301. [DOI] [Google Scholar]
  34. Giannazzo F.; Fisichella G.; Piazza A.; Agnello S.; Roccaforte F. Nanoscale Inhomogeneity of the Schottky barrier and Resistivity in MoS2 Multilayers. Phys. Rev. B 2015, 92, 081307 10.1103/PhysRevB.92.081307. [DOI] [Google Scholar]
  35. Giannazzo F.; Fisichella G.; Piazza A.; Di Franco S.; Oliveri I.; Agnello S.; Roccaforte F. Current Injection from Metal to MoS2 Probed at Nanoscale by Conductive Atomic Force Microscopy. Mater. Sci. Semicond. Process. 2016, 42, 174–178. 10.1016/j.mssp.2015.07.062. [DOI] [Google Scholar]
  36. Bampoulis P.; Sotthewes K.; Siekman M. H.; Zandvliet H. J. W.; Poelsema B. Graphene Visualizes the Ion Distribution on Air-Cleaved Mica. Sci. Rep. 2017, 7, 43451 10.1038/srep43451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Fuhrer M. S.; Hone J. Measurement of Mobility in Dual-Gated MoS2 Transistors. Nat. Nanotechnol. 2013, 8, 146–147. 10.1038/nnano.2013.30. [DOI] [PubMed] [Google Scholar]
  38. Radisavljevic B.; Kis A. Reply to ’Measurement of Mobility in Dual-Gated MoS2 Transistors. Nat. Nanotechnol. 2013, 8, 147–148. 10.1038/nnano.2013.31. [DOI] [PubMed] [Google Scholar]
  39. Jena D. Tunneling Transistors Based on Graphene and 2-D Crystals. Proc. IEEE 2013, 101, 1585–1602. 10.1109/JPROC.2013.2253435. [DOI] [Google Scholar]
  40. Son Y.; Wang Q. H.; Paulson J. A.; Shih C.-J.; Rajan A. G.; Tvrdy K.; Kim S.; Alfeeli B.; Braatz R. D.; Strano M. S. Layer Number Dependence of MoS2 Photoconductivity using Photocurrent Spectral Atomic Force Microscopic Imaging. ACS Nano 2015, 9, 2843–2855. 10.1021/nn506924j. [DOI] [PubMed] [Google Scholar]
  41. Hwang J. H.; Lee H.; Kwon S.; Jeong J. H.; Song H. C.; Choi J. I. J.; Park J. Y. Local Conductance Mapping of Water-Intercalated Graphene on Mica. Appl. Phys. Lett. 2016, 109, 241602 10.1063/1.4972233. [DOI] [Google Scholar]
  42. Inoue A.; Komori T.; Shudo K.-i. Atomic-Scale Structures and Electronic States of Defects on Ar+-ion Irradiated MoS2. J. Electron. Spectrosc. Relat. Phenom. 2013, 189, 11–18. 10.1016/j.elspec.2012.12.005. [DOI] [Google Scholar]
  43. González C.; Biel B.; Dappe Y. Theoretical Characterisation of Point Defects on a MoS2 Monolayer by Scanning Tunnelling Microscopy. Nanotechnology 2016, 27, 105702 10.1088/0957-4484/27/10/105702. [DOI] [PubMed] [Google Scholar]
  44. Whangbo M.-H.; Ren J.; Magonov S.; Bengel H.; Parkinson B.; Suna A. On the Correlation between the Scanning Tunneling Microscopy Image Imperfections and Point Defects of Layered Chalcogenides 2H-MX2 (M= Mo, W; X= S, Se). Surf. Sci. 1995, 326, 311–326. 10.1016/0039-6028(94)00800-0. [DOI] [Google Scholar]
  45. Murata H.; Kataoka K.; Koma A. Scanning Tunneling Microscope Images of Locally Modulated Structures in Layered Materials, MoS2 (0001) and MoSe2 (0001), Induced by Impurity Atoms. Surf. Sci. 2001, 478, 131–144. 10.1016/S0039-6028(01)00904-9. [DOI] [Google Scholar]
  46. Lu C.-P.; Li G.; Mao J.; Wang L.-M.; Andrei E. Y. Bandgap, Mid-Gap States, and Gating Effects in MoS2. Nano Lett. 2014, 14, 4628–4633. 10.1021/nl501659n. [DOI] [PubMed] [Google Scholar]
  47. Yankowitz M.; McKenzie D.; LeRoy B. J. Local Spectroscopic Characterization of Spin and Layer Polarization in WSe2. Phys. Rev. Lett. 2015, 115, 136803 10.1103/PhysRevLett.115.136803. [DOI] [PubMed] [Google Scholar]
  48. Koenraad P. M.; Flatté M. E. Single Dopants in Semiconductors. Nat. Mater. 2011, 10, 91–100. 10.1038/nmat2940. [DOI] [PubMed] [Google Scholar]
  49. Sinthiptharakoon K.; Schofield S. R.; Studer P.; Brázdová V.; Hirjibehedin C. F.; Bowler D. R.; Curson N. J. Investigating Individual Arsenic Dopant Atoms in Silicon Using Low-Temperature Scanning Tunnelling Microscopy. J. Phys. Condens. Matter 2013, 26, 012001 10.1088/0953-8984/26/1/012001. [DOI] [PubMed] [Google Scholar]
  50. Lee D.; Gohlke D.; Benjamin A.; Gupta J. A. Influence of the Local Environment on Mn Acceptors in GaAs. J. Phys. Condens. Matter 2015, 27, 154202 10.1088/0953-8984/27/15/154202. [DOI] [PubMed] [Google Scholar]
  51. Liu L.; Yu J.; Lyding J. W. Atom-Resolved Three-Dimensional Mapping of Boron Dopants in Si(100) by Scanning Tunneling Microscopy. Appl. Phys. Lett. 2001, 78, 386–388. 10.1063/1.1339260. [DOI] [Google Scholar]
  52. Liu K.; Zhang B.; Wan M.; Chu J.; Johnston C.; Roth S. Measurement of Electron Affinity in Boron-Doped Diamond from Capacitance Spectroscopy. Appl. Phys. Lett. 1997, 70, 2891–2893. 10.1063/1.119044. [DOI] [Google Scholar]
  53. Kim K. S.; Zhao Y.; Jang H.; Lee S. Y.; Kim J. M.; Kim K. S.; Ahn J.-H.; Kim P.; Choi J.-Y.; Hong B. H. Large-Scale Pattern Growth of Graphene Films for Stretchable Transparent Electrodes. Nature 2009, 457, 706–710. 10.1038/nature07719. [DOI] [PubMed] [Google Scholar]
  54. Kwon S.; Choi S.; Chung H.; Yang H.; Seo S.; Jhi S.-H.; Young Park J. Probing Nanoscale Conductance of Monolayer Graphene Under Pressure. Appl. Phys. Lett. 2011, 99, 013110 10.1063/1.3609317. [DOI] [Google Scholar]
  55. Heui Hwang J.; Kwon S.; Park J.; Hun Kim J.; Lee J.; Sung Kim J.; Lyeo H.-K.; Young Park J. Strain Effects on In-Plane Conductance of the Topological Insulator Bi2Te3. Appl. Phys. Lett. 2014, 104, 161613 10.1063/1.4873389. [DOI] [Google Scholar]
  56. Werner J. H. Schottky Barrier and pn-Junction I/V Plots-Small Signal Evaluation. Appl. Phys. A 1988, 47, 291–300. 10.1007/BF00615935. [DOI] [Google Scholar]
  57. Nouchi R. Extraction of the Schottky Parameters in Metal-Semiconductor-Metal Diodes from a Single Current-Voltage Measurement. J. Appl. Phys. 2014, 116, 184505 10.1063/1.4901467. [DOI] [Google Scholar]
  58. Lee M. H.; Hwang C. S. Resistive Switching Memory: Observations with Scanning Probe Microscopy. Nanoscale 2011, 3, 490–502. 10.1039/C0NR00580K. [DOI] [PubMed] [Google Scholar]
  59. Schlaf R.; Lang O.; Pettenkofer C.; Jaegermann W. Band Lineup of Layered Semiconductor Heterointerfaces Prepared by van der Waals Epitaxy: Charge Transfer Correction Term for the Electron Affinity Rule. J. Appl. Phys. 1999, 85, 2732. 10.1063/1.369590. [DOI] [Google Scholar]
  60. Zhong H.; Quhe R.; Wang Y.; Ni Z.; Ye Z.; Song M.; Pan Y.; Yang J.; Yang L.; Lei M.; Shi J.; Lu J. Interfacial Properties of Monolayer and Bilayer MoS2 Contacts with Metals: Beyond the Energy Band Calculations. Sci. Rep. 2016, 6, 21786 10.1038/srep21786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Kim C.; Moon I.; Lee D.; Choi M. S.; Ahmed F.; Nam S.; Cho Y.; Shin H.-J.; Park S.; Yoo W. J. Fermi Level Pinning at Electrical Metal Contacts of Monolayer Molybdenum Dichalcogenides. ACS Nano 2017, 11, 1588–1596. 10.1021/acsnano.6b07159. [DOI] [PubMed] [Google Scholar]
  62. Gong C.; Colombo L.; Wallace R. M.; Cho K. The unusual Mechanism of Partial Fermi Level Pinning at Metal-MoS2 Interfaces. Nano Lett. 2014, 14, 1714–1720. 10.1021/nl403465v. [DOI] [PubMed] [Google Scholar]
  63. Kang J.; Liu W.; Sarkar D.; Jena D.; Banerjee K. Computational Study of Metal Contacts to Monolayer Transition-Metal Dichalcogenide Semiconductor. Phys. Rev. X 2014, 4, 031005 10.1103/PhysRevX.4.031005. [DOI] [Google Scholar]
  64. Tung R. Formation of an Electric Dipole at Metal-Semiconductor Interfaces. Phys. Rev. B 2001, 64, 205310 10.1103/PhysRevB.64.205310. [DOI] [Google Scholar]
  65. Robertson J. Band Offsets, Schottky Barrier Heights, and Their Effects on Electronic Devices. J. Vac. Sci. Technol., A 2013, 31, 050821 10.1116/1.4818426. [DOI] [Google Scholar]
  66. Guo Y.; Liu D.; Robertson J. 3D Behavior of Schottky Barriers of 2D Transition-Metal Dichalcogenides. ACS Appl. Mater. Interfaces 2015, 7, 25709. 10.1021/acsami.5b06897. [DOI] [PubMed] [Google Scholar]
  67. Allain A.; Kang J.; Banerjee K.; Kis A. Electrical Contacts to Two-Dimensional Semiconductors. Nat. Mater. 2015, 14, 1195. 10.1038/nmat4452. [DOI] [PubMed] [Google Scholar]
  68. Kaushik N.; Nipane A.; Basheer F.; Dubey S.; Grover S.; Deshmukh M. M.; Lodha S. Schottky Barrier Heights for Au and Pd Contacts to MoS2. Appl. Phys. Lett. 2014, 105, 113505 10.1063/1.4895767. [DOI] [Google Scholar]
  69. Su J.; Li N.; Zhang Y.; Feng L.; Liu Z. Role of Vacancies in Tuning the Electronic Properties of Au-MoS2 contact. AIP Adv. 2015, 5, 077182 10.1063/1.4927853. [DOI] [Google Scholar]
  70. McDonnell S.; Smyth C.; Hinkle C. L.; Wallace R. M. MoS2-Titanium Contact Interface Reactions. ACS Appl. Mater. Interfaces 2016, 8, 8289–8294. 10.1021/acsami.6b00275. [DOI] [PubMed] [Google Scholar]
  71. Smyth C. M.; Addou R.; McDonnell S.; Hinkle C. L.; Wallace R. M. Contact Metal-MoS2 Interfacial Reactions and Potential Implications on MoS2-Based Device Performance. J. Phys. Chem. C 2016, 120, 14719–14729. 10.1021/acs.jpcc.6b04473. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am7b02739_si_001.pdf (2.1MB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES