Shear bands as manifestation of a criticality in yielding amorphous solids

Significance

The art of making structural, polymeric, and metallic glasses is rapidly developing with many applications. A limitation is that, under increasing external strain, all amorphous solids have a yield stress, which when exceeded, results in a plastic response leading to mechanical failure. Understanding this is crucial for assessing the risk of failure of glassy materials under loads. The universality of the mechanical yield requires a theory that is general enough to transcend the microscopic details of different glasses, which all show similar stress–strain curves with a yield point. We provide a general theory that is thermodynamic in nature, showing that the mechanical yield is a spinodal criticality in an appropriately constructed free energy landscape.

Abstract

Amorphous solids increase their stress as a function of an applied strain until a mechanical yield point whereupon the stress cannot increase anymore, afterward exhibiting a steady state with a constant mean stress. In stress-controlled experiments, the system simply breaks when pushed beyond this mean stress. The ubiquity of this phenomenon over a huge variety of amorphous solids calls for a generic theory that is free of microscopic details. Here, we offer such a theory: The mechanical yield is a thermodynamic phase transition, where yield occurs as a spinodal phenomenon. At the spinodal point, there exists a divergent correlation length that is associated with the system-spanning instabilities (also known as shear bands), which are typical to the mechanical yield. The theory, the order parameter used, and the correlation functions that exhibit the divergent correlation length are universal in nature and can be applied to any amorphous solids that undergo mechanical yield.

A solid, be it crystalline or amorphous, is operatively defined as any material capable to respond elastically to an externally applied shear deformation (1). However, any solid material, when subject to a large-enough shear strain, finally undergoes a mechanical yield. Here, we focus on the mechanical yield of amorphous materials, such as molecular and colloidal glasses, foams, and granular matter. The phenomenology exhibited by the yielding point within this vast class of materials, as reported in countless strain-controlled simulations (2–8) and experiments (9–11), shows a remarkable degree of universality, despite the highly varied nature of the model systems involved. Among these universal features is the presence, at the onset of flow at yielding, of system-spanning excitations referred to as shear bands (12, 13), wherein the shear strongly localizes, leaving the rest of the material unperturbed. This phenomenon is of capital importance for engineering applications, because it is responsible for the brittleness typical of glassy materials, in particular metallic glasses (14), whose potential for practical use is stymied by their tendency to shear band and fracture (13, 15, 16).

In athermal amorphous solids, the phenomenon has universal features. For strains $\gamma$ smaller than some critical value denoted as ${\gamma }_Y$, the stress in the material grows on the average when the strain is increased. After yield, the stress cannot grow on the average, no matter how much the strain is increased. The universality of the basic phenomenology of yielding begs a picture of its characteristics in terms of a universal theory, in the sense that such a theory should rely on a statistical–mechanical framework and be independent of details, such as chemical composition and production process of the material. This need was addressed in a recent work (17), wherein building up from ideas first advanced in ref. 18, there emerged a picture of mechanical yielding as a first-order phenomenon [i.e., as a discontinuous phase transition in a suitable overlap order parameter $Q_{ab}$ (defined in Eq. 1 below), which jumps from a value of order one to a value of order zero as strain is increased above the yielding threshold ${\gamma }_Y$]. The physical meaning of this observation is that, before yielding, the amorphous system was limited to a small patch in the configuration space, very far from any kind of ergodicity. The yielding transition is an opening of a much larger available configuration space, whereupon the system is ergodized subject to the constraint of constant mean stress. Within this framework, the yielding transition is essentially envisioned as a spinodal point (19) (i.e., the point where the metastable, high-$Q_{ab}$ glassy patch of available configurations becomes unstable with respect to a new phase with low $Q_{ab}$) associated with an ergodized system in the presence of disorder (20). A paradigmatic example of such a spinodal is the mode coupling cross-over (12) characterized by dynamical slowing down and heterogeneities, with behavior that is characterized by a dynamical length scale, which can be extracted from suitable multipoint correlators (12). According to our picture, this kind of critical behavior should also be found at the yielding transition, conditional that one is able to derive the expression of the right correlator to measure. This suggestion seems even more reasonable in light of a recent study (21), wherein the similarity of shear bands with dynamical heterogeneities has been pointed out; also, some oscillatory shear simulations seem to indicate that a slowdown of the dynamics on approaching yielding may indeed be present (22, 23). It is important to stress here that the reason that a spinodal point can be exposed and measured is that the glassy timescales and the athermal conditions stabilize the metastable system until the spinodal point is crossed and the system becomes unstable against constrained ergodization.

Within a generic statistical–mechanical theory, formulated in terms of a suitable Gibbs free energy $G[\varphi ]$ (i.e., the free energy for fixed order parameter $\varphi$), stable phases are identified with its points of minimum in $\varphi$, and phase transitions happen when the curvature of these minima goes to zero, inducing a critical behavior that manifests diverging susceptibilities–fluctuations, critical slowing down of the dynamics, and growing correlation lengths (24). At a spinodal point, for example, one such minimum becomes unstable and transforms into a saddle. In the case of the order parameter $Q_{ab}$, the general form of the free energy $s[Q_{ab}]$ had been already derived and studied (ref. 25 has a review) in the context of the theory of replicas originally developed for the study of spin glasses, and its properties, at least at mean field level, are well-known (we refer to refs. 18 and 26 for the derivation of $s[Q_{ab}]$ in the specific case of mean field hard spheres); the matrix of second derivatives (or using a more field-theoretic terminology, the mass matrix) is not diagonal in the base of $Q_{ab}$ and after diagonalization, is found to have only three distinct modes or masses (25). Of these masses, the most relevant ones are the so-called replicon mode ${\lambda }_R$, which for example, goes to zero at the newly proposed Gardner transition (27), and the longitudinal mode ${\lambda }_L$, which is, instead, related to spinodal points (18, 19), such as our yielding transition. In SI Text, we review briefly the background theory that is at the basis of this approach.

In this paper, we build up from the results of ref. 17, and following the line of reasoning formulated above, we use the expression of the correlation function relative to the longitudinal mode ${\lambda }_L$ as it can be derived from the replicated field theory (25) to reveal the critical features of the yielding transition. We measure this correlator in numerical simulation and use it to expose the critical properties of the yielding transition, showing how shear bands manifest the diverging correlation length encoded in this correlator. We show how the order parameter $Q_{ab}$ and its associated replicated field theory are thereby able to provide a unified and universal picture of the yielding transition in terms of a spinodal point in the presence of disorder, with an associated criticality.

Correlation Functions

The relevant order parameter for the problem at hand is the overlap function $Q_{ab}$, which measures the distance between two configurations $a$ and $b$ of the same system. Denoting the position of the $i$th particle as ${𝐫}_i^a$ in configuration $a$ and ${𝐫}_i^b$ in configuration $b$, we define

$$Q_{ab}\equiv \frac{1}{N}\sum _{i=1}^N\theta (\mathrm{\ell }-|{𝐫}_i^a-{𝐫}_i^b|),$$ [1]

where $\theta (x)$ is the Heaviside step function, and $\mathrm{\ell }$ is a constant length, which is taken below to be 1/3 in Lennard–Jones units (numerical details are given below). Thus, $Q_{ab}=\mathrm{\hspace{0.17em}1}$ for two identical configurations, and $Q_{ab}=\mathrm{\hspace{0.17em}0}$ when the distance between the positions of all of the particles $i$ in the two configurations exceeds $\mathrm{\ell }$. Based on the introductory discussion, we now derive an expression for the correlator associated with the longitudinal mode, from whence one can extract the correlation length associated with the onset of criticality at the yielding point and define an associated susceptibility, which will shoot up as the yielding point is approached. The first step is to “localize” the overlap function and define the $r$-dependent quantity

$$Q_{ab}(𝐫)\equiv \sum _{i=1}^N\theta (\mathrm{\ell }-|{𝐫}_i^a-{𝐫}_i^b|)\delta (𝐫-{𝐫}_i^a).$$ [2]

Next, as mentioned above, the expression for the longitudinal correlator in terms of four-replica correlation functions can be found by diagonalization of the correlation matrix $G_{ab;cd}$, which is defined as the inverse of the mass matrix $M_{ab;cd}$ of the replicated field theory of the overlap order parameter $Q_{ab}$ (25). The derivation is a matter of standard diagonalization algebra, and therefore, we shall not report it here and refer to SI Text for the details. The expression, used, for example, in refs. 28 and 29 in the case of a model with spins on a lattice, reads for athermal systems

$$G_L(𝐫)=2G_R(𝐫)-{\mathrm{\Gamma }}_2(𝐫),$$ [3]

with the definitions

$$G_R(𝐫)\equiv \overline{⟨Q_{ab}(r)Q_{ab}(0)⟩}-2\overline{⟨Q_{ab}(r)Q_{ac}(0)⟩}+\overline{⟨Q_{ab}(r)⟩⟨Q_{cd}(0)⟩},$$ [4]

$${\mathrm{\Gamma }}_2(𝐫)\equiv \overline{⟨Q_{ab}(𝐫)Q_{ab}(0)⟩-⟨Q_{ab}(𝐫)⟩⟨Q_{ab}(0)⟩}.$$ [5]

Here, angular brackets denote a thermal average in the thermal case and an evaluation in an inherent state in the athermal case; an $\overline{(\bullet )}$ indicates an average over different samples of the glass. The quantity $G_R(r)$ is the correlation function of the replicon mode (25), and ${\mathrm{\Gamma }}_2(r)$ is just the garden variety four-point correlator.

Using these definitions and taking Eq. 2 into account, the quantities that we compute in numerical simulation, before taking the ensemble average, are (SI Text) (30)

$${\stackrel{\sim }{\mathrm{\Gamma }}}_2(𝐫)=\frac{\sum _{i\ne j}(u_i^{ab}-Q_{ab})(u_j^{ab}-Q_{ab})\delta (𝐫-({𝐫}_i^a-{𝐫}_j^a))}{\sum _{i\ne j}\delta (𝐫-({𝐫}_i^a-{𝐫}_j^a))}$$ [6]

and

$${\stackrel{\sim }{G}}_R(𝐫)=\frac{\sum _{i\ne j}[u_i^{ab}{u}_j^{ab}-2u_i^{ab}{u}_j^{ac}+Q_{ab}{Q}_{cd}]\delta (𝐫-({𝐫}_i^a-{𝐫}_j^a))}{\sum _{i\ne j}\delta (𝐫-({𝐫}_i^a-{𝐫}_j^a))}$$ [7]

with

$$u_i^{ab}\equiv \theta (\mathrm{\ell }-|{𝐫}_i^a-{𝐫}_i^b|).$$ [8]

These four-replica objects can be computed for any quadruplet of distinct replicas. The ensemble averaged correlation functions are simply obtained as ${\mathrm{\Gamma }}_2\equiv \overline{{\stackrel{\sim }{\mathrm{\Gamma }}}_2}$ and $G_R\equiv \overline{{\stackrel{\sim }{G}}_R}$ (compare with SI Text for a proof). We stress that one must keep the full space dependence of the correlators in the definitions above, because the introduction of shear breaks the rotational symmetry of the glass samples, and therefore, the correlators are not just functions of a distance $r$.

Numerics

To measure the quantities defined above, we performed molecular dynamics simulations of a Kob–Andersen 65–35% Lennard–Jones Binary Mixture in $2d$. We have three system sizes: $N=\mathrm{1,000}$, $N=\mathrm{\hspace{0.17em}4},000$, and $N=\mathrm{\hspace{0.17em}10},000$. We chose $Q_{12}$ with $\mathrm{\ell }=\mathrm{\hspace{0.17em}0.3}$ in Lennard-Jones units but verified that changes in $\mathrm{\ell }$ leave the emerging picture invariant.

Following the procedure reported in ref. 17, as a first step, we prepared a glass by equilibrating the system at $T=\mathrm{\hspace{0.17em}0.4}$ and then quenching it (the rate is ${10}^{-6}$) down to $T=\mathrm{\hspace{0.17em}1}\cdot {\mathrm{\hspace{0.17em}10}}^{-6}$ into a glassy configuration. The sample is then heated up again to $T=\mathrm{\hspace{0.17em}0.2}$, and a starting configuration of particle positions is chosen at this temperature. Note that, whereas at $T=\mathrm{\hspace{0.17em}0.4}$, equilibration is sufficiently fast, at $T=\mathrm{\hspace{0.17em}0.2}$, the computation time is much shorter than the relaxation time. The configuration is then assigned a set of velocities randomly drawn from the Maxwell–Boltzmann distribution at $T=\mathrm{\hspace{0.17em}0.2}$, and these different samples are then quenched down to $T=\mathrm{\hspace{0.17em}0}$ at a rate of $0.1$. This procedure can be repeated any number of times (say 100 times), and it allows us to get a sampling of the configurations, or replicas, inside one single “glassy patch.” We then perform this procedure again, each time using a different configuration from the parent melt at $T=\mathrm{\hspace{0.17em}0.4}$, and in doing so, we get an ensemble of these glassy patches, each of them representing a distinct glass sample. For each of these patches, we measure the four-replica correlators defined above for any distinct quadruplet of replicas, averaging the result over any possible permutations of the quadruplet to gain statistics (29). The ensemble average is then performed by averaging the result over all of the glass samples. To perform these measurement, below, we use 100 patches for $N=\mathrm{\hspace{0.17em}1},000$ (each with 100 configurations), 100 patches for $N=\mathrm{\hspace{0.17em}4},000$ (each with 50 configurations), and 50 patches for $N=\mathrm{\hspace{0.17em}10},000$ (each with 50 configurations). A strain ${\gamma }_{xy}$ (denoted below as $\gamma$) is then applied quasistatically to all configurations in all patches. In this protocol, after every step of increased strain, the system undergoes energy gradient minimization to return to mechanical equilibrium. This procedure creates an ensemble of strained patches for every value of the strain parameter $\gamma$, from whence we measure again the above defined correlators, which then become functions of the strain $\gamma$. This behavior is simply a consequence of the response of the configurations [i.e., each position ${𝐫}_i$ in the definitions above becomes ${𝐫}_i(\gamma )$]. Thus, for example, $G_R(r)$ becomes $G_R(r;\gamma )$, etc. We are interested in the behavior of the correlators as the yielding point ${\gamma }_{\mathrm{Y}}$ is approached.

Results

We consider first the susceptibilities ${\chi }_{G_L},{\chi }_{G_R}$ and ${\chi }_{{\mathrm{\Gamma }}_2}$ that can be obtained from the correlators; for example,

$${\chi }_{G_L}(\gamma )\equiv \int d^{2}x{G}_L(x,y;\gamma ).$$ [9]

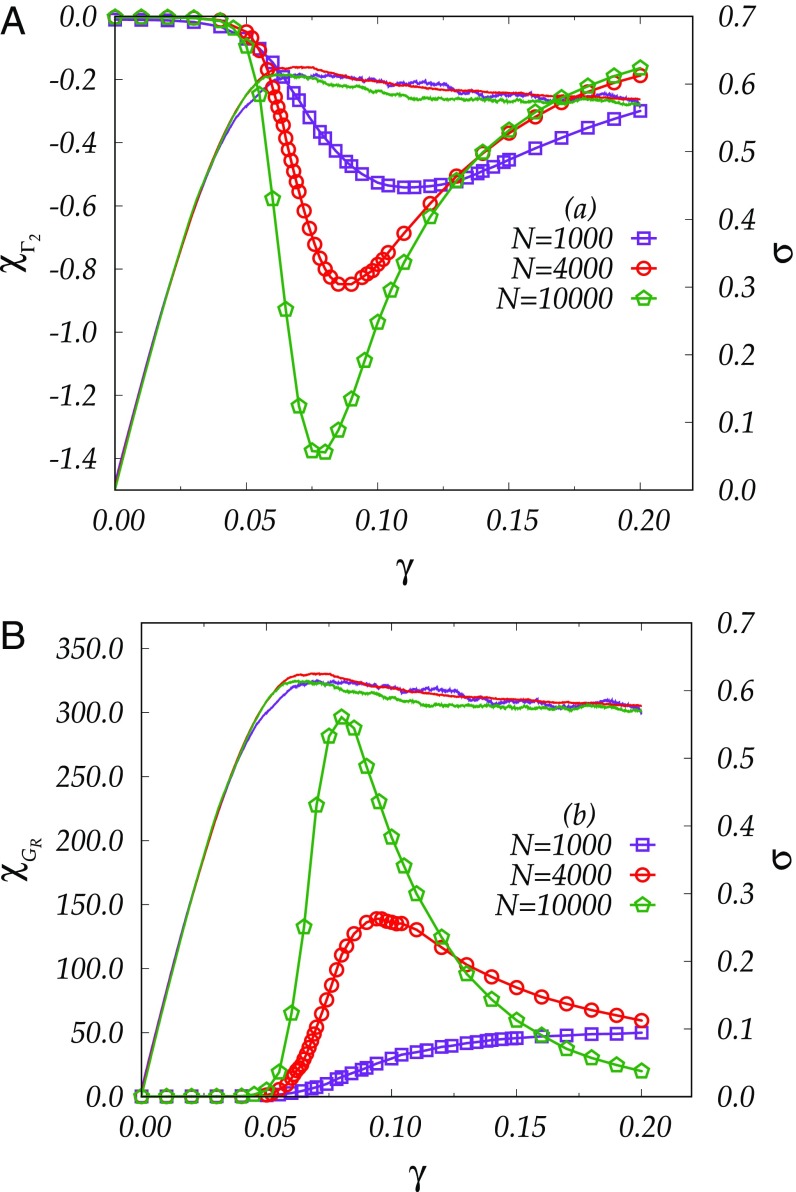
In Fig. 1, Upper, we show the susceptibility ${\chi }_{{\mathrm{\Gamma }}_2}$ as a function of $\gamma$ for three system sizes at our disposal. Superimposed are the stress versus strain curves obtained by averaging the individual curves over all of the available configurations and glass samples. One sees very clearly the singularity that develops near the yield point as a function of the system size. In Fig. 1, Lower, we show the susceptibility ${\chi }_{G_R}$ as a function of the strain $\gamma$, again with the stress–strain curve superimposed for comparison. As we expected, the susceptibilities show a distinct peak at the spinodal point ${\gamma }_Y$, wherein yielding occurs. Because ${\chi }_{{\mathrm{\Gamma }}_2}$ is much smaller in amplitude than ${\chi }_{G_R}$, there is not much new information in ${\chi }_{G_L}$, which is ∼2${\chi }_{G_R}$.

Fig. 1.

The susceptibilities (A) ${\chi }_{{\mathrm{\Gamma }}_2}$ and (B) ${\chi }_{G_R}$ as a function of $\gamma$ for three systems sizes available. Superimposed are the stress versus strain curves for comparison. The color code is violet for $N=\mathrm{\hspace{0.17em}1},000$, red for N = 4,000 and green for N = 10,000.

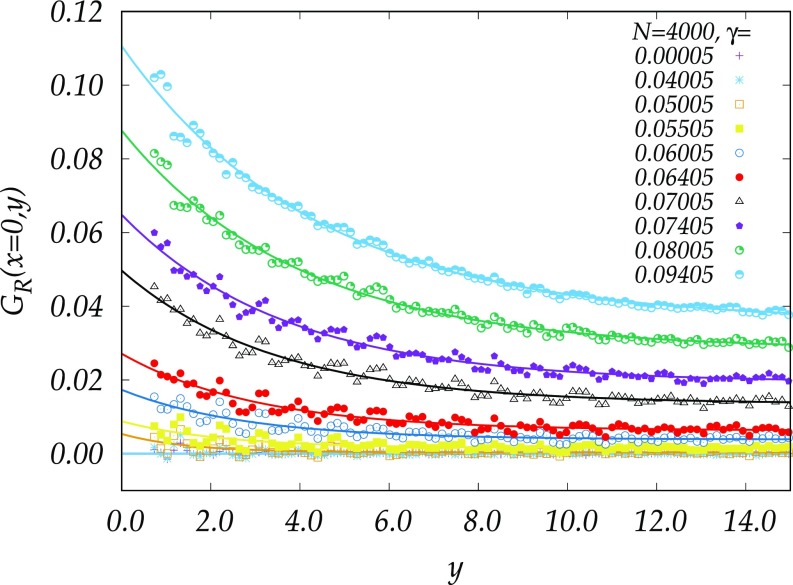
More detailed information is provided by the full dependence of the correlators on their arguments. To see most clearly the change in the correlators as the spinodal point is approached, it is best to consider, for example, the 1D function $G_R(x=\mathrm{\hspace{0.17em}0},y;\gamma )$, shown for $N=\mathrm{\hspace{0.17em}4},000$ in Fig. 2. Similar results for the other systems sizes are available in SI Text. We note that the correlator changes in both amplitude and extent when we approach the critical point. To quantify these changes, we fit a three-parameter function to $G_R(x=\mathrm{\hspace{0.17em}0},y)$ in the form

$$G_R(x=0,y;\gamma )\approx C+A\exp (-\frac{y}{\xi }),$$ [10]

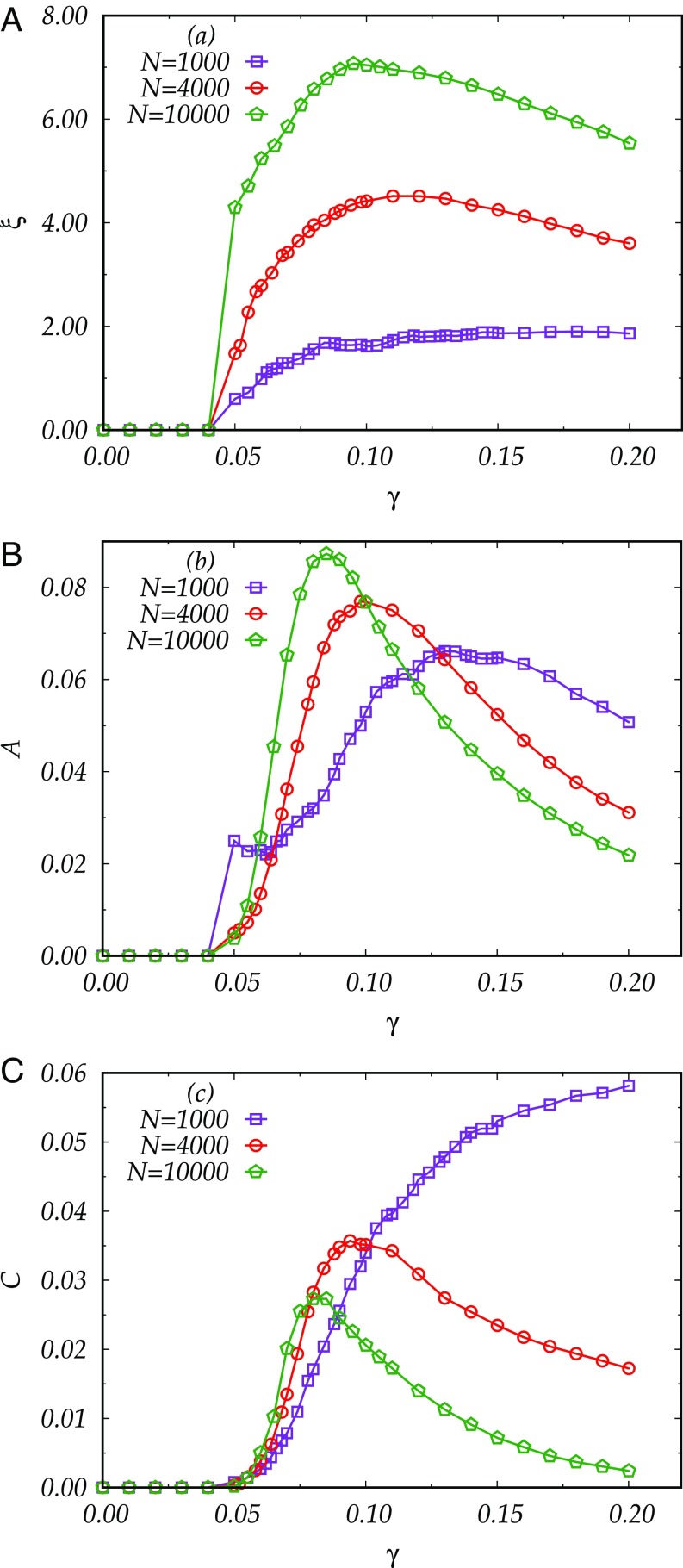
where all of the fitting coefficients are functions of $\gamma$. In Fig. 3, we present the $\gamma$ dependence of the amplitude $A(\gamma )$, the constant $C(\gamma )$, and the correlation length $\xi (\gamma )$.

Fig. 2.

The function $G_R(x=\mathrm{\hspace{0.17em}0},y;\gamma )$ for various values of $\gamma$ from $5\times {\mathrm{\hspace{0.17em}10}}^{-5}$ to 0.09405. Note the increase in the overall amplitude of the correlator as well as the increase in the correlation length. The lines through the data are the fit function 10.

Fig. 3.

The $\gamma$ dependence of the correlation length $\xi (\gamma )$ (A), the amplitude $A(\gamma )$ (B), and the constant $C(\gamma )$ (C) in the best fit to the function $G_R(x=\mathrm{\hspace{0.17em}0},y;\gamma )$ (compare with 10).

It is interesting to notice that the constant $C$ decreases with the system size, presumably becoming irrelevant in the thermodynamic limit. The amplitude $A$ is still increasing with the system size, and it is difficult to assert whether it converges or not. However, we can safely conclude that the data present a strong evidence for the increase in the correlation length; it is very likely that it should diverge in the thermodynamic limit.

Relevant questions are whether one can define critical exponents that can also be measured in experimental situations and whether such exponents can be computed from theory, even on the mean field level. Clearly, the standard thermal mean field approach cannot be used, because averages here are computed over replicas at $T=\mathrm{\hspace{0.17em}0}$, and fluctuations caused by quenched disorder are expected to dominate the thermal fluctuations that stem only from the mother supercooled liquid from which the replicas at $T=\mathrm{\hspace{0.17em}0}$ are created. Considerations of the effect of such fluctuations are beyond the scope of this paper and will be discussed elsewhere.

Physical Interpretation

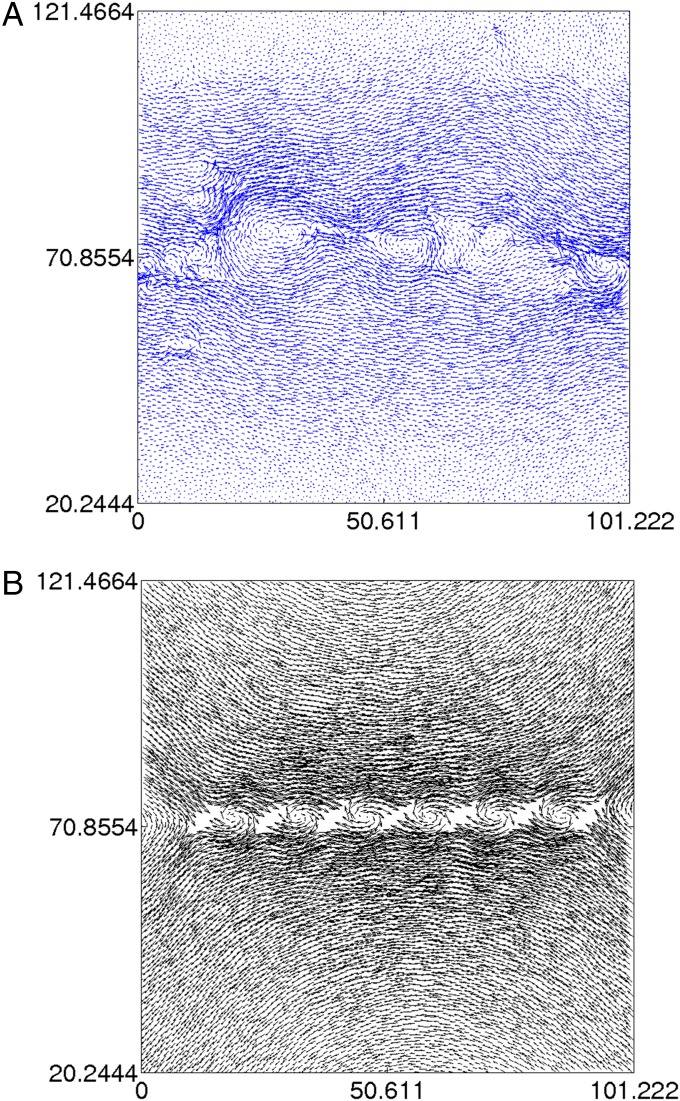
To conclude this paper, we present a physical interpretation to these insights, connecting them to what is known about the mechanical yield in athermal amorphous solids. The most important characteristic of the mechanical yield in athermal amorphous solids is the change from plastic responses that are localized, typically in the form of Eshelby quadrupoles, to subextensive plastic events that are system-spanning (31, 32). The energy drops associated with the localized Eshelby quadrupoles are system size-independent, scaling like $N^0$, where $N$ is the total number of particles in the system. Mechanical yield is associated with the spontaneous appearance of concatenated lines of quadrupoles [in two dimensions or planes in three dimensions (13, 15, 16)]. The latter are associated with energy drops that are subextensive, scaling like $N^{1/3}$ in two dimensions. Importantly, the concatenated lines of quadrupoles change drastically the displacement field associated with the plastic events. Each quadrupole has an arm with a displacement field pointing outward and an arm with the displacement field pointing inward. When the quadrupole is isolated, the displacement field decays algebraically to infinity. In contrast, when the quadrupoles are organized in the line, there is a global connection between the outgoing direction of one quadrupole and the incoming direction of the next, making the displacement field strongly localized around the line of quadrupoles (or around a plane in three dimensions), and all of the shear is there. This excitation is a microscopic shear band. An example of the displacement field associated with such a system-spanning event is shown in Fig. 4 (details are in ref. 13). The main point of this paper is that the highly correlated phenomenon of such a shear band can only occur when there exists a correlation length that approaches the system size in magnitude. This length is the correlation length $\xi$ that is identified in this paper (compare with Fig. 3, Top).

Fig. 4.

Example of the spontaneous plastic event exhibiting a concatenation of a series of Eshelby quadrupoles resulting in a correlated displacement field with shear localization over a thin region, which is system-spanning. (A) Direct numerical simulations. (B) Inserted line of Eshelby quadrupoles.

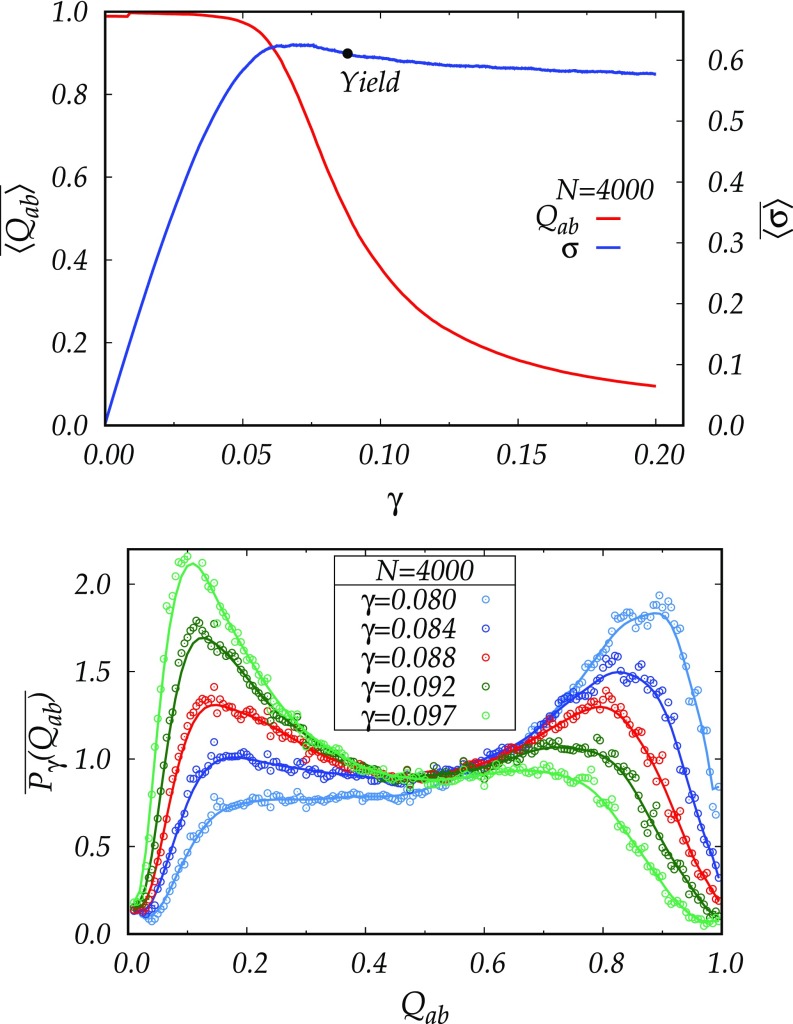
To understand the relevance of the spinodal point for this scenario, we provide two figures that were obtained in ref. 17. In Fig. 5, Upper, one sees the order parameter $Q_{ab}$ as a function of $\gamma$ superimposed on the stress versus strain curve of the system under study. The point “yield” was obtained with the help of the results shown in Fig. 5, Lower, in which the probability of observing $Q_{ab}$ is plotted for values of $\gamma$ around the mechanical yield point ${\gamma }_Y$. The yield itself is identified when the probability distribution function has two peaks of the same height. The spinodal point is at a slightly higher value of $\gamma$, where the peak occurring around high values of $Q_{ab}$ is about to disappear, with a characteristic spinodal vanishing of the slope. This spinodal is occurring in this system around $\gamma =\mathrm{\hspace{0.17em}0.1}$. Of course, in the thermodynamic limit, the whole range of $\gamma$ values where the exchange of stability is occurring is becoming very narrow.

Fig. 5.

(Upper) The order parameter $\overline{Q_{ab}}$ as a function of the strain $\gamma$ superimposed on the stress versus strain curve. (Lower) The probability distribution function $P(\overline{Q_{ab}})$ for different values of $\gamma$ in the vicinity of the mechanical yield value ${\gamma }_Y$.

It is important to stress again that the ability to observe the divergence of the susceptibility and the correlation length caused by the spinodal phenomenon stems from the fact that we deal with an athermal glassy system with typical relaxation times that are immense. In a liquid system, the fluctuations would have caused the system to make the transition before the spinodal point is reached.

Conclusions

In conclusion, we have presented evidence that the yielding transition is a spinodal point with disorder characterized by a criticality with features that can be picked up by suitable multipoint correlators, with expression that can be obtained from replica theory. The treatment presented here pertains to an athermal setting, but an obvious direction for future research will be the application of these ideas to thermal glasses under shear (21); in the finite temperature case, the system will generally be able to escape through thermal activation from the high-$Q_{ab}$ minimum before this has a chance to flatten and the relative susceptibility to diverge. However, because the nucleation time will anyway be fairly long, one should anyway be able to observe transient shear bands/heterogeneities as long as the temperature is low enough that nucleation does not take place until the system is close to the spinodal, which interestingly, is precisely the behavior of transient shear bands as reported in ref. 21. In this thermal setting, we expect that the study of the ideas presented in this paper will have to proceed much as it does in the case of dynamical heterogeneities around the mode coupling cross-over, entailing, for example, the definition and study of time-dependent multipoint susceptibilities and correlators.

SI Text

Let us start from the expression of the free energy of a glass state prepared by equilibrating a generic glass former down to a glass transition temperature $T_g$ and then quenching it out of equilibrium to a given temperature $T$. Such a free energy was first defined in ref. 33 in the context of spin glass physics. Its definition in the case of structural glasses and its computation in the particular case of hard spheres were first discussed in ref. 26. The definition, in the case of a generic glass former made of $N$ particles with positions $X\equiv {\{\text{𝒙}\}}_{i=1}^N$ and generic interaction potential $V(X)$, is

$$f[T,T_g]\equiv -\frac{1}{\beta N}\int dR\frac{e^{-{\beta }_{g}V(R)}}{Z_g}\times \log \left[\int dX{e}^{\beta V(X)}\delta (q_r-Q(X,R))\right].$$ [S1]

The idea is to consider the free energy at temperature $T$ of the glass former with it constrained to stay close to a configuration $R$ (i.e., the amorphous lattice of the glass), which is selected with the equilibrium, canonical distribution when the glass falls out of equilibrium at $T_g$; therefore, $Q(X,R)$ is a notion of similarity between two configurations of the system. In the case of ref. 26, the mean square displacement (MSD) between the two configurations was used:

$$Q(X,R)\equiv \mathrm{\Delta }(X,R)=\frac{d}{N}\sum _{i=1}^N{|{\text{𝒙}}_i-{\text{𝒓}}_i|}^2,$$ [S2]

whereas for example, in ref. 17, one used the definition

$$Q(X,R)\equiv \frac{1}{N}\sum _{i=1}^N\theta (a-|{\text{𝒓}}_i-{\text{𝒙}}_i|),$$ [S3]

where $a$ is a coarse-graining parameter (in ref. 17, $a\simeq 0.3$ in Lennard–Jones units). The actual definition is not important for what concerns the critical properties of the system, which we shall see below.

The properties and computation of the free energy [S1] are discussed extensively in refs. 18 and 26, and therefore, we refer the interested reader to those works. Here, we just sketch how its definition leads naturally to a mean field theory in terms of an overlap order parameter and how one can extract the critical properties of a glass state from such a theory.

The outermost integral in [S1] can be computed with the replica trick,

$$f[T,T_g]=\underset{s\to 0}{lim}{\partial }_s\mathrm{\Phi }[T,T_g],$$ [S4]

where $\mathrm{\Phi }$ is defined as

$$\mathrm{\Phi }[T,T_g]=-\frac{1}{\beta N}\log \int dRd{X}^1\mathrm{\cdots }d{X}^s{e}^{-{\beta }_{g}V(R)}{e}^{-\beta V(X^1)}\times \delta (q-Q(X_1,R))\mathrm{\cdots }{e}^{-\beta V(X^s)}\times \delta (q-Q(X_s,R)),$$ [S5]

and therefore, we are considering $s$ replicas of the $X$ configuration. One can then prove that the functional defined above can generally be written as

$$\mathrm{\Phi }=-\frac{1}{\beta N}\int \mathcal{D}{Q}_{ab}{e}^{-dN\beta S(Q_{ab})},$$ [S6]

where $Q_{ab}$ is the notion of similarity between two replicas $a$ and $b$: for example,

$$Q_{ab}=\frac{1}{N}\sum _{i=1}^N\theta (a-|{\text{𝒙}}_i^a-{\text{𝒙}}_i^b|),$$ [S7]

$\mathcal{D}{Q}_{ab}$ denotes an integration measure over all of the distinct $Q_{ab}$ values (we have stipulated that the configuration $R$ is replica zero),

$$\mathcal{D}{Q}_{ab}\equiv \prod _{a<b}^{0,s}d{Q}_{ab},$$ [S8]

and $d$ is the number of spatial dimensions. In the mean field limit $d\to \mathrm{\infty }$, the integral above can be computed via the saddle point method (34), which means that one must consider the optimum points in $Q_{ab}$ of the replica action $S(Q_{ab})$. This fact means that $S(Q_{ab})$ plays the role of a Gibbs free energy (i.e., the free energy for fixed order parameter). An illustrative example is the case of a Curie–Weiss model (mean field ferromagnet), wherein for the Helmholtz free energy $F$ in zero magnetic field, one has (35)

$$F(h=0,T)=\underset{m}{min}G(m,T),$$ [S9]

where $G(m,T)$ is indeed the Gibbs free energy for fixed magnetization $m$. The minimization equation for $G$ is then the celebrated equation for the spontaneous magnetization

$$\frac{\partial G}{\partial m}=0⟹m=tanh(\beta m),$$ [S10]

and the ferromagnetic phase transition takes place when the paramagnetic $m=\mathrm{\hspace{0.17em}0}$ minimum of $G$ flattens and splits in two degenerate minima with $m\ne \mathrm{\hspace{0.17em}0}$, which implies that, at the critical temperature, ${\partial }^{2}G/\partial m^2=\mathrm{\hspace{0.17em}0}$. The derivation of the $S(Q_{ab})$ action in the case of mean field hard spheres and with the MSD, ${\mathrm{\Delta }}_{ab}$, used as order parameter can be found in ref. 36.

In this case, $f[T,T_g]$ plays the role of the Helmholtz free energy $F$ and the $S(Q_{ab})$ of the Gibbs free energy $G$. With this analogy, one can understand how the critical properties of glass states are related to the matrix of second derivatives of the replica action $S(Q_{ab})$,

$$M_{ab;cd}\equiv \frac{{\partial }^{2}S}{\partial Q_{a<b}\partial Q_{c<d}},\hspace{1em}a,b\in [1,s],$$ [S11]

in the limit $s\to \mathrm{\hspace{0.17em}0}$ (we have stipulated that the configuration $R$ is replica zero). The inverse $G_{ab;cd}$ of the tensor $M$, defined as

$$\sum _{e\ne f}{M}_{ab;ef}{G}_{ef;cd}=\frac{{\delta }_{ac}{\delta }_{bd}+{\delta }_{ad}{\delta }_{bc}}{2},$$ [S12]

is then the covariance matrix of the mean field theory,

$$G_{ab;cd}=⟨(Q_{ab}-⟨Q_{ab}⟩)(Q_{cd}-⟨Q_{cd}⟩)⟩,$$ [S13]

and encodes the critical fluctuations of the system near the critical points. whereupon the tensor $M_{ab;cd}$ develops a zero mode.

Let us now assume that the glass state under study is a single minimum of the free energy landscape of the system, wherein all replicas from one to $s$ can move ergodically; this picture implies that the replicas are all equivalent and that the matrix $Q_{ab}$ must then be invariant by any replica permutation, a hypothesis referred so as replica-symmetric (RS).

In ref. 26, it discussed how this is not true in all cases (i.e., there exists a regime, wherein the glass basin undergoes an ergodicity breaking and fractures into subbasins). Nevertheless, here we stick to the simple RS ansatz. In this case, because the action $S(Q_{ab})$ must, in turn, be invariant for any replica permutations, the most general form that the Hessian $M$ can take is

$$M_{ab;cd}=M_1\left(\frac{{\delta }_{ac}{\delta }_{bd}+{\delta }_{ad}{\delta }_{bc}}{2}\right)+M_2\left(\frac{{\delta }_{ac}+{\delta }_{bd}+{\delta }_{ad}+{\delta }_{bc}}{4}\right)+M_3,$$ [S14]

and the same goes for the covariance matrix $G_{ab;cd}$. This form is completely general, because it only descends for the RS symmetry; then, the only model dependence is in the parameters $M_1$, $M_2$, and $M_3$, which must be computed case by case and are generally dependent on the external parameters, like temperature of magnetic field.

The diagonalization of the tensor $M_{ab;cd}$ is an exercise of standard linear algebra and has been already carried out many times (for example, refs. 25, where it is proposed as an exercise, and 37–39). It is found that the tensor $M$ has only three distinct eigenvalues:

$${\lambda }_R=M_1,$$ [S15]

$${\lambda }_L=M_1+(s-1)(M_2+s{M}_3),$$ [S16]

$${\lambda }_A=M_1+\frac{s-2}{2}{M}_2,$$ [S17]

and the same goes for the tensor $G$. Those three eigenvalues (or modes) are called the replicon, longitudinal, and anomalous, respectively (39).

We are interested in the longitudinal mode (which in the limit $s\to \mathrm{\hspace{0.17em}0}$, is degenerate with the anomalous one), which becomes soft at the yielding transition (18, 19). Let us consider the $G$ tensor. Because of replica symmetry, there are only three distinct correlators that one can define, namely

$$G_{12;12}=\frac{G_1}{2}+\frac{G_2}{2}+G_3,$$ [S18]

$$G_{12;13}=\frac{G_2}{4}+G_3,$$ [S19]

$$G_{12;34}=G_3,$$ [S20]

and in the limit $s\to \mathrm{\hspace{0.17em}0}$, we know that

$$\frac{1}{{\lambda }_L}=G_1-G_2.$$ [S21]

It is then immediate to check that

$$G_{12;12}-2G_{12;13}+G_{12;34}=\frac{G_1}{2}\propto \frac{1}{{\lambda }_R}\equiv G_R,$$ [S22]

$$G_{12;12}-4G_{12;13}+3G_{12;34}=\frac{G_1-G_2}{2}\propto \frac{1}{{\lambda }_L}\equiv G_L,$$ [S23]

which then implies

$$G_L(\text{𝒓})=2G_R(\text{𝒓})-{\mathrm{\Gamma }}_2(\text{𝒓}),$$ [S24]

with the definitions

$$G_R(\text{𝒓})\equiv ⟨Q_{ab}(r)Q_{ab}(0)⟩-2⟨Q_{ab}(r)Q_{ac}(0)⟩+⟨Q_{ab}(r)⟩⟨Q_{cd}(0)⟩,$$ [S25]

$${\mathrm{\Gamma }}_2(\text{𝒓})\equiv ⟨Q_{ab}(\text{𝒓})Q_{ab}(0)⟩-⟨Q_{ab}(\text{𝒓})⟩⟨Q_{ab}(0)⟩,$$ [S26]

as in the text. We have used ${\mathrm{\Gamma }}_2=G_{12;12}-G_{12;34}$, which derives from replica symmetry, as $⟨Q_{12}⟩⟨Q_{12}⟩=⟨Q_{12}{Q}_{34}⟩$ in the RS phase.