Controllable load sharing for soft adhesive interfaces on three-dimensional surfaces

Significance

In transfer printing, robotics, and precision manufacturing, adhesion-controlled grasping of complex 3D surfaces is very challenging because the adhesive must be soft enough to enable intimate contact under light pressure but stiff enough to support high load and fracture strength. We address this dilemma by replacing the adhesive with a pressurized microfiber array that enables independent control of 3D conformability and bond strength. This architecture exhibits enhanced and robust adhesion on various sizes of 3D and deformable surfaces. In contrast to other microfiber adhesives, it has the area scalability of the natural gecko footpad. These features suggest that the proposed soft-gripping system can outperform conventional adhesive systems for a broad range of surface shapes and length scales.

Abstract

For adhering to three-dimensional (3D) surfaces or objects, current adhesion systems are limited by a fundamental trade-off between 3D surface conformability and high adhesion strength. This limitation arises from the need for a soft, mechanically compliant interface, which enables conformability to nonflat and irregularly shaped surfaces but significantly reduces the interfacial fracture strength. In this work, we overcome this trade-off with an adhesion-based soft-gripping system that exhibits enhanced fracture strength without sacrificing conformability to nonplanar 3D surfaces. Composed of a gecko-inspired elastomeric microfibrillar adhesive membrane supported by a pressure-controlled deformable gripper body, the proposed soft-gripping system controls the bonding strength by changing its internal pressure and exploiting the mechanics of interfacial equal load sharing. The soft adhesion system can use up to ∼26% of the maximum adhesion of the fibrillar membrane, which is 14× higher than the adhering membrane without load sharing. Our proposed load-sharing method suggests a paradigm for soft adhesion-based gripping and transfer-printing systems that achieves area scaling similar to that of a natural gecko footpad.

By exploiting principles of equal load sharing (1) and interfacial crack pinning (2), geckos’ fibrillar foot-hairs can firmly adhere to a wide range of surfaces using intermolecular interactions, such as van der Waals forces (3). Using the same attachment method, gecko-inspired synthetic elastomeric fibrillar adhesives achieve bond strengths of over 100 kPa on smooth flat surfaces (4), surpassing the performance of the gecko on such surfaces (5), and exhibit quick release through peeling (6) or buckling (7) of the microfibers. For the past decade, gecko-inspired adhesives have been applied to a variety of systems including numerous robotic applications for wall climbing (8, 9), perching devices for flyers (10), and grippers (11–14). However, difficulties arise in dealing with 3D surfaces because the current gecko-inspired synthetic adhesive systems are often supported by a rigid backing, which limits their ability to conform to nonplanar surfaces. In our previous work, we created elastomeric fibrillar adhesives integrated with a soft membrane, which we named as fibrillar adhesives on a membrane (FAM), and fixed the membrane onto a 3D-printed rigid plastic body so that the system could handle various 3D objects (15). Despite demonstrating a significant improvement over an unstructured elastomeric membrane with 10× higher adhesion, the tested FAM could achieve only 2 kPa of adhesion stress, a small fraction of the 55 kPa measured with rigid-backed microfiber arrays (16). This implies that the improved conformability to 3D surfaces enabled by the more compliant membrane backing is at the expense of a 96% reduction in adhesion strength. Considering that the adhesion of a membrane scales with the circumferential length of the contact interface and not with the area (15), the results above suggest that the size of the membrane, whether containing structures or not, has to be vastly increased to support a high load-carrying capacity.

Enhancing the adhesion strength of an adhering membrane requires more uniform load sharing throughout the contact interface (17). Hawkes et al. proposed a frictional attachment system that could improve the lateral load-sharing capability and friction of microwedge structures by scaling up to larger areas on flat and slightly curved surfaces (18). However, no adhesion-based attachment system has succeeded in improving the perpendicular load sharing and adhesion of fibrillar structures for complex 3D surfaces. A backing layer made out of stiffness-tunable materials such as granular materials (19), liquid metals (20), thermoplastics (21, 22), or shape memory polymers (23, 24) can adapt to 3D surfaces when they are soft and support high fracture strength when they are hardened. However, challenges still remain in managing deformable substrates (e.g., plastic foils, rubber-like stretchable surfaces, thin metal films) because the stiffened backing cannot accommodate deformation, resulting in stress concentrations at the contact edges. Therefore, all adhesive gripping tasks are limited by a fundamental trade-off between compliance/conformability and rigidity/bond strength (25). Whereas adhesives must be compliant enough to conform to complex 3D or deformable geometries, the same system must remain rigid enough to maximize interfacial (mode I) fracture strength to support the object’s weight.

This work aims at eliminating this trade-off through a soft adhesion-based gripping system shown in Fig. 1, which allows the control of internal pressure to achieve equal load sharing on the interface over a large 3D surface. Our soft adhesion system increases adhesion through a combination of two fundamental mechanisms: (i) using a negative pressure differential to distribute the load more uniformly on the interface, and (ii) taking advantage of passive deformation of the soft system in response to the reduced chamber pressure, which can prevent the adhering membrane from peeling at a high negative pressure differential. Pneumatic pressure has been a popular choice as an actuator for soft systems due to its low drag resistance and rapid transport, abundant accessibility, and environmental compatibility (26, 27). Here, we show that the pressure differential is also effective for enhancing the adhesion of a membrane-backed microfiber array on a wide range of curved geometries. This is accomplished with the existing pneumatic system used for gripping actuation and does not require the introduction of additional hardware, including sensors and electronics. Experimental results show that pressure-controlled load sharing among the microfibers in contact with the surface does not only enhance adhesion but also leads to an area scaling law similar to that of the natural geckos' adhesive system. Such area scalability suggests that improved interfacial load sharing is critical when grasping 3D nonplanar geometries.

Fig. 1.

Demonstration of the proposed soft adhesion-based gripping system holding various 3D objects such as (A) a rounded glass flask filled with 200 mL of liquid (total weight of 307 g), (B–D) a 118-g coffee cup, (E) a 41-g pair of of cherry tomatoes, and (F) a 139-g plastic bag. (Scale bar, 10 cm.)

Results

Structure and Basic Mechanism of the Soft Adhesion System.

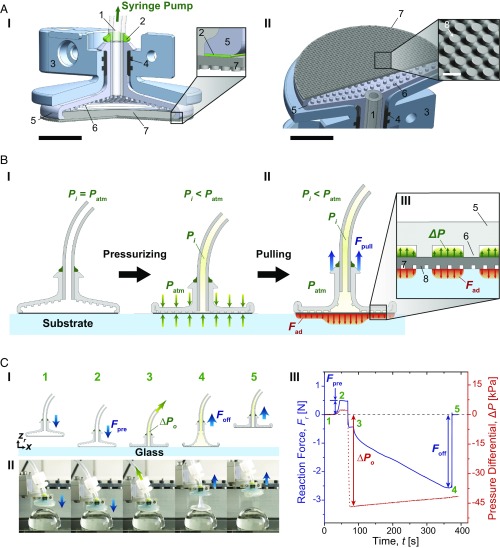
Fig. 2A details structural features of the proposed soft adhesion system. An FAM is supported by a soft, deformable chamber, which is connected to a syringe pump to allow control of the system internal pressure (Fig. 2 A, I). The soft gripper chamber is 18 mm in diameter, 600 μm thick, and contains 400-μm-diameter pillar-like internal spacers made out of a soft and highly stretchable silicone elastomer. The soft chamber is bracketed by a 3D-printed plastic outer case, ensuring evenly distributed preload over the whole contact area. Each silicone component of the system is bonded using a vinylsiloxane elastomer. The FAM is composed of an array of vertically aligned, mushroom-shaped, polydimethylsiloxane (PDMS) microfibers with 69-μm tip diameter, 31-µm spacing, and 42-µm height, supported by a thin PDMS backing layer with 250-μm thickness (SI Appendix, Figs. S2 and S3). As shown in Fig. 2 A, II, the microfibers (Fig. 2 A, II, 8) covering the entire area of the membrane provide a gap between the substrate and the membrane, allowing air to seamlessly travel through the contact interface, preventing development of any suction that could contribute to the soft system adhesion. The FAM can be cleaned using a wet (28) or dry process (29), allowing reliable and repetitive performance, which can otherwise be influenced with the buildup of dust, oil, or dirt (30).

Fig. 2.

Schematics of structure, mechanism, and a representative adhesion test of the soft adhesion system. (A) A cross-section of 3D assembly of the proposed system from side (I) and from bottom (II) of the system. 1: silicone tubing, 2: vinylsiloxane, 3: outer case, 4: rubber ring, 5: soft chamber, 6: spacer between the chamber and the FAM, 7: FAM, and 8: mushroom-shaped PDMS microfibers. [Larger scale bars (black) indicate 5 mm, whereas the smaller scale (white) inside of the inset in II corresponds to 100 μm.] (B) A schematic of the proposed system when pressurized with a negative pressure differential (ΔP) (I) and pulled with a pull-up load (F_pull) (II). The inset (III) shows a schematic of pressure distribution between the spacers in the soft chamber and adhesion stress on the contact interface. (C) Adhesion test of the soft system. A schematic of experimental procedure (I), snapshots of the soft system under a negative pressure differential on a 30-mm-diameter glass hemisphere in accordance with each step (II), and corresponding profiles of reaction force (F_r) and pressure differential inside the chamber with respect to elapsed time (III). The initial pressure (ΔP_o) here is approximately −47 kPa. The numbers indicated in green are correlated with the experimental procedure 1: approaching, 2: preloading, 3: applying initial pressure, 4: pulled off, and 5: detached.

The effect of a negative pressure differential (ΔP) on the load sharing is shown in Fig. 2B. Here, the internal pressure (P_i) corresponds to the air pressure in the gripper chamber, tubing, and syringe pump and is always positive. The pressure differential is defined as the internal pressure subtracted by the atmospheric pressure (P_atm), and can be either positive or negative. Therefore, a negative pressure differential means that an absolute value of the internal pressure is lower than the atmospheric pressure (101.3 kPa). Likewise, a high negative pressure differential indicates that the internal pressure is substantially lower than the atmospheric pressure. Under a high negative pressure differential, the atmospheric pressure forces the chamber to collapse over the FAM (Fig. 2 B, I). The spacers in the chamber (Fig. 2 B, III, 6) ensure that the FAM is exposed to the pressure differential even when the chamber has collapsed (Fig. 2 B, III). In contrast to typical adhesion systems that peel and exhibit poor adhesion under large deformations during pulling, our gripping system benefits from deformation because it allows the spacers in the soft chamber to lift up from the backing and exposes a larger area of the membrane to the negative pressure differential. This, in turn, enhances the load sharing by enabling the negative pressure differential to more uniformly distribute the interfacial tensile stress and improve bonding strength (F_ad) (Fig. 2 B, II).

Fig. 2C and Movie S1 show a representative force measurement of the soft adhesion system with its corresponding force (blue) and pressure (red) curves. Fig. 2 C, III gives reaction force (F_r) as a function of time (t). First, the soft adhesion system approaches a substrate (Fig. 2 C, I, 1) and is brought to contact (Fig. 2 C, I, 2) with a compressive preload force (F_pre) induced at the interface. The preload is the maximum reaction force as shown in Fig. 2 C, III, ranging from 0.5 to 1.0 N depending on the substrate radius of curvature. A negative pressure differential is applied to the inside of the soft chamber during a predefined contact time, then the system is slowly retracted at 50 μm·s⁻¹ unloading speed to minimize possible viscoelastic effects on the adhesion. The pressure differential at the beginning of the retraction (Fig. 2 C, I, 3) is defined as initial pressure (ΔP_o), which can be either positive or negative. The reaction force decreases during the retraction until it reaches the pull-off force (F_off) (Fig. 2 C, I, 4), which corresponds to the minimum reaction force in Fig. 2 C, III. The soft adhesion system snaps off from the substrate instantaneously after the pull-off force is reached (Fig. 2 C, I, 5), as shown in Fig. 2 C, III.

Modeling the Effect of Pressure Differential on Adhesion.

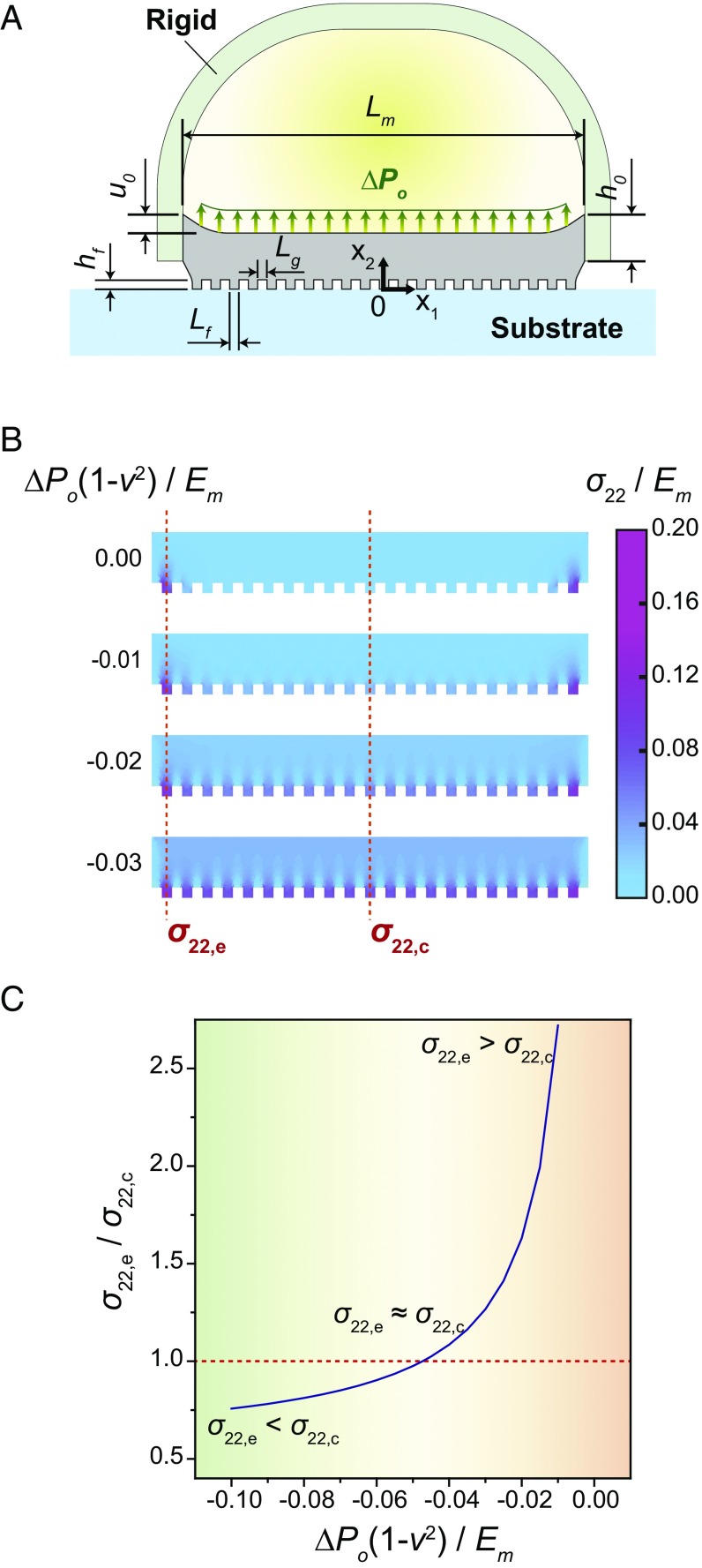
We used principles of elasticity and stationary potential to examine the influence of internal pressure differential (ΔP_o) on the distribution of load among the microfibers in contact with the surface and to estimate the membrane adhesion on curved surfaces. To develop a qualitative understanding of the load distribution among fibers, the axisymmetric array on the FAM is modeled using 2D plane–strain linear elasticity (31). As shown in Fig. 3A, the FAM is simplified as an incompressible Hookean solid [Young’s modulus E_m = 2.1 MPa (32)], which has a diameter L_m = 2.15 mm and thickness h₀ = 250 µm. The edge of the FAM is subject to a vertical displacement (u₀) corresponding to 5% of its thickness. Each microfiber has a width L_f = 50 µm, height h_f = 50 µm, and spacing L_g = 50 µm, and is assumed to remain in contact with the substrate under the prescribed loading conditions.

Fig. 3.

Finite-element analysis for modeling vertical stress within the FAM. (A) A schematic of dimensions and boundary conditions of the FAM clamped at the edge and being pulled up by a rigid support under an internal pressure differential (ΔP_o). (B) A colormap of normalized vertical stress (${\sigma }_{22}/E_m$) within the FAM for selected normalized pressures $\widehat{p}=\left(1-{\nu }^2\right)\mathrm{\Delta }{P}_o/E_m$. (C) A ratio in the vertical stress between the edge and the center (${\sigma }_{22,\text{e}}/{\sigma }_{22,\text{c}}$) depending on the normalized pressure $\widehat{p}$. Here, ${\sigma }_{22,\text{e}}$ is the vertical stress on the first fiber from the edge of the FAM and ${\sigma }_{22,\text{c}}$ is on the fiber at the center.

The governing Navier–Lamé equations follow the standard displacement formulation for divergence-free stress within the Hookean solid and are presented in SI Appendix, section S1. Of particular interest is the vertical stress σ₂₂ within the microfibers, which is normalized by the Young’s modulus E_m. It is also convenient to define a normalized surface pressure $\widehat{p}=\left(1-{\nu }^2\right)\mathrm{\Delta }{P}_o/E_m$. In the absence of a negative pressure differential (i.e., $\widehat{p}=0$), stress is concentrated in the outermost fibers when the edges of the membrane (thickness h₀) are lifted by the prescribed vertical displacement (Fig. 3B). Decreasing the pressure leads to a more uniform stress distribution, with the vertical stress at the center fiber (σ_22,c) approaching the stresses at the edge (σ_22,e). Referring to Fig. 3C, the ratio σ_22,e/σ_22,c steadily decreases and can even drop below 1.0 for a sufficiently high negative pressure differential. Although these results are based on 2D plane–strain elasticity, they nonetheless give qualitative insights on how negative pressure can be used to control the load distribution within the axisymmetric system.

To investigate the influence of internal air pressure on membrane adhesion to nonplanar 3D geometries, we adapt our previous analysis (33) based on the principle of minimum potential energy (34–36). As shown in Fig. 4A, this rigid version of the adhesion system is composed of the circular FAM supported along its edge by a hemispherical chamber. The chamber has the same 18-mm diameter, but slightly thicker wall of 1 mm, compared with the soft chamber. As with the soft gripper, the FAM used for the rigid gripper is composed of PDMS and has a thickness of 250 μm. Examining this alternative system simplifies the analysis by eliminating the elastic deformation of the chamber and allowing us to instead focus on the deformation of the membrane. In particular, it enables us to examine the influence of various design parameters (e.g., membrane thickness and elastic modulus) and identify conditions that lead to more uniform load-sharing control.

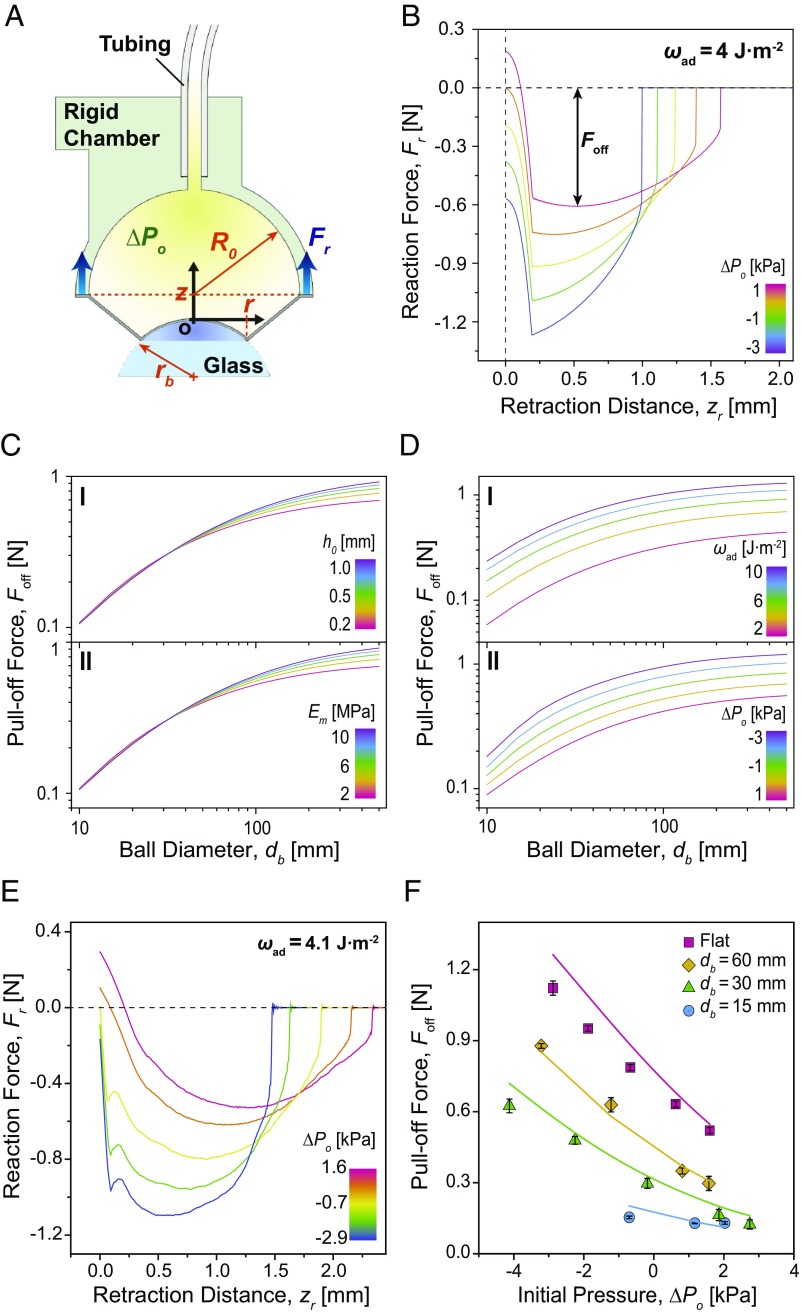
Fig. 4.

Analysis and force measurements in the rigid adhesion system for different 3D geometries. (A) A schematic of the rigid adhesion system being pulled off from a spherical substrate under a negative pressure differential. Blue arrows indicate the direction of reaction force (F_r). (B) Calculated reaction force (F_r) profiles on a flat glass surface versus retraction distance (z_r) for various initial pressures (ΔP_o). (C) Calculated pull-off force (F_off) as a function of diameter (d_b) of glass spheres for various thicknesses (h₀) (I), and Young’s moduli (E_m) (II). (D) Calculated pull-off force (F_off) as a function of diameter (d_b) of glass spheres for various works of adhesion (ω_ad) (I) and initial pressures (ΔP_o) (II). In all of these plots, the default parameter values are h₀ = 0.2 mm, E_m = 2.1 MPa, ω_ad = 4.0 J·m⁻², and ΔP_o = 0 kPa. (E) Measured reaction force profiles on a flat glass surface with respect to retraction distance, depending on different initial pressures. (F) Measured pull-off forces on glass substrates with different curvatures depending on the initial pressures. Each point indicates an average of five measurements, and error bars are ±1 SD.

As with the fiber array load-distribution model, the purpose of the membrane adhesion theory is to establish a qualitative understanding of how a negative pressure differential influences the interfacial mechanics. To further simplify the analysis, while still preserving the primary mechanics that govern adhesion, we make the following assumptions. First, the fibrillar interface is assumed to be an unstructured adhesive surface. Next, the elastomeric FAM is assumed to be incompressible, has a uniform thickness over the entire area, and deforms into the shape of a truncated cone. These assumptions imply the principal stretches in the circumferential (λ_ρ), meridional (λ_φ), and thickness (λ_t) directions as ${\lambda }_{\rho }=\sqrt{{\left(z+r_b-\sqrt{{r_b}^2-r^2}\right)}^2+{\left(R_0-r\right)}^2}/\left(R_0-r\right)$, ${\lambda }_{\phi }=1$, and ${\lambda }_t=1/{\lambda }_{\rho }·{\lambda }_{\phi }$. Such a simple geometry assumption for the deformed shape is reasonable for a membrane that is subject to a relatively low negative pressure differential (ΔP_o) and high work of adhesion (ω_ad). Here, R₀ is the radius of the FAM, which is 8 mm, r_b is the radius of a curved surface, z is the vertical position of the rigid adhesion system with respect to the top of the curved surface where the origin (o) is located, and r is the contact radius at the given z (Fig. 4A).

Details of the model are presented in SI Appendix, section S2. Fig. 4B shows the calculated profiles of reaction forces (F_r) between the rigid system and a flat glass substrate depending on different initial pressures (ΔP_o) with respect to retraction distance (z_r). Before the retraction (unloading) occurs, a decrease in the internal pressure pulls the soft adhesion system toward the interface, which explains the initial negative reaction force in Fig. 4B. As long as adhesion of the FAM can sustain the applied internal pressure, the decrease in the initial reaction force can be estimated by the initial pressure multiplied by the actual contact area. This adhesion, however, is not due to any suction but instead arises from the uniform distribution of the interfacial load among the fibers in contact with the surface, as simulated in Fig. 3. At the beginning of the retraction, the reaction force shows a significant drop until the edge of the FAM in contact reaches its critical interfacial strength and starts peeling off. According to our model, the drop becomes less steep with a smaller initial contact area, requiring a longer retraction distance to reach the critical interfacial strength for peeling (SI Appendix, Fig. S8). After transitioning through the dramatic decrease, the reaction force begins increasing in accordance with the peeling mechanics of the adhesive membrane, until the FAM is completely detached.

A higher negative pressure differential can result in higher pull-off force of the rigid adhesion system by distributing the load over the entire contact area more uniformly (Fig. 4B). Meanwhile, the negative pressure differential could accelerate detachment of the FAM by additional tensile stress and a higher peeling angle (37) caused by the deformation of the membrane as it is pulled into the inner chamber of the rigid adhesion system (SI Appendix, Fig. S7C). Fig. 4 C and D shows calculations of the pull-off forces (F_off) on spherical glass substrates with diameters (d_b) ranging from 10 to 500 mm for various design parameters of the FAM. The results indicate that its thickness (h₀) and Young’s modulus (E_m) are not effective for increasing the pull-off force for small spherical geometries (Fig. 4C). On the other hand, both the effective work of adhesion (ω_ad) and negative pressure differential (ΔP_o) could increase the pull-off force for all spherical geometries (Fig. 4D). Actively tuning the effective work of adhesion is often difficult once the membrane is fabricated. Potential methods for tuning include heating (38), electrostatic charging (39), or other forms of active stimulation. Among these methods, pressure-controlled adhesion tuning is attractive because it can be easily combined with other pneumatic elements, which already exist for actuating a soft robotic system (40). Our analysis in Fig. 4 D, II predicts that the adhesion can be doubled with respect to a decrease in the initial pressure by 4 kPa for the entire range of examined 3D surface curvatures.

Fig. 4F shows the pull-off force of the rigid adhesion system for different initial pressures tested on flat and spherical glass substrates with 15-, 30-, and 60-mm diameter. The experimentally measured reaction force profiles for adhesion to the flat substrate are also presented in Fig. 4E. The effective work of adhesion of the FAM and corresponding adhesion stress were estimated to be 4.1 J·m⁻² and 101 kPa, respectively (SI Appendix, Fig. S9B and Table S3). Various initial pressures were applied depending on the spherical curvatures by means of volume changes in the syringe pump. The positive initial pressure is caused by compression of the system during preloading when no air volume is withdrawn.

The experimental reaction forces on the flat glass substrate in Fig. 4E show reasonable qualitative agreement with the theoretical model (Fig. 4B) for how the reduction in the initial pressure results in a higher pull-off force and shorter retraction distance for detachment. The measured pull-off forces in Fig. 4F are close to the theoretical predictions, shown as solid lines, with an average deviation of only 11% from the experimental results. The applicable maximum negative initial pressure was only −4.1 kPa on the glass sphere with 30-mm diameter, and became even smaller for the glass sphere with 15-mm diameter. For the latter case, the maximum negative initial pressure reduced to −0.7 kPa and corresponded to a small contact area and lower peel resistance, as shown in Fig. 4F. The pull-off force on the flat glass was increased by 2.2×, while it was enhanced up to 5× on the glass sphere with 30-mm diameter at maximum. We observed an improvement of only 1.2× in the pull-off force on the sphere with a 15-mm diameter.

Characterization of the Soft Adhesion System.

The rigid system does show some benefit from a negative pressure differential in increasing interfacial bonding strength. However, a fully soft adhesion system exhibits an even more dramatic improvement by overcoming some of the limitations, when applying a high negative pressure differential for various nonplanar 3D geometries. As shown in Fig. 2 B, I, the deformation of the soft chamber eliminates the unfavorable air pocket, allowing over −50 kPa of high negative pressure differentials for all examined substrates––15-, 30-, and 60-mm-diameter glass spheres, a flat glass, and a soft elastomeric film with 400-μm thickness made out of Ecoflex 00–30 (Smooth-On Inc.). This is ∼10× greater than the highest negative initial pressure possible with the rigid system. In particular, the FAM on the soft adhesion system remains in contact and enhances the adhesion to the 15-mm-diameter glass sphere with a 70× larger negative pressure differential.

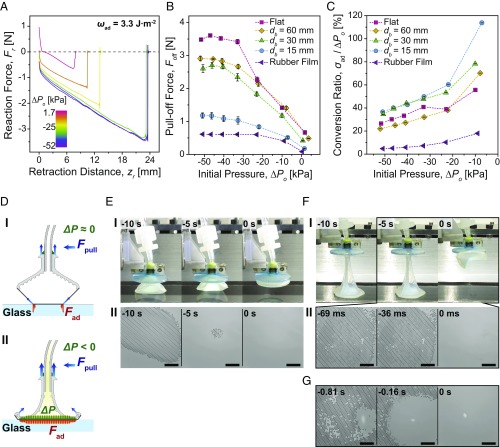
The FAM of the soft adhesion system is less adhesive than that of the rigid system, which exhibits an effective work of adhesion and adhesion stress of 3.3 J·m⁻² and 73 kPa, respectively (SI Appendix, Fig. S9A and Table S4). Fig. 5B shows the pull-off force (F_off) measurements of the soft adhesion system as a function of different initial pressures (ΔP_o). In general, the pull-off force increases when the initial pressure decreases and converges to a maximum when the pressure is between −40 and −50 kPa. However, 90% of this maximum pull-off force can be achieved with a pressure differential of roughly −35 kPa. On the flat glass, the pull-off force of the soft adhesion system is increased by 5.4× compared with the force without a high negative pressure differential. Of particular interest is the superior performance shown for highly curved 3D geometries like the 15-mm-diameter glass sphere, for which the pull-off force could be improved by 6.7×. Even on deformable and stretchable substrates, where the FAM and many other adhesives easily peel off, the soft system could remain in contact under the high negative pressure differential and improve the pull-off force by 7.2×.

Fig. 5.

Characterization results of the soft adhesion system. (A) Measured reaction force (F_r) profiles on a flat glass surface with respect to retraction distance, depending on different initial pressures (ΔP_o). (B) Measured pull-off forces (F_off) on various substrates depending on the initial pressures. (C) Conversion ratio (σ_ad/ΔP_o) on various substrates as a function of initial pressure. Each point in B and C indicates an average of five measurements, and error bars are ±1 SD. (D) Schematics of the soft system being pulled off from the flat glass without a change in the internal pressure (I), and under a high negative pressure differential (ΔP) (II). (E) Side views of the soft system being pulled off from the flat glass at 1.7 kPa of the initial pressure (I), and corresponding microscopic images of the contact interface (II). The estimated crack propagation speed is 1.5 m·s⁻¹. (F) Side views of the soft system being pulled off from the flat glass at −52 kPa of the initial pressure (I), and corresponding microscopic images of the contact interface (II). The estimated crack propagation speed is 179 m·s⁻¹. (G) Microscopic images of the contact interface of the soft system with a less adhesive FAM being pulled off from the flat glass at −46 kPa of the initial pressure. (Scales in E, II, F, II, and G indicate 1 mm.) The moment at which the FAM is detached is set to be 0 s.

Fig. 5C shows conversion ratios (σ_ad/ΔP_o) of the soft adhesion system on different substrates, defined as percentages of the adhesion stress (σ_ad) normalized by the applied initial pressure (ΔP_o). The soft adhesion system exhibits high conversion ratios at low negative pressure differentials, as the microfibers on the FAM can still exert some adhesion without relying on the pressure differential. It shows even higher than 100% of the conversion ratio on 15-mm-diameter spherical glass at −10 kPa. At high negative pressure differentials, on the other hand, the conversion ratios decrease significantly, when the system cannot achieve the adhesion as high as the applied negative pressure differential. Among the different diameter of spherical glasses, the smaller sphere shows higher conversion ratios. In case of the same contact areas between the 60-mm-diameter sphere and flat glass, the flat surface shows superior conversion ratios to the curved substrate. In general, the soft adhesion system can achieve 30∼50% of the conversion ratio at −35 kPa of the initial pressure on glass. However, these values are highly dependent on the adhesiveness of the membrane. As already shown in Fig. 5B, the soft adhesion system cannot achieve as high an adhesion on the rubber film as it does on the glass substrates, with a conversion ratio well below 20% for all initial pressures. This leads us to the conclusion that the conversion ratios on the glass substrates would be higher if a more adhesive membrane was used. Therefore, the maximum allowable adhesion of our adhesion systems is fundamentally limited by the maximum adhesion strength of the fiber–surface contact interface. Nonetheless, negative pressure differential will change how the interfacial load is distributed among the microfibers in contact with the surface and enhance adhesion performance within the limits of what the total sum of the contacts can support.

Previous microscale contact experiments have revealed that microfibers with optimized tip shapes show greater pull-off force due to equal load sharing, characterized by longer retraction distances for detachment accompanied with a fast crack propagation (41–45). Our soft system achieves similar characteristics at the macroscale with 4 orders of magnitude larger contact area by improving the load sharing. Unlike the short retraction that accompanies the higher pull-off force of the rigid system, Fig. 5A shows that our soft system could increase the pull-off force while delaying the detachment with a negative pressure differential. Fig. 5 D–F shows schematics, side-view, and microscopic images of the soft system on flat glass interface, respectively. In the absence of the negative pressure differential, no collapse of the soft chamber occurs and the FAM experiences high stress concentration at the contact edge (Fig. 5 D, I). This induces slow peeling from the interface (Fig. 5 E, II and Movie S2) during a short retraction distance up to 8 mm (Fig. 5 A and E, I and Movie S3). On the contrary, the soft chamber collapses and strongly suppresses the peeling of the FAM at a high negative pressure differential, allowing the soft system to remain in contact for a 3× longer retraction distance (Fig. 5 F, I and Movie S4). At the moment when the soft system is pulled off, the extremely large stretch of the soft chamber causes a shear force higher than the critical shear stress, peeling is induced, and the FAM starts detaching from the contact edge (Fig. 5 D, II). Because the equal load-sharing interface can withstand high tensile forces, small loss in contact area can trigger an immediate detachment of the entire FAM (Fig. 5 F, II and Movie S5). In this case, the crack propagation is roughly 110× times faster than without a negative pressure differential, strongly indicating the significant influence of equal load sharing.

Within the range of negative pressure differentials allowed by our experimental setup, the FAM for the soft system always detaches from the contact edge. As shown in Fig. 5G and Movie S6, however, a similar amount of the negative pressure differential could cause a crack propagation initiated at the center when we used a less adhesive FAM (effective work of adhesion and adhesion stress of 3.1 J·m⁻² and 56 kPa, respectively). The results in Fig. 5 E–G show that our soft adhesion system is able to manipulate crack initiation by changing the load distribution over a large area with the controlled pressure differential, as theoretically expected in our analysis shown in Fig. 3.

Direct comparison of the pull-off force between the soft and rigid adhesion systems cannot be made, as the FAMs on two systems have different effective works of adhesion. To compare the performance of the rigid and soft systems with respect to load sharing, we use adhesion efficiency (ε_ad), which is defined as a percentage of the adhesion stress of an adhesive system normalized by that of the microfiber array on the FAM. If a load is equally shared over the entire interface until detachment, the adhesive system will reach the maximum adhesion stress of the microfiber arrays (i.e., ε_ad = 100%). The rigid adhesion system could achieve only 6.6% of the maximum adhesion efficiency on the flat glass surface under a negative pressure differential. If no air is removed from the chamber, then the efficiency drops down to 1.8% on a 60-mm-diameter glass and the interface readily fails. The soft adhesion system, on the other hand, can use up to 19.5% adhesion efficiency on the flat glass. The system is even more effective for small and highly curved geometries where a full contact is not established. The maximum adhesion efficiency was 25.7% on a 15-mm-diameter glass, which is 14× larger than the rigid adhesion system efficiency without the pressure control on nonplanar surfaces.

More detailed information on the characterization results of the rigid and soft adhesion systems is presented in SI Appendix, Tables S1 and S2, respectively. In Fig. 1, the reversible load-sharing mechanism of the soft adhesion system is demonstrated as a soft adhesive pick-and-place gripper, enabling manipulation of various objects with complex 3D and deformable geometries. Our soft adhesion system could conform to a convex (Fig. 1B) or a concave curvature (Fig. 1C), and provide a sufficiently high payload to support over 300 g with 2.5 cm² of contact area (Fig. 1A and Movie S7). In Fig. 1D and Movie S8, the soft system can increase the adhesion on a highly curved geometry smaller than the FAM and lift up a weight as much as it could with the full contact in Fig. 1 B and C. Unlike geckos' biological foot-hairs, synthetic microfibers are highly sensitive to surface roughness (46), requiring very smooth surfaces like glass for high adhesion. However, the soft system can enhance the weak adhesion of the microfibers on slightly rough surfaces such as cherry tomatoes (Fig. 1E and Movie S9). The soft adhesion system is also successful for handling soft and deformable surfaces, which would not be possible for controllable adhesion mechanisms based on stiffness-tunable materials (20, 21). As shown in Fig. 1F and Movie S10, the soft system remains in contact even when the object is deformed and effectively preserves the adhesive attachment during manipulation.

Discussion

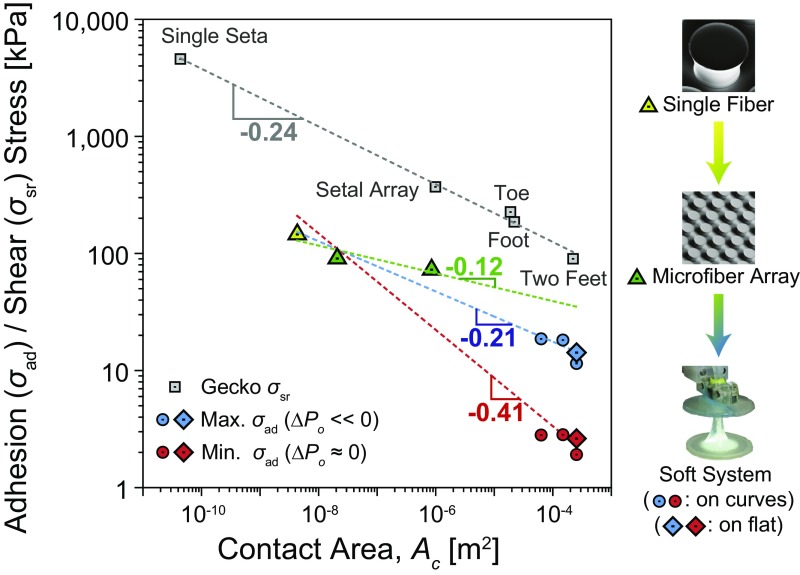
An ideally scaled-up macroscale adhesion system would have no loss in adhesive force compared with its microscale counterparts. Equal load sharing plays a critical role in approaching ideal bonding conditions and maximizing load capacity over a prescribed contact area (A_c) (47). Geckos have been used as a benchmark to judge the scaling efficiency of man-made adhesion systems (17, 18). Whereas shear stress (σ_sr) of the geckos' adhesion system, from bonding of a single seta to the attachment of two feet, has been reported to follow a scaling power law σ_sr ∝ A_c^-0.24 on a flat glass surface (48), no conclusive estimate is available on the scaling law for pure normal adhesion stress (σ_ad), as adhesion of the gecko is strongly coupled with friction. Labonte and Federle have recently reported that the geckos' scaling trend in adhesion coupled with shear forces is very similar to its scaling in shear stress for a range from the seta to the animal level (49). Therefore, we took the scaling of the gecko in the shear direction as a standard to evaluate the scaling performance of our adhesion system in the adhesion stress, assuming the gecko would have similar scaling efficiencies in both lateral and normal directions.

The adhesion stresses of a single fiber, a microfiber array, and our soft adhesion system on different sizes of spherical and flat glass substrates are plotted with the shear stress of the geckos' foot-hairs, as shown in Fig. 6. Estimation of the adhesion stress of the single fiber and the microfiber arrays with a small contact area are detailed in SI Appendix, Fig. S10 and Table S5. The scaling relation between the single fiber and the microfiber array, which are fixed on a rigid backing, is estimated as a power law of σ_ad ∝ A_c^-0.12 by the least-squares method, indicated as the green dashed line. This scaling relation provides a theoretical upper limit of the scaling efficiency that an adhesion system with the fibrillar adhesives could achieve at maximum.

Fig. 6.

Scaling of the soft adhesion system compared with a flat microfiber array and biological gecko adhesives. The scaling of geckos’ foot-hair adhesion is for shear stress (σ_sr) on a flat substrate, whereas the other results in the soft system are for normal adhesion stress (σ_ad) on both 3D curved (circles) and flat surfaces (rhombuses). Dashed lines are the least-squares trends in the adhesion stress of a single fiber, the microfiber array, and the soft system measured on both flat glass and spheres with 15-, 30-, and 60-mm diameters with (blue) and without (red) a negative initial pressure. The green line is the scaling from the single fiber to the microfiber array. Each data point indicates an average of five experimental measurements.

Unlike the case of single fiber and microfiber array on a rigid backing shown as the green dashed line, the adhesion stress of the compliant FAM on our soft load-sharing system deviates from the linear trend of the theoretical maximum due to a significant loss in fracture strength by introducing stress concentration. The dashed red and blue lines in Fig. 6 show the scaling trends of our soft system from the single fiber, microfiber array, and overall soft system calculated by the least-squares method. Without a negative pressure differential (the red line in Fig. 6), the stress concentration results in a poor scalability of σ_ad ∝ A_c^-0.41. Under a high negative pressure differential (the blue line in Fig. 6), on the other hand, our soft load-sharing system can minimize the stress concentration with the same compliant membrane and improves the scaling efficiency by recovering it up to σ_ad ∝ A_c^-0.21, which is slightly higher than that of the gecko on various flat and curved 3D surfaces.

Hawkes et al. developed a synthetic adhesion system (18) with the scaling efficiency related to σ_ad ∝ A_c^-0.02 for the shear stress on flat or slightly curved surfaces. Our soft adhesion system, on the other hand, is the geometry-insensitive load sharing mechanism with an area scaling efficiency comparable to that of the natural geckos' adhesion system for the normal adhesion stress. Therefore, the concept of our soft adhesion system can provide significant benefits in a broad range of adhesion applications requiring high adhesion on various sizes of 3D surfaces. This includes transfer-printing systems (14, 50–52) and robotic manipulators (15) capable of handling a wide range of sizes and curvatures of rigid and deformable substrates as well as mobile robots that can climb on complex 3D surfaces, such as aircraft, space shuttle, or pipe surfaces (9, 53, 54).

Several future studies still remain to evaluate this approach to soft robotic grasping. Whereas our soft elastomeric system possesses high 3D surface conformability, a large amount of stretch under a high load generates shear stresses at the edge of contact, causing a stress concentration. Using a soft but nonstretchable elastomer for the chamber may resolve this problem and further improve the performance. This work has focused on enhancing the adhesion capacity of a membrane by equal load sharing, and there has not been an attempt to optimize the performance of our adhesion system for releasing lightweight objects. In our previous work, we leveraged the stretch of a membrane to peel the microfibers in contact, reducing the bonding strength of the FAM down to the adhesion of a single fiber (33). Combining the proposed soft load-sharing mechanism with the stretchable FAM in the future, we may achieve high load capacity and controllability in adhesion with a controlled pressure differential. In our analytic model for the FAM, the structured fibrillar surface has been approximated as a flat surface and the shape of deformation has been simplified as a truncated cone, even under a reduced internal chamber pressure. Taking the fibrillar structures into account along with more realistic kinematics of the membrane deformation would allow for a more quantitatively accurate predictive model. Such a model represents a potential opportunity for future work. In particular, it could lead to further insights into the contact mechanics of a soft and structured interface and be used in optimized soft system designs for specific applications.

Conclusion

In summary, we present a soft load-sharing system that controls normal load distribution on 3D surfaces by exploiting the influence of internal pressure on interfacial load sharing. This soft-system architecture addresses the fundamental challenge of having high surface conformability while simultaneously maintaining high fracture strength. By using a soft and deformable body and controlling the negative pressure differential acting on the interface, the proposed system pushes the upper limit on the maximum adhesion-controlled gripping strength that can be achieved on nonplanar 3D geometries. Our equal load-sharing method represents a paradigm for adhesion-based systems that outperform previous systems using microfibrillar adhesives in handling complex 3D and deformable objects and surfaces.

Materials and Methods

Fabrication of the Elastomeric FAM.

Soft PDMS molds containing cylindrical cavities were obtained by replicating SU-8 lithographic templates as previously reported (55, 56). Sylgard 184 siloxane base and curing agent were mixed in a 10:1 ratio, degassed, and casted on the PDMS mold shaped in the cylindrical cavities. The excess prepolymer was removed by a bar coater (K-Hand-Coater, Erichsen GmbH & Co. KG) creating an ∼250-µm thin backing layer. The sample was cured in a vacuum oven at 90 °C for 1 h and demolded (SI Appendix, Fig. S1). Micropatterns with 52-µm diameter, 48-µm spacing, and 38-µm height were received (SI Appendix, Fig. S2). Sylgard 184 prepolymer was poured on a glass plate and a thin film of ∼20-µm thickness was created by a film applicator (Multicator 411, Erichsen GmbH & Co. KG). The thin polymer film was precured in the oven at 90 °C for 3 min. The cylindrical fibers, fabricated in the previous step, were manually inked onto the precured thin film and placed on a perfluorinated silicon wafer. The precuring of the polymer film is necessary to increase its viscosity, thereby enhancing the transfer of the polymer material to the fibers for creating optimal mushroom-shaped tips. After curing at 90 °C for 1 h, the printed patterns were carefully peeled off and the FAM with 69-µm tip diameter, 31-µm spacing, and 42-µm-height mushroom-shaped microfibers were obtained (SI Appendix, Figs. S2 and S3).

Fabrication of the Rigid Adhesion System.

The rigid chamber was designed with a computer-aided design (CAD) software (SolidWorks) and fabricated by a 3D printer (Objet260 Connex, Stratasys Ltd.) using VeroClear as the rigid material. The printed rigid chamber was thoroughly cleaned with 1 mol of NaOH solution to remove supporting materials. Surface modification on the chamber was performed by inking the chamber into a primer (1200 OS Primer, Dow Corning), followed by a drying step at room temperature for 30 min. The surface modification is important to ensure strong bonding between the chamber and the FAM. A silicone adhesive (Sil-Poxy, Smooth-On Inc.) was poured on a glass plate and a thin film of ∼50 μm in thickness was created by a film applicator (Multicator 411, Erichsen GmbH & Co. KG). The chamber was inked into the thin Sil-Poxy film and placed onto the FAM. After curing at room temperature for 30 min, the FAM was strongly bonded to the rigid chamber (SI Appendix, Fig. S4).

Fabrication of the Soft Adhesion System.

A negative mold made out of Ecoflex 00–30 (Smooth-On Inc.) for the soft chamber was obtained by replicating a 3D-printed composite model shaped as the chamber. The composite model was designed with a CAD software and fabricated by a 3D printer (Objet260 Connex, Stratasys Ltd.) using VeroClear as rigid and TangoBlack as soft materials. The rigid axis grants stability to the model, while the soft body facilitates the peeling. The printed chamber model was thoroughly cleaned with 1 mol of NaOH solution to remove supporting materials. The chamber was fixed using a double-sided tape in a small plastic Petri dish. A 1:1 ratio of Ecoflex 00–30 prepolymer and cross-linker was mixed, degassed, and casted into the Petri dish and cured at room temperature for 6 h (SI Appendix, Fig. S5). After the elastomer was cured, the composite model of the soft chamber was carefully demolded. The fabricated negative mold of the soft chamber was treated in an oxygen plasma at 100 W for 2 min, followed by the surface modification using Hexadecafluoro-1,1,2,2-tetrahydrooctyltrichlorosilane for 1 h in vacuum and cured at 90 °C for 30 min. The perfluoro coating of the mold is important to reduce the adhesion of the casting materials in the following replication process. The mold consists of two components: the soft negative of the chamber and a thin metal bar used for a spacer to create an air channel in the chamber (SI Appendix, Fig. S5). A 1:1 ratio of Ecoflex 00–50 (Smooth-On Inc.) Parts A and B were mixed, degassed, and injected inside of the negative mold using a syringe. After curing at room temperature for 6 h, the mold and the soft chamber were carefully demolded. A vinylsiloxane polymer (Flexitime Medium Flow, Heraeus Kulzer GmbH) was applied on a glass plate and a thin film of ∼50-µm thickness was created by a film applicator (Multicator 411, Erichsen GmbH & Co. KG). The soft chamber was manually inked into the polymer film and placed on the FAM. The vinylsiloxane could develop a strong bond between the soft chamber and the FAM after 5 min of curing at room temperature.

Experimental Setup.

The customized adhesion measurement setup was mounted on an inverted optical microscope (Axio Observer A1, Zeiss) with a video camera (Grasshopper3, Point Gray Research Inc.) to visualize and record the contact interface (SI Appendix, Fig. S6). The reaction forces between an adhesion system and a substrate were measured by high-resolution load cells (GSO-25, GSO-500, and GSO-1K, Transducer Techniques). The load cell was attached on a computer-controlled high-precision piezo motion stage (LPS-65 2″, Physik Instrumente GmbH & Co. KG) in the z direction, with a resolution of 5 nm and the maximum velocity of 10 mm·s⁻¹. A long-ranged motor stage (M-605 2DD, Physik Instrumente GmbH & Co. KG) was used for the y direction with 1-µm resolution and high maximum velocity up to 50 mm·s⁻¹. The substrate was fixed onto a sample holder within the focal range of the microscope and moved in the x direction by the piezo stage (LPS-65 2″, Physik Instrumente GmbH & Co. KG). Also, fine positions in the x- and y directions were determined by a manual xy stage (NFP-2462CC, Positionierungstechnik Dr. Meierling). Angular misalignments were adjusted by two goniometers (M-GON65-U, Newport) according to the substrate. A syringe pump (Legato 210P, KDScientific Inc.) with an accuracy of ±0.35% was used for pressure control inside of the adhesion system. The motion of the piezo stages and the data acquisition were performed by a customized code in Linux (Ubuntu, Canonical Ltd.). The program allowed automated data acquisition and enabled the user to control velocities, preloads, displacements in the x- and z directions, and contacting time. The load cell was connected to the computer via a signal conditioner (BNC-2110, National Instruments) and the force signal was exported as a voltage through a data acquisition board (PCIe-6259, National Instruments). Motion control of the piezo stages was conducted through a motor controller (Nexact E-861, Physik Instrumente GmbH & Co. KG).