Spread of Zika virus in the Americas

Significance

Mathematical and computational modeling approaches can be essential in providing quantitative scenarios of disease spreading, as well as projecting the impact in the population. Here we analyze the spatial and temporal dynamics of the Zika virus epidemic in the Americas with a microsimulation approach informed by high-definition demographic, mobility, and epidemic data. The model provides probability distributions for the time and place of introduction of Zika in Brazil, the estimate of the attack rate, timing of the epidemic in the affected countries, and the projected number of newborns from women infected by Zika. These results are potentially relevant in the preparation and analysis of contingency plans aimed at Zika virus control.

Abstract

We use a data-driven global stochastic epidemic model to analyze the spread of the Zika virus (ZIKV) in the Americas. The model has high spatial and temporal resolution and integrates real-world demographic, human mobility, socioeconomic, temperature, and vector density data. We estimate that the first introduction of ZIKV to Brazil likely occurred between August 2013 and April 2014 (90% credible interval). We provide simulated epidemic profiles of incident ZIKV infections for several countries in the Americas through February 2017. The ZIKV epidemic is characterized by slow growth and high spatial and seasonal heterogeneity, attributable to the dynamics of the mosquito vector and to the characteristics and mobility of the human populations. We project the expected timing and number of pregnancies infected with ZIKV during the first trimester and provide estimates of microcephaly cases assuming different levels of risk as reported in empirical retrospective studies. Our approach represents a modeling effort aimed at understanding the potential magnitude and timing of the ZIKV epidemic and it can be potentially used as a template for the analysis of future mosquito-borne epidemics.

The Zika virus (ZIKV) is an RNA virus from the Flaviviridae family, genus Flavivirus (1, 2), first isolated in the Zika Forest of Uganda in 1947 (3). It generally results in a mild disease characterized by low-grade fever, rash, and/or conjunctivitis, although only ∼20% of those infected are symptomatic (4). Although there have been instances of sexual and perinatal/vertical transmission (5–12) and the potential for transmission by transfusion is present (13), ZIKV spreads primarily through infected Aedes mosquitoes (14, 15).

Until recently, ZIKV was considered a neglected tropical disease with only local outbreaks (4, 16–18). The association of ZIKV with the reported microcephaly case clusters in Brazil during 2015 (19) led the director-general of the WHO to declare on February 1, 2016, a Public Health Emergency of International Concern (PHEIC) (20) that lasted for nearly 10 mo. During this period, ZIKV spread throughout the Americas, with 47 countries and territories in the region reporting autochthonous transmission (21, 22). Many other countries with ZIKV outbreaks besides Brazil have reported cases of microcephaly and other birth defects associated with ZIKV infection during pregnancy (Zika congenital syndrome) (23), and the epidemic has been under close scrutiny by all of the major public health agencies around the world.

Although enhanced surveillance and new data have improved our understanding of ZIKV (24–29), many unknowns persist. There is uncertainty surrounding the time of introduction of the virus to the region, although epidemiological and genetic findings estimate that ZIKV arrived in Brazil between May and December 2013 (nextstrain.org/zika; ref. 30). Furthermore, although mathematical and computational models have tackled the characterization of the transmissibility and potential burden of ZIKV (31–35), little is known about the global spread of the virus in 2014 and 2015, before the WHO’s alert in early 2016. Using a data-driven stochastic and spatial epidemic model, we present numerical results providing insight into the first introduction in the region and the epidemic dynamics across the Americas. We use the model to analyze the spatiotemporal spread and magnitude of the epidemic in the Americas through to February 2017, accounting for seasonal environmental factors and detailed population data. We also provide projections of the number of pregnancies infected with ZIKV during the first trimester, along with estimates for the number of microcephaly cases per country using three different levels of risk based on empirical retrospective studies (36, 37).

Results

Introduction of ZIKV to the Americas.

We identify 12 major transportation hubs in areas related to major events held in Brazil, such as the Soccer Confederations Cup in June 2013 and the Soccer World Cup in June 2014 and assumed a prior probability of introduction proportional to the daily passenger flow to each hub. We then consider introduction dates between April 2013 and June 2014, including the time frame suggested by phylogenetic and molecular clock analyses (nextstrain.org/zika; ref. 30) through to the 2014 Soccer World Cup. Using Latin square sampling over the two-dimensional space (date–location), we calculated the likelihood of replicating the observed epidemic peak in Colombia ($\pm$1 wk), as reported by Colombia’s National Institute of Health (38), and the resulting posterior density of each location and date combination. The Colombian epidemic was used to calibrate this analysis because of the large number of cases observed and overall consistency in reporting.

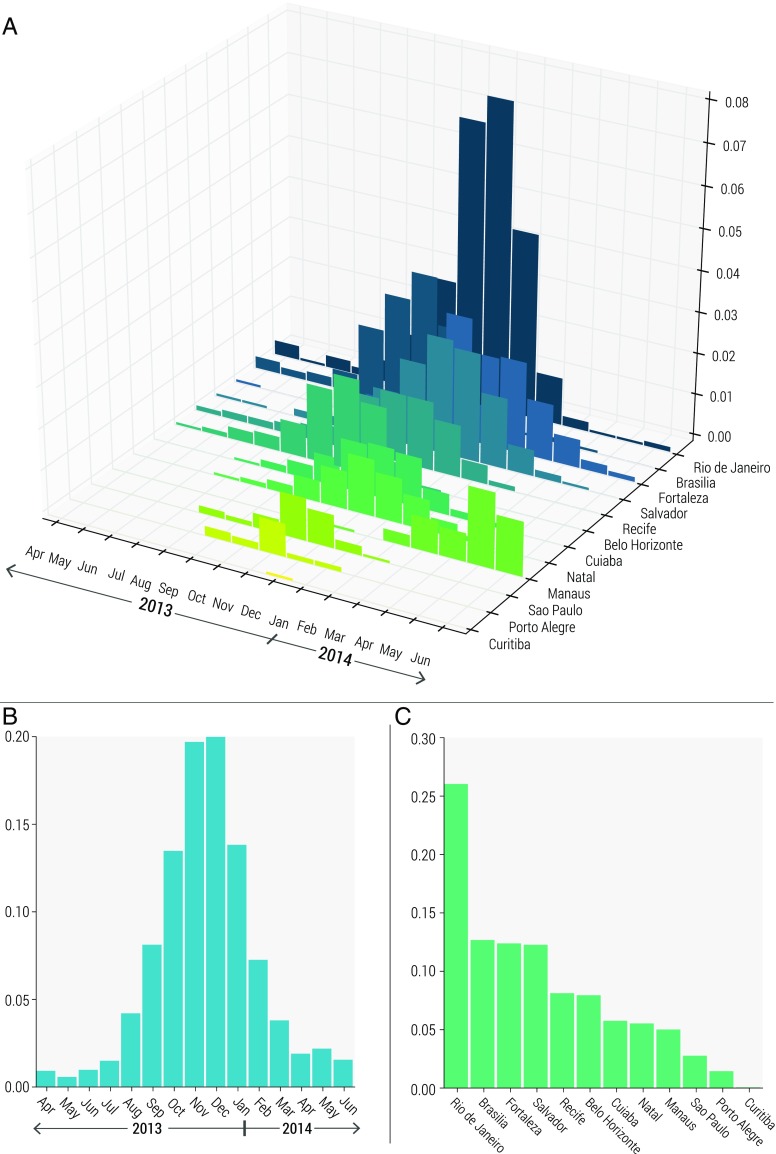
In Fig. 1A we plot the posterior distribution as a function of introduction date and location, and in Fig. 1 B and C we plot the marginal posterior distributions of introduction date and location separately. The largest posterior density is associated with an introduction in Rio de Janeiro in December 2013. The 90% credible interval for the most likely date extends from August 2013 to April 2014, with the mode in December 2013, in agreement with phylogenetic and molecular clock analyses (nextstrain.org/zika; ref. 30). The most likely locations of ZIKV introduction, in descending order, are Rio de Janeiro (southeast), Brasilia (central), Fortaleza (northeast), and Salvador (northeast). Although Rio de Janeiro experiences the greatest passenger flow, the city also experiences more seasonality in mosquito density, making its likelihood to seed an epidemic sensitive to introduction date. The cities located in the northeast of Brazil have lower passenger flow compared with Rio de Janeiro but have higher mosquito density and dengue virus (DENV) transmission all year round. Brasilia, in comparison, has little seasonality in terms of mosquito density and high traffic flow, although the area has low DENV transmission.

Fig. 1.

Posterior distribution for ZIKV introductions in 12 major transportation hubs in Brazil between April 2013 and June 2014, incorporating the likelihood of replicating the observed epidemic peak in Colombia. (A) Full posterior distribution as a function of location and time of introduction. (B) Marginal posterior distribution for time (month) of introduction. (C) Marginal posterior distribution for location of introduction.

Spatiotemporal ZIKV Spread.

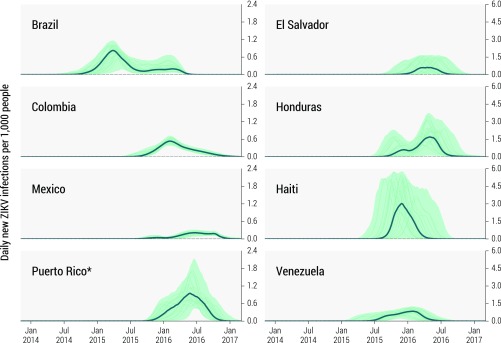
Stochastic realizations reproducing the observed peak in Colombia define the model output used to provide the spatiotemporal pattern of ZIKV spread in the Americas through to February 2017. In Fig. 2 we plot the simulated epidemic profiles of incident ZIKV infections for several countries in the region, and in Table 1 we report the associated infection attack rates (ARs) through to February 1, 2016, when the WHO declared a PHEIC, and through to February 28, 2017. In SI Appendix we report maps with the cumulative number of cases at the scale of 1 km × 1 km. The infection AR is defined as the ratio between the cumulative number of new infections (both symptomatic and asymptomatic) during the period of consideration and the total population of a given region. Estimates for additional countries in the Americas are provided in a publicly available database (www.zika-model.org). The earliest epidemic is observed in Brazil, followed by Haiti, Honduras, Venezuela, and Colombia. The model indicates that the epidemics in most countries decline after July 2016, a finding supported by epidemiological surveillance in the region. The decline of the epidemic is mostly due to the fact that large outbreaks greatly deplete the pool of susceptible individuals who can be exposed to the disease. In some countries (for instance, Puerto Rico) the seasonal variation plays a role in the quick decline of the epidemic; however, the first wave is generally the most important in terms of magnitude. Although the model projects activity in many places throughout the Americas in 2017, the incidence is extremely small compared with the cumulative incidence of 2015/2016.

Fig. 2.

Estimated daily number of new ZIKV infections (per 1,000 people) in eight affected countries in the Americas between January 2014 and February 2017. The bold line and shaded area refer to the estimated median number of infections and 95% CI of the model projections. Rates include asymptomatic infections. The median incidence is calculated each week from the stochastic ensemble output of the model and may not be representative of specific epidemic realizations. Thin lines represent a sample of specific realizations. Note that the scales on the y axes of the subplots vary. *Puerto Rico curves are constrained under the condition that the peak of incidence curve is after March 1, 2016, based on the surveillance reports (72).

Table 1.

Projected ZIKV infection ARs through the time of the WHO declaration of a PHEIC on February 1, 2016, and through February 28, 2017, in eight affected countries in the Americas

	Infection AR %		Cumulative microcephaly cases (median with 95% CI)
	(median with 95% CI)		First-trimester risk: 0.95%		First-trimester risk: 2.19%		First-trimester risk: 4.52%
	Feb. 1, 2016	Feb. 28, 2017	Feb. 1, 2016	Dec. 10, 2017	Feb. 1, 2016	Dec. 10, 2017	Feb. 1, 2016	Dec. 10, 2017
Brazil	16 [13 to 18]	18 [16 to 19]	839 [138 to 1,140]	1,297 [1,190 to 1,428]	1,934 [318 to 2,628]	2,991 [2,744 to 3,291]	3,992 [656 to 5,424]	6,173 [5,664 to 6,792]
Colombia	4 [3 to 7]	12 [11 to 14]	0 [0 to 4]	219 [194 to 248]	0 [0 to 10]	504 [447 to 572]	1 [0 to 20]	1,041 [922 to 1,180]
Mexico	1 [0 to 2]	5 [4 to 6]	0 [0 to 2]	314 [226 to 367]	0 [0 to 5]	723 [522 to 845]	1 [0 to 11]	1,493 [1,077 to 1,744]
Puerto Rico*	2 [0 to 7]	20 [13 to 28]	0 [0 to 0]	19 [13 to 26]	0 [0 to 0]	43 [29 to 60]	0 [0 to 0]	88 [60 to 124]
El Salvador	1 [0 to 13]	16 [13 to 18]	0 [0 to 0]	39 [32 to 47]	0 [0 to 0]	91 [75 to 108]	0 [0 to 1]	187 [154 to 223]
Honduras	8 [0 to 28]	35 [30 to 39]	0 [0 to 1]	144 [124 to 163]	0 [0 to 3]	332 [286 to 376]	0 [0 to 7]	686 [590 to 775]
Haiti	43 [1 to 54]	49 [43 to 55]	0 [0 to 54]	316 [276 to 357]	0 [0 to 124]	728 [637 to 824]	0 [0 to 256]	1,502 [1,315 to 1,700]
Venezuela	13 [5 to 19]	19 [16 to 21]	2 [0 to 96]	271 [237 to 308]	5 [0 to 221]	624 [546 to 711]	9 [0 to 456]	1,288 [1,127 to 1,468]

Median estimates and 95% CIs are provided. ZIKV ARs include asymptomatic infections. The denominator is the entire population of the country, including regions not exposed to the vector. Cumulative microcephaly cases due to ZIKV infection during the first trimester of pregnancy through the time of the WHO declaration of a PHEIC on February 1, 2016, and through December 10, 2017, in eight affected countries in the Americas. We consider three different risks of microcephaly associated with ZIKV infection during the first trimester: 0.95% first-trimester risk based on a study of the 2013–2014 French Polynesian outbreak (36) and 2.19% (100% overreporting) and 4.52% (no overreporting) first-trimester risks, based on a study of Bahia, Brazil (37), given a model-estimated 31% infection AR in Bahia.

^*Puerto Rico curves constrained under the condition that the peak of ZIKV incidence curve is after March 1, 2016, based on surveillance data (72).

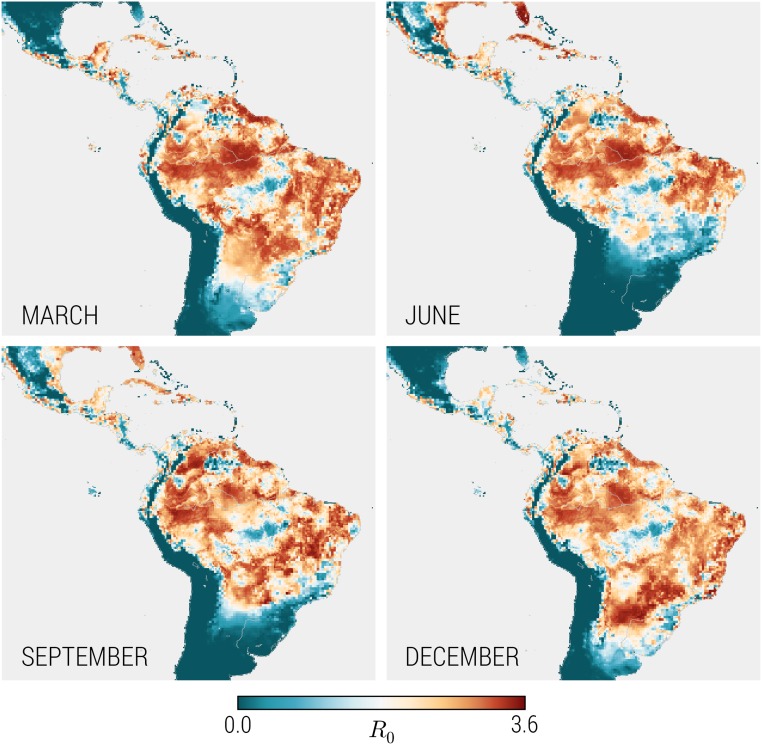
National infection ARs are projected to be high in Haiti, Honduras, and Puerto Rico. Countries with larger populations and more heterogeneity in mosquito density and vector-borne disease transmission, such as Mexico and Colombia, experience much lower infection ARs. For example, nearly half of Colombia’s population resides in areas of high altitude where sustained vector-borne ZIKV transmission is not possible. Due to the model’s fine spatial and temporal resolution, we are able to observe significant variability in the ZIKV basic reproductive number $R_0$ across locations, and even within the same location at different times. These differences are driven by temperature, the vector distribution, and socioeconomic factors, among other variables (additional details are provided in Materials and Methods). In Fig. 3 we plot $R_0$ in a number of areas at different times throughout the year. Equatorial regions experience less seasonality than nonequatorial regions, where changes in temperature have a strong impact on the mosquito population, and thus $R_0$. Large areas with unexposed populations are visible, such as in high-altitude regions of Colombia. It is also worth remarking that maximum $R_0$ is not the sole determinant of the epidemic magnitude, because seasonality patterns and a small fraction of exposed individuals may not allow large outbreaks to occur.

Fig. 3.

Monthly seasonality for the time- and location-dependent basic reproductive number, R₀. The equatorial regions display less seasonality than the nonequatorial regions, where the changes of the season have a strong impact on the temperature and consequently on the basic reproductive number, R₀.

Projected ZIKV Infections in Childbearing Women and Microcephaly Cases.

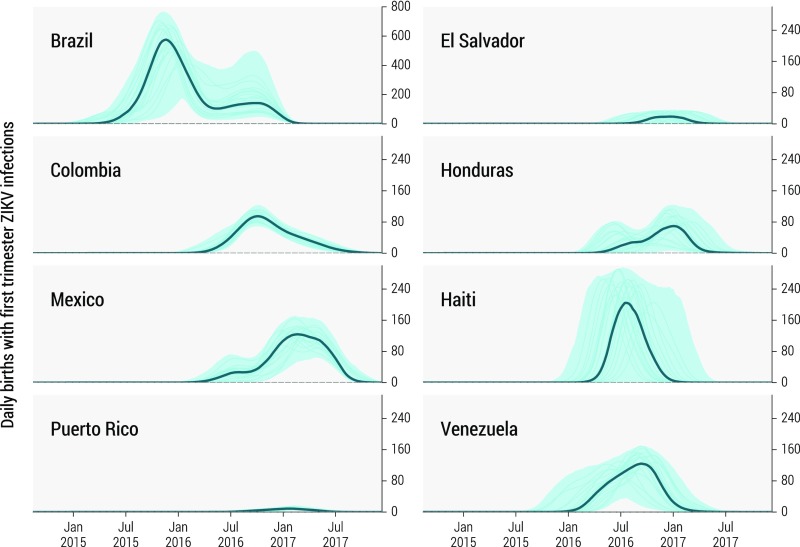
Using the epidemic profiles generated by the model we project the number of ZIKV infections in childbearing women following the model proposed in the study of ZIKV–microcephaly association for the 2013–2014 French Polynesia outbreak (36). In Fig. 4 we plot the daily number of births through December 2017 from women infected with ZIKV during their first trimester of pregnancy in several countries. Indeed, the first trimester of pregnancy is when the risk of microcephaly is the highest (36, 37, 39). The curves closely resemble the epidemic profiles in Fig. 2 but shifted forward in time by about 40 wk. We construct our estimates using country-specific birth rates, as detailed in SI Appendix, section 4.

Fig. 4.

Estimated daily number of births between October 2014 and December 2017 from women infected with ZIKV during the first trimester of pregnancy in eight affected countries in the Americas. The bold line and shaded area refer to the estimated median number of births and 95% CI of the model projections, respectively. Note that Brazil is plotted on a different scale. The median curve is calculated each week from the stochastic ensemble output of the model and may not be representative of specific epidemic realizations. Thin lines represent a sample of specific realizations.

To estimate the number of microcephaly cases we adopt three different probabilities, as reported in two empirical retrospectives studies (36, 37). The first estimate of microcephaly risk for ZIKV infected pregnancies is $0.95\%$ (95% confidence interval (CI) [0.34 to 1.91%]), from a study in French Polynesia (36). The remaining two estimates come from a study performed in Bahia, Brazil (37). Given an overall ZIKV infection AR of $31\%$ (95% CI [26 to 36%]) in Bahia through February 2016, as determined by our model, the estimated first trimester microcephaly risks are $2.19\%$ (95% CI [1.98 to 2.41%]), assuming 100% overreporting of microcephaly cases, and $4.52\%$ (95% CI [4.10 to 4.96%]), assuming no overreporting. These estimates do not account for miscarriages or other complications that may occur during pregnancy.

In Table 1 we report the projected cumulative number of microcephaly cases up to February 1, 2016, and December 10, 2017. By the time the WHO declared a PHEIC, Brazil was the only country with a substantial (>100) number of ZIKV-attributable microcephaly cases, with cases expected to appear through July 2017. For Colombia, the model projects a considerable number of new microcephaly cases until March–April 2017. In Venezuela, the peak in microcephaly cases was projected to start in September/October 2016, continuing through February 2017. In Puerto Rico, microcephaly cases were expected to occur mostly from December 2016 to April 2017. It is important to remark, however, that the microcephaly incidence tail extends for most of the countries up to July/August 2017. Along with the microcephaly risk, other birth defects and pregnancy complications are associated with ZIKV infection during pregnancy (36, 37, 39). Although we do not explicitly tabulate here specific projections, they can be calculated from our model by applying the estimated risk for any other complication to our daily number of births from women infected with ZIKV.

Sensitivity to Mosquito Vector.

Simulations reported here consider both Aedes aegypti and Aedes albopictus as competent ZIKV vectors, although less is known about the vectorial capacity of A. albopictus. A sensitivity analysis considering A. aegypti as the only competent vector is provided in SI Appendix with all figures and tables replicated for this scenario. Overall, results are similar because transmission due to A. aegypti increases to compensate for the absence of the other vector. Differences in the infection ARs, however, are observed in areas where A. albopictus is the most common or the only vector. For example, the infection AR in Brazil up to February 28, 2017, decreases from $18\%$ (95% CI [16 to 19%]) to $16\%$ (95% CI [14 to 17%]) if we consider only A. aegypti. During the same time period, the infection AR in Mexico decreases from $5\%$ (95% CI [4 to 6%]) to $4\%$ (95% CI [2 to 5%]). A more thorough analysis of the differences between the two scenarios is reported in SI Appendix. At the country scale, in Brazil and other key countries those differences seem small because A. aegypti and A. albopictus have very similar presence. However, we see noticeable differences in the infection AR as soon as the country extends to north and south of the equator and we look at specific geographical areas where only A. albopictus are present.

Model Validation.

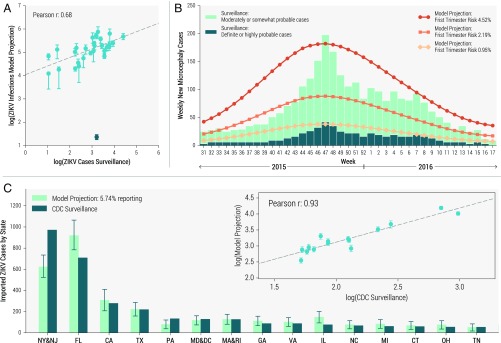
Our results have been validated comparing our projections with surveillance data that were not directly used to calibrate the model: the number of ZIKV infections by states in Colombia, the weekly counts of microcephaly cases reported in Brazil, and the number of importations of ZIKV infections in the continental United States (USA), as shown in Fig. 5. In Fig. 5A we compare model-based projections of the number of ZIKV infections for states in Colombia with observed surveillance data through October 1, 2016 (38). As expected for a typically asymptomatic or mild disease, the model projects a much larger number of infections than that captured by surveillance, suggesting a reporting and detection rate of $1.02\%\pm 0.93\%$ (from linear regression analysis). However, the observed data and model estimates are well-correlated (Pearson’s $r=0.68$, $P<0.0001$), replicating the often several-orders-of-magnitude difference in infection burden across states within the same country.

Fig. 5.

(A) Correlation between the number of ZIKV cases by state in Colombia as reported by surveillance data through October 1, 2016 (38), compared with state-level model projections of infections (median with 95% CI). Pearson’s r correlation coefficient is reported for the linear association on the log scale. The outlier (in dark green) excluded from the statistical analysis corresponds to the Arauca region. (B) Timeline of microcephaly cases in Brazil through April 30, 2016. Bar plots show weekly definite (or highly probable cases) and moderately (or somewhat probable cases) from surveillance data (40). Line plots indicate estimated weekly new microcephaly cases given three levels of first trimester risk: 4.52% (circles) (37), 2.19% (squares) (37), and 0.95% (diamonds) (36). (C) Bar plot of ZIKV infections imported into the USA by state(s) as reported by CDC surveillance through October 5, 2016 (41), and compared to model projections (median with 95% CI) for the same period assuming 5.74% reporting/detection. (Inset) The correlation between CDC surveillance data and model projections (median with 95% CI).

In Fig. 5B we compare observed data on weekly counts of microcephaly cases reported in Brazil through April 30, 2016 (40) with estimates from the model for each projected level of microcephaly risk given first-trimester ZIKV infection. The three model projection curves vary in magnitude but replicate peaks consistent with the observed data. Because the fraction of cases confirmed in Brazil is relatively low, it is not possible to identify the most likely level of risk, although the figure suggests that the risk might exceed the lowest estimate of 0.95% (36).

Because the computational approach explicitly simulates the number of daily airline passengers traveling globally, the microsimulations allow us to track ZIKV infections imported into countries with no autochthonous transmission. In Fig. 5C we plot the number of importations into states in the USA through October 5, 2016, as reported by the CDC (41) and compare these results with model projections. Because the detection rate of ZIKV infections is very low, there are significantly fewer reported cases than projected; we estimate through a linear regression fit that $5.74\%\pm 1.46\%$ of both symptomatic and asymptomatic imported infections are detected. Nonetheless, model projections are highly correlated with the observed data (Pearson’s $r=0.93$, $P<0.0001$), as shown in Fig. 5C, Inset. A further validation of the model is provided by the reported number of ZIKV cases of pregnant women in the USA. A high detection rate is expected in this closely monitored population. As of September 29, 2016, $837$ pregnant women in the USA were laboratory-confirmed for ZIKV, all of whom were imported cases. Because pregnant women comprise ∼$1\%$ of incoming airline traffic flow from the rest of the Americas (42), one can roughly estimate $\mathrm{83,700}$ infections. Although this is a rough estimate, because of fluctuations in pregnant women traffic flow and testing rates, it is in the ballpark of our modeling results projecting $\mathrm{57,910}$ (95% CI [50, 138 to 66, 608]) infections imported into the USA by early October 2016. These results are relevant for ZIKV risk assessment in the USA (43, 44). In SI Appendix we provide additional validation tests by looking at case reporting in Brazil at the state level, and the detection of travel related cases in European countries.

Discussion

We use computational modeling to reconstruct the past and project the future spatiotemporal spread of ZIKV in the Americas. To identify the likely date and location of ZIKV’s first introduction to the Americas, posterior densities are estimated for 12 major travel hubs in Brazil over a range of dates. The marginal posterior distributions suggest an introduction between August 2013 and April 2014 in a number of potential locations, including Rio de Janeiro, Brasilia, Fortaleza, and Salvador. This date range overlaps with that suggested by a recent phylogenetic analysis (nextstrain.org/zika; ref. 30), although our estimate also includes later potential introductions. The model seems to rule out an introduction concurrent to the Soccer World Cup in June 2014.

The model is able to generate epidemic curves in time for incident ZIKV cases for about two dozen countries in the Americas. Although for the sake of space we report on only eight countries, the full database is publicly available (www.zika-model.org). The results obtained are in good agreement with model-based projections achieved with a different approach developed by Perkins et al. (32) using location-specific epidemic ARs on highly spatially resolved human demographic projections. Although the approach of Perkins et al. (32) does not provide information on the dynamic of the epidemic, it estimates ZIKV infections in the first-wave epidemic in the most-affected countries such as Brazil and Colombia, where the approach projects a median infection AR of 19 and 14%, respectively, which falls within the CI of the results provided here.

Although the initial introduction of ZIKV could date back to August 2013, most countries did not experience the first wave of the epidemic until the early months of 2016. Brazil is the only country that seems to have a well-defined first peak in March 2015, consistent with reports from the northeast region (45). The model suggests two epidemic waves in Brazil. The first wave, occurring between January and July 2015, corresponds to early outbreaks in the northeast region (Maranhao, Bahia, and Rio Grande do Norte) and later on in the rest of the country. This first wave was not recognized as ZIKV until early 2016. The second wave, between January and May 2016, affected mostly southern states in Brazil (46). This progression of the epidemic is in agreement with the reconstruction of the movement of ZIKV in Brazil using confirmed cases at the municipal level (33).

The virus also circulated early on in the Caribbean, with ZIKV samples isolated in Haiti at the end of 2014, and a possible first peak occurred in October 2015 (47). Colombia first isolated ZIKV in October 2015, at which time it spread rapidly from the Caribbean coast to cities infested with A. aegypti (48). The model suggests an introduction to Colombia as early as March–April 2015, potentially overlapping with the Easter holiday, which is a period of high mobility within and between countries in the region. ZIKV transmission in Venezuela follows a similar trajectory, first isolated in November 2015 and present in all states by July 2016 (49). Since March 2016, reported cases have declined in both countries, consistent with our model estimates.

Our model estimates ZIKV transmission in El Salvador and Honduras increasing around July 2015. ZIKV was first detected in El Salvador in November 2015 and in Honduras in December 2015 (50, 51). Although the first ZIKV infection was confirmed in Puerto Rico in the last week of December 2015 (52), the model estimates ZIKV transmission in Puerto Rico beginning around August 2015. In Mexico, the first infection was reported to the surveillance system at the end of November 2015 (53), although circulation may have begun in September 2015.

The epidemic has moved slowly and is mostly constrained by seasonality in ZIKV transmissibility. Seasonal drivers and time of introduction result in multiple waves (54) across several countries, as projected for Brazil, Honduras, and Mexico. To show the importance of the seasonal drivers in shaping the epidemic, we report in SI Appendix the analysis of two counterfactual scenarios in which we eliminate the differences in the seasonal drivers across the region. This analysis clearly shows that ignoring the spatial variation of seasonal drivers gives rise to unrealistic patterns incompatible with the observed data.

Another relevant result of the model is that incidence rates dramatically decrease in all considered countries by the end of 2016. The drop in incidence in the model is largely due to the epidemic’s depleting the susceptible pool. This implies that ZIKV epidemics could settle into the typical seasonal pattern of mosquito-borne diseases such as DENV. Transmission may be low for several years with a gradual buildup in susceptibility due to births (55). In the real world, however, other factors such as vector control and/or specific local weather conditions could have contributed to the drop of incidence along with herd immunity. Because these factors might change in the future, subsequent epidemic waves may occur. Precise projection of long-term ZIKV transmission is crucial to plan for future Zika control activities and for finding sites for phase-III Zika vaccine trials. This is a topic for future research.

Another prominent feature emerging from the numerical results is the extreme heterogeneity in the infection ARs across countries. We find more than a sevenfold difference between Honduras and Mexico, exhibiting infection ARs of $35\%$ (95% CI [30 to 39%]) and $5\%$ (95% CI [4 to 6%]), respectively. These large differences in infection ARs, which are also observable at finer geographical resolutions, stem from variation in climatic factors, mosquito densities, and socioeconomic factors.

We project the numbers of births from women who were infected with ZIKV during the first trimester of their pregnancy. There is a well-defined time lag between the epidemic curve and this birth curve. Brazil, which likely experienced its first ZIKV epidemic peak in March 2015, had a sharp rise in microcephaly cases in September 2015, consistent with what was observed in the field (40). In Colombia 132 confirmed cases of congenital Zika syndrome had been observed as of March 11, 2017 (56). However, at the same date, $538$ additional cases are under study, thus not yet allowing a risk factor estimate from the model. Note that the projected number of microcephaly cases estimated by the model varies considerably depending on the assumed first-trimester risk, for which only retrospective estimates are available (36, 37). We also note that with as many as 80% of ZIKV infections being asymptomatic (4, 39), most of ZIKV-infected pregnant women giving birth may not have experienced symptoms during pregnancy. Thus, clinicians should be cautious before ruling out ZIKV as the cause of birth defects. The results presented here, however, could be used as a baseline to uncover possible disagreement with the observed data and highlight the need for additional key evidence to enhance our understanding of the link between ZIKV and birth defects (57).

Available data on the ZIKV epidemic suffer from several limitations. Although the disease has likely been spreading in the Americas since late 2013, infection detection and reporting began much later and likely increased after the WHO’s declaration of a PHEIC in February 2016. Case reporting is inconsistent across countries. Furthermore, comparatively few infections are laboratory-confirmed; this presents an additional challenge because symptomatic cases with other etiologies may be misdiagnosed, and asymptomatic infections are almost entirely missed. Once a reliable ZIKV antibody test is available, seroprevalence studies can help determine the full extent of these outbreaks. For external validation, we compare modeling results with data from Brazil, Colombia, and the USA that were not used to calibrate the model. We are able to replicate relative trends, although we estimate significantly higher absolute numbers, suggesting reporting and detection rates ranging from 1% to about 6% depending on the country.

The modeling approach presented here is motivated by the need for a rapid assessment of the ZIKV epidemic, and it contains assumptions and approximations unavoidable due to the sparsity of available data. As a result, transmission is modeled assuming ZIKV behaves similarly to DENV and other mosquito-borne diseases. This includes the use of some expressions for temperature dependence of transmissibility that are modeled on DENV data. Although this assumption is plausible, more data specific to ZIKV are certainly needed. The model has been calibrated by using data from French Polynesia and the observed epidemic peak in Colombia ($\pm$ 1 wk), as reported by Colombia’s National Institute of Health (38); further research is needed to provide ZIKV-specific parameter estimates and more accurate local calibrations. Mosquito presence/absence maps are available from published data but have limitations as detailed in the literature (32, 34, 58). Sexual and other modes of transmission are not incorporated in the model. The sexual component of the transmission, however, might acquire relevance in areas where the mosquito-borne transmission has a small reproductive number and low incidence (9–12, 59). The specific socioeconomic features of airline travelers are also not included. Finally, we do not model public health interventions to control the vector population or behavioral changes due to increased awareness. These results may change as more information becomes available from ZIKV-affected regions to refine the calibration of the model.

Conclusions

The model presented here provides a methodological framework for the analysis of the global spread of ZIKV. The model captures the slow dynamic of the epidemic characterized by heterogeneity in the infection AR as well as the temporal pattern resulting from local weather, population-level characteristics, and human mobility:

• •The model yields a probability distribution for the time and place of introduction of ZIKV in Brazil, generating a comprehensive picture of the past dynamics of the epidemic.
• •The numerical simulations allow estimates of the spatiotemporal spread of ZIKV in the Americas through February 2017. In particular, it provides estimates for the infection ARs and epidemic timing in ZIKV affected countries.
• •The integration of airline travel data allows the explicit estimation of the number of travel-related cases into the USA and other countries.
• •The model allows estimation of the number of newborns from women infected by ZIKV during the first trimester of pregnancy and the potential number of microcephaly cases through 2017 assuming different levels of risk. These projections could be checked against observed data in the future.

Although the modeling results should be interpreted cautiously in light of the assumptions and limitations inherent to the approach, the framework emerging from the numerical results may help in the interpretation of observed surveillance data and provide indications for the magnitude and timing of the epidemic, as well as aid in planning for international and local outbreak response, and for the planning of phase-III ZIKV vaccine trial sites. The study presented here also provides a computational modeling framework that can potentially be generalized to other Aedes-transmitted vector-borne diseases, such as dengue and chikungunya.

Materials and Methods

Model Summary.

To study spatiotemporal ZIKV spread, we use the Global Epidemic and Mobility Model (GLEAM), a previously described individual-based, stochastic, and spatial epidemic model (60–65). This model integrates high-resolution demographic, human mobility, socioeconomic (gecon.yale.edu), and temperature data (climate.geog.udel.edu/∼climate/html_pages/Global2011/GlobalTsT2011.html); because no human subject research/analysis was performed, IRB approval was not required. Here we expanded to incorporate data on Aedes mosquito density (58) and the association between socioeconomic factors and population risk of exposure (32, 66). Similar to previous arbovirus modeling approaches (18), we use a compartmental classification of the disease stages in the human and mosquito populations, assigning plausible parameter ranges based on the available ZIKV literature and assumed similarities between ZIKV and DENV.

Global Model for the Spread of Vector-Borne Diseases.

The GLEAM model is a fully stochastic epidemic modeling platform that uses real-world data to perform in silico simulations of the spatial spread of infectious diseases at the global level. GLEAM uses population information obtained from the high-resolution population database of the Gridded Population of the World project from the Socioeconomic Data and Application Center at Columbia University (sedac.ciesin.columbia.edu). The model considers geographical cells of $0.25°\times 0.25°$, corresponding to an approximately $25-\text{km}\times 25-$km square for cells along Earth’s equator. GLEAM groups cells into subpopulations defined by a Voronoi-like tessellation of the Earth’s surface centered around major transportation hubs in different urban areas. The model includes over 3,200 subpopulations in roughly $230$ different countries (numbers vary by year).

Within each subpopulation, a compartmental model is used to simulate the disease of interest. The model uses an individual dynamic where discrete, stochastic transitions are mathematically defined by chain binomial and multinomial processes. Subpopulations interact through the mechanistically simulated mobility and commuting patterns of disease carriers. Mobility includes global air travel (www.oag.com), and GLEAM simulates the number of passengers traveling daily worldwide using available data on origin–destination flows among indexed subpopulations.

The transmissibility of vector-borne diseases is associated with strong spatial heterogeneity, driven by variability and seasonality in vector abundance, the temperature dependence modulating the vector competence, and the characteristics of the exposed populations. Many locations, such as those at high elevation, are not at risk for autochthonous ZIKV transmission simply because the vector is absent. In other locations the vector may be present but sustained transmission is not possible because of environmental factors that affect the vector’s population dynamics, such as temperature or precipitation. Housing conditions, availability of air conditioning, and socioeconomic factors also contribute significantly to determining the fraction of the population likely exposed to the vector. To extend the GLEAM model to simulate vector-borne diseases, a number of new datasets with high spatial resolution are integrated, including the following:

• •Global terrestrial air temperature data: The global air temperature dataset (climate.geog.udel.edu/∼climate/html_pages/Global2011/GlobalTsT2011.html) contains monthly mean temperatures at a spatial resolution of $0.5°\times 0.5°$. To match the spatial resolution of GLEAM’s gridded population density map, the temperature for each population cell is extracted from the nearest available point in the temperature dataset. Daily average temperatures are linearly interpolated from each population’s monthly averages.
• •Global A. aegypti and A. albopictus distribution: The global A. aegypti and A. albopictus distribution database provides uncertainty estimates for the vector’s distribution at a spatial resolution of $5\text{km}\times 5$ km (58).
• •Geolocalized economic data: The geophysically scaled economic dataset (G-Econ), developed by Nordhaus et al. (67), maps the per capita Gross Domestic Product [GDP, computed at purchasing power parity (PPP) exchange rates] at a $1°\times 1°$ resolution. To estimate the per capita gross cell product at PPP rates, the amount is distributed across GLEAM cells proportionally to each cell’s population size. The data have also been rescaled to reflect 2015 GDP per capita (PPP) estimates.

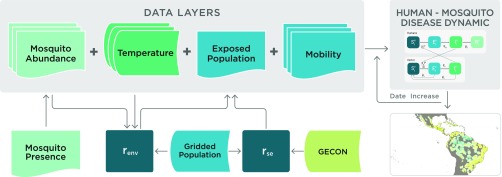
These databases are combined to model the key drivers of ZIKV transmission, as illustrated in combination with necessary parameters in Fig. 6. Temperature affects many important disease parameters, including the time- and cell-specific values of $R_0$, whose variation induces seasonality and spatial heterogeneity in the model. Temperature data are also used together with the mosquito presence distribution data to define the daily mosquito abundance (number of mosquitoes per human) in each cell, as detailed in SI Appendix, section 2. Data on mosquito abundance and temperature are used to identify cells where ZIKV outbreaks are not possible because of environmental factors. The human populations in these cells are thus considered unexposed to ZIKV and susceptible individuals are assigned an environmental rescaling factor, $r_{\mathrm{en}}$, as described SI Appendix, section 3. Finally, we use historical data and G-Econ to provide a socioeconomic rescaling factor, $r_{\mathrm{se}}$, reflecting how exposure to the vector is impacted by socioeconomic variables such as availability of air conditioning. The derivation of these rescaling factors is provided in SI Appendix, section 3.

Fig. 6.

Schematic representation of the integration of data layers and the computational flow chart defining the GLEAM model for ZIKV.

Once the data layers and parameters have been defined, the model runs using discrete time steps of one full day to simulate the transmission dynamic model (described in detail below), incorporating human mobility between subpopulations, and partially aggregating the results at the desired level of geographic resolution. The model is fully stochastic and from any nominally identical initialization (initial conditions and disease model) generates an ensemble of possible epidemics, as described by newly generated infections, time of arrival of the infection in each subpopulation, and the number of traveling carriers. The Latin square sampling of the initial introduction of ZIKV in Latin America and the ensuing statistical analysis is performed on 150,000 stochastic epidemic realizations. From those realizations we find the probability $p(x)$ and $p(x|\theta )$, defined as the probability of the evidence (the epidemic peak in Colombia as from surveillance data) and the likelihood of the evidence given the parameters $\theta$ specifying the date and location of introduction of ZIKV in Brazil. From those distributions we can calculate the posterior probabilities of interest. The sensitivity analysis for the others scenarios considers an additional 200,000 simulations in total.

ZIKV Transmission Dynamics.

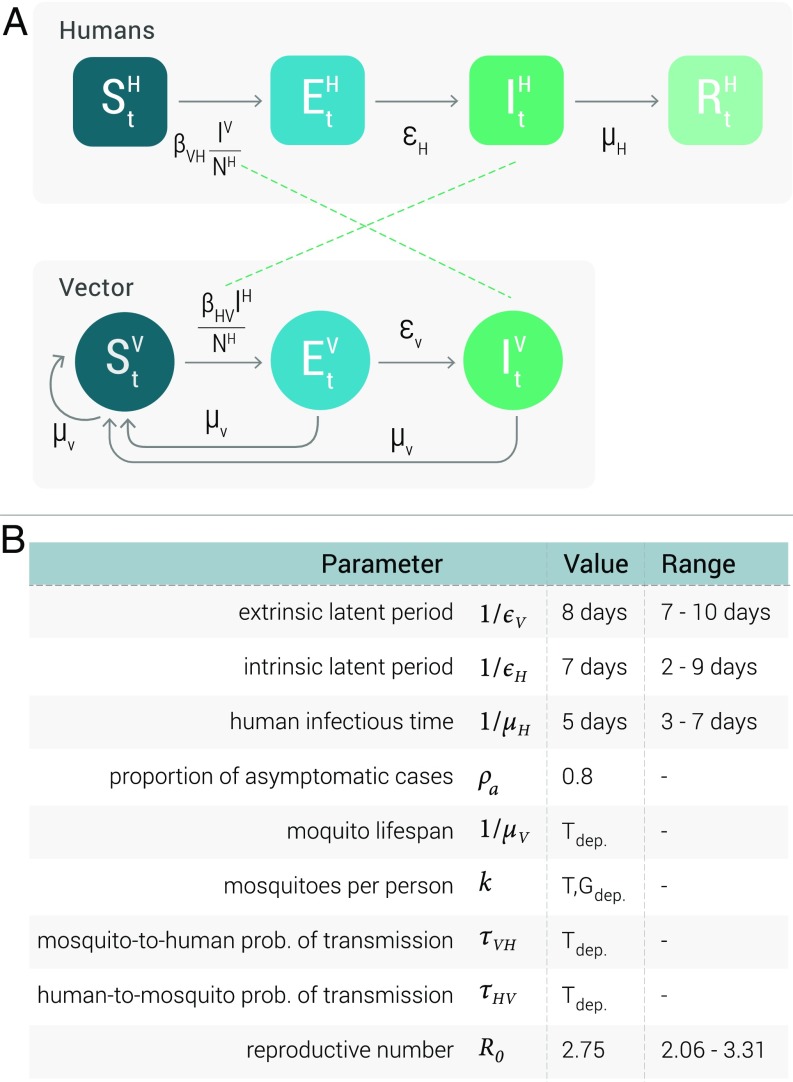
Fig. 7A describes the compartmental classifications used to simulate ZIKV transmission dynamics. Humans can occupy one of four compartments: susceptible individuals $S^H$ who lack immunity against the infection, exposed individuals $E^H$ who have acquired the infection but are not yet infectious, infected individuals $I^H$ who can transmit the infection (and may or may not display symptoms), and removed individuals $R^H$ who no longer have the infection and are immune to further ZIKV infection. We consider the human population size to be constant, that is, $S^H+E^H+I^H+R^H=N^H$. The mosquito vector population is described by the number of susceptible $S^V$, exposed $E^V$, and infectious mosquitoes $I^V$. The transmission model is fully stochastic. Transitions across compartments, the human-to-mosquito force of infection, and the mosquito-to-human force of infection are described by parameters that take into account the specific abundance of mosquitoes and temperature dependence at the cell level. Exposed individuals become infectious at a rate ${ϵ}_H$, which is inversely proportional to the mean intrinsic latent period of the infection (68). These infectious individuals then recover from the disease at a rate ${\mu }_H$ (18), which is inversely proportional to the mean infectious period. The mosquito-to-human force of infection follows the usual mass-action law and is the product of the number of mosquitoes per person, the daily mosquito biting rate, and specific ZIKV infection transmissibility per day, the mosquito-to-human probability of transmission (69), and the number $I^V$ of infected mosquitoes. Exposed mosquitoes transition to the infectious class at a rate ${ϵ}_V$, which is inversely proportional to the mean extrinsic latent period in the mosquito population (2). Susceptible, exposed, and infectious mosquitoes all die at a rate that is inversely proportional to the mosquito lifespan, ${\mu }_V$ (70). The mosquito-to-human force of infection follows the usual mass-action law in each subpopulation whose linear extension varies from a few miles to about 50 miles depending on the population density and specific area of the world. A full description of the stochastic model and the equations is provided in SI Appendix.

Fig. 7.

(A) Compartmental classification for ZIKV infection. Humans can occupy one of the four top compartments: susceptible, which can acquire the infection through contacts (bites) with infectious mosquitoes; exposed, where individuals are infected but are not able yet to transmit the virus; infectious, where individuals are infected and can transmit the disease to susceptible mosquitoes; and recovered or removed, where individuals are no longer infectious. The compartmental model for the mosquito vector is shown below. (B) Summary of the parameters of the model. $T_{\mathrm{dep}}$ denotes parameters that are temperature-dependent. $T\mathit{\text{,}}{G}_{\mathrm{dep}}$ denotes parameters that are temperature- and geolocation-dependent. Specific values for the parameters can be found in refs. 2, 4, 18, 55, and 68–70.

A summary of the parameters defining the disease dynamics is reported in Fig. 7B. The empirical evidence related to the ZIKV infection in both human and mosquito populations is fairly limited at the moment. We have performed a review of the current studies of ZIKV and collected plausible ranges for these parameters. As in other studies, we have assumed that the drivers of ZIKV transmission are analogous to those of DENV. In particular, we have considered that mosquito lifespan, mosquito abundance, and the transmission probability per bite depend on the temperature level.

Model Calibration.

The calibration of the disease dynamic model is performed by a Markov chain Monte Carlo analysis of data reported from the 2013 ZIKV epidemic in French Polynesia (18). Setting the extrinsic and intrinsic latent periods and the human infectious period to reference values and using average daily temperatures of French Polynesia, we estimate a basic reproduction number at the temperature $T=25°$C for French Polynesia $R_0^{FP}=$2.75 (95% CI [2.53 to 2.98]), which is consistent with other ZIKV outbreak analyses (18, 31). Because the reproduction number depends on the disease serial interval, we report a sensitivity analysis in SI Appendix considering the upper and lower extremes of plausible serial intervals. Briefly, the estimated $R_0^{FP}$ values are 2.06 (95% CI [1.91 to 2.22]) and 3.31 (95% CI [3.03 to 3.6]) for the shortest and longest serial intervals, respectively. The $R_0$ values are in the range of those estimated from local outbreaks in San Andres Island ($R_0=1.41$) and Girardot, Colombia ($R_0=4.61$) (71); however, it is worth recalling that the reproductive number depends on the location and on time through seasonal temperature changes. The calibration in French Polynesia provides the basic transmissibility of ZIKV. However, variations in temperature and mosquito abundance yield varying $R_0$ in each subpopulation tracked by the model as discussed in SI Appendix.