Stem cell migration and mechanotransduction on linear stiffness gradient hydrogels

Significance

Mechanobiology is receiving an increasing amount of focus, but the mechanics of cell-substrate behavior are often neglected in cell biology. As such, novel materials and systems that are simple to build and share in a nonengineering laboratory are sorely needed. We have fabricated gradient hydrogels with continuous linear gradients above and below the durotactic threshold, making it possible to pinpoint optimal stiffness values for a wide range of biological phenomena without the confounding effects of durotaxis. This system has the potential for wide adoption in the cell biology community because of its ease of fabrication, simple material ingredients, and wide gradient possibilities in a single well.

Abstract

The spatial presentation of mechanical information is a key parameter for cell behavior. We have developed a method of polymerization control in which the differential diffusion distance of unreacted cross-linker and monomer into a prepolymerized hydrogel sink results in a tunable stiffness gradient at the cell–matrix interface. This simple, low-cost, robust method was used to produce polyacrylamide hydrogels with stiffness gradients of 0.5, 1.7, 2.9, 4.5, 6.8, and 8.2 kPa/mm, spanning the in vivo physiological and pathological mechanical landscape. Importantly, three of these gradients were found to be nondurotactic for human adipose-derived stem cells (hASCs), allowing the presentation of a continuous range of stiffnesses in a single well without the confounding effect of differential cell migration. Using these nondurotactic gradient gels, stiffness-dependent hASC morphology, migration, and differentiation were studied. Finally, the mechanosensitive proteins YAP, Lamin A/C, Lamin B, MRTF-A, and MRTF-B were analyzed on these gradients, providing higher-resolution data on stiffness-dependent expression and localization.

Stem cells receive a myriad of chemical and mechanical cues from their environment and must integrate those signals to commit to a specific lineage. Although the ability of chemical signals (soluble and/or substrate-immobilized) to dictate stem cell behavior in the microenvironment has been appreciated for decades, only recently has significant research focus shed light on the mechanical forces that shape organismal development and direct disease response (1–3). Chemical gradients impacting stem cell migration, proliferation, and differentiation are well-described, and methods permitting their wide-scale use now allow efficient investigation of the effects they elicit (4–6).

Mechanotransduction is arguably more intuitive, as the functional boundaries at multiple length scales in living systems attest. Physiological interfaces, such as those at neuromuscular junctions, and pathological boundaries, e.g., infarcted fibrous heart tissue adjacent to healthy myocardium, are prevalent in vivo and imply that mechanical cues not only help guide differentiation but play critical regulatory roles in disease response. Recent studies have identified substrate stiffness as a significant factor in cell spreading (7, 8), migration (9), proliferation (10), and differentiation (11, 12) using both adipose-derived (13) and bone marrow-derived stem cells (14). When mimicking the stiffness of neural (∼1 kPa), muscle (∼12 kPa), and bone (∼30 kPa) tissues (15, 16), substrate stiffness can induce differentiation toward those specific tissue types. Furthermore, stem cells will migrate toward regions of higher stiffness in a process known as “durotaxis” (17–19), whereas neurons have shown preference for softer regions (20, 21). Additionally, some cancer cell lines are inversely sensitive to substrate stiffness and thus show markedly different migration phenotypes (22–24). Given these complex and differential responses, it is apparent that any thorough in vitro investigation of stem cell behavior must consider both the absolute substrate stiffness value and the underlying stiffness gradient strength.

To create stiffness gradients in vitro, a multitude of diverse methods have been proposed, including repeated freeze–thaw methods with liquid nitrogen and cylindrical polyvinyl alcohol columns (25), heat gradients within polymerizing polydimethylsiloxane (PDMS) (10), polyelectrolyte monolayers with a patterned cross-linker (26), inclusion of rigid particles in a soft hydrogel (27), and microfluidic mixing of different polyacrylamide (PA) solutions. However, all require significant technical background or equipment or are exceedingly expensive. Other less complex methods use photoinitiators and a patterned (28–30) or moving (31–33) photomask overlying a polymerization chamber to create stiffness gradients, although they are limited by the penetration depth of the light source, nonhomogeneous diffusion of photons, and residual toxicity of initiators left within the polymerized gel. Indeed, studies performed with gradient photomasks for UV photopolymerization have shown poor reproducibility and gradient linearity (19). Recent work has demonstrated the ability to build stiffness gradients in PA based on diffusion-driven gradients, although these methods require photolithography and microfluidics (34). Thus, although simple methods exist to produce chemical gradients (4–6), protocols to create simple (i.e., not requiring a clean room or photolithography facility) and highly reproducible [i.e., not relying on photopolymerization or PDMS interfaces] linear mechanical gradients spanning all biologically relevant ranges remain elusive (Table S1) (15, 35). Our aim is to develop a simple, nontoxic, cost-effective, and highly reproducible culture surface that puts stiffness gradient control into the hands of cell biology researchers who may not otherwise have access to more complex methods. To do so, we have investigated the stiffness-sensitive expression of the known mechano-regulator YAP (Yes-associated protein), the nuclear “mechanostat” Lamin A and its less stiffness-sensitive counterpart Lamin B, and the transcription factors MRTF-A and MRTF-B to a higher stiffness resolution than previously attained, revealing heretofore unobserved “transition zones” between basal and saturated levels of mechanosensitive proteins.

Table S1.

Comparison of current gradient hydrogel systems

Refs.	Gradient (surface area in cm2)	Cells per experiment*	Gradient strength, kPa/mm	Gradient range, kPa	Cells per kPa*	Photopolymerization	Photolithography	PDMS interface	Microfluidics
This study	4.8 (2.4 × 2.0)	24,000	0.5	01.-6.6	∼3,700
			2.9	2.4–38.1	∼670
			8.2	3.2–159.2	∼150
Isenberg et al., 2009 (36)	0.54 (3 × 0.18)	2,700	10	29.6–51.6	∼125	×	×	×	×
			20	0.93–41.7	∼65
			40	4.64–80.1	∼35
Hartman et al., 2016 (34)	0.1 (0.5 × 0.2)†	500	2.9	0.5–10	∼50	×	×	×
			10	0.5–20	∼25
			71.7	7–170	∼3
Chao et al., 2014 (37)	0.1 (0.1 × 1)	500	1.2	0.4–1.6	∼415			×
			17.4	4.5–20	∼30
Vincent et al., 2013 (19)	2.5 (2.5 × 1)	12,500	0.38	1.5–5.5	∼3,125	×
			2.4	2–20	∼700
			4.33	2.5–27.5	∼500
Wong et al., 2003 (30)	2.54 (18 mm ø)	12,700	∼0.94	2.5–11	∼1,500	×
Choi et al., 2012 (17)	0.025‡ (0.01 × 2.5)	125‡	275	2–14	∼10		×

^*Cells per experiment and per kilopascal are calculated at a standard density of 5,000 cells/cm².

^†Hydrogel width not given in publication, estimated at 5 mm.

^‡Value given for one ‘stripe’; each gel contained up to 200 stripes.

Results and Discussion

Stiffness Gradient Hydrogel Fabrication: A Two-Step Polymerization Process.

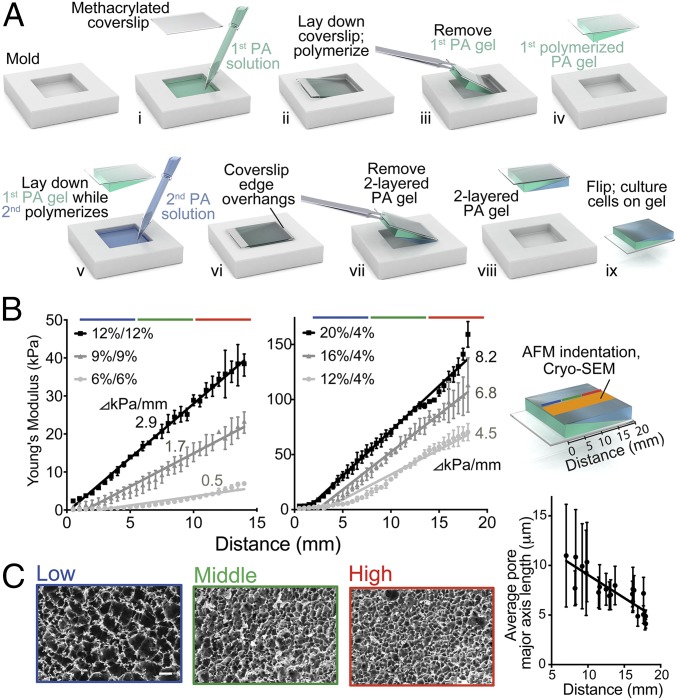
Previous methods of reproducing in vivo stiffness gradients in culture systems are either complex (19, 30, 34, 36, 37) or lack the stiffness or gradient range (9, 30, 32) to interrogate the physiological mechanical landscape fully (Table S1). Therefore, we developed a method to fabricate planar PA hydrogels with linear stiffness gradients capable of spanning both biologically relevant ranges and disease conditions. Briefly, 24 × 20 × 1 mm glass molds were constructed from glass slides, coverslips, and cyanoacrylate. Aliquots (250 µL) consisting of a defined acrylamide monomer concentration (4, 6, 9, 12, or 15%) and 0.4% N, N methylene-bis-acrylamide cross-linker (Fig. 1 A, i) were poured into a dichlorodimethylsilane (DCDMS)-treated glass mold and covered with a 3-(trimethoxysilyl)-propyl methacrylate (3-TMPM)–treated glass coverslip so that the polymerization chamber assumed the shape of a right-angled ramp with a 3° angle in the vertical plane (Fig. 1 A, ii). The functionalized coverslip reacts with the PA solution and subsequently serves as a support for manipulating the hydrogel. After polymerization and removal from the mold (Fig. 1 A, iii and iv), a second 280-µL aliquot of acrylamide (6, 9, 12, 15, 16, or 20%) was poured into the mold and covered with the first PA gel (Fig. 1 A, v) so that the coverslip edge overhangs (Fig. 1 A, vi). After polymerization of the second component, the compound structure was removed from the mold (Fig. 1 A, vii and viii), yielding a 24- × 20- × 1-mm PA hydrogel composed of two sequentially polymerized, inversely oriented, ramp-shaped components. Ultimately, this system requires only acrylamide/bis-acrylamide solution, DCDMS, 3-TMPM, glass slides and coverslips, and cyanoacrylate glue (as few as five common laboratory chemicals and supplies) for the fast formation of gradient hydrogels suitable for cell biology studies. Furthermore, because of the large, consistent surface area presented to the cells, this system can assay higher numbers of cells per gel than any other stiffness-gradient tool available (Table S1).

Fig. 1.

Fabrication and characterization of stiffness gradient PA hydrogels. (A) A 24- × 20-mm rectangular mold is used to fabricate hydrogels in a double polymerization process creating a two-layered PA hydrogel. (B) AFM was used to probe the surface Young’s modulus, E, for hydrogels composed of 12/12% = 2.9 kPa/mm (R² = 0.9965) (black squares); 9/9% = 1.7 kPa/mm (R² = 0.9764) (dark gray triangles); or 6/6% = 0.5 kPa/mm (R² = 0.9041) (light gray circles) (Left) or 20/4% = 8.2 kPa/mm (R² = 0.9783) (black squares); 16/4% = 6.8 kPa/mm (R² = 0.9532) (dark gray triangles); or 12/4% = 4.5 kPa/mm (R² = 0.9415) (light gray circles) (Right). (C, Left) Cryo-SEM images of a 12/12% PA hydrogel surface at low (blue), middle (green), and high (red) stiffness ranges. (Scale bar: 25 µm.) (Right) The corresponding graph shows pore size is inversely proportional to stiffness where the slope = −0.4676 µm/mm (R² = 0.7312).

Topographical and Mechanical Characterization.

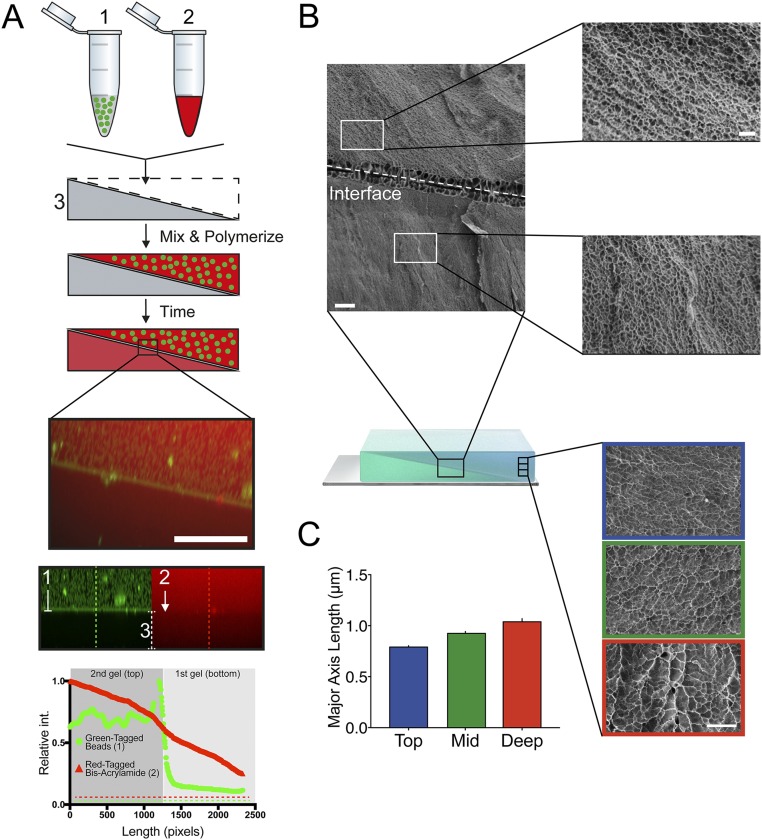
Varying the concentration of acrylamide monomer can substantially alter the stiffness of a planar PA surface (38). We therefore postulated that an interface with a uniform slope between two sequentially polymerized components of a compound PA hydrogel would result in depletion of monomer and cross-linker from the second component at a rate proportional to the relative thicknesses and acrylamide/bis-acrylamide concentrations of those two components (Fig. S1A). To test this hypothesis, we added Texas red-labeled bis-acrylamide cross-linker and 100-nm green fluorescent beads to the second PA-forming solution. Fig. S1A demonstrates that bis-acrylamide leaches readily from the second PA-forming solution into the first PA hydrogel, but large objects (i.e., the green microbeads) do not. This result supports the idea that unpolymerized components are absorbed by the already-polymerized component, which is unsurprising given that solute diffusion through hydrogels, which has been shown to be slower than through water (39), is a feature in many drug-delivery applications (40). Furthermore, because the first component is sloped, an inherent acrylamide gradient dynamically forms within the top gel as polymerization progresses. The formation of this gradient is enhanced by the fact that as the hydrogel polymerizes, acrylamide chains lengthen and become incorporated into the cross-linked network, decreasing their diffusion coefficient and preserving the concentration gradient formed by fast diffusion into the first component. This gradient was confirmed with cryo-scanning electron microscopy (cryo-SEM) of 12/12% (vol/vol) PA hydrogels (second polymerized PA hydrogel/first polymerized PA hydrogel) at 1,000× and 5,000× magnification. Images show that the average pore size is larger in the second (top) hydrogel component although both solutions contain the same initial acrylamide:bis-acrylamide ratio (Fig. S1B). Although other systems have used polymerized PA above prepolymerized PA (17), those systems had very small diffusion distances from the surface of the gel to the underlying prepolymerized gel (∼25 μm), allowing (i) an equilibrium concentration to form before polymerization occurs and (ii) the mechanical properties of the underlying stiffness layer to influence those of the upper layer.

Fig. S1.

Observing differential polymerization in hydrogel layers. (A) Schematic showing 100-nm green fluorescent beads (1), red fluorescent-tagged bis-acrylamide mixed with acrylamide (2), and the first polymerized PA hydrogel (3). The green fluorescent beads and the red fluorescent-tagged bis-acrylamide are mixed and polymerized on top of first polymerized PA hydrogel. Monomer/cross-linker depletion from the second (top) PA gel into the first polymerized PA hydrogel occurs, resulting in an observed red color throughout both layers, but the green fluorescent beads are too large to cross the interface. (Scale bar: 20 µm.) In channel-separated images below, green fluorescent beads can be seen in the second/top polymerized PA hydrogel, hindered from entering the first/bottom gel, whereas the red-tagged bis-acrylamide can be seen throughout both gels. Fluorescence intensity across lines perpendicular to the interface (dashed lines show examples) is quantified in the graph below. (B) Cryo-SEM images of the interface in a 12/12% PA hydrogel depicting differences in pore size between the top and the bottom PA hydrogels. (Scale bars: 10 µm, Left; 2 µm, Right.) (C) Cryo-SEM images of the cross-section in the second polymerized hydrogel near the top (blue), in the middle (green), and deep (red). (Scale bar: 5 µm.) The mean length of the major axis (in micrometers, ± SEM) is quantified in the graph. int, intensity.

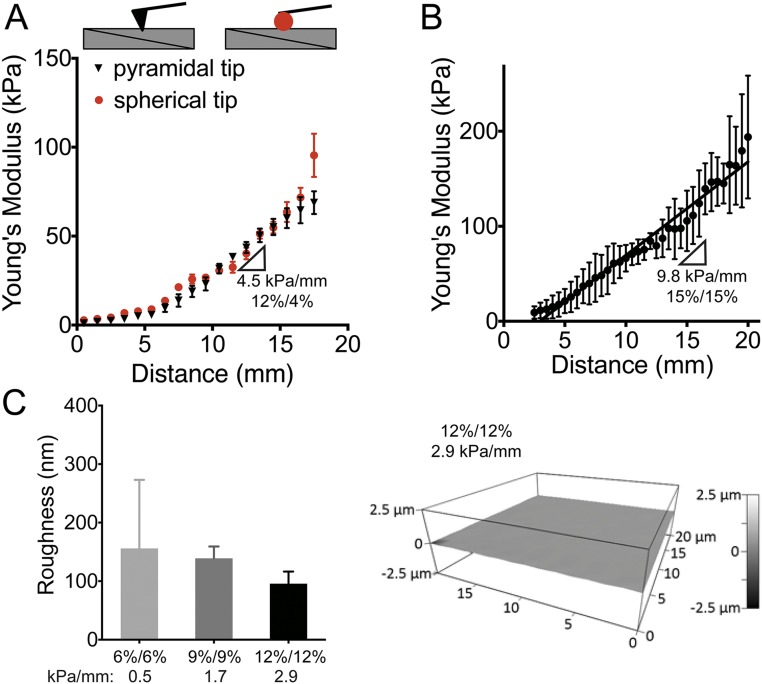
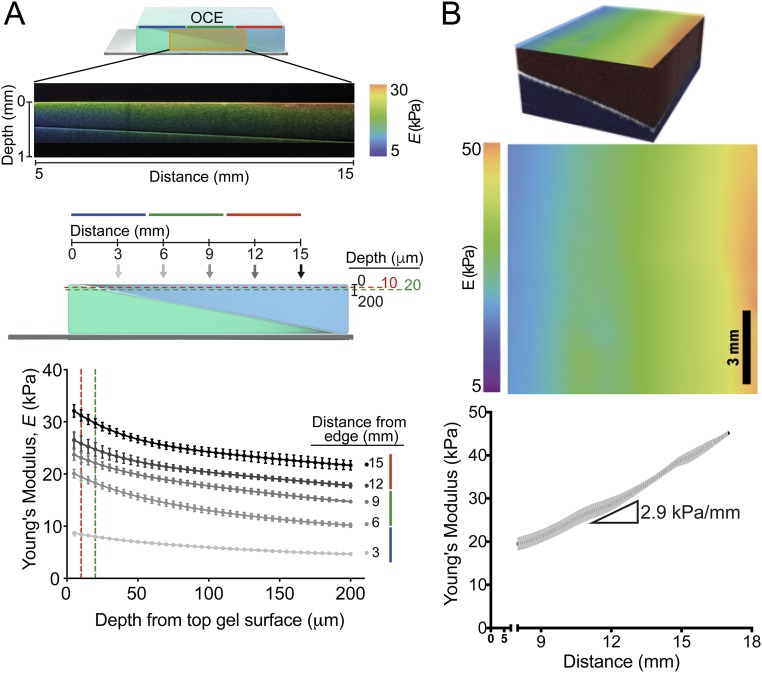
Because the thinnest areas of the second hydrogel component suffer the greatest proportional loss of monomer/cross-linker, a stiffness gradient subsequently results. To examine this gradient, we measured the Young’s modulus of these hydrogels parallel to the ramp axis with atomic force microscopy (AFM) (41). For 20/4, 16/4, 12/4, 12/12, 9/9, and 6/6% (top gel/bottom gel, vol/vol) acrylamide solutions in which bis-acrylamide was held constant at 0.4%, linear stiffness gradients of 8.2, 6.8, 4.5, 2.9, 1.7, and 0.5 kPa/mm were observed, respectively (Fig. 1B and Table S2). Mechanical probing was repeated with a larger AFM tip to assess whether stiffness varied appreciably with probe area. Fig. S2A shows that differences in the stiffness data obtained by different AFM tip geometries are insignificant. We also used compression optical coherence elastography (OCE) (42) to characterize further any potential stiffness gradient in the z axis (depth), because previous studies have suggested that cells are able to feel up to 10–20 µm below the substrate surface (43, 44) when plated on very soft (∼1 kPa) hydrogels. We found a maximal softening of 3.3% at a depth of 10 µm and 9.0% at a depth of 20 µm for the stiffest regions of the gradient hydrogels (Fig. S3A and Table S3). On the softest region of ∼10 kPa, a depth of 20 μm shows a softening of less than 1 kPa. Although measurable, these differences are likely inconsequential for mechanosensitive responses (e.g., both 9 and 10 kPa are myogenic). This progressive softening in the z axis also correlates to cryo-SEM images taken of hydrogel cross-sections (Fig. S1C), which show increasing pore size with increasing distance from the culture surface.

Table S2.

Tabulated summary of PA gel concentrations and corresponding measured stiffness and gradient strength values (Fig. 1B)

Gel, %	Top (second gel)		Bottom (first gel)		Range, kPa	Slope, kPa/mm
	Acryl, %	Bis-acryl, %	Acryl, %	Bis-acryl, %
20/4	20	0.4	4	0.4	3.2–159.2	8.2
16/4	16	0.4	4	0.4	1.3–113.2	6.8
12/4	12	0.4	4	0.4	1.1–70.4	4.5
12/12	12	0.4	12	0.4	2.4–38.1	2.9
9/9	9	0.4	9	0.4	0.9–23.0	1.7
6/6	6	0.4	6	0.4	0.1–6.6	0.5

Fig. S2.

Further characterization of gradient stiffness hydrogels by AFM. (A) Surface elastic moduli (in kilopascals) of a 12/4% hydrogel measured with AFM using pyramidal (black triangles) and spherical (red circles) tips over the length of the gel. (B) Surface elastic moduli measured with AFM for a 15/15% hydrogel. Stiffness gradient = 9.8 kPa/mm (R² = 0.8244). Data are shown as mean ± SD (n = 3). (C) Surface roughness (in nanometers) measured with AFM on 6/6%, 9/9%, and 12/12% PA hydrogels (P = 0.2840). The representative image is from a 12/12% PA hydrogel. All data are shown as mean ± SD (n = 3).

Fig. S3.

OCE characterization of the stiffness gradient PA hydrogel. (A, Top) Cross-sectional OCE image expressed as heat map of the stiffness distribution of 12/12% stiffness gradient PA hydrogel showing graded stiffness vs. depth where orange indicates stiffest and violet indicates softest. (Middle) Schematic showing OCE-collected data at 3, 6, 9, 12, and 15 mm from the coverslip edge through a depth of 200 µm into the gel. The10-µm (red) and 20-µm (green) depths are marked with dashed lines (Bottom). Data from the schematic graphed as the Young’s modulus (measured in kilopascals) vs. the depth from surface of the top gel (in micrometers) for distances of 3 (light gray) through 15 mm (black) from the edge of the gel. Data are shown as mean ± SEM. (B, Upper) 3D OCT image (faux color illustrating gel layer) and surface heat map of a 12/12% PA hydrogel showing graded stiffness changes; orange indicates stiffest, and violet indicates softest. (Lower) Graphical representation of Young’s modulus using OCE confirming a stiffness change of 2.9 kPa/mm (R² = 0.9939) as shown in Fig. 2A. Data are shown as mean ± SEM (n = 3).

Table S3.

Tabulated summary of stiffness changes in depth by OCE (Fig. S3A)

	3 mm		6 mm		9 mm		12 mm		15 mm
Depth, μm	E, kPa	%, to 5 μm	E, kPa	%, to 5 μm	E, kPa	%, to 5 μm	E, kPa	%, to 5 μm	E, kPa	%, to 5 μm
5	8.68	100	20.09	100	23.70	100	26.48	100	32.09	100
10	8.44	97.1	19.43	96.7	23.12	97.5	25.84	97.6	31.22	97.3
15	8.21	94.5	18.83	93.7	22.58	95.3	25.25	95.4	30.43	94.8
20	8.00	92.1	18.27	91.0	22.09	93.2	24.72	93.3	29.72	92.6

All data (shown as mean ± SEM) are summarized in the table for a depth of 5–20 µm.

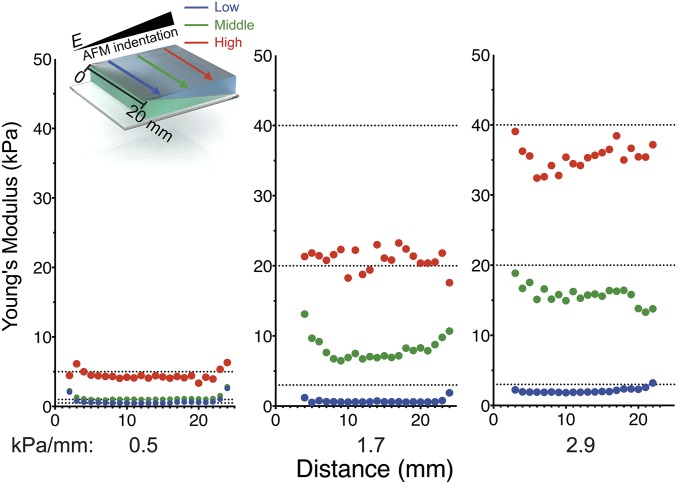
The highest stiffness gradients measured here are mimetic of pathological stiffness gradients in vivo (i.e., myocardial infarction, ∼7 kPa/mm) (45). Furthermore, one of the gradients (2.9 kPa/mm) spans several physiologically relevant ranges from adipose (∼2 kPa) to osteoid tissue (∼35 kPa) (1). As acrylamide concentration increases, e.g., 15/15% (vol/vol) acrylamide, the steepest gradients are achieved (9.8 kPa/mm), but limited monomer depletion from the second layer can compromise reproducibility (see larger error bars in Fig. S2B). For hydrogels with lower absolute acrylamide concentrations (i.e., 6/6%: 0.5 kPa/mm; 9/9%: 1.7 kPa/mm; and 12/12%: 2.9 kPa/mm), we found homogenous stiffness values perpendicular to the ramp axis, ensuring homogeneous polymerization along stiffness lines (Fig. S4).

Fig. S4.

Characterization of uniformity perpendicular to the gradient by AFM. Young’s moduli measured with AFM in multiple planes perpendicular to the stiffness gradient axis on hydrogels of indicated stiffness strengths (0.5, 1.7, and 2.9 kPa/mm). Blue, low-stiffness; green, mid-stiffness; red, high-stiffness ranges of each PA hydrogel.

To confirm Young’s moduli gradients independently in high resolution, we used OCE (42) to capture 3D images with experimentally measured axial and lateral resolutions of 7.8 and 11 µm, respectively, up to 2–3 mm into the hydrogels (Fig. S3B). 3D reconstruction of a 12/12% (2.9 kPa/mm) PA hydrogel visualizes the stiffness gradient at the surface (Fig. S3B) as well as the ramp-angle interface between the first and second layers (Fig. S3B, Top, white line). The 5% compression required for OCE imaging resulted in a slight absolute change in reported moduli, whereas the slope of the gradient was unchanged at 2.9 kPa/mm (Fig. S3B).

The mechanism creating this stiffness gradient also suggests an accompanying pore-size gradient along the hydrogel surface, because higher degrees of crosslinking would result in smaller pore sizes in stiffer regions (38). Cryo-SEM images at 500× magnification taken at the low, middle, and high stiffness ranges on the surface of 2.9 kPa/mm PA hydrogels confirm a pore size gradient from largest (11 ± 5.2 µm) to smallest (4.1 ± 0.4 µm) from the soft to stiff ends, respectively (Fig. 1C). Stiffness-dependent behavior does not depend on pore size (38), but surface topography is known to influence cell migration (46). To exclude pore size as an influence on surface topography, 20- × 20-µm surface AFM scans corresponding to low, middle, and high stiffness ranges were generated. We found insignificant variation in surface topography between hydrogel formulations, thus excluding roughness as an influence on observed cellular behavior (Fig. S2C).

Cell-Adhesive Protein Functionalization of Gradient Hydrogels.

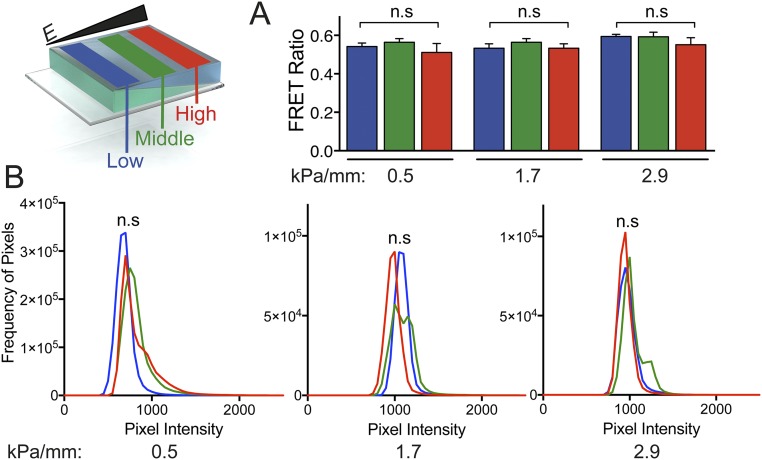
PA hydrogels do not contain cell-adhesive domains and thus require a covalently attached protein coat such as fibronectin or collagen (8). Previous studies have confirmed that the overall amount of protein that can bind to differentially cross-linked PA does not change as stiffness increases (36). However, concerns have been raised regarding the degree of protein tethering as a function of pore size (47), which we have shown varies across the gradient surface. To ensure that any subsequent observed differences in interaction between cells and PA hydrogels is not a result of differential levels of protein tethering, Förster resonance energy transfer (FRET) (38) was used to measure the degree of fibronectin unfolding across the gradient. ECM proteins are exposed to traction force before any subsequent ECM deformation; thus this FRET sensor is not a metric of overall traction force, which is stiffness-dependent (48, 49), but rather is a confirmation that the ECM protein itself does not experience any differential unfolding as the result of potential changes in protein–hydrogel tethering. The unfolding of the protein layer was measured as a function of the ratio of the maximum intensities of the second fluorophore (acceptor) to those of the first fluorophore (donor). FRET ratios for PA gradient hydrogels (0.5, 1.7, and 2.9 kPa/mm) in each stiffness condition (low, middle, and high) showed no significant differences (Fig. S5A). To characterize the adhesive protein layer further using a different ECM protein, collagen-coated PA hydrogels were immunostained, and pixel-intensity histograms were computed for PA hydrogels at all stiffness conditions as described in Wen et al. (38). One-way ANOVA was used to compare the area under the curve (AUC) of these histograms within each hydrogel. The 0.5, 1.7, and 2.9 kPa/mm hydrogels showed no significant differences in collagen functionalization across their surfaces (P > 0.05) (Fig. S5B).

Fig. S5.

Characterization of extracellular protein binding to the gradient hydrogels. The schematic shows hydrogel regions examined for low (blue), middle (green), and high (red) stiffness regions. (A) Fibronectin FRET intensity ratios for hASCs on PA hydrogels at low (blue), mid (green), and high (red) stiffness ranges in 0.5-, 1.7-, and 2.9-kPa/mm gradient hydrogels. Data are shown as mean ± SD (n = 3). (B) Pixel-intensity histograms for collagen I coating on 0.5, 1.7, and 2.9 kPa/mm hydrogels showing overlapping fluorescent (anti-collagen staining) signatures for low (blue), mid (green), and high (red) stiffness ranges within each hydrogel. AUCs were compared using one-way ANOVA with n = 3. n.s, not significant.

Cell Migration and Durotaxis.

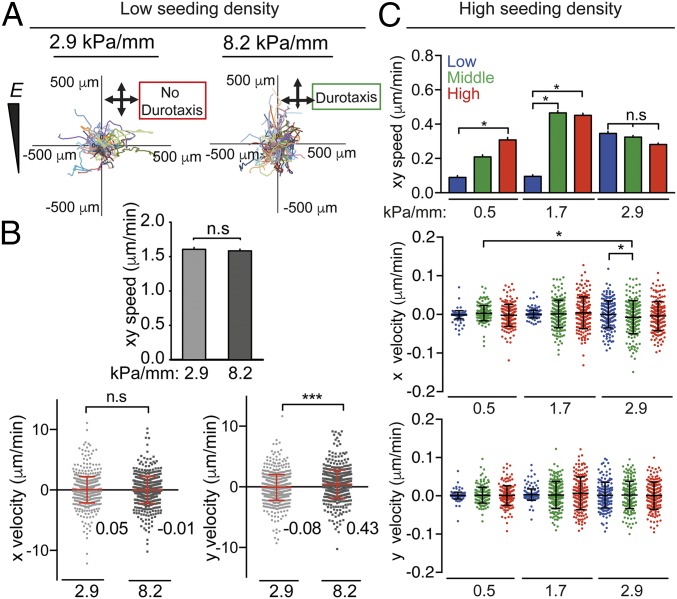
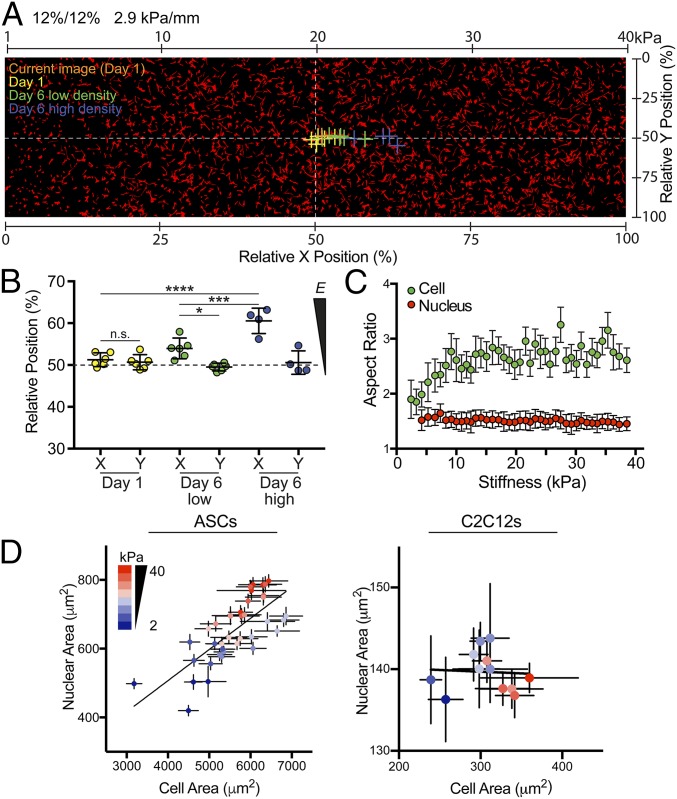
To investigate cell migration on fibronectin-coated stiffness gradients, we used time-lapse microscopy to observe human adipose-derived stem cells (hASCs) (Fig. 2, Fig. S6, and Movies S1–S11). Durotaxis, or migration in response to a stiffness gradient, generally causes cells to migrate toward stiffer regions, with cell velocity correlating to gradient strength (19). Therefore we compared the migration of sparsely plated hASCs on a shallow gradient (2.9 kPa/mm) with the migration on a steep, pathology-mimicking gradient (8.2 kPa/mm) by calculating the instantaneous speed and direction of cells from multiple regions over 72 h (Fig. 2A). Average cell speed was similar on both gradients (Fig. 2B); however, when the cell speed was divided into components either perpendicular to or parallel to the gradient direction (x and y, respectively), the steep gradient (8.2 kPa/mm) exhibited significantly higher y velocities, indicating durotaxis toward the stiffer region (Fig. 2 A and B). Because the average y velocity of cells on the 2.9-kPa/mm hydrogel was not significantly different from zero, we can conclude that the gradient did not induce biased migration. These data improve upon the durotactic threshold suggested in previous studies (17, 19) by narrowing the range in which the threshold potentially occurs to above 2.9 kPa/mm and below 8.2 kPa/mm. To rule out the possibility that cell attachment or cell proliferation is biased by the stiffness gradients, the centroid of all measured cells was calculated at low (20,000 cells per hydrogel) and high (50,000 cells per hydrogel) density cell seeding on the 2.9-kPa/mm hydrogels (depicted and quantified in Fig. 3 A and B, respectively). For all samples collected after 1 d, the centroid was not significantly different from 50% in either x or y, indicating that cell attachment was not biased (Fig. 3 A and B). After 6 d on the gradient hydrogels, low-density populations exhibited a slight shift toward the stiffer region (∼4%). In high-density populations, this shift was much higher (∼11%), suggesting that cell density plays a role in stiffness-based proliferation changes (Fig. 3 A and B).

Fig. 2.

Migration of hASCs on stiffness gradient hydrogels. (A) Representative hASC migration plots on 2.9-kPa/mm (Left) and 8.2-kPa/mm (Right) fibronectin-coated PA stiffness gradient hydrogels over 72 h. (B) The xy speed, x velocity, and y velocity (in micrometers per minute) on 2.9- and 8.2-kPa/mm fibronectin-coated PA gels on which the positive y velocity vector is toward the stiffest end of the hydrogel. (C) Average speed (xy) and x and y velocity over 72 h of hASCs on low (blue), middle (green), and high (red) stiffness ranges of 0.5-, 1.7-, and 2.9-kPa/mm gradient hydrogels. Cells were seeded at low density (<20,000 cells per well) for A and B and at high density (>50,000 cells per well) for C. For A and B, all data are shown as mean ± SEM (speed) and mean ± SD (velocity) (>695 cells analyzed). For C, n = 6 (30 cells tracked per n). In stiffness runs along the y axis, more positive = stiffer. Blue = low, green = middle, and red = high stiffness range. For all: *P < 0.05, ***P < 0.001; n.s., not significant.

Fig. S6.

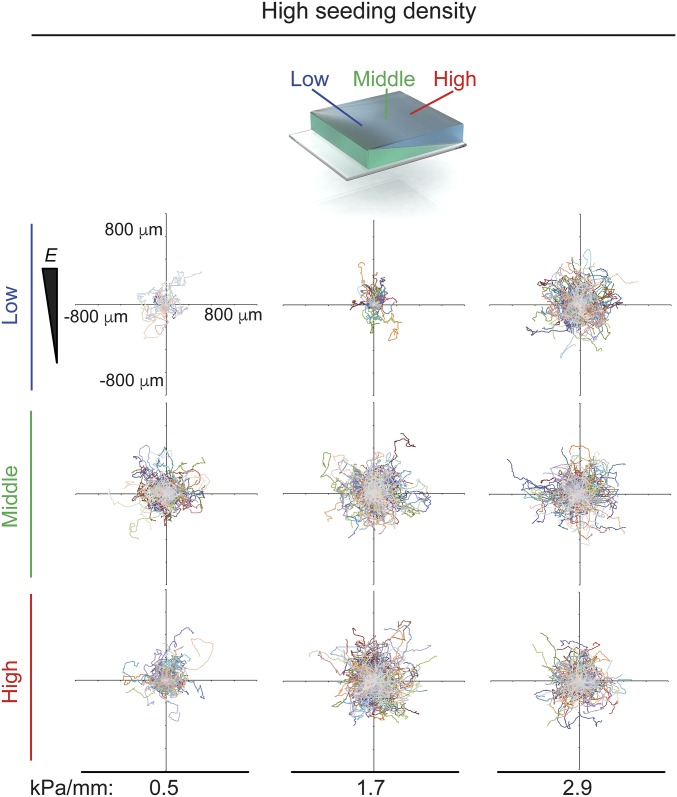
Representative plots of hASC migration over 72 h on low (blue), middle (green) and high (red) stiffness ranges of 0.5-, 1.7-, and 2.9-kPa/mm gradient hydrogels.

Fig. 3.

Centroid and morphological characteristics of hASCs and C2C12s on stiffness gradient hydrogels. (A) Centroids of cell on gradient gels are indicated with a cross for current image at day 1 (orange), day 1 (yellow), day 6 at low density (green), and day 6 at high density (blue). White dashed lines intersect at the center of the image (relative x and y positions of 50%). (B) Relative x and y positions from A are graphed. (C) Cellular (green) and nuclear (red) aspect ratios are plotted as a function of Young’s modulus, E. (D) Nuclear area (in square millimeters) vs. cell area (in square millimeters) for hASCs (Left) and C2C12s (Right) as a function of stiffness (2 kPa: blue to 40 kPa: red). *P < 0.05, ***P < 0.001, ****P < 0.0001, n.s, not significant.

Once we established that the durotactic threshold for hASCs was above 2.9 kPa/mm, we characterized cell migration on three nondurotactic gradient gels (0.5, 1.7, and 2.9 kPa/mm). Although hASCs migrated at different speeds according to their local stiffness (i.e., cells moved faster on higher-stiffness regions), they did not exhibit any bias in the x or y direction, indicating that durotaxis was not occurring (Fig. 2C and Fig. S6). This absence of durotaxis means that cells plated on these gradient hydrogels will not preferentially move to stiffer regions, allowing the examination of cell behavior and protein expression in response to a continuous range of stiffnesses without the confounding effect of biased migration.

Stem Cell Mechanotransduction and Differentiation.

In this set-up, gradients can be fabricated both above and below the durotactic threshold, giving this system dual utility. As explored above, gels with gradients above the durotactic-promoting threshold can be used to analyze cell migration toward stiffer or softer regions. Perhaps more interestingly, gels with gradients below the durotactic threshold can be used as single-well platforms for analyzing cellular responses to a wide range of static substrate stiffnesses without the confounding effect of biased cell migration. We used the inability of the 2.9-kPa/mm gradients to induce durotaxis (Fig. 2C and Fig. S6) to our advantage to investigate mechanotransduction and differentiation decoupled from durotaxis.

To demonstrate the ability to assess cellular morphological characteristics in a high content fashion, nuclei and the actin cytoskeleton were stained on these gradient hydrogels, allowing the analysis of thousands of cells in a single well (Fig. 3A). We found that in hASCs, both the cell-spread area and the nuclear area increase with stiffness (Fig. 3D). In addition, despite steady increases in cross-sectional area, the aspect ratio of both cells and nuclei remained consistent across the entire stiffness range, suggesting that the stresses contributing to nuclear expansion were isotropic (Fig. 3C). This finding is in contrast to data obtained from C2C12 mouse myoblasts, in which the cellular-spread area increased with stiffness but the nuclear cross-sectional area remained generally constant (Fig. 3D). Because nuclear stiffness has been shown to increase as differentiation progresses, it follows that nuclei in more terminally differentiated cells would compress less in response to traction forces (50). Thus, this system presents an opportunity for high content analysis of simple morphological responses of different cell types. This system can also be extended to specialized cell populations (i.e., knockouts) in which interesting morphological changes (cell aspect ratio, focal adhesion area, and so forth) in response to substrate stiffness can be assessed.

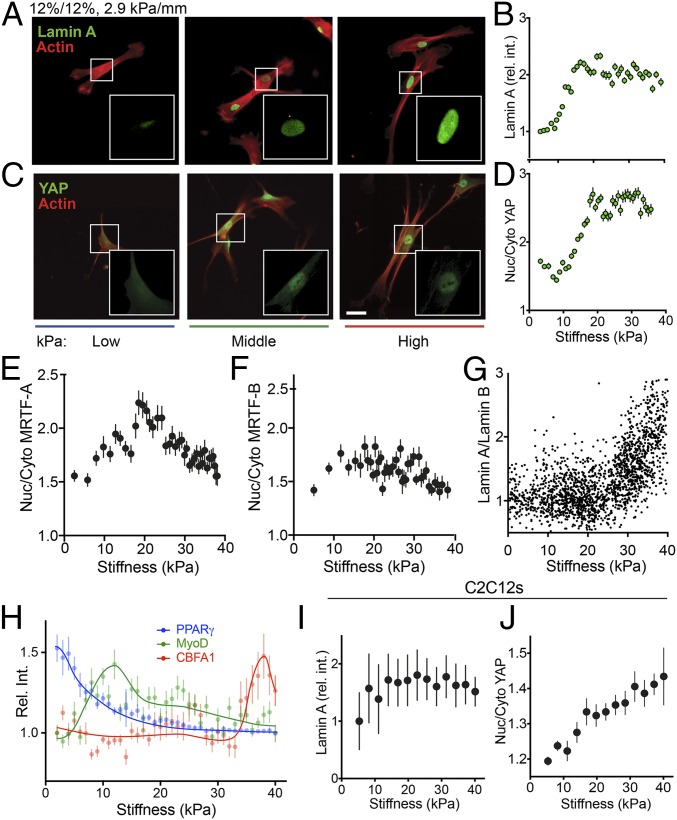
The use of immunofluorescence allows the examination of stiffness-dependent cell behavior beyond morphological characterization. The nuclear intermediate filament Lamin A exhibits scaled expression with tissue stiffness (51) and a dose-dependent mechanosensing response. To determine to what extent switch-like vs. dose-dependent signaling regulates behavior at intermediate stiffness in single cells, hASCs were stained for Lamin A and Lamin B on 2.9-kPa/mm-gradient hydrogels (Fig. 4A). Lamin A expression was found to scale in a logarithmic dose-dependent manner in response to stiffness (Fig. 4B), i.e., exhibiting quick increases in intensity between 2 and 18 kPa and marginally slower increases above 18 kPa. These high stiffness-resolution data are consistent with previous reports of logarithmic increases of Lamin A expression in single cells that assayed only three distinct stiffness values (51). Furthermore, by staining the same cell populations for Lamin A and Lamin B, we obtained individual Lamin A/Lamin B ratios for thousands of cells over a range of physiological stiffnesses, revealing an exponential increase in this ratio as stiffness increases (Fig. 4G). In contrast with hASCs, C2C12 cells showed less stiffness-dependent Lamin A expression, with nuclear Lamin A levels saturating above 10 kPa (Fig. 4I). Again, this finding mirrors previous observations that more terminally differentiated cells tend to have more stable patterns of Lamin A expression (52).

Fig. 4.

Mechanotransduction and differentiation of hASCs on stiffness gradient hydrogels. (A) Representative images of hASCs plated on fibronectin-coated stiffness gradient hydrogels stained for Lamin A (green) and actin (red) for low (blue), middle (green), and high (red) stiffness regions of the hydrogel. (B) Lamin A relative intensity (rel. int.) plotted vs. stiffness. (C) Representative images for YAP (green) and actin (red) as in A. (D) Nuclear-to-cytoplasmic ratio (Nuc/Cyto) of YAP. (E and F) Nuclear-to-cytoplasmic ratio of MRTF-A (E) and MRFT-B (F) plotted as a function of stiffness. (G) The ratio of Lamin A to Lamin B is plotted vs. stiffness. (H) Expression of differentiation markers (rel. int.) of PPARγ (blue), MyoD (green), and CBFA1 (red) vs. stiffness. (I and J) C2C12 cells were examined for Lamin A expression (rel. int.) (I) and nuclear to cytoplasmic ratio of YAP (J) as a function of stiffness. (Scale bar: 50 μm; scale in A is identical to C.)

YAP displays a biphasic regulation pattern by alternatively localizing to the cytoplasm on soft matrices and to the nucleus on stiff matrices (53). This substrate stiffness-dependent behavior was recently analyzed in more detail, increasing the stiffness resolution to six discrete static PA hydrogels, allowing discernment of the specific stiffness regime in which YAP translocates to the nucleus (49). However, these and other studies have struggled to identify the stiffness range that shows a transition-level translocation, as opposed to on/off behavior. On 2.9-kPa/mm gradient hydrogels, the nucleus/cytoplasm ratio of YAP appeared sigmoidal, with a minimum ratio found from 2–12 kPa, followed by a linear increase in nuclear localization from 12–20 kPa and a saturated nuclear localization state above 20 kPa (Fig. 4 C and D). This result suggests that the nuclear translocation of YAP is indeed stiffness-dose dependent for certain stiffness ranges, with a fairly broad sigmoidal transition zone that includes physiological stiffness values, in contrast to prior suggestions of binary, switch-like localization patterns. Finding transition zones like these can have important implications in the understanding of many signaling pathways, because they indicate that intermediate levels of expression or localization potentially could result in outcomes different from “on” or “off.” Indeed, C2C12 myoblasts, which have been shown to have a pattern of YAP expression and nuclear localization different from that of stem cells, were found to have a much broader transition zone, with nuclear localization increasing steadily from 2 to 38 kPa (Fig. 4J) (54).

The transcription factors MRTF-A and MRTF-B, also known as “Mkl1/MAL” and “Mkl2/MAL16,” have been shown to shuttle naturally between the cytoplasm and the nucleus (55), to play a role in myogenic differentiation (56), and to be directly affected by the actin polymerization state of the cell (57). MRTF-A interactions with YAP have generated substantial interest in the nuclear localization patterns of MRTF-A (58–60), but to date nearly all investigations that test stiffness variations have analyzed only two distinct values (61, 62). Leveraging our gradient system, we analyzed expression patterns of MRTF-A and MRTF-B in hASCs plated for 24 h on 2.9-kPa/mm hydrogels and found that although MRTF-B localization was independent of stiffness (Fig. 4F), MRTF-A expression peaked at ∼20 kPa (Fig. 4E). This finding is in contrast with reported time-dependent increases in nuclear localization of MRTF-A in hMSCs on 100-kPa PA substrates (62), although we did not analyze supraphysiological stiffnesses higher than 40 kPa. However, these results are intriguing in that MRTF-A has been shown to regulate miRNAs with roles in myogenic differentiation, a process that occurs near the stiffness region at which we observed MRTF-A to peak in ref. 63.

To explore this platform’s utility further, specifically in the context of stem cells, we analyzed stiffness-dependent hASC differentiation after 6 d on 2.9-kPa/mm gradient hydrogels. In agreement with previous studies (1), the expression of the adipogenic marker PPARγ was found to peak at low stiffnesses (E <3 kPa) and to decrease quickly as stiffness increased (Fig. 4H, blue). Similarly, expression of the myogenic transcription factor MyoD was found to peak at E∼12 kPa (Fig. 4H, green), and CBFA1, an osteogenic marker, was highest around E∼36 kPa (Fig. 4H, red), also in agreement with a large body of literature on mechanosensitive myogenic and osteogenic differentiation.

Conclusion

Nearly all phenomena in cell biology are affected to some degree by substrate stiffness, from stem cell differentiation (1) to cancer cell chemoresistance (64) to heart cell function (65). The stiffness gradient platform described here allows the investigator to test a wide range of mechanical induction signals on the same surface. Furthermore, because the slope of stiffness built into this technology is easily tunable, it can be customized to a wide variety of biological conditions or disease processes under investigation; shallow slopes can isolate stiffness as an inductive factor, and steeper slopes can elicit durotaxis. This method offers a simpler solution than those previously available to fabricate synthetic stiffness gradients and is easily reproducible because it requires only a few simple components that can be procured and assembled in any biochemistry laboratory. Most importantly, the shallower gradients created by this method enable observations of more subtle behaviors in stem cells, e.g., the dose-dependent rather than switch-like responses of YAP to intermediate stiffness values, exemplifying the utility of these gradient hydrogels.

Materials and Methods

PA gradient hydrogels were fabricated using a two-layer polymerization method. After characterization of hydrogels, human ASCs or C2C12 cells were cultured on fibronectin-functionalized hydrogels. Time-lapse microscopy was used to study cell migration, and immunocytochemistry was used to measure cell distribution and to show cell mechanotransduction and stem cell differentiation. Further details about mold fabrication, cell assays, and statistical analyses can be found in SI Materials and Methods.

The use of freshly aspirated human adipose tissue was approved by the University of California, San Diego human research protections program (Project # 101878).

SI Materials and Methods

Mold Fabrication.

Molds were fabricated with one 76- × 51- × 1-mm glass slide (ProSciTech) forming the base, two 76- × 26- × 1-mm glass slides (HD Scientific Supplies) forming the lateral edges, and two stacks of five 24- × 24-mm coverslips (ProSciTech) forming the distal edges (Fig. 1A). All pieces were attached with common super glue (cyanoacrylates), yielding an open-topped glass mold with dimensions of 24 × 20 × 1 mm. The glass surface of the mold was coated with 30 µL DCDMS (Sigma-Aldrich) to ensure a nonadherent surface for the removal of the PA hydrogel. Coverslips were cleaned on both sides with ozone (Bioforce Nanosciences UV/Ozone ProCleaner) for 1 min and then were functionalized in a solution containing 100 µL 3-(trimethoxysilyl)propyl methacrylate (Sigma-Aldrich), 600 µL acetic acid, and 20 mL ethanol for 5 min to facilitate covalent attachment of acrylamide polymers.

PA Hydrogel Fabrication.

Polymer solutions containing 4, 6, 9, 12, 15, 16, or 20% (vol/vol) acrylamide monomers (Bio-Rad) with 0.4% (vol/vol) N,N′-methylene-bis-acrylamide cross-linker (Bio-Rad) were prepared in 1× Dulbecco’s PBS without Mg²⁺ and Ca²⁺ (Life Technologies). After 1-mL aliquots were degassed for 5 min, 10 µL of 10% (wt/vol) ammonium persulfate (APS) (Sigma-Aldrich) was added and mixed for 0.5 s; then 1 µL N,N,N′,N′-tetramethylethylenediamine (TEMED) (Bio-Rad) was added quickly and mixed for 1 s. Two hundred fifty microliters of this solution were pipetted into the glass mold, and a functionalized glass coverslip was placed over the solution at an angle so that no air remained under the coverslip. This solution was allowed to polymerize for 15 min and then was removed from the mold with the coverslip attached. The addition of APS and TEMED was repeated with a new aliquot of the same monomer concentration, and a second 280-µL aliquot of that solution was pipetted into the same mold. The first ramp-shaped PA hydrogel, with coverslip attached, was then placed gel-down onto the second aliquot of solution. The edges of the coverslip bridged the roof of the mold so that air was excluded from the polymerization chamber, preventing oxygen inhibition. The second gel was allowed to polymerize for exactly 15 min and then was removed from the mold with its coverslip base still attached. Gels were rinsed and stored in 1× PBS without Mg²⁺ and Ca²⁺ for further use.

AFM.

The compression stiffness of the fabricated gels was verified using an MFP-3D atomic force microscope (Asylum Research). Two hundred-micrometer chromium/gold-coated, silicone-nitride cantilevers with pyramid-shaped tips or 2-μm spherical tips, 17-kHz resonant frequencies, and ∼20–25-pN/nm nominal spring constants were used (Nano World model PRP-TR-20). Samples were immersed in 1× PBS without Mg²⁺ and Ca²⁺, indented in triplicate at an approach velocity of 2 µm/s until a 2-nN trigger force was registered, and then retracted at 10 µm/s. Samples were indented at 500-µm intervals along the gradient axis of compound PA hydrogels. The linear portion of the contact-generated force curves were analyzed with custom-written code in Igor Pro to determine Young’s modulus as previously described (1). Triplicate data points representing three separate hydrogels were averaged, and the stiffness in kilopascals was plotted against displacement along the gradient axis of the PA hydrogels using GraphPad Prism. Surfaces of the compound PA hydrogels were further analyzed for roughness in a 256-point grid with a 20- × 20-µm surface area using a 4-µm/s approach velocity, 2-nN trigger point, and 10-µm/s retraction velocity.

OCE.

The gradient of Young’s modulus measured in the depth direction in the hydrogel was imaged using a compression OCE method (42). OCE was performed with a Fourier-domain optical coherence tomography (OCT) system. The OCT system operates on the principle of low-coherence interferometry by illuminating a sample with a broad optical bandwidth, focused beam of light with a central wavelength of 845 nm. It is nonionizing and low power (∼7.5 mW). The light back-scattered from inside the sample is captured, and the time-delay information is used to reconstruct a depth profile of sample microstructure. The system can capture 2D or 3D images with experimentally measured axial and lateral resolutions of 7.8 and 11 μm, respectively, up to 2–3 mm in depth.

The hydrogel was compressed to 5–10% of its initial thickness by a compliant silicone or PA gel stress sensor. A further microscale compression was applied and the local deformation in the direction of the optical beam was measured from the phase changes in the scattered light. The relative deformation between the precharacterized stress layer and the hydrogel was used to reconstruct the local, spatially resolved Young's Modulus. The advantage of the OCE method over standardized compression testing and indentation methods is that Young’s modulus can be resolved within a volume (with z-resolution of 100 μm and lateral resolution of 10 μm) with a field of view of over 15 mm in less than 10 min.

PA Hydrogel Functionalization.

PA hydrogels in Hepes (pH 8.5) buffer (Life Technologies) were sterilized under 302 nm UV light for 15 min. The pH 8.5 Hepes was removed, and the PA hydrogels were covered with 2 mL of 1 mg/mL N-sulphosuccinimidyl-6-(4’-azido-2’-nitrophenylamino) hexanoate (sulpho-SANPAH; Thermo Scientific) in pH 8.5 Hepes and were activated under 365-nm UV light for 10 min. Sulpho-SANPAH was removed, and PA hydrogels were washed three times with pH 8.5 Hepes, covered with 2 mL of 0.25 µg/mL human plasma fibronectin (Life Technologies), and incubated overnight at 37 °C. This protocol was used for both migration and differentiation assays.

Adipose-Derived Stem Cell Isolation and Culture.

hASCs were isolated from freshly aspirated human s.c. adipose tissue (donor age 26–31 y) according to the method described elsewhere (13), with approval of the University of California, San Diego human research protections program (Project no. 101878). hASCs were cultured in DMEM with 10% FBS (HyClone) and 1× antibiotics (Life Technologies). hASCs were seeded on PA hydrogels to obtain an estimated 30% confluence for normal experiments and were seeded at a 10% confluence level for low-density experiments.

hASC Migration Assay (Manual).

The EVOS FL Auto cell imaging system (Life Technologies) with a 5% CO₂ and 37 °C incubation chamber was used to obtain time-lapsed micrographs of cell cultures every 15 min for 72 h. Fiji Image J software with a chemotaxis tool was used to track cell migration over 72 h, and composite migration data were analyzed in GraphPad Prism and Microsoft Excel 2013.

hASC Migration Assay (Automated).

Detection and tracking of multiple cells was fully automated using a spot-detection algorithm in conjunction with an optimal Bayes multiobject tracking algorithm. Cell migration was studied by examining the trajectories of the cells and analyzing their behavior. The cells were detected from each image using a spot-detection algorithm with adaptive wavelet threshold (66). A multiobject tracker was needed to process the sequence of detections to produce estimate the cell trajectories. The latest state-of-the-art multiobject tracker that addresses all these challenges under one unifying mathematical framework is the generalized labeled multi-Bernoulli (GLMB) filter (67). This filter is an analytic solution to optimal Bayes formulation of the multiobject tracking problem and captures all statistical information about the cell population for the duration of the experiment.

FRET.

Fibronectin was prepared as described previously (38). Briefly, human serum fibronectin was denatured for 15 min in 4 M guanidine hydrochloride (GdnHCl). Denatured fibronectin was then incubated in a 30-fold molar excess solution of Alexa Fluor 546 C5 Maleimide (Life Technologies) for 2 h followed by buffer exchange into 0.1 M sodium bicarbonate (pH 8.3) using a spin desalting column (Thermo Scientific) according to the manufacturer’s instructions. Then the single-labeled fibronectin was incubated with 40-fold molar excess Alexa Fluor 488 succinimidyl ester (Life Technologies) for 1 h. Dual-labeled fibronectin was stored with 10% glycerol at −20 °C. The average number of Alexa Fluor 546 and Alexa Fluor 488 fluorophores per fibronectin dimer was 3.6 and 8.8, respectively, and was determined using published extinction coefficients and the absorbance of the dual-labeled fibronectin at 280, 498, and 556 nm.

FRET Imaging.

Images of cells on hydrogels coated with FRET-fibronectin were acquired on a Zeiss LSM 780 Confocal Microscope and analyzed using a custom MATLAB script, as previously described (38). Briefly, images were sliding block averaged, and perinuclear regions of Hoechst stained cells were chosen for analysis. The FRET ratio for each pixel was calculated by dividing the pixel’s intensity in the acceptor (Alexa Fluor 546) image by its corresponding intensity in the donor (Alexa Fluor 488) image. FRET ratios less than 0.05 and greater than 1.0 were excluded from analysis. The mean FRET ratio within the selected regions was calculated for each cell and then averaged over all of the cells in each condition.

Cryo-SEM.

Cryo-SEM was used to examine the native pore size across the hydrogel surface and in cross-section. Twelve percent acrylamide hydrogels were mounted (flat for top surface evaluation and at a 90° angle for cross-section evaluation), flash frozen in liquid nitrogen, and sublimated first from −150 °C to −120 °C at a rate of 5 °C/min, then from −120 °C to −90 °C at a rate of 2 °C/min, and then held at −90 °C for 1 h using a Freeze Fracture System Leica EM BAF060 fitted with a VCT 100 BAS Rev 04 Controller (Leica Microsystems). Hydrogels used for cross-section examination were freeze-fractured with the built-in microtome before sublimation. After sublimation, samples were transferred to the microscope (Zeiss Ultra 55 fitted with a Gemini Electron Beam and Baltec LE 02567 mn/140 Controller; Carl Zeiss NTS GmbH) and evaluated at 1.5–3 kV, depending on charging effects, with the secondary electron detector. Images were captured at multiple locations along the length of the hydrogel and recorded with x and y coordinates.

Pore Size Analysis.

A custom CellProfiler (68) pipeline was used on cryo-SEM images to identify and analyze pore size distribution automatically. Briefly, an adaptive maximum correlation method with a correction factor of 0.75 was used to threshold cryo-SEM images, followed by the identification of pores as primary objects in conjunction with separation of intensity-distinguished clumped objects. The major axis length of each identified pore was then calculated.

Immunofluorescence.

After culturing for 24 h, hASCs were fixed with 3.7% formaldehyde for 15 min at room temperature and permeabilized with 1% Triton-X for 5 min at 37 °C. Cells were then stained with primary antibodies against YAP1 (no. 4912; Cell Signaling Technology), Lamin A (NB100-74451; Novus Biologicals), Lamin B1 (sc-374015; Santa Cruz), MRTF-A (sc-398675; Santa Cruz), MRTF-B (AMAB90887; Sigma), PPARγ (sc-7196; Santa Cruz), MyoD (sc-377460; Santa Cruz), and CBFA1 (sc-101145; Santa Cruz). Corresponding secondary antibodies were conjugated to Alexa Fluor 488 (FITC) or Alexa Fluor 647 (Cy5) (Invitrogen). The actin cytoskeleton was stained with rhodamine-conjugated phalloidin (Invitrogen), and cells were mounted in Fluoromount G with DAPI (SouthernBiotech).

High-Content Imaging and Analysis.

Gradient gels were imaged on a Zeiss Axio Observer Z1 fitted with an AxioCam MRm. Briefly, an image mosaic spanning the length of the gradient was collected in TXRD, CY5, DAPI, and FITC, with autofocus using DAPI as a reference channel occurring every position. The image mosaic was then stitched in Zeiss Zen software. Resulting stitched images were analyzed using a semiautomated image analysis pipeline in CellProfiler (68). Nuclear outlines were obtained as primary objects with manual thresholding, and cell outlines were obtained using the TXRD channel as secondary objects using a Watershed Gradient algorithm. The pipeline calculated morphological attributes, e.g., cell area, aspect ratio, and eccentricity for each cell and nucleus, as well as the mean and integrated density of the FITC and CY5 channel signal in nuclei, cell outlines, and cytoplasm outlines. From these data, nuclear-to-cytoplasmic expression ratios could also be calculated. To obtain background intensity values, ImageJ/Fiji was used to determine intensity values at all positions without cells. A sixth-order polynomial fit was applied to these data and was used to predict background intensities for each individual cell based on its position along the gradient. Data analysis was performed with Microsoft Excel and GraphPad Prism.

Statistical Analysis.

Data are expressed as mean ± SD, SEM, or 95% confidence intervals as indicated. For statistical analyses, Student’s t test was performed on the data presented in Fig. 2B. One-way ANOVAs were performed on all other data where significance is shown. Multiple comparisons Tukey post tests were performed where appropriate. Differences were considered significant when *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001. All experiments were performed in triplicate unless otherwise noted, and in such cases, the number of cells used in the measurement has been stated.