Energetic cost of building a virus

Significance

Viruses rely entirely on their host as an energy source. Despite numerous experimental studies that demonstrate the capability of viruses to rewire and undermine their host’s metabolism, we still largely lack a quantitative understanding of an infection’s energetics. However, the energetics of a viral infection is at the center of broader evolutionary and physical questions in virology. By enumerating the energetic costs of different viral processes, we open the door to quantitative predictions about viral evolution. For example, we predict that, for the majority of viruses, translation will serve as the dominant cost of building a virus, and that selection, rather than drift, will govern the fate of new genetic elements within viral genomes.

Abstract

Viruses are incapable of autonomous energy production. Although many experimental studies make it clear that viruses are parasitic entities that hijack the molecular resources of the host, a detailed estimate for the energetic cost of viral synthesis is largely lacking. To quantify the energetic cost of viruses to their hosts, we enumerated the costs associated with two very distinct but representative DNA and RNA viruses, namely, T4 and influenza. We found that, for these viruses, translation of viral proteins is the most energetically expensive process. Interestingly, the costs of building a T4 phage and a single influenza virus are nearly the same. Due to influenza’s higher burst size, however, the overall cost of a T4 phage infection is only 2–3% of the cost of an influenza infection. The costs of these infections relative to their host’s estimated energy budget during the infection reveal that a T4 infection consumes about a third of its host’s energy budget, whereas an influenza infection consumes only ≈ 1%. Building on our estimates for T4, we show how the energetic costs of double-stranded DNA phages scale with the capsid size, revealing that the dominant cost of building a virus can switch from translation to genome replication above a critical size. Last, using our predictions for the energetic cost of viruses, we provide estimates for the strengths of selection and genetic drift acting on newly incorporated genetic elements in viral genomes, under conditions of energy limitation.

Viruses are biological “entities” at the boundary of life. Without cells to infect, viruses as we know them would cease to function, as they rely on their hosts to replicate. Although the extent of this reliance varies for different viruses, all viruses consume from the host’s energy budget in creating the next generation of viruses. There are many examples of viruses that actively subvert the host transcriptional and translational processes in favor of their own replication (1). This viral takeover of the host metabolism manifests itself in a variety of forms such as in the degradation of the host’s genome or the inhibition of the host’s mRNA translation (1). There are many other experimental studies (discussed in SI section I) (2–6) that demonstrate viruses to be capable of rewiring the host metabolism. These examples also suggest that a viral infection requires a considerable amount of the host’s energetic supply. In support of this view are experiments on T4 (7), T7 (8), Pseudoalteromonas phage (9), and Paramecium bursaria chlorella virus-1 (PBCV-1) (10), demonstrating that the viral burst size correlates positively with the host growth rate. In the case of PBCV-1, the burst size is reduced by 50% when its photosynthetic host, a freshwater algae, is grown in the dark (10). Similarly, slow-growing Escherichia coli with a doubling time of 21 h affords a T4 burst size of just one phage (11), as opposed to a burst size of 100–200 phages during optimal growth conditions.

These fascinating observations led us to ask the following questions: what is the energetic cost of a viral infection, and what is the energetic burden of a viral infection on the host cell? To our knowledge, the first attempt to address these problems is provided through a kinetic model of the growth of Qβ phage (12). A more recent study performed numerical simulations of the impact of a T7 phage infection on its E. coli host, yielding important insights into the time course of the metabolic demands of a viral infection (13).

To further explore the energetic requirements of viral synthesis, we made careful estimates of the energetic costs for two viruses with very different characteristics, namely the T4 phage and the influenza A virus. T4 phage is a double-stranded DNA (dsDNA) virus with a 169-kb genome that infects E. coli. The influenza virus is a negative-sense, single-stranded RNA virus (–ssRNA) with a segmented genome that is 10.6 kb in total length. The influenza virus is a eukaryotic virus infecting various animals, with an average burst size of 6,000, although note that the burst size depends upon growth conditions (14). Similar to many other dsDNA viruses, T4 phage infections yield a relatively modest burst size, with the majority of T4 phages resulting in a burst size of ≈ 200 during optimal host growth conditions (15). To determine the energetic demand of viruses on their hosts, the cost estimate for building a single virus has to be multiplied by the viral burst size and placed in the context of the host’s energy budget during the viral infection.

Concretely, the costs associated with building a virus can be broken down into the following processes that are common to the life cycles of many viruses: (i) viral entry, (ii) intracellular transport, (iii) genome replication, (iv) transcription, (v) translation, (vi) assembly and genome packaging, and (vii) exit. Our strategy was to examine each of these processes for both viruses in parallel, comparing and contrasting the energetic burdens of each of the steps in the viral life cycle.

Energetic Cost Units and Definitions

Given that the energetic processes of the cell take place in many different energy currencies ranging from ATP and GTP hydrolysis to the energy stored in membrane potentials, it is important to have a consistent scheme for reporting those energies. ATP serves as the most common energy currency of the cell, a function that is universally conserved across all known cellular life-forms (16, 17). The triphosphate group in ATP contains phosphoanhydride bonds, which upon hydrolysis result in a large negative free-energy change. Specifically, the hydrolysis of ATP into ADP and orthophosphate (P_i) is responsible for roughly a −30 kJ/mol free-energy change at standard conditions (25 °C, 1 atm, pH 7, and 1 M concentration of reaction components) (16, 18). Under physiological conditions more typically found in cells, the hydrolysis of ATP usually releases about −50 kJ/mol (16, 18). In addition to ATP, which most commonly serves as the energy currency of the cell, there are other nucleoside triphosphates such as GTP that are approximately energetically equivalent to ATP. We will refer to these molecules as ATP-equivalent.

Although the change in free energy under standard conditions is a constant, the actual change in free energy in a given biochemical reaction is variable and dependent on the concentrations of reactants and products (19). In the absence of exact concentration measurements throughout viral processes of interest here, calculating the actual change in free energy for each reaction is not feasible. Hence, we follow others in their reporting of cellular costs by using the number of ATP (and ATP-equivalent) hydrolysis events as a proxy for energetic cost. Similar to Lynch and Marinov (20), we will use the symbol P as a shorthand notation to represent an ATP (or an ATP-equivalent) hydrolysis event. We will additionally use subscripts to clearly label the results obtained under different energetic cost definitions, which will be introduced in the following paragraphs. Last, in reporting some of our final cost estimates, we will convert the number of ATP (or ATP-equivalent) hydrolysis events to units of joules and k_BT by assuming 50 kJ of negative free-energy change per mole of P at physiological conditions.

In making viral energetic cost estimates, we are guided by two energetic cost definitions, which despite sharing the same unit of energy have very different physical interpretations. In our first definition of energetic cost, termed “direct cost” or $E_{\mathrm{D}}$, we will only account for the explicit number of ATP and ATP-equivalent hydrolysis events required during viral synthesis. This is the definition that is implicitly used in some of the earliest investigations into cellular energetics (21). Estimates made under this definition will be denoted in the previously described units of P, however, with a subscript (P_D) to make it clear we are talking about energy that is expended in viral synthesis processes. This definition will include costs such as those incurred during the synthesis and polymerization of building blocks. See Fig. S1 (steps 3 and 4) and SI section II for a more detailed description of direct cost.

In our second definition, termed “total cost” or $E_{\mathrm{T}}$, we not only account for the direct costs, but also for the “opportunity cost” of building blocks, $E_{\mathrm{O}}$, required during viral synthesis; hence, $E_{\mathrm{T}}=E_{\mathrm{D}}+E_{\mathrm{O}}.$ We define the opportunity cost of a building block as the number of ATP (and ATP-equivalent) molecules that could have been generated had the building block not been used in viral synthesis and will label these costs with the notation P_O (Fig. S1, steps 1–4, and SI sections II, III, and IV). In the more recent works on cellular energetics, it is the total cost definition that the authors implicitly adhere to (22, 23). The units for the total cost definition will be denoted by the symbol P_T. A more detailed explanation and derivation of these two cost components can be found in the SI (SI sections II–IV, Dataset S1, and Figs. S1–S3).

The distinction between these two different energetic cost definitions is that, under the total cost definition, in addition to accounting for direct costs, we attribute an energetic cost to the building blocks that are usurped from the host during viral synthesis. Both energetic cost definitions have physical significance. For example, the direct cost definition is the more appropriate choice when estimating heat production and power consumption of a viral infection (SI sections II–IV). The total cost definition, on the other hand, is aligned with traditional energetic cost estimates made from growth experiments in chemostats, where substrate consumption and cell yield is monitored, and allows for a clear comparison between the cost of an infection and the cost of a cell (SI sections II–IV). This is because the cost of a cell, derived through chemostat experiments, implicitly includes the opportunity cost component, which is the cost of diverting precursor metabolites from energy-producing pathways toward the synthesis of molecular building blocks. In addition, although our approach would certainly benefit from detailed experimental studies that reveal the fluxes in the host metabolome during an infection, the assignment of an energetic value to each metabolite allows us to simplify the problem from reporting changes in the concentration of hundreds of metabolites to reporting a single energetic value associated with the viral infection. This value can then be compared with the cellular energy budget.

We will generally estimate the cost of a certain viral process for a single virus, and then multiply this cost by the viral burst size to determine the infection cost of a given process. Subscript v will denote the cost estimates made for a single virus, and the subscript i will refer to a cost estimate made for an infection. We relegate the energetic cost estimates for all viral processes to SI sections V–XI.

Results

The Energetic Costs of T4 and Influenza.

By estimating the energetic costs of influenza and T4 life cycles, we show that, surprisingly, the costs of synthesizing an influenza virus and a T4 phage are nearly the same (Table 1). The outcome of the analysis to be discussed in the remainder of the paper is summarized pictorially in Fig. 1 for bacteriophage T4 and Fig. 2 for influenza. For both viruses, the energetic cost of translation outweighs other costs (Table 1 and Figs. 1–3), although as we will show at the end of the paper, because translation scales with the surface area of the viral capsid and replication scales with the volume of the virus, for dsDNA phages larger than a critical size, the replication cost outpaces the translation cost.

Table 1.

The direct, opportunity, and total energetic costs of viral processes for T4 and influenza

Cost			Replication	Transcription	Viral entry	Packaging	Intracellular transport	Viral exit	Translation	Sum
Direct cost (PD)	Per virion	T4	4 × 106	7 × 105	—	3 × 105	—	—	7 × 106	107
		Flu	3 × 105	7 × 104	—	—	103	2 × 106	107	107
	Per infection	T4	9 × 108	108	—	7 × 107	—	—	109	3 × 109
		Flu	2 × 109	4 × 108	103	—	6 × 106	1010	6 × 1010	8 × 1010
Opportunity cost (PO)	Per virion	T4	107	7 × 105	—	—	—	—	3 × 107	4 × 107
		Flu	8 × 105	2 × 105	—	—	—	3 × 107	5 × 107	9 × 107
	Per infection	T4	2 × 109	108	—	—	—	—	6 × 109	8 × 109
		Flu	5 × 109	109	—	—	—	2 × 1011	3 × 1011	5 × 1011
Total cost (PT)	Per virion	T4	2 × 107	106	—	3 × 105	—	—	4 × 107	6 × 107
		Flu	106	3 × 105	—	—	103	4 × 107	6 × 107	108
	Per infection	T4	3 × 109	3 × 108	—	7 × 107	—	—	8 × 109	1010
		Flu	6 × 109	2 × 109	103	—	6 × 106	2 × 1011	4 × 1011	6 × 1011

The T4 infection costs are estimated based on an average burst size of 200, and the influenza infection costs are based on an average burst size of 6,000. Direct costs shown represent the number of phosphate bonds directly hydrolyzed during the viral lifecycle (P_D), whereas the total costs (P_T) include both direct costs (P_D) as well as opportunity costs (P_O) incurred during the viral life cycle (SI sections V–XI). Empty entries correspond to viral processes that did not result in an energetic cost or were not applicable to the given virus. Note that, to obtain the total cost estimates, the sum of opportunity and direct costs used exact numbers and was then rounded (this is why the sum of the rounded versions of direct and opportunity costs do not exactly match up to the total costs presented in this table).

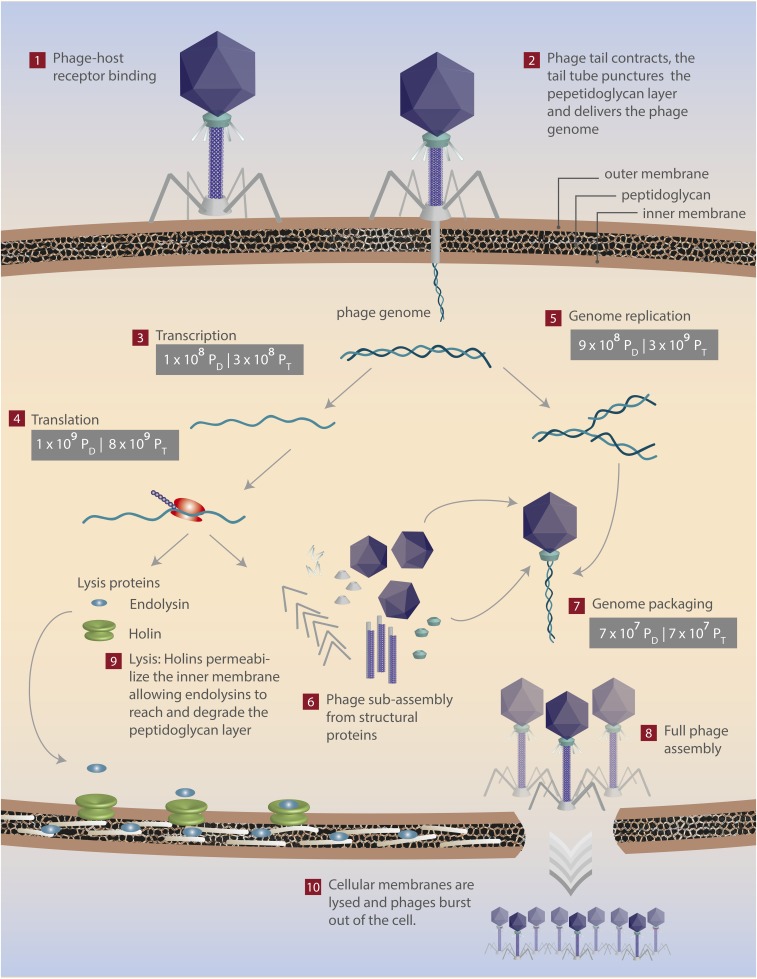
Fig. 1.

The energetics of a T4 phage infection. The direct and total costs of viral processes are denoted and can be distinguished by their subscripts (P_D and P_T, respectively). The energetic requirements of transcription (step 3), translation (step 4), genome replication (step 5), and genome packaging (step 7) are shown. See SI sections V–XI and Table 1.

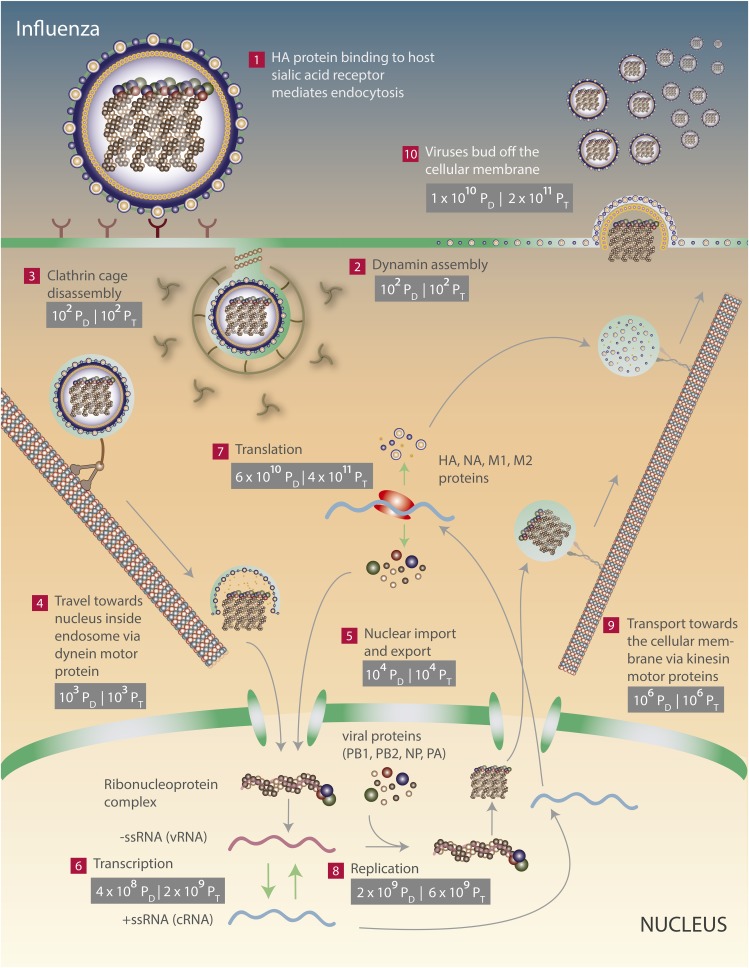
Fig. 2.

The energetics of an influenza infection. The direct and total costs of viral processes are denoted and can be distinguished by their subscripts (P_D and P_T, respectively). The energetic requirements of viral entry (steps 2 and 3), intracellular transport (steps 4, 5, and 9), transcription (step 6), translation (step 7), genome replication (step 8), and viral exit (step 10) are shown. See SI sections V–XI and Table 1.

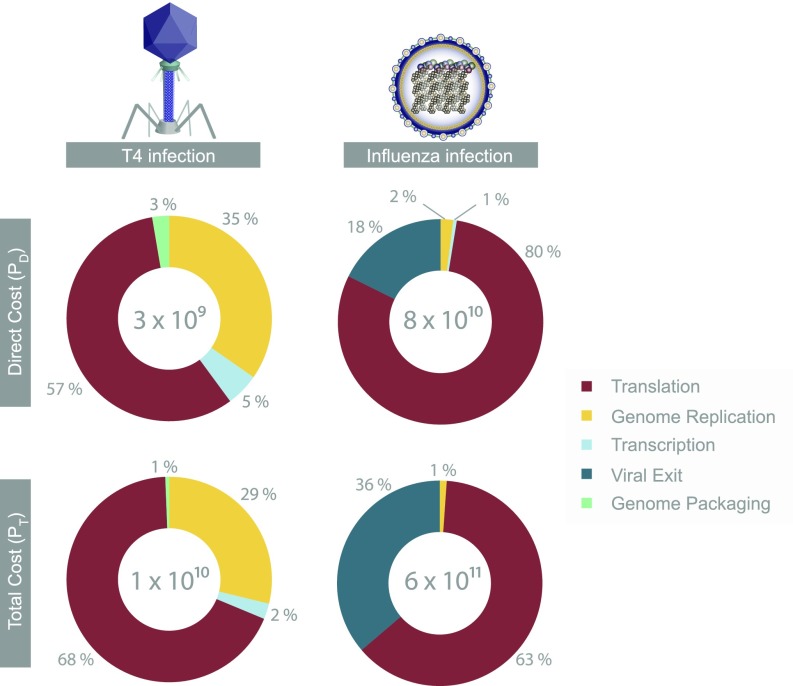
Fig. 3.

A breakdown of the direct cost (Top) and the total cost (Bottom) of various viral processes during T4 (Left) and influenza (Right) viral infections (normalized to the sum of all costs during an infection, as shown in the center of each pie chart). The direct cost of a T4 phage infection is ≈ 3 × 10⁹ P_D, whereas the total cost is 10¹⁰ P_T. The direct and total costs of an influenza infection are ≈ 8 × 10¹⁰ P_D and 6 × 10¹¹ P_T, respectively. Numbers are rounded to the nearest percent, and viral processes costing below 0.5% of the infection’s cost are not shown. See SI sections V–XI for energetic cost estimates for viral entry, intracellular transport, transcription, viral assembly, and viral exit.

To get a sense for the numbers, here we provide order-of-magnitude estimates of both the costs of translation and replication and refer the interested reader to SI sections II–XI for full details. As detailed in the Tables S1 and S2, both T4 and influenza are composed of about 10⁶ amino acids. We can estimate the total cost of translation by appealing to a few simple facts. First, the average opportunity cost per amino acid is about 30 P_O. Second, the average direct cost to produce amino acids from precursor metabolites is 2 P_D per amino acid. Finally, each polypeptide bond incurs a direct cost of 4 P_D. We can see that the total cost of an amino acid is ≈ 36 P_T (30 P_O + 6 P_D). As a result, the translational cost of an influenza virus and a T4 phage both fall between 10⁷ to 10⁸ P_T (Table 1).

The cost of viral replication can be approximated in a similar fashion: we have to consider that the T4 genome is composed of roughly 4 × 10⁵ DNA bases and that the influenza genome is composed of an order of magnitude fewer RNA bases ($\approx$ 10⁴). The total costs of a DNA nucleotide and an RNA nucleotide, including the opportunity costs as well as the direct costs of synthesis and polymerization, are ≈ 50 P_T (SI sections II–IX, Figs. S1–S3, and Dataset S1). As a result of T4’s longer genome length, its total cost of replication ($\approx$ 10⁷ P_T) is about an order of magnitude higher than that of an influenza genome (Table 1, Figs. 1 and 2, and SI section VII).

The cost estimates of different viral processes during T4 and influenza infections are summarized in Figs. 1–3 and Table 1. The overall cost of a T4 infection is obtained by the sum of replication ($E_{REP/i}$), transcription ($E_{TX/i}$), translation ($E_{TL/i}$), and genome packaging ($E_{Pack/i}$) costs required during the infection (SI sections V–XI, Table 1, and Figs. 1 and 3). These costs together amount to $\approx$ 3 × 10⁹ P_D in direct cost and 1 × 10¹⁰ P_T in total cost (SI sections V–XI, Table 1, and Figs. 1 and 3, assuming a burst size of 200). The total cost of a T4 infection is also equivalent to the aerobic respiration of $\approx$ 4 × 10⁸ glucose molecules by E. coli [26 ATP per glucose (24)]. Alternatively, it is equivalent to $\approx$ 2 × 10¹¹ k_BT (assuming 1 ATP $\approx$ 20 k_BT) (25).

Similarly, the cost of an influenza infection is obtained by adding up the costs of entry ($E_{Entry}$), intracellular transport ($E_{Transit/i}$), replication ($E_{REP/i}$), transcription ($E_{TX/i}$), translation ($E_{TL/i}$), and exit ($E_{Exit/i}$) required during the infection (SI sections V–XI, Table 1, and Figs. 2 and 3). These processes have a cumulative cost of $\approx$ 8 × 10¹⁰ P_D and 6 × 10¹¹ P_T, for the assumed burst size of 6,000. The sum of costs in an influenza infection (6 × 10¹¹ P_T) is equivalent to the aerobic respiration of $\approx$ 2 × 10¹⁰ glucose molecules by a eukaryotic cell (32 ATP per glucose). It is also equivalent to $\approx$ 10¹³ k_BT. It is interesting to note that, for both viral infections, the opportunity cost component is the dominant component of the total cost (Table 1).

Even though individually a T4 phage and an influenza virus have comparable energetic costs, because of their different burst sizes, the direct cost of a T4 phage infection is $\approx$ 3% of the direct cost of an influenza infection. Similarly, the total cost of a T4 phage infection is $\approx$ 2% of the total cost of an influenza infection. To contextualize these numbers, the host energy budget during the infection has to be taken into account. The total cost of a cell is experimentally tractable through growth experiments in chemostats, in which cultures are maintained at a constant growth rate. The number of glucose molecules taken up per cell per unit time can be determined. The number of glucose molecules can then be converted to an energetic supply by assuming typical conversion ratios of 26 or 32 ATPs per glucose molecule depending on the organism (24). This energetic cost estimate will be a total cost estimate because not all glucose molecules taken up by the cell are fully metabolized to carbon dioxide and water to generate ATPs and are used as building blocks for biomass components instead. During the cellular life cycle, the cell has to double its number of building blocks before division, and to do so, a fraction of glucose molecules taken up is diverted away from energy production toward biosynthesis pathways. Hence, cellular energetic cost estimates that are derived from chemostat experiments are total cost estimates because they report on the combined opportunity and direct costs of a cell (SI sections II–IV).

Based on chemostat growth experiments (20), the total energy used by a bacterium and a mammalian cell with volumes of 1 and 2,000 μm³, respectively, are $\approx$ 3 × 10¹⁰ P_T and $\approx$ 5 × 10¹³ P_T, during the course of their viral infections (SI section XII). A simpler estimate for arriving at the total cost of E. coli with a 30-min doubling time is by considering the dry weight of E. coli ($\approx$ 0.6 pg at this growth rate) (ref. 26; BNID 100089). Given that about one-half of the cell’s dry weight is composed of carbon (ref. 26; BNID 100649), an E. coli is composed of $\approx$ 2 × 10¹⁰ carbons, supplied from $\approx$ 3 × 10⁹ glucose molecules, because each glucose contributes 6 carbons. With the 26 ATP per glucose conversion for E. coli, this is equivalent to a total cost of $\approx$ 7 × 10¹⁰ P_T, which is similar to the number obtained from chemostat growth experiments (20) (SI section XII).

Moreover, we estimate the fractional cost of a viral infection as the ratio of total cost of an infection, $E_{T/i}$, to the total cost of the host during the infection, $E_{T/h}$. For the T4 infection with a burst size of 200 virions, $E_{T/i}$ $\approx$ 1 × 10¹⁰ P_T (Table 1) and $E_{T/h}\approx$ 3 × 10¹⁰ P_T; therefore, the fractional cost of the T4 infection is $\approx$ 0.3. Interestingly, a calorimetric study of a marine microbial community demonstrated that 25% of the heat released by microbes is due to phage activity (27). If we assume that the majority of the direct cost of a cell is associated with translation (20, 25), these calorimetric studies square well with our estimate for the ratio of direct costs. In contrast, the influenza infection despite its larger burst size (6,000 virions) leading to a higher $E_{T/i}$ ($\approx$ 6 × 10¹¹ P_T) has a fractional cost of just 0.01 as the host cell is much bigger. Finally, we estimate that the heat release due to the T4 and influenza viral infections are approximately 0.2 and 2 nJ, respectively (SI section XIII). Although an influenza infection results in an order of magnitude more heat, the average power estimates of both infections are surprisingly very similar, on the order of 200 fW (SI section XIII).

Scaling of Viral Energetics with Size for dsDNA Phages.

Although we have concluded that for the influenza virus and the T4 phage the translational cost outweighs the replication cost, the ratio of these two costs varies according to the dimensions of a virus. In the case of T4 and influenza, these two viruses have comparable dimensions and consequently were composed of a similar number of amino acids (Tables S1 and S2). However, because for dsDNA phages the capsid is mostly comprised of proteins whereas the virion interior is mostly dedicated to the genetic material (28), it follows that with the diminishing surface area-to-volume ratio of a spherical object as it grows in size, the ratio of translational cost to replication cost also diminishes. This simple rule governs not just nucleotide or amino acid composition of a virus, but more fundamentally, it governs the elemental composition of viruses with spherical-like geometries (28).

The full derivation of replication and translational cost estimates as a function of viral capsid inner radius, $r$, can be found in SI section XIV. From these expressions, it is clear that the translational cost of a virus scales with $r^2$, whereas the replication cost scales with $r^3$ (Fig. 4). The critical radius at which replication will outweigh translation in cost is ≈ 60 nm for total cost estimates, $r_{crit-Tot}$ (Fig. 4 and SI section XIV). For the direct cost estimates, the critical radius, $r_{crit-Dir}$, is ≈ 40 nm. Interestingly, a survey of structural diversity encompassing 2,600 viruses inhabiting the world’s oceans reveals that the average outer capsid radius is 28 nm (29) (25-nm inner radius), which is much smaller than the critical radii at which replication becomes the dominant cost (Fig. 4). As such, for the majority of viruses, we predict translation is the dominant cost of a viral infection.

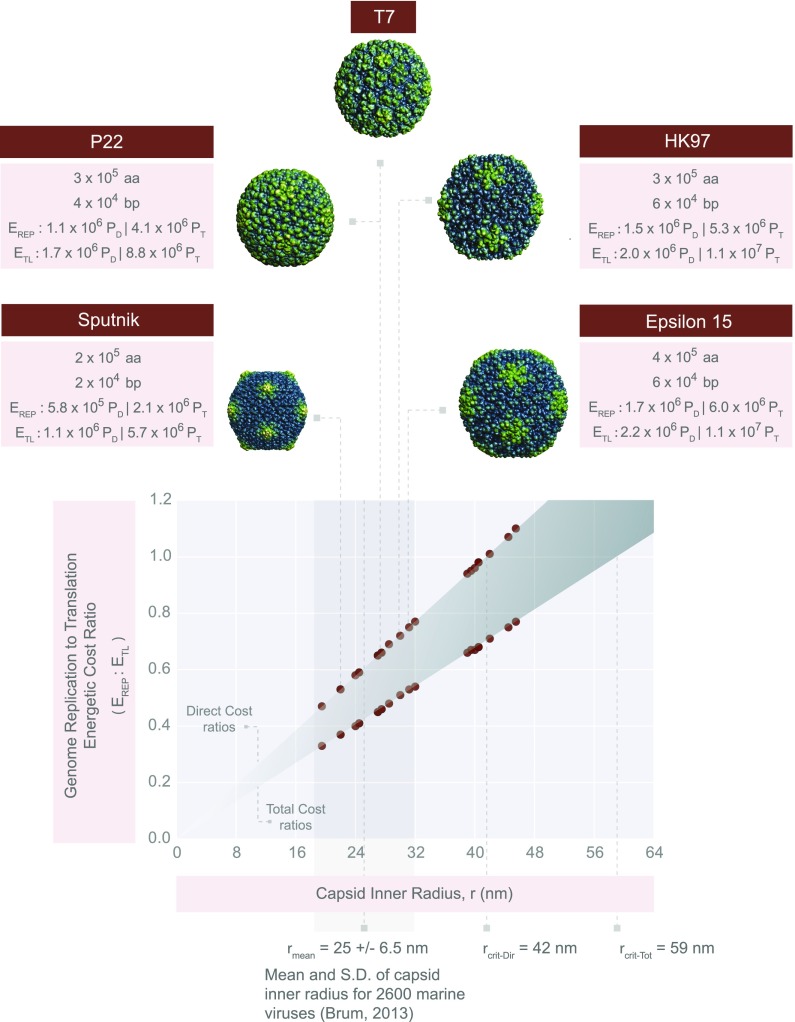
Fig. 4.

Generalizing viral energetics. A plot of the genome replication cost ($E_{REP}$)-to-translational cost ($E_{TL}$) ratio as a function of the virus inner radius, r. The plot uses the geometric parameters of dsDNA viruses with icosahedral geometries (Dataset S2 and SI section XIV). The predicted numbers of amino acids and nucleotides are derived in Dataset S2. Cost ratios are shown for both direct and total cost estimates. All viruses shown infect bacteria except Sputnik, which is a satellite virus of the giant Mimivirus. We have zoomed in on viruses Sputnik (r = 22 nm), P22 (r = 27.5 nm), T7 (r = 27.5 nm), HK97 (r = 30 nm), and Epsilon15 (r = 31.2 nm). The capsid structures for these representative viruses were obtained from the VIPERdb (43), and image sizes were scaled based on radii shown in Dataset S2 to accurately represent the relative sizes of each capsid. The critical radii for the total cost ($r_{crit-Tot}$) and the direct cost ($r_{crit-Dir}$) estimates are shown. We have also included the mean ($r_{mean}$ = 25 nm) and SD (gray vertical box, $\pm$ 6.5 nm) of viral capsid inner radii from 2,600 viruses collected by the Tara Oceans Expeditions (29). Note, here, we have subtracted the mean capsid thickness (3 nm) from the mean capsid radius reported by Brum et al. (29) to arrive at the mean inner capsid radius.

Furthermore, we provide genome replication to translation cost ratios for about 30 different double-stranded viruses, primarily phages (Dataset S2 and Fig. 4). Although we have omitted calculations for the virus tails, they can be simply treated as hollow cylinders and will further decrease the expected replication-to-translation cost ratio for the tailed viruses. Although we have calculated these ratios primarily for dsDNA phages, similar principles can be applied to modeling the energetics of other viral groups.

Forces of Evolution Operating on Viral Genomes.

Inspired by efforts to consider the evolutionary implications of the cost of a gene to cells of different sizes (20, 23), we were curious whether similar considerations might be in play in the context of viruses. For example, we asked which evolutionary forces are prominently operating on neutral genetic elements that are incorporated into viral genomes, either by horizontal gene transfer, gene duplication, or other similar types of events. We further asked whether the viral size is a parameter of interest in the tug of war between different forces of evolution. We will address these topics by assuming that the viral infection, consistent with our findings for T4, consumes a substantial portion of the host energy budget. We further assume that the energetic cost of a genetic element translates to a proportional fitness cost. We believe this assumption to be relevant when the host growth condition is energy or carbon substrate limited.

For a genetic element to remain in the population, regardless of whether it is beneficial or not, it must face the consequences of genetic drift, which scales with the viral effective population size, $N_e$, as ${N_e}^{-1}$. We follow the treatment of Lynch and Marinov who argue that the net selective advantage of a genetic element is $s_n=s_a-\hspace{0.17em}{s}_c$, where $s_a$ and $s_c$ denote the selective advantage and disadvantage, respectively (Fig. 5B). For a genetic element within a viral genome that is nontranscribed and nontranslated (Fig. 5C), only the energetic cost of its replication poses a selective disadvantage. Assuming the genetic element provides no benefit to the virus ($s_a=0$), the net selective advantage can be stated as $s_n=-s_c$, the absolute value of which must be much greater than ${N_e}^{-1}$ for selection to operate effectively. Following Lynch and Marinov and others (23, 30), we make the simplifying assumption that a neutral genetic element’s selection coefficient, $s_c$, is proportional to its fractional energetic cost, $E_g$ (Fig. 5C). This means that the viral infection is energy (or carbon source) limited. Because we assumed that the energetic cost of a viral infection is comparable to the total energy budget of a cell, any increase to the cost of a virus would necessitate a smaller burst size. Using the viral burst size as a proxy for the viral growth rate, we are then able to relate the additional fractional energetic cost of a neutral genetic element to a fitness cost.

Fig. 5.

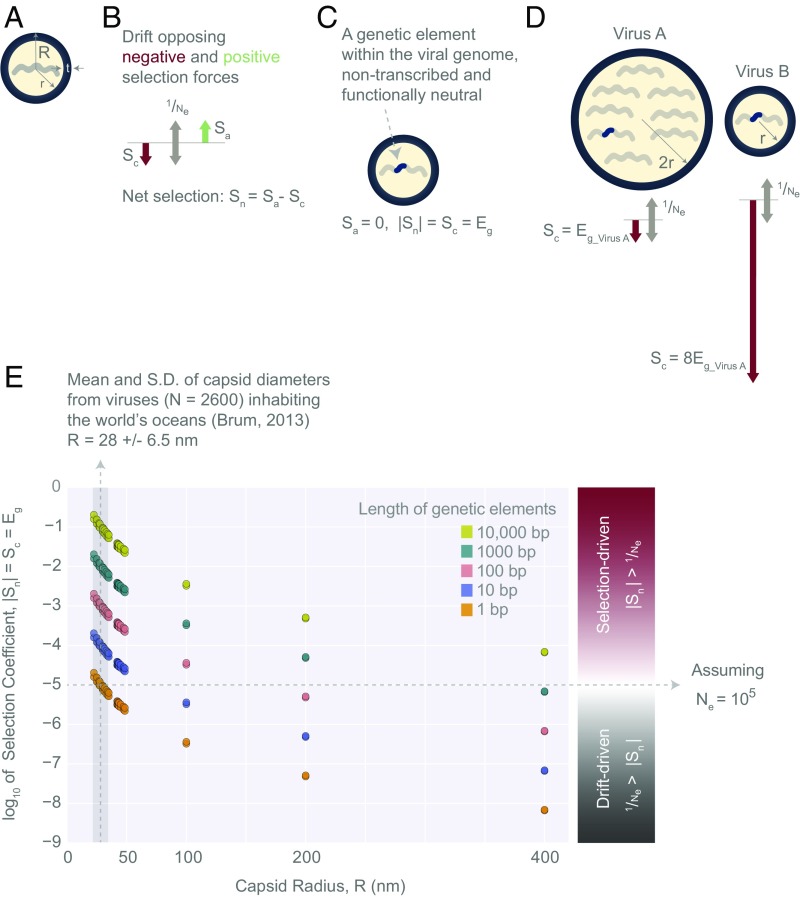
Evolutionary forces acting on genetic elements within viral genomes. (A) Schematic of a virus as a spherical object, with an inner radius, r, an outer radius, R, and a capsid thickness, t. The capsid is composed of viral proteins, whereas the inner volume holds the viral genome. (B) Positive and negative selective forces ($s_a$ and $s_c$) at a tug of war with the force of genetic drift, which scales as ${N_e}^{-1}$, where $N_e$ is the viral effective population size. (C) A schematic of a genetic element within a viral genome. It is assumed to be nonfunctional ($s_a$ = 0) and nontranscribed, resulting in $\left|s_a\right|$ = $s_c$ = $E_g$, where $s_a$ corresponds to the net selection coefficient and $E_g$ corresponds to the fractional cost of a genetic element. (D) The evolutionary forces acting on a genetic element within virus A and virus B genomes. The fractional cost of a genetic element in virus B, $E_{g\_VirusB}$, is eight times higher than the fractional cost of the same element in virus A, $E_{g\_VirusA}$. Note that virus A has twice the radius of virus B, and therefore its genome is eight times longer than that of virus B (schematically represented by the number of genetic segments). Both viruses are assumed to have radii greater than critical radii, $r_{crit-Tot}$ and $r_{crit-Dir}$. (E) Log₁₀ $E_g$ estimates for nontranscribed and neutral genetic elements of different lengths (1–10,000 bp) within the context of 30 dsDNA viruses ranging from ≈ 20 to 400 nm in radius (Dataset S3; viruses with R > 50 nm are hypothetical dsDNA viruses). Log₁₀ $E_g$ estimates derived from both direct and total cost estimates are included (there is minimal difference between these estimates, which is not visible in this figure; Dataset S3). Assuming $N_e$ = 10⁵, the region above the horizontal dashed line represents a selection-dominated regime, and the region below it represents a drift-dominated regime. For comparison, we have included the mean (vertical dashed line, 28 nm) and SD (gray vertical box, $\pm$ 6.5 nm) of viral capsid outer radii obtained from 2,600 viruses collected during the Tara Oceans Expeditions (29).

In the case of a nontranscribed genetic element, $E_g=E_{REP/v}/E_v$, where $E_{REP/v}$ corresponds to its replication cost and $E_v$ is the sum of all costs of a virus (Fig. 5C). Given that replication cost scales as $r^3$, the effects of selection relative to genetic drift could be different for viruses of different sizes. Consider two viruses with the same burst size, with virus A, having a radius that is two times larger than that of virus B (Fig. 5D). Because both viruses are assumed to have radii larger than the critical radius, we imagine the scenario in which the cost of genome replication is the dominant cost of synthesizing these viruses. The fractional cost of a genetic element in the smaller virus, $E_{g\_Virus\hspace{0.17em}B}$ is then equal to $8E_{g\_Virus\hspace{0.17em}A}$, where $E_{g\_Virus\hspace{0.17em}A}$ is the fractional cost of the genetic element in the larger virus. This is because the length of the genome is proportional to $r^3$, and consequently, $E_g$ is inversely proportional to $r^3$ (Fig. 5D).

Fig. 5E and Dataset S3 provide $E_g$ estimates for genetic elements of different lengths (1–10,000 bp) within 30 dsDNA viruses. To illustrate the effect of scaling in the example provided above, we made the simplifying assumption that the viruses are large enough that their $E_v$ are approximately equal to their replication costs. However, for $E_v$ values in Fig. 5E and Dataset S3, we provide more precise estimates, treating $E_v$ as the sum of both the replication cost and the translational cost of a virus. The cost of replicating a double-stranded genetic element can be obtained from Eq. S3. For a 1-kb element, which is about the average length of a bacterial gene, the direct and total costs of its replication per virus, $E_{REP/v},$ are 3 × 10⁴ P_D and 9 × 10⁴ P_T, respectively. Both direct and total cost estimates indicate that the strength of selection acting on a 1 kb, nontranscribed element ranges from 2 × 10⁻² to 7 × 10⁻⁶ (Dataset S3 and Fig. 5E) when considering viruses with radii ranging from ≈ 20 to 400 nm. The difference between direct and total estimates of selection strength is minimal within this range of capsid radii and continues to diminish as the capsids grow in size.

To examine whether selection or genetic drift will decide the fate of a genetic element, we need to assess each virus’s effective population size. This is difficult because the effective population size of most viruses is unknown and subject to great variability due to several environmental factors (31). The current effective population size estimates regarding HIV, influenza, dengue, and measles fall within 10¹ to 10⁵ (31–33). Based on the wide range of variation in these effective population sizes, it is difficult to make conclusive statements. It is, however, apparent that the strength of selection on neutral genetic elements is a nonlinear function of the viral capsid radius and becomes much weaker as viruses get larger (Fig. 5E). In fact, for giant viruses (with outer-radius R > 200 nm), assuming an ${N_e}^{-1}$ = 10⁻⁵, genetic drift could overpower selection, allowing for the persistence of neutral elements of lengths 100 bp or shorter in the population. For the majority of viruses [R $=$ 28 $\pm$ 6.5 nm (29)], however, selection is likely to be the dominant force and drift may only play a role for genetic elements that are just a few base pairs long (Fig. 5E and Dataset S3).

Discussion

There have been several experiments that imply that a viral infection requires a significant portion of the host energy budget (3, 5, 10, 11, 34–36). Following these experimental hints, we enumerated the energetic requirements of two very different viruses on the basis of their life cycles, and thereby estimated the energetic burdens of these viral infections on the host cells. According to our total cost estimates, a T4 infection with a burst size of 200 will consume a significant portion (about 30%) of the host energy supply. This result, demonstrating a significant fraction of the host energy used by an infection, supports the experimental findings that the T4 burst size is correlated positively with the host growth rate (7, 11). It also lends further credence to the hypothesis that auxiliary metabolic genes within phage genomes are not just evolutionary accidents; rather, they have come to serve a functional role in boosting the host’s metabolic capacity, which translates into larger viral burst sizes (3, 4, 36, 37). These calculations make it all the more interesting to develop high-precision, single-cell calorimetry techniques to monitor energy use during viral infections. Perhaps the most promising support for T4’s cost estimate is the observation that the maximum T4 burst size is 1,000 virions (15). Using the total cost to make new viruses, at a burst size of 1,000, the viral infection would consume 170% of the host normal energy supply at a 30-min growth rate, consistent with the observed apparent upper limits on burst size.

It is, however, important to note that, in all of our estimates, we make the assumption that the sources of nitrogen, sulfur, phosphorus, and other trace elements are in excess, which is typical of culture conditions in the laboratory and from which most burst measurements are obtained (SI section II), but this assumption may not be valid in certain natural environments as demonstrated by the phosphorus-limited environments of marine ecosystems (38). In such limited environments, phages are shown to carry auxiliary genes and to actively rewire the host metabolism (full discussion can be found in SI section I). It would be interesting to have additional experimental studies that go beyond the ideal conditions of a laboratory experiment to fully explore the range of possible limiting factors in a viral infection.

Although there are several fascinating studies that explore the link between the host metabolism and phage infections (3, 6, 12, 13), similar studies focusing on viruses of multicellular eukaryotes are largely lacking. To that end, we chose to estimate the energetic cost of a representative virus for this category, namely, the influenza virus. The influenza virus and T4 phage are functionally and evolutionarily very different viruses. However, they have a very similar per-virus cost, regardless of whether the total or the direct cost estimates are being considered. This is primarily due to the fact that they have a similar translational cost, which dominates all other costs. Their comparable cost of translation is due to the fact that these viruses have similar dimensions and are both composed of about a million amino acids. Perhaps even more surprising is that both viral infections have very similar average power consumptions, on the order of 200 fW (SI section XIII).

Even with its higher burst size, an influenza infection has a total cost that is just 1% of the total energetic budget of a eukaryotic cell over the characteristic time of the viral infection. This is because a typical eukaryotic cell is estimated to have much higher energy supply than a typical bacterium under the same growth conditions. So far in our estimates, we do not account for the possible inefficiencies at various stages of the viral infection, which may drain more of the host energy than we estimated. Specifically, burst sizes are typically reported from plaque assays, which count the number of infectious virions that create plaques. However, we do not have a good estimate for the number of noninfectious viruses that arise from faulty genome replication, transcription, or viral assembly, for example. This point is especially important when considering RNA-based viruses such as influenza or HIV, which have higher mutation rates [10⁻⁴ to 10⁻⁶ mutations per base pair per generation (39)] compared with dsDNA viruses such as T4 [10⁻⁶ to 10⁻⁸ mutations per base pair per generation (39)]. As a result of these higher error rates, RNA-based viruses may have greater hidden costs associated with aborted or faulty viral synthesis.

Even infectious viruses cannot all be guaranteed to enter the lytic cycle upon infecting a host cell. For example, only 10% of influenza-infected host cells have been shown to generate infectious virions (40), demonstrating the cumulative inefficiency of an influenza infection. Hence, counting plaques to measure viral burst sizes likely underestimates the true burst size and results in an underestimation of the infection cost. As such, single-cell studies of viral infection could provide a detailed breakdown of inefficiencies at various steps of the viral life cycle and enable more exact cost estimates. We further explore other factors related to the fractional cost of influenza and T4 infections in SI section XV.

Finally, we will need future experimental studies to test the assumptions underlying the relationship between the fractional cost of a neutral genetic element and the strength of negative selection acting on the viral population. There is also a great need for estimates of the effective population sizes of different viruses within their natural environments. With current effective population size estimates for viruses, it appears that selection likely determines the fate of genetic elements for the majority of viruses, which have on average 28-nm radii (29) (Fig. 5E and Dataset S3). However, for larger viruses (R > 200 nm), the diminishing, fractional cost of a gene may enable the interference of genetic drift to the extent that neutral genetic elements could persist in the viral population. The result of such a phenomenon could be genome expansions in the form of gene duplication events, cooption of previously noncoding, horizontally transferred elements into functional genes and regulatory domains, and perhaps even a trend toward greater autonomy over large evolutionary timescales. This effect may explain the unusual number of duplication events in the genomes of giant viruses such as that of the Mimivirus (41, 42).