Abstract
A highly CO2-tolerant green alga, Chlorococcum littorale, was investigated at temperatures ranging from 8 to 28 °C, light intensities from 30 to 170 μmol m−2 s−1, a constant CO2 concentration of 5% (v/v) and atmospheric pressure. The experimental results showed that a specific growth rate μ, defined in terms of cell growth rate under a logarithmic growth phase, increased with temperature up to the maximum value (ca. 22 °C), while the μ decreased at higher temperatures. These promotion and inhibition of the cell growth rate were expressed by both a multiple linear regression and a mathematical model taking account of the Arrhenius activation/deactivation energies. Light intensity affected on the cell growth was independently treated in the mathematical model. The proposed growth model agreed well with the experimental data to within 6.6 %, which provides good correlation for both temperature and light intensity effects on the microalgal cell growth.
Keywords: Algal growth, Chlorococcum littorale, Microalgae
1. Introduction
Algae have many potentials to be studied with a view toward food science and technology [1], energy [4], [7], environment and global warming issues [12], since they can produce valuable metabolites like carbohydrates, proteins, lipids and pigments using highly efficient photosynthesis processes [16]. In these days, researches on microalgae for multifunctional applications have been increased, which can be derived from their advantages of fast growth and good environmental adaptability over normal land biomass resources. High-density growth can also be one of their advantages that could allow efficient production of the above-mentioned biochemicals in opened and/or closed culture systems [14], [19].
Among many microalgal species existing in the nature, Chlorococcum littorale is one of candidates leading to high density cultures, because the cells can thrive at concentration growing up to 84 g/dm3 by using a flat-panel photobioreactor from literature [2]. They also possess a high CO2-tolerance up to 65 % of CO2 concentration [5], [9], [10], although most microalgae thrive at suitable CO2 concentrations, likely from 1 to 5% (v/v). The reason for the high CO2-tolerance can be evaluated by the growth rate in the logarithmic growth phase under photoautotrophic culture systems. Kurano and Miyachi collected experimental data for evaluating CO2-tolerance and applied to a growth inhibition model describing the growth rate of C. littorale [8]. The model was able to represent the experimental growth rate data at CO2 concentrations lower than 20%, however, results at higher CO2 concentrations do not allow sufficient evaluation. Our previous report found that the cell growth model agreed well with the experimental data under rich HCO3-/CO2 conditions [10]. Moreover, at these conditions, production of fatty acids were also promoted during nitrate deficient conditions in culture media based on artificial sea water and low dissolved oxygen concentrations to prevent photorespiration [9], [11].
It is fundamentally another issue of debate to evaluate effects of temperature and light intensity on the C. littorale growth. The growth rate of this strain in the logarithmic growth phase was highly maintained at even extra-high light intensities (<2000 μmol m−2 s−1), which was reported in literature [8]. Although temperature effect was also investigated [8], the interaction between the effects of light intensity and temperature was not reported on the C. littorale growth. For Nannochloropsis oculata, however, the interaction between temperature and light intensity was not observed from both experimental data analyzed by a statistical regression [17], although the findings are different from the report on Microcystis aeruginosa growth [20].
Evaluation of complex parameters related to the microalgal growth rate was needed to develop culture systems. For this aim, a green microalga C. littorale was chosen for study because the strain possesses a high CO2 uptake rate [2] in addition to the above-mentioned advantages [6]. Experiments were planned to prevent photorespiration with having ignored influence of dissolved oxygen gas and to develop a new growth model applicable to a wide range of temperature and light intensity conditions. To evaluate both temperature and light intensity effects and their interaction on C. littorale growth, a multiple linear regression analysis was firstly examined using the experimental data. For this regression process, a simple experimental design method was used for setting the experimental conditions of the variables to examine the correlation between the two variables with respect to cultural growth rate. Since a lot of mathematical models have been proposed to elucidate temperature and light intensity effects, models that describe the obtained experimental data with high accuracy was secondly examined for evaluating C. littorale growth.
2. Materials and methods
A green unicellular alga C. littorale (NBRC 102761) originally isolated by Marine Biotechnology Institute Co., Ltd. was used as received from National Institute of Technology and Evaluation (NBRC, Japan). Culture medium was based on the Daigo IMK medium (Nihon-Seiyaku Co., Ltd.) in artificial seawater made by mixing the Daigo SP (Nihon-Seiyaku Co., Ltd.) with the distilled water. The detailed experimental procedure was shown elsewhere [10]. A 10 cm3 of preculture sample maintained at 22 °C and a photosynthetic photon flux density (PPFD) of ca. 14 μmol m−2 s−1 using a LED light source (TAITEC corporation, LC-LED450W) was added aseptically to a 200 cm3 of fresh culture medium within a flask. The flask was placed on the LED light source, illuminated at a given intensity, I, within an uncertainty of ±5 μmol m−2 s−1 in an air bath (TAITEC, BR-43) where temperature, T, was controlled at a given temperature to within an uncertainty of ±0.5 °C. A flow rate of bubbling gas was regulated at 100 cm3 min−1 at 100 kPa and CO2 concentration was fixed at 5% by mixing CO2 (99.5%) and N2 (99.9%). Growth rate was monitored by means of changes in turbidity of the culture medium (optical density at 750 nm: OD750) using a spectrophotometer (JASCO, V-570). Biomass concentration X [g-dry weight/dm3] at a given incubation time was determined from a calibration curve between the available OD750 and the biomass concentration (g-dry weight/dm3). Initial biomass concentration, X0, was ca. 1.5 ± 1.0 mg/dm3 for each experiment.
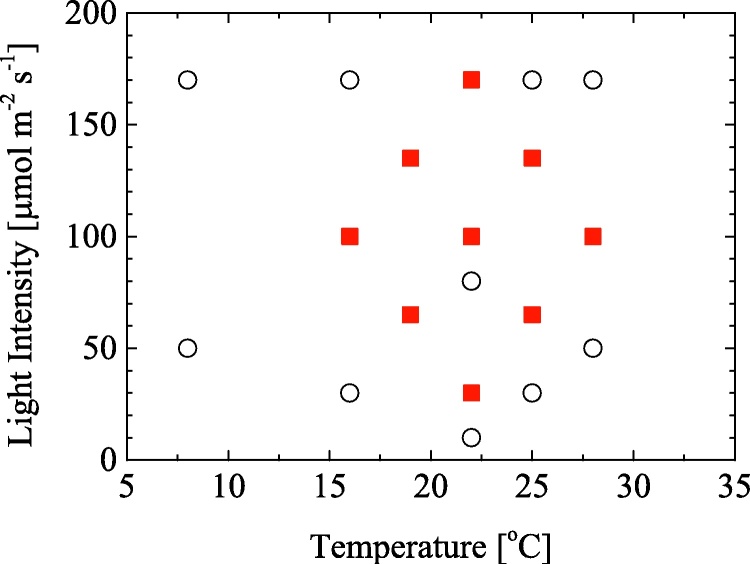
Fig. 1 and Table 1 show the experimental temperature and light intensity conditions chosen in this work. This work focused on temperature and light intensity as key variables to optimize the culture conditions of C. littorale. Since there is a possibility of having interactive relation between these two variables, a simple experimental design method was used for setting the experimental conditions of the variables to examine the correlation between the two variables with respect to cultural growth rate. Firstly, we set a central condition as 22 °C and 100 μmol m−2 s−1 with considering our experimental set up capability, then set a unit scale as 3 °C for temperature and 35 μmol m−2 s−1 for light intensity by considering the weight of effect of each variable on algal cultivation. Consequently, we varied the temperature form −2 to +2 scales and the light intensity from −2 to +2 scales with 1.0 interval, leading to 9 conditions as shown by filled square symbols in Fig. 1.
Fig. 1.
Experimental temperature and light intensity conditions chosen in this study. Symbol of square and circle show the conditions selected with the experimental design method and the extra experiments, respectively.
Table 1.
Correlation of the relative growth rate μ under different temperature and light intensity conditions.
| Run | Number of data | Temperature [°C] | Light intensity [μmol m−2 s−1] |
μ [h−1] | R2 [–] |
|---|---|---|---|---|---|
| 1 | 6 | 16 | 100 | 0.066 | 0.995 |
| 2 | 6 | 19 | 65 | 0.073 | 0.998 |
| 3 | 5 | 19 | 135 | 0.087 | 0.996 |
| 4 | 6 | 22 | 30 | 0.051 | 0.997 |
| 5 | 4 | 22 | 100 | 0.091 | 0.983 |
| 6 | 6 | 22 | 170 | 0.110 | 0.999 |
| 7 | 6 | 22 | 65 | 0.077 | 0.995 |
| 8 | 6 | 25 | 135 | 0.103 | 0.992 |
| 9 | 4 | 28 | 100 | 0.037 | 0.993 |
3. Results and discussion
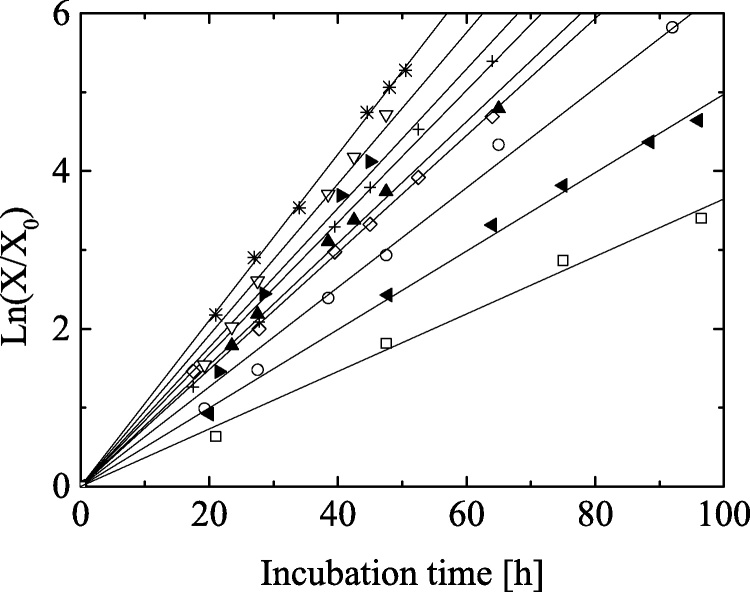
Fig. 2 shows that a plot of the logarithmic relative biomass concentration, ln X/X0, against incubation time, t, under different temperature and light intensity conditions. For each experiment, ln X/X0 increased proportionally with incubation time, of which corresponds to a logarithmic growth phase. The growth rates increased with light intensity, but varied with temperature conditions. With regard this point, a multiple linear regression analysis was carried out for discussion. Because temperature and light intensity have dimension and the absolute values are different each other, a normalization technique was adopted to the experimental data as follows:
| (1) |
| (2) |
T0, I0, ΔT and ΔI were determined from the experimental set up to be 22 °C and 100 μmol m−2 s−1, 6 °C and 70 μmol m−2 s−1, respectively. Thus, an average of the normalized data for each x value was 0 and a maximum absolute deviation was 1.
Fig. 2.
Logarithmic relative concentration, ln (X/X0), as a function of incubation time. Symbols show circles for Run 1, diamonds for Run 2, + marks for Run 3, left pointing triangles for Run4, right pointing triangles for Run 5, asterisks for Run 6, triangles for Run 7, upside-down triangles for Run 8 and squares for Run 9, respectively.
To begin with discussion about interaction between temperature and light intensity on the C. littorale growth rate, the following equation was formulated:
| (3) |
where, x1 and x2 as defined in Eq. (3) mean variables of temperature and light intensity, respectively and a values show the coefficient of each variable. A term of x1x2 shows the interaction between temperature and light intensity. y means a specific growth rate, μ, as defined in the following equation:
| (4) |
where X and t are biomass concentration [g-dry weight/dm3] and incubation time [h], respectively. Standardizing Eq. (4) with X0 which is the initial biomass concentration leads to the following equation:
| (5) |
The obtained specific growth rate, μ, under different temperature and light intensity conditions were listed in Table 1.
When a regression formula (Eq. (3)) includes unnecessary variable number, the expression was not explained statistically. Therefore, variable numbers were selected for the formulated regression. There are several ways for the selection of variable numbers. The method falls roughly into two categories. One is all possible regression and another is iteration technique which was adopted in this work because of convenient usefulness and the calculated load. Excel 2013 was used for this analysis.
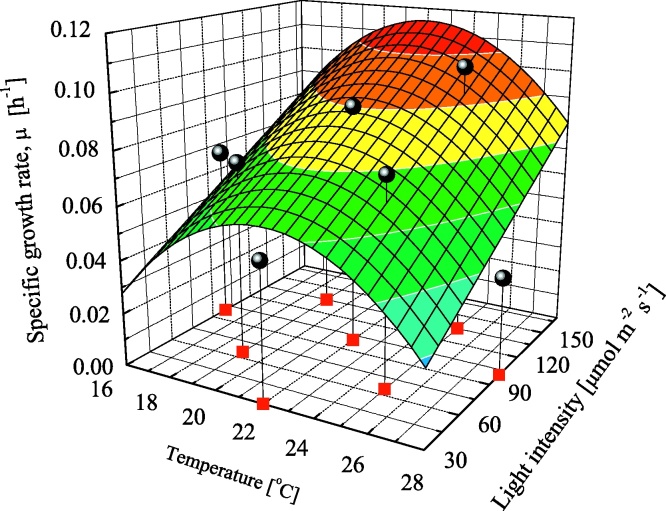
If the F-test for the model after regression is significant at the 5% level (i.e., P < 0.05), there is evidence that the model can explain the variation in the response. The regression results as shown in Table 2a for the first calculation (Model A) using all terms in Eq. (3) show that the model cannot satisfactorily explain the effects of two factors on the C. littorale growth (Prob. < F = 0.129) although R2 = (0.878) can be almost suitable. From the resulted coefficient values as shown in Table 2b, the effects of a1 and a12 were decided to be too small to be removed for better regression. By iteration process, a22 can be removed, but if a11 was removed, the F value did not become feasible, then the iteration process quitted for the second calculation (Model B). The obtained results listed in Table 2a shows that the model B can satisfactorily explain the above effects (Prob. < F = 0.008). As mentioned above, the F-test for the model after regression is significant at the 5% level (i.e., P < 0.05) and there is evidence that the model B can explain the variation in the response. The correlated results using model B, of which fitting parameters were listed in Table 2b, revealed that the experimental data agreed well with the calculation results as shown in Fig. 3. From the correlation, an average relative deviation (ARD) as defined in Eq. (6) was within 14.6 %, meaning that the C. littorale growth was not strongly affected by the interaction between temperature and light intensity (a12), which well supported for the discussion of N. oculata growth [17], although the findings are different from the report on M. aeruginosa growth [20].
| (6) |
Table 2a.
Correlation of the relative growth rate μ under different conditions.
| Run | Number of experiments for the calculation | Number of variables in the model | Prob. > F |
|---|---|---|---|
| Model A | 9 | 6 | 0.129 |
| Model B | 9 | 3 | 0.008 |
Table 2b.
Calculation results for Model A and B.
| Variable | Coefficient | Model A | Model B |
|---|---|---|---|
| – | a0 | 0.0969 | 0.0888 |
| x1 | a1 | −0.0064 | – |
| x2 | a2 | 0.0262 | 0.0262 |
| x11 | a11 | −0.0440 | −0.0349 |
| x22 | a22 | −0.0440 | – |
| x12 | a12 | −0.0151 | – |
Fig. 3.
Experimental data for C. littorale growth under different temperature and light intensity conditions accompanied with calculation results by model B.
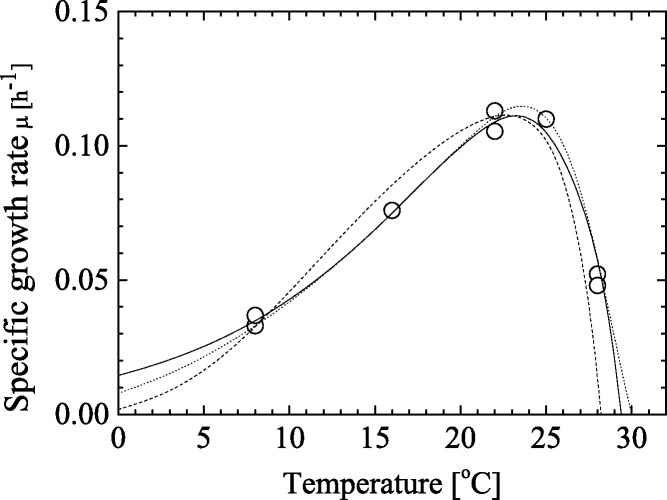
Because another evaluation technique was necessary to elucidate the effects between temperature and light intensity on C. littorale growth, the mathematical modeling was examined in this study. Extra experiments were carried out for this purpose, which was shown in Fig. 1. Fig. 4 shows a specific growth rate μ as defined in Eq. (4) as a function of temperature at a light intensity of 170 μmol m−2 s−1 and a CO2 concentration of 5% with diluted nitrogen gas. From the Fig. 4, the μ values increased with temperature up to ca. 22 °C, although those decreased at the higher temperature conditions.
Fig. 4.
Specific growth rate μ as a function of temperature. The results of fitting by Eqs. (7)–(9) to the experimental data show continuous line, dashed line and dotted line, respectively.
For modeling the fundamental experimental data, the several mathematical models proposed in literatures were selected. Perez et al. examined Eq. (7) from Phaeodactylum tricornutum cultures [13] using the following equation:
| (7) |
The first term of the right-hand side shows a promotion effect on microalgal growth, while the second term shows an inhibition effect. The reference temperature (T0) was arbitrary value in the literature and defined at the first treatment as 22 °C chosen in this work. Fitting parameters are frequency factors A0 and B0 and activation energies Ea and Eb, respectively.
Ratkowsky et al. proposed a subduplicate empirical model [15] as follows:
| (8) |
Tmin and Tmax mean a minimum and a maximum temperature at which the cell can grow, respectively and b and c are constants.
Huang et al. proposed combination of Eyring model derived from the Arrhenius equation with the subduplicate empirical model [3] as defined in the following equation:
| (9) |
ΔG means the Gibbs activation energy for cell growth and fitting parameters are A and B. The calculation results with these model were shown in Fig. 4. Available parameters are listed in Table 3. From the ARD analysis with Eq. (6), the Arrhenius-type equation Eq. (7) was the most suitable among the three models because the ARD value is the smallest (3.86%). However, the treatment of T0 is an issue of debate, and thus, we examined how the fitting is affected by various T0 as shown in Table 4. From the table, there are not large deviation with the various T0 changed. Thus, the reference temperature of 22 °C was also adopted in the following section.
Table 3.
Fitting parameters by each model and the resulted ARD.
Table 4.
Fitting parameters of A0, B0, Ea and Eb in Eq. (7) estimated as a function of arbitrary T0 and the resulted ARD.
| T0 [K] | 273 | 293 | 296 (Tmax) | 313 | 333 |
|---|---|---|---|---|---|
| A0 [h−1] | 0.015 | 0.124 | 0.168 | 0.838 | 4.12 |
| B0 [h−1] | 0.000 | 0.025 | 0.056 | 4.60 | 436 |
| Ea [kJ/mol] | 71.2 | 71.4 | 71.5 | 72.4 | 71.0 |
| Eb [kJ/mol] | 198 | 199 | 199 | 199 | 199 |
| ARD [%] | 3.82 | 3.81 | 3.78 | 3.69 | 3.59 |
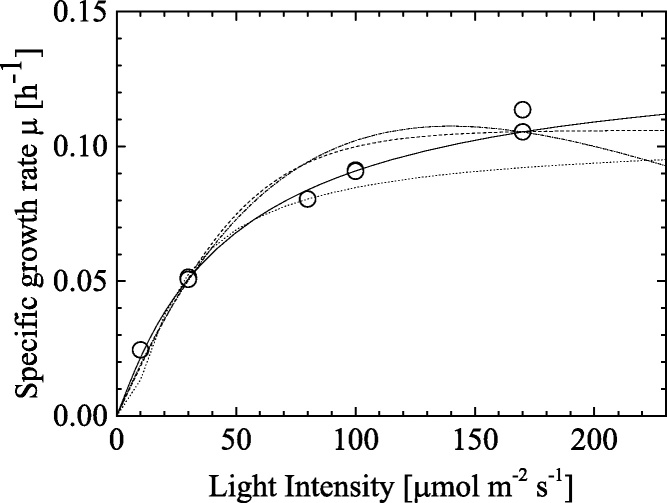
Next, we discussed about the effect of light intensity on the C. littorale growth with taking account of the above-mentioned Arrhenius-type equation that described the temperature effect well. Fig. 5 shows the specific growth rate μ as a function of light intensity. The μ values increased with light intensity at low light intensities and then the slope was changed and gradually increased with light intensity at high light intensities. According to the experimental data, we selected models from the following 4 types of equations, which would satisfactorily explain the phenomenon.
| (10) |
| (11) |
| (12) |
| (13) |
Fig. 5.
Specific growth rate μ as a function of light intensity. The results of fitting by Eqs. (10)–(13) to the experimental data show dashed line, dotted line, continuous line and dashed-dotted line, respectively.
Eqs. (10) and (11) include hyperbolic tangent and exponential functions, respectively. Both functions can be used for expression of activity of photosynthesis [8]. For Eq. (12), the functional form resembles the Monod type equation for modeling of enzymatic reactions [18]. Eq. (13) is extended for the expression of exponential function of Eq. (10). We used the four models for comparing with our obtained experimental data, which was shown in Fig. 5. All the models were fitted well with some errors. From the ARD analysis as shown in Table 5, the Monod-type equation in Eq. (12) showed the smallest (3.34%) among the four models, which describes our experimental data the best. Thus, we chose the Eq. (12) for the next discussion.
Table 5.
Fitting parameters from each equation with ARD.
| μm [h−1] | Ik [μmol m−2 s−1] | ARD [%] | |
|---|---|---|---|
| Eq. (10) | 0.106 | 56.5 | 8.34 |
| Eq. (11) | 0.104 | 20.4 | 13.7 |
| μm [h−1] | KI [μmol m−2 s−1] | ARD [%] | |
|---|---|---|---|
| Eq. (12) | 0.136 | 49.7 | 3.34 |
| μm [h−1] | Iopt [μmol m−2 s−1] | ARD [%] | |
|---|---|---|---|
| Eq. (13) | 0.108 | 140 | 7.79 |
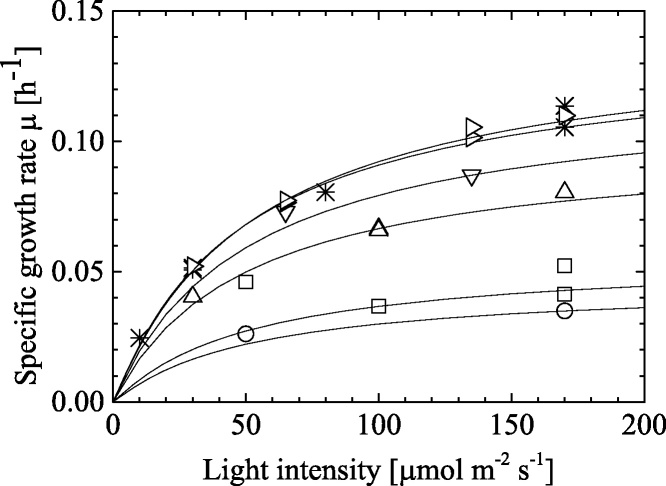
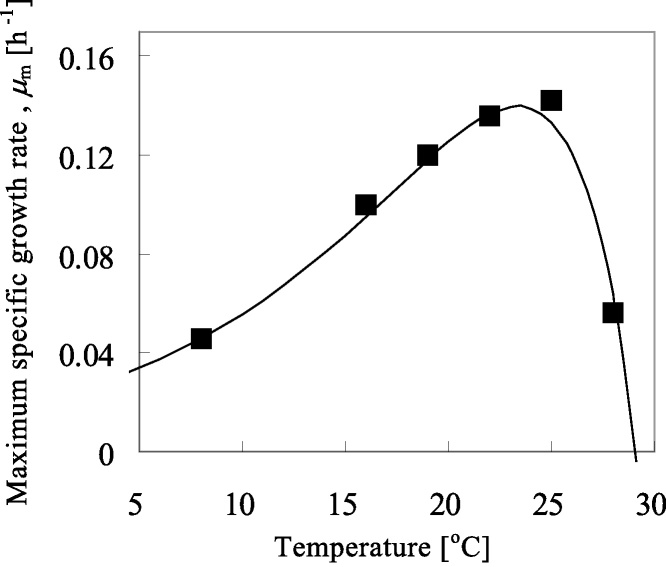
Fig. 6 shows that the μ as a function of light intensity under different temperatures with correlation results using Eq. (12) The good agreement was observed in calculations with experimental data. The resulted fitting parameter using Eq. (12) depended on temperature was listed in Table 6. A half-saturation number of KI was the almost same with the different temperature conditions, while maximum specific growth rate, μm, were varied with temperatures. The effect of temperature on the μm was plotted in Fig. 7. The μm value increased with temperature up to ca. 25 °C, while that decreased at the higher temperature conditions. Because the function was very similar to the Arrhenius-type model in Eq. (7), which was as shown in Fig. 4, here we used the following model for this expression:
| (14) |
Fig. 6.
Specific growth rate μ as a function of light intensity under different temperature conditions. In Figure, symbols show circles for 8 °C, triangles for 16 °C, upside-down triangles for 19 °C, asterisks for 22 °C, right pointing triangles for 25 °C and squares for 28 °C, respectively. Continuous line shows the correlation results by Eq. (12).
Table 6.
Temperature dependence of fitting parameters with the resulted ARD.
| Temperature [°C] |
KI [μmol m−2 s−1] | μm [h−1] | ARD [%] |
|---|---|---|---|
| 8 | 53.2 | 0.046 | 7.48 |
| 16 | 50.0 | 0.100 | 3.09 |
| 19 | 51.5 | 0.120 | 4.07 |
| 22 | 49.7 | 0.136 | 3.34 |
| 25 | 54.0 | 0.142 | 1.64 |
| 28 | 52.9 | 0.056 | 15.5 |
Fig. 7.
Maximum specific growth rate, μm, as a function of temperature. Continuous line shows the correlation results by using Eq. (14).
The parameters obtained from fitting to our experimental data were listed in Table 7. The model was a good agreement within ARD of 1.52%. From activation energy balance analysis, a deactivation energy (Eb = 198.4 kJ mol−1) overcame an activation energy (Ea = 73.4 kJ mol−1). From kinetic model for growth of P. tricornutum, Ea and Eb showed 117.0 kJ mol−1 and 163.0 kJ mol−1, respectively [13] and the orders of activation energies were comparable between our results and literature [13]. Thus, the final expression of the growth model was shown as follows:
| (15) |
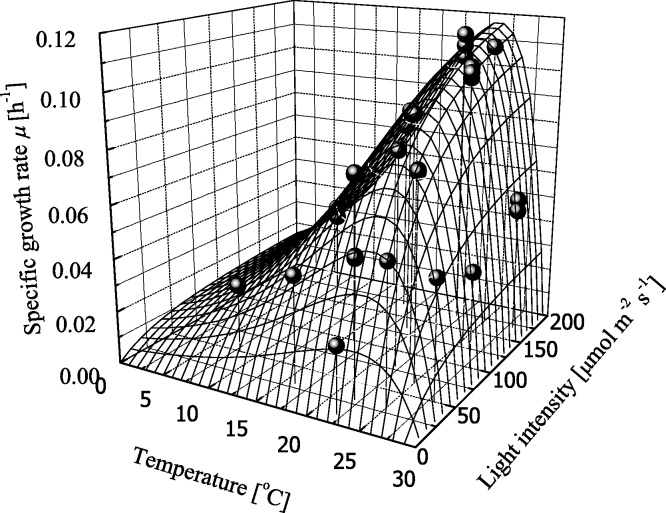
As mentioned in Table 6, KI was independent of temperature and light intensity and assumed to be the averaged value (51.8 μmol m−2 s−1). From the obtained parameters in Table 7, the results using the growth model was in Fig. 8. ARD for this calculation within 6.6% showed a good agreement between experimental and calculation to be achieved.
Table 7.
The obtained fitting parameters with the resulted ARD.
| A0 [h−1] | B0 [h−1] | Ea [kJ mol−1] | Eb [kJ mol−1] | ARD [%] |
|---|---|---|---|---|
| 0.192 | 0.079 | 73.4 | 198.4 | 1.52 |
Fig. 8.
Specific growth rate, μ, as a function of temperature and light intensity. Symbol of circle shows experimental data with continuous line showing correlation by Eq. (15).
Consequently, the above-mentioned two analyses with regression and mathematical modeling showed that the cell growth of C. littorale can discriminate between temperature and light intensity effects. The temperature given for the maximum growth rate for this strain was ca. 25 °C and light intensity effect was expressed by the Monod-type equation. The results obtained by mathematical models were well supported by the multiple linear regression analysis.
4. Conclusions
A highly CO2-tolerant green alga, C. littorale, was investigated for clarification of the effects of both temperatures and light intensities on the C. littorale growth. From analyses by a multiple linear regression, the C. littorale growth was affected independently by each temperature and light intensity and not strongly affected by the interaction between temperature and light intensity. A mathematical model taking account of the Arrhenius activation/deactivation energies expressed the temperature-dependent promotion and inhibition of the cell growth rate. Light intensity affected on the cell growth was independently treated in the mathematical model. The proposed growth model agreed well with the experimental data to within 6.6 %, which provides good correlation for both temperature and light intensity effects on the microalgal cell growth.
Acknowledgements
The financial aids given by the Grant-in-Aid for and Next-generation Energies for Tohoku Recovery (NET) project of the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) are gratefully acknowledged.
Footnotes
Available online 7 May 2015
References
- 1.Harker M., Tsavalos A.J., Young A.J. Factors responsible for astaxanthin formation in the chlorophyte Haematococcus pluvialis. Bioresour. Technol. 1996;55:207–214. [Google Scholar]
- 2.Hu Q., Kurano N., Kawachi M., Iwasaki I., Miyachi S. Ultrahigh-cell-density culture of a marine green alga Chlorococcum littorale in a flat-plate photobioreactor. Appl. Microbiol. Biotechnol. 1998;49:655–662. [Google Scholar]
- 3.Huang L.H., Hwang A.D., Phillips J. Effect of temperature on microbial growth rate–mathematical analysis: the arrhenius and Eyring–Polanyi connections. J. Food Sci. 2011;76:E553–E560. doi: 10.1111/j.1750-3841.2011.02377.x. [DOI] [PubMed] [Google Scholar]
- 4.John R.P., Anisha G.S., Nampoothiri K.M., Pandey A. Micro and macroalgal biomass: a renewable source for bioethanol. Bioresour. Technol. 2011;102:186–193. doi: 10.1016/j.biortech.2010.06.139. [DOI] [PubMed] [Google Scholar]
- 5.Kodama M., Ikemoto H., Miyachi S. A new species of highly CO2-tolerant fast growing marine microalga suitable for high density culture. J. Mar. Biotechnol. 1993;1:21–25. [Google Scholar]
- 6.Kodama M., Ikemoto H., Miyachi S. A new species of highly CO2-tolerant fast growing marine microalga suitable for high density culture. J. Mar. Biotechnol. 1993;1:21–25. [Google Scholar]
- 7.Konur O. The scientometric evaluation of the research on the algae and bio-energy. Appl. Energy. 2011;88:3532–3540. [Google Scholar]
- 8.Kurano N., Miyachi S. Selection of microalgal growth model for describing specific growth rate-light response using extended information criterion. J. Biosci. Bioeng. 2005;100:403–408. doi: 10.1263/jbb.100.403. [DOI] [PubMed] [Google Scholar]
- 9.Ota M., Kato Y., Watanabe H., Watanabe M., Sato Y., Smith R.L., Inomata H. Fatty acid production from a highly CO2 tolerant alga, Chlorocuccum littorale, in the presence of inorganic carbon and nitrate. Bioresour. Technol. 2009;100:5237–5242. doi: 10.1016/j.biortech.2009.05.048. [DOI] [PubMed] [Google Scholar]
- 10.Ota M., Kato Y., Watanabe M., Sato Y., Smith R.L., Rosello-Sastre R., Posten C., Inomata H. Effects of nitrate and oxygen on photoautotrophic lipid production from Chlorococcum littorale. Biosour. Technol. 2011;102:3286–3292. doi: 10.1016/j.biortech.2010.10.024. [DOI] [PubMed] [Google Scholar]
- 11.Ota M., Watanabe H., Kato Y., Watanabe M., Sato Y., Smith R.L., Jr., Inomata H. Effect of inorganic carbon on photoautotrophic growth of a microalga Chlorococcum littorale. Biotechnol. Prog. 2009;25:492–498. doi: 10.1002/btpr.123. [DOI] [PubMed] [Google Scholar]
- 12.Packer M. Algal capture of carbon dioxide; biomass generation as a tool for greenhouse gas mitigation with reference to New Zealand energy strategy and policy. Energy Policy. 2009;37:3428–3437. [Google Scholar]
- 13.Perez E.B., Pina I.C., Rodriguez L.P. Kinetic model for growth of Phaeodactylum tricornutum in intensive culture photobioreactor. Biochem. Eng. J. 2008;40:520–525. [Google Scholar]
- 14.Posten C., Schaub G. Microalgae and terrestrial biomass as source for fuels—a process view. J. Biotechnol. 2009;142:64–69. doi: 10.1016/j.jbiotec.2009.03.015. [DOI] [PubMed] [Google Scholar]
- 15.Ratkowsky D.A., Olley J., McMeekin T.A., Ball A. Relationship between temperature and growth-rate of bacterial cultures. J. Bacteriol. 1982;149:1–5. doi: 10.1128/jb.149.1.1-5.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Singh S., Kate B.N., Banerjee U.C. Bioactive compounds from cyanobacteria and microalgae: an overview. Crit. Rev. Biotechnol. 2005;25:73–95. doi: 10.1080/07388550500248498. [DOI] [PubMed] [Google Scholar]
- 17.Spolaore P., Joannis-Cassan C., Duran E., Isambert A. Optimization of Nannochloropsis oculata growth using the response surface method. J. Chem. Technol. Biotechnol. 2006;81:1049–1056. [Google Scholar]
- 18.Tamiya H. Some theoretical notes on the kinetics of algal growth. Syokubutsugaku Zasshi. 1951;64:167–173. [Google Scholar]
- 19.Ugwu C.U., Aoyagi H., Uchiyama H. Photobioreactors for mass cultivation of algae. Bioresour. Technol. 2008;99:4021–4028. doi: 10.1016/j.biortech.2007.01.046. [DOI] [PubMed] [Google Scholar]
- 20.Yang Z., Geng L.L., Wang W., Zhang J. Combined effects of temperature, light intensity, and nitrogen concentration on the growth and polysaccharide content of Microcystis aeruginosa in batch culture. Biochem. Syst. Ecol. 2012;41:130–135. [Google Scholar]