Efficient utilisation of hydrogel preparations with encapsulated enzymes – a case study on catalase and hydrogen peroxide degradation

Graphical abstract

Highlights

• •We present a model for the process of enzyme encapsulation in hydrogels.
• •Parameters influencing the process efficiency and substrate conversion rate are selected.
• •The diameter of the gel capsule used for enzymatic preparation influences the process efficiency.
• •Encapsulated enzymes remain more active than native enzymes and enzymes immobilised on solid supports.

Abstract

The size of the gel preparation, the concentration of the encapsulated enzyme and the ratio of the preparation volume to the volume of the reaction mixture influence the reaction efficiency with encapsulated biocatalysts. A model of first order enzymatic reaction with substrate diffusion is presented and validated by the decomposition reaction of hydrogen peroxide by catalase. The Thiele modulus (Ф) contains the modified (including the enzyme concentration) enzymatic reaction constant (k′). Based on the model analysis, the Thiele modulus should not exceed a value of 2 (optimally less than 0.5). This value can be controlled by appropriate selection of the enzyme concentration inside and the size of the capsule. A lower Ф value gives a flat substrate concentration profile inside the gel capsule and all the enzyme molecules are involved in the reaction. The optimal diameter of the gel capsule with respect to their separation from the reaction mixture is 1–2 mm.

Nomenclature

a

Constant

b

Constant

C_E,imm

Enzyme concentration inside alginate structure, g l⁻¹

C_S,in

Substrate concentration in the entering stream, g l⁻¹

C_S

Substrate concentration, g l⁻¹

C_S,m

Average substrate concentration inside alginate structure, g l⁻¹

C_S,out

Substrate concentration in the outgoing stream, g l⁻¹

D_S

Diffusion coefficient m² s⁻¹

k_1,imm

Kinetic constant, l g⁻¹ h⁻¹

k′

Modified kinetic constant, h⁻¹

m_S

Mass of substrate, g

N

Number of capsules

P_S

Equilibrium coefficient

Q

Stream, l h⁻¹

R

Capsule radius, m

r

Local capsule radius, m

v_imm

Reaction rate inside alginate structure, g l⁻¹ h⁻¹

v_m

Average reaction rate inside alginate structure, g l⁻¹ h⁻¹

t

Time, h

V_alg

Volume of alginate flat structure, l

V_cap

Volume of alginate capsule, l

V_res

Volume of substrate reservoir, l

Φ

Thiele modulus

τ

Residence time, h

1. Introduction

Enzymes are immobilised to increase their thermal stability, operational stability and facilitate their reuse. There are two general strategies for enzyme immobilisation: surface immobilisation by chemical or physical interaction on a solid support and biocatalyst encapsulation inside matrices such as hydrogels or within solid membranes [16], [29], [2], [31], [19], [21].

The key parameters that allow hydrogels to be used as carriers for immobilised enzymes include the type and origin of the hydrogel, the hydrogel molecular structure (i.e. linear polymers, block-copolymers or graft polymer multicomponent mixtures) and the hydrogel physicochemical properties (e.g. pore size, water absorption capacity, mechanical strength, resistance to high temperatures and pH changes and the amount and quality of reactive functional groups that can interact with the biocatalyst).

Chitosan, alginate and gelatine are the most commonly used hydrogels for enzyme and microbial cell immobilisation [11], [5], [7], [20], [25]. These polymers are inexpensive, derived from natural sources, inert, strongly hydrophilic and biocompatible. Thus, they are attractive for the immobilisation of active, sensitive compounds. The hydrogel encapsulation systems can be designed with various shapes and sizes. Depending on the reactants, the polymer concentration and the rate of gelation, the hydrogels may exhibit either homogeneous or inhomogeneous distribution of structural components [3], [13].

Any ingredients dissolved or suspended in the solution during gelation become encapsulated inside the hydrogel structure after gelation. If the pores size of the hydrogel is less than the diameter of the particles, the particles remain in encapsulated form in the hydrogel preparation (smaller molecules diffuse gradually to the external environment). Thus, this immobilisation strategy can be used for each kind of biocatalyst and for whole enzymatic systems.

Various enzymes have been encapsulated in hydrogels including glucose oxidase [18], [4], β-galactosidase [23], [9], invertase [8], [15], tyrosinase [30], [1] and catalases [10], [22].

Catalases (EC 1.11.1.6) decompose hydrogen peroxide to water and oxygen. Catalase may be used to degrade H₂O₂ after textile bleaching [6], [17] after cold pasteurisation of milk and other liquids [24], [28] to remove H₂O₂ from reactions coupled with oxidases and in biosensor system to determine H₂O₂ or glucose concentrations [14].

The enzyme encapsulation papers mentioned above are typical experimental reports describing the immobilisation method and process conditions. The experiments were carried out using a wide, randomly selected range of parameters. The authors reported an increase in the stability of the immobilised biocatalysts after storage and increased thermal stability. The enzymes could also be used multiple times without significant loss of catalytic activity, demonstrating the attractiveness of the immobilisation preparations. However, there is a need to resolve the randomness of the application parameters.

Here, we present a model for choosing process parameters such as the size of the gel preparation, the concentration of the encapsulated enzyme and the ratio of the volume of the preparation to the total volume of the system. The optimization based on the model takes into consideration the process productivity (amount of conversed substrate molecules over time) and efficiency with respect to the enzyme (utilisation of all of the enzyme molecules). Because the study was carried out with catalase, the enzyme applied in food industry and medicine, we chosen the alginate – the biocompatible hydrogel, acceptable for the contact with food.

2. Model of the process

Because the enzyme is usually the most expensive component of the system, the aim is to utilise all of the encapsulated biocatalyst molecules. This will occur if the reaction is significantly slower than the diffusion of the substrate into the interior of the hydrogel (the catalytic regime). For this case, it can be assumed with good accuracy that the substrate concentration profile across the hydrogel capsule will be flat, and its value is only a function of the substrate concentration in the solution surrounding the capsules. In the diffusive regime, however, a fast reaction occurs at the surface of the capsules and the substrate does not diffuse into the capsules. Thus, enzymes located near the centre of the capsule will not be involved in reaction. To summarise, in the catalytic regime, the reaction is slow, but the enzyme is fully utilised (good efficiency), while in the diffusive regime, the reaction is fast (high productivity), but some of the enzyme is not used. The values of k′, D_S, R included in the Thiele modulus (Φ) determine the process regime.

The model can be used to select the most effective (high substrate conversion rate) and economic (all enzyme is used) parameters. To describe the mass transport of the biochemical reaction in the capsule, the following assumptions were made:

• 1.The capsules are spherical with radius R.
• 2.The interior of the capsule is homogeneous and the catalyst is encapsulated homogeneously at a known concentration.
• 3.A substrate penetrates the capsule, where it is reacted. Its concentration in a homogeneous liquid medium surrounding the capsule is C_S,out, which changes with time C_S,out(t).
• 4.
  The concentration at the interface of the capsule C_S(R) and the concentration of the surrounding liquid C_S,out are in equilibrium described by an equilibrium coefficient P_S.

  $$C_s(R,t)=P_s\times C_{s,\mathrm{out}}(t)$$ (1)
• 5.Transport inside the capsule occurs by diffusion. There is no convection.
• 6.
  The reaction follows first-order kinetics.

  $$v_{\mathrm{imm}}={-k}_{1,\mathrm{imm}}\times C_{E,\mathrm{imm}}\times C_s=k^{\prime }\times C_s$$ (2)
• 7.The reaction product does not affect the diffusion or the reaction rate.

The substrate concentration in the capsule is a function of location and time = >C_S(r, t). The substrate accumulation is equal to the difference in the rate of diffusion and the reaction rate, as described by the following equation:

$$\frac{\partial C_S}{\partial t}=D_S\times {\nabla }^2{C}_S-v_{\mathrm{imm}}$$ (3)

The Laplacian in the spherical system is calculated according to the following equation:

$${\nabla }^2{C}_S=\frac{1_{\mathrm{}}}{r^2}\times \frac{\partial }{\partial r}\left(r^2\frac{\partial C_S}{\partial r}\right)=(\frac{{\partial }^2{C}_S}{\partial r^2}+\frac{2}{r}\frac{\partial C_S}{\partial r})$$ (4)

Thus, the model equation takes the following form:

$$\frac{\partial C_S}{\partial t}=D_S\times (\frac{{\partial }^2{C}_S}{\partial r^2}+\frac{2}{r}\frac{\partial C_S}{\partial r})-k^{\prime }\times C_S$$ (5)

Under steady-state conditions, C_S is only a function of the location. The solution of Eq. (5) can thus be determined using the following expression:

$$r\times C_S(r)=a\times \text{sinh}(r\times \sqrt{\frac{k^{\prime }}{D_S}})+b\times \text{cosh}(r\times \sqrt{\frac{k^{\prime }}{D_S}})$$ (6)

To determine constants a and b​, the boundary conditions were defined. The first boundary condition resulted from the symmetry (Eq. (7)).

$$r=0\frac{\partial C_S}{\partial r}=0$$ (7)

The second boundary condition resulted from assumption (Eqs. (8) and (4)).

$$C_S(R)=P_S\times C_{S,\text{out}}$$ (8)

Using the above conditions, b = 0 and

$$a=\frac{P_S\times C_{S,\mathrm{out}}\times R}{\sinh (R\times \sqrt{k^{\prime }/D_S})}$$ (9)

the substrate concentration profile inside the capsule can be described by the following equation:

$$C_S(r)=P_S\times C_{S,\mathrm{out}}\times \frac{R}{r}\times \frac{\sinh (r\times \sqrt{k^{\prime }/D_S})}{\sinh (R\times \sqrt{k^{\prime }/D_S})}$$ (10)

Using the Thiele modulus, we obtain the following:

$${\mathrm{\Phi }}^2=R^2\times \frac{k^{\prime }}{D_S}$$ (11)

Eq. (10) thus takes the following form:

$$C_S(r)=P_S\times C_{S,\mathrm{out}}\times \frac{R}{r}\times \frac{\sinh (r\times \mathrm{\Phi })}{\sinh (\mathrm{\Phi })}$$ (12)

Using Eq. (12), the average concentration of substrate inside capsule is expressed as follows:

$$C_{S,m}={\displaystyle \underset{0}{\overset{R}{\int }}}\frac{C_S^{\mathrm{}}(r)\times A(r)\times \text{d}r}{V_{\text{cap}}}$$ (13)

After integration, we obtain the following.

$$\begin{array}{l}{C}_{S,m}=\frac{3\times P_S\times C_{S,\mathrm{out}}\times D_S}{k^{\prime }\times R^2\times \sinh (\mathrm{\Phi })}\times [\mathrm{\Phi }\cdot \cosh (\mathrm{\Phi })-\sinh (\mathrm{\Phi })]=\\ \frac{3\times P_S\times C_{S,\mathrm{out}}}{{\mathrm{\Phi }}^2\times \sinh (\mathrm{\Phi })}\times [\mathrm{\Phi }\times \cosh (\mathrm{\Phi })-\sinh (\mathrm{\Phi })]=\frac{3\times P_S\times C_{S,\mathrm{out}}}{{\mathrm{\Phi }}^2}\times [\mathrm{\Phi }\times \cosh (\mathrm{\Phi })-1]\end{array}$$ (14)

The model parameters of the Thiele modulus include the diffusion coefficient, kinetic constant and equilibrium coefficient. These values should be determined in independent experiments. The procedures and the values obtained for the decomposition of hydrogen peroxide by catalase are described below.

3. Materials and methods

3.1. Materials

Catalase (hydrogen peroxide oxidoreductase, EC 1.11.1.6.) from bovine liver (2000–5000 U mg⁻¹), alginic acid sodium salt, HEPES (2-(4-(2-hydroxyethyl)-1-piperazinyl) ethanesulfonic acid), tris (2-amino-2-hydroxymethyl-propane-1,3-diol) were purchased from Sigma Chemical Co., hydrogen peroxide and other chemicals were obtained from POCH.

3.2. Immobilisation of catalase into alginate capsules

For the formation of alginate capsules containing catalase, two solutions in 0.05 M HEPES–tris buffer, pH 6.4 were prepared: alginic acid sodium salt (20 g l⁻¹) and catalase (2 or 4 mg l⁻¹). The freshly prepared catalase solution (50 ml) was suspended in 50 ml of alginate solution. This suspension was injected into the crosslinking solution. To prepare the crosslinking solution, 30 g of calcium chloride was added to 300 ml of distilled water. The enzyme (0.3 or 0.6 mg) was also added to this solution (to prevent transport by diffusion during gelation). The alginate capsules were hardened for one hour at 4 °C and washed twice with 0.05 M HEPES–tris buffer. The capsules were stored at 4 °C in the buffer. Before and after formation of the capsules the enzyme concentration in the crosslinking solution was determined by the Lowry method [12]. The mass of the enzyme in the solution before and after the process was equal. Thus, the enzyme concentration within the capsules was the same as the concentration in the injected solution.

3.3. Estimation of the kinetics parameter

To avoid mass transfer resistance from the solution to the capsule surface, the kinetics measurements were performed in a flow system with a fixed bed of alginate. The flat alginate structure, V_alg = 0.8 ml, was crosslinked with calcium (under the same conditions described in Section 3.2) with an enzyme concentration of either 1.0 or 2.0 mg l⁻¹. The substrate solution (30 ml of 0.05 M HEPES–tris buffer, pH 6.4) was circulated through the alginate structure at a maximum pressure of 0.2 MPa. In each experiment, a new alginate structure was used to prevent the influence of enzyme inactivation. The activity assay was applied for different H₂O₂ concentrations (up to 3 g l⁻¹). With fast circulation of the substrate solution, a constant substrate concentration (the same as in the solution) inside the structure could be achieved.

The temperature was maintained at 11 °C in the first series of experiments and at 24 °C in the second series of experiments. Samples were taken every 20 s for the first five minutes, then every 2 min for 30 min. The concentration of H₂O₂ was determined spectrophotometrically (Shimadzu UV-1800) at 230 nm using a standard curve A(230) = 1.97 C_S (g l⁻¹).

The stability of the encapsulated catalase was assessed by measuring the residual activity after incubation in 0.05 M HEPES–tris buffer (pH 6.4) at 11 and 24 °C for different incubation times (every day for the first five days, then every 2–3 days for two months).

3.4. Estimation of the equilibrium coefficient

The equilibrium between the substrate concentration inside the alginate structure and the concentration in solution (0.05 M HEPES–tris buffer, pH 6.4) was verified at 11 and 24 °C. The initial hydrogen peroxide concentration was 0.50–0.91 g l⁻¹. The study was conducted in several series, at ratios of the volume of the capsules to the solution volume of 1:1.28, 1:2.6 and 1:5.1. The volume of the capsules was determined from their geometric structures. The diameter of the selected for each temperature 50 capsules was measured by calliper. Thus calculated the average volume of a single capsule was 0.055 ± 0.002 ml at 11 °C and 0.059 ± 0.002 ml at 24 °C. The volume of the alginate structures increased at higher temperatures.

The study was conducted in a stirred tank for 30 min. The H₂O₂ concentration was measured spectrophotometrically in the buffer until a steady state was obtained. The equilibrium concentration inside the capsule was calculated from the mass balance.

3.5. Estimation of the diffusion coefficient

The diffusion coefficient was determined in a diffusion cell according to the procedure described previously [27]. Flat alginate structures with thicknesses of 3–6 mm were prepared. H₂O₂ at a concentration of 0.7–2.8 g l⁻¹ was circulated on one side of the alginate structure. Water was circulated on the other side. The temperature was maintained at 11 °C in the first series of experiments and at 24 °C in the second series of experiments. The process was conducted for one hour. The H₂O₂ concentration in both phases was monitored spectrophotometrically.

3.6. Model validation in the continuous process

Experiments were carried out under process conditions (11 and 24 °C, pH 6.4) in a stirred reactor. The alginate capsules with a catalase concentration of 2 mg l⁻¹ had a diameter of 5.05 mm. The diameter of outlet hose was less than the diameter of the capsules, so that they could not leave the reactor. The ratio of the capsule volume to the volume of the surrounding solution was 1:3 (74 capsules were added to 15 ml of 0.05 M HEPES–tris buffer, pH 6.4). The substrate (H₂O₂) concentration in the feed stream was 2.5 g l⁻¹. The residence time was 0.25–3 h. The process was established after 6 exchanges of volume.

4. Experimental results

Preliminary tests were intended to designate the parameters used in the model. As described earlier [28], encapsulated catalase exhibits a maximum activity at 24–35 °C. The study was also conducted at 11 °C, where the activity of catalase was approximately 40% of maximum (10–11 °C is the temperatures at which catalase is applied to remove H₂O₂ from beverages) [28].

4.1. Estimation of the kinetics parameters

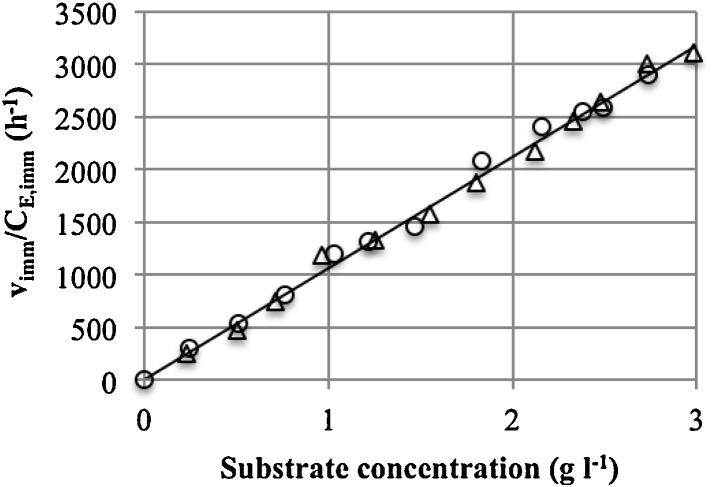
The rate of H₂O₂ degradation was determined at a substrate concentration of 0.2–3.0 g l⁻¹ and enzyme concentrations of 1 and 2 mg l⁻¹. In this range, the kinetics are first order with respect to the substrate and enzyme (Fig. 1). The reaction rate can be expressed by Eq. (15).

$$v_{\mathrm{imm}}=-\frac{1}{V_{\mathrm{cap}}}\times \frac{\text{d}{m}_S}{\text{d}t}=-\frac{V_{\mathrm{res}}}{V_{\mathrm{cap}}}\times \frac{\mathrm{d}{C}_{S,\mathrm{out}}}{\text{d}t}=k_{1,\mathrm{imm}}\times C_{E,\mathrm{imm}}\times C_S=k^{\prime }\times C_S$$ (15)

Fig. 1.

The dependence of the reaction rate per unit (v_imm/C_E,imm) on the concentration of substrate (11 °C, pH 6.4). Data are from the series with C_E,imm = 1 mg l⁻¹ (○) and 2 mg l⁻¹ (△).

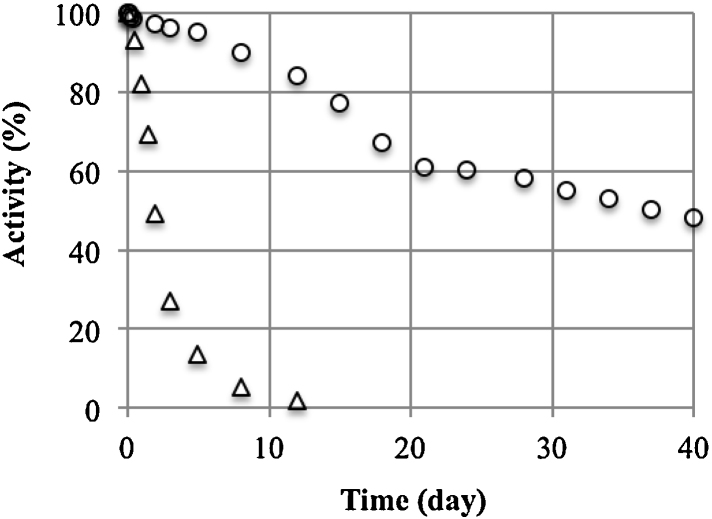
The stability of the immobilised catalase under the process conditions (11 and 24 °C, pH 6.4) (Fig. 2) was described assuming first-order kinetics of inactivation. On this basis, the half-life time [26] was calculated (Table 1).

Fig. 2.

Decrease in enzymatic activity at 11 °C (○) and 24 °C (△) at pH 6.4.

Table 1.

Values of the kinetic equation constant, the inactivation constant and the half-life time of the enzymatic activity at 11 °C and 24 °C (pH 6.4).

Temperature (°C)	Kinetic constant k1,imm (l g−1 h−1)	Inactivation constant (day−1)	Half life time (day)
11	1064.5	0.0195	35.5
24	2656.4	0.339	2.04

4.2. Estimation of the equilibrium coefficient and diffusion coefficient

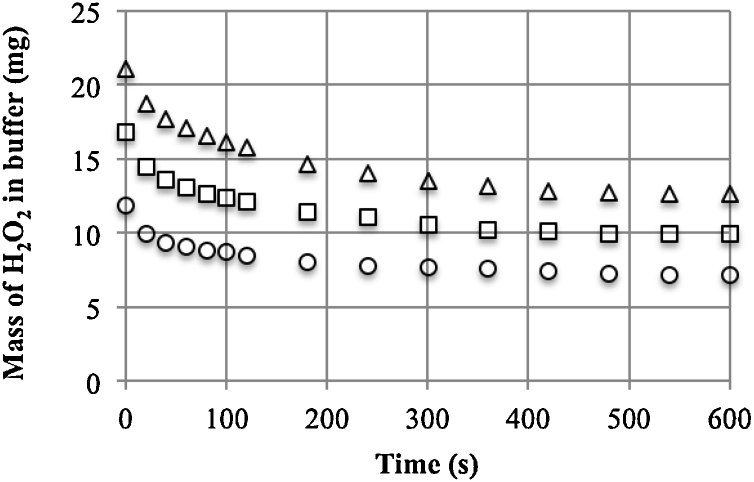
After placing the capsules in the H₂O₂ solution, concentration changes were monitored spectrophotometrically. A steady-state was observed after 10 min (Fig. 3). Based on the mass balance, the equilibrium coefficient (P_S) was defined as the ratio of the concentration inside the capsule to the concentration in the buffer (0.84 ± 0.3 at 11 °C and 0.88 ± 0.2 at 24 °C). At the test concentration, the coefficient did not depend on the concentration.

Fig. 3.

The change in mass of H₂O₂ in the buffer during diffusion into the alginate capsules (V_cap/V_res = 0.78, 24 °C, initial concentrations of H₂O₂ of 0.50, 0.71 and 0.90 g l⁻¹).

The effective diffusion coefficient was determined from the mass stream obtained at different initial values of the concentration of H₂O₂, and at different alginate layer thicknesses. Experiments were carried out according to a procedure described previously [27]. On the base of 9 series of experiments for each temperature, the effective diffusion coefficient was calculated as 1.48 × 10⁻⁹ ± 0.12 × 10⁻⁹ m² s⁻¹ at 11 °C and 2.01 × 10⁻⁹ ± 0.23 × 10⁻⁹ m² s⁻¹ at 24 °C.

4.3. Model validation

The study was carried out in a continuous stirred reactor with the catalase encapsulated in the alginate capsules. The capsules did not leave the reactor. According to the bioreactor balance equation we obtain the following:

$$Q\times C_{S,\mathrm{in}}=Q\times C_{S,\mathrm{out}}+N\times {\displaystyle \underset{0}{\overset{R}{\int }}}A(r)\times v_{\mathrm{imm}}^{\mathrm{}}(C_S^{\mathrm{}}(r))\times \text{d}r\cong Q\times C_{S,\mathrm{out}}+V_{\mathrm{cap}}^{\mathrm{}}\times v_{\mathrm{imm}}^{\mathrm{}}(C_{S,m}^{\mathrm{}})$$ (16)

Introducing τ

$$\tau =\frac{V_{\mathrm{res}}}{Q}$$ (17)

the value of the substrate concentration in the stream leaving the reactor is as follows:

$$C_{S,\mathrm{out}}=\frac{C_{S,\mathrm{in}}}{1+V_{\mathrm{cap}}/V_{\mathrm{res}}\times \tau \times k^{\prime }\times 3P_S/{\mathrm{\Phi }}^2\times [\mathrm{\Phi }\times \cosh (\mathrm{\Phi })-1]}$$ (18)

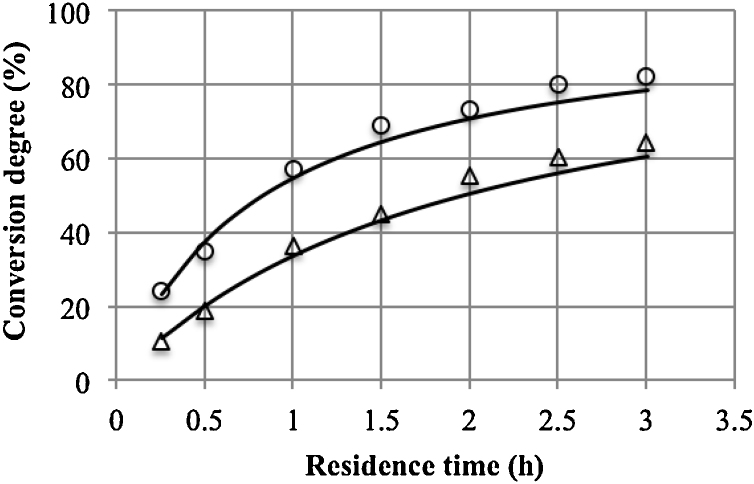
A steady-state was achieved after 6 volume exchanges. Depending on the residence time, this corresponds to 1.5–18 h of the process. With respect to this time, having regard to the inactivation of the enzyme, the value of the kinetic constant k′ and the Thiele modulus was corrected. Fig. 4 gives the model values calculated on the basis of Eq. (18) and the values obtained experimentally. The average relative error was 7.3% at 11 °C and 4.3% at 24 °C.

Fig. 4.

Model validation at 11 °C (△) and 24 °C (○) (points – experimental data, lines – model values).

5. Parameters influencing the efficiency and rate of the process – the model analysis

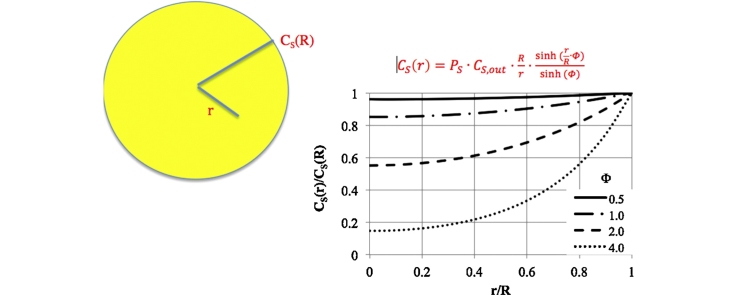
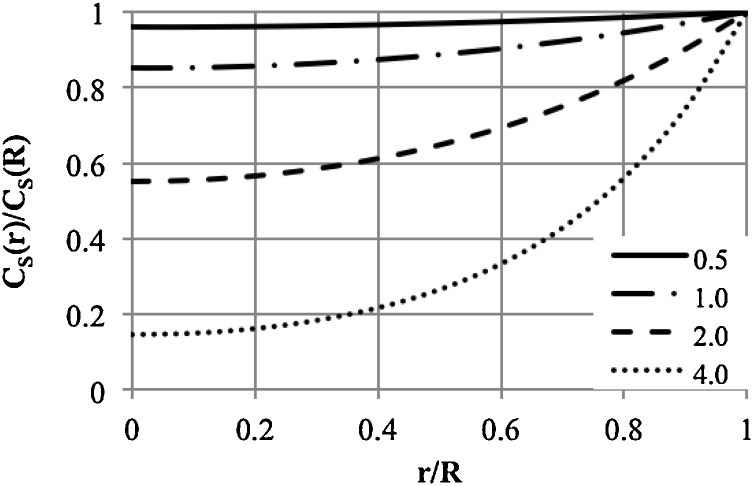
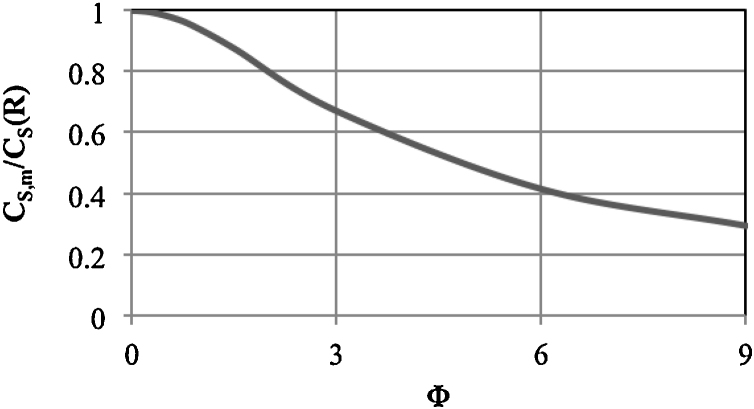
According to Eq. (12), the profile of the substrate concentration inside the capsule depends on the Thiele modulus (Fig. 5). For Φ < 0.5, the concentration profile is almost flat. The concentration at each location in the capsule is close to the concentration at the surface. The enzyme molecules encapsulated uniformly throughout the capsule volume are thus fully utilised. With an increase in Φ, the substrate concentration gradient between the surface and the capsule centre increases. This gives the average substrate concentration inside the capsule, according to Eq. (14) (Fig. 6). Analysing the values ​​shown in Fig. 6, for efficient utilisation of the enzyme, the value of Φ should be not greater than 2.

Fig. 5.

Substrate concentration profile inside the capsule based on the Thiele modulus.

Fig. 6.

Effect of the Thiele modulus on the average substrate concentration inside the capsule in relation to the concentration at the surface.

The kinetic constant k_1,imm and the diffusion coefficient included in the Thiele modulus are constant (under selected temperatures). The fully controllable parameters are the diameter of the capsule and the catalyst concentration. The capsule diameter is directly proportional to Φ. A short diffusion path tends to reduce the concentration gradient. The concentration of the biocatalyst is directly proportional to the value of k′, accounting for the reaction rate. Using Eqs. (11) and (14) the average rate of the reaction (v_m) can be expressed as follows:

$$v_m=k^{\prime }\times C_{S,m}=\frac{3\times k^{\prime }\times P_S\times C_{S,\mathrm{out}}}{{\mathrm{\Phi }}^2}\times (\mathrm{\Phi }\times \cosh (\mathrm{\Phi })-1)=\frac{3\times D_S\times P_S\times C_{S,\mathrm{out}}}{R^2}\times (R\times \sqrt{\frac{k^{\prime }}{D_S}})\times \coth (R\times \sqrt{\frac{k^{\prime }}{D_S}})-1)$$ (19)

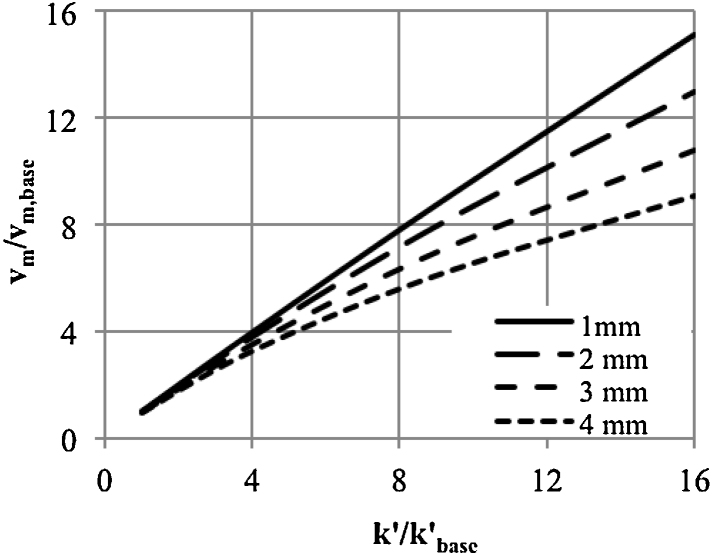
based on the above equation, the effect of the rate constant (k′) with different sized capsules on v_m can be analysed. Fig. 7 shows the relative values ​​according the reaction rate obtained for R = 1 mm and $\sqrt{k_{\text{base}}^{\prime }/D_s}$ = 250 m⁻¹.

Fig. 7.

Effect of increasing the kinetic rate constant on the reaction rate for capsules with diameters of 1–4 mm (v_m,base corresponds to R = 1 mm, $\sqrt{k_{\text{base}}^{\prime }/D_s}$ = 250 m⁻¹).

Increasing the k′ results in a proportionately higher the enzyme concentration. Thus, we can expect a proportional increase in the reaction rate. However, as shown in Fig. 7, such an effect is obtained only for capsules with R = 1 mm (and smaller). Thus, increasing the capsules diameter, reduces the process efficiency.

6. Discussion

The biggest advantage of hydrogel preparations is that they can be used as various size and shape carriers for encapsulated active ingredients. The size of the capsule with encapsulated enzyme influences the profile of substrate concentration inside the capsule. This directly impacts the rate of the reaction process. For small diameter capsules, the concentration in the core is close to the concentration at the surface. Thus, all of the enzyme molecules are utilised.

However, the diameter of the hydrogel capsule must be considered for separation as well. One advantage of immobilised preparations is that they can be easily separated from the reaction mixture and processed in a column reactor. Therefore, a lower value for the size of the capsules is suggested to be R = 1 mm.

The aim should be to obtain small values of Φ (preferably below 0.5). The upper limit of this value is 2. At a constant value of k_1,imm and D_S and a limited capsule size, Φ is controlled by the enzyme concentration. The calculation of the conversion degree should be based on the selection of small capsules with the previously calculated enzyme concentration. The second controllable parameter is usually the residence time, which is related to enzyme inactivation. In the case of a reaction with native enzyme, inactivation results in a proportional decrease in the rate of the reaction. According the model for the encapsulated enzyme, lower enzymatic activity reduces the value of k′ and thus the value of Φ. The substrate concentration profile thus becomes flatter and the average concentration inside the capsule increases slightly. Thus slightly increases the average process rate. As a result, inactivation of the encapsulated enzymes is less noticeable than for native enzymes and enzymes immobilised on solid supports.