Compressed glassy carbon: An ultrastrong and elastic interpenetrating graphene network

The compression of glassy carbon forms a series of lightweight, ultrastrong, hard, elastic, and conductive carbons.

Abstract

Carbon’s unique ability to have both sp² and sp³ bonding states gives rise to a range of physical attributes, including excellent mechanical and electrical properties. We show that a series of lightweight, ultrastrong, hard, elastic, and conductive carbons are recovered after compressing sp²-hybridized glassy carbon at various temperatures. Compression induces the local buckling of graphene sheets through sp³ nodes to form interpenetrating graphene networks with long-range disorder and short-range order on the nanometer scale. The compressed glassy carbons have extraordinary specific compressive strengths—more than two times that of commonly used ceramics—and simultaneously exhibit robust elastic recovery in response to local deformations. This type of carbon is an optimal ultralight, ultrastrong material for a wide range of multifunctional applications, and the synthesis methodology demonstrates potential to access entirely new metastable materials with exceptional properties.

INTRODUCTION

High-performance materials that couple low weight and high strength with elasticity are demanded for a vast range of applications. Finding the optimum strength-to-weight ratio is not an easy task, and certain compromises must generally be made between different classes of materials. Common metals are ductile yet heavy and have maximum yield strengths limited to about 2 GPa (1). The elastic strain of metals is usually limited to <2% because of dislocation or twin formation when the applied stress reaches a critical value. High-tech ceramics have superior compressive strengths and hardness over metals (2, 3). For example, cemented tungsten carbide has an extreme compressive strength up to 9 GPa, but its heavy weight leads to excessive energy consumption. Light-element compounds, such as silicon carbide and boron carbide, are low-density and high-strength and are thus preferred materials for military armor and aerospace shields to protect certain vital equipment. Nevertheless, most ceramics can only withstand small elastic strains (<2%) and undergo brittle fracture immediately after deformation. By virtue of martensitic transformations, fine-scale ceramics can simultaneously increase elasticity and strength (4). However, so far, it remains a major challenge to make ceramics with the optimum combination of weight, strength, and elastic properties.

Carbon gives rise to remarkable classes of materials with combined properties, such as low weight, high strength, hardness, elasticity, and tunable electronic properties, because of the flexibility to form sp-, sp²-, and sp³-hybridized bonds. Diamond, entirely composed of sp³ bonds, is a three-dimensional (3D) superhard insulator, whereas fully sp² graphene is a 2D Dirac semimetal with out-of-plane flexibility. Mixed sp²- and sp³-bonded carbon phases are expected to have advantages by integrating mechanical and electrical properties. By introducing local sp³ buckling between graphene sheets, hard and elastic semiconducting thin films of amorphous carbon have been produced by multiple deposition techniques (5). Unfortunately, these films have significant residual internal stresses, which limit their thickness and usefulness (6). As a result, it is desirable to synthesize uniform bulk forms of mixed sp²-sp³ carbons with manageable microstructures and versatile capabilities.

The most direct means to synthesize mixed sp²-sp³ forms of carbon is by the controlled compression of pure sp² carbons. For example, both highly sp²-hybridized graphite-like and sp³-hybridized diamond-like amorphous carbons can be quenched from compressed fullerenes (7, 8), and some of them also show high hardness and elastic recovery but with a very low compressive strength of 0.2 to 0.3 GPa, probably due to the restructuring heterogeneity from the collapse of fullerenes (9). Glassy carbon (GC), as a typical disordered sp² carbon, can be manufactured into various shapes with a great variety of unique material properties, including high strength, low density, high-temperature resistance in inert gas up to 3000°C, and extreme corrosion resistance. Type I GC, which is produced by firing polymeric precursors at temperatures below 2000°C, mainly consists of randomly distributed curved graphene layer fragments (10, 11). Type II GC, fabricated at higher temperatures above 2500°C, contains self-assembled fullerene-like spheroids of nanometer sizes, dispersed within and interconnected by a 3D disordered multilayer graphene matrix (10, 11). During cold compression of type I GC to 44.4 GPa, synchrotron x-ray Raman spectroscopy revealed a continuous pressure-induced sp²-to-sp³ bonding change (12). The transition appeared to be reversible upon releasing pressure so that the cold-compressed GC was not quenchable to ambient pressure (12). While overheating GC at pressures above 15 GPa, fully sp³ superhard nanocrystalline diamonds were produced (13, 14). Thus, there is a gap to synthesize recoverable sp²-sp³ carbons from GC conversion and to further explore the suitable synthetic conditions needed. Moreover, it is well known that the sp² carbon precursors with different crystal structures would undergo distinct phase transitions under pressure due to kinetic factors, which makes the phase diagrams unexpectedly complex, for example, the transitions of typical graphite and fullerenes (7, 15). Therefore, the comprehensive search of metastable phase transitions of various carbon precursors with pressure is needed because this may reveal key insights for producing more new carbon allotropes with unprecedented properties.

Here, we report a series of lightweight, ultrastrong, hard, elastic, and conductive type of amorphous carbons in bulk form by compressing GC at previously unexplored moderate temperatures. Structure and bonding were studied by x-ray diffraction (XRD), high-resolution transmission electron microscopy (HRTEM), electron energy loss spectroscopy (EELS), and Raman spectroscopy. Indentation hardness and elastic recovery were derived from the load/unload-displacement curves, whereas axial compressive stress-strain relations were established using a diamond anvil cell (DAC) technique.

RESULTS

Microstructure

The millimeter-sized pillars of compressed GCs were quenched to ambient conditions after compressing type I GC (Alfa Aesar) at pressures of 10 to 25 GPa and temperatures of 400° to 1100°C. Figure 1 and figs. S1 to S5 show the structural properties of compressed GCs measured at ambient condition. From the XRD results (Fig. 1A), the recovered materials remain amorphous, with the most notable changes occurring at the first diffraction peak centered around 2.7 to 4.5 Å, which is analogous to the interlayer distance of 3.35 Å in graphite. In comparison with the broad range of interlayer distances in raw GC, the compressed GCs have more uniform and shortened distances. The mean interlayer distances for compressed GCs are 3.46, 3.36, 3.22, and 3.13 Å, respectively, and gradually decrease with increasing synthesis temperatures from 400 to 1000°C and keeping synthesis pressure of 25 GPa. In addition, the d spacing near 1.6 to 1.8 Å corresponds to higher-order diffraction between layers, like (004) in graphite, and it is also shortened with increased synthesis temperatures and has a similar trend with the first main peak. The slightly shortened interlayer distances indicate that the main skeleton in compressed GCs is still composed of sp² bonds with only partial sp³ linkages between interlayers, whereas the decreased peak widths of the first sharp diffraction peak indicate increased correlation lengths within the samples. There is no obvious difference of intralayer d spacings at ~2, 1.2, 1, 0.8, 0.7, and 0.6 Å, which are comparable with those of graphite. Note that the diamond phase was produced when heating GC at 1200°C and pressure of 25 GPa (fig. S1A).

Fig. 1. XRD and sp²/sp³ component of compressed GCs (Com.GCs) measured at ambient conditions.

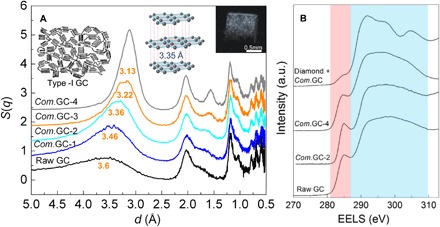
The Com.GC numbers (1 to 4) and Diamond + Com.GC represent the samples recovered after compressing GCs at 25 GPa and temperatures of 400°, 600°, 800°, 1000°, and 1200°C, respectively. (A) The graphite-like interlayer distances for compressed GCs gradually reduced with the increase of synthesis temperatures. The S(q) data are unscaled but successively shifted from the raw GC data by 0.6 units in the vertical axis. The insets show Franklin’s model of nongraphitizing carbon (11), ordered graphite structure with standard interlayer distance of 3.35 Å, and the bulk morphology of recovered sample rods. (B) EELS change showing the decreased sp² component in the compressed GCs relative to the raw material. The pink and light blue regions represent 1s-π* and 1s-σ* transitions of carbon, respectively.

The sp² and sp³ components in compressed GCs were measured using EELS (Fig. 1B and figs. S4 and S5). The 1s-σ* peak at 292 eV is the signature of σ bonding, whereas the 1s-π* peak at 285 eV represents π bonding. By using raw sp² GC or graphitized carbon black as the calibration material, the ratio of the integrals under the 1s-π* and the 1s-σ* peaks is used to estimate the fraction of sp² carbon present. The quantitative sp³ fractions of compressed GCs recovered from 25 GPa and temperatures of 400°, 600°, 800°, and 1000°C, are 9 (±2%), 10 (±3%), 16 (±3%), and 22% (±5%), respectively. The relatively larger error in compressed GC from 1000°C may be due to the bonding nonuniformity of the sample. In comparison, the sample recovered from 25 GPa and 1200°C is mainly sp³ diamond with a weak 1s-π* peak at 285 eV. In addition, the right shift of low-loss EELS of compressed GC compared with raw GC also indicates an increase of sp³ bonding (fig. S4C). Therefore, the compressed GCs are a class of mixed sp²-sp³ hybridized carbons with a low sp³ component.

The microscopic atomic structure of compressed GCs was further investigated by using selected area electron diffraction (SAED) and HRTEM. The broad diffraction rings observed in the SAED patterns indicate the disordered character, consistent with the XRD results, and there were no preferred diffraction orientations observed at linear dimensions of ~150 and 800 nm, respectively (fig. S2). The HRTEM images show the fringe of interpenetrating graphene sheets with long-range disorder and short-range order (Fig. 2A and fig. S3). The domains of locally ordered carbon nanolattices persist across lateral dimensions of 1 to 5 nm and exhibit lattice spacings of 3 to 5 Å, randomly distributed in the disordered network. Considering that the EELS data show partial sp³ bonding in the microstructure, a physical mechanism for the formation of the networks would consist of local buckling or linkage of disordered graphene sheets through sp³ carbon nodes. Figure 2B shows the schematic linkage types between the graphene layers. During compression, the sp³ bonds would be readily formed at the high-energy curved surfaces of graphene layer fragments with distinct orientations and also easily formed through the partial buckle of multigraphene interlayers like the process during compressing layered carbon nitride (16). When the buckle of graphene sheets becomes locally ordered, the short-range ordered carbon nanolattice would be formed. Furthermore, the local sp³ linkage inevitably leads to the decrease of interlayer distance, consistent with the XRD result above (Fig. 1A).

Fig. 2. Nanoscale structure of compressed GCs.

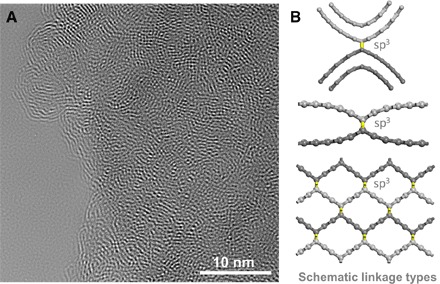
(A) Raw HRTEM image showing the interpenetrating graphene networks with long-range disorder and short-range order (also see fig. S3). The local order has a lateral dimension of 1 to 5 nm and exhibits lattice spacings of 3 to 5 Å. (B) Schematic linkage types between the graphene layers. The layers are distinguished by different colors, that is, light and dark gray, respectively. Under pressure, the sp³ bonds colored by yellow are readily formed at the curved surfaces of graphene layers with different orientations (top) and are also easily formed between the interlayers (center). In addition, orderly buckled graphene sheets would form the short-range ordered carbon nanolattice (bottom).

Raman spectra were collected from random regions of the samples (fig. S6). Like other amorphous carbons (17), the compressed GCs have two broad Raman-active modes at approximately 1600 cm⁻¹ (G band) and 1400 cm⁻¹ (D band) originating from sp² carbon. Under the “molecular” interpretation (18), the G band is attributed to bond stretching of all sp² pairs, whereas the D band is associated with breathing modes of sp² atoms in rings and is distinct from the sharp Raman line of diamond observed at 1332 cm⁻¹. The T peak lying about 1060 cm⁻¹ appears in ultraviolet (UV) Raman due to the sp³ vibrations (19). A reduced I(D)/I(G) intensity ratio observed for recovered GC samples (fig. S6) is also consistent with an increased fraction of sp³ carbon (20).

Hardness and elastic recovery

The indentation hardness at peak load, reduced modulus (E_r), and indentation elastic recovery were determined from the load-displacement relationship according to the model of Oliver and Pharr (figs. S7 to S10) (21). To eliminate the indentation size effect, we applied large loads of 0.98 to 9.8 N. The indentation measurements were also carried out with varying loading, holding, and unloading time (fig. S9). The compressed GCs recovered from 25 GPa and temperatures of 400° and 600°C have similar hardness near 15 GPa, whereas the samples from 800° and 1000°C have similar asymptote hardness of about 26 GPa (Fig. 3A). As a comparison, the raw GC has a low hardness of only 5 GPa. The reduced modulus E_r can be determined by the contact stiffness and project area and is related to the Young’s modulus E and Poisson’s ratio of the specimen (21). By assuming Poisson’s ratio of 0.2 for all GCs, the estimated Young’s moduli of raw GC and compressed GCs from 25 GPa and temperatures of 400°, 600°, 800°, and 1000°C are 35, 121, 130, 313, and 289 GPa, respectively. Notably, the compressed GCs recovered from 10 to 16 GPa and 900° to 1100°C have the similar structures and mechanical properties with those of compressed GC from 25 GPa and 600°C (figs. S1 and S8). Furthermore, the Vickers hardness of samples was examined, and the measured Vickers hardness for compressed GC recovered from 25 GPa and 600°C was 15.4 GPa (±1.3), consistent with the result of indentation hardness above (fig. S11, B and C). Note that no crack was produced on compressed GCs after unloading from 4.9 N. In comparison, the obvious brittle cracks were observed on diamond single crystal after unloading (fig. S11A). More intuitively, the hardness characterization of compressed GC was carried out with a qualitative scratch test, that is, Mohs hardness test. The edge of compressed GC rod recovered from 25 GPa and 800°C readily scratched both the (0001) crystal planes of Al₂O₃ (Mohs scale, 9) and SiC single crystals (Mohs scale, 9.5), demonstrating its high hardness (fig. S12). The high hardness and Young’s moduli of compressed GCs is due to the pressure-induced increase of sp³ bonding in the structure.

Fig. 3. Indentation hardness and elastic recovery of compressed GCs.

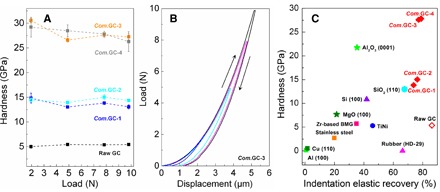
(A) The indentation hardness as a function of applied load. The loads of 1.96, 4.9, 7.84, and 9.8 N were applied, respectively. (B) The loading/unloading-displacement curves of compressed GCs showing the high elastic recovery. (C) Hardness and elastic recovery of compressed GCs in comparison with common ceramics, polymers, and metals estimated from the nanoindentation testing (see Materials and Methods). The compressed GCs have an unprecedented combination of hardness and elastic recovery.

The load-displacement curves of compressed GCs are distinct from those of fully plastically deformable metals and partially elastic ceramics (Fig. 3B and figs. S7 to S9). As suggested from the measured curves, the compressed GCs demonstrate significant elastic recovery, which is further evidenced by the bowed edges of the indentations (figs. S10 and S11). Note that a small amount of bulging at the indent faces was previously observed in Ti₃N₄ nanocomposite ceramics and was related to the ductile/brittle behavior of the material (22). However, the indentation measurements are still performed within the elastic-plastic regime so that the hardness and load-displacement analyses are completely valid. The indentation elastic recovery was calculated using the ratio of area integrals under the unloading and loading curves, respectively. The compressed GCs have remarkable elastic recoveries above 70%, obviously higher than common metals and ceramics and even higher than the shape-memory TiNi alloy, organic rubber, and silica with known excellent elasticity (Fig. 3C). The compressed GCs inherit the high elasticity of raw GC that originates from the out-of-plane flexibility of sp² bonds (10, 23). This mechanism is different from the reversible martensitic transformation in shape-memory alloys (1) but is similar with those in rubber and silica, that is, by the compressibility and stretchability of molecular chains (24) and rotation or bending of the SiO₄ tetrahedra during indentation, respectively (25).

Strength and thermal stability

The axial compressive stress-strain relationships for compressed GCs were established using DAC equipment (Fig. 4). Polished samples were placed between the two parallel diamond anvils, and fine ruby powder was dispersed on the surface of sample. During compression, the stress was directly obtained from the ruby pressure (26), and the strain was estimated from the decrease in sample thickness measured by optical interferometry (fig. S13). Using this approach, the raw type I GC and standard type II GC were determined to have compressive strengths of 1.2 and 1.3 GPa as well as yield strains of about 3 and 3.5%, respectively (Fig. 4A and fig. S14), which are consistent with the previous report (10). The compressed GCs have the similar yield strains but with remarkably higher yield strengths of ~3 and 9 GPa for the samples recovered from 25 GPa and temperatures of 400° and 800°C, respectively. The high strength is also related to the high Young’s moduli derived from the linear elastic stress-strain relationship. The obtained Young’s moduli are also consistent with the aforementioned results from unload-displacement relationships during indentation measurements. The high compressive strength up to 9 GPa of compressed GCs is about five times stronger than common metals and alloys (1) and also greater than common ceramics with strengths of 1 to 5 GPa (2, 3).

Fig. 4. Compressive stress-strain curves and specific strength of compressed GCs.

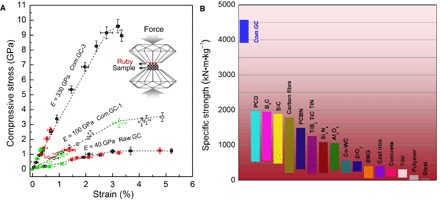
(A) The compressed GCs exhibit high compressive strength up to 9 GPa and large axial elastic strains near 3%. The Young’s moduli E are derived from the linear stress-strain relationship before yield. The inset shows a schematic of the measurement method in the DAC. (B) The specific compressive strength of compressed GCs in comparison with available data on known ceramics, polymers, and metals (2, 3). When normalized by density, the compressed GCs are about two to four times stronger than commonly used carbon fibers, cemented diamond, cemented cubic BN, SiC, and B₄C.

Materials with high strength and low density provide a high specific strength and are ideal for applications where weight savings are more important than material cost. The specific strength is characterized by the strength-to-density ratio. The compressed GCs have densities of 2.0 to 2.5 g/cm³, as measured directly from the mass and cylindrical sample volume. Their densities are higher than that of raw GC (1.5 g/cm³) and close to the density of graphite (2.25 g/cm³). Figure 4B shows the specific compressive strength of various materials. The compressed GCs have ultimate specific compressive strengths as high as 4600 kN·m·kg⁻¹, which is about two to four times higher than those of commonly used carbon fibers, cemented diamond, cemented cubic BN, SiC, and B₄C. In addition, the compressed GCs are all conducting with room temperature electrical resistivities of 6 to 16 milliohm·cm compared with that (3 to 4 milliohm·cm) of graphite along its interlayer direction. The compressed GCs also have a high thermal stability, for example, the samples recovered from 25 GPa and 800°C have an oxidation resistance temperature about 160°C higher than that of raw GC at air condition, and are still stable at argon condition up to the measurement temperature of 1400°C (fig. S15).

DISCUSSION

In summary, this class of mixed sp²-sp³ compressed GCs combines a variety of features into one material, including extraordinary specific compressive strength, high hardness, indentation elastic recovery, and electrical conductivity for many potential applications. In the disordered array of compressed GCs, domains of ordered interpenetrating graphene planes can form local lattices with open pores on the scale of several angstroms, representing a class of carbon allotropes with potentially variable structures and properties. Some possible structures have been proposed with peculiar electronic behaviors, such as anisotropic Dirac and classic fermions simultaneously (27), Weyl-like loops and points (28), and semiconducting behavior or node-loop/node-line semimetal properties (29), offering a strong motivation for both theorists and experimentalists to pursue this class of cross-linked graphene configurations.

MATERIALS AND METHODS

Sample synthesis

High-pressure and high-temperature experiments were performed in a large-volume multianvil system at Yanshan University, identical to that described in the study by Huang et al (30). Temperature was measured in situ by C-type W-Re thermocouples, and pressures were estimated from previously obtained calibration curves at different temperatures. The raw GC rod (type I GC, Alfa Aesar) was loaded into an h-BN capsule with 2-mm (used at 10 to 15 GPa) or 1.2-mm (used at 16 to 25 GPa) inner diameter and 2- to 2.3-mm length, and then assembled into a hole in the center of a 10- or 8-mm spinel (MgAl₂O₄) octahedron with an Re heater and an LaCrO₃ thermal insulator. Pressure loading/unloading rates were 2 GPa/hour. When the target pressure was reached, the sample was heated with a rate of 100°C/min to peak temperature, and then was maintained for 2 hours and finally quenched by turning off the electric power supply. The recovered sample rods had both a diameter and height of about 1 to 1.7 mm.

X-ray diffraction

Structural characterization was performed by the multiangle, energy-dispersive XRD technique carried out at 16-BM-B beamline of High Pressure Collaborative Access Team (HPCAT) at the Advanced Photon Source (see result in Fig. 1A). The diffraction patterns were collected at multiple diffraction angles (2θ: 3°, 4°, 5°, 7°, 9°, 12°, 16°, 21°, 27°, and 33°). All patterns were collected until the maximum intensity reached at least 2000 counts to ensure reliable counting statistics. The structure factors S(q) were deduced using the approach developed by Kono et al (31). In addition, the recovered samples were also analyzed by XRD with a Cu Kα radiation (diffractometer: Bruker D8 Discover) (fig. S1).

Transmission electron microscopy

Microstructures of the recovered samples were characterized by a monochromated, aberration-corrected FEI Titan³ 60-300 S/TEM at Pennsylvania State University with an accelerating voltage of 80 kV, FEI Titan 80-300 Cs corrector TEM at Tsinghua University with an accelerating voltage of 300 kV, and TEM (JEM-2010) at Yanshan University with an accelerating voltage of 200 kV. To prepare a TEM sample, the recovered sample was crushed and ground in the agate mortar. The crushed small particles were dispersed in ethanol solution by ultrasonic treatment and drop-casted on a carbon-coated copper grid and then dried for TEM analysis. The sample was also prepared by focused ion beam milling for comparison, and the collected EELS spectra are shown in fig. S5A. Note that all the microstructure information except that shown in fig. S5A was from the samples prepared by the first method. The sp²/sp³ ratios were estimated from the EELS of compressed GCs with all-sp² raw GC or graphitized carbon black standard (Electron Microscopy Sciences #80037) as a reference. The spectra were deconvoluted and the background was subtracted using a power-law model. The sp² ratio was determined by integrating the π* peak and the remaining area starting at the σ* edge, and then calculating the normalized integrated ratio using the equation (32) ${\mathit{N}}_{\text{int ratio}}=\frac{\raisebox{1ex}{${\mathit{I}}_{\mathrm{\pi }}^{\text{CG}}$}\!\left/ \!\raisebox{-1ex}{${\mathit{I}}_{\mathrm{\sigma }}^{\text{CG}}$}\right.}{\raisebox{1ex}{${\mathit{I}}_{\mathrm{\pi }}^{\text{RG or CB}}$}\!\left/ \!\raisebox{-1ex}{${\mathit{I}}_{\mathrm{\sigma }}^{\text{RG or CB}}$}\right.}$, where CG, RG, and CB represent compressed GCs, referenced raw GC, or carbon black, respectively. The sp² fraction, x, was calculated from the equation (32) N_{int ratio} = 3x/(4 − x).

Raman spectroscopy

The UV Raman spectra were measured at room temperature by using Renishaw’s micro-Raman spectroscopy system with 325-nm laser as the excitation source. The spot size of the laser on the sample was about 2 μm².

Hardness and elastic recovery measurement

Indentation hardness and elastic recovery were derived from the load-displacement curves established by the three-sided pyramidal Berkovich diamond indenter (Keysight Nano Indenter G200). The indenter parameters were first calibrated against hard materials with a wide hardness range, including fused quartz, Al₂O₃, and SiC. The measured hardness for these materials was consistent with the referenced data. The applied standard loading time to peak load was 15 s, the peak holding time was 10 s, and the unloading time was 15 s. In addition, the indentation measurements were also carried out with varying loading, holding, and unloading times. The applied time has no significant effect on the elastic modulus, elastic recovery, and hardness (see fig. S9). The applied loads were 0.98 to 9.8N for the GCs, Si, SiO₂, MgO, and Al₂O₃, whose hardness and elastic recovery had little change with the loads, especially above 4.9 N. The applied loads were 0.49 to 4.41 N for Cu and Al, and the obtained hardness and elastic recovery were almost unchanged with the loads. The standard shore hardness test block of the HD-29 rubber is too soft; thus, we had to use a small load of 0.049 N to obtain a standard load-displacement curve. When larger loads were used, the hops were not anticipated to appear on the curve, possibly due to the breaking of rubber. In addition, the hardness and elastic recovery of steel, TiNi, and bulk metallic glass were estimated from the previous research. For the nanoindentation method, the hardness was estimated by the peak load and projected area of indentation determined by the indenter displacement (that is, indentation depth) at peak load and the indenter geometries. The reduced modulus E_r was determined by the contact stiffness and project area. By assuming a Poisson’s ratio of 0.2 for all GCs, their Young’s moduli were estimated. The indentation elastic recovery was calculated using the ratio of area integrals under the unloading and loading curves, respectively.

The standard Vickers hardness (H_v) measurement was also carried out, and the indentation experiments were performed on the polished samples using a four-sided pyramidal diamond indenter. The loading force of the microhardness tester was 4.9 N. The loading and dwell times were both 15 s. Under each sample, six indentations were made. H_v is defined as the applied load P(N) divided by the surface area of the impression after unloading: H_v = 1854.4P/d², where d is the arithmetic mean of the two diagonals of the indent in micrometers (μm).

The hardness characterization of compressed GC was also carried out with a qualitative scratch test (that is, Mohs hardness test). The edge of the Com.GC-3 sample rod readily scratched the (0001) crystal planes of Al₂O₃ (Mohs scale, 9) and SiC single crystals (Mohs scale, 9.5) (see fig. S12). This means that the hardness of Com.GC-3 is comparable to or even higher than those of Al₂O₃ and SiC. The hardness of (0001) crystal planes of Al₂O₃ and SiC single crystals we measured are 22 and 33 GPa, respectively, which are consistent with other reports.

Compressive strength test

Axial compressive stress-strain relations were established in a simple DAC. The samples were first polished on two sides to a length of 300 to 500 μm and thickness of 100 to 200 μm, and then placed on the surface of the 1000-μm culet diamond anvil. Then, fine ruby powder was dispersed onto the surface of another diamond anvil. During compression, the stress was obtained from the ruby pressure, and the strain was derived from the thickness decrease of sample measured by optical interferometry. The fluorescence peaks of Ruby became broadened and shifted to higher wavelength with the increase of axial stress, and the center position of the R1 fluorescence peak was used to determine the pressure value according to nonhydrostatic calibration (26). The period of the interference fringes from transmitted light is related to the distance between the two diamond anvils (that is, thickness of sample), and at least 10 interference peaks were used to reduce errors. A confocal spatial filter was used to discriminate light at the sample position. The compression tests were also performed in other standard materials including raw type I and type II GCs (fig. S14). The obtained compressive strength values were consistent with published literature (10), demonstrating the accuracy of the method.

Thermal stability test

The thermal stability of compressed GC was studied by measuring differential scanning calorimetry (DSC) and thermogravimetry (TG) in both air and inert conditions using Netzsch STA 449 C with a heating rate of 10°C/min over the temperature range 20° to 1400°C (fig. S15, A and B). To check the energy release from stress-strain, we chose the thermal analyzer of PerkinElmer DSC 8000 with higher sensitivity and accuracy, and the samples were measured with a heating rate of 5°C/min and temperatures up to the limit of 500°C (fig. S15C).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/6/e1603213/DC1

fig. S1. XRD of compressed GCs recovered after compressing raw GC at pressures of 10 to 25 GPa and temperatures of 600° to 1200°C.

fig. S2. SAED patterns of compressed GCs measured at different length scales.

fig. S3. Local order in compressed GC.

fig. S4. The sp³ component of compressed GCs measured at ambient condition.

fig. S5. The sp³ component of compressed GC and microstructure of raw GC.

fig. S6. UV Raman spectroscopy of compressed GCs.

fig. S7. The loading/unloading-displacement curves of compressed GCs in comparison with raw GC, Cu, and MgO.

fig. S8. The loading/unloading-displacement curves, indentation hardness, and elastic recovery of compressed GCs synthesized at moderate pressures and temperatures.

fig. S9. The loading/unloading-displacement curves, hardness, Young’s modulus, and indentation elastic recovery of compressed GC at varied loading, holding, and unloading times.

fig. S10. Indentation morphology after unloading three-sided pyramidal Berkovich diamond indenter, showing significant elastic recovery.

fig. S11. Optical images of the indentations on diamond and Com.GC-2 after unloading a four-sided pyramidal diamond indenter.

fig. S12. Mohs hardness of compressed GC (Com.GC-3) characterized with qualitative scratch tests.

fig. S13. Axial compressive stress-strain relations established in a simple DAC.

fig. S14. Compressive strength tests for standard materials including type I and II GCs in a simple DAC.

fig. S15. Comparison of thermal stability of compressed GC (Com.GC-3) with raw GC at air and inert argon (Ar) or nitrogen (N₂) conditions, respectively.