Abstract
This paper describes the break-up behavior of a concentrated emulsion comprising drops stabilized by amphiphilic silica nanoparticles flowing in a tapered microchannel. Such geometry is often used in serial droplet interrogation and sorting processes in droplet microfluidics applications. When exposed to high viscous stresses, drops can undergo break-up and compromise their physical integrity. As these drops are used as micro-reactors, such compromise leads to a loss in the accuracy of droplet-based assays. Here, we show droplet break-up is suppressed by replacing the fluoro-surfactant similar to the one commonly used in current droplet microfluidics applications with amphiphilic nanoparticles as droplet stabilizer. We identify parameters that influence the break-up of these drops and demonstrate that break-up probability increases with increasing capillary number and confinement, decreasing nanoparticle size, and is insensitive to viscosity ratio within the range tested. Practically, our results reveal two key advantages of nanoparticles with direct applications to droplet microfluidics. First, replacing surfactants with nanoparticles suppresses break-up and increases the throughput of the serial interrogation process to 3 times higher than that in surfactant system under similar flow conditions. Second, the insensitivity of break-up to droplet viscosity makes it possible to process samples having different composition and viscosities without having to change the channel and droplet geometry in order to maintain the same degree of break-up and corresponding assay accuracy.
I. INTRODUCTION
In recent years, droplet microfluidics has grown into an interdisciplinary platform where fluid dynamics, chemistry, and bioengineering meet. Applications of droplet microfluidics are broad, ranging from disease diagnostics, drug discovery, to the synthesis of novel materials.1–3 Droplet microfluidics has multiple advantages: (1) The ability to generate monodisperse drops reproducibly allows accurate control of the size of the drops. (2) The small volume (pL to nL) of the drops, which act as micro-reactors, can accelerate some reactions that would be too slow to take place in bulk. (3) The ability to generate, interrogate, and sort drops at high rates enable the rapid screening of many samples in a massively parallel manner.4,5 These advantages make droplet microfluidics a strong candidate for the next generation of high-throughput screening platform.2,6,7 To further increase the throughput of droplet applications, the ability to control and employ concentrated emulsions (defined here as emulsions having a droplet volume fraction φ exceeding 80%) will become essential, since it reduces the volume of the continuous phase that must be handled otherwise in dilute emulsions for the same number of drops. In these high-throughput applications, it is also critical that the physical integrity of droplets is preserved. In contrast to solid wells in their multi-well plate counterparts, drops are prone to instabilities of the liquid-liquid interface and can undergo coalescence or break-up. While coalescence has been successfully avoided by using appropriate stabilizers,8,9 the break-up of drops, especially those within a concentrated emulsion, can limit the ultimate throughput of the assay.2,10,11
The deformation and break-up of isolated single drops has been well studied in the field of low Reynolds number hydrodynamics.12–17 For a single drop, the interface can be described by assigning a surface tension if the interface is a simple liquid-liquid interface. The deformation of the drop is determined by capillary number (Ca), viscosity ratio, flow type, and confinement. There exists a threshold or critical Ca, above which a drop fails to sustain its stable shape and undergoes break-up. The critical Ca is, in turn, dependent on factors including viscosity ratio, flow type, and confinement.17–19
More recent studies have extended this simple description of interface to complex interfaces, which can display rich dynamics in the presence of surface viscosity, surface elasticity, or both. For instance, a Newtonian viscous interface can be modeled by the Boussinesq-Scriven constitutive law.20–22 In addition to Ca, the Boussinesq number (Bq), which represents the effect of surface viscosity relative to bulk viscosity, plays a critical role in determining drop deformation. Previous numerical and analytical works have shown that as the interfacial viscosity (and hence Bq) increases, drop deformation decreases at a fixed Ca.21–24 When drops are enclosed by a solid deformable membrane (also known as capsules), depending on the composition of the membrane, the deformation exhibits different modes from that of a pure liquid drop.25–28 In particular, it has been shown that the deformation is significantly restricted by increasing the elasticity of the interface.28,29 When drops are stabilized by densely packed particles, a rigid barrier is formed at the interface, which shows a strong viscoelastic behavior.30–32 Similar to a capsule, previous work has reported that a particle-stabilized drop deforms less than a pure liquid drop at comparable flow conditions.31 When subject to sufficiently large deformation induced by strong external flow, break-up was always observed for capsules and particle-stabilized drops.31,33,34 The break-up process can still be described by a deterministic behavior: above a certain critical Ca, drops fail to sustain a steady large deformation and undergo break-up.25,31,35 In addition to viscosity ratio, flow type, and confinement, the value of the critical Ca is dependent on interfacial viscoelasticity.
In contrast to single drops, the corresponding problem of drops within a concentrated emulsion in microfluidic channels is less explored and is not well understood. Previously, we have found that, unlike single drops, the break-up of drops within a concentrated emulsion is not deterministic but is stochastic.10,11 At a given flow condition, only a fraction of the drops breaks. The stochasticity arises from the time-varying droplet-wall and droplet-droplet interactions not present in single-drop systems. We have further identified that the break-up probability can be described by the product of three dimensionless groups: capillary number, viscosity ratio, and confinement factor.10,11 For the conditions tested, the break-up probability increases with increasing value of the product of these three dimensionless groups.
In this paper, we investigate the break-up behavior of a concentrated emulsion comprising drops stabilized by amphiphilic silica nanoparticles instead of the fluoro-surfactant similar to the one commonly used in current droplet microfluidics applications. The key motivation for replacing surfactants with nanoparticles (referred to as “NPs” hereafter) is that NPs mitigate surfactant-mediated inter-drop transport of small molecules such as model drugs and fluorophores commonly used in fluorogenic enzyme substrates.8,36–38 Such transport leads to the undesirable cross-talk of droplet contents and destroys the accuracy of droplet-based assays.39 In addition, we found that NPs provide a sufficiently rigid interface that supports the attachment and growth of adherent cells, a capability not possible in surfactant systems.8 Previously, we have demonstrated that these NPs are effective in stabilizing drops against coalescence. Here, we show that replacing the fluoro-surfactant molecules with NPs as droplet stabilizers reduces the break-up of drops within a concentrated emulsion flowing as a two-dimensional monolayer in a tapered geometry. Such geometry is often used in droplet interrogation and sorting processes, which are typically performed in a serial manner by flowing a concentrated emulsion into a tapered channel leading to a narrow constriction, whose height and width are comparable to the diameter of a drop.2 In addition, we identify important parameters that influence the break-up of drops stabilized by these NPs in the concentrated emulsion (referred to as “NP drops” herein). While extensive work has described the stability of NP drops (also referred to as “Pickering emulsions”), most had focused on the stability of the emulsions against coalescence, rather than the break-up of the emulsion into small drops.40–43 In fact, it is not at all obvious what the combined effect of NPs and confinement—arising from both the channel wall and the high volume fraction of the drops within the concentrated emulsion—should have on the suppression or enhancement of break-up of these drops. As such, the key significance and novelty of this work lies in the elucidation of the fate and dynamics of individual NP drops within a highly confined concentrated emulsion, a regime that no work has reported before. We expect our results here to lay the foundation for the further development of theoretical framework for both NP-laden drops and concentrated emulsion.
II. EXPERIMENTAL METHOD
A. Materials
All chemicals were used as purchased without purification. Absolute ethanol (EtOH) (99%), tetraethyl orthosilicate (TEOS) (98%), ammonium hydroxide solution (NH4OH) (28 wt. %), and 1H,1H,2H,2H-Per-fluorooctyltriethoxysilane (FAS) (97%) were purchased from Sigma-Aldrich. HFE-7500 was purchased from 3M.
B. Synthesis of amphiphilic fluorinated silica nanoparticles
We synthesized amphiphilic fluorinated silica nanoparticles following our protocol published previously.36 We generated three sizes of NPs having diameters of 30 nm, 100 nm, and 200 nm, respectively. For 30 nm NPs, 3.57 ml of TEOS was added to a solution mixture containing 50 ml of ethanol (EtOH), 1 ml of deionized water, and 1.43 ml of NH4OH (28 wt. %). The solution was stirred vigorously (∼800 rpm) at room temperature for 12 h. 5 ml of neat FAS was then added directly to every 30 ml of the synthesized SiO2 NPs dispersion obtained above, followed by vigorous stirring (∼800 rpm) at room temperature for 6 h. We diluted the reacting solution by adding EtOH to terminate the reaction with a dilution factor of 5. The nanoparticles were then spun down by centrifugation (Sorvall LEGEND X1R) at 10 350 rpm for 30 min. After the supernatant in the mixture was removed, the solid particles were isolated by desiccation overnight and then redispersed in HFE-7500.
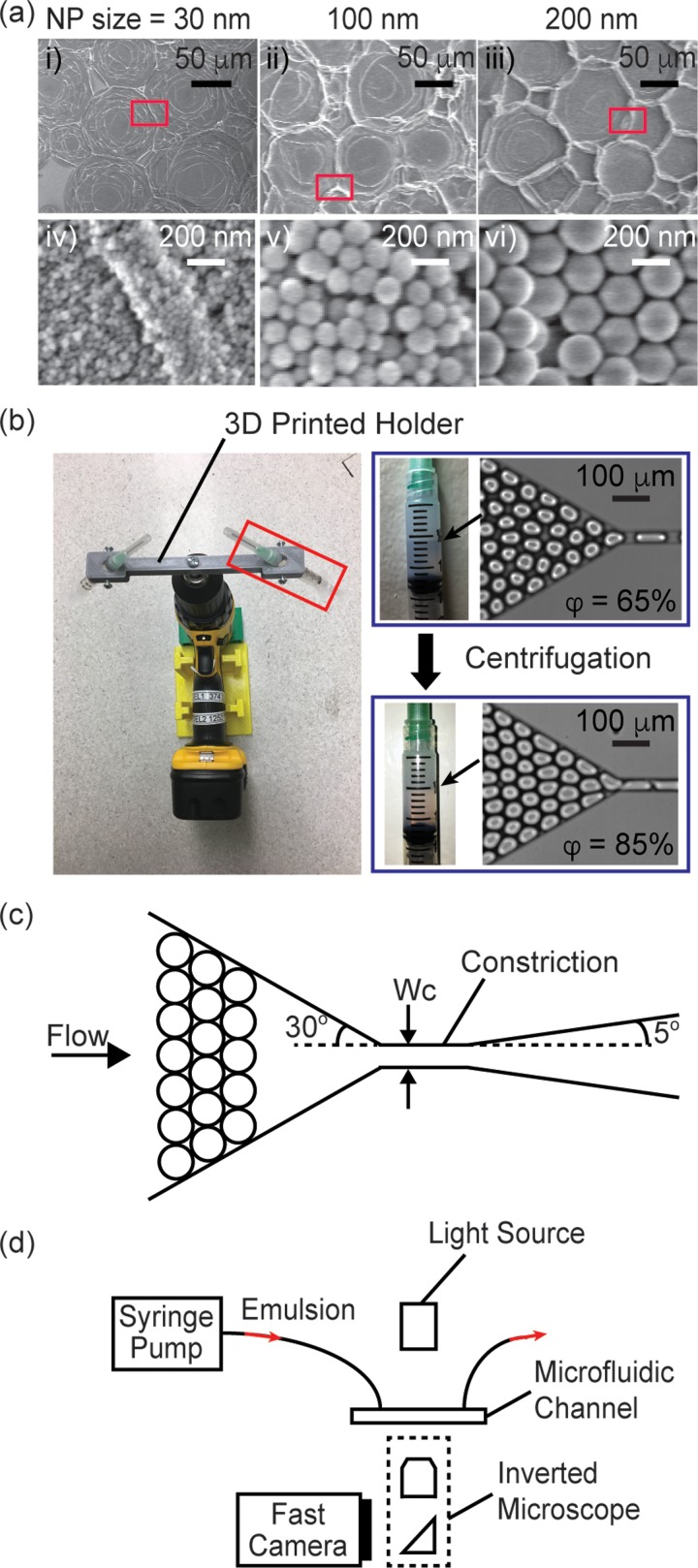
The synthesis was similar for NPs of other sizes, except that the volumes of deionized water, NH4OH, TEOS, and FAS were adjusted. For 100 nm NPs, 3.13 ml of deionized water, 1.49 ml of NH4OH, and 3.72 ml of TEOS were used for the solution mixture. For 200 nm NPs, 4.55 ml of deionized water, 5.04 ml of NH4OH, and 4.06 ml of TEOS were used for the solution mixture. For both sizes, 3 ml of neat FAS was used for every 30 ml of the synthesized SiO2 NPs dispersion. The size of the particle was measured by scanning electron microscope (SEM). SEM images of the particles are shown in Fig. 1(a).
FIG. 1.
(a) SEM images of dried droplets that were stabilized by NPs with diameter of: (i), (iv) 30 nm, (ii), (v) 100 nm, and (iii), (vi) 200 nm, respectively. (iv)–(vi) are enlarged views corresponding to regions inside the red boxes in (i)–(iii), respectively. (b) (Left) Image of the electric drill/driver fitted with a custom 3D-printed syringe holder for centrifugation and concentration of the emulsion. (Right) The volume fraction of the emulsion increased from 65% to 85% after the centrifugation step. (c) Scheme of the channel. (d) Experimental setup.
C. Droplet generation and emulsion preparation
We fabricated all microchannels in poly(dimethylsiloxane) (PDMS) using methods in soft lithography. The microchannels were rendered hydrophobic by treatment with Aquapel (Pittsburgh, PA) to prevent droplets from wetting the wall. We used flow-focusing nozzles to generate monodisperse droplets. The disperse phase was deionized water, and the continuous phase was HFE-7500 containing amphiphilic fluorinated silica nanoparticles (6% w/w). The dispersity of the drops was less than 3% in volume. We used a serpentine channel with a length of 1.37 cm downstream of the nozzle to ensure sufficient time for the NPs to adsorb to the droplet interface to prevent their coalescence upon their collection off-chip. Even though the flow was in the low Reynolds number regime, diffusion was not the only means by which the particles were transported from the bulk continuous phase to the droplet surface. In the presence of flow and confinement, the convective effect arising from the lubrication film between the drops and the channel wall also contributed to accelerate the transport process.44,45 We collected the drops generated from the flow-focusing nozzles into plastic syringes (Normject 3 ml). The drops were then stored for 30 min, during which additional NPs in continuous phase continued to adsorb to the droplet interface. As a result, the drop interface was expected to possess a high surface coverage of NPs. Supplementary material, Note S1, shows our estimation of the surface coverage of NPs on the drops. The coverage was found to be similar for drops coated with 30 nm-NPs and 200 nm-NPs, at ∼1.31 and 1.57 times the value when the drops were covered by a monolayer of randomly close-packed NPs, respectively (see supplementary material, Note S1). We are in the process of investigating the origin of this coverage and using other methods to verify the estimations here. Nevertheless, the coverage ratios of drops coated by these two different NP sizes were similar. Furthermore, since the desorption energy of the NPs was on the order of 104 –105 kBT, the NPs were expected to be irreversibly adsorbed at the droplet interface.8 As such, the drops were stable against coalescence even after we washed off excess NPs in the continuous phase (see supplementary material, Fig. S1).
For the results on the break-up of surfactant-stabilized drops, details can be found in our prior publications.10,11 Briefly, the disperse phase consisted of a mixture of deionized water and glycerol at different mixing ratios, and the continuous phase consisted of a hydrofluoroether HFE-7500 (3M, St. Paul, MN) containing an ammonium salt of Krytox (2% w/w) as surfactant to prevent droplet coalescence.11 The interfacial tension between water and HFE-7500 containing this surfactant (2% w/w) was measured to be 26.3 mN/m using a pendant drop goniometer. We have used only one surfactant here because: (1) This surfactant was similar to the fluoro-surfactant commonly used for stabilizing water drops in fluorinated oil in droplet microfluidics applications.9 (2) This surfactant was the only one with which data were available for the break-up of concentrated emulsions for direct comparison with the results presented in this work.
To obtain emulsions with volume fraction φ > 85%, the drops were centrifuged in the syringes at 374 rpm for 10 min using a centrifuge modified from a hand drill with a 3D-printed custom holder for syringes [Fig. 1(b)].46 After centrifugation, the volume fraction of the emulsion increased from ∼65% to ∼85%. No coalescence was observed during centrifugation, and the size of the drops remained unchanged after centrifugation. We then reinjected the emulsion into a microchannel to examine break-up.
D. Droplet reinjection and channel geometries
Figure 1(c) shows a scheme of the microchannel. The height of the channel was smaller than the diameter of a drop when spherical. The emulsion thus flowed as a monolayer. In the absence of break-up, drops would be forced to pass through the narrow constriction in a serial manner as the width of the constriction was smaller than the diameter of a drop. The entrance angle of the constriction was fixed at 30°, and the exit angle of the constriction was fixed at 5°. Table I lists the experimental parameters tested. We used a Rame-Hart 290 goniometer to measure surface tension between the disperse phase and the continuous phase. After the pendant drop was formed, we waited 35 min before taking the measurement to allow sufficient time for NPs to adsorb to the interface, such that the measured surface tension has already reached an equilibrium value.8 The dynamic viscosity of water and glycerol mixture were based on previous literature.47 We used a Cannon 9722-D50 viscometer to measure the viscosity of the continuous phase containing different NPs at different concentrations. For each set of break-up experiment, we used a syringe pump (Kent Scientific) to vary the flow rate.
TABLE I.
Experimental parameters.
| Experiment # | Disperse phase | (mPa s) | Continuous phase | (mPa s) | λ | (mN/m) | Constriction height, H (μm) | Constriction width, Wc (μm) | Droplet volume (pL) | Confinement factor, cf |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | Water | 1 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 0.78 | 31.25 | 30 | 45 | 70 | 1.42 |
| A2 | Water | 1 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 0.78 | 31.25 | 25 | 30 | 50 | 1.68 |
| A3 | Water | 1 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 0.78 | 31.25 | 20 | 25 | 65 | 2.24 |
| A4 | Water | 1 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 0.78 | 31.25 | 25 | 25 | 65 | 2.01 |
| A5 | Water | 1 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 0.78 | 31.25 | 30 | 38 | 70 | 1.51 |
| A6 | Water | 1 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 0.78 | 31.25 | 25 | 40 | 76 | 1.71 |
| B1 | 20 wt. % glycerol solution | 1.76 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 1.38 | 33.74 | 30 | 38 | 70 | 1.51 |
| B2 | 40 wt. % glycerol solution | 3.71 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 2.90 | 36.12 | 30 | 38 | 70 | 1.51 |
| B3 | 70 wt. % glycerol solution | 22.5 | HFE7500 + 30 nm NPs (6% w/w) | 1.28 | 17.04 | 35.51 | 30 | 38 | 70 | 1.51 |
| C1 | Water | 1 | HFE7500 + 100 nm NPs (6% w/w) | 1.31 | 0.76 | 30.18 | 30 | 38 | 70 | 1.51 |
| C2 | Water | 1 | HFE7500 + 200 nm NPs (6% w/w) | 1.32 | 0.76 | 27.69 | 30 | 38 | 70 | 1.51 |
E. Measurement and analysis of droplet break-up
We imaged the emulsion flow in the microchannel by a high-speed camera (Phantom v7.3) mounted on an inverted microscope [Fig. 1(d)]. We used MATLAB to track the position, size, and shape of all drops in each frame. We defined the break-up fraction as the total number of drops that had been split downstream of constriction divided by the total number of drops injected into the channel. We obtained the number of split drops by comparing the drop size distributions upstream and downstream of the constriction (see details in our previous works10,11). We assumed that a parent drop split once only at the constriction, and a break-up event led to two daughter drops. We verified this assumption for all flow conditions tested in this paper.
III. RESULTS
A. The effect of confinement
We first varied the drop size, constriction size, and flow rates to study the break-up behavior of NP drops. Figure 2 shows the break-up fraction as a function of the capillary number. The capillary number Ca is defined in the following equation:
| (1) |
where is the dynamic viscosity of the continuous phase, G is the strain rate in the constriction, r is droplet radius, and is the interfacial tension between the continuous phase and the disperse phase. We also plotted the results in terms of an alternative definition of Ca where the effective viscosity of the emulsion was used (details in supplementary material, Fig. S2). Here, we had presented the break-up results of NP drops in terms of Ca for direct comparison with previous results on surfactant drops.10,11 The break-up process, however, was determined not only by a balance between viscous effect and surface tension effect but also by interfacial viscoelasticity, drop-drop interaction, and drop-wall interaction as shown in Sections III D, and IV. Nevertheless, Ca was still a useful quantity that was used routinely to describe the deformation and break-up of drops with viscoelastic interface despite the increased complexity of the interface.21,31,35,48
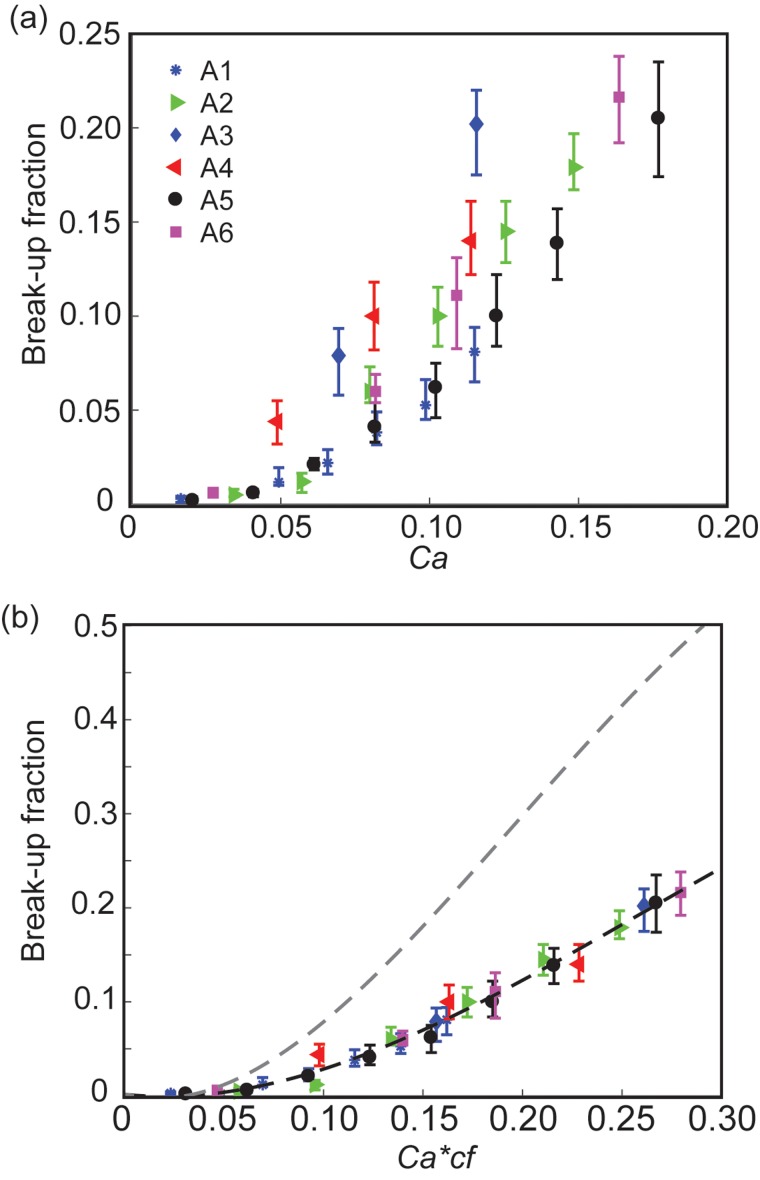
FIG. 2.
Effect of confinement on the break-up of NP drops within a concentrated emulsion. (a) Break-up fraction as a function of capillary number (Ca) at different drop sizes and constriction geometries. The data are from experiments A1-A6 as listed in Table I. (b) Break-up fraction as a function of the product of capillary number (Ca) and confinement factor (cf). The black dashed line is a guide to the eye only. The gray dashed line is the visual guide adopted from surfactant drops from our previous work.10 See supplementary material, Fig. S1, of our prior work for a detail discussion of error bars.11
Similar to our previous results,10 we found that most break-ups took place close to or inside the constriction. We thus approximated the strain rate G experienced by the drops as the shear strain rate in the constriction in the following equation:49
| (2) |
where is the apparent shear rate experienced by a Newtonian fluid, Wc is constriction width, H is channel height (H/Wc < 1), and Q is the volumetric flow rate. f*, a*, b* are functions of H/Wc only, and we set n = 0.5 based on the work of Princen and Kiss50 to represent the index of a power-law concentrated emulsion (see supplementary material, Note S2, and our previous work for more details10).
We can make three immediate observations. First, as Ca increased, the break-up fraction increased for a fixed drop size and constriction geometry. Second, at the same Ca, the break-up fraction increased with increasing confinement factor cf. The confinement factor is defined in Eq. (3), where rh is the hydraulic radius of the constriction.10
| (3) |
Third, by plotting the break-up fraction as a function of Ca, the data failed to collapse into a single curve. This result indicates that Ca alone was insufficient to describe the break-up behavior of NP drops. Figure 2(b) plots the break-up fraction as a function of Ca*cf for datasets A1-A6 in Table I. As can be seen, the data collapsed into a single curve. Similar to surfactant drops, this result implies that confinement, along with Ca which describes viscous stress and interfacial tension, govern droplet break-up.
B. The effect of viscosity ratio
Figure 3 examines the effect of viscosity ratio. The viscosity ratio is defined as the ratio of the dynamic viscosity of the disperse phase to that of the continuous phase as shown in the following equation:
| (4) |
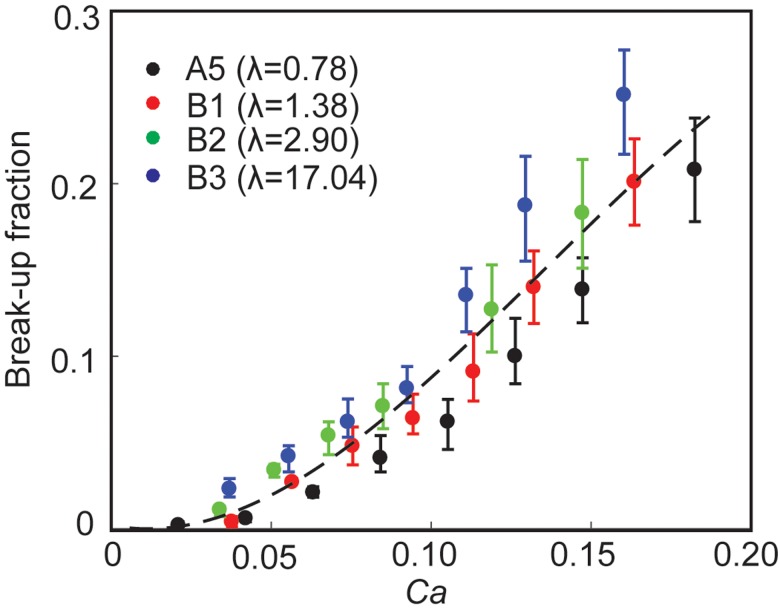
FIG. 3.
Effect of viscosity ratio on break-up. Break-up fraction as a function of capillary number at different viscosity ratios (λ). The data are from experiments A5 (λ = 0.78), B1 (λ = 1.38), B2 (λ = 2.90), and B3 (λ = 17.04) as listed in Table I. The dashed line is for visual guide only.
We plotted the break-up fraction as a function of Ca for 4 sets of experiments for λ = 0.78, 1.38, 2.90, and 17.04 corresponding to datasets A5, B1, B2, and B3, respectively, in Table I. In our previous study on surfactant system, we found that was a critical parameter that determined the break-up fraction. Specifically, at the same Ca and cf, the break-up fraction increased with increasing . In contrast, we found that the break-up fraction of NP drops was not sensitive to within the range tested.
C. The effect of NP size
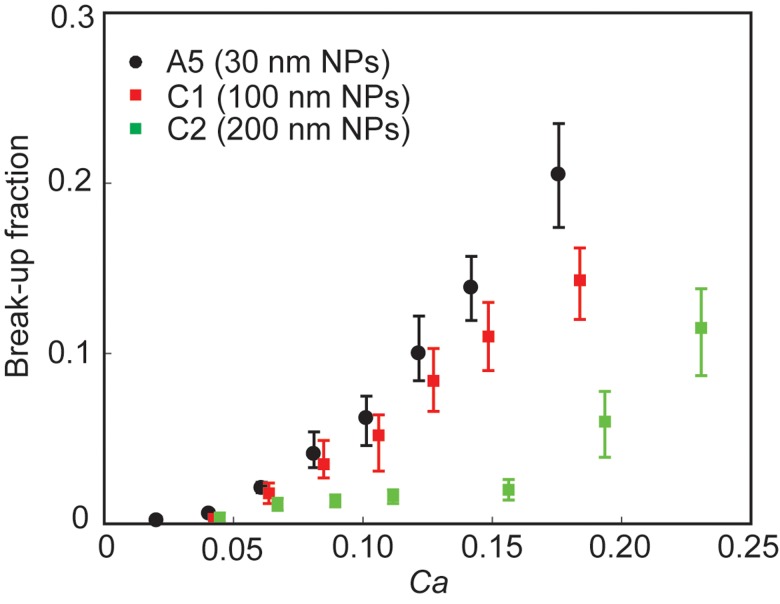
Figure 4 reports the effect of NP size on break-up fraction. The differences in break-up fraction start to be observable from Ca = 0.08, below which the break-up fractions were low (<5%) and not significantly different for the three NP sizes. At Ca > 0.08, a decrease in break-up fraction was observed as the diameter of NPs increased.
FIG. 4.
Effect of particle size on break-up. Break-up fraction as a function of capillary number for drops stabilized by NPs with different sizes. The data are from experiments A5 (30 nm NPs), C1 (100 nm NPs), and C2 (200 nm NPs) as listed in Table I.
D. Local break-up dynamics
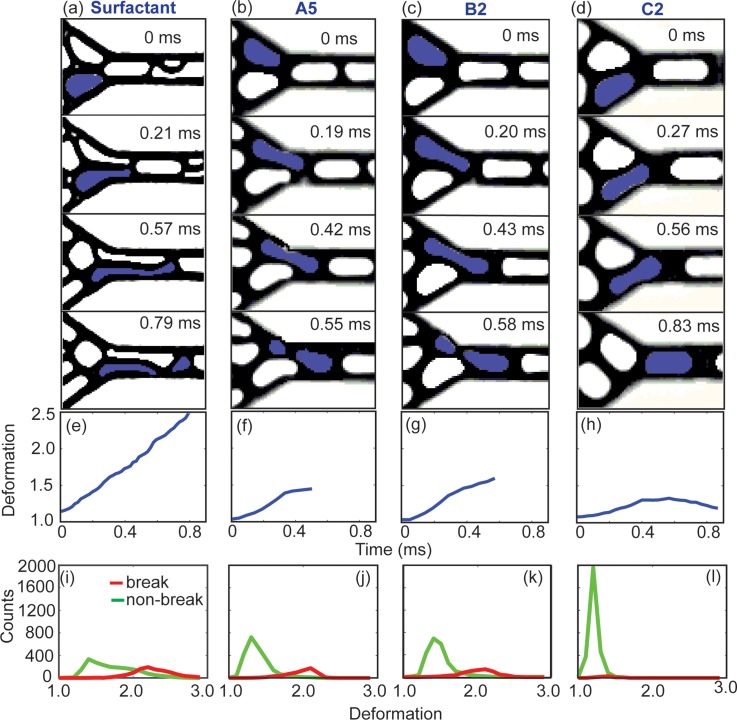
To further investigate the break-up phenomena, here we focus on the dynamics of individual drops close to the entrance to the constriction where majority of the break-up events took place. Figures 5(a)–5(d) show snapshots of four pairs of drops during their flow through the constriction. Figures 5(e)–5(h) plot the deformation of the drops highlighted in blue in Figs. 5(a)–5(d) as a function of time. The deformation D is defined in the following equation:
| (5) |
where P and A are the projected perimeter and area of the drop, respectively.10,11 Three parameters remained constant in the four cases shown: cf, Ca, and the relative position between the two drops entering the constriction. Comparing Figs. 5(a) and 5(b) shows that in both surfactant and NP system, droplet break-up occurred primarily from the pinching of a drop by another against the wall. Comparing Figs. 5(b) and 5(c) shows that the effect of viscosity ratio had insignificant effect on droplet deformation and the break-up dynamics. Comparing Figs. 5(b) and 5(d) shows that drops stabilized by large NPs (200 nm) experienced less deformation than drops stabilized by small NPs (30 nm).
FIG. 5.
A series of snapshots showing the deformation of drops for: (a) surfactant drops, (b) NP drops in experiments A5, (c) B2, and (d) C2, respectively, all at capillary number Ca ∼ 0.15. The value of confinement factor cf is identical in (a)–(d). λ shown in (a) is identical to that in A5. (e)–(h) The deformation of the drop highlighted in blue as a function of time, corresponding to the snapshots in (a)–(d). (i)–(l) Histograms showing the distribution of the maximum deformation a drop experienced during its flow in the field of view as shown in (a)–(d). 3000 drops were recorded for each plot. The red curves denote drops that underwent break-up, and the green curves denote drops that did not undergo break-up.
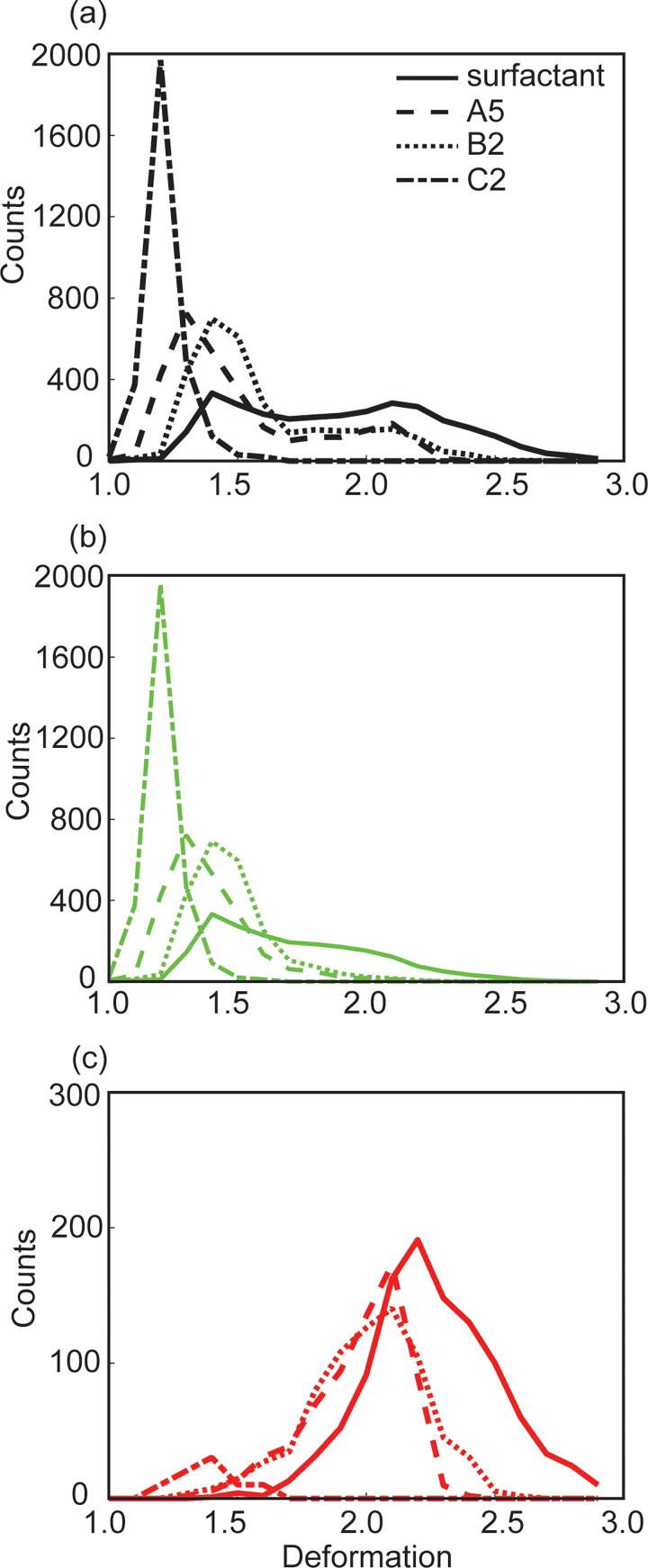
To generate Figs. 5(a)–5(d), we purposely chose drop pairs having the same relative positions or packing configuration, in which the two drops were synchronized as they entered the constriction. The packing configuration of the drops in the rest of the emulsion was not fixed but time-varying, however.10,11 In Figs. 5(i)–5(l), we plotted the distribution of the maximum deformation (Dmax) of a large number of drops (N = 3000) with different packing configurations and tracked their subsequent fate (break-up or not) in the same region shown in Figs. 5(a)–5(d). To facilitate comparison, we combined the histograms from Figs. 5(i) to 5(l) in Fig. 6. For a concentrated emulsion comprising surfactant drops, we have previously identified a critical deformation value D ∼ 1.7, beyond which break-up started occurring and the break-up probability increased with drop deformation.10,11 In Fig. 6(c), we noticed the break-up of NP drops started to occur at a deformation value D ∼ 1.4, slightly lower than that of surfactant drops. The origin of this difference is under current investigation. Despite this small difference, the trend of break-up probability of NP drops was similar to that of surfactant drops: once break-up started, increasing drop deformation resulted in increasing break-up probability. We also note that the break-up probability relied not only on the absolute value of this critical deformation D but also on the proportion of drops within the emulsion with deformation exceeding this critical value. As such, even the critical deformation value for NP drops was slightly smaller than that for surfactant drops, the smaller proportion of drops having deformation exceeding this critical value led to a smaller break-up probability.
FIG. 6.
(a) Distribution of the maximum deformation of 3000 drops, including both break-up and non-breakup drops. (b) The same distribution as that in (a), but for non-breakup drops only. (c) The same distribution as that in (a), but for break-up drops only. The curves in (a)–(c) correspond to datasets shown in Figs. 5(i)–5(l), respectively.
IV. DISCUSSION
A. Confinement enhances the deformation and break-up of NP drops
Previously, the confinement of a drop has been shown to be critical in determining the deformation and break-up of a drop, both for single drops and for drops within a concentrated emulsion stabilized by surfactants. The effect of confinement on the deformation of a single drop was analytically studied by Shapira and Haber, who modified Taylor's small deformation theory and combined with Lorentz's reflection method to introduce confinement.51 While the analysis was based on small deformation theory, its prediction was in good agreement with experimental results at moderate and large Ca.52,53 Subsequent analytical, simulation, and experimental works confirmed that confinement enhances droplet deformation.51–57 For capsules and particle-stabilized drops, the motion and deformation modes were different from that of a pure drop owing to the different nature of the interface, where interfacial viscoelastic response must be considered in addition to surface tension. The general effect of confinement on deformation, however, remains qualitatively similar: as confinement increases, the deformation of the drop also increases.48,58,59 The effect of confinement on break-up has been mixed, however. Depending on the details of flow type, viscosity ratio, the presence and the composition of surfactants and viscoelastic components, break-up has been enhanced or suppressed.19,48,53–57,60
Nevertheless, confinement is still expected to play an important role in our system in determining the break-up of NP drops, as it does on the break-up of surfactant drops within a concentrated emulsion. The mechanism responsible for the break-up of NP drops was similar to that of surfactant drops, as can be seen by comparing Figs. 5(a) to 5(b) and 5(c). As a drop flowed through the constriction, it deformed to an elongated shape. Break-up occurred when another drop attempted to squeeze into the constriction at the same time, eventually pinching and splitting the first drop into two daughter drops. Similar to surfactant drops, strong confinement led to increased deformation of NP drops and facilitated their pinch-off in the constriction. As such, increasing confinement also led to an enhancement of break-up for NP drops.
B. Replacing surfactants with NPs suppresses droplet break-up
In comparison to drops stabilized by the fluoro-surfactant studied, the break-up fraction of NP drops was significantly lower than that of surfactant drops at the same values of Ca*cf [Fig. 2(b)]. This result is also supported by considering droplet deformation. At the same Ca and cf, NP drops deformed less than surfactant drops, as seen by comparing Figs. 5(e) and 5(f). Although both highlighted drops in Figs. 5(a) and 5(b) pinched off, the maximum deformation of the drops immediately before break-up was very different. The highlighted surfactant drop deformed significantly with a maximum deformation value Dmax ∼ 2.5, while the highlighted NP drop deformed to a maximum value of Dmax ∼ 1.47 only. Figure 6 shows similar trends for a large number of drops in the emulsion. Specifically, Fig. 6(a) shows that NP drops rarely reached a deformation beyond Dmax ∼ 2.5, while a considerable portion of surfactant drops had deformation beyond Dmax ∼ 2.5 at a fixed set of values for Ca and cf.
Here, the comparison between NP and surfactant system was performed at the same capillary number, where any difference in interfacial tension was already accounted for. If interfacial tension was the only contributing factor to the results, the data for surfactant and NP-stabilized drops should have collapsed onto a single curve in Fig. 2(b). Here, the suppression of deformation and break-up in NP drops was likely due to the larger viscoelastic contribution from the NP-covered interface than that from a surfactant interface.61–66 To further illustrate the difference between the surfactant and NPs studied, we consider the stress boundary condition in determining drop deformation. In the absence of Marangoni effect, the boundary condition can be written in a general form as shown in Eqs. (6) and (7), which correspond to the local stress balance at the interface in tangential direction and in normal direction, respectively21,67–70
| (6) |
| (7) |
where T is the stress tensor (including both viscous stress and pressure) of bulk fluid evaluated at the interface, τs is the surface stress tensor arising from interfacial viscoelasticity, and are unit normal and unit tangential vectors, respectively, is the interfacial tension as defined before, and denotes surface gradient along the interface. We used * to denote parameters of the flow of the disperse phase.
For the surfactant we used, we believe that the primary effect of the surfactant was to modify the overall interfacial tension, and the contribution from viscoelasticity was small and negligible. The boundary conditions can then be simplified to
| (8) |
| (9) |
Equations (8) and (9) imply that the deformation of a simple surfactant drop is solely determined by balancing the stress difference of the bulk fluids across the interface (which tends to deform the drop) and surface tension (which tends to resist the deformation).
In the case of an interface coated with NPs, the presence of interfacial viscoelasticity introduces additional dynamics that is reflected in the terms associated with τs in both Eqs. (6) and (7). The constitutive equation of τs, however, was not trivial. Depending on the particle size, wettability, concentration, and many other factors, the constitutive model of particle-laden interface was complex and often non-linear.61,64,65,70 Nevertheless, the equations here qualitatively reveal that the boundary conditions are very different in the case of NPs versus the case of surfactant.
In general, both elastic and viscous modulus of a particle-laden interface were reported to be significantly higher than that stabilized by typical surfactant molecules.64,65,71 Both viscous and elastic components of the interface constrain the degree at which a drop can deform.21,31 Therefore, it follows that the deformation of a NP drop was less than that of a surfactant drop. In our system, increasing drop deformation was correlated with increasing break-up fraction.10,11 As NPs suppressed deformation, the break-up fraction in NP drops decreased accordingly.
We found that the break-up fraction was not sensitive to the NP concentrations used for the range of values tested (supplementary material, Fig. S1). The transport of NPs from the continuous phase onto the increased interfacial area caused by drop deformation was unlikely to be significant in our case. This result was largely due to the different time scales for drop deformation and for NP transport.17,40,44,45,48,53,72 In our system, the time scale for drop deformation and relaxation was <1 ms [Figs. 5(a)–5(h)], while the transport of NPs was expected to take >10 ms (see supplementary material, Note S3). Although we could not easily estimate the effect of convection and adsorption kinetics on the actual time scale of NP transport, the adsorption process was known to be slow and rate-limiting, especially when the droplet surface was already densely packed with NPs.45,73–75 The results in Fig. S1 (supplementary material) indicate that the time scale for NP transport arising from the combined effect of diffusion, particle interaction, and convection should be slow compared with that of droplet deformation in our system. Furthermore, at the highest bulk NP concentration (6% w/w) used in our experiment, the continuous phase had the same viscosity as neat oil and was not expected to raise any viscoelastic response.76 Therefore, extra NPs in the continuous phase had insignificant effect on drop deformation and break-up.
C. Break-up of NP drops is insensitive to viscosity ratio
Unlike surfactant drops, both the deformation and break-up fraction of NP drops were insensitive to the viscosity ratios tested in this paper. The insensitivity of deformation is clearly seen by comparing Figs. 5(f) and 5(g). Increasing λ from λ = 0.78 to λ = 2.90 increased Dmax from Dmax ∼ 1.47 to Dmax ∼ 1.58 only for the highlighted NP drops. This increment of 0.11 was small compared with surfactant case in our previous study, in which the increment in Dmax was almost 1 by changing λ from λ = 0.81 to λ = 2.02.10 Figures 6(a)–6(c) further confirm that changing λ did not significantly alter NP drop deformation, as seen by the similar distributions of drop deformation between experiments A5 and B2.
The insensitivity to λ for NP drops appears in line with earlier work on droplet break-up in the presence of surface-active polymers, where the critical Ca and droplet deformation at critical condition were reported to be independent of λ.16,77,78 The independence was caused by the use of a convection-dominant surfactant giving rise to a strong Marangoni stress, which retarded interfacial flow substantially. As a result, the effect of viscosity ratio on retarding interfacial flow and drop deformation was only incremental. This explanation does not apply here, however. We tested different concentrations of NPs in the continuous phase, and found that the break-up fraction was insensitive to NP concentration (see supplementary material, Fig. S1). The convective effect of NPs at the interface did not cause strong Marangoni flow, and Marangoni effect was unlikely to be significant in our system.
Here, we propose this insensitivity to viscosity ratio as another consequence of increased interfacial viscoelasticity. In the presence of NPs at the interface, the large interfacial viscoelastic contribution overtook the viscous stress contribution from the flow of the internal disperse phase, and appeared as a dominant term in the boundary conditions as shown in Eqs. (6) and (7). In this case, the contribution from internal fluid viscous stress became an incremental term. As a result, the internal fluid and λ virtually ceased to play a role in determining drop deformation. In our system, we have shown the break-up fraction is correlated to drop deformation. It thus follows that λ did not affect the break-up fraction here.
While our proposal has to be verified with measurements of the viscoelastic properties of interfaces coated with our NPs, it is in line with previous studies.71,79,80 As a note, the surfactant used in our previous study was unlikely to have given rise to an interface with large viscoelastic modulus. This fact was in part supported by the dependence of droplet deformation and break-up fraction on λ, as well as our micro-particle imaging velocimetry results which showed that the strength of inner fluid recirculation decreased with increasing viscosity ratio.81
We note that the range of viscosity we could test was limited by the availability of fluids with which we can form stable concentrated emulsions. Even the range tested was relatively narrow, the results were still useful since: (1) Practically, most droplet microfluidics applications are performed in this viscosity range. (2) Fundamentally, the insensitivity of our results in comparison with the surfactant system was sufficient to reflect the different flow physics induced by the differences in the interfacial properties given by NPs and surfactant.
D. The use of large NPs suppresses droplet break-up
Figure 4 shows that an increase in NP size leads to a decrease in break-up fraction in our system. Such result is again consistent with the trend of droplet deformation. In Fig. 5(h), the deformation of the drop stabilized by 200 nm-NPs increased gradually as the drop attempted to squeeze into the constriction. A maximum deformation Dmax ∼ 1.34 was reached when the leading edge of the drop was inside the constriction, while the rear end of the drop was still outside the constriction. The drop successfully overtook the neighboring drop and entered the constriction completely without being pinched off. After passing through, the deformation value decreased as the drop relaxed inside the constriction. On the other hand, the drop stabilized by 30 nm-NPs [Fig. 5(f)] reached a deformation of Dmax ∼ 1.47 and eventually underwent break-up. This trend was the same in the entire emulsion, as seen by comparing the distributions of drop deformation from experiment C2 where 200 nm-NPs were used, and that from experiment A5 where 30 nm-NPs were used [Figs. 6(a) and 6(b)]. In addition, from Fig. 6(c), the total number of split drops in experiment C2 was significantly lower than all other cases.
Particle size, from the nanometer to micrometer range, has been shown to be of paramount importance in determining the structure and viscoelastic response of a two-dimensional Langmuir monolayer with particles.61,82 Among other factors, increasing particle size at a fixed surface particle density was shown to induce a transition from a liquid-like to solid-like state in a monolayer of charged polystyrene microparticles; such transition could then change the shear response of the interface.61,82 Dynamically, from direct interfacial shear measurement on the viscoelastic response of two-dimensional particle surfaces laden by gold NPs, an increase in particle size from 7 nm to 80 nm led to increases in both elastic and viscous moduli.61,62 Assuming that size was the only major difference in the three sets of particles used in our system, the observation of suppressed break-up with increasing NP size can be reasoned as an increase in the interfacial viscous and elastic moduli. Such an increase stiffened the interface and constrained droplet deformation,21,62,83 thereby decreasing break-up fraction in our system. To predict and explain the trend more quantitatively requires measuring the viscoelastic properties of interfaces laden with different NP sizes at different surface densities, and is under current investigation.
V. CONCLUSIONS
In summary, we have compared the break-up of drops stabilized by NPs with those stabilized by the fluoro-surfactant similar to the one commonly used in droplet microfluidics in a concentrated emulsion flowing in a tapered microfluidic channel. We showed that break-up was suppressed by replacing surfactant with amphiphilic NPs as droplet stabilizer. The break-up fraction of NP drops was not sensitive to λ for the range of values tested, and it decreased with increasing NP size. To further understand and predict the break-up behavior of NP drops, work is in progress to characterize the rheological properties of interfaces laden with our NPs, and to derive the dependence on particle size, concentration, as well as fluid properties.
Practically, our results indicate two key advantages of NPs with direct applications in droplet microfluidics. First, since droplet break-up is insensitive to viscosity ratio, one can use the same droplet size and channel geometry—that is, the same confinement factor—for samples having different viscosities (e.g., polymer or protein solutions that can be more viscous than water) and maintain the same degree of break-up and corresponding assay accuracy. This feature is an advantage over the surfactant system studied. For surfactant-stabilized drops, the break-up fraction scales with the product of confinement factor and viscosity ratio. The droplet size and/or the constriction geometry must therefore be redesigned and customized separately for samples with different viscosities in order to maintain the same break-up fraction. Second, replacing surfactants with NPs increases the throughput of the serial droplet interrogation process. For example, if a tolerance of 3% of droplet break-up is acceptable in a microfluidic assay, the highest throughput is ∼7100 drops/s for 70 pL-drops flowing in a 30° taper with a confinement factor of 1.51 when the drops are stabilized by 200 nm-NPs. This throughput is 3 times faster than the case when the drops are stabilized by the surfactant studied here.
VI. SUPPLEMENTARY MATERIAL
See supplementary information for the (1) effect of NP concentration on break-up fraction, (2) break-up results in terms of alternative definition of capillary number, (3) estimation of NP coverage on droplet interface, (4) calculation of values for f*, a*, and b* in Eq. (2) in the main text, and (5) estimation of time scale for drop deformation and NP diffusion, respectively.
ACKNOWLEDGMENTS
We acknowledge support from the National Science Foundation through the NSF CAREER Award No. #1454542. We also acknowledge additional support from Agilent Technologies University Research Program Award No. #4023. We also thank Guanya Shi and Jian Wei Khor for assistance with initial experiments and discussions.
References
- 1. Teh S.-Y., Lin R., Hung L.-H., and Lee A. P., Lab Chip 8(2), 198–220 (2008). 10.1039/b715524g [DOI] [PubMed] [Google Scholar]
- 2. Rosenfeld L., Lin T., Derda R., and Tang S. K., Microfluid. Nanofluid. 16(5), 921–939 (2014). 10.1007/s10404-013-1310-x [DOI] [Google Scholar]
- 3. Breslauer D. N., Lee P. J., and Lee L. P., Mol. Biosyst. 2(2), 97–112 (2006). 10.1039/b515632g [DOI] [PubMed] [Google Scholar]
- 4. Köster S., Angile F. E., Duan H., Agresti J. J., Wintner A., Schmitz C., Rowat A. C., Merten C. A., Pisignano D., and Griffiths A. D., Lab Chip 8(7), 1110–1115 (2008). 10.1039/b802941e [DOI] [PubMed] [Google Scholar]
- 5. Kim M., Pan M., Gai Y., Pang S., Han C., Yang C., and Tang S. K., Lab Chip 15(6), 1417–1423 (2015). 10.1039/C4LC01465K [DOI] [PubMed] [Google Scholar]
- 6. Agresti J. J., Antipov E., Abate A. R., Ahn K., Rowat A. C., Baret J.-C., Marquez M., Klibanov A. M., Griffiths A. D., and Weitz D. A., Proc. Natl. Acad. Sci. U.S.A. 107(9), 4004–4009 (2010). 10.1073/pnas.0910781107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Guo M. T., Rotem A., Heyman J. A., and Weitz D. A., Lab Chip 12(12), 2146–2155 (2012). 10.1039/c2lc21147e [DOI] [PubMed] [Google Scholar]
- 8. Pan M., Rosenfeld L., Kim M., Xu M., Lin E., Derda R., and Tang S. K., ACS Appl. Mater. Interfaces 6(23), 21446–21453 (2014). 10.1021/am506443e [DOI] [PubMed] [Google Scholar]
- 9. Holtze C., Rowat A., Agresti J., Hutchison J., Angile F., Schmitz C., Köster S., Duan H., Humphry K., and Scanga R., Lab Chip 8(10), 1632–1639 (2008). 10.1039/b806706f [DOI] [PubMed] [Google Scholar]
- 10. Gai Y., Khor J. W., and Tang S. K. Y., Lab Chip 16(16), 3058–3064 (2016). 10.1039/C6LC00478D [DOI] [PubMed] [Google Scholar]
- 11. Rosenfeld L., Fan L., Chen Y., Swoboda R., and Tang S. K., Soft Matter 10(3), 421–430 (2014). 10.1039/C3SM51843D [DOI] [PubMed] [Google Scholar]
- 12. Taylor G. I., Proc. R. Soc. London, Ser. A 138(834), 41–48 (1932). 10.1098/rspa.1932.0169 [DOI] [Google Scholar]
- 13. Taylor G., Proc. R. Soc. London, Ser. A 146(858), 501–523 (1934). 10.1098/rspa.1934.0169 [DOI] [Google Scholar]
- 14. Bentley B. and Leal L., J. Fluid Mech. 167, 241–283 (1986). 10.1017/S0022112086002811 [DOI] [Google Scholar]
- 15. Stone H. A. and Leal L., J. Fluid Mech. 198, 399–427 (1989). 10.1017/S0022112089000194 [DOI] [Google Scholar]
- 16. Stone H. and Leal L., J. Fluid Mech. 220, 161–186 (1990). 10.1017/S0022112090003226 [DOI] [Google Scholar]
- 17. Stone H. A., Annu. Rev. Fluid Mech. 26(1), 65–102 (1994). 10.1146/annurev.fl.26.010194.000433 [DOI] [Google Scholar]
- 18. Grace H. P., Chem. Eng. Commun. 14(3–6), 225–277 (1982). 10.1080/00986448208911047 [DOI] [Google Scholar]
- 19. Vananroye A., Van Puyvelde P., and Moldenaers P., Langmuir 22(9), 3972–3974 (2006). 10.1021/la060442+ [DOI] [PubMed] [Google Scholar]
- 20. Boussinesq J., Ann. Chim. Phys. 29(349), 349–357 (1914). [Google Scholar]
- 21. Gounley J., Boedec G., Jaeger M., and Leonetti M., J. Fluid Mech. 791, 464–494 (2016). 10.1017/jfm.2016.39 [DOI] [Google Scholar]
- 22. Reusken A. and Zhang Y., Int. J. Numer. Methods Fluids 73(12), 1042–1058 (2013). 10.1002/fld.3835 [DOI] [Google Scholar]
- 23. Flumerfelt R. W., J. Colloid Interface Sci. 76(2), 330–349 (1980). 10.1016/0021-9797(80)90377-X [DOI] [Google Scholar]
- 24. Phillips W. J., Graves R. W., and Flumerfelt R. W., J. Colloid Interface Sci. 76(2), 350–370 (1980). 10.1016/0021-9797(80)90378-1 [DOI] [Google Scholar]
- 25. Barthès-Biesel D., Annu. Rev. Fluid Mech. 48, 25–52 (2016). 10.1146/annurev-fluid-122414-034345 [DOI] [Google Scholar]
- 26. Barthes-Biesel D., Diaz A., and Dhenin E., J. Fluid Mech. 460, 211–222 (2002). 10.1017/S0022112002008352 [DOI] [Google Scholar]
- 27. Lac E. and Barthès-Biesel D., Phys. Fluids 17(7), 072105 (2005). 10.1063/1.1955127 [DOI] [Google Scholar]
- 28. Barthes-Biesel D., Phys. A 172(1–2), 103–124 (1991). 10.1016/0378-4371(91)90314-3 [DOI] [Google Scholar]
- 29. Barthes-Biesel D., Biomater., Artif. Cell Immobilization Biotechnol. 21(3), 359–373 (1993). 10.3109/10731199309117374 [DOI] [PubMed] [Google Scholar]
- 30. Arditty S., Schmitt V., Lequeux F., and Leal-Calderon F., Eur. Phys. J. B 44(3), 381–393 (2005). 10.1140/epjb/e2005-00137-0 [DOI] [Google Scholar]
- 31. Mei Y., Li G., Moldenaers P., and Cardinaels R., Soft Matter 12(47), 9407 (2016). 10.1039/C6SM02031C [DOI] [PubMed] [Google Scholar]
- 32. Lee M. N., Chan H. K., and Mohraz A., Langmuir 28(6), 3085–3091 (2012). 10.1021/la203384f [DOI] [PubMed] [Google Scholar]
- 33. Chang K. and Olbricht W., J. Fluid Mech. 250, 609–633 (1993). 10.1017/S0022112093001582 [DOI] [Google Scholar]
- 34. Chang K. and Olbricht W., J. Fluid Mech. 250, 587–608 (1993). 10.1017/S0022112093001570 [DOI] [Google Scholar]
- 35. Williams A., Janssen J., and Prins A., Colloids Surf., A 125(2), 189–200 (1997). 10.1016/S0927-7757(96)03972-6 [DOI] [Google Scholar]
- 36. Pan M., Kim M., Blauch L., and Tang S. K., RSC Adv. 6(46), 39926–39932 (2016). 10.1039/C6RA03950B [DOI] [Google Scholar]
- 37. Lyu F., Xu M., Cheng Y., Xie J., Rao J., and Tang S. K., Biomicrofluidics 9(4), 044120 (2015). 10.1063/1.4928879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Litten B., Blackett C., Wigglesworth M., Goddard N., and Fielden P., Biomicrofluidics 9(5), 052607 (2015). 10.1063/1.4927324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Chen Y., Gani A. W., and Tang S. K., Lab Chip 12(23), 5093–5103 (2012). 10.1039/c2lc40624a [DOI] [PubMed] [Google Scholar]
- 40. Zhou Q., Sun Y., Yi S., Wang K., and Luo G., Soft Matter 12(6), 1674–1682 (2016). 10.1039/C5SM02924D [DOI] [PubMed] [Google Scholar]
- 41. Destribats M., Lapeyre V., Wolfs M., Sellier E., Leal-Calderon F., Ravaine V., and Schmitt V., Soft Matter 7(17), 7689–7698 (2011). 10.1039/c1sm05240c [DOI] [Google Scholar]
- 42. Destribats M., Gineste S. P., Laurichesse E., Tanner H., Leal-Calderon F., He´roguez V. R., and Schmitt V. R., Langmuir 30(31), 9313–9326 (2014). 10.1021/la501299u [DOI] [PubMed] [Google Scholar]
- 43. Tambe D. E. and Sharma M. M., Adv. Colloid Interface Sci. 52, 1–63 (1994). 10.1016/0001-8686(94)80039-1 [DOI] [Google Scholar]
- 44. Kotula A. P. and Anna S. L., Soft Matter 8(41), 10759–10772 (2012). 10.1039/c2sm25970b [DOI] [Google Scholar]
- 45. Anna S. L., Annu. Rev. Fluid Mech. 48, 285–309 (2016). 10.1146/annurev-fluid-122414-034425 [DOI] [Google Scholar]
- 46. Kim M., Shi G., Pan M., Blauch L., and Tang S. K. Y., see http://blogs.rsc.org/chipsandtips/2016/10/17/electric-drilldriver-as-centrifuge-with-3d-printed-custom-holders-for-non-conventional-containers/ for “ Chips & tips: Electric drill/driver as centrifuge with 3D-printed custom holders for non-conventional containers,” Lab Chip, October 17, 2016.
- 47. Cheng N.-S., Ind. Eng. Chem. Res. 47(9), 3285–3288 (2008). 10.1021/ie071349z [DOI] [Google Scholar]
- 48. Mulligan M. K. and Rothstein J. P., Langmuir 27(16), 9760–9768 (2011). 10.1021/la201523r [DOI] [PubMed] [Google Scholar]
- 49. Son Y., Polymer 48(2), 632–637 (2007). 10.1016/j.polymer.2006.11.048 [DOI] [Google Scholar]
- 50. Princen H. and Kiss A., J. Colloid Interface Sci. 128(1), 176–187 (1989). 10.1016/0021-9797(89)90396-2 [DOI] [Google Scholar]
- 51. Shapira M. and Haber S., Int. J. Multiphase Flow 16(2), 305–321 (1990). 10.1016/0301-9322(90)90061-M [DOI] [Google Scholar]
- 52. Vananroye A., Van Puyvelde P., and Moldenaers P., J. Rheol. 51(1), 139–153 (2007). 10.1122/1.2399089 [DOI] [Google Scholar]
- 53. Sibillo V., Pasquariello G., Simeone M., Cristini V., and Guido S., Phys. Rev. Lett. 97(5), 054502 (2006). 10.1103/PhysRevLett.97.054502 [DOI] [PubMed] [Google Scholar]
- 54. Christopher G., Bergstein J., End N., Poon M., Nguyen C., and Anna S. L., Lab Chip 9(8), 1102–1109 (2009). 10.1039/b813062k [DOI] [PubMed] [Google Scholar]
- 55. Janssen P., Vananroye A., Van Puyvelde P., Moldenaers P., and Anderson P., J. Rheol. 54(5), 1047–1060 (2010). 10.1122/1.3473924 [DOI] [Google Scholar]
- 56. Guido S., Curr. Opin. Colloid Interface Sci. 16(1), 61–70 (2011). 10.1016/j.cocis.2010.12.001 [DOI] [Google Scholar]
- 57. Cardinaels R. and Moldenaers P., Microfluid. Nanofluid. 10(6), 1153–1163 (2011). 10.1007/s10404-010-0743-8 [DOI] [Google Scholar]
- 58. Dawson G., Häner E., and Juel A., Procedia IUTAM 16, 22–32 (2015). 10.1016/j.piutam.2015.03.004 [DOI] [Google Scholar]
- 59. Hu X.-Q., Sévénié B., Salsac A.-V., Leclerc E., and Barthès-Biesel D., Phys. Rev. E 87(6), 063008 (2013). 10.1103/PhysRevE.87.063008 [DOI] [PubMed] [Google Scholar]
- 60. Mulligan M. K. and Rothstein J. P., Phys. Fluids 23(2), 022004 (2011). 10.1063/1.3548856 [DOI] [Google Scholar]
- 61. Mendoza A. J., Guzmán E., Martínez-Pedrero F., Ritacco H., Rubio R. G., Ortega F., Starov V. M., and Miller R., Adv. Colloid Interface Sci. 206, 303–319 (2014). 10.1016/j.cis.2013.10.010 [DOI] [PubMed] [Google Scholar]
- 62. Orsi D., Baldi G., Cicuta P., and Cristofolini L., Colloids Surf., A 413, 71–77 (2012). 10.1016/j.colsurfa.2012.01.001 [DOI] [Google Scholar]
- 63. Cicuta P., Stancik E. J., and Fuller G. G., Phys. Rev. Lett. 90(23), 236101 (2003). 10.1103/PhysRevLett.90.236101 [DOI] [PubMed] [Google Scholar]
- 64. Maestro A., Santini E., Zabiegaj D., Llamas S., Ravera F., Liggieri L., Ortega F., Rubio R. G., and Guzman E., Adv. Condens. Matter Phys. 2015, 917516. 10.1155/2015/917516 [DOI] [Google Scholar]
- 65. Krägel J. and Derkatch S. R., Curr. Opin. Colloid Interface Sci. 15(4), 246–255 (2010). 10.1016/j.cocis.2010.02.001 [DOI] [Google Scholar]
- 66. Reynaert S., Moldenaers P., and Vermant J., Phys. Chem. Chem. Phys. 9(48), 6463–6475 (2007). 10.1039/b710825g [DOI] [PubMed] [Google Scholar]
- 67. Scriven L., Chem. Eng. Sci. 12(2), 98–108 (1960). 10.1016/0009-2509(60)87003-0 [DOI] [Google Scholar]
- 68. Gardner J., Addison J., and Schechter R., AlChE J. 24(3), 400–406 (1978). 10.1002/aic.690240303 [DOI] [Google Scholar]
- 69. Ponce-Torres A., Montanero J., Herrada M., Vega E., and Vega J., Phys. Rev. Lett. 118(2), 024501 (2017). 10.1103/PhysRevLett.118.024501 [DOI] [PubMed] [Google Scholar]
- 70. Erni P., Soft Matter 7(17), 7586–7600 (2011). 10.1039/c1sm05263b [DOI] [Google Scholar]
- 71. Safouane M., Langevin D., and Binks B., Langmuir 23(23), 11546–11553 (2007). 10.1021/la700800a [DOI] [PubMed] [Google Scholar]
- 72. Rallison J., Annu. Rev. Fluid Mech. 16(1), 45–66 (1984). 10.1146/annurev.fl.16.010184.000401 [DOI] [Google Scholar]
- 73. Kutuzov S., He J., Tangirala R., Emrick T., Russell T., and Böker A., Phys. Chem. Chem. Phys. 9(48), 6351–6358 (2007). 10.1039/b710060b [DOI] [PubMed] [Google Scholar]
- 74. Manga M. S., Cayre O. J., Williams R. A., Biggs S., and York D. W., Soft Matter 8(5), 1532–1538 (2012). 10.1039/C1SM06547E [DOI] [Google Scholar]
- 75. Du K., Glogowski E., Emrick T., Russell T. P., and Dinsmore A. D., Langmuir 26(15), 12518–12522 (2010). 10.1021/la100497h [DOI] [PubMed] [Google Scholar]
- 76. Merkel T., Henne J., Hecht L., Graef V., Walz E., and Schuchmann H. P., Colloids Surf., A 470, 179–187 (2015). 10.1016/j.colsurfa.2015.01.080 [DOI] [Google Scholar]
- 77. Milliken W. and Leal L., J. Non-Newtonian Fluid Mech. 40(3), 355–379 (1991). 10.1016/0377-0257(91)87018-S [DOI] [Google Scholar]
- 78. Milliken W., Stone H., and Leal L., Phys. Fluids A 5(1), 69–79 (1993). 10.1063/1.858790 [DOI] [Google Scholar]
- 79. Ramanujan S. and Pozrikidis C., J. Fluid Mech. 361, 117–143 (1998). 10.1017/S0022112098008714 [DOI] [Google Scholar]
- 80. Park S.-Y. and Dimitrakopoulos P., Soft Matter 9(37), 8844–8855 (2013). 10.1039/c3sm51516h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Leong C. M., Gai Y., and Tang S. K., Phys. Fluids 28(11), 112001 (2016). 10.1063/1.4968526 [DOI] [Google Scholar]
- 82. Bonales L., Rubio J., Ritacco H., Vega C., Rubio R., and Ortega F., Langmuir 27(7), 3391–3400 (2011). 10.1021/la104917e [DOI] [PubMed] [Google Scholar]
- 83. Lishchuk S. and Halliday I., Phys. Rev. E 80(1), 016306 (2009). 10.1103/PhysRevE.80.016306 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary information for the (1) effect of NP concentration on break-up fraction, (2) break-up results in terms of alternative definition of capillary number, (3) estimation of NP coverage on droplet interface, (4) calculation of values for f*, a*, and b* in Eq. (2) in the main text, and (5) estimation of time scale for drop deformation and NP diffusion, respectively.