Right Ventricular Fiber Structure as a Compensatory Mechanism in Pressure Overload: A Computational Study

Abstract

Right ventricular failure (RVF) is a lethal condition in diverse pathologies. Pressure overload is the most common etiology of RVF, but our understanding of the tissue structure remodeling and other biomechanical factors involved in RVF is limited. Some remodeling patterns are interpreted as compensatory mechanisms including myocyte hypertrophy, extracellular fibrosis, and changes in fiber orientation. However, the specific implications of these changes, especially in relation to clinically observable measurements, are difficult to investigate experimentally. In this computational study, we hypothesized that, with other variables constant, fiber orientation alteration provides a quantifiable and distinct compensatory mechanism during RV pressure overload (RVPO). Numerical models were constructed using a rabbit model of chronic pressure overload RVF based on intraventricular pressure measurements, CINE magnetic resonance imaging (MRI), and diffusion tensor MRI (DT-MRI). Biventricular simulations were conducted under normotensive and hypertensive boundary conditions using variations in RV wall thickness, tissue stiffness, and fiber orientation to investigate their effect on RV pump function. Our results show that a longitudinally aligned myocardial fiber orientation contributed to an increase in RV ejection fraction (RVEF). This effect was more pronounced in response to pressure overload. Likewise, models with longitudinally aligned fiber orientation required a lesser contractility for maintaining a target RVEF against elevated pressures. In addition to increased wall thickness and material stiffness (diastolic compensation), systolic mechanisms in the forms of myocardial fiber realignment and changes in contractility are likely involved in the overall compensatory responses to pressure overload.

Introduction

Right ventricular failure (RVF) is a deadly deterioration of pump function that can occur from a variety of etiologies including congenital heart disease, pulmonary hypertension, and indirect pressure-overload from ischemic and nonischemic cardiomyopathies [1–4]. While a great deal of research has been focused on elucidating progression of left ventricular (LV) failure via structural and functional analysis, knowledge concerning the failing and recovering right ventricle (RV) is limited and currently insufficient for systematic development of effective treatment strategies [5]. Preclinical research and computational tools are important for bridging this knowledge gap by identifying compensatory mechanisms, designing and testing of treatments, and enhancing monitoring techniques. In the context of RVF, all of these can have significant impact due to the number of conditions associated with RV hypertension.

Pressure overload-induced RVF has been shown to incur diastolic and contractile deficiencies linked to wall stiffening mediated by hypertrophy and interstitial fibrosis [6–8]. From a biomechanical standpoint, these mediating factors can be conceptualized as compensatory mechanisms for limiting the magnitude of internal wall stresses, namely: Hypertrophy, which enables distribution of internal forces along larger cross-sectional areas, and fibrosis with increased perimysial collagen content resulting in tissue stiffening [9,10]. Structural remodeling in terms of fiber orientation is also of interest not only because it can be related to passive tissue stiffening, but also because it has been shown to be a significant contributor to systolic organ function in terms of interventricular septal compression and LV kinematics [11–13]. Despite abundant investigations in the LV (or its indirect influence on RV function) [14–17], the relative contributions between different compensatory mechanisms applicable to the RV (hypertrophy, fibrosis, and changes in fiber orientation) have been less studied, and have become more accessible with improved experimental techniques [9,18].

Experimental observations show that, as in the LV, myocytes in the RV aggregate or align in fibers following a helical structure quantified in terms of elevation (or helix) angles with respect to the circumferential direction tangent to the ventricular wall [19,20]. In the healthy epicardium, the angles are mostly negative resulting in left-handed fiber helixes, and the opposite is true in the endocardium. Angles in between are conceptualized as varying smoothly from positive to negative in a quasi-linear manner. Although detailed causal knowledge relating RVF to structural and functional compensatory mechanisms, especially those detectable via noninvasive means, remains lacking, hypertension-induced structural alterations in the RV have been the focus of previous investigations in animal models. Pulmonary artery (PA) banding is the most common means of inducing RV pressure overload, and the basis of previous studies. Longitudinal alignment of myocardial fibers, equivalent to an increase in the transmural helix angle slope (HAS), has been observed after chronic RV pressure overload via microstructural characterization using microscopy and high-resolution speckle tracking [9,18]. However, possibly due to the relatively large measurement errors involved, no significant change was detected in diffusion tensor MRI (DT-MRI) studies [20,21]. The functional consequences of fiber remodeling in light of this discrepancy remain understudied.

Computational studies allow parameterization of individual modeling features and provide the distinct flexibility of isolating one particular modeling parameter at the time, and evaluating its effect on simulated outputs. Classical and recent computational studies have demonstrated the importance of fiber structure on simulated organ function. For example, local LV fiber orientation not only affects net cardiac pump function but is also a key determinant in stress distribution [14,15]. Additional studies strongly suggest a natural tendency for lowering and reducing spatial variability of stresses in the line of action of cardiac fibers [16,17]. However, studies focusing on the RV are limited, partly because computational studies are susceptible to inaccuracies in geometry, material parameters, and boundary conditions [15,22]. Augmentation of numerical approaches with medical imaging technology and other experimental data provides the means to manage these limitations.

Based on experimental reports of fiber remodeling, we hypothesized that longitudinal alignment of RV fibers would be associated with improved RV function in pressure overload. This hypothesis was tested with a parameter sensitivity analysis, which was conducted using animal-specific finite element (FE) models based on experimental data, including DT-MRI.

Materials and Methods

Being a parameter sensitivity analysis, the study was conducted by comparing simulated output as a function of different combinations of modeling parameters. The strategy is visually represented in Fig. 1, and comprised two experiments performed with animal-specific, finite element (FE) models of rabbit ventricles (n = 3):

Fig. 1.

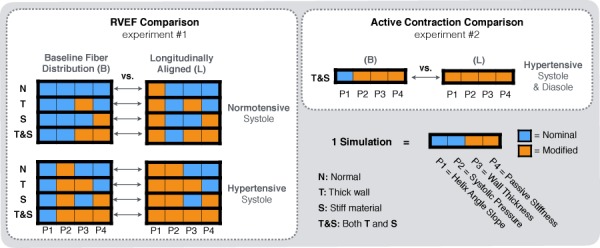
Numerical experiments. The sensitivity study encompassed two experiments aimed at determining differences between models with baseline and baseline fiber distribution. The first experiment (left) looked at differences in RV ejection fraction (RVEF). The second experiment (right) investigated differences in active contraction, or contractility given a target RVEF. Each of the modeling parameters included a nominal value based on normal RVs and a modification based on pressure overload.

The goal of the first experiment was to determine whether or not longitudinal alignment had a positive effect in simulated ventricular function (per RVEF) across different conditions associated with pressure overload. In particular, we compared simulated RVEF as a function of four modeling parameters applied to the RV. Each parameter included two states, as follows:

• (1)Fiber orientation: Nominal versus longitudinally aligned (simulated remodeling)
• (2)Systolic pressure: Normotensive and hypertensive ventricular afterload
• (3)Wall thickness: Nominal and increased (simulated effect of hypertrophy)
• (4)Passive stiffening: Nominal and stiffened (simulated effect of fibrotic stiffening)

The states, or modifications from nominal values, were selected based on empirical observations. The combination between modeling parameters and their modified states yielded a total of 16 possible combinations, where each combination of parameters corresponded to a simulation, as illustrated in Fig. 1 (left). Because the main comparison involved models with baseline fiber distribution (B) versus models with longitudinally aligned fibers (L), we collapsed all the comparisons into B versus L pairs. These comparisons were grouped into normotensive and hypertensive groups to determine if the effects caused by longitudinal alignment became more or less pronounced in pressure overload. Thus, the 16 simulations per animal yielded eight (B versus L) comparisons: four in the normotensive group and four in the hypertensive group. Each comparison compared the RVEF output models with combinations of the remaining modeling parameters. That is, B versus L comparisons in models with normal wall parameters (N), thicker RV wall (T), stiffer material parameters (S), and with both of these features (T&S). Active stresses in each animal-specific model were kept constant during this experiment.

The second experiment consisted of finding the magnitude of active stress necessary to maintain a normal RVEF in simulations with and without longitudinal fiber alignment (Fig. 2, right). This set of simulations was carried out because ejection fraction has been observed to remain constant during pressure overload [6,9,23,24]. The goal of this experiment was to observe any differences in active stress level and fiber strain between two simulations differing only in fiber alignment, but exhibiting signs or chronic pressure overload, i.e., elevated pressure, increased wall thickness, and higher tissue stiffness. To achieve this, we modified the simulations in the last (B versus L) comparison from the previous experiments (i.e., the last B versus L pair T&S simulations in the hypertensive group, Fig. 1): First, diastolic pressure was increased to reflect the diastolic enlargement observed experimentally (the new diastolic pressure was held constant in both simulations). Second, the magnitude of the active contractile stress, a measure of contractility [25,26], was adjusted separately in each simulation. Thus, active stress became the independent variable, and RVEF was set to the same value, which corresponded to the normal RVEF per MRI measurements for the given animal. This strategy enabled interpretation of any B versus L differences shown in the first experiment in the context of active contraction against pressure overload with preserved RVEF.

Fig. 2.

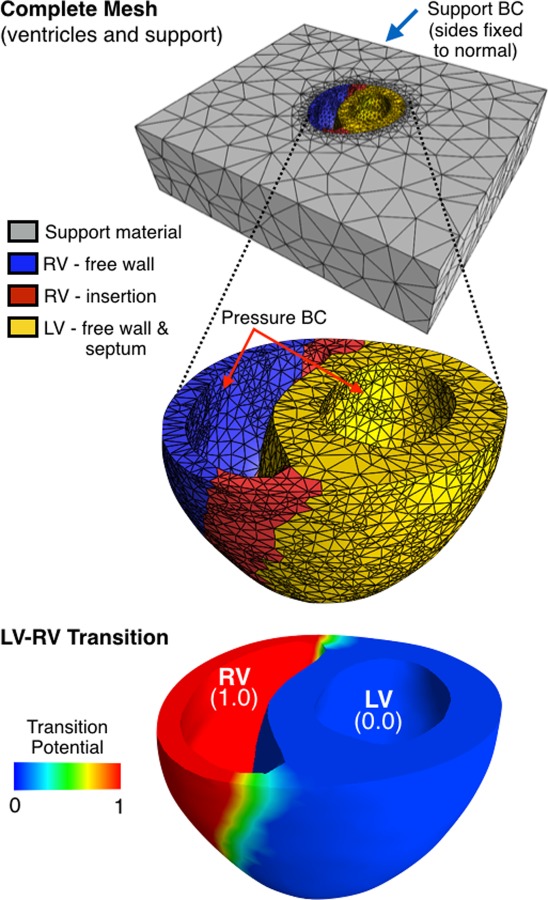
Biventricular mesh. The complete mesh (top) was subdivided into four compartments: the RV free wall, the RV insertion, the LV (including the septum), and a low-stiffness support material. The potential distribution (bottom) was used as rule for fiber distribution, which provided a smooth transition from LV to RV for modeling differences in HAS.

Animal Model.

Geometry (shape and wall thicknesses), pressure boundary conditions, and fiber orientation were extracted using an animal model of chronic, reversible RV failure induced by pressure overload. Detailed information regarding methods for experimental RVF can be found in a published description of the animal model based on New Zealand white rabbits [24]. Briefly, in order to induce RV overload, animals (2.0–2.5 kg, n = 3) were outfitted with fully implantable, PA bands (Access Technologies, Skokie, IL). After recovery from band implantation, injection of aqueous 0.9% Normal Saline into a subcutaneous port tightened the band according to estimates of RV end-systolic pressure (RVESP) obtained via transthoracic echo. Regular band tightening at weekly intervals was continued until RVESP measurements reached values over 25 mmHg, then it was maintained over a period of 2 weeks until evidence of RVF was observed (the signs included a shift of the interventricular septum toward the left side, and onset of hepatic congestion). A group of animals (n = 3) were used as controls; these animals underwent sham procedures without band implantation.

Modeling parameters were extracted from direct imaging observations as detailed below and from the literature. All animal protocols were subject to established guidelines and approved by the Institutional Animal Care and Use Committee at the University of Utah.

Model Geometry.

The geometry for the baseline biventricular FE models was obtained based on CINE MRI of control animals. To obtain imaging information, each rabbit was anesthetized with 1–3% isoflurane and 0.6–0.9 L/min O2 and placed inside a 150 mm imaging RF coil (Bruker, MA). Continuous monitoring of vital signs (respiration, temperature, electrocardiogram (ECG), and oxygen saturation) was performed using an MR-compatible physiological monitoring system (SA Instruments, Stony Brook, NY), and cardiac CINE-MRI was obtained by applying a multislice FLASH sequence (retrospectively gated, 10-slices FOV 80 × 80 mm 256 × 256 pixels, 15 deg flip angle). The resulting volumetric data at early diastole, when the mechanical load of the ventricles is at is minimum, were delineated using a semi-automated approach (Amira, FEI Life Sciences, Hillsboro, OR), and a computational mesh was constructed based on labeled surfaces (TetGen, WIAS, Berlin, Germany). The mesh was composed of 33–36 thousand quadratic tetrahedra (10-point formulation) after a 2% convergence analysis of peak strain due to diastolic pressurization. The complete mesh (Fig. 2, top) consisted of the ventricles and a support. As shown in Fig. 2, the ventricular space was subdivided to accommodate some degree of spatial heterogeneity in terms of material properties; the division included the RV free wall, the RV insertion, and the LV, which included the LV free wall and the interventricular septum. The insertion extent was assigned based on visual inspection of the RV wall thickness.

The thickness of the meshed RV wall was altered to model the observed increase due to pressure overload. This was accomplished as a modification to the nominal computational models to enable paired comparison with wall thickness as an independent modeling parameter. RV thickness was increased via an ancillary simulation with an isotropic compressible material (neo-Hookean, with stiffness coefficient of 1 kPa, and Poisson ratio of 0.1), fixed epicardial (EPI) and septal nodes, and a negative pressure load applied to the RV endocardium (on the order of 1 kPa). The resulting deformation map was then applied to the reference geometry to obtain a new mesh with thicker RV wall (labeled as T, in Fig. 1). The target thickness of the modified meshes was obtained from ex vivo, high-resolution imaging via DT-MRI of hypertrophic animals acquired as described in the Fiber Distribution and Material Parameters section.

Fiber Distribution and Material Parameters

Fiber Orientation.

In pressure overload, fiber orientation from DT-MRI measurements suggests that helix angle remains conserved, while longitudinal alignment of cardiac fibers has been measured with alternative means [9,18,20,21]. Here, high-resolution DT-MRI was performed to provide a nominal HAS value for modeling, and to quantify the variability of this measurement. The modification in HAS was kept under in the variability in helical angle measurements, and was modeled as an increase (under which fibers move away from the circumferential direction into longitudinal alignment [9]). Fiber orientation was parameterized using a linear function with negative values at the epicardium, and positive values in the epicardium. The transition in fiber orientation between the LV and the RV was assumed to be smooth, and was applied using a modified rule-based algorithm [27]. The modification consisted of defining the additional potential distribution shown in Fig. 2 (bottom), which enabled application of longitudinal alignment to the RV, while leaving a nominal fiber distribution in the LV. Tractography of baseline and longitudinally aligned models appears in Fig. 3.

Fig. 3.

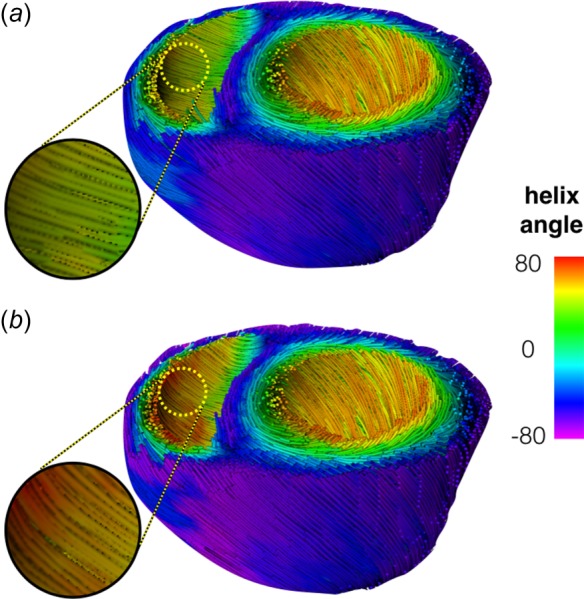
Modeled fiber distribution. The tractographical representation of a baseline model (a) and a model with longitudinally aligned fibers (b) show differences in RV fiber orientation (circle). The baseline fibers are more circumferential and have less steep angles than the longitudinally aligned fiber distribution.

The DT-MRI acquisition was performed ex vivo. Shortly after extraction, the hearts were cannulated at the aorta, and perfused with 0.9% potassium chloride to evacuate blood from myocardial vasculature and cause cardiac arrest. An amount equivalent to systolic volume, 500–900 μl, of alginate (Smooth-On, Macungie, PA) was injected inside the ventricles to prevent collapse. The samples where fixed in formalin to stabilize geometry and diffusion parameters (6–8 h prior and during scanning) [28,29], but were scanned within 48 h to avoid undesired fixation effects [30]. Each heart was scanned using a 50 mm-inner diameter quadrature volumetric coil (Rapid MRI, Columbus, OH) with a Bruker Biospec 7 T imaging instrument. High-resolution 3D DT-MRI was obtained by applying a spin echo sequence (FOV 30 × 30 × 30 mm, 128 × 85 × 85 pixels, TR 500 ms, TE 23 ms, 12 directions, and 1000 mm/cm b-value) over a period of 13 h.

Constitutive Modeling.

Ventricular myocardium was modeled as a solid mixture composed of a passive solid and an active stress was applied in the direction of local fibers. The passive material response was assumed to be a transversely isotropic Fung-type hyperelastic solid with strain energy

$$W=\frac{1}{2}c\left(e^Q-1\right)+\frac{1}{2}K\ln \left(J\right)$$ (1)

where $c$ was adjusted based on the passive volumetric response at end diastole from CINE-MRI, $K$ represents the bulk modulus (200 kPa), $J$ is the relative change in volume, and

$$Q=c_1{E}_{\mathit{f}\mathit{f}}^2+c_2(E_{\mathit{s}\mathit{s}}^2+E_{\mathit{n}\mathit{n}}^2+E_{\mathit{s}\mathit{n}}^2+E_{\mathit{n}\mathit{s}}^2)+c_3(E_{\mathit{f}\mathit{s}}^2+E_{\mathit{s}\mathit{f}}^2+E_{\mathit{n}\mathit{f}}^2+E_{\mathit{f}\mathit{n}}^2)$$ (2)

Because Eq. (1) is an uncoupled, nearly incompressible formulation, the strain components in Eq. (2) correspond to the deviatoric Green Lagrange strain in the local coordinate system with respect to the fiber ($f$), sheet ($s$), and normal ($n$) directions. Despite some evidence to the contrary, the material model was assumed to be stress-free in the reference configuration. However, changes in ejection fraction are relatively low with respect to residual stress [31,32], which did not justify the additional effort necessary to include this phenomena given the scarcity of experimental data. Nominal material coefficients $c_1$ through $c_3$ were obtained from the literature: $c_1$ = 9.13, $c_2$ = 2.32, and $c_3$ = 3.70 [33,34]. Active contraction was simulated with a steady-state specialization of the time-varying elastance modification to Hill's active muscle contraction [26,35,36]. The nominal magnitude of active stress (maximum contractility, or $T_{\text{max}}$) was scaled to match systolic volume CINE-MRI against systolic pressure. Support material followed a coupled neo-Hookean formulation with stiffness coefficient set at 0.1 kPa and a Poisson ratio of zero. The support strategy provides numerical stability, but has a negligible effect in cavity volumes (an increase, or decrease, in support stiffness by a factor of 10 resulted in less than 0.01% change in ventricular volume [37]).

In experiment 1, the nominal material coefficients were modified to reflect remodeling-based stiffening after chronic pressure overload. Previous experimental observation of this phenomenon quantifies these changes as two–fold increase in $c_1$ and $c_2$, based on fitting load-displacement data [9]. For the contractility comparison experiment, $T_{\text{max}}$ was manually adjusted to match normal RVEF values.

Loads and Boundary Conditions.

Intraventricular catheterization (SPR-882, AD Instruments, Colorado Springs, CO) was used to measure ventricular pressures relative to atmosphere with an accuracy of approximately 0.26 kPa (2 mmHg). This procedure was performed in controls (n = 3) and in banded animals (n = 6). Prior to sacrifice, animals were intubated and anesthetized (1–3% isoflurane and 0.6–0.9 L/min O2), while pressure waveforms were extracted over 5–8 heartbeats. To avoid artifacts, a short breath hold was induced during the measurements. Nominal pressure boundary conditions were derived from average waveforms of control animals. No pressure boundary conditions were applied in the epicardium, which was lightly constrained by the support material. However, the boundary nodes of the support material and the basal cut of the ventricles were constrained as shown in Fig. 1. Modified pressure values were derived from differences between controls and animals with chronic pressure overload.

Solution and Postprocessing.

The modeling aspects of this study, which included solving mechanical boundary value problems and visualization of biomechanical simulations, were performed using the structural mechanics solver included in the febio software suite version 2.3, with parallel linear solver [38], in a 12-core (1.4 GHz per core) 32 GB ram processing server. The average computational time per simulation was approximately 6.2 ± 2.1 h. Volumes were approximated using triangulation of cavity surfaces using customized matlab scripts (Mathworks, Natick, MA—version 2013 b), where ejection fraction was defined as stroke volume (difference between diastolic and systolic volumes) divided by diastolic volume.

Statistical Comparisons.

On the experimental side, differences in pressure measurements, wall thickness, and fiber orientation were compared using an unpaired nonparametric Wilcoxon test (prism, GraphPad Software, La Jolla, CA) because the same animals were not in the control and RVF groups. On the numerical side, simulated RVEF values were compared using a paired version of the test above because the outcome of each simulation is systematically determined by its modeling parameters. The test was applied between B and L groups (baseline and longitudinally aligned fibers, respectively). The simplest and least conservative assessment of overall effect of fiber alignment was performed via single measures. A more conservative comparison was made treating each animal model as an independent repeated measurement because this strategy included variation across animals. The difference in fiber-mediated changes in RVEF between the hypertensive and normotensive groups was comparing similarly (single and repeated measures). Differences from a hypothetical value were tested via two-tailed T-tests. The alpha level for statistical significance was 0.05. In the models under pressure overload conditions, the spatial variation of element-wise fiber strain was quantified using the minimum and maximum values, and visual inspection.

Results

Experimental Observations.

This section describes the experimental (noncomputational) results and how they were incorporated in the parameter sensitivity analysis. Relevant modeling parameters used in the simulations were tabulated in Table 1.

Table 1.

Nominal and modified modeling coefficients. The modifications were used in the numerical experiments per Fig. 1.

Parameter		Nominal value	Source	Modification	Modified value	Modification source
Fiber orientation	HAS/DF (deg)	120/±60	DT-MRI	Longitudinal alignment	156/±78	Observed in Refs. [9] and [10]
+30% HAS	within DT-MRI variability [11]
Ventricular pressure	ESP/DSP (mmHg)	11.0/2.7	Intraventricular catheter	Pressure overload	15.7/4.7	Differences between normal and banded animals, and diastolic enlargement [43]
				+25% ESP
+75% EDPa
Wall thickness	Mean±SD (mm)	1.2 ± 0.2	Hi-res MRI	Hypertrophy	1.8 ± 0.3	Differences between normal and banded animals [43]
+50% thickness
Material parameters	$c_1$  = 9.13, $c_2$  = 2.32, $c_3$  = 3.70 and Table 2		[33,34] animal-specific per CINE-MRI	RV Remodeling	$c_1$  = 18.3	Stiffening observed in Ref. [9]
+200% in c2 and c3	$c_2$  = 4.64

^aModified values for end-diastolic RV pressure were used only in experiment 2 to produce diastolic enlargement.

Ventricular volumes derived from in vivo imaging appear in Table 2. These values were used as volume targets in the simulations where all parameters had nominal values. The mean diastolic RV volume across all animals was 932 ± 152 μl, while the systolic measurement was 547 ± 136 μl; thus, the mean RV stroke volume was 386 ± 17 μl with an RVEF of 0.42 ± 0.06. The same measurements in the LV yielded 1299 ± 22 μl (diastolic volume), 656 ± 87 μl (systolic volume), 642.89 ± 22 μl (stroke volume), 0.49 ± 0.06 (ejection fraction). Note the discrepancy on RV stroke volume with respect to the LV.

Table 2.

Measured (via in vivo MRI) and simulated RV volumes. The measured diastolic and systolic values (respectively, RVED and RVES) were used to calculate animal-specific stiffness passive stiffness $c$, and active contraction $T_{\text{max}}$.

		RVED				RVES				RVEF
	Animal	MRI (μl)	Sim. (μl)	Diff. (%)	$c$ (kPa)	MRI (μl)	Sim. (μl)	Diff. (%)	$T_{\text{max}}$ (kPa)	MRI (-)	Sim. (-)
RV	A1	757	702	7.3	0.5	391	362	7.4	21	0.48	0.48
	A2	1012	1020	−0.8	2.7	609	648	0.2	54	0.36	0.36
	A3	1029	1030	−0.1	1.3	641	691	−1.5	42	0.34	0.33
Avg.	933 ± 152	917 ± 187	2.1 ± 4.5	1.5 ± 1.1	547 ± 136	567 ± 179	2.3 ± 8.4	39 ± 17	0.42 ± 0.06	0.39 ± 0.08
LV	A1	1299	1265	2.6	0.9	556	561	−0.9	18	0.57	0.56
	A2	1321	1217	7.9	0.6	713	659	7.6	17	0.46	0.46
	A3	1277	1247	2.3	0.8	701	679	3.1	19	0.45	0.46
Avg.	1299 ± 22	1243 ± 24	4.3 ± 3.1	0.8 ± 0.1	657 ± 87	633 ± 63	3.3 ± 4.2	18 ± 1.0	0.49 ± 0.07	0.49 ± 0.06

Note: Simulated values (Sim.) were obtained using nominal simulations. Averaged values (Avg.) appear as mean ± SD.

As expected, helix angle measurements from ex vivo DT-MRI showed no differences in HAS between control and banded animals. This was the case in the RV with 77 deg ± 12 versus 89 deg ± 34, and the LV 120 deg ± 23 versus 118 deg ± 40 (control versus banded, respectively). For illustration, Fig. 4 shows these measurements from representative basal slices. Unlike the LV, the basal distribution in the RV showed more nonlinearity with slope values (extrapolating to each side) of roughly 140 deg in the endocardial (ENDO) half, and a less steep epicardial half with an approximate HAS of 60 deg. The nominal transmural distributions used in the simulations consisted of a HAS of 120 deg (i.e., − 60 deg to 60 deg endocardium to epicardium). This maintained consistency with the LV, but fell slightly above the measurements in the RV, as shown in Fig. 5. The modified value for HAS, which was applied only to the RV, consisted of an increase of 30%. This value was roughly one standard deviation in banded animals (which was 34 deg or 38%). Note that the modified value yields larger differences in fiber distribution in the epicardial half of the RV, Fig. 5.

Fig. 4.

Helix angle measurements from basal DT-MRI slices and linear approximations. The RV (left) exhibits more nonlinearity than the (LV). The RV has a steeper distribution on the endocardial (ENDO) half, compared to its epicardial (EPI) counterpart. The nominal linear fiber distributions were the same in the LV and the RV, and modifications were only applied to the RV.

Fig. 5.

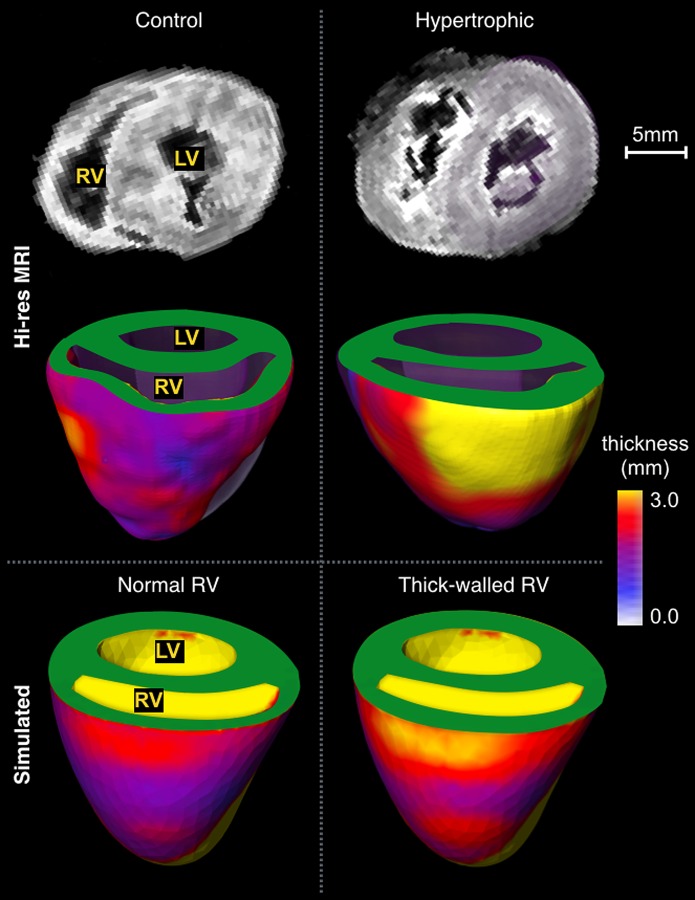
High-resolution imaging of the ventricles. Imaging from a representative control animal (left column) exhibits relatively thin RV wall compared to the LV (right column). These differences were captured by the meshes with (thick-walled RV) and without (normal) modifications in wall thickness.

Analysis of high-resolution imaging data showed differences in RV wall thickness between control animals and RVF, but no noticeable differences in septal and LV free wall. Hypertrophic hearts exhibited wall thickening across most of the RV, but it was more pronounced in the free wall, as shown in Fig. 5. Marked differences are evident in the 3D rendering of wall thickness: Compared to the control, the hypertrophic heart exhibits wall enlargement of almost two–fold concentrated across an area roughly two-thirds the RV wall. The measurements suggest a difference in thickness of approximately 50% (1.3 ± 0.1 in controls, and 2.0 ± 0.4 in banded animals, p = 0.04), which was used to modify the nominal meshes. Mesh modification resulted in a concentric wall thickness increase of roughly 55%. The nominal average RV wall in the models was 1.2 ± 0.2 mm, while the same measurement in the modified meshes was 1.8 ± 0.3 mm. A model with and without wall thickness modification appears at the bottom of Fig. 4.

Intraventricular catheter measurements showed that pulmonary artery banding resulted in significant differences in RV end-systolic pressure with respect to the control group. This measurement was 20.8 ± 3.8 mmHg (mean ES ± SD) in banded animals, and 14.0 ± 3.6 mmHg in controls—a 25% increase (p = 0.02). No significant differences were observed in RV end-diastolic pressure (1.8 ± 2.0 mmHg in banded animals versus 2.7 ± 1.8 mmHg in controls). Likewise, no differences were detected in LV pressures, either systolic (46.5 ± 7.8 versus 33.3 ± 6.4 mmHg) or diastolic (2.7 ± 3.4 versus 5.3 ± 3.2 mmHg, banded versus controls, respectively). Based on these observations, the nominal pressure boundary conditions for the RV included 2.7 mmHg (0.36 kPa) in diastole, and 11.0 mmHg (1.47 kPa) in systole. The modified value for systole in the hypertensive group was 15.8 mmHg (2.1 kPa), per the observed difference in this study. Despite not detecting significant differences in our measurements, the modified value for diastolic pressure used in experiment 2 was increased by 1.75 to reproduce diastolic enlargement of the RV.

Numerical Experiment 1: Sensitivity Analysis.

Figure 6 shows the main stages of the cardiac cycle, which correspond to passive pressurization by diastolic pressure (simulated end diastole), and active contraction against systolic pressure (end systole). These show the expected change in volume associated with cardiac contraction in the normal simulation (Fig. 6, left column). The volume predictions using the simulations with nominal parameters are also included in Table 2 along with the MRI measurements. After adjusting the passive stiffness coefficient $c$ and the magnitude of active contraction $T_{\text{max}}$, the average error in volume predictions was approximately 2% of the corresponding measurements (with a maximum of 7.3% and a minimum of − 0.1%). The average RVEF in nominal simulations was 0.39 ± 0.08. In the LV, the average error in volume prediction was roughly 4% (7.9% max., −0.9% min.). Average LV ejection fraction was 0.49 ± 0.06. By design, stroke volumes were similar to imaging measurements.

Fig. 6.

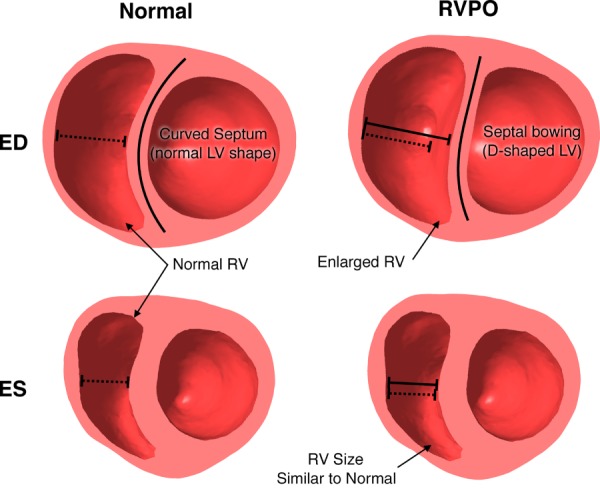
Comparison between normal and RVPO simulations. Introducing pressure overload conditions (increased boundary pressures) results in marked diastolic ventricular deformation characterized by an enlarged RV and septal bowing, which give the LV a “D” shape. These differences are virtually unnoticeable during systole.

Figure 7 shows the simulated RV volumes, and the difference in RVEF between models with B and L fiber distributions in each of the three animals (A1–A3). Each of the bars represents an average of the variations of each model in the normotensive and hypertensive group (i.e., N, T, S, and T&S in Fig. 1). In each of the cases, models with L fiber distribution resulted in reduced systolic volume when compared to B fiber distribution. The difference was small, (3%), but highly significant (p = 0.0001) when lumping all B versus L comparisons, and remained significant when treating each animal as a repeated measure (p = 0.03). Reduction in systolic volume effectively increased stroke volume and, consequently, increased RVEF. Thus, the difference in RVEF was positive. It was also more pronounced in the hypertensive group. While averaging variations of the same animal model (Fig. 7) showed no systematic changes in diastolic volume, grouping by model type (Fig. 8) made apparent the relationship between diastolic volume and stiffness: Independent increases in geometric and material stiffness (introduced by increases in RV thickness and material coefficients) reduced diastolic volume and negatively affect stroke volume and RVEF. As before, Fig. 7 also shows that longitudinal alignment results in increased stroke volume and RVEF. In this grouping, the improvement continued to be more pronounced in the hypertensive group. Overall, the differences in RVEF per model ranged from 3.1% to 5.9% in the normotensive group, and 4.2% to 10.8% in the hypertensive group. The difference was significantly more pronounced than the latter group (p = 0.001) when lumping all B versus L comparisons, but was not significant when treating each animal as a repeated measure (p = 0.125). Left-ventricular volumes remained virtually unchanged.

Fig. 7.

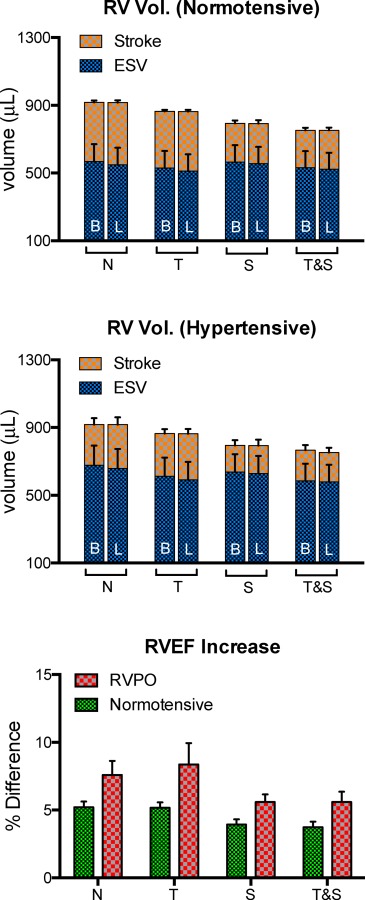
Per-animal (A1–A3) grouping of differences between baseline (B), and longitudinally aligned (L) fiber distribution. A small but consistent decrease in systolic volume was observed both in the normotensive (top) and the hypertensive (middle) groups. This change produced an increment in stroke volume, and, consequently, RVEF. The differences in RVEF (bottom) are more pronounced in the hypertensive group.

Fig. 8.

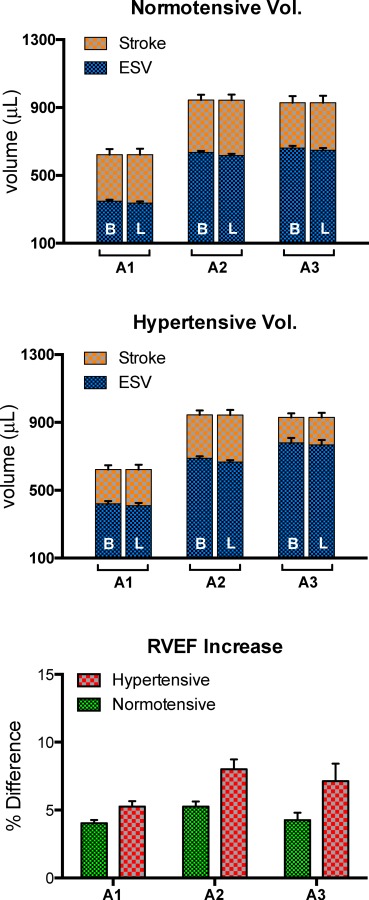
Simulation type grouping of differences between B and L fiber distribution. This grouping shows a similar trend to Fig. 7, with the L group resulting in lowered systolic volumes compared to B, in both the normotensive (top) and the hypertensive (middle) groups. Grouping the results by simulation type shows the effect of stiffness on diastolic volume. Compared to nominal models (N), models with a thicker wall (T) were more stiff and this translated to a reduction in diastolic volume. Increased material stiffness (S), and a combination of T and S (T&S) progressively exacerbated these reductions. As in the per-animal grouping, the differences in RVEF (bottom) were more pronounced in the hypertensive group.

Numerical Experiment 2: Simulations Under Pressure Overload Conditions.

A simulation of RV pressure overload is shown in Fig. 6 (right column). Compared to the nominal version of the same model (left column), the increase in pressure boundary conditions brought about notable distortion in both ventricles. Following a change in curvature in the interventricular septum, the diastolic LV changed from mostly circular to having a “D” shape. The differences in shape were much less pronounced during systole.

The average volume in the RV in these simulations was 907 ± 198 μl in diastole, and 559 ± 186 μl. Note that these values are similar to the nominal models (with a mean of 932 μl and 547 μl, respectively) despite the difference in pressures, but constituted an increase of roughly 20% in diastolic volume compared to models with thicker and stiffer RV wall under normal pressures.

The target RVEF values were matched within 2% with respect to experimental measurements, and the difference in RVEF from models with B and L fiber alignment was 0.7%, 0.1%, and 0.3% for each of the respective geometries. The contractility values necessary to achieve the target RVEF are shown in Fig. 9. Compared to the normal models (i.e., simulations with nominal parameters), all of the models under pressure overload conditions (i.e., thicker RV wall, stiffer tissue, and higher systolic pressure) required greater contractility to achieve the target RVEF. However, the models with longitudinally aligned fiber orientation (RVPO-L) required approximately 5% less contractile stress to maintain the target RVEF compared to those with nominal fiber orientation (p = 0.03) (RVPO-R).

Fig. 9.

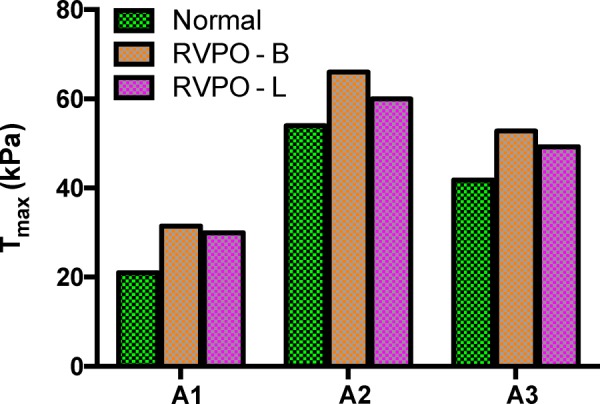
Contractility differences for maintaining normal RVEF. Because models in pressure overload conditions (RVPO) change volume against higher pressures, contractility values are larger than in the normal simulations. However, modifying the models to include longitudinal alignment (L) results in a small, but consistent reduction in contractility compared to the baseline fiber orientation (B).

In both, models with B and L fiber distributions, LV diastolic fiber stretch was greater in the endocardium with respect to the epicardium. The RV exhibited a similar pattern but only in free wall. Diastolic fiber stretch in models with longitudinally aligned fibers was identical to that from models with nominal fiber orientation, but longitudinally aligned fibers showed smaller concentrations around peak values. Although no significant differences in mean systolic fiber stretch values were measured, the simulations with longitudinally aligned fibers had the tendency of having higher absolute stretch values, i.e., less contraction (0.87 ± 0.06 versus 0.85 ± 0.07), and more positively spread spatial distribution (maximum measured at 1.08 ± 0.04 versus 1.02 ± 0.04, minimum measured at 0.77 ± 0.03 versus 0.76 ± 0.03). These results indicate a slight reduction in absolute and concentrated fiber stretch.

Discussion

The principal finding of this study is that, with all other variables held constant, longitudinal alignment of RV fibers provides a reduction in simulated systolic volumes and, consequently, a boost in ejection fraction. The parameter sensitivity analysis (Figs. 7 and 8) revealed that the increase in RVEF, per the above mechanism, was persistent across simulations with all the studied variations in the models (increased systolic pressure, wall thickness, material stiffening, or combinations of these alterations). This result was also consistent with the second part of the study because longitudinal alignment reduced the active stress necessary for maintaining a target RVEF as shown in Fig. 9. On the one hand, this numerical evidence, in conjunction with previous experimental observations [9,18], suggests that RV longitudinal fiber alignment plays a role as a systolic compensatory mechanism. On the other hand, if longitudinal alignment is achieved in a relatively short period, longitudinal alignment could constitute a mechanism of ventricular reserve—note that the boost in RVEF is more prevalent under pressure overload per the differences between normotensive and hypertensive groups shown in the bottom panel of Figs. 7 and 8.

The above findings further underscore the importance of myocardial fiber orientation in organ function already observed in the healthy LV [15], and its potential role in terms of LV disease progression [14]. Nevertheless, the magnitude of changes in fiber orientation needed to influence simulated RV function, although observable at a histological level [9], or other local approaches [18], can also fall slightly outside population-based DT-MRI measurements per our results, and the level of variability observed in previous DT-MRI studies [20,39]. This is consistent with the results in this study because the magnitude of the fiber orientation changes used in the models were both, within the variability of the DT-MRI measurements, and sufficient to yield a consistent functional differences. Unfortunately, the same results suggest that nondestructive (and also noninvasive) detection of these functionally relevant fiber orientation changes, at least within the scope of this parameter sensitivity analysis, is not yet within reach. However, despite its current limitations, in vivo DT-MRI offers the potential for studying longitudinal data from the same animal (which is not possible ex vivo), and may reveal information associated with fiber orientation variations [40,41].

From a methodological standpoint, this study provided a modeling pipeline for simulation of variations in fiber orientation (Figs. 3 and 4) and wall thickening (Fig. 5). The wall thickening was qualitatively similar, albeit in a lesser extent, to the observations in the high-resolution data. The resulting models exhibited some of the characteristics seen in experimental studies, for instance: the relationship between diastolic volume and stiffness show in the simulation type grouping of the results (Fig. 8) is consistent with diastolic deficiency induced by pressure overload [6]. Likewise, having a greater diastolic fiber stretch in the endocardium with respect to the epicardium is consistent with imaging-based data [42]. The models with pressure overload conditions (higher pressures, thicker wall, and stiffer material model) resulted in septal bowing and changes in chamber size [12,43]. These models also required increased contractility to compress against higher afterload, which has been reported during pulmonary hypertension [44,45]. The results are also consistent with a recent finding suggesting that fiber orientation (longitudinal alignment) is necessary to reproduce pulmonary hypertension geometry using computational models [45].

At the same time, there are aspects in this study that do not agree with physiological expectations, namely, the pressures measured via intraventricular catheter and the inconsistency in LV and RV stroke volumes. While pressures fall below physiological expectations [46], these are likely due to the anesthetic used during the measurement. Some consistency is expected, as this was the same agent used to anesthetize the animals during imaging. The inconsistency in stroke volumes can be traced to the slice placement, which requires a longitudinally symmetric LV having the tendency to place the most basal LV slice somewhat below the RV. We expect our results to stand despite this inconsistency, because there was good agreement between simulated and imaging results, and because the RVEF-based comparisons were done on a per-volume basis. Being a numerical study, generous assumptions have been made, particularly in the overload conditions. These assumptions limit the overall capacity of the methodology herein to the realm of description rather than prediction. These assumptions include using a transverse isotropic material symmetry (Eqs. (1) and (2)) with a limited level of spatial heterogeneity (Fig. 2), and assuming that no residual stress was present in the unloaded configuration. Thus, the presented analysis is an extension of traditional stress–strain analyses using geometrical simplifications (for the most part, in the LV) where some or all of these assumptions have been successfully employed [14,47], except that emphasis has been placed on the RV and some realism in the definition of geometry and boundary conditions has been added through the use of imaging and other experimental data. Therefore, care must be employed when extrapolating the results and methodology from their current form to actual modeling of RVF, in particular due to all of the biological processes and feedback pathways that take place in organ and systemic RVF arising from pressure overload or other causes [23,24]. Further, this research used a relatively small number of animals, which largely limits the results to paired comparisons of a given model and variations of itself (justified given that the simulation process is highly deterministic), and not in situations where models from different animals are treated as a population. Hence, more importance is placed on differences in RVEF and active stress than to their absolute values as a population sample.

Fiber alignment and other alterations in this study were applied to the RV, to reduce any indirect effects resulting from interaction with the LV and interventricular septum, which would warrant a separate study. In the LV, the relationship between systolic volume and fiber has been explained through changes in ventricular torsion [48].

Our results, at least phenomenologically, suggest that a similar fundamental relationship mediated by a transmurally variant fiber orientation may be at play here. However, asymmetry in the RV makes a direct analogy intractable, which would also warrant further investigation. An additional direction for future research stems from one of the ultimate goals of computational biomechanics, which is to generate predictions of the degree of RV failure in patients. In that way, decisions on treatments or interventions can be made based on these predictions. As an intermediate step toward this goal, the modeling approaches discussed here could be combined with modeling of interstitial growth to incorporate wall thickening, material stiffening, and residual stress [49,50]. It is possible also that the results in this study (and others) can be linked to the biological pathways responsible for fiber realignment [9]. Such a link has the potential for aiding the design of possible treatments, should the effect of longitudinal alignment be confirmed via longitudinal data. The ability to perform image-based biomechanical analysis of patients with heart failure can also benefit from improvements in imaging (particularly DT-MRI [40]) and the reduction of the effort necessary to produce adequate models.

Summary and Conclusion

This study was aimed at evaluating the role of longitudinal alignment of cardiac fibers as a plausible compensatory mechanism for pressure overload via computational analysis. Using methods for assigning fiber orientation, increasing wall thickening, and material stiffening, the effect of longitudinal alignment of myofibers was tested under normal and increased systolic pressures. The observed changes in RVEF and contractility suggest that longitudinal alignment of similar extent as in previous experimental observations via histology, but below detection using DT-MRI, produces in an improvement in simulated stroke volume, and reduces the magnitude of contractile stress necessary to maintain cardiac output. This research points at improvements in image acquisition needed for determining the precise extent of this type of remodeling in vivo.

Nomenclature

$c$ =

stress scaling factor

$c_i$ =

deviatoric material coefficients

$E$ =

Green–Lagrange strain

$f$ =

index denoting fiber direction

$J$ =

Jacobian of deformation gradient

$K$ =

bulk modulus

$n$ =

direction normal to fiber and cross-fiber directions

$Q$ =

deviatoric scaling term

$s$ =

cross-fiber direction

$T_{\text{max}}$ =

active stress magnitude

$W$ =

strain energy