Abstract
The stress in a cell due to extracellular mechanical stimulus is determined by its mechanical properties, and the structural organization of many adherent cells suggests that their properties are anisotropic. This anisotropy may significantly influence the cells' mechanotransductive response to complex loads, and has important implications for development of accurate models of tissue biomechanics. Standard methods for measuring cellular mechanics report linear moduli that cannot capture large-deformation anisotropic properties, which in a continuum mechanics framework are best described by a strain energy density function (SED). In tissues, the SED is most robustly measured using biaxial testing. Here, we describe a cellular microbiaxial stretching (CμBS) method that modifies this tissue-scale approach to measure the anisotropic elastic behavior of individual vascular smooth muscle cells (VSMCs) with nativelike cytoarchitecture. Using CμBS, we reveal that VSMCs are highly anisotropic under large deformations. We then characterize a Holzapfel–Gasser–Ogden type SED for individual VSMCs and find that architecture-dependent properties of the cells can be robustly described using a formulation solely based on the organization of their actin cytoskeleton. These results suggest that cellular anisotropy should be considered when developing biomechanical models, and could play an important role in cellular mechano-adaptation.
Introduction
Active mechanical feedback between cells and their environment has important implications for tissue homeostasis and repair as it influences stem cell differentiation [1], tissue self-organization [2,3], and the ability of tissues to adaptively grow and remodel in response to mechanical forces [4,5]. Many tissues are composed of highly organized fibrous matrices with anisotropic mechanical properties [6,7], to which cells are highly attuned [8], suggesting an important role for anisotropy in mechanobiology. Cells found in mechanically dynamic tissues, like muscle and arteries, have similarly organized structure [9,10], likely resulting in tissuelike anisotropic mechanical properties, and potentially influencing mechanotransductive signaling [11–14]. However, the general approach using current methods (e.g., bead cytometry [15], micropipette aspiration [16], atomic force microscopy [17]) for measuring cellular elastic mechanical properties report linear moduli [18,19] intended for assessment of small-strain isotropic materials.
A description of the full large-strain anisotropic properties of cells is necessary for developing robust mathematical models of tissue biomechanics. Cells that exist in dynamic mechanical environments must constantly adapt to maintain tissue integrity [20]. Growth and remodeling theory often posits that this adaptation is driven by changes in cell stress [21]. Theoretical approaches that capture this mechano-adaptation could be used to develop model-aided individualized medicine to, for example, predict aneurysm growth and rupture [22,23]. Modern tissue modeling approaches, like constrained mixture [24–28] and multiscale [29–31] models, require mechanical descriptions of each of the constituents in the tissue. So, for these models to be successful, it is vital that we understand how the complex forces and deformations impact cellular mechanics and mechanotransduction. But, the large-strain anisotropic properties needed for the models have not been empirically determined.
Here, we seek to measure large-strain anisotropic properties of cells, which can be used to improve multiscale models of tissues. In continuum mechanics, the full elastic mechanical behavior of a material is described by the SED [32]. The gold standard method for measuring the SED of tissue samples is biaxial testing [6,7]. While tissue-scale biaxial testing requires samples to be physically clamped or sutured to the testing apparatus, this is not feasible with individual cells. Thus, we have developed cellular microbiaxial stretching (CBS) microscopy to measure the large-deformation SED of micropatterned adherent cells by modifying tissue-scale stretching methods and coupling them with traction force microscopy [33]. Using this approach, we find that VSMCs with nativelike elongated geometries have highly anisotropic cell shape-dependent mechanical properties, and can be described by a simple SED determined by the organization of the VSMC actin cytoskeleton.
Methods
Substrate Fabrication and Cell Micropatterning.
Micropatterned polyacrylamide-elastomer composites were fabricated by combining the methods of Simmons et al. [34] and Polio et al. [35] (Fig. 1(a)). Elastomer membranes (0.01 in thick, Specialty Manufacturing, Saginaw, MI) were clamped into membrane grips and placed under slight tension using custom fabricated grip holders so that the membranes were taut. Glass slides were adhered to the bottom of the membranes to prevent oxygen diffusion into the membrane during subsequent steps. Polydimethylsiloxane (PDMS) rings (30 mm diameter × 3 mm wall thickness) were then bonded to the membrane to retain cell culture media. Ideally, biaxial stretching would be performed using a large number of stretching protocols on a single sample [6,36]. However, cells remodel in response to mechanical load [37], which limits the number of protocols to which a single cell can be exposed. To overcome this limitation, VSMCs were micropatterned with identical architectures, conferring a uniform geometry for direct comparison between cells exposed to different stretching protocols. Standard photolithography techniques were used to design PDMS stamps with arrays of 4000 μm2 features, as previously published [38], of varying aspect ratios (ARs). Aspect ratios (AR1: 63 μm × 63 μm; AR2: 91 μm × 44 μm; AR4: 127 μm × 32 μm; AR8: 175 μm × 22 μm) were chosen to mimic the ranges of physiological shapes ranging from cobblestone shapes in blood vessel bifurcations and more elongated geometries seen in unbranched blood vessels [10]. Stamps were inked with 100 μg/mL of human fibronectin (BD Biosciences, Bedford, MA) for 1 h. The stamps were blown dry with air, then placed in conformal contact with an O2-plasma treated 15 mm glass coverslips for 30 min. Elastomer membranes were functionalized with photoinitiator benzophenone (10% w/v in 35:65 water/acetone) by placing 1 mL of solution onto the center of the membrane within the boundary of the PDMS ring for 1 min. The membranes were then rinsed 3× with methanol and degassed for 30 min to remove oxygen. Prepolymer gel solution was prepared with 10/0.13/0.005% w/v acrylamide/bisacrylamide/acrylic acid N-hydroxysuccinimide (Sigma-Aldrich, St. Louis, MO), 0.014% 1 M HCl, 0.01% 0.2 μm red fluorescent beads (Polysciences, Warrington, PA) and degassed for 15 min, then, 0.002/0.05% w/v of tetramethylethylenediamine/ammonium persulfate (Sigma-Aldrich) was added. Degassed and functionalized membranes were vented to N2 gas. 10 μL of the prepolymer solution was deposited onto the functionalized elastomer and covered with the micropatterned coverslip (patterned side down). The gels were then exposed to UV illumination using a Jelight 342 UVO Cleaner for 30 min approximately 1 in away from the UV lamp. After polymerization, gels were hydrated in 1× phosphate-buffered saline for 15 min and the coverglasses were removed. Gels were then passivated with 4% bovine serum albumin for 1 h and then incubated in cell growth media for 48 h at 37 °C to remove residual benzophenone and unreacted prepolymer constituents. Gel moduli were measured by fabricating dog-bone shaped (∼5 mm width, ∼5 mm thick, ∼50 mm length) gels in a custom mold and performing uniaxial testing using an Instron biaxial stretcher (Tissue Mechanics Lab, University of Minnesota).
Fig. 1.
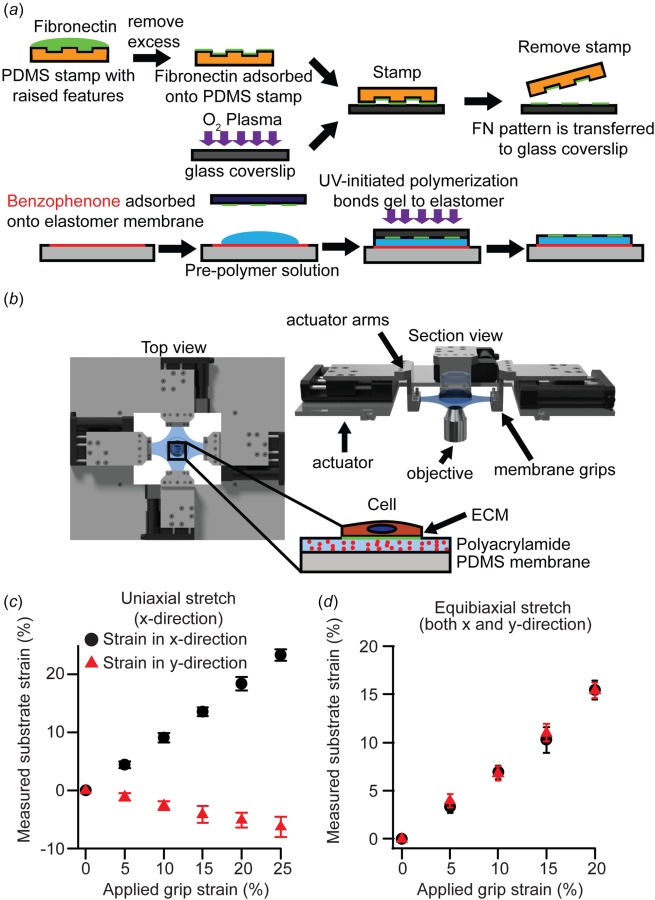
Fabrication of substrate and cellular microbiaxial stretching device: (a) schematic representation of substrate fabrication process, (b) schematic representation of the CBS device. Inset: cell substrate, (c) grip strain versus measured substrate strain under applied uniaxial grip strain (n = 10), and (d) grip strain versus measured substrate strain under equibiaxial grip strain. Error bars: standard deviation (n = 10).
Stretcher Design.
Cellular microbiaxial stretching (CBS) was used for simultaneous stretching and imaging of cells. The CBS device consists of four independent linear actuators (M-111.1DG, M-110.1DG, Physik Instrumente, Auburn, MA) (Fig. 1(b)) with a total travel range of 20 or 30 mm (50% or 75% strain), controlled by a servomotor controller (C-863, Physik Instrumente), and mounted on to the microscope stage. Custom stainless steel arms and membrane grips (Fig. 1(b)) mounted to the actuators constrained a cruciform shaped elastomer membrane. Computer-aided design plans for all custom-designed parts will be provided on request. Grip strain was calculated by measuring distance between the grips with respect to the initial distance between the grips. Substrate strain to grip strain calibration was performed by tracking bead displacement in the top layer of the gel during cell-free stretch (see Fig. 2(d)) applied by the actuator membrane grips and calculating strain (Figs. 1(c) and 1(d)). We define a ∼50 μm × 50 μm region centered about the microscope field of view and measure the locations of the beads in the corner of the region. The substrate strains were then calculated by measuring relative displacement of beads with respect to the original locations for each step of grip strain.
Fig. 2.
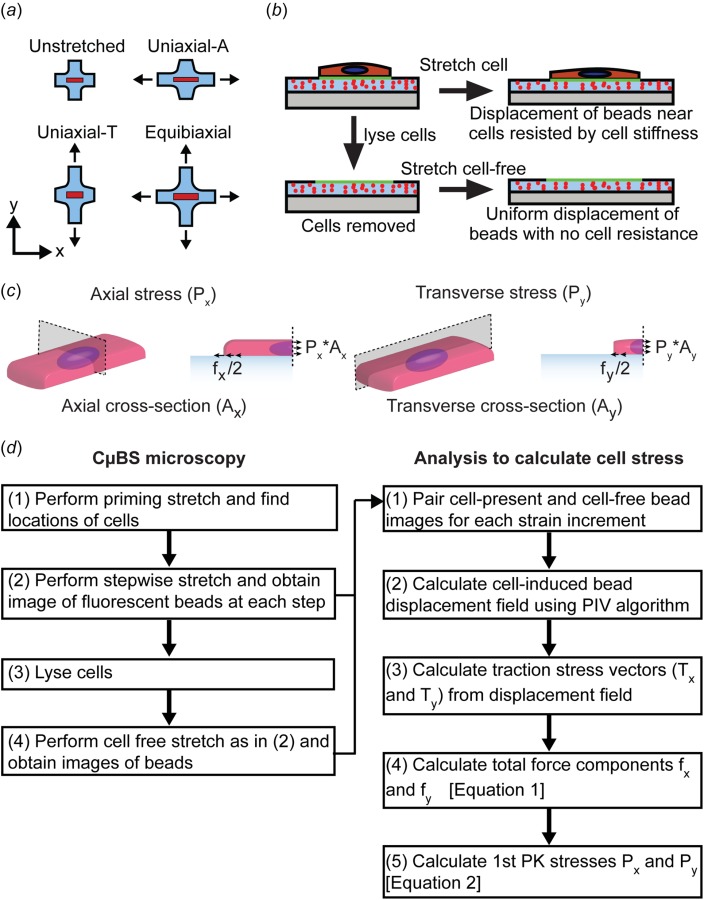
Cell stretching and stress measurement: (a) uniaxial and biaxial stretching protocols, (b) protocol to determine substrate displacements used to calculate cell-induced substrate traction force, (c) schematic for calculating first Piola–Kirchhoff stress from measured substrate traction force, and (d) flowchart describing CBS microscopy technique and cell stress calculation
Cell Culture.
Human umbilical artery vascular smooth muscle cells (VSMCs) were purchased from Lonza at passage 3 and cultured at 37 °C and 5% CO2 in a growth medium consisting of Medium 199 (GenDEPOT, Baker, TX) supplemented with 10% fetal bovine serum (Gibco, Grand Island, NY), 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (Gibco), 3.5 g L−1 glucose (Sigma-Aldrich, St. Louis, MO), 2 mg L−1 vitamin B12 (Sigma-Aldrich), 50 U mL−1 penicillin–streptomycin (Gibco), 1× minimal essential medium nonessential amino acids (Gibco), and 2 mM L-glutamine (Gibco). All experiments were conducted at passages 5–7. Cells were seeded at a density of 5000–150,000 cells per gel-membrane construct overnight in growth media to allow cells to adhere to micropatterns. After overnight seeding, cells were serum starved for a minimum of 24 h prior to all experiments to induce a physiological phenotype [39]. All experiments were conducted at 37 °C in Tyrode's solution.
Cell Structure Determination.
Cells were fixed using 4% paraformaldehyde (Electron Microscope Sciences, Hardfield, PA) for 5 min then stained for F-actin (Alexa Fluor 488 Phalloidin, Life Technologies, Eugene, OR), nuclei (DAPI, 4’, 6-diamiidino-2-phenylindole, Life Technologies), and microtubules (YL ½ hybridoma, Sigma-Aldrich). F-actin and microtubules were imaged using an Olympus X-81 fluorescent microscope at 40× magnification (UPLSAPO40X2, NA 0.95) using a Hamamatsu ORCA-R2 (C10600) CCD camera, and fiber distributions were measured using a custom matlab code [40,41]. F-actin stacks were obtained using an Olympus FluoView FV1000 BX2 laser-scanning confocal microscope (UPlanFLN, 40X, NA 1.30) at the University Imaging Centers (University of Minnesota). Cell thicknesses and volume were determined using a custom matlab script [41]. Cell cross-sectional area was determined by integrating the cell thickness over the cell width. The axial midplane area () was taken as the mean area over the middle 50% of the cell. The transverse midplane area () was calculated similarly. Cell architecture was determined using at least ten cells per micropattern aspect ratio.
Single Cell Biaxial Testing.
For the standard experiment, substrates were stretched by applying increments of 5% grip strain up to 25% uniaxial (uniaxial-axial (uniaxial-A), in the direction of cell alignment, or uniaxial-transverse (uniaxial-T), transverse to cell alignment) and 20% equibiaxial strains at 0.1%/s (Figs. 2(a) and 2(b)). Note: 5% grip strain equated to ∼4% substrate strain at the cell/gel interface (see Fig. 1(c)). At each increment, brightfield images of the cells and fluorescent images of the beads at the top layer of the gel were obtained at 40× magnification (UPLSAPO40X2, NA 0.95, Olympus X81). The cells were then lysed with 0.1% sodium dodecyl sulfate and the stretching protocol was repeated (Fig. 2(b)). For the repeated stretch experiments, the stretch was repeated four times prior to cell lysis. To determine the contribution of major cytoskeletal components to the cell properties, cells were treated with nocodazole (20 μM) to inhibit microtubule polymerization or cytochalasin D (0.5 μM) to inhibit f-actin polymerization prior to stretch for 1 h [42–44]. A maximum of five micropatterned cells per substrate were imaged and analyzed in any single stretching experiment, to maintain consistency between experiments. Only cells with single nuclei, confirmed by nuclear staining poststretch, were analyzed.
Pre- and postlysis bead images were compared using particle image velocimetry (PIV) to determine the cell-induced substrate deformation [45]. Displacement fields were calculated using 5 × 5 μm2 grids interrogated every 2.5 μm. Average experimental displacement maps were generated assuming cell quarter symmetry. The displacement of the substrate about each cell quadrant was averaged for all cells of each aspect ratio.
Individual cell traction stress vectors were determined from bead displacements using an unconstrained Fourier transform traction cytometry (FTTC) algorithm [45] with a regularization factor of 1 × 10−9 and assumed Poisson's ration of 0.5, yielding a grid of substrate traction stresses vectors given by where is the unit vector in the direction. The total traction force components and are given as
| (1) |
where , is the area (6.25 μm2) of discrete surface , and is the vector that described the location of surface with respect to the center of the cell [38]. The first Piola–Kirchhoff stresses (force with respect to undeformed cross-sectional area) and were taken as
| (2) |
Planar Biaxial Strain Energy Density Determination.
The cell was treated as an anisotropic incompressible material exposed to planar biaxial deformation (no shear). The deformation tensor was taken as the observed deformation of the cell, where are the stretch ratios in the direction (x: parallel to the long axis of the cell, y: parallel to the short axis of the cell, and the z: perpendicular to the gel surface). The first Piola–Kirchhoff stress in the direction is given by
| (3) |
where is the SED of the cell, , and .
The cell was assumed to be composed of prestressed actin fibers within an isotropic matrix. The shear modulus of the matrix is given by . The actin fiber stiffness is characterized by the parameter , and the stress-free shortening that the fiber would undergo if it was unconstrained is given by . The fibers were assumed to be oriented as described by the measured whole-cell orientation probability density in the x–y plane and with an assumed Gaussian distribution out of the x–y plane. The fiber orientation was used to determine a structure tensor , as defined by Gasser et al. [46]. ( values for each AR can be found in Table 1.)
Table 1.
Actin fiber structure tensor values
| AR1 | 0.486 | 0.486 | 0.028 | 0 | 0 | 0 |
| AR2 | 0.846 | 0.126 | 0.028 | 0.023 | 0 | 0 |
| AR4 | 0.928 | 0.044 | 0.028 | 0.010 | 0 | 0 |
| AR8 | 0.945 | 0.027 | 0.028 | 0.011 | 0 | 0 |
Briefly, fiber orientation was described by the unit vector where and are Eulerian angles with respect to the and axes, respectively, and is the unit vector in the direction. The density function was normalized so that
| (4) |
and the structure tensor was given by
| (5) |
When the fiber distribution is included, the SED of the cell was given as
| (6) |
Parameter optimization was performed by comparing predicted versus experimental stress and at the six uniaxial stretches and five equibiaxial stretches corresponding with the measured substrate deformations (uniaxial: in the directions of stretch and transverse to the stretch. Equibiaxial: in both directions). The range of possible parameters was limited to , , and . This parameter range was determined using both the practical constraints of the model and physical assumptions of the cell. A too large mismatch between and caused the finite element (FE) model used to validate this model (see Finite Element Model section) to be unable to converge, limiting the range of . In the previous models, was assumed to be 0.9 at homeostasis, with a minimum possible value (during maximum stimulation) of 0.6 [27]. Since our cells were not being stimulated, we limited the range of . The parameter set that best fit the experimental data, as determined by least squares fitting, was determined to be optimal.
Finite Element Model.
To validate the SED determined using planar biaxial assumptions, a quarter symmetry finite element model of the cell and underlying polyacrylamide and elastomer substrates was developed using COMSOL Multiphysics 4.2. The cell was modeled as hyperelastic and nearly incompressible with a SED of
| (7) |
where , , , , and is the bulk modulus. The gel and elastomer membrane were modeled as neo-Hookean, with a strain energy density function of
| (8) |
where is the shear modulus and is the first Lamè parameter. Gel parameters were taken from the experimentally determined Young's modulus () and assumed Poisson's ratio () based on the relations and . Elastomer parameters were based on standard PDMS values [47,48].
The model geometry was meshed with tetrahedral elements using COMSOL's physics-controlled meshing sequence. The AR1 model had 21,204 elements (cell: 821, gel: 10,005, membrane: 10,378). The AR2 model had 21,265 elements (cell: 850, gel: 9945, membrane: 10,470). The AR4 model had 22,435 elements (cell: 929, gel: 11,173, membrane: 10,333). The AR7 model had 23,870 elements (cell: 1146, gel: 12,205, membrane: 10,429). Displacement consistent with experimental strains was applied to the membrane and gel on the nonsymmetry x–y planes. The top surface was free and the bottom surface was constrained from displacement in z. The governing equations were solved via quasi-static analysis. Prior to displacing the boundaries, the activation tensor, which is initially , was incremented linearly with time until . The nonsymmetry boundaries were then incremented linearly with time, while was not varied. Cell-induced displacement () was determined as where and are the displacements of the top surface of the gel in and and and are the expected displacements due to the prescribed boundary displacement. Model-predicted cell-induced substrate displacements () were then compared to the average experimental substrate displacements.
Statistical Analyses.
Differences in stress as a function of strain were compared by using a one-way analysis of variance (ANOVA), and pairwise comparison significance was performed using a Holm–Sidak test. Differences in Px and Py as a function of strain were compared by using a two-way ANOVA and pairwise comparison significance was performed using a Holm–Sidak test. Similarly, nocodazole and cytochalasin D treatment were compared to control stress values for each aspect ratio cell and stretch using a two-way ANOVA and pairwise comparison significance was performed using a Holm–Sidak test. Computational fits to experimental data were compared by computing . Sum of squares of residuals and the total sum of squares were computed as and over n values over i, where yi are data values, fi are predicted values, and is the mean of data.
Results
Single-Cell Biaxial Stretching With CBS Microscopy.
To perform single-cell biaxial stretching, we developed the CBS microscopy method to measure the stress in cells adhered to a deformable elastomer substrate. The CBS device (Fig. 1(b)) can apply any combination of x–y strains up to 25% grip strain (Fig. 2(a)). Cells were micropatterned on a fluorescent bead-doped layer of polyacrylamide (Young's modulus: 13.5 ± 2.2 kPa) adhered to an elastomer membrane and stretched by increments of 5% grip strain up to 25%, while the deformation of the substrate beneath the cell was measured using the displacement of the embedded beads. Traction force microscopy methods [33] were used to determine the traction stresses applied to the substrate by the cell at each stretch increment, by comparing substrate deformation during identical stretching protocols with the cells intact and after cell lysis.
VSMCs With Nativelike Architecture Exhibit Anisotropic Material Properties.
In vivo, VSMCs are normally organized into elongated spindles wrapped circumferentially around blood vessels [10]. To mimic this architecture, the cells were micropatterned with an aspect ratio (AR) of 4:1 (AR4) (Fig. 3(a)). When the cells were stretched uniaxially parallel to their long axes (uniaxial axial, uniaxial-A) (Movie S1, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection), the cell-induced substrate deformation and traction force increased with increasing applied strain and decreased with decreasing strain (Figs. 3(a) and 3(b)). VSMCs were consecutively stretched four times over 110 min (Fig. 3(b)), during which we observed hysteresis during unloading, consistent with previous viscoelastic [49–53] or soft glassy [54] descriptions of cells. However, the cellular traction forces during both loading and unloading were consistent over the four stretches (Figs. 3(c) and 3(d)). The cycle-independent nature of the force-strain behavior indicates that the VSMCs were not plastically deforming [55] or significantly remodeling [56] during the stretching protocol, allowing their elastic properties to be measured. For the remainder of this work, we focused only on the first extension (increasing strain) of each cell, and did not perform repeated stretch.
Fig. 3.
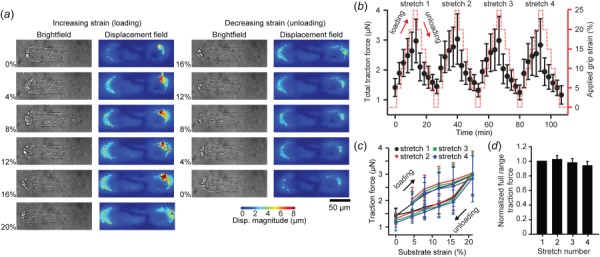
Repeated cell stretching and hysteresis: (a) representative images of a single AR4 VSMC during one cycle of loading and unloading. Left columns: brightfield image of cell. Right columns: cell-induced bead displacement field. (b) Total traction force generated by AR4 cells undergoing loading and unloading cycles during repeated uniaxial-A stretch (n = 9). (c) Total traction force exerted by AR4 cells during cyclic loading over four sequential stretches (n = 5). (d) Normalized cycle-to-cycle total traction force relative to the first stretching cycle for cells exposed to four sequential uniaxial-A stretches. All error bars: standard deviation.
Confocal microscopy was used to determine the 3D geometry of the micropatterned cells. The mean axial and transverse cross-sectional areas were determined to be Ax = 78 μm2 and Ay = 278 μm2, respectively. The undeformed geometry was used to calculate the midplane first Piola–Kirchhoff stress [32] during stretching. For uniaxial-A stretching (Fig. 4(a)), the stresses in the direction of stretch () increased with strain, while transverse stresses () were lower and nearly constant (Fig. 4(b)). However, when the cells were stretched uniaxially parallel to their short axes (uniaxial transverse, uniaxial-T) (Fig. 4(c), Movie S1, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection) the stresses in both the stretched () and unstretched () directions were nearly unchanged over 0–20% strain (Fig. 4(d)). When equibiaxially stretched (Fig. 4(e), Movie S1, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection), the cells' stress–strain behavior in each direction mimicked that of the uniaxial stretch (Fig. 4(f)). This large-deformation mechanical anisotropy is consistent with previous small-deformation studies in micropatterned cells [57]. Taken together, these data demonstrate that there is significant material anisotropy in VSMCs with nativelike elongated architecture [10].
Fig. 4.
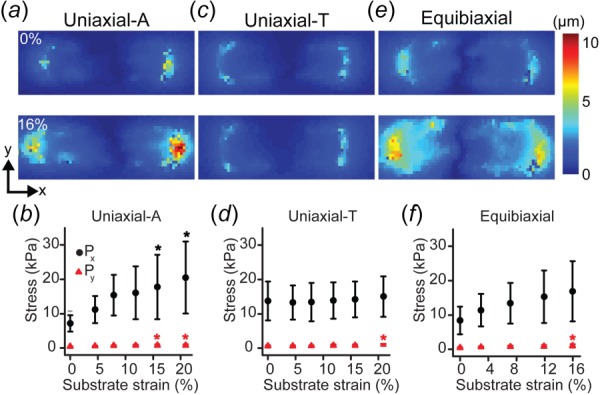
Mechanical anisotropy in biaxially stretched micropatterned VSMCs. (a), (c), and (e) Representative cell-induced displacement fields for unstretched and 16% strain AR4 VSMCs undergoing (a) uniaxial-A (n = 10), (c) uniaxial-T (n = 13), and (e) equibiaxial stretch (n = 9). (b), (d), and (f) First Piola–Kirchhoff stresses in AR4 cells during (b) uniaxial-A (*, * = significant from 0%, p < 0.05), (d) uniaxial-T (* = significant from 0%, 4%, 8%, p < 0.05), and (f) equibiaxial stretching (* = significant from 0%, p < 0.05). All error bars: standard deviation.
Cellular Architecture Dictates VSMC Material Properties.
The stereotypical elongated VSMC architecture is dramatically altered near small artery bifurcations [10]. It is notable that cerebral aneurysms, which are thought to initiate due to a weakening of the artery wall, occur disproportionately around these bifurcations [58]. To determine the effect of cellular architecture on mechanical properties, we performed CBS microscopy on VSMCs micropatterned with matching adhesive areas, but varying aspect ratios (1:1 (AR1), 2:1 (AR2), 4:1 (AR4), 8:1 (AR8)) (Fig. 5(a)). VSMC volume was fairly consistent in the patterned cells (AR1: 7841 ± 2512 μm3, AR2: 8954 ± 3323 μm3, AR4: 10,164 ± 3452 μm3 AR1: 8831 ± 2984 μm3; only AR1 and AR4 were statistically different). But the cross-sectional areas were altered by the micropatterning such that larger aspect ratios had decreasing axial cross section (Ax) and increasing transverse cross section (Ay) (Fig. 5(b)). VSMCs with larger ARs had greater axial prestress and were stiffer when stretched parallel to their long axes, compared to VSMCs with smaller ARs (Fig. 5(c)). Conversely, cells with larger aspect ratios had lower transverse prestress and were less stiff when stretched transverse to their long axes (Fig. 5(c)). These trends were consistent for equibiaxial stretching (Fig. 5(c)). These results, taken as a whole, indicate that anisotropic prestress and resistance to strain depend on cellular architecture [10].
Fig. 5.
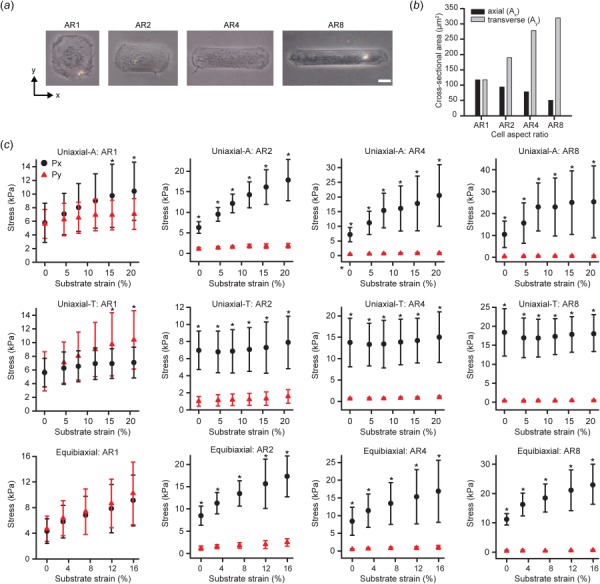
Cell shape influences mechanical properties. (a) Brightfield images of micropatterned cells with identical adhesive area, but varied aspect ratios (1:1 (AR1), 2:1 (AR2), 4:1 (AR4), 8:1 (AR8)). Scale bar: 20 μm. (b) Measured cell cross-sectional areas from average cell thickness maps. (c) First Piola–Kirchhoff stresses for all active cells during uniaxial-A, uniaxial-T, and equibiaxial stretching. Error bars: standard deviation. Uniaxial-A: AR1 (n = 10), AR2 (n = 10), AR4 (n = 10), AR8 (n = 9). Uniaxial-T: AR1 (n = 10), AR2 (n = 11), AR4 (n = 13), AR8 (n = 9). Equibiaxial: AR1 (n = 10), AR2 (n = 10), AR4 (n = 9), AR8 (n = 10). (* = Px significant from Py at same strain, p < 0.05).
Actin Cytoskeleton Mediates Whole-Cell Mechanical Anisotropy.
The actin and microtubule cytoskeletons are critical structural components of cells [19]. We asked whether the observed cell shape-dependent mechanical properties were a result of changes in cytoskeletal architecture. To quantify their organization, we stained VSMCs for actin and microtubule filament systems (Fig. 6(a)) and found that both are highly anisotropic in high AR VSMCs (Figs. 6(b) and 6(c)), and increasing anisotropic alignment correlates with increasing mechanical anisotropy (Figs. 6(b)–6(e)). To determine the contributions of these filament systems to the mechanical properties of VSMCs, axial and transverse uniaxial stretching was performed in cells treated with nocodazole or cytochalasin D, which act to depolymerize microtubule or actin filaments, respectively [43]. While nocodazole treatment hardly altered the mechanical behavior of VSMCs (Figs. 6(f) and 6(g)), cytochalasin D treatment significantly reduced VSMC rigidity in comparison to control cells (Figs. 6(h) and 6(i)). Thus, these data suggest that the mechanical properties of VSMCs are mediated by the intact actin cytoskeleton.
Fig. 6.
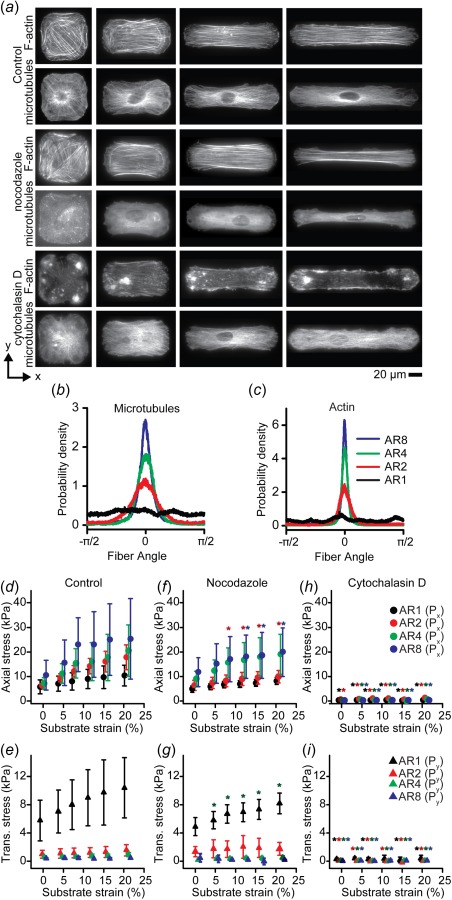
Cytoskeletal structure influences mechanical properties. (a) Representative immunofluorescent images of F-actin and microtubules in representative micropatterned cells for each aspect ratio. Top: dimethyl sulfoxide control. Middle: nocodazole treated. Bottom: cytochalasin D treated. (b) Microtubule filament orientation. Measured from n = 10 cells. (c) Actin filament orientation. Measured from n = 10 cells. (d), (f), and (h) Axial first Piola–Kirchhoff stress () in VSMCs during uniaxial stretch in axial direction (d) control cells (n = 10). (f) Nocodazole treated (n = 10). (h) Cytochalasin D treated (n = 6). (e), (g), and (i) Transverse first Piola–Kirchhoff stress () in VSMCs during uniaxial stretch in the transverse direction (e) control cells (n = 13). (g) Nocodazole treated (n = 4). (i) Cytochalasin D treated (n = 6). All error bars: standard deviation. Note: data staggered about strain values to prevent overlapping data. (d), (f), and (h) Y-axis scaled to maximum of Px. (e), (g), and (i) Y-axis scaled to maximum of Py. (*, *, *, * = significant from control at same strain with same AR p < 0.05 for respective aspect ratios).
Actin Organization-Based SED Is Sufficient to Characterize VSMC Mechanical Properties.
To determine the SED of VSMCs at the single-cell level, we first analyzed the CBS method as planar biaxial stretching (i.e., no shear), as previously described for tissue-scale biaxial tests [6]. We assumed that cellular deformation and material properties were uniform and described by a three-parameter SED using the measured actin orientation to define a distribution of prestressed fibers within an isotropic matrix [46] (see Table 1). Parameters were optimized so that the model reproduced the experimentally measured AR4 first Piola–Kirchhoff stresses for all stretching protocols (Fig. 7(a), Table 2). Next, we asked whether the AR4 SED could be generalized for any cellular architecture for which the actin orientation is known. To do this, we simulated planar biaxial tests of VSMCs with varying ARs. All parameters were identical to those determined for the AR4 cell, except the actin orientation, which was based on those measured for VSMCs of each aspect ratio (Table 1). For each of the experimental stretching protocols, this simple model was able to capture the stress–strain behavior of VSMCs of most ARs (Fig. 7(b)).
Fig. 7.
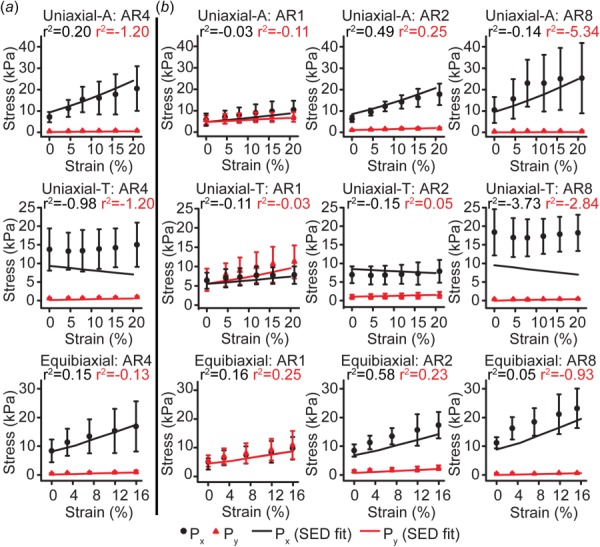
Mechanical models using actin organization-based SED recapitulate experimental results. (a) AR4 experimental data used to determine SED parameters and planar biaxial model fit. (b) AR1, AR2, and AR8 experimental data and planar biaxial model prediction. Error bars: standard deviation.
Table 2.
Calculated cell properties and assumed gel and membrane properties in the model
| Cell properties |
| Gel properties |
| Membrane properties |
Adhered VSMCs are likely not truly undergoing shear-free planar biaxial deformation. To determine whether our planar biaxial model recapitulates the true dynamics of the cell, we developed a 3D quarter symmetry finite element (FE) model of the AR4 cell and its underlying substrate (Fig. 8(a)). When this model was used to replicate the three experimental stretching protocols (Movie S2, which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection), the VSMC-induced substrate deformation in the model mirrored the experimentally measured mean displacement throughout each stretching protocol (Figs. 8(b)–8(d)), suggesting that our planar biaxial assumptions do not create excessive error. There was good agreement between FE model-predicted and experimentally measured substrate deformations for most ARs (Fig. 9), with AR1 deformations varying the most from the experimental, likely due to greater spatial heterogeneity in actin orientation. Thus, these data demonstrate that a simple SED-based solely on the organization of the actin cytoskeleton can be used to describe the elastic properties of VSMCs.
Fig. 8.
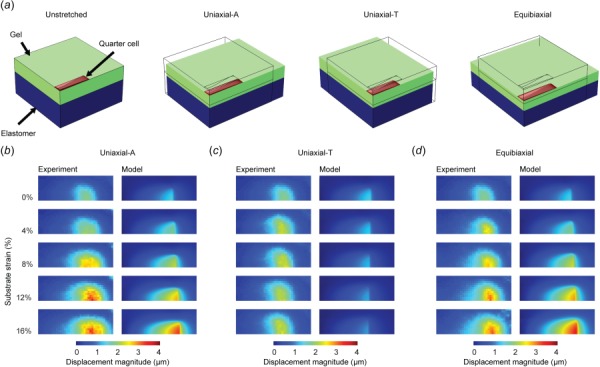
FE model for validating cell stretching experiment. (a) Quarter symmetry cell and substrate model generated in COMSOL of AR4 cell undergoing prescribed uniaxial-axial, uniaxial-transverse, and equibiaxial stretch. (b) and (c) Comparison of model and experimental cell induced substrate displacements during (b) uniaxial-axial, (c) uniaxial-transverse, and (d) equibiaxial stretch.
Fig. 9.
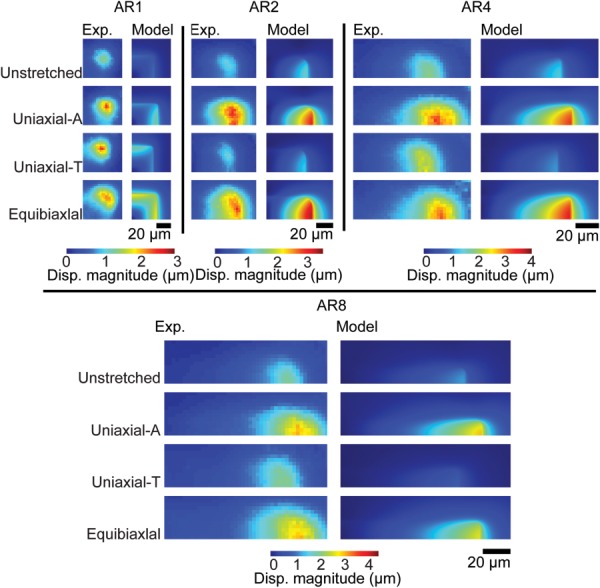
Quarter-symmetry FE model-predicted substrate displacement compared to the mean experimental substrate displacements. All stretched images represent 16% strain cases.
Discussion
To determine the cellular stress induced by extracellular mechanical stimuli, it is necessary to know the mechanical properties of the cells. Here, we describe the CBS method for performing biaxial tests on individual cells to determine the SED that fully describes their elastic mechanical properties. Standard methods for measuring cellular elastic properties, such as atomic force microscopy indentation [59], micropipette aspiration [60], magnetic tweezers [50], and magnetic twisting cytometry [61], report isotropic descriptions of the cell's properties, like Young's modulus. While this is sufficient for comparative studies [62], most adherent cells are not well described by a single modulus due to their structural anisotropy. Our results show that VSMCs patterned with in vivo like architecture are highly anisotropic. Elongated cells were markedly stiffer when stretched parallel to their long axes, compared to their short axes. It is also notable that we found limited orthogonal coupling in VSMCs, which is unlike intact arteries, where axial stretch significantly alters pressure-radius behavior in vessel inflation tests [63].
VSMCs in arteries can undergo physiological strains of up to 15–25%, per cardiac cycle [64,65], and under extreme conditions such as aneurysm growth, chronic strains may be markedly larger. In this study, we used strains up to 20%, to measure large-deformation anisotropic mechanical properties that are appropriate for these cells. Many tissues, including arteries, have highly nonlinear material properties when exposed to large strains [63,66]. However, we did not find significant nonlinearity in VSMC stress–strain behavior, though it is notable that our strains were not as large as those in many tissue studies.
The primary aim of this study was to determine the SED of VSMCs. It is important to know the SED, rather than a simple modulus, when developing computational models of cells and tissues. Cutting edge models of tissue mechanics, like rule-of-mixtures [24–28] and multiscale [29–31] models, consider the contribution of each tissue constituent independently. As a result, the assumed properties of these constituents can significantly alter model predictions [67]. Thus, for models that simulate complex loads, the full anisotropic description captured by the SED is necessary. Here, we characterized nativelike AR4 VSMCs with a simple three parameter SED that incorporates actin cytoskeletal organization. With only actin alignment altered, this SED was also able to describe cells patterned into other ARs, demonstrating that an architecture-dependent SED can robustly describe VSMCs.
In this study, we found that VSMCs with larger ARs have greater prestress and are stiffer in their long axes, which is consistent with evidence that cells with greater prestress exhibit increased stiffness [68]. In a related study, it was found that in highly aligned confluent engineered tissues, VSMC AR influences tissue prestress, even when actin organization is not significantly altered [69]. In those tissues, agonist-induced contractility also increases with increased AR, possibly due to altered phenotype expression [69], suggesting that a model that considers both cytoskeletal organization and expression of a set of key phenotype markers could improve on the one presented here.
The CBS method requires several assumptions that may affect experimental robustness. We assume that the cell is a continuum body with a uniform SED throughout, ignoring the contribution of the nucleus [70,71] and spatial variation of cytoskeletal organization. Thus, we report an average planar cell stress, with no assumptions of the stress distribution in the cell. We ignored viscous behavior and assumed that the cells were purely elastic when determining the SED. However, we observed hysteresis during cell unloading, demonstrating time-dependent mechanical properties that have been previously described with both viscoelastic [49–53] and soft glassy rheology [54] theories. Another shortcoming of this study is that we did not study the range of possible SEDs, only one formulation. In addition, due to constraints in the data range over which the model would converge, we did not sample the entire possible parameter space. This is most notable in our fitting of , which is at the bottom of our tested data range and for which there is no physical reason that it could not be lower. Finally, CBS only truly measures two-dimensional properties, and it has been shown that adherent cells exert forces normal to their substrates [72,73]. In the VSMCs studied, the primary orientation of the actin cytoskeleton is in 2D plane measured, so though there is out-of-plane rigidity, it is likely that it is relatively low. Although beyond the scope of this study where we study mechanical properties of single cells, multicellular monolayers have been shown to exhibit complex material properties due to cell–cell contact. In the future, CBS microscopy can be extended to study mechanical properties of multicellular monolayers [74].
Early elasticity-based measurements, like biaxial testing, formed the basis of the field of modern soft-tissue biomechanics [6]. These studies not only demonstrated the complex structure-function relations of tissues [75–77], but also laid the foundation for the tissue-scale growth and remodeling theory currently used to model how tissue function is affected by mechanical perturbations [78,79]. Today, mechanobiology researchers are making great strides toward understanding how cells transduce mechanical forces [80–82]. However, nearly all of these studies describe the properties of the cells and their environment in terms of a modulus or stiffness. Our demonstration that cells, like tissues, have complex anisotropic properties suggests their mechanotransductive response to applied loads may be similarly anisotropic, which must be taken into consideration.
Supplementary Material
Acknowledgment
We acknowledge financial support from the U.S. National Science Foundation (NSF): CMMI 1553255 (P.W.A.), American Heart Association (AHA): 13SDG14670062 (P.W.A.), 16PRE27770112 (Z.W.), Dystonia Medical Research Foundation (G.W.G.L.), the Paul and Sheila Wellstone Muscular Dystrophy Center NIAMS P30 Grant (G.W.G.L.), and University of Minnesota Doctoral Dissertation Fellowship (Z.W.). Parts of this work were carried out in the University Imaging Centers at the University of Minnesota and the Minnesota Nano Center, which receives partial support from NSF through the NNIN program.
Contributor Information
Zaw Win, Department of Biomedical Engineering, , University of Minnesota-Twin Cities, , 312 Church Street SE NHH 7-105, , Minneapolis, MN 55455 , e-mail: winxx005@umn.edu.
Justin M. Buksa, Department of Biomedical Engineering, , University of Minnesota-Twin Cities, , 312 Church Street SE NHH 7-105, , Minneapolis, MN 55455 , e-mail: buksa002@umn.edu
Kerianne E. Steucke, Department of Biomedical Engineering, , University of Minnesota-Twin Cities, , 312 Church Street SE NHH 7-105, , Minneapolis, MN 55455 , e-mail: steu0057@umn.edu
G. W. Gant Luxton, Department of Genetics, , Cell Biology, and Development, , University of Minnesota-Twin Cities, , 420 Washington Avenue SE MCB 4-128, , Minneapolis, MN 55455 , e-mail: gwgl@umn.edu
Victor H. Barocas, Department of Biomedical Engineering, , University of Minnesota-Twin Cities, , 312 Church Street SE NHH 7-105, , Minneapolis, MN 55455 , e-mail: baroc001@umn.edu
Patrick W. Alford, Department of Biomedical Engineering, , University of Minnesota-Twin Cities, , 312 Church Street SE NHH 7-105, , Minneapolis, MN 55455 , e-mail: pwalford@umn.edu.
References
- [1]. Engler, A. J. , Sen, S. , Sweeney, H. L. , and Discher, D. E. , 2006, “ Matrix Elasticity Directs Stem Cell Lineage Specification,” Cell, 126(4), pp. 677–689. 10.1016/j.cell.2006.06.044 [DOI] [PubMed] [Google Scholar]
- [2]. Trepat, X. , Wasserman, M. R. , Angelini, T. E. , Millet, E. , Weitz, D. A. , Butler, J. P. , and Fredberg, J. J. , 2009, “ Physical Forces During Collective Cell Migration,” Nat. Phys., 5(6), pp. 426–430. 10.1038/nphys1269 [DOI] [Google Scholar]
- [3]. Shyer, A. E. , Tallinen, T. , Nerurkar, N. L. , Wei, Z. Y. , Gil, E. S. , Kaplan, D. L. , Tabin, C. J. , and Mahadevan, L. , 2013, “ Vilification: How the Gut Gets Its Villi,” Science, 342(6155), pp. 212–218. 10.1126/science.1238842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Humphrey, J. D. , Eberth, J. F. , Dye, W. W. , and Gleason, R. L. , 2009, “ Fundamental Role of Axial Stress in Compensatory Adaptations by Arteries,” J. Biomech., 42(1), pp. 1–8. 10.1016/j.jbiomech.2008.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Alford, P. W. , Dabiri, B. E. , Goss, J. A. , Hemphill, M. A. , Brigham, M. D. , and Parker, K. K. , 2011, “ Blast-Induced Phenotypic Switching in Cerebral Vasospasm,” Proc. Natl. Acad. Sci. U.S.A., 108(31), pp. 12705–12710. 10.1073/pnas.1105860108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Sacks, M. S. , and Sun, W. , 2003, “ Multiaxial Mechanical Behavior of Biological Materials,” Annu. Rev. Biomed. Eng., 5(1), pp. 251–284. 10.1146/annurev.bioeng.5.011303.120714 [DOI] [PubMed] [Google Scholar]
- [7]. Humphrey, J. D. , Strumpf, R. K. , and Yin, F. C. , 1990, “ Determination of a Constitutive Relation for Passive Myocardium: I. A New Functional Form,” ASME J. Biomech. Eng., 112(3), pp. 333–339. 10.1115/1.2891193 [DOI] [PubMed] [Google Scholar]
- [8]. Kim, D. H. , Lipke, E. A. , Kim, P. , Cheong, R. , Thompson, S. , Delannoy, M. , Suh, K. Y. , Tung, L. , and Levchenko, A. , 2010, “ Nanoscale Cues Regulate the Structure and Function of Macroscopic Cardiac Tissue Constructs,” Proc. Natl. Acad. Sci. U.S.A., 107(2), pp. 565–570. 10.1073/pnas.0906504107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Gerdes, A. M. , Kellerman, S. E. , Moore, J. A. , Muffly, K. E. , Clark, L. C. , Reaves, P. Y. , Malec, K. B. , McKeown, P. P. , and Schocken, D. D. , 1992, “ Structural Remodeling of Cardiac Myocytes in Patients With Ischemic Cardiomyopathy,” Circulation, 86(2), pp. 426–430. 10.1161/01.CIR.86.2.426 [DOI] [PubMed] [Google Scholar]
- [10]. Ushiwata, I. , and Ushiki, T. , 1990, “ Cytoarchitecture of the Smooth Muscles and Pericytes of Rat Cerebral Blood Vessels. A Scanning Electron Microscopic Study,” J. Neurosurg., 73(1), pp. 82–90. 10.3171/jns.1990.73.1.0082 [DOI] [PubMed] [Google Scholar]
- [11]. Makhija, E. , Jokhun, D. S. , and Shivashankar, G. V. , 2016, “ Nuclear Deformability and Telomere Dynamics Are Regulated by Cell Geometric Constraints,” Proc. Natl. Acad. Sci. U.S.A., 113(1), pp. E32–40. 10.1073/pnas.1513189113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Rothenberg, K. E. , Neibart, S. S. , LaCroix, A. S. , and Hoffman, B. D. , 2015, “ Controlling Cell Geometry Affects the Spatial Distribution of Load Across Vinculin,” Cell. Mol. Bioeng., 8(3), pp. 364–382. 10.1007/s12195-015-0404-9 [DOI] [Google Scholar]
- [13]. Versaevel, M. , Grevesse, T. , and Gabriele, S. , 2012, “ Spatial Coordination Between Cell and Nuclear Shape Within Micropatterned Endothelial Cells,” Nat. Commun., 3, p. 671. 10.1038/ncomms1668 [DOI] [PubMed] [Google Scholar]
- [14]. Versaevel, M. , Braquenier, J. B. , Riaz, M. , Grevesse, T. , Lantoine, J. , and Gabriele, S. , 2014, “ Super-Resolution Microscopy Reveals LINC Complex Recruitment at Nuclear Indentation Sites,” Sci. Rep., 4, p. 7362. 10.1038/srep07362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Wang, N. , Naruse, K. , Stamenovic, D. , Fredberg, J. J. , Mijailovich, S. M. , Toric-Norrelykke, I. M. , Polte, T. , Mannix, R. , and Ingber, D. E. , 2001, “ Mechanical Behavior in Living Cells Consistent With the Tensegrity Model,” Proc. Natl. Acad. Sci. U.S.A., 98(14), pp. 7765–7770. 10.1073/pnas.141199598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Diez-Silva, M. , Dao, M. , Han, J. Y. , Lim, C. T. , and Suresh, S. , 2010, “ Shape and Biomechanical Characteristics of Human Red Blood Cells in Health and Disease,” MRS Bull., 35(5), pp. 382–388. 10.1557/mrs2010.571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Kuznetsova, T. G. , Starodubtseva, M. N. , Yegorenkov, N. I. , Chizhik, S. A. , and Zhdanov, R. I. , 2007, “ Atomic Force Microscopy Probing of Cell Elasticity,” Micron, 38(8), pp. 824–833. 10.1016/j.micron.2007.06.011 [DOI] [PubMed] [Google Scholar]
- [18]. Janmey, P. A. , and McCulloch, C. A. , 2007, “ Cell Mechanics: Integrating Cell Responses to Mechanical Stimuli,” Annu. Rev. Biomed. Eng., 9(1), pp. 1–34. 10.1146/annurev.bioeng.9.060906.151927 [DOI] [PubMed] [Google Scholar]
- [19]. Rodriguez, M. L. , McGarry, P. J. , and Sniadecki, N. J. , 2013, “ Review on Cell Mechanics: Experimental and Modeling Approaches,” ASME Appl. Mech. Rev., 65(6), p. 060801. 10.1115/1.4025355 [DOI] [Google Scholar]
- [20]. Taber, L. A. , 1995, “ Biomechanics of Growth, Remodeling, and Morphogenesis,” ASME Appl. Mech. Rev., 48(8), pp. 487–545. 10.1115/1.3005109 [DOI] [Google Scholar]
- [21]. Taber, L. A. , 1998, “ Biomechanical Growth Laws for Muscle Tissue,” J. Theor. Biol., 193(2), pp. 201–213. 10.1006/jtbi.1997.0618 [DOI] [PubMed] [Google Scholar]
- [22]. Malkawi, A. H. , Hinchliffe, R. J. , Xu, Y. , Holt, P. J. , Loftus, I. M. , and Thompson, M. M. , 2010, “ Patient-Specific Biomechanical Profiling in Abdominal Aortic Aneurysm Development and Rupture,” J. Vasc. Surg., 52(2), pp. 480–488. 10.1016/j.jvs.2010.01.029 [DOI] [PubMed] [Google Scholar]
- [23]. Doyle, B. J. , Cloonan, A. J. , Walsh, M. T. , Vorp, D. A. , and McGloughlin, T. M. , 2010, “ Identification of Rupture Locations in Patient-Specific Abdominal Aortic Aneurysms Using Experimental and Computational Techniques,” J. Biomech., 43(7), pp. 1408–1416. 10.1016/j.jbiomech.2009.09.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Humphrey, J. D. , and Rajagopal, K. R. , 2003, “ A Constrained Mixture Model for Arterial Adaptations to a Sustained Step Change in Blood Flow,” Biomech. Model. Mechanobiol., 2(2), pp. 109–126. 10.1007/s10237-003-0033-4 [DOI] [PubMed] [Google Scholar]
- [25]. Gleason, R. L. , and Humphrey, J. D. , 2004, “ A Mixture Model of Arterial Growth and Remodeling in Hypertension: Altered Muscle Tone and Tissue Turnover,” J. Vasc. Res., 41(4), pp. 352–363. 10.1159/000080699 [DOI] [PubMed] [Google Scholar]
- [26]. Wagenseil, J. E. , 2011, “ A Constrained Mixture Model for Developing Mouse Aorta,” Biomech. Model. Mechanobiol., 10(5), pp. 671–687. 10.1007/s10237-010-0265-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Alford, P. W. , Humphrey, J. D. , and Taber, L. A. , 2008, “ Growth and Remodeling in a Thick-Walled Artery Model: Effects of Spatial Variations in Wall Constituents,” Biomech. Model. Mechanobiol., 7(4), pp. 245–262. 10.1007/s10237-007-0101-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Soares, J. S. , and Sacks, M. S. , 2016, “ A Triphasic Constrained Mixture Model of Engineered Tissue Formation Under In Vitro Dynamic Mechanical Conditioning,” Biomech. Model. Mechanobiol., 15(2), pp. 293–316. 10.1007/s10237-015-0687-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. Sander, E. A. , Stylianopoulos, T. , Tranquillo, R. T. , and Barocas, V. H. , 2009, “ Image-Based Multiscale Modeling Predicts Tissue-Level and Network-Level Fiber Reorganization in Stretched Cell-Compacted Collagen Gels,” Proc. Natl. Acad. Sci. U.S.A., 106(42), pp. 17675–17680. 10.1073/pnas.0903716106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Shah, S. B. , Witzenburg, C. , Hadi, M. F. , Wagner, H. P. , Goodrich, J. M. , Alford, P. W. , and Barocas, V. H. , 2014, “ Prefailure and Failure Mechanics of the Porcine Ascending Thoracic Aorta: Experiments and a Multiscale Model,” ASME J. Biomech. Eng., 136(2), p. 021028. 10.1115/1.4026443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Edgar, L. T. , Maas, S. A. , Guilkey, J. E. , and Weiss, J. A. , 2015, “ A Coupled Model of Neovessel Growth and Matrix Mechanics Describes and Predicts Angiogenesis In Vitro,” Biomech. Model. Mechanobiol., 14(4)(4), pp. 767–782. 10.1007/s10237-014-0635-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Taber, L. A. , 2004, Nonlinear Theory of Elasticity: Applications in Biomechanics, World Scientific Publishing, Singapore. [Google Scholar]
- [33]. Butler, J. P. , Tolic-Norrelykke, I. M. , Fabry, B. , and Fredberg, J. J. , 2002, “ Traction Fields, Moments, and Strain Energy That Cells Exert on Their Surroundings,” Am. J. Physiol.: Cell Physiol., 282(3), pp. C595–605. 10.1152/ajpcell.00270.2001 [DOI] [PubMed] [Google Scholar]
- [34]. Simmons, C. S. , Ribeiro, A. J. , and Pruitt, B. L. , 2013, “ Formation of Composite Polyacrylamide and Silicone Substrates for Independent Control of Stiffness and Strain,” Lab Chip, 13(4), pp. 646–649. 10.1039/c2lc41110e [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Polio, S. R. , Rothenberg, K. E. , Stamenovic, D. , and Smith, M. L. , 2012, “ A Micropatterning and Image Processing Approach to Simplify Measurement of Cellular Traction Forces,” Acta Biomater., 8(1), pp. 82–88. 10.1016/j.actbio.2011.08.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Vande Geest, J. P. , Sacks, M. S. , and Vorp, D. A. , 2006, “ The Effects of Aneurysm on the Biaxial Mechanical Behavior of Human Abdominal Aorta,” J. Biomech., 39(7), pp. 1324–1334. 10.1016/j.jbiomech.2005.03.003 [DOI] [PubMed] [Google Scholar]
- [37]. Kaunas, R. , and Hsu, H. J. , 2009, “ A Kinematic Model of Stretch-Induced Stress Fiber Turnover and Reorientation,” J. Theor. Biol., 257(2), pp. 320–330. 10.1016/j.jtbi.2008.11.024 [DOI] [PubMed] [Google Scholar]
- [38]. Ye, G. J. C. , Aratyn-Schaus, Y. , Nesmith, A. P. , Pasqualini, F. S. , Alford, P. W. , and Parker, K. K. , 2014, “ The Contractile Strength of Vascular Smooth Muscle Myocytes Is Shape Dependent,” Integr. Biol., 6(2), pp. 152–163. 10.1039/c3ib40230d [DOI] [PubMed] [Google Scholar]
- [39]. Han, M. , Wen, J.-K. , Zheng, B. , Cheng, Y. , and Zhang, C. , 2006, “ Serum Deprivation Results in Redifferentiation of Human Umbilical Vascular Smooth Muscle Cells,” Am. J. Physiol.: Cell Physiol., 291(1), pp. C50–58. 10.1152/ajpcell.00524.2005 [DOI] [PubMed] [Google Scholar]
- [40]. Feinberg, A. W. , Alford, P. W. , Jin, H. , Ripplinger, C. M. , Werdich, A. A. , Sheehy, S. P. , Grosberg, A. , and Parker, K. K. , 2012, “ Controlling the Contractile Strength of Engineered Cardiac Muscle by Hierarchal Tissue Architecture,” Biomaterials, 33(23), pp. 5732–5741. 10.1016/j.biomaterials.2012.04.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Alford, P. W. , Nesmith, A. P. , Seywerd, J. N. , Grosberg, A. , and Parker, K. K. , 2011, “ Vascular Smooth Muscle Contractility Depends on Cell Shape,” Integr. Biol. (Cambridge), 3(11), pp. 1063–1070. 10.1039/c1ib00061f [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42]. Ingber, D. E. , Prusty, D. , Sun, Z. Q. , Betensky, H. , and Wang, N. , 1995, “ Cell Shape, Cytoskeletal Mechanics, and Cell Cycle Control in Angiogenesis,” J. Biomech., 28(12), pp. 1471–1484. 10.1016/0021-9290(95)00095-X [DOI] [PubMed] [Google Scholar]
- [43]. Luxton, G. W. , Lee, J. I. , Haverlock-Moyns, S. , Schober, J. M. , and Smith, G. A. , 2006, “ The Pseudorabies Virus VP1/2 Tegument Protein Is Required for Intracellular Capsid Transport,” J. Virol., 80(1), pp. 201–209. 10.1128/JVI.80.1.201-209.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Fletcher, D. A. , and Mullins, R. D. , 2010, “ Cell Mechanics and the Cytoskeleton,” Nature, 463(7280), pp. 485–492. 10.1038/nature08908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45]. Tseng, Q. , Duchemin-Pelletier, E. , Deshiere, A. , Balland, M. , Guillou, H. , Filhol, O. , and Thery, M. , 2012, “ Spatial Organization of the Extracellular Matrix Regulates Cell-Cell Junction Positioning,” Proc. Natl. Acad. Sci. U.S.A., 109(5), pp. 1506–1511. 10.1073/pnas.1106377109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Gasser, T. C. , Ogden, R. W. , and Holzapfel, G. A. , 2006, “ Hyperelastic Modelling of Arterial Layers With Distributed Collagen Fibre Orientations,” J. R. Soc., Interface, 3(6), pp. 15–35. 10.1098/rsif.2005.0073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47]. Steucke, K. E. , Tracy, P. V. , Hald, E. S. , Hall, J. L. , and Alford, P. W. , 2015, “ Vascular Smooth Muscle Cell Functional Contractility Depends on Extracellular Mechanical Properties,” J. Biomech., 48(12), pp. 3044–3051. 10.1016/j.jbiomech.2015.07.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Palchesko, R. N. , Zhang, L. , Sun, Y. , and Feinberg, A. W. , 2012, “ Development of Polydimethylsiloxane Substrates With Tunable Elastic Modulus to Study Cell Mechanobiology in Muscle and Nerve,” PLoS One, 7(12), p. e51499. 10.1371/journal.pone.0051499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Puig-de-Morales-Marinkovic, M. , Turner, K. T. , Butler, J. P. , Fredberg, J. J. , and Suresh, S. , 2007, “ Viscoelasticity of the Human Red Blood Cell,” Am. J. Physiol.: Cell Physiol., 293(2), pp. C597–C605. 10.1152/ajpcell.00562.2006 [DOI] [PubMed] [Google Scholar]
- [50]. Bausch, A. R. , Ziemann, F. , Boulbitch, A. A. , Jacobson, K. , and Sackmann, E. , 1998, “ Local Measurements of Viscoelastic Parameters of Adherent Cell Surfaces by Magnetic Bead Microrheometry,” Biophys. J., 75(4), pp. 2038–2049. 10.1016/S0006-3495(98)77646-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Bausch, A. R. , Moller, W. , and Sackmann, E. , 1999, “ Measurement of Local Viscoelasticity and Forces in Living Cells by Magnetic Tweezers,” Biophys. J., 76(1 Pt 1), pp. 573–579. 10.1016/S0006-3495(99)77225-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Putman, C. A. , van der Werf, K. O. , de Grooth, B. G. , van Hulst, N. F. , and Greve, J. , 1994, “ Viscoelasticity of Living Cells Allows High Resolution Imaging by Tapping Mode Atomic Force Microscopy,” Biophys. J., 67(4), pp. 1749–1753. 10.1016/S0006-3495(94)80649-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53]. Trepat, X. , Grabulosa, M. , Puig, F. , Maksym, G. N. , Navajas, D. , and Farre, R. , 2004, “ Viscoelasticity of Human Alveolar Epithelial Cells Subjected to Stretch,” Am. J. Physiol.: Lung Cell. Mol. Physiol., 287(5), pp. L1025–1034. 10.1152/ajplung.00077.2004 [DOI] [PubMed] [Google Scholar]
- [54]. Trepat, X. , Deng, L. , An, S. S. , Navajas, D. , Tschumperlin, D. J. , Gerthoffer, W. T. , Butler, J. P. , and Fredberg, J. J. , 2007, “ Universal Physical Responses to Stretch in the Living Cell,” Nature, 447(7144), pp. 592–595. 10.1038/nature05824 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55]. Bonakdar, N. , Gerum, R. , Kuhn, M. , Sporrer, M. , Lippert, A. , Schneider, W. , Aifantis, K. E. , and Fabry, B. , 2016, “ Mechanical Plasticity of Cells,” Nat. Mater., 15(10), pp. 1090–1094. 10.1038/nmat4689 [DOI] [PubMed] [Google Scholar]
- [56]. Weng, S. , Shao, Y. , Chen, W. , and Fu, J. , 2016, “ Mechanosensitive Subcellular Rheostasis Drives Emergent Single-Cell Mechanical Homeostasis,” Nat. Mater., 15(9), pp. 961–967. 10.1038/nmat4654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57]. Hu, S. , Eberhard, L. , Chen, J. , Love, J. C. , Butler, J. P. , Fredberg, J. J. , Whitesides, G. M. , and Wang, N. , 2004, “ Mechanical Anisotropy of Adherent Cells Probed by a Three-Dimensional Magnetic Twisting Device,” Am. J. Physiol.: Cell Physiol., 287(5), pp. C1184–1191. 10.1152/ajpcell.00224.2004 [DOI] [PubMed] [Google Scholar]
- [58]. Schievink, W. I. , 1997, “ Intracranial Aneurysms,” N. Engl. J. Med., 336(1), pp. 28–40. 10.1056/NEJM199701023360106 [DOI] [PubMed] [Google Scholar]
- [59]. Radmacher, M. , Tillmann, R. W. , Fritz, M. , and Gaub, H. E. , 1992, “ From Molecules to Cells—Imaging Soft Samples With the Atomic Force Microscope,” Science, 257(5078), pp. 1900–1905. 10.1126/science.1411505 [DOI] [PubMed] [Google Scholar]
- [60]. Schmidschonbein, G. W. , Sung, K. L. P. , Tozeren, H. , Skalak, R. , and Chien, S. , 1981, “ Passive Mechanical-Properties of Human-Leukocytes,” Biophys. J., 36(1), pp. 243–256. 10.1016/S0006-3495(81)84726-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Wang, N. , and Ingber, D. E. , 1995, “ Probing Transmembrane Mechanical Coupling and Cytomechanics Using Magnetic Twisting Cytometry,” Biochem. Cell Biol., 73(7–8), pp. 327–335. 10.1139/o95-041 [DOI] [PubMed] [Google Scholar]
- [62]. Qiu, H. , Zhu, Y. , Sun, Z. , Trzeciakowski, J. P. , Gansner, M. , Depre, C. , Resuello, R. R. , Natividad, F. F. , Hunter, W. C. , Genin, G. M. , Elson, E. L. , Vatner, D. E. , Meininger, G. A. , and Vatner, S. F. , 2010, “ Short Communication: Vascular Smooth Muscle Cell Stiffness as a Mechanism for Increased Aortic Stiffness With Aging,” Circ. Res., 107(5), pp. 615–619. 10.1161/CIRCRESAHA.110.221846 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63]. Matsumoto, T. , and Hayashi, K. , 1996, “ Stress and Strain Distribution in Hypertensive and Normotensive Rat Aorta Considering Residual Strain,” ASME J. Biomech. Eng., 118(1), pp. 62–73. 10.1115/1.2795947 [DOI] [PubMed] [Google Scholar]
- [64]. Zhou, J. , and Fung, Y. C. , 1997, “ The Degree of Nonlinearity and Anisotropy of Blood Vessel Elasticity,” Proc. Natl. Acad. Sci. U.S.A., 94(26), pp. 14255–14260. 10.1073/pnas.94.26.14255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65]. Bell, V. , Mitchell, W. A. , Sigurethsson, S. , Westenberg, J. J. , Gotal, J. D. , Torjesen, A. A. , Aspelund, T. , Launer, L. J. , de Roos, A. , Gudnason, V. , Harris, T. B. , and Mitchell, G. F. , 2014, “ Longitudinal and Circumferential Strain of the Proximal Aorta,” J. Am. Heart Assoc., 3(6), p. e001536. 10.1161/JAHA.114.001536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66]. Bonifasi-Lista, C. , Lake, S. P. , Small, M. S. , and Weiss, J. A. , 2005, “ Viscoelastic Properties of the Human Medial Collateral Ligament Under Longitudinal, Transverse and Shear Loading,” J. Orthop. Res., 23(1), pp. 67–76. 10.1016/j.orthres.2004.06.002 [DOI] [PubMed] [Google Scholar]
- [67]. Lai, V. K. , Hadi, M. F. , Tranquillo, R. T. , and Barocas, V. H. , 2013, “ A Multiscale Approach to Modeling the Passive Mechanical Contribution of Cells in Tissues,” ASME J. Biomech. Eng., 135(7), p. 071007. 10.1115/1.4024350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68]. Kollmannsberger, P. , and Fabry, B. , 2011, “ Linear and Nonlinear Rheology of Living Cells,” Annu. Rev. Mater. Res., 41(1), pp. 75–97. 10.1146/annurev-matsci-062910-100351 [DOI] [Google Scholar]
- [69]. Win, Z. , Vrla, G. D. , Steucke, K. E. , Sevcik, E. N. , Hald, E. S. , and Alford, P. W. , 2014, “ Smooth Muscle Architecture Within Cell-Dense Vascular Tissues Influences Functional Contractility,” Integr. Biol. (Cambridge), 6(12), pp. 1201–1210. 10.1039/C4IB00193A [DOI] [PubMed] [Google Scholar]
- [70]. Caille, N. , Thoumine, O. , Tardy, Y. , and Meister, J. J. , 2002, “ Contribution of the Nucleus to the Mechanical Properties of Endothelial Cells,” J. Biomech., 35(2), pp. 177–187. 10.1016/S0021-9290(01)00201-9 [DOI] [PubMed] [Google Scholar]
- [71]. Isermann, P. , and Lammerding, J. , 2013, “ Nuclear Mechanics and Mechanotransduction in Health and Disease,” Curr. Biol., 23(24), pp. R1113–R1121. 10.1016/j.cub.2013.11.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72]. Maskarinec, S. A. , Franck, C. , Tirrell, D. A. , and Ravichandran, G. , 2009, “ Quantifying Cellular Traction Forces in Three Dimensions,” Proc. Natl. Acad. Sci. U.S.A., 106(52), pp. 22108–22113. 10.1073/pnas.0904565106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73]. Legant, W. R. , Choi, C. K. , Miller, J. S. , Shao, L. , Gao, L. , Betzig, E. , and Chen, C. S. , 2013, “ Multidimensional Traction Force Microscopy Reveals Out-of-Plane Rotational Moments About Focal Adhesions,” Proc. Natl. Acad. Sci. U.S.A., 110(3), pp. 881–886. 10.1073/pnas.1207997110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74]. Harris, A. R. , Peter, L. , Bellis, J. , Baum, B. , Kabla, A. J. , and Charras, G. T. , 2012, “ Characterizing the Mechanics of Cultured Cell Monolayers,” Proc. Natl. Acad. Sci. U.S.A., 109(41), pp. 16449–16454. 10.1073/pnas.1213301109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75]. Tong, P. , and Fung, Y. C. , 1976, “ The Stress-Strain Relationship for the Skin,” J. Biomech., 9(10), pp. 649–657. 10.1016/0021-9290(76)90107-X [DOI] [PubMed] [Google Scholar]
- [76]. Choi, H. S. , and Vito, R. P. , 1990, “ Two-Dimensional Stress-Strain Relationship for Canine Pericardium,” ASME J. Biomech. Eng., 112(2), pp. 153–159. 10.1115/1.2891166 [DOI] [PubMed] [Google Scholar]
- [77]. Billiar, K. L. , and Sacks, M. S. , 2000, “ Biaxial Mechanical Properties of the Natural and Glutaraldehyde Treated Aortic Valve Cusp—Part I: Experimental Results,” ASME J. Biomech. Eng., 122(1), pp. 23–30. 10.1115/1.429624 [DOI] [PubMed] [Google Scholar]
- [78]. Fung, Y. C. , 1991, “ What Are the Residual Stresses Doing in Our Blood Vessels?,” Ann. Biomed. Eng., 19(3), pp. 237–249. 10.1007/BF02584301 [DOI] [PubMed] [Google Scholar]
- [79]. Taber, L. A. , 1998, “ A Model for Aortic Growth Based on Fluid Shear and Fiber Stresses,” ASME J. Biomech. Eng., 120(3), pp. 348–354. 10.1115/1.2798001 [DOI] [PubMed] [Google Scholar]
- [80]. Chan, C. E. , and Odde, D. J. , 2008, “ Traction Dynamics of Filopodia on Compliant Substrates,” Science, 322(5908), pp. 1687–1691. 10.1126/science.1163595 [DOI] [PubMed] [Google Scholar]
- [81]. Dupont, S. , Morsut, L. , Aragona, M. , Enzo, E. , Giulitti, S. , Cordenonsi, M. , Zanconato, F. , Le Digabel, J. , Forcato, M. , Bicciato, S. , Elvassore, N. , and Piccolo, S. , 2011, “ Role of YAP/TAZ in Mechanotransduction,” Nature, 474(7350), pp. 179–183. 10.1038/nature10137 [DOI] [PubMed] [Google Scholar]
- [82]. Guilluy, C. , Osborne, L. D. , Van Landeghem, L. , Sharek, L. , Superfine, R. , Garcia-Mata, R. , and Burridge, K. , 2014, “ Isolated Nuclei Adapt to Force and Reveal a Mechanotransduction Pathway in the Nucleus,” Nat. Cell Biol., 16(4), pp. 376–381. 10.1038/ncb2927 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


