Tactile Sensing with Whiskers of Various Shapes: Determining the Three-Dimensional Location of Object Contact Based on Mechanical Signals at the Whisker Base

Abstract

Almost all mammals use their mystacial vibrissae (whiskers) as important tactile sensors. There are no sensors along the length of a whisker: all sensing is performed by mechanoreceptors at the whisker base. To use artificial whiskers as a sensing tool in robotics, it is essential to be able to determine the three-dimensional (3D) location at which a whisker has made contact with an object. With the assumption of quasistatic, frictionless, single-point contact, previous work demonstrated that the 3D contact point can be uniquely determined if all six components of force and moment are measured at the whisker base, but these measurements require a six-axis load cell. Here, we perform simulations to investigate the extent to which each of the 20 possible “triplet” combinations of the six mechanical signals at the whisker base uniquely determine 3D contact point location. We perform this analysis for four different whisker profiles (shapes): tapered with and without intrinsic curvature, and cylindrical with and without intrinsic curvature. We show that whisker profile has a strong influence on the particular triplet(s) of signals that uniquely map to the 3D contact point. The triplet of bending moment, bending moment direction, and axial force produces unique mappings for tapered whiskers. Four different mappings are unique for a cylindrical whisker without intrinsic curvature, but only when large deflections are excluded. These results inform the neuroscience of vibrissotactile sensing and represent an important step toward the development of artificial whiskers for robotic applications.

Introduction

Vibrissae (whiskers) or tactile hairs provide many animals with a rich sense of touch. These animals can use their whiskers to tactually determine an object's location as well as its shape, size, orientation, compliance, and texture.^1–10

Artificial whiskers could provide robots with similarly sophisticated tactile capabilities. For an artificial whisker to extract an object's contours, it is important to determine the three-dimensional (3D) location of whisker-object contact. To date, however, studies have only determined at most two coordinates of the contact point,^11–15 limited contacts to occur at the tip,¹⁶ or used a six-axis load cell to determine 3D contact point location.^17,18

Our laboratory recently developed a mechanical model to calculate all mechanical signals at the whisker base as the whisker is deflected in 3D.^19,20 Given the location of the point of contact between the whisker and an object, the model can compute all six components of force and moment at the whisker base.

The goal of the present work was to invert this process, that is, to use measurements of force and moment at the whisker base to infer the 3D contact point location. To avoid use of a six-axis load cell, which is bulky and expensive, we included the additional constraint that only three of the six mechanical variables at the whisker base could be used, thus creating mappings from three mechanical variables to the 3D contact point location. We examined all 20 possible combinations of triplets of mechanical variables and determined whether they provided unique mappings to contact point location.

We also examined how these mappings changed with different whisker profiles (i.e., intrinsic whisker shape). Whiskers, by nature, have a tapered and intrinsic curvature, but it is easiest to create robotic whiskers that are straight, cylindrical segments of plastic or wire. We therefore analyzed the mappings for four different whisker profiles: curved tapered, curved cylindrical, straight tapered, and straight cylindrical. For each profile, we evaluate which mapping is the best suited to extract the 3D contact point locations.

The results of the present work enable the development of modular and replaceable artificial whiskers for robotics that minimize sensors and wiring and reduce signal processing requirements. Potential applications include obstacle localization and avoidance, contour following and navigation, extraction of 3D object geometry, improved instrument placement, and increased mobility, maneuverability, and autonomy.

Materials and Methods

Elastica3D: A 3D model for whisker bending

Whiskers often deflect against objects with a single point of contact. The overall goal of the present work was to characterize and construct the mappings from forces and moments at the whisker base to the 3D contact point location. We aimed at constructing a set of “inverse models” that permit the determination of 3D contact point location based on mechanical signals at the whisker base. To generate the data to create the mappings from mechanical signals to the 3D contact point, we used a 3D frictionless and quasistatic whisker model that had been previously described in detail.^19–21 We call the model Elastica3D because it is based on the Euler-Bernoulli equations for 3D elastic beam bending. We first describe the general form of Elastica3D. We then describe the “basic mode” and “contact point” mode of Elastica3D, the latter of which is used in the present work.

In Elastica3D, the whisker is represented as a series of 99 rigid links of a uniform length that are connected by nodes. The model whisker can be deformed by application of a point load at any point along its length. The nodes allow rotation in all three dimensions, and rotation magnitude is constrained by torsional springs. The stiffness of each spring is dictated by linear elastic beam bending, as described in Equations (2.1) and (2.2). The angle dθ through which each node rotates is given by:

where ds is the length of the link, M_B is the bending moment at that node, E is Young's modulus, and I is the area moment of inertia of the whisker at that node. Although Young's modulus is known to vary somewhat along the whisker length,^22–24 here we use a constant average value of 3.3 GPa. The value of I at each node was calculated as I = πr⁴/4, where r is the whisker's radius at that node.

The amount that each node rotated in a twisting motion about the axis of the immediately distal link was determined by:

where τ is the twisting moment at each node, G is the shear modulus, and J is the polar moment of inertia. G was calculated by using the Equation G = E/(2 × (1+ν)), where ν is Poisson's ratio. The value of ν was set to 0.38, which is typical for alpha keratin that composes the whisker.²⁵ The polar moment of inertia was calculated as J = πr⁴/2. A rigid boundary condition was imposed at the whisker base, meaning that the basepoint of the whisker could not move and the initial slope of the whisker at its base could not change.

The “basic mode” of Elastica3D applies a point force (F_applied) at a specified arc length along the whisker (s_applied) and at a specified angle about the whisker axis (ζ_applied). Because the model assumes frictionless conditions, the force is always applied perpendicular to the whisker. The model then calculates the appropriate whisker deflection due to this point force and returns the resultant forces and moments at the whisker base. It also outputs the shape of the deflected whisker, including the location of the point force acting on the deflected whisker.

In the present work, however, Elastica3D was used in “contact point” mode, in which the inputs are not (F_applied, s_applied, ζ_applied) but rather the location of the 3D contact point and the undeflected whisker shape. The model then uses the MATLAB™ optimization function fminsearch that runs a Nelder-Mead algorithm. It optimizes over (F_applied, s_applied, ζ_applied) with the goal of minimizing the Euclidean distance from the contact point location to the location of the point force acting on the deflected whisker. When this distance is zero, the model has found the solution and returns the deflected whisker shape as well as the forces and moments at the base. If the optimization could not converge to a zero distance, then it was determined that the whisker could not reach that contact point. The whisker would have slipped off the object before deflecting that far.

Validation of Elastica3D

The forces and moments output by Elastica3D for a straight, cylindrical beam were validated against an analytical solution.²⁶ The output of Elastica3D for tapered beams was validated against a finite element model (FEM) constructed in ABAQUS. The FEM model was also used to validate the shape of the deflected straight cylindrical whisker because the analytical model did not give a solution for the full whisker shape.

The ABAQUS model enforced a rigid boundary condition at the beam base, a traction-free boundary condition at the tip, and applied a prescribed point force at a node at a specified location along the beam, s_applied. A follower load was used to ensure that the point force rotated with the node at which it was applied. To enable the rotational degrees of freedom for the follower load, 3D linear beam elements were used to discretize the tapered beam. Five hundred Timoshenko beam elements in ABAQUS (B31) were used to fully capture the effects of shear deformation that are omitted in Euler Bernoulli beam bending.

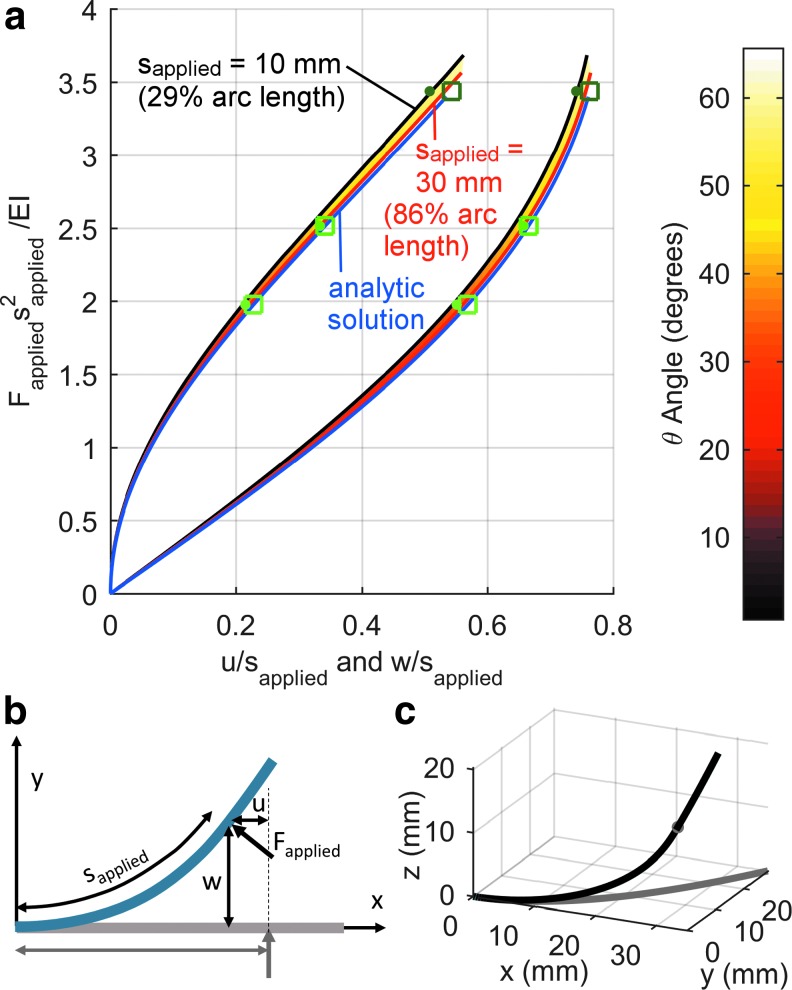
Figure 1a replicates figure 5.2 from Mattiasson,²⁶ which plots the nondimensional solution to the bending of a straight cylindrical beam, and Figure 1b presents a diagram for the variables used in Figure 1a. Results from the FEM whisker matched the Mattiasson solution perfectly. The blue lines in Figure 1a are the results from Mattiasson/FEM, and the colored regions bordered by black and red lines represent all the solutions from Elastica3D. Results from Elastica3D are not single lines because the number of nodes depends on s_applied. For a shorter s_applied, fewer nodes are rotated in Elastica3D.

FIG. 1.

Results from Elastica3D were a good match to analytical and FEM solutions of whisker bending. (a) A nondimensional plot of whisker bending is reproduced from Mattiasson²⁶ figure 5.2, and results from Elastica3D are overlaid. The value on the y-axis is determined by the magnitude of the applied force (F_applied) and the arc length at which the force was applied (s_applied). The values on the x-axis show the amount of deflection at the point of contact in the x- and y-directions (u and w, respectively) normalized to s_applied. The blue lines reproduce Mattiasson's values, and the colored regions bordered by black and red lines represent the results from Elastica3D. The coloring within the regions is determined by the angle of deflection, which is directly related to the values u/s_applied and w/s_applied. The coloring emphasizes that larger angles of deflection result in larger errors. The black lines are the deflections when s_applied was set to its smallest value (10 mm or 29% of the whisker arc length), and the red lines are the deflections for a much larger value of s_applied (30 mm or 86% of the whisker arc length). When s_applied was greater than 30 mm, the whisker was not able to deflect through as large an angle and, therefore, does not extend out as far along the x-axis. The green dots and boxes mark three specific examples in which the identical force was applied to the FEM model and Elastica3D. Boxes mark the analytical solution, and dots mark the Elastica3D solution. (b) This diagram depicts the variables used in (a). The gray line is the undeflected straight, cylindrical whisker, and the blue line is the whisker shape once the force has been applied. The values of u and w show the amount of deflection at the point of applied force in the x and y directions, respectively. (c) A comparison of the FEM solution and the Elastica3D solution for a tapered whisker with intrinsic curvature. The undeflected whisker shape is shown in gray. Results for the deflected whisker shape from the FEM (blue) and Elastica3D model (black) are indistinguishable in the plot. The 3D contact points from the two models are plotted in blue and gray and are also indistinguishable. 3D, three-dimensional; FEM, finite element model.

It is apparent that the force and moments output from Elastica3D drift slightly from the analytical solution, especially when the arc length of contact is small and the deflection angle is large. However, the shapes of the deflected whiskers were visually indistinguishable. A few specific cases are highlighted by three sets of boxes and dots in Figure 1a and tabulated in Table 1. The maximum deviation from the analytical model was 1.2%.

Table 1.

Validation of the Elastica3D Model Against a Finite Element Solution in ABAQUS and/or Against the Analytic Solution

	sapplied(mm)	Fapplied(mN)	Error	Error (percent whisker arc length)
Cylindrical whiskers: Error is the distance between the contact point location (rcp, θcp, φcp) computed by using Elastica3D and computed via the analytic solution.
Figure 1a, case 1	13.9	2.4	0.31 mm	0.88
Figure 1a, case 2	31.4	6.0	0.36 mm	1.03
Figure 1a, case 3	10.0	8.1	0.41 mm	1.2
Compare cylindrical and tapered whiskers: Error is the distance between the contact point location (rcp, θcp, φcp) computed by using Elastica3D and computed by using FEM.
Cylindrical (no figure)	22.7	0.1	38.4 μm	0.11
Tapered (no figure)	22.7	0.1	26.6 μm	0.076
Tapered whisker with intrinsic curvature: Error is the distance between the contact point location (rcp, θcp, φcp) computed by using Elastica3D and computed by using FEM.
Figure 1c	34.5	0.4	40.8 μm	0.087

For the cases identified in the first column, we applied the same force (F_applied) at the same location along the whisker arc length (s_applied) to Elastica3D and the FEM model. Top rows: In the case of cylindrical whiskers, where the FEM solution matched the analytic solution, the errors remained below 1.5% of the whisker arc length. Middle rows: Errors between the FEM solution and Elastica3D were smaller for tapered whiskers than cylindrical whiskers when the same load was applied at the same arc length. Bottom row: Errors remained small for tapered whiskers with intrinsic curvature.

3D, three-dimensional; FEM, finite element model.

Errors in Elastica3D were smaller for tapered whiskers than for cylindrical whiskers, as shown in the middle section of Table 1. Errors for a whisker with intrinsic curvature were also small, as illustrated in Figure 1c and tabulated in the last row of Table 1.

Generating data for mappings

A mapping consists of a set of forces and moments that are measured at the whisker base and that point to the 3D location of whisker-object contact. To generate the mappings, we first had to generate all the force and moment data for all contact points.

Data were generated for four different whisker profiles: straight cylindrical, straight tapered, curved cylindrical, and curved tapered. Whisker dimensions were based on the dimensions of a rat C2 whisker. All whiskers had an arc length (S) of 3.5 cm^27,28 and a base radius (R_base) of 100 μm. The intrinsic curvature was defined by the parabolic function y = 23.3 x², where the coefficient has units of m⁻¹.²⁷ Tapered whiskers had a base-to-tip radius ratio of 15^28–30, resulting in a tip radius (R_tip) of 6.67 μm. Cylindrical whiskers had a radius of 100 μm along their entire length.

All simulations were performed in whisker-centered coordinates, which have been previously described in detail.^{11,13,19–21,31–35} Whisker-centered coordinates place the origin at the whisker base with the x-axis aligned with the proximal linear portion of the whisker. The positive y-direction for a whisker with intrinsic curvature is defined as the direction in which the tip curves concave forward (CF). Thus, all whiskers are defined to lie in the x-y plane when undeflected.

To generate the mechanical data, we deflected the whisker to all contact points that it could reach within a given range. The 3D contact point location was defined in spherical coordinates (r_cp, θ_cp, φ_cp). The radial distance, r_cp, was varied from 11 to 35 mm (29–100% of the whisker arc length). The azimuthal angle (θ_cp) was varied from −60° to 60° for a straight whisker and from −65° to +65° for a curved whisker. The elevation angle (φ_cp) was varied from −60° to +60° for all whiskers. The resulting forces and moments for each contact point in this space that the whisker was able to reach were then determined by using Elastica3D.

Determining uniqueness of mappings

Visual inspection often served as a quick tool to determine whether a mapping was unique. Many mappings were obviously nonunique. For example, the obvious overlap in the monochromatic surfaces for the mapping that involves F_x, F_T, and F_D (Fig. 6a of Results) immediately classified it as nonunique. Other mappings (e.g., Fig. 7a, b) were obviously unique by visual inspection: there was no possibility that the monochromatic surfaces overlapped.

FIG. 6.

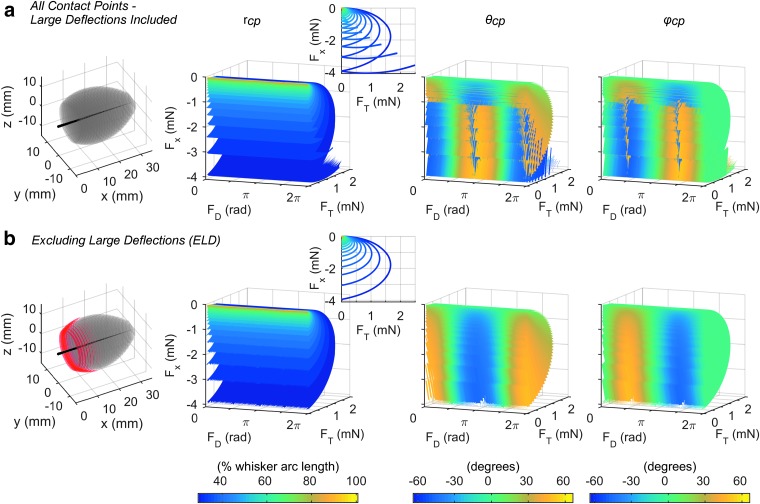
The mapping of F_x, F_T, and F_D is not unique for a straight, tapered whisker unless contact points with large deflections are excluded. Color scales are identical for (a) and (b). (a) These four panels show that mappings between F_x, F_T, and F_D and the 3D contact point location (r_cp, θ_cp, φ_cp) are not unique when large angle deflections are included. The first panel shows all 3D contact point locations for a straight, tapered whisker. The whisker is depicted as a tapered, black line, and the gray volume shows all the 3D contact point locations that the whisker was able to reach. Panels 2–4 show the mapping between F_x, F_T, and F_D and r_cp, θ_cp, and φ_cp when all these contact points are included. The panels are color coded for r_cp, θ_cp, and φ_cp, respectively. As in Figure 5, the data points that compose the mappings for all three variables are identical, but their shape appears different because they are constructed of surfaces that slice through the solid differently. The inset to the plot for r_cp shows the mapping projected into the F_x, F_T plane to reveal that the monochromatic surfaces overlap. Overlap is also clearly visible in the mappings for θ_cp, and φ_cp, as seen in the blue appearing to penetrate the yellow. These regions of overlap indicate that the mapping is nonunique and can be more clearly visualized in Supplementary Video S4. (b) These four panels show that mappings between F_x, F_T, and F_D and the 3D contact point location (r_cp, θ_cp, φ_cp) become unique when large angle deflections are excluded. The first panel is identical to the first panel in (a), except that the contact points classified as large deflections are plotted as red dots. Panels 2–4 show the mapping between F_x, F_T, and F_D and r_cp, θ_cp, and φ_cp when the red contact points involving large angle deflections are excluded. The monochromatic surfaces no longer overlap, so the mapping is unique. Supplementary Video S4 shows these mappings rotating in 3D.

FIG. 7.

Each of the four rows of the figure depicts the best mapping for a different whisker profile. (a) The F_x, M_B, and M_D mapping is best for the curved, tapered whisker. (b) The F_x, M_B, and M_D mapping is best for the straight, tapered whisker. (c) The M_x, M_B, and M_D mapping is best for the curved, cylindrical whisker. (d) There are four mappings with equivalent performances for the straight, cylindrical whisker; all are unique only when large deflections are excluded. Here, we show the F_x, F_T, and F_D mapping. Supplementary Video S5 shows these mappings rotating in 3D.

Many mappings, however, could not be visually classified as unique or nonunique, and therefore, a neural network was used as a second method to examine uniqueness. The intuition here was that the neural network would be trained on a set of data to learn a function approximation to the input-output mapping. The network would then be tested on an independent set of test data. If there had been degenerate outputs for an input, then the network would have learned a degenerate input-output mapping and would provide poor output estimates for the test data.

The neural network construction and training algorithm were the same for all mappings. MATLAB built-in neural network functions were used, and the structure of the network was designed to solve a complex nonlinear function. The neural network had three input and three output nodes with two hidden layers of ten nodes each. The hidden layers used a hyperbolic tangent sigmoid function, and the output layer used a linear transfer function. Levenberg-Marquardt backpropagation was used to train the network, and the performance function was the mean squared normalized error. The networks were trained on 35% of the data; MATLAB built-in training functions tested network training completion on another 7.5% of the data and validated it on a further 7.5% of the data, all of which were chosen at random. The remaining 50% of the data was used to calculate errors to determine uniqueness.

For a mapping to be considered unique, the neural network had to be able to solve for the mapping within certain error thresholds for r_cp, θ_cp, and φ_cp. The thresholds were set by the largest weighted median errors that were associated with mappings that were obviously unique by visual inspection. The error thresholds were as follows: 1 mm in r_cp (3% of the whisker arc length), and 1.5° for θ_cp and φ_cp. For a mapping to be declared unique, it had to meet two criteria: (1) it could have no regions of large, obvious visual overlap, and (2) the error had to be below threshold.

There is a subtlety in establishing the median errors. Because the contact points were distributed evenly in spherical coordinates (r_cp, θ_cp, φ_cp), they were not distributed evenly in Cartesian coordinates. The points were denser at smaller values of r_cp and at higher values of φ_cp. Therefore, the median errors over the space of contact points were calculated by weighting the data points by .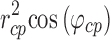

There is an additional subtlety when determining whether the solution found by the neural network is unique. Imagine that the forces and moments map to two different sets of (r_cp, θ_cp, and φ_cp) throughout a large portion of the force/moment space, meaning that the mapping is nonunique. But now imagine further that one (r_cp, θ_cp, φ_cp) set is dense, involving the majority of contact points, whereas the other (r_cp, θ_cp, φ_cp) set is sparse, having relatively few points distributed within the force/moment space.

In this imagined scenario, there will be extensive and obvious overlap of the monochromatic surfaces in the mapping visualization, similar to the surfaces shown in Figure 6a in the Results section. However, because the dense (r_cp, θ_cp, φ_cp) set contains more points, the neural network will converge on this set. Consequently, the neural network will return small errors for the large number of data points in the densely populated (r_cp, θ_cp, φ_cp) set and return large errors only for the small number of data points in the sparse set. When averaged, it is entirely possible that the total error could be below the uniqueness thresholds established for the three variables (r_cp, θ_cp, φ_cp), despite the nonuniqueness permeating a large fraction of the mapping.

It is for this reason that we required a mapping to be unique by visual inspection as well as below the error threshold to be formally declared unique.

For each of the four whisker profiles, we tested the 20 different triplet combinations of force and moment for uniqueness. We also tested each of these combinations for uniqueness by using only subsets of the mappings (e.g., small angle deflections, concave forward only, etc…), as will be described further in the Results section. These uniqueness results are tabulated in Table 2.

Table 2.

Conditions in Which Each Mapping for Each Whisker Profile Is Unique

	Inputs			When is the mapping unique?
	1	2	3	Curved, tapered	Curved, cylindrical	Straight, tapered	Straight cylindrical
1	Fx	MB	MD	All	CF	All	not unique
2	Fx	MB	FD	ELD	ELD CF	ELD	not unique
3	Fx	FT	MD	ELD CF	ELD CF	ELD	ELD
4	Fx	FT	FD	ELD	ELD CF / ELD CB	ELD	ELD
5	FT	MB	MD	ELD CF	ELD CF	ELD	ELD
6	FT	MB	FD	CB**	ELD CB	ELD	ELD
7	Fx	MB	FT	not unique	not unique	not unique	not unique
8	Fx	MD	FD	All*	ELD CF* / CB*	not unique	not unique
9	MD	MB	FD	All*	All*	not unique	not unique
10	FT	MD	FD	All*	ELD* / CF* / CB*	not unique	not unique
11	Mx	MD	FD	All*	CB	not unique	not unique
12	Mx	MB	MD	All*	All*	not unique	not unique
13	Mx	MB	FD	CF*	ELD CF*	not unique	not unique
14	Mx	FT	MD	ELD CF*	ELD* / CF*	not unique	not unique
15	Mx	FT	FD	ELD CF*	ELD CF*	not unique	not unique
16	Mx	Fx	MD	not unique	ELD* / CB*	not unique	not unique
17	Mx	Fx	FD	CB*	not unique	not unique	not unique
18	Mx	MB	FT	ELD CF	ELD CF	not unique	not unique
19	Mx	MB	Fx	CB / CF	not unique	not unique	not unique
20	Mx	Fx	FT	not unique	not unique	not unique	not unique

Cells marked “All” mean that the mapping is unique for the entire contact point space, and cells marked “not unique” mean that the mapping is not unique. Cells marked “ELD” mean that the mapping is unique when large deflections are excluded, and cells marked “CF” or “CB” mean that the mapping is unique when only concave-forward or concave-backward contact points are considered. Cells marked “ELD CF” mean that the mappings are unique only when concave-forward points are included and large deflections are excluded. Similarly, cells marked “ELD CB” are unique when only concave-backward points are included and large deflections are excluded. Cells that are split by slashes had multiple conditions under which the mapping became unique. For example, the way to read Row 4 of the table is that if it is known that the whisker is in the CF region, or it is known that the whisker is in the CB region, then the mapping is unique if large deflections are excluded. If it is not known whether the whisker is in the CB or CF region, then the mapping is not unique. ^*The mapping is nonunique only in the x-y plane. ^**The mapping is nonunique in the curved surface that defines the crossover to large angle deflections.

CF, concave forward; CB, concave backward; ELD, excluding large deflections.

Two nonunique mappings for a straight, cylindrical whisker required a different approach to determine uniqueness, and they are shown in rows 1 and 2 of Table 2 of the Results section. The mapping in row 1 is based on the axial force (F_x), the magnitude of the bending moment (M_B), and the direction of bending moment (M_D); the mapping in row 2 is based on F_x, M_B, and the direction of the transverse force (F_D).

Initial results of the neural network analysis demonstrated that both of these mappings had regions of uniqueness, but the equivalent two-dimensional (2D) version of these mappings had previously been shown to be nonunique.¹¹ Visual inspection was inconclusive. To resolve this matter, we used Equations (5.1)–(5.9) from Mattiasson, 1979,²⁶ which describe the contact point location for an applied load (Fig. 1a). Solving these equations in Mathematica™ showed that the same values of the mechanical signals could be associated with entire families of contact points, verifying that these two mappings were nonunique.

Finally, we note that occasionally mappings contained small, highly localized regions of nonuniqueness but had acceptable median errors, and they were classified as unique. For example, all mappings for curved, cylindrical whiskers that include both M_D and F_D (lines 8–11 of Table 2 in the Results section) contain a small region of nonuniqueness in the concave-forward collision regime when θ_cp is positive. These are regions in which the whisker is being “straightened out” in the top-down view. Nevertheless, errors were small enough for the average error to be passed within the acceptable limit and the mapping to be still classified as unique. As a result, though, in Figure 7, we chose to present the mapping that contains M_x instead of F_D because of this nonunique region.

Results

Problem statement: What combination(s) of mechanical signals at the whisker base uniquely identify contact point location?

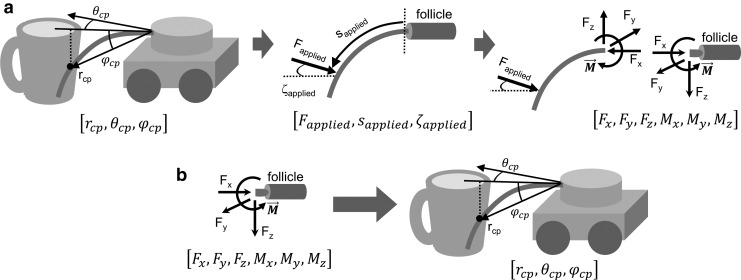
Deflection of a whisker against an object typically generates a single point of contact. We describe this contact point by using slightly nonstandard spherical coordinates (r_cp, θ_cp, φ_cp), as shown in the left panel of Figure 2a. These coordinates differ from standard spherical coordinates only in that φ_cp is measured from the x-y plane instead of from the positive z-axis. The point of contact exerts an external point force on the whisker, which is described by (F_applied, s_applied, ζ_applied) as illustrated in the middle panel of Figure 2a. F_applied is the magnitude of the applied force, s_applied is the arc length from the whisker base to the location of the applied force, and ζ_applied is the orientation of the applied force about the axis of the whisker. Because this study assumes frictionless conditions, the applied force is always perpendicular to the axis of the whisker.

FIG. 2.

Graphical depictions of a 3D contact point location resulting in mechanical signals at the whisker base and a mapping of the inverse. (a) Elastica3D finds the forces and moments at the whisker base given the 3D contact point location. When a whisker contacts an object, it generates a single contact point between the whisker and the object (r_cp, θ_cp, φ_cp) (left panel) and a point force on the whisker (F_applied, s_applied, ζ_applied) (center panel). Elastica3D can be used to compute the resultant forces and moments at the whisker base (F and M) (right panel) and has been the subject of several previous studies.^19–21 (b) The goal of the present work was to use Elastica3D to invert the process described in (a), in other words, to determine the 3D contact point location given various combinations of forces and moments at the whisker base.

The applied force creates reaction forces and moments at the base of the whisker, as illustrated in the right panel of Figure 2a, which can then be sensed by mechanoreceptors within the follicle. Although forces and moments are generally expressed in Cartesian coordinates [F_x, F_y, F_z, M_x, M_y, M_z], the radial symmetry at the whisker base lends itself to expressing these mechanical signals in cylindrical coordinates [F_x, F_T, F_D, M_x, M_B, M_D]. F_x is the axial force directed along the axis of the whisker at its base. F_T is the magnitude of the transverse force, defined by 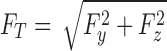; F_D is the direction of this transverse force about the axis at the whisker base, defined as 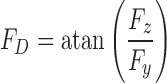. M_x is the twisting moment about the whisker's axis at its base; M_B is the magnitude of the bending moment, defined by 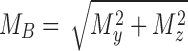; and M_D is the direction of the bending moment, defined as 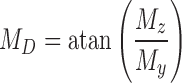. All these forces and moments are described in whisker-centered coordinates (see the Materials and Methods section).

As described in the Materials and Methods section, we used Elastica3D^19,20 to find these six forces and moments, F and M.

The central question of the present study involves inverting the process illustrated in Figure 2a and is schematized in Figure 2b. We aim at using forces and moments at the whisker base to determine the contact point location. Theoretical work has shown that the use of all six forces and moments uniquely determines contact point location.¹⁸ Therefore, we sought to reduce the dimensionality of the input by asking what combinations of three of these six mechanical variables map uniquely to the contact point location.

The reachable space for whiskers with different profiles (shapes)

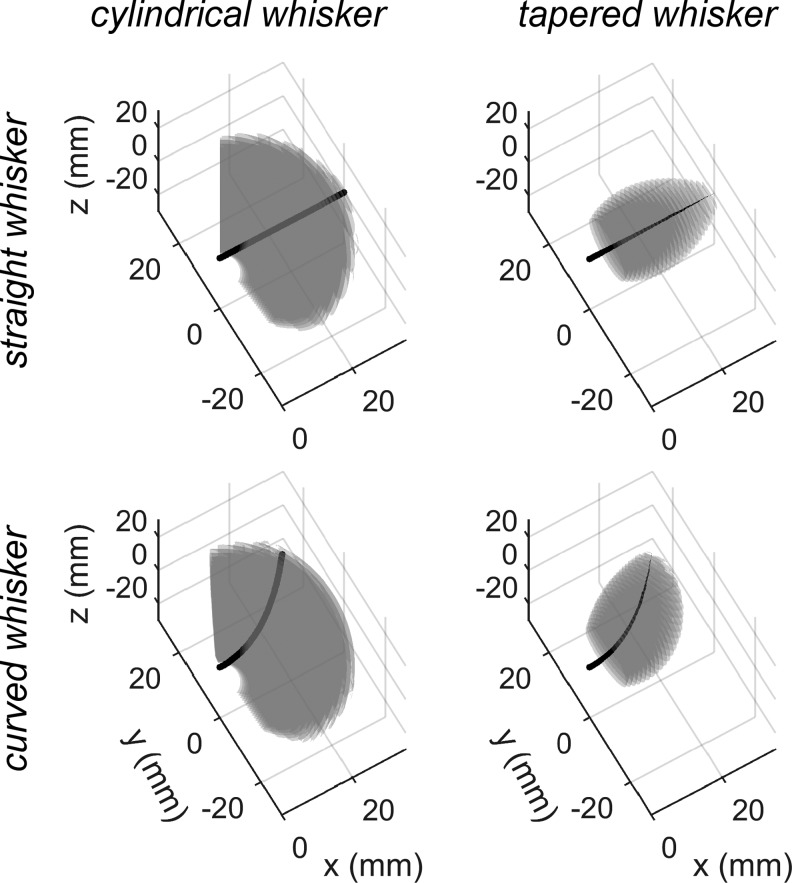
To investigate these mappings, we simulated deflections of the whisker to all contact points within its reach (see the Materials and Methods section) and determined forces and moments at the whisker base. Four different whisker profiles were simulated: straight cylindrical, straight tapered, curved cylindrical, and curved tapered. These profiles were chosen, because natural whiskers are curved and tapered, but straight and cylindrical whiskers are the easiest to construct in hardware for robotic applications.

The gray volumes shown in Figure 3 and Supplementary Video S1 (Supplementary Data are available online at www.liebertpub.com/soro) show the 3D contact point locations that each of the whiskers was able to reach before slipping off. The limits for whisker slipoff were identified as cases when the optimization in Elastica3D could not converge to zero.

FIG. 3.

Whiskers with different profiles (shapes) are able to reach different regions of the 3D contact point space. All subplots in this figure were created by drawing surfaces at each discrete radial distance value, which makes the edges of the workspace appear to have “ripples.” Each panel represents the (x, y, z) point cloud of contact point locations that are reachable by four whiskers with different profiles: straight cylindrical, straight tapered, curved cylindrical, and curved tapered. Note that the tapers are not drawn to scale; they are for illustrative purposes only. Supplementary Video S1 shows these four point clouds rotating in 3D.

The most striking feature of Figure 3 is that each whisker profile can reach very different regions of the 3D space. The curved whiskers have reachable spaces that curve with them, and the cylindrical whiskers can reach much larger regions, especially for more distal radial contacts. This effect occurs because cylindrical whiskers are stiffer near their tip than are tapered whiskers and therefore experience less deflection for the same contact point. The increased stiffness allows cylindrical whiskers to deflect much more before slipping off, revealing a distinct advantage of using cylindrical whiskers.

Mechanical signals at the base of each whisker

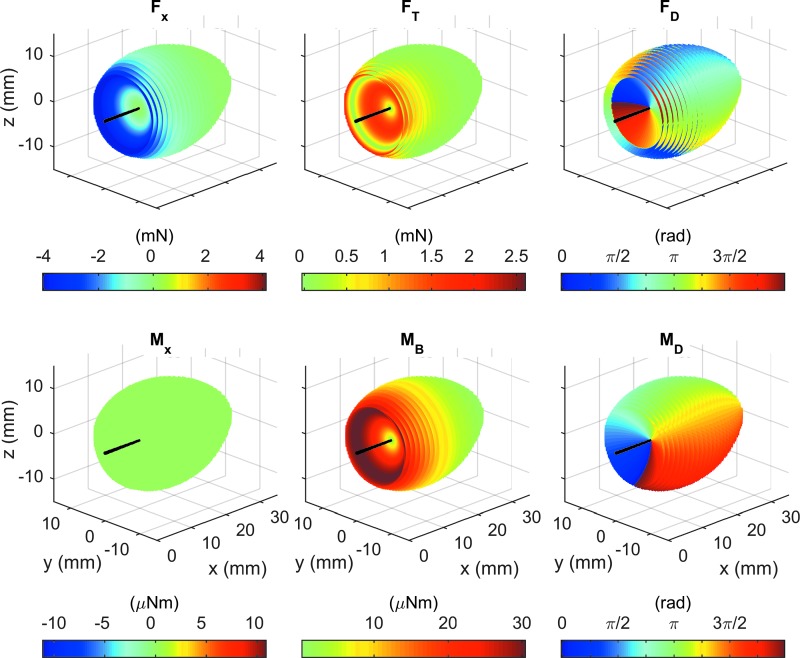
The next step is to determine the values of F and M for each of the contact point locations shown in Figure 3. Figure 4 and Supplementary Video S2 show these six forces and moments for the example of a straight, tapered whisker. This example was chosen because it highlights several important features of the relationships between mechanical signals and contact point location.

FIG. 4.

Trends in the spatial distribution of forces and moments can be observed when the 3D contact point locations are appropriately color coded, as shown for the example of a straight, tapered whisker. All of the panels in this figure replicate the spatial distribution of contact points shown for the straight, tapered whisker in the top right panel of Figure 3. However, instead of coloring the contact points gray, each panel color codes the contact points according to one of six mechanical signals at the whisker base, as indicated in the titles (F_x, F_T, F_D, M_x, M_B, M_D). Supplementary Video S2 shows these mapping clouds rotating in 3D.

The volumes in each subplot of Figure 4 are identical to the volume shown in the top right panel of Figure 3, but the gray point cloud has now been colored to represent each of the six mechanical signals at the whisker base. A number of key trends in the forces and moments are easy to observe for different contact point locations.

First, an obvious feature of Figure 4 is that M_x is zero for all contact points. This effect occurs because the whisker is straight. M_x is nonzero only for whiskers with intrinsic curvature. Therefore, for straight whiskers, M_x contains no information on contact point location.

Second, the magnitudes of F_x and M_B are the largest when both the radial distance of contact (r_cp) is small and the deflection angle is large. These mechanical signals are much smaller for distal contacts and small deflection angles. Note, however, that even though F_x and M_B share this trend, they are not proportional to each other because they follow different gradients.

Third, a sudden 180° change in F_D occurs as contact points deflect farther from the resting whisker. This inversion is visible as a “ring” of color change in the proximal contact points in the F_D subplot of Figure 4. The sudden change occurs because, at this angle of deflection, the whisker has bent so far that the applied force points directly in the negative x-direction. Past this point of deflection, the transverse force points in the opposite direction. M_D does not exhibit an abrupt transition because the bending moment does not change direction. Note that even with this flip, F_D and M_D always remain 90° offset from each other, which is true for all straight whiskers.

The point at which F_D flips by 180° marks the cutoff that defines “large deflections.” Although these large deflections are more numerous and more easily visible at proximal contact point locations, large deflections also occur at distal contact point locations. This cutoff occurs at a wide range of angles depending on the radial distance of contact, but most large deflections are found at a cutoff of over 40°.

The demarcation into large deflections is also visible in the F_T output as a “ring” of zero values. At these locations, the whisker is bent so that all the applied force acts in the x-direction.

The switch to large deflections is slightly different for whiskers with intrinsic curvature in that F_T does not become zero. However, F_D experiences a similar switch in direction, and large deflections remain easy to identify.

An example of a unique mapping: F_x, M_B, and M_D for a straight, tapered whisker

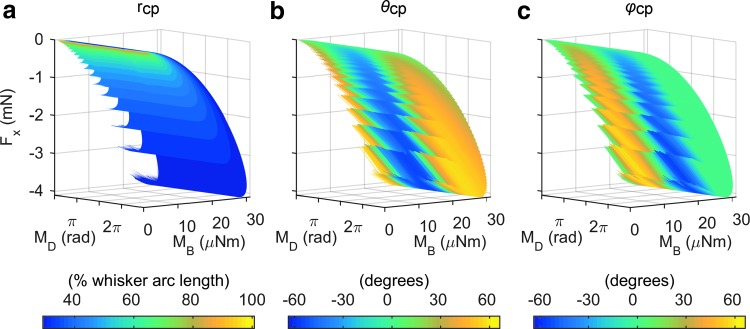
The next step in our analysis was to test different triplet combinations of mechanical variables to determine whether they generate a unique mapping to the contact point location, as described by r_cp, θ_cp, and φ_cp. A visualization of one mapping is shown in Figure 5 and Supplementary Video S3. The figure shows a mapping that uses F_x, M_B, and M_D for a straight, tapered whisker. We examine this mapping first because we recently showed—for the 2D case—that F_x and M_B at the base of a straight, tapered whisker uniquely determine r_cp and θ_cp for contact points in the x-y plane.¹¹ Adding M_D as the third mechanical variable is a natural 3D extension of this 2D mapping.

FIG. 5.

Visualization of the F_x, M_B, and M_D mapping for a straight, tapered whisker. The data points in the mappings are identical in all three panels: They represent the values of F_x, M_B, and M_D for all 3D contact point locations. As described in the text, the “solids” shown in the three panels of this figure are actually composed of a set of surfaces that have a resolution determined by the discretized steps in creating the mappings. Thus, although the data points in the three subpanels are identical, the shapes look different because they are constructed of monochromatic surfaces that “slice through” the solid differently. These surfaces are easier to visualize in Supplementary Video S3. The color code changes between the three panels: The left panel (a) is color coded to describe r_cp, the middle panel (b) is color coded for θ_cp, and the right panel (c) is color coded to describe φ_cp. This mapping is unique because the surfaces that make up each solid do not intersect each other. The “feathered edges” seen in all panels of this figure (particularly in the mapping for r_cp) are not scientifically relevant; they are caused by the discretization used when generating all F and M values. Running simulations at a finer resolution would generate smoother edges. Supplementary Video S3 shows these mappings rotating in 3D.

The visualization is created by plotting the values of three selected mechanical variables in a single 3D plot. The three subplots of Figure 5 all contain identical points; that is, each triplet of F_x, M_B, and M_D identifies a point (r_cp, θ_cp, φ_cp). Each subplot shows a multi-colored solid shape. For easier visualization (MATLAB cannot plot solids), the solids are plotted as a series of monochromatic surfaces; that is, each solid is sliced along a single color value. The surfaces are colored differently, based on r_cp, θ_cp, or φ_cp. For instance, one monochromatic surface in Figure 5a contains all contact points that have the same radial distance. Similarly, one monochromatic surface in Figure 5b contains all contact points that have the same value of θ_cp. These discrete surfaces are more easily visible in Supplementary Video S3.

Note that because the solids are sliced differently (according to r_cp, θ_cp, φ_cp), their shapes appear slightly different. In addition, data were generated at finer resolutions for θ_cp and φ_cp values than for r_cp, resulting in more monochromatic surfaces and a higher resolution for the two angular variables than for r_cp. The lower resolution of the r_cp mapping accounts for the apparent “step-like” gaps seen in Figure 5a.

Two important features can be observed in the mapping of Figure 5. First, although M_D contains no information about r_cp, it plays a large role in determining θ_cp and φ_cp. In Figure 5a, r_cp does not change along the M_D axis; however, in Figure 5b, c, both θ_cp and φ_cp change mostly along the M_D axis.

Second, M_B and F_x generally increase and decrease together. When both signals are large, r_cp is small, and either θ_cp or φ_cp is large. Conversely, when both M_B and F_x are small, both θ_cp and φ_cp are also small, but r_cp is unconstrained. This result can be observed on close examination of the top of Figure 5a, where all monochromatic surfaces converge to a line. Note that this feature is consistent with Figure 4, in that both M_B and F_x were largest at large deflections at small radial distances and smallest for large radial distances or small deflections.

The most important feature of a mapping is the extent to which it maps uniquely to contact point locations. A mapping is unique when one reading of the specified mechanical variables uniquely determines a single contact point location. If a mapping is unique, it can be used to identify contact point location, which is the first step toward feature extraction.

One method to determine mapping uniqueness is by visual inspection. A mapping is nonunique if any of the monochromatic surfaces that compose the solid intersect each other because such an intersection would demonstrate that a single reading of the mechanical triplet results in two or more different contact point locations. A careful visual examination of the F_x, M_B, and M_D mapping in Figure 5 indicates that it is a unique mapping, and it fell well within the error limit for uniqueness established by the neural network (see the Materials and Methods section).

It is important to keep in mind that although a given mapping depends on only three of the six mechanical variables, the remaining three mechanical variables cannot vary independently. For instance, in the unique mapping of Figure 5, it is impossible for F_T, F_D, or M_x to change without also altering the variables plotted on the axes, F_x, M_B, and M_D. In other words, because the mapping is unique, we can say that the variables F_x, M_B, and M_D fully define the whisker state, which includes r_cp, θ_cp, φ_cp, F_applied, s_applied, ζ_applied, the deflected whisker shape, and the remaining mechanical variables F_T, F_D, and M_x.

In contrast, for a nonunique mapping, an example of which follows, certain combinations of the three chosen mechanical variables—or sometimes all combinations of these variables—do not uniquely identify a contact point location or the complete whisker state.

Some nonunique mappings are unique in a subset of the contact point space

An example of a nonunique mapping, F_x, F_T, and F_D for a straight, tapered whisker is shown in Figure 6a. The left-most panel shows all the contact points used in the three other panels. Visual inspection immediately reveals that the monochromatic surfaces intersect. A reading of F_x, F_T, and F_D within the region of intersecting layers will result in two possible contact point locations. The insets to the mapping for radial distance show a different viewing angle so as to more clearly reveal the overlapping surfaces.

Because the mapping using F_x, F_T, and F_D was found to be nonunique for a straight, tapered whisker, we next searched for ways to make the mapping unique. We began by eliminating all contacts with large deflections, as determined by the points at which F_D flips direction by 180° (c.f., Fig. 4). These contact point locations are highlighted in red in the left-most panel of Figure 6b. When these points are removed, the mapping shown in the three other panels of Figure 6b contains no overlapping surfaces and is, therefore, unique. Thus, the F_x, F_T, and F_D mapping is unique for a straight, tapered whisker as long as large deflections are excluded. Supplementary Video S4 provides rotating 3D views of the panels in Figure 6.

An alternative approach to render a nonunique mapping unique is to consider either only concave-forward or only concave-backward contact points. Of course, this distinction can apply only to whiskers with intrinsic curvature. A concave-forward contact point is defined as one in which the whisker would have to collide concave forward into a point object to reach the contact point, and a concave-backward contact point is defined as one that would result from a concave-backward collision.³⁰ Concave-forward contact points generally create negative M_z bending moments. Conversely, concave-backward contact points generally create positive resultant M_z moments.

Different whisker profiles have different optimal mappings

In Figures 5 and 6, uniqueness was determined based only on a visual estimate of overlap. A more rigorous approach to quantifying uniqueness involves the use of a neural network (see the Materials and Methods section). We used this method to tabulate the regions of uniqueness for mappings of all four whisker profiles, as shown in Table 2. Boxes that are blacked out and contain the words “not unique” represent force and moment combinations that never resulted in unique mappings. All other boxes describe the conditions in which the mapping was determined to be unique.

Boxes marked “All” identify cases in which the mappings are unique when all possible contact points are considered. More commonly, boxes are marked “ELD” for “Excluding Large Deflections,” which indicates that the mappings are unique only when the large deflections are excluded. Boxes could also be marked as “CF” for “Concave Forward,” meaning that the mappings are unique when only contact points that are concave forward are included, or “CB” for “Concave Backwards,” meaning that the mappings are unique when only concave-backward points are considered. Only whiskers with intrinsic curvature can be marked “CF” or “CB.”

Mappings can also be marked with asterisks to indicate mappings that have an infinitesimally thin surface in 3D space where the mapping is nonunique. A single asterisk means that contact points in the x-y plane cannot be distinguished from one another, and two asterisks mean that contact points in the border space that marks the crossover into large deflections cannot be distinguished. However, since these areas of nonuniqueness are only infinitesimal curved planes, they hardly affect the mapping's overall uniqueness.

A comparison of mappings across Table 2 reveals some interesting trends. Straight whiskers have nonunique mappings in all cases when M_x is included (rows 11–20) because M_x for a straight whisker is always zero, as previously noted in Figure 3. The number of input dimensions to these mappings is thus reduced to two, which is insufficient to determine the 3D contact point location. Straight whiskers also have nonunique mappings in all cases when both M_D and F_D are used (rows 8–11) because these variables always differ by exactly 90°, again decreasing the input dimensionality.

Interestingly, the combination of M_D and F_D guarantees nonuniqueness for straight whiskers, whereas mappings that include these variables for a curved, tapered whisker are always unique for all contact points except for those in the whisker plane.

Another example in which the number of input dimensions is reduced can be seen in the mappings marked with a single asterisk (e.g., rows 8–17). In these mappings, which are nonunique in the x-y plane, two of the input signals have constant values when the contact point is in the whisker plane. F_D is either 0° or 180°, and M_D is either 90° or 270°. M_x will always be zero. Any mapping that has two of these three mechanical inputs is, therefore, nonunique in the whisker plane.

Most notably, the only mapping that is unique for all contact points without exception is the F_x, M_B, and M_D mapping for tapered whiskers. This indicates that this mapping would be the best to use for tapered whiskers to determine contact point location.

Optimal mappings for the four different whisker profiles

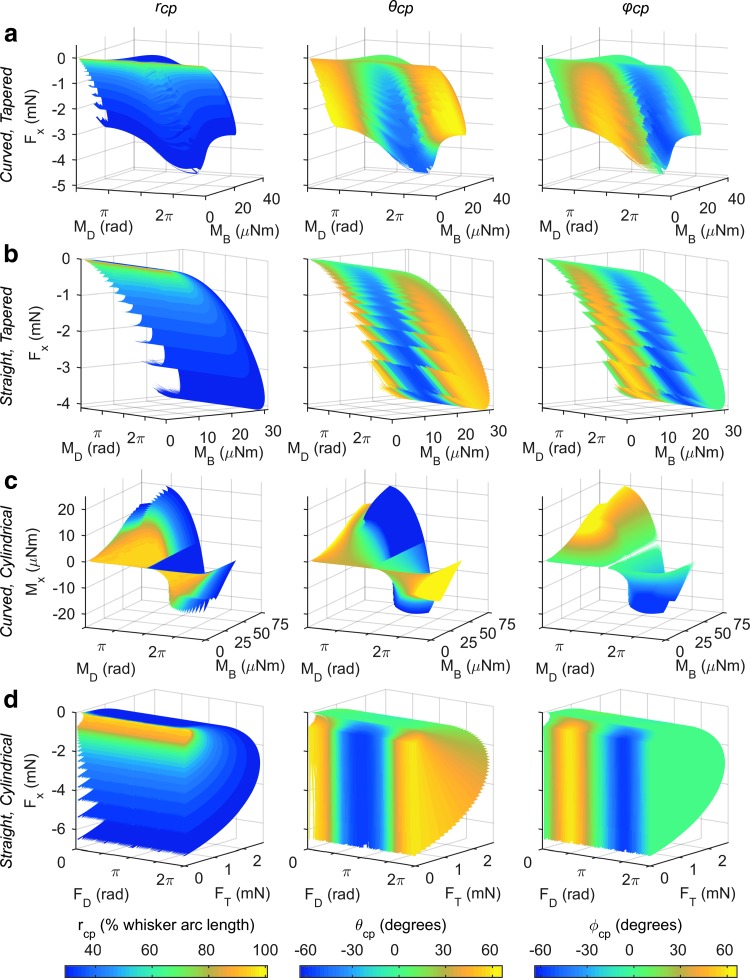
The results of the present work are summarized in Figure 7 and Supplementary Video S5, which illustrate the best mappings for all four whisker profiles.

For tapered whiskers, regardless of intrinsic curvature, the best mapping is F_x, M_B, and M_D, which is unique in all regions of the 3D contact point space. These mappings are shown in Figure 7a, b.

For cylindrical whiskers with intrinsic curvature, two mappings are unique for all contact points, except those in the whisker plane: (F_D, M_B, M_D) and (M_X, M_B, M_D), shown in rows 9 and 12 of Table 2. However, the mapping containing F_D contained a small region of nonuniqueness in the concave-forward collision regime (see the Materials and Methods section), so the mapping containing M_x is shown in Figure 7c.

For a straight, cylindrical whisker, no mapping was found that was unique for all contact points, but four mappings were unique when large deflections were excluded (rows 3–6 of Table 2). These four mappings had approximately similar shapes and performance. We have chosen one, F_x, F_T, and F_D, to be displayed in Figure 7d.

Discussion

Advantages and limitations of Elastica3D

The present work has explored how a thin, flexible cantilever beam (a “whisker”) can be used to determine 3D contact point location based on reading triplets of various mechanical signals at the whisker base. The work has also shown that the whisker profile has a profound effect on which combinations of forces and moments result in unique mappings. We chose to examine four whisker profiles—curved tapered, curved cylindrical, straight tapered, and straight cylindrical—because most whiskers found in nature are curved and tapered, but whiskers that are the easiest to construct (e.g., wire segments) are straight and cylindrical.

The whisker model used in this study, Elastica3D, was validated against analytic and FEM results and was found to contain only slight inaccuracies in determining contact point location for a given applied force (maximum error <1.5% whisker length). Because these inconsistencies varied systematically with arc length and the magnitude of the applied force, they are highly unlikely to affect the results of the present work.

The primary advantage of Elastica3D compared with other modeling tools is its speed and ease of use. Contact point mode of Elastica3D can take an undeflected beam and a desired contact point and solve for the necessary applied force (F_applied, s_applied, ζ_applied); such a computation is possible in ABAQUS but more difficult to achieve. In addition, the calculations for beam deflection are much faster in Elastica3D than in ABAQUS. Elastica3D can solve for a deflected beam shape and resultant forces and moments given an applied force in a fraction of a second, whereas the same calculation can take tens of seconds in ABAQUS.

Because Elastica3D is relatively fast and easy to use, we could rapidly create and analyze the mappings from mechanical signals at the whisker base to 3D contact point location, leading to several novel findings. Previous studies that have identified 3D contact point location for rigid and/or whisker-like probes have required all six components of force and moment to be measured at the whisker base.^17,18 This solution requires the use of a six-axis load cell, which is bulky and expensive. Using Elastica3D, we found that certain triplet combinations of these components are sufficient for unique 3D mappings.

Two limitations of the Elastica3D model are that it is quasistatic and assumes frictionless contact.

Because Elastica3D is quasistatic, the mechanical signals that are associated with transient dynamic effects after a collision would render incorrect contact point position readings from the mappings. Three ways to combat this effect are to use whiskers with high damping, to push slowly against objects, or to wait for dynamic effects to damp out before determining contact point location. Notably, recent behavioral work has demonstrated that rats press their vibrissae against surfaces for durations between 20 and 50 msec.^36,37 These durations exactly match those that are required to damp out dynamic effects.³⁸

As a frictionless model, Elastica3D generates a unique deflected whisker shape for a single contact point and thus returns a unique set of forces and moments at the base. In contrast, if friction is present, a single contact point can result in many possible deflected whisker shapes depending on the history of contact. The mechanical signals at the whisker base will therefore vary based on the contact history. Although friction will not significantly affect bending moment for small deflections for a straight whisker,¹³ it will change all other mechanical variables,^9,19,34 and the accuracy of all mappings is likely to be reduced. Frictional effects could be minimized by using whiskers with low friction coefficients and by avoiding long, sweeping contacts.

A caveat to the present work pertains to the determination of uniqueness for the different mappings. Although many mappings (e.g., those shown in Figs. 5–7) can be easily classified as unique or nonunique, other mappings are more difficult to assess for uniqueness. For example, the mappings for the curved, tapered whiskers in rows 8–11 of Table 2 had regions of nonuniqueness that were too small to warrant classifying the entire mappings as nonunique; their weighted median errors fell in the acceptable range. Other mappings had acceptable weighted median errors but had visual overlap that, though sparse, covered a significant portion of the mapping, and they were labeled nonunique. Table 2 provides expected uniqueness for each mapping, but researchers using these results to determine contact point location should examine the mapping carefully to be sure it satisfies application demands.

Expected generalization to whiskers with different geometric and mechanical parameters

The mappings in this study were created by using whiskers with parameters similar to those of a C2 rat vibrissa. Altering some of these parameters will perfectly scale the mappings and not affect uniqueness, whereas other parameters may alter the mappings and change their uniqueness.

Three parameters that only scale the mappings are Young's modulus, the radius at the whisker base, and the length of the whisker. Because Young's modulus has been taken as constant, it simply scales the moment and forces at the base. If the material responses were nonlinear or the modulus varied along the whisker, this simple scaling would not apply. Altering the radius of the whisker base scales the mappings as long as the base radius to tip radius ratio, R_base/R_tip, stays constant. Similarly, changing the length of the whisker will also only scale the mappings when r_cp is measured as a percent of whisker arc length.

Changing the base radius to the tip radius ratio of the whisker can have highly nonlinear effects on the mappings. It is easiest to imagine the changes associated with this ratio by examining Figure 7b, which shows the mapping of F_x, M_B, and M_D for a straight, tapered whisker. This figure shows several distinct monochromatic surface layers. Each layer corresponds to a different radial distance, and the layers are far enough apart from each other that the mapping is unique. In contrast, the same mapping for a straight, cylindrical whisker is nonunique because all of the layers fall exactly on top of each other. For this particular mapping, the degree of taper is related to the distance between the layers. In general, however, changing the taper can change the mappings in highly unintuitive ways.

The uniqueness of the mappings will also change with whisker curvature. Adding curvature to a whisker will result in nonzero values for M_x, potentially increasing uniqueness for the ten mappings that employ this mechanical variable (lines 11–20 of Table 2). Similarly, adding curvature to a whisker ensures that M_D and F_D no longer have a fixed offset, increasing uniqueness for the four mappings that contain both these variables (lines 8–11 of Table 2). For the remaining seven mappings (lines 1–7), further work is required to determine the extent to which the magnitude of curvature is a decisive factor in uniqueness.

Resolution of the mappings

How fine a resolution must a sensor have to obtain a particular accuracy for the estimate of r_cp, θ_cp, and φ_cp? The question of mapping resolution is complicated because a shift in the reading of any one mechanical signal will change all three r_cp, θ_cp, and φ_cp values. In addition, the magnitude of the change in r_cp, θ_cp, and φ_cp will depend on the point's location within the mapping; in other words, mapping resolution varies throughout the contact space. Examples can be seen in Figures 7a, b, and d. In these figures, small changes in the magnitude of a force or moment are associated with a larger change in contact point location when r_cp is large. Sensors measuring these forces and moments will require higher resolution to distinguish between r_cp, θ_cp, and φ_cp for distal, rather than proximal, contacts.

It is also important to keep in mind that although some mappings may technically be unique, they could include one or more regions where resolution demands are impractical. Mappings also run the risk of having too wide a range of required resolutions over the contact point space. Gain control could help ensure that whisker sensors navigate the tradeoff between ensuring fine-sensing capabilities in some regions without saturating in others.

Practical considerations

From an applications standpoint, it is essential to consider how easy it is to measure each mechanical variable. For instance, although the combination of F_D and M_D results in a unique mapping for a curved, tapered whisker, it is likely to be difficult to distinguish between these two signals at the whisker base. It will be similarly challenging to distinguish F_T from M_B. Although all six mechanical signals can be determined with a six-axis load cell,¹⁷ this is an expensive solution, may be difficult to implement at smaller scales, and does not exploit the triplet combinations found in the present work. Here, we evaluate the mappings found for each whisker profile through the lens of practicality.

For the straight, cylindrical whisker, four mappings are unique when large deflections are avoided (rows 3–6 of Table 2). The difficulty with these mappings, however, is that they all require F_T, which will be difficult to distinguish from M_B. A straight, cylindrical whisker would require a load cell to measure F_y and F_z to uniquely determine contact point locations.

By adding curvature to the cylindrical whisker, we obtain two mappings that are unique for all contact points except for those in the whisker plane (rows 9 and 12 in Table 2). These mappings present their own challenges, however, because one requires reading both M_D and F_D, whereas the other requires M_x. Simultaneous readings of M_D and F_D necessitate a six-axis load cell, and reading M_x would require a torque sensor.

For tapered whiskers, the mapping with the largest region of uniqueness is F_x, M_B, and M_D, which is shown in row 1 of Table 2. For both whisker profiles, it is the only mapping that is unique for the entire contact point space, without any exceptions. Furthermore, this mapping requires adding only a measure of F_x to the bending moment measurements that are already used by many artificial whisker sensors.^{12–15,17,33,35,39,40}

The conclusions from comparing results across these four different whisker profiles indicate that a tapered whisker is best for contact point localization, and they suggest that tapered whiskers may be essential for robots if they are to extract 3D object features.

Conclusions and future work

The present study demonstrates that—given quasistatic, frictionless conditions—three mechanical signals at the base of a tapered whisker are sufficient to determine the 3D location of a contact point with an object. Our results confirm and extend previous 2D results that demonstrated that one component of the bending moment and the axial force are sufficient to determine two coordinates (r_cp, θ_cp) of the contact point.¹¹

The only previous studies that have determined all three coordinates of the whisker-object contact point have either required a six-axis force-torque sensor at the whisker base¹⁷ or limited the contact location to the tip of the whisker.^16,41 One other study¹² determined contact point location in two dimensions for both tip and transverse contact, but it again required a load cell to distinguish the bending moment from transverse force. The present results demonstrate that two components of bending moment and axial force are sufficient to uniquely determine the 3D contact point location for a tapered whisker, regardless of its intrinsic curvature. Our results obviate the need for an expensive and bulky six-axis force-torque sensor, and they permit contact to occur anywhere along the whisker's length. Although tapered whiskers have been used in some robotic applications,^42,43 these studies have focused on control and search strategies rather than on contact point determination.

Our approach also stands in distinct contrast to earlier studies that have estimated the radial distance of contact (r_cp) based on the rate of change of bending moment as the whisker taps or sweeps against an object.^{13,14,33–35,44,45} This technique requires knowledge of how far the whisker has deflected against the object, requiring an encoder or a similar sensor to be placed on the actuator. In contrast, the present work shows that mechanical variables at every instant of time are sufficient to determine contact point location. Because the computation does not depend on the time history of the mechanical signals, the 3D contact point can be calculated at every instant of time as a whisker is increasingly deflected against an object. Rates of change of mechanical signals could then be used to sense object compliance or object motion.^9,11

The present work indicates the powerful potential of artificial whiskers as sensors. Robotic whisker systems could be used for high-fidelity tactual exploration to determine object contour and shape. These systems could be used as a complement to cameras and optical encoders for accurate navigation and exploration, particularly under conditions of darkness, glare, or fog. Potential applications include accurate instrument placement, hazard avoidance, and extraction of information about shape and surface texture.

The present results may also help guide the study of primary sensory neurons within the trigeminal ganglion.^31,46,47 If these neurons are found to encode the combinations of the mechanical signals identified here, the nervous system of the rat could exploit similar “mappings” to determine object location and contours.

Acknowledgments

This work was supported by NSF awards CAREER IOS-0846088 and EFRI-0938007 as well as NIH R01-NS093585 to M.J.Z.H. and J.W.R. L.A.H. received support from DoD, Air Force Office of Scientific Research, National Defense Science and Engineering Graduate (NDSEG) Fellowship, 32 CFR 168a. The authors would like to extend their thanks to Mr. SE Lin for constructing and conducting the FEM whisker simulations in ABAQUS, to Anastasia Mavrommati for helpful discussions and keen insights into how to validate mapping uniqueness, and to Dr. Todd Murphey for useful discussions.

Author Disclosure Statement

No competing financial interests exist.