Probabilistic Modeling of Reprogramming to Induced Pluripotent Stem Cells

Abstract

Reprogramming of somatic cells to induced pluripotent stem cells (iPSCs) is typically an inefficient and asynchronous process. A variety of technological efforts have been made to accelerate and/or synchronize this process. In order to define a unified framework to study and compare the dynamics of reprogramming under different conditions, we developed an in silico analysis platform based on mathematical modeling. Our approach takes into account the variability in experimental results stemming from probabilistic growth and death of cells and potentially heterogeneous reprogramming rates. We suggested that reprogramming driven by the Yamanaka factors alone is a more heterogeneous process possibly due to cell-specific reprogramming rates, which could be homogenized by the addition of additional factors. We validated our approach using publicly available reprogramming data sets, including data on early reprogramming dynamics as well as cell count data, and thus demonstrated the general utility and predictive power of our methodology for investigating reprogramming and other cell fate change systems.

Graphical abstract

eTOC

Liu et al. use probabilistic models to interrogate the dynamics of reprogramming from somatic cells to iPS cells. These studies demonstrate that the general two-type (or multi-type) birth-death-transition process is a useful mathematical framework to answer and raise important biological questions, such as inferring the reprogramming rate, whether cells are homogeneous in terms of properties including division rates, apoptosis rates and reprogramming rates.

Introduction

Somatic cells can be experimentally reprogrammed into induced pluripotent stem cells (iPSCs) through overexpression of the four transcription factors Oct3/4, Sox2, Klf4, and c-Myc (OSKM) (Takahashi et al., 2007; Takahashi and Yamanaka, 2006; Yamanaka, 2009). The reprogramming process usually takes weeks, yielding iPSCs at extremely low efficiency (Hanna et al., 2009; Hanna et al., 2007; Rais et al., 2013; Takahashi et al., 2007; Takahashi and Yamanaka, 2006; Yamanaka, 2009). Several efforts have improved the efficiency of the reprogramming process; for example, Hanna et al. (2009) reported that inhibition of the p53/p21 pathway or overexpression of Lin28 resulted in acceleration of reprogramming by increasing cell proliferation, whereas Nanog overexpression improved reprogramming in a cell-division independent manner. Subsequently, reduction of the methyl-binding protein Mbd3 during reprogramming was also shown to ensure that almost all responding somatic lineages form iPSCs within 8 days, consistent with a deterministic process (Rais et al., 2013). Similarly, another study argued that a subset of “privileged” somatic cells appear to acquire pluripotency in a deterministic manner, indicating a latent intrinsic heterogeneity within the starting population either prior to or following OSKM induction (Guo et al., 2014). Induction of C/EBPα in B-cells expressing OSKM provides another approach to activate the Oct4-GFP transgene in the majority of responding cells within a few days (Di Stefano et al., 2014). Most recently, two different studies optimized extrinsic conditions that facilitate iPSC formation from somatic progenitor cells within one week, thus avoiding the need for additional genetic manipulation (Bar-Nur et al., 2014; Vidal et al., 2014). For example, exposing somatic cells expressing OSKM to ascorbic acid and a GSK3-β inhibitor (AGi) was demonstrated to result in synchronous and rapid reprogramming (Bar-Nur et al., 2014).

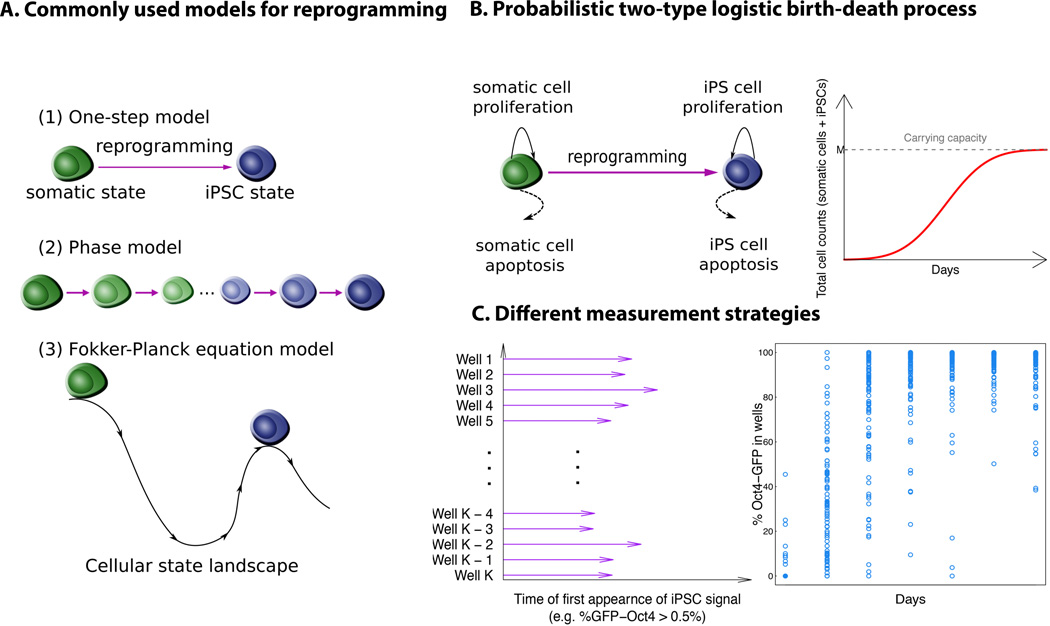
Mathematical modeling has been a valuable approach to better understand the reprogramming process. For example, Hanna et al. (2009) used a simple death process model to explain the dynamics under different conditions of reprogramming (Figure 1A). Cell cycle modeling previously used to describe isotype switching in immune system development, in particular B-cell development and lineage commitment (Duffy et al., 2012), can also provide a good fit to experimental data in the induced reprogramming setting using Mbd3 knock-down (Rais et al., 2013). In conditions using OSKM overexpression only, however, neither the cellcycle model nor a model assuming deterministic reprogramming can explain the complex lineage histories that lead to iPSCs (Rais et al., 2013). Alternatively, the iPSC dynamics can be explained with a phase-type model (Figure 1A) (Rais et al., 2013), assuming a finite number of intermediate phases between the initial somatic cell and the final iPSC state. In this type of model, the number of parameters linearly depends on the number of phases and their values are difficult to select using underlying biological knowledge; this model also ignored the effects of proliferation and apoptosis of different cell types on the population dynamics. However, it is difficult to interpret the number of phases inferred from this type of model and more difficult to verify such result experimentally. Lastly, from a statistical physics perspective, Fokker- Planck equations were also employed to construct the probability density function of the latency time to reprogramming, and then an inverse problem was solved to estimate the parameters from experimental data (Morris et al., 2014). Though these predictions led to a good fit to the data with out-of-sample validation, the choice of the functional form for the potential is quite ad hoc and not subject to experimental validation based on currently available technology (Figure 1A).

Figure 1. A schematic illustration and comparison between alternative modeling approaches.

A. Previous modeling approaches mainly include (1) a one-step process, in which the model considers the reprogramming event from a somatic cell state to the iPSC state as a single switch-like transition; (2) a phase-type model, in which the model assumes an unknown number of intermediate cellular states between the somatic cell and iPSC states; and (3) a Fokker-Plank equation-based model, which assumes a Waddington epigenetic landscape between different cellular states, derived using a potential function to establish transition barriers. B. A probabilistic logistic birth-death process that accounts for proliferation and apoptosis events of both the founding somatic and iPSC states, as well as the transition between states during reprogramming. The carrying capacity reflects the number of cells in the cultured plate at confluence without passaging. C. Previous modeling efforts to describe the reprogramming process primarily consider the time of the first appearance of Oct4-GFP⁺ signals in each well or colony by setting a binarizing score for reporter activation, and there is no universal standard for how to choose this threshold. Here we focus directly on the percent of Oct4-GFP cells in each well or colony as a measure of the percentage of iPSCs generated over time.

The framework of continuous-time birth-death processes (Parzen, 1999) provides an alternative perspective to describe cellular reprogramming, including essential elements of the dynamics such as cell growth, death, and cell fate change (i.e. transition). One advantage of the birth-death-transition process approach is that it appreciates probabilistic effects of division, death, and reprogramming on the final outcome, either represented by the distribution of first passage times or the percentage of iPSCs at a certain time point. Another advantage is that the birth-death-transition process helps us better understand the sources of the variation observed from the data. Here we designed a generalizable probabilistic model with simple and explicit interpretations of all parameters to explore alternative explanations of the dynamics of reprogramming. Using this approach, we explicitly modeled reprogramming dynamics to analyze the cell dynamic data from different experimental setups. We first utilized cell proliferation data from Bar-Nur et al. (2014) to parameterize the probabilistic model. We found that the use of a low and heterogeneous reprogramming rate, in the context of our mathematical model, could explain the OSKM data, while a high and homogeneous reprogramming rate recapitulated the OSKM + AGi results. Data from other sources (Rais et al., 2013; Vidal et al., 2014) were then used to further validate our approach and test its ability to also recapitulate early phase reprogramming dynamics (Hanna et al., 2009; Smith et al., 2010). A summary of the data used in this paper is listed in Table S1. Our approach allows quantification of reprogramming dynamics using the widely variable experimental setups of different studies (Table S1 and Figure 1A). For example, Rais et al. (2013) collected data on the first passage time of the percentages of Oct4-GFP signal in each well surpassing some threshold, whereas Bar-Nur et al. (2014) recorded the percentages of Oct4-GFP-positive cells in each well at several time points. In order to obtain as much information as possible from these types of experiments, we recommend collecting the full time course of the reprogramming signal instead of the first passage time only.

Our flexible approach provides a theoretical framework for describing cellular reprogramming under any condition. Importantly, it also establishes a quantitative method to compare between reprogramming systems. From a practical perspective, our modeling approach provides a platform to determine both the rate and homogeneity of any given cell fate conversion. Quantitative assessment of these parameters is particularly important for large-scale mechanistic studies that demand large cell numbers or for the design of differentiation protocols generating therapeutic cell types. For example, global transcriptomic or proteomic analyses often require bulk cell culture; our modeling approach could be used to identify reprogramming systems or time points well suited for these applications based on the reprogramming rate and its uniformity. Alternatively, such a model could be employed as an empirical standard to quantify the uniformity and kinetics of any given cell fate conversion under different conditions to optimize improved protocols or understand the contributions of specific growth factors. Thus, in addition to the more fundamental modeling role, we anticipate that our approach will be useful for mapping the precise molecular trajectories of somatic cells acquiring pluripotency and for identifying novel reprogramming intermediates.

Results

I. Induced reprogramming can be modeled as a two-type continuous-time Markov process

We began to explore the kinetics of iPSC generation by analyzing previous data obtained from a doxycycline-inducible, polycistronic reprogramming system (Bar-Nur et al., 2014). In this study, granulocyte-macrophage progenitors (GMPs) were exposed to doxycycline for varying time periods before scoring for activation of an OCT4-GFP reporter (Bar-Nur et al., 2014). Using this data set, we designed a two-type probabilistic logistic birth-death-transition process with a carrying capacity to model the dynamics of cellular reprogramming (Figure 1B). Such a process describes the growth and death of individual cells while the population as a whole initially expands exponentially but then reaches a maximum cell number, the “carrying capacity” due to the resource limitation of the in vitro cell culture system. In this model, we ignore any spatial interactions between different cells (Pour et al., 2015). The population of cells is composed of two different cell types – somatic cells and iPSCs, whose numbers at time t are denoted by X_S(t) and X_I(t), respectively. Initially, somatic cells and iPSCs proliferate with rates λ₁ and λ₂ and die with rates φ₁ and φ₂ per day per cell, respectively, when population sizes are sufficiently small such that they are not yet impacted by the carrying capacity. The maximum total number of cells for each well is M, i.e. X_S(t) + X_I(t) ≤ M if the culture is not split after the exponential growth phase. Therefore, as the population of cells increases, the growth pattern of cells depreciates according to the logistic function (see Materials and Methods). The reprogramming rate from somatic cells into iPSCs is given by γ per day per cell. In one infinitesimally small time interval, only the following events can occur: one somatic cell may divide or die, one iPSC may divide or die, or one somatic cell may transition to one iPSC; all other events have very small probabilities of occurrence. Detailed mathematical definitions are provided in Materials and Methods and SI. Without a carrying capacity, the numbers of cells at day 8 in the OSKM + AGi and at day 12 in the OSKM conditions are predicted to be much larger than M (Table S2), which is inconsistent with experimental results; therefore a carrying capacity was included in the model. All results considering carrying capacity shown in the main text are based on M = 100,000, but sensitivity analyses (see Supplementary Information, SI) demonstrated that perturbations of this and other parameters did not significantly change the dynamics. Our probabilistic model explicitly distinguishes the effects of cell growth, death and fate change on the reprogramming dynamics.

Using this approach, we then aimed to predict the percentage of iPSCs at time t. We approximated the expected proportion of iPSCs at a certain time point t as E[X_I(t)/(X_S(t) + X_I(t))] ≈ E[X_I(t)]/E[X_S(t) + X_I(t)] + g (E[X_S(t)], E[X_I(t)]) followed from multivariate Taylor expansion, where the form of g(E[X_S(t)], E[X_I(t)]) can be found in SI Equation (10). With the probability generating function for the process, we obtained a system of two coupled first order ordinary differential equations for the following quantities: κ₁(t) = E[X_S(t)], κ₂(t) = E[X_I(t)], κ₃(t) = E[X_S(t)²], κ₄(t) = E[X_I(t)²], κ₅(t) = E[X_S(t)X_I(t)] (see the SI for details and derivations). We then obtain:

$$\frac{d{k}_1(t)}{dt}=({\lambda }_1-{\phi }_1-\gamma )k_1(t)-\frac{{\lambda }_1}{M}(k_3(t)+k_4(t)),$$ (1)

$$\frac{d{k}_2(t)}{dt}=\gamma k_1(t)+({\lambda }_2-{\phi }_2)k_2(t)-\frac{{\lambda }_2}{M}(k_4(t)+k_5(t)),$$

where at time t = 0 (i.e., the start of the experiment), we have initial conditions κ₁(0) = 1, κ₂(0) = 0, κ₃(0) = 1, κ₄(0) = 0, κ₅(0) = 0. This system of differential equations was solved using the moment closure approximation (Murrell et al., 2004; Nasell, 2003) followed by Euler’s method to solve the approximate system of differential equations numerically (Smith, 1965); the complete formula for this system of differential equations involving higher-order moments as well as the R code for solving such systems can be found in SI Equation (9). To demonstrate the utility of this analytical approximation and the numerical method, we examined the consistency between the analytical approximation and exact numerical computer simulations of the process and concluded that the analytical approximation is sufficiently accurate to be used in our setting (Figure S1). The utility of this approximation is to aid in our parameter estimation procedure (Materials and Methods). Unfortunately, no approximation of the variance of the iPSC proportion Var[X_I(t)/(X_S(t) + X_I(t))] is available, and therefore this quantity was investigated based on computer simulations (Materials and Methods).

II. Mathematical modeling reveals different modes of reprogramming dynamics

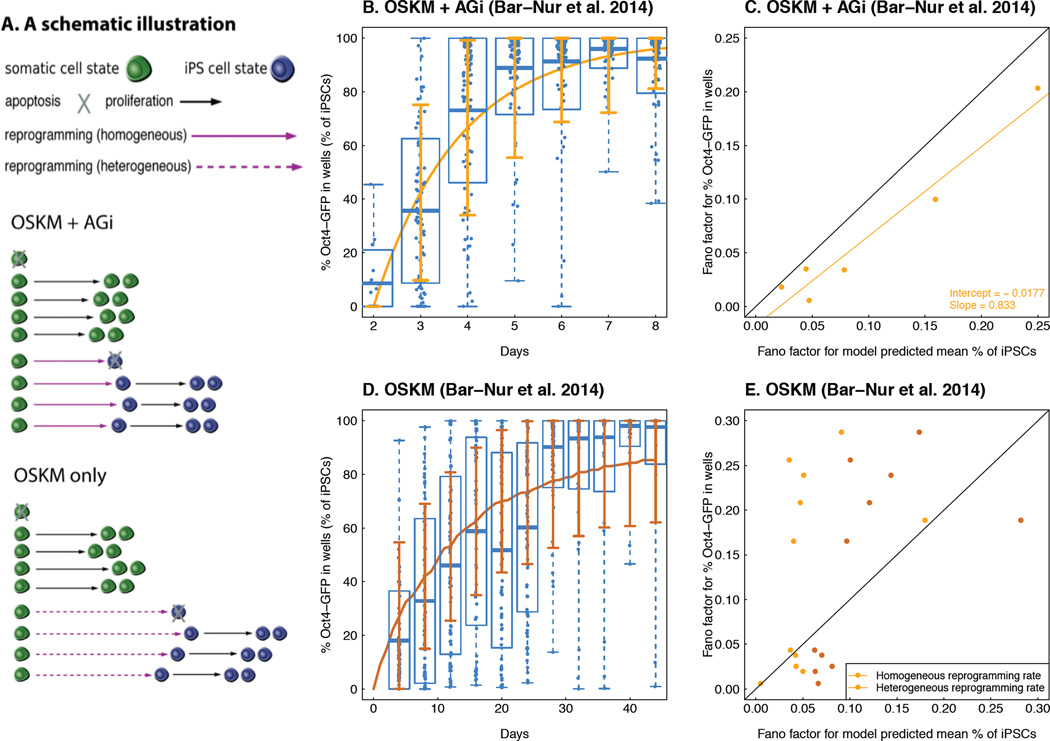
We then utilized our mathematical model to analyze the time-course Oct4-GFP percent data from Bar-Nur et al. (2014) with the goal of studying the dynamics of reprogramming under two growth conditions: somatic cells cultured in the presence of ascorbic acid and a GSK3-β inhibitor in addition to ectopic expression of the OSKM factors (the “OSKM + AGi” condition) and cells cultured with OSKM overexpression alone (the “OSKM” condition, Figure 2A). We first obtained the parameter values for the proliferation and apoptosis rates of somatic cells under these two conditions from the proliferation data provided in Table 1 (Materials and Methods); note that we do not provide a confidence interval for these estimates because the sample size is too small (n = 3). To this end, we counted the number of cells in wells of a 12-well dish at day 1 and day 2 as well as the percentage of live and dead cells. In particular, we used annexin staining with DAPI as a viability dye to determine cells that were apoptotic in order to directly estimate the apoptosis rate from the dead cell count. We then estimated proliferation and apoptosis rates together with the mean and standard deviation of cell counts at day 2 (Table 1). The net growth rate of iPSCs was calculated from an empirically derived iPSC doubling time of approximately 10.2 hours. However, since the cell doubling time might not be a very accurate way to estimate the proliferation rate, sensitivity analyses were conducted (SI). The apoptosis rate of iPSCs was considered equal to that of somatic progenitor cells. Sensitivity analyses to account for imprecise estimation showed that slight perturbations of the proliferation and apoptosis rates did not modify our results (Figures S3 – S5).

Figure 2. Probabilistic modeling of Oct4-GFP activation reveals distinct dynamics between the OSKM vs. OSKM + AGi conditions.

A. A schematic illustration of the modeling results. In both the OSKM and OSKM + AGi experiments, the proliferation and apoptosis rates for somatic cell and iPSC states are considered to be a fixed homogeneous variable. Due to the probabilistic nature of the model, the waiting time of cellular division and death are random variables, reflected by the variable lengths of the black solid (division) and dashed (death) arrows in the figure. In the OSKM + AGi experiment, a single reprogramming rate (0.55 per day) from the somatic cell to iPSC state best fit the data, which is greater than that estimated for the OSKM experiment (0.08 per day) and reflected by the overall shorter waiting time for successful reprogramming events or shorter purple arrows in the figure. In the OSKM + AGi condition, a fixed homogeneous reprogramming rate can recapitulate the variability observed from the data, whereas a fixed homogeneous reprogramming rate underestimates the variability in OSKM only. Instead, a log-normal distribution with mean 0.08 and standard deviation 0.75 recapitulates the variability observed in the latter, and this heterogeneity is reflected by the dashed purple arrows in the figure. B and D. A comparison between the model-predicted mean % iPSC trajectory (B: OSKM + AGi and D: OSKM condition; curves indicates mean % iPSC dynamics generated by analytical approximation in B or by 1,000 simulations in D; error bar corresponds to “mean ± s.d”, where standard deviations are based on 1,000 simulations) and observed Oct4-GFP % in each well over time (dots are the Oct4-GFP % in each well at each time point; in each box, the two ends of the dashed line are the maximum and minimum of the % iPSCs at each time point; the edges of the box correspond to the “mean ± s.d” of the % iPSCs computed from the data; and the horizontal line within the box is the mean % iPSC at each time point). In both experiments, we obtain a correlation between model prediction and observed data of above 0.95, indicating a good fit of our model. C and E. A comparison of the Fano factors (dispersion of the data over the mean) between the observed percent Oct4-GFP in each well and model prediction. The black line corresponds to the 45 degree “y = x” curve. In C, the yellow dots correspond to the Fano factors predicted from a homogeneous reprogramming rate 0.55 per day. In E, brown dots are Fano factors corresponding to a heterogeneous reprogramming rate drawn from a log-normal distribution with mean 0.08 per day and standard deviation 0.75, whereas yellow dots are Fano factors corresponding to the constant reprogramming rate with mean 0.08 per day.

Table 1.

The number of live cells on day 1 and day 2, together with the percentage of live and dead cells, and the estimated proliferation and apoptosis rates for GMPs in the OSKM and OSKM + AGi conditions (data from Bar-Nur et al. 2014).

	OSKM			OSKM + AGi
	Cell counts on day 1	Live cell counts on day 2	% Live cells at day 2	Cell counts on day 1	Live cell counts on day 2	% Live cells on day 2
Replicate 1	13,000	63,900	96.2	10,400	52,200	96.0
Replicate 2	11,700	66,600	92.6	10,100	58,200	88.3
Replicate 3	13,300	75,900	86.1	13,400	59,100	96.9
Mean	12,666.67	68,800	91.63	11,300	56,500	93.73
Standard deviation	850.49	6,295.24	5.12	1,824.83	3,751.00	4.73
Mean model prediction		69,223.00			55,927.98
SD model prediction		4,451.80			8,619.29
Proliferation rate for GMPs λ1		1.84			1.71
Apoptosis rate for GMPs φ1		0.09			0.06

We then estimated the reprogramming rate γ from the experimental data by identifying the value that minimized the mean squared difference between the model-predicted mean percentage of iPSCs and the experimentally observed empirical mean of the percentage of cells with the Oct4-GFP signal. For the OSKM + AGi condition, we used the first measurement as the initial time point because only 8 out of 96 wells showed any signal. Using the estimation strategy detailed in Materials and Methods, we identified γ = 0.55 day⁻¹ (with 95% confidence interval [0.50, 0.61] day⁻¹ obtained from a nonparametric bootstrap (Efron and Tibshirani, 1993) in the OSKM + AGi condition. Next, we evaluated the consistency for the model prediction compared to the data using the maximum squared distance between model-predicted mean and sample average proportion of iPSCs over all six measurement occasions (0.0074), and found a correlation coefficient of R² = 0.99, suggesting consistency between the model predictions and the observed data (Figure 2B). The relative overestimation of the model-predicted iPSC percentage on day 2 could potentially be explained by the results in Smith et al. (2010). Furthermore, to evaluate whether the model-based variability of the percentage of iPSCs at each time point was significantly different from the empirical variability, we calculated both the model-based and empirical Fano factors (defined as the ratio between the variance and mean) and performed a linear regression (adjusted R² = 0.9386), finding that the intercept of the linear regression output (−0.0177 with standard error 0.0122) was not significantly different from zero and the slope was not significantly different from one (0.833 with standard error 0.0947) (Figure 2C); we thus demonstrated that in the OSKM + AGi condition, the model prediction does not underestimate the variability of the observed data. These findings indicate that, even when assuming constant proliferation, apoptosis, and reprogramming rates across time and individual cells, the level of variability observed in this condition can be determined by the probabilistic nature of the model itself, and is not necessarily due to any heterogeneous properties of the cells or reprogramming process themselves.

We then sought to utilize the same approach to analyze data from the OSKM condition (Figure 2D). Using constant per-cell proliferation, apoptosis and reprogramming rates, we found that the reprogramming rate for the OSKM condition (γ = 0.080 day⁻¹ with 95% confidence interval [0.073, 0.088] day⁻¹ again computed from a nonparametric bootstrap) was significantly lower (p-value < 0.05) than for the OSKM + AGi condition (γ = 0.56 day⁻¹ with 95% confidence interval [0.50, 0.61] day⁻¹), indicating that AGi exposure induces a dramatic increase in reprogramming efficiency (Figure S2A and Figure 2B). Similarly, we evaluated the consistency of the model prediction compared to the data using the maximum squared distance between the model-predicted mean and the average proportion of iPSCs over all eleven measurements (0.045, mainly driven by the fifth (day 20) and sixth (day 24) measurements during which the cell culture was split randomly; when removing these two points, the maximum squared distance was 0.0025), and correlation coefficients (R² = 0.96) (Figure S2A). We also found similar proliferation and apoptosis rates between the two conditions, which are thus unlikely to contribute significantly to the different reprogramming efficiencies between them (Table 1). Interestingly, the model-predicted variability did not provide as good a match to the data in the OSKM condition as in the OSKM + AGi condition. A visualization of Fano factors between the model prediction and the data demonstrates that only four time points out of eleven are localized on or below the 45-degree line (Figure 2E and Figure S2B). We decided not to evaluate the linear model between predicted and empirical Fano factors in this comparison because of lack of fit of linear regression (adjusted R² = 0.06). In addition, the average squared distance between model-based and data-based Fano factors in the OSKM condition is 0.0140, which is larger than that in the OSKM + AGi condition (0.006). There exist multiple explanations for the underestimated variability by the model. Measurement errors in the GFP read-out could be one possibility. However, to estimate the measurement errors, more experimental data obtained in different laboratories is necessary. Here we proposed another biologically plausible possibility – if the reprogramming rate γ is a heterogeneous random variable instead of a homogeneous constant, the underestimation can also be compensated. As an example, considering a lognormal distribution of γ in the OSKM condition, we identified the parameters (a log-normal distribution with mean 0.08 and standard deviation 0.75) such that the variance of the model prediction based on 1000 simulations matched the empirical data with mean squared distance 0.007 (Figure 2E and Figure S2). The maximum squared distance between simulation-based and data-based mean % iPSCs was 0.035 (when not considering days 20 and 24, decreasing to 0.01). A similar Fano factor comparison (Figure 2E) showed that more than half of the data points were located below the 45-degree line, suggesting that a heterogeneous reprogramming rate can capture the variability observed in the data better than a homogeneous reprogramming rate.

It is possible that a heterogeneous proliferation and/or apoptosis rate can also contribute to the increased extent of variability observed in the experiments compared to the model prediction. For instance, Figures S4–S5 show that a heterogeneous proliferation or apoptosis rate can also provide model predictions with a good fit for the data in terms of both mean and variance time trajectory, and hence the source of extra variability must be identified using additional data. We thus used the proliferation data (Table 1) and compared the model predictions, based on different assumptions about the variability of the proliferation and death rates, to the experimental data (Table S3 and S4). These investigations indicate that the proliferation and/or apoptosis rates are not heterogeneous, hence supporting a heterogeneous reprogramming rate in order to explain the data if assuming that the additional variability is due to a heterogeneous property of the cells themselves. Together, these observations might suggest a heterogeneous reprogramming process in the OSKM condition but a homogeneous process during OSKM + AGi treatment when using GMPs as starting cells. However, other possibilities are still possible, such as measurement error or lineage priming. We also performed sensitivity analyses based on analytical approximations to test the robustness of our results; we obtained consistent results when considering data variability such as potential counting inaccuracies and insufficient data to estimate the iPSC apoptosis rate (Figure S3). Finally, we performed sensitivity analyses for the OSKM condition by changing the magnitude of proliferation and apoptosis rates of iPSCs but fixing the net growth rate of iPSCs to test whether that approach would increase the intrinsic variability of the reprogramming dynamics when considering a homogeneous reprogramming rate. Figure S6A and Figure S6B shows that even when increasing the apoptosis rates of iPSCs from 0.1 to 1.0, the empirical variance was still underestimated. We want to again emphasize that such additional analyses cannot rule out other possibilities, without further experiments.

III. The probabilistic two-type logistic process modeling reprogramming dynamics has predictive power

One criterion for evaluating the generalizability and utility of a quantitative model is to evaluate its out-of-sample predictive power (Gelman and Hill, 2006). To this end, we first used a subset of time points from the experiments in Bar-Nur et al. (2014) to predict the iPSC trajectories, in an approach similar to that used in Morris et al. (2014). We then investigated whether the model predictions based on a subset of time points was similar to that based on all time points. In the OSKM + AGi condition, the estimated reprogramming rate based on only the first three out of seven time points (0.52 day⁻¹) was similar to the estimate using all time points (0.55 day⁻¹) (Figure S6 C–E); in the OSKM condition, we observed similar results (Figure S6 F–I).

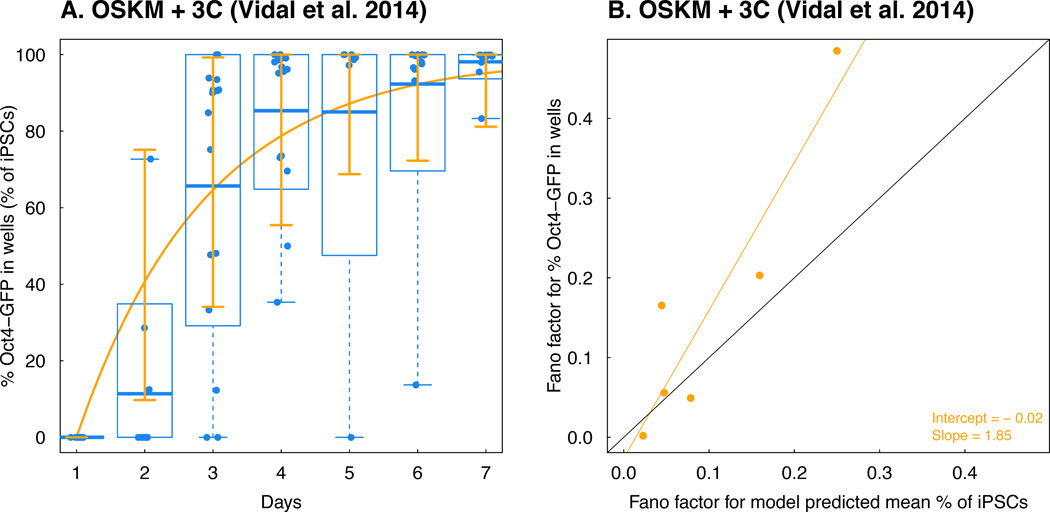
We next aimed to evaluate the model with an independent dataset (Vidal et al., 2014) in which somatic cells were exposed to either OSKM overexpression alone or in combination with ascorbic acid treatment, TGF-β inhibition, and GSK3-β inhibition. There was insufficient data available for the OSKM experiment to evaluate the model fit; the other growth condition, however, was amenable for analysis. We thus compared this dataset with the model prediction using parameters obtained from the investigation of data from Bar-Nur et al. (2014) and achieved an excellent fit (R² = 0.96, Figure 3A). We also estimated the reprogramming rate (0.52 per day, with confidence interval [0.42, 0.61]) from this new dataset, which is very similar to the one estimated from the OSKM + AGi experiment. Our model thus has significant predictive power when applied to independent datasets. In addition, when comparing the Fano factors calculated from model predictions and the data (Figure 3B) using linear regression (adjusted R² = 0.81), we found again that the intercept was not significantly different from 0 (−0.02 with standard error 0.050) and the slope was not significantly smaller than 1 (1.85 with standard error 0.40) respectively, indicating that a constant reprogramming rate can capture the variability of the observed data.

Figure 3. Model validation using time-series Oct4-GFP % in different colonies.

A. A comparison between the model-predicted mean percent iPSC trajectory using the data in the OSKM + AGi experiment from Bar-Nur et al. 2014 and observed percent Oct4-GFP in each colony over time in the OSKM + 3C experiment from Vidal et al. 2014. Again, we obtain a correlation between the observed data and model prediction > 0.95. B. Comparison between Fano factors of percent Oct4-GFP in each colony over time in the OSKM + 3C experiment from Vidal et al. 2014 and model-predicted Fano factors based on data from the OSKM + AGi experiment from Bar-Nur et al. 2014. The black line corresponds to the 45 degree “y = x” curve.

IV. The probabilistic two-type birth-death process can model the first appearance time of the iPSC signal

Aside from collecting the time-series percentages of certain markers (such as Oct4-GFP or Nanog-GFP) representing the level of iPSC formation, another common approach is to measure the time of the first appearance of some signal of these markers across multiple replicates (wells or colonies) (Hanna et al., 2009; Rais et al., 2013) (Figure 1C). We thus also utilized the multi-type birth-death-transition process to analyze such datasets (Hanna et al., 2009; Rais et al., 2013) to further demonstrate the generalizability of our approach. We did not consider a carrying capacity due to the frequent plate splitting in the experiments (Hanna et al., 2009; Rais et al., 2013), which is nearly equivalent to our logistic birth-death process when M becomes very large (SI). To find out the first passage time when the percentage of iPSCs reached a certain threshold (0.5%), we performed Monte Carlo simulations to generate 1000 replicates for a range of reprogramming rates and searched for the rate that minimized the maximum squared distance between the simulation and the observed data over all measurements.

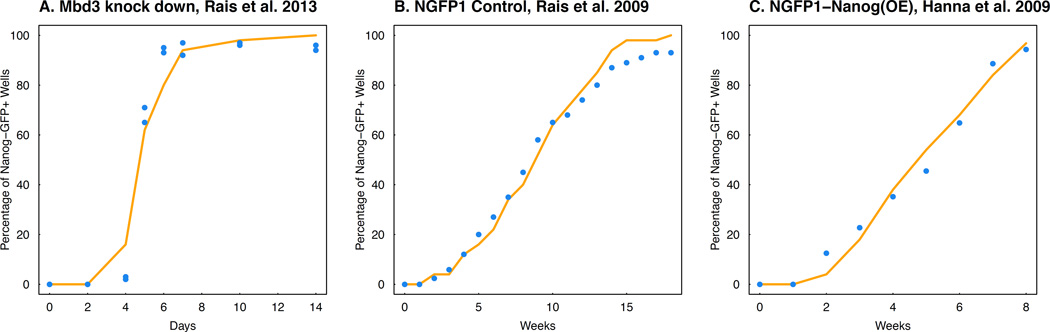
We first studied the Mbd3 knock-down experiment (Rais et al., 2013), which was interpreted by the authors to lead to a relatively fast and deterministic transition. Assuming exponential growth, the proliferation rate (0.853 day⁻¹) for MEF cells was directly estimated from the raw cell-doubling time (19.5 hrs) shared by the authors. Unfortunately, no other information was available to estimate the apoptosis rate. We found that a delayed constant reprogramming rate explained the data (Figure 4A, R² = 0.98 for both replicate experiments), where the delayed reprogramming rate was a step function equal to zero before day 1 and equal to 0.344 week⁻¹ after day 1. Otherwise, without this delayed effect, the predicted percentage of wells with more than 5% iPSCs at day 2 is larger than zero. Here we again used the procedure described in Materials and Methods by identifying the reprogramming rate that minimizes the maximum squared distance between the model prediction based on the simulation and the experimental data. Such delayed effects might be observed due to multiple reasons; it could be due to the detection sensitivity (Hanna et al., 2009; Rais et al., 2013), or because cells in culture need to pass through unobserved intermediate states before dividing or reprogramming. Unfortunately, there was no higher-resolution time-series data available to address such questions. Furthermore, we found that our multi-type birth-death-transition process model without delayed reprogramming can explain the relatively low efficiency NGFP1 control experiment (Rais et al., 2013) (Figure 4B, reprogramming rate is 8.57 × 10⁻⁶ week⁻¹, R² = 0.99) as well as the NGFP1-Nanog(OE) experiment performed by Hanna et al. (2009) (Figure 4C, reprogramming rate is 6.4 × 10⁻⁴ week⁻¹, R² = 0.99). A similar result is shown in Figure S7A–C for a heterogeneous reprogramming rate drawn from a lognormal distribution with standard deviation 0.75 and mean equal to the same estimated reprogramming rates as above. Unfortunately, the standard deviation could not be inferred due to insufficiently many replicates.

Figure 4. Modeling the time of first appearance of iPSC signals.

The figure shows the model-predicted percentage of replicates having surpassed a certain threshold of percent iPSC at each time point (red line) and the corresponding quantity measured from data (blue dots): A. NGFP1 Mbd3 knock down experiments; B. NGFP1 control experiment; C. NGFP1-Nanog^OE experiment.

V. The probabilistic birth-death-transition process can model the colony cell count data

We then collected data of three distinct cell fate types defined by Smith et al. (2010), in which cells were not selected for iPSC potency and were categorized into fast-dividing (FD), slowly-dividing (SD) and iPSC-forming lineages after doxycycline induction (Figure 5A). We observed that the cellular growth patterns satisfied an exponential growth model without reaching confluence (Figure 5B), and therefore used a linear birth-death process without a carrying capacity to model the cellular growth based on the cell count data described in Result IV. Since the cell count data over multiple time points for the three cell fates were measured retrospectively and conditional on lineage non-extinction, i.e. colony formation (Figure 5C), we first calculated the theoretical mean and variance of cell counts at different time points conditional on population non-extinction (SI). We then used the empirical mean and variance computed from the data halfway to the end of follow-up to estimate the growth and death rates of the three cell types (Table 2). Based on these rates, we then compared the model prediction and the empirical data in terms of both mean and standard deviation of the cell count trajectory over time (Figure 5B and 5C), demonstrating that our approach can also be used to model cellular growth data in this experimental setup. Finally, using the estimated birth and death rates for FD cells and iPSCs, and the estimated reprogramming rate for iPSCs (0.01 per day) from Pour et al. (2015) and for FD (~10⁻⁸ per day) from Hanna et al. (2009), we simulated the reprogramming dynamics for a mixture of FD cells and iPSC-forming lineages with the empirically determined mixture ratios of FD:iPSC = 6:58 and FD:iPSC = 6:19. Using this approach, we obtained lower predicted early-phase iPSC dynamics for admixtures as compared to homogeneous iPSC populations (Figure 5D). This population admixture effect captured in the early phase of reprogramming in Smith et al. (2010) and Pour et al. (2015) might explain the overestimation of our model prediction for the percentage of iPSCs in the earliest measured time points of the OSKM + AGi condition in Bar-Nur et al. (2014) (Figure 2B) and possibly also the overestimation of the model proposed in Hanna et al. (2009) for the early phase Nanog-GFP+ well percentages.

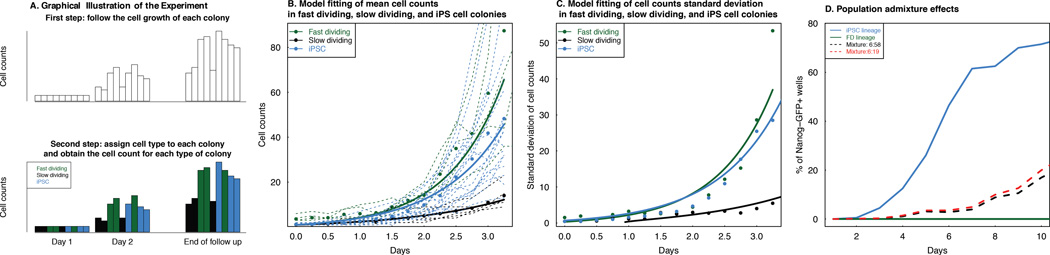
Figure 5. Validation of the model utility when cell count data is available.

A. A schematic description of a lineage tracing experiment (Smith et al. 2010) that assigned different morphological responses to OSKM induction in a standard reprogramming experiment using clonally inducible fibroblasts (fast dividing or FD, slow dividing or SD, and iPSC-generating, iPSC). Initially, labeled cells are tracked over time. Then, conditioning on colony formation or non-extinction, cell lineages are retrospectively assigned as FD (green), SD (grey), or iPSC (blue) and characterized as distinct groups. B. The mean cell count dynamics of FD, SD and iPSC are accurately described by our model. Since in the experiment no confluence was observed, the carrying capacity is set to infinity. The model prediction (lines) fit the observed cell counts very well (correlation above 0.95 in all three types of cells). Solid line: model-predicted cell counts over time; Dots: mean cell count dynamics averaging over all colonies belonging to each cell type; Dashed lines: cell counts for each colonies obtained from the data. C. The standard deviation of cell count dynamics of FD, SD and iPSC are also consistent with our model. Again the correlation between model prediction and data is above 0.95 in all three types of cells. Solid Line: model-predicted standard deviation of cell counts over time; Dots: standard deviation of cell counts obtained from the data. D. Population admixture of FD and iPSC cells can decrease the iPSC level dynamics compared to a homogeneous iPSC population. Blue solid line: uniform iPSC population; green solid line: uniform FD population; black dashed line: FD:iPSC = 6:58 mixture; red dashed line: FD:iPSC = 6:19 mixture.

Table 2.

Growth and death rates with their 95% confidence intervals (based on nonparametric bootstrapping) estimated for FD, SD, and iPSC fates (data from Smith et al. 2010).

	Proliferation rate (day−1)	Apoptosis rate (day−1)
FD cells	1.724 [1.612, 1.836]	0.553 [0.441, 0.665]
SD cells	0.964 [0.825, 1.103]	0.330 [0.191, 0.469]
iPSCs	1.567 [1.454, 1.680]	0.483 [0.370, 0.596]

VI. Identification of the reprogramming dynamics for any culture condition

Finally, we sought to investigate the ability of our model to identify the reprogramming dynamics for any culture condition used in potential future studies. To this end, we tested the ability of our model to identify the reprogramming rates based on simulating realistic experimental settings. The input of our approach includes the proliferation and apoptosis rates of somatic cells and iPSCs, in addition to the time course trajectory of the percentage of iPSCs. We first examined whether our approach could robustly identify the reprogramming rate when the number of measurements during the experiment decreases. In Figure S7D, we compared the consistency between the identified reprogramming rates when very sparse measurements were performed. The correlation between the model prediction and the mean percentage of iPSCs from the simulation was approximately 0.96, suggesting that our method can be applied even when very few time points are available. We then explored two efficient hypothetical reprogramming regimes, one with a higher reprogramming rate and the other with a higher proliferation rate of iPSCs (Figure S7E), and found that our model was able to distinguish between these two situations and render model predictions consistent with the data (correlations of 0.99 and 0.97, respectively). We are thus very confident that our analysis approach will prove useful for the investigation of any future reprogramming experiments.

Discussion

Here we designed a two-type probabilistic logistic process model to investigate the dynamics of induced reprogramming from somatic cells into iPSCs. We found that this birth-death-transition process with a constant (or homogeneous) reprogramming rate can recapitulate the dynamics of iPSCs after exposure to chemical supplements in addition to OSKM overexpression from two independent datasets (Bar-Nur et al., 2014; Vidal et al., 2014). For experiments with only ectopic expression of OSKM, the same process applies but with a heterogeneous instead of constant reprogramming rate. Our investigations thus reveal two different modes of cellular reprogramming dynamics: OSKM expression alone leads to heterogeneous reprogramming while OSKM plus certain other factors homogenizes the dynamics.

Unlike previous methods focusing on statistics such as the first passage time (Hanna et al., 2009; Morris et al., 2014; Rais et al., 2013; Yan et al., 2014), our approach explicitly models the reprogramming rate and thus can be used to make direct computational inferences about the heterogeneity of cellular populations with regard to induced reprogramming. Furthermore, by carefully considering the effects of proliferation, apoptosis, reprogramming and the carrying capacity, we were able to identify differences in the reprogramming rate itself that resulted in the acceleration of reprogramming in the OSKM + AGi as compared to the OSKM condition. We further explored the source of variability leading to the increased variance observed in the OSKM data. However, due to lack of sufficiently many replicates and longer follow-up times when counting the cell numbers, further work is warranted to better assess the variability of cell growth and death in different conditions. It will also be necessary to conduct follow-up experiments to further address whether the additional variability comes from measurement error or heterogeneous cell population. In addition, the log-normal distribution of the reprogramming rate used in our paper is only one out of infinitely many possibilities based on the current data. A recent paper (Tran et al., 2015) also showed that combining ascorbic acid (AA) and 2i (MAP kinase and GSK inhibitors) can synergize reprogramming. Even though our modeling does not directly model the first passage time, it is not difficult to use our model to study such data (Figure 4). Since we can always transform the time course percent iPSC data into first passage time data, we argue for collecting time course percent iPSC whenever possible since such data allows for more detailed characterization of the reprogramming dynamics.

Although our current framework is promising for modeling induced reprogramming or more general cellular fate change phenomena, several caveats apply. First, we do not have enough information to distinguish between different OKSM systems. For instance, Hanna et al. (2009) used OSKM while Bar-Nur et al. (2014) used OKSM; however, we cannot directly compare the data because of different data collection processes employed by these two laboratories. As a result, we used the same terminology “OSKM” to indicate the overexpression of Yamanaka factors. Second, we estimated the parameters in the two-type model by minimizing the squared distance between the model prediction and observed data; an alternative inference strategy would include likelihood-based methods to obtain the maximum likelihood estimator with good statistical properties (Crawford et al., 2014). Though some recent advances have been reported (Ho et al., 2016), the tools needed to make inferences about the reprogramming rate in the two-type case, however, are currently unavailable. Furthermore, likelihood-based methods such as the EM algorithm are usually computationally intensive when applied to situations with population sizes at the scale of millions (Crawford et al., 2014). More carefully designed experiments (Dinh et al., 2014) and advanced technology to collect single cell as well as molecular data would also allow for better model design and parameterization. Another implication of our model is that there is a positive probability of acquiring pluripotency immediately after the start of the experiment, when AGi is added, which might suggest acceleration of the transition from an early population with a heterogeneous capacity of acquiring pluripotency towards a more deterministic or homogeneous process occurring later (Buganim et al., 2012). To delineate these possibilities and to retrace the early events in relatively fast regimes such as with addition of AGi, data needs to be collected frequently in the very early phases of the experiment. Also, when analyzing the data from Rais et al. (2013), we observed time-delayed reprogramming rates, especially in the relatively slow reprogramming regimes. These results might be partly due to the use of different biomarkers for tracing reprogramming events (Table S1), thus emphasizing the need to standardize approaches and biomarker usage in the field to enable a quantitative comparison of results and processes. Furthermore, it is possible that the ‘conversion to iPSC’ does not represent the immediate acquisition of all iPSC characteristics but rather the symmetrical transmission of iPSC competence to all subsequent progeny – i.e. the switch to deterministic acquisition of pluripotency after an initially probabilistic event (Buganim et al., 2012; Pasque et al., 2014; Polo et al., 2012; Polo et al., 2010).

To robustly test the assumptions and the consequences of the multi-type birth-death-transition process model exploited in this paper, experiments from different laboratories will be necessary to account for potential confounders such as batch effects of these cellular dynamic/kinetic experiments. Also, to test whether the assumption of the model listed in Materials and Methods, one need cell count measurements for more time points instead of two time points, to test the relation between the population cell growth and the current population size. In addition, to test heterogeneity in reprogramming rate vs. measurement error, the same 96-well plates experiment repeated multiple times will be important to infer the well-to-well variability in different “batches”. Our approach can further be extended to explicitly study the effects of cell cycle times on reprogramming dynamics. For instance, Guo et al. (2014) reported that fast cycling cells tend to reprogram more efficiently than slow cycling ones. To directly test such a hypothesis in our system, data on cell division kinetics for both fast and slow cycling cells are required together with data for dissecting the time-ordering between reprogramming and proliferation, but unfortunately such data is currently not available.

Apart from the probabilistic birth-death-transition process framework, several studies have explored different modeling perspectives for studying reprogramming dynamics (Duffy et al., 2012; Hanna et al., 2009; Morris et al., 2014; Rais et al., 2013; Yamanaka, 2009; Yan et al., 2014). Most of these directly model the reprogramming latency time. In this paper, we also demonstrated that the current probabilistic logistic birth-death-transition process model can be applied to study the latency time distribution by calculating, at each time point, the fraction of wells surpassing a certain threshold. However, to our best knowledge, there is no available standard of choosing such as threshold, and therefore we suggest that experimentalists collect the iPSC percentage for all wells rather than discontinuing to follow the dynamics when the signal first appears.

In summary, we have developed a new two-type probabilistic logistic birth-death model to interrogate the dynamics of transcription factor-induced reprogramming of somatic cells into iPSCs following different genetic or environmental perturbations by independent laboratories. We anticipate that our methodology will be applicable to other reprogramming systems utilizing different transcription factor combinations and cell fate conversion systems such as the reprogramming of epiblast stem cells into embryonic stem cells or cellular transdifferentiation. Likewise, our approach is useful for interrogating the dynamics of forward differentiation approaches using pluripotent stem cells.

Materials and Methods

Two-type stochastic logistic process

Our two-type stochastic logistic process is a continuous-time Markovian process – suggesting that (1) events can happen at any point in time (i.e., continuous time) and (2) the future state of the system is independent of the past when conditioning on the present (i.e. Markovian property). Our model contains two types of cells (somatic cells and iPSC), and each can divide and die with a certain proliferation and apoptosis rate, respectively. Furthermore, a somatic cell state can transition to an iPSC state, which then cannot change back into a somatic cell. The two-type stochastic logistic process is defined using infinitesimal transition probabilities (Equation (6) in SI). At time t, with X_S(t) somatic cells and X_I(t) iPSCs in the system, the following possible events may occur during the next infinitesimally small time interval Δt:

1. With probability λ_* · (1 − (X_S(t) + X_I(t))/M) · X_*(t) · Δt + o(Δt), one of the type-* cells (where * refers to either somatic cells or iPSCs) divides into two, where λ_* is the per-cell intrinsic proliferation rate when population sizes are sufficiently small such that they are not yet impacted by the carrying capacity. If the number of somatic cells is large then the probability of one somatic cell dividing is also large and this probability increases if the time interval becomes longer. The term (1 − (n + m)/M) penalizes the proliferation dynamics such that the total number of somatic cells and iPSCs does not exceed M. The term o(Δt) is an extremely small quantity compared to Δt;

2. With probability σ_* · X_*(t) ·; Δt + o(Δt), one of the type-* cells dies and the population size decreases by one;

3. With probability γ · X_S(t) · Δt + o(Δt), one of the somatic cells transitions to an iPSC and the size of the population stays constant;

4. The probability of no events in next Δt time interval is the complement of the sum of the above probabilities;

5. The probability of all other possible events is of much smaller order than Δt.

With the infinitesimal transition probabilities outlined above as a building block, we can derive important quantities such as the master equation, the probability-generating function, moment-generating function, sojourn time, and others (Taylor and Karlin, 2014). More detailed explanations can be found in the SI. Note that all rate parameters can in principle be time-dependent and random variables instead of constants.

Parameter estimation

To estimate the proliferation and apoptosis rates of somatic cells provided in Table 1, we first divided the real line into fixed size grids. We then searched within the grid to obtain a value of the proliferation rate that minimized the maximum squared difference over all measurements between the analytic approximation of the mean cell number trajectory predicted using the one-type probabilistic logistic process (details in Supplementary Materials) and the mean cell counts while assuming an apoptosis rate of 0. The mean cell counts were calculated from taking the product of the mean live cell counts and the mean live cell percentage from Table 1. Using this identified proliferation rate, we then chose the value of the apoptosis rate that minimized the maximum squared difference over all measurements between the analytic approximation and the mean live cell counts shown in Table 1. In particular, the proliferation rate estimator is of the form

$$\widehat{{\lambda }_{\iota }}={\mathit{\text{argmin}}}_{\lambda \in {ℝ}_{>0}}{\mathit{\text{max}}}_{k\in \{1,2,\cdots ,K\}}\left\{{\left(Ê\right(X_{*,\mathit{\text{live}}}(t_k))-Ě(X_{*,\mathit{\text{live}}}(t_k)))}^2\right\},$$

where Ê(X_*,live(t_k)) is the average live cell count of type-* cells at time t_k, and Ě(X_*,live(t_k)) is the model-based mean cell count for type-* cells at time t_k assuming no death rate. Here the initial cell count is set as the average cell count at day 1, listed in Table 1. The death rate estimator is of a similar form by plugging in $\widehat{{\lambda }_{\iota }}$:

$${\hat{\phi }}_{\iota }={\mathit{\text{argmin}}}_{\lambda \in {ℝ}_{>0}}{\mathit{\text{max}}}_{k\in \{1,2,\cdots ,K\}}\left\{{\left(Ê\right(X_{*}(t_k))-{Ě}_{\widehat{{\lambda }_{\iota }}}(X_{*}(t_k)))}^2\right\},$$

where Ê(X_*(t_k) is the average total cell count of type-* cells at time t_k, and Ě(X_*(t_k)) is the model-based mean cell count of type-* cells at time t_k. We used the same strategy for the estimation procedure for the results in Figure 5 involving cell count data from Smith et al. (2010) as well as for the reprogramming rate, which was identified by

$$\hat{\gamma }={\mathit{\text{argmin}}}_{\gamma \in {ℝ}_{>0}}{\mathit{\text{max}}}_{k\in \{1,2,\cdots ,K\}}\left\{{(Ê[X_I(t)/(X_S(t)+X_I(t))]-Ĕ[X_I(t)/(X_S(t)+X_I(t))])}^2\right\}$$

where K is the number of measurements in each experiment, Ê[X_I(t)/X_S(t) + X_I(t))] is the empirical average proportion of iPSCs at time t_k, and Ě[X_I(t)/X_S(t) + X_I(t))] is the model-based prediction of the average iPSC proportion at time t_k. With such an estimation strategy, the parameters are determined such that the difference between the model-based prediction and the empirical observation is small over all measurements.

To obtain confidence interval of these rates when the sample size is reasonably large (excluding the cell count data in Table 1), we employed the nonparametric bootstrap resampling approach (Efron and Tibshirani, 1993) by sampling with replacement from the replicates and repeating the above procedures for 1,000 bootstrap samples. Then the 95% confidence interval can be obtained from computing the 2.5% and 97.5% quantile of the 1,000 bootstrap estimates.

Numerical modeling

All computer simulations (Gillespie, 1977) were performed using C++ and we used 1,000 replicates to obtain the summary statistics of the simulations. We used the open source R “deSolve” (Soetaert et al., 2010) function to numerically solve the differential equations (equation (1) and those in the SI) with Euler methods (Smith, 1965), discretizing the time into 0.001-day unit intervals.

Highlights.

• A stochastic process model for reprogramming dynamics from somatic cells to iPS cells

• Model-based analysis of dynamic reprogramming data from multiple sources

• Dissecting model-intrinsic variability and empirical variability from the data