Mapping complex traits as a dynamic system

Abstract

Despite increasing emphasis on the genetic study of quantitative traits, we are still far from being able to chart a clear picture of their genetic architecture, given an inherent complexity involved in trait formation. A competing theory for studying such complex traits has emerged by viewing their phenotypic formation as a “system” in which a high-dimensional group of interconnected components act and interact across different levels of biological organization from molecules through cells to whole organisms. This system is initiated by a machinery of DNA sequences that regulate a cascade of biochemical pathways to synthesize endophenotypes and further assemble these endophenotypes toward the end-point phenotype in virtue of various developmental changes. This review focuses on a conceptual framework for genetic mapping of complex traits by which to delineate the underlying components, interactions and mechanisms that govern the system according to biological principles and understand how these components function synergistically under the control of quantitative trait loci (QTLs) to comprise a unified whole. This framework is built by a system of differential equations that quantifies how alterations of different components lead to the global change of trait development and function, and provides a quantitative and testable platform for assessing the multiscale interplay between QTLs and development. The method will enable geneticists to shed light on the genetic complexity of any biological system and predict, alter or engineer its physiological and pathological states.

1. Introduction

The past two decades have witnessed increasing applications of quantitative genetics to a wide spectrum of life sciences from plant and animal breeding to clinical medicine [16,101,118,142]. However, a considerable body of research has shown that quantitative traits are extremely difficult to study because their formation involves many unknown physiological mechanisms that guide or are guided by the underlying genetic factors that operate in a complicated way [7,100]. By regressing phenotypic values of traits directly on molecular markers from the genome, Lander and Botstein [78] have pioneered an approach for mapping and identifying specific genetic loci, known as quantitative trait loci (QTLs), that contribute to trait variation. Depending on the type of segregating populations used, this approach is called linkage mapping for controlled crosses or association mapping for natural populations [110]. With the increasing availability of inexpensive DNA sequencing and genotyping techniques, it has become a routine tool to dissect the genetic architecture of complex traits, providing unprecedented promises to construct the genotype-phenotype predictive map [62]. However, thousands of thousands of significant QTLs identified so far in a variety of species by this approach have gained little mechanistic insight because a majority of these loci have not been translated into genes and pathways [20]. The translation of functional QTLs requires knowledge of how they act and interact through a series of biochemical pathways toward the end-point phenotype.

To understand the genetic control of QTLs over the process of trait formation, a dynamic model, called functional mapping, has been developed [98,174] and recognized as an important approach for genetic mapping [69,131,141,188]. By integrating the dynamic pathways underlying phenotypic formation using mathematical equations, this model is renovated to identify QTLs involved in rate-limiting processes and to quantify the dynamic effect pattern of these genes across a time and space scale [58,89]. More recently, functional mapping has been extended to systems mapping by viewing a phenotype as a dynamic system [46,47,176]. The key insight of systems mapping is that the dynamics of a complex system depends on how its elements causally influence each other by means of QTLs. By identifying QTLs that determine information flows between different elements, systems mapping can reconstruct a genotype-phenotype map from developmental pathways [12].

Many existing genetic approaches are built on a direct genotype-phenotype association. Although this is a simple strategy easy to be used, it neglects the biology inside the “black box” that links genotype and phenotype through causal networks of interacting genes and pathways. Several authors have recognized the essentiality of incorporating transcript, protein and metabolite abundance into genotype-phenotype prediction models and constructing transcriptional and regulatory networks affecting high-order phenotypes [20,101]. With these established networks, the causative and downstream effects of DNA sequences on phenotypic variation can be clearly understood by perturbing gene expression, proteins and metabolities that play a critical role in the connectivity of DNA variation through endophenotypes to the end-point phenotype.

Figure 1 illustrates a big picture of the formation process of a complex trait from DNA to a final phenotype through a cascade of regulatory pathways. This picture presents a general system of information flow applicable for any trait or disease, but its implementation into a practical genetic study is extremely difficult, if not impossible. At the current level of biotechnology, however, it is feasible to dissolve the whole process of trait formation into multiple continuous smaller-scale systems, in each of which the comprising elements can be readily identified from prior knowledge, and further connect these systems in tandem as a functional whole. A system is defined by the elements that it constitutes, the interactions between these elements, and the natural rules of the system [113,147]. The system rules operate through individual or subsystem elements, but are effective only at the entire system level. How the function of a system is recognized and emphasized depends on the investigator or user’s perspective [5].

Figure 1.

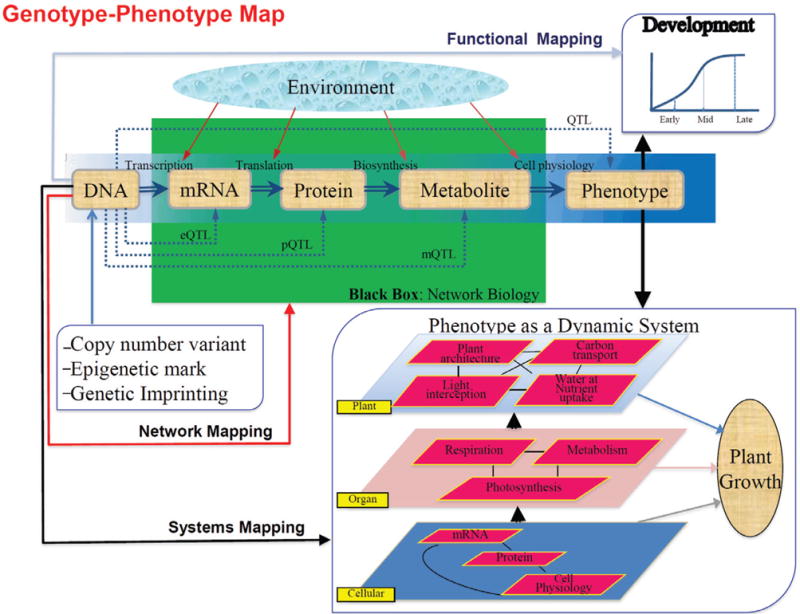
Genetic mapping of complex phenotypes toward constructing a genotype-phenotype map of plant growth. Traditional direct DNA-phenotype associations to find the underling QTLs are reformed by functional mapping that considers the developmental process of phenotypic traits, systems mapping that treats phenotypic formation as a dynamic system composed of many interactive, functional elements at different levels of organization, and network mapping that integrates the regulatory pathways from DNA sequences to endophenotypes providing essential materials for the physiological function of cells.

In this review, we present a general philosophy of mapping complex traits by broadly dissecting trait formation into its three interactive underlying systems, (1) a static system of genetic architecture composed of DNA-based variants, (2) a dynamic system of morphogenesis from early to adult phenotypes, and (3) a dynamic system of regulatory networks originated from DNA and ended at the molecules as precursors for synthesizing the phenotype. Phenotypic formation of one organism may not only be affected directly by its own genes, but also indirectly by genes of its conspecific in a community. We also discuss how a dynamic system of ecological interactions determines the phenotypic variation of a complex trait. We describe the basic principle of dissecting each of these systems and the computational framework of modeling the structure, organization and function of a system through differential equations. As an approach of genetic mapping, we pinpoint several commonly used types of mapping populations that accommodate to key characteristics of different species. To the end, this review provides a dynamic strategy for using the genotype of an organism to predict its phenotype across a range of environments. Our review does not simply provide literature documentation for results of genetic mapping, rather than attempts to provide a broad picture of mapping complex traits from a systematic standpoint, which is inevitably unbalanced in the coverage and references of the presentation. Despite their significant contributions to genetic mapping, we apologize in advance to those authors whose work is not cited in this review.

2. Modeling the genetic architecture of complex traits

There has been a wealth of seminal reviews on the status and opportunities of studies on genetic architecture by leading quantitative geneticists [7,61,63,99–101]. Hansen [55] discussed the pattern of how genetic architecture evolves and how it influences evolution. All the approaches for studying genetic architecture are to link individual DNA variants to the end-point phenotype (Fig. 1). Here, we define the genetic architecture of a complex trait from a systems perspective and review statistical methods for estimating the structure and organization of such a high-dimensional system.

2.1 A traditional strategy of mapping complex traits

The genetic theory for analyzing quantitative traits has well been established since the early twenty century [42]. This theory, equipped with statistical methods, such as the analysis of variance and path coefficients invented by Fisher [42] and Wright [170], enables geneticists to estimate the resemblance between relatives and partition phenotypic variation into its genetic (including additive, dominant and epistatic) and environmental components. By implementing the quantitative genetic theory into the design of experiment derived from various mating designs, Cockerham [21] translated the estimates of experimental variances into the estimates of additive and dominant variance components, largely expanding the practical application of the original theory to dissecting quantitative traits. Wu [173] further integrated clonal replicates, which can be available for many species, such as forest trees, into Cockerham’s [21] analytical model to extract part of the epistatic genetic variance.

Pure quantitative genetic analysis cannot reveal the “black box” behind quantitative genetic variation that is believed to involve many loci with unknown actions and interactions [33,97,101] until the revolutionary emergence of DNA recombinant technologies in the 1980s. Taking advantage of the rapid development of statistical and computational techniques, Lander and Botstein [78] pioneered an innovative approach for dissecting quantitative traits into their underlying genetic components, i.e., QTLs, at the DNA level. This so-called interval mapping has quickly demonstrated its widespread application in quantitative genetic studies for a wide range of species including microorganisms, plants, animals and humans (reviewed in 7,33,61,63,99–101) and has also received extensive modifications and reformations for different purposes [15,68,71,102,112,129,186,187,191,194,198]. While genetic mapping is usually based on a genetic linkage map constructed from molecular markers, which may not have a detailed coverage of the genome, a more in-depth genetic approach, genome-wide association studies (GWAS), has emerged as a powerful tool since high-throughput single nucleotide polymorphism (SNP) genotyping techniques have become available [57,62,82]. GWAS attempts to search for all possible genes that control a complex trait or disease in a way a fisherman fishes from a big pool of water by using a high-density web.

As shown in Fig. 1, a conventional analytical strategy of genetic mapping and GWAS is based on a simple regression model that directly associates individual markers with a phenotype without considering the intermediate process from DNA to the end-point phenotype. This analysis is conducted on a controlled cross of segregating individuals, such as the backcross or F2, initiated with two inbred lines, with the model expressed as

$$y_i=\mu +{\xi }_i{a}_j+{\zeta }_i{d}_j+e_i$$ (1)

where y_i is the phenotypic value of individual i; μ is the overall mean; a_j and d_j are the additive and dominant genetic effects of the jth QTL, respectively; ξ_i and ζ_i are the indicator variables that define the genotype of a QTL, expressed as

$${\xi }_i=\{\begin{array}{ll}1\hfill & \mathrm{If}\text{the}\text{QTL}\text{is}\text{the}\text{homozygote}AA\hfill \\ 0\hfill & \mathrm{If}\text{the}\text{QTL}\text{is}\text{the}\text{homozygote}Aa\hfill \\ -1\hfill & \mathrm{If}\text{the}\text{QTL}\text{is}\text{the}\text{homozygote}aa\hfill \end{array},$$ (2)

$${\zeta }_i=\{\begin{array}{ll}1\hfill & \mathrm{If}\text{the}\text{QTL}\text{is}\text{the}\text{homozygote}Aa\hfill \\ 0\hfill & \mathrm{If}\text{the}\text{QTL}\text{is}\text{the}\text{homozygote}AA\text{or}aa\hfill \end{array};$$ (3)

and e_i is the residual error, assumed to be normally distributed with mean 0 and variance σ².

Statistical methods, such as maximum likelihood or regression analysis, have been implemented to estimate the genetic effects and other model parameters [78]. After these parameters are estimated, hypothesis tests are performed to test whether the genetic effects are significant singly or jointly. In genetic mapping, permutations tests are usually used to determine the genome-wide critical threshold for claiming the significance of the QTLs detected. For GWAS, each SNP is subject to statistical analysis by the regression model (1), obtaining a p-value from the significance test. Put together, the p-values are plotted against the genome locations of all SNPs to produce a Manhattan plot, from which a final set of significant SNPs are determined after the adjust for multiple comparisons using Bonferroni correction, false discovery rate or other approaches.

As an example, Figure 2 shows the application of genetic mapping and GWAS in an F₁ family of interspecific hybrids in poplar. By scanning a linkage group based on the log-likelihood ratio (LR) test, a peak, beyond the critical threshold at the 5% significance level determined from permutation tests, was identified between markers AG/CGC-235R and GT/CAT-430RD, suggesting the existence of a significant QTL for stem diameter growth in this marker interval (Fig. 2A). The same hybrid population, genotyped for about 110,000 SNPs, was analyzed for the same trait by GWAS (R. Wu and M. Huang, unpublished data). From the Manhattan plot obtained, we identify several significant loci at the 5% significant level after Bonferroni correction (Fig. 2B). As like in genetic mapping, we need to estimate the proportion of total phenotypic variance explained by each significant locus. This proportion is called single-QTL heritability that contributes to the overall heritability of 11-year stem diameter.

Figure 2.

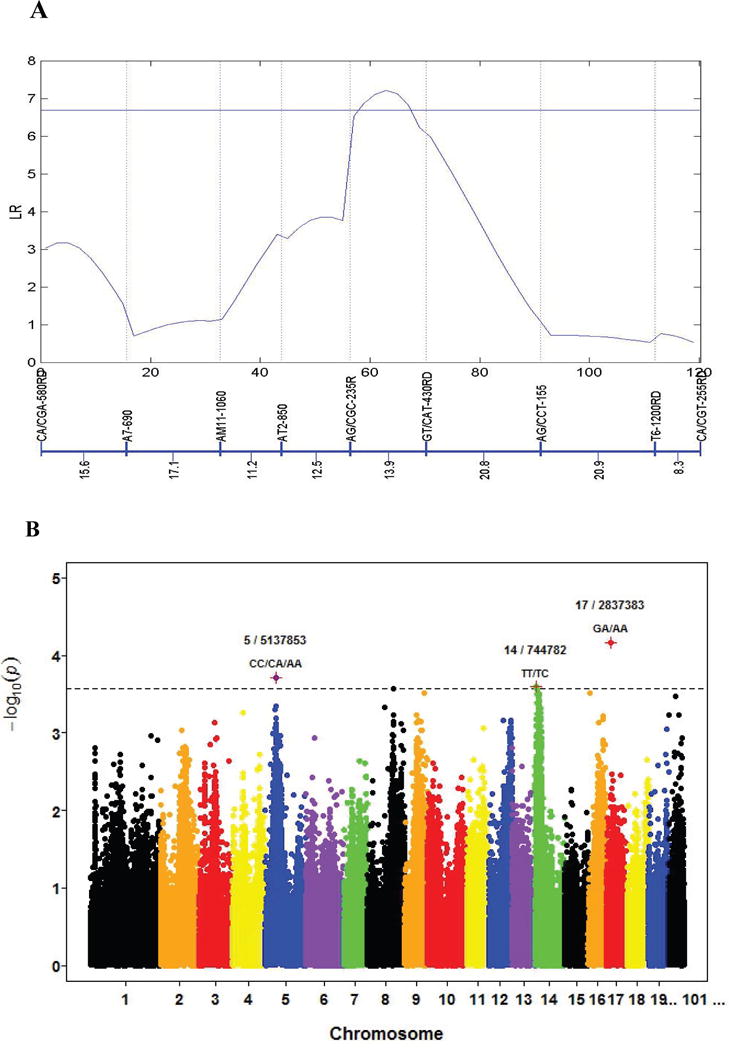
Graphic presentation of the results by linkage mapping and GWAS for 11-year stem diameter growth in a full-sib family of interspecific hybridization between different Populus species. (A) Plot of log-likelihood ratio (LR) test statistics for testing the existence of a significant QTL on a linkage group, with the names and genetic distances (in cM) of molecular markers given beneath. The horizontal line denotes the genome-wide threshold at the 5% significance level determined from permutation tests. (B) Manhattan plot of minus log(p) values against the genome locations of SNPs distributed throughout the genome. The horizontal dash line indicates the 5% significance level after the adjustment for multiple testing from Bonferroni correction. Several significant loci are shown. Data was supplied by Prof. Minren Huang at Nanjing Forestry University with permission.

Linkage mapping and association studies have provided a powerful tool to illustrate a trait’s genetic architecture by identifying the numbers and genome locations of genes that affect the trait, the magnitude of their unique effects and pleiotropic effects, and the relative contributions of additive, dominant, and epistatic genetic effects. The traditional single-locus/single-phenotype analysis used, however, is not able to provide a precise picture of genetic architecture for complex traits because it is not implemented with the intrinsic complexity of genetic control. It has been widely recognized that complex traits are determined simultaneously by a number of genes, each acting singly or interacting with other genes and environmental factors to different degrees [33,97]. Such multifactorial nature of a complex trait has made the description of its underlying genetic architecture a difficult and challenging task.

2.2 Genetic actions and interactions

A gene exerts its effects on a complex trait in a complicated manner. It may act singly through main effects, or interact with other genes via epistasis, forming a network of actions and interactions. For a single gene, its main effect can be partitioned into additive and dominant components, whereas the epistasis of a given pair of genes includes additive × additive, additive × dominant, dominant × additive and dominant × dominant interactions [42]. By charting such a genetic network, we can comprehend the genetic control mechanisms of a complex trait and elucidate the rules for translating genetic variation to the phenotypic variation of the trait. We diagrammatize the genetic architecture of botanical traits for a plant composed of all possible genes distributed on its total five chromosomes (Fig. 3). Some genes are collectively distributed on a small region (e.g., chromosome 2), whereas the others have a sporadic distribution throughout a wide region of the genome. Some interacts with many other genes (e.g., gene 1), some only have a few interactions (e.g., gene 2), and the others have no interactions (e.g., genes 24 and 25). Some genes tend to interact with those within the same region (e.g., genes on chromosome 5), whereas others only interact with those from different chromosomes (e.g., genes on chromosome 1).

Figure 3.

A network of genetic actions and interactions among genes distributed on different chromosomes that affect leaf trait and root traits of a plant. The plant in the diagram contains five chromosomes (I – V) on which the locations of genes, labelled by 1 – 26, are indicated. The direct effects of genes are indicated by green lines for leaf traits and brown lines for root traits. The epistatic interactions of different genes are indicated by blue lines.

Pleiotropy, believed to play an important role in the genotype-phenotype relationship, is the other main element in genetic architecture. A gene is thought of being pleiotropic if it affects two or more traits at the same time [146]. Of the genes that affect an above-ground trait of the plant, some also pleiotropically influence its below-ground trait (e.g., genes 2, 3, 15 among others; Fig. 3). These genes are one of the causes for the genetic correlation between these two types of traits. Of course, the two traits are correlated partly because of the genetic linkage between two genes, each controlling a different trait (e.g., two adjacent genes 3 and 4). Although the below-ground trait is highly related to the above-ground trait, they obviously present two different modules because of distinct discrepancy in their underlying genetic basis. As shown in Fig. 3, a large portion of genes that affect the below-ground trait are not involved in variation in the above-ground trait. On the other hand, the genes for the above-ground trait are generally also responsible for the below-ground trait. This difference suggests that this particular below-ground trait is more autonomous than the above-ground trait assumed.

Given that the complexity of a phenotypic trait arises from the highly interactive relationships of its underlying components, it is reasonable to hypothesize that the metabolic pathways for trait formation involve multiple interacting gene products and regulatory loci [106]. Three-way interactions among different QTLs were believed to be involved in metabolic pathways toward a complex trait [134]. A mathematical approach was derived to describe multi-way genetic interactions to study the genetic structure of fitness landscapes for Escherichia coli [9]. A genome-scale knockout design was framed to detect high-order epistatic relationships between components of large metabolic networks [66]. Hansen and Wagner [56] showed that higher-order genetic interactions play a pivotal role in trait phenotype if the total genomic mutation rate is large and the interaction density among loci is not too low.

2.3 Genetic imprinting and epigenetic actions

Many recent studies have unraveled the importance of genomic imprinting and epigenetic modification as a mechanism for genetic variation [19,90,92,148,149]. Genomic imprinting is a genetic phenomenon by which certain genes are expressed or repressed depending on their parental origin [79]. Violating the classical Mendelian inheritance, imprinted genes are either expressed only from the allele inherited from the mother, such as H19 or CDKN1C, or from the allele inherited from the father, such as IGF-2. From a quantitative genetic perspective, genomic imprinting may provide organisms with evolutionary merits by contributing additional genetic variation and conferring a fitness benefit in changing environments [120]. Nowadays, different forms of genomic imprinting have been detected in a variety of species and thought to play an important role in regulating crucial aspects of embryonic growth and development as well as pathogenesis. Recent bioinformatic analyses suggest that the number of imprinted genes may be higher than we thought previously but this remains to be demonstrated experimentally [67].

One of the forces causing genetic imprinting is systematic or stochastic changes in chromatin states, such as DNA methylation, chromatin remodeling, histone modification and RNA interference [17,157]. These epigenetic modifications have also been thought to provide an additional driving force for phenotypic variation in complex traits and diseases [31,39,40,70,122,123]. Different chromatin states, called epialleles, that occur in the same sequence allele cannot be captured by an analysis based on DNA sequence alone (Johannes et al. 2008). With the increasing availability of epigenome technologies, there has been an unprecedented opportunity to understand the role of epiallelic variants in maintaining and inducing functional variation for organisms to better buffer against environmental perturbations. Like genetic imprinting, epigenetic variants should also been considered for elucidating the genotype-phenotype map.

Genetic mapping has been used as an appealing approach to discovering imprinted QTLs (iQTLs) based on particular mating designs. Basically, these designs include outcrossed families [29,74], sex-specific linkage analysis [19,25], reciprocal crosses [90,148,149,192], multigenerational pedigrees [92], open-pollinated populations [138] and case-control studies [87]. From these designs, significant imprinted QTLs were detected for body composition and body weight in pigs, chickens, sheep and canine, endosperm traits in maize, and stem growth in hickory tree. Computational models have also been developed to detect and map epiQTLs, i.e, those QTLs at which epigenetic marks are differentially expressed in response to environmental changes [137]. Wang et al. [155] proposed a model to estimate the relative contribution of epiQTLs to overall genetic variation in a natural population.

2.4 Genotype-environment interactions

In order to adapt to the new or fluctuating environment, the organism will often change its phenotypic expression, a phenomenon called phenotypic plasticity [126,144]. Differences in the capacity of phenotypic plasticity among individuals cause genotype-environment interactions. This explains a vast body of observations of why the genetic effect of a QTL detected on a phenotypic trait depends on the environmental and developmental context, such as temperature, irradiation, nutrition, or age [101,154]. Obviously, genotype-environment interactions are a key factor that determines the pattern of the genetic architecture of a complex trait. The investigations of genotype-environment interactions will not only help to design an efficient breeding program as like a traditional consideration, but also are being integrated into conceptual model construction for evolutionary, climate change and clinical studies [8,32,108].

Special attention has been paid to study the genetic mechanisms of phenotypic plasticity [127]. More recently, El-Soda et al. [32] summarized five genetic models proposed to explain the genetic basis of phenotypic plasticity: (1) Overdominance: phenotypic plasticity is negatively correlated with the number of heterozygous loci; i.e., the more homozygous a genotype, the more plastic it is. (2) Allelic sensitivity or incomplete pleiotropy: the magnitude of allelic effects at a gene varies among different environment; the gene has a pleiotropic but different effect on the same trait expressed in different environments. (3) Epistasis: loci causing plasticity regulate other genes through epistatic interactions to be switched on or off in a particular environment. (4) Linkage: alleles responsible for plasticity may be linked with alleles that produce either low or high fitness. (5) Epigenesis: an epiallele of a gene becomes sensitive to the environment due to chromatin modification and DNA methylation, while the standard allele is stable. All possible models implicate the mechanistic complexity of genotype-environment interactions, making it essential to chart genetic architecture from a systems perspective.

Most studies of genotype-environment interactions focus on genetic variation in phenotypic plasticity between two discrete environments [32]. Such studies are not able to unravel phenotypic response, or reaction norms, to a gradient of environmental conditions [145]. Wang et al. [154] implemented a dynamic model to study the genetic architecture of the gradient expression of a complex trait across a range of environments. This model was framed on mathematical aspects of phenotypic plasticity, equipped with a capacity to unravel the quantitative attribute of trait response to the environment. By testing the curve parameters that specify reaction norm trajectories, the model enables geneticists to test a series of fundamental hypotheses a quantitative way about the interplay between genes and environmental sensitivity. The model can also make the dynamic prediction of genetic control over phenotypic plasticity within the context of changing environments.

2.5 Direct and indirect genetic effects from genome-genome interactions

Increased recognition has been given to the role of genetic interactions between QTLs from different genomes in both direct and indirect ways [75,77,168,196]. For example, in flowering plants that undergo a double-fertilization process leading to the differentiation of the embryo and endosperm in the seed, seed traits are controlled simultaneously by three genomes, diploid offspring (embryo), triploid offspring (endosperm), and the maternal plant which carries the seed. While offspring genomes confer direct genetic effects on the seed, the maternal genome provides an indirect genetic effect. Seed development is thus the result of a mosaic of different gene expression programs occurring in parallel in different compartments. Wu and group have developed a series of statistical models that can characterize the genetic effects on seed traits derived from the maternal genome, the offspring genome and material-offspring interactions [22–24,26,150,178,180]. Likewise, given that a tumor is supplied with nutrients from normal tissues, its growth should depend on an interactive effect of genes directly from the normal tissue and indirectly the tumor tissue [88].

When different organisms grow in the same environment, the phenotype of an organism may be determined not only by its own genome, but also by the genome of the other organisms around it and genetic interactions between different genomes. In a gene expression study of plant-pathogen interactions, Zhu et al. [196] identified the genetic architecture of plant resistant traits composed of genes from the host and pathogen. Kolenbrander et al. [75] reviewed evidence for intimate interactions between genomes of the human and microorganisms in dental plaque communities. Lambrechts [77] argued that the phenotype of viral infection does not merely result from additive effects of host and pathogen genotypes, but also from a specific interaction between the two genomes. Wolf et al. [169] integrated genetic mapping and structural equation models to detect a QTL for flowering time in focal plants that pleiotropically affects the expression of developmental traits in the neighbor plants. Also, there has been a body of other literature that reports the detection of QTLs for phenotypic traits related to interspecific interactions, such as immune response [80], tolerance to herbivory [160], mate recognition [130], or predator-defense traits [96], by using conventional mapping approaches.

3.6 High-dimensional model of inferring a complete picture of genetic architecture

Despite the complexity of the underlying process from genes to phenotype, the vast majority of genetic analysis is built around a very simple model of associating genotype with phenotype. To overcome this simplicity of trait analysis, a more sophisticated statistical model based on high-dimensional variable selection has been developed, allowing a large number of SNPs to be analyzed simultaneously [83]. This model involves a two-stage procedure for multi-SNP modeling and analysis in GWAS, by first producing a “preconditioned” response variable using a supervised principle component analysis and then formulating Bayesian LASSO to select a subset of significant SNPs. This model has proven to be particularly powerful for selecting the most relevant SNPs for GWAS where the number of predictors exceeds the number of observations.

More recently, high-dimensional variable selection has been extended to an ultrahigh-dimensional scale which enables the modeling and estimation of SNP-SNP interactions in GWAS [85]. The extended model incorporates a two-stage sure independence screening (TS-SIS) procedure [36]: first, to generate a pool of candidate SNPs and interactions served as predictors to explain and predict the phenotypes of a complex trait; and second, regularization regression methods, such as LASSO or smoothly clipped absolute deviation (SCAD) [34,35], are applied to further identify important genetic effects. A rates adjusted thresholding estimation (RATE) approach was used to control the false positive rate of the selected model by a general independent screening procedure.

Consider a GWAS in which a simple regression model (1) was extended to include all possible main effects (including the additive and dominant) and interaction effects, as well as all possible covariates. Thus, the phenotypic value of a particular individual i can be expressed as

$$\begin{array}{l}{y}_i=\mu +{\displaystyle \sum _{k=1}^q{x}_{ki}}{\alpha }_k+{\displaystyle \sum _{j=1}^p{\xi }_{ji}}{a}_j+{\displaystyle \sum _{j=1}^p{\zeta }_{ji}}{d}_j+{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{j\prime =1}^p{\xi }_{ji}}{\xi }_{j\prime i}{I}_{jj\prime }^{aa}}+{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{j\prime =1}^p{\xi }_{ji}}{\zeta }_{j\prime i}{I}_{jj\prime }^{ad}}\\ +{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{j\prime =1}^p{\zeta }_{ji}}{\xi }_{j\prime i}{I}_{jj\prime }^{da}+{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{j\prime =1}^p{\zeta }_{ji}}{\zeta }_{j\prime i}{I}_{jj\prime }^{dd}+{\epsilon }_i,}i=1},\dots ,n;j<j\prime \end{array}$$ (4)

where μ is the overall mean, x_ki is the kth covariate for individual i, which could be either discrete or continuous, α_k is the effect of the kth covariate (k = 1, …, q), a_j and d_j are the additive effect and dominant effect of the jth SNP (j = 1, …, p), respectively, $I_{jj\prime }^{aa}$, $I_{jj\prime }^{ad}$, $I_{jj\prime }^{da}$ and $I_{jj\prime }^{dd}$ are the additive × additive, additive × dominant, dominant × additive and dominant × dominant epistatic effects between SNP j and j′ (j < j′ = 1, …, p), respectively, and ε_i is the residual error assumed to follow an N(0; σ²) distribution. For individual i, ξ_ji and ζ_ji are the indicators of the additive and dominant effects of the jth SNP, respectively, as explained in equations (2) and (3).

Let D_a and D_d denote a set of additive and dominant effect indices, respectively. The first round SIS is conducted on $D_a^{(0)}=\{1,\dots ,p\}$ and $D_d^{(0)}=\{1,\dots ,p\}$ for all SNPs. After the first stage SIS, a subset of SNPs with potential nonzero additive $(D_a^{(1)})$ and dominant effects $(D_d^{(1)})$ is selected. Note that each SNP in any subset may either have true nonzero main effects, or serve as a root in a two-way interaction. Let $(D_{aa}^{(2)})$, $(D_{ad}^{(2)})$, $(D_{da}^{(2)})$ and $(D_{dd}^{(2)})$ denote a set of selected roots for additive × additive, additive × dominant, dominant × additive and dominant × dominant epistatic effects, respectively.

After two-stage sure independence screening, the dimensionality of GWAS model has greatly reduced. In order to precisely select important SNPs and epistatic interactions from a pool of candidate effects, penalized regressions widely used in main-effect analysis could be incorporated here. Specifically, we put penalties on the sizes of additive, dominant and all epistatic effects and minimize the following penalized least squares:

$$\begin{array}{l}\frac{1}{2n}{\Vert y-Ey\Vert }^2+{\displaystyle \sum _{j\in D_a^{(1)}}{p}_{\lambda }(|a_j|)}+{\displaystyle \sum _{j\in D_d^{(1)}}{p}_{\lambda }(|d_j|)}\\ +{\displaystyle \sum _{j\in D_{aa}^{(2)}}{p}_{\lambda }(|I_{jj\prime }^{aa}|)}+{\displaystyle \sum _{j\in D_{ad}^{(2)}}{p}_{\lambda }(|I_{jj\prime }^{ad}|)+{\displaystyle \sum _{j\in D_{da}^{(2)}}{p}_{\lambda }(|I_{jj\prime }^{da}|)}+{\displaystyle \sum _{j\in D_{dd}^{(2)}}{p}_{\lambda }(|I_{jj\prime }^{dd}|)}}\end{array}$$ (5)

where the penalty function p_λ(·) is implemented to shrink sufficiently small effects to zero and thus exclude the inactive predictors. The SCAD penalty least squares function, characterized by unbiasedness, continuity and sparsity properties [36], has been used to solve model (5), with the estimates of regression coefficients being estimated with the aid of local linear approximation. Note that the SCAD penalized least squares (5) can be easily minimized using L₁ penalized regression.

Results from simulation studies show that the TS-SIS procedure is computationally efficient and has an outstanding finite sample performance in selecting potential SNPs as well as gene-gene interactions. The procedure was used to analyze an ultra-high dimensional GWAS dataset from the Framingham Heart Study [28], leading to the detection of 32 significant SNPs including 42 epistatic interactions for body mass index (BMI) (Fig. 4). We summarized the results as follows: (1) Epistasis appears to be distributed randomly throughout the genome, although a few SNPs, such as ss66142093 on chr 3, ss66249128 and ss66468842 on chr 7 tend to interact with many other SNPs. (2) Active epistasis may not be due to interactions between two SNPs both of which display active marginal effects. Of the 42 selected pairs, there are five cases in which both SNPs have active marginal effects and there are 21 cases in which only one SNP has an active marginal effect whereas the counterpart has not. There are as many as 16 pairs in which no SNP is active for its marginal effect. Notably, the DD interaction between SNP ss66249128 on chr 7 and SNP ss66451087 on chr 12 can explain 2.32% of the BMI variation, although the latter is marginally uncorrelated with BMI. In the presence of SNP ss66451087, the D effect of SNP ss66249128 is dramatically impacted.

Figure 4.

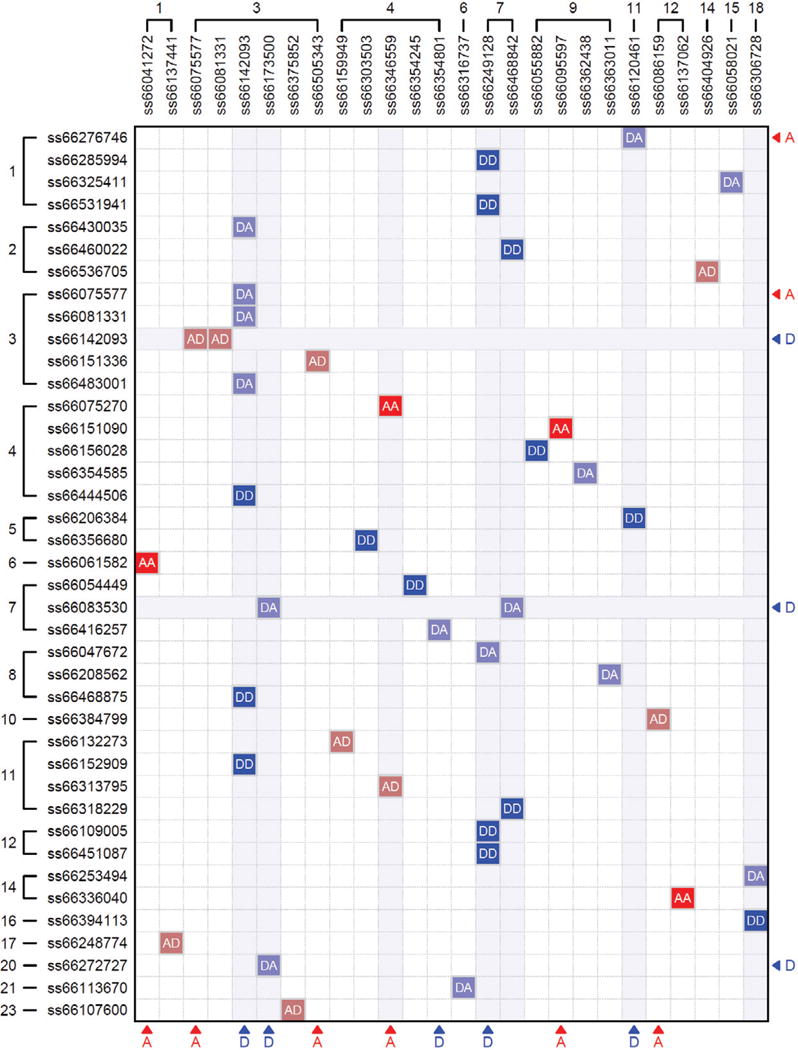
A picture of significant genetic interactions between different SNPs that determine BMI in the Framingham Heart Study. The numbers beside SNPs are chromosome numbers. The SNPs that display significant main additive (A) and dominant (D) genetic effects are indicated by arrows. AA, AD, DA and DD represent four corresponding types of epistasis. Modified from Li et al. [85].

Since this ultrahigh-dimensional GWAS model can analyze a large number of SNPs and interactions simultaneously, the resulting discoveries should be statistically powerful to chart the genetic architecture of a complex trait than those from traditional single-SNP approaches. Genetic loci detected by this approach show high more biological relevance. For example, SNP ss66142093 on chromosome 3, detected to explain 2.97% single-locus heritability, is near a candidate gene ANAPC13 involved in pathways for bone and cartilage development that affects human height and stature through cell cycle regulation and mitosis [158]. Also, significant loci detected on chromosomes 3, 4, 6, 9 and 12 are within the genes responsible for type 2 diabetes, a disease highly correlated with BMI [44]. These results demonstrate the capability of the TS-SIS model to resolve the complexity of genetic control mechanisms.

3. Developmental dissection of complex traits

The formation of every trait undergoes a series of developmental changes in an organism’s ontogeny. For example, in the lifecycle of a soybean (Fig. 5), plant development includes a broad spectrum of processes, i.e., the formation of a complete embryo from a zygote, seed germination, the elaboration of a mature vegetative plant from the embryo, the formation of flowers, fruits, and seeds, and many of the plant’s responses to its environment. Each of these processes is fundamental to determine the size, shape and production of a higher plant. Knowledge of the genetic basis of the variation in each process is important for understanding adaptive evolution and deriving elite domestic crop varieties. Traditional approaches map a phenotype by measuring it at a fixed time point (Fig. 1), view the process of trait formation as a “black box” and, thus, fail to capture the dynamic structure and pattern of the process. A conceptual functional mapping model has been derived to address this issue by considering biological mechanisms and processes of phenotypic formation ([98,174]; Fig. 1). By measuring a phenotypic trait repeatedly at a series of time points, a biologically meaningful curve, e.g., growth curve, can be used to fit to these observations. This procedure has been integrated into functional mapping which thus unifies the strengths of statistics, genetics, and developmental biology to facilitate the test of the interplay between genetic action and development and the characterization of physiological and developmental pathways involved in the function of genes [181]. Here we do not focus on the review of functional mapping because it has been described elsewhere [58,88].

Figure 5.

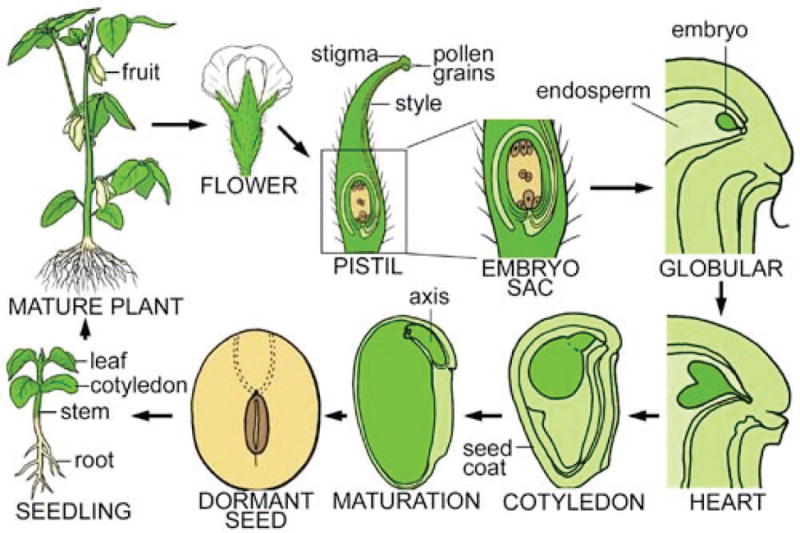
Lifecycle of a typical flowering plant – soybean, which experiences many distinct stages of vegetative and reproductive growth. Key organs of the plants are shown.

3.1. From functional mapping to systems mapping

Although functional mapping is a big jump in exploring the developmental machineries of trait formation from Lander and Botstein’s [78] internal mapping model, it is still too simple to chart a complete dynamic picture of trait formation. In general, a phenotypic trait, such as biomass, is formed through complex interactions and coordination of the underlying components expressed at different organizational levels. Given that biology is multifactorial, any analytical tools used to study biology should be sophisticated sufficiently to capture such complexity. By viewing a complex phenotype as a dynamic system, Wu et al. [176] extended functional mapping to the level of systems mapping. The central principle of systems mapping is to dissect a trait into its underlying components, coordinate the interactions of different components in terms of biological laws through mathematical equations, and map specific genes that mediate each component and its connection with other components. As a bottom-top model, systems approach can identify specific QTLs that govern the developmental interactions of various components giving rise to the function and behavior of the system. By estimating and testing mathematical parameters that specify the system, systems mapping enables the prediction or alteration of the physiological status of a phenotype based on the underlying genetic control mechanisms.

Biomass partitioning

Here, we use an example of biomass partitioning to explain systems mapping. To best adapt to a particular environment, a plant tends to allocate its biomass into living parts in an optimal way that channels a maximum amount of resources to the target of harvest (leaves, stem, roots, or fruits) (Fig. 6; [50]). Given its such an ecological interest [105], theoretical modeling of biomass allocation pattern has received considerable attention [18,50]. Modeling work has focused on the understanding of how different organs of a plant coordinate and interact to optimize the capture of nutrients, light, water, and carbon dioxide in a manner that maximizes plant growth rate through a specific developmental program. Chen and Reynolds [18] developed coordination theory to model the dynamic allocation of carbon to different organs during growth in relation to carbon and water/nitrogen supply by a group of differential equations. To maintain the growth of a plant, its organs, the leaf, stem, branch, coarse root and fine root, should coordinate as a cohesive whole. Wu et al. [176] integrated the coordination and optimization model to study the pattern of biomass partitioning by incorporating the allometric scaling theory [161–163] into a system of ordinary differential equations (ODE), expressed as

$$\begin{array}{l}\frac{d{M}_{\mathrm{F}}}{dt}={\alpha }_{\mathrm{F}}{M}^{{\beta }_{\mathrm{F}}}-{\lambda }_{\mathrm{F}}{M}_{\mathrm{F}}\\ \frac{d{M}_{\mathrm{S}}}{dt}={\alpha }_{\mathrm{S}}{M}^{{\beta }_{\mathrm{S}}}\\ \frac{d{M}_{\mathrm{B}}}{dt}={\alpha }_{\mathrm{B}}{M}^{{\beta }_{\mathrm{B}}}\\ \frac{d{M}_{\mathrm{R}}}{dt}={\alpha }_{\mathrm{R}}{M}^{{\beta }_{\mathrm{R}}}\\ \frac{d{M}_{\mathrm{H}}}{dt}={\alpha }_{\mathrm{H}}{M}^{{\beta }_{\mathrm{H}}}-{\lambda }_{\mathrm{H}}{M}_{\mathrm{H}}\end{array}$$ (6)

where M_F, M_S, M_B, M_R, and M_H are the biomasses of the foliage (F), stem (S), branches (B), roots (R) and root hairs (H), respectively, with whole-plant biomass M = M_F + M_S + M_B + M_R + M_H; α and β are the constant and exponent power of an organ biomass scaling as whole-plant biomass; and λ is the rate of eliminating ageing leaves or root hairs [177].

Figure 6.

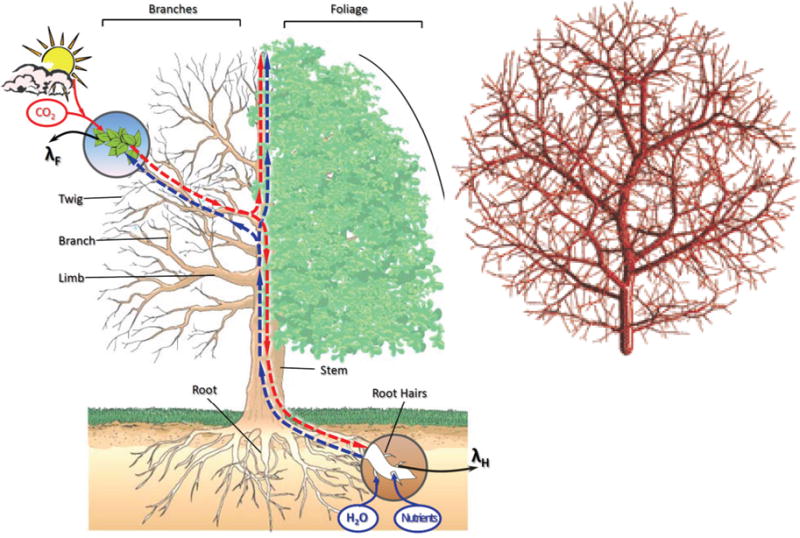
Biological design principles that build the system of ordinary differential equations (6). Left: Botanical architecture of a living plant and the pathways of absorbing water and nutrients from root hairs and transporting carbohydrates from leaves that perform photosynthesis with CO₂ and sunlight. Right: A fractal model that is used to explain universal allometric scaling laws that constrain the relationship of physiology and body size in living systems.

The complex interactions between different parts of a plant that underlie design principles of plant biomass growth can be modeled and studied by estimating and testing the ODE parameters (α_F, β_F, λ_F; α_S, β_S; α_B, β_B; α_R, β_R; α_H, β_H, λ_H). For example, plants are equipped with a capacity to optimize their fitness under low nutrient availability by shifting the partitioning of carbohydrates to processes associated with nutrient uptake at a cost of carbon acquisition [59]. These parameters can be used to quantify and predict such regulation between different plant parts in response to environmental and developmental changes.

Model

Assume a plant’s mapping population composed of n RILs, initiated with two inbred lines. This population is genotyped by a panel of molecular markers from which a genetic linkage map is constructed. All RILs are phenotyped for biomass traits, separately for the foliage (F), stem (S), branches (B), roots (R) and root hairs (H), at a multitude of T time points on the ontogeny of the plants. Let $y_i=(y_i^{\mathrm{F}};y_i^{\mathrm{S}};y_i^{\mathrm{B}};y_i^{\mathrm{R}};y_i^{\mathrm{H}})=(y_i^{\mathrm{F}}(1),\dots ,y_i^{\mathrm{F}}(T);y_i^{\mathrm{S}}(1),\dots ,y_i^{\mathrm{S}}(T);y_i^{\mathrm{B}}(1),\dots ,y_i^{\mathrm{B}}(T);y_i^{\mathrm{R}}(1),\dots ,y_i^{\mathrm{R}}(T);y_i^{\mathrm{H}}(1),\dots ,y_i^{\mathrm{H}}(T))$ denote the vector of time-dependent biomass traits of RIL i measured for five organs. Consider a QTL or a set of QTLs that affect the dynamic changes of five biomass traits at a time. Based on Lander and Botstein’s [78] theory, we formulate a mixture-based likelihood expressed as

$$\mathrm{L}(y)={\displaystyle \sum _{i=1}^n\left[{\omega }_{1|i}{f}_1(y_i^{\mathrm{F}};y_i^{\mathrm{S}};y_i^{\mathrm{B}};y_i^{\mathrm{R}};y_i^{\mathrm{H}})+\dots +{\omega }_{J|i}{f}_J(y_i^{\mathrm{F}};y_i^{\mathrm{S}};y_i^{\mathrm{B}};y_i^{\mathrm{R}};y_i^{\mathrm{H}})\right]}$$ (7)

where ω_j|i (j = 1, …, J) is the conditional probability of the jth QTL genotype given the marker genotype of RIL i that are linked with the QTLs, and $f_j(y_i^{\mathrm{F}};y_i^{\mathrm{S}};y_i^{\mathrm{B}};y_i^{\mathrm{R}};y_i^{\mathrm{H}})$ is a high-dimensional multivariate normal distribution density function of RIL i with mean vector for QTL genotype j expressed as

$$\begin{array}{r}({\mu }_j^{\mathrm{F}};{\mu }_j^{\mathrm{S}};{\mu }_j^{\mathrm{B}};{\mu }_j^{\mathrm{R}};{\mu }_j^{\mathrm{H}})=({\mu }_j^{\mathrm{F}}(1),\dots ,{\mu }_j^{\mathrm{F}}(T);{\mu }_j^{\mathrm{S}}(1),\dots ,{\mu }_j^{\mathrm{S}}(T);{\mu }_j^{\mathrm{B}}(1),\dots ,{\mu }_j^{\mathrm{B}}(T);\\ {\mu }_j^{\mathrm{R}}(1),\dots ,{\mu }_j^{\mathrm{R}}(T);{\mu }_j^{\mathrm{H}}(1),\dots ,{\mu }_j^{\mathrm{H}}(T))\end{array}$$ (8)

and covariance matrix, expressed as

$$\sum =\left(\begin{array}{lllll}{\sum }_{\mathrm{F}}\hfill & {\sum }_{\mathrm{F}}^{\mathrm{S}}\hfill & {\sum }_{\mathrm{F}}^{\mathrm{B}}\hfill & {\sum }_{\mathrm{F}}^{\mathrm{R}}\hfill & {\sum }_{\mathrm{F}}^{\mathrm{H}}\hfill \\ {\sum }_{\mathrm{S}}^{\mathrm{F}}\hfill & {\sum }_{\mathrm{S}}\hfill & {\sum }_{\mathrm{S}}^{\mathrm{B}}\hfill & {\sum }_{\mathrm{S}}^{\mathrm{R}}\hfill & {\sum }_{\mathrm{S}}^{\mathrm{H}}\hfill \\ {\sum }_{\mathrm{B}}^{\mathrm{F}}\hfill & {\sum }_{\mathrm{B}}^{\mathrm{S}}\hfill & {\sum }_{\mathrm{B}}\hfill & {\sum }_{\mathrm{B}}^{\mathrm{R}}\hfill & {\sum }_{\mathrm{B}}^{\mathrm{H}}\hfill \\ {\sum }_{\mathrm{R}}^{\mathrm{F}}\hfill & {\sum }_{\mathrm{R}}^{\mathrm{S}}\hfill & {\sum }_{\mathrm{R}}^{\mathrm{B}}\hfill & {\sum }_{\mathrm{R}}\hfill & {\sum }_{\mathrm{R}}^{\mathrm{H}}\hfill \\ {\sum }_{\mathrm{H}}^{\mathrm{F}}\hfill & {\sum }_{\mathrm{H}}^{\mathrm{S}}\hfill & {\sum }_{\mathrm{H}}^{\mathrm{B}}\hfill & {\sum }_{\mathrm{H}}^{\mathrm{R}}\hfill & {\sum }_{\mathrm{H}}\hfill \end{array}\right).$$ (9)

Systems mapping uses ODE (6) to model the time-dependent mean vectors for each QTL genotype j using ODE parameters $({\alpha }_j^{\mathrm{F}},{\beta }_j^{\mathrm{F}},{\lambda }_j^{\mathrm{F}};{\alpha }_j^{\mathrm{S}},{\beta }_j^{\mathrm{S}},{\lambda }_j^{\mathrm{S}};{\alpha }_j^{\mathrm{B}},{\beta }_j^{\mathrm{B}},{\lambda }_j^{\mathrm{B}};{\alpha }_j^{\mathrm{R}},{\beta }_j^{\mathrm{R}},{\lambda }_j^{\mathrm{R}};{\alpha }_j^{\mathrm{H}},{\beta }_j^{\mathrm{H}},{\lambda }_j^{\mathrm{H}})$ (j = 1, …, J). A basic mathematical algorithm for ODE solving, the fourth Runge-Kutta, has been incorporated into mixture model to estimate these QTL genotype-specific ODE parameters [46,47,174]. Because the covariance matrix Σ contains longitudinal structure, it can be modeled by some parsimonious approaches. Zhao et al.’s [195] multivariate structured antedependence (SAD) model can be implemented within systems mapping. The SAD is found to have an advantage in capturing the covariance structure with a few parameters.

The existence of significant QTLs involved in the ODE system can be detected by scanning the linkage group using a log-likelihood ratio profile, a method as shown in Fig. 2A. After a significant QTL is detected, systems mapping provide an elegant procedure to test mechanistic hypotheses of biological relevance [151]. They include:

1. Size-shape relationship: Given the ODE parameters for system (6), one can see how much biomass has been allocated to the leaves, stem, branches, roots and root hairs. It is possible that some plants have a dominant main stem, with less leaves, while some plants allocate more carbon to the roots than the leaves, stem and branches. Systems mapping can estimate specific effects of a QTL on a plant’s size and form or shape and, furthermore, quantify how the QTL governs the dynamic relationship between size and shape.

2. Structural-functional relationship: The structure of a system can determine its function. On other hand, function may also lead to the change of structure. In general, a plant in drought soil would allocate more energy into its root system in order to increase its survival rate and fitness. Systems mapping enables geneticists to predict the dynamical change of such structural-functional relationships and gain new insight into the genetic mechanisms involved in balancing vegetative and reproductive growth.

3. Cause-effect relationship: All organs contribute to the whole-plant biomass through a complex web of direct and indirect relationships. The foliage performing photosynthesis may not only make a direct contribution to the whole-plant biomass by producing carbohydrates, but also affect the latter through an indirect relationship of other traits, such as roots and root hairs. Systems mapping can estimate the genetic effects on these direct and indirect relationships.

4. Sink-source relationship: In plants, leaves serve as main supply areas (sources) that produce and transport carbohydrates through the phloem to areas of growth or storage (sinks). Sinks can locate at many places including the stem and root system. The rate at which carbohydrates are transported is primarily dependent on the sink strength of plant organs. The specific QTLs that affect these sink-sources relationships can be identified from systems mapping.

Example

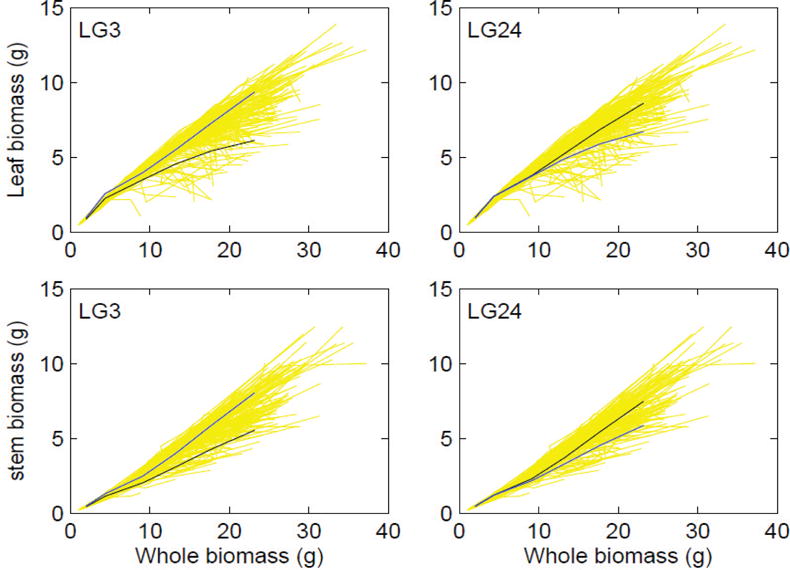
We used systems mapping to analyze the dynamic changes of above-ground biomass composed of the stem and leaves (including foliage and branches) in a soybean RIL mapping population derived from two cultivars, Kefeng No.1 and Nannong1138-2. Systems mapping detects two QTLs, one on linkage group 3, named dynQ1, and the second on linkage group 24, named dynQ2 (Fig. 7). The two QTLs were found to determine the functional relationship between leaf and stem and whole-plant biomass. dynQ1 triggers its effect on organ biomass growth immediately when seeds germinate into seedlings, whereas dynQ2 is operational when the seedlings have grown into a certain size. At dynQ1, alleles inherited from Kefeng No.1 contributes to the favorable allometric correlation of leaf and stem biomass with the whole-plant biomass. The alleles for dynQ2 that favorably affect this correlation are derived from Nannong1138-2. These findings suggest that specific QTLs are involved in the control of developmental timing and the structural-functional relationship of biomass allocation, with the pattern of action being taken to cope with genetic background.

Figure 7.

Dynamic pattern of biomass allocated to the leaves and stem for two different genotypes (dark curves) at each of the two QTLs, dynQ1 and dynQ2, detected on LG3 and LG24, respectively, detected from a recombinant inbred line population of soybean. Curves in yellow each represent the biomass growth trajectory of a progeny in soybean. The system of ODEs (1) is reduced to a two-dimensional system, expressed as

$$\begin{array}{l}{\dot{M}}_F={\alpha }_F{W}^{{\beta }_F}-{\lambda }_F{M}_F\\ {\dot{M}}_S={\alpha }_S{W}^{{\beta }_S}\end{array}$$

where W = M_L + M_S is the sum of the foliage (M) and stem biomass (S). Data was supplied by Prof. Junyi Gai at Nanjing Agricultural University with permission.

3.2. The application of systems mapping in pharmacology

In clinical pharmacology for HIV/AIDS, the response of a patient to an antiviral drug or multiple drugs can be viewed as a system in which the body interacts with the drug through biochemical and biophysical principles to control or eliminate the expansion of virus. Because this process is under the joint control of genes derived from the host and pathogen [3], an understanding of the genetic architecture of drug response is important for designing personalized medicines to effectively combat HIV/AIDS. Systems mapping is shown to be particularly powerful for tackling the complexity of the genetic control mechanisms of virus-host interactions [54,184]. The decline trend of viral load in the host after an antiviral therapy, followed by the possible emergence of drug resistant viruses in the therapy, can be described by a high-dimensional group of ordinary differential equations (ODE). By incorporating the difference of wild-type and mutant viruses, Bonhoeffer et al. [13] obtained the following ODE:

$$\begin{array}{l}\frac{dx}{dt}=\lambda -dx-{\beta }_{1}x{v}_1-{\beta }_{2}x{v}_2\\ \frac{d{y}_1}{dt}={\beta }_1(1-\mu )x{v}_1+{\beta }_2\mu x{v}_2-a{y}_1\\ \frac{d{y}_2}{dt}={\beta }_1\mu x{v}_1+{\beta }_2(1-\mu )x{v}_2-a{y}_2\\ \frac{d{v}_1}{dt}=k_1{y}_1-u{v}_1\\ \frac{d{v}_2}{dt}=k_2{y}_2-u{v}_2\end{array}$$ (10)

where there are five variables: uninfected cells, x, cells infected by wild-type virus, y₁, cells infected by mutant virus, y₂, free wild-type virus, v₁, and free mutant virus, v₂. These five types of cells interact with each other to determine the pharmacodynamic changes of drug resistant virus in a host’s body. The mutation rate between wild-type and mutant is given by μ (in both directions). For a small μ, the basic reproductive ratios of wild-type and mutant virus are R₁ = β₁λk₁/(adu) and R₂ = β₂λk₂/(adu). The system (7), defined by nine parameters (λ, d, β₁, β₁, μ, a, k₁, k₂, u), shows that the expected pretreatment frequency of resistant mutant depends on the number of point mutations between wild-type and resistant mutant, the mutation rate of virus replication, and the relative replication rates of wild-type virus, resistant mutant, and all intermediate mutants [13].

Mathematical models of pharmacodynamics reactions (10) have proved very powerful for characterizing complex three-way interactions among the host, pathogen and drug to provide quantitative insights into the biochemical mechanisms that leads to drug sensitivity and resistance. Now, these models have been integrated into systems mapping, gleaning an additional dimension of how genes participate in drug response [54,184]. The basic condition of this integration is to genotype a panel of patients for molecular markers who are measured for those five variables that constitute ODE (7) repeatedly at a series of time. Founded on mixture (7), this integration is implemented with linkage disequilibria between markers and QTLs since the mapping population is derived from a natural population. Guo et al. [54] gave a procedure for the pattern of genetic control over the dynamic change of uninfected cells, cells infected by wild-type virus, cells infected by mutant virus, free wild-type virus and free mutant virus after the patients are administered. This procedure can particularly test whether and how genetic pleiotropy impacts on the correlated change of these different cell and virus types. Such genetic information is helpful for clinical professionals to design and deliver the drug in an effective way based on a patient’s genetic blueprint [152].

3.3. Systems mapping meets stochastic biology

There are fundamental physical reasons why biochemical processes might be subject to noise and stochastic fluctuations [125]. A stochastic modeling approach based on the probabilistic description of the transition rates of different stages has been shown to be useful for predicting the dynamic behavior of a system. It is thought to produce more accurate results than the deterministic approach. One interesting application of the stochastic model is to study the degree of increase of disease risk with age. For example, based on the mutation accumulation hypothesis stating that cancer arises through the sequential accumulation of mutations within cell lineages, Frank [43] proposed a system of differential equations to describe how the mutations increase with age to lead to cancer, expressed as

$$\begin{array}{l}\frac{d{y}_0}{dt}=-u_0{y}_0\\ \frac{d{y}_b}{dt}=u_{b-1}{y}_{b-1}-u_b{y}_b,b=1,\dots ,M-1\\ \frac{d{y}_M}{dt}=u_{M-1}{y}_{M-1}\end{array}$$ (11)

where y_m (m = 0, …, M) is the number of cell lineages with m mutations at age t; and u_m is the rate at which lineages progress from having m mutations to having m + 1 mutations. It is assumed that an individual has cancer once she has a single lineage with M mutations. The simplest deterministic model assumes that the u_m values are constant over age. But a realistic model is based on a system of stochastic differential equations (SDE), which views these values as changing with age. The advantage of SDEs is that they allow the decomposition of the noise affecting the system into a system noise term representing unknown or incorrectly specified dynamics and a measurement noise term accounting for uncorrelated errors. This advantage will help to increase the flexibility of the models for describing the system.

To reflect that cancer arises as uncontrolled clonal growth of cancerous cells following several mutations, Frank [43] implemented clonal expansion into the model (11). A new model is written as

$$\begin{array}{l}\frac{d{y}_0}{dt}=y_0{D}_0(t,0)\\ \frac{d{y}_b}{dt}={\displaystyle {\int }_0^t{u}_{b-1}{y}_{b-1}}{D}_b(t,s)ds,b=1,\dots ,M-1\\ \frac{d{y}_M}{dt}={\displaystyle {\int }_0^t{u}_{M-1}{y}_{M-1}}ds\end{array}$$ (12)

where u_b−1y_b−1 is the influx of cells with b − 1 mutations at time s, $D_b(t,s)=\exp \left(-{\displaystyle {\int }_s^t{u}_b(Z)dZ}\right)$ is the decay or outflux of these cells over the remaining period from s to t, with Z being the number of cells in the clone. Clonal expansion y follows a logistic equation, expressed as

$$Z_b=\frac{K_b{e}^{r_{b}t}}{K_b+e^{r_{b}t}-1}$$ (13)

where K_b is the carrying capacity and r_b is the intrinsic rate of increase of the clone with b mutations [43]. It is possible that clones with different numbers of mutations have different carrying capacities and rates of increase. Let v denote the mutation rate per cell, which, multiplied by the clone size, is the total mutational capacity of a cell lineage. Thus, we have

$$D_b(t,s)=\exp \left(-{\displaystyle {\int }_s^t{v}_b{Z}_b(\tau )d\tau }\right)={\left(\frac{K_b}{K_b+e^{r_b(t-s)}-1}\right)}^{\frac{v_b{K}_b}{r_b}}.$$

The total transition rate from cells with b mutations to cells with b + 1mutations is the mutation rate per cell, v_b, multiplied by the average size of clones with b mutations, which leads ultimately to

$$U_b=v_b{\displaystyle {\int }_0^t{u}_{b-1}{y}_{b-1}{D}_b(t,s)Z_b(t-s)ds/y_b.}$$ (14)

Being more sophisticated than SDE (11), SDE (12) integrates mutation accumulation and clonal expansion to model age-specific accelerations of cancer via two types of parameters (v_b, r_b, K_b), allowing the estimation of any number of rounds of clonal expansion. If these two types of SDE are incorporated into systems mapping, we can construct a predictive model for the occurrence of cancer from an individual’s genetic structure based on prior knowledge obtained from a genetic mapping study. Assume that such a study is launched, which contains a set of genotyped individuals whose number of cell lineages with different numbers of mutations is measured at different ages. By analyzing the marker and phenotypic data, systems mapping enables the characterization of specific QTLs involved in age-specific acceleration of cancer.

Suppose that, from the above-mentioned study, a significant QTL has been detected by implementing equations (12). For each of three possible genotypes of this QTL, a different set of SDE parameters was estimated, with which the curves of acceleration were drawn (Fig. 8). The patterns of age-specific acceleration were found to be very different, depending on QTL genotypes. QTL genotype qq, with three rounds of clonal expansion, display a pronounced peak in the acceleration curve of cancer at age 60 years, which is much higher and more delayed than the other genotype Qq and QQ with two and one round of clonal expansion. From this hypothesized example, it is shown that systems mapping has great power to predict the pattern and time of cancer occurrence based on patient’s genotypes at significant loci.

Figure 8.

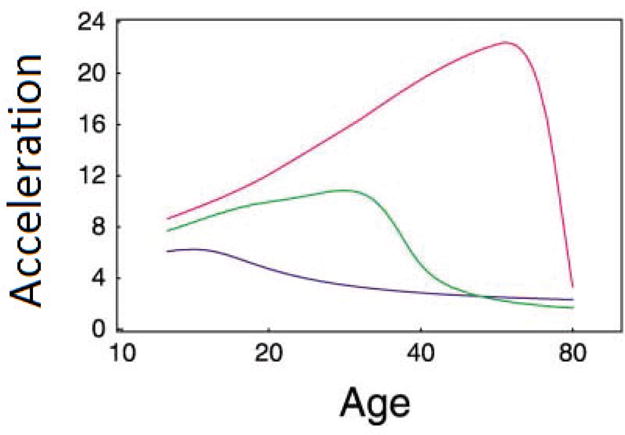
Patterns of age-specific acceleration for different genotypes at a hypothesized QTL. Three genotypes show different forms of acceleration curves, indicating the role of the QTL in cancer pathogenesis. The first genotype QQ is denoted by a blue curve, for which clonal expansion occurs only in the last round before cancer, so K_{M − 2} = K_{M − 3} = 1; the second genotype is denoted by a green curve, whose clonal expansion occurs in the last two rounds before cancer, with K_{M − 2} = 10⁶ and K_{M − 3} = 1; and the third genotype is denoted by a red curve, where clonal expansion occurs in the last three rounds before cancer, with K_{M − 2} = K_{M − 3} = 10⁶. The mutation rates for these three genotypes are v_m = 5.8 × 10⁻⁴, 9.3 × 10⁻⁵, and 1.55 × 10⁻⁶ for m mutations to keep the total incidence of cancer at 10%, respectively. Basic parameters are M = 4, x₀(0) = 10⁴, r_m = 0.5 for all m, K₀ = 1, and K _{M − 1} = 10⁶. This example was made up from Frank’s [43] analysis.

3.4. Systems mapping of phenotypic landscapes

The development of complex traits is the consequence of interactions among a multitude of genetic and environmental factors that each trigger an impact on every step of trait development. This process is inherently complicated, but can be illustrated by a landscape of phenotype formed by genetic and environmental variables [121,168]. The surface of such a phenotype landscape defines the phenotype determined by a particular combination of underlying genetic (such as additive, dominant or epistatic) and environmental factors (such as temperature, light or moisture) that interact with each other through developmental pathways. The number of underlying factors contributing to phenotypic variation defines the number of dimensions of the landscape space. In theory, the number of underlying factors can be unlimited, implying that a landscape can exist in a very high dimensional space (i.e., hyperspace) [168]. By characterizing the topographical features of such a landscape, typically including slope, curvature, peak-valley and ridge [168], a fundamental question of how each underlying factor contributes to phenotypic expression individually or through an interactive web can be addressed.

The topography of a phenotypic landscape can be determined by the degree and pattern of phenotypic changes in response to different environmental factors. For example, photosynthesis as the primary process in plant growth is determined by many biotic or abiotic environmental factors, such as leaf age, CO2 concentration, temperature, irradiance, nutrient, and water potential. The responsiveness of photosynthetic rate to each of these factors follows different physiological mechanisms during a multi-step of development, leading to a particular phenotypic landscape of photosynthesis. Wu et al. [171] integrated functional mapping to determine the genetic machinery of the reaction norms of photosynthetic rate simultaneously to these factors by using mechanistic or empirical models for describing the relationship of various biotic or abiotic factors, separately or jointly, with photosynthetic rate [139,172].

Systems mapping can play a central role in illustrating an overall picture of the genetic control of phenotypic sensitivity to multiple environmental factors and discerning the differences of genetic control over response to each environmental factor. This can be done by integrating a system of partial differential equations (PDE) that can deal with functions of multiple variables, beyond ordinary differential equations describing functions of a single variable. Consider plant height growth as a phenotypic landscape. It is determined by many factors, but two of which, temperature (f₁) and nutritional concentration (f₂), are considered. The PDE that specifies the topography of plant height growth (H) is expressed as

$$\frac{dH}{dt}=rH\left(1-\frac{H}{K}\right)+D_1\left(\frac{{\partial }^{2}H}{\partial f_1^2}\right)+D_2\left(\frac{{\partial }^{2}H}{\partial f_2^2}\right)$$ (14)

where r is the plant’s intrinsic rate of growth, K is the carrying capacity, and D₁ and D₂ are the diffusion coefficients that measures the rates of change per temperature and nutritional concentration, respectively. By estimating a set of PDE parameters (r, K, D₁, D₂), we can visualize the phenotypic landscape of plant height growth.

Systems mapping allows QTL genotype-specific PDE parameter sets to be estimated and tested and, therefore, is empowered with a capacity to test how a specific QTL affects the slope, curvature, peak-valley and ridge of the growth landscape. This test enables geneticists to understand the mechanistic formation of the landscape. More interestingly, it can also test whether there is the common genetic basis for different environmental responses and how the QTL affects a web of interactions between different environmental responses toward plant height growth curves. Mathematically, SDE (14) is fairly flexible to accommodate to multiple developmentally related phenotypic traits, such as plant height and diameter growth. The integration of these high-dimensional SDE into systems mapping can enhance the level of addressing biological questions, such as physiological pleiotropy of different traits [93], ecological pleiotropy of phenotypic plasticity to different environmental factors [135], and developmental pleiotropy of the same trait varying over time [117]. Because SDE has not been popular to geneticists, a heavy involvement of applied mathematicians is essential for the implementation of SDE into systems mapping and the mechanistic underpinnings and interpretation of SDE models in a biologically intuitive way.

4. Ecological dissection of complex traits

There has been increasing recognition that the traits of an individual are not only influenced by its own genes but also strongly by the genotypes of its neighbors [75,77]. For example, the feather condition of a laying hen is controlled both by its own genes and the genes of its partners through some serotonin pathway [11]. Using integrated genetic mapping and structural equation models, a QTL was detected for flowering time in focal plants that pleiotropically affects the expression of developmental traits in the neighbor plants [169]. Given these findings, phenotypic formation can be viewed as a system of cooperative or competing interactions between biological entities. Game theory can be integrated to quantify the extent of individual-individual interactions [107,114] and reveal the genetic machineries for cooperation and competition that take place in a community.

4.1. Dynamic game theory

Game theory, originally developed to study conflict and cooperation between decision makers, has found its implications in biology because of the pioneering work of evolutionary game theory by John Maynard-Smith and George R. Price [104]. On a dynamic scale, the evolutionary game theory can be mathematically formulated to describe the growth of two individuals in the shared environment by using a coupled group of ODE, expressed as

$$\begin{array}{l}\frac{dx}{dt}={\alpha }_x-{\beta }_{x}x-F(x,y;{\gamma }_{x\leftarrow y})\\ \frac{dy}{dt}={\alpha }_y-{\beta }_{y}y-F(x,y;{\gamma }_{y\leftarrow x})\end{array}$$ (15)

which characterize the rate of change of sizes of the two individuals, x and y. The first two terms of equations (15) on the right-hand side describe neighbor-independent growth in terms of a Gompertz model, where α_x and α_y are thought of as an intrinsic growth rate due to the uptake of resources, and β_xx and β_yy are a metabolic loss proportional to the size of the individuals. The last term on the right-hand side couples the growth of the neighboring individual by means of a kernel function F(x,y), which in general depends at least on the size of the target individual and the size of the neighbor, with the extent characterized by γ_x←y (quantifying how individual y affects individual x) and γ_y←x (quantifying how individual x affects individual y). Many studies have discussed the choice of the kernel function although more work is needed to obtain an optimal function [128].

We can cast this formulation in a game theoretic context in the following way. Given equations (15), we may assume that a rest point for the ODE is an energy minimizing (payoff maximizing) point for the two individuals engaged in competition. In this case, we can write

$$\begin{array}{l}{\pi }_x(x,y)={\alpha }_{x}x-\frac{1}{2}{\beta }_x{x}^2+F(x,y;{\gamma }_{x\leftarrow y})\\ {\pi }_y(x,y)={\alpha }_{y}x-\frac{1}{2}{\beta }_y{x}^2+F(x,y;{\gamma }_{y\leftarrow x})\end{array}$$ (16)

as the two payoff functions (energy-cost functions) of the individual. A first order necessary condition for a Nash equilibrium is [111,124]:

$$\begin{array}{l}\frac{\partial {\pi }_x}{\partial x}={\alpha }_x-{\beta }_{x}x+F(x,y;{\gamma }_{x\leftarrow y})=0\\ \frac{\partial {\pi }_y}{\partial y}={\alpha }_y-{\beta }_{y}y+F(x,y;{\gamma }_{y\leftarrow x})=0\end{array}$$ (17)

when we assume that

$$\begin{array}{l}\frac{\partial f(x,y;{\gamma }_{x\leftarrow y})}{\partial x}=F(x,y;{\gamma }_{y\leftarrow x})\\ \frac{\partial f(x,y;{\gamma }_{y\leftarrow x})}{\partial y}=F(x,y;{\gamma }_{x\leftarrow y})\end{array}$$ (18)

Thus, Nash equilibrium in the two-player continuous strategy game implies a fixed point in the differential system (16). Following Antoniadis et al. [4], if we assume an evolutionary rule given by a better response function (i.e., Jacobi iteration) as opposed to the traditional replicator dynamics of evolutionary game theory [159], then we recover exactly the dynamics in equations (15) as a result of co-evolution.

After a proper kernel function is chosen, the test of parameters γ_x←y, γ_y←x can provide information about how the growth of one individual is affected by the second individual. If γ_x←y, γ_y←x = 0, the two individuals are independent. If γ_x←y, γ_y←x < 0, this suggests that the two individuals are of conflict, while if γ_x←y, γ_y←x > 0 they are thought to be cooperative. Such mathematical formulation of conflict and cooperation allows game theory to be quantified and further used for the ecological dissection of trait expression. By embedding it into systems mapping, this theory helps to characterize the genetic components that contribute to the formation and progression of complex traits driven by ecological interactions.

4.2. Game theory meets system mapping

Are there specific genes that control the strengths and patterns of interactions between different species in a dynamic community and ecosystem? This question has been raised intensively because of the recent emergence of community and ecosystem genetics as a new discipline aimed to study how genetic variation in one species influences the composition of associated communities and the functioning of ecosystems [1,6,10,60,164–166]. The integration of systems mapping and evolutionary game theory can address this question, enabling the genetic mapping of genes involved in a network of interspecific interactions. It is likely that this integration can facilitate the movement of community genetics research from its first generation focusing on intra- and interspecific genetic variation to its second generation seeking for a mechanistic understanding of genes that structure communities and ecosystems [2].

While broad-scale empirical and theoretical efforts have addressed the relative importance of inter- and intra-specific effects and variation on community processes, it is now a time to initiate fine-scale genetic mechanistic approaches through systems mapping. The confluence of two traditionally separated areas, statistical genetics and game theory, helps to build a cohesive and predictive framework between community ecology, evolutionary biology, genetics and genomics.

5. Regulatory dissection of complex traits

The development of any trait can be modeled as a dynamic system consisting of various biological parts which coordinate to determine a final phenotype through genetic regulation (Fig. 1). In this section, we focus on regulatory pathways from DNA to cellular physiology through transcript, protein and metabolic expression. We do not review specific examples of how to construct genotype-phenotype maps with regulatory data (see [20]), rather than provide a general procedure of integrating this information flow into systems mapping.

5.1. Network mapping

To measure a cellular system, an understanding of how gene, protein, metabolic and physiological events are expressed in time course is crucial. Attempts to correlate gene expression data with proteomic and metabolomic data have been made by using classic correlation methods or multivariate statistics. However, they have often proved to be unsatisfactory in large part because the timescales of various biological control functions are either very different or simply unknown. Figure 9, modified from Nicholson et al. [113], shows such a problem, in which two pairs of gene-protein couples are expressed in time course. It can be seen that the levels of mRNA transcripts are not consistent with protein levels on timescales. If the action of the stimulus, such as environmental intervention, is at the genetic level, it will take a finite amount of time in a cell for the associated protein synthesis (or post-translational modification) to occur. Also, the duration of the gene events (t_g) and protein events (t_p) may be very different. All this will lead to the consequence that the observed covariance of the gene and protein events is highly dependent on sampling time point and frequency. In some instances, a single sampling point (say τ₃) might result in the incorrect assumption that gene 2 co-varied with protein 1. The times of maximal activity or expression for protein may not be constant; for example, the t_p values and related turnover times are larger for protein 2 than protein 1. A problem also exists when attempting to correlate proteomic with metabolomic data. Currently proteomic data sets contain no information on the activity of specific proteins, which is dependent on their location in the cell and the presence of cofactors or inhibitors.

Figure 9.

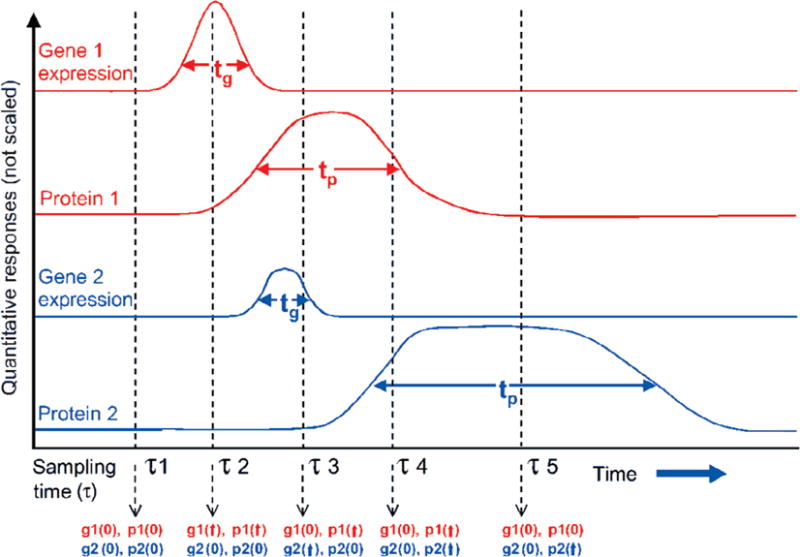
Dynamic changes of two hypothesized gene-protein couples (relating transcription activity to protein level) that are expressed in response to an environmental stimuli at time zero. g₁(0), g₂ (↑); p₁(0), p₂(↑) describe the relative condition for the expression of each gene and protein at a given time-point (e.g. τ₁, τ₂, etc.), where (0) indicates baseline level and (↑) indicates expression. It can be seen that the post intervention observation of relative state is dependent on sampling time-point, which can be considered by differential equations. Adapted from Nicholson et al. [113].

To understand true quantitative relationships between thousands of gene-protein couples or protein-metabolite couples in a cellular system, a series of high-dimensional systems of differential equations have been established by considering several critical factors, such as the time displacement of the genetic and protein synthetic and post-translational events, their different timescales and their half-lives [14,72,81,113]. These mathematical equations are integrated with systems mapping, leading to the birth of a new mapping model, called network mapping, which can map interactive eQTLs, pQTLs, and mQTLs underlying transcriptional, proteomic, and metabolomic profiles and interaction networks among these different profiles [155]. The model has power to test what are the most important pathways that cause final phenotypes and how QTLs control these pathways.

5.2. Dissecting rhythmic biology

The molecular bases of circadian rhythms have been clarified during the past decade by experimental advances, first in Drosophila and Neurospora, and more recently in cyanobacteria, plants and mammals [30,52,193]. In view of the large number of variables involved and of the complexity of feedback processes that generate oscillations, mathematical models are necessary to comprehend the transition from simple to complex oscillatory behavior and to delineate the conditions under which they arise [52].

Based on the negative control exerted by the PER protein on the expression of per, a molecular model governed by a set of five ordinary differential equations was derived [51]. In the model (Fig. 10a), the per gene is first expressed in the nucleus and transcribed into per mRNA. The latter is transported into the cytosol, where it is translated into the PER protein, P₀, and degraded. The PER protein undergoes multiple phosphorylation, from P₀ into P₁ and from P₁ into P₂. These modifications, catalyzed by a protein kinase, are reverted by a phosphatase. The fully phosphorylated form of the protein is marked up for degradation and transported into the nucleus in a reversible manner. The nuclear form of the protein (P_N) represses the transcription of the gene.

Figure 10.

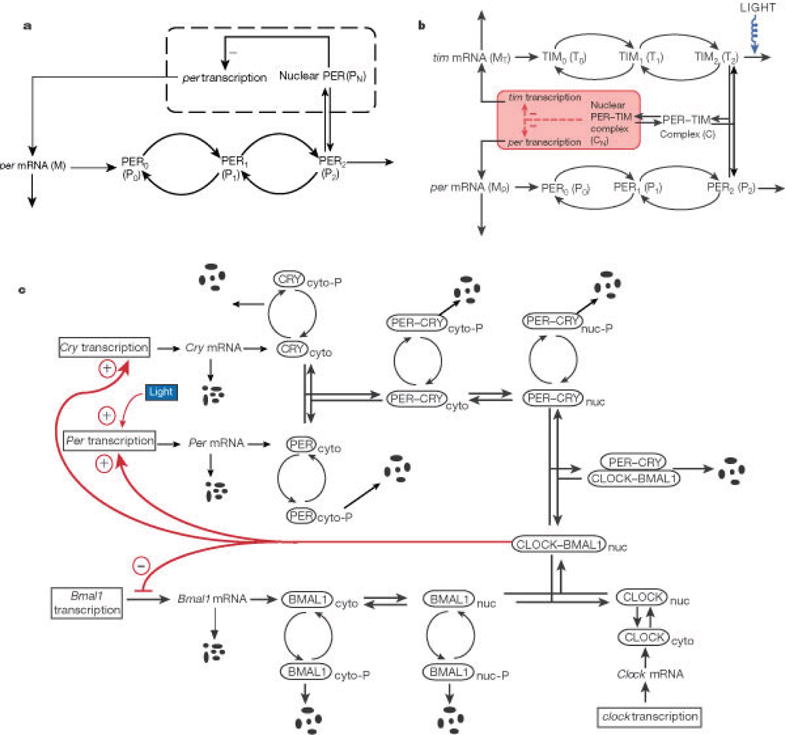
Molecular models for explaining circadian oscillations. (a) Model for circadian oscillations in Drosophila based on negative autoregulation of the per gene by its protein product PER. (b) Model for circadian oscillations in Drosophila incorporating the formation of a complex between the PER and TIM proteins. (c) Model for circadian oscillations in mammals incorporating indirect, negative autoregulation of the Per and Cry genes through binding of the PER–CRY dimer to the complex formed between the two activating proteins CLOCK and BMAL1. Adapted from Goldbeter [52].

In the model, the temporal variation of the concen- trations of mRNA (M) and of the various forms of the regulatory protein–cytosolic (P₀,P₁,P₂) or nuclear (P_N)–is governed by the following system of ODE:

$$\begin{array}{l}\frac{dM}{dt}=\frac{v_s{K}_I^n}{K_I^n+P_N^n}-\frac{v_{m}M}{k_m+M}\\ \frac{d{P}_0}{dt}=k_{s}M-\frac{V_1{P}_0}{K_1+P_0}+\frac{V_2{P}_1}{K_2+P_1}\\ \frac{d{P}_1}{dt}=\frac{V_1{P}_0}{K_1+P_0}-\frac{V_2{P}_1}{K_2+P_1}-\frac{V_3{P}_1}{K_3+P_1}+\frac{V_4{P}_2}{K_4+P_2}\\ \frac{d{P}_2}{dt}=\frac{V_3{P}_1}{K_3+P_1}-\frac{V_4{P}_2}{K_4+P_2}-k_1{P}_2+k_2{P}_N-\frac{v_d{P}_2}{K_d+P_2}\\ \frac{d{P}_N}{dt}=k_1{P}_2-k_2{P}_N\end{array}$$ (19)

where per mRNA (M) is synthesized in the nucleus and transfers to the cytosol (where it accumulates at a maximum rate v_d) and it is degraded by an enzyme of maximum rate v_m and Michaelis constant K_m, and the rate of synthesis of the PER protein, proportional to M, is characterized by an apparent first-order rate constant k_s. Parameters V₁, …, V₄ and K₁, …,K₄ denote the maximum rate and Michaelis constant of the kinase(s) and phosphatase(s) involved in the reversible phosphorylation of P₀ into P₁ and P₃ into P₂, respectively. The fully phosphorylated form (P₂) is degraded by an enzyme of maximum rate v_d and Michaelis constant K_d, and transported into the nucleus at a rate characterized by the apparent first-order rate constant k₁. Transport of the nuclear, bisphosphorylated form of PER (P_N) into the cytosol is characterized by the apparent first-order rate constant k₂. The negative feedback exerted by nuclear PER on per transcription is described by an equation of the Hill type, in which n denotes the degree of cooperativity, and K_I denotes the threshold constant for repression. A more sophisticated set of differential equations can be derived when the pathways in Fig. 10b or 10c are considered.

We integrate five-variable ODE (19) into network mapping to identify QTLs for circadian rhythms and test how these QTLs have sustained oscillations of the system. Figure 11 illustrates the rhythmic curves of three genotypes at a QTL assumed to be detected by network mapping. When plotting the time evolution of per mRNA (M) as a function of the total amount of PER protein (P_tot), these oscillations evolve toward a limit cycle (i.e., a closed curve) (Fig. 11). It is interesting to see that the shapes and periods of rhythmic curves are very sensitive to different combinations of the parameters that determine the rhythms. A small change will lead to marked differences in rhythmic curves (Fig. 11), suggesting that testing genetic differences in parameter combinations is an effective way for understanding the genetic mechanisms for biological rhythms.

Figure 11.

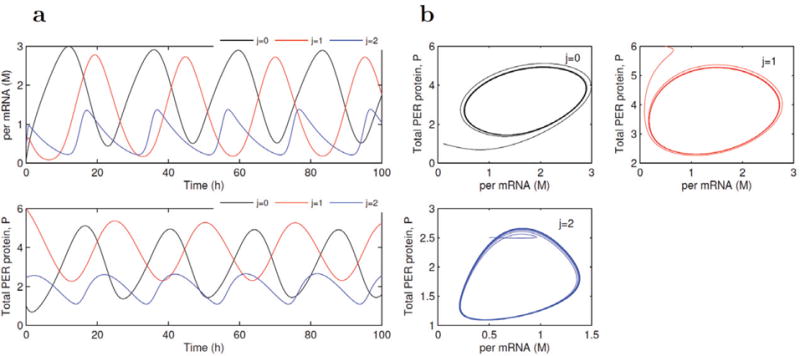
Sustained oscillations of per mRNA and the total amount of PER protein and limit cycle generated by ODE (19). Rhythmic curves for three genotypes. j = 0 for qq, 1 for Qq, and 2 for QQ, at a hypothesized QTL are determined by a combination of parameters, i.e., (v_s,v_m,K_s,v_d,k₁,k₂,K_l,K_d,K₁,K₂,K₃,K₄, n,v₁,v₂,v₃,v₄,K_m) = (0.76, 0.65,0.38,0.95,1.9,1.3,1,0.2, 2,2,2,2,4, 3.2,1.58,5,2.5,0.5) for curve genotype j = 0, (0.82,0.5,0.28,0.6,2.3,1,1.6, 0.5,2.2,2.2,2.2,2.2,6,2.2,1.38, 8,1.5,0.7) for curve genotype j = 1, and (0.30,0.48,0.75,1.5,0.8,0.6,0.7,2.5,2.5, 2.5,2.5,9.9,4.2,1.8,1.2,9,0.5, 1.5) curve genotype j = 2.

In several studies of drug response, the so-called clock genes were found to affect patients’ circadian rhythms through clock-controlled transcription factors, holding a promise for the determination of an individualized optimal body time for drug administration based on a patient’s genes. It has been suggested that drug administration at the appropriate body time can improve the outcome of pharmacotherapy by maximizing potency and minimizing the toxicity of the drug, whereas drug administration at an inappropriate body time can induce severe side effects [116]. In practice, body time-dependent therapy, termed “chronotherapy” [53,76], can be optimized by implementing the patient’s genes that control expression levels of his/her physiological variables during the course of a day.

Network mapping has great power to unravel the genetic control of different aspects of biological rhythms and determine the best time for “chronotherapy” based on individual patient’s genetic background. Also, some fundamental questions will be addressed from these tests: (1) How do QTLs determine periodic motions in a biological system? (2) How can the synchronization of different variables be achieved in a rhythmic system through genetic regulation? (3) How can mathematical equations be integrated into genetic mapping models for circadian rhythms related to clock-and-wavefront, reaction- diffusion, and cell-cycle processes?

6. Genetic and statistical considerations

In the preceding sections, we have described and reviewed basic principles of dissecting complex traits in terms of their underlying genetic, developmental and regulatory underpinnings using genetic mapping approaches. Genetic mapping relies on two issues, mapping population and statistical approach. Lander and Botstein’s [78] original mapping population is based on an experimental cross. Other types of mapping populations can also be used, depending on the organism. We will describe those commonly used mapping populations. Although there have been numerous statistical approaches developed for genetic mapping, we will briefly review the mathematical and statistical methods that are critically used in systems mapping and network mapping.

6.1. Genetic designs

Experimental crosses

Advanced generations, like the backcross, F₂ or recombinant inbred lines (RILs), produced through continuous controlled crosses initiated with two inbred strain, form a segregating population suitable for genetic mapping. In many non-model outcrossing species, such as forest trees, the F₁ generation from two heterozygous parents, called the full-sib family, can produce the segregation of marker genes. However, unlike the advanced-generation populations, the full-sib family contains inconsistent patterns of marker segregation. The algorithm has been developed to simultaneously analyze all these different marker types [94,133,182]. Genetic mapping with experimental crosses is founded on linkage analysis of the recombination fraction between different loci.

Multigenerational families

In humans, neither adequate numbers of progeny can be generated from a single family nor can any controlled cross be made possible. A nuclear family with multiple successive generations in humans is often used in order to accumulate a sufficient number of progeny for genetic mapping. The recombination fraction and identical by decent (IBD) coefficient are the key determinants of genetic mapping with multigenerational families.

Unrelated individuals randomly sampled from natural populations

The genetic mapping of complex traits can be conducted by sampling a collection of unrelated individuals at random from a natural population. In a population, different loci are genetically associated, with the extent described by a parameter called the linkage disequilibrium (LD). By making use of recombinants accumulated over a long history of generations, LD-based mapping is meritorious in terms of high-resolution dissection of a target QTL into a narrow genomic region [132].

Unrelated families randomly sampled from natural populations

Although LD mapping has tremendous potential to fine map functional genes for a complex trait, it may provide a spurious estimate of LD in practice when the association between genetic loci is due to evolutionary forces, such as mutation, drift, selection, population structure, and admixture. A mapping strategy that samples unrelated families (composed of parents and offspring) from a natural population is helpful for overcoming the limitation of LD mapping by simultaneously estimating the linkage and linkage disequilibrium [64,84,175,179]. This design can also estimate the genetic imprinting effect of QTLs by discerning the difference of maternal- and paternal-inherited alleles [138].

Natural populations with related families

Genetic studies of some particular complex traits require a mapping population to be derived from multiple related families. For such a genetic design, the recombination fraction, IBD, and linkage disequilibrium will be needed to be estimated at a time, tracing the co-transmission of alleles from parents to their offspring. This design is powerful for studying the evolution of genes that control human traits, such as drug response.

6.2. Mathematical and statistical solutions

The methodological challenge of systems mapping and network mapping are that we need to implement and develop rigorous mathematical and statistical approaches for resolving differential equations. The recent years have seen tremendous developments in addressing these challenges. Our review is focused on those which have been used or have a direct application to the problems described in this article. Interested readers are referred to the relevant mathematical or statistical literature [95,119,185].

How to solve high-dimensional ordinary differential equations (HiODE)

As the dimension of a system increases, it is crucial to better handle HiODE. Convergence rates and estimation consistency are important for the parameter estimation of HiODE. Mathematical analysis and computer simulation have been heavily used to investigate the mechanistic underpinnings of HiODE and the behavior of dynamic systems described by these equations [95].

How to solve delay differential equations (DDEs)

While modeling the oscillation behavior of mRNA and protein concentrations, we often encounter time delays of a system. Feng and Navaratna [41] and Verdugo and Rand [143] developed mathematical approaches for manipulating linear or nonlinear relationships between the dependent variables and time delays. When a DDE contains multiple time delays, the following questions should be addressed: (1) in which range of each of differential parameters, does Hopf bifurcation occur, i.e., there are sustained oscillations? (2) how do different time delays determine periodic motions in a biological system? (3) how can the synchronization of different variables be achieved in a rhythmic system? (4) how can mathematical equations be integrated into biological models for circadian rhythms, such as the clock-and-wavefront model, the reaction-diffusion model, and the cell-cycle model?

How to solving stochastic differential equations (SDE)

Numerical solution of SDE is a relatively young field. Almost all algorithms used for the solution of ODE may work poorly for SDEs. A few basic algorithms, such as Euler’s method and Itō’s method, have been proposed for solving SDE (incorporating white noise) [73]. These algorithms can provide the condition under which a given a given SDE has a solution, and determine whether or not the solution is unique.

How to solve partial differential equations (PDE)

PDE and their solutions exhibit rich and complex structures. The finite element discretization method has been implemented for solving SDEs. This numerical approach can easily handle geometrically complicated domains and construct high-order interactions. No prior knowledge is needed for this method [140].

6.3. Modeling covariance structure

Robust modeling of longitudinal covariance structure (9) is a prerequisite for appropriate statistical inference of genetic effects on longitudinal traits. Several different approaches are available for covariance modeling, including parametric, nonparametric, and semiparametric.

Parametric modeling

The advantage of parametric approaches includes the existence of closed forms for the determinant and inverse of a longitudinal matrix. This will greatly help to enhance computational efficiency. The following is a list of existing parametric approaches used to model functional mapping: stationary parametric model – assuming the stationarity of variance and correlation (e.g., autoregressive (AR) model) [98], non-stationary parametric model – variance and correlation may not be stationary (e.g., structured antedependence (SAD) model) [195,197], and general parametric model (autoregressive moving average model ARMA(p,q)) [86]. For each model above, it is important to determine its optimal order for covariance structure modeling in the most parsimonious way by a model selection criterion.

Nonparametric modeling

In many cases, the covariance structure may not follow a parametric structure, which can be better modelled by a nonparametric approach. There is a nonparametric estimator derived to model the covariance structure without assuming stationarity using kernel-weighted local linear regression smoothing of sample variograms ordinates and of squared residuals [197]. Das et al. [27] implemented a B-spline approach for modeling time-varying covariances and covariances for longitudinal traits.

Semiparametric modeling

More recently, Fan et al. [38] proposed a semiparametric model for the covariance structure of irregular longitudinal data, in which they approached the time-dependent correlation by a parametric function and the time-dependent variance by a nonparametric kernel function. The Fan et al. model’s advantage lies in the combination between the flexibility of nonparametric modeling and parsimony of parametric modeling. The establishment of a robust estimation procedure and asymptotic properties of the estimators will make this semiparametric model useful in the practical estimation of the covariance function [190].

In many longitudinal trials, data are often collected at irregularly spaced time points and with measurement schedules specific to different subjects. The efficient estimation of covariance structure in this situation will be a significant concern for detecting the QTLs that control dynamic traits. Although there are many challenges in modeling the covariance structure of subject-specific irregular longitudinal data, many workers have considered this issue using different approaches. These include nonparametric analysis derived from a two-step estimation procedure [37,183], a semiparametric approach [35], a penalized likelihood approach [65], and functional data analysis [189].

7. Discussion and prospects

The genetic mapping of complex traits has developed to a point at which current sequencing technologies can allow trait phenotypes to be partitioned into their underlying components at the DNA, regulatory, cellular and developmental levels [20,48,115]. As shown in a diagram of genetic mapping that links DNA variants with final phenotypes at different levels (Fig. 1), genetic mapping can be performed by five approaches. First, genetic mapping, originally proposed by Lander and Botstein [78], is a fundamental approach for linking DNA polymorphisms with end-point phenotypes measured at a static point. Second, beyond the original mapping approach, functional mapping has been derived for mapping QTLs that govern the developmental process of trait development through mathematical equations [98,174]. Third, functional mapping has been extended to systems mapping in which a phenotype is mapped by treating it as a dynamic system composed of interacting components linked through a system of differential equations [12,176]. Fourth, to identify the pathway mediating the genetic effect on the physiological phenotype, network mapping has been developed [155]. This approach is grounded on the regulatory process of genes that govern mRNA and protein expression toward phenotypic formation through cellular metabolism, a process characterized as a dynamic system by a group of differential equations [81]. All these mapping approaches have afforded an unprecedented understanding of how the control of trait formation is triggered by the interplay between genetic, epigenetic, and environmental factors, facilitating the construction of a precise genotype-phenotype map. Especially, functional mapping can identify developmental genes, supporting evolutionary developmental biology (evo-devo) theory concerned with the discovery and understanding of the changes in developmental mechanisms and their role in the evolutionary origin of aspects of the phenotype [109].

The biological process of trait formation is extremely complex from an ecological view. One cause of this ecological complexity is, as Strauss et al. [136] articulated in their review article, “…species exhibit traits shaped by collections of other species that co-occur with them,” leading to “… every effect of a species on a community will loop back to influence the species itself, either positively or negatively” [167]. Thus, to chart a complete picture of quantitative genetic architecture, we need to study how the traits of one organism are affected by the genes from its own genome and by those from the genome of its partner in the community. It is also possible that epistasis takes place not only among genetic loci in the same genome, but also across genomes [45]. All this growing recognition of the role of ecological interactions in shaping complex traits [1, 6,10,60, 136,164–166] appeals the emergence of the fifth approach for genetic mapping, ecosystem mapping of complex traits.

A biological system, even a cellular system, involved in phenotypic formation, can be dissected into countless continuous subsystems in tandem spanning from DNA variants through regulatory pathways to cellular and developmental processes toward the end-point phenotype. Each subsystem is affected in a complex, usually nonlinear, manner, by biotic and abiotic factors. Todays’ sequencing, genotyping and phenotyping technologies have made available large stores of expression data from different levels of organization. The challenge will never be how these data are collected, rather than how the experiment is designed to maximize the use and interpretation of the data, from which biological rules for the formation and control of every part of a living system can be extracted. The use of genetic mapping from a systematic perspective can facilitate our understanding of how different parts are coordinated and organized into a whole system and what are the genetic roots of the function of these parts. To the end, by altering the pathways of one or more parts, the behavior and outcome of this system can be changed toward what we expect.

Highlights.

• Phenotypic formation is dissolved into several parts, each modeled as a system.

• We review a conceptual framework for genetic mapping of each of these systems.

• This framework is equipped by differential equations to map a system’s structure.

• Systems mapping identifies QTLs useful to construct genotype-phenotype map.