A data-driven approach to prostate cancer detection from dynamic contrast enhanced MRI

Abstract

Magnetic resonance imaging (MRI), particularly dynamic contrast enhanced (DCE) imaging, has shown great potential in prostate cancer diagnosis and staging. In the current practice of DCE-MRI, diagnosis is based on quantitative parameters extracted from the series of T1-weighted images acquired after the injection of a contrast agent. To calculate these parameters, a pharmacokinetic model is fitted to the T1-weighted intensities. Most models make simplistic assumptions about the perfusion process. Moreover, these models require accurate estimation of the arterial input function, which is challenging. In this work we propose a data-driven approach to characterization of the prostate tissue that uses the time series of DCE T1-weighted images without pharmacokinetic modeling. This approach uses a number of model-free empirical parameters and also the principal component analysis (PCA) of the normalized T1-weighted intensities, as features for cancer detection from DCE MRI. The optimal set of principal components is extracted with sparse regularized regression through Least Absolute Shrinkage and Selection Operator (LASSO). A support vector machine classifier was used with leave-one-patient-out cross validation to determine the ability of this set of features in cancer detection. Our data is obtained from patients prior to radical prostatectomy and the results are validated based on histological evaluation of the extracted specimens. Our results, obtained on 449 tissue regions from 64 images, show that the proposed data-driven features outperform the traditional pharmacokinetic parameters with an area under ROC of 0.86 for LASSO-isolated PCA parameters, compared to 0.78 for pharmacokinetic parameters. This shows that our novel approach to the analysis of DCE data has the potential to improve the multiparametric MRI protocol for prostate cancer detection.

1. Introduction

Prostate cancer is the second leading cause of cancer-related death among males [1]. Morbidity is often due to the metastasis of cancer from prostate to bones, which happens only in a small percentage of cases. However, the existing diagnostic techniques cannot adequately determine the stage of prostate cancer. The most commonly used method to detect prostate cancer is a transrectal ultrasound (TRUS) guided biopsy. Although, TRUS provides outstanding details about the boundaries of the gland and bladder, it has a limited ability to accurately image prostate tissues and differentiate malignant from benign tissues [2]. As a result, TRUS-guided biopsy is essentially a blind, systematic procedure which suffers from gross sampling errors. Small cancers may be missed and large or multifocal tumors may be under-sampled (false negative) [3]. Due to the limitations of the existing diagnostic techniques, radical prostatectomy is often used in treating the disease, including instances when the cancer is either pathologically insignificant at one extreme or incurable at the other [4]. This surgery can impact a man’s quality of life by causing urinary incontinence or sexual dysfunctions. Therefore, there is a need for more reliable techniques to confirm cancer location, extent and its stage, prior to deciding on the optimal course of treatment in a given individual. With reliable imaging techniques, approaches such as focal therapy and active surveillance of the patients with lower risk tumors, and avoidance of surgery in non-operable cases become possible.

Since the mid-1980s, magnetic resonance imaging (MRI) has shown great potential in visualization and characterization of prostate anatomy using T2-weighted imaging [5, 6, 7]. However, the sensitivity and specificity acquired from conventional T2-weighted MRI is insufficient for prostate cancer diagnosis and particularly grading of cancer [8, 9, 10]. As a result, the addition of multiple MR modalities (multiparametric-MRI), such as spectroscopy, diffusion imaging, and perfusion imaging, are under study for better tissue characterization [11]. Among these, dynamic contrast enhanced (DCE) MRI is a very promising methodology [12]. The pharmacokinetic parameters extracted from DCE MR images provide physiological information about tissue microvasculature and may be linked to active cancer growth [13, 14]. These parameters, when used in a supervised machine learning framework with diffusion tensor features [15, 16], or with T2-weighted and diffusion weighted features [17], have shown great potential in prostate cancer detection.

The pharmacokinetic parameters are extracted by fitting a model to the the concentration values measured from T1-weighted intensities acquired after the injection of a contrast agent. The sequence of contrast agent concentration values is fitted to one of the several pharmacokinetic models that characterize the perfusion pattern. One of the most commonly used models is the two-compartment Kety model [18]. Accurate pharmacokinetic modeling of DCE MRI data also requires the knowledge of the concentration of the contrast agent in the external iliac or femoral arteries over time, which is known as the Arterial Input Function (AIF). The extraction of AIF requires the segmentation of the cross section of the artery, which is a subjective process. There has been work done with population averaged AIF [18, 19], but with limited temporal resolution of MRI, there is no significant difference between population averaged and individually measured AIF in terms of their diagnostic power [20]. Besides, the modeling process is sensitive to noise and fitting instabilities [21], and the fitting process is complex and difficult for clinical use [22]. Furthermore, most pharmacokinetic models make simplistic assumptions about the perfusion process in tissue. This issue has resulted in limited correlation between individual DCE parameters and the stage of the disease [23, 24], despite the strong evidence of correlation between increase in microvasculature and the pathologic stage of cancer [25, 26]. Therefore, there is a need for new methods for the analysis of the DCE T1-weighted intensities. We address this need by proposing a data-driven and model-free parameterization process for the DCE T1-weighted signal intensities. Model-free parameters are reported in the literature for breast and prostate DCE MRI [27, 28]. In this paper, we further investigate this approach to develop a framework for MRI-targeted prostate biopsies.

Our approach is to devise a learning agent that can detect cancer directly from the T1-weighted intensities without modeling the physical perfusion phenomenon. We investigated two different sets of parameters in terms of their capability to classify prostate cancers. The first set of parameters consists of six empirical model-free parameters that describe the shape of the kinetic curves of DCE T1-weighted signal intensity. The second set of parameters is generated by reducing the dimensionality of the T1-weighted intensities using Principal Component Analysis (PCA). An important question in the use of PCA for feature reduction is the determination of the optimal number of components that will be included in the model. It is also not guaranteed that the components that can explain most of the variance of the data also provide the highest classification accuracy. So we have devised a new solution of extracting the optimal set of features from PCA. To reduce the dimensionality in the PCA space, we used a Least Absolute Shrinkage and Selection Operator (LASSO) model, along with cross-validation to determine the most effective principal components. The resulting parameters were used with Support Vector Machine (SVM) classification. These parameters were generated directly from the DCE MRI signal intensities and therefore do not make any assumption about the perfusion pattern. We compared the proposed features with the traditional pharmacokinetic parameters in terms of their ability to detect cancer. We show that the proposed framework of learning the tissue signature directly from T1-weighted intensities is a promising approach for cancer detection from DCE MRI data.

2. Materials and Methods

2.1. Data Collection Protocols

The data used in this work was obtained in 2010–2011 for a multiparametric MRI study. The study was approved by the Clinical Research Ethics Board of the University of British Columbia and the patients had given their written consent before entering the study. These patients were scheduled for radical prostatectomy and they went through an MRI imaging session before their surgery. The MRI examination was scheduled 3–48 days before the surgery date. The mean time between the MRI session and the radical prostatectomy was 14 days for these patients. The patients recruited for this study had not received any form of therapy before their radical prostatectomy. Detailed information about the patients are given in Table 1.

Table 1.

Clinical data of 16 patients.

Patient	Age (years)	PSA (ng/mL)	Pathology stage	Prostatectomy Gleason score
P041	66.8	6.5	pT3c	3+4
P044	63.9	2.6	pT2c	3+3
P045	60.9	8.3	pT3c	4+4, 3+4, 3+4+5
P047	52.7	4.9	pT2c	3+3
P049	62.3	7.2	pT3a	3+3, 3+4
P050	67.5	5.3	pT3a	3+3, 3+4
P052	61.3	2.9	pT3a	3+3, 3+4
P056	63.0	5.8	pT2c	3+4
P057	66.3	11.4	pT2a	3+3
P058	69.0	5.4	pT2a	3+3
P059	49.6	6.6	pT3b	3+3, 3+4, 4+3
P060	61.8	7.4	pT3a	3+3, 3+4
P061	56.8	11.0	pT3a	3+4
P062	64.4	n/a	pT2c	3+3, 3+4
P063	67.2	7.0	pT2a	3+4
P064	64.8	4.9	pT2c	3+4

2.1.1. MRI Imaging Protocol

MRI examinations were performed on a 3 Tesla MRI scanner (Achieva, Philips Healthcare, Best, The Netherlands) and the signals were acquired with a combination of an endorectal coil (Medrad, Pittsburgh, PA) and a cardiac phased-array coil (Philips Healthcare, Best, The Netherlands). Fast spin-echo T2-weighted images were acquired in the axial and coronal planes using repetition time (TR) of 1851 ms and an effective echo time (TE) of 80 ms with 14 cm field of view (FOV) (284×225 matrix, 3 averages). Each slice was 4 mm thick and there were no gaps between the slices. 12 axial slices were selected from this sequence and used for DCE MRI scans. T2-weighted images were used to identify the anatomical details of the prostate gland to match MR-slices with histology. The majority of the glands were smaller than 48 mm along slice selection direction.

DCE T1-weighted images were acquired using a three-dimensional T1-weighted spoiled gradient echo-sequence with a field of view of 24 cm (TR/TE = 3.4/1.06 ms, flip angle = 15°, 256×163 matrix, 2 averages). The contrast agent used here was Gd-DTPA (Magnevist, Berlex Canada) and 0.1 mmol/kg of Gd-DTPA was injected with a motorized power injector within 10 s at the rate of 2 mL/s, followed by a 20 mL flush of saline. To calculate the contrast agent concentration in the prostate, at first proton density (PD) images were acquired (TR/TE = 50/0.95 ms, flip angle = 45°). Subsequently a series of 75 T1-weighted dynamics were acquired, where 3 dynamics were acquired before the injection of the contrast agent, and the remaining 72 images were acquired following the injection of the contrast agent. The time resolution was 10.6 s per dynamic and the slice thickness was 4 mm. T1 values were calculated based on PD-weighted and T1-weighted images according to the procedure described by Parker et al [29]. DCE MRI data were processed off-line using Matlab (Mathworks, Natick, MA) and Igor Pro (WaveMetrics, Portland, OR).

2.1.2. Pathology Data

After imaging, patients went through surgery. The radical prostatectomy specimens were dissected and histopathologically examined in a uniform manner to acquire the whole-mount analysis. The external surfaces were inked, seminal vesicles were amputated, the apical and bladder neck tissue slices were removed and the specimens were dissected following a minimum of 24-h fixation in 10% buffered formalin. A device described in Drew et al [30] was used to cut the prostate gland from inferior to superior in serial transverse cuts perpendicular to the posterior capsule, at 4 mm intervals, which allowed reasonably good correspondence between the pathology slides and the MR slices. The multi-bladed cutting device consists of an adjustable box that holds the prostate, a plunger tool that prevents rolling or sliding of prostate, and a knife assembly that holds the blades at 4 mm intervals. Once the prostate specimen is placed on the base, the specimen is rotated manually to the orientation that produces the proper slice orientation. The adjustable box was designed to hold the prostate in the correct orientation for matching the MRI and the histology sections. The walls of the device and the plunger include vertical slots to allow the blades of the knife to pass through it. The slots are at 4 mm intervals and the slots on opposite walls are lined up with each other to ensure parallel cuts. The blades of the knife assembly fit through the vertical slots in the adjustable box and cut simultaneously through the sample. The multi-blade device ensures that the histology sections are parallel to each other and exactly 4 mm apart - requirements that are difficult to achieve with manual cutting using a single blade. In addition, careful positioning of the specimen inside the cutting device results in the orientations of the MRI slices and histology sections being very close to each other. Fig. 1 shows different parts of the prostatectomy sectioning device.

Figure 1.

Prostatectomy sectioning device with walls (LW, lateral walls; SIW, superior-inferior walls) inserted in the base (A), multi-bladed knife (B), the rack (C) used to hold the blades while they are cleaned in solution. Reproduced with permission from [30].

A Lieka RM2245 whole body rotary microtome was used to cut the whole mount sections and the sections were submitted as intact transverse sections mounted on oversize glass slides for hematoxylin and eosin staining. In the pathology slides, the regions of prostatic carcinoma were outlined and assigned a Gleason score by an anatomic pathologist with over 20 years of experience.

2.2. Registration

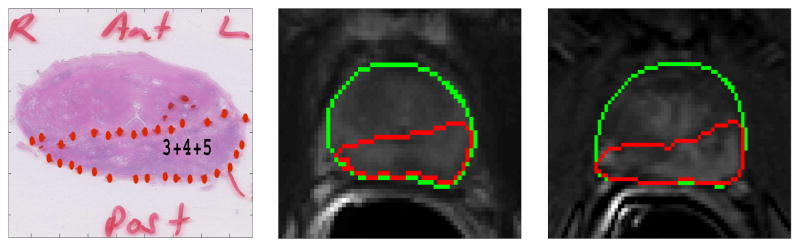
Our tissue cutting protocol and device ensured that the histopathology slides and the T2-weigthed MR slices could be matched. However, due to shrinkage of the tissue after surgery, deformable registration was required to map the histology findings to the MR images. Registration of DCE images to T2-weighted images were also needed to compensate for the motion of the prostate during the prolonged DCE MRI scan. The whole-mount pathology slides were registered with the corresponding T2-weighted MR images by affine registration followed by deformable B-spline registration. T2-weighted images were also registered to the corresponding DCE-MR images following similar procedures. These two transformations were used successively on the pathology slides to register it to DCE-MR images. To register the images, the prostate region was manually segmented in both the fixed (MRI) and the moving images and registration was applied on the segmented region only. Mutual information was used as the similarity measure and adaptive stochastic gradient descent was used as the optimizer to guide the registration process. After registration, the computed transformations were applied to map tumor regions from the pathology slides to the corresponding T2-weighted and DCE-MR images. For registration, we used elastix, which is an open source software for image registration [31]. We used Dice Similarity Coefficient (DSC) to validate the registration. The average DSC value between the pathology and T2-weighted images after registration was 0.94, and between registered T2-weighted and DCE image it was 0.95. Fig. 2 and 3 show two cases where the tumor regions from the pathology slides are mapped to the corresponding T2-weighted and DCE MRI slices.

Figure 2.

Registration example 1: Peripheral zone tumor from pathology slide (left) was mapped to the corresponding T2-weighted (middle) and DCE-MRI slice (right). The green contour represents the boundary of the prostate gland.

Figure 3.

Registration example 2: Peripheral zone tumor from pathology slide (left) was mapped to the corresponding T2-weighted (middle) and DCE-MRI slice (right). The green contour represents the boundary of the prostate gland.

2.3. Data-driven Parameterization of DCE T1-weighted Time Course

The normal and cancer regions were mapped from the pathology slides to the corresponding DCE slides by registration and the mapped regions were then used to extract features. To extract features, these mapped regions were divided into square regions of interest (ROI) of size 4.7 mm × 4.7 mm in the DCE image. The intensity values within each ROI were averaged and an average T1-weighted signal was formed. Thereby, each ROI was used to form one T1-weighted signal and the model-free and PCA features were extracted from this average T1-weighted signal. The true label (class) of the feature vector was determined from the pathology image. Fig. 4 shows the kinetic curves of contrast agent concentration in the prostate. These curves are generated by averaging over all the ROIs of the tumor and normal regions. The difference in the pattern of perfusion is evident: the contrast agent concentration increases faster and stronger within the tumor.

Figure 4.

Kinetic curves of Gadolinium concentration versus time for tumor (red) and normal (blue) regions generated by averaging intensities over all regions of interest.

2.3.1. Model-free Empirical Parameter Calculation

Radiologic evaluation of the DCE time course is typically performed by examining the kinetics of the concentration time course [2]. As part of our data-driven approach to parameterization of the DCE data, we extracted six model-free empirical features from the DCE T1-weighted signal intensities. These features were extracted from the relative signal intensity calculated by the following equation:

$$i_{\mathit{rel}}(t)=\frac{i(t)-i_{\mathit{pre}}}{i_{\mathit{pre}}}$$ (1)

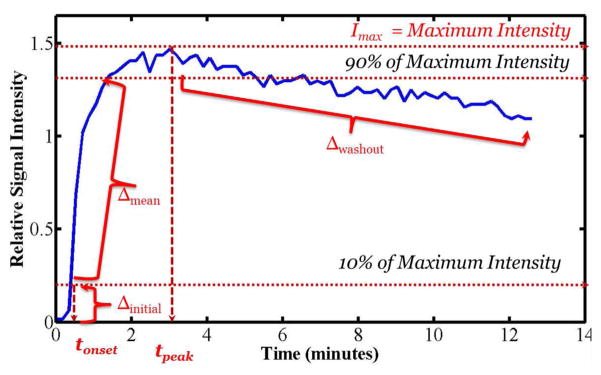
where i_pre is the average pre-injection signal intensity over an ROI and i(t) is the average signal intensity at time t. Fig. 5 shows the change in the relative intensity over time for a single ROI. The features extracted from the relative signal intensity, i_rel(t) are:

Figure 5.

Changes in the relative signal intensity over time for a region of interest and the illustration of the empirical model-free parameters.

• Maximum signal intensity (I_max): defined as the peak relative signal intensity in DCE time course.

• Time-to-peak (t_peak): defined as the time to reach the maximum signal intensity.

• Onset time (t_onset): defined as the time to reach 10% of the maximum signal intensity.

• Initial gradient (Δ_initial): defined as the mean gradient from the time of injection to the time when the intensity is 10% of the maximum signal intensity.

• Mean gradient (Δ_mean): defined as the mean gradient calculated between the time points when signal intensity goes from 10% to 90% of the maximum intensity.

• Washout gradient (Δ_washout): defined as the average rate of change in relative signal intensity from the maximum intensity to the end of the scanning period.

2.3.2. Principal Component Analysis of the T1-weighted intensity

An alternative approach to data-driven characterization of the DCE T1-weighted intensities is to use a dimensionality reduction method to convert the time series of normalized contrast enhanced T1-weighted intensities to an optimally sized vector of features. We used Principal Component Analysis (PCA) for this purpose. PCA uses an orthogonal transformation to map a high dimensional data of possibly correlated variables into a low dimensional representation with linearly uncorrelated variables, called principal components. The first principal component has the largest variance, or it inherits the maximum variability of the data. Each successive component in turn accounts for the highest variance possible under the constraint that it is orthogonal to the preceding components [32]. For a p-dimensional data-set, PCA analysis gives p number of eigenvectors and projects the data into a p-dimensional principal component space. We use the notation I for the N × 72 dimensional matrix obtained by the PCA transformation of the 72-dimensional T1-weighted intensities for all the N training ROIs.

2.3.3. Feature Selection by LASSO

The 72-dimensional principal components extracted from the DCE T1-weighted intensities were ranked in terms of class separability using LASSO [33]. The L1-norm regression problem in our work was formulated as:

$$\widehat{\beta }=\underset{\beta }{argmin}(\frac{1}{2}\sum _{j=1}^N{(y_j-{\beta }_0-\sum _{k=1}^p{I}_{jk}{\beta }_k)}^2+\lambda \sum _{k=1}^p\mid {\beta }_k\mid )$$ (2)

where I_jk are elements of I, y_j is the label (0 or 1) for the jth ROI, λ is the regularization parameter and the vector β includes the LASSO coefficients. This L1-norm regression forces some coefficients to zero. The 72 features are ranked according to the magnitude of their corresponding β_k. To solve the regression problem, cylindrical coordinate descent algorithm was used [34] and the value of λ was determined by 10-fold cross validation on the entire dataset targeted to minimize the mean squared error. Among 72 PCA features, 32 components were identified as the significant features by LASSO with non-zero coefficients. Leave-one-patient-out cross-validation with forward search showed that the maximum Area Under receiver operating characteristics Curve (AUC) was obtained when the 11 top-ranked PCA features were used together to train and test the classifier.

2.4. Pharmacokinetic Modeling

In order to compare our data-driven approach to the traditional pharmacokinetic parameter based approach to prostate cancer detection, we generated pharmacokinetic parameter maps for the patients. AIF was extracted from the external iliac or femoral arteries in the center-slice of the DCE MRI data. The MR images used in this work were acquired using the 3D technique. This technique minimizes the blood in-flow effect, as opposed to the 2D multislice technique; and therefore slice selection has a minimal effect on the arterial input function. We selected the center-slice to extract AIF as this slice best visualizes the arteries. We used local population averaged AIF, called local Gaussian AIF [20], to calculate the pharmacokinetic parameters. Here the AIF is calculated in the form of two Gaussians plus an exponential function, as proposed by Parker [19], but fitted to the average of individual AIFs measured from the patients in our study.

The extracted AIF was then used to calculate the pharmacokinetic parameters: volume transfer constant, K^trans, fractional volume of extravascular extracellular space, v_e, and fractional plasma volume v_p. These parameters were calculated by fitting the extended Kety model to the contrast agent concentration curves [35]. Fitting was carried out in every pixel of every slice within a region of interest encompassing the prostate gland.

The two-compartmental Kety model is a standard tracer kinetics model, which assumes that the tracer (contrast agent) can reside in two compartments: blood plasma space and extra-vascular extra-cellular space EES (the assumption is that the tracer does not cross the cellular membranes). Following intravenous injection of a bolus of a contrast agent, the agent passes through the arteries and its concentration can be measured in the supplying arteries this is known as the AIF. Transfer of the contrast agent from blood plasma to interstitial space is driven by the concentration gradient. Initially, when blood plasma concentration is high, the agent diffuses into EES through the capillaries microscopic pores. When the plasma concentration becomes lower than the EES concentration, the contrast agent diffuses back to the plasma space. Overall concentration of the agent (plasma + EES) is additionally affected by the clearance of the agent through kidneys and liver. The rate at which this transfer of contrast agent between plasma and EES occurs is known as the volume transfer constant, K^trans and it depends on the permeability of capillary wall and the flow of blood. In the flow-limited condition (i.e. when the vessels are very leaky and the contrast agent leaves the plasma space very quickly), K^trans equals to the blood plasma flow per unit volume of tissue. In the permeability-limited condition (i.e. when the vessels permeability is very low), K^trans equals to the permeability surface area product per unit volume of tissue. The fractional volumes of the EES and plasma compartments are known as v_e and v_p respectively. Fig. 6 shows the relative signal intensity pattern for two regions, with significantly different K^trans values. As can be seen from the figure, region with high K^trans exhibits higher and faster intake and faster washout rate than the region with low K^trans. It should be noted that the pharmacokinetic parameters measure physical quantities such as the transfer rate. The transfer rate also drives the changes in the image intensity. As such, not surprisingly, as Fig. 6 shows, higher K^trans values can be attributed to a fast increase in the intensity after injection, followed by a fast decrease.

Figure 6.

Changes in the relative signal intensity pattern for two different pixels with significantly different K^trans values: the pixel with higher K^trans value is from a tumor region and pixel with a lower K^trans value is from a normal region. The pixels are from the peripheral zone of the same patient and from the same MRI slice.

2.5. Classification and Cross-validation

Support vector machine (SVM) classifier was used to classify cancer and normal tissues with different feature combinations. SVM classifier constructs a maximum-margin hyperplane or a set of hyperplanes in a high-dimensional space to separate the input data into different classes. Typically, a kernel function is used with SVM to map the data into a high-dimensional space. The optimization process that trains SVM is based on maximizing the distance between the hyperplane and the nearest training data points (support vectors). In our work, we used a radial basis function (RBF) as the kernel. The RBF kernel was used due to its ability for nonlinear mapping of the data. RBF outperforms a linear kernel in terms of classification accuracy in our data. The classifier was a soft margin classifier where the cost or error penalty, c, and the RBF kernel parameter, γ, were the two parameters to tune. For the classifier we used LIBSVM, which is a C++ implementation of the SVM algorithm [36]. Since SVM is a non-probabilistic binary classifier, it cannot give a posteriori probability values. Therefore, in order to evaluate the a posteriori class probability based on SVM classification, we used the methodology proposed by Platt [37, 38]. This method estimates the class probability in form of a sigmoid function of the estimated SVM hyperplane equation. The parameters of this sigmoid function were estimated using maximum likelihood estimation on the training data. By applying a cutoff threshold to the cancer probability value acquired for each ROI we were able to calculate confusion matrices and plot the Receiver Operating Characteristic (ROC) curves.

We investigated the performance of different feature combinations in classifying tumor tissues. Six different SVM classifiers were trained on the following combinations of the features: the six dimensional empirical model-free parameters, the five dimensional PCA features (consisted of the PCA features that can explain 97% variance of the data), the combination of empirical model-free features with pharmacokinetic parameters, the combination of 5-dimensional PCA and pharmacokinetic parameters, 11-dimensional LASSO-isolated PCA features and the three dimensional pharmacokinetic feature vector. For each of these cases, the SVM classifier was tuned by cross-validation. The cross-validation was performed on a leave-one-patient-out basis, where for each combination of c and γ the classifier was trained on 15 patients and tested on the other patient. This process was carried out for all of the patients with the cross-validation targeted to maximizing the total area under ROC. We investigated the possible combinations of c and γ by a grid search on c ∈ {2⁻¹⁰, 2^−9.5, ..., 2¹⁰} and γ ∈ {2⁻¹⁰, 2^−9.5, ..., 2¹⁰}.

3. Results

We used 449 regions of interest from 64 images in data from 16 patients to train and test the classifier. This covered the peripheral zone of the prostate gland in these cases. Out of these samples, 219 were from cancer regions and the remaining 230 were from normal areas. These samples were extracted from the slices where the tumor was larger than 0.5 cm² in area. The mean and the standard deviation of the pharmacokinetic parameters, the empirical model-free parameters and the first five PCA features are shown in Tables 2, 3 and 4.

Table 2.

Statistics of the three pharmacokinetic parameters in the format of mean (standard deviation)

	Ktrans	ve	vp
Normal	0.053 (0.03)	0.187 (0.08)	0.022 (0.02)
Cancer	0.104 (0.06)	0.214 (0.07)	0.018 (0.01)

Table 3.

Statistics of the six empirical model-free features in the format of mean (standard deviation)

	Imax	tpeak	tonset	Δinitial	Δmean	Δwashout
Normal	1.536 (0.50)	5.195 (2.75)	0.491 (0.11)	0.341 (0.14)	0.644 (0.48)	−0.053 (0.09)
Cancer	1.937 (0.55)	3.535 (2.22)	0.452 (0.08)	0.465 (0.18)	1.718 (1.6)	−0.069 (0.04)

Table 4.

Statistics of the first five PCA features in the format of mean (standard deviation)

	feature-1	feature-2	feature-3	feature-4	feature-5
Normal	5.122 (1.76)	0.461 (0.52)	−0.269 (0.09)	−0.227 (0.12)	−0.078 (0.08)
Cancer	6.204 (1.7)	1.245 (0.81)	−0.314 (0.11)	−0.259 (0.18)	−0.043 (0.14)

The classifiers were trained on a leave-one-patient-out basis. With the empirical model-free parameters, the overall Area Under the ROC (AUC) was 0.78, with a standard deviation of 0.16. This was obtained when the SVM parameters were c = 0.04 and γ = 0.02. When the classifier was trained on the first five PCA features alone, with c = 0.7 and γ = 0.001, the AUC was found to be 0.79 with a standard deviation of 0.18. For a cutoff value of 0.43 applied to the a posteriori class probability, the sensitivity and specificity were 71.2% and 72.2% respectively. When only the pharmacokinetic parameters were used, the AUC was 0.78.

We defined slice-level sensitivity to quantify the classifier’s performance in detecting tumor regions. To define slice-level sensitivity we took the prediction of the classifier as a ‘true positive’ if it can correctly classify more than 50% of the total tumor area in a slide, and as a ‘false negative’ otherwise. With this measure, we found that in 23 out of 33 slides with peripheral zone cancer, the classifier can detect more than 50% of the tumor area, resulting in a slice-level sensitivity of 70%, when the classifier was trained on the PCA features and also when trained on model-free empirical parameters, separately.

We also examined the cancer detection capability of the DCE method when the pharmacokinetic parameters were used along with the model-free parameters. We trained a classifier with K^trans and model-free empirical parameters together. Adding v_e and v_p to this set did not improve the result and therefore we included only K^trans in this analysis. The optimum parameters found for the SVM classifier were c = 0.06 and γ = 0.008 and the area under ROC curve was 0.8 with a standard deviation of 0.14. The slice-level sensitivity was found to be 73%, meaning that in 73% of the slices with a pathologic finding, more than 50% of the tumor area was classified as cancer.

When the classifier was trained on the first five PCA features along with K^trans, with c = 0.5 and γ = 0.001, the AUC was 0.8 with a standard deviation of 0.14. Note that the increase, compared to only using PCA, was not statistically significant. At the cutoff value of 0.42 for the posterior class probability, 163 tumor samples were correctly classified while 56 tumor samples were missed. The sensitivity and specificity were found to be 74.4% and 70.9% respectively. The slice-level sensitivity was 75.8%.

We ranked the PCA features based on the magnitude of their corresponding coefficient in LASSO regression and selected the optimal number of features by forward search and leave-one-patient-out cross-validation. The maximum AUC was obtained when 11 PCA features isolated by LASSO were used to train the classifier. With the LASSO-isolated 11 PCA components of the T1-weighted intensities, we obtained an AUC of 0.86, with a standard deviation of 0.12. At the cutoff value of 0.46, the sensitivity and specificity were 80% and 77.8% respectively. In 27 out of 33 tumor slices, more than 50% area was detected, with the slice-level sensitivity of 81.8%. The statistical significance test performed between the LASSO-isolated PCA features and the pharmacokinetic parameters generated a p-value of 0.16.

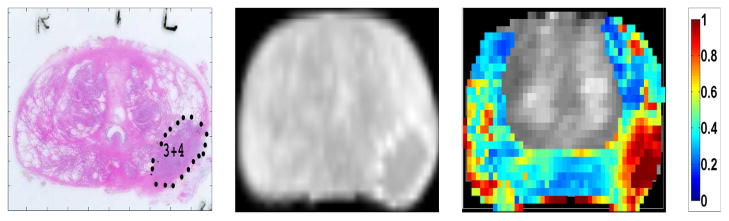
Table 5 summarizes the classifiers’ performances. We used the classifier trained on K^trans and PCA features to generate cancer probability maps for the entire peripheral zone of the gland. To generate cancer probability maps, the classifier was trained on all other patients. Then each pixel from the DCE MRI image of interest was used as a test sample for the classifier. The six features (K^trans value and five PCA components) were extracted for each pixel. The predicted a posteriori class probability of the classifier was mapped onto the T1-weighted image as a cancer probability map. Figure 7 shows the probability map for one patient generated with this method. The probability map was plotted using standard Jet colormap, where hot colors represent higher probability values. In Figure 7, the main pathologic finding is a 3+4 tumor in the left peripheral zone. The generated probability map shows higher probability of cancer in the left peripheral zone, consistent with the pathologic finding.

Table 5.

Area under receiver operating characteristic curve (AUC), sensitivity, specificity and slice-level sensitivity with different feature combinations. Slice-level sensitivity is defined as the percentage of cases where the classifier can detect more than 50% of the total tumor area.

Features	AUC	Sensitivity	Specificity	Slice-level sensitivity
Pharmacokinetic Parameters	0.78 ± 0.14	76.1%	63.9%	78.8%
Model-free Empirical Parameters	0.78 ± 0.16	75.3%	64.0%	70.0%
Ktrans and Empirical Parameters	0.80 ± 0.14	75.3%	67.8%	73.0%
PCA features	0.79 ± 0.18	71.2%	72.2%	70.0%
Ktrans and PCA features	0.80 ± 0.14	74.4%	70.9%	75.8%
LASSO-isolated PCA features	0.86 ± 0.12	80.0%	77.8%	81.8%

Figure 7.

Left: Peripheral zone tumor marked in pathology slide for one patient. Middle: Pathology slide registered to corresponding DCE MR image. Right: The generated cancer probability map superimposed on the DCE T1-weighted image. Note that the classifier is only trained on the peripheral zone. The classifier is trained on all other cases.

4. Discussion

In this work, we developed a model-free framework for prostate cancer detection by principal component analysis of DCE T1-weighted intensities. We used the LASSO method to isolate an optimal subset of PCA features. Model-free empirical and the PCA parameters gave close results and the difference was not statistically significant. This finding is not surprising as these two sets of parameters are essentially two different ways of summarizing the DCE T1-weighted intensity, one empirically and the other statistically.

We generated cancer probability maps for the peripheral zone of the prostate, which can be used in MRI-targeted biopsies. These maps show cancer probability of each pixel and hence highlight the region from where the biopsy samples should be taken. This will become even more important if, with a larger dataset, we can show that there is a correlation between the markers of risk and aggressiveness of cancer, such as Gleason score, and the calculated probability. Then we will be able to decrease the possibility of missing clinically significant and potentially aggressive tumors.

In this work, we did not use pixel resolution for feature extraction in training set to ensure that the training set does not get trained on data that is affected by registration error or imaging noise. Averaging over a region of interest makes the classifier less sensitive to noisy pixels. Also, our target is to detect clinically significant prostate cancer. A prostate tumor is accepted as clinically significant if its volume exceeds 0.5 mL [2]. However, while generating probability maps, we used each pixel as a test sample for the trained classifier and predicted the cancer probability values for each pixel. To compare the data-driven approach to the traditional model-based approach, the pharmacokinetic parameters were calculated for each pixel and then averaged over an ROI to train and test the classifier based on these parameters. This typical pixel-based calculation of the pharmacokinetic parameters could be one of the reasons for the lower performance.

The use of SVM enables us to perform classification without the need for estimating the probability distributions of the features, as needed in Bayesian approaches. The SVM solution is also a convex optimization problem, which reduces the risk of local minima. In our previous work with DCE data, we have shown that random forest classification does not provide improved classification accuracy [39], potentially due to the fact that random forest is designed to enhance the accuracy of classification through bagging and bootstrapping of data with high-dimensional feature vectors. In our case, the feature vectors are relatively small.

The proposed method does not replace accurate physical modeling of the perfusion process. Those models provide physical and physiological insights for understanding the process of cancer growth. Here, we show that our data-driven method provides improved diagnosis. Although the differences between enhancement curves from normal and cancerous tissue analyzed by the PCA come from differences in perfusion patterns, the model-free empirical or the PCA method in itself does not provide any insight into these differences.

It should be noted that since both the model-free empirical and the PCA analysis rely on the normalized image intensity, the results could depend on the pulse sequence parameters. On the other hand, pharmacokinetic parameters are calculated from the contrast agent concentration values and are quantitative physical parameters. Therefore, they should be, theoretically, less dependent on the pulse sequence parameters. As discussed in the introduction, this theoretical advantage of the pharmacokinetic parameters is not translated into a clinical advantage due to the sensitivity of the calculation process to noise and to the accurate extraction of the AIF. Even though the pharmacokinetic modeling provides results that can be pulse sequence independent, clinically the most important issue is the ability to detect cancer, which appears to be improved with the use of the model-free approach demonstrated here.

Our immediate goal is to implement this model-free method for cancer detection in the central and transition zone of the gland and generate cancer probability maps for the entire gland. Since the normal prostate tissue varies in different zones, we will train zone-specific SVM classifiers. We have started with peripheral zone as this is the target for transrectal biopsies. Accurate cancer detection in the peripheral zone can enable targeting of the biopsy procedure. On the other hand, due to the limited access to the central and transition zones during biopsy, an image-based method of cancer detection in those areas is also a pressing clinical need.

In clinical use, DCE is often one component of a multiparametric strategy for cancer detection with MRI. It should be emphasized that the most accurate methods of MRI-based prostate cancer detection are typically multiparametric and include diffusion imaging, which is a very effective modality in prostate cancer detection [2, 40]. In our previous work we have shown that diffusion imaging outperforms DCE in detection of cancer from biopsy cases and that the combination of the two methods is the most effective solution [16]. Therefore, we expect a significantly improved performance resulting from adding the diffusion parameters to our feature vector in the current wholemount prostatectomy study as well.

5. Conclusion

We have developed a novel data-driven and model-free framework for prostate cancer detection using DCE MRI. We report an area under ROC curve of 0.86 with our proposed LASSO-isolated PCA features extracted from the DCE T1-weighted intensities. The comparisons in this paper show that the LASSO-isolated features outperform both the quantitative pharmacokinetic modeling, and the currently available model-free methods such as empirical analysis. We are currently recruiting patients to study and validate the clinical impact of the proposed method.

In conclusion, the proposed data-driven approach to prostate cancer detection from DCE-MR images shows an improvement compared to traditional pharmacokinetic modelling. Even though the improvement is not statistically significant most likely due to our limited sample size, the data-driven approach removes the need for AIF calculation and modeling. Our method also generates helpful cancer probability maps for MRI-targeted biopsies. Both the empirical model-free parameterization of the normalized T1-weighted intensity and the principal component analysis of the T1-weighted intensities result in features for cancer detection that are effective, in terms of AUC, when compared with the standard pharmacokinetic parameters. This novel approach can significantly simplify and streamline the use of DCE imaging for prostate cancer detection.

Highlights.

• A data-driven approach for analysis of the dynamic contrast enhanced MRI of prostate.

• No need for pharmacokinetic modeling and knowledge of the arterial input function.

• LASSO is used to find an optimal set of principal components of the T1 time course.

• The area under ROC curve increased from 0.78 to 0.86 with the data-driven approach.

• Prostate Cancer probability maps are generated using the proposed features.