On the Possibility of Facilitated Diffousion of Dendrimers Along DNA

Abstract

We investigate the electrostatics, energetics and dynamics of dendrimer-DNA interactions that mimic protein-DNA complexes as means to design facilitated mechanisms by which dendrimers can slide and search DNA for targets. By using all-atom molecular dynamics simulations, we calculated the free energy profiles of dendrimer-binding around the DNA via umbrella sampling. We also calculated electrostatic interaction maps in comparison to proteins, as well as the dynamical changes induced by DNA-dendrimer interactions via NMR-measurable order parameters. Our results show that for dendrimers to go around DNA there is a free energy barrier of 8.5 kcal/mol from the DNA major groove to DNA minor groove, with a minimum in the major groove. This barrier height makes it unlikely for an all-amine dendrimer to slide along DNA longitudinally, but following a helical path may be possible along the major groove. Comparison of the non bonded interaction energy and the interaction free energy profiles reveal a considerable entropic cost as the dendrimer binds to DNA. This is also supported by the mobility patterns obtained from NMR-measurable order parameter values, which show a decreased mobility of the dendrimer N-H bond vectors in the DNA-binding mode.

Graphical abstract

Introduction

Proteins that bind DNA have critical functions in many genetic transactions, including DNA replication, unwinding, supercoiling, recombination, and damage repair, to name just a few.¹ These vital biological processes rely on the fast search for binding targets along DNA by the proteins. For example, DNA transcription factors recognize a target sequence of just a few DNA base pairs within a couple of seconds; after taking into account the length of DNA and typical transcription factor concentration, this corresponds to an average scanning rate of about 10⁵ sites per second.^2,3

The phenomenology of search and recognition has been puzzling for decades due to the remarkable speed and accuracy involved. Such a fast search creates a speed-stability paradox, given the mutually exclusive energy requirements for fast searching and for high stability of the protein-DNA complex.⁴ It is thought that behind the observed speed and accuracy of the facilitated search process lies the ability of the proteins to use a combination of four different modes of searching, i.e., sliding, hopping, jumping, and intersegmental transfer.^4–7 A combination of these search modes will determine the speed with which a protein finds its target. Several studies tackled this issue by taking into account factors such as protein conformational change upon binding,^4,8 complementarity of the DNA and protein charge patterns,⁹ shape of the protein and its charge distribution,¹⁰ and the location of the target site.¹¹ Some other studies questioned the existence of speed-stability paradox¹² and argued that this so called paradox is an artifact of continuum models of the protein search process, which are only valid for scanning lengths significantly greater than the size of the binding site.¹² By introducing the scanning length as a critical parameter, the authors developed a discrete-state stochastic model which allows different scalings for search times as a function of DNA length for different search regimes. However, existing studies of protein-DNA interactions have not provided, as of yet, an effective atomistic picture of this nonspecific protein-DNA interaction or of the resulting search process.

Our study herein targets a biomimetic approach to the facilitated diffusion of DNA binding proteins in which we are interested in replacing proteins with dendritic nanoparticles that bind DNA. Related studies^13–15 suggest that the protein-DNA interaction is dominated by electrostatic interactions when the protein is in its nonspecific search mode. Therefore, with the proper adjustment of surface charge density and distribution of a charged nanoparticle, the theoretical possibility exists to mimic the facilitated search process of DNA-binding proteins.

Our chosen model for the proteins are poly-amidoamine (PAMAM) dendrimers,¹⁶ which are highly charged functional nano-particles that can be considered as artificial proteins for targeted delivery of drugs and genetic material into cells. Their size, charge, and surface properties can be easily controlled synthetically.¹⁷ Because of their interesting properties, they have potential in areas such as gene transfection, drug delivery, in vivo imaging, and biosensing.^18–21 The interaction of dendrimers with DNA has been explored recently.^22–32

A factor that affects the sliding ability of a protein is the shape of the free energy landscape along the DNA. Using detailed theoretical analyses, Slutsky et al.⁴ showed that the experimentally reported rapid search is possible when a three-dimensional search process is combined with a one-dimensional search along DNA, and that the optimum search time is obtained when the time spent on the one-dimensional search is equal to the time spent on the three-dimensional search. While the three-dimensional search time is determined by nonspecific interactions between the protein and the DNA phosphate backbone, the one-dimensional search time may additionally depend on sequence-specific interactions.

The nonspecific binding energy contribution to the total binding energy is estimated to be in the range 10k_BT – 15k_BT for proteins (from an Arrhenius-type dependence of the dissociation rate).⁴ Moreover, by assuming that the specific binding energies can be described by a Gaussian distribution with variance σ², it can be shown⁴ that one-dimensional search can be described by normal diffusion with a diffusion constant that depends exponentially on σ, with σ being a measure of the roughness of the specific binding energy landscape as the protein slides along DNA. Because of this exponential dependence, the diffusion constant decays rapidly with σ. For rapid search to be possible, the specific binding energy landscape must be smooth, such that σ ≲ 2k_BT .^4,33 For example, experiments done with proteins hOgg1³⁴ and p53³⁵ reported values of σ < k_BT for sliding along DNA, supporting this argument. On the other hand, Slutsky and et al.⁴ also estimated that the high stability requirement at the target site requires s to be at least 5k_BT for a genome of about 10⁶ base pair long. This requirement for stability is obviously in contradiction with the speed requirement. In order to address this paradox, a two state model was developed.^4,8 This model suggests a conformational difference between non-specific protein-DNA interactions and specific protein-DNA interactions. It emphasizes the significance of conformational flexibility in nonspecific searches. Several studies showed that the existence of disordered domains in protein structures promotes the speed in the nonspecific search process. For example, the p53 core domain that recognizes a specific DNA sequence has a slower search compared with the disordered C-domain.³⁶ The disordered tails are also shown to promote intersegmental transfer through a ‘monkey bar’ mechanism, which can help the protein explore more distant regions and to reduce the redundancy in one dimension.³⁷

Besides the free energy landscape and the existence of flexible regions, another factor that affects the search speed is the electrical charge. For example, the disorder as well as the positive charge on certain domains is shown to increase the non-specific search speed for p53;^36,38 p53 is shown to maintain constant contact with DNA as it slides.³⁵ A considerable difference in the electrostatic potential surface of a DNA binding protein when it is in complex with nonspecific DNA sequence versus when it is in complex with specific DNA sequence has been found.³⁹ In the former case, there are negatively charged pockets scattered among positively charged regions on the DNA binding face of the protein. In the latter case, however, positive charges are observed to focus more on the DNA binding regions. This shows that charge redistribution plays an important role in distinguishing between specific and nonspecific complexes.

Due to the low affinity of nonspecific protein-DNA complexes, there are available only a few nonspecifically-bound protein-DNA structures, including EcoRV,⁴⁰ BamHI,³⁹ BstYI,⁴¹ and Lac Repressor.¹⁵ A structural analysis of these complexes indicates that the interactions are mainly between negatively charged phosphate groups and positively charged protein domains.¹⁴ In addition, a comparison of salt dependence of the interaction, as well as hydration differences between specific and nonspecific complexes show that nonspecific interactions are dominated by electrostatic interactions.¹⁴

With the lessons learned from DNA-sliding proteins in mind, we seek to find if and how nanoparticles can be used, instead of proteins. Functionalized nanoparticles hold great promise for various biomedical applications, which include their potential use as biosensors, cell-labeling agents, imaging or contrast agents, artificial catalytic sites, and DNA/protein microarrays, to name just a few.^42,43 They can also be used in targeted gene or drug delivery.^{17–19,21,44–47} For our purposes, we propose that polyamidoamine (PAMAM) den-drimers,^16,17,19 which are charged nanoparticles, can serve as first model systems to mimic the electrostatic nature of protein-DNA interactions.

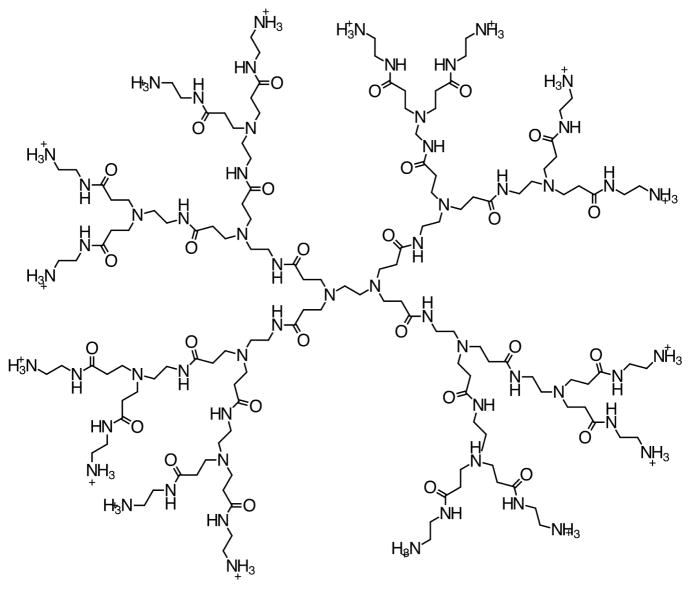
PAMAM dendrimers (Figure 1), often referred to as “artificial proteins”,²⁰ resemble proteins in their chemical structure. Their size and surface chemistry can be controlled and their toxicity can be reduced by adjusting the surface charge size or core chemistry.^44,48 They can be conjugated with different surface modifiers such as amino acids⁴⁹ and in principle they can be used to mimic the non-specific search along DNA, the firm binding to a target sequence and possibly subsequent catalytic events. For many such possible applications of dendrimers, it is crucial to explore the dendrimer-DNA interactions in general, and the diffusion properties of dendrimers along DNA in particular, in atomistic detail.

Figure 1.

Structure of generation 2 dendrimer. A generation number is defined as the number of branching points.

Cationic dendrimers of generation 5 (G5) or larger are shown to bind to DNA irreversibly^24,26 and can condense DNA. On the other hand, there is evidence from computational studies that cationic dendrimers of generation 3 slightly bend DNA locally, but do not condense it.²³ Moreover, sliding of third generation (G3) and fourth generation (G4) dendrimers along DNA, until they find an ideal binding location, has been reported in a molecular dynamics study.²⁵ Considering the fact that G3 is highly flexible and positively charged (at physiological pH), it can be an ideal candidate to mimic the nonspecific search process along DNA. Moreover, importantly, the energy landscape it sees along and around DNA can be modified by adjusting its terminal charges. Therefore, the flexibility of a lower generation dendrimer combined with optimum terminal charges have the potential to overcome the strong attraction due to DNA that would lead to balancing association and dissociation, which is necessary for nonspecific search mechanism.

In a previous study, we computed the binding free energy profile along the radial direction for an all-amine terminated G3 dendrimer interacting with DNA; the profile exhibited a well-depth of −13.5 kcal/mol.²³ When this value is compared with the nonspecific binding energy required for facilitated search of DNA binding proteins (estimated to be in the 10k_BT – 15k_BT range, or 5.93 – 8.895 kcal/mol at room temperature⁴) G3 has about two times higher a nonspecific binding energy than typical proteins. A similar study done with G3 (surface charge +32) and higher generation dendrimers G4 (surface charge +64) and G5 (surface charge +128) reported that the binding free energy increases almost linearly with the generation.²⁷ While a dendrimer of such charge size is unlikely to dissociate from DNA in the radial direction, we should also note that the free energy depends on the tension on DNA. It has been shown that as the tension on DNA increases, the free energy barrier decreases for a given dendrimer size and charge.²³ This information can be used as a starting point and the linear dependence can be used to estimate an optimum charge size that would facilitate diffusion along DNA. For this purpose, we setup to explore the free energy profiles along longitudinal sliding pathways. The organization of the rest of this paper is as follows: In the next section (Theory and Methods), we describe the system setup and simulation details after which we provide a theoretical framework for potential of mean force and NMR order parameter calculations. We then continue with a Results section, in which we compare electrostatic potential maps for some DNA binding proteins and dendrimer interacting non-specifically with DNA. We also present potential of mean force and NMR order parameter calculation results for dendrimer interacting with DNA in the Results section. We end with a Concluding Discussion.

Theory and Methods

Simulation Methods

In all simulations, CHARMM 27 all-atom force field for nucleic acids^50,51 was used with the CHARMM software (Chemistry at HARvard Macromolecular Mechanics), version c34b2.^52–54 Langevin dynamics is used with a friction coefficient of 10 ps⁻¹ applied on non-hydrogen atoms and an implicit solvent model (GBMV2)⁵⁵ is used. The accuracy of generalized Born methods rely highly on the accuracy of the Born radii, i.e. the distance of a charge location from the solvent boundary in a given molecule. GBMV2 method is shown to give highly accurate Born radii such that the relative error in total electrostatics solvation energy is shown to be ≤ 1% between GBMV and Poisson theory.^56,57 The nonbonded cutoff distance was 21 Å, with a switching function from 16 Å to 18 Å. The SHAKE algorithm ⁵⁸ was used to constrain the distance of covalent bonds to hydrogen atoms, enabling a 2 femtosecond time step. A third generation PAMAM dendrimer, G3, with all-amine terminations was generated using parameters obtained as described in C. V. Kelly et al.⁵⁹ Double stranded B-DNA, 48 base pairs in length and a repeat of the CGAT sequence was generated using the program NAB.⁶⁰ This sequence was used as a model for a “generic” DNA sequence⁶¹ that mixes all possible base pairings. DNA and G3 were initially prepared separately as follows. Each one was first minimized in vacuum using 1000 steps of steepest descent and 2000 steps of adopted basis Newton-Raphson (ABNR). This was followed by 2000 steps of ABNR in implicit solvent. It was then heated for 50 ps while a harmonic constraint with a force constant of 1 kcal/mol/Ų was applied on all atoms. This was followed by an equilibration for about 2 ns with all the harmonic constraints were gradually removed. For DNA only, after the removal of constraints, the relative distances between complimentary base pairs at each end were restrained with a harmonic potential by using NOE-type restraints in order to prevent fraying.

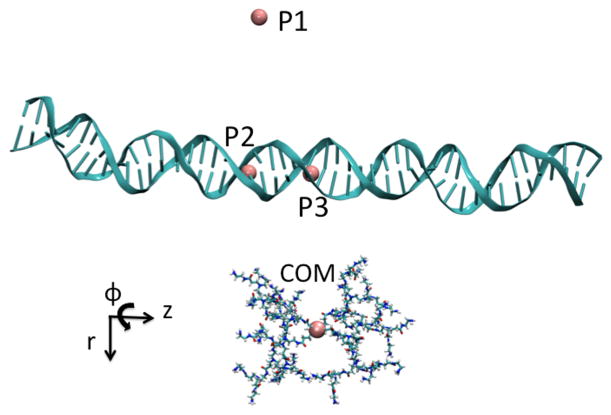
The DNA axis was defined by the line connecting the center of geometry of the (DNA1)29th-(DNA2)68th base pairs and the center of geometry of the (DNA1)19th-(DNA2)78th base pairs. Three separate systems were prepared by combining the dendrimer and DNA at three distances of 25 Å, 35 Å, and 45 Å, which we label as r25, r35, and r45, respectively. Intermolecular distances were calculated from the dendrimer center of mass (COM) to the middle of the DNA axis. The longest axis of the dendrimer was placed to be parallel to the DNA axis. For each system, the dendrimer was then rotated rigidly around the defined DNA axis by 10 degrees to obtain multiple windows. Rotation was done in such a way that the same side of the dendrimer was facing the DNA. Figure 2 shows a snapshot of system r45 where the dendrimer is positioned at a dihedral angle value of 180 degrees defined by the dummy atoms and the dendrimer center of mass (P1:P2:P3:G3 COM). The entire range of the dihedral values (0–360°) was sampled. For each system, after a brief equilibration period of 40 ps, DNA atoms were harmonically restrained to their most recent positions with a harmonic force constant of 100 kcal/mol/Ų in order to maintain DNA shape and orientation with respect to the dendrimer. Additional windows are added as needed for PMF calculations which resulted in 61 windows for system r25, 129 windows for system r35, and 155 windows for system r45.

Figure 2.

The dendrimer is shown at a pseudo dihedral value of ϕ = 180° and a distance of r = 45 Å, defined by three points and the dendrimer center of mass: P1:P2:P3:G3 COM.

Potential of Mean Force

The umbrella sampling method⁶² was used to obtain a potential of mean force (PMF)⁶³ around the DNA. A reaction coordinate was defined between two states, then the reaction coordinate was divided into multiple overlapping windows and the system was restrained around each window with a harmonic biasing force. This helps to sample all regions, including the higher energy regions which are difficult to sample within the accessible time scale of molecular dynamics simulations.

The biasing potential

$$U_b(r,\varphi ,z)=\frac{1}{2}{k}_r{(r-r_0)}^2+\frac{1}{2}{k}_{\varphi }{(\varphi -{\varphi }_0)}^2+\frac{1}{2}{k}_z{(z-z_0)}^2$$ (1)

was used, where r is the radial distance between DNA axis and the dendrimer center of mass, z is the displacement of the dendrimer center of mass along the DNA axis, and ϕ is the pseudo dihedral angle as defined by the three fixed points and the dendrimer center of mass (See Figure 2). For all PMF simulations, z₀ = 0 and r₀=25 Å, 35 Å or 45 Å. The force constants k_r and k_z are 500 kcal/mol/Ų. We used various values for the force constant k_ϕ which varied between 2.5, 10, 25, 50, 100, 200, and 250 kcal/mol/rad², depending on the overlap of the probability distribution of the reaction coordinate between neighboring windows. The length of the simulations for the different windows varied between 4 ns and 25 ns because of the difference in the force constant values. The weighted histogram analysis method (WHAM)^64,65 was used to unbias the simulation results, with multiple restraints handled through a minor modification in the WHAM code.

In order to investigate the sliding of a PAMAM dendrimer along DNA, the free energy profile along one DNA turn was obtained. In our previous study,²³ we showed that the interaction of the dendrimer with DNA bases is not significant and is nonspecific. Here, we are mostly interested in the change in interaction due to minor and major groove variations and not due to larger DNA conformational differences. Therefore we want to avoid changes in DNA conformations, such as untwisting, bending, groove width differences etc. along sliding pathways. This can be achieved by taking advantage of the helical symmetry of DNA. Accordingly, for an ideal DNA, the sliding surface along a line parallel to DNA axis is periodic with a period of one DNA turn. The landscape that would be seen for longitudinal sliding should be identical to the surface that would be seen in the case of rotation around the DNA on a plane orthogonal to DNA axis. A similar approach has been previously used in calculating the variation of electrostatic binding energy with respect to the minor and major groove interactions of a BamHI-DNA complex.⁶⁶ Therefore, we define our reaction coordinate along a circular path of constant radius around DNA axis on a plane perpendicular to DNA axis. This reaction coordinate is defined to be a pseudo dihedral angle with respect to the fixed points represented in Figure 2.

Calculating NMR Order Parameters

The MD simulations were used to compute NMR-based order parameters, which have been previously used to characterize the dynamics of biomolecules.^67–69 According to the Lipari-Szabo model,⁷⁰ the degree of spatial restriction of motion and the rate of that motion for subnanosecond motion was described by the model-free NMR order parameters S² and τ_e respectively, where S² is a generalized order parameter and τ_e is an effective correlation time. Order parameter values can further be used to estimate the configurational entropy change due to bond vector motions.⁷¹

NMR order parameter S² for the dendrimer N1-H5 bond vectors were calculated from the molecular dynamics trajectories. The equilibrium expression,^72,73

$$S^2=\frac{1}{2}[3\sum _{i=1}^3\sum _{j=1}^3{\langle {\mu }_i{\mu }_j\rangle }^2-1]$$ (2)

was used, where μ_i represent the Cartesian coordinates of the normalized internuclear vector after alignment of the MD snapshots with respect to the dendrimer core carbon and nitrogen atoms. Alternatively, S² was also calculated from the tail values of internal correlation functions using the following relation assuming internal and overall motions are not correlated and internal fast and slow motions are not correlated:^67,68

$$C_i(t)=S^2+(1-S_f^2)e^{-t/{\tau }_f}+(S_f^2-S^2)e^{-t/{\tau }_s}$$ (3)

Here, $S^2=S_f^2{S}_s^2$ corresponds to the tail value of the correlation function and f and s indicate ”fast” and ”slow” motions, respectively.

Poisson-Boltzmann Calculations

The PBEQ module in CHARMM was used to solve the linearized Poisson-Boltzmann equation numerically.⁷⁴ The dielectric boundary was determined from the molecular surface with a probe radius of 1.4 Å and atomic Born radii values calculated from free energy calculations for standard amino acids and DNA^75,76 were used. A grid spacing of 1 Å before focusing and 0.5 Å after focusing was used. A dielectric constant of 1 was used for the molecules, and a value of 80 was used for the solvent. Salt concentration was 0.15 M. Images were obtained by using PyMOL.⁷⁷

Results

Electrostatic Potential Surfaces

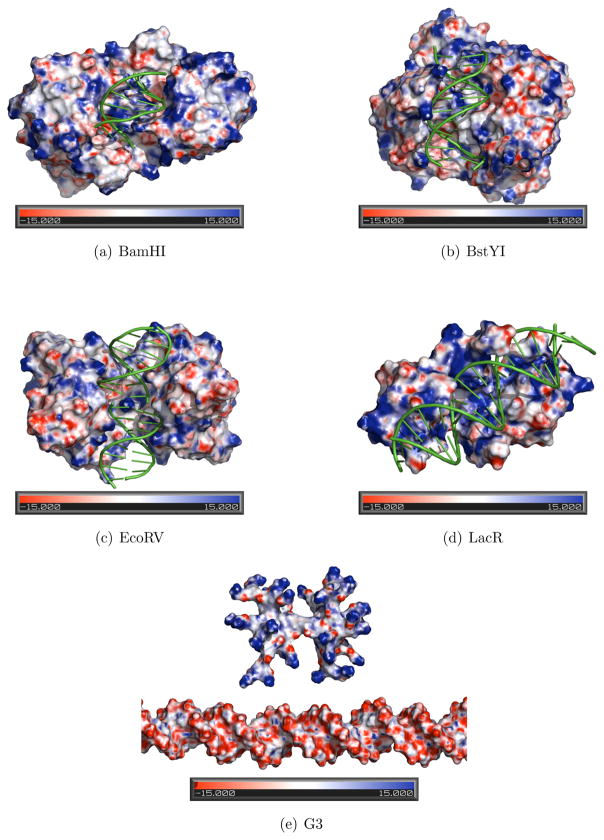
As Honig and Nicholls⁷⁸ point out, the surface electrostatic potential is influenced not only by the charge size or distribution near the molecular surface, but also by surface geometry. For example, narrow regions or clefts (as found in many DNA binding proteins or DNA minor groove) are shown to enhance the electrostatic potential,⁷⁹ an effect known as “electrostatic focusing”.⁷⁹ Therefore, in order to understand the role of electrostatics in protein sliding, it is useful to compare the surface electrostatic potential map of the dendrimer-DNA complex to proteins complexed with DNA nonspecifically. We obtained electrostatic potential surface maps for the following nonspecific protein-DNA structures: BamHI (PDB ID: 1ESG),³⁹ BstYI (PDB ID: 2POJ)⁴¹ EcoRV (PDB ID: 2RVE),⁴⁰ and Lac Repressor (PDB ID: 1OSL).¹⁵

As shown in Figure 3, a large positive charge concentration is evident on the DNA binding surface of proteins. While positively charged regions are dominant on these surfaces, there are some smaller pockets of negatively charged regions scattered among positive regions as well. It is possible that the existence of these negatively charged regions may be needed to help the protein dissociate easily from a nonspecific DNA site.

Figure 3.

Electrostatic potential surfaces as calculated with PBEQ module of CHARMM shown for proteins: (a) BamHI (PDB ID 1ESG); (b) BstYI (PDB ID 2POJ); (c) EcoRV (PDB ID 2RVE); and (d) Lac Repressor (PDB ID 1OSL) complexed with DNA nonspecifically; and (e) G3. Images were made by PyMOL. Negative regions are shown with red, and positive regions are shown with blue. Heat map color scale is from −15.0 kT/e to 15.0 kT/e.

For comparison with these proteins, we also generated the electrostatic potential surface map for the G3-DNA system, using the same method as described above for the proteins (See Figure 3(e)). Based on the comparison, it can be argued that although a high attraction is expected between the positively charged dendrimer terminals and the negatively charged DNA sugar phosphate backbone, the repulsion due to the observed negative regions located on the branches may reduce this attraction to some extent. Another interesting property of the dendrimer is that since its branches are very flexible, the branches are observed to repel each other when they get closer. This effect also prevents the dendrimer to stick to the DNA. Therefore the theoretical possibility exists for the dendrimer to mimic the sliding motion of proteins along DNA, likely following a helical path.

Interaction Energy

To map the energy profile for the interaction between the two molecules in three dimensional space, the interaction energy was calculated along various radial as well as angular coordinates as follows. First we kept the distance constant at 45 Å, and calculated the interaction energy map around the DNA axis for two different planes orthogonal to the DNA axis positioned at half DNA turn apart. The interaction energy was calculated as the sum of electrostatic and van der Waals energies:

$$E_{\mathit{ind}}=E_{\mathit{elect}}+E_{\mathit{vdw}}$$ (4)

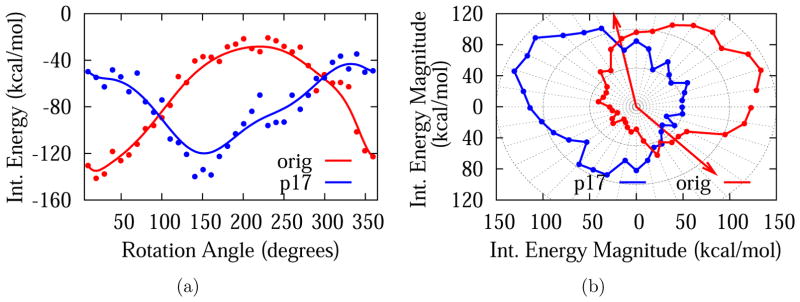
Figure 4 shows the variation of the interaction energy around DNA at an intermolecular distance of 45 Å at two different planes orthogonal to DNA axis: the z = 0 plane (red), which is the plane that intersects the DNA axis orthogonally at its center, and the z = 17 plane (blue), which is separated from the former by 17 Å, i.e., half DNA turn. The sugar-phosphate group is marked with arrows to distinguish minor and major groove positions on the z = 0 plane. Note that the angle measure on the minor groove side is about 145³, consistent with typical B-form values. The nonbonded interaction, which is predominantly electrostatic in nature, is significantly more favorable (by about 100 kcal/mol) when the dendrimer center of mass is on the minor groove. This is consistent with previous electrostatic potential calculations of B-form DNA, which show that the electronegative potential is enhanced in the narrow minor groove due to electrostatic focusing.^79,80 Also noticeable is a shift of the pattern when the dendrimer is placed on the z = 17 plane. This is expected due to the helical symmetry of the DNA structure, verifying that the observed interaction pattern is due to the positions of negatively charged phosphates on DNA backbone.

Figure 4.

Interaction energy plots for G3-DNA separation of 45 Å at two different planes orthogonal to DNA axis: the z = 0 plane (red) and the z = 17 Å plane (blue) in cartesian 4(a) and polar 4(b) representations. In 4(a) smoothing line is used to guide the eye. In 4(b) the positions of sugar-phosphate group is marked with arrows to distinguish minor and major grooves on the z = 0 plane. Note that the radius is proportional to the magnitude of the interaction energy.

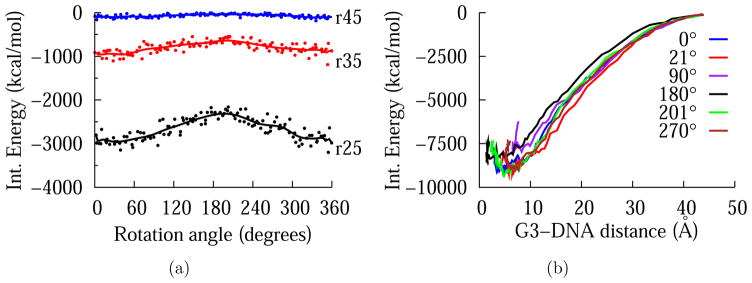
Interaction energies for intermolecular distances of 25 Å and 35 Å were also calculated on the z = 0 plane to gauge how the energy profile changes as the dendrimer gets closer to DNA. Figure 5(a) shows that while the interaction energy values are much lower at distances closer to DNA (as expected), the shape of the energy profile in angular directions is maintained. Table 1 lists the values of the interaction energy and its components at minor and major grooves for three intermolecular distances. Finally, starting from a distance of 45 Å, the dendrimer is pulled towards the DNA axis along the radial direction with a constant force of magnitude 10 pN for various dihedral angle values (See Figure 5(b)). These interaction energy profiles around the DNA and in the radial direction show that the difference between dendrimer-minor groove interaction and dendrimer-major groove interaction is amplified as the dendrimer gets closer to DNA. The difference in the DNA-G3 interaction energy at the minor groove and major groove is about 100 kcal/mol for r45, 300 kcal/mol for r35, and 600 kcal/mol for r25.

Figure 5.

5(a) A comparison of interaction energy calculated at three G3-DNA separation around DNA axis. 5(b) Dependence of interaction energy on radial distance for various dihedral angle values.

Table 1.

Contributions of electrostatic and van der Waals energies to interaction energy at minor and major grooves.

	Electrostatic (kcal/mol)	vdW (kcal/mol)	Interaction En. (kcal/mol)
r25
Minor Groove	−2787.17	−17.5468	−2804.72
Major Groove	−2344.03	−16.5974	−2360.63
r35
Minor Groove	−937.139	−0.642	−937.139
Major Groove	−624.75	−0.449	−625.199
r45
Minor Groove	−140.382	−0.028	−140.410
Major Groove	−28.196	−0.0016	−28.194

The closest distance at which the dendrimer approaches the DNA when the dendrimer is restrained to the z = 0 plane and at various dihedral values when no distance restraint applied, varied between 17 Å and 28 Å over a simulation of length 4 ns (data not shown). Therefore a distance of 25 Å can be safely considered to represent a binding mode.

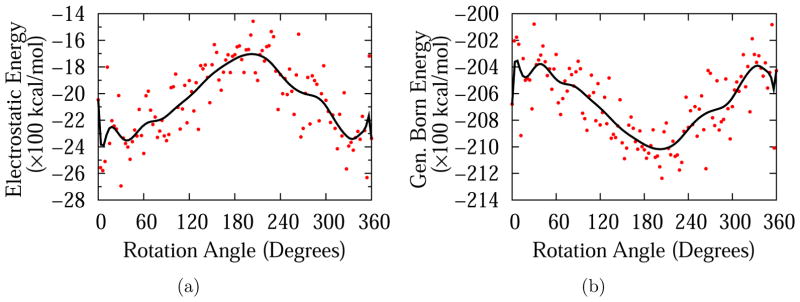
Figure 6 shows a comparison of the electrostatic component of the total energy value (Figure 6(a)) for the dendrimer-DNA system with the electrostatic contribution to the generalized Born solvation energy as obtained from the GBMV2 module⁵⁵ in CHARMM (Figure 6(b)); anticorrelated behavior is observed. Total electrostatic, van der Waals and generalized Born solvation energy contributions are also calculated for r35 and r45, which are reported in Table 2. The generalized Born solvation energy is a continuum approximation to the electrostatic contribution to solvation energy.⁵⁵ According to Figure 6(b), solvation energy at the minor groove is higher than the solvation energy at the major grove. In other words, in the region where interaction energy, which is predominantly electrostatic in nature, is more favorable (minor groove), solvation energy is less favorable. This opposite behavior of solvation energy and electrostatic energy is in agreement with Honig et al. in that the charged or polar groups are a source of destability for molecules or complexes in aqueous solutions.⁷⁸ This is because desolvation costs for binding of opposing charges are larger than Coulombic attractions.

Figure 6.

Electrostatic 6(a) and Generalized Born 6(b) components of total energy for G3-DNA separation of 25 Å

Table 2.

Contributions of electrostatic and van der Waals energies to total system energy and electrostatic contribution to Generalized Born solvation energy.

	Electrostatic	vdW	Total Nonbonded	Gen. Born Electr. Solvation Energy
	(kcal/mol)	(kcal/mol)	(kcal/mol)	(kcal/mol)
r25
Minor Groove	−2325.35	−464.2	−2789.55	−20407.8
Major Groove	−1683.99	−461.66	−2145.65	−21036
r35
Minor Groove	−415.27	−442.772	−858.04	−22304.7
Major Groove	−126.82	−444.38	−571.21	−22588.4
r45
Minor Groove	526.5	−446.88	79.62	−23298.8
Major Groove	581.952	−452.75	129.2	−23251

In another computational study of dendrimer-DNA interactions performed in explicit solvent, the authors reported a total electrostatic energy of −22400 kcal/mol for a complex consisting of G3 and a 38 basepair DNA including the interactions due to ions and water.²⁵ In our implicit solvent simulations, this corresponds to the sum of the total system electrostatic energy and the electrostatic contribution to generalized Born energy, which are listed in Table 2. Since the DNA we use in our study is longer, i.e. 48 basepairs, we expect the total electrostatic energy in our system to be slightly lower. As expected, for an interaction distance of 25 Å, we find −22720 kcal/mol and −22733 kcal/mol for major groove and minor groove binding modes, respectively. While a one-to-one comparison cannot be made due to the different number of DNA atoms in the two studies, this close agreement in total electrostatic energy values suggest that the use of implicit solvent model used in our study yields results consistent with explicit solvent simulations.

Another similar molecular dynamics study which compared the non-bonded interactions of a charged nano-particle with DNA minor groove versus major groove reported a preference for the major groove.⁸¹ In that study, gold nanoparticles functionalized with thiolated alkane ligands carrying a small charge of +6 (AuNP-NH3) were used. The authors reported an electrostatic energy difference of 658.36 kJ/mol between minor and major groove electrostatic interactions, which corresponds to 157.2 kcal/mol overall or 26.2 kcal/mol per amine charge. Our results for a distance of 25 Å show a difference of 641.36 kcal/mol overall or 20.04 kcal/mol per amine charge, which is comparable to the above results in magnitude, but contradict them in terms of the preferred region. While we did not observe much difference between the van der Waals interactions for both modes of binding, the gold nanoparticle study reported a difference of 330.08 kJ/mol in the van der Waals interactions between the two modes of interactions, which favor the minor groove. The difference in nano-particle composition, size and flexibility may be a factor in explaining this difference in the two studies. Another explanation of this difference may be that in the mentioned study, DNA was free to move, resulting in DNA bending and adjustment of the groove width. In our study, on the other hand, DNA is kept straight and the widths of the minor and major grooves are maintained.

Based on the results mentioned above, we infer that for a longitudinal sliding motion along DNA to be possible, a free energy barrier is expected between the minor groove and major groove positions. Its height will determine whether or not the barrier can be scaled by thermal fluctuations, resulting in a random or, respectively, a helical sliding motion.

While the calculations reported above are useful to understand binding vs. sliding, the interaction energy values mentioned above are only enthalpic contributions to the free energy profiles. In order to include the entropic contributions, further calculations of the potentials of mean force around DNA are needed.

Potentials of Mean Force

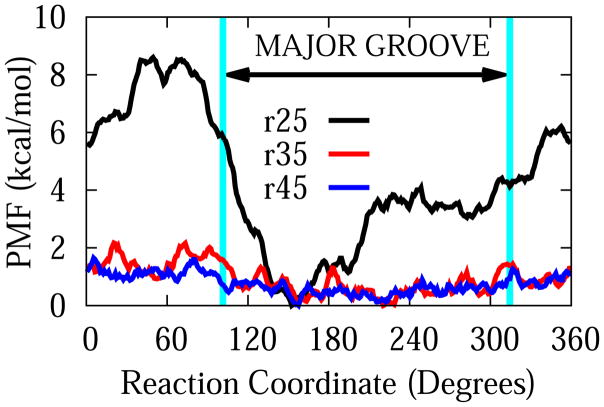
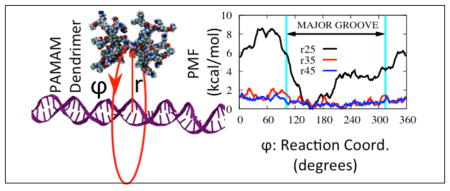
The potential of mean force around DNA for G3-DNA center of mass separations of 25 Å, 35 Å, and 45 Å along the pseudo-dihedral angle reaction coordinate are shown in Figure 7. Contrarily to the interaction energy patterns described above, the free energy minimum was located in the major groove. While the free energy is almost smooth at a distance of 45 Å, the preference for the major groove starts to be felt at a distance of 35 Å with a barrier of about 2 kcal/mol. When the dendrimer is at a distance of 25 Å, the free energy barrier gets close to 8.5 kcal/mol.

Figure 7.

Potentials of Mean Force along circular reaction coordinates around DNA axis for dendrimer-DNA distances of 25 Å, 35 Å, and 45 Å.

For comparison of our results with protein-DNA interactions, we need to consider studies of PMF that explore the free energy profiles along possible sliding pathways along DNA. For example, Marklund et al.⁸² explored the PMF for LacI head domain nonspecifically interacting with DNA along a helical reaction coordinate and in the radial direction. In the radial direction, they found the barrier to be 12k_BT ( or 7.15 kcal/mol at room temperature), which is within the theoretically estimated range for facilitated diffusion of proteins.⁴ This is almost half of the value we reported for G3 (13.5 kcal/mol) in a previous study.²³ Marklund et al. also obtained the PMF along the helical direction, and they found it to be periodic, with a periodicity of one base pair, and a barrier of no larger than 3.5 k_BT (or 2.1 kcal/mol). This value is close to the estimated value required for facilitated diffusion, which is estimated to be less than 2k_BT.⁴

Based on the PMF results for G3, it is unlikely that G3 will dissociate from DNA due to the high barrier in the radial direction. In the longitudinal direction, we identified the major groove as the region of more favorable interaction, with a barrier of 8.5 kcal/mol, which is high enough to make the motion in this direction also unlikely. There exists the possibility, however, that the dendrimer may follow a helical path, similar to some DNA binding proteins such as LacI,⁸² human hOgg1, BstYI. MutY, E. coli MutM M74A, and BamHI, etc.⁸³ Free energy profiles along helical coordinates will need to be determined to verify this. In any case, we believe that based on the assumptions mentioned earlier about the almost linear dependence of PMF barrier along radial direction, if the dendrimer charge size is reduced by half, this may result in cutting the barriers in both radial direction and sliding direction by half, which in turn may result in values close to the ones reported for LacI above.

We note that our study uses implicit solvent and therefore, does not include any structural effects of water or salt. An earlier study showed the important effects of ordered water layers in dendrimer-DNA interactions.²² Due to the dominant electrostatic nature of the interactions, the role of salt will also be important. However, these effects can be assumed to have effects of similar magnitude for major and minor grooves such that the relative interactions reported here are still valid.

NMR Order Parameters

In order to understand the dendrimer dynamics as the dendrimer interacts with DNA, we calculated NMR generalized order parameters S² for the dendrimer N-H bond vectors at multiple positions around DNA using both the equilibrium expression and the tail value of the autocorrelation functions (See Methods). The tail values were calculated from the average of the last 300 ps of the trajectory. Sample correlation functions are shown in the Supporting Information (Figure S1) for system r25. Except for residues 7 and 16, all correlation functions converge on the nanosecond time scale. This is because dendrimer motions are well sampled within this time scale.

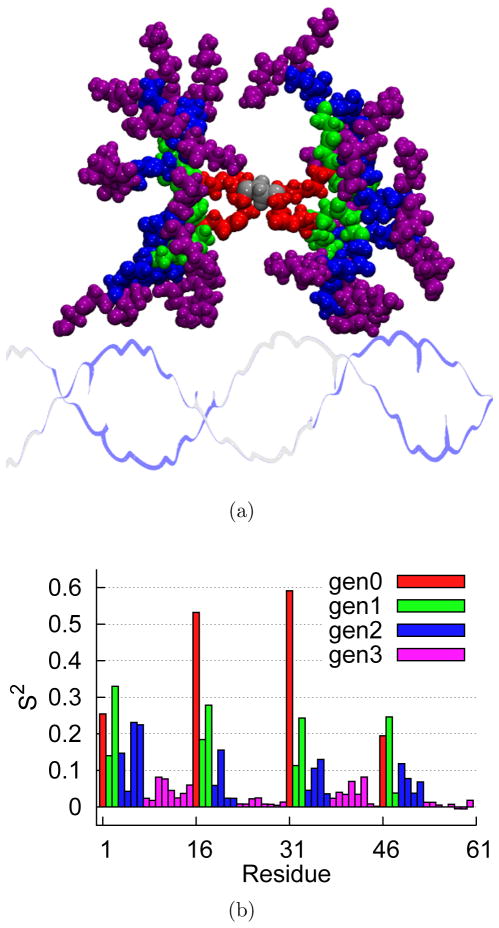
According to the model-free approach,⁷⁰ the lower S² value for a given residue corresponds to more mobile motion, whereas a higher S² value corresponds to more restricted motion. For a protein, the residues closer to the N-terminal and C-terminal are more mobile while the residues in the interior regions are more restricted. This results in a “frowning” pattern in which the residues closer to the two termini have lower S² values and the residues closer to the central regions have higher S² values. In contrast, dendrimers have a different pattern of mobility, in which all termini are flexible, not just the C- and N-termini in the protein case. Figure 8(b) shows the pattern of order parameter values, which are color coded according to generation as shown in Figure 8(a) for one prototypical example. More S² plots for various positions of dendrimer around DNA are included in the Supporting Information (Figures S2 – S7). Accordingly, N-H bonds in the innermost layer (generation 0), have consistently higher S² values compared with bonds in the outer layers (generations 1 – 3). That is, the motion is more restricted in the inner layers than in the outer layers, as expected from the branching geometry. Moreover, S² values approach zero for the terminals showing unrestricted motion.

Figure 8.

The dendrimer placed at a distance of r = 25 Å and a dihedral angle of ϕ = 150° is shown in 8(a) color coded by generation as follows: generation 0 (red), generation 1 (green), generation 2 (blue), and generation 3 (purple). The core is shown in silver color. Corresponding S² values are shown in 8(b).

When the mobility patterns at different dendrimer-DNA interaction distances are compared, it is observed that S² values for an interaction distance of 25 Å are usually higher than S² values for interaction distances of 35 Å and 45 Å. This shows that mobility is more restricted as the dendrimer gets closer to DNA and as the terminals start to make more contacts with the DNA. This behavior is consistent with that of many (but not all) proteins, which are known to show a rigid behavior upon binding,^84–86 resulting in higher S² values.

Our findings in the area of bond motion via S² could be readily verifiable by NMR liquid state experiments,^67,87 in which one can label the nitrogens with ¹⁵N isotopes, and can reveal binding dynamics through the measurement of order parameters.

Concluding Discussion

In this study, we analyzed the potential use of cationic PAMAM dendrimers to mimic the facilitated search mechanism of proteins along DNA. With this goal in mind, we investigated the energetics and dynamics of dendrimer-DNA binding interactions. We calculated the interaction energy by using all-atom molecular dynamics simulations and mapped the free energy along a circular reaction coordinate around DNA via umbrella sampling. We also calculated NMR order parameters, first time to our knowledge for a PAMAM dendrimer, to understand the dynamics in different binding modes, comparing minor and major groove binding.

Based on a comparison of energetics, we concluded that, despite considerably more favorable electrostatic interactions in the minor groove, the free energy is lower in the major groove than minor groove. This can be explained by a high entropic cost as the dendrimer is attracted to DNA in the minor groove. The higher values of NMR order parameters when the dendrimer is in minor-groove binding mode supported this explanation. The free energy barrier between the minor and major groove interactions was found to be about 8.5 kcal/mol, a value high enough to likely inhibit a possible sliding motion along DNA axis. Our result not only quantifies the free energy barrier introduced due to major groove-minor groove variations in DNA landscape, but also identifies the helical path along DNA major groove as a suitable reaction coordinate to study possible diffusion of dendrimers. The possibility of a sliding motion along a helical axis (similarly to some DNA-sliding proteins) will be dictated by the PMF along a helical axis spiraling through the major groove. Alternatively, the overall charge size may be reduced to half of its current value to obtain free energy values comparable to proteins. This is the first study to our knowledge, in which a potential of mean force of interaction around DNA is calculated for a cationic, flexible molecule. This information will benefit various fields of DNA nanotechnology, in which not only dynamic, but also static DNA structures are used for various potential applications, some of which involve the interaction of DNA with other molecules similar to dendrimers. Moreover, our PMF profile is a significant contribution in itself in any area that involves dendrimer-DNA interactions. Our results can be used in the fields of bionanomedicine and bionanotechnology that involve dendrimer-DNA interactions and in designing artificial walking molecules.