A tiered, Bayesian approach to estimating of population variability for regulatory decision-making

Summary

Characterizing human variability in susceptibility to chemical toxicity is a critical issue in regulatory decision-making, but is usually addressed by a default 10-fold safety/uncertainty factor. Feasibility of population-based in vitro experimental approaches to more accurately estimate human variability was demonstrated recently using a large (~1000) panel of lymphoblastoid cell lines. However, routine use of such a large population-based model poses cost and logistical challenges. We hypothesize that a Bayesian approach embedded in a tiered workflow provides efficient estimation of variability and enables a tailored and sensible approach to selection of appropriate sample size. We used the previously-collected lymphoblastoid cell line in vitro toxicity data to develop a “data-derived prior distribution” for the uncertainty in the degree of population variability. The resulting “prior” for the toxicodynamic variability factor (the ratio between the median and 1% most sensitive individual) has median (90% CI) of 2.5 (1.4–9.6). We then performed computational experiments using a hierarchical Bayesian population model with lognormal population variability with samples sizes of n=5 to 100 to determine the value-added in terms of precision and accuracy with increasing sample size. We propose a “tiered,” Bayesian strategy for fit-for-purpose population variability estimates: (1) a “default” using the “data-derived prior distribution”; (2) a “preliminary” or “pilot” experiment using samples sizes ~20 individuals that reduces prior uncertainty by >50% with >80% balanced accuracy for classification; and (3) a “high confidence” experiment using sample sizes ~50–100. We propose that this approach efficiently uses in vitro data on population variability to inform decision-making.

1. Introduction

The growing list of chemical substances in commerce and the complexity of exposures in the environment present enormous challenges for ensuring safety while promoting innovation. Because of the limitations of the current human and animal data-centric paradigm of chemical hazard and risk assessment in terms of cost, time, and throughput, the next generation of human health assessments has no choice but to use the information on chemical structure and from molecular and cell-based assays (NAS, 2007). Combined with the ever increasing power of modern biomedical research tools to probe biological effects of chemicals at finer and finer resolutions, 21st century toxicology is taking shape (Tice et al., 2013; Kavlock et al., 2012).

In addition to addressing only a fraction of the chemicals in commerce, current hazard testing approaches usually do not take into account the genetic diversity within populations, overlooking uncertainties about how genetic variability might interact with environmental exposures to affect risk (Rusyn et al., 2010). As a result, while characterization of human variability in susceptibility to chemical toxicity is a critical issue in toxicology, public health, and risk assessment, it is usually addressed by a generic 10-fold safety/uncertainty factor despite encouragement to generate and use chemical-specific data (WHO/IPCS, 2005). The recent use of population-based animal in vivo (Rusyn et al., 2010; Chiu et al., 2014) and human in vitro (Abdo et al., 2015b; Abdo et al., 2015a; Eduati et al., 2015; Lock et al., 2012) experimental models that incorporate genetic diversity provide an opportunity to more precisely estimate human variability and increase confidence in decision-making. The technical feasibility and the scientific and practical value of large-scale in vitro population-based experimental approaches to more accurately estimate human variability, thereby avoiding the using of animals, has been firmly established in experiments with hundreds of single chemicals (Abdo et al., 2015b), as well as with several mixtures (Abdo et al., 2015a). Such an experimental approach fills a critical gap in large-scale in vitro toxicity testing programs, providing quantitative estimates of human toxicodynamic variability and generating testable hypotheses about the molecular mechanisms that may contribute to inter-individual variation in responses to particular agents. However, it is not feasible or practical to employ in vitro screening for population variability using thousands of cell lines to test thousands of chemicals and an infinite number of mixtures and real-life environmental samples.

Two approaches are possible to address the challenges in cost and effort of embedding population variability into large-scale in vitro testing programs. One solution is to develop computational models based on the already collected data, either to predict susceptibility to chemicals based on the constitutional genetic makeup of an individual or to forecast which chemicals may be most prone to eliciting widely divergent responses in a human population. Indeed, the large-scale population based in vitro toxicity data of Abdo et al. (2015b) enabled development of an in silico approach to predicting individual- and population-level toxicity associated with unknown compounds (Eduati et al., 2015). This exercise showed that in silico models could be developed producing predictions were statistically significantly better than random, but the correlations were modest for individual cytotoxicity response and only somewhat better for population-level responses, consistent with predictive performances for complex genetic traits. A second solution is to devise a tiered experimental strategy, flagging compounds with greater-than-default variability that may benefit from additional testing to more fully characterize the extent of a population-wide response.

Here we hypothesized that a Bayesian approach embedded in a tiered workflow will enable one to efficiently estimate population variability, and to sequentially determine the number of individuals needed to provide sufficiently accurate variability estimates. The acceptable degree of uncertainty in population variability differs depending on the risk assessment decision-making context as well as other sources of uncertainty. Our approach combines a data-derived-default and Bayesian estimation of uncertainty to provide sufficient flexibility to develop fit-for-purpose estimates of human toxicodynamic variability as part of broader, more generic decision-making frameworks (e.g., Keisler and Linkov, 2014). This approach avoids use of animals to fill a critical need for decision-making, and also provides a template to minimize sample sizes that can be applied to reduction in the use of animals, both of which are in keeping with the 3R concept of Russel and Burch (1959).

2. Materials and methods

2.1. Population cytotoxicity data and measures of toxicodynamic variability

The chemicals, cell lines, and cytotoxicity assays were previously described in Abdo et al. (2015b). Briefly, concentration-response data consisted of intracellular ATP concentrations evaluated 40 hr after treatment with 170 unique chemicals at concentrations from 0.33 nM to 92 µM in lymphoblastoid cell lines from 1,086 individuals. Data were collected in 6 batches, and included some within-batch and some between batch replicates, with a total of 1–5 replicates for each chemical/cell-line combination. In all there were 351,914 individual concentration-response profiles, each consisting of 8 concentrations of a chemical in a specific cell line. The data were renormalized so that 0 corresponded to control levels (number of cells in each well) and −100 corresponded to a maximal response (complete loss of viable cells).

For each chemical and individual, the EC₁₀ (concentration associated with a 10% decline in viability) was used as an indicator of a toxicodynamic response. The variation across individuals in the EC₁₀ was then used as an indicator of population variability in toxicodynamic response. Specifically the toxicodynamic variability factor at 1% (TDVF₀₁) is defined as the ratio of the EC₁₀ for the median individual (EC_10,50) to the EC₁₀ for the more sensitive 1^st percentile individual (EC_10,01): TDVF₀₁ = EC_10,50 / EC_10,01. Additionally, we define the toxicodynamic variability magnitude (TDVM) as the base 10 logarithm of the TDVF: TDVM = log₁₀(TDVF), or TDVF = 10^TDVM. The default fixed uncertainty factor for toxicodynamic variability is 10^½ (WHO/IPCS, 2005), or half an order of magnitude, corresponding to TDVF = 3.16 and TDVM = ½.

2.2. Estimating population variability for each chemical using a Bayesian approach

Abdo et al. (2015b) used maximum likelihood to fit a logistic model to each concentration-response dataset, averaging EC₁₀ estimates across replicates to estimate the EC₁₀ each individual, with TDVF₀₁ estimated by the ratio between the median individual’s EC₁₀ and the 1% most sensitive individual’s EC_10, using a simple correction for measurement-related sampling variation using the variation among replicates. This method of using the sample quantiles to estimate TDVF₀₁ is subject to increasing sample variation for sample sizes much less than ~1000, and is not be feasible for smaller sample sizes <100 (the 1% most sensitive EC₁₀ would not be part of the sample). However, if using a parametric distributional fit, then in principle any quantile can be estimated, along with (importantly) the uncertainty in this estimation.

Hierarchical Bayesian methods provide a natural approach to this type of challenge. The TDVF can be viewed as following a random effects models, with underlying parameters estimated using a Bayesian approach. Specifically, these methods they allow for a multi-level structure in which individual-level parameters are viewed as drawn from a distribution governed by hyperparameters. Various levels of uncertainty can then be quantified and described through posterior distributions. The modelling workflow is shown in Figure 1, and described in more detail as follows.

Figure 1.

Bayesian modeling, evaluation, and prediction workflow. See text for details.

2.2.1. Bayesian concentration-response modeling for each chemical

The first step in the workflow (Figure 1) is specifying the statistical and concentration-response model that will be applied for each dataset. We analyzed each chemical separately, combining all the datasets that used the same chemical. Thus, for each chemical, each dataset j corresponds to a particular individual i[j] and batch b[j]. For each dataset j, the concentration-response data are assumed to follow a logistic model, as was assumed previously by Abdo et al. (2015b). Recognizing the issue of outliers, we assume that deviations between the data and the model follow a student-t distribution instead of a normal distribution (Bell and Huang, 2006). Specifically, the logistic model we used is (see bottom left panel, Figure 1):

• y_j(x_jk) = θ_0,j + (θ_1,j – θ_0,j) inv.logit(β_0,i[j] + β_1,i[j] x_jk) + ε_jk

• x_jk = ln(concentration_jk)

• ε_jk ~ T₅(0,σ_b[j])

• inv.logit(u) = exp(u)/[1+exp(u)]

θ_1,j was assigned a fixed value of –100 because many chemicals did not reach a maximal response in the dose range used, and in these instances θ₁ could not be reliably estimated from the data. In addition, T₅(0,σ) denotes a student-t distribution with 5 degrees of freedom, centered on 0, with scale parameter σ. Recognizing potential differences across batches, we allowed σ to vary across each batch b. We fixed the student-t degrees of freedom at 5 based on examining residuals from preliminary fits to the data. Additionally, the EC₁₀ for individual i is given by

• EC_10,i=exp([ln(0.1/0.9) – β_0,i ]/β_1,i),

which depends only on β_0,i and β_1,i.

Prior distributions were specified as follows (middle and top left panels, Figure 1). Parameter θ_0,j was estimated separately for each dataset j, as there was some apparent drift in the normalization, with a normal prior distribution across datasets j of θ_0,j ~ N(m_θ0 , sd_θ0). We assumed a normal population distribution across individuals i for β_0,i ~ N(m₀,sd₀) and β_1,i ~ N(m₁,sd₁), with respective means m₀ and m₁ and standard deviations sd₀ and sd₁. We used normal priors with wide variances for m₀ and m_θ0 , and half-normal priors with wide variances for m₁, sd₀, sd₁, sd_θ0, and σ (restricted to being positive).

The joint posterior distribution of the parameters ϕ given the data D is equal to

• P(φ|D) = P(φ) P(D|φ)/P(D)

Here, P(φ) is the prior distribution of the individual model parameters and hyperparameters, P(D|φ) is the likelihood, and P(D) can be treated as a normalization factor.

2.2.2. Model computation, convergence, and evaluation

Although our model is straightforward, the fitting and computation of posteriors cannot be feasibly performed deterministically, and so the posterior distribution was sampled using the Markov Chain Monte Carlo (MCMC) algorithm (large left arrow, Figure 1) implemented in the software package “Stan” version 2.6.2 (Gelman et al., 2015). Computations were performed in the Texas A&M University high performance computing cluster with four MCMC chains run per chemical. Evaluation of the model performance had several components as follows (middle panels, Figure 1).

Convergence was assessed using the potential scale reduction factor R (Gelman and Rubin, 1992), which compares inter- and intra-chain variability. Values >>1 indicate poor convergence, and asymptotically approach 1 as the MCMC chain converges. Parameters with values of R ≤ 1.2 are considered converged.

The model fit was evaluated in three ways. First, because some chemicals showed very little response at the concentrations tested, the model could not confidently estimate an EC₁₀. A large value for the scale parameter for the error term σ is an indicator of poor model fit, so chemicals were dropped if the median estimate for any of the σ≥10. Additionally, chemicals were dropped if (a) the EC₁₀ for the median individual was outside the tested concentration range or (b) more than 1% of the individual EC₁₀ estimates have a 90% confidence range ≥1000-fold.

The model also estimates the overall population distribution of EC₁₀ values, so it is necessary to check the fit at the population, and not just the individual level. Specifically, we checked the assumption that β₀ and β₁ are unimodal, normally distributed, and independent. For unimodality, we used Hartigans’ dip test (Hartigan and Hartigan, 1985); for normality, we visually examined quantile-quantile plots; and for independence, we required that the correlation coefficient among posterior samples be < 0.5 (i.e., an R² of <0.25).

2.2.3. Model predictions

At the individual level, the model predicts posterior distributions of β₀ and β₁ for each individual, which can be used to estimate uncertainty in each individual’s EC₁₀ (upper right panel, Figure 1). Note that these estimates are already corrected for measurement errors. Thus, these EC₁₀ values can be used to derive an “individual-based” estimate for TDVF₀₁ as long as the number of individuals (n_indiv) ≥ 100, because we are using the 1^st percentile.

This approach infeasible for n_indiv < 100 because the 1^st percentile is not part of the sample. However, in the hierarchical Bayesian model, population predictions can still be made using the estimated values of the population-level parameters rather than the individual-level parameters (lower right panel, Figure 1). Specifically, in this case, the model predicts a posterior distribution for the population parameters m₀, m₁, sd₀, and sd₁, from which a “virtual” population of β₀ and β₁ can be generated via Monte Carlo sampling. Because the posterior distributions of m₀, m₁, sd₀, and sd₁ are also sampled (via MCMC), this is in essence a “two-dimensional Monte Carlo,” separately evaluating uncertainty and variability. The specific procedure to derive this “population-based” estimate for TDVF₀₁ is as follows:

• (1)Uncertainty loop – randomly sample populations l = 1…10³ from the posterior distribution of m₀, m₁, sd₀, and sd₁. Thus, the distribution across l represents the uncertainty in the population means and standard deviations.
• (2)Variability loop – for a given set m_0,l, m_1,k, sd_0,l, and sd_1,l. draw i = 1…10⁵ individual pairs of β_0,l,i ~ N(m₀, sd₀) and β_1,l,i ~ N(m₁, sd₁). Thus each l,i pair represents an individual i (representing variability) drawn from the population l (representing uncertainty).
• (3)For each individual i, calculate the predicted EC_10,l,i = exp([ln(0.1/0.9) – β_0,l,i ]/β_1,l,i). The distribution of EC_10,l,i over i (for fixed l), is the variability in the EC₁₀ for population l.
• (4)For each population l, calculate the TDVF_01,l, which is the ratio of the median to the 1% quantile of the EC_10,l,i.
• (5)The distribution of TDVF_01,l over l reflects the uncertainty in the degree of variability in the population.

2.3. Data-derived prior distribution for population variability in toxicodynamics (“Default distribution”)

2.3.1. Coverage of chemical space

The first element of the tiered approach is the development of a data-derived prior distribution for population variability. The principle behind such a default distribution is the assumption that the chemicals for which data were previously collected are sufficiently representative of chemical space so that a new chemical can be reasonably considered a “random draw” from the same distribution. To check this assumption, the chemicals examined by Abdo et al. (2015b) were compared with the over 32,000 chemicals in the CERAPP predication dataset (Mansouri et al., 2016), a virtual chemical library has undergone stringent chemical structure processing and normalization for use in the QSAR modeling. Chemical structures were mapped to chemical property space using DRAGON descriptors (Talete, 2010), as implemented in ChemBench (Walker et al., 2010).

2.3.2. Deriving the “Default distribution”

The “default distribution” was estimated using the “individual-based” estimates for TDVF₀₁. Specifically, for each of the chemicals for which the “individual” EC₁₀ estimates for the individual cell lines tested were considered reliable, the median EC₁₀ estimate of each of the 1086 individuals was used to construct the population variability distribution for that chemical. The TDVF₀₁ for each chemical is the ratio between the median and 1% quantile of the 1086 individual EC₁₀ estimates. The “individual-based” estimate of TDVF₀₁ was chosen to represent the “default distribution” because it is less dependent on model assumptions, and thus was reliability estimated for more chemicals. Additionally, it is most similar to the approach used by Abdo et al. (2015b), the only difference being the method of estimating the individual EC₁₀s.

The “default distribution” across chemical-specific TDVF₀₁ values was fit to a lognormal distribution in TDVM₀₁ = log₁₀ TDVF₀₁ [i.e., ln (log₁₀ TDVF₀₁) is fit to a normal distribution). This choice of distribution was motivated by several considerations. First, because TDVF₀₁ is restricted to be >1, this implies TDVM₀₁ is restricted to be > 0, and the lognormal distribution is a natural choice for strictly positive values. Additionally, previous analyses of in vivo human data that found toxicokinetic and toxicodynamic variability to be consistent with such a distribution (Hattis et al., 2002; WHO/IPCS, 2014). This choice was further checked using the Shapiro-Wilk test for normality (Royston, 1995) with a p-value threshold of 0.05.

The sensitivity of the resulting “default distribution” to the above choices was assessed in ways: (1) using “individual-based” estimates for the chemicals that passed the model fit test at both the population level as well as the individual level; (2) using “population-based” estimates instead of “individual-based” estimates; and (3) leaving one chemical out at a time.

2.4. Computational experiments with smaller sample sizes

In order to characterize the value-added as a function of sample size, sub-samples of individuals with n_indiv=5, 10, 20, 50, and 100 were drawn for each chemical, and the TDVF₀₁ re-estimated using the smaller sample. Ten (10) different replicate sub-samples were drawn for each value of n_indiv. Because only population-based estimates of TDVF₀₁ are feasible for these sample sizes, the computational experiments were restricted to the chemicals that had reliable population-based predictions.

Additionally, two estimates of TDVF₀₁ were derived for each experiment. The first estimate used the same Bayesian modeling workflow used to derive the data-derived prior distribution, including the same prior distributions for the model parameters. This posterior distribution is denoted “Data” distribution because it is based largely on the chemical-specific data, as the priors are broad enough to be unrestrictive as to the value of TDVF₀₁. A second “Default+Data” distribution estimate is derived based on combining the “Data” distribution with the “Default distribution” derived from the full dataset. This approach essentially treats the “Default” distribution as a Bayesian prior for TDVF₀₁, in which case the “Default+Data” distribution is the appropriate Bayesian posterior for TDVF₀₁.

The accuracy and precision of the “Default,” “Data,” and “Default+Data” distributions were evaluated in two illustrative types of prediction: “classification” and “estimation.” “Classification” involves separating chemicals into two bins of “high” or “low” variability, defined as having TDVF₀₁ > or < than the median value from the “default distribution.” Different percentiles of each distribution were used as “estimators” of TDVF₀₁ (e.g., 5^th percentile, median, 95^th percentile) to reflect different tolerances for false positives and negatives. The rates of true/false positives and negatives were compiled as a function of sample size n_indiv, assuming the estimate based on 1086 individuals was the “true” value. The results were summarized in an ROC curve, balanced accuracy, and AUC.

“Estimation” involves providing a numerical value for a chemical’s TDVF₀₁. The accuracy of each distribution as a function of sample size n was evaluated by comparing each median prediction with “true” value assumed to be the median estimate based on 1086 individuals, and quantified in terms of the slope and intercept of a linear regression. Because the uncertainty in TDVM₀₁ = log₁₀(TDVF₀₁) was found to be approximately lognormally distributed, the linear regression was performed on ln(TDVM₀₁). The precision of each distribution was quantified in terms of the R² of the linear regression as well as the geometric standard deviation of TDVM₀₁. The degree of uncertainty was compared using the corresponding log-transformed variance var(ln TDVM₀₁) = (ln GSD_TDVM)².

2.5. Software

MCMC computations and analyses of the convergence diagnostic R were performed with Stan version 2.6.2. The Stan statistical model code is included in Supplemental Materials and Methods. All other statistical analyses were performed using R version 3.1.1.

3. Results

3.1. Estimating population variability for each chemical

For most chemicals, convergence was reached for all parameters with a chain length of 8000, where the first 4000 “warmup” samples of each chain were discarded, and the final 4000 samples were used for evaluation of convergence, model fit, and inference. If a chemical had not achieved convergence for all parameters after chain lengths of 128,000 (64,000 warmup), then it was dropped due to poor convergence. One hundred and thirty-eight (138) of the original 170 chemicals passed both convergence checks as well as checks related to model fit. For these chemicals, “individual” EC₁₀ estimates for the individual cell lines tested were considered reliable. The 32 chemicals that failed these checks are listed in Supplemental Table 1, along with the rationale for their exclusion.

One hundred nineteen (119) of the original 170 chemicals also passed these additional checks related to normality and unimodality of the population distribution. For these chemicals, “population” EC₁₀ estimates (e.g., individuals generated via Monte Carlo) were also considered reliable. The 19 chemicals with reliable individual-based estimates, but less than reliable population-based estimates are listed in Supplemental Table 2, along with the rationale for their exclusion and the individual-based TDVF₀₁ estimate. The 119 chemicals with reliable individual- and population-based estimates are listed in Supplemental Table 3, along with both TDVF₀₁ estimates.

3.2. Default distribution for population variability in toxicodynamics

3.2.1. Coverage of chemical space

Figure 2 shows a visualization of the overlap between the Abdo and CERRAP chemicals, using the first three principal components in chemical property space (which account for 48% of the variance). Quantitatively, using Euclidean distance in chemical space as a measure of similarity (Zhu et al., 2009), greater than 97% of the CERAPP chemicals are within 3 standard deviations of the nearest neighbor distances across the Abdo chemicals. Thus, the Abdo et al. (2015b) chemicals represent a highly representative dataset from which to derive a data-derived prior distribution for population variability. For shorthand, this distribution is denoted the “default distribution.”

Figure 2.

Chemical space coverage of 170 chemicals from Abdo et al. (2015b) as compared to >32,000 chemicals in the CERAPP chemical library (Mansouri et al., 2016), based on principal component analysis of chemical descriptors.

3.2.2. Default distribution

Using the 138 chemicals with reliable individual-based EC₁₀ estimates, the distribution of TDVF₀₁ estimates ranged from 1.15 to 30.4, with a median of 2.6. As hypothesized, the distribution across chemicals of TDVM₀₁ = log₁₀(TDVF₀₁) was consistent with a lognormal distribution by the Shapiro-Wilk test (p = 0.32). The distribution of TDVF₀₁ estimates, along with the lognormal fit to TDVM₀₁, are shown in Figure 3. The parameters for the fit distribution, as well as their sensitivity to alternative methods, are shown in Table 1. As is evident from these results, alternative analyses lead to very small changes in the resulting “default distribution” of toxicodynamic variability. Therefore, the “default distribution” using individual-based estimates for the larger dataset of 138 chemicals is considered robust and will be used in subsequent analyses.

Figure 3.

Default distribution for toxicodynamic variability factor TDVF₀₁ based on cytotoxicity profiling, contrasted with a lognormal fit to TDVM₀₁ = log₁₀(TDVF₀₁).

Table 1.

Default distribution for population variability in toxicodynamics based on cytotoxicity profiling and Bayesian modeling.

Analysis	nchem	Lognormal distribution of TDVM01	Distribution for TDVF01 Median (90% CI)
Individual-based estimates, larger dataset	138	GM=0.39 GSD=1.74	2.48 (1.44, 9.57)
Alternative with population-based estimates, smaller dataset	119	GM=0.37 GSD=1.74	2.36 (1.41, 8.52)
Alternative with individual-based estimates, smaller dataset	119	GM=0.37 GSD=1.73	2.35 (1.41, 8.15)
Range of alternatives with individual based estimates, leave-one-one, full dataset	137	GM= 0.39–0.40 GSD=1.70–1.74	2.46–2.51 (1.44–1.47, 9.04–9.67)

Note: The toxicodynamic variability factor at 1% (TDVF₀₁) is defined as ratio of the EC₁₀ for the median person (EC_10,50) to the EC₁₀ for the more sensitive 1^st percentile person (EC_10,01): TDVF₀₁ = EC_10,50 / EC_10,01. The toxicodynamic variability magnitude (TDVM) as the base 10 logarithm of the TDVF: TDVM = log₁₀(TDVF), or TDVF = 10^TDVM.

3.3. Computational experiments with smaller sample sizes

A total of 5950 computational experiments were run, comprising 119 chemicals, five values of n_indiv (5, 10, 20, 50, and 100), and 10 replicates each. Figure 4 illustrates two typical results from these computational experiments. In each panel, the curves represent the Bayesian distributions for TDVF₀₁ based on (1) only the “Data”, (2) only the “Default”, and (3) the combined “Data+Default.” The chemical in the left panel has high variability, and the chemical on the right panel has low variability. Three key results are as follows:

Figure 4. Illustration of the effect of sample sizes on Bayesian estimates of the toxicodynamic variability factor TDVF₀₁ based on cytotoxicity profiling.

The chemical on the left has “high” variability and the chemical on the right has “low” variability. For each chemical and sample size (n = 5 … 1086), three distributions reflecting uncertainty in the value of TDVF₀₁ are shown, along with the median estimate. The “Data” distribution is the estimate only on the chemical-specific data using the Bayesian workflow illustrated in Figure 1. The “Default” distribution is the estimate without using any chemical-specific data, but assuming the chemical is randomly drawn from the distribution of chemicals as shown in Figure 3. The “Data+Default” distribution is the result of combining these distributions, i.e., the Bayesian posterior distribution treating the “Default” as a prior.

• At small values of n_indiv, the “Data” distribution is wider than the “Default” distributions, indicating that the chemical-specific data provide a less precise estimate of toxicodynamic variability than do data on other chemicals. In the case of a high variability chemical, the precision of the estimate based on n_indiv=5 is orders of magnitude worse than the precision of the “Default.” This is to be expected in a Bayesian context where informative prior information (here derived from large experiments with many chemicals) can “outweigh” a small amount of new data. Only at n_indiv~20 does the “Data” begin to have comparable precision to the “Default.”

• The Bayesian approach of combining the “Data” and “Default” leads to estimates that are both more accurate (with less bias) and more precise (with narrower confidence intervals), even at small values of n_indiv. Even for n_indiv as small as 5, the median of the “Data+Default” distribution is closer to the “true value” estimated for n_indiv = 1086 than the “Data” distribution. Additionally, by combining the two distributions, the resulting estimate is also more precise, as evident from the narrower width of the “Data+Default” distributions.

• In the case of a “low variability” chemical, the concordance between “Data” and “Data+Default” is higher, presumably because it is closer to the median across all chemicals (i.e., more similar to the “prior”).

These results hold generally across all the chemicals analyzed. Their implications are illustrated through two representative types of predictions: (i) classification of high/low variability chemicals and (ii) estimation of a chemical-specific TDVF₀₁.

3.3.1. Classification

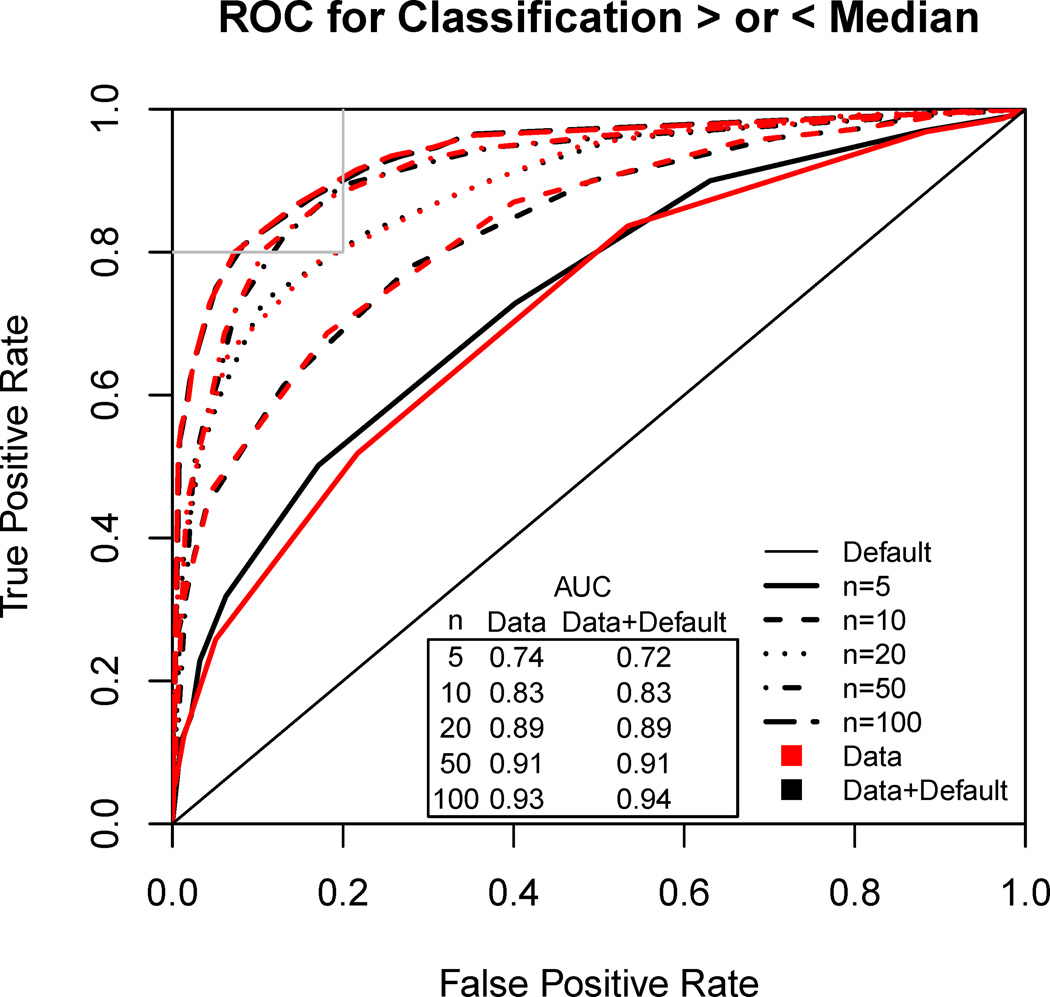
The purpose of classification is to place one or more chemicals into bins of “high” and “low” population variability, and the key question is characterizing the rates of true/false positives and negatives. For illustration, we assume that the threshold is the median of the “default distribution” = 2.48, with the implication that without any chemical-specific information, there is a 50–50 chance of a correct classification. Figure 5 shows the Receiver Operating Characteristic (ROC) and corresponding AUC for different values of n_indiv. We find that a sample size of at least n_indiv = 20 is required to achieve both 80% specificity and 80% sensitivity, and even n_indiv = 100 cannot achieve 90% balanced accuracy.

Figure 5.

Receiver Operative Characteristic (ROC) curve and AUCs for classifying a chemical as “high” or “low” population variability, defined by > or < median of the default.

The results for classification are similar whether the “Data” or “Data+Default” distribution is used. This can be explained by noting that the result of “Data+Default” is simply to “shrink” the estimates toward the median, in comparison to using “Data” alone. Because the classification is based on > or < the median, this shrinkage, while producing more accurate predictions, does not change the classification, leading to similar ROC curves.

3.3.2. Chemical-specific toxicodynamic variability estimation

Estimates of a chemical-specific TDVF₀₁ can be used in calculating a human health toxicity value such as a Reference Dose. The key questions here are the accuracy and precision of the estimate as a function of sample size. These are illustrated graphically in Figure 6, which shows scatter plots of the predictions for n_indiv=5…100 as compared to the predictions for n_indiv=1086. Also shown are the linear regression lines on ln(TDVM₀₁), along with slope β and R². Several key results are noteworthy:

Figure 6. Scatter plots (dots) and linear regression (red line) of predictions for n_indiv = 5…100 as compared to the predictions for n_indiv = 1086.

The R² and slope β of the linear regression are also shown. The black line is the slope=1 line, and the dotted lines separate the “high” and “low” values of variability with the median across chemicals as the “cut-point.” Note that the axis scales are “double log” transformed.

• At all sample sizes, the “Data” predictions have less accuracy (β further from 1) and less precision (smaller R²) as compared to the “Data+Default” predictions. This bias tends to be positive for “high variability” chemicals and negative for “low variability” chemicals, as is evident from the regression line intersecting the β=1 line at approximately the median value. This explains the similar ROC curves for “Data” and “Data+Default” in Figure 5.

• In some cases, the values of the “Data” predictions were extremely high, with absurdly unrealistic estimates of population variability, whereas the “Data+Default” predictions were much more reasonable due to the influence of the “prior.” For instance at n_indiv=10, across the 1190 computational experiments, the top 1% of the “Data” predictions for TDVF₀₁ ranged from 1800 to 10⁶¹ (!), whereas the top 1% of the “Data+Default” predictions ranged from 16 to 31. This shows how “unstable” estimates of population variability are with small sample sizes in the absence of accounting for prior information.

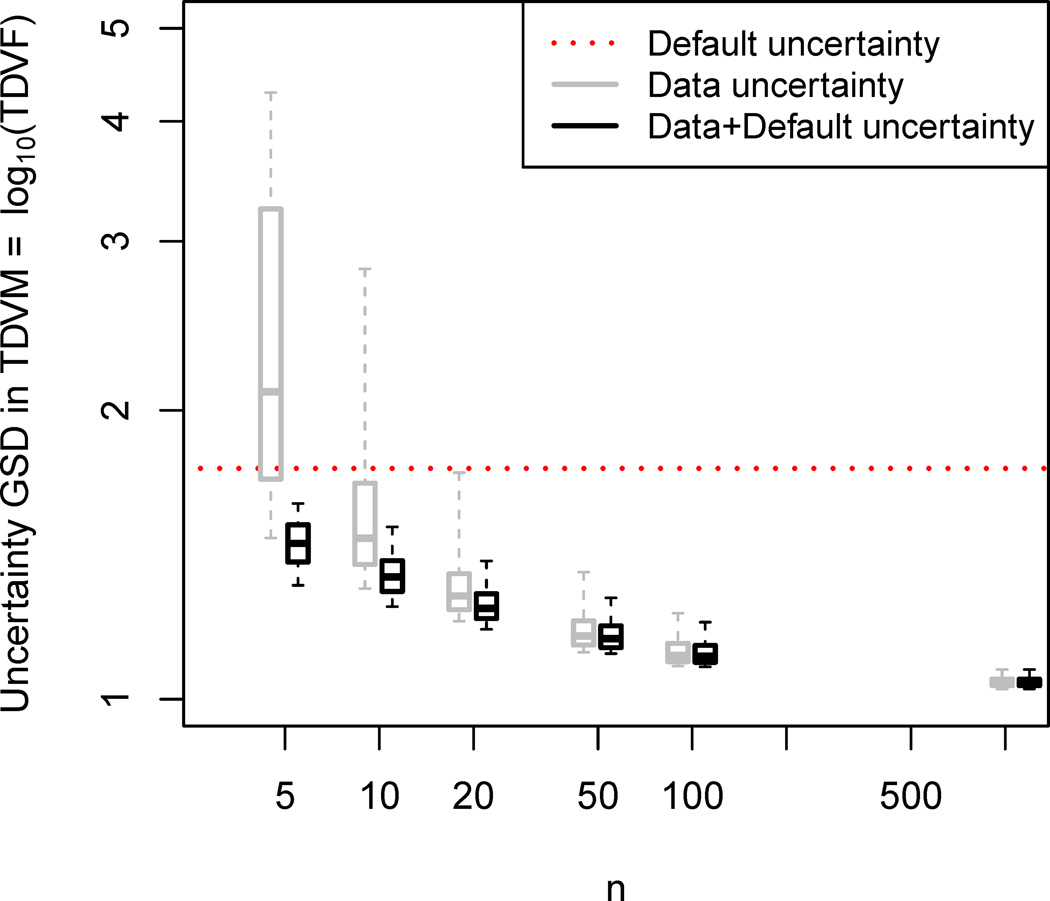
• In all cases, for the same value of n_indiv, the “Data+Default” prediction had better precision, as evidenced by the higher R², as compared to the “Data” prediction. This is further illustrated in Figure 7, which shows how the uncertainty in the TDVF₀₁ estimate decreases with increasing sample size. Only for n_indiv ≥ 20 does the “Data” prediction have an uncertainty smaller than the “Default” at least 95% of the time. By contrast, at n_indiv ≥ 20, in more than 99% of the “Data+Default” predictions the uncertainty is reduced by 2-fold compared to the “Default,” with a reduction in uncertainty of at least 5-fold 75% of the time.

Figure 7. Uncertainty in estimate of toxicodynamic variability as a function of sample size, comparing “Default” (red dotted line), “Data” predictions (grey box plot), and “Data+Default” predictions (black box plot).

The box plots represent the median (horizontal bar), interquartile range (box), and 95%ile range (whiskers) across the 1190 computational experiments for each value of n_indiv. The measure of uncertainty shown is the posterior GSD of the TDVM₀₁ = log₁₀ TDVF₀₁. For example, if the central estimate of TDVF₀₁ = 10^½ = 3.16, then the central estimate of TDVM₀₁ = ½. If GSD of TDVM₀₁ = 1.5, then its 90% CI is ¼ to 1, which in turn implies the 90% CI of TDVF₀₁ is 10^{¼ to 1} = 1.8 to 10.

Overall, for estimating chemical-specific toxicodynamic variability, the “Data+Default” predictions combining chemical-specific data with the “default distribution” as the prior are more accurate and more precise than the “Data” predictions based on chemical-specific data alone. Additionally, the “Data+Default” predictions begin to provide substantial improvement over the default distribution alone at n_indiv ≥ 20.

4. Discussion

Our results provide scientific justification for a tiered experimental strategy applicable to fit-for-purpose population variability estimation in in vitro screening, as illustrated in Figure 8. The first tier relies on the “default distribution” derived from the large scale study of >100 chemicals in >1000 individual cell lines (Abdo et al., 2015b). We have demonstrated that the chemicals used to derive this distribution provide wide coverage of the chemical space occupied by the environmental and industrial compounds (Figure 1), and that this default distribution is robust to multiple sensitivity analyses (Table 1). For many risk assessment applications and regulatory decision, this default distribution may be deemed adequate, for example if margins of exposure are high/estimated health risks are low even assuming a “worst case” of high variability. Moreover, although the default distribution is based on data from a single cell type, the resulting distribution is very similar to that based on available in vivo human data on toxicodynamic variability across a range of endpoints (Abdo et al., 2015b; WHO/IPCS, 2014). Therefore, as a “default,” this distribution is likely to be adequate regardless of the endpoint of interest.

Figure 8. Tiered workflow using a Bayesian approach to estimate toxicodynamic population variability.

After each tier, a decision is made as to whether the information from that tier is adequate to make the risk assessment decision

In addition, further refinement of the “prior” distribution may be possible through chemo-informatic approaches – using chemical structure information to give greater “weight” to chemicals in the database that are more “similar” to the chemical of interest, such as incorporating the models reported in Eduati et al. (2015). Indeed, we found the distance between chemicals in chemical property space (e.g., as in Figure 1) have a small, but statistically significant, correlation (r=0.12, p = 0.03, by the Mantel test (Mantel, 1967)) with the “distance” between chemicals in terms of their TDVF, consistent with a small degree of “clustering” in chemical properties among chemicals with similar TDVF values.

The second tier focuses on “preliminary” or “pilot” experiments that provide a first level of refinement to the question of population variability. The results of this experiment could be used, for instance, to classify a large group of chemicals into bins of “high” and “low” population variability, or to provide a chemical-specific estimate of population variability for a particular substance or multiple agents at a reasonable cost. Based on the results with respect to accuracy and precision, sample sizes ~20 individuals have >80% balanced accuracy for classification and reduce prior uncertainty by >50% for estimation. For classification, similar results are obtained from the estimates based on the “Data” alone (using only chemical-specific data) or based on combining the “Data” and “Default” in a Bayesian manner. However, for quantitatively estimating a chemical-specific population variability, combining the “Data” and “Default” in a Bayesian manner results in a much more accurate and precise estimate. It is anticipated that this tier will address the needs of most of the risk assessment applications and regulatory decisions for which the default distribution alone is deemed to be inadequate.

The third tier is for deriving “high confidence,” chemical-specific estimates of toxicodynamic variability using sample sizes n_indiv > 20. While the difference between the “Data” and “Data+Default” results are more similar for these sample sizes, the latter would be more consistent with the overall Bayesian framework. This tier may be repeated iteratively with progressively larger sample sizes until the information is considered adequate for the regulatory decision at hand.

One uncertainty in the experimental (i.e., second and third) tiers of this approach is possible differences among cell types. The experiments reported in (Abdo et al., 2015b) which form the basis of these analyses were in lymphoblastoid cells, and it is not clear the extent to which the degree of variability correlates across different cell types. Therefore, while the “default” distribution based on lymphoblastoid cells is likely to be adequate across endpoints, given the similarity with the distribution based on in vivo data across multiple endpoints, it is less clear that chemical-specific variability can be assessed using only one cell type. However, it is anticipated that induced pluripotent stem cell (iPSC)-based technologies will enable tissue-type specific analyses of population variability, and such experiments are already underway for iPSC-derived cardiomyocytes from individuals with familial cardiovascular syndromes (Chen et al., 2016).

The Bayesian approach illustrated in these analyses also naturally interfaces with an overall probabilistic approach to dose-response assessment, as advocated by the National Academy of Sciences and the World Health Organization International Program on Chemical Safety (NAS, 2009; WHO/IPCS, 2014). Specifically, by providing a distribution reflecting uncertainty in the degree of variability, the Bayesian estimates of TDVF₀₁ can be used directly in the recent probabilistic framework developed by WHO/IPCS (2014) and summarized by Chiu and Slob (2015). This framework was developed as an extension of the current approach for deriving toxicity values using uncertainty and variability distributions based on historical in vivo data. In particular, with respect to the factor for human variation, WHO/IPCS (2014) and Chiu and Slob (2015) argued that this probabilistic approach provides substantial value-added in comparison with the usual 10-fold factor by explicitly quantifying both a “level of conservatism” (e.g., 90%, 95%, or 99% confidence) as well as a “level of protection” in terms of what residual fraction of the population may experience effects (e.g., 0.1%, 1%, or 5%). Thus, one consequence of the current 10-fold factor approach is that risk management judgements such as the levels of confidence and protection are “hidden” in the risk assessment, whereas a probabilistic approach that requires estimates such as the TDVF₀₁ and its uncertainty allow for such judgments to be made transparent and explicit.

More broadly, the approach proposed here suggests that an overall Bayesian framework can substantially reduce required sample sizes, particularly if there is an existing database from which to derive “informed” prior distributions. The same three-tier approach may indeed be applicable not only to other studies of population variability, but also perhaps other in vitro assays and in vivo studies as well, leading to a reduction in the number of animals used per experiment. This generic approach would consist of the following:

1. Tier 1. Developing prior distributions through re-analysis of existing data that can be used in the absence of chemical-specific data. These distributions could not only replace the current “explicit” defaults (such as 10-fold safety factors), but also “implicit” defaults such as “no data=no hazard=no risk.” This approach is consistent with recommendations from the NAS (2009) to replace current “defaults” with those based on the best available science.

2. Tier 2. Developing a suite of “preliminary” or “pilot” experimental designs with smaller sample sizes that could provide an improvement in precision and accuracy over the “default” but with smaller sample sizes than current testing regimes. The ability to use smaller sample sizes rests on the Bayesian approach of combining the prior information with the chemical-specific information, thereby increasing overall accuracy and precision at a lower “cost.” Additionally, other alterations in study design and statistical analyses could make more efficient use of samples (e.g., designing studies with benchmark dose modeling in mind, rather than pairwise statistical tests) (Slob, 2014a, b).

3. Tier 3. Only as a “last resort” would larger sample sizes like those traditionally used in toxicity testing be required.

A limitation of this approach is that developing an informative “prior” relies on the existence of a large dataset across chemicals. Even if it were not feasible to newly generate such a large dataset, it may be possible to mine existing databases, such as EPA’s ACToR System (Judson et al., 2012).

In sum, we have demonstrated that a Bayesian approach embedded in a tiered workflow enables one to reduce the number of individuals needed to estimate population variability. A key component of this approach is using the existing database of large sample size experiments across are large number of chemicals to develop an informed prior distribution for the extent of toxicodynamic population variability. For many applications, this prior distribution may well be adequate for decision-making, so no additional experiments may be needed. In cases where this “default distribution” is too uncertain, experiments with modest sample sizes of ~20 individuals can, if combined with the prior, provide a substantial increase in accuracy and precision. Only for the rare cases where a high confidence estimate is required would larger samples sizes of up to ~100 individuals used. Based on these results, we suggest that a tiered, Bayesian approach may be useful more broadly in toxicology and risk assessment.