Reconstructing blood stem cell regulatory network models from single-cell molecular profiles

Abstract

Adult blood contains a mixture of mature cell types, each with specialized functions. Single hematopoietic stem cells (HSCs) have been functionally shown to generate all mature cell types for the lifetime of the organism. Differentiation of HSCs toward alternative lineages must be balanced at the population level by the fate decisions made by individual cells. Transcription factors play a key role in regulating these decisions and operate within organized regulatory programs that can be modeled as transcriptional regulatory networks. As dysregulation of single HSC fate decisions is linked to fatal malignancies such as leukemia, it is important to understand how these decisions are controlled on a cell-by-cell basis. Here we developed and applied a network inference method, exploiting the ability to infer dynamic information from single-cell snapshot expression data based on expression profiles of 48 genes in 2,167 blood stem and progenitor cells. This approach allowed us to infer transcriptional regulatory network models that recapitulated differentiation of HSCs into progenitor cell types, focusing on trajectories toward megakaryocyte–erythrocyte progenitors and lymphoid-primed multipotent progenitors. By comparing these two models, we identified and subsequently experimentally validated a difference in the regulation of nuclear factor, erythroid 2 (Nfe2) and core-binding factor, runt domain, alpha subunit 2, translocated to, 3 homolog (Cbfa2t3h) by the transcription factor Gata2. Our approach confirms known aspects of hematopoiesis, provides hypotheses about regulation of HSC differentiation, and is widely applicable to other hierarchical biological systems to uncover regulatory relationships.

Throughout adult life, the mammalian blood system is maintained by hematopoietic stem cells (HSCs). HSCs are able to differentiate into all mature blood cell types, as well as self-renew to maintain the blood stem cell pool. Although alternative fate choices can be made by individual cells, the output toward different mature cell types is balanced and regulated at the population level. An imbalance of fate choices leads to biased production of cell types, which can result in severe blood disorders such as acute myeloid leukemia. It is therefore important to understand how fate decisions are controlled during blood cell development.

Hematopoiesis is an extensively studied and well-characterized system (1), and yet it is only with the recent development of high-throughput single-cell technologies that we are understanding how heterogeneity within hematopoietic stem and progenitor cell (HSPC) populations is related to fate choices in the blood (2, 3). Unlike bulk population studies, which measure average states of expression and assume homogeneity within a population, single-cell assays can resolve the molecular basis of cell type heterogeneity. Methods such as quantitative real-time PCR (qRT-PCR) and RNA sequencing (RNA-Seq) can be performed in individual cells to obtain single-cell gene expression profiles (4).

Cellular decision-making is heavily influenced by transcription factors acting as components of transcriptional regulatory networks (5). Identifying true transcriptional interactions remains an enormous challenge, at least in part because the experimental validation of functional relationships between regulator and target genes does not readily scale to a system-wide approach. Computational network inference methods have therefore become widely used to predict these functional relationships. However, the application of most network reconstruction methods has been restricted to expression data measured on whole populations of cells. The power of single-cell data has previously been recognized in discovering simple regulatory relationships in blood systems (6, 7). More recently, approaches have emerged basing network reconstruction on single-cell data (8–11).

As well as identifying regulatory relationships, network inference methods can also allow in silico simulation of gene expression. Computational modeling of gene regulatory networks has been applied to a variety of systems, in particular, developmental gene networks, providing new understanding about gene regulatory processes. Several studies have used a mathematical approach to study the role of gap genes in patterning the Drosophila embryo (12) where constructing gene circuit models improved understanding of the interactions present in the gap gene network (13). In the developing sea urchin embryo, Peter et al. (14) used extensive experimental evidence of transcriptional regulation to create a computational network model that recapitulated known patterning behavior, and was capable of making predictions by simulating perturbations.

To address the question of how HSPC fate decisions are controlled, we have used single-cell gene expression profiling to infer transcription factor regulatory relationships. To provide a large pool of cells for this investigation, qRT-PCR data we previously published (2) were extended to obtain comprehensive coverage of the murine bone marrow HSPC compartment. Using these data, differentiation trajectories from HSCs to progenitor cells were constructed. These were used to infer and validate regulatory network models, thereby gaining greater insight into the transcriptional programs governing HSC differentiation.

Results

Single-Cell Snapshot Measurements Capture Progression Through HSPC Differentiation.

To study the transcriptional control of HSPC differentiation, we previously collected single-cell qRT-PCR data for HSCs and progenitor cells, in which we quantified the expression levels of 48 genes in 1,626 HSPCs using the Fluidigm Biomark system (2). This study profiled megakaryocyte–erythroid progenitors (MEPs), granulocyte–monocyte progenitors (GMPs), lymphoid-primed multipotent progenitors (LMPPs), common myeloid progenitors (CMPs), HSCs with finite self-renewal (FSR-HSCs), and long-term HSCs (LT-HSCs). However, the primary focus was to resolve heterogeneity within four different LT-HSC populations isolated by fluorescence-activated cell sorting. Furthermore, the study profiled a limited number of progenitor populations. As we were interested in understanding progression through differentiation, we generated equivalent expression profiles for over 500 single cells from three additional populations to increase the coverage of intermediate cell stages and therefore improve our resolution of the hematopoietic hierarchy (Fig. 1A). FSR-HSC2, multipotent progenitor (MPP), and pre-megakaryocyte-erythroid progenitor (preMegE) (15) populations were profiled using the same single-cell qRT-PCR assays as before. Combined with the earlier profiles, these data provide extensive coverage of murine HSPC populations (Fig. 1A). The gene set used included 33 transcription factors known to play a role in HSC or myeloid differentiation, 12 nontranscription factor genes implicated in HSPC biology, and three housekeeping genes.

Fig. 1.

Single-cell gene expression profiling captures the transcriptional landscape of HSC differentiation. (A) The hematopoietic hierarchy, with populations profiled by qRT-PCR highlighted in boxes. The sorting strategies used to isolate each population are displayed to the right of the lineage tree. The three cell types with starred sorting strategies were collected and profiled specifically for this study; unstarred populations were profiled in our previous study, and the lineage tree diagram is also adapted from this paper (2). (B) Diffusion map dimensionality reduction of the populations highlighted in A based on gene expression as quantified by qRT-PCR. MolO stem cells (a subset of the LT-HSC sorting strategies enriched for functional LT-HSCs) are shown in purple, MEPs in red, and LMPPs in blue. All other cell types are in gray. For diffusion map, principal component analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) plots showing all cell types see SI Appendix, Fig. S1. (C) Diagram highlighting how these single-cell data capture HSC fate choice. HSCs can self-renew, or differentiate toward alternative lineages. Single-cell expression data are sampled from a transcriptional landscape that contains cells at different stages along differentiation trajectories toward MEP or LMPP progenitor cells.

To visualize the broader expression landscape captured by these 2,167 single-cell transcriptional profiles, we used diffusion maps (16). Diffusion maps use properties of random walks between cells to describe the underlying structure of the data. This method offers an advantage over linear dimensionality reduction techniques, such as principal component analysis, as it can capture a variety of more complex structures. The diffusion map method has been specifically adapted for use with single-cell expression data (17) and has proved to be a powerful tool for representing spatial heterogeneity in single-cell data from mouse embryos (18), and branching differentiation dynamics for both single-cell qRT-PCR data describing embryonic blood development (10) and single-cell RNA sequencing (scRNA-Seq) data for adult HSPCs (19).

When applied to our data, diffusion map analysis using all of the genes analyzed by single-cell qRT-PCR demonstrated that the new and old data sets integrated well (SI Appendix, Fig. S1). The location of specific HSPC populations in the diffusion map was consistent with known lineage relationships between mature cell types and their respective precursor populations. Fig. 1B highlights two progenitor cell populations, MEPs and LMPPs, along with the so-called molecular overlap, or “MolO” HSCs, as identified by Wilson et al. (2). MolO cells are HSCs with a shared transcriptional profile and increased probability of long-term multilineage reconstitution upon single-cell transplantation. Cells belonging to intermediate populations, such as MPPs and preMegEs, were present in regions of the diffusion map between the highlighted cell types. Taken together, diffusion map analysis of this comprehensive single-cell data set reveals a transcriptional landscape of expression states characteristic for early HSPC differentiation (Fig. 1C). In addition, the coordinates of the data in the diffusion map provide more than a visualization, as distances in diffusion space represent a measure of similarity between cells that avoids some of the effects of noise present in single-cell expression measurements (11, 20).

Single-Cell Expression Profiles Can Be Used to Construct Differentiation Trajectories.

Motivated by the consistency between the location of HSPC populations in the diffusion map and the hematopoietic hierarchy, we aimed to use the underlying coordinate space to better understand transcriptional changes throughout differentiation. Recent work introduced the concept of inferring “pseudotime” trajectories from single-cell expression data, where a sample of cells is ordered by progress through differentiation based on the strength of similarities between individual expression profiles (21, 22). From our diffusion map, two lineage branches originating from HSCs were identified with either MEPs or LMPPs as terminal cells. Cells belonging to each of these branches were ordered into the two respective pseudotime differentiation trajectories (Fig. 2A) to allow investigation of gene expression dynamics during HSPC differentiation.

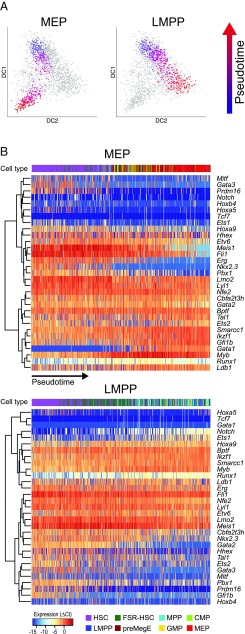
Fig. 2.

Computationally ordering single cells along differentiation trajectories captures gene expression dynamics. (A) Diffusion map showing cells on MEP or LMPP trajectories. Cells are colored by their pseudotime value, with blue cells early in the differentiation trajectory and red cells later. (B) Heatmaps showing changes in transcription factor expression levels along pseudotime for MEP and LMPP trajectories. Dendrograms on the left of the heatmap indicate the results of hierarchical clustering on genes. Colored bars at the top of the heatmaps indicate the types of cells along the pseudotime ordering.

Several factors displayed strong dynamics in one or both of the lineages, with differences between the two trajectories visible. For example, the expression of the developmental regulator Notch increased along the LMPP trajectory yet was largely undetected in the MEP trajectory. Expression of the transcription factor Gata1, however, was specifically activated during differentiation toward MEPs. The path toward MEPs mostly passes through MEP cells near the end of its trajectory. In contrast, the end of the LMPP path is composed of a mixture of cell types. This finding may be attributed, at least in part, to the nature of our gene set, and is also seen in the diffusion map representation of the data, where LMPPs appear closely related to CMPs and GMPs (SI Appendix, Fig. S1).

Gene Regulatory Network Models Can Be Inferred from the Pseudotime Dynamics of Single-Cell Data.

Variation in gene expression dynamics between the two differentiation trajectories suggested that these orderings could be used to help understand differences between the regulatory programs controlling differentiation toward alternative blood fates. Previous studies have successfully used Boolean abstraction to model transcriptional regulatory networks in HSCs (23), embryonic blood development (10), and embryonic stem cells (8, 24).

A clear limitation of Boolean network modeling, however, is that expression levels must be converted to binary ON/OFF values. From our data, it was clear that some transcription factors exhibited more complex behavior, with changes in the expression levels of genes visible throughout pseudotime (Fig. 2B). For example, Myb expression increases along both trajectories but is expressed throughout differentiation; considering only binary data would lose this information. We therefore reasoned that it would be valuable to use information about continuous gene expression levels to identify potential regulatory relationships (Fig. 3A). Using the single-cell expression data, pairwise correlations between genes were calculated, and a network of potential regulators for each gene was formed from the gene pairs with the strongest correlation. Partial correlations were then abstracted to a set of potential Boolean functions to model the regulation of each of the transcription factor genes (Fig. 3B).

Fig. 3.

Single-cell molecular profiles allow inference of regulatory network models. (A) Schematic showing the network inference steps starting from gene expression profiling using single-cell qRT-PCR data. (B) Potential regulators of each gene are identified by calculating a pairwise gene–gene correlation network. The highest correlating gene pairs are linked in the gene network. Activating (red edge) or repressing (blue edge) relationships correspond to positive or negative correlations, respectively. The regulators of each gene then define a set of potential Boolean functions governing the expression of that gene. Three of the possible functions for $G_1$ are shown here. (C) The pseudotime trajectory is then used to identify the most suitable Boolean functions. Cells are ordered in pseudotime (based on continuous expression data) and then converted to binary expression. Pairs of cells a fixed distance apart then represent input–output pairs to the Boolean function. These pairs are used to score a Boolean function $F$ by comparing $F(I_k)$ to $O_k$ for a pair $(I_k,O_k)$. The highest scoring function is the one where these values agree for the greatest number of pairs.

A method was needed, however, to identify the most suitable Boolean function for each gene from this set of potential functions. In single-cell data, the binary expression data for each individual cell can be considered as an allowed state of the Boolean network, and it has been established that transitions between these states can be used to identify Boolean functions (10, 25). As discussed above, differentiation is a dynamic process, which we captured by finding pseudotime orderings of the two lineage branches. Here we propose that the binary gene expression for pairs of cells from an ordered trajectory can be considered as input–output states for a Boolean function, and therefore provide an opportunity to identify the most relevant functions. To this end, each Boolean function from the partial correlation analysis was scored based on how frequently it agreed with the output cell when applied to the input cell (Fig. 3C). As well as providing a score for the Boolean functions, this method can also enable a direction of regulation to be inferred from the undirected correlation network. Using this method, we identified potential transcriptional regulatory network models for differentiation from HSCs to MEPs and LMPPs, with regulatory rules for each gene given by the highest scoring Boolean functions (see SI Appendix, Table S1 for full set of results). Examples of the dynamic expression patterns seen in Fig. 2B can be readily explained by the Boolean rules, such as differences in Notch expression between the two trajectories. In the LMPP trajectory, the expression increases throughout differentiation, whereas the majority of cells on the MEP differentiation trajectory do not express Notch. Investigating the Boolean rules for Notch shows that it is predicted within the LMPP trajectory to be regulated via Lmo2 AND NOT (Gata2 AND Gfi1b). A similar rule was found as one of the alternatives for the MEP trajectory [Lmo2 AND NOT (Gata2 OR Gfi1b) activates Notch]. The different behavior of Gata2 and Gfi1b along both trajectories can account for the different dynamics of Notch expression, as Gata2 and Gfi1b are downregulated toward LMPPs but remain expressed in MEPs.

Stable State Analysis of Network Models Identifies States Corresponding to in Vivo Cell Types.

The Boolean network models reconstructed from pseudotime ordering of LMPP and MEP differentiation trajectories were found to have complex structures, with each gene receiving inputs from an average of four upstream regulators, often as part of composite Boolean functions such as “(Notch AND Tcf7) AND NOT Etv6 activates Ets1.” Simplified graphical representation, depicting regulation as only activation or repression rather than the Boolean AND/OR relations forming the regulatory rules, illustrates the highly connected nature of both networks (Fig. 4A and SI Appendix, Fig. S2). To assess whether the reconstructed LMPP and MEP network models were able to recapitulate HSPC differentiation, we identified the stable states of both models. Importantly, this analysis demonstrated that, within the set of stable states for the MEP network model, there were several states exactly matching binary gene expression profiles of MEP but not LMPP cells, with the other MEP stable states having expression close to cells on the MEP trajectory. Similarly, for the LMPP network model, stable states were found that either closely or exactly matched the expression profiles of LMPP cells from the primary bone marrow data (SI Appendix, Fig. S3). To visualize how closely these stable states matched the location of cells sorted on LMPP and MEP surface markers, we also projected the stable states onto the diffusion map (Fig. 4B). Close matches between the sorted qRT-PCR data and the stable states were seen along the relevant lineage trajectories for both network models.

Fig. 4.

Stable state analysis demonstrates biological relevance of the networks for HSC differentiation. (A) Transcriptional regulatory network models for differentiation from HSCs to MEPs or HSCs to LMPPs. Activation is indicated with a red pointed arrow, and repression is indicated with a blue flat-headed arrow. A full description of Boolean rules for both networks is available in SI Appendix, Table S1. (B) Stable states of MEP (red) and LMPP (blue) networks projected onto the diffusion map of the primary bone marrow qRT-PCR data (small gray points). For each stable state, its nearest neighbors were found in the binary gene expression data. The average expression of these nearest neighbors (in the nonbinary data) was then projected into the diffusion map and highlighted (large red/blue circles). The intensity of the color of each state indicates how closely it matches binary measured expression values; for example, a value of zero indicates an exact match to the primary bone marrow data, and a value of 1 means that the stable state matched the primary bone marrow data except for a single gene.

Stable state analysis identifies all stable states of the network model, regardless of whether they can be reached from a biologically meaningful starting condition. We therefore simulated the network with initial conditions corresponding to binary expression in MolO cells (see Materials and Methods for details). Simulations starting from several of the MolO binary states could stabilize on both the MEP and LMPP binary states when simulated with the relevant networks, demonstrating that the two network models could recapitulate differentiation trajectories from HSCs to MEPs and LMPPs, respectively.

Differences in Network Model Connectivity Are Supported by Transcription Factor Binding.

Given the differences in dynamic expression of genes such as Notch and Gata1 between the two differentiation trajectories, it was not unexpected that the inferred Boolean networks for the two trajectories show differences in the regulatory rules for some genes. Comparing rules in the two network models highlighted a trio of genes with regulation unique to the MEP network model (Fig. 5A). In the MEP network model, Gata2 positively regulates Cbfa2t3h and Nfe2, with this regulation not present in the LMPP network model. Classical assays for the functional validation of the specificity of regulatory relationships require the use of model cell lines. We therefore considered previously published single-cell expression profiles of the 416B myeloid progenitor cell line (26, 27), which can be induced toward megakaryocyte differentiation (28). Projection of the 416B expression profiles onto our bone marrow HSPC diffusion map indeed demonstrated that 416B cells occupy a territory that forms part of the MEP differentiation trajectory (Fig. 5B). The HoxB8-FL cell line was recently reported to have both myeloid and lymphoid potential (29). We therefore also generated expression profiles for 107 HoxB8-FL single cells, which, when projected onto the diffusion plot, confirmed that the HoxB8-FL expression state resembles that of primary bone marrow cells from the LMPP trajectory.

Fig. 5.

Regulatory relationships unique to the MEP network model are supported by transcription factor binding. (A) Diagram of the trio of genes with a regulatory pattern identified as unique to the MEP network model. Red arrows indicate binding and positive regulation of genes by Gata2. (B) Diffusion map with projected qRT-PCR data for 416B and HoxB8-FL cells, showing gene expression similarities between the cell lines and in vivo data. (C) ChIP-Seq analysis of Gata2 in 416B and HoxB8-FL cell lines, showing Gata2 binds the Cbfa2t3h promoter in 416B cells only, and binds the Nfe2 enhancer in both cell lines but with greater binding in 416B cells. (D) Fold change in luciferase activity at the Cbfa2t3h promoter and Nfe2 enhancer, comparing the wild-type and Gata2 mutant regulatory regions. (*P < 0.05, **P < 0.01, ***P < 0.001; two-tailed unpaired t test, n = 3 $\pm$ SD.)

We interrogated existing Chromatin Immunoprecipitation Sequencing (ChIP-Seq) data for Gata2 in 416B cells (27) and generated new ChIP-Seq data for Gata2 in HoxB8-FL cells to investigate binding of Gata2 to Cbfa2t3h and Nfe2 (Fig. 5C). At the Cbfa2t3h locus, two prominent binding peaks were identified at the promoter region in 416B cells. The two peaks represent the minimal and full promoter, the minimal promoter being the most conserved region. Our single-cell profiling of HoxB8-FL cells showed that, just like in primary bone marrow LMPP cells, only a small minority of cells express Gata2. In accordance, only very limited Gata2 binding was observed at the Cbfa2t3h locus in HoxB8-FL cells, consistent with the specificity of our Gata2-activates-Cbfa2t3h rule found only in the MEP network model. At the Nfe2 locus, a prominent peak was identified at the $-$7-kb enhancer region in 416B cells, and, again, Gata2 binding in HoxB8-FL cells was at a much lower level.

To validate whether the binding of Gata2 in 416B cells causes transcriptional activation as predicted by our model, we generated reporter constructs for the Cbfa2t3h minimal and full promoter, as well as the Nfe2 enhancer, which were complemented by corresponding constructs with relevant Gata2 binding sites mutated. Luciferase reporter assays in 416B cells demonstrated that wild-type constructs showed significant fold activation over promoter/enhancer-less control constructs (Fig. 5D). Moreover, mutation of Gata2 binding sites resulted in significantly reduced luciferase activity, and was therefore consistent with the proposed role of Gata2 activation of both Cbfa2t3h and Nfe2 during MEP differentiation. Therefore, both ChIP-Seq and Luciferase assays served to validate the regulatory relationships proposed in silico between Gata2 and Cbfa2t3h, and between Gata2 and Nfe2. Several of the Boolean rules for the MEP predicted network model have been previously reported [growth factor independent 1B (Gfi1b) being regulated via the transcription factors T-cell acute lymphocytic leukemia protein 1 (Tal1)/Ets/Gata or friend leukemia integration 1 (Fli1) being regulated via Ets factors], thereby reiterating the utility of the proposed Boolean network model in this study (27, 30).

Discussion

In this study, we used single-cell gene expression profiling to define two transcriptional regulatory network models capturing differentiation toward alternative blood lineages. By contrasting the network rules, we identified Gata2 control of Nfe2 and Cbfa2t3h unique to the MEP network model, which we found to be supported by experimental evidence.

Our network inference method combines recently developed ideas about pseudotime trajectories with Boolean network modeling to exploit the dynamic information captured by single-cell data. Boolean models can easily be used to simulate network perturbations and readily relate to experimental approaches feasible in the laboratory. Using models to develop and test hypotheses on the effect of network perturbations will improve our understanding of how cell fate decisions are regulated in the blood. As disruption of regulatory programs is linked to serious blood conditions such as leukemia (31), discovering the mechanisms regulating differentiation of blood stem cells can provide insights into the role that subverted cell fate decisions play in these disorders.

Many methods exist with the aim of constructing regulatory network models from gene expression data. Transcription factor networks have been successfully modeled using methods such as Bayesian networks (27), which are computationally efficient and allow network perturbations to be simulated. However, Bayesian network topology is limited to acyclic graphs and therefore cannot capture feedback between transcription factors in the network. An advantage of Boolean network modeling, as used in this work, is that it does not suffer from this limitation. A recent study used Boolean abstraction to model the pluripotency network in embryonic stem cells (24), and was able to predict the results of experimental network perturbations. However, this study relied on performing gene expression profiling in multiple experimental conditions, which is not always feasible, and was limited to bulk rather than single-cell data. Several studies have used single-cell data to discover regulatory relationships, but only focused on simple correlation analyses (6, 7), which cannot infer the direction of regulation without additional experimental data.

More recently, single-cell gene expression data have been used to construct Boolean network models, but the models either relied on the assumption of cells being in a steady-state (8), which is not applicable to differentiating systems, or only used binary gene expression data, thereby losing information present in the level of gene expression (10). Regulatory factors in Boolean rules with many OR logic inputs could play different roles in the regulation of expression levels, which would not be captured by the Boolean model. For example, when Gata2 is predicted by our model to act in OR logic control of Nfe2, this would lead to the prediction that the loss of Gata2 is as important as any of the other factors also involved in the OR rules. This may not be true in vivo, as the relative expression levels of genes will vary, and loss of a transcription factor that is very highly expressed may have different consequences than that of the loss of a factor that is lowly expressed. An alternative approach, using the pseudotime ordering of single-cell expression profiles to construct an ordinary differential equation network model, was recently described (11). This approach can model more sensitive changes in gene expression levels, but is limited to smaller networks. We believe that the ability of our method to simulate and infer larger networks is a reasonable trade-off for modeling binary gene expression states.

Our method is particularly useful for studying regulation of differentiation processes, as it uses the dynamic pseudotime ordering to identify regulatory rules. A limitation of using qRT-PCR profiling is that it can only measure the expression of a limited number of genes. This restriction will affect the accuracy of the pseudotime ordering and means some important regulatory relationships cannot be described in the network, as the relevant genes were not included. Nevertheless, this study demonstrates an advantage to performing single-cell rather than bulk expression analysis, as it allows the construction of differentiation trajectories (11, 21, 22) and the reconstruction of transcriptional relationships involved in HSC cell fate decisions made by single cells. Future work may focus on expanding the set of profiled genes by using other high-throughput single-cell approaches, such as RNA-seq, which may also resolve heterogeneities within HSPC populations linked to fate choices (3, 32, 33). However, single-cell RNA-seq is currently less sensitive than qRT-PCR, which presents its own set of challenges for network inference methods.

The two MEP trajectory-specific network rules we identified, namely, the positive regulation of Cbfa2t3h and Nfe2 by Gata2, are both consistent with the known biological functions of the genes involved. Cbfa2t3h functions as a key component of multimeric transcription factor complexes that regulate both erythroid and megakaryocytic expression programs (34–36), whereas Nfe2 was originally discovered as an upstream regulator of globin gene expression (37) and is required for megakaryocyte maturation (38). Gata2 is primarily recognized as a regulator of HSPC function (39, 40). It is involved in HSC maintenance and expansion, playing a role in early hematopoietic cell formation (41), where Gata2 knockout mice display defects in primary hematopoiesis (42). Cbfa2t3h encodes the transcription factor Eto2, a corepressor in complex with Scl/Tal1 (43). Gata2 binds and activates Cbfa2t3h and, during differentiation, Eto2 represses its own promoter, leading to erythroid maturation and a Gata1-driven transcriptional program (44). Directly linking Gata2 to Cbfa2t3h and Nfe2 in the MEP regulatory network model but not the LMPP network model therefore provides an illustration of how differences in network topology guide the interaction between HSPC regulators such as Gata2 and more lineage-restricted regulators such as Cbfa2t3h and Nfe2. Interestingly, although Cbfa2t3h is traditionally reported to be a corepressor, our model predicts that it would activate several genes in the network. This activity could be directly a result of Cbfa2t3h (depending on its cofactors) or a double repressive link (involving a gene not included in our dataset). An important area of future research will be the identification of the mechanisms that direct stem cells into entering specific differentiation trajectories. By identifying and validating simple rules in the MEP and LMPP network models, we show the value of using in silico network inference to guide in vitro and in vivo investigations. By doing these in silico investigations, we can also gain information not available from gene knockouts alone, such as combinations of genes that interact, as well as specific cell types that may be affected by mutation.

In conclusion, we present an algorithm for discovering the transcriptional regulatory programs governing cell differentiation. We use this to describe regulatory network models in blood stem and progenitor cells, and provide validation of differences between the two network models. Our network models capture known biology and provide hypotheses about how HSC differentiation is regulated, and our network inference approach will be widely applicable to other differentiating biological systems.

Materials and Methods

Purification of Stem and Progenitor Cells.

Bone marrow cells were isolated from the femurs, tibiae, and iliac crest of 8- to 12-wk-old C57BL/6 mice and red-cell-depleted by ammonium chloride lysis (STEMCELL Technologies). Cells were lineage-depleted using the EasySep^TM Mouse Hematopoietic Progenitor Cell Enrichment Kit (STEMCELL Technologies). Antibodies used for isolation of FSR-HSC2, MPPs, and PreMegEs are listed in SI Appendix, Table S2. Single cells were sorted, using a five-laser Becton Dickinson Influx sorter, into individual wells of a 96-well PCR plate.

Single-Cell Gene Expression Analysis.

Single-cell gene expression analysis was performed as previously described (2, 6, 45) (see SI Appendix). Diffusion map dimensionality reductions were calculated using the Destiny R package (46) using centered cosine distance and $\sigma =\mathrm{\hspace{0.17em}0.3}$. Cell line data were projected onto the diffusion map using the dm.predict function from the Destiny R package. All qRT-PCR data can be downloaded from blood.stemcells.cam.ac.uk/single_cell_qpcr.html.

Pseudotime Inference.

Before pseudotime ordering, two lineage branches (HSC to MEP and HSC to LMPP) were identified following the method of Ocone et al. (11). Briefly, MolO, MEP and LMPP cells were highlighted on the diffusion map, and this visualization was used to select a start and end cell for each trajectory from within these populations. Branches were then identified by constructing a $k=\mathrm{\hspace{0.17em}30}$ nearest-neighbor graph using Euclidean distance on the first four diffusion components. Using Dijkstra’s algorithm, the shortest path from the start to the end cell was found, and the branch formed from the $n=\mathrm{\hspace{0.17em}100}$ nearest neighbors of each cell on this path. Cells on this path were then ordered in pseudotime using the Wanderlust algorithm with default parameters (21).

Network Construction.

To construct an initial network, partial correlation coefficients were calculated on all pairs of transcription factors using functions from the ppcor R package. Correlation coefficients with significance $>0.01$ were set to zero. The top 100 correlating pairs, plus self-activation for each gene, were taken as potential edges (distribution of correlation values is available in SI Appendix, Fig. S4). A step-size parameter $k=\mathrm{\hspace{0.17em}3}$ was used to generate the input–output pairs from the pseudotime order. After pseudotime ordering, gene expression was converted to binary (ON/OFF) expression. Binary expression in each cell is represented by a vector $c_i$, where ${(c_i)}_j$ is equal to the expression level of gene $j$ in cell $i$. Consider ordered cells $(c_0\mathit{\text{,}}{c}_1\mathit{\text{,}}\mathrm{\dots }\mathit{\text{,}}{c}_n)$. The set of input–output pairs $\{(I_t\mathit{\text{,}}{O}_t)\}$ were then generated by taking ${(I_t)}_j=mode[{(c_{t-k-1})}_j\mathit{\text{,}}{(c_{t-k})}_j\mathit{\text{,}}{(c_{t-k+1})}_j]$ and ${(O_t)}_j={(c_t)}_j$.

For a gene, the edges of the partial correlation network define its sets of possible activators $\{a_i\}$ and repressors $\{r_j\}$. Boolean functions $f$ of the form $f=f_1\wedge \mathrm{\neg }{f}_2$ were considered, where $f_1$ represents the activating part of the function and $f_2$ represents the repressing part. Here $f_j$ is a Boolean function restricted to AND nodes and OR nodes of in-degree 2. The functions $f_1\mathit{\text{,}}{f}_2$ were formed from, at most, $d_1$ and $d_2$ regulating TFs, respectively, with these parameters set to a default of $d_1=\mathrm{\hspace{0.17em}4},d_2=\mathrm{\hspace{0.17em}2}$ for each gene.

To identify the best rules for a gene $g$, we defined the score function $S$. For activating genes $a\mathit{\text{,}}b$, repressing genes $r\mathit{\text{,}}s$, and $m$ input–output pairs ${\{(I_t\mathit{\text{,}}{O}_t)\}}_{t=1}^m$, we have $f(I_t)=f_1[{(I_t)}_a\mathit{\text{,}}{(I_t)}_b]\wedge \mathrm{\neg }{f}_2[{(I_t)}_r\mathit{\text{,}}{(I_t)}_s]$ and

$$S(f)=\sum _{t=1}^m{s}_t(f)\mathit{\text{,}}{s}_t(f)=\{\begin{array}{cc}1\mathit{\text{,}}\hspace{1em}\hfill & \text{if}{[f(I_t)]}_g={(O_t)}_g\hfill \\ 0\mathit{\text{,}}\hspace{1em}\hfill & \text{otherwise}\hfill \end{array}.$$

This function counts how many times the predicted output of a function calculated from the pseudotime input agrees with the observed pseudotime output.

To find the rule for a gene $v$, the algorithm then searches for functions of the above form satisfying the following criteria: (i) $f_1=f_1(a_i)$, $f_2=f_2(r_j)$ for activators $\{a_i\}$ and repressors $\{r_j\}$ of $v$ as defined above. (ii) The allowed function(s) maximize the score $S(f)$.

The above criteria were encoded as a Boolean satisfiability problem to find rules for each gene. This method was implemented in the Python programming language using the Z3 solver (z3.codeplex.com/) to encode satisfiability constraints. Python code for performing this network inference can be downloaded from https://github.com/fionahamey/Pseudotime-network-inference. For many genes, the method gave several functions with equally high scores. In this case, the results were simplified to the minimum set of simplest functions. For example, if functions Gata1 and Gata1 $\wedge$ Nfe2 had equal scores, the former would be chosen, as it is simpler and contained within the latter. When rules could not be simplified in this way, multiple rules were retained. If possible, the list of rules was also simplified to reduce the total number of rules. For example, if three functions Gata1, Gfi1b, and Gata1 $\vee$ Nfe2 were returned, then only the OR rule would be retained, as it contains the other two rules.

Stable State Analysis.

Stable states of the network were identified using the GenYsis algorithm using asynchronous updates (expression of one randomly chosen gene changing at a time) (47). To identify the states reachable from MolO starting points, Boolean rules for a network were encoded in R and simulated with asynchronous updates until the network stabilized and no genes could change expression. For MEP and LMPP networks, 1,000 simulations were run starting from each of the 237 binary expression states corresponding to MolO cells, and the stable end state of the simulation was recorded.

To project stable states onto the diffusion map, states were compared with binary primary bone marrow expression data. For each stable state, its nearest neighbor was identified and highlighted in the diffusion map. If more than one neighbor was the best match, the continuous gene expression levels were averaged across neighbors, and the average expression state was projected onto the diffusion map using the dm.predict function from the Destiny R package.

Chromatin Immunoprecipitation Sequencing.

ChIP assays were performed as previously described (48) (see SI Appendix for details). Raw and processed ChIP-Seq data have been submitted to the NCBI Gene Expression Omnibus with identifier GSE84328.

Luciferase Assays.

Luciferase assays were performed as previously described (49) (see SI Appendix for details).