Significance
Focal adhesions play crucial roles in mechanotransduction and regulate processes such as spreading, proliferation, differentiation, and motility. It is well known that cells develop larger adhesions when cultured on stiffer elastic hydrogels, but the native extracellular matrix (ECM) is fibrous, nonlinear, and dissipative. We developed a multiscale model showing that adhesion size decreases with increasing stiffness in fibrous matrices, in excellent agreement with our experiments on engineered fibrous matrices. Our model shows that this is due to the feedback between cell contractility and the physical remodeling of ECM, which does not exist in elastic substrates. The basic stiffness–adhesion size principle uncovered can be applied to understand tumor progression fundamentally or to better design biomaterial scaffolds to control cell behavior.
Keywords: focal adhesion, mechanosensing, cell contractility, matrix physical remodeling, Rho pathway
Abstract
We describe a multiscale model that incorporates force-dependent mechanical plasticity induced by interfiber cross-link breakage and stiffness-dependent cellular contractility to predict focal adhesion (FA) growth and mechanosensing in fibrous extracellular matrices (ECMs). The model predicts that FA size depends on both the stiffness of ECM and the density of ligands available to form adhesions. Although these two quantities are independent in commonly used hydrogels, contractile cells break cross-links in soft fibrous matrices leading to recruitment of fibers, which increases the ligand density in the vicinity of cells. Consequently, although the size of focal adhesions increases with ECM stiffness in nonfibrous and elastic hydrogels, plasticity of fibrous networks leads to a departure from the well-described positive correlation between stiffness and FA size. We predict a phase diagram that describes nonmonotonic behavior of FA in the space spanned by ECM stiffness and recruitment index, which describes the ability of cells to break cross-links and recruit fibers. The predicted decrease in FA size with increasing ECM stiffness is in excellent agreement with recent observations of cell spreading on electrospun fiber networks with tunable cross-link strengths and mechanics. Our model provides a framework to analyze cell mechanosensing in nonlinear and inelastic ECMs.
Focal adhesions (FAs) are large macromolecular assemblies through which mechanical force and regulatory signals are transmitted between the extracellular matrix (ECM) and cells. FAs play important roles in many cellular behaviors, including proliferation, differentiation, and locomotion, and pathological processes like tumorigenesis and wound healing (1–4). For this reason, intense efforts have been devoted to understanding how key signaling molecules and ECM characteristics influence the formation and growth of FAs. In particular, in vitro studies using elastic hydrogels have shown that forces generated by actomyosin contraction are essential for the stabilization of FAs (5, 6). Numerous observations have convincingly demonstrated that cells form larger FAs as well as develop higher intracellular traction forces on stiffer ECMs (7, 8), evidencing the mechanosensitive nature of FAs which has been quantitatively modeled using different (continuum, coarse-grain, and molecular) approaches (9, 10).
It must be pointed out that in all of the aforementioned investigations, the substrates considered were flat (2D) and linear elastic. However, in vivo, many cells reside within 3D fibrous scaffolds where the density and diameter of fibers can vary depending on the nature of the tissue (11–13). The local architecture of these fibrous networks may change significantly when cells exert forces on them, leading to phenomena such as nonlinear stiffening, reorientation, and physical remodeling of the ECM (14, 15). Our recent study on cells in synthetic fibrous matrices with tunable mechanics and user-defined architecture showed that increasing fiber stiffness suppresses spreading, in contrast to hydrogels, where increased stiffness always promotes cell spreading (16). Other recent studies have found that the spreading of cells cultured on soft viscoelastic substrates that exhibit stress relaxation is greater than those on elastic substrates of the same modulus but similar to that of cells spreading on stiffer elastic substrates (17). Although these studies demonstrate a clear departure from the well-described relationship between material stiffness and spreading established with elastic hydrogel surfaces, a quantitative description of how cells are able to physically remodel matrices to mature FAs, which in turn can lead to greater spreading, is currently lacking. In particular, models that connect ECM structure (i.e., fiber properties such as size and stiffness and the strength of cross-links) with cell adhesion formation and spreading can guide the development of materials to engineer the cellular responses, as well as to better understand the cell–matrix interactions in physiologically relevant states.
Here we propose a multiscale chemomechanical model to describe the evolution of FAs in cross-linked fibrous networks that resemble native ECMs. Specifically, possible breakage of cross-links in the fibrous network is considered, which allows contractile cells to recruit fibers and increase the density of ligands available for the formation of adhesions. By combining the mechanics of fiber recruitment with stress-dependent growth kinetics of FA plaques, we predict a phase diagram for the stable size of focal adhesions as a function of the ECM stiffness and a parameter we introduce, namely, the recruitment index of the ECM that characterizes how easily fibers can be recruited by the contractile cells. Our model explains how cell-driven fiber recruitment can lead to a departure from the monotonic stiffness versus cell spreading relationship observed in hydrogels.
Materials and Methods
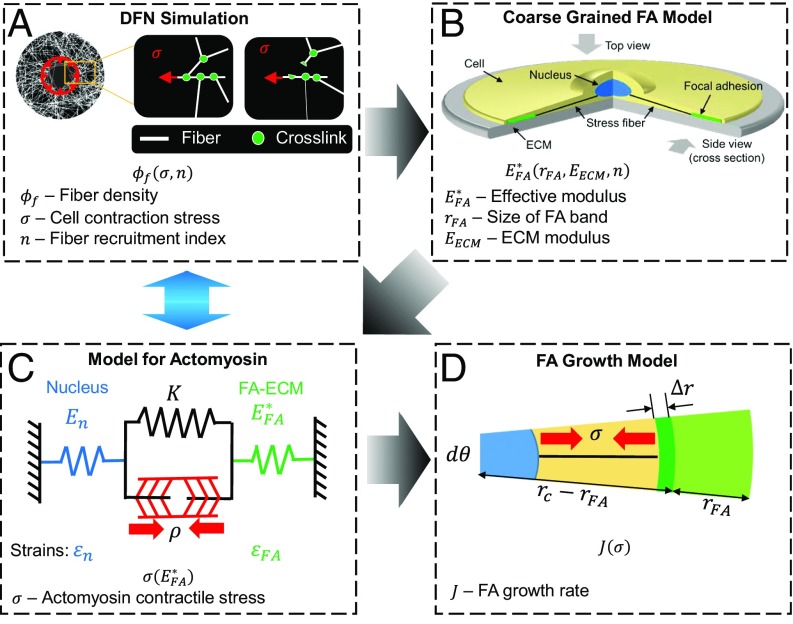
To understand the influence of cell-driven fiber recruitment on the formation of FAs, we developed a multiscale chemomechanical model. Specifically, the correlation between fiber density (which then determines the density of ligand/integrin bonds composing FAs) and cell contractility is first obtained using discrete fiber network (DFN) simulations. The mechanical response of the FA–ECM complex to actomyosin contractile forces is then determined by developing a coarse-grained model, where discrete FAs are homogenized and treated as an adhesion band along the rim of the cell. By coupling the stiffness dependence of the actin contractile force and the stress-dependent kinetics of adding new adhesion plaque units, the growth dynamics of the FA band and its equilibrium size are evaluated. The details of each of the elements of the model are described in the following sections.
Discrete Fiber Network Model for the ECM.
Following our earlier work on active biopolymer networks (14, 15), 2D fiber networks representing electrospun matrices were created with randomly organized linear elastic fibers and breakable cross-links. The fiber properties used in our DFN simulations were based on recent experiments on electrospun methacrylated dextran (16) scaffolds. Specifically, individual fibers were modeled as beams having circular cross-sections with Young’s moduli, Poisson’s ratios, and radii of 140 MPa, 0.3, and 1.8 µm, respectively. The initial configuration was created by randomly placing discrete fibers in a 2D plane and cross-linking the fibers that are closer than a threshold value. New fibers were added until the experimentally observed network pore size was reached. A circular void was introduced in the middle to represent the contractile cell which applies a uniformly distributed and radially directed force to the network near the periphery of the hole (Fig. S1). During the simulation, the force applied at the cell periphery was raised incrementally, whereas the network displacement was fixed at the outer boundaries, far from the hole. The cross-links were checked at each loading increment and removed if the transmitted strain energy exceeded a threshold value. This allowed for the detachments of fibers from their initial positions and densification toward the cell area. Fiber recruitment was quantified as the number of fibers that were pulled into the cell area.
Fig. S1.
Snapshots of the discrete fiber network contracted by a cell. (A) Distribution of strain energy in the fibers. (B) Forces in the fibers oriented radially (tensile) and circumferentially (compressive).
Coarse-Grained Model for the Mechanical Response of the FAs.
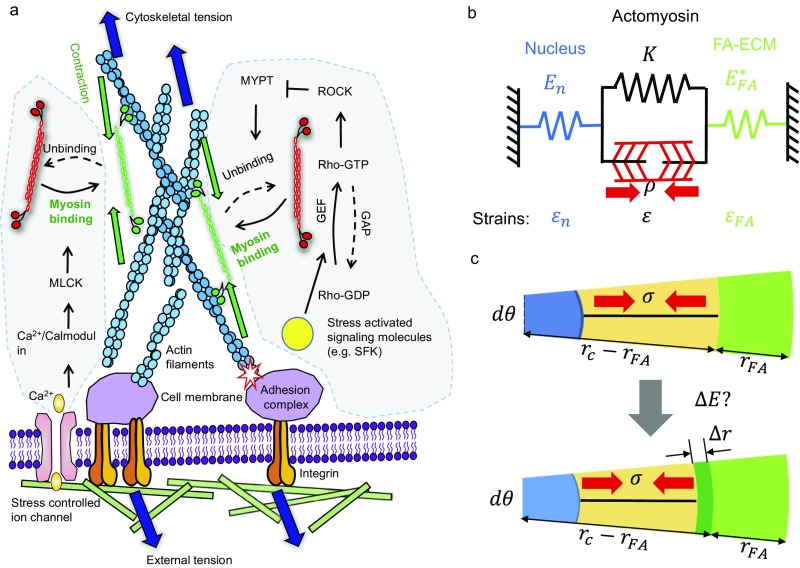
It is well known that FAs, which consist of clusters of integrins that bind to the ECM and to an intracellular plaque of reinforcing actin binding proteins, are connected to the cell nucleus via actomyosin stress fibers as shown in Fig. S2. Furthermore, such assemblies are mostly distributed at the cell periphery (18, 19), as shown in Fig. 1A. Based on these observations, we proceed by adopting an axially symmetric coarse-grained computational model where we represent the focal adhesions as a band (with width ) along the rim of a circular cell (Fig. 1A). The discrete FAs are not considered here, but we adopt a homogenized description where the total area of the adhesions is predicted based on the effective width of the band. The FA band is treated as an elastic plaque representing the stiffness of the constituent molecules (with Young’s modulus ) connected to the ECM through an array of integrins (modeled as springs with stiffness ) whose density () is assumed to be proportional to the fiber density () underneath the cell. Although more complicated models with strain-dependent detachment rates can be used for integrins, recent experiments have shown that a simple description (i.e., treating the integrin as a linear spring) can capture the response of integrins sufficiently because the timescale for integrin binding dynamics [i.e., a few seconds (9, 20)] is much shorter than that for FA growth [i.e., a few minutes (18)]. In addition, the proximal end of the band is connected to the cell nucleus through stress fibers (Fig. 1B) that generate contractile forces.
Fig. S2.
Schematic representation of the components of the cell–ECM adhesions.
Fig. 1.
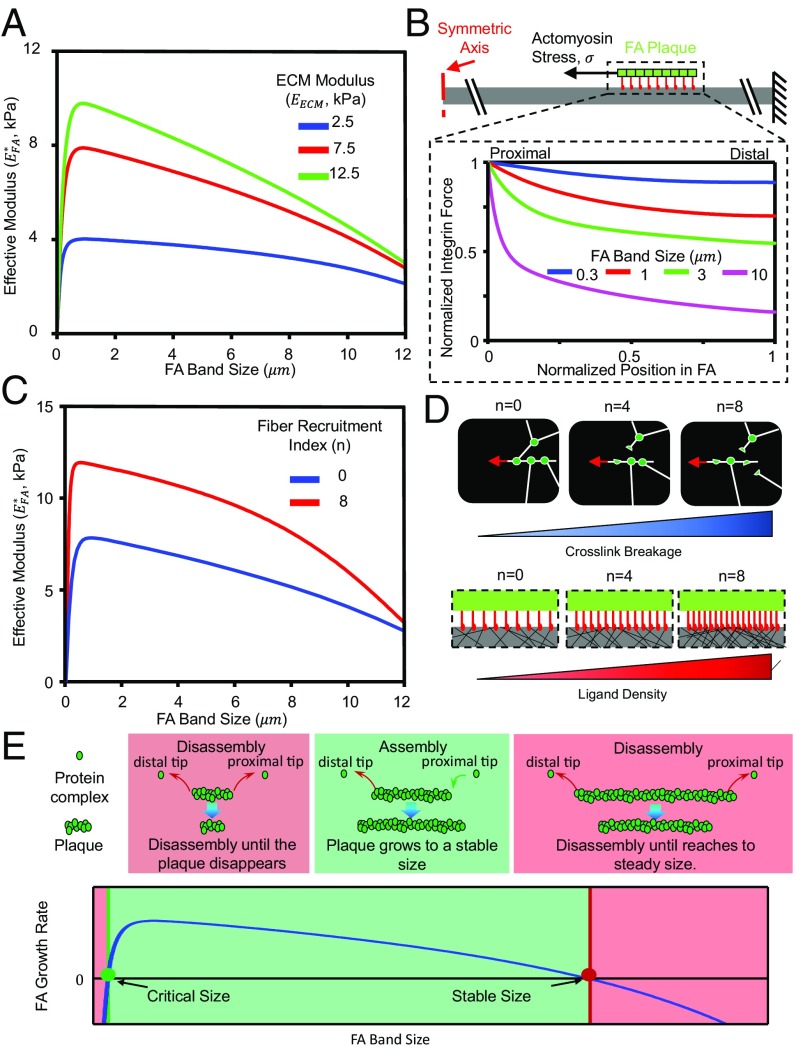
Coarse-grained model for the mechanical response of the FAs. (A) Schematic of a cell adhered to fibrous ECM. Cell contraction deforms the fibrous ECM through the FAs. The FAs are formed at the periphery of the cell. Based on this observation, an axially symmetric coarse-grained model is proposed, in which FAs are treated as a band at the periphery of the cell. (B) Schematic of the coarse-grained model: Stress fibers connect the FA band/plaque and the nucleus. The FA band/plaque is connected to ECM through an integrin layer whose density is positively correlated with the fiber density underneath the cell. The ECM is treated as an elastic material. (C) Schematic of the mechanical model: the deformation field induced by an actomyosin stress σ applied at the proximal edge of the FA band/plaque connected to the ECM via integrin layer. The FA plaque and the ECM are treated as elastic materials. The integrin layer is treated as a thin elastic layer consisting of springs.
Increases in the density of ECM fibers () underneath a cell can occur as the contractile forces break the cross-links in the ECM and recruit fibers, which will further influence the integrin–ECM bond density (; for simplicity, we assume that ). Specifically, our DFN simulations show that the fiber density () increases with the applied force (once it exceeds a threshold value) before saturating at large levels of force. To capture this behavior, is phenomenologically related to the contractile stress () as
| [1] |
Here is the initial fiber density, corresponds to the threshold stress for fiber recruitment, erf stands for the error function, and (recruitment index) is a measure of the ease with which fibers can be recruited. Physically, large values of correspond to the cases where cross-links are weak (i.e., can be broken easily), and therefore, more fibers will be recruited by the cell. As we show below (Cross-Link Breakage Enables Ligand Recruitment in Fibrous Networks), Eq. 1 captures the essential features of cross-link failure and fiber recruitment observed in our DFN simulations. With this description in hand, we can then use our coarse-grained model to address the outstanding issue of how cellular contraction influences the formation of FAs (via remodeling the ECM) within a continuum framework. The limitations of applying Eq. 1 to the 1D model for FA growth are discussed in Supporting Information.
When the actomyosin system applies a stress at the proximal edge of the FA band/plaque (as shown in Fig. 1C), the FA–ECM system deforms in response, leading to spatially varying elastic fields. To determine the stress and strain distributions, we implemented the coarse-grained model shown in Fig. 1B (governing equations and the boundary conditions are given in Supporting Information), together with the phenomenological description for fiber recruitment (Eq. 1), in the finite element method package (COMSOL 5.1). The effective modulus of the FA–ECM complex (i.e., the modulus sensed by the cell through active contraction) can be expressed as
| [2] |
where is the radial strain of the plaque at the proximal edge, which depends on the stiffness of the ECM, the size of the adhesion plaque as well as the degree of fiber recruitment. Note that because the contractile stress depends on the effective stiffness , the mechanical deformation of the FA–ECM complex has to be obtained in a self-consistent manner due to chemomechanical feedback (Fig. 2C; see Supporting Information for details).
Fig. 2.
Flowchart depicting the simulation steps. Blue arrow indicates the cross-talk between cell contractility and ECM remodeling. (A) DFN simulations predict fiber density (ϕf) as a function of cell contraction stress (σ) and fiber recruitment index (n). The prediction about fiber density is implemented in the coarse-grained FA model (B) to estimate the effective FA–ECM modulus ( ), which is used to evaluate the level of the contractile force (σ) using a chemomechanical feedback model for the actomyosin system (C; see Supporting Information for details). (D) Finally, all of the insights are combined to study the evolution dynamics of FA (in terms of its growth rate J) and give its equilibrium size.
Model for Stress-Dependent Growth of the FA Band.
Given that integrin binding/unbinding occurs within seconds (9, 20), whereas the assembly of proteins in the FA takes several minutes (18), the growth of FA should primarily depend on how fast adhesion proteins are added/removed from the plaque. Furthermore, as suggested by experiments, we proceed by assuming that protein recruitment/disassembly can only take place at the edge of the FA plaque (21). Finally, the driving force for growth of the plaque is assumed to be the chemical potential difference between plaque units recruited to the plaque and those in the cytosol. In particular, the work done by the contractile stress as the new units are recruited is expected to facilitate their incorporation in the plaque (22). Following this line of reasoning, we express the free energy difference for a segment of the plaque (with size and radial angle as shown in Fig. 2D and Fig. S3C) as
| [3] |
Fig. S3.
(A) The actomyosin activity in the cell is mediated by mechanochemical processes, such as the rho–ROCK and calcium-mediated pathways. (B) Schematic for the mechanical model of active contractile stress generation. The stress fibers are modeled as a spring in parallel with an active contractile element, which ensures that stiffer ECMs will generate larger contractile stresses. (C) Schematic for the plaque protein complex recruitment process.
where is the thickness of the FA plaque and (with unit ) represents the free energy gained per unit area for growing the plaque. The first term corresponds to the mechanical work performed by the actomyosin fibers when a new plaque unit is incorporated. When is negative in the presence of sufficiently large actomyosin contractile force, FA growth becomes energetically favorable. The total plaque recruitment flux (i.e., the FA growth rate) can then be related to as
| [4] |
where is a constant describing the kinetics of plaque assembly. In steady state (), the stress generated by the actomyosin system must satisfy, . Next we discuss how the laws for plaque incorporation (Eq. 4), actomyosin force generation, and effective modulus (Eq. 2) can be combined to predict the stable size of FA plaques.
Putting It All Together: Prediction of the Stable FA Size Based on Mechanical Response.
The rate-limiting step in the growth of the FAs is the incorporation of new plaque units, a process influenced by the stress level in the plaque exerted by the actomyosin network. The contractility of the network, in turn, depends on the effective stiffness of the adhesion complex determined by the size of the plaque, the stiffness of the ECM, and the density of integrin links between the ECM and the plaque. For ECMs that can be remodeled by cells, the integrin density is expected to be proportional to the density of fibers that can be recruited by the cells as they break the cross-links, which is controlled by the contractile force. Thus, predicting the growth kinetics and size of focal adhesions requires us to consider the two-way cross-talk between matrix reorganization and cell contractility. This is achieved by adopting the following multiscale procedures: (i) Using discrete fiber network simulations, the density of cross-links that are broken and hence the density of the recruited fibers (), as well as the integrin density increase that occurs in the process, are determined for a given level of contractile force (Fig. S1). (ii) Based on the integrin bond density, determine the effective stiffness () of the adhesion complex as a function of the plaque size () and ECM stiffness/modulus () from a coarse-grained model (Fig. 1 B and C). (iii) Using the effective stiffness () from step ii, evaluate the level of the contractile force () using a chemomechanical feedback model for the actomyosin system we previously developed (Fig. 2C and Fig. S3 A and B). (iv) Combining insights from steps i to iii, with the knowledge of the contractile force, study the evolution dynamics of FA (in terms of its growth rate ) as well as its equilibrium size (Fig. 2D and Fig. S3C).
It must be pointed out that the feedback between steps i and iii (i.e., actin contractile stress induces change in integrin density, whereas in return, a higher integrin–ECM bond density could vary the effective stiffness of FAs and eventually the generation of contractile stress) was carried out self-consistently in the above procedures as illustrated in Fig. 2. The parameters used in the model and along with their sources are listed in Table S1.
Table S1.
List of parameters used in the model
| Model parameter | Description | Value | Source |
| FA plaque modulus | ∼0.05 kPa | Estimated from Fisher et al. (41) | |
| ECM modulus | ∼0–20 kPa | Typical value for ECM modulus | |
| Integrin stiffness | 5 pN/nm | Estimated from Fisher et al. (41) | |
| Nucleus modulus | ∼5–10 kPa | Caille et al. (42) | |
| Stiffness of the cytoskeleton | ∼1 kPa | Chiron et al. (43) | |
| Initial myosin motor density | ∼0.5 kPa | Wang et al. (44) | |
| Chemo-mechanical coupling parameters related to the molecular mechanisms that regulate the engagement of motors | ∼ Pa | Shenoy et al. (33) | |
| Chemo-mechanical coupling parameters related to the molecular mechanisms that regulate the stress-dependent signaling pathways | ∼ Pa | Shenoy et al. (33) | |
| Thickness of FA plaque | ∼ | Kanchanawong et al. (45) | |
| Energy barrier for protein recruitment without mechanical load | ∼ | Estimated from Nicolas et al. (21) | |
| Size of the recruited segment | ∼ | Estimated from Kanchanawong et al. (45) | |
| Initial ligand density | ∼ | Cavalcanti-Adam et al. (46) | |
| Cell radius | ∼ | Typical value of cell radius | |
| ECM radius | ∼ | Set much larger than cell size to eliminate boundary effect. |
Results
Cross-Link Breakage Enables Ligand Recruitment in Fibrous Networks.
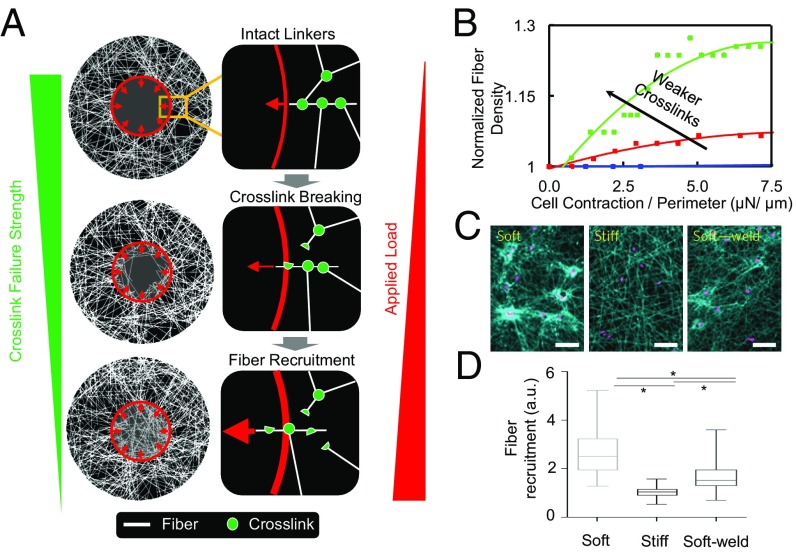
Our DFN simulations showed that the fiber strains decay gradually away from the periphery of the cell where contractile forces are applied (Fig. S1A). Furthermore, fibers oriented in the radial direction are stretched, whereas strains in the fibers aligned circumferentially were predominantly compressive (Fig. S1B). As the level of contractile force increases, the compressed fibers buckle, whereas the cross-links between the radial fibers could undergo higher stretching. Rupture of cross-links takes place once the forces the cross-links transmitted exceed a critical level, eventually allowing the fibers to be pulled into the cell area. As expected, significant fiber recruitment (to the circular region shown in Fig. S1) was observed in networks with weak cross-links (Fig. 3A) that could rupture easily, whereas no recruitment was observed when the fibers were welded together, in agreement with experimental observations (Fig. 3 C and D). The density of fibers (underneath the cell) under different levels of contractile stresses and cross-link strength are shown in Fig. 3B. Increases in the density of recruited fibers with force can be well fitted by the phenomenological relationship, Eq. 1, that is characterized by two parameters, namely, the fiber recruitment index () and the threshold stress for the cross-links to rupture (). We found that ECM stiffness indeed had a significant effect on fiber recruitment. Specifically, the cell recruits significantly fewer fibers on stiffer ECMs, as shown in Fig. 3 C and D, a phenomenon that is well captured by our model (Fig. S4).
Fig. 3.
Discrete fiber network simulation shows that cross-link breakage leads to fiber recruitment. (A) Tensile forces generated by cellular contraction leads to the breakage of the fiber cross-links, which allows the cell to recruit more fibers. The fiber recruitment index increases when the cell contractile force increases and more cross-links break. The red circle denotes the outline of the cell. (B) Normalized fiber density as a function of cell contraction for networks with cross-links of different breaking strengths. (C) The cell induces large deformations to the soft network, whereas induced deformations are much smaller for the stiff and welded soft network (stronger cross-links). (D) Quantitative measurements verified that the welded soft network shows fiber recruitment index as stiff networks, indicating that strong cross-links inhibit fiber recruitment. C and D adapted with permission from ref. 16.
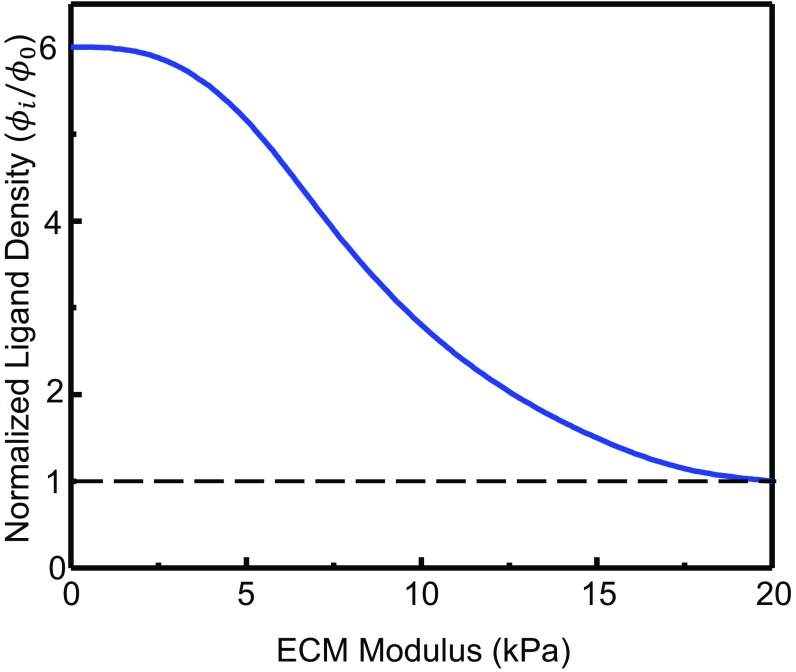
Fig. S4.
Normalized ligand density vs. ECM modulus. Model parameters are rFA = 8 µm and n = 8.
Nonuniform Stress Distribution in the FA Leads to Biphasic Stiffness Sensing by the Actomyosin System.
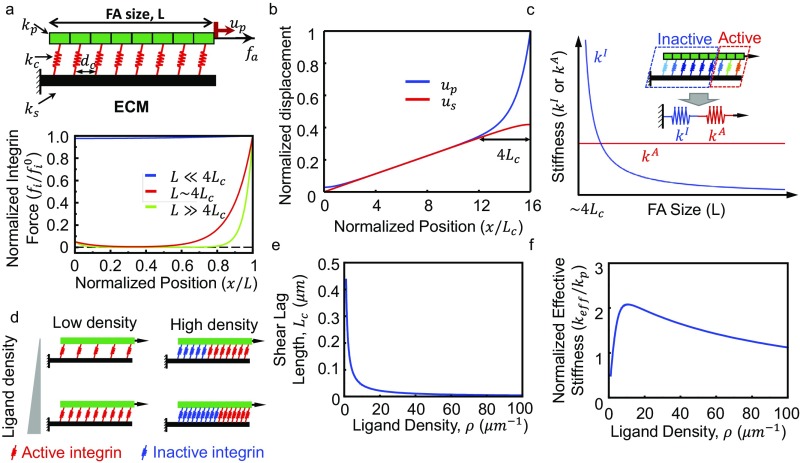
A quantity of key interest is the effective stiffness () of the FA–ECM complex, which physically represents the apparent mechanical modulus of the extracellular environment that a cell senses through the FA. This quantity is determined using the coarse-grained model and plotted as a function of the FA size in Fig. 4 A and C for different values of the ECM moduli () and fiber recruitment indexes (), respectively. In both cases, is small when the FA band size is either very large or very small but reaches a maximum at a certain intermediate FA band size. To understand this biphasic behavior, the force distribution in the integrin layer is first examined in the absence of fiber recruitment. As shown in Fig. 4B, the force transmitted to the ECM is distributed almost uniformly over all of the integrins for small FAs (solid blue curve), whereas the load distribution becomes highly nonuniform for large FAs, with the proximal edge carrying the majority of the transmitted force (solid magenta curve). This is known as the shear lag effect (23), where the stresses get unevenly distributed in the connecting layer (integrin layer) due to the difference in the deformation of the connected elements (the FA plaque and the ECM). The nonuniform distribution of force in the integrin layer becomes significant above a critical size of the FA, namely, the shear lag length (23). This length is determined by the stiffnesses of the FA plaque, integrins, and ECM, as well as the density of integrins (see the detailed form in Supporting Information and Fig. S5B). Hence, for FAs that are smaller than this characteristic size, the load is almost evenly shared by the integrins, and their growth results in bringing more active (i.e., load bearing) integrins and leads to a monotonic increase of . In contrast, for larger FAs (much larger than the shear lag length), the load is concentrated in a limited region at the proximal edge, and only inactive (i.e., those carrying no load) integrins are introduced as they grow. The effective stiffness of this inactive part correlates negatively to its size, whereas the response of the active part is not sensitive to how large the adhesion plaque is (refer to Fig. S5B and related discussion for details). Hence, decreases for large FAs as they grow.
Fig. 4.
Mechanosensing of the FA shows biphasic behavior with respect to the FA size. (A) Effective stiffness of a FA as a function of its size and the ECM modulus. (B) Normalized integrin force distribution for FAs of different sizes with EECM = 7.5 kPa. For small FAs, integrin force is almost uniformly distributed. The force is concentrated at the proximal edge as the FA becomes larger. (C) Influence of fiber recruitment index on the effective stiffness–FA size profile with EECM = 7.5 kPa. Fiber recruitment significantly increases the effective stiffness of FA–ECM complex. (D) Schematics for the influence of fiber recruitment: higher fiber recruitment index indicates more cross-link breakage, leading to more fibers and ligands, providing more integrins within the FA. Therefore, fiber recruitment significantly increases the effective stiffness. (E) Generic shape of the FA growth rate as a function of FA size, from which two quantities of central interest, i.e., the nucleation size for the nascent adhesions to develop into mature ones and the stable size for a fully developed FA, can be identified. The value of FA growth rate is only positive when FA size is between these two sizes. E reprinted with permission from ref. 24, with permission from Elsevier (www.sciencedirect.com/science/journal/00063495).
Fig. S5.
(A) Schematics of the 1D FA–ECM model. The integrin force distribution is very sensitive to FA size. For small FAs, integrin force is distributed almost uniformly; regions where integrins are force-free appear when FA size is comparable to 4Lc. The leading edge carries the majority of integrin force, and the size of this highly loaded region is a constant if FA size is much larger than 4Lc. A large FA (≫4Lc) can be divided into two parts based on the magnitude of the integrin force; the effective stiffnesses of the two parts are shown in C. Notice that the horizontal axis in C starts from L ∼ 4Lc. A and C are reprinted with permission from ref. 24, with permission from Elsevier (www.sciencedirect.com/science/journal/00063495). (B) Normalized displacement field (with respect to the maximum displacement) for FA plaque (up) and ECM (us) for an FA of size 16Lc. Note the size of the region of displacement mismatch between the FA plaque and the ECM is ∼4Lc. (D) At low ligand densities, more active integrins are introduced as ligand density increases because the characteristic length is large (E); at high ligand density, a part of the integrins become inactive and the inactive region becomes larger as ligand density increases because the characteristic length decreases (E). (F) Normalized effective stiffness as a function of ligand density for FAs of 0.1 µm, indicating ligand density has similar biphasic influence on stiffness sensing as FA size.
When recruitment of fibers due to breaking of the cross-links is considered, the effective stiffness of the FA–ECM complex () increases significantly compared with the case where fiber recruitment is not possible (Fig. 4C). For ECMs of the same modulus, higher fiber recruitment index (larger ) means more cross-links can break for the same level of applied load (as shown in Fig. 4D, Top). As a result, the cell can recruit more fibers and form more integrin–ECM bonds (as shown in Fig. 4D, Bottom), which contributes to additional stiffness and ultimately leads to the overall increase of effective stiffness ().
The Growth Model Predicts a Nucleation Size and Stable Size of the FAs That Depends on the ECM Stiffness and the Level of Fiber Recruitment.
As demonstrated both experimentally and theoretically (5, 6, 24), FA growth is largely determined by the level of actomyosin stress, which is sensitive to the effective stiffness of the FA–ECM complex () as described by the two-way mechanochemical feedback (Fig. 2C). Because this effective stiffness depends on the FA size (Fig. 4 A and C), the ECM modulus and the fiber recruitment index, these parameters in turn influence how fast the FAs grow. The generic behavior of the FA plaque recruitment flux (FA growth rate) as a function of FA size predicted by our model is shown in Fig. 4E. An immediate observation is that the value of is positive only when , where stands for the nucleation size. A nascent FA must be larger than this size to grow, whereas is the stable size for the FA. The FA growth can then be divided into three regimes as depicted in Fig. 4E: newly nucleated FAs with sizes smaller than will disassemble and eventually disappear; in comparison, FAs that are larger than will increase in size toward a stable size (); and very large FAs (), on the other hand, are predicted to shrink until they reach back to the stable size ().
This nonmonotonic growth rate–FA size relation can be understood by examining the intracellular contractile stress as a function of the size of the FA. Specifically, because of the biphasic dependence of on the FA size, a similar trend is expected for the contractile stress because a stiff FA–ECM complex induces a higher level of cell contractility (Eq. 3). As a result, cells cannot generate sufficient contractile stresses necessary for the further growth of the FAs when the sizes of FAs are either too small or too large, which produces the biphasic shape of FA growth profile as shown in Fig. 4E. Of course, the exact shape of the growth rate profile varies with the ECM moduli and the fiber recruitment indexes, leading to different stable sizes of the FA band.
FA Size–ECM Modulus Relation Becomes Nonmonotonic When Cells Can Recruit Fibers.
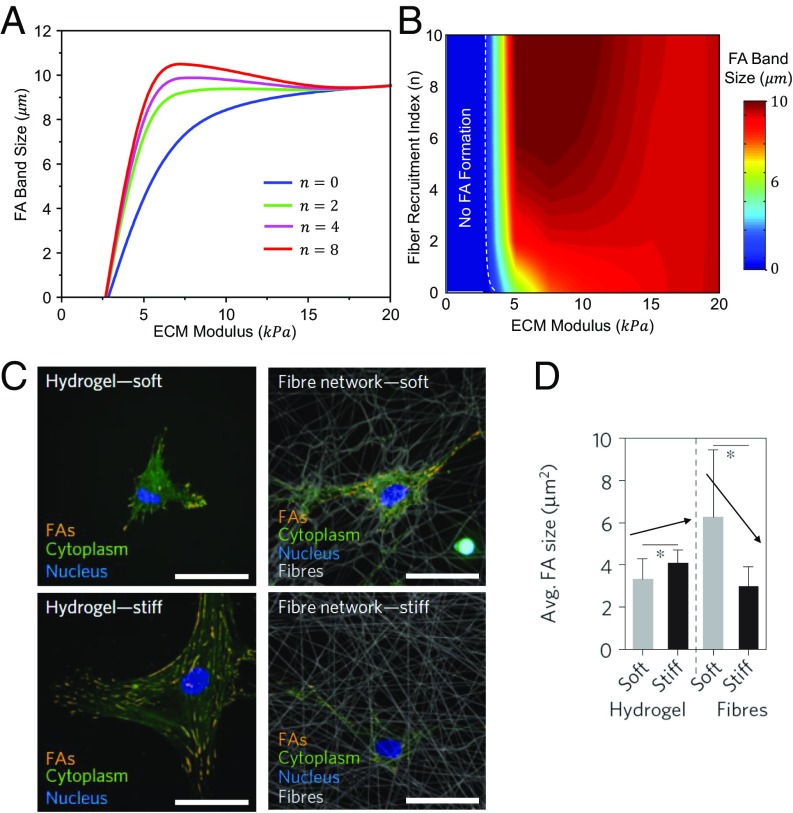
We first examined the correlation between FA size and ECM modulus without fiber recruitment, a scenario relevant to most elastic hydrogels and cross-linked ECMs that cannot be physically remodeled by the cells. As shown in Fig. 5A, we found that cells cannot form stable FAs on very soft ECMs. Furthermore, FA size increases monotonically with the ECM modulus. This can be explained by the fact that higher contractile stress will be developed on stiffer ECMs, which eventually leads to larger FAs.
Fig. 5.
Fiber recruitment promotes FA formation. (A) Stable FA band size plotted as a function of the ECM modulus at three different fiber recruitment indices. With no fiber recruitment and intermediate levels of fiber recruitment, FA size shows a positive correlation with ECM modulus; at high levels of fiber recruitment, FA size shows a nonmonotonic relation with respect to ECM modulus in an intermediate range of ECM modulus. The nonmonotonicity becomes less significant by reducing the fiber recruitment index. (B) Heat map of the stable FA band size as a function of the ECM modulus and the fiber recruitment index. (C) FA formation of representative hMSCs seeded on methacrylated dextran (DexMA) hydrogels of low and high stiffness, as well as on DexMA fiber networks of low and high stiffness. (Scale bars, 50 µm.) (D) Cell forms larger FAs on stiff hydrogel and soft fiber networks, verified by quantitative measurement. C and D adapted with permission from ref. 16.
When cells can recruit fibers [as in the case of fibrous ECMs with breakable cross-links (16)], the stable FA size increases compared with the cases without fiber recruitment (solid red curve in Fig. 5A) for a given level of ECM stiffness. This is because more integrins are available with the recruitment of fibers, leading to a stiffer FA–ECM complex as shown in Fig. 4C and therefore to higher levels of contractility. The FA size will reach its maximum at a certain intermediate ECM modulus when fiber recruitment is possible (Fig. 5A), in direct contrast to the monotonic trend observed on substrates that cannot be remodeled. The reason is that cross-links are ruptured more easily in a softer ECM due to the large deformation caused by cell contraction. Consequently, more integrin–ECM bonds will be formed in the FA, which will result in a stiffer FA–ECM complex (and hence a larger FA) even though the ECM modulus is smaller. This competition between increases in the fiber/integrin density and the ECM modulus (both promoting the formation of larger FAs) leads to a peak in the FA size at intermediate levels of the ECM modulus (Fig. 5A). These findings are consistent with our recent experimental observations where the FA size was found to increase with the stiffness of the hydrogel substrate that cannot be remodeled (i.e., n = 0), whereas larger FAs can be formed on softer remodelable fibrous scaffolds (refer to Fig. 5 C and D). When the recruitment index is at an intermediate level (n = 2, solid green curve in Fig. 5A), the FA size–ECM modulus relation still shows a monotonic variation. These results predict that a critical level of fiber recruitment is essential for the presence of a nonmonotonic FA size–ECM modulus relation. Above this critical level, the nonmonotonicity become less significant by reducing the fiber recruitment index (n = 4; solid magenta curve in Fig. 5A), which has been validated by our experiments (16).
By varying the values of and , the stable FA band size as a function of the ECM modulus and the fiber recruitment index is shown in Fig. 5B. The heat map predicts how the FA size varies with the ECM modulus and the fiber recruitment index. Similar to previous studies (24), our model suggests that the cell cannot form stable FAs on very soft ECMs. The threshold modulus for stable FA formation decreases with increasing fiber recruitment index because FA formation is favored at higher ligand densities. The cells can form stable FAs in ECMs with weak cross-links. In that case, FA growth may be favorable by an increase in ligand density resulting from the recruitment of fibers. Another key prediction of the model is the increase of FA size with stiffness in an intermediate range of stiffness and decrease of FA size at larger matrix stiffness (e.g., the red and magenta curve in Fig. 5A); we have not been able to engineer our ECMs to span the entire phase space to validate the predictions of the model. We hope these predictions can provide guidelines to design matrices to engineer the cell response.
Discussion
In summary, we developed a multiscale coarse-grained chemomechanical model to describe the evolution of FAs in cross-linked fibrous networks that resemble native ECMs as well as widely used hydrogel ECM systems. In particular, by considering the elastic deformation and fiber recruitment within the ECM along with the stress-dependent growth kinetics of the FA, we predict the stable FA band size as a function of ECM modulus and fiber recruitment index. Our results show that, FA size is positively correlated with ECM modulus for ECMs that cannot be remodeled (i.e., hydrogels), but the relation departs if the ECM is remodelable for cells (i.e., fibrous network), as shown in Fig. 5A. The reported FA size–ECM modulus relation is consistent with recent experiments (Fig. 5 C and D) (16).
To further understand the nonmonotonic behavior of the FA size as a function of the level of fiber recruitment, we study how FA adhesion size varies when the ligand density and the ECM modulus are independently altered based on our recent published 1D FA model. This analysis was motivated by the experimental work of Engler et al. (25), who controlled the density of collagen on the surface of hydrogels (of fixed stiffness) and hence effectively designed a method to decouple the effects of ligand density and ECM stiffness. They found a nonmonotonic dependence of cell area on ligand density; the cell area shows a peak at an intermediate density of ligands on the surface. They also suggested that other cellular responses (focal adhesion growth, cell shape, and cytoskeletal organization) should follow similar trends (25). However, an explanation for these phenomena is still lacking (26). Specifically, we found that (the shear lag length that determines the size over which contractile stresses are transmitted to the ECM) decreases with increasing ligand density (Fig. S5E), which results in a larger value of the ratio even if the FA size () remains unchanged. As we have shown earlier, this ratio determines the integrin force distribution profile: at small , integrin force distributes uniformly, whereas the force becomes highly localized at the proximal end when is large (Fig. S5A). This change in the integrin force distribution (induced by either increasing or decreasing ) eventually leads to the biphasic response of the effective stiffness of FA. Therefore, increasing ligand density () has a similar effect on as that of increasing the FA size (); that is, the effective stiffness of FA increases with the growing initially, reaches its maximum, and then decreases gradually as the ligand density further increases (refer to Fig. S5F and related discussions). By coupling the effective stiffness of FAs with the stiffness-dependent generation of actin contractile stress and the force-dependent kinetics of adding new adhesion plaque units, the stable FA size as a function of ECM stiffness and ligand density can be obtained. As shown in Fig. S6, cells respond positively to ECM stiffness (i.e., forming larger FAs) but nonmonotonically to ligand density, which is consistent with the observations on cellular contractility and spreading (1, 25). Specifically, the effective stiffness of FA–ECM complex (with fixed ECM stiffness) will be small if the ligand density is either too low or too high, leading to low intracellular contractility. Because cells form larger FAs at higher contractility levels, the stable size of FAs will reach its maximum at intermediate ligand density. In comparison, under fixed ligand density, stiffer ECM always results in higher contractility and consequently a monotonic increase in the FA size. We carried out steps b–d (Fig. 2) by treating ligand density and ECM modulus as two independent parameters and obtained the FA size profile as shown in Fig. S6B, which shows trends similar to the 1D model (Fig. S6A). In summary, we predicted the nonmonotonic FA size–ECM stiffness–ligand density map (Fig. S6) that was pointed out previously (1, 25) but thus far has not been explained from a theoretical perspective.
Fig. S6.
FA size as a function of ligand density and ECM stiffness/modulus: (A) 1D predictions and (B) 3D predictions.
The behavior of cells on different ECM systems is best summarized by the nonmonotonic response map (Fig. S6). In particular, for ECMs that cannot be remodeled (i.e., hydrogels), the ECM modulus and ligand density are decoupled from each other (this is applicable for most artificial ECM systems, as shown in Fig. 6A). Therefore, as ECM becomes stiffer, the response of cells follows a linear path with no variation in ligand density (Fig. 6C), resulting in positive correlation between FA size and ECM modulus (Fig. 6E). In comparison, for fibrous ECMs that can be remodeled (such as DexMA fiber network), cells are able to recruit more fibers from their soft microenvironment and hence form more integrin bonds (Fig. 6B), as demonstrated by recent experiments (16) and our simulations (Fig. S4). Because the ligand/integrin density and ECM modulus are coupled in this case, the cells will react to changes in the properties of their surroundings along a much more complicated path where ligand density decreases with increasing ECM modulus as shown in Fig. 6D, leading to the nonmonotonic FA size–ECM modulus relationship (Fig. 6F). Of course, the actual shape of the path has to be determined by the cross-talk among cell contraction, fiber recruitment, and ECM stiffness.
Fig. 6.
Ligand recruitment leads to nonmonotonic behavior of FA size with stiffness. On ECMs that the cells cannot remodel [(A) e.g., hydrogel and welded fibrous networks], the contractile stress increases with stiffness of the ECM, which makes FA growth more favorable. As a result, FA size is positively correlated with the ECM modulus (C and E). However, on ECMs that can be remodeled [(B) e.g., cross-linked fibrous networks], cellular contraction induces deformation of the ECM leading to recruitment of fibers on softer ECMs. In this case, when matrix mechanics are enhanced, cells sense matrix properties that vary along a more complicated path in the ligand density–ECM stiffness space (D). Therefore, a departure from the monotonic FA size–ECM modulus relation found in the case of hydrogels is observed (F). Quantitative comparisons against experimental results are shown in Fig. S7.
We must point out that local fiber recruitment is closely related to the inelastic (history-dependent) bulk response of biopolymer networks (27–29). In particular, mechanical straining accelerates the dissociation of weak cross-links (30), leading to macroscale plastic deformation of the matrix. It had been shown that such an effect is more prominent at long timescales (27) and large strains (28, 29), whereas it diminishes with the addition of permanent covalent cross-links (28, 29). In contrast, networks that only have weak cross-links are more dissipative and undergo larger stress relaxations (29). In this regard, it is expected that the fiber recruitment index, , introduced here is a quantitative measure of the plastic response of the ECM, a parameter that has not been considered and appreciated in previous theoretical investigations. By introducing this parameter, we are able to characterize the coupled relation between ligand density and ECM stiffness for fibrous ECMs. Recently, the influences of time-dependent matrix properties [such as viscoelasticity (17) and viscoplasticity (31)] on cell behaviors have drawn lots of attention. By applying the corresponding theoretical models, we may be able to characterize the corresponding recruitment index for these matrices and therefore apply the proposed multiscale model to probe the cellular mechanosensing in these matrices. Experiments have shown that matrix degradation by the action of enzymes such as MMPs decreases with increasing tensile forces (32), but this newly described phenomenon of force-mediated changes in active, cell-induced matrix degradation is not considered here, because cells cannot degrade the synthetic DexMA fibers considered in our experimental study. Our model generically applies to fibrous ECMs with interfiber bonds that follow a Bell-like breaking behavior, where cross-links dissociate more readily with increasing levels of force. Recent experiments (29) on the nonlinear viscoelastic response of collagen suggest that cross-link breaking in collagen networks is facilitated by tensile forces, in agreement with the assumptions of our model. Because cross-link breakage occurs within 1–10 s (29), which is separable from the timescale for FA growth and evolution (5–10 min) (18), our model can be applied to address viscoelastic effects of the ECM. Incorporating properties such as cell-mediated matrix degradation and synthesis into the current model will be critical in the future to capture the long-term evolution of cell–matrix interactions in natural matrices.
To summarize, our results from the multiscale chemomechanical model and recent reports (16) show that as studies move from smooth and flat hydrogel surfaces to more complicated 2D or 3D fibrous scaffolds (mimicking in vitro ECMs), the ability of cells to remodel their microenvironment needs to be taken into consideration when modeling the growth of focal adhesions. In addition to providing explanation for a variety of experimental observations, this study can serve as a theoretical framework for assessing the role of FAs in cell functions such as cell spreading, migration, and differentiation in nonlinear extracellular environments.
SI Materials and Methods
Limitation of Dimensionality: 1D vs. 3D Models for FA Growth.
Integrin/ligand density can vary in both 1D and 3D (or more precisely, quasi-3D, because the cell is not fully encapsulated in the matrices) models, but there are significant differences in the physical phenomenon described by Eq. 1 in 1D vs. 3D. In 1D environments, there are no cross-links involved because only a single fiber is considered. In that case, integrin/ligand density increases along individual fibers as a result of compressive strains. On the other hand, in 3D environments, integrin/ligand density changes when fibers are recruited by the cells after breaking interfiber cross-links. Because RGD ligand attached to DexMA fibers are not mobile, collective recruitment is crucial to increase local ligand density. Therefore, although an increase in density of ligands can be achieved in 1D using Eq. 1, the parameters in this equation only make physical sense when applied to the 3D model. In addition to providing a more accurate description of densification, the 3D setup allows for quantitative analysis of mechanotranduction at the cellular level and therefore can be used to study more complicated problems such as spreading, migration, and cell–cell interactions where the geometry of cells becomes important.
Two-Way Feedback Between Active Contractile Stresses and the Effective Stiffness of the FA–ECM Complex.
The tensile forces applied by the actomyosin stress fibers on the FA can stabilize the whole structure as well as trigger a variety of biochemical events (33) as shown in Fig. S3A. One example is the conformational changes of vinculin and p130Cas that expose binding sites of Src-family kinases (SFKs) (34, 35). SFKs act on Rho-GTPases by controlling the activity of guanine nucleotide exchange factors (GEFs) and GTPase activating proteins (GAPs). Increased activity of Rho promotes phosphorylation of myosin phosphatase targeting protein (MYPT) and, ultimately, down-regulates motor unbinding from the stress fiber (36). Meanwhile, the appearance of contractile forces can also trigger Ca2+ flux into the cytoplasm, which facilitates the binding of myosin motors to the cytoskeleton (37). Clearly, these observations show a positive feedback between cell contractility and the growth of FAs. To capture such mechanochemical coupling in a simple manner, we proceed by expressing the contractile stress as (33) , where and represent the strain and passive stiffness of stress fibers, whereas corresponds to the density of force dipoles (representing myosin motors) in the contracting filaments. The contractility itself depends on the mechanochemical coupling discussed above (i.e., the positive feedback) and can be written (33) as
| [S1] |
with being the baseline contractility of cells in the absence of external stress/constraints and and representing mechanochemical coupling parameters reflecting the molecular mechanisms that regulate the stress-dependent signaling pathways and engagement of motors, respectively, and satisfy the criterion (33) that . From Eq. S1, it is clear that higher contractile stresses will be generated for larger feedback parameter values, i.e., when .
Because the contractile stress (generated in the stress fiber) must be transmitted to the ECM as well as to the cell nucleus, we have , where and (or and ) are the effective stiffness and strain of the nucleus (or FA), respectively (Fig. S3B). In addition, the geometric constraint requires that (indicating the total strain is zero; refer to Fig. 2C and Fig. S3B). Based on these relations, the contractile stress , defined as , can be expressed as
| [S2] |
where . The above equation shows that increasing the stiffness of either the nucleus or the FA–ECM complex will lead to a higher contractile force, consistent with recent experimental observations (38, 39), and that the maximum level of contractility [] is achieved when . The effective stiffness of the FA–ECM complex, in turn, depends on the size of the FA, which we consider next by studying the kinetics of incorporation of new adhesion plaque units.
Treatment of Integrins and Their Connections to the ECM.
Integrins are stretched by the FA plaque once engaged successfully; therefore, they are treated as springs in this study to estimate the force they carry. It is well known that the bonds formed between integrins and ECM are highly dynamic (9, 20, 40). Specifically, it was reported (20) that the - and -mediated catch bonds are responsible for force transmission between the cell and ECM, whereas talin unfolding and binding to vinculin (both exhibiting slip bond behaviors) trigger other signaling processes and lead to adhesion growth. The integrin binding/unbinding can occur within seconds (9, 20, 40), whereas talin unfolds instantaneously if force exceeds a threshold (∼5 pN) (20). Both timescales are much faster than the assembly of proteins in the FA (taking minutes to complete) (18). Therefore, we assume that the assembly of the adhesion plaque is the rate-limiting step, whereas new integrin bonds will be formed instantaneously as the FA grows. In other words, the integrins will reach a steady state within the timescale that is interested in this study (a few minutes). The density of integrins in our model is the effective density in the quasi-static limit, which is determined by the balance between bond on and off rates.
Governing Equations and Boundary Conditions.
The stresses in the FA plaque and the ECM along radial direction are denoted as and , respectively, equilibrium requires that
where is the stress in the integrin layer and can be expressed as
where is the integrin density; and are the displacements of the FA plaque and ECM, respectively; and is the stiffness of the individual integrins along the in-plane direction, whereas the out-plane stiffness of integrins is set to be extremely high ( times stiffer than that along the in-plane direction) to ensure that the FA plaque will not detach from the ECM.
Because ECM is treated as a very large disk with its edge fixed, the boundary conditions are
where , , and are the sizes of the ECM, the cell, and the FA, respectively, and is the contraction stress applied by the cell.
Influence of Integrin/Ligand Density on Cellular Stiffness Sensing.
As revealed by previous studies (1, 16), integrin/ligand density has a significant effect on the formation and the size of FAs. To demonstrate this in the simplest manner, we examine the problem with a recently developed the 1D model (24), as shown in Fig. S5A. The mechanical response and force transmission mechanisms in the 1D model are similar to the 3D coarse-grained model. The ligand density () in this case can be defined as the number of ligands per unit length (), expressed as , where is the integrin spacing. The effective stiffness of the FA–ECM complex (, equivalent as in 3D) can be found as (24)
with
where is the shear lag length (i.e., the length scale over which actomyosin forces are transmitted to the ECM); is the FA size; and , , and are the stiffnesses of the plaque, integrin clutches, and the ECM, respectively. This characteristic size emerges due to the mismatch between the displacement fields of the FA plaque and the ECM as shown in Fig. S5B. Clearly, depends on the normalized FA size () for a given set of stiffness parameters.
As illustrated in our previous study (24), is very sensitive to the size of FAs (with respect to the shear lag length, ). Specifically, as shown in Fig. S5A, integrins carry the load uniformly for small FAs (), whereas a force-free region emerges at the center when the FA size reaches ∼. For very large FAs (), only a few integrins at the leading edge carry the majority of the applied force, and the size of this region remains the same regardless of actual FA size. This is an inherent feature of the so-called shear lag loading scenario, where the transmitting range of contractile stresses into the ECM is limited by a critical shear lag length () (23). Therefore, for a small FA (), more active integrins are introduced to evenly share the load as FA grows, resulting in an increase in with respect to FA size. In contrast, a larger FA () can be divided into an inactive and an active part, based on the integrin loading pattern. As shown in Fig. S5C, the elastic response of the active part is insensitive to FA size, whereas the compliance of the inactive part increases with L. Hence, the effective stiffnesses for large FAs decrease as they grow. Essentially the same nonmonotonic dependence of effective stiffness on FA size was also predicted from the present 3D coarse-grained model.
One important observation that emerges from the above analysis is that the shear lag length is influenced by the density of ligands/bonds. Specifically, was found to decrease from 0.436 to as ligand density increases from 1 to 100 as shown in Fig. S5E. Consequently, the effective stiffness of FA should also be a function of the ligand density. To understand this more clearly, we proceed by calculating how the effective stiffness, , of a FA whose size is varies with respect to the ligand density. As shown in Fig. S5F, the effective stiffness of a small FA increases with the ligand density initially. This is because although decreases with the increasing integrin density, it is still much larger than the FA size () when the ligand density is relatively low. Therefore, will first increase with the integrin density because more active integrins are introduced. However, as the integrin density keeps increasing, the shear lag length will eventually decrease to a level much smaller than the FA size (). In this case, newly incorporated integrins are not active (Fig. S5D, Right), leading to the decrease in . To summarize, as ligand density increases, the normalized FA size () increases monotonically, leading to the integrin force distribution changing from an almost uniform one to a concentrated distribution at the leading end. The distribution pattern change, which is similar as the effect brought by increasing FA size, eventually leads to the biphasic dependence of on increasing ligand density.
By coupling the effective stiffness with the stiffness-dependent actin contractile stress and the force-dependent kinetics of adding new adhesion plaque units (as illustrated in the main text), the stable FA size as a function of ECM stiffness and ligand density can be obtained as shown in Fig. S6A. By treating the ligand density and ECM modulus as two independent parameters, we achieved the FA size profile from the 3D multiscale model as shown in Fig. S6B. Clearly, both heat maps show similar trends.
Quantitative Comparison Between Experimental Results and Model Predictions.
In our coarse-grained model, the cell is assumed to be circular, and the FAs are treated as a continuous band along the periphery of the cell (Fig. 1A). The predicted FA band size is not a direct description of average FA size but should be proportional to it because experiments show that there are one or two adhesions along the radial direction in the band (18, 19), as shown in Fig. 1A. We quantitatively compared the normalized FA band size (with respect to the FA size on the stiff fibrous ECM) from model predictions to the normalized average FA size measured in our experiments. The key physical parameters for the ECM in our model and the experiments are ECM stiffness/modulus and ligand density. We chose two fibrous ECMs whose moduli are different, and the variations of ligand density are comparable to experimental measurements between the two groups. Next, we considered two hydrogels that have the same ligand density but different elastic moduli. By choosing these parameters, the model mimics the experimental conditions: two fibrous ECMs where the soft ECM has higher ligand density than the stiff ECM, whereas both the soft and stiff hydrogels have similar ligand density. The model predictions are in good agreement with the experimental results quantitatively as shown in Fig. S7.
Fig. S7.
Quantitative comparison between experimental results (16) and model predictions for the normalized FA size.
Acknowledgments
The theoretical part of the work was supported by National Cancer Institute Grants U01CA202177 and U54CA193417 (to V.B.S.), NIH Grant R01EB017753 (to V.B.S.), and National Science Foundation Grant 1548571 (to V.B.S.). B.M.B. acknowledges financial support from an NIH Pathway to Independence Award (HL124322). J.A.B. acknowledges financial support from NIH Grant R01AR056624.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 5772.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1620486114/-/DCSupplemental.
References
- 1.Discher DE, Janmey P, Wang Y-L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 2.Jaalouk DE, Lammerding J. Mechanotransduction gone awry. Nat Rev Mol Cell Biol. 2009;10:63–73. doi: 10.1038/nrm2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fenteany G, Janmey PA, Stossel TP. Signaling pathways and cell mechanics involved in wound closure by epithelial cell sheets. Curr Biol. 2000;10:831–838. doi: 10.1016/s0960-9822(00)00579-0. [DOI] [PubMed] [Google Scholar]
- 4.Kumar S, Weaver VM. Mechanics, malignancy, and metastasis: The force journey of a tumor cell. Cancer Metastasis Rev. 2009;28:113–127. doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Riveline D, et al. Focal contacts as mechanosensors: Externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J Cell Biol. 2001;153:1175–1186. doi: 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Han SJ, Oak Y, Groisman A, Danuser G. Traction microscopy to identify force modulation in subresolution adhesions. Nat Methods. 2015;12:653–656. doi: 10.1038/nmeth.3430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Peyton SR, Putnam AJ. Extracellular matrix rigidity governs smooth muscle cell motility in a biphasic fashion. J Cell Physiol. 2005;204:198–209. doi: 10.1002/jcp.20274. [DOI] [PubMed] [Google Scholar]
- 8.Goffin JM, et al. Focal adhesion size controls tension-dependent recruitment of alpha-smooth muscle actin to stress fibers. J Cell Biol. 2006;172:259–268. doi: 10.1083/jcb.200506179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 10.Gao H, Qian J, Chen B. Probing mechanical principles of focal contacts in cell-matrix adhesion with a coupled stochastic-elastic modelling framework. J R Soc Interface. 2011;8:1217–1232. doi: 10.1098/rsif.2011.0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pedersen JA, Swartz MA. Mechanobiology in the third dimension. Ann Biomed Eng. 2005;33:1469–1490. doi: 10.1007/s10439-005-8159-4. [DOI] [PubMed] [Google Scholar]
- 12.Pathak A, Kumar S. Biophysical regulation of tumor cell invasion: Moving beyond matrix stiffness. Integr Biol. 2011;3:267–278. doi: 10.1039/c0ib00095g. [DOI] [PubMed] [Google Scholar]
- 13.Baker BM, Chen CS. Deconstructing the third dimension: How 3D culture microenvironments alter cellular cues. J Cell Sci. 2012;125:3015–3024. doi: 10.1242/jcs.079509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Abhilash AS, Baker BM, Trappmann B, Chen CS, Shenoy VB. Remodeling of fibrous extracellular matrices by contractile cells: Predictions from discrete fiber network simulations. Biophys J. 2014;107:1829–1840. doi: 10.1016/j.bpj.2014.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang H, Abhilash AS, Chen CS, Wells RG, Shenoy VB. Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers. Biophys J. 2014;107:2592–2603. doi: 10.1016/j.bpj.2014.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baker BM, et al. Cell-mediated fibre recruitment drives extracellular matrix mechanosensing in engineered fibrillar microenvironments. Nat Mater. 2015;14:1262–1268. doi: 10.1038/nmat4444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chaudhuri O, et al. Substrate stress relaxation regulates cell spreading. Nat Commun. 2015;6:6364. doi: 10.1038/ncomms7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stricker J, Aratyn-Schaus Y, Oakes PW, Gardel ML. Spatiotemporal constraints on the force-dependent growth of focal adhesions. Biophys J. 2011;100:2883–2893. doi: 10.1016/j.bpj.2011.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Elineni KK, Gallant ND. Regulation of cell adhesion strength by peripheral focal adhesion distribution. Biophys J. 2011;101:2903–2911. doi: 10.1016/j.bpj.2011.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Elosegui-Artola A, et al. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nat Cell Biol. 2016;18:540–548. doi: 10.1038/ncb3336. [DOI] [PubMed] [Google Scholar]
- 21.Nicolas A, Geiger B, Safran SA. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc Natl Acad Sci USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Grashoff C, et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cox HL. The elasticity and strength of paper and other fibrous materials. Br J Appl Phys. 1952;3:72–79. [Google Scholar]
- 24.Cao X, et al. A chemomechanical model of matrix and nuclear rigidity regulation of focal adhesion size. Biophys J. 2015;109:1807–1817. doi: 10.1016/j.bpj.2015.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Engler A, et al. Substrate compliance versus ligand density in cell on gel responses. Biophys J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nisenholz N, et al. Active mechanics and dynamics of cell spreading on elastic substrates. Soft Matter. 2014;10:7234–7246. doi: 10.1039/c4sm00780h. [DOI] [PubMed] [Google Scholar]
- 27.Müller KW, et al. Rheology of semiflexible bundle networks with transient linkers. Phys Rev Lett. 2014;112:238102. doi: 10.1103/PhysRevLett.112.238102. [DOI] [PubMed] [Google Scholar]
- 28.Münster S, et al. Strain history dependence of the nonlinear stress response of fibrin and collagen networks. Proc Natl Acad Sci USA. 2013;110:12197–12202. doi: 10.1073/pnas.1222787110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nam S, Hu KH, Butte MJ, Chaudhuri O. Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels. Proc Natl Acad Sci USA. 2016;113:5492–5497. doi: 10.1073/pnas.1523906113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 31.Liu AS, et al. Matrix viscoplasticity and its shielding by active mechanics in microtissue models: Experiments and mathematical modeling. Sci Rep. 2016;6:33919. doi: 10.1038/srep33919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Flynn BP, Tilburey GE, Ruberti JW. Highly sensitive single-fibril erosion assay demonstrates mechanochemical switch in native collagen fibrils. Biomech Model Mechanobiol. 2013;12:291–300. doi: 10.1007/s10237-012-0399-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shenoy VB, Wang H, Wang X. A chemo-mechanical free-energy-based approach to model durotaxis and extracellular stiffness-dependent contraction and polarization of cells. Interface Focus. 2016;6:20150067. doi: 10.1098/rsfs.2015.0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sawada Y, et al. Force sensing by mechanical extension of the Src family kinase substrate p130Cas. Cell. 2006;127:1015–1026. doi: 10.1016/j.cell.2006.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Puklin-Faucher E, Sheetz MP. The mechanical integrin cycle. J Cell Sci. 2009;122:179–186. doi: 10.1242/jcs.042127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Katoh K, et al. Rho-kinase–mediated contraction of isolated stress fibers. J Cell Biol. 2001;153:569–584. doi: 10.1083/jcb.153.3.569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Matthews BD, et al. Ultra-rapid activation of TRPV4 ion channels by mechanical forces applied to cell surface beta1 integrins. Integr Biol. 2010;2:435–442. doi: 10.1039/c0ib00034e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ghibaudo M, et al. Traction forces and rigidity sensing regulate cell functions. Soft Matter. 2008;4:1836–1843. [Google Scholar]
- 39.Mitrossilis D, et al. Single-cell response to stiffness exhibits muscle-like behavior. Proc Natl Acad Sci USA. 2009;106:18243–18248. doi: 10.1073/pnas.0903994106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Plotnikov SV, Pasapera AM, Sabass B, Waterman CM. Force fluctuations within focal adhesions mediate ECM-rigidity sensing to guide directed cell migration. Cell. 2012;151:1513–1527. doi: 10.1016/j.cell.2012.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fisher TE, Oberhauser AF, Carrion-Vazquez M, Marszalek PE, Fernandez JM. The study of protein mechanics with the atomic force microscope. Trends Biochem Sci. 1999;24:379–384. doi: 10.1016/s0968-0004(99)01453-x. [DOI] [PubMed] [Google Scholar]
- 42.Caille N, Thoumine O, Tardy Y, Meister J-J. Contribution of the nucleus to the mechanical properties of endothelial cells. J Biomech. 2002;35:177–187. doi: 10.1016/s0021-9290(01)00201-9. [DOI] [PubMed] [Google Scholar]
- 43.Chiron S, et al. Complex interactions between human myoblasts and the surrounding 3D fibrin-based matrix. PLoS One. 2012;7:e36173. doi: 10.1371/journal.pone.0036173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang H, et al. Necking and failure of constrained 3D microtissues induced by cellular tension. Proc Natl Acad Sci USA. 2013;110:20923–20928. doi: 10.1073/pnas.1313662110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kanchanawong P, et al. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–584. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cavalcanti-Adam EA, et al. Lateral spacing of integrin ligands influences cell spreading and focal adhesion assembly. Eur J Cell Biol. 2006;85:219–224. doi: 10.1016/j.ejcb.2005.09.011. [DOI] [PubMed] [Google Scholar]