3D-3D Registration of partial capitate bones using spin-images

Abstract

It is often necessary to register partial objects in medical imaging. Due to limited FOV, the entirety of an object cannot always be imaged. This study presents a novel application of an existing registration algorithm to this problem. The spin-image algorithm [1] creates pose-invariant representations of global shape with respect to individual mesh vertices. These ‘spin-images,’ are then compared for two different poses of the same object to establish correspondences and subsequently determine relative orientation of the poses. In this study, the spin-image algorithm is applied to 4DCT-derived capitate bone surfaces to assess the relative accuracy of registration with various amounts of geometry excluded.

The limited longitudinal coverage under the 4DCT technique (38.4mm, [2]), results in partial views of the capitate when imaging wrist motions. This study assesses the ability of the spin-image algorithm to register partial bone surfaces by artificially restricting the capitate geometry available for registration. Under IRB approval, standard static CT and 4DCT scans were obtained on a patient. The capitate was segmented from the static CT and one phase of 4DCT in which the whole bone was available. Spin-image registration was performed between the static and 4DCT. Distal portions of the 4DCT capitate (10–70%) were then removed and registration was repeated. Registration accuracy was evaluated by angular errors and the percentage of sub-resolution fitting. It was determined that 60% of the distal capitate could be omitted without appreciable effect on registration accuracy using the spin-image algorithm (angular error < 1.5 degree, sub-resolution fitting > 98.4%).

1. INTRODUCTION

In medical image processing, it is often necessary to register partial objects. For example, due to limited field-of-view (FOV), the entirety of an object cannot always be imaged and the complete geometry of the object is not available for registration. The purpose of this study was to examine the potential use of the spin-image algorithm [1] as a means to calculate rigid body transformations required to register partial bone surfaces acquired using a recently developed 4DCT imaging approach [2]. In particular, the capitate bone is of interest because of the significant variation in the portions of the bone that are visible in the frames of wrist motion obtained using 4DCT.

Spin-image based registration was chosen as the method to register partial bone surfaces because of its robustness to occlusion [1]. Specifically, the algorithm is relatively insensitive to the ‘completeness’ of the mesh of an object because it is a correspondence-based approach to surface matching. An additional advantage of correspondence-based approaches is that a closed-form solution for orientation is applicable [1, 3], eliminating the problem of local-minima present in entirely optimization-based solutions. In the case of 4DCT imaging, the absence of a portion of the capitate bone due to FOV restriction is treated as complete occlusion of the geometry that could not be imaged. This presents a challenge to most registration algorithms as additional geometry generally makes the object more orientable.

The objective of this study was to assess how well spin-image registration can accommodate limited geometries acquired from 4DCT of the wrist. Based on extant literature describing the algorithm, it is hypothesized that when sufficient information (orientable geometry) is available, the algorithm will be able to accurately register the capitate meshes. In this study we examine the quantity of geometry necessary to achieve accurate registration and quantify the effects of limited geometry on relative registration accuracy. This information is useful because omission of a large, continuous portion of an object may influence the algorithm’s ability to register the remaining portion of the object, potentially preventing accurate registration. With respect to the capitate, this is especially true as the proximal pole of the capitate is practically hemispherical and largely devoid of salient features.

2. OVERVIEW OF SPIN-IMAGE ALGORITHM

The spin-image algorithm is a pose-independent method for registration, i.e. it produces identical results regardless of the initial orientations and positions of the registered surfaces [1]. The algorithm is initialized by loading point clouds (surface mesh vertices) for both a model and scene. The model is typically a complete surface mesh or point cloud representation of the object being registered and the scene mesh or cloud contains some subset of the object’s geometry. The algorithm then generates spin-maps (figure 1, left) of all vertices in each mesh. These are 2D mappings of the locations of vertices into the radial (α) and longitudinal coordinates (β) of all points in the meshes with respect to the normal and location of the point for which the map is being generated. The third (angular) dimension of a cylindrical coordinate system is omitted, making the spin-map pose-invariant. Spin-maps are converted to spin-images—2D histograms of the distribution of vertices in spin-map space (figure 1, right). The process of generating histograms of the points’ distributions abates the effects of different mesh samplings of the same object’s surface (i.e. different scans of the same object) through bilinear weighting of each point’s contribution to the histogram bins.

Figure 1.

Example spin-map (left) and the resulting spin-image (right).

Correlation coefficients weighted by the number of occupied bins (called similarity measures), are then calculated for all compared spin-image pairs to establish likely point correspondences between model and scene. A randomly-sampled subset of scene spin-images (approx. 200) is compared to all model spin-images. ‘Likely’ correspondences are those for which the similarity measure exceeds a threshold based on the statistical distribution of similarity measures between the particular scene spin image and all model spin images. Likely correspondences are then filtered and grouped using geometric consistency in spin-map space. Once grouped, the groups of correspondences are used to calculate their respective transformations to register the model to the scene using a closed-form solution, after Horn [3]. Deviating from Johnson and Herbert’s approach [1], the current implementation determines the fit of each group’s registration by calculating the portion of scene vertices that are within the mean edge length of the mesh of the nearest registered model vertex.

The grouping with the greatest portion of points meeting this criterion is then refined. Refinement begins with correspondence spreading, whereby the number of corresponding points is grown by adding those points neighboring each correspondence in the model that fall within a specified threshold distance of their nearest neighbor in the scene. In the current implementation the threshold is set at twice the model mesh resolution. Iterative closest point (ICP) matching [4] is then applied to the resulting sets of points to refine the fit. Although ICP is optimization-based, the initial alignment obtained from spin-image matching provides an accurate initialization, avoiding detrimental local minima. The two resulting rigid-body transformations in both the spin-image and the ICP refinement steps are combined to produce a single transformation from model to scene.

3. METHODS

Following IRB approval and informed consent of the subject, an established 4DCT imaging technique [2] was used to acquire an 18-volume motion sequence of the wrist during a flexion motion cycle. A conventional static CT scan of the wrist was also obtained to acquire the surfaces and positions of the carpal bones in a neutral posture. The voxel dimensions for the scans were 0.234mm in-plane and 0.4mm along the bore, and image volumes were subsequently converted to isotropic at the planar resolution of 0.234mm. From the motion sequence, a single volume in which the entirety of the capitate was visible was selected. The capitate bone was segmented from both this single 4DCT volume and the conventional CT, using global thresholding followed by a graph-based connected component method [5]. Subsequently, the segmented capitates were meshed using an adaptive deformation approach [6]. Segmentation and meshing were done using Analyze 10.0 software (Mayo Clinic Biomedical Imaging Resource, Rochester, MN).

The meshes were then reduced to their external hulls using a hidden-points-removal (HPR) algorithm, developed by Katz, et al. [7]. The HPR algorithm determines which constituent nodes in a mesh are visible from the perspective of a given view point. In our implementation of HPR, the viewpoint was initially placed a fixed distance (50mm) from the centroid of each mesh. In order to obtain the entire externally visible mesh, the algorithm was run iteratively as the viewpoint was rotated completely around each mesh in 18° increments to obtain all externally visible points on the mesh. The meshes were then ‘rebuilt’ by removing the non-visible vertices and re-enumerating the visible mesh faces. The benefits of using the HPR algorithm are two-fold; it reduces total spin image computation time by directly reducing the number of comparisons necessary and it also eliminates points from the interior surfaces that are dissimilar between model and scene.

The resulting mesh from the conventional CT (model) was then fit to the mesh from the motion sequence (the ‘scene’) using the spin-image algorithm. Both meshes contained complete capitate geometry. Due to slight differences in segmentation and mesh sampling they are not identical; the complete scene mesh contains fewer vertices than the complete model mesh (4260 scene versus 4422 model). The fit obtained here was used as the ground-truth for how the algorithm would perform in subsequent partial bone registrations. The proximal 90% of the scene capitate mesh (as measured along the long axis of the bone) was then used as the scene mesh and the algorithm was again applied. This was repeated for 80% to 30% of the mesh, in 10% increments. Both the HPR and spin-image algorithm were applied using purpose-written computer code in MATLAB (Release 2011b, The MathWorks, Natick, MA).

Relative registration quality was determined as the portion of mesh points in the scene that were within the median mesh edge length of their nearest neighbor in the model after registration, (% sub-resolution fitting (%SRF), Table 1). Additionally, the point-point distances between model and scene nearest neighbors were calculated as an additional indicator of fit quality. Sub-resolution fitting calculations used the mesh-resolution of the model mesh to maintain a constant threshold for comparisons across all registrations.

Table 1.

Fit quality, relative mesh sizes, and relative errors. Gray columns indicate metrics relating model to scene in each registration. White columns indicate metrics between partial and whole mesh registrations.

% length of whole bone	% model vertices	angular error (°)	RMS point location error (mm)	point-point distance (mm)	% sub-resolution fitting (SRF)
40	35.3	1.35	0.207	0.255	98.9
50	45.0	1.15	0.210	0.267	98.6
60	54.8	1.44	0.308	0.261	98.4
70	65.1	1.13	0.178	0.264	98.9
80	76.1	1.29	0.188	0.260	99.0
90	84.8	0.83	0.144	0.261	99.1
100	96.3	–	–	0.265	99.1

The extent to which limited geometry affected registration was assessed through angular error and RMS point location error measures. Angular error was computed as the angular difference between the ground-truth registration (using 100% of scene mesh) and the individual partial mesh registrations. This was calculated by transforming an arbitrary unit vector by the registrations’ transformation matrices, and determining the angle between the resulting vectors (as the inverse cosine of the dot product of the two vectors). Root-mean-square (RMS) point location error was determined by transforming separate instances of the complete model mesh by the 100%-length mesh registration and each partial mesh registration.

4. RESULTS

At 30% the algorithm ceased to accurately register the model mesh to the partial mesh. To give a qualitative sense of the similarity of spin-images constituting a match, figure 3 shows the spin-images of one correspondence used in the registration of the model to the 60% partial scene. Additionally, figure 4 shows the original, unregistered orientation of the model mesh in addition to the partial scene mesh (left), and their resulting alignment after registration (center). Figure 4 also shows a ‘fit map’ (right) of the registration of the model to the 60% partial scene, showing the extent of geometry that falls within the mesh resolution (units are distance as a multiple of median edge length—approx. 0.63mm).

Figure 3.

Matched spin-images from scene and model.

Figure 4.

Capitate meshes before (left) and after (center) registration. 60% partial scene (black) and model (grey). ‘Fit Map’ of registration to 60% partial capitate (right) 98.4% SRF; gray level indicates distance between nearest points in model and complete scene mesh in units of the median edge length.

In addition to the above assessments of partial-capitate registration, spin-image registration was also applied to 20 wrists for which 4DCTs were collected (under IRB approval) for two different wrist motions: radial/ulnar deviation and flexion/extension. A total of 720 capitates were registered. Qualitatively, the obtained registrations and derived kinematics revealed that 703 capitates were well registered (98% total). The unsatisfactory registrations of the remaining 17 capitates were attributable to motion artifacts/blur in the original image sets.

Application of the HPR algorithm resulted in appreciable reduction of mesh size (approx. 6500 points, 13000 faces to approx. 4350 points and 8600 faces), while maintaining the relevant, more reproducible cortical geometry of the bone. To confirm the benefit of the HPR algorithm, the original pre-HPR meshes were used for registration and yielded a SRF fitting of 94.4%, angular error of 0.94°, and 0.354 mm RMS location error, indicating that the non-cortical geometry differs between the meshes and that this difference adversely affects registration performance.

5. DISCUSSION and CONCLUSIONS

In this assessment of the spin-image method, the algorithm proved capable of registering the model to the partial scene meshes from 40% to 100% of the original mesh length. Fit quality for these partial scene registrations was strong, based on low angular and point location errors and high %SRF. However, the 30% partial scene was not registerable using the spin-image algorithm. The reason for this is likely because the amount of geometry remaining in the 30% scene is not sufficiently orientable; that is, the remaining scene geometry does not contain sufficient information to establish a unique orientation.

As shown in figure 5, the remaining geometry in the 30% partial capitate is practically semi-circular in profile, and there are relatively few salient features of the 30% bone when compared with the 40% partial capitate’s orientable features (black arrows). The spin-image algorithm is not a ‘feature-based’ approach to registration, rather it requires enough unique geometry to make spin-images distinguishable in order for correspondences to be established. An example of this problem is a sphere, i.e. a non-orientable body. The lack of any difference in the global geometry as perceived from any point on the sphere means that all spin-images generated for its mesh will be identical, and hence all correspondences are equally likely and a unique solution for registration will be unattainable.

Figure 5.

Capitate geometry of various lengths (as % of total length). Arrows indicate orientable features present on the 40% capitate mesh.

Note that 40% is not a finite limit, and the amount of requisite geometry required to yield favorable registrations will vary from object to object and, with regard to the present application, from patient to patient. The only true requirement is that the remaining geometry is adequately distributed relative to the orientable geometry of the bone. For example, if the capitate mesh had been cut along a plane preserving the palmar or dorsal surfaces, the amount of requisite bone geometry for registration would likely be much smaller. In the case of 4DCT of the wrist, the portion of the capitate most frequently omitted is the more orientable portion of the geometry (figure 5). For this reason, and the FOV constraints in our present 4DCT approach, distal geometry removed longitudinally constitutes the worst case and is most representative of the challenges of registering these capitates.

The metrics for comparing registration accuracy were chosen in lieu of a fiducial marker set and determining absolute registration errors as the data were obtained in-vivo and skin movement would likely overshadow the magnitude of the differences in partial bone registrations. Comparison of the full mesh registration to a purely ICP based approach (using post-HPR meshes) indicates that the spin-image approach yields better results. Specifically, the ICP-only registration resulted in a %SRF of 98.5 and RMS location error 0.258 mm, indicating a lower fit quality than most of the partial mesh registrations using the spin-image algorithm. This also illuminates spin-image’s role in the larger task of registering partial objects: it serves as a method for providing an initializing transformation for the ICP refinement, resulting in a better quality registration. Regarding the magnitudes of the relative errors seen in this study, the location specific metrics (mean point-point distance and RMS location error) are appreciably smaller (2–2.5×) than the mesh resolution and are much closer to the in-plane resolution of the original images from which the meshes were derived.

The novelty of the current implementation of the spin-image algorithm is that it utilizes the hidden-points-removal algorithm to automatically reduce meshes to their external surfaces. This is ideal for registering carpal bones, including the capitate, in 4DCT imaging because the motion during acquisition influences signal intensity (and thus apparent density) of cancellous bone, resulting in dissimilar geometry on the interior of the bone when it is segmented and meshed. This would impede registration if it were not removed as demonstrated above. Conversely, the exterior surface of the bone is generally well defined during 4DCT and conventional CT imaging, allowing for consistent segmentation, and subsequent registration. The exclusion of the interior surfaces of the bones also allows for registration between CT/4DCT and other imaging modalities that can similarly establish the external geometry of the bone, e.g. laser or structured-light scanning. Additionally novel, rather than studying scattered occlusion/omission [1] of object geometry, this study looked at complete omission of large amounts of continuous object geometry and found that a significant portion of an object can be occluded or omitted with little effect on registration quality.

Although spin-images and similar methods have been previously used to register bone [1] and tooth [8] surfaces, extraction of meshes that can be registered from these objects was unnecessary due either to the original image acquisition method (3D laser range scans produce external point cloud data directly) or the innate ease in establishing the complete external surface of the objects (i.e. larger bones have thicker cortices and their segmentation is less susceptible to partial-volume effects). In the absence of these advantages, the HPR algorithm was successfully applied to this problem. As currently coupled with the HPR algorithm, the spin-image algorithm is well suited to the registration of partial capitate bone geometries derived from 4DCT.

Figure 2.

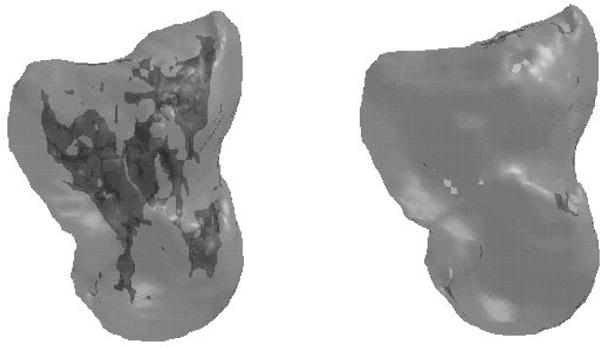
Partially transparent model capitate showing the entire mesh including interior elements (6526 points, 13232 faces, left) and the HPR reduced mesh showing the remaining exterior surfaces (4422 points, 8776 faces, right).