Characterization and Interspecies Scaling of rhTNF-α Pharmacokinetics with Minimal Physiologically Based Pharmacokinetic Models

Abstract

Tumor necrosis factor-α (TNF-α) is a soluble cytokine and target of specific monoclonal antibodies (mAbs) and other biologic agents used in the treatment of inflammatory diseases. These biologics exert their pharmacological effects through binding and neutralizing TNF-α, and thus they prevent TNF-α from interacting with its cell surface receptors. The magnitude of the pharmacological effects is governed not only by the pharmacokinetics (PK) of mAbs, but also by the kinetic fate of TNF-α. We have examined the pharmacokinetics of recombinant human TNF-α (rhTNF-α) in rats at low doses and quantitatively characterized its pharmacokinetic features with a minimal physiologically based pharmacokinetic model. Our experimental and literature-digitalized PK data of rhTNF-α in rats across a wide range of doses were applied to global model fitting. rhTNF-α exhibits permeability rate–limited tissue distribution and its elimination is comprised of a saturable clearance pathway mediated by tumor necrosis factor receptor binding and disposition and renal filtration. The resulting model integrated with classic allometry was further used for interspecies PK scaling and resulted in model predictions that agreed well with experimental measurements in monkeys. In addition, a semimechanistic model was proposed and applied to explore the absorption kinetics of rhTNF-α following s.c. and other routes of administration. The model suggests substantial presystemic degradation of rhTNF-α for s.c. and i.m. routes and considerable lymph uptake contributing to the overall systemic absorption through the stomach wall and gastrointestinal wall routes of dosing. This report provides comprehensive modeling and key insights into the complexities of absorption and disposition of a major cytokine.

Introduction

Tumor necrosis factor-α (TNF-α) is one of the soluble proinflammatory cytokines that mediate many inflammatory diseases. TNF-α has a molecular size of 17 kDa and exists in homo-trimeric form. Through binding to cell surface receptors, i.e., tumor necrosis factor receptors (TNFRs) 1 and 2, TNF-α exerts its versatile biologic functions (Bradley, 2008). Endogenous TNF-α expression is fairly low in healthy subjects (serum concentrations ∼25 pg/ml), but increases by 2- to 3-fold in patients with inflammatory diseases (Manicourt et al., 1993). Biologics that selectively neutralize TNF-α have shown great potential in the treatment of rheumatoid arthritis and other inflammatory diseases. The magnitude of their pharmacological effects depends not only on the binding and pharmacokinetics (PK) of these biologics, but also on the turnover of endogenous TNF-α in the body.

The PK features of TNF-α were extensively examined in various animal species as an anti-cancer agent (Kojima et al., 1988; Ferraiolo et al., 1989; Greischel and Zahn, 1989; Zahn and Greischel, 1989), but no quantitative characterization of its PK has been established. It was noted that TNF-α exhibited nonlinear PK. The clearance of TNF-α was attributed to: 1) a saturable elimination process mediated by TNFR binding and disposition, as demonstrated by concomitant administration of excess amounts of tumor necrosis factor-β (TNF-β), which competes with TNF-α in binding to the TNFRs (Greischel and Zahn, 1989; Zahn and Greischel, 1989); and 2) renal filtration as demonstrated by changes of PK produced by nephrectomy (Ferraiolo et al., 1989). However, these animal studies applied therapeutic doses and created circumstances of extremely high TNF-α exposure in plasma compared with endogenous TNF-α baselines. The dynamics of endogenous TNF-α might behave differently. Therefore, in this study we sought to assess TNF-α PK at lower doses in rats, quantitatively characterize its PK with pharmacokinetic modeling approaches, and integrate our findings with data from the literature.

The first-generation minimal physiologically based pharmacokinetic (mPBPK) models (Cao and Jusko, 2012) provide a suitable modeling platform for assessing pharmacokinetic features of small molecule drugs as well as smaller size proteins and peptides. Inheriting and lumping together all major physiologic attributes from full physiologically based pharmacokinetic (PBPK) models, the model includes blood/plasma and lumped tissue compartments connected in an anatomic manner. Distribution of drug molecules to tissues is assumed driven by Fick’s laws of perfusion and diffusion. In addition, the mPBPK models have the flexibility to include organs such as liver and kidney to account for their elimination mechanisms if necessary.

Classic allometric scaling approaches, which assume that different species share similar anatomic, physiologic, and biochemical properties, have been widely applied to anticipate drug PK across animal species (Mordenti, 1986). This approach relates the PK parameters (θ) across species to the body weight (BW) with the following equation:

(1)

where a is the allometric coefficient and b is the allometric exponent. Integration of empirical allometric scaling principles into PBPK models provides a more advanced approach for interspecies PK prediction. This approach is applicable when PK measurements from one species are available. More importantly, PBPK and mPBPK models separate drug- and system-specific parameters. Thus, species-specific physiologic information, such as target expression and target binding affinity, can be used to account for the complexities of nonlinear drug disposition. Our laboratory has assessed the feasibility of implementing allometric scaling principles into mPBPK models to relate the interspecies PK of monoclonal antibodies (mAbs) (Zhao et al., 2015).

Administration of therapeutic proteins via the s.c. route offers several advantages over i.v. including convenience, tolerance, and prolonged exposure. However, less is known about the process of s.c. absorption for both mAbs and other protein therapeutics. The kinetics of s.c. absorption for protein drugs are fairly complicated, involving presystemic degradation and absorption via both blood and lymphatic transport. Uptake by lymph at s.c. injection sites is assumed to be the main route for their systemic absorption (Charman et al., 2001). The relative contribution of lymph transport to systemic absorption varies with size and charge of the proteins (Swartz, 2001), as well as the animal species and site of injection (McDonald et al., 2010; Kagan et al., 2012).

In the present study, we examined the plasma PK of recombinant human TNF-α (rhTNF-α) in rats at relatively low doses and quantitatively characterized its pharmacokinetic properties with mPBPK models. Experimental and literature-digitalized PK data of rhTNF-α in rats across a wide range of doses were applied for model fitting and to assess consistency across studies. The resulting model integrated with classic allometry was further applied for interspecies PK scaling in monkeys. In addition, a semimechanistic model was proposed and applied to explore the absorption kinetics of rhTNF-α following s.c. and other routes of administration.

Materials and Methods

Test Compound.

rhTNF-α was purchased from R&D Systems (Minneapolis, MN) and reconstituted with sterilized phosphate-buffered saline (pH 7.4) containing 0.1% bovine serum albumin at 2 mg/ml. The reconstituted rhTNF-α was stored in aliquots at −80°C before use.

Animals.

Male Lewis rats weighing approximately 300 g were purchased from Harlan (Indianapolis, IN). Animals were housed individually in the University Laboratory Animal Facility and acclimatized for 1 week with free food and water access at constant environmental conditions (22°C, 72% humidity, and 12-hour light/12-hour dark cycles). All animal study protocols followed the Principles of Laboratory Animal Care (National Research Council, 2011) and were approved by the University at Buffalo Institutional Animal Care and Use Committee.

Pharmacokinetic Study of rhTNF-α.

Healthy Lewis rats (n = 14) were randomly assigned to four groups for rhTNF-α PK studies. The i.v. bolus group (n = 3) received a single bolus dose of rhTNF-α at 5 μg/kg via penile vein injection. At sampling time, animals were briefly anesthetized by inhalation of 3% isoflurane. Serial blood samples were collected at 3, 10, 20, and 30 minutes, and 1, 2, 4, and 6 hours from the saphenous vein and at 24 hours upon sacrifice by exsanguination from the abdominal aorta. The s.c. bolus group (n = 3) received the rhTNF-α dose of 16 μg/kg on the upper back. Serial blood samples were collected at 15 and 30 minutes, and 1, 2, 3, 4, 6, and 8 hours from the saphenous vein and at 24 hours from the abdominal aorta upon sacrifice. The low-dose s.c. infusion group (n = 4) received rhTNF-α at 11.74 μg/kg/d for 8 hours (infusion rate 8 μl/h) using Alzet Model 2001D micro-osmotic pumps (Durect Corporation, Cupertino, CA). The pumps were implanted into a skin pocket on the back under isoflurane anesthesia. The rats were monitored for allergic and toxic reactions and rectal temperatures were recorded periodically. The pumps were removed at the end of infusion. The rhTNF-α solutions remaining in the pumps were collected for stability tests. Serial blood samples were collected at 1, 1.5, 2, 2.25, 2.5, 3, 4, 5, 6, 7, 8, 8.25, 8.5, 9, and 9.5 hours from the saphenous vein and at 10 hours from the abdominal aorta upon sacrifice. The high-dose s.c. infusion group (n = 4) received 117.4 μg/kg/d of rhTNF-α for 48 hours (infusion rate 1 μl/h) using Alzet Model 1003D micro-osmotic pumps (Durect Corporation), implanted as described previously. Serial blood samples were collected at 1, 2, 3, 5, 10, 15, 17, 20, and 30 hours from the saphenous vein and at 40 and 48 hours from the abdominal aorta upon sacrifice. Blood samples were taken from at least two rats at each time point in all studies. Blood samples were immediately centrifuged at 2000g, at 4°C for 15 minutes. The plasma fraction was aliquoted and stored at −80°C.

Quantification of rhTNF-α.

The rhTNF-α concentrations in plasma samples and the solutions remaining in the pumps were measured with the human TNF-α Quantikine HS enzyme-linked immunosorbent assay kit (R&D Systems) following the manufacturer’s instructions. The standard curve was fitted to a four-parameter logistic model and was in the range of 0.5–32 pg/ml. Between-assay variability was tested with quality control samples (2 and 20 pg/ml) prepared by adding rhTNF-α to blank rat plasma, and was typically less than 15%. The cross-species reactivity was reported as minimal.

Literature Data Sources.

Concentration-time profiles of rhTNF-α in rats were digitalized (Plot Digitizer, free software) from the literature for model development (Kojima et al., 1988; Ferraiolo et al., 1989; Zahn and Greischel, 1989). Another data set of rhTNF-α concentration-time profiles following i.v. administration in monkeys was digitalized and applied for making comparison with allometric scaling PK predictions (Greischel and Zahn, 1989). All rhTNF-α PK studies used are summarized in Table 1. Units of rhTNF-α concentrations were converted to ng/ml.

TABLE 1.

Literature sources of rhTNF-α pharmacokinetic data

Species (Strain)	Sex	Body Weight	Dosing Route	Duration	Number Studied (n)	Specific Activity	Dose	rhTNF-α Assay	Additional Comments
		kg		h		U/µg	µg/kg
Rata (Wistar)	M	0.200–0.250	i.v. infusion	0–0.5	4		2	ELISA
					4		10
					5		20
					5		100
					6		500
					4		2		Excess TNF-βb
Ratc (Sprague- Dawley)	M	0.200–0.400	i.v. bolus		12		10	ELISA
					6		25
					6		46
					3		10		Nephrectomizedd
					6		46		Nephrectomizedd
Rate (Wistar)	M	0.280–0.300	i.v. bolus		5	2.9 × 103	114	L-M cell toxicity assay	Lymph concentrationsf
			s.c.		4		114
			i.m.		4		114
			i.p.		5		114
			SW		5		114
			GW		5		114
Monkeyg (Rhesus)	M	3–10	i.v. infusion	0–0.5	3		10	ELISA
					3		20
					3		30
					2		120
				0.5–7	3		22
					1		54
					1		135
					3		325
					3		22		Excess TNF-βb

ELISA, enzyme-linked immunosorbent assay.

^aZahn and Greischel (1989).

^bSaturable receptor-mediated elimination pathway is blocked in the presence of excess TNF-β.

^cConcentrations measured in serum and assume serum and plasma concentrations are equivalent (Ferraiolo et al., 1989).

^dAnimals were nephrectomized to abolish rhTNF-α elimination via renal filtration.

^eKojima et al. (1988).

^fLymph was collected from thoracic duct and rhTNF-α concentrations in lymph were measured.

^gGreischel and Zahn (1989).

mPBPK Model Development.

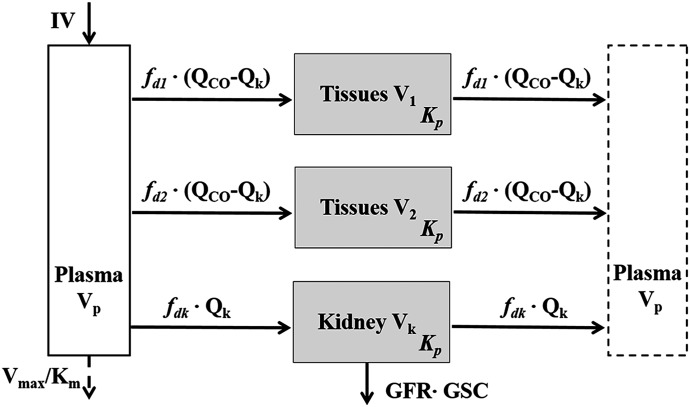
The first-generation mPBPK model (Cao and Jusko, 2012) was applied to characterize the plasma PK of rhTNF-α. Concentration-time profiles of rhTNF-α following i.v. doses from our study (5 mg/kg) and from the literature were simultaneously fitted. The model includes plasma, two lumped tissue compartments, and the kidney connected in an anatomic manner (Fig. 1). The model assumes that rhTNF-α is eliminated via saturable receptor-mediated disposition and renal filtration. The model equations are

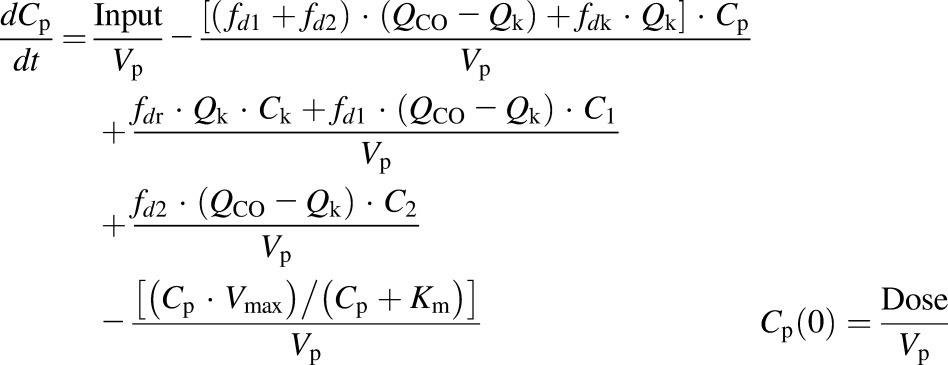(2)

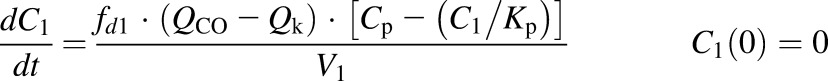(3)

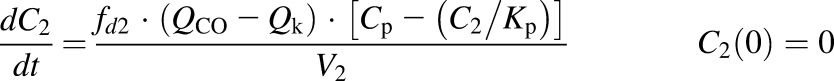(4)

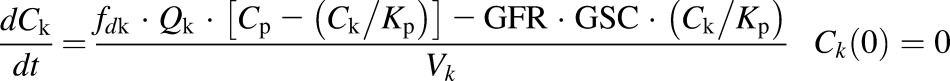(5)

where C_p, C₁, C₂, and C_k are the concentrations of rhTNF-α in plasma (V_p), two tissue interstitial fluid compartments (V₁ and V₂), and kidney interstitial fluid (V_k), respectively; Q_CO is the cardiac plasma flow; Q_k is the kidney plasma flow (Shah and Betts, 2012); f_d1 and f_d2 are the fractions of Q_CO for V₁ and V₂, respectively; f_dk is the fraction of Q_k for V_k; K_p is the tissue partition coefficient; GFR is the glomerular filtration rate (Davies and Morris, 1993); GSC is the glomerular sieving coefficient; and V_max and K_m account for nonlinear elimination. The GFR was set to zero in rats subjected to nephrectomy and V_max was set to zero when excess TNF-β was present. All physiologic volumes and flows used for rats in the mPBPK model are listed in Table 2.

Fig. 1.

Extended first-generation mPBPK model for characterization of rhTNF-α plasma PK. Model includes plasma compartment (V_p), two types of tissue compartments (V₁ and V₂) and a kidney compartment (V_k). Distribution of rhTNF-α to tissues is assumed driven by perfusion and diffusion. Symbols are defined in Tables 2 and 3.

TABLE 2.

Physiologic parameter values

Parameter	Definition	Rat (280 g)	Monkey (6.2 kg)
Vp (ml)	Plasma volume	9.06	187
VECF (ml)	Tissue extracellular fluid volume	48.72	993
QCO (ml/h)	Cardiac plasma output flow	2945	22,433
Qk (ml/h)	Renal plasma flow	365	3237
Vk (ml)	Kidney extracellular fluid volume	0.361	4.09
GFR (ml/h)	Glomerular filtration rate	78.6	624

All parameter values except the GFR were obtained from Shah and Betts (2012) and the GFR values were obtained from Davies and Morris (1993).

Allometric Scaling.

The developed mPBPK model was scaled to generate rhTNF-α PK predictions in monkeys. Physiologic flows and volumes of monkey were used and are listed in Table 2. Classic principles of allometry were applied to scale model parameters between species (eq. 1). The V_max was scaled to body weight with an exponent factor 0.75. Human TNF-α exhibits binding affinity for various animal species, and we assumed that the binding affinity (K_m) of rhTNF-α to its receptors is the same in rats and monkeys. The ratio of V₁/(V₁ + V₂) was also assumed to be the same in both species. Other parameters were shared between two species.

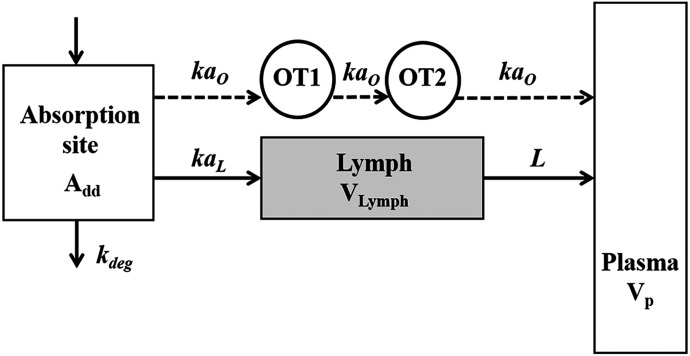
Absorption Model.

A semimechanistic model was proposed for rhTNF-α absorption kinetics given by different dosing routes. As depicted in the model scheme in Fig. 2, rhTNF-α reaches the blood through lymph uptake and other pathways including absorption via capillaries but is also degraded at the injection site. Presystemic degradation is assumed saturable for s.c. doses. The PK data of rhTNF-α following other routes of administration were only available for one dose, thus linear degradation was assumed. The model was described as

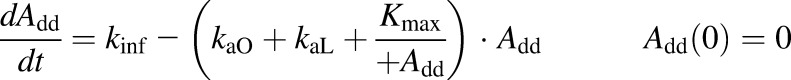(6)

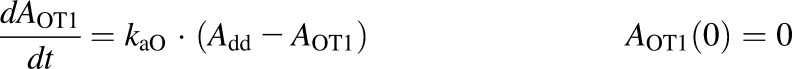(7)

(8)

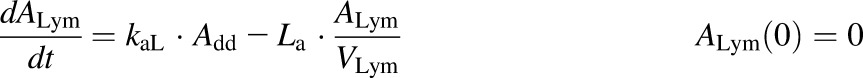(9)

where A_dd, A_Lym, A_OT1, and A_OT2 are the amounts of rhTNF-α at the s.c. injection site, lymph, and two transit compartments, respectively; V_Lym is the lymph volume, which equals the blood volume; L_a is the lymph flow rate measured by thoracic duct cannulation (0.6 ml/h) (Kojima et al., 1988); k_aL and k_aO are absorption rate constants for rhTNF-α for lymph uptake and other routes, respectively; and k_deg is the presystemic degradation rate constant at the absorption site.

Fig. 2.

Semimechanistic model for rhTNF-α absorption kinetics. Model includes the absorption site, lymph, plasma, and two transit compartments (OT1 and OT2). The absorption of rhTNF-α is via lymph uptake and other routes. Symbols are defined in Tables 2 and 4.

For s.c. administration

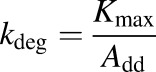(10)

For other routes of administration

(11)

The amount of rhTNF-α that enters the systemic circulation (input) is described as

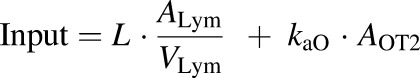(12)

For animals that underwent thoracic duct cannulation, the input is

(13)

Bioavailability (F) and percentage absorption via lymph (%Abs_Lymph) were also calculated using

(14)

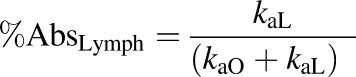(15)

Experimentally measured plasma concentration-time profiles of rhTNF-α following s.c. doses and infusions and literature digitalized rhTNF-α concentrations in plasma and lymph following s.c., i.m., i.p., stomach wall (SW), and gastrointestinal wall (GW) routes were simultaneously fitted with the model. Parameter estimates obtained from the plasma PK were fixed when assessing the absorption process.

Data Analysis.

Noncompartmental analysis was performed with WinNonlin 6.1 (Phoenix, Pharsight Corporation, Palo Alto, CA). The areas under the concentration time curves of rhTNF-α in plasma were estimated by the trapezoidal rule. Model fittings were performed with the ADAPT 5 computer program (Biomedical Simulations Resource, University of Southern California, Los Angeles, CA) using the naive, pooled data population approach and maximum likelihood algorithm. The variance model was defined as 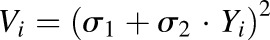, where V_i is the variance of the ith observation, σ₁ and σ₂ are additive and proportional variance model parameters, and Y_i is the ith model prediction. Model performance was evaluated by goodness-of-fit plots and Akaike information criterion values. The GraphPad Prism (GraphPad Software Inc., San Diego, CA) was used to generate graphs.

Results

rhTNF-α Pharmacokinetics in Plasma.

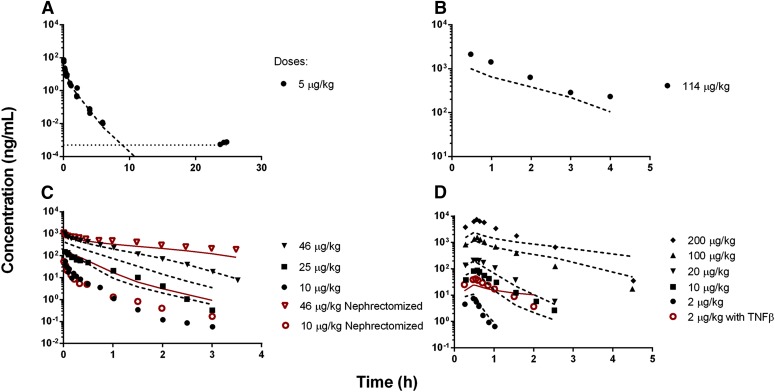
Following the i.v. bolus dose of 5 µg/kg, rhTNF-α exhibited rapid elimination in rats (Fig. 3A). The plasma half-life is approximately 6 minutes, which is much shorter than literature reported values (30 minutes to 1 hour) (Ferraiolo et al., 1989; Greischel and Zahn, 1989; Zahn and Greischel, 1989). The extended first-generation mPBPK model was applied to simultaneously fit both experimental and literature reported rhTNF-α PK following i.v. doses. The model-fitted plasma concentration-time profiles of rhTNF-α were overlaid with observed data from different studies in rats (Fig. 3). The parameter estimates are listed in Table 3. Overall, the model was able to describe the plasma concentration profiles of rhTNF-α reasonably well despite the animal, study, digitizing, and assay variability. Interestingly, the model described the change in rhTNF-α plasma profiles quite well when mechanistic disturbances were introduced. The model predicted less impact on rhTNF-α PK profiles in nephrectomized rats compared with normal rats at lower doses since the saturable receptor-mediated binding and disposition is the dominant elimination pathway (Fig. 3C). Also, in the presence of excess amounts of TNF-β, the receptor-mediated elimination of rhTNF-α is saturated and rhTNF-α is retained in the blood circulation for longer times (Fig. 3D).

Fig. 3.

Model-fitted plasma rhTNF-α concentration versus time profiles from experimental (A) and literature reported studies in rats (B–D) (Kojima et al., 1988; Ferraiolo et al., 1989; Zahn and Greischel, 1989). Symbols are observed concentrations and lines depict model fittings using parameters from Tables 3 and 4. The dotted line indicates the lower limit of assay quantification.

TABLE 3.

Summary of model parameter estimates for rhTNF-α plasma PK

Parameter	Definition	Estimate	CV
			%
fd1	Fraction of (QCO–Qk) for V1	0.6663	380
fd2	Fraction of (QCO–Qk) for V2	0.007463	18.5
fdk	Fraction of Qk for Vk	0.8	Fixed
Kp	Partition coefficient	0.5172	11.9
V1 (ml)	ECF volume for tissue compartment 1	13.10	19.5
Vmax (ng/h)	Michaelis Menten capacity constant	3152	11.3
Km (ng/ml)	Michaelis Menten affinity constant	31.72	19.3
GSC	Glomerular sieving coefficient	0.1031	14.9

ECF, extracellular fluid.

The fraction term f_d is a hybrid parameter that describes both the ratio of the total cardiac plasma output distributing into each tissue and the permeability of that specific tissue. Therefore, if the sum of all f_d is less than 1, the studied compound exhibits permeability issues. The fractions of cardiac plasma output flow for the two lumped tissue compartments (f_d1 and f_d2) are moderate and small (0.6663 and 0.0075), suggesting the occurrence of permeability rate–limited tissue distribution of rhTNF-α. The f_dk could not be precisely estimated and thus was fixed at 0.8. The kidney is a highly perfused organ and the permeability of rhTNF-α in the kidney should resemble the tissues with greater f_d. Also, the renal plasma flow Q_k was used with the ratio of plasma flow distribution into the kidney. Therefore, f_dk falls in the range of 0.6663–1 and was not sensitive for model fitting and estimation of other parameters within this range. The partition coefficient (K_p) of 0.5172 indicates that about 50% of the interstitial fluid space is available for rhTNF-α distribution. The GSC is 0.1031. Proteins are hindered for glomerular filtration in proportion to their size, charge, and structure. Trimeric units of rhTNF-α have a molecular size of ∼51 kDa and the estimated GSC for rhTNF-α corresponds to that for other proteins with similar size (e.g., Bence Jones, 44 kDa, reported GSC of 0.08) (Wallace et al., 1972; Heinemann et al., 1974). The receptor binding affinity of rhTNF-α is 0.5 nM when converted to molar concentration, which is within the range of binding affinity of TNF-α to TNFR1 (0.1 nM) and TNFR2 (greater or less than 0.1 nM) (Kull et al., 1985; Tsujimoto et al., 1985; Scheurich et al., 1986; Tartaglia et al., 1993; Van Ostade et al., 1993; Grell et al., 1998; MacEwan, 2002). This indicates that the saturable elimination pathway of TNF-α is dominantly mediated by binding and disposition to TNFRs. The estimated V_max and K_m values (3152 ng and 31.72 ng/ml) yield a maximum clearance of 100 ml/h, which controls rhTNF-α elimination at lower doses in comparison with renal filtration of 7 ml/h (GFR × GSC).

Allometric Scaling.

The resulting mPBPK model for rats, integrated with allometric scaling, was used to project the PK of rhTNF-α in monkeys. The model-simulated concentration-time profiles of rhTNF-α are overlaid with literature reported data in Fig. 4. The allometric predictions are in good agreement with the experimental PK in monkeys, with some underprediction at higher doses following long-term infusion. TNF-α was reported to induce glomerular damage in rabbits following 5-hour i.v. infusions at high doses (Bertani et al., 1989), which possibly explains the discrepancy between model predictions and experimental measurements at higher rhTNF-α doses for 6.5-hour infusions. Surprisingly, the model predicts very well the changes of rhTNF-α PK in the presence of excess TNF-β, suggesting that the nonlinear clearance pathway mediated by receptor binding and disposition is reliably projected.

Fig. 4.

Allometric-scaled plasma rhTNF-α concentration versus time profiles in monkeys. Symbols are observed concentrations from literature reported studies (Greischel and Zahn, 1989) and lines depict interspecies predictions using the parameters listed in Tables 3 and 4.

Absorption Kinetics.

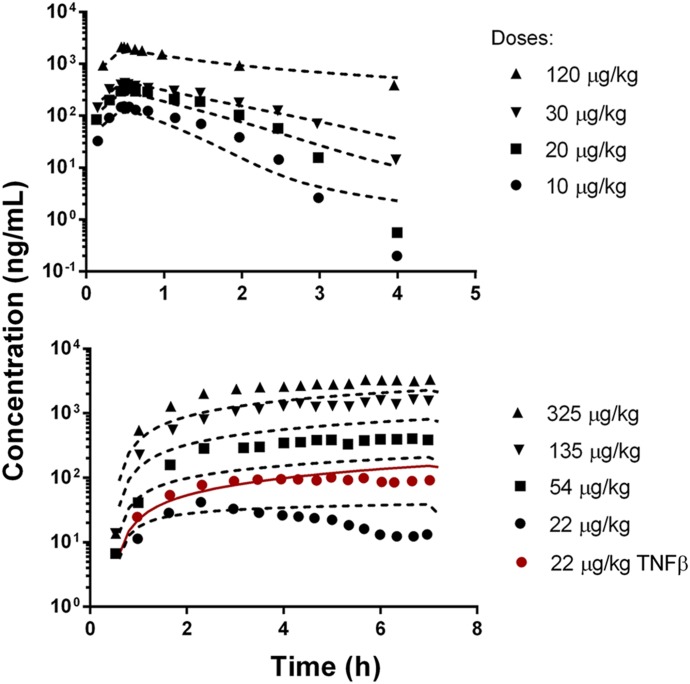
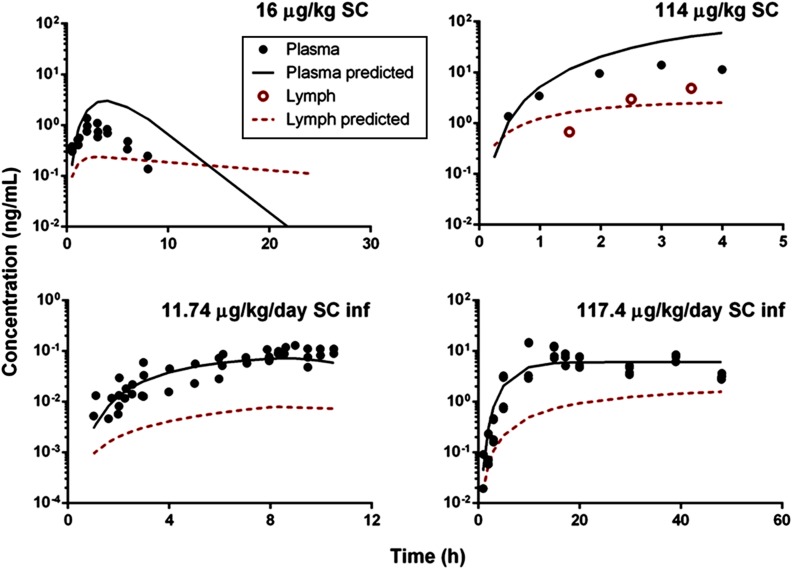
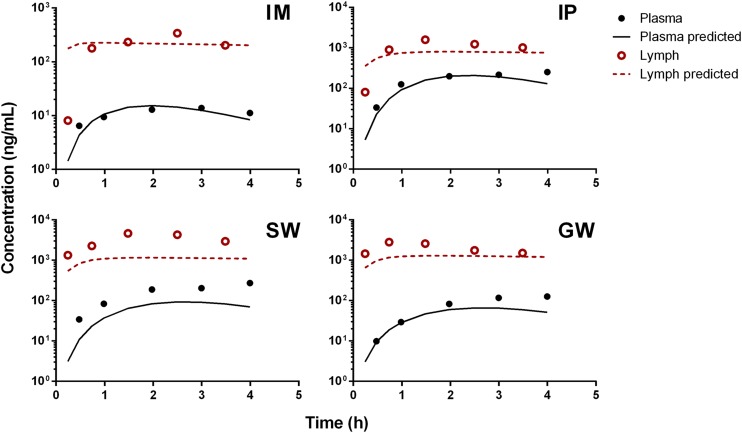
Animals subjected to s.c. infusions of rhTNF-α experienced a transient mild fever between 5 and 10 hours. Stability tests demonstrated that rhTNF-α in the pump remains intact during infusions and degradation within the pump container is negligible. Noncompartmental analysis showed dose-dependent bioavailability of rhTNF-α following s.c. bolus and infusions, assuming linear clearance at the given dose range. Bioavailability was generally poor and increased with dose (6.7% versus 36% following 11.74 and 117.4 µg/kg/d s.c. infusions). Therefore, our model assumed a saturable presystemic degradation pathway to account for the dose dependency of bioavailability. The model-predicted plasma and lymph concentration-time profiles of rhTNF-α following s.c. doses were overlaid with experimental measurements (Fig. 5). The model reasonably described the absorption kinetics of rhTNF-α following s.c. routes of bolus doses as well as short- and long-term infusions. The absorption kinetics of rhTNF-α following other routes of administration was also characterized. The model-predicted rhTNF-α concentration-time profiles in plasma and lymph agreed well with the experimental data (Fig. 6). The model parameter estimates for the absorption processes are listed in Table 4. The degradation rate constants following i.p., SW, and GW routes were estimated to be close to zero and were thus fixed at zero. The estimated absorption rate constants via lymph (k_aL) suggest much faster and more efficient transport of rhTNF-α into lymph following SW and GW doses in comparison with other routes. The absorption rate constants via other routes (k_aO) are quite close following different dosing routes, indicating possibly similar non-lymph–mediated absorption mechanisms. Also, the presystemic degradation rates following s.c. and i.m. administration are comparable (6 and 4 hour⁻¹). This is reasonable since catabolic environments are considered similar at the s.c. and i.m. dosing sites.

Fig. 5.

Model-fitted rhTNF-α concentration versus time profiles in plasma and lymph following s.c. administration from our experimental (A, C, and D) and literature reported studies in rats (B) (Kojima et al., 1988). Solid circles are observed plasma concentrations and open circles are observed lymph concentrations. Solid and dashed lines depict model-fitted concentration profiles in plasma and lymph, respectively, with the parameters listed in Table 4.

Fig. 6.

Model-fitted rhTNF-α concentrations versus time profiles in plasma and lymph following i.m., i.p., SW, and GW routes of administration from literature reported studies in rats (Kojima et al., 1988). Solid circles are observed plasma concentrations and open circles are observed lymph concentrations. Solid and dashed lines depict model-fitted concentration profiles in plasma and lymph, respectively, with the parameters listed in Table 4.

TABLE 4.

Summary of model parameters and estimates [mean (CV%)] for rhTNF-α absorption kinetics

Parameter	Definition	Route of Administration
		Subcutaneous	Intramuscular	Intraperitoneal	Stomach Wall	Intestinal Wall
kaO (1/h)	First-order absorption rate constant via other routes	0.4114 (0.077)	0.8045 (12.0)	1.219 (15.1)	0.9087 (21.2)	0.7963 (18.3)
kaL (1/h)	First-order absorption rate constant via lymph	0.0007969 (0.95)	0.6161 (26.2)	0.8306 (28.9)	1.193 (40.3)	1.371 (36.6)
kdeg (1/h)	Degradation rate constant at dose depot		3.886 (25.9)	0 (Fixed)	0 (Fixed)	0 (Fixed)
Kmax (ng/h)	Maximum degradation capacity at dose depot	899.9 (1.33)
KD50 (ng)	Dose amount causing 50% of Kmax	137.0 (21.2)
F	Bioavailability	>0.06	0.27	1	1	1
AbsLymph (%)	Percentage absorption via lymph uptake	0.19	43	41	57	63

Following s.c. and i.m. routes, appreciable portions of rhTNF-α are lost presystemically, whereas close to 100% of rhTNF-α is available for systemic absorption following i.p., SW, and GW doses. This might be explained by the presence of more proteases in skin versus the outer walls of the stomach and intestine. Also, the slower absorption rates through the lymph and bloodstream for s.c. and i.m. routes lead to prolonged retention of rhTNF-α at the dosing site and thus results in more presystemic degradation. In addition, the model suggests that less than 1% of rhTNF-α absorption occurs via lymph transport following s.c. routes, which agrees with previously studies (Bocci et al., 1986; Kagan et al., 2007). On the other hand, following SW and GW doses, lymph transport accounts for more than 50% of the overall rhTNF-α absorption; this is due to the rapid lymph formation in the gastrointestinal tract compared with other organs. Of the total lymph production, over 50% is formed in the gastrointestinal tract (Alexander et al., 2010).

Discussion

Soluble cytokines are therapeutic targets of mAbs and other biologics for the treatment of many inflammatory diseases. These biologics serve as neutralizing agents, binding to the cytokines, preventing them from interacting with cell surface receptors, and thus achieving beneficial pharmacological effects. The interrelationship between biologic agents and targeted cytokines can be characterized by target-mediated drug disposition kinetics (Mager and Jusko, 2001). The kinetic properties of cytokines are important determinants of both the PK and the pharmacological effects for therapeutic biologics. In this study, we have comprehensively and quantitatively summarized from the literature and characterized the available pharmacokinetic data for TNF-α in rats.

An extended first-generation mPBPK model with addition of the kidney was applied to the rhTNF-α PK. The whole body PBPK models as well as reduced and semimechanistic modeling approaches have been adapted for the mechanistic characterization of small molecule drug PK (Zhang et al., 2011; An and Morris, 2012). The mPBPK models bridge whole body PBPK models and empirical PK models, offer characterization of drug pharmacokinetic features in physiologic and mechanistic ways, and separate drug- and system-specific components using only plasma concentration profiles. The first-generation mPBPK models were applied for antibiotics and other small molecule drugs (Cao and Jusko, 2012). Here, we show that the first-generation mPBPK modeling approach is also suitable to describe the PK of proteins with smaller sizes. Our extended model accounts for both the nonlinear elimination and tissue distribution properties of rhTNF-α. Advantage was taken of published studies that perturbed receptor binding and renal extraction of TNF-α to gain modeling insights. These literature and modeling perspectives help to better understand the fate of TNF-α in vivo and may allow for improved prediction of the magnitude of pharmacological effects when integrating the PK features of therapeutic agents with TNF-α as their cytokine target.

TNF-α is systemically cleared via a saturable pathway mediated by TNFR binding and disposition and the linear clearance from renal filtration. At lower doses, TNFR-mediated binding and disposition dominate the elimination of rhTNF-α, whereas at high doses TNFR-mediated elimination is saturated and renal filtration is the main loss pathway. Mechanistically characterizing the elimination kinetics of rhTNF-α with the mPBPK model explains some contradictory observations concerning the contribution of different organs to TNF-α clearance. Liver and lung are supposedly the major organs accounting for TNF-α catabolism because of the reticulo-endothelial system. However, lung was reported to play a minimal role in rhTNF-α tissue uptake and elimination in rats (Pessina et al., 1995). In another study with rabbits and monkeys, very little liver catabolism of rhTNF-α was observed by isolated organ perfusions (Pessina et al., 1987). Both studies applied much higher doses of rhTNF-α and therefore the catabolism pathway of rhTNF-α mediated by TNFRs would be saturated.

Classic allometric scaling principles, which assume that PK attributes across species are related to body weight (eq. 1), have been extensively applied for interspecies PK predictions of small molecule drugs. Such principles were extended for interspecies predictions with macromolecules. In general, classic allometric scaling approaches yield reliable predictions of mAb clearances from monkey to man for mAbs exhibiting linear PK (Ling et al., 2009; Wang and Prueksaritanont, 2010; Deng et al., 2011). Also, clearances of proteins across a wide range of molecular sizes can be predicted with simple allometry or with adjustment to brain weights but require two or more animal species (Mahmood, 2004). However, the performance of classic allometry is less satisfactory for mAbs and other proteins with nonlinear PK (Ling et al., 2009). Integration of simple allometry with mechanism-based pharmacokinetic/pharmacodynamic models improves interspecies PK predictions of proteins with complex pharmacokinetic behaviors (Kagan et al., 2010). The feasibility of implementing simple allometry in mPBPK models for mAb PK predictions was also successful (Zhao et al., 2015). Our work provides an example and further extends efforts to integrate simple allometry with mPBPK models for PK prediction of smaller size protein cytokines. Our mPBPK model mechanistically explains the nonlinear clearance of rhTNF-α, which allows reliable prediction of clearance in monkeys with simple allometric rules. More importantly, the mPBPK model includes all major contributing pathways for TNF-α elimination, and thus has the ability to make projections of changes of rhTNF-α PK when elimination pathways are disrupted under disease conditions such as kidney failure and altered expression of TNFRs with disease.

Our semimechanistic model explores the absorption kinetics of rhTNF-α following s.c. and other routes of administration. Absorption kinetics of mAbs and other therapeutic proteins are complicated and include presystemic degradation, direct absorption through capillaries, and indirect absorption via lymph transport. Despite efforts seeking to understand the key determinants of s.c. absorption kinetics, knowledge in this area is still incomplete. Our model delineates major components of protein absorption in a semimechanistic manner with limited experimental data and provides an attempt to improve the understanding of the attributes of protein absorption processes. A particular feature is the use and concordance of lymph concentrations, which enables the differentiation of the absorption pathways via lymph and other routes. Our findings about the lymph uptake contribution in s.c. administration agree with some previous studies with interferon, albumin, and erythropoietin (Bocci et al., 1986; Kagan et al., 2007), but contradict a report on polyethylene glycol 30/erythropoietin (Wang et al., 2012). This could be explained by the size and diameter of the molecules. Polyethylene glycol 30/erythropoietin has a molecular size of 70 kDa with a large diameter produced by pegylation, which confines its entry through capillaries. Also, lymph samples were collected by thoracic duct cannulation, which drains lymph generated from only parts of the body including upper extremities, trunk, and hind legs (Tilney, 1971; Wang et al., 2012). Therefore, the s.c. dosing site matters. The data sets applied in our model development were from rats receiving s.c. doses at the upper back, and rhTNF-α may enter systemic circulation via lymph at other entries rather than the thoracic duct. The contribution of lymph uptake on overall absorption may be underrated.

Our model has some limitations. It was noted that presystemic degradation happened at both the s.c. dosing site and during lymph transport (Charman et al., 2000; Wang et al., 2012). However, with rather limited data, model simplifications were made by lumping the presystemic degradation and assuming the degradation is only present at the s.c. dosing site. In addition, this model is not able to address the structural and physiologic differences of skin between species, as well as the use of unrealistic large injection volumes in experimental animals, which further hinder reliable scale-up of absorption in man (McDonald et al., 2010). A physiologic model accounting for these unaddressed issues has been proposed in theory (Fathallah and Balu-Iyer, 2015). However, more sophisticated animal studies and experimental data are required to allow application of such complicated models.

In conclusion, we characterized the PK of rhTNF-α in rats with mPBPK models across a wide range of doses that cause no pathophysiological changes (nontoxic doses). The model accounts for rhTNF-α exhibiting permeability rate–limited tissue distribution and elimination comprised of a saturable clearance pathway mediated by TNFR binding and disposition coupled with renal filtration. The knowledge obtained allows better understanding of the fate of TNF-α in vivo, allows improved interspecies scale-up of rhTNF-α PK, and importantly may enable projections of the magnitude of pharmacological effects of therapeutic proteins targeting TNF-α. Also, the absorption kinetics of rhTNF-α following s.c. and other routes of administration were assessed with a semimechanistic model. The model suggests substantial presystemic degradation of rhTNF-α for s.c. and i.m. routes and greater contributions of lymph uptake to the overall systemic absorption through SW and GW dosing. Despite the model limitations, simplifications, and diverse sources of data, the model included all major pathways of absorption and disposition, offers a reasonable means to quantitatively understand the global kinetics of rhTNF-α, and improves the understanding and scale-up of its PK across species.

Abbreviations

GFR

glomerular filtration rate

GSC

glomerular sieving coefficient

GW

gastrointestinal wall

mAb

monoclonal antibody

mPBPK

minimal physiologically based pharmacokinetic

PBPK

physiologically based pharmacokinetic

PK

pharmacokinetics

rhTNF-α

recombinant human tumor necrosis factor-α

SW

stomach wall

TNF-α

tumor necrosis factor-α

TNF-β

tumor necrosis factor-β

TNFR

tumor necrosis factor receptor

Authorship Contributions

Participated in research design: Chen, DuBois, Almon, Jusko.

Conducted experiments: Chen, DuBois.

Performed data analysis: Chen, Jusko.

Wrote or contributed to the writing of the manuscript: Chen, DuBois, Almon, Jusko.