Intermolecular interactions in the condensed phase: Evaluation of semi-empirical quantum mechanical methods

Abstract

To facilitate further development of approximate quantum mechanical methods for condensed phase applications, we present a new benchmark dataset of intermolecular interaction energies in the solution phase for a set of 15 dimers, each containing one charged monomer. The reference interaction energy in solution is computed via a thermodynamic cycle that integrates dimer binding energy in the gas phase at the coupled cluster level and solute-solvent interaction with density functional theory; the estimated uncertainty of such calculated interaction energy is $\pm 1.5$ kcal/mol. The dataset is used to benchmark the performance of a set of semi-empirical quantum mechanical (SQM) methods that include DFTB3-D3, DFTB3/CPE-D3, OM2-D3, PM6-D3, PM6-D3H+, and PM7 as well as the HF-3c method. We find that while all tested SQM methods tend to underestimate binding energies in the gas phase with a root-mean-squared error (RMSE) of 2-5 kcal/mol, they overestimate binding energies in the solution phase with an RMSE of 3-4 kcal/mol, with the exception of DFTB3/CPE-D3 and OM2-D3, for which the systematic deviation is less pronounced. In addition, we find that HF-3c systematically overestimates binding energies in both gas and solution phases. As most approximate QM methods are parametrized and evaluated using data measured or calculated in the gas phase, the dataset represents an important first step toward calibrating QM based methods for application in the condensed phase where polarization and exchange repulsion need to be treated in a balanced fashion.

INTRODUCTION

There is currently a resurgent interest in semi-empirical quantum mechanical (SQM) methods due to the importance of balancing computational efficiency and accuracy in many chemical and biological applications.^1–12 Due to approximations in SQM methods, such as NDDO^13,14 and DFTB^15–17 methods, they are often not quantitatively accurate as compared to high level ab initio calculations. For example, errors in thermochemical properties such as proton affinity and reaction energy are often in the range of 5-10 kcal/mol;^7,18–21 a recent barrier height benchmark for enzyme models conducted by us found that errors can often reach the range of 10-15 kcal/mol.²² Thus systematic improvements of SQM methods are required to make them robust in mechanistic studies of reactive processes.

For non-covalent interactions, on the other hand, SQM methods augmented with empirical corrections^2,7,23–31 yield results that can rival modern density functional theory (DFT) and ab initio methods (e.g., SCS-MP2³²) in accuracy.^2,4 For instance, for the S66 dataset,³³ which consists of 66 dimers and their gas-phase interaction energies calculated at the Coupled Cluster with Singles and Doubles with Perturbative Triples and Complete Basis Set extrapolation (CCSD(T)/CBS) level of theory, the Root Mean Squared Deviation (RMSD) interaction energy is $<1$ kcal/mol for both DFT and a set of empirically corrected SQM methods.⁴ However, we note that empirically adjustable parameters of SQM methods are usually fitted to experimental data or high-level QM data in the gas phase.^18,34,35 While datasets generated with high-level QM methods, such as CCSD(T)/CBS³⁶ or SAPT,³⁷ can be highly accurate, it is unclear whether parameters fitted to such data are transferable to condensed-phase systems, where both many-body polarization effects and exchange repulsion need to be treated in a balanced manner.^23,38 For example, Yalmazer and Korth found the mean absolute deviation between interaction energies for 695 protein-ligand complexes computed at the PM6-DH+ and BP86-D2/TZVP levels of theory to be as large as 14 kcal/mol.³⁹

In this work, we initiate the development of a dataset for intermolecular interaction energies in the solution phase, such that it is possible to calibrate and improve current SQM methods for condensed phase applications. The dataset is also useful for benchmarking various ab initio QM methods for condensed phase problems, as previous efforts focused on pair-wise interactions in the gas phase,^33,40 although the clusters might have been obtained from biomolecules;³⁶ there are also datasets that include solid crystals.² As described in the section titled Dataset and computational methods, we extend the dataset of Řezáč and Hobza²⁹ and construct a dataset that consists of small molecule dimers solvated by a water droplet; the intermolecular binding energy for the dimer solute is computed via a thermodynamic cycle that integrates CCSD(T) calculations for the dimer interaction in the gas phase and DFT calculations for the solute-solvent (water) interactions. For the SQM methods, we include DFTB3⁴¹ and DFTB3-CPE,²³ which improves the description of polarization via a chemical potential equalization model,^42–44 several variants of the PM6 model^24,28 and the OM2-D3 model;³⁵ we also test the HF-3c model,⁴⁵ which employs Hartree-Fock with a minimal basis along with several empirical corrections. Among those, we note that most empirical corrections are mechanical in nature (i.e., decoupled from the determination of the wavefunction or electron density), with the exception of DFTB3-CPE,²³ in which the auxiliary response function is self-consistent with the DFTB3 density. Therefore, we expect that the DFTB3-CPE model is more likely to be transferable to the solution phase, although parameters were determined entirely based on gas phase systems. This was already evident from our recent analysis²³ of “large” water clusters (which contain 6-17 water molecules⁴⁶), for which empirically corrected PM6 models were found to give rather large errors in the binding energies, despite their excellent performance for dimeric systems.

In the following, we first describe the model systems and the computational approach we take to calculate the intermolecular binding energies in the solution phase. We then present the benchmark results for a set of SQM methods. We conclude with a few remarks and comments on future work.

DATASET AND COMPUTATIONAL METHODS

Description of the dataset

The dataset presented herein consists of 15 different dimers motivated by biologically relevant molecules (see Table I) and they are embedded in a water droplet; three droplets that contain water molecules within 4, 6, and 8 Å of the solute are studied for each dimer. An example is shown in Fig. 1 for the formaldehyde ⋅ imidazolium dimer with a 4.0 Å thick water shell, which roughly corresponds to the first solvation shell. Table I lists the computed interaction energies for the 15 dimers in the gas phase and in the 8.0 Å water shell, which roughly corresponds to inclusion of up to the third solvation shell with a total of around 600 atoms. We limit discussion to the 8 Å systems in the main text, and results for smaller water shells are summarized in the supplementary material.

TABLE I.

Computed intermolecular binding energy in the gas-phase (g) and in an 8.0 Å water shell (aq) following the thermodynamic cycle in Fig. 2.^a

ID	Complex	$\mathrm{\Delta }{E}_{\left(g\right)}$b	$\mathrm{\Delta }{E}_{\left(aq\right)}$
1	Acetate ⋅ methanol	−19.8	−12.6
2	Acetate ⋅ water	−21.1	−15.3
3	Acetate ⋅ methylamine	−11.5	−0.5
4	Methylammonium ⋅ formaldehyde	−19.1	−11.9
5	Methylammonium ⋅ methylamine	−28.6	−22.6
6	Methylammonium ⋅ methanol	−21.2	−15.5
7	Methylammonium ⋅ water	−18.5	−13.8
8	Guanidinium ⋅ formaldehyde	−18.1	−13.0
9	Guanidinium ⋅ methylamine	−20.2	−16.0
10	Guanidinium ⋅ methanol	−19.8	−15.4
11	Guanidinium ⋅ water	−17.5	−14.0
12	Imidazolium ⋅ formaldehyde	−16.4	−11.7
13	Imidazolium ⋅ methylamine	−26.0	−23.1
14	Imidazolium ⋅ methanol	−18.9	−14.0
15	Imidazolium ⋅ water	−16.5	−12.1

^aIntermolecular binding energies are calculated using a combined CCSD(T)/DFT approach [see Eq. (3)]. The uncertainty is $\pm 0.2$ kcal/mol for $\mathrm{\Delta }{E}_{\left(g\right)}$ and $\pm 1.5$ kcal/mol for $\mathrm{\Delta }{E}_{\left(aq\right)}$. All energies are listed in units of kcal/mol.

^bGas-phase interaction energies calculated at the CCSD(T)/CBS level are taken from the work of Řezáč and Hobza.²⁹

FIG. 1.

An example for the dimer systems studied in the current work. The dimer between formaldehyde and imidazolium is studied in both the (a) gas phase and (b) solution phase, which is modeled by a water droplet that includes water molecules within a given distance (4, 6, or 8 Å) from the solute. The model in (b) contains water molecules within 4 Å from the solute. Discussion is limited to the 8 Å systems in the main text, and results for smaller water shells are summarized in the supplementary material.

Calculation of reference binding energies in the solution phase

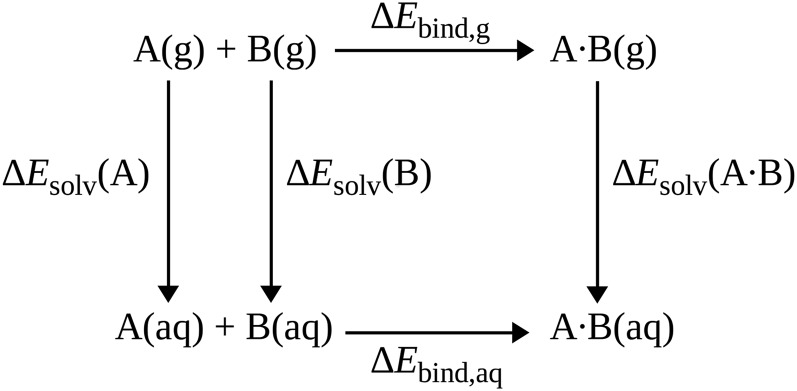
To compute the reference value for the binding energies in solution, we use an approach similar to the thermodynamic cycle (summarized in Fig. 2) used to compute binding free energies in solution.^47,48 The dimer complex of monomers A and B is placed in a water droplet, and after equilibration with molecular dynamics (see below), the dimer complex and a surrounding shell of water molecules are extracted. The binding energy in the gas phase ($\mathrm{\Delta }{E}_{bind,g}$) is simply calculated as

$$\mathrm{\Delta }{E}_{bind,g}=E_{A\cdot B\left(g\right)}-\left[E_{A\left(g\right)}+E_{B\left(g\right)}\right].$$ (1)

For the values of $\mathrm{\Delta }{E}_{bind,g}$, we use those calculated by Řezáč and Hobza²⁹ at the level of CCSD(T)/CBS. For the “solvation energies” (note that no entropic contribution is considered in the current work), considering the large size of the water droplet, we compute these values at the DFT level (PBE0⁴⁹/def2-TZVP-D3),

$$\mathrm{\Delta }{E}_{solv}\left(\mathrm{X}\right)=E\left(X\cdot W\right)-\left[E\left(\mathrm{X}\right)+E\left(\mathrm{W}\right)\right],$$ (2)

where X is either one of the monomers A or B, or the complex A ⋅ B, and W is the water shell surrounding the complex. Note that the same geometry of W (extracted from the molecular dynamics snapshot for a solvated dimer AB) is used for the monomers (A and B) as for the dimer AB.

FIG. 2.

The thermodynamic cycle used to calculate the binding energy in the solution phase.

The final reference binding energy ($\mathrm{\Delta }{E}_{bind,aq}$) is then calculated by combining the gas phase binding energy and the “solvation energies,”

$$\begin{array}{rcl}\mathrm{\Delta }{E}_{bind,aq}& =& \mathrm{\Delta }{E}_{bind,g}^{CCSD\left(T\right)}+\mathrm{\Delta }{E}_{solv}^{DFT}\left(A\cdot B\right)\\ & & -\left[\mathrm{\Delta }{E}_{solv}^{DFT}\left(\mathrm{A}\right)+\mathrm{\Delta }{E}_{solv}^{DFT}\left(\mathrm{B}\right)\right].\end{array}$$ (3)

The values of $\mathrm{\Delta }{E}_{bind,aq}$ for each complex in the dataset are listed in Table I. For each dimer AB, only one solvent snapshot is used in the current work to estimate the “solvation energies” (although three water droplets of different sizes are examined, see the supplementary material) and this is done considering the large computational cost associated with DFT calculations for systems that consist of hundreds of atoms. The dataset can be systematically expanded by including additional snapshots for each dimer.

We note that the solvated binding energy, $\mathrm{\Delta }{E}_{bind,aq}$, is not meant to estimate an average binding energy or binding free energy since the water molecules are not equilibrated when the molecules are removed. Rather $\mathrm{\Delta }{E}_{bind,aq}$ is a measure of the binding interaction between the two molecules for a specific conformation of the molecular complex in the presence of surrounding water molecules.

For the SQM methods tested here, the same equation [Eq. (3)] is used, except that all components (gas phase binding and “solvation energies”) are computed at the same respective SQM method; the structures are not re-optimized, all reported values in Table II are based on single point energies at the SQM levels, and original binding energies are summarized in the supplementary material.

TABLE II.

The root mean squared error (RMSE) and mean error (Mean) to reference binding energy values for 7 methods on the C15 and solvated C15 datasets in units of kcal/mol. Note that the mean error of the null model is 0 kcal/mol by construction.

	Gas		Solution
Method	RMSE	Mean	RMSE	Mean
DFTB3-D3	5.0	3.6	3.9	0.6
DFTB3/CPE-D3	1.9	0.9	2.2	−0.6
HF-3c	4.4	−3.6	7.0	-6.6
OM2-D3	2.1	1.8	1.9	−1.4
PM6-D3	2.1	0.9	3.5	−2.6
PM6-D3H+	2.2	1.3	3.7	−3.0
PM7	1.9	1.0	2.9	−2.2
Null	3.8	(0.0)	4.9	(0.0)

Generation of solvated structures

The MP2-optimized structures from the dataset of 15 charged dimers from the work of Řezáč and Hobza²⁹ (hereafter abbreviated as “C15”) are placed in a 20 Å radius water shell with the standard stochastic boundary condition,⁵⁰ and MD simulations are carried out with the CHARMM program.⁵¹ The dimer is treated with DFTB3/3OB¹⁸ and water is treated with a modified TIP3P model;^52,53 the internal structure of the dimer is held fixed during the molecular dynamics (MD) simulations, which are conducted for 1 ns with a time step of 2 fs. SHAKE⁵⁴ is applied to constrain the structure of the water molecules, and non-bonded interactions are treated using extended electrostatics⁵⁵ and a switching function⁵⁶ for the van der Waals interaction between 8 and 12 Å. The structure from the very last step in the 1 ns MD simulation is used to construct the various water droplet models.

QM calculations

ORCA⁵⁷ version 3.0.3 is used for all PBE0/def2-TZVP-D3 and HF-3c calculations. The RIJCOSX approximation is used for PBE0 to make the largest calculations computationally tractable. MOPAC2012⁵⁸ 15.229L is used for PM6-D3 and PM7 calculations, while a developmental version of GAMESS⁵⁹ is used for PM6-D3H+ calculations. MNDO2005⁶⁰ version 7.0 is used for the OM2 calculations, along with the DFT-D3 program^61,62 for calculating the D3 dispersion energy term for OM2-D3. CHARMM⁵¹ version c41a1 is used for all DFTB3-D3 and DFTB3/CPE-D3 calculations and for the DFTB3/3OB/TIP3P MD simulations to generate the solvated dimer structures. We note that all corrections to the approximate QM methods⁴ discussed here, the D3 models for empirical dispersion, the H+ model for hydrogen-bonding interactions, and the “3c” correction for HF, are all mechanical in nature in that they are not coupled with the wavefunction/density determination. By contrast, the CPE correction is fully self-consistent with the determination of density in the DFTB3/CPE model.²³

RESULTS

Uncertainty estimates for the reference binding energies

First, we estimate the uncertainty in the reference binding energies [$\mathrm{\Delta }{E}_{bind,aq}$, see Eq. (3)] that arises due to the choice of the method and basis set, using a standard propagation of error. For the gas phase binding energy, $\mathrm{\Delta }{E}_{bind,g}^{CCSD\left(T\right)}$, the error in the CCSD(T)/CBS values is about 1.5% of the total interaction energies, which corresponds to 0.2 kcal/mol on average for the dataset.⁶³ For the solvation energies, we estimate the uncertainty as follows: the calculations of $\mathrm{\Delta }{E}_{solv}$ are repeated for three cases (acetate ⋅ methanol, acetate ⋅ water, and guanidinium ⋅ formaldehyde complexes) with the smallest solvent shell (i.e., within 4 Å of the solute) with four additional functionals: B3LYP,⁶⁴ M06-2X,⁶⁵ TPSS,⁶⁶ and PBE,⁶⁷ and the basis sets def2-TZVP and def2-QZVP of these interaction energies are displayed in Table S7 of the supplementary material. In all cases, the differences in interaction energies between different DFT functionals are less than 1.1 kcal/mol. Likewise, the differences between results using the def2-TZVP and def2-QZVP basis sets are less than 1.0 kcal/mol.

Using the difference between the five different DFT functionals and the difference between def2-TZVP and def2-QZVP calculations as estimates for the uncertainty in choice of method and basis set, it is possible to use propagation of error to calculate an uncertainty estimate: under the assumption that these errors are random in nature, the total error is $\pm 1.5$ kcal/mol for the binding energies in solution ($\mathrm{\Delta }{E}_{bind,aq}$). Although such uncertainty is larger than the “chemical accuracy” (usually defined as $<1$ kcal/mol), it is small compared to the precision of the SQM methods assessed in this work.

Accuracy of semi-empirical quantum methods

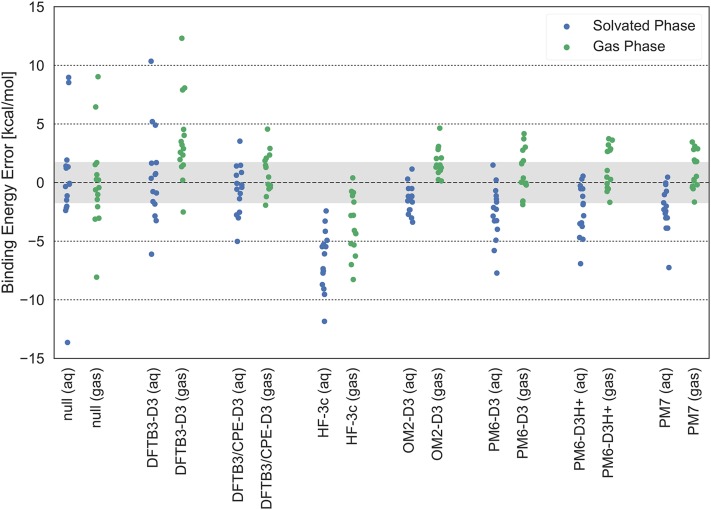
In this section, we use the dataset to benchmark the performance of the SQM methods DFTB3-D3, DFTB3/CPE-D3, OM2-D3, PM6-D3, PM6-D3H+, and PM7 as well as the HF-3c method in solution phase.^{14,23,28,34,35,41} An overview of the root-mean-squared error (RMSE) in binding energies and mean errors is summarized in Table II. Graphical overviews of the errors are presented in Figs. 3 and 4.

FIG. 3.

The deviation (error) between binding energies calculated using various semi-empirical methods and reference values (see Table I), for the set of 15 dimers in the gas phase (gas) or solution phase (aq). The gray line denotes an estimated $\pm 1.5$ kcal/mol uncertainty in the reference values in the solution phase. The gas-phase reference of CCSD(T)/CBS is expected to carry only a small uncertainty of $\pm 0.2$ kcal/mol for which the gray error bar is not representative. See text for the discussion of the null models.

FIG. 4.

Root-mean-squared error (RMSE) between binding energies calculated using various semi-empirical methods and reference values (see Table I), for the set of 15 dimers in the gas phase (gas) or solvated phase (aq). Error bars denote the 95% confidence interval, obtained via a boot-strapping procedure. See text for the discussion of the null models.

For DFTB3-D3, the error in the gas-phase is dominated by complexes with binding interactions with the nitrogen lone pair in methylamine. This problem has been noted previously and likely reflects the monopole approximation for lone pairs in charge-charge interactions in the current DFTB framework.²³ On average, DFTB3-D3 exhibits systematic underbinding in the gas-phase for all complexes, except for the acetate ⋅ water complex, by 3.6 kcal/mol. In the solution phase, DFTB3-D3 does not systematically predict over- or underbinding, except for the complexes containing methylamine, which are still systematically predicted to underbind by 5-10 kcal/mol.

The polarization-corrected method DFTB3/CPE-D3²³ has been parametrized based on the gas-phase dataset (with the formaldehyde ⋅ imidazolium complex excluded) and is therefore by design more balanced and accurate for the gas-phase data. Encouragingly, this trend is maintained for the solution phase dataset DFTB3/CPE-D3, which exhibits the smallest mean error (−0.6 kcal/mol) among the SQM methods tested here, suggesting that the CPE correction is transferable to the solution phase. The RMSE values relative to the reference binding energies are comparable in the gas phase (1.9 kcal/mol) and solution phase (2.2 kcal/mol).

The three methods of the PMx family we benchmark here, PM6-D3, PM6-D3H+, and PM7, have been parametrized predominantly based on experimental heats of formation and they display a similar degree of accuracy in both the gas and solution phases. In all cases, the RMSE relative to the reference binding energies is around 2 kcal/mol in the gas-phase and around 3 kcal/mol in the solution phase; these are slightly larger, especially the solution phase values, than DFTB3/CPE-D3. All three PMx methods predict underbinding by around 1 kcal/mol in the gas phase and overbinding by between 2 and 3 kcal/mol in the solution phase. The use of the third-generation hydrogen-bond correction H+ (and slight reparametrization of the D3 parameters), in the case of PM6-D3H+, does not increase nor decrease the accuracy of the PM6 model when compared to PM6-D3. This presumably reflects the mechanical nature of the H+ model, which does not account for the missing many-body polarization in the PM6 method.

The orthogonalization-corrected OM2-D3 method shows very encouraging performance. In the gas phase, interaction energies are predicted to overbind by 1.8 kcal/mol on average, but with a small random error. In the solution phase, the RMSE of 1.9 kcal/mol is the lowest among all SQM methods tested here; although the mean error of −1.4 kcal/mol is slightly larger than that of DFTB3/CPE-D3, the accuracy of the methods does not differ with any statistical significance ($p<0.05$).

The method tested with the least empiricism, HF-3c, which has only 9 adjustable parameters, is observed to overbind systematically in both the gas and solution phases. In fact, HF-3c systematically overbinds by −3.6 kcal/mol on average in the gas phase, and this error increases to −6.6 kcal/mol in the solution phase. These rather large errors suggest that parameters in the geometric counter-poise correction (gCP) and the short-range basis set-incompleteness correction (SRB) are not tuned adequately for the solution environment.

As a statistical test, we also compare all models to a null model. The null model has one degree of freedom which we simply fit to the mean reference value. Thus the null model yields the binding energy −19.5 kcal/mol for complexes in the gas phase, and −14.1 kcal/mol for the solvated complexes. The RMSE for the null models is 3.8 kcal/mol for the gas-phase complexes and 4.9 kcal/mol for the solvated complexes. Using the statsig program,⁶⁸ only the OM2 and DFTB3/CPE methods show up as being significantly different (with $p<0.05$) from the constructed null model for the solvated complexes—in both cases being more accurate than the null model. For the gas-phase reference data, only PM7 is significantly different from the null-model with $p<0.05$, although the accuracy of PM7 is very comparable with an RMSE within few tenths of a kcal/mol to those of the methods DFTB3/CPE-D3, OM2-D3, PM6-D3, and PM6-D3H+. A detailed statistical comparison between the various methods is summarized in Tables S5 and S6 of the supplementary material.

We note that the acetate ⋅ water complex appears as a sort of an outlier with the largest negative binding energy error (i.e., predicted to bind too strong compared to the reference method) for all methods except OM2-D3 (see, e.g., Fig. 3). Since the error is systematic across all methods, it is entirely possible that the DFT reference is not accurate enough for this particular case—if the reference value had been 2-3 kcal/mol stronger, corresponding to 1-2 times the estimated uncertainly, the complex would not show up as a significant outlier. Despite this uncertainty, it is still apparent that most methods predict very strong overbinding for this complex—much larger than those that can be explained by errors in the reference binding energies.

CONCLUSION

We have developed a new dataset of intermolecular interaction energies for molecules in the solution phase, approximated by water shells that include up to the third solvation shell. The dataset is available under the terms of the CC0 license at https://github.com/Cuigroup/c15solv. The reference binding energies are computed using a thermodynamic cycle that integrates CCSD(T)/CBS binding energies in the gas phase and DFT solute-solvent interaction energies; the estimated uncertainty of the reference values is $\pm 1.5$ kcal/mol. The reference values are used to benchmark a set of SQM methods that include DFTB3-D3, DFTB3/CPE-D3, OM2-D3, PM6-D3, PM6-D3H+, and PM7 as well as the HF-3c method. Among these, only the two methods OM2 and DFTB3/CPE are better than the null model with statistical significance ($p<0.05$).⁶⁸ It is encouraging that the CPE-correction developed for DFTB3 is transferable to the solution phase since all parameters were developed based entirely on gas phase molecules. By contrast, the PMx family of methods appears to be somewhat more accurate in the gas phase but systematically predicts overbinding in the solution phase, and the addition of the H+ correction neither increases nor decreases the accuracy in the gas or the solution phase. These observations highlight the merits of developing systematic improvements of SQM methods that are explicitly coupled to the electronic density in a self-consistent manner.

We hope that the database will facilitate further calibration and developments of SQM methods and other approximate QM methods for the description of non-covalent interactions in the condensed phase. The thermodynamic cycle approach can also be used to estimate accurate binding interactions in heterogeneous environments such as proteins, nucleic acids, and lipid bilayers. Including additional snapshots will also help calibrate approximate QM methods for the description of entropic aspects of intermolecular interactions in the condensed phase. Further exploration for the relative orientations and separations of the solute molecules is also essential for ensuring continuous potential energy surfaces with proper geometries for key stationary points.³¹

SUPPLEMENTARY MATERIAL

See supplementary material for detailed benchmark data for gas-phase and different solution phase systems.