Efficient Descriptor-Based Segmentation of Parotid Glands with Non-Local Means

Abstract

Objective

We introduce descriptor-based segmentation that extends existing patch-based methods by combining intensities, features and location information. Since it is unclear which image features are best suited for patch selection, we perform a broad empirical study on a multitude of different features.

Methods

We extend non-local means segmentation by including image features and location information. We search larger windows with an efficient nearest neighbor search based on kd-trees. We compare a large number of image features.

Results

The best results were obtained for entropy image features, which have not yet been used for patch-based segmentation. We further show that searching larger image regions with an approximate nearest neighbor search and location information yields a significant improvement over the bounded nearest neighbor search traditionally employed in patch-based segmentation methods.

Conclusion

Features and location information significantly increase the segmentation accuracy. The best features highlight boundaries in the image.

Significance

Our detailed analysis of several aspects of non-local means based segmentation yields new insights about patch and neighborhood sizes together with the inclusion of location information. The presented approach advances the state-of-the-art in the segmentation of parotid glands for radiation therapy planning.

I. Introduction

The automatic segmentation of parotid glands in head and neck CT images supports intensity-modulated radiation therapy planning. Atlas-based segmentation methods often use deformable image registration to associate each voxel in a test image with a set of voxels in training images, and apply a label propagation scheme to segment the test image [1]–[5]. Instead of registering whole images, patch-based segmentation compares patches of intensity values to establish correspondences between test and training voxels of similar local image content [6]–[9]. However, intensity values are just one possible description of image content. We present a natural generalization of patch-based segmentation to descriptor-based segmentation by including image features and location information as well as patches of intensity values in descriptor vectors representing local image content. Our results show that the additional discriminative information in the descriptor improves segmentation accuracy.

Our method is based on the non-local means (NLM) framework introduced in [10], which produces state-of-the-art results for patch-based segmentation [6], [7]. The principal idea behind NLM is to compare patches across the entire image domain and to base the comparison solely on patch intensity values without taking their locations in the image domain into account. In the actual implementation of NLM for image denoising [10], the search window is reduced from the entire image domain to neighborhoods of 21 × 21 pixels to address computational concerns. Similarly, [6] and [7] restrict the search window to range from 9×9×9 to 15×15×15 voxels to improve computational efficiency, assuming an initial affine alignment of the images. In our study, we employ an efficient approximate nearest neighbor search allowing us to work with larger search windows that contain the entire parotid gland, which better reflects the original idea of NLM to consider the entire image domain. Counter-intuitively, our experimental results show that larger search windows lead to less accurate segmentation results. This suggests that the spatial information implicitly incorporated by restricting the search to small windows not only improves computational efficiency but also has a direct influence on segmentation accuracy. However, spatially biasing the result by restricting search windows has two disadvantages: (1) it imposes a hard spatial cutoff and therefore a discontinuous rather than a soft bias; and (2) it does not provide spatial context within the search window. Contrary to the idea behind NLM, we explicitly incorporate location information in the comparison of patches, introducing a soft bias towards spatially closer patches. With the explicit inclusion of location information, we extend the search window from small neighborhoods to regions containing the entire target structure. The computational concerns accompanying these large search regions are addressed with an approximate nearest neighbor search. We find that this approach yields a significant improvement in segmentation accuracy over an exact nearest neighbor search within a restricted search window.

In addition to location information, we incorporate image features into the descriptor. A large number of image features have been proposed in the computer vision literature and a priori it is unclear which of these features best complement patch intensity values for segmenting medical images. In this study, we empirically evaluate the performance of 15 features. Some of these features were initially proposed for two-dimensional images – we discuss and evaluate three-dimensional extensions of these features. We investigate the parameters involved in descriptor-based segmentation, e.g., patch sizes, feature and location weights, the composition of the descriptor and the number of nearest neighbors. This comprehensive analysis leads to new insights into the behavior of NLM segmentation methods in general. Notably, we find that decoupling the size of the intensity patch and the size of the label patch in the multi-point label propagation method improves segmentation accuracy. We also introduce multi-scale patches that combine the intensity information from multiple scales and therefore provide additional context.

We evaluate our descriptor-based framework by applying it to the segmentation of parotid glands of patients undergoing radiation therapy. In intensity-modulated radiation therapy, experts delineate the most critical structures, also known as organs at risk, and use the generated segmentations to reduce the irradiation of healthy tissue and potential side effects. The parotid glands are critical salivary glands. Irradiation of the parotid glands in patients with head and neck cancer leads to xerostomia, a condition that interferes with mastication, deglutition, and speech in patients. The automatic segmentation of parotid glands is particularly challenging due to the low soft tissue contrast in CT images and the high anatomical variability of the glands among patients.

A. Related Work

Atlas-based segmentation of parotid glands with deformable registration has been previously investigated [11], [12]. In [13], an active shape model of parotid glands was constructed with the atlas images. The refinement of head and neck segmentations based on patch classification with features was proposed in [14]. The approach in [15] applied label fusion to initialize a segmentation pipeline that employs statistical appearance models and geodesic active contours.

Patch-based segmentation approaches as described within the NLM framework were proposed by [6], [7]. Recently, the PatchMatch algorithm [16] was applied for NLM-based segmentation [17]. In contrast to our work, features and explicit location information were not included. For the segmentation of the hippocampus, the application of ball trees in combination with location was proposed [18]. In previous work, we used a patch-based method to segment the parotid glands using the NLM framework and a random forest classifier [8], [9]. We refined the initial segmentations based on image contours with Gaussian process regression. Sparse coding is a related extension of patch-based segmentation which was combined with the Haar-wavelet, histogram of oriented gradients and local binary patterns image features by [19]. In [20], three specific features (intensity, gradient, context) were evaluated for the segmentation of cardiac MR. To summarize, our approach is different from existing work by combining intensity, patches and location; by comparing a much larger number of different features; and by contrasting bounded search techniques with the explicit integration of location information. A preliminary version of this work was presented at a workshop [21] and has been substantially extended.

II. Method

A. Review of Non-Local Means Segmentation

Given an atlas 𝒜 = (ℐ, 𝒮) that contains images ℐ = {I₁, . . . , I_n} and their corresponding segmentations 𝒮 = {S₁, . . . , S_n} over a common image domain, our objective is to compute the segmentation S of a new image I. Patch-based methods are based on the rationale that locations with similar image content should have similar segmentations, where local image content is represented by the intensity values in a patch centered at each voxel. For a patch P(x) from the test image at a location x ∈ Ω and the collection of all patches in the training images ℘, we seek the closest patch P_atlas(x) in the training set

$$P_{\text{atlas}}(\mathbf{x})=arg\underset{P\in \mathcal{P}}{min}{\left|\right|P(\mathbf{x})-P\left|\right|}_2.$$ (1)

Associated with the image patch P_atlas(x) is the segmentation patch S_x, which is used to infer the segmentation S(x) in the test image around location x. Beyond the nearest neighbor $P_{\text{atlas}}(\mathbf{x})=P_{\text{atlas}}^1(\mathbf{x})$, we can identify a set of k-nearest neighbor patches from the atlas $P_{\text{atlas}}^1(\mathbf{x}),\dots ,P_{\text{atlas}}^k(\mathbf{x})$. Two methods of label propagation are commonly used: (1) point-wise (PW) estimation that only considers the center location of the patch S_x[x]; and (2) multi-point (MP) estimation [7] that considers the entire segmentation patch S_x. The label map L is computed under the two approaches as

$$L^{\text{PW}}(\mathbf{x})=\frac{{\sum }_{i=1}^{k}w(P(\mathbf{x}),P_{\text{atlas}}^i(\mathbf{x}))·S_{\mathbf{x}}^i[\mathbf{x}]}{{\sum }_{i=1}^{k}w(P(\mathbf{x}),P_{\text{atlas}}^i(\mathbf{x}))},$$ (2)

$$L^{\text{MP}}(\mathbf{x})=\frac{{\sum }_{\mathbf{y}\in {\mathcal{N}}_{\mathbf{x}}}{\sum }_{i=1}^{k}w(P(\mathbf{y}),P_{\text{atlas}}^i(\mathbf{y}))·S_{\mathbf{y}}^i[\mathbf{x}]}{{\sum }_{\mathbf{y}\in {\mathcal{N}}_{\mathbf{x}}}{\sum }_{i=1}^{k}w(P(\mathbf{y}),P_{\text{atlas}}^i(\mathbf{y}))},$$ (3)

where 𝒩_x is the patch neighborhood around x and S_y[x] is the label on the location x of the segmentation patch S_y centered at y. The weight w between patches is defined as

$$w(P,P^{\prime })=exp\left(-\frac{{\left|\right|P-P^{\prime }\left|\right|}_2^2}{2{\sigma }^2}\right),$$ (4)

where σ² is the variance of the intensity values estimated from the entire training set. We also consider an unweighted version of the label propagation with w ∝ 1. To obtain the segmentation S of the test image I, each voxel is assigned to the parotid glands or the background, depending on which of the labels receives the most votes.

B. Descriptor-Based Segmentation

We extend patch-based segmentation to descriptor-based segmentation by including image features and location information as descriptors of image content. Image features capture additional information about contours, gradients, and texture in the image. The specific features used in this work are described in Section III. We also include location information in the descriptor by adding the xyz-coordinates of the center voxel in the patch, where we assume a rough spatial alignment of the images. Outside of the head, the spatial normalization may be more challenging so that distances to anatomical landmarks may be suitable alternative for the location information. Location information imposes a soft spatial constraint on the nearest neighbor search. This bias is especially important when working with large search windows, as described in Section II-C. The descriptor vector D(x) is the concatenation of a patch P(x), an image feature F(x), and location information L(x)

$$D(\mathbf{x})=\left(\begin{array}{l}\frac{1}{{\sigma }_P·{\mid P(\mathbf{x})\mid }^{1/2}}P(\mathbf{x})\hfill \\ \frac{f^{1/2}}{{\sigma }_F·{\mid F(\mathbf{x})\mid }^{1/2}}F(\mathbf{x})\hfill \\ \frac{{\ell }^{1/2}}{{\sigma }_L·{\mid L(\mathbf{x})\mid }^{1/2}}L(\mathbf{x})\hfill \end{array}\right),$$ (5)

where f and ℓ are positive weights and each sub-vector is normalized by dividing by the square root of the number of entries | · |^1/2 and the corresponding standard deviation σ. These standard deviations are estimated for each sub-vector from the training set. The normalization ensures that the expected contributions of each descriptor type to the squared distances ${\left|\right|D-D^{\prime }\left|\right|}_2^2$ is independent of descriptor-specific magnitudes and depends only on the weights f and ℓ. The patch weight in Eq. (4) becomes a descriptor weight

$$w(D,D^{\prime })=exp\left(-\frac{{\left|\right|D-D^{\prime }\left|\right|}_2^2}{2(1+F+\ell )}\right),$$ (6)

where the denominator 2(1 + f + ℓ) normalizes the expected value of the exponent to −1. This can be seen by noting that if P and P′ are assumed to be independent then the expected value of ${\left|\right|P-P^{\prime }\left|\right|}_2^2$ is $2{\sigma }_P^2$; combining this with symmetric results for F and L gives that the expected value is −1. We use this updated definition of the weight for the label propagation in Eqs. (2) and (3) when working with patch descriptors.

Figure 1 presents an overview of the descriptor-based segmentation algorithm. In the first step, the patch intensity values P(x), image features F(x) and location information L(x) are extracted and combined to form the descriptor D(x) for each voxel x in both the training and test images. The segmentation patches S_x are extracted from the training images. In the second step, a search is performed over all training image descriptors to find k nearest neighbors to descriptors in the test image. In the third step, one of the label propagation methods in Eqs. (2) and (3) is used to segment the test image using the label information of the k nearest neighbors.

Fig. 1.

Overview of the descriptor-based segmentation algorithm: (1) descriptors consisting of patch intensity values, features and location information are extracted from the training and test images; labels are extracted from the training images; (2) a k-nearest neighbor (k-NN) search is performed over the descriptors from the training images for each descriptor from the test image; and (3) the labels of the nearest neighbors are used in label propagation to segment the test image. We compare the performance of a variety of features in (1), of bounded and approximate k-NN searches in (2), and of point-wise and multi-point label propagation methods in (3).

C. Nearest Neighbor Search

We evaluate two approaches to performing the k-nearest neighbor search in Eq. (1): a bounded and an approximate k-nearest neighbor search. The bounded nearest neighbor (BNN) method searches over all locations y within a cubic search window of side length r centered at $\mathbf{x}({\left|\right|\mathbf{y}-\mathbf{x}\left|\right|}_1<\frac{r}{2})$. This replicates the search method used by [6], [7], where the search is restricted to boxes of sizes between 9 × 9 × 9 and 15 × 15 × 15 voxels to reduce computation time. To achieve a similar behavior, we restrict the search window to 11×11×11 by setting r = 11.

A disadvantage of BNN is the hard spatial cutoff it imposes during search. Increasing the size of the search window rectifies the problem at additional cost of computational complexity. As a compromise, we consider an unbounded approximate nearest neighbor (ANN) search. We use the randomized kd-tree algorithm implemented in FLANN [22]. The kd-tree algorithm is a frequently used for ANN. While the method’s performance generally decreases on high-dimensional data, it has been shown that kd-trees perform well on high-dimensional data from image patches, likely due to strong correlations in images [22]. The randomized kd-tree algorithm splits data along a dimension randomly chosen among the dimensions of highest variance, rather than that of highest variance as in the classic kd-tree algorithm. Searching over multiple randomized kd-trees improves the performance of the algorithm. The randomized kd-tree algorithm commonly provides more than 95% of the correct neighbors and is two or more orders of magnitude faster than the exact search [22].

III. Image Features

In this section, we describe a large variety of features that we evaluate as candidates for the descriptor-based segmentation. Next to basic features, we include advanced features that are popular in computer vision. The features are illustrated in Figure 2. For most of the image features considered, we first process the entire image to produce a feature image and then extract a patch from the feature image. For example, in filtering the feature F(x) is the patch of the filtered image around x. The size of the patches for which F(x) is extracted varies according to the feature and is specified later in this section. The features F(x) are combined with the intensity patches P(x). We evaluate our method on intensity patch sizes ranging from 3×3×1 to 9×9×5 voxels, which includes patch sizes have been previously proposed for patch-based segmentation [3], [4], [6]–[9]. Small patch sizes yield localized features, which is desirable to support segmentation. But at the same time, small patches only provide few samples for the reliable estimation in the presence of noise. Consequently, the selection of the patch size is a trade-off and it is a priori not clear, which patch sizes are best suited for which feature. We state the used patch ranges in the following sections; the best patch sizes are listed in the section about optimal parameter settings. Next to isotropic patches, we particularly consider for larger patch sizes also anisotropic patches to account for the anisotropy of the voxels of head and neck CT scans.

Fig. 2.

Feature images computed from the intensity image shown in (a) with the corresponding manual segmentation (b). Mean, median, Gaussian, variance and standard deviation (STD) images are computed using 5 × 5 × 3 windows. Entropy is computed over 5 × 5 × 5 patches. Two different filter orientations are shown for Sobel and Haar; one orientation is shown for the Gabor wavelet. Two of the eight bins of histogram of oriented gradients (HoG) are shown along with the sum of all eight bins. Feature images for Laplacian filter, gradient magnitude features, multi-scale probability of boundary (mPb), and local binary patterns (LBP) and are also shown.

Multi-Scale Patches

Patch-based approaches contain limited spatial context information, leading to undesirable pairings in the nearest neighbor search. Extracting intensity values from larger patches increases the context considered but leads to higher memory consumption and computation times. Increasing the patch size also leads to a sharp decrease in the influence of voxels close to the center voxel on the distances ${\left|\right|D-D^{\prime }\left|\right|}_2^2$ relative to that of peripheral voxels. For example, using a 5 × 5 × 5 patch instead of a 3 × 3 × 3 patch results in more than a four-fold increase in the number of voxels, causing the added 98 outer voxels to dominate the distances ||D − D′||² in comparison to the original 27 inner voxels. Another natural approach to expanding the limited spatial context is to employ a multi-scale approach, creating a Gaussian pyramid and downsampling the images and segmentations. However, downsampling the segmentations is nontrivial along the boundary of the organ where downsampled voxels correspond to both organ and background in the original resolution of the image.

We introduce multi-scale patches that combine high resolution at their center and low resolution in the surrounding area (see figure on the right for a 2D illustration). In addition to the standard intensity patch P(x) in the center, we consider a 3 × 3 × 3 grid of blocks of the same size as P(x) centered at x. The multi-scale patch consists of P(x) and a summary statistic for each of the 27 blocks, which we take to be the mean intensity value. The multi-scale patch spatially covers a volume 27 times as large as the intensity patch while increasing the length of the descriptor D(x) by only 27 entries. Going back to our 2D example, the intensity patch P is a 3×3 patch and the feature F contains 9 mean values, each computed in a block of size 3×3. Since the resolution considered by the multi-scale patch decreases significantly outside of P(x), peripheral voxels in this region do not dominate the distances ${\left|\right|D-D^{\prime }\left|\right|}_2^2$. This design is motivated by the human visual system, where spatial acuity peaks at the central fovea and diminishes with distance. In this study, we consider only two scales; however, this feature has a natural extension to additional scale levels. We compute multi-scale patch features using intensity patch sizes from 3 × 3 × 1 to 9 × 9 × 5.

Filter-Based Features

A variety of image features can be obtained by filtering. We consider mean, median, Gaussian, variance, standard deviation (STD), Sobel [23], gradient magnitude (GradM), Laplacian and Gabor wavelet [24], [25] filter features. We extract features from neighborhoods of size 1×1×1, 3×3×3 and 5 × 5 × 5 from each of the filtered images.

The mean, median, Gaussian, variance and standard deviation filtered images are computed using masks of size 5×5×3 and 9×9×5. Of the feasible mask sizes, 5×5×3 best captures image characteristics around the parotid glands as shown in Figure 2. A mask size of 9 × 9 × 5 is also tested for comparison. The covariance matrix of the Gaussian filters applied is set to be a diagonal matrix with diagonal entries $\mathbf{m}=\frac{1}{32log2}·{[553]}^T$. This choice of covariance matrix ensures that the full width at half maximum is equal to half of the mask size. Variance and standard deviation images are computed using a uniform weighting over the mask.

Sobel image features are computed using two methods: (1) standard 2D Sobel kernel in the two planar orientations along each axial direction to produce six feature images; and (2) 3D Sobel kernel along each axial direction to produce three feature images. Gradient magnitude features are computed as the magnitude of the vector at each voxel consisting of three or six Sobel values, respectively. Laplacian features are computed by applying a 3D Laplacian filter of size 3 × 3 × 3. Gabor wavelet features are computed with 11×11×11 filters with bandwidth 4, ψ = 0 and λ = 2.5 in 16 directions (θ, ϕ) = (iπ/4, jπ/4) for i, j = 0, 1, 2, 3, yielding 16 feature images. These parameters setting were manually varied and determined to be reasonable given the image domain. As shown in Figure 2, filtering with these parameters captures effectively image characteristics around the parotid glands and in the remainder of the image domain.

Entropy Image

Entropy images have been first developed for multi-modal image registration [26]. The information content of a patch is measured with the Shannon entropy, which is computed and stored at the center voxel of the patch. Repeating this calculation for all voxels in the image yields the entropy image, which represents the structural information in the image. Entropy image features measure statistical dispersion in a similar way to variance filters and bear similarities to gradient magnitude features. However, unlike variance filters and many gradient features, the entropy image is independent of the magnitude of intensity values and intensity differences. The entropy image also faithfully captures the information in complex setups such as triple junctions. We compute the entropy of patches of size 5 × 5 × 5 and 9 × 9 × 5 voxels and while using 64 bins for density estimation. We extract patches of size 1, 3, and 5 from the entropy image as features.

Histogram of Oriented Gradients

To compute histogram of oriented gradients (HoG) features, we construct 3D image gradients in each patch of the image [27]. These gradients are used to produce a histogram over gradient orientations, where the contribution of each gradient to the histogram is equal to its magnitude. Gradients created from image noise therefore have a lower impact than strong gradients at image boundaries. The histograms produced have 8 bins corresponding to the 8 octants that the 3D vector can lie in. For applications in computer vision, gradient strengths are locally normalized to account for changes in illumination [27]. Since we work with CT scans, where intensities are measured in Hounsfield units, we do not apply such a normalization. We evalute the neighborhood size for histogram of gradients computation from 3×3×3 to 9 × 9 × 5.

Multi-scale Probability of Boundary

We compute the multi-scale probability of boundary (mPb) as defined in [28]. In the first step, we estimate image and texture gradients per slice with the oriented gradient signal. This method calculates the χ² distance between the histograms of two half-discs at each location for various orientations and at multiple scales. Textons are computed to quantify the texture by convolving the image with 17 Gaussian derivative and center-surround filters and by subsequently clustering with k-means into 64 classes [29]. Image and texture gradients of multiple scales are added to yield the multi-scale probability of boundary. Features are extracted in 1 × 1 × 1, 3 × 3 × 3 and 5 × 5 × 5 neighborhood from the mPb image.

Local Binary Patterns

Local binary patterns (LBP) [30] measure the co-occurence relations between a voxel and its neighbors, encoding these relations into a binary word and quantifying the texture in a local region. LBP is primarily used for 2D images. We work with a 2D implementation applied on all xy, xz and yz planar slices¹ in the volume. The concurrence statistics for these three planes are concatenated. Features are extracted from 1×1×1, 3×3×3 and 5×5×5 patches of the feature image computed using 3 × 3 and 5 × 5 LBP masks.

Haar-like Features

Haar-like features [31] are computed by considering adjacent rectangular regions at a specific location in a detection window, summing the pixel intensities in each region and evaluating the difference between these sums. The key advantage of Haar-like features over most other features is their low computation time. Integral images enable rapid feature calculation at many scales. Haar-like features bear a certain similarity to Haar basis functions but also consider patterns that are more complex than Haar filters. Haar-like features are computed using 106 2D integral kernels approximating horizontal and vertical derivatives, second order partial derivatives and Gaussian second order partial derivatives. Since 106 filtered images are created in this step, we extract voxels rather than patches from each of the filtered images to be part of the descriptor.

IV. Experiments

We evaluate each of the methods described in Section II and each of the features introduced in Section III on a dataset of 18 CT scans of patients with head and neck cancer. Each image was labeled by a trained anatomist for treatment planning. The images contain between 80 and 200 axial slices with a slice thickness of 2.5mm. We resampled all 18 images to the same in-plane resolution, since we compare voxels and they should represent the same physical space. The in-plane resolution selected was the most commonly encountered in-plane spacing, which was 0.976mm. In case of substantial variations in image resolution, which was not the case on our image corpus, more attention has to be paid to the re-sampling, where particularly up-sampling is not advised. All images have the left parotid labeled. The right parotid gland was consumed by a tumor in one patient. Three of the 18 patients have dental artifacts that modify the image intensity values in regions around the parotid glands. We segment the left and right parotid glands in each image in a leave-one-out procedure, using the remaining 17 subjects as training images. To limit the number of patches, we only consider every other patch in the training set in a way similar to [7]. We measure segmentation quality by calculating the Dice volume overlap score [32] and modified Hausdorff distance [33] between the automatic and manual segmentations. We identify a bounding box around the parotid glands by template matching the mandible bone, which is adjacent to the parotid glands. This bounding box acts as the common image domain Ω used by the segmentation method as described in Section II-A.

Below is an outline of our experiments in the following sections.

IV-A.	Comparison of point-wise and multi-point methods in combination with location information
IV-B.	Comparison of bounded and approximate nearest neighbor search in combination with entropy features
IV-C.	Evaluation of descriptor composition (intensity, location, feature) for varying patch and multipoint sizes
IV-D.	Comparison of 15 features in combination with intensities and location
IV-E.	Evaluation of optimal feature parameters
IV-F.	Evaluation of the multi-scale patch

In the experiments, we use the following settings if not specified otherwise: 9 × 9 × 5 patches and k = 10 nearest neighbors. To perform the approximate nearest neighbor search, we employ the kd-tree algorithm with 8 trees and 64 checks, specifying that at most 64 leaves can be visited in a single search. We threshold the image at −100 and 150 Hounsfield units, which roughly corresponds to the range of intensity values in the parotid glands, to lessen the effects of dental artifacts and image noise on the computed distances between descriptors. Images are thresholded before feature extraction.

A. Evaluation of Location and Label Propagation Methods

In this section, we evaluate the inclusion of location information in the descriptor and compare point-wise (PW) and multi-point (MP) label propagation methods. We also compare the weighted and unweighted variants of the multi-point method. Figure 3 reports the segmentation results for these methods applied to the left parotid gland, results for the right parotid are shown in the supplementary material. We use paired t-tests to evaluate the statistical significance of the differences between the results for each of the methods. We observe a significant improvement using multi-point label propagation over point-wise label propagation, which is consistent with the results in [7]. We further observe a significant improvement when including location information (Loc) in the descriptor with both point-wise and multi-point label propagation methods. Figure 3 shows that there is no significant difference between the segmentation results obtained using the unweighted and weighted variants of multi-point label propagation. We apply the unweighted multi-point variant in the remainder of our experiments, since it involves a simpler voting scheme.

Fig. 3.

Comparison of Dice volume overlap and modified Hausdorff distances for pointwise (PW), weighted multipoint (W-MP), unweighted multipoint (U-MP) and the inclusion of location information (+Loc) for the left parotid gland. The red line indicates the median, the boxes extend to the 25th and 75th percentiles, and the whiskers reach the most extreme values not considered outliers (red crosses). *, ** and *** indicate statistical significance levels of 0.05, 0.01 and 0.001, respectively.

As shown in Figure 3, there are three outlier Dice scores in the results of the point-wise and multi-point labeling for the left parotid. These outliers correspond to patients with dental artifacts. Figure 4 provides a visualization of qualitative segmentation results for one of the subjects with dental artifacts together with the corresponding Dice scores. The input CT slice demonstrates the strong impact of the dental artifact on the image. Including location information yields a clear improvement in the generated segmentation as illustrated by Figure 4 and the Dice increase by about 0.7. In this case, location information spatially regulates the segmentation, discouraging the selection of patches from distant locations in the training images, which have a similar intensity profile but correspond to a different anatomical structure. Furthermore, the multi-point method smoothes the generated segmentation along the boundary of the parotid gland and yields a single connected component. Based on the results in this section, we apply the unweighted multi-point label propagation method with location information in all further experiments.

Fig. 4.

Comparison of segmentation results for left parotid gland in a patient with dental artifacts and corresponding Dice scores. We evaluated (a) multi-point with location (MP+Loc), (b) point-wise with location (PW+Loc), (d) multi-point (MP) and (e) point-wise (PW). The expert segmentation is shown in (c). The CT slice in (f) illustrates the strong impact of the dental artifact.

B. Evaluation of Nearest Neighbor Methods

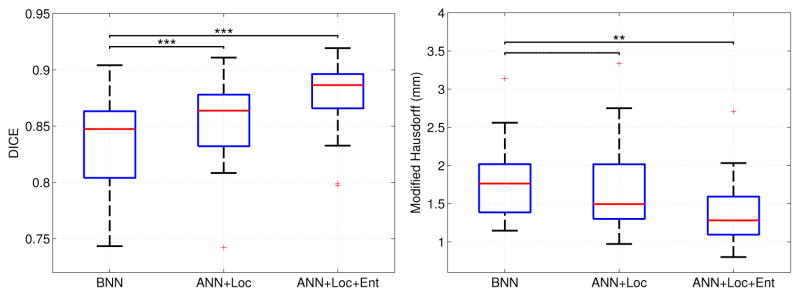
In this section, we compare the segmentation results obtained by applying the bounded k-nearest neighbor search (BNN), which restricts to a 11 × 11 × 11 search window, and the approximate k-nearest neighbor search with location information (ANN+Loc). We also evaluate the inclusion of features in the descriptor by adding entropy features, which we find in Section IV-D are the optimal image features for this task, to the comparison using the approximate search with location information (ANN+Loc+Ent). Figure 5 reports the segmentation results for these three methods. As shown, there is an improvement in both Dice scores and modified Hausdorff distances on applying ANN with location over BNN. Paired t-tests show that there is a significant improvement in Dice scores when using ANN with location. Adding entropy image features to the descriptor further improves the Dice scores and Hausdorff distances over BNN. This suggests that entropy image features significantly improve the quality of the generated segmentation along its boundary. In both cases, the proposed methods yield significant improvements over the traditional bounded search.

Fig. 5.

Comparison of Dice volume overlap and modified Hausdorff distances on the left parotid when using bounded nearest neighbor (BNN), approximate nearest neighbor with location information (ANN+Loc) and approximate nearest neighbor with location information and entropy image features (ANN+Loc+Ent). The red line indicates the median, the boxes extend to the 25th and 75th percentiles, and the whiskers reach the most extreme values not considered outliers (red crosses). *, ** and *** indicate significance levels at 0.05, 0.01 and 0.001, respectively.

To further examine the improvement of ANN with location information over BNN, we compare the spatial distances between the nearest neighbors selected by the two methods. About one fourth of the nearest neighbors found using ANN with location information are outside the 11 × 11 × 11 search window of BNN. This implies that BNN excludes a substantial fraction of the nearest neighbors found using ANN with location. Since ANN with location significantly outperforms BNN, this supports the argument made in Section I that the hard cutoff imposed by the restricted search window in BNN leads to less accurate segmentations than the soft bias imposed by location information on using ANN. Note that the additional effect of the location information in favoring more central patches within the search window is not covered by this analysis.

C. Descriptor Composition

While Section IV-A highlighted the importance of including location information in the descriptor, it is unclear whether using only image features or image features in combination with intensity patches leads to the best performance. In this section, we evaluate these different compositions of the descriptor and the influence of the size of the intensity patch and the size of the multi-point neighborhood. We use entropy images as a representative feature in this evaluation.

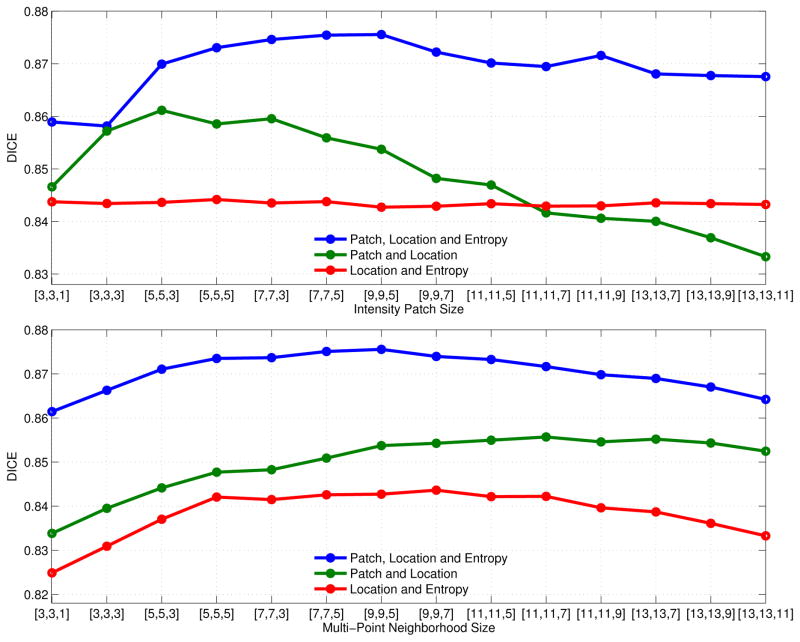
Figure 6 reports segmentation results for each of the three compositions of the descriptor that include location information: (1) patch intensity values, location information and entropy image features; (2) patch intensity values and location information; and (3) location information and entropy image features. We plot the resulting mean Dice scores while varying (a) the size of the intensity patch P(x); and (b) the size of the neighborhood 𝒩_x used in multi-point label propagation as described in Section II-A. In the first plot, the size of patch P(x) varies while the size of 𝒩_x is held constant at 9 × 9 × 5, and in the second plot, the size of 𝒩_x varies while the size of P(x) is held constant at 9 × 9 × 5. The experiments depicted in Figure 6 decouple the sizes of the intensity patch P(x) and neighborhood 𝒩_x, which are typically taken to be equal [7]. We observe that the best results are achieved with smaller intensity patches of 5 × 5 × 3 to 7 × 7 × 3 voxels. In contrast, comparatively larger neighborhoods of 11 × 11 × 7 and 13×13×7 voxels are required to maximize segmentation accuracy. As discussed in Section III, peripheral voxels tend to dominate the distances ||D − D′||₂ used by ANN as the patch size increases, potentially leading to less desirable matches. This effect may explain the less accurate segmentations observed at larger patch sizes. Selecting larger multi-point neighborhood sizes transfers larger local patterns from the training to the test image. The increased regularization imposed by summing over larger neighborhoods 𝒩_x in Eq.(3) may be the reason for the improved segmentation results – it causes the generated segmentations to account for the presence of strong spatial correlations in CT scans of the parotid glands.

Fig. 6.

Mean Dice volume overlap for segmentations of the left parotid such that the descriptor contains: (1) patch intensity values, location information and entropy image features; (2) patch intensity values and location information; and (3) location information and entropy image features. The first sub-figure plots the mean Dice scores for each of these three compositions against different sizes of the intensity patch P(x). The second sub-figure plots these Dice scores against different sizes of the multi-point label propagation neighborhood 𝒩_x. The size that is not varied is set to 9 × 9 × 5. Note that the intensity patch size has no influence on the entropy features, yielding a constant curve with slight variations only to the randomness of the ANN search.

Figure 6 also implies that patch intensities with location generally improve over entropy image features with location while the combination of all three consistently yields the best segmentation results. The results for patch intensities and location falls below that of entropy and location for patch sizes above 11 × 11 × 5. Because entropy image features are independent of patch size, the mean Dice scores shown in the first subplot in Figure 6 are approximately constant, with slight variation caused by the randomness of the ANN search. Furthermore, the combination of patch intensity values, entropy features and location does not exhibit the previously described preference for small patch and large neighborhood sizes. Instead, this combination achieves its best performance at medium neighborhood and patch sizes of 9 × 9 × 5 voxels. Based on these results, we use intensity patch and multi-point neighborhood sizes of 9 × 9 × 5 voxels when evaluating other image features below.

D. Comparison of Features

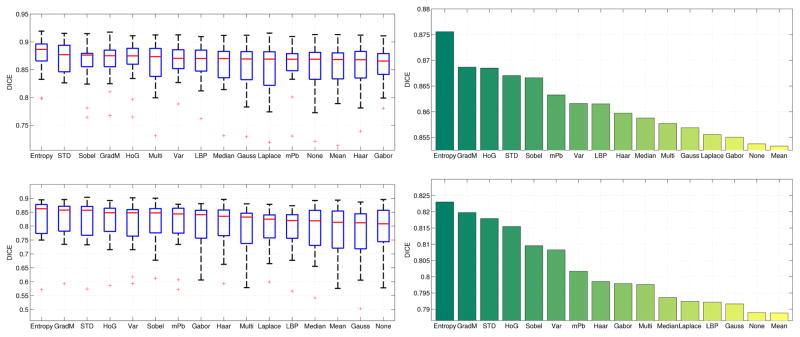
In this section, we present the results of an empirical study that seeks optimal feature selection. As motivated in the previous sections, we apply the unweighted multipoint method for label propagation and use approximate neighbor search. Further, based on the results of section IV-C, we use features in combination with intensity and location information. The presented results in this section are therefore not for using the feature in isolation, but always in combination with intensities and location. Figure 7 compares the segmentation results for the left and right parotid glands achieved using each of the features described in Section III to compute the descriptor D(x). For both parotid glands, entropy image features perform considerably better than any other image features. The next three highest performing features are gradient magnitude, histogram of oriented gradients and standard deviation for both the left and right parotid glands. These features are followed by Sobel, multi-scale probability of boundary and variance image features. The only feature that performs slightly worse than including no additional image features in the descriptor is the mean image. Details on the parameters for each image feature are listed in the supplementary material.

Fig. 7.

Comparison of Dice scores for the left and right parotid glands by feature. The top two plots show results for the left parotid gland; the bottom two plots show results for the right parotid gland. In the box-and-whisker diagrams, the red line indicates the median, the boxes extend to the 25th and 75th percentiles, and the whiskers reach the most extreme values not considered outliers (red crosses). The bar plots show the mean Dice scores obtained by each feature. Features in the plots are ordered by median Dice and mean Dice, respectively. Note that different scales on the y-axis are used in these plots.

A major difference between the results for the left and right parotid glands is that local binary patterns is one of medium performing features for the left parotid but one of the worst performing features for the right parotid, dropping from 8th to 13th place in relative feature rankings. Gabor wavelet image features exhibit a similar decrease in relative feature rankings from the right to left parotid glands, from 9th to 14th place. Other than these differences, the relative order of the performances of each feature is fairly consistent from the left to right parotid glands. The best performing features measure contours in the image (entropy, gradient magnitude, HoG, STD, Sobel, mPb and variance). It seems reasonable that adding contour information to the descriptor improves performance since this captures the change from foreground to background in patches. Instead of only matching patches that have an overall similar appearance, adding gradient-based features ensures that the matched patches contain similar contours. In contrast, smoothing filter features such as mean, median, or Gauss features provide less information complementary to the intensity patch and do not yield a large improvement over patch intensity values alone.

E. Optimal Feature Parameters

This section discusses the optimal weights f and ℓ for each feature and the optimal feature-specific parameters and implementations outlined in Section III. The weights f and ℓ determine the influence of the feature and location component in the descriptor, cf. Eq. (5). Table I reports the range of feature weights f and location weights ℓ that achieved the mean Dice scores within 0.002 of the highest mean Dice for each feature in the results for the left parotid and within 0.003 of the highest mean Dice in the results for the right parotid. Different thresholds were chosen to account for the difference in the ranges of mean Dice scores for the left and right parotids. We evaluated weights f and ℓ in the range from 0.01 to 5.0. As shown in the table, the optimal location weights ℓ were between 0.2 and 1.0. The optimal feature weights f varied significantly between different features. The features with the highest segmentation accuracy such as entropy image features and gradient image features generally performed well with higher feature weights. The features with the lowest segmentation accuracy yielded similar Dice scores with both low feature weights of at most 0.1 and high feature weights of at least 1.0. Features such as the mean image exhibited this trend, which may reflect the limited additional discriminative ability conferred by smoothed intensity values over patch intensity values alone.

Table I.

Mean Dice and ranges of optimal feature weights f and location weights ℓ for each feature for the left parotid.

Left Parotid
Feature	Entropy	Grad	HoG	STD	Sobel	mPb	Var	LBP	Haar	Median	Multi	Gauss	Laplace	Gabor	None	Mean
Mean Dice	0.8756	0.8687	0.8685	0.8670	0.8666	0.8633	0.8616	0.8615	0.8597	0.8588	0.8577	0.8569	0.8563	0.8556	0.8537	0.8533
Optimal f	1.0–2.0	0.2–0.5	0.05–0.2	0.05–0.5	0.5–2.0	0.2–0.5	0.05–0.2	0.2–0.2	0.2–5.0	1.0–5.0	0.05–0.2	1.0–5.0	0.01–1.0	0.01–1.0	NA	0.01–2.0
Optimal ℓ	0.2–0.4	0.2–1.0	0.2–1.0	0.2–0.9	0.6–2.0	0.3–0.6	0.2–0.9	0.2–0.8	0.4–5.0	0.6–1.0	0.3–1.0	0.4–1.0	0.2–0.6	0.2–0.4	0.2–0.6	0.2–1.0

The optimal composition of the descriptor is patch intensity values, location information and entropy image features. The patch sizes should be selected between 7×7×3 and 9×9×5; the location weights between ℓ = 0.3 and ℓ = 0.6; and the feature weights between f = 1.0 and f = 2.0. Segmenting a single test subject using the other 17 image-segmentation pairs as an atlas ran in about three minutes in Matlab. We believe that further optimization could improve this runtime considerably.

F. Multi-Scale Patch

As shown in Figure 6, more accurate segmentation results are generally obtained when the multi-point neighborhood size 𝒩_x exceeds the size of the intensity patch. However, using a larger multi-point neighborhood size causes voxels outside the patch size, which were not considered in computing the distances, to be used for label propagation. This effect can lead to poor pairings in the ANN search that could have been avoided by considering additional context within the image. The multi-scale patch overcomes this issue by considering additional context while using a smaller core set of patch intensity values. Figure 8 shows the improvement on using (1) multi-scale patch intensity values and location information over (2) patch intensity values and location information. In (1), the multi-point neighborhood size is set equal to the total extent of the multi-scale patch, which is three times the intensity patch size along each dimension. For instance, a patch size of 7 × 7 × 3 yields to a multi-scale patch that covers a region of 21 × 21 × 9 voxels, which is also multi-point size. In (2), the multi-point neighborhood size is set equal to the patch size. The multi-scale patch presents an interesting new patch design that provides wider context without having peripheral voxels dominate distances computed in the nearest neighbor search. In this study, we compute mean intensity values as summary statistics in generating the multi-scale patch. A future research direction is to instead generate the multi-scale patch with image features other than intensity values and to consider a summary statistic different from the mean.

Fig. 8.

Comparison of mean Dice overlap scores for segmentations of the left parotid such that the descriptor contains: (1) multi-scale patch intensity values and location information; and (2) patch intensity values and location information. The differences are not statistically significant. The multi-point neighborhood size is set equal to the total extent of the multi-scale patch, which is three times the intensity patch size along each dimension, in (1). The multi-point neighborhood size is set equal to the patch size in (2).

V. Discussion

Our results indicate that including patch intensity values, location information, and image features in the descriptor yields the highest segmentation accuracy. The first conclusion that can be drawn from our results is the importance of location information. As mentioned in Section I, including location information in the descriptor diverges from the location-independent comparisons used in non-local means [10]. However, the high performance of non-local means segmentation methods [6], [7] can be attributed to the implicit inclusion of location as a descriptor by restricting the search to small local windows. Our results demonstrate that the explicit integration of location information into the descriptor yields better segmentation results than the hard spatial cutoff imposed by small search windows. This effect results from the potential to simultaneously select distant patches as nearest neighbors and impose spatial constraints on the nearest neighbor search. This additional flexibility is important when segmenting structures with large shape variations in the training set and when the initial alignment is of limited accuracy. In our method, the location weight parameter permits direct control over the influence of location information on the distances used in the ANN search. The spatial regularization imposed by location is especially important when the training set or test image contains image distortions that lead to the propagation of incorrect labels when considering image information only. In the segmentation of parotid glands, this effect is most commonly seen in segmenting images of patients with dental implants, which can create strong artifacts in the image.

Our second conclusion is that features improve the performance of intensity values. Other than at very large patch sizes, including only image features in the descriptor leads to worse segmentation results than those obtained using only patch intensity values. Features should therefore not replace patch intensities but rather augment them with additional information in order to obtain more accurate segmentations. From this perspective, features that provide information complementary to patch intensities can be expected to yield the best results. The high Dice scores achieved by entropy, HoG, and Sobel image features suggest that image gradients and contours provide complementary information to patch intensities for the purpose of image segmentation. In contrast, smoothing filters do not add much additional information to the patch description of an image.

A general note for non-local means segmentation is that a rough initial alignment of the structures of interest is required. Otherwise the definition of local search windows is not meaningful. Similarly for our descriptor-based approach, we need rough correspondences between images to obtain comparable location information. For domains where it is complicated to obtain an alignment of the structures of interest with affine registration the segmentation with non-local means techniques is challenging. Our proposed approach is likely to offer advantages in such situations because we do not work with a hard cut-off but instead use a soft spatial prior in combination with larger search windows.

Our results compare positively to the approach presented in [15], which combines label fusion with statistical appearance models and geodesic active contours. On the same dataset, a mean dice of 0.84 was reported for the left parotid and 0.81 for right parotid. Comparing to the results presented in Fig. 7, we see that all features for the left parotid are above 0.84 dice, with the best performing entropy features resulting in a dice of 0.875. For the right parotid gland, entropy features result in a dice of 0.823. The reported run-time in [15] is 15 minutes per subject, where our presented method runs in about 3 minutes. These results highlight the large potential of descriptor-based segmentation.

VI. Conclusions

We introduced a generalization of non-local means segmentation by moving from comparing patches to descriptors. The proposed descriptor consists of patch intensity values, location information and image features. We investigated larger search windows than previous studies that employed non-local means, enabled by an efficient nearest neighbor search. In an extensive comparison of features for segmentation, we found the best performance for entropy image features, which have not yet been used for patch-based segmentation. Taken together, our analysis did not only provide new insights into NLM-based segmentation but also demonstrated the importance of including location and features.