NEUTRON RADIOGRAPHY MEASUREMENT OF SALT SOLUTION ABSORPTION IN MORTAR

Abstract

Some concrete pavements in the US have recently exhibited premature joint deterioration. It is hypothesized that one component of this damage can be attributed to a reaction that occurs when salt-laden water is absorbed in the concrete and reacts with the matrix. This study examines the absorption of CaCl₂ solution in mortar via neutron imaging.

Mortar specimens were prepared with water to cement ratios, (w/c), of 0.36, 0.42 and 0.50 by mass and exposed to chloride solutions with concentrations ranging from 0 % to 29.8 % by mass. Depth of fluid penetration and moisture content along the specimen length were determined for 96 h after exposure. At high salt concentration (29.8 %), the sorption rate decreased by over 80 % in all samples. Along with changes in surface tension and viscosity, CaCl₂ reacts with the cement paste to produce products (Friedel’s salt, Kuzel’s salt, or calcium oxychloride) that block pores and reduce absorption.

INTRODUCTION

Concrete pavements represent a large portion of the transportation infrastructure. While many of these pavements provide excellent long-term performance, some pavements, particularly in the northern region of the US, have recently exhibited premature joint deterioration. This damage can shorten the life of an otherwise well-functioning pavement or can necessitate costly repairs. Recently, studies have been conducted to examine causes, early detection, and mitigation of joint deterioration [1]–[6].

Other research has focused on the development of approaches to predict how long freeze-thaw damage will take to occur. These models use fluid absorption to aid in the determination of the degree of saturation [7]. The degree of saturation influences the freeze-thaw performance of concrete [8], [9]. The addition of salts to the pore fluid can increase the degree of saturation due to the higher equilibrium relative humidity of the solution [10], [11]. The addition of salts will alter properties of the fluid such as surface tension and viscosity, therefore altering the transport properties such as absorption. The fluid viscosity and surface tension both increase with an increase in concentration of salts, but the viscosity more so than the surface tension, which will decrease the rate of absorption. Furthermore, salt can also precipitate out of solution and block pores, preventing further fluid ingress and increasing the local degree of saturation [12].

In many cold climates, salt solutions are used on concrete roads and sidewalks to minimize the formation of ice by lowering the freezing temperature of the solution. However, calcium chloride (CaCl₂) can react with the calcium aluminate phases (C₃A) of cement clinker or monosulfate (Afm) to create Friedel’s salt [13], [14]. The calcium sulfo-aluminate phases (Afm and ettringite) can further react with chloride-based salts to form Kuzel’s salt [15]. Additionally, calcium chloride can react with calcium hydroxide to form calcium oxychloride at room temperature (Equation 1). All three products can precipitate and grow in the voids, reducing fluid ingress, as well as reducing the volume of empty pores, thereby increasing the local degree of saturation.

$$3\text{Ca}{(\text{OH})}_2+{\text{CaCl}}_2+12{\mathrm{H}}_2\mathrm{O}\to 3\text{Ca}{(\text{OH})}_2·{\text{CaCl}}_2·12{\mathrm{H}}_2\mathrm{O}$$ Equation 1

A standardized test method for quantifying absorption of water in concrete is ASTM C1585 [16]. This test was developed for water and does not provide corrections for fluids with viscosities and surface tensions that differ from those of deionized water. Additionally, the absorption behavior is influenced by the initial conditioning [17]. According to the standard, the absorption, I (mm³/mm² [in³/in²]), can be computed as shown in Equation 2:

$$I=\frac{m_t}{a·\rho }$$ Equation 2

where m_t is the change in specimen mass (g [lb]) at the time t after exposure to the fluid, a is the exposed surface area of the specimen (mm² [in²]) and ρ is the density of water (g/mm³ [lb/in³]). Additionally, ASTM C1585 instructs users to plot the results of the test as mm³ [in³] of water absorbed normalized by the surface area of the specimen in mm² [in²] versus the square root of time. This calculation provides a result in units of mm [in] that many mistakenly interpret as the depth of water ingress. However, the test does not account for the total pore volume, which can affect the interpretation of the results.

The initial rate of absorption, or sorptivity as defined by ASTM C1585, S_i (mm/s^1/2 [in/s^1/2]) is the slope of the absorption versus the square root of time up to 6 h. The secondary sorptivity, S_s (mm/s^1/2 [in/s^1/2]) is the slope of the absorption versus the square root of time achieved between 1 d and 7 d. However it should be noted that these times are dependent on the sample height and fluid properties, both of which are specified in the ASTM C1585 test method [11], [18], [19].

While Equation 2 is used for absorption and the ASTM method for determining S_i and S_s are useful for qualifying the absorption behavior of concrete, it may not be representative of the actual depth of penetration into the specimen. The rate at which the fluid travels is dependent on the fluid properties (such as surface tension, viscosity and density) and the volume of pores, as well as their connectivity in the paste [18], [20]–[22]. To overcome this shortcoming, some have used the intrinsic absorption as defined in Equation 3 [19].

$$I_{int}=\frac{m_t}{a·\rho ·\mathrm{\Phi }·(1-D_0)}·\sqrt{\frac{{\gamma }_w{\eta }_s}{{\gamma }_s{\eta }_w}}$$ Equation 3

where I_int (mm [in]) is the intrinsic absorption, Φ is the volume fraction of porosity, D₀ is the volume fraction of the initial degree of saturation, η_w and η_s are the viscosities of water and solution (mN•s/m² [lbf-s/in²]), respectively; and γ_w and γ_s are the surface tensions of water and solution (mN/m [lbf/in]), respectively. The quantity under the square root represents the theoretical influence of fluid surface tension and viscosity on the absorption.

Neutron imaging is an accurate and powerful method of monitoring fluid penetration in porous media and has been used by many researchers to study fluid permeation in concrete [23]–[25]. The gray level of a pixel in a radiograph is proportional to the number of neutrons that made it through the object. Hydrogen has a large neutron attenuation coefficient, meaning materials rich in hydrogen appear dark in images. This nondestructive test method can be used to monitor the actual depth of fluid penetration continuously for long periods of time. The volume of water in the system can be accurately quantified, in addition to the ability to visually monitor fluid movement in situ [26]–[28]. This allows for the calculation of the degree of saturation in the system which is directly related to long term performance, particularly during exposure to freeze-thaw cycles.

RESEARCH SIGNIFICANCE

One approach to achieving sustainable concrete construction is to increase its service life and minimize the need for costly repairs. The deterioration of joints in pavements is one example where foundational efforts are needed to better understand the contributing phenomena and to develop functional approaches to reducing damage and cracking. This experimental study investigates the fundamental transport of calcium chloride solutions into mortar, permitting a quantitative description of the saturation (and salt) profile of the exposed specimen. Understanding how these salts penetrate into and react with the concrete will promote the development of mitigation strategies to effectively reduce and perhaps one day eliminate premature joint deterioration.

EXPERIMENTAL INVESTIGATION

Sample Preparation

Mortar specimens were mixed in accordance with ASTM C192/C192M-13 using the mixture proportions in Table 1. All materials were weighed to the nearest 0.01 g [0.00002 lb]. Both ASTM C150 Type I and Type V cements were used in this study. The composition of each cement is listed in Table 2. It is expected that mortars made using Type V cement will produce less Friedel’s and Kuzel’s salts when exposed to CaCl₂ due to their lower amount of aluminates (C₃A), although these compounds may still form due to the increased presence of C₄AF [13], [29].

Table 1.

Mixture proportions for the four mortars used in absorption experiments

Mix ID	Type I Cement, kg/m3 (lb/yd3)	Type V Cement, kg/m3 (lb/yd3)	Water, kg/m3 (lb/yd3)	Fine Aggregate (SSD), kg/m3 (lb/yd3)	w/c
1	632.62 (1066.3)	--	227.74 (383.86)	1363.11 (2297.59)	0.36
2	581.01 (979.32)	--	244.02 (411.31)	1368.34 (2306.41)	0.42
3	524.01 (883.24)	--	262.01 (441.63)	1363.11 (2297.59)	0.50
4	--	581.01 (979.32)	244.02 (411.31)	1363.11 (2297.59)	0.42

Table 2.

Chemical and physical properties of ordinary Portland cement

	Percent by Mass (%)
Component	Type I	Type V
SiO2	19.3	21.3
Al2O3	5.2	2.6
Fe2O3	2.9	4.2
CaO	64.0	63.2
MgO	2.6	4.5
SO3	3.3	2.8
C3S	63.4	64.0
C2S	8.4	13.1
C3A	9.0	0.0
C4AF	8.7	12.8
Blaine Fineness [cm2/g]	3680	3160
(in2/lb)	(259000)	(222000)

The mortar was cast in prism molds with nominal dimensions of 76.2 mm by 101.6 mm by 406.4 mm [3 in by 4 in by 16 in]. After setting, the mortar prisms were removed from their molds, sealed, and kept at 23 °C ± 1 °C [73.4 °F ± 1.8 °F] until they reached 60 % hydration. The curing time to reach the desired degree of hydration was estimated using isothermal calorimetry. The time to reach 60 % hydration was 27 d, 78 h, 55 h, and 21 d for mixtures 1 through 4, respectively. The mortar prism was cut with a wet saw to 76.2 mm [3 in] wide by 50 mm ± 1.1 mm [2.0 in ± 0.04 in] high by 20 mm ± 1.2 mm [0.79 in ± 0.05 in] thick slices. Since the field of view of the neutron camera (75 mm [2.95 in]) was smaller than the nominal width of the specimen, the width of individual specimens was not measured. The cut specimens were then placed in a chamber at 23 °C [73.4 °F] and 50 % relative humidity (RH) for 1 month. Equilibrium was determined when the change in mass was less than 0.02 % for a 15 d period [17]. Four sides of the specimens were then wrapped in aluminum tape to prevent moisture loss. The top and bottom surfaces of the 50 mm [2.0 in] high specimens were subsequently exposed for absorption tests.

Additional 76.2 mm wide by 50 mm high by 20 mm [3 in by 2.0 in by 0.79 in] samples of each mixture were oven dried and vacuum saturated to 100 % degree of saturation. A group of additional mortar specimens with a w/c of 0.42 and Type I ordinary Portland cement (OPC) were conditioned differently in order to compare the degree of saturation as determined from neutron images and by mass measurements. Samples were conditioned to degrees of saturation between 30 % and 90 % by saturating samples and letting them dry in air for various amounts of time. One sample for each degree of saturation shown in Figure 1b was prepared. Once dried to the desired moisture content (mass), each sample was rewrapped in aluminum tape and allowed to re-equilibrate for at least 24 h.

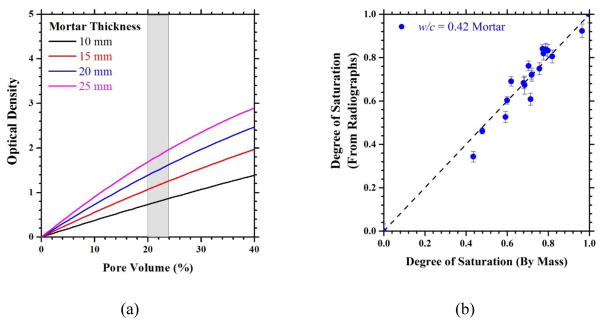
Fig. 1.

(a) Influence of mortar thickness on optical density. The shaded region is the total porosity of the four mortar samples used. (b) Relationship between the degrees of saturation as determined by neutron radiographs and by mass measurements. Error bars indicate +/− one standard deviation in the experimental measurements.

Calcium chloride solutions were prepared as percent of CaCl₂ to water by mass. Solutions ranging from 0 % (deionized water) to 29.8 %, the eutectic concentration of calcium chloride and water, were used for this study in order to include the spectrum of concentrations that may be seen in pavements in the field. The fluid properties of each solution are summarized in Table 3 [11], [30]. The viscosity of the solution increases by a factor of 3.3, while the surface tension only increases by a factor of 1.13 over the full range of concentrations investigated in the present study. The sorptivity of a fluid is proportional to the square root of the ratio of the surface tension to the viscosity [20], so the relatively larger increase in viscosity will result in an overall decrease in sorptivity.

Table 3.

Fluid properties at 25 °C for concentrations of CaCl₂ solutions used in this study [11], [30].

CaCl2 Concentration (% by mass)	Density, kg/m3 (lb/ft3)	Viscosity via rheometer, mN·s/m2 (10−7 lbf-s/in2)	Surface Tension via Du Noüy tensiometer, mN/m (10−4 lbf/in)	Theoretical Normalized Sorptivity
0	997 (62.2)	0.905 (1.13)	72.8 (4.16)	1.00
10	1087 (67.86)	1.045 (1.52)	75.02 (4.28)	0.94
20	1189 (74.23)	1.675 (2.43)	79.47 (4.54)	0.77
29.8	1291 (80.59)	2.975 (4.31)	85.88 (4.90)	0.60

Neutron Imaging

Imaging was performed at the Neutron Imaging Facility at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR) in Gaithersburg, Maryland. The imaging facility is located at Beam Tube 2 as shown in Figure 2. The thermal neutron source is a 20 MW [18969 Btu/s] heavy-water fission reactor operated at 37 °C [98.6 °F]. A collimation ratio (L/D) of 450 and a neutron fluence rate of 1.4 x 10⁷ cm⁻¹s⁻¹ [3.55 x 10⁷ in⁻¹s⁻¹] were used for the sorption experiments. A scientific complimentary oxide semiconductor (sCMOS) camera viewed a gadolinium oxysulfide scintillator through a Nikon^* 85 mm f/1.8 lens with a PK-11a extension tube to create a neutron detector with an effective pixel pitch of 30 μm [3.94 x 10⁻⁵ in].

Fig. 2.

Plan view of the Neutron Imaging Facility at NIST

The experiment was set up such that five samples could be imaged in each test series. The samples were placed on a motorized table so that they could be repositioned in the beam line without the beam being turned off, as shown in Figure 3. Nine images of each sample were taken with an exposure time of 60 s to serve as reference images of the specimen at 50 % RH before being exposed to the chloride solutions. Nine images of similar geometry samples cut from the same prism in the oven dried and fully saturated conditions were also taken to determine the degree of saturation during absorption.

Fig. 3.

Experimental set up for chloride ponding tests.

After the reference images were captured, fluid ingress could be measured. The ponding reservoirs on top of the samples were filled with approximately 30 mL [1.0 fl. oz. (US)] of solution and the mortar began absorbing the fluid. Three images were captured of each sample before the stage moved to the next position to image the next sample. Including the time to move the table to each position, approximately 30 min elapsed between each set of images per specimen.

Image Processing and Analysis

Images were combined with a median filter in groups of 9 for the reference images or 3 for images taken during absorption. 30 flat field (open beam) and dark (closed beam) images were also taken and combined with a median filter. The use of a median filter (in time) eliminated the appearance of streaks due to gamma rays and fast neutrons depositing energy directly into the sCMOS.

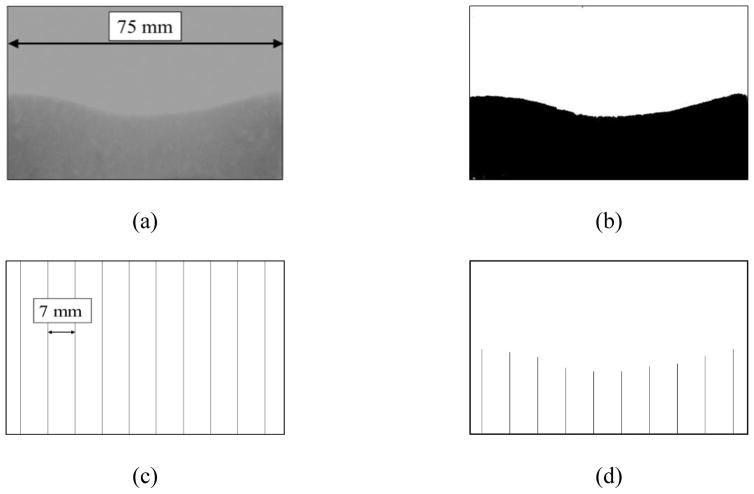
The images of the mortar in the wet state at time t after exposure to fluid were normalized to the reference image before exposure to fluid and converted to binary form as shown in Figure 4a and 4b. The depth of penetration was measured at 10 points, excluding the edges, equally spaced at 7 mm [0.28 in] according to Figure 4c, along the water front as shown in Figure 4d.

Fig. 4.

Image analysis process for determining the average depth of penetration. (a) Normalized images were (b) converted to binary. (c) A mask of vertical lines was subtracted from the binary images to result in (d) 10 measurable lines of the fluid front.

Beam hardening effects, where the effective attenuation coefficient decreases due to an increased mass of high energy neutrons in the effective cross section, can be seen in neutron images containing relatively large quantities (thicknesses) of water [26], [31]. These effects can make quantifying water difficult. However, with total water thicknesses less than about 5 mm [0.20 in], the relationship between optical density and water thickness remains approximately linear [26], [32]. The optical density is defined as

$$OD=-ln\left(\raisebox{1ex}{$I$}\!\left/ \!\raisebox{-1ex}{$I_0$}\right.\right)$$ Equation 4

where OD is the optical density, I is the measured intensity and I₀ is the intensity of the flat field.

Figure 1a illustrates a calculation of optical density as a function of pore volume in mortar for different sample thicknesses. The approximate volume fraction of the pores at 60 % degree of hydration was determined using Powers Model and is summarized in Table 4 [33]. The theoretical capillary porosity for 0.36, 0.42, and 0.50 w/c mortars ranged from approximately 19 % to 24 % and is indicated in the gray shaded region of Figure 1a. The volume fraction was then applied to various thicknesses of mortar to determine the extent of beam hardening that can be expected.

Table 4.

Calculated components of porosity according to Powers model [33]

	Mixture No.
	1	2	3	4
Capillary Porosity	0.071	0.097	0.128	0.099
Gel Porosity	0.073	0.065	0.058	0.066
Chemical Shrinkage	0.024	0.022	0.019	0.022
Measured Air	0.020	0.035	0.040	0.026
Total Calculated Porosity	18.8 %	21.8 %	24.4 %	21.3 %

$$OD(t_w)={\mu }_w{t}_w+{\beta }_w{t_w}^2$$ Equation 5

where t_w is the thickness of water, μ_w is 0.38483 mm⁻¹ [9.69 in⁻¹], and β_w is −0.00947 mm⁻² [6.10 in⁻²], as taken from [26]. When using a 20 mm [0.79 in] thick mortar sample as in the case of this study, beam hardening will not be significant as t_w ≤ 4.8 mm [0.19 in]. This indicates that the relationship between the optical density and the water content can be assumed to be linear between oven dried mortar and 100 % saturated mortar.

The optical density can be normalized by the sample thickness to define the composite attenuation coefficient of the mortar (μ_mortar) [32]. By normalizing to the thickness of the sample (t_sample), the optical densities from multiple mortar samples can be compared to each other.

$${\mu }_{\mathit{mortar}}=\frac{{OD}_{\mathit{mortar}}}{t_{\mathit{sample}}}$$ Equation 6

The degree of saturation in the mortar is calculated from the radiographs using the optical density normalized to the sample thickness of an oven dried sample (S=0) and a completely saturated sample (S=1) as calculated in Equation 7

$$S=\frac{{\mu }_{\mathit{mortar}}-{\mu }_{\mathit{DRY}}}{{\mu }_{\mathit{SAT}}-{\mu }_{\mathit{DRY}}}\times 100\%$$ Equation 7

where μ_DRY and μ_SAT are the attenuation coefficients of the mortar in the oven dried and saturated states, respectively.

Figure 1b is a plot of degree of saturation (S) obtained via neutron radiographs versus the degree of saturation determined gravimetrically. A good one-to-one correlation exists between the degrees of saturation calculated from the radiographs to the actual degree of saturation determined by mass. The error associated with the calculated value of S is largely attributed to the variation of sample thickness.

EXPERIMENTAL RESULTS AND DISCUSSION

Depth of Fluid Penetration

The average depth of penetration was measured every 30 min for the first 12 h of exposure to the chloride solution. After 12 h, the depth of penetration was measured at 25 h (300 s^1/2) and 40 h (400 s^1/2). The results from each series (mixtures 1–4) are plotted in Figure 5.

Fig. 5.

Average depth of penetration of four concentrations of CaCl₂ solution for mortars composed of (a) w/c of 0.36 and Type I cement, (b) w/c of 0.42 and Type I cement, (c) w/c of 0.50 and Type I cement, and (d) w/c of 0.42 and Type V cement. Dashed lines represent a linear best fit. Coefficient of variation is less than 7 % for measured depths.

In general, the rate of fluid penetration decreases as the concentration of chlorides in the solution increases as shown in Figure 5. This is consistent with previous studies [11], [12], [19], [34] where the rate of salt solution absorption decreases as the concentration of salts increase. When normalized to the sorptivity of water, there is a clear decrease in sorptivity with an increase in chloride concentration as shown in Figure 6. The theoretical influence of the altered fluid properties (surface tension and viscosity), i_fluid, is calculated by Equation 8 [11], [20] and is plotted as a function of calcium chloride concentration in Figure 6.

Fig. 6.

Normalized sorptivity with an increase in CaCl₂ concentration in the ponded fluid. Sorptivity values were normalized to those of DI water for each respective mortar.

$$i_{\mathit{fluid}}=\sqrt{\frac{{\gamma }_s{\eta }_w}{{\gamma }_w{\eta }_s}}$$ Equation 8

When exposed to 10 % CaCl₂, mortar prepared with Type V cement remains on the theoretical line, meaning the specimen sorptivity is only influenced by the fluid properties. Mortar prepared with Type I cement also shows a decrease in absorption due to fluid properties when exposed to 10 % CaCl₂ solution, however the value of normalized sorptivity deviates from the theoretical curve due to a decrease in porosity from the reaction between C₃A and calcium chloride resulting in the precipitation of Friedel’s and Kuzel’s salts [13], [19]. At room temperature, calcium oxychloride can form when the CaCl₂ concentration is over 12 % by mass [35]. When exposed to solutions with 20 % and 29.8 % CaCl₂, all samples experienced a significant decrease in sorptivity beyond that predicted by the change in fluid properties. This additional decrease in sorptivity is the effect of the formation of calcium oxychloride, in addition to the formation of Friedel’s and Kuzel’s salts in the Type I mortar [2], [19], [36]. Although salt formation cannot be directly detected with neutron radiography, the hindered rate of fluid ingress is likely attributed to the formation of calcium oxychloride and Friedel’s salt that occupies space in the pores and effectively decreases the local pore volume of the matrix. Table 5 summarizes the sorptivity (rate of fluid penetration), the normalized sorptivity and the percent difference between the experimental normalized sorptivity and the theoretical value.

Table 5.

Summary of measured sorptivity and normalized sorptivity for mortar samples exposed to CaCl₂ solutions.

Mixture No.	Sample Description	CaCl2 Solution (%)	Sorptivity1 (mm/s1/2)	Normalized Sorptivity (Ssolution/Swater)	% Deviation from Theoretical Value
1	w/c = 0.36, Type I	0	0.214 ± 0.006	1.00 ± 0.03	0.0
		10	0.138 ± 0.002	0.64 ± 0.01	28.9
		20	0.097 ± 0.002	0.45 ± 0.01	41.0
		29.8	0.039 ± 0.002	0.18 ± 0.01	69.7
2	w/c = 0.42, Type I	0	0.277 ± 0.003	1.00 ± 0.01	0.0
		10	0.210 ± 0.003	0.76 ± 0.01	16.3
		20	0.144 ± 0.003	0.52 ± 0.01	32.3
		29.8	0.035 ± 0.003	0.13 ± 0.01	78.9
3	w/c = 0.50, Type I	0	0.311 ± 0.019	1.00 ± 0.06	0.0
		10	0.235 ± 0.009	0.76 ± 0.03	16.2
		20	0.160 ± 0.006	0.52 ± 0.02	32.9
		29.8	0.051 ± 0.003	0.16 ± 0.01	72.4
4	w/c = 0.42, Type V	0	0.361 ± 0.007	1.00 ± 0.02	0.0
		10	0.327 ± 0.007	0.91 ± 0.02	0.3
		20	0.224 ± 0.004	0.62 ± 0.01	19.1
		29.8	0.074 ± 0.004	0.20 ± 0.01	65.8

¹1 mm/s^1/2 = 0.039 in/s^1/2

Change in Degree of Saturation

The change in moisture content was monitored continuously for 10 h to 12 h. Since the samples were conditioned to 50 % RH, the initial degree of saturations were approximately 20 %, 16 %, 15 %, and 18 % for Mixtures 1 through 4 respectively. The following figures monitor the change in degree of saturation with respect to the distance from the wetting edge. The degree of saturation was calculated using Equation 7.

Figure 7a and 7b exhibit moisture profiles with a steep gradient at the wetting front that maintain a constant shape as time increases, as expected [18], [32]. However, in Figure 7c and 7d, there is a clear increase in the change in degree of saturation at the far end of the sample after the water front reaches that edge, as indicated by the local peak in the 10 h data at a distance of about 48 mm. All the small pores (gel and capillary pores [33]) quickly fill as the water front advances due to the high capillary pressure in these pores, and once the water front reaches the edge of the sample, larger pores (entrapped and entrained air) begin to fill slowly as the mortar continues to absorb water [18].

Fig. 7.

Degree of saturation when exposed to deionized water for mortar with (a) w/c of 0.36 with Type I cement, (b) w/c of 0.42 with Type I cement, (c) w/c of 0.50 with Type I cement, and (d) w/c of 0.42 and Type V cement.

The increase in salt concentration to 10 % by mass does not greatly influence the change in degree of saturation. However, as noted in the previous section, it does decrease the rate of fluid penetration in mortars prepared with Type I cement. The moisture profiles have similar gradients at the wetting front as compared to deionized water. Again, in Figure 8d, there is an increase in the degree of saturation at the far edge of the sample after the moisture front reached that edge.

Fig. 8.

Degree of saturation when exposed to 10% by mass CaCl₂ solution for mortar with (a) w/c of 0.36 with Type I cement, (b) w/c of 0.42 with Type I cement, (c) w/c of 0.50 with Type I cement, and (d) w/c of 0.42 and Type V cement.

With higher chloride concentrations, such as the 20 % by mass shown in Figure 9, the slope of the fluid front becomes less sharp. In addition, there is a gradient throughout the entire distance of the wetted portion, rather than a relatively constant change in moisture content followed by a sharp decrease at the wetted front. In the case of deionized water and 10 % CaCl₂ solution in Figure 7 and Figure 8, the moisture content through the wetted portion was generally constant. This could be due to the change in fluid properties with highly concentrated solutions. The viscosity of CaCl₂ solution doubles when the solution concentration is increased from 10 % to 20 % by mass [10]. It can also be due to the formation of calcium chloroaluminate phases (Friedel’s and Kuzel’s salts) decreasing the pore volume. When these phases form and fill porosity, the resulting thickness of water measured will decrease.

Fig. 9.

Degree of saturation when exposed to 20 % by mass CaCl₂ solution for mortar with (a) w/c of 0.36 with Type I cement, (b) w/c of 0.42 with Type I cement, (c) w/c of 0.50 with Type I cement, and (d) w/c of 0.42 and Type V cement.

Finally, at very high concentrations of CaCl₂, 29.8 % by mass, it is clear that the penetration of fluid has been greatly hindered in all mortar samples including the one prepared with the Type V cement. In Figure 10, there is a two-part moisture front. There is a highly saturated portion near the exposed surface followed by a sharp decrease in moisture content for the remainder of the wetted portion. There may be a build-up of chlorides near the exposed surface that accounts for the peaks seen within the first 5 mm (0.20 in). Chlorine has an attenuation coefficient that is approximately one third that of hydrogen [37] so it could influence the attenuation of neutrons if there are large quantities accumulated. The wetting front gradually declines, which is a much different behavior compared to that of the mortars exposed to lower concentrations of calcium chloride.

Fig. 10.

Degree of saturation when exposed to 29.8% by mass CaCl₂ solution for mortar with (a) w/c of 0.36 with Type I cement, (b) w/c of 0.42 with Type I cement, (c) w/c of 0.50 with Type I cement, and (d) w/c of 0.42 and Type V cement. (Note change in x-axis scaling)

In many of the mortars, the fluid front reached the edge of the sample within 10 h (See Figure 7 and Figure 8). By 24 h, the deionized water, 10% CaCl₂, and 15% CaCl₂ solutions had completely penetrated the mortar. The mortar continued to absorb fluid after 24 h until monitoring stopped at 96 h. This slow uptake in fluid corresponds to the secondary sorptivity in ASTM C1585. Figure 11 shows the continued increase in the degree of saturation after the fluid reached the edge of the sample between 24 h and 96 h. The rate of absorption is much slower at longer times (days) due to the low capillary suction in the larger voids [38]. The measured entrapped air volume of the 0.42 Type I sample was higher than that of the 0.36 Type I sample (See Table 4), which results in less matrix porosity and therefore a lower degree of saturation when the small pores are initially filled.

Fig. 11.

Increase in degree of saturation of mortars exposed to deionized water up to 96 h.

CONCLUSIONS

This study utilized neutron radiography to measure the depth of fluid penetration and the degree of saturation in four mortars (Type I cement with w/c’s of 0.36, 0.42, and 0.50 and Type V cement with a w/c of 0.42) exposed to varying concentrations of CaCl₂. The addition of chlorides influences the transport properties of fluid in mortar due to changes in the fluid properties such as surface tension, viscosity and density. In addition, CaCl₂ salt solutions can react with the cement paste resulting in the formation of expansive reaction products such as Friedel’s salts, Kuzel’s salts and calcium oxychloride that can fill in the porosity and potentially damage the matrix. At a low concentration (10 % by mass), mortars prepared with Type I cement experienced a reduction in sorptivity between 20 % and 38 % due to a change in fluid properties and the creation of Friedel’s and Kuzel’s salts, whereas the mortar prepared with Type V cement only reduced in sorptivity by 10 %, due to the change in fluid properties. Cements containing aluminates (C₃A) will react with CaCl₂ even at low concentrations to produce pore-blocking salts that reduce the subsequent rate of absorption. These pore-blocking salts also reduce the effective pore volume and increase the degree of saturation which can lead to premature freeze-thaw damage in pavement joints. At high concentrations, all mortars experienced a dramatic decrease (between 80 % and 87 %) in sorptivity due to the change in fluid properties (increases in viscosity and surface tension) and the formation of calcium oxychloride.

The neutron radiographs enabled the fluid ingress depth and change in degree of saturation to be accurately calculated. From this information, the shape or gradient of the wetting front could be monitored. The wetting front became clearly less sharp as the concentration of chlorides increased. In addition, the phenomenon of pore-blocking with chlorides was observed at high concentrations (29.8 %). In this scenario, there is a build-up of chlorides close to the fluid source and a sharp decrease in the amount of fluid past the build-up. This implies that the pores have decreased in volume, therefore the volume of fluid that can penetrate past that barrier decreases as does the rate of further ingress.

Biographies

ACI member Catherine L. Lucero is a civil engineer at the Concrete, Geotechnical and Structural Laboratory of the US Bureau of Reclamation in Denver, CO. She received her BSCE from the University of New Mexico and her MSCE from Purdue University.

ACI member Robert P. Spragg is a PhD candidate at Purdue University. He received his BSCE and MSCE degrees from Purdue University.

ACI member Dale P. Bentz is a chemical engineer in the Materials and Structural Systems Division, National Institute of Standards and Technology (NIST), Gaithersburg, MD. He is a member of ACI committees 232, Fly Ash; 308, Curing Concrete; and 546, Concrete Repair. His research interests include experimental and computer modeling studies of the microstructure and performance of cement-based materials.

Daniel S. Hussey is a Physicist at the National Institute of Standards and Technology, which he first joined as a National Research Council Postdoctoral Fellow. He received his PhD in Physics from Indiana University, Bloomington, and his BS in physics from the University of New Hampshire. His research interests are focused on neutron imaging and optics and the application of neutron imaging and scattering techniques to problems of porous media.

David L. Jacobson is a Physicist at the National Institute of Standards and Technology, which he first joined as a National Research Council Postdoctoral Fellow. He received his PhD in Physics from the University of Missouri, Columbia, and his BS in physics from Westminster College (Missouri). His research interests are focused on neutron interferometry, imaging and optics.

Jason Weiss, FACI, is the Edwards Professor of Engineering and Head of the school of Civil and Construction Engineering at Oregon State University. He earned a BAE from Penn State University and a MS and PhD from Northwestern University. His research interests include shrinkage, early age behavior, cracking and moisture transport in concrete.