Robust and scalable inference of population history from hundreds of unphased whole-genomes

Abstract

It has recently been demonstrated that inference methods based on genealogical processes with recombination can reveal past population history in unprecedented detail. However, these methods scale poorly with sample size, which limits resolution in the recent past, and they require phased genomes, which contain switch errors that can catastrophically distort the inferred history. Here, we present SMC++, a new statistical tool capable of analyzing orders of magnitude more samples than existing methods, while requiring only unphased genomes (its results are independent of phasing). SMC++ can jointly infer population size histories and split times in diverged populations, and it employs a novel spline regularization scheme that greatly reduces estimation error. We apply SMC++ to analyze sequence data from over a thousand human genomes in Africa and Eurasia, hundreds of genomes from a Drosophila population in Africa, and tens of genomes from zebra finch and long-tailed finch populations in Australia.

INTRODUCTION

Encoded in the genome of every living organism is a wealth of information about its antecedents. Unlocking this information promises to provide exciting new insights into the history of humans and many other species. Apart from its intrinsic interest, such knowledge is useful for understanding patterns of historical migration^1–4, natural selection^1,5,6, the relationship between humans and other hominids^7–10, and even distantly related phenomena like global climate change^11,12.

Over the past few years, there has been a surge of interest in using whole-genome sequence data from multiple individuals to learn about population demographic histories. There are two popular approaches to this problem: one based on the Poisson Random Field model¹³ using the sample frequency spectrum¹⁴, and the other based on the sequentially Markov coalescent^15–17. SFS/PRF methods^18,19 employ results from the diffusion or coalescent theory to characterize the sampling distribution of unlinked segregating sites in a random sample of DNA sequences. This distribution can be efficiently computed for a very large sample size²⁰ and for complex demographic models with multiple populations²¹, but the model is incorrect when applied to modern whole-genome sequence (WGS) data due to correlation among neighboring sites. Also, the number of parameters that can be estimated using SFS-based methods is bounded by the sample size.

With the increasing prevalence of WGS data, attention has shifted to more complex models that incorporate recombination and linkage disequilibrium (LD) information. It has been shown that this approach can reveal past population history in unprecedented detail²². Owing to the linear structure of DNA, these models commonly employ some form of hidden Markov model (HMM)^22–28. Exploiting LD gives these methods more power to reconstruct past demographic events. At the same time, it entails an added level of mathematical and computational sophistication, such that state-of-the-art methods are limited to analyzing whole genome samples from only a few genomes at a time. Also, most of these methods require as input computationally phased haplotypes, entailing a costly and potentially error-prone preprocessing step. As we show later, switch errors in phasing can catastrophically distort the inferred history.

In this paper, we present a new inference framework called SMC++ that combines the computational efficiency of the SFS and the advantage of utilizing LD information in coalescent HMMs. Our method is designed to take advantage of modern data sets consisting of hundreds of unphased whole-genomes. It can also analyze pairs of diverged populations, allowing it to pool information from both populations, as well as directly estimate the time of divergence. We believe that this is the first demographic inference method capable of analyzing unphased whole genome data from a large number of individuals in a computationally efficient and stable manner, while taking linkage information into account.

RESULTS

We first demonstrate the accuracy and efficiency of our method SMC++ on simulated data. Then we apply the method to analyze real data from several large-scale whole-genome sequencing projects for various species: over a thousand genomes from eight human populations in Africa and Eurasia, hundreds of genomes from a Drosophila population in Africa, and tens of genomes from zebra finch and long-tailed finch populations in Australia. Throughout the rest of the paper, we denote the haploid sample size of a data set by n.

Accuracy and computational performance on simulated data

The exact details of our simulation procedure are described in ONLINE METHODS. Briefly, each scenario consisted of ten replicates of 3Gb of data simulated under either a “sawtooth” demography²⁴ featuring repeated exponential expansions and crashes over the last 1 million years; or “recent expansion”, a stylized model of European population growth involving a bottleneck 200 kya and tenfold expansion over the last 10 ky.

Effect of phasing error

Many inference procedures in population genetics require phased sequence data, which leads to an unavoidable and potentially significant source of computational expense and error. Since current phasing methods work best when large reference panels are available²⁹, these problems are especially acute when studying new populations for which a suitable reference panel is not available.

Phasing errors confound demographic inference by breaking up identity-by-state tracts in closely related haplotypes, biasing downwards the number of inferred coalescences in the recent past and causing haplotype-based inference methods to infer large recent effective population sizes. To quantify this effect, we simulated n = 4 genomes under the sawtooth demography to generate three input datasets for MSMC and SMC++. One version of the dataset contained the exact haplotypes generated by the simulation. The other two contained artificially induced “switch errors” at rates of 1% and 5%, which are approximate upper and lower bounds on the accuracy of existing phasing algorithms^29,30.

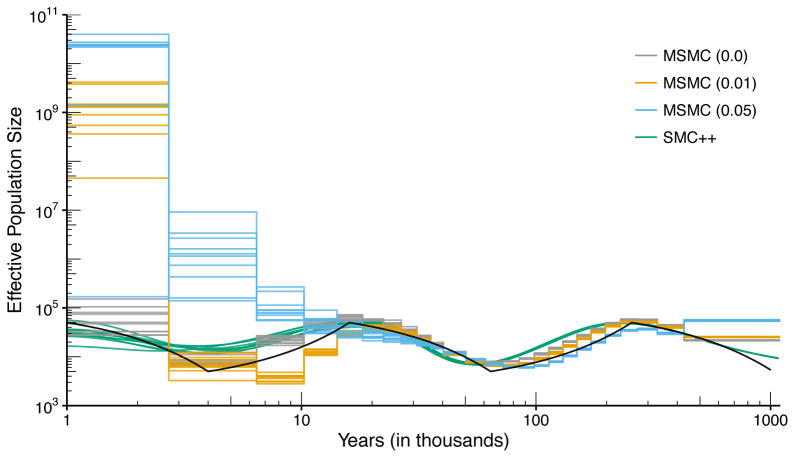
Fig. 1 shows the result of running SMC++ and MSMC on these datasets. There are three lines corresponding to the performance of MSMC at each level of switch error. (Since it is invariant to phasing, only a single line is plotted for SMC++.) All of the fits exhibit some bias, but the methods show fairly good agreement and low dispersion in the distant past. In the recent past, large differences emerge in the performance of MSMC as error increases. With 1% switch error, MSMC has difficulty accurately inferring the demography more recently than 20 kya, with highly divergent estimates (off by four orders of magnitude) over the past 3 ky. With 5% phasing error performance further deteriorates, with estimates diverging from substantially from the truth beginning 20 kya. With no phasing error, the accuracy of MSMC is similar to that of SMC++, with SMC++ producing higher resolution in the recent past. While we have used MSMC for illustrative purposes, we expect any demographic inference procedure which relies on phased data to exhibit similar inaccuracies in the presence of phasing error.

Figure 1. The effect of phasing error.

The true population size history is indicated by a bold black line, while colored lines indicate inferred histories for ten simulations each with sample size n = 4. For MSMC, switch error was introduced at the rate of 0%,1%, or 5%, indicated in parenthesis in the legend. SMC++ does not require phased data and its results are insensitive to phasing errors. With phasing error, MSMC estimates can be off by orders of magnitude in the recent past. In the absence of phasing error, the accuracy of MSMC is comparable to that of SMC++, with SMC++ producing higher resolution in the recent past.

SMC++ compared to other methods

Next, we compared SMC++ with MSMC and the SFS-based inference method ∂a∂i¹⁸. Based on the findings in the preceding section, we introduced phasing errors into the data at a switch error rate of 1%. (Note that ∂a∂i is also invariant to phasing.)

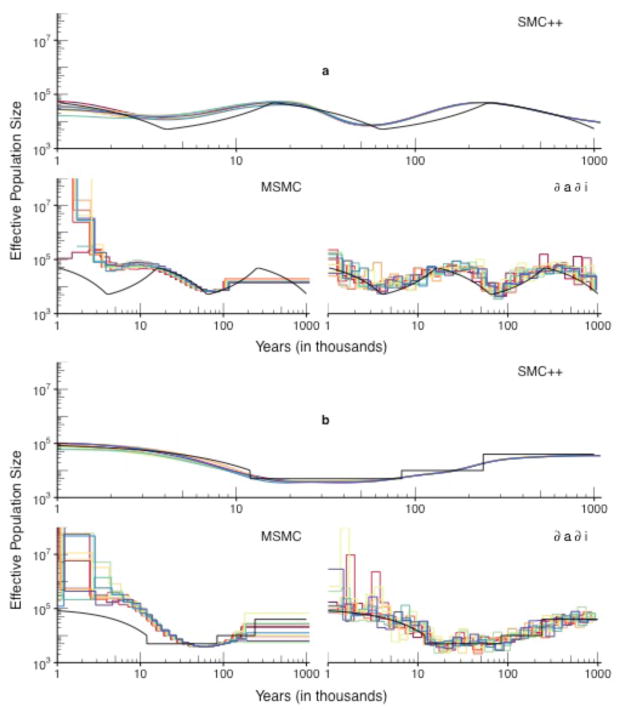
For both the sawtooth and recent-expansion simulations, SMC++ estimates are much more tightly concentrated around the true demography (shown in black) than either of the other two methods. The spline-based regularization scheme (ONLINE METHODS) employed by SMC++ effectively trades a small amount of bias for greatly reduced variance. Estimates obtained from ∂a∂i appear to be biased only slightly, but vary significantly from run to run and fluctuate substantially across epochs. MSMC has difficulty accurately inferring the true history, with estimates diverging quite severely for the very recent past. We note that these findings are somewhat at odds with the simulation results reported by Schiffels and Durbin²⁴, which appear to have been performed on error-free data.

The estimates in Fig. 2a seem to deviate more from the truth than in Fig. 2b; in general the sawtooth demography seems to be harder to accurately infer compared to the recent-expansion demography. This may in part be due to the somewhat pathological nature of the sawtooth demography, which experiences several rapid crashes over a relatively short period of time. It is known, for example, that a strong bottleneck complicates efforts to accurately estimate size change events which occurred before the bottleneck³¹. For the recent-expansion demography (Fig. 2b), SMC++ tends to smooth over abrupt changes in the historical effective population size, a phenomenon which has been witnessed previously in related methods²².

Figure 2. Performance of SMC++ compared to MSMC and ∂a∂i.

(a) The sawtooth demography. (b) The recent-expansion demography. Each method was used to analyze ten simulated datasets generated according to the demography shown in black. SMC++ was given sequence data from n = 100 lineages, and ∂a∂i analyzed the SFS from that data set. MSMC analyzed n = 8 of those lineages, the largest sample size for which it successfully ran. For this simulation, we introduced switch errors at a rate of 1% at segregating sites. All plots are on the same axes to aid in comparing the methods, but note that the MSMC fits again diverged to very large values (as high as O(10¹⁰)) in the recent past. (MSMC and ∂a∂i use the same breakpoints from run to run; we jittered the x-values of the fits slightly to prevent overlaying.)

Estimating the rate of recombination

In the preceding simulations, we assumed that the recombination rate (denoted by ρ/2) was known ahead of time. When ρ is unknown, SMC++ can estimate this quantity simultaneously with the demography. To test this, we generated additional data sets with n = 50 under the recent expansion demography, varying ρ within the range [0.1θ, 10θ] with θ/2 being the mutation rate. We then used SMC++ to jointly infer both the demography and the recombination rate. Results for the recombination rate estimation are shown in Supplementary Figure 1. SMC++ is able to estimate the rate of recombination fairly accurately over two orders of magnitude. It is most accurate when the ratio of recombination rate to mutation rate is below one. As ρ approaches 10θ, the estimates of the ratio ρ/θ exhibit some downward bias, which causes the inferred demographies to become too large. In this regime recombinations are roughly as common as mutations along the genome, complicating efforts by the HMM to establish the marginal time to the most recent common ancestor (TMRCA). The resulting demographic estimates exhibited additional variation but were qualitatively similar to those obtained when the recombination rate was known (Fig. 2b and Supplementary Figure 1).

Inference of split times

SMC++ can analyze pairs of populations simultaneously to infer divergence times jointly with population size histories. The current version of our implementation assumes a “clean split” model, in which no gene flow occurs after the populations split (S3 in the Supplementary Note). As in the one-population case, divergence time estimates and the jointly inferred demographies do not depend on phasing.

We verified by additional simulations that SMC++ can accurately determine the divergence time and demography in the clean split case. For these simulations we focused on somewhat smaller sample sizes of n = 10 lineages in each population. This illustrates the performance of our method when there are limited data; additionally, the computations needed to jointly analyze two populations have higher computational complexity, so it is expedient to fit the joint model to somewhat smaller data sets.

The two populations were simulated according to the “recent expansion” demography described above. At a time which varied from simulation to simulation, population 2 splits from population 1 (moving forward in time) and maintains a constant effective population size until the present, while population 1 continues to follow the “recent expansion” demography. No gene flow occurs between the two populations after the split.

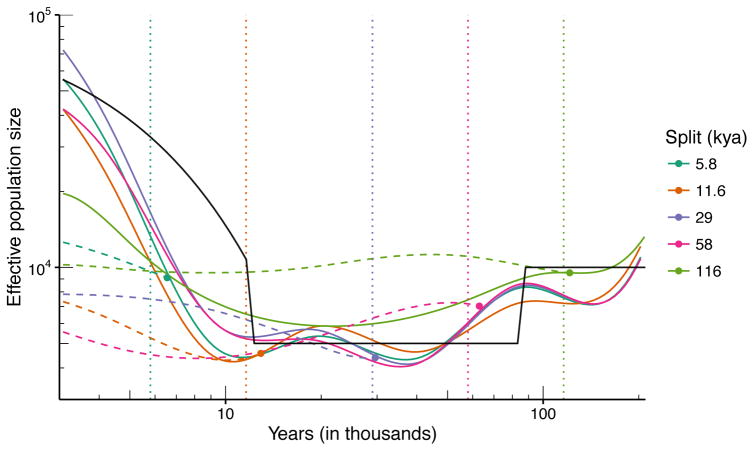
Simulation results are shown in Fig. 3. Over the range of approximately 6–120 kya, SMC++ is able to infer divergence times with low error. Additionally, the inferred demographies exhibit an acceptable level of accuracy. In situations where additional data are available, SMC++ can also estimate the demography of each population separately and then combine this information to infer the joint demography and divergence time.

Figure 3. SMC++ results of jointly inferring population size histories and divergence times.

Two populations were simulated under the “recent-expansion” demography described above. Each population consisted of n = 10 lineages. Different colors correspond to different divergence times. From the point of divergence until present, population 2 maintains a constant effective population size equal to the value it had at the time of the split. The solid colored lines indicate the inferred demography for population 1, which should follow the solid black line indicating the simulated demography. The dashed colored lines indicate the inferred demography for population 2, which should be flat from the time of the split onwards. The vertical dotted lines represent the true value of the split, whereas solid dots in corresponding color represent the value of the inferred split time. This result shows that our method is able to infer divergence times with low error over a wide range of split times, spanning approximately 6–120 kya.

Computational performance

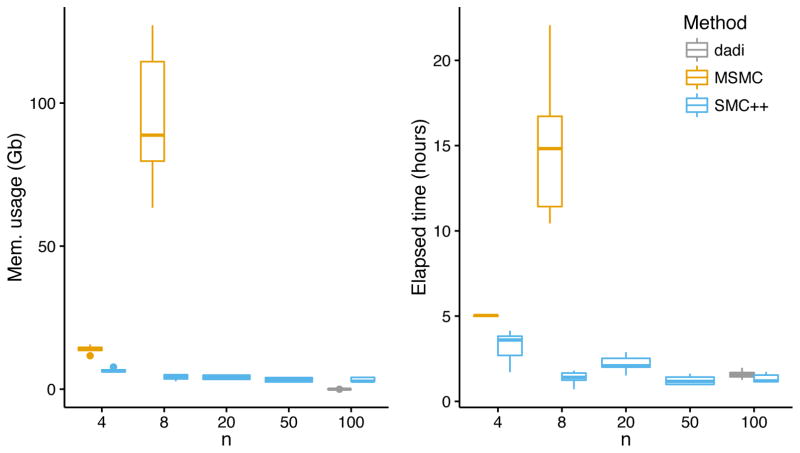
We recorded the run time and peak memory consumption for SMC++, ∂a∂i and MSMC while analyzing the simulated data sets mentioned above. To allow for fair comparison, we restricted SMC++ and MSMC to six threads, though we note that SMC++ is capable of exploiting all cores when possible. Results are shown in Fig. 4. At n = 8, the largest setting for which we were able to successfully run MSMC, SMC++ requires roughly an order of magnitude less memory and time. ∂a∂i, which operates on the SFS rather than sequence data, required extremely little memory (roughly 100Mb per run) and ran in roughly the same amount of time as SMC++.

Figure 4. Computational performance of SMC++, MSMC, and ∂a∂i.

The plots show median memory usage and runtime; error bars denote interquartile range. Each datum comprises ten repetitions on 3Gb of simulated data. The largest sample size for which we were able to successfully run MSMC was n = 8. For large sample sizes (n ≥ 8), SMC++ requires orders of magnitude less memory and time than does MSMC. The lower and upper hinges represent 25th and 75th percentiles; the middle line is the median. Whiskers extend to the nearest observation less than 1.5IQR beyond the corresponding hinges.

For larger sample sizes, memory consumption with SMC++ is approximately constant, and running time also scales quite favorably. It may seem odd that SMC++ running time actually decreases slightly as n grows. This is due to the fact that our method’s computational performance improves as the density of segregating sites decreases (EM algorithm in ONLINE METHODS), which occurs when we “thin” the data more aggressively at larger sample sizes in order to break up correlations in the underlying ancestral recombination graph (see Thinning in ONLINE METHODS). All told, even though there are fewer segregating sites in the thinned data for large n, they are more demographically informative.

Improvement in posterior decoding

In addition to demographic inference, SMC++ can also be used to locally infer the time to the most recent common ancestor (TMRCA) of the distinguished lineages. We hypothesized that the CSFS, by establishing a link between the coalescence time of the distinguished pair and the allelic status of the rest of the sample, could help to obtain an improved posterior distribution on the former quantity. To check this, we simulated additional 10 Mb stretches of sequence data and compared true TMRCA at each position in the distinguished pair with the posterior obtained by running our method. To quantify changes in accuracy, we calculated the root mean-squared error between the inferred and true TMRCA. (See Posterior decoding in ONLINE METHODS for a precise definition.)

Supplementary Table 1 shows the results of these simulations. For each scenario, the corresponding table entry gives the average RMSE relative to the PSMC (n = 2) baseline decoding. The table has three strata. The outermost indicates the result of varying the ratio of recombination rate to mutation rate. The next stratum shows the effects of introducing genotype error, and the innermost shows the effects of introducing missingness into the simulations. (See Posterior decoding in ONLINE METHODS for a description of how we simulated these errors.) A “*” in columns 4–6 indicates that the ratio of RMSEs is different from 1 at a 5% significance level.

In general, the table confirms that incorporating additional information from the CSFS improves the posterior decoding. For large values of the ρ/μ, the effect is on the order of 1–2% and is statistically significant in all scenarios. On the other hand, for very low values of recombination (ρ/μ = 0.1) the results exhibited considerable variance, with certain combinations of simulation parameters leading to substantial improvements, and others resulting in no significant improvement. Manually comparing the posterior decoding and true TMRCA in these cases revealed long spans with very recent coalescence times, which did not accumulate enough mutations to make reliable inference on the TMRCA.

The middle section of the table examines the case when mutation and recombination occur at comparable rates, and is the most relevant for analyzing human data. For high levels of genotype error (0.1% of sequenced bases) we see a very substantial decrease in RMSE as the sample size increases. This could potentially be useful in low coverage sequencing applications. Lower genotype error rates saw improvements of 1–2% when there was 10% missingness in the data, and 5–6% with 20% missingness. Finally, we found that increasing the sample size from 5 to 10 and then to 25 generally decreased the error, but did not observe much of an improvement beyond that. We suspect that this is because the amount of correlation between the CSFS and the TMRCA of the distinguished pair declines marginally as additional samples are added.

Inference of human demography

We used SMC++ to infer the historical effective size of eight human populations from Africa and Eurasia. We obtained whole-genome sequences from Complete Genomics³² and the 1000 Genomes Project². The Complete Genomics data consist of 54 unrelated individuals obtained from various populations and have average coverage in excess of 45×. The 1000 Genomes data has a larger sample size (typically 50–100 individuals per population) but lower coverage data. We combined these datasets by treating the genomes of each individual from the Complete Genomics data as “distinguished” lineages and computing the full “conditioned SFS” using all available individuals (see the Supplementary Note for the details of these concepts). Within each population, we fit a model using composite likelihood, whereby SMC++ was instantiated once for each available pair of distinguished lineages, and the sum of their log-likelihoods maximized using EM. Additionally, we analyzed a single ancient individual (“Ust’-Ishim”) who lived ∼45 kya in western Siberia³³. The data used in this portion of the analysis are summarized in Supplementary Tables 2 and 3.

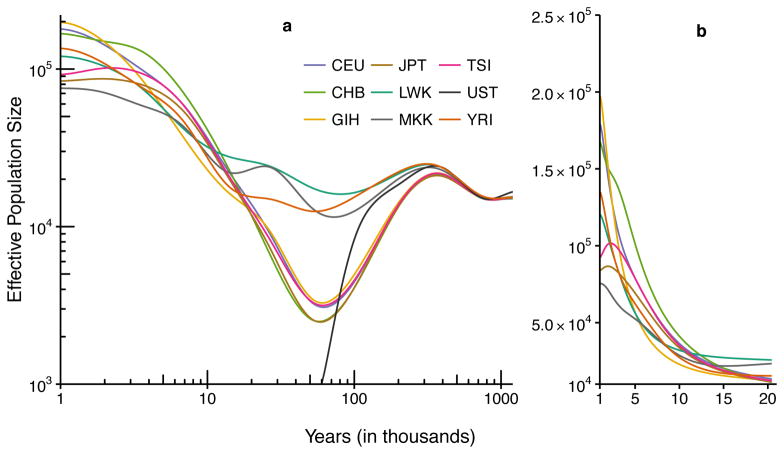
Results across all populations are shown in Fig. 5, with estimates broken out by continent in Supplementary Figures 2—4. A constant generation time of 29 years³⁴ was used to convert each figure from the coalescent time to calendar time, though we caution that the generation time(s) of ancient human populations are not known precisely, potentially distorting x-coordinates of the plots in the distant past. The per-generation mutation rate was fixed at 1.25×10⁻⁸ per base pair for all extant populations and 1.45×10⁻⁸ for the Ust’-Ishim individual³³.

Figure 5. Results of effective population size inference across eight extant human populations and an ancient Ust’-Ishim individual.

A generation time of 29 years was used to convert the coalescent scaling to calendar time. (a) Results for all populations on a log-log scale. Plot assumes that the Ust’-Ishim individual lived until 45 kya. (b) Results for present-day populations on a linear scale over the past 20 ky. See Supplementary Table 2 for a description of the populations and sample sizes.

In Fig. 5 and Supplementary Figures 2–4, we show the inferred size history over the period 1 Mya–1 kya in panel (a), as well as the size history for the past 20 kya on a linear scale in panel (b). Several interesting features emerge. In the period from 1 Mya to 300 kya, all population size histories experience similar dynamics. Around 300 kya, we begin to see the African size histories deviating from all other populations, potentially reflecting the existence of population structure within Africa. In the period from 300 kya to 100 kya, the African and non-African populations start to diverge significantly. During this period the non-African populations experience a steep decline in effective population size, while the African populations experience a more moderate decline. There is strong concordance in the population size histories of the European and Asian populations over this time interval, consistent with the notion that they split from a common ancestral population more recently than 100 kya.

Turning to the period more recent than 100 kya, all of the various populations become more distinct. Part of the observed short-term variability is due to the increased variance of our estimates as we approach the present (Supplementary Figure 5), but differences in the global pattern should reflect real differences between population size histories. The African populations (Supplementary Figure 2) all experience a relatively mild bottleneck followed by growth in the period 100–10 kya. The Luhya (LWK) and Maasai (MKK) reach a nadir around 70–80 kya, and the Yoruba (YRI) somewhat later, around 50 kya. All three populations seem to experience growth from at least 50 kya until present, with a noticeable uptick starting approximately 15 kya. Note that additional variability and lower recent effective population size seen for Maasai is likely due in part to the much smaller sample size of this population (Supplementary Table 2).

Among the Asian populations (Supplementary Figure 3), a somewhat different pattern emerges. All three populations experience a sharp bottleneck reaching a nadir around 55 kya, followed by growth until the present. Sudden rapid growth is experienced by the Gujarati (GIH) population around 5–10 kya, whereas in the other two populations (CHB, JPT) growth begins earlier, around 15 kya. It is interesting to note that the Gujarati population appears distinct from the East Asian populations starting around 100 kya.

The European populations (Supplementary Figure 4) experience a similar bottleneck as Asians ending around 50 kya, followed by a period of rapid growth starting 10–15 kya. The size histories of the Tuscan (TSI) and northern European (CEU) populations are nearly identical until around 5 kya.

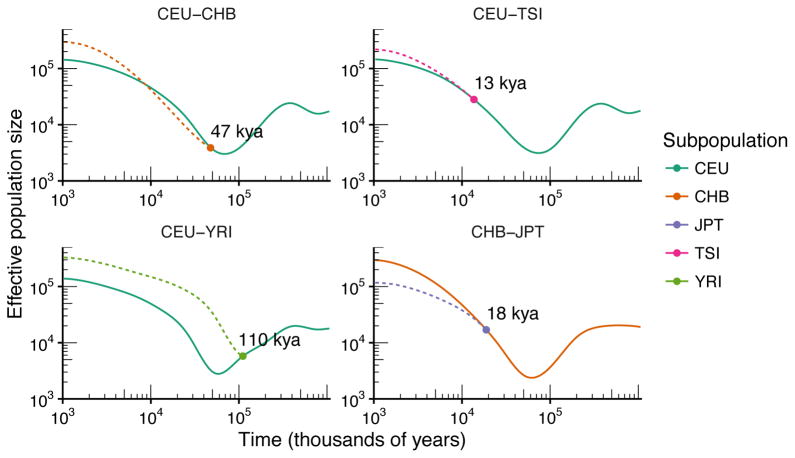
The plots show that several of the populations in the sample experienced similar size histories before diverging at some point in the recent past. To study this further, we jointly estimated their size histories and split times using the two-population model described above. Results are shown in Fig. 6. Our model estimates a divergence time of 13 kya for the European and Tuscan populations; 18 kya for the Han Chinese and Japanese; 47 kya for the European and Han; and 110 kya for the northern European and Yoruban. The joint estimates of population sizes shown in Fig. 6 differ slightly from the marginal estimates shown in Fig. 5, because the assumption of continuity between the two size histories at the time of divergence places additional constraint on the estimation problem. Overall, however, the estimates are quite consistent between the two figures.

Figure 6. Inference of split times in modern humans.

Results of jointly estimating population size histories and split times in a two-population model. The same data and generation times as in Fig. 5 were used to generate the plot.

Finally, we note the close agreement between the Ust’-Ishim individual (black line) and modern populations in Fig. 5 over the period 45 kya–1 Mya. The highly disparate origins of these samples—the former consisting of ancient DNA, the latter obtained from present-day individuals—gives us confidence that the features emerging in this plot correspond to actual historical events, and not data or modeling artifacts.

Inference of demography in other species

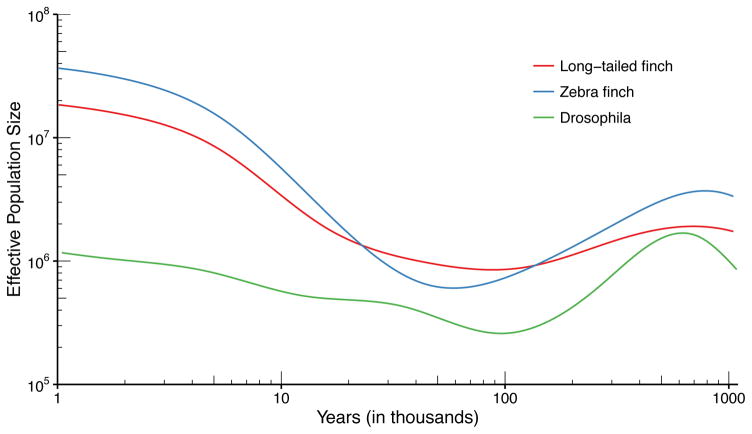
To verify that SMC++ has applications beyond human demographic inference, we also inferred population size histories for two species of finch (the zebra finch, Taeniopygia guttata, and the long-tailed finch, Poephila acuticauda) from Australia³⁵, as well as a wild African population of D. melanogaster from Zambia³⁶. These datasets are described in Supplementary Table 3. For the finch, we assumed a generation time of 3 months and a per-generation mutation rate of 7×10⁻¹⁰ per base pair³⁵. For D. melanogaster, we assumed a generation time of 1 month and a per-generation mutation rate of 3×10⁻⁹ per base pair³⁷. Due to uncertainty surrounding the generation times of these species, we also plotted these results in generations (Supplementary Figure 6). For all three species we estimated the per-generation recombination rate from data. The genome-wide average ratios of recombination to mutation were estimated to be 1.6: 1 (D. melanogaster), 1.15: 1 (P. acuticauda) and 1.1: 1 (T. guttata).

Results of demographic inference are shown in Fig. 7. The two finch species have similar, stable size histories between 500 kya and 1 Mya. Starting around 500kya, the populations experienced a decline which persisted until about 60–80kya, depending on species. This was followed by a period of expansion, which accelerated around 15 kya and led to more than tenfold increase in effective population size by 1 kya.

Figure 7. Results of effective population size inference for two finch species and D. melanogaster.

Generation times of 3 months (finch) and 1 month (D. melanogaster) were used to convert the coalescent scaling to calendar time. See Supplementary Table 3 for a description of the populations and sample sizes.

Estimates for D. melanogaster are overall lower, though we caution that the short generation time of the Drosophila, combined with smaller genome size, complicate efforts to peer this far back into its past using genetic data. D. melanogaster appears to decline from 600–100 kya, at which point it experiences steady growth leading to present. Unlike the other species analyzed in this paper, we do not see as much evidence of a sudden increase in effective population size in the recent past.

DISCUSSION

In this paper, we have presented SMC++, a new demographic inference method capable of analyzing hundreds of unphased whole-genome sequences at a time, while being fast, robust and easy to use. The ability to analyze much larger sample sizes makes our method’s estimates substantially more accurate than previous methods, especially in the recent past. On simulated data, we obtain accurate estimates of the true effective population size history across a time span of three orders of magnitude. Furthermore, our method is able to estimate population split times with low error over a wide range of timescale. In real data we obtain convincing estimates of the effective population size history of a number of different populations. In most cases our estimates agree with previous findings concerning divergence times and historical migration patterns, while also bringing to light some intriguing new features that could merit further study.

Two aspects of our method in particular are worth re-emphasizing. We have shown using simulations that introducing a modest amount of phasing error can severely corrupt the estimates of an existing demographic inference method. We conjecture that any method which is not invariant to phasing suffers from similar issues. Hence, the phase invariance of our method makes it more robust. Additionally, it eliminates a burdensome preprocessing step when analyzing real data.

We have also demonstrated that SMC++ requires an order of magnitude less memory and processing time than existing methods. We have found in practice that this is extremely useful for exploring and testing hypotheses in real data. The results of any demographic analysis depend on a number of a priori modeling assumptions, such as the functional form of the demography and various tuning parameters. At present we lack a theoretical understanding of how to optimally choose these parameters. This is an important area for future research, and in the meantime the ability to explore the model space and receive rapid feedback from the algorithm is essential.

Our general theoretical framework, which couples the genealogical process for a given diploid individual with the allele frequency information in a large collection of other individuals, can be extended to more complex demographic models. In particular, we plan to extend our method to incorporate gene flow between populations. We believe that this approach opens up a new window of opportunity to utilize the information contained in a large collection of whole-genomes to infer population demographic history in finer detail and higher accuracy than previously possible.

URLs

PopGenMethods repository: https://github.com/popgenmethods/smcpp Complete Genomics diversity panel: http://www.completegenomics.com/public-data/69-genomes/

1000 Genomes Phase 3: ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502/Drosophila Genome Nexus: http://www.johnpool.net/genomes.html

ONLINE METHODS

SMC₊₊ stands for “Sequential Markov Coalescent + Plenty of Unlabeled Samples.” SMC₊₊ unites the PRF and coalescent HMM approaches, combining the strengths of each while overcoming several of their limitations. The inclusion of “unlabeled samples” into the standard coalescent HMM is achieved via novel theoretical results on what we term “conditioned SFS” (CSFS), the sample frequency spectrum conditioned on the coalescence time and allelic state of a distinguished diploid individual. Compared to existing methods, the main advantages of SMC₊₊ are:

1. Scalability: SMC₊₊ can analyze hundreds of individuals at a time while requiring a modest amount of memory and processing time. Analyzing a hundred human genomes takes roughly an hour on a laptop.

2. Accuracy: By accommodating larger sample sizes, SMC₊₊ has significantly improved power to infer demographic events, particularly in the recent past.

3. Phase invariance: SMC₊₊ only requires unphased sequence data as input (i.e., results do not depend on phasing).

4. Regularity: SMC₊₊ uses cubic splines to enforce a smoothness constraint on the inferred demographies. Compared with existing methods, the resulting estimates exhibit far less variance, with only a minimal increase in bias.

SMC₊₊ extends a line of work which approximates the intractable sampling distribution of a contiguous segment of DNA (that of the so-called ancestral recombination graph³⁸) by a tractable Markov process. We first give a brief overview of these related methods, followed by a description of the novel aspects of SMC₊₊.

Related work

The starting point for our model is the well known pairwise sequentially Markov coalescent²². That paper applied a simple likelihood model for the pattern of genetic mutations observed in a single diploid individual, and showed that it had surprising power to infer the history of the individual’s population. PSMC works as follows: each pair of chromosomes is divided into blocks of 100 base pairs, and then mapped to a binary string according to whether each block contained one or more heterozygous sites. These “emitted” symbols are modeled as an HMM whose hidden state is the marginal TMRCA, assumed constant within each block. Conditional on the TMRCA being equal to T, the probability of observing a heterozygous block is 1 − e^−100θT where θ/2 is the per-base mutation rate. The distribution of the TMRCA is discretized into a number of disjoint intervals, and its stationary distribution and (discrete) transition function are then computed with respect to a piecewise-constant population size history. The transition function, which describes the conditional distribution of TMRCA between neighboring sites, is intractable in its exact form¹⁵. Instead, a simple Markov approximation is used¹⁶. The stationary, emission, and transition probabilities together define a map from population size history to sampling distribution via the HMM. The likelihood function is then maximized iteratively using the EM algorithm.

Despite its apparent simplicity, PSMC has proved very effective in practice and has been utilized in hundreds of subsequent analyses of many different species. Nevertheless, there are a few clear areas where PSMC could be improved:

• The so-called SMC approximation¹⁶ utilized to calculate transition probabilities in PSMC is inaccurate. A slight modification known as SMC’¹⁷ results in a much more accurate approximation of the transition matrix, with negligible added computational burden^39,40.

• The computational performance of PSMC, though adequate, can be substantially improved via parallelism on modern, many-core workstations. Doing so renders the blocking approximation unnecessary.

• More fundamentally, PSMC is limited to analyzing a single diploid individual. This strongly limits the power of PSMC, particularly in the recent past where there will be few coalescent events in a sample of size two.

A follow-on method called MSMC²⁴ extends PSMC to larger sample sizes, and also allows for the analysis of multiple populations. MSMC does so by redefining the HMM hidden variable to be the first coalescent event among the n haplotypes in the sample, with transition probabilities based on SMC’. For the emission probabilities, MSMC mainly uses the singleton mutations, only using the higher-frequency mutations to disallow certain coalescence events (if the 2 coalesced haplotypes have different alleles the emission probability of the non-singleton mutation is 0, otherwise the mutation is ignored). For the case of n = 2, MSMC essentially reduces to PSMC. Since the time to first coalescence depends more strongly on recent demography for larger sample sizes, MSMC has greater power to infer size changes in the recent past. On the other hand, the computational burden of MSMC also grows substantially with sample size, such that it is limited, in practice, to analyzing no more than four diploid whole genome samples.

A different approach to performing demographic inference via a coalescent HMM may be found in diCal²⁷ and related methods^28,41. These rely on the so-called conditional sampling distribution (CSD), which characterizes the probability of observing an k-th sampled chromosome conditional on the previously observed k − 1 samples. Computing the CSD becomes substantially more difficult for larger sample sizes, so that even the most recent version of diCal is limited to analyzing no more than 10 samples at a time at whole-genome scale. On the other hand, diCal is capable of analyzing complex demographic scenarios involving size changes, admixture, migration and population splits.

Theoretical model for SMC₊₊

Above, we described how MSMC generalizes PSMC in two different directions, by altering both the hidden state space as well as the space of emitted symbols used in the HMM. We also demonstrated in simulation that MSMC has difficulty scaling to large n. This is partly due to the fact that there are O(n²) pairs of haplotypes that may be involved in the first coalescence; thus, the HMM must integrate over O(n²) hidden states per time interval per locus.

To scale to larger sample sizes, SMC₊₊ generalizes PSMC in a different direction. The hidden state of SMC₊₊ is exactly the same as in PSMC; specifically, the hidden state is the TMRCA between the 2 haplotypes of a single individual. Where SMC₊₊ and PSMC differ are in the observed state. Whereas PSMC emits a binary symbol indicating whether the individual is heterozygous, SMC++ additionally emits the allele frequency of an extra n − 2 haplotypes. Specifically, the emission probability of SMC₊₊ is based on the site frequency spectrum^14,42, conditioned on the TMRCA of a single “distinguished” individual.

The differences between these three approaches are depicted in Supplementary Figure 7. PSMC and SMC₊₊ track the same hidden information, but their emissions are different. Whereas the PSMC emissions are binary symbols, SMC₊₊ emissions are 2-tuples (a, b) ∈ {0,1,2}×{0,1,…, n − 2}. Here a and b denotes the number of derived alleles present in the “distinguished” individual and the additional “undistinguished” n − 2 haplotypes, respectively. We refer to the distribution of these tuples as the conditioned SFS (CSFS): the site frequency spectrum conditional on the event that the TMRCA of the distinguished member falls in a given interval. The CSFS is a two-dimensional generalization of the site frequency spectrum; indeed, summing the CSFS across rows exactly recovers the standard site frequency spectrum on n haploids. We explicitly define the SMC₊₊ emission probability, and rigorously derive the CSFS using coalescent theory, in the Supplementary Note.

In order to calculate the CSFS we assume that the mutation rate is known. Uncertainty in the mutation rate can potentially alter the estimates of SMC₊₊, though in practice this effect will be attenuated by also using linkage information to infer the demography.

Thinning

An important caveat to our approach concerns correlation between observations of the conditioned SFS. The hidden Markov model formally assumes that neighboring observations are independent conditional on knowing the underlying hidden state. If we just use the distinguished individual, without the additional undistinguished haplotypes, this assumption is correct (up to the SMC’ approximation and time discretization). However, the conditional independence assumption is violated when we add the additional undistinguished lineages: correlations in branch lengths of the sample’s underlying genealogy will remain even after conditioning on the TMRCA within the distinguished individual. Emitting the “full” conditioned SFS at every site therefore leads to model misspecification. To prevent this we adopt a “thinning” strategy, in which the full conditioned SFS is emitted only at every k-th site for some pre-specified constant k.

In this paper we adopted the heuristic k = Cn for a large constant C, so that the density of full SFS emissions decreases linearly in sample size. We found that C = 400 worked well in practice and all analyses reported in this paper are the result using that choice of parameter.

Transition function

As discussed earlier, the SMC’ transition function more accurately approximates the sequential coalescent. In SMC++ we employ a continuous time, conditioned Markov chain approximation to the sequential coalescent³⁹. This approximation, which derives from the exact continuous time description of the two-locus coalescent with recombination⁴³, is actually slightly more accurate than SMC’ as originally formulated¹⁷ since it integrates over any number of recombinations and back-coalescences occurring between neighboring sites.

EM algorithm

For a hidden Markov model with M hidden states and L observations, the complexity of the forward-backward algorithm is O(M²L). Genetic data usually contains long stretches of monomorphic sites, a fact which can be used to decrease the running time of this algorithm to O(M²L_p), where p is the number of polymorphic loci in the data set⁴⁴.

However, extending this speedup to the EM algorithm is nontrivial: in particular, it was previously unknown how to compute the posterior expected number of transitions and emissions from each hidden state, which are needed to execute the “M” step of the EM algorithm during model fitting. In the Supplementary Note, we present new results to compute these posterior expectations by taking advantage of the sparsity of polymorphic sites. The complexity of our modified algorithm is O(M³L_p) which improves the running time O(M²L) of the non-sparse algorithm when ML_p < L. For large sample sizes L = O(10²L_p) so this requires that M = O(10), a setting which we found produces acceptable results in practice.

Regularization

As mentioned above, we found that regularization dramatically improved convergence of our algorithm and the quality of the resulting estimates. SMC₊₊ enforces a mild smoothness constraint by fitting a cubic spline to the data. Hence, the space of models considered by our algorithm consists of continuously twice-differentiable (C²) curves. (A weaker constraint requiring only C¹ smoothness is also available to the user.)

In addition to this “implicit” regularization scheme, we added an explicit “roughness” penalty to the optimization. Here roughness is defined as

$$\mathcal{P}(f)\stackrel{\text{def}}{=}{\int }_R{(f^{″})}^2,$$

where R is the (compact) support of the spline f. The penalized likelihood used for fitting is then 𝒬(f) − λ℘(f), where 𝒬(f) is the so-called complete log-likelihood used in the EM algorithm⁴⁵, and λ > 0 is the regularization parameter.

By penalizing curvature, this type of regularizer shrinks to a linear fit, and encodes our prior belief that real populations are unlikely to experience repeated crashes and expansions over short time intervals. For our simulated results, we found that λ = 0.01 worked well. On real data, which contains noise, missingness, and other model violations, we found that slightly larger values, ranging from λ = 1.0 to λ = 10.0 depending on the amount and quality of available data, were necessary to obtain smooth fits.

Simulation procedure

We used the coalescent simulation program scrm⁴⁶ to generate simulated data sets. Each simulated data set consisted of 30 independently generated chromosomes of length 100Mb. Ten replications were performed for each combination of demography, inference procedure, and sample size. When running MSMC we fixed the value of the recombination rate to its true value, while for SMC++ the recombination rate was estimated from the simulated data.

The command line used to simulate from the sawtooth demography was:

scrm <n> 1 -p 10 -t 71560.0
-r 17889.9998211 100000000
-oSFS -seeds <s1> <s2> <s3> -eN 0.0 5.0
-eG 0.0 0.0 -eN 0.000582262 5.0
-eG 0.000582262 1318.18 -eN 0.00232905 0.500002043581
-eG 0.00232905 -329.546 -eN 0.00931919 5.00496081234
-eG 0.00931919 82.3865 -eN 0.0372648 0.500618264601
-eG 0.0372648 -20.5966 -eN 0.149059 5.0061592508
-eG 0.149059 5.14916 -eN 0.596236 0.500615510407
-eG 0.596236 0.0

The command line used to simulate from the human demography was:

scrm <n> 1 -p 10 -t 50000.0
-r 12499.999875 100000000
-oSFS -seeds <s1> <s2> <s3> -eN 0.0 10.0
-eG 0.0 230.258509299 -eN 0.01 0.5 -eG 0.01 0.0
-eN 0.07 1.0 -eG 0.07 0.0 -eN 0.2 4.0 -eG 0.2 0.0

In these commands <n> is the (haploid) sample size, which varied from experiment to experiment, and <s{1,2,3}> are random number generator seeds, which varied from experiment to experiment but were retained to enable reproducibility.

To model the effect of computational phasing we introduced switch error into the data sets using the following procedure. Let X ∈ {0,1}^2×S be a binary matrix representing a pair of dimorphic haplotypes at S segregating sites. The ith column of X is denoted X_i = (X_i,1, X_i,2). Also let U_i, i = 1,…, S denote a sequence of i.i.d. Uniform(0,1) random variables and let α denote the switch error rate. Execute the following random algorithm:

1. set switch_error = False

2. For i = 1,…, S

   1. If U_i < α then switch_error = ¬ switch_error

   2. If switch_error = True, then Y_i,1 = X_i,2 and Y_i,2 = X_i,1; else Y_i = X_i.

3. Return Y ∈ {0,1}^2×S.

Posterior decoding

The root mean squared error between the true TMRCA and inferred posterior is defined as

$$\text{RMSE}={[\sum _{\ell =1}^L\sum _{m=1}^M{\gamma }_{\ell m}{(h_m-t_{\ell })}^2]}^{1/2}.$$

Here, γ_ℓm is the posterior probability of coalescence in the m-th hidden state for position t_ℓ is the true TMRCA at position ℓ, and h_m is the expected coalescence time conditional on coalescence occurring in hidden state m.

To simulate genotype error, we “flipped” a Poisson-distributed number of randomly chosen bases in each simulation. To simulate missingness, we replaced a Poisson-distributed number of segregating sites in each sample with missing values. The means of the Poisson distributions were chosen such that in expectation, the fraction of bases affected by each type of error equaled the corresponding value in columns 2–3 of Supplementary Table 1.