Multimodal Registration of White Matter Brain Data via Optimal Mass Transport

Abstract

The elastic registration of medical scans from different acquisition sequences is becoming an important topic for many research labs that would like to continue the post-processing of medical scans acquired via the new generation of high-field-strength scanners. In this note, we present a parameter-free registration algorithm that is well suited for this scenario as it requires no tuning to specific acquisition sequences. The algorithm encompasses a new numerical scheme for computing elastic registration maps based on the minimizing flow approach to optimal mass transport. The approach utilizes all of the gray-scale data in both images, and the optimal mapping from image A to image B is the inverse of the optimal mapping from B to A. Further, no landmarks need to be specified, and the minimizer of the distance functional involved is unique. We apply the algorithm to register the white matter folds of two different scans and use the results to parcellate the cortex of the target image. To the best of our knowledge, this is the first time that the optimal mass transport function has been applied to register large 3D multimodal data sets.

1 Introduction

Registration is an important pre-processing step for many automatic approaches that extract cortical structures from Magnetic Resonance Images (MRI) [9, 22, 11]. Common approaches for aligning the atlas of the segmenter to the patient MRI are based on the B-spline representation [11, 19] and continuum and fluid mechanics, [7, 15, 6, 21]. The accuracy of these approaches generally depends on how well they are tuned to the sequence of patient scan. Tuning these algorithms often requires expertise about the underlying algorithm. Clinicians scanning with new acquisition sequences are therefore often concerned on how to post-process these scans. In this paper, we propose a parameter-free algorithm for the registration of MRIs.

We model the registration of images as an optimal mass transport problem. Introduced by Monge and Kantorovich [13], the solution to the problem is an optimal mapping û (in some sense) between two densities μ₀ > 0 and μ₁ > 0. If we now define d as the dimension of the image domain, det() as the determinant, u as a mapping from Ω → Ω with Ω a subdomain of ℝ^d, and represent by ρ(.,.) : Ω · Ω → ℝ⁺ a distance function between two points in Ω, then the problem can be formalized as

$$\begin{array}{c}\widehat{u}\stackrel{\mathrm{\Delta }}{=}\underset{u\in \mathcal{U}}{min}\frac{1}{2}{\displaystyle {\int }_{{\mathrm{\Omega }}^d}{\mu }_0\left(x\right)\mathrm{\rho }\left(u\left(x\right),x\right)dx},\\ \text{where}\mathcal{U}=\{u:\mathrm{\Omega }\to \mathrm{\Omega }|c\left(u\right)=\det \left(\nabla u\right){\mu }_1\left(u\right)-{\mu }_0=0\}.\end{array}$$ (1.1)

We refer to the constraint c(u) = 0 as the mass preserving (MP) property.

For the remainder of this note, we take ρ(·,·) to be the squared distance function $\mathrm{\rho }\left(u\left(x\right),x\right)\stackrel{\mathrm{\Delta }}{=}{\Vert u\left(x\right)-x\Vert }^2.$ Even for the simple L²-norm, (1.1) defines a highly non-linear optimization problem. While there exists a large body of literature which deals with the analysis of the problem, such as [1, 8], only a smaller number of papers discuss efficient numerical solutions for the problem. Benamou and Brenier [5] estimate û by relating Equation (1.1) to the minimization of a certain kinetic energy functional with a space-time transport partial differential equation (PDE) constraint. Their approach not only estimates the optimal mapping but also provides the transportation path between the densities. A computationally faster solution to (1.1) was proposed by Angenent et al. [3]. Their algorithm directly estimates û by first computing a transformation u₀ that fulfills the MP property. Afterwards, the algorithm improves u₀ by concatenating the mapping with the transformation,

$$\begin{array}{c}\widehat{s}\stackrel{\mathrm{\Delta }}{=}\underset{s\in \mathcal{S}}{min}\frac{1}{2}{\displaystyle {\int }_{{\mathrm{\Omega }}^d}{\mu }_0\left(x\right){\left(u_0\left(s^{-1}\left(x\right)\right)-x\right)}^{2}dx,}\\ \text{where}\mathcal{S}=\{s:\mathrm{\Omega }\to \mathrm{\Omega }|\stackrel{\sim }{c}\left(s\right)=\det \left(\nabla s\right){\mu }_0\left(s\right)-{\mu }_0=0\}.\end{array}$$ (1.2)

We refer to the second equation in (1.2) as the $\stackrel{\sim }{c}$ constraint. This means that $s\in \mathcal{S}$ is an MP mapping from μ₀ to itself. The authors in [3] show that ŝ can be estimated via a steepest descent flow. To register 2D MRIs, they implement the method using forward Euler equation scheme for time stepping and a simple finite difference discretization of the spatial derivatives. The approach, however, does not enforce the MP constraint at each step of the numerical algorithm, so that the final solution generally does not fulfill the MP property. In addition, steepest descent is very slow in estimating the solution to Equation (1.2). For these reasons it would be very challenging to efficiently register 3D medical images with this approach. To overcome this hurdle, this paper describes a faster numerical solution to Equation (1.2) that enforces the MP constraint.

Unlike [3], we solve the optimization problem via an approach where we choose a direction other than steepest descent and show that it converges faster (see Section 2). Furthermore, we derive a numerical approach that uses a consistent conservative discretization method and enforces the MP constraint at each update of the solution (Section 3). In Section 4, we test the robustness of our approach by registering the white matter folds of two MRIs. The first MRI scan is part of a publicly available atlas [14] with detailed anatomical information about the scan. The second scan was acquired using a very different scanning protocol. Our approach accurately aligns the two scans. We then use the aligned atlas to outline the cortical folds in the new scan.

We end this section with the comment that our approach most closely relates to those registration approaches based on fluid mechanics. The optimal warping map of the L² Monge-Kantorovich equation may be regarded as the velocity vector field which minimizes a standard energy integral subject an Euler continuity equation constraint [5]. In particular, in the fluid mechanics framework, this means that the optimal Monge-Kantorovich solution is given as a potential flow.

2 Obtaining the descent direction

We now quickly review the derivation presented in [12] but within a variational framework. Assuming that the MP constraint condition is valid, we take a perturbation in s which stays on the MP constrained manifold. This leads to

$$\begin{array}{l}0=c\left(s+\mathrm{\delta }s\right)-c\left(s\right)=\text{det}\left(\nabla \left(s+\mathrm{\delta }s\right)\right){\mu }_0\left(s+\mathrm{\delta }s\right)-\text{det}\left(\nabla s\right){\mu }_0\left(s\right)\\ =\text{det}\left(\nabla s\right)(\nabla \cdot (\mathrm{\delta }s(s^{-1}))\left(s\right)){\mu }_0\left(s\right)+\text{det}\left(\nabla s\right)\nabla {\mu }_0\left(s\right)\cdot \mathrm{\delta }s.\end{array}$$

This expression can be simplified as long as the constraint is valid. Since det(∇u) > 0 we can divide, and rearranging we have

$$\begin{array}{l}0=({\mu }_0\nabla \cdot (\mathrm{\delta }s(s^{-1})))(s)+\nabla {\mu }_0(s)\cdot \mathrm{\delta }s\\ ={\mu }_0\nabla \cdot (\mathrm{\delta }s(s^{-1}))+\nabla {\mu }_0\cdot \mathrm{\delta }s(s^{-1})=\nabla \cdot ({\mu }_0\mathrm{\delta }(s^{-1}).\end{array}$$

Defining δζ = μ₀δs(s⁻¹), we see that ∇· δζ = 0. Next, looking at u = u₀ (s⁻¹), we can write u(s) = u₀ which implies that,

$$\left(\nabla u\left(s\right)\right)\mathrm{\delta }s+\mathrm{\delta }u\left(s\right)=0\Rightarrow \mathrm{\delta }u=-\left(\nabla u\right)\mathrm{\delta }s(s^{-1}).$$

Using the definition of δζ we obtain that as long as the constraint is valid and that u(s) = u₀ we have

$$\mathrm{\delta }u=-{\mu }_0^{-1}\left(\nabla u\right)\mathrm{\delta }\zeta ,$$ (2.3a)

$$0=\nabla \cdot \mathrm{\delta }\zeta .$$ (2.3b)

Let M be defined as the objective function in (1.2) then it can be shown that

$$\mathrm{\delta }M={\displaystyle {\int }_{\mathrm{\Omega }}u\cdot \mathrm{\delta }\zeta dx.}$$ (2.4)

In the the original paper [12], it is suggested to use the Helmholtz decomposition in order to obtain a descent direction. Here we employ a different approach. First, we note that the divergence constraint can be eliminated by selecting δζ = ∇ × δη, and thus to reduce M we need to obtain a direction that yields a negative δM, that is we seek a direction, δη such that $\mathrm{\delta }M={\displaystyle {\int }_{\mathrm{\Omega }}u}\cdot \nabla \times \mathrm{\delta }\mathrm{\eta }dx<0$. Using the Gauss theorem, we obtain that

$${\displaystyle {\int }_{\mathrm{\Omega }}u}\cdot \nabla \times \mathrm{\delta }\mathrm{\eta }dx={\displaystyle {\int }_{\mathrm{\Omega }}\nabla \times u\cdot \mathrm{\delta }\mathrm{\eta }dx+{\displaystyle {\int }_{\mathrm{\partial }\mathrm{\Omega }}\left(u\cdot (\mathrm{\delta }\mathrm{\eta }\times \overrightarrow{n}\right)}}dx$$

and therefore the steepest descent direction is given by

$$\mathrm{\delta }\mathrm{\eta }=\nabla \times u,\mathrm{\delta }\mathrm{\eta }\in \mathrm{\Omega }:\mathrm{\delta }\mathrm{\eta }\times \overrightarrow{n}=0,\mathrm{\delta }\mathrm{\eta }\in \mathrm{\partial }\mathrm{\Omega }$$

which leads to the update δζ = ∇ × ∇ × u, and finally to the steepest descent direction in u $\mathrm{\delta }u=-\frac{1}{{\mu }_0}\left(\nabla u\right)\nabla \times \nabla \times u$ or, in symmetric form

$${\mu }_0{\left(\nabla u\right)}^{-1}\mathrm{\delta }u=-\nabla \times \nabla \times u.$$ (2.5)

The operator −∇ × ∇× is negative and elliptic thus, the equation can be thought of as a parabolic PDE as long as real part of the eigenvalues of ∇u are positive. Using the above decomposition a family of different directions may be obtained. Note that in order to reduce the objective ${\displaystyle {\int }_{\mathrm{\Omega }}\nabla }\times u\cdot \mathrm{\eta }dx$ any vector field of the form δη = A∇ × u can be used where A is a symmetric positive definite matrix. For example, a choice that leads to a similar method to the one derived in the original paper [12] in 2D is A = −Δ⁻¹, which leads to the update

$${\mu }_0{\left(\nabla u\right)}^{-1}\mathrm{\delta }u=\nabla \times {\mathrm{\Delta }}^{-1}\nabla \times u.$$ (2.6)

Using the above calculation it is easy to see that the flow (2.6) is valid also in 3D. Moreover, it is easy to verify that given a smooth u the second formulation (2.6) leads to a more stable method that should converge faster compared with the first formulation (2.5), because the operator ∇ × Δ⁻¹∇ × is compact while the ∇ × ∇× operator is unbounded. In this work, we therefore derive a numerical method for (2.6) rather than for (2.5).

3 Deriving an efficient numerical method

In this section, we derive an efficient numerical method for the solution of the flow. The proposed method has three main components: a conservative discretization of differential operators, a criterion to choose step size, and a method to correct steps that deviate from the mass preservation constraint.

3.1 Conservative discretization

The applications we have in mind derive from medical imaging where images are discretized on a regular grid. We therefore construct our discretization based on a finite volume/difference approach. To derive and analyze our discretization we introduce a new variable δp = Δ⁻¹∇ × u and rewrite (2.6) as

$$\left(\begin{array}{cc}{\mu }_0{\left(\nabla u\right)}^{-1}& \nabla \times \\ 0& \mathrm{\Delta }\end{array}\right)\begin{array}{l}\left(\begin{array}{c}\mathrm{\delta }u\\ \mathrm{\delta }p\end{array}\right)\hfill \end{array}=\left(\begin{array}{c}\begin{array}{c}0\\ \nabla \times u\end{array}\end{array}\right).$$ (3.7)

In order for the discrete system to be well posed we need consistent discretizations for Δ, ∇u and ∇ × u. There are a number of possible discretizations that lead to a well-posed system.

We divide Ω into n₁ × … × n_d cells, each of size h₁ × … × h_d where d is the dimension of the problem. We discretize all the components of u at the nodes of each cell to obtain d grid functions û¹,…û^d. Since δp is connected to u by the curl operator, we employ a staggered grid and place δp at cell centers. To approximate ∇u at each node, we use long differences. Thus, in 3D, the discretized (1,1) block in (3.7) is a matrix of the form

$$\left({\nabla }_h\widehat{u}\right)=\frac{1}{h}\left(\begin{array}{lll}\text{diag}\left(D_1{\widehat{u}}^1\right)\hfill & \text{diag}\left(D_2{\widehat{u}}^1\right)\hfill & \text{diag}\left(D_3{\widehat{u}}^1\right)\hfill \\ \text{diag}\left(D_1{\widehat{u}}^2\right)\hfill & \text{diag}\left(D_2{\widehat{u}}^2\right)\hfill & \text{diag}\left(D_3{\widehat{u}}^2\right)\hfill \\ \text{diag}\left(D_1{\widehat{u}}^3\right)\hfill & \text{diag}\left(D_2{\widehat{u}}^3\right)\hfill & \text{diag}\left(D_3{\widehat{u}}^3\right)\hfill \end{array}\right),$$ (3.8)

where D_j is a matrix of long differences in the j^th direction. To obtain a consistent discretization of the Laplacian we use a standard discretization (5 point stencil in 2D and 7 point stencil in 3D) with Dirichlet boundary conditions. Finally, we employ short differences in one direction averaged in the other direction to obtain a cell centered approximation of ∇ × u.

3.2 Computation of a step

The computation of each step requires two parts. Firstly, the solution of (3.7) and secondly, a way to determine if it is an acceptable step. The solution of the system (3.7) is straightforward. Any fast Poisson solver can be used for the task. Here we have used a standard multigrid method with weighted Jacobi smoothing, bilinear prolongation and its adjoint as a restriction.

The validity of the update is determined using the following procedure. Assume that at iteration n we have û_n as an approximation to u and that we computed δû. The update is then performed using,

$${\widehat{u}}_{n+1}=\mathcal{P}\left({\widehat{u}}_n+\mathrm{\alpha }\mathrm{\delta }\widehat{u}\right),$$ (3.9)

where $\mathcal{P}$ is an orthogonal projection discussed in Section 3.3 below, that projects û_n + αδû into the mass preserving manifold. The step size α is then chosen such that the objective function is decreased and that the real part of the eigenvalues of (∇_hû) is positive. The whole algorithm is outlined Algorithm 1.

Algorithm 1.

Solution of OMT:

û ← OMTsol(μ0, μ1);

Use μ0 and μ1 to compute a mass preserving u0

while true do

Solve (3.7) for δû

line search: set α = 1

while true do

${\widehat{u}}_{n+1}=\mathcal{P}\left({\widehat{u}}_n+\mathrm{\alpha }\mathrm{\delta }\widehat{u}\right)$

$\mathrm{if}{\Vert {\widehat{u}}_{n+1}-x\Vert }_{\mu 0}<{\Vert {\widehat{u}}_n-x\Vert }_{\mu 0}\text{and}Re\left(\mathrm{\lambda }\left({\nabla }_h{u}_{n+1}\right)\right)>0\mathrm{then}$

Break

end if

α ⇐ α/2

end while

end while

3.3 Orthogonal projection into the mass preserving constraint

Assume that we have computed a mass preserving mapping û_n, and that we have updated it to obtain v_n = û_n +αδû. It should be noted that an infinitesimal δû does not guarantee mass preservation. Furthermore, we aim to take large steps in δû, and therefore the MP constraint is likely to be invalid. To correct for this we use orthogonal projections. The goal is to compute a vector field δv such that c(v + δv) = 0. Obviously, δv is non-unique and therefore we seek a minimum norm solution that is we seek δv such that

$$\underset{v}{min}\frac{1}{2}{\Vert \mathrm{\delta }v\Vert }_{{\mu }_0}^2\text{subject}\text{to}c\left(\mathrm{\delta }v\right)={\mu }_0\left(v+\mathrm{\delta }v\right)\text{det}\left(\nabla \left(v+\mathrm{\delta }v\right)\right)-{\mu }_1=0.$$

It is easy to verify that a correction for δv can be obtained by solving the system $\mathrm{\delta }v\approx c_v^{\top }{\left(c_v{c}_v^{\top }\right)}^{-1}c\left(v\right)$. The system $c_v{c}_c^{\top }$ can be thought as an elliptic system of equations. The system is solved using preconditioned conjugate gradient with an incomplete Cholesky preconditioner.

4 Registration of Brain Data

Our goal is the identification of cortical structures by mapping a publicly available atlas[14] to the scan of a patient. In our scenario, the scanning sequence of the atlas is very different from the one of the patient. The MRI of the atlas is a spoiled gradient recalled image acquired on a 1.5-Tesla General Electric Signa System (GE Medical Systems, Milwaukee) with 256×256×124 voxels and voxel dimension of 0.92 × 0.92 × 1.5 mm. The patient scan is a MPRAGE acquired on a Siemens 3T long bore machine using a 8 channel head coil. The resolution of the scan is 256 × 256 × 144 with voxel dimension 0.54 × 0.54 × 1.0 mm (See Figure 1(b).

Figure 1.

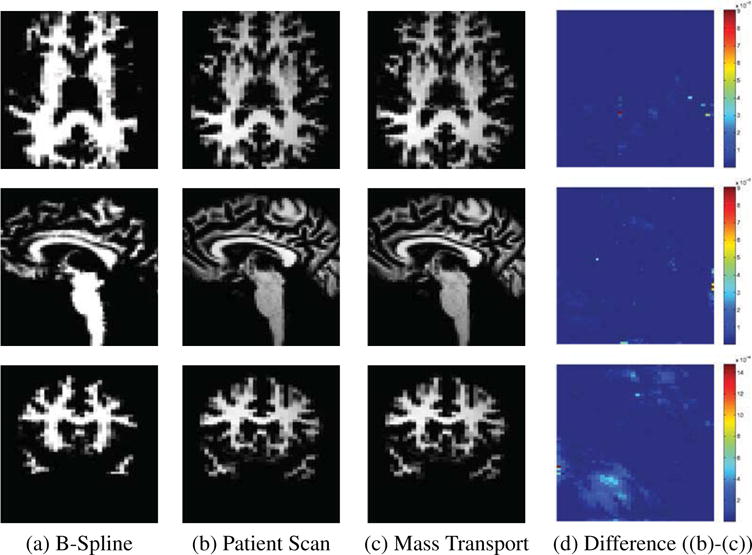
Registration results.

The parcellation of the cortex can be encoded by partitioning the boundary between cortex and white matter into anatomical regions [9]. The label map of cortical structures can then be inferred from this partition by propagating the labeling along the boundary to the entire cortex. The pipeline described below will apply this concept for the parcellation of the cortex to the high resolution scan.

The input of the pipeline consist of the atlas, the high resolution scan as well as a segmentation of the scan into the major tissue classes. In the first step, we coarsely align the atlas to the image data using the B-spline implementation by Rohlfinger[19] with a final spacing of the grid nodes of 2.5 mm. This results in a coarse alignment of the scans. The algorithm has difficulties in mapping the folds of the white matter due to the inherent constraints of the B-spline representation. We then reduce the atlas to the white matter including the parcellation of the cortex along the boundary between gray and white matter (see Figure 1(a)). Afterwards, we refine the alignment of this new atlas to the white matter of the high resolution scan using our Optimal Mass Transport registration approach. Registration using Optimal Mass Transport is a highly flexible approach that is, unlike B-Splines, not constrained to a set of control points. The intensities in the two input datasets are first normalized and rescaled to make sure that both have the same total mass. The white matter registration with the proposed algorithm took just 12 iterations to converge with 2 iterations of the projection to constraint per iteration. This is a huge improvement over algorithm proposed in [12] where thousands of iterations were required for convergence with roughly the same computational complexity per iteration. The ∇ × u (convergence metric) was reduced to an order of 10⁻³ indicating an optimal map. Figure 1(c) shows the resampled images with 3D views of the corresponding deformation grid in Figure 2. The difference (Figure 1(d)) between target (Figure 1(b)) and resampled image indicates that our approach accurately aligned the folds. After this local alignment, the folds of the atlas should perfectly align with the ones of the high resolution scan. The parcellation of the folds of the atlas, therefore, also encodes the parcellation of the same region in the high resolution scan. We then complete the cortex parcellation of the high resolution scan by confining the Voronoi diagram of the aligned atlas to the gray matter mask of the high resolution scan. The results in Figure 3 show the corresponding segmentation when applying the deformation map of the B-Spline registration and our approach to the the label map of [14], and propagating the labels to the cortex via the Voronoi diagram.

Figure 2.

Deformed Grid on white matter Slices (left) and 3D volume (right).

Figure 3.

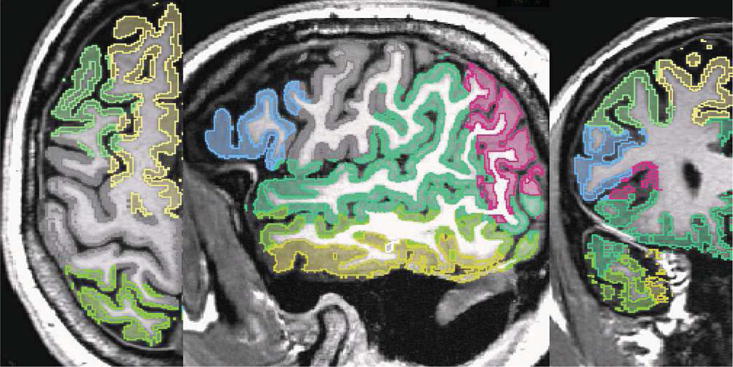
Parecellation results

We are aware of the variety of other methods for registering and segmenting cortical structures. We also note that our segmentation results are by no means perfect. However, to the best of our knowledge, this is the first time in medical imaging that a parameter-free registration tool has been used for registering the cortical folds of 3D MRIs.

5 Conclusions

The difficulties of aligning cortical folds is reflected by the large body of literature discussing this topic. Registration approaches based on continuum and fluid mechanics are often applied to this problem. However, the accuracy of these approaches generally depends on how well they are tuned to the sequence of patient scan. We view Optimal Mass Transport (OMT) as part of these types of registration approaches. Unlike the current state of the art, OMT is parameter free. It is, therefore, especially suited to align new acquisition sequences, which the other methods have not yet been tuned to.

In this paper we presented an efficient variational methodology for the computation of the optimal L² mass transport mapping based on the formulation of [12]. Although, the theory was rigorous in [12], the proposed numerics were problematic. All of these problems have been addressed in our approach. This has lead to an efficient robust elastic deformation algorithm which is guaranteed to converge to the optimal solution of the Monge-Kantorovich problem. We applied the approach to register the white matter between two MRI datasets. We then use the results to resample the label map of the source providing us with a parcellation of the cortex of the target image. We note that the approach is applicable to a whole range of registration and image morphing problems where the mass preservation constraint makes sense. Based on deriving this numerical framework, we are quite sure that in the near future we will be able to provide cases in which we show superior performance to other well established tools in the community. Finally, the set-up can be extended directly to optimal transport on a manifold as in [4].