Temporally Factorized Network Modeling for Evolutionary Network Analysis

Abstract

The problem of evolutionary network analysis has gained increasing attention in recent years, because of an increasing number of networks, which are encountered in temporal settings. For example, social networks, communication networks, and information networks continuously evolve over time, and it is desirable to learn interesting trends about how the network structure evolves over time, and in terms of other interesting trends. One challenging aspect of networks is that they are inherently resistant to parametric modeling, which allows us to truly express the edges in the network as functions of time. This is because, unlike multidimensional data, the edges in the network reflect interactions among nodes, and it is difficult to independently model the edge as a function of time, without taking into account its correlations and interactions with neighboring edges. Fortunately, we show that it is indeed possible to achieve this goal with the use of a matrix factorization, in which the entries are parameterized by time. This approach allows us to represent the edge structure of the network purely as a function of time, and predict the evolution of the network over time. This opens the possibility of using the approach for a wide variety of temporal network analysis problems, such as predicting future trends in structures, predicting links, and node-centric anomaly/event detection. This flexibility is because of the general way in which the approach allows us to express the structure of the network as a function of time. We present a number of experimental results on a number of temporal data sets showing the effectiveness of the approach.

1. INTRODUCTION

Temporal networks have become ubiquitous because of the numerous applications that generate network structures in a time-dependent way. In recent years, a significant amount of work has been done on the area of evolutionary network analysis [1, 2], which examines various problems in the context of network evolution. Some examples of such problems are as follows:

• Based on the trends in the past, which links are most likely to be received at a future point in time? How does the likelihood change with increasing value of time. Note that this is a more refined problem than traditional link prediction [3, 4], in which one simply predicts the links based on a static state of the network.

• How do communities evolve over time? Which communities grow, and which ones shrink? Which ones are expected to grow in the future? Numerous works have been proposed in this context [5, 6, 7], although none of these methods fully capture the evolving nature of the underlying network.

• One would like to predict surprising or anomalous events in different regions of the networks [8, 9, 10]. These could represent sudden regions of change [10], or other structural changes in the network [6].

Although many individual solutions exist for these problems, a broader question is whether we can directly characterize the structure of the network as a function of time. The ability to characterize the structure of the network as a function of time is crucial in using it in different application settings, because such a characterization can capture very rich information about the structure of the underlying network. In this paper, we discuss one such model, with the use of matrix factorization methods.

Matrix factorization is a natural method to express the evolutionary structure of networks because of its ability to leverage the structural correlations among the edges in the network. The basic idea of temporal matrix factorization methods is to extract a low rank representation of the underlying adjacency matrices, in a way which are parameterized with time, as shown in Figure 1. This temporally parameterized factorization can be used to reconstruct the structure of the network at any time t, including at times in the past or future where the network has not been observed. This ability to reconstruct the adjacency structure of the network at any time t is crucial; it allows one to make far more general predictions. Furthermore, it can be viewed as a compressed representation of not just the current state of the network, but the entire dynamic profile of the network over time. This comprehensive characterization is crucial in enabling an effective solution to a variety of problems. We view our solution as generic, as it is not specific to a particular problem, but it enables solutions across a wider variety of settings.

Figure 1.

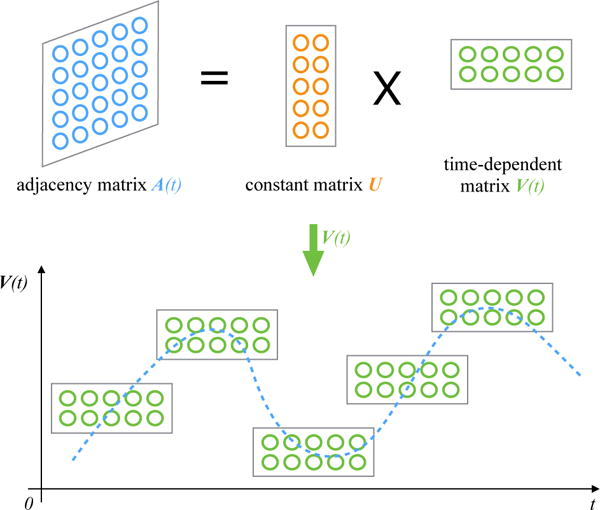
Illustration of Temporal Matrix Factorization Model

The rest of the paper is organized as follows. Section 2 introduces the temporal matrix factorization model and its solutions. Section 3 presents the methods and experimental results of temporal matrix factorization model in link prediction, including link-weight prediction and new link prediction. Sections 4 and 5 describe the use of temporal matrix factorization model in event detection and evolving community detection, respectively. The survey of the related work is presented in Section 6. Finally, we conclude in Section 7.

2. THE TEMPORAL MATRIX FACTORIZATION MODEL

In this section, we will first introduce the problem setting, and then discuss the temporal matrix factorization model (short for TMF) for dynamic network analysis. In the following, we will generally assume that we have a temporal network G(t) = (N, A(t)), where N is set of nodes in the networks, and A(t) is the adjacency matrix of the edges, as a function of time. We assume that the size of A(t) = [a_ijt] is n × n, where |N| = n. For unweighted networks, the matrix A(t) is binary, whereas for weighted networks, the matrix A(t) might contain arbitrary weights which change with time. For example, in the case of the DBLP network, a_ijt might represent the number of publications between authors i and j at time t. These weights might even be negative for dynamic signed networks such as a dynamic Epinions network with shifting trust relationships. In general, the way in which A(t) changes will depend on the specific application at hand, and it is completely agnostic to the model discussed in our paper. It is assumed that the time stamp t is a continuous variable that varies from 1 through T.

Note that the set of nodes in the current state of the network is also a function of time, but in practice, one can only work with the set of nodes that one has seen so far historically. Therefore, the set N is fixed to the union of all nodes received so far at the current time t, at which the analysis is performed. It is generally relatively easy to also provide estimations of the number of new nodes that various parts of the network can receive as neighbors in the future. If the network G(t) is directed, the basic temporal rank-k matrix factorization model assumes that the matrix A(t) can be factorized as follows:

$$\mathit{A}\left(t\right)=f(\mathit{UV}{\left(t\right)}^T)$$ (1)

Here, both U and V (t) are n × k matrices. The main difference between U and V(t) is that U is a constant matrix and V (t) is time-dependent. The function f (·) is an elementwise function on elements of the matrix in UV(t), which is useful in certain settings. For example, if the elements in A(t) are normalized to the range (0,1), then one can use a logistic function for f (·).

Obviously, results from Eq.(1) are trivially generalizable to undirected networks, since undirected networks are special cases of directed networks. For undirected networks, the matrix A(t) is symmetric. We can simply average UV(t)^T and its transpose as the prediction of A(t). It can also be factorized as the product of a time-dependent matrix V(t) and its transpose:

$$\mathit{A}\left(t\right)=f(\mathit{V}\left(t\right)\mathit{V}{\left(t\right)}^T)$$ (2)

Note that one can also make both U and V(t) time-dependent, although the simpler model can often achieve good approximations and avoid overfitting. Furthermore, it is also possible to make U time-dependent instead of V(t) to achieve similar results. It is possible to simplify the aforementioned relation, by not using a functional transformation f (·), and simply expressing A(t) as follows:

$$\mathit{A}\left(t\right)=\mathit{UV}{\left(t\right)}^T\text{or}\mathit{A}\left(t\right)=\mathit{V}\left(t\right)\mathit{V}{\left(t\right)}^T$$ (3)

The function V(t) can take on any canonical form, such as linear models, polynomial models, and so on. The choice of models is, however, orthogonal to the key ideas in this paper as shown in Section 2.1.

How does one determine the values of U and V(t) ? The standard approach in matrix factorization is to set up a least squares optimization problem, so that the A(t) matches f (UV (t)^T) as closely as possible. This can be achieved by minimizing the sum of the squares of the entries in A(t) − f(UV(t)^T). Therefore, one can express this optimization problem as the minimization of the time-decayed sum of the Frobenius norms of the matrix A(t) − f (UV(t)^T) over all values of t from 1 to the current time T.

$$\underset{\mathit{U},\mathit{V}}{\min }J\left(\mathit{U},\mathit{V}\right)={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}{\Vert \mathit{A}\left(t\right)-f\left(\mathit{UV}{\left(t\right)}^T\right)\Vert }_F^2}$$ (4)

Here, D(t) is a decay function with time t that regulates the greater importance of the current state of the network with respect to the past time stamps. For example, one might choose the decay function as the exponential decay function with parameter θ > 0:

$$D\left(t\right)=e^{-\theta \left(T-t\right)}$$ (5)

One challenge with the use of this approach is that the network may be very large, and only a small number of edges may be present in A(t). For a network with n nodes, the O(n²) objective function expressed above might simply be computationally too expensive to even represent effectively. In such cases, the presence of an edge between a pair of nodes in A(t) is more significant than the absence of an edge. The absence of an edge, in fact, often conveys far more noisy information in real settings. Therefore, the aforementioned objective function should be tailored to edge presence rather than edge absence. However, we do need a sample of absent edges to properly train the model. Let S(t) be a sample of edges (i,j) at time-stamp t such that the value of a_ijt is 0. At time t, let E(t) be the set of edges for which the weights in A(t) are non-zero at time t. Therefore, we have the following:

$$E\left(t\right)=\{\left(i,j\right)|a_{\mathit{ijt}}>0\}\cup S\left(t\right)$$ (6)

Note that the size of the set E(t) is much smaller than O(n²) because real networks are sparse in real settings. Then, one can express the aforementioned objective function in terms of the edges that are present in the network as follows:

$$J\left(\mathit{U},\mathit{V}\right)={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}{\displaystyle \sum _{\left(i,j\right)\in E\left(t\right)}{(a_{\mathit{ijt}}-f{(\mathit{UV}{\left(t\right)}^T)}_{ij})}^2}}$$ (7)

Similarly, for undirected network we have

$$J\left(\mathit{V}\right)={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}{\displaystyle \sum _{\left(i,j\right)\in E\left(t\right)}{(a_{\mathit{ijt}}-f{(\mathit{V}\left(t\right)\mathit{V}{\left(t\right)}^T)}_{ij})}^2}}$$ (8)

Note that the number of terms in this objective is dependent on the number of edges in the network, which is much easier to handle in practical settings. We also need to add a regularization term to reduce the model variance. However, the specific regularization term will be discussed in the next section, because it depends on the choice of the temporal function V (t).

2.1 Model Choices

In this section, we will set up various forms of the model for various choices of f(·), and V(t). One typical choice for f(·) include the use of the identity function, and that for V(t) is a polynomial function. In such a case, we can represent V (t) as follows:

$$\mathit{V}\left(t\right)={\mathit{W}}^{\left(0\right)}+{\mathit{W}}^{\left(1\right)}t+\dots +{\mathit{W}}^{\left(d\right)}{t}^d={\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}{t}^i}$$ (9)

Here ${\{{\mathit{W}}^{\left(i\right)}\}}_{i=0}^d$ are all n × k matrices, which need to be learned from the model along with U. d ∈ N₊ and d≥ 1, when d = 1, V(t) is the simplest linear function. Given the definition of V(t), the matrix form of Eq.(7) becomes the following with added regularization:

$$J\left(\mathit{U},\mathit{W}\right)={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}\Vert 1_{E\left(t\right)}(\mathit{A}\left(t\right)-\mathit{U}{({\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}{t}^i})}^T){\Vert }_F^2+\frac{\alpha }{2}\Vert \mathit{U}{\Vert }_F^2+{\displaystyle \sum _{i=0}^d\frac{{\beta }_i}{2}\Vert {\mathit{W}}^{\left(i\right)}{\Vert }_F^2}}$$ (10)

where,

$$1_{E\left(t\right)}\left(X\right)=\{\begin{array}{cc}{X}_{ij}& \mathrm{if}\left(i,j\right)\in E\left(t\right),\\ 0& \mathrm{if}\left(i,j\right)\notin E\left(t\right).\end{array}$$ (11)

The regularization terms add the Frobenius norms of the matrices U and W⁽ⁱ⁾, so as to minimize overfitting. Similarly, for undirected graphs, we obtain the following loss function:

$$J\left(\mathit{W}\right)={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}\Vert 1_{E\left(t\right)}(\mathit{A}(t)-({\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}{t}^i}){({\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}{t}^i})}^T){\Vert }_F^2+{\displaystyle \sum _{i=0}^d\frac{{\beta }_i}{2}\Vert {\mathit{W}}^{\left(i\right)}{\Vert }_F^2}}$$ (12)

2.2 Model Solutions

In this section, we first compute the partial derivatives of objective functions Eq.(10) and Eq.(12), with respect to U and W to derive updates. Then we present the temporal matrix factorization algorithms for both asymmetric and symmetric adjacency matrices.

Consider the model for directed networks, one needs to minimize the loss function J (U, W),

$$\underset{\mathit{U},\mathit{W}}{\min }J\left(\mathit{U},\mathit{W}\right)={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}\Vert 1_{E\left(t\right)}(\mathit{A}(t)-\mathit{U}{({\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}{t}^i})}^T){\Vert }_F^2+\frac{\alpha }{2}\Vert \mathit{U}{\Vert }_F^2+{\displaystyle \sum _{i=0}^d\frac{{\beta }_i}{2}\Vert {\mathit{W}}^{\left(i\right)}{\Vert }_F^2}}$$ (13)

We introduce a “decayed error term” ξ(t) for each time stamp t, as follows:

$$\xi \left(t\right)=D\left(t\right)1_{E\left(t\right)}(\mathit{A}(t)-\mathit{U}{({\displaystyle \sum _{j=0}^d{\mathit{W}}^{\left(j\right)}{t}^j})}^T)$$ (14)

To compute the gradient, we will need to differentiate our error function. Since our function is defined by parameter matrices U and W⁽ⁱ⁾, we will need to compute a partial derivative for each. These derivatives work out to be:

Algorithm 1.

Algorithm for TMF model

Input:	temporal adjacency matrices ${\{A(t)\}}_{t=1}^T$ the order d of V(t) and latent dimension k.
Output:	results of factor matrices U and ${\{{\mathit{W}}^{(i)}\}}_{i=1}^d$ and the predict adjacency matrix A(T + 1).
1.	Set k and d.
2.	Randomly initialize U and ${\{{\mathit{W}}^{(i)}\}}_{i=1}^d$.
3.	while not stopping criterion do
4.	Compute “decayed error term” ξ(t) for each time stamp t.
5.	Compute partial derivatives $\frac{\partial J\left(\mathit{U},\mathit{W}\right)}{\partial \mathit{U}}$ and $\frac{\partial J\left(\mathit{U},\mathit{W}\right)}{\partial {\mathit{W}}^{(i)}}$ using ξ(t) by Eq.(15) and Eq.(16).
6.	Determine the step size λ by line search.
7.	Update $\mathit{U}=\mathit{U}-\lambda \frac{\partial J\left(\mathit{U},\mathit{W}\right)}{\partial \mathit{U}}$
8.	for i = 1,…,d do
9.	Update ${\mathit{W}}^{(i)}={\mathit{W}}^{(i)}-\lambda \frac{\partial J\left(\mathit{U},\mathit{W}\right)}{\partial {\mathit{W}}^{(i)}}$
10.	end
11.	end
12.	Compute predict adjacency matrix $A\left(T+1\right)=\mathit{UV}{\left(T+1\right)}^T=\mathit{U}{({\displaystyle {\sum }_{i=0}^d{\mathit{W}}^{(i)}}{(T+1)}^i)}^T$

$$\frac{\partial J\left(\mathit{U},\mathit{W}\right)}{\partial \mathit{U}}={\displaystyle \sum _{t=1}^T\xi \left(t\right)(-{\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}{t}^i})+\alpha \mathit{U}}$$ (15)

$$\frac{\partial J\left(\mathit{U},\mathit{W}\right)}{\partial {\mathit{W}}^{\left(i\right)}}={\displaystyle \sum _{t=1}^T\xi {\left(t\right)}^T}(-\mathit{U}{t}^i)+{\beta }_i{\mathit{W}}^{\left(i\right)}$$ (16)

We now have all the derivatives needed to run gradient descent. Pseudocode of the full approach is given in Algorithm 1, where λ is the learning rate. To train this model, we can now repeatedly take steps of gradient descent to reduce our cost function J(U, W). Note that TMF is a general framework, which can be adapted for both directed and undirected networks.

For undirected networks, the adjacency matrices are symmetric, thus we can leverage symmetric matrix factorization technique [11] to deal with the undirected networks. Then one needs to minimize the loss function J(W),

$$J(\mathit{W})={\displaystyle \sum _{t=1}^T\frac{D\left(t\right)}{2}\Vert 1_{E\left(t\right)}(\mathit{A}(t)-({\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}}{t}^i){({\displaystyle \sum _{i=0}^d{\mathit{W}}^{\left(i\right)}}{t}^i)}^T){\Vert }_F^2+{\displaystyle \sum _{i=0}^d\frac{{\beta }_i}{2}}\Vert {\mathit{W}}^{\left(i\right)}}{\Vert }_F^2$$ (17)

In order to infer the parameter W, we need to compute the derivatives of Eq.(17). Similar to the derivative calculation for directed network model, we introduce an “error term” ψ(t) for each time stamp t of undirected networks, as follows:

$$\psi \left(t\right)=1_{E\left(t\right)}(\mathit{A}(t)-({\displaystyle \sum _{j=0}^d{\mathit{W}}^{\left(j\right)}}{t}^j){({\displaystyle \sum _{j=0}^d{\mathit{W}}^{\left(j\right)}}{t}^j)}^T)$$ (18)

Note that, the error matrix in ψ(t) has already projected to indices set defined by E(t). Thus, the derivatives of Eq.(17) with regularization term can be calculated as,

$$\frac{\partial J\left(\mathit{W}\right)}{\partial {\mathit{W}}^{\left(i\right)}}=-{\displaystyle \sum _{t=1}^{T}D\left(t\right)(\psi \left(t\right)}{\displaystyle \sum _{j=0}^d{\mathit{W}}^{\left(j\right)}}{t}^j+\psi {\left(t\right)}^T{\displaystyle \sum _{j=0}^d{\mathit{W}}^{\left(j\right)}}{t}^j)t^i+{\beta }_i{\mathit{W}}^{\left(i\right)}$$ (19)

2.3 Computational Analysis

To help in analyzing the complexity of the algorithm, we assume that the number of nodes in G(N, A(t)) is n, the number of edges is m, and the rank of the factorization is k. The gradient-descent method is implemented for M iterations. Here, d is the (polynomial) order of the time-dependent matrix V(t). Furthermore, it is assumed that there are T time-stamps for the temporal method.

In each of the M iterations, the bottleneck step involves updating all the parameters. The number of parameters in U is nk. The same number for V(t) is nk(d+1), because we need to sum over the d polynomial orders. for ${\{{\mathit{W}}^{(i)}\}}_{i=1}^d$, respectively. For the derivative computation of each parameter, one needs to multiply the corresponding k dimensional columns of matrices U and ${\displaystyle {\sum }_{i=0}^d{\mathit{W}}^{\left(i\right)}}{t}^i$, and then compute the derivative. This requires time of the order of magnitude of the sum of the corresponding node degrees in the adjacency matrix A(t). By summing up these costs, we obtain:

$$MT{\displaystyle \sum _{\{i,j\}\in \mathit{U}}({\mathit{degree}}_{i,j}}+kd)+MT{\displaystyle \sum _{\{i,j\}\in \mathit{W}}({\mathit{degree}}_{i,j}}+kd)=\mathit{MTmk}\left(d+2\right)+\mathit{MTn}{k}^{2}d\left(d+2\right)$$ (20)

The order d of the polynomial is set to a small number such as 1 or 2. Thus, the asymptotic running time is O(MTmk + MTnk²). Since M, T and k are much smaller than n and m, the time complexity is approximately O(m+ n).

2.4 Leveraging the Factorization in Different Application Settings

The most interesting aspect of the models discussed in this section is its extraordinary generality in terms of its applicability to various settings. Most of the existing methods for evolutionary network analysis [1] are focused on specific problems like link prediction [4], dynamic community detection [5, 6, 7, 12, 13], anomaly detection [9, 10] and compression [14]. Here we provide a very general purpose framework TMF and symmetric TMF (s-TMF), which can perform almost all of these tasks within a single unified approach. In the following sections, we will describe how the methods described in this section can be used to accomplish these tasks.

3. TEMPORAL MATRIX FACTORIZATION MODEL IN LINK PREDICTION

Link prediction and network reconstruction are almost trivial in this setting because the entire network is expressed as a function of time with the use of latent variables. The main advantage of link prediction with temporal matrix factorization model over traditional link prediction methods is that it can not only predict new links at any time T in the future, but also predict the weight of each link. Note that traditional link prediction is only able to predict new links at “some” point in the future based on the current snapshot, but it does not really provide temporally sensitive analysis. Given the advantages of the proposed model described above, we evaluate the performance of the TMF model and symmetric TMF (s-TMF) model in two aspects, corresponding to link-weight prediction and new link prediction.

3.1 Dataset Description

To verify the performance of the proposed model, we conducted experiments on a variety of dynamic networks from different domains as shown in Table 1. First three networks, UCI Messages, Digg and Epinions, are directed and the rest three are undirected. Note that the symmetric algorithm is relevant only to the undirected setting.

Table 1.

Temporal dataset description

Dataset	Vertices	Edges	Max Weight	|T|
UCI Messages	1,899	20,296	98	7 months
Digg	30,398	86,404	25	14 days
Epinions	131,828	841,372	1	32 months
Infectious	410	2,765	191	8 hours
arXiv hep-th	6,798	214,693	66	7 years
DBLP	315,159	743,709	159	34 years

UCI Messages (directed) [15]

This directed network is based on an online community of students at the University of California, Irvine. A node represents a user that has sent or received messages. The weight of a directed edge represents the number of sent messages.

Digg (directed)¹

This is the reply network of the news aggregator website digg.com. Each node is a Website user, and each weighted edge denotes the number of replies.

Epinions (directed) [16]

This is the trust and distrust network of Epinions, an online product rating site. The network contains individual users connected by directed trust and distrust links. Edges have the weight 1 for trust and −1 for distrust.

Infectious (undirected) [17]

This network contains the daily dynamic contact networks collected during the Infectious SocioPatterns event that took place at the Science Gallery in Dublin, Ireland. Nodes represent exhibition visitors; edge weights represent face-to-face contact times.

arXiv hep-th (undirected) [18]

This collaboration network is from arXiv and covers scientific collaborations between authors and papers submitted to High Energy Physics - Theory category (hep-th). Nodes represent the authors, and edge weights between two authors represents the number of coauthored publications. Time-stamps denote the date of a publication.

DBLP (undirected)²

This undirected collaboration graph of authors is from the DBLP computer science bibliography. Similar to arXiv hep-th, the nodes in this network represent the authors, and edge weights represent the number of co-authorships between two authors.

3.2 Comparative Methods

The comparative methods used in this paper are summarized as follows. We consider the canonical link prediction methods as well as recent algorithms. Let Γ(x) denote the set of neighbors of node x in network G(N, A(t)), and w_x,y denote the link weights between nodes x and y.

Common Neighbors (CN) [19]

For any pair of nodes x and y, the link prediction strategy is to define the score(x, y) = |Γ(x) ∩ Γ(y)|, the number of common neighbors between x and y. The weighted version of common neighbors (w-CN) [20, 21] is defined as $\mathit{score}\left(x,y\right)={\displaystyle {\sum }_{z\in \mathrm{\Gamma }\left(x\right)\cap \mathrm{\Gamma }\left(y\right)}\frac{w_{x,z}+w_{y,z}}{2}}$, but here we normalize the score by the size of common neighbors, thus $\mathit{score}\left(x,y\right)=\frac{1}{|\mathrm{\Gamma }\left(x\right)\cap \mathrm{\Gamma }\left(y\right)|}{\displaystyle {\sum }_{z\in \mathrm{\Gamma }\left(x\right)\cap \mathrm{\Gamma }\left(y\right)}\frac{w_{x,z}+w_{y,z}}{2}}$.

Adamic Adar (AA) [22]

This method assigns larger weights to less-connected neighbors. The weighted version (w-AA) [20, 21] is $\mathit{score}\left(x,y\right)={\displaystyle {\sum }_{z\in \mathrm{\Gamma }\left(x\right)\cap \mathrm{\Gamma }\left(y\right)}\frac{w_{x,z}+w_{y,z}}{2}}\times \frac{1}{\log \left(1+s_z\right)}$, where s_z=Σ_z′∈Γ(z)w_z,z′.

High-performance Link Prediction (HPLP) [23]

This is a supervised classification framework to predict the new links. The weighted version (w-HPLP) is using the same features to train a regression model to predict the link weights.

Preferential Attachment (PA) [24]

This unweighted method corresponds to the measure score(x,y) = |Γ(x)|·|Γ(y)|. The basic premise is that the probability that a new edge involves node x is proportional to |Γ(x)|.

Nonparametric Link Prediction (NP) [25]

This method predicts links based on the features of its endpoints, as well as those of the local neighborhood around the endpoints.

Link Prediction via Matrix Factorization (Fact-Sq) [26]

This method solves the link prediction problem in graphs using a matrix factorization based approach. This baseline uses the square loss and the same latent dimension k as the proposed model in this paper.

CP Tensor Model (CP-Tensor) [27]

This is a tensor-based method for predicting future links for bipartite graphs that evolve over time. In our problem setting, we apply this method to homogeneous graphs.

Our models are denoted as TMF and s-TMF, respectively, where the term s stands for symmetric. We attach a suffix (say, d=1), to represent the order of V (t) for the corresponding model.

3.3 Link Weight Prediction

In this section, we evaluate the link-weight prediction accuracy of each method. For each of the six networks, three directed networks (asymmetric adjacency matrices) and three undirected networks (symmetric adjacency matrices), we choose the first T − 1 time-stamps as training set, and the T^th time-stamp as test set, here T varies from 2 to the total time-stamps of each dataset. We analyze the algorithms by measuring the accuracy of the weight prediction based on root mean-squared error (RMSE). We obtained the RMSE at different T for link prediction as presented in Figure 2.

Figure 2.

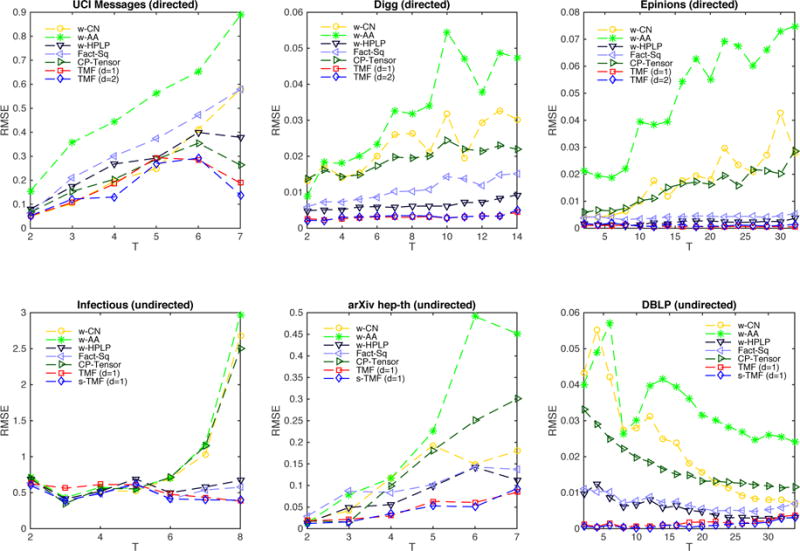
Prediction RMSE at time-stamp T (training with first T − 1 time-stamps)

For the first three directed networks UCI Messages, Digg and Epinions in Figure 2, we compute the RMSE of all five weighted baselines and our models TMF. Here we set d, the order of the time-dependent matrix, V (t), to 1 (linear) and 2 (quadratic). The other parameter settings are as follows: latent dimension k = 10, exponential decay function parameter θ = 0.3, regularizer weights α = β_i = 0.01. The maximum iteration of TMF models is set to 500. The upper three figures show that the best prediction results are achieved by our TMF models, namely TMF (d=1) and TMF (d=2). The performance of TMF models are very similar with respect to different values of d. The RMSE of TMF models in the last time-stamp of these three directed networks are only 15.58%, 9.49% and 1.34% of the worst baseline, and 36.48%, 48.39% and 26.89% of the best baseline.

For the lower three undirected networks, referred to as Infectious, arXiv hep-th and DBLP in Figure 2, we compute the RMSE of all five weighted baselines, TMF and symmetric TMF (s-TMF). Note that we can still use the TMF model for the undirected networks. In this case, E(t) in Eq.(6) is the non-zero entries of the upper triangular matrices of the undirected networks. In these detailed figures, we show the results when d = 1 (since the results are very similar for d = 2) although all results are presented in tabular form in Table 2. All the remaining parameter settings are the same. It is evident that TMF and s-TMF provide the best overall performance, which are consistent with the good performance of different values of T in undirected networks. The average RMSE of s-TMF is smaller than TMF, which will be shown in Table 2. The RMSE of s-TMF models of these three undirected networks are only 9.49%, 16.78% and 9.13% of the worst baseline, and 42.15%, 67.08% and 73.33% of the best baseline, showing the advantage of TMF and s-TMF models in link-weight prediction.

Table 2.

Average RMSE over all time-stamps

Methods	UCI Messages	Digg	Epinions	Infectious	arXiv hep-th	DBLP
w-CN	0.2649	0.0229	0.0171	0.9386	0.1167	0.0227
w-AA	0.5101	0.0325	0.0483	1.0192	0.2295	0.0350
w-HPLP	0.2653	0.0064	0.0021	0.5802	0.0785	0.0056
Fact-Sq	0.3324	0.0107	0.0021	0.5215	0.0970	0.0071
CP-Tensor	0.2215	0.0191	0.0150	0.9321	0.1440	0.0170
TMF (d=1)	0.1853	0.0031	0.0007	0.5304	0.0464	0.0016
TMF (d=2)	0.1673	0.0032	0.0012	0.5398	0.0436	0.0014
s-TMF (d=1)	–	–	–	0.4743	0.0432	0.0011
s-TMF (d=2)	–	–	–	0.4391	0.0427	0.0012
Average	0.2773	0.0139	0.0123	0.6911	0.0986	0.0117

Table 2 displays the average prediction RMSE over all time frames of each dataset. It is evident that TMF and s-TMF models have a lower RMSE than the five weighted baselines. Note that, for undirected networks, s-TMF models always perform better than TMF models, though the RMSE differences are not that large when compare to other baselines. However, the advantage of TMF models is that they can also be applied to directed networks.

Although one might expect the prediction RMSE to decrease with increasing T (and more data), this is not the case for all data sets. It was only in the UCI Messages and Infectious data sets that the RMSE reduced. For the other four datasets, the RMSE increased. The reason is that the network showed increasing rates of evolution over time with rapid formation of new links. As a result, it became harder to predict more accurately with passage of time. Nevertheless, the incorporation of temporal information still has an inherent temporal advantage over the use of static models; this is the reason that the approach outperforms the baselines.

3.4 New Link Prediction

The TMF model is not designed for new link prediction since we use Frobenius norm to define the loss function, as shown in Eq.(10) and Eq.(12). However, one can still apply it to unweighted data sets. In this section, we predict new links using TMF model on Epinions data set in which the maximum link weight is 1.

We measure the accuracy of new link prediction by using the area under curve (AUC) of the receiver operating characteristics (ROC) analysis. The ROC is designed to work in the binary class setting with positive and negative samples. When predicting the new links at time-stamp T, the new edges to be predicted are treated as the “positive” samples. We use the absolute values of our prediction results, so that the new edges (both with +1 weights and −1 weights) to be predicted are treated as the positive samples. We then randomly sample the same number of node pairs without an edge between them at time T as “negative” samples (S(t) in Eq.(6)). The parameter settings remain the same as previous experiments. We compare TMF (d=1) model with six baselines which is shown in Figure 3. In the Epinions network, the TMF model outperforms the baseline methods by 15.53% on average. It outperforms Common Neighbors by more than 21.55% across all time-stamps. We attribute this success to the temporal nature of the factorization that can predict trends over time, rather than simply relying on a static model.

Figure 3.

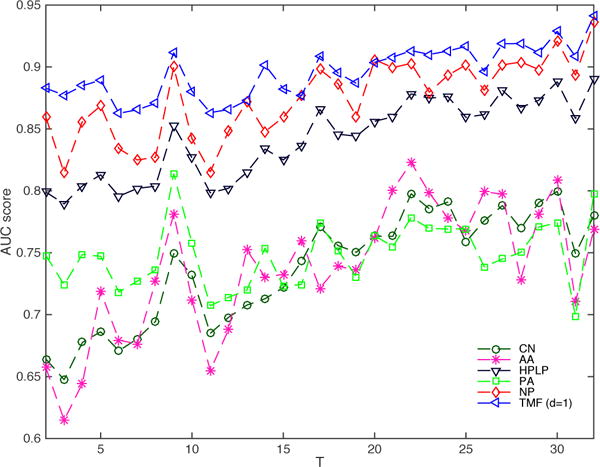
New link prediction AUC at T for Epinions network (training with first T − 1 time-stamps)

3.5 Sensitivity Analysis

The loss function defined by Eq.(10) is dependent on parameters denoted by k, θ and the regularizer weight α and β_i. Normally, we set the regularizer weight to a relatively small value such as 0.01. Therefore, in this section, we conduct sensitivity analysis on k, the latent dimension of V (t) and θ, the parameter of the exponential decay function D(t).

We used the Infectious and UCI Messages data sets for sensitivity analysis; the first is a fast evolving undirected network and the second is a slowly evolving directed network. We choose values between k from 5 to 100 for Infectious and 10 to 300 for UCI Messages The value of θ varied from 0.1 to 1.0 with interval 0.1. The results are summarized in Figure 4. It is evident that RMSE initially improves with k but further improvements are harder beyond a certain point. But from the effectiveness analysis in Section 2.3 we can see that, the time complexity is proportion to O(k²) for fixed networks. Taking both prediction error and computational time into consideration, we will choose a relative small k from 10 to 100.

Figure 4.

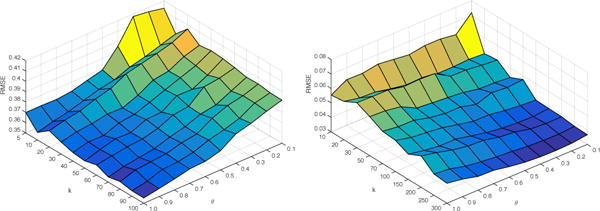
Last time-stamp prediction RMSE of Infectious(top) and UCI Messages(bottom) with different parameter pairs

The value of θ has a significant impact on prediction results, and it is in fact sensitive to the data set. For the Infectious dataset, when θ increases, the proposed model will have a better RMSE. This means that as we assign less weight on the early time-stamps, it will achieve better prediction results. Thus, we can infer that for a fast evolving network, higher exponential weight decay brings better prediction accuracy. For UCI Messages dataset, we obtain a totally different trend. As θ increases, RMSE increases. This means that for a slowly evolving network like UCI Messages, we should assign more weights to the early time-stamps.

4. TEMPORAL MATRIX FACTORIZATION MODEL IN TEMPORAL ANOMALIES AND EVENTS DETECTION

Temporal anomalies and events are often defined by unexpected changes in the network structure over time, which are different from their forecasted values. Consider the scenario, where the training data at time stamps 1 … T has been used to learn the network A(t). We would like to use the learned training data to determine the anomalies in A(T + 1), when the network at time (T + 1) is received. Let the predicted network at time (T + 1) according to the aforementioned model be denoted by Â(T + 1), and the true network state at time (T + 1) be A(T + 1). Then, the unexpected part of the change in network structure, is given by the following:

$$\mathrm{\Delta }\mathit{A}\left(T+1\right)=\widehat{\mathit{A}}\left(T+1\right)-\mathit{A}\left(T+1\right)$$ (21)

Large absolute values in ΔA(T+1) correspond to edges with unusual levels of activity:

$$F\left(t\right)=\{\left(i,j\right):|{\left[\mathrm{\Delta }\mathit{A}\left(T+1\right)\right]}_{ij}|>\delta \}$$ (22)

One can use a Z-statistic or t-statistic over the values of |ΔA(T + 1)| to determine the value of δ at which the change is significant. As in the case of communities, one can discover the connected components in such edge sets, and report the anomalous change regions in the network. It is also possible to discover the individual node hot spots, by first quantifying the level L(T + 1,i) of anomalous activity adjacent to each node i at time (T + 1) as follows:

$$L\left(T+1,i\right)={\displaystyle \sum _{j:\{i,j\}\in F\left(t\right)}|{\left[\mathrm{\Delta }\mathit{A}\left(T+1\right)\right]}_{ij}}|$$ (23)

Nodes with large anomalous values of L(T +1,i) correspond to hot-spots of activity. One can use a Z-statistic or t-statistic to determine thresholds on the value of L(T + 1,i). For example, in a DBLP network, such nodes might correspond to researchers who had a sudden change in their coauthorship activity as a result of an event, such as change of institution. Therefore, the structural and node events tell us a lot about unusual events in the underlying network activity.

4.1 Discovering Temporal Anomalies and Events: A Case Study

In this section, we detect temporal anomalous coauthors and individual authors on DBLP dataset using TMF model. Based on aforementioned analysis, we first show the trends of maximum absolute values in ΔA(T + 1) and maximum anomalous values of level L(T + 1,i). Then we present the top 10 pairs of anomalous coauthors and authors.

The blue dashed line in Figure 5 shows the maximum absolute value in ΔA(T + 1) at each time-stamp T, while the red dashed line shows the maximum anomalous value of L(T + 1,i). Therefore, these two lines respectively represent the trends of top anomalous coauthor and top anomalous author at each time-stamp. It can be seen that as T increases, the anomalous level increases in terms of both quantifications. This can be explained by the fact that recent years have experienced a larger volume of publications; therefore, the corresponding anomalous trends increase in absolute magnitude. Furthermore, the statistical correlation between these two lines is very high (0.9308), which is evidence that anomalous author-events are usually caused by underlying anomalous co-authorship events.

Figure 5.

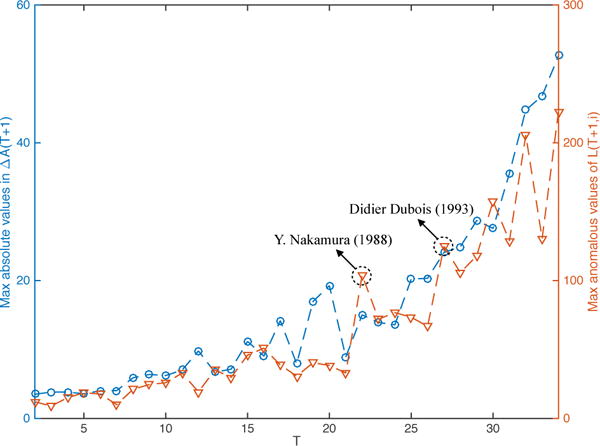
Maximum absolute values in ΔA(T + 1) and maximum anomalous values of L(T + 1,i) of all time-stamps

Additionally, we labeled two anomalous peaks, corresponding to Y. Nakamura (1988) and Didier Dubois (1993) in Figure 5. These two authors represent different types of abnormalities. According to DBLP, Y. Nakamura has only one publication (in 1982) before 1988 but has 15 in 1988, which is unusual. For Didier Dubois, the abnormality is a result of the fact that he has an unusually large number of new coauthors in 1993.

We then detect the anomalous coauthors by calculating the unexpected part of the change ΔA(T + 1) in network structure. Table 3 represents the top 10 pairs of anomalous coauthors sorted by |[ΔA(T + 1)]_ij|. The experiment is conducted with the same parameter settings described in Section 3.3. Surprisingly, the pair of authors Sudhakar M. Reddy and Irith Pomeranz appears 4 times. The total coauthor papers between them from 1997 to 2000 are 92, 116, 135 and 159, respectively. But before 1991, they have no coauthor papers. This could be the reason that why they are titled “top anomalous coauthor” by our model.

Table 3.

Top 10 pairs of anomalous coauthors sorted by |[ΔA(T + 1)]_ij| (denoted as Δ in the table)

#	Δ	Coauthors	Year
1	52.6421	Sudhakar M. Reddy, Irith Pomeranz	1999–2000
2	46.8029	Sudhakar M. Reddy, Irith Pomeranz	1998–1999
3	44.7452	Sudhakar M. Reddy, Irith Pomeranz	1997–1998
4	36.8849	Raj Jain, Sonia Fahmy	1997–1998
5	36.877	Raj Jain, Rohit Goyal	1997–1998
6	35.5676	Sudhakar M. Reddy, Irith Pomeranz	1996–1997
7	35.2318	Divyakant Agrawal, Amr El Abbadi	1999–2000
8	34.876	Sonia Fahmy, Rohit Goyal	1997–1998
9	32.2694	Divyakant Agrawal, Amr El Abbadi	1998–1999
10	30.5123	Didier Dubois, Henri Prade	1997–1998

Additionally, we calculate L(T + 1,i) of all time-stamps and show the top 10 anomalous values in Table 4. We can verify the authors who receive large anomalous values with DBLP database. For example, the DBLP homepage shows that Robin J. Chapman, the top 1 “anomalous” author, had no coauthor paper in 1999, but 21 coauthor papers in 2000³.

Table 4.

Top 10 anomalous authors sorted by the level of anomalous activity L(T + 1,i)

#	L(T + 1,i)	Author	Year
1	222.799	Robin J. Chapman	1999–2000
2	205.561	Hector Garcia-Molina	1997–1998
3	190.993	John H. Lindsey II	1999–2000
4	168.677	Raj Jain	1997–1998
5	157.488	Alberto L. S.-V.	1995–1996
6	152.147	David Callan	1999–2000
7	149.377	Rohit Goyal	1997–1998
8	148.404	Sonia Fahmy	1997–1998
9	147.063	Hugo De Man	1999–2000
10	144.791	Alberto L. S.-V.	1999–2000

5. TEMPORAL MATRIX FACTORIZATION MODEL IN EVOLUTIONARY COMMUNITY ANALYSIS

The temporal matrix factorization approach can be naturally used for discovering the rate of evolution of each edge in the network at any given time t. This may be expressed in the form of the following matrix A′ (t) at any given time t:

$$\mathit{A}\prime \left(t\right)=\frac{\partial \mathit{A}\left(t\right)}{\partial t}=\frac{\partial f\left(\mathit{UV}{\left(t\right)}^T\right)}{\partial t}$$ (24)

Here we only consider the temporal matrix factorization model for directed network, since it is trivially generalizable to undirected network. Note that A′(t) can vary with t, when a nonlinear expression is used for f (UV(t)^T). When a polynomial expression of V(t) is used, the above partial derivative evaluates to

$$\frac{\partial f\left(\mathit{UV}{\left(t\right)}^T\right)}{\partial t}=\mathit{U}{({\displaystyle \sum _{i=1}^d{\mathit{W}}^{\left(i\right)}}{t}^{i-1}i)}^T)$$ (25)

The partial derivative of Eq.(25) is equal to UW⁽¹⁾ when V(t) is linear (i = 1). Note that edges (i,j) for which ${\left[\mathit{A}\prime \left(t\right)\right]}_{ij}={\displaystyle {\sum }_{p=1}^k\left(u_{ip}{\displaystyle {\sum }_{q=1}^d{w}_{jp}^{\left(q\right)}}{t}^{q-1}q\right)>0}$ correspond to edges in which the weights are increasing with time. When the sign is negative, it corresponds to edges with reducing weights. One approach to discover expanding communities, is to isolate the following edge set for some threshold δ > 0:

$$I\left(t\right)=\{\left(i,j\right):{[\mathit{A}\prime \left(t\right)]}_{ij}>\delta \}$$ (26)

The connected components of this network yield the expanding communities. By varying the value of δ, one can obtain expanding communities at different threshold levels of evolution. A similar approach can be used to determine the contracting communities. It is noteworthy that the discovery of expanding or contracting communities is almost trivial once the network has been expressed in functional form.

5.1 Discovering Expanding Communities: A Case Study

Expanding and contracting community detection techniques are essential for finding trends in time-series data, such as the discovery of hot research topics. In this section, we report the expanding community detection examples from the DBLP data set using the TMF model.

In order to interpret each expanding community detected by the proposed model, we label the coauthor edges with their dominant venues (journals or conferences). For example, if author a₁ and a₂ coauthored 10 papers (7 in SIGIR, 2 in WWW and 1 in WSDM), we label the coauthor edge e_a1,a2 with SIGIR. We utilize asymmetric TMF model with linear V(t) in this experiment. The gradient threshold δ is set to 0.01. We filter out the graph noise by building a set of trees using breadth-first search (BFS) over the entire vertex set of the network and then considering only those trees whose vertex set size are at least 4. The other parameter settings remain the same as Section 3.3. The expanding communities are shown in Figure 6.

Figure 6.

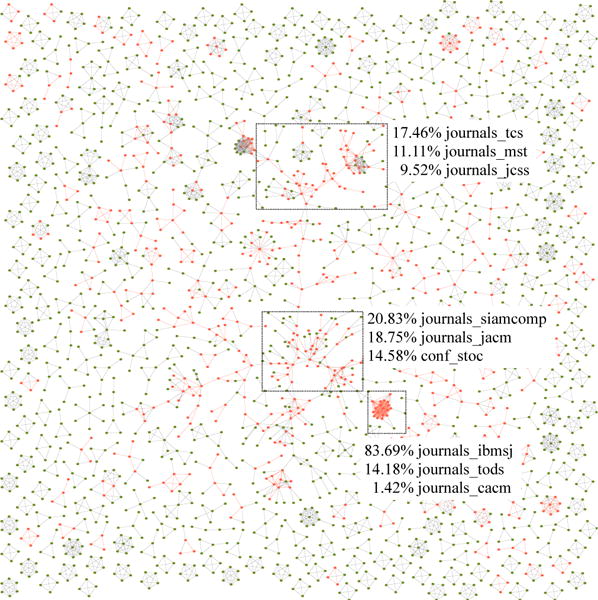
Expanding communities from 1980 to 1981. Edges (i,j) with red color correspond to the gradients that meet [A′(t)]_ij > δ. Three largest expanding communities are marked with rectangles.

Figure 6 illustrates three largest expanding communities in DBLP from 1980 to 1981. The top three venues of each community are also listed. It can be seen that, the largest expanding community has 17.46%, 11.11% and 9.52% of the weight increasing edges labeled with journals_tcs (Theoretical Computer Science), journals_mst (Mathematical Systems Theory) and journals_jcss (Journal of Computer and System Sciences). Notably, these three venues belong to the same area Computer Science Theory which is consistent with the increasing prominence of theoretical computer science in the early eighties. Similar analytical results were obtained from the other two expanding communities. Among the edges with increasing weight, the second community has 20.83%, 18.75% and 14.58% of the edges labeled with journals_siamcomp (SIAM Journal on Computing), journals_jacm (Journal of the ACM) and conf_stoc (Symposium on Theory of Computing). These venues also tend to contain theoretical topics. The third community is a highly compact sub-network where 83.69% edges are labeled with journals_ibmsj (IBM Systems Journal).

Another interesting finding from Figure 6 is that most of the cliques contain fewer edges with increasing weight. This means that stable groups of persistent co-authors often have a tendency to not evolve too much with time. This is consistent with the intuition that most evolution in network structures is caused by dynamically changing co-authorships. On the other hand, connected components with a greater number of branches also tend to have more edges with increasing weight. This is because these components contain groups of authors that are more open to initiating new cross-collaborations with different groups. In these sense evolutionary community detection can provide insights about the causality of the underlying network changes because of its summary representation.

6. RELATED WORK

Evolutionary networks [1, 2] have recently found increasing importance because of their numerous applications for trend detection in the network. Numerous methods have been proposed in the context of dynamic community detection [5, 6, 12, 7], link prediction [4, 20, 21], compression [14], mixed membership modeling [28, 29], and anomaly detection [9, 10]. The approach in [29] uses non-negative matrix factorization to extract features in a sequence of graphs which is different from the structural factorization model in the paper. The applications in [29] are implicitly regulated by the nature of the node features that are extracted, and cannot fully characterize the structure of the network over time or directly express the network structure as a function of time, once the features have been extracted. The fully parameterized model in this paper is more general, and it can be used to reconstruct the approximate future structure in the network at any point in time. Recently, some interest has been focused on the use of rth order tensors [3, 30] for expressing dynamic networks. Tensors are, however, inherently designed for the case when the other (r − 2) dimensions of interest (than source node and destination node) are discrete variables rather than continuous; time is a continuous variable. Although some temporal applications have been designed with tensors [3], by treating time as a discrete variable, the applicability of these methods to express the network as a continuous function of time is limited. Temporal matrix factorization has recently been used successfully in the context of collaborative filtering [31]. In this paper, we explore temporal matrix factorization in the context of network-centric applications. We show that a significant number of evolutionary network applications can be addressed with the use of the factorization framework.

7. CONCLUSION

In this paper, we developed a novel temporal matrix factorization model for dynamic network analysis. This model has the advantage of significant generality in addressing various temporal applications because of its ability to explicitly represent the network as a function of time. As specific examples, we provide results for (temporal) weight trend prediction, link prediction, dynamic community detection and event detection within this unified framework. Even though we provide a more general model, our results show that its specific instantiation to weight prediction and link prediction performs better than state-of-the-art techniques. We also show that the approach is able to provide useful intuitions about the community changes and events in the underlying network.