Three-Dimensional Localization of Single Molecules for Super-Resolution Imaging and Single-Particle Tracking

Abstract

Single-molecule super-resolution fluorescence microscopy and single-particle tracking are two imaging modalities that illuminate the properties of cells and materials on spatial scales down to tens of nanometers, or with dynamical information about nanoscale particle motion in the millisecond range, respectively. These methods generally use wide-field microscopes and two-dimensional camera detectors to localize molecules to much higher precision than the diffraction limit. Given the limited total photons available from each single-molecule label, both modalities require careful mathematical analysis and image processing. Much more information can be obtained about the system under study by extending to three-dimensional (3D) single-molecule localization: without this capability, visualization of structures or motions extending in the axial direction can easily be missed or confused, compromising scientific understanding. A variety of methods for obtaining both 3D super-resolution images and 3D tracking information have been devised, each with their own strengths and weaknesses. These include imaging of multiple focal planes, point-spread-function engineering, and interferometric detection. These methods may be compared based on their ability to provide accurate and precise position information of single-molecule emitters with limited photons. To successfully apply and further develop these methods, it is essential to consider many practical concerns, including the effects of optical aberrations, field-dependence in the imaging system, fluorophore labeling density, and registration between different color channels. Selected examples of 3D super-resolution imaging and tracking are described for illustration from a variety of biological contexts and with a variety of methods, demonstrating the power of 3D localization for understanding complex systems.

1. Introduction

Fluorescence microscopy has been a mainstay of biological and biomedical laboratories since its inception.(1) Labeling specific proteins or oligonucleotides with a small fluorophore (2) or an autofluorescent protein (3, 4) lights up those molecules of interest against a dark background in a relatively non-invasive way, painting a picture of subcellular structures and intermolecular interactions. Imaging of fluorescent labels has also been applied to the study of non-biological materials such as polymers and glasses,(5) mesoporous materials,(6) and directly to natively-fluorescent antenna complexes.(7) The resulting fluorescence images have provided useful information about structures, dynamics, and interactions for decades, first with wide-field epifluorescence microscopes.

A major advance occurred more than 27 years ago, specifically the advent of the ability to optically detect and spectrally characterize single molecules in a condensed phase by direct detection of the absorption,(8) followed a year later by detection of single-molecule absorption by sensing emitted fluorescence in solids (9) and in solution.(10) Single-molecule spectroscopy (SMS) and imaging allows exactly one molecule hidden deep within a crystal, polymer, or cell to be observed via optical excitation of the molecule of interest. This represents the ultimate sensitivity level of ~1.66 × 10⁻²⁴ moles of the molecule of interest (1.66 yoctomole), but the detection must be achieved in the presence of billions to trillions of solvent or host molecules. Successful experiments must meet the requirements of (a) guaranteeing that only one molecule is in resonance in the volume probed by the laser, and (b) providing a signal-to-noise ratio (SNR) for the single-molecule signal that is greater than unity for a reasonable averaging time. The first of these two requirements means that at room temperature, the single molecules need be farther apart than about 500 nm, so that the diffraction-limited spots from each do not overlap, and this is generally achieved by dilution. The power of the method primarily rests upon the removal of ensemble averaging: in contrast to traditional spectroscopy, it is no longer necessary to average over billions to trillions of molecules to measure optical quantities such as brightness, lifetime, emission spectrum, polarization, and so on. Therefore, it becomes possible to directly measure distributions of behavior to explore hidden heterogeneity, a property that would be expected in complex environments such as in cells, polymers, or other materials. In the time domain, the ability to optically sense internal states of one molecule and the transitions among them allows measurement of hidden kinetic pathways and the detection of rare intermediates. Because typical single-molecule labels behave like tiny light sources roughly 1–3 nm in size and can report on their immediate local environment, single-molecule studies provide a new window into the nanoscale with intrinsic access to time-dependent changes. The basic principles of single-molecule optical spectroscopy and imaging have been the subject of many reviews(11–21), and books (22–25)

This article considers two applications of single-molecule spectroscopy as extended to three spatial dimensions, “single-particle tracking” (SPT) of individual molecules in motion, and “super-resolution” (SR) microscopy of extended structures to provide details of the shape of an object on a very fine scale. Both of these methods rest on imaging of single molecules, where the x–y position is extracted from the image to localize the position of the molecule. (For concision, we will generally refer to point emitters as single fluorescent molecules, since quantum dot nanocrystals, metallic nanoparticles, etc. can be localized similarly.) Many types of microscopes can be used,(18) including wide-field, confocal, total-internal-reflection, two-photon, etc. to measure the positions of isolated single molecules, but a key point is: How precisely can the position or location of a single molecule be determined? Unfortunately, fundamental diffraction effects (26) blur the molecule’s detected emission profile, limiting its smallest width on the camera in sample units to roughly the optical wavelength λ divided by two times the numerical aperture (NA) of the imaging system (Figure 1A). Since the largest values of NA for state-of-the-art, highly corrected microscope objectives are in the range of about 1.3–1.5, the minimum spatial size of single-molecule spots is limited to about ~200 nm for visible light of 500 nm wavelength. Nevertheless, the measurement of the shape of the spot is useful information, in that a fitting function can be fit to the measured pixelated image to obtain the molecular position. The precision of this localization can be far smaller than the diffraction-limited width of the spot, and is limited primarily by the number of photons detected from the molecule. Both the precision and accuracy of this localization process are described in detail in Sections 2 and 3 of this paper, not only for 2D, but also for 3D determinations of the molecular position.

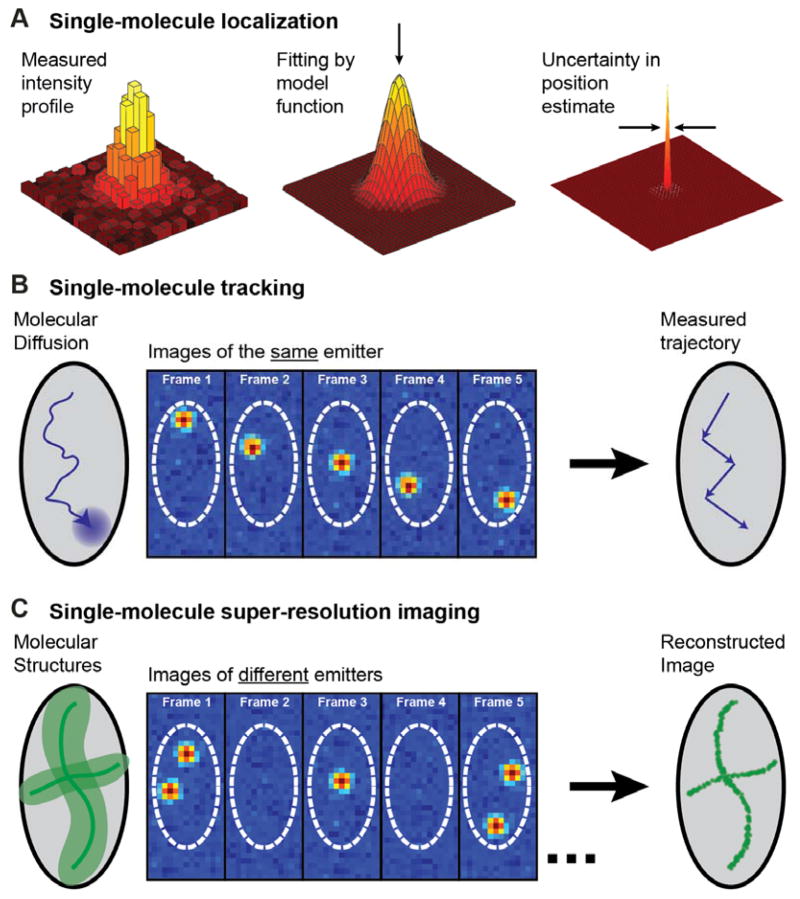
Figure 1.

The principles of single-molecule localization and its applications to particle tracking and super-resolution. (A) The pattern of light formed on a camera by a single fluorescent molecule is blurred by diffraction, but can be fit by a model function to yield a localization with uncertainty at least an order of magnitude lower than the diffraction-limited resolution, depending upon the photons detected. (B) If only one fluorescing molecule is present in a diffraction-limited volume, its motion can be localized in successive frames to build up a track of its motion, as illustrated for an abstraction of a cell. (C) Alternatively, single-molecule localization can surpass diffraction-limited resolution (left, light green area) when imaging extended structures (dark green lines). By (photo)chemically or photophysically limiting the number of simultaneously active immobile emitters, different labels are turned on, localized, and turned off in many successive frames, building up a super-resolution reconstruction of the underlying structures. Inspired by ref. (27).

Single-particle-tracking (SPT) is one method that applies single-emitter localization to answer key questions in both biology and materials science. In a SPT experiment, the spatial trajectory of a given molecule is determined by repeatedly detecting and localizing it at many sequential time points (Figure 1B).(28) Analysis of the resulting single-molecule tracks provides information on the mode of motion of the set of labelled molecules, which may be diffusive, motor-directed, confined or a mixture of these modes.(29–34) For materials science applications and in vitro reconstitutions of biological systems, dilution of the fluorescent probe used is typically sufficient to achieve single-molecule concentration. For fluorescently tagged biomolecules in living cells, it is sometimes necessary to use other means to lower the emitter concentration. These include lowering the expression levels of genetically encoded labels,(35) quenching or photobleaching an initially large number of emitters, chemical generation of emitters, or sparse activation of only a few photoactivatable molecules at a time.(36, 37) While in vitro measurements are simpler, because intracellular crowding and binding interactions with cellular structures influence measured trajectories, it is more representative to observe the motion of the molecule of interest as it performs its function in the native biological environment, either in the cytoplasm or the membrane.(38)

Turning now to the second method, let us pose a problem: how can one extract images of structures, if the power of optical microscopy to resolve two closely spaced-emitters is limited by the fundamental effects of diffraction? This problem has been overcome by the invention of “super-resolution” optical microscopy, recognized by the Nobel Prize in Chemistry in 2014, awarded to one of us (W.E.M.)(39), Eric Betzig(40) and Stefan Hell(41), an achievement which has continued to stimulate a revolution in biological and materials microscopy. Hell pursued Stimulated Emission Depletion Microscopy (STED) and its variants, while the focus of this paper is on approaches to overcome the diffraction limit using single molecules which rely on a clever modification of standard wide-field single-molecule fluorescence microscopy,(42–44) described in more detail in other papers in this special issue.

These single-molecule super-resolution (SR) imaging approaches are summarized in Figure 1C. As opposed to tracking of the same molecule, SR determines the positions of different molecule labels at different times to resolve a static structure. The essential requirements for this process are (a) sufficient sensitivity to enable imaging of single-molecule labels, (b) determination of the position of a single molecule with a precision better than the diffraction limit, and (c) the addition of some form of on/off control of the molecular emission to maintain concentrations at very low levels in each imaging frame. This last point is crucial: the experimenter must actively pick some photophysical, photochemical, or other mechanism which forces most of the emitters to be off while only a very small, non-overlapping subset is on. If these labelled copies are incorporated into a larger structure, such as a polymeric protein filament, then their positions recorded from different imaging frames randomly sample this structure. A point-by-point reconstruction can then be assembled by combining the localized positions of all detected molecules in a computational post-processing step. Importantly, because all molecules are localized with a precision of tens of nanometers, this approach circumvents the diffraction limit that otherwise limits image resolution to 200–300 nm in conventional fluorescence microscopy.

The required sparsity in the concentrations of emitting molecules can be achieved by a variety of methods. The PAINT method(45) (Points Accumulation for Imaging in Nanoscale Topography) relies upon the photophysical behavior of certain molecules that light up when bound or constrained, and this idea was initially demonstrated with the twisted intermolecular charge transfer turn-on behavior of Nile Red.(46) PAINT has advantages that the object to be imaged need not be labeled and that many individual fluorophores are used for the imaging, thus relaxing the requirement on the total number of photons detected from each single molecule. In the STORM approach (44) (Stochastic Optical Reconstruction Microscopy), cyanine dye molecules (e.g. Cy5) are forced into a dark state by photoinduced reaction with nearby thiols. A small subset of the emitters return from the dark form either thermally or by pumping of a nearby auxiliary molecule like Cy3. In the (f)PALM approach (42, 43) (fluorescence PhotoActivated Localization Microscopy), a photoactivatable fluorescent protein label is used, and a weak activation beam creates a small concentration of emitters which are localized until they are bleached, and the process is repeated many times.

Other active control mechanisms have been demonstrated giving rise to a menagerie of acronyms and names, including dSTORM (direct STORM) (47), GSDIM (Ground-State Depletion with Individual Molecule return)(48), “Blink Microscopy” (49), SPDM (Spectral Precision Determination Microscopy) (50), and many others. Photoactivation methods have been extended to organic dyes,(51, 52) photorecovery and/or photoinduced blinking can be used for SR with fluorescent proteins such as eYFP,(53, 54) and even enzymatic methods produce turn-on which may be controlled by the concentration of substrate and the enzymatic rate.(55)

Between the large improvement in resolution (a factor of 5 or more, typically down to the 20–40 nm range) of SR microscopy, and the dynamical information and understanding of heterogeneity available from SPT, single-molecule localization has revealed structures and processes that were previously unresolvable. As treated in previous reviews,(56–65) and discussed throughout this special issue, these improvements have allowed scientists to address many long-standing questions spanning the fields of biology and materials science. The methodological challenge that we focus on in this review, of how to best obtain 3D information in SPT and SR microscopy, touches all of these subject areas. The reason 3D information is needed is simple: the world is three-dimensional, so that if we can only make 2D measurements, we will likely miss critical information. For example, as shown in Figure 2, motion on a 3D object such as the surface of a spherical cell appears contracted and warped when only 2D information is available. In the 3D trajectory, it is easy to observe that the molecule diffusely freely over the surface, while in the 2D projection, it is not even clear whether the molecule is surface-associated.

Figure 2.

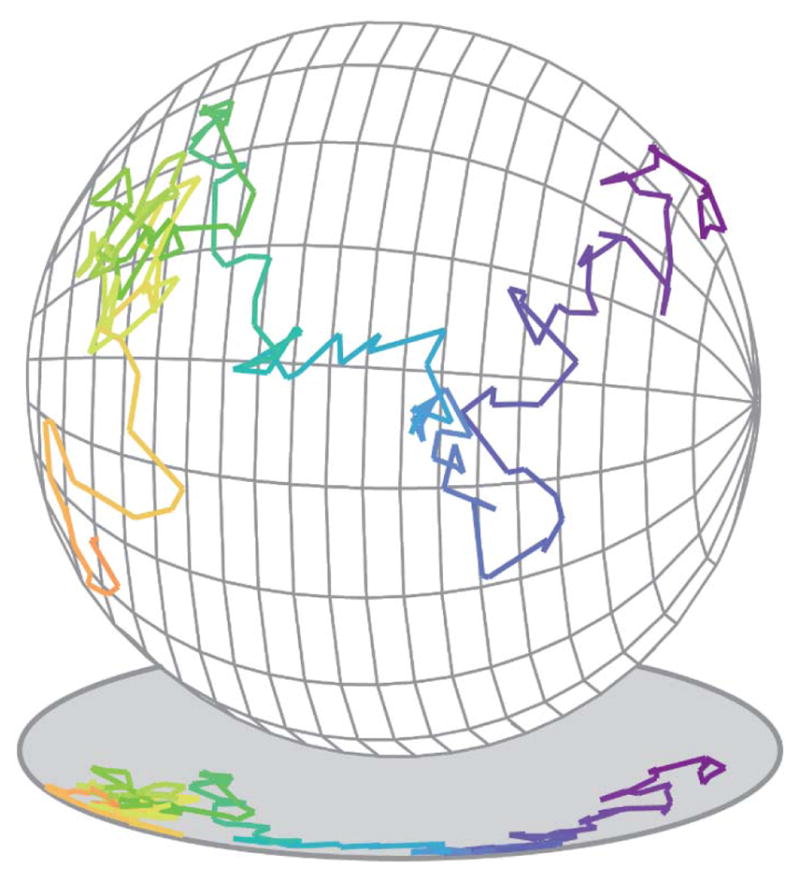
Illustration of the 3D motion of a single molecule moving on the surface of a spherical cell, and its projection into 2D. The 3D trajectory shows that the molecule diffuses freely over the surface of the sphere, while the 2D projection is ambiguous.

Precise and accurate single-molecule localization is the foundation for all quantitative SR and SPT studies, and we begin in Section 2 by introducing the key principles of single-molecule detection and position estimation for the general case of 2D localization. In Section 3, we catalog and compare many of the creative and elegant means by which these measurements have been extended into the third dimension. In Section 4, we treat the physical and theoretical limits of these techniques: the possible resolution that can be attained, the corrupting influence of aberrations and other systematic errors, and how these limits have been pushed. Finally, in Section 5, we show the power of 3D localization microscopy by examining several case studies where 3D SR and SPT have offered new insights.

2. Basic Principles of Single-Molecule Localization

Many of the experimental and analytical considerations in 3D single-molecule microscopy can be seen as an extension of those in “traditional” 2D single-molecule localization experiments. To introduce vocabulary and context that is shared between many 3D localization modalities, we first give a brief overview of instrumentation and statistical theory used to localize single molecules in two dimensions. We encourage readers new to localization microscopy to peruse reviews that specifically treat these topics in detail for further background (18, 66, 67).

2.1 Detecting Single Molecules

The most common imaging geometry used in 2D single-molecule wide-field imaging experiments is sketched in Figure 3A, and provides the basis for 3D single-molecule microscopes. In most details, this is equivalent to the epifluorescence microscopes used for diffraction-limited microscopy. Here, we briefly review the foundational instrumental principles true of both 2D and 3D before discussing the microscope modifications allowing 3D localization in later sections.

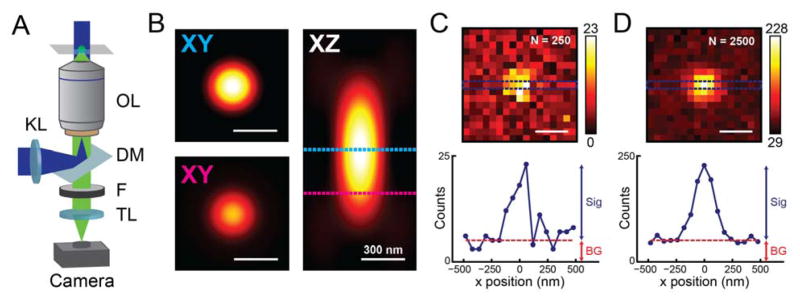
Figure 3.

Instrumentation and detection in a 2D single-molecule microscope. (A) The imaging geometry used in epifluorescence (inverted microscope shown). KL: Köhler lens; OL: objective lens; DM: dichroic mirror; F: filter(s); TL: tube lens; sample plane shown at the top. (B) Simulated x–y and x–z slices of the microscope PSF (λ_em = 600 nm, NA = 1.4) for scalar diffraction of an emitter near the coverslip(68) using the PSF Generator ImageJ plugin(69). Top x–y slice, in-focus PSF; bottom x–y slice, PSF at 300 nm defocus, same color scale. (C), (D) Simulated images of an in-focus single molecule formed on the camera under the same conditions, showing the effect of Poisson noise given 250 (2500) total signal photons collected and 5 (50) background photons per 60 nm (in sample plane) pixel. Counts in units of detected photons. The corresponding line profiles through the centers of the single-molecule images show the contributions to the image from signal and background. All scalebars are 300 nm.

In contrast to confocal microscopes, which scan a diffraction-limited focused laser spot across the sample, epifluorescence microscopes often produce a larger Gaussian illumination spot ranging from 1 to 100 μm in diameter in the object plane. In this way, all actively emitting fluorescent molecules in the sample can be detected simultaneously without scanning. To produce a broad illumination profile, the light source (typically a laser beam) is focused at the back focal plane of the microscope objective using a Köhler lens positioned externally to the inverted microscope body. The fluorescence from excited molecules is then collected back through the objective and imaged onto an array detector (i.e. a camera) with a separate tube lens. The objective lens is the most important detection optic in the system, and its most important parameter is numerical aperture, NA = n × sin(θ) with n the refractive index of the medium between the sample and objective and θ the objective’s maximum collection half-angle. The highest θ available from conventional objective lenses is roughly 72°, and by using high-index media such as immersion oil (n = 1.51), typical objectives used for single-molecule imaging achieve NA = 1.3–1.5.

The objective NA is a major determinant of image quality. As discussed in the introduction, optical resolution is limited by blurring of image features finer than the diffraction limit. The lateral resolution of wide-field fluorescence microscopy is thus limited to 0.61 λ_em, or at best ~200–250 nm for emission wavelengths λ_em in the visible range. Axial resolution is even more dependent on NA, and is at best roughly equal to 2λ_em/NA² (~550–700 nm). Much of the behavior of the microscope is defined by the “point spread function” (PSF), which describes how light collected from a point emitter is transformed into an image. Mathematically, diffraction blur is equivalent to a convolution of the true labeled structure with the microscope’s three-dimensional PSF, shown in Figure 3B for a NA 1.4 objective and an emitter near the coverslip. This blur is directly responsible for the inability of conventional diffraction-limited microscopy to record fine details. The image formed on the camera by an ideal point emitter is a cross-section of the 3D PSF, dependent on the position of the emitter relative to the focal plane. The ~250 nm transverse width of the in-focus PSF is clearly apparent (Figure 3B, top x–y slice). By contrast, the PSF at 300 nm defocus is more diffuse and appears dimmer (bottom x–y slice). As can been seen in the x–z profile, within the scalar approximation, defocused emission profiles from above and below the focal plane are indistinguishable. As suggested by the resolution criteria above, higher NA objectives provide more compact PSFs; they also improve total signal, as light collection efficiency scales with the square of the NA.

However, even the best collection optics and brightest fluorophores available will not be enough if the signal from single molecules is drowned out by background light, and filtering this background while keeping as many signal photons as possible is a well-known requirement for every single-molecule experiment (18, 70). Carefully selected spectral filters are absolutely essential to reduce background from autofluorescence and scattering, and it is common to image at relatively red wavelengths (500–700 nm) to avoid spectral regions of particularly high cellular autofluorescence. Yet when imaging samples such as thick cells, even optimal spectral filtering may not be sufficient, as autofluorescence, scattering, and fluorescence from out-of-focus fluorophores all increase with the illuminated sample volume. In these cases, it is necessary to consider alternate illumination geometries from epiillumination. One way to reduce background is excitation by total internal reflection (thus TIR fluorescence or TIRF) which makes use of the 100–200 nm thick evanescent field generated from the excitation beam at incidence angles greater than the critical angle of the interface between the coverslip and the sample.(71–73) However, while TIRF greatly reduces out-of-focus background fluorescence above the 100–200 nm illumination region, yielding excellent results for thin imaging volumes,(74–77) having a limited axial reach away from the coverslip makes TIRF less useful for 3D imaging inside cells.

Detection is the last part of the imaging process, and the development of new, more sensitive cameras has been crucial to the progress of single-molecule microscopy. To maximize collected signal from the molecule, a single-molecule detector must have high quantum efficiency in the conversion of photons to photoelectrons. Further, all detectors introduce noise due to thermally generated current (“dark noise,” dependent on temperature and integration time) and noise from the electronics that convert the photocurrent of each pixel to a signal voltage (“read noise,” roughly constant for a given detector). For conventional detectors used in diffraction limited fluorescence microscopy such as Charge Coupled Device (CCD) cameras, this added noise can overwhelm the small signal from single molecules, and must be reduced. State-of-the-art cameras that address these needs include Electron-Multiplying CCD (EMCCD) and scientific Complementary Metal Oxide Semiconductor (sCMOS) cameras. EMCCDs have long achieved quantum efficiencies on the order of 95%, making them a common choice for single-molecule imaging, while sCMOS cameras have become increasingly popular in recent years thanks to rapid development in detector technology, and have recently reached quantum efficiencies of 95% as well (Photometrics Prime 95B; Tucson, AZ, USA). These cameras each overcome read noise in their own way, either by charge multiplication before readout (EMCCD) or by engineering extremely low read noise in the first place (sCMOS).

The contributions to the image formed on the camera from single-molecule fluorescence and background are summarized in Figure 3C,D. To design effective single-molecule experiments, whether in 2D or 3D, it is important to consider what determines the quality of such an image. Signal-to-background ratio (SBR) or contrast is a common metric in many imaging modalities, but is less informative in single-molecule imaging. As the difference between Figure 3C and Figure 3D shows, even when maintaining the same SBR, increasing the total detected photons (as is done by increasing the integration time or illumination intensity) improves the signal-to-noise ratio given shot noise statistics. That is, background is fundamentally a problem because it adds noise, rather than decreases contrast.

While increasing the pumping irradiance can greatly improve signal-to-noise (SNR), there is an upper limit to the signal available from single molecules. On a fundamental photophysical level, the emission rate from the molecule might saturate while that from the background might not. In most cases, a more serious limit is photochemical stability, i.e. the maximum possible emitted photons from single-molecule fluorophores before photobleaching. This quantity is often more important than brightness per se. For modern detectors and under most imaging conditions, these photon statistics are overwhelmingly the largest noise source, though the detector noise floor (i.e. read noise, dark noise, and other factors such as clock induced charge in EMCCDs) becomes highly significant under certain conditions with low signal in each pixel.(78) With such noise statistics in mind, we now turn to the question of how exactly we can infer accurate and precise molecular positions from the images collected by our microscope.

2.2 Estimating Single-Molecule Position

After acquiring single-molecule data, the task remains to implement algorithms that faithfully extract molecule positions from noisy, complicated images. While this task poses challenges, the reward – nanoscale position estimates of potentially millions of individually resolved molecules within a sample – is a worthy one. As with instrumentation, many of the principles of image analysis in 2D and 3D single-molecule localization are analogous. Here, we describe how molecular positions are extracted from image data in 2D, and introduce a general framework for evaluating and comparing localization methods in 3D.

Most fitting algorithms used for SR and SPT assume spatiotemporal sparsity, such that regions of interest (ROIs) can be defined in each image frame that each contain the intensity pattern of only one single-molecule emitter. As discussed in Section 2.1, under ideal conditions, the average intensity produced by a point emitter is proportional to a cross-section of the microscope’s 3D PSF, scaled by the total signal photons N_sig plus a constant background per unit area N_bg, giving us the imaging model

$$I(u,v)=H(x,y,z,N_{\mathit{sig}},N_{bg})=H(\mathit{\theta })$$ (1)

defined for position u,v in the image plane when the emitter is at position x, y, z in the sample space, where θ represents these position and photon parameters, plus any other parameterizations of the PSF. The actual image from the detector is subject to noise and binned into pixels, producing a signal n_k at each of the pixels w_k within the ROI. Phrased this way, single-molecule localization is revealed to be an inverse problem: given the pixelated and noisy image vector n and our knowledge of H, how can we accurately and precisely estimate the molecule’s position x = (x, y, z)?

Accuracy means that our chosen position estimator must not be systematically biased away from the true value, while precision means that the estimator makes effective use of all the available data to minimize random error. Estimators can be very simple, but not necessarily very accurate or precise. For example, since the 2D microscope PSF is brightest close to the molecule’s position, we could take the brightest of the pixel vector w of the PSF as a position estimate, $\widehat{\mathit{x}}=\underset{\mathit{w}}{argmax}(\mathit{n})$, a “max-value” estimator. Or, applying the same logic slightly differently, we could use a weighted average of all the N pixels in the ROI,

$$\widehat{\mathit{x}}=\frac{{\sum }_k^N{n}_k{w}_i}{{\sum }_k^N{n}_k},$$ (2)

i.e. a centroid estimator. Such estimators are computationally convenient, but limited: the max-value estimate is sensitive to noise and limited by pixel size, and so has low precision, while the centroid estimate is biased towards the center of the ROI by the background in outlying pixels, making it inaccurate (Figure 4).

Figure 4.

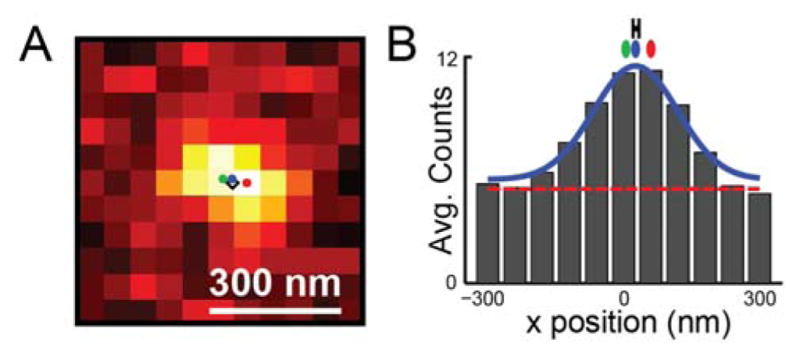
Accurate localization requires unbiased estimators, an illustrative example. (A) One simulated image of a single molecule at position (x₀ = 27 nm, y₀ = 0 nm) with 250 signal photons and 5 background photons per pixel. Black diamond: true emitter position. Red, green, and blue dots: estimated position from max-value, centroid, and Gaussian fit estimators, respectively. (B) Image counts of (A) averaged along the x axis, with background level marked by the red dotted line, the Gaussian fit drawn in blue, and position estimates marked as in (A). Estimator accuracy and precision was tested for 10,000 simulated frames with the same parameters: Gaussian fitting accurately estimates true molecular position (mean value biased by < 0.1 nm) with a localization precision of 10.0 nm, marked by the black error bar. For the same data, the max-value estimator has a precision of 34 nm and a bias of −0.9 nm, while the centroid estimator has a precision of 5.4 nm and a bias of −20 nm.

How can one do better? While it is possible to create effective, unbiased estimators that use only basic assumptions about the PSF, such as radial symmetry,(79) the most powerful estimators implement a more detailed PSF model to solve the inverse problem of eq. (1). Least-squares (LS) fitting and maximum likelihood estimation (MLE) are two such methods that are adaptable to many models.

LS and MLE fit the image data to a model function. As implied by eq. (1), the imaging model H(θ) produces an expected value of the image, I(u,v; θ), and the best guess of θ is found by optimizing I to match the observed PSF. While tracking of the positions of large biological objects has a long history,(29, 30) deep considerations of the fitting procedure are relatively recent. LS was one of the first relatively unbiased localization algorithms used,(80, 81) and is familiar from its ubiquitous application to scientific regression problems and curve fitting. The scoring method of LS is to minimize the square error between the PSF model μ(θ) and the observed data n,

$$S=\sum _{k=1}^N{[n_k-{\mu }_k(\mathit{\theta })]}^2,$$ (3)

where x̂ is included in the optimized parameter estimate θ̂. This optimization strategy follows from the statistical assumption that each pixel value n_k is an observation with normally, independently and identically distributed noise, which is generally only approximately true.(82, 83)

We must still define the imaging model H that produces the parametrized image I(u, v; θ). After more than a century of study, there is a sophisticated understanding of the standard microscope PSF, and this quantitatively describes the way light from a molecule is collected by the microscope.(26, 68, 84–86) When molecules emit light isotropically, without net polarization, the scalar approximation allows for a comprehensive treatment of the imaging system.(68) As shown in Figure 3, the image of an ideal, in-focus emitter at the coverslip is an Airy disk,

$$I(u,v)=C{\left(\frac{J_1(k\text{NA}\rho )}{k\text{NA}\rho }\right)}^2$$ (4)

with J₁ the first order Bessel function of the first kind, k the wavenumber 2π/λ, ρ the distance from the point source in the image plane, i.e. $\rho =\sqrt{{(u-u_0)}^2+{(v-v_0)}^2}$, and C a constant for a given number of total detected photons. While the Airy disk has several relatively dim rings, most of the PSF’s intensity is concentrated in the center. For this reason, a Gaussian function is a tractable and reasonably accurate approximation, and it is extremely common to fit single-molecule data with a symmetric Gaussian plus a constant background with the width σ the size of the spot arising from the diffraction limit(82, 87):

$$I(u,v)=\frac{N_{\mathit{sig}}}{2\pi {\sigma }^2}exp\left(-\frac{{\rho }^2}{2{\sigma }^2}\right)+N_{bg}$$ (5)

As shown in Figure 4 for a simulation with N_sig = 250 photons and N_bg = 5 photons/pixel, performing nonlinear LS fitting with a Gaussian model retrieves a position estimate ( $\widehat{x_0},\widehat{y_0}$) close to that of the true position, and avoids the bias of the simpler estimators. We must next ask how precise an individual localization is. To empirically test the random error in our measurement, we can either simulate or measure the spread of position estimates obtained from the same molecule emitting over many frames. As shown in Figure 4B, repeated least-squares localizations on simulated data give a range of estimates ( $\widehat{x_0},\widehat{y_0}$) normally distributed around the true values, with standard deviation, or “localization precision,” σ ≈ 10 nm. The localization precision is dependent on the estimator: for example, max-value estimation is much less precise, resulting in a localization precision of 34 nm for the exact same data. A well-known analytical expression was developed for the localization precision of LS Gaussian fitting by Thompson et al., with later corrections by Mortensen et al.:(85, 88)

$${\sigma }^2=\frac{{\sigma }_{\text{PSF}}^2+a^2/12}{N_{\mathit{sig}}}\left(\frac{16}{9}+\frac{8\pi N_{bg}({\sigma }_{\text{PSF}}^2+a^2/12)}{N_{\mathit{sig}}{a}^2}\right)$$ (6)

This equation assumes the PSF is a Gaussian with standard deviation σ_PSF detected with pixels of diameter a, and gives the correct result within a few percent even if the true PSF is an Airy disk (such as simulated in Figure 4). For low background and ignoring pixelation, eq. (6) reduces to the approximate relationship

$$\sigma \propto \frac{{\sigma }_{\text{PSF}}}{\sqrt{N_{\mathit{sig}}}},$$ (7)

highlighting the importance of high photon counts. Eq. (6) has been widely applied to Gaussian LS estimation, but it only holds for the special case of aberration-free, in-focus, 2D PSFs, and does not reveal whether it might be possible to achieve a better precision with a different estimator. The question of how to define – and achieve – the best possible precision for an arbitrary 3D PSF is found in maximum-likelihood-estimation methods. MLE is rooted in a statistical framework that attempts to estimate a set of underlying parameters yielding a given measurement, accounting for the signal generating model (image formation) and noise statistics. Given image formation and noise models, one attempts to find the set of underlying parameters θ that maximizes the likelihood function, or, equivalently, the log-likelihood.(89, 90) Assuming shot (Poisson) noise dominates, the log-likelihood function is(82, 91)

$$\mathcal{L}(\theta \mid \mathit{n})=\sum _{k=1}^N[n_{k}ln\left({\mu }_k(\mathit{\theta })\right)-{\mu }_k(\mathit{\theta })]$$ (8)

where we drop terms not dependent on θ for clarity. Equivalently, MLE means seeking the set of parameters for which the measurement is most probable.

The preceding has discussed several estimators for determining molecule position. This leaves the question as to how to define the best possible precision one can achieve. This is of interest, both for practical reasons, such as estimating the resolution of an image, for designing a better imaging system, and for fundamental theoretical reasons. A useful and elegant framework for the quantification of localization precision stems from recognizing that emitter localization is a parameter estimation problem. As such, tools from estimation theory can be used to analyze it. Specifically, Fisher information is a mathematical measure of the sensitivity of an observable quantity (image) to changes in its underlying parameters (e.g. emitter position).(91–93) Intuitively, an image that is more sensitive to the emitter’s position contains more information about the position. Mathematically, Fisher information is given by:

$$\mathrm{I}(\theta )=E\left[{\left(\frac{\partial lnf(s;\theta )}{\partial \theta }\right)}^{\mathrm{T}}\left(\frac{\partial lnf(s;\theta )}{\partial \theta }\right)\right],$$ (9)

where f(s; θ) is the probability density, i.e. the probability of measuring a signal s given the underlying parameter vector θ, T denotes the transpose operation, and E denotes expectation over all possible values of s. In the special case where Poisson noise is dominant and there is spatially uniform background, eq. (9) becomes:

$$\mathrm{I}(\theta )=\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{p}}}\frac{1}{\mathrm{\mu }(\mathrm{k})+\mathrm{\beta }}{\left(\frac{\partial \mathrm{\mu }(\mathrm{k})}{\partial \theta }\right)}^{\mathrm{T}}\left(\frac{\partial \mathrm{\mu }(\mathrm{k})}{\partial \theta }\right),$$ (10)

where μ(k) is the model of the PSF in pixel k and β is the number of background photons per pixel. More sophisticated models can be used that account for the noise characteristics of EMCCD(94) and sCMOS detectors,(95) and calibration of the pixel-to-pixel variation of sCMOS detectors is necessary for accurate localization.

The use of Fisher information in localization analysis is motivated by its relation to precision. The inverse of the Fisher information is the Cramér-Rao lower bound (CRLB), which is the lower bound on the variance with which the set of parameters θ can be estimated using any unbiased estimator.(96) For the position coordinates (x,y,z), this translates to the optimal precision with which the source can be localized for a given imaging modality, signal, background, and noise model. The CRLB is not a quantity of merely theoretical importance – it has been shown that the CRLB can be approached in practice.(82, 85, 97) As long as the imaging model matches the experiment, the precision of MLE will always be superior to LS methods, and will generally achieve the CRLB. However, LS estimators also have merits: they do not require a comprehensive noise model and are simpler to implement, and can achieve precisions close to the CRLB for high background levels, where noise statistics are similar between pixels.(82, 83) As we discuss further in Section 3, CRLB comparisons allow us to systematically compare 3D localization methods, and are important in the design of new PSFs for 3D imaging.

3. Methods for 3D Localization

The 3D PSF shape of a standard fluorescence microscope changes relatively slowly with changing axial position relative to the focal plane (Figure 3). This is equivalent to having low Fisher information, or poor precision for determining z (see Figures 5 and 7 for comparisons of CRLB analysis of several PSFs including the standard PSF). Further, in the absence of aberrations, the PSF is symmetric above and below the focal plane, making it difficult to assign a unique z position to the emitter. While some tracking experiments have achieved nanometer axial precision with the standard PSF, these required extremely bright nanoparticle emitters and working away from focus to remove ambiguity.(98, 99) In most cases, the low photon budget of probes used in single-molecule microscopy severely limits axial localization precision with a conventional fluorescence microscope, especially over extended axial ranges.

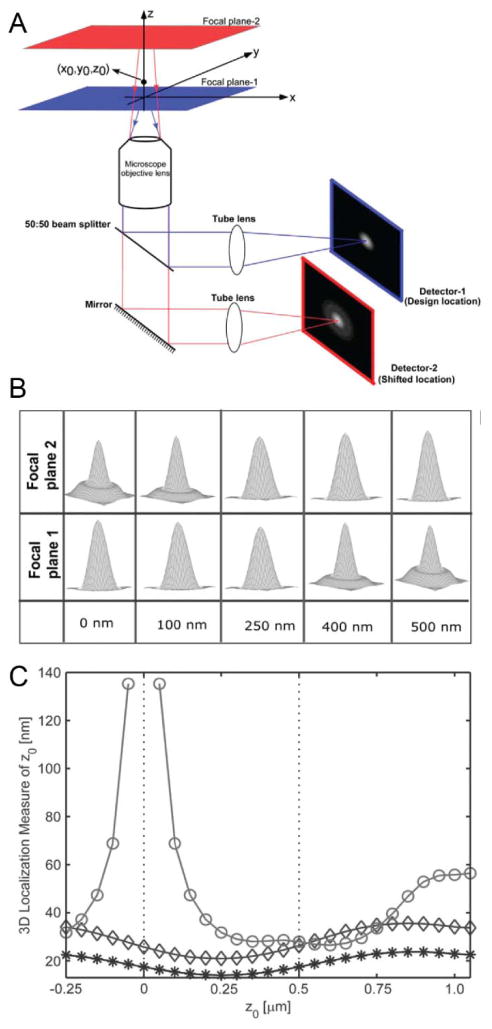
Figure 5.

Multifocal microscopy with a biplane setup. (A) The fluorescence from a point emitter at position (x_0,y₀,z₀) is collected by the objective and directed to two different detectors using a 50:50 beamsplitter. The focal plane detected by the second detector is shifted by changing the separation between the detector and the tube lens. (B) Simulated PSFs of each channel as a function of emitter axial position relative to focal plane 1. The PSF changes relatively slowly within ~250 nm of focus. (C) The CRLB for axial localization for a conventional microscope (○) and biplane microscope with 500 nm plane separation (◇) with 2000 total detected photons and 160 background photons per ~160 nm pixel (80 photons per pixel for biplane detection). NA 1.45, λ_em = 655 nm, 6 e⁻/pixel read noise. Doubling the acquisition time (*) improves the axial CRLB for biplane localization by a factor of approximately $\sqrt{2}$. Reprinted from ref. (103), Copyright 2008, with permission from the Biophysical Society.

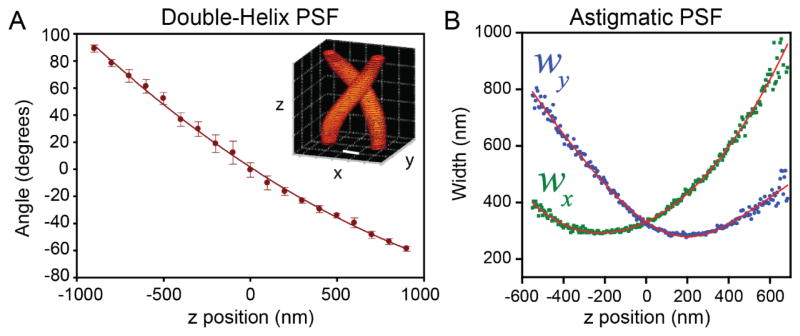
Figure 7.

Calibration curves associated with the double-helix PSF and the astigmatic PSF. (A) The angle of the line between two revolving DH-PSF lobes changes monotonically as a function of z position. Inset: intensity profile of the DH-PSF. Scale bar and grid spacing: 400 nm. Adapted from ref. (126). Copyright 2009 the authors. (B) The x and y widths w_x, w_y, of asymmetric Gaussian fits to the astigmatic PSF change with z position in a well-defined manner. Adapted from ref. (123). Reprinted with permission from AAAS.

Several microscope modifications have emerged that obtain high Fisher information for both axial and transverse localization, allowing precise 3D imaging for a wide range of conditions. These modifications can be classified based on the optical principle they employ: these include multifocus methods, where multiple focal planes are imaged simultaneously; PSF engineering methods, where the PSF of the microscope is altered to encode axial position in its shape; and interference-, interface-, or intensity-sensing methods, which measure the position of the molecule relative to features in the imaging geometry instead of fitting the shape of the PSF. All of these methods are compatible with a wide range of emitting labels, and are sometimes creatively combined to take advantage of the strengths of multiple approaches.

3.1 Multifocus Methods to Extend the Standard PSF

As summarized above, the standard PSF has clear limitations for 3D imaging. These limitations follow from the need to estimate molecule position from a single 2D slice of the PSF; if we were to measure the entire 3D PSF, it would be possible to fit the axial position just as we fit the lateral position. Such volumetric imaging is common in confocal microscopy, where scanning the focal spot to acquire a stack of z-slices gives axial information with gives axial sectioning to diffraction-limited resolution, even though the larger extent of the PSF in the axial direction reduces attainable precision. Since single-molecule imaging is inherently dynamic due to e.g. the movement of molecules in a tracking experiment or the blinking process in a super-resolution experiment, scanning through a focal stack is an unattractive approach.

Widefield multifocal imaging employs a microscope modification that avoids scanning and makes multiple simultaneous measurements of the 3D PSF at different focal planes. The simplest implementation of multifocal imaging, also known as biplane or bifocal imaging, splits fluorescence equally into two channels that are imaged either onto two cameras(100) or onto different regions of the same camera,(99, 101) where shifting the camera placement (or adding another lens) in one channel causes different focal planes to be detected in each channel (Figure 5A). The PSFs with focal planes at 0 nm (channel 1) and 500 nm (channel 2) are shown in Figure 5B. Near focus, each PSF is bright and changes slowly as a function of z position (good lateral precision, poor axial precision), and away from focus, each PSF is spread out but changes shape more quickly (poor lateral precision, better axial precision). When imaged together, the two channels complement each other, allowing good lateral and axial localization precision over a large axial range, as well as removing ambiguity about which side of the focal plane the emitter is on. This is described quantitatively by CRLB analysis: biplane imaging gives more significantly more precise axial localization than single-plane imaging, and has an axial range of ~1.5 μm (Figure 5C). (The best choice of spacing distance between focal planes for a given application has been investigated using CRLB analysis.(102)) Biplane data is usually fit following the approach of eq. (1), where a model of how the PSF of each channel changes as a function of the 3D emitter position (x₀, y₀, z₀) is used to simultaneously fit both channels. The fitting task can be defined by LS or MLE with either theoretically derived or empirically measured 3D PSFs.(103, 104)

Multifocal/biplane imaging has been applied to several systems, including single-particle tracking using quantum dots(103, 105) and super-resolution imaging with synthetic dyes and fluorescent proteins(101, 106, 107) in cells. By adding additional planes,(103, 105, 108) it is possible to capture a larger depth of field at the cost of either additional cameras or lateral field of view on a single camera. For example, multifocal imaging with four planes has yielded 3D trajectories of quantum dots in cells with an axial range up to 10 μm.(105)

For high-NA optics, refocusing by displacing the camera is not exactly equivalent to displacing the emitter position within the sample, and can introduce spherical aberration for larger displacements.(109) Aberration-free refocusing can be realized in multifocal microscopy by the application of diffractive optics analogous to those used in PSF engineering (Section 3.2).(108, 110–112) By placing a custom-fabricated optical element into the detection path, the image is diffracted into many orders, each of which has a different phase term that closely mimics the effect of axial displacement within the sample, avoiding aberrations. Such an optical element effectively replaces the functions of the beamsplitter and camera displacement shown in Figure 5. While diffractive optics may incur some loss of photons, this approach has achieved up to ~84% diffraction efficiency for the case of nine planes ranging over 4 μm (113) and is compatible with single-molecule tracking(111) and super-resolution imaging with small molecules.(112) A drawback of multifocal methods that span a large axial range is inefficient use of signal, especially at the extremes of the focal stack, where much of the signal is split into planes that are too out of focus to provide useful information. To improve the 3D precision attainable from each plane, multifocal imaging has been combined with astigmatism (see section 3.2),(114, 115) and we anticipate the possibility of further interesting modifications to multifocus techniques.

Another set of microscope designs related to multifocal imaging achieve high axial resolution by viewing the emitter from multiple angles. One such approach, termed “Parallax”,(116) splits the angular distribution of detected light into two channels by placing a mirror into a plane conjugate to the back focal plane. The axial position is measured from the relative displacement between the PSF in each channel, while the lateral position is read out from the average position. This method, and an earlier version using a prism to split the light, have been applied to the 3D single-molecule tracking of motor proteins.(117, 118) Alternatively, a virtual side view of the sample can be created by mounting the sample onto a fabricated micromirror sitting at a roughly 45° angle to the optical axis. The PSFs in this virtual image can be fit to directly extract axial position. While it complicates sample preparation, this approach has been successfully demonstrated for particle tracking and for super-resolution imaging.(119, 120)

3.2 Accessing the Third Dimension via PSF Engineering

The limitations of the standard PSF make it difficult to extract emitter z position from a single image, but this need not be true for all microscope PSFs. An alternate set of methods attain precise axial localization of a point source by encoding the emitter’s depth in the shape of the PSF. This can be achieved with simple phase aberrations, such as by inserting a weak cylindrical lens before the tube lens to induce astigmatism, where the eccentricity of the PSF changes as a function of axial position (Figure 6A).(121–123) A more general-purpose way to induce phase aberrations is to place a programmable phase-modulator in a plane conjugate to the objective back focal plane, i.e. the Fourier plane of the microscope (Figure 6). (While one could modulate amplitude in addition to phase using absorptive optics, this would cause the loss of precious photons.) Performing phase modulation in this specific geometry provides a useful mathematical framework for synthesizing new PSFs, and is necessary in order to impart the same modulation throughout the field of view.(124) The relation between the electromagnetic fields in the back focal plane and the image plane is given by

Figure 6.

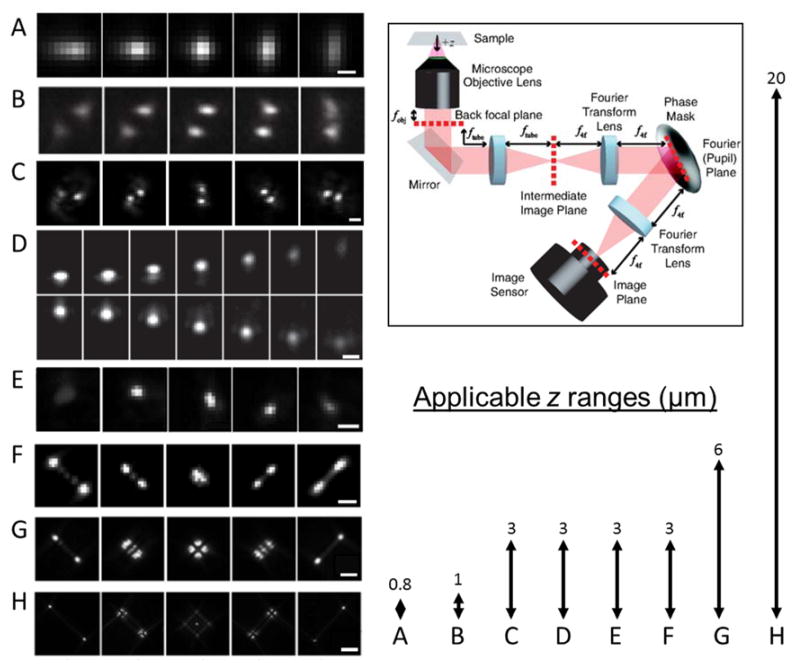
Various experimentally measured PSFs for 3D localization microscopy shown as a function of axial position of the emitter (ranges shown in lower right). Adapted from ref. (134) (A) Astigmatism. Scale bar ≈ 0.5 μm. From ref. (123). Reprinted with permission from AAAS. (B) Phase-ramp. Ref. (128) Copyright Tsinghua University Press and Springer-Verlag Berlin Heidelberg 2011, with permission of Springer. (C) Double-Helix. Scale bar = 2μm. Adapted from ref. (126). Copyright 2009 the authors. (D) Accelerating beam (split onto two camera regions). Scale bar = 1 μm. Reprinted with permission from Macmillan Publishers Ltd: Nature Photonics ref. (129), copyright 2014. (E) Corkscrew. Scale bar = 1 μm. Adapted from ref. (127). Copyright 2011 the authors. (F) A 3 μm range Tetrapod (also known as the saddle-point PSF). Scale bar = 1 μm. Reprinted figure with permission from ref. (130). Copyright 2014 by the American Physical Society. (G), (H) 6 and 20 μm range Tetrapods. Scale bars =2 μm and 5 μm, respectively. Reprinted with permission from ref. (131). Copyright 2015 American Chemical Society. The arrows (right) represent the z-ranges over which the PSFs on the left were imaged, which correspond to their applicable depth ranges. Top right: experimental setup for PSF engineering based on back focal plane modulation. Reprinted figure with permission from ref. (130). Copyright 2014 by the American Physical Society.

$$I(u,v;x,y,z)\propto {\left|\mathcal{F}\{\mathrm{E}(x^{\prime },y^{\prime };x,y,z)·\mathrm{P}(x^{\prime },y^{\prime })\}\right|}^2$$ (11)

where E(x′,y′) is the electric field in the back focal plane caused by a point source at (x,y,z), the 3D position relative to the focal plane and the optical axis. The function P(x′,y′) is a phase pattern imposed by optics in the Fourier plane. We denote by ℱ the 2D Fourier transform. To broadly summarize the implications of eq. (11) for PSF engineering, an axial (z) displacement of the emitter from the focal plane is equivalent to curvature in the phase of E(x′,y′), and the phase pattern P(x′,y′) changes how this manifests in the image I(u,v).

The z-dependent curvature term of the electromagnetic field at the back focal plane can be approximated by

$$E(x^{\prime },y^{\prime })\propto e^{-{\mathit{ikn}}_1{z}_1}\sqrt{1-{\left(\frac{NA}{n_1}\rho \right)}^2}+{\mathit{ikn}}_2{z}_2\sqrt{1-{\left(\frac{NA}{n_2}\rho \right)}^2},$$ (12)

derived from the scalar approximation in the Gibson-Lanni model.(68) This model assumes a two-layer experimental system consisting of a sample of refractive index n₂ (e.g. water), and glass/immersion oil which have matched refractive index of n₁. The distance between the emitter and the interface separating layer 1 and layer 2 (namely, the distance from the surface of the glass coverslip) is given by z₁, and the distance between the microscope focal plane and the interface is denoted by z₂, with k the wavenumber 2π/λ, and $\rho =\sqrt{{x^{\prime }}^2+{y^{\prime }}^2}$ denoting normalized polar pupil plane coordinates. Phase curvature is added to the phase pattern P(x′,y′), and the measured PSF I(u,v) reflects both P(x′,y′) and z.(86) In the absence of a phase mask (i.e., if P(x′,y′) is a constant), z displacements appear as defocus blur. The goal of PSF engineering is to choose a pattern P(x′,y′) that makes the amount of phase curvature, and thus z position, easier to detect from the image.

There are multiple ways in which a phase mask can encode the axial position of an emitter in the shape of the PSF, and various PSF designs have been used in recent years. These include an elliptical (astigmatic) PSF,(121–123) the rotating double-helix PSF (DH-PSF),(125, 126) the corkscrew PSF,(127) the phase ramp PSF,(128) the self-bending PSF(129) and the saddle-point/Tetrapods(130, 131) (Figure 6). These engineered PSFs span different axial ranges and exhibit a wide variety of shapes, but all have distinct features that change rapidly as a function of z position, such as changing eccentricity (Figure 6A), relative motion of two lobes (Figure 6B–D), lateral translation (Figure 6E), or relative motion, splitting, and recombining of multiple lobes (Figure 6F–H).

As mentioned above, these PSFs can be generated using several approaches. Simpler phase patterns can be induced using optics such as a cylindrical lens(123) or a glass wedge,(128) while other patterns require control over the phase pattern, as can be attained with a deformable mirror (DM),(132) a lithographically etched dielectric (e.g. quartz),(62) or a liquid crystal spatial light modulator (SLM).(126, 129–131) SLMs and DMs can be flexibly programmed to generate different phase patterns, and have advantages and disadvantages. SLMs have many pixels, but are designed to work for a specific linear polarization of light, halving the photons collected. This limitation can be avoided if necessary by using a “pyramid geometry” that collects both polarizations.(133) DMs have negligible loss, but generally have a limited number of actuators and cannot generate patterns with phase singularities or other fine features. Glass or quartz optics can generate features limited in fineness only by the fabrication method and have minimal loss, but are fabricated into a set pattern and cannot be changed.

There are multiple ways to determine z positions from image features in engineered PSFs. An intuitive and widely-applied approach is to choose an easily identifiable parameter in the image and generate a calibration curve relating that parameter and z. Such calibration curves can be derived from a theoretical model of the PSF or from empirical measurement of fluorescent beads or other bright fiducials, where the focal plane is translated by changing the distance between the objective and sample. For the case of the DH-PSF (Figure 6C), the angle of the two revolving PSF lobes are such a calibration parameter (Figure 7A). For the astigmatic PSF (Figure 6A), the relevant parameters are the PSF width along the x and y axes (Figure 7B), such that z is estimated from the value that best matches the observed pair (w_x,w_y). These parameters are measured by fitting image data to an approximation of the PSF, such as a pair of 2D Gaussian functions fit to the DH-PSF lobes, or an asymmetric 2D Gaussian fit to the astigmatic PSF.

While intuitive, such parametrizations do not use all the data in the image. Most 3D PSFs have features that are not accurately fit by a Gaussian function; for example, it is difficult to imagine a simple parameter that uses all the information present in complicated-looking PSFs such as the Tetrapod family (Figure 6F–H). To make use of this information, one can instead fit the observed PSF to a 3D model function of the PSF. Such a model function can be numerically generated or interpolated from an experimental calibration. In this way, fine features of the PSF contribute to the estimate, improving the precision. (MLE, rather than LS fitting, is particularly desirable when fitting a complete PSF model, as MLE uses information from dim pixels more correctly.) Because the PSF need not have a single, easily-interpretable feature, this broadens the range of possible 3D PSFs.

Engineered PSFs exhibit a wide range of behavior in terms of size, applicable z-range, and attainable precision. For example, the astigmatic PSF has a small footprint on the detector, allowing for potentially more emitters per unit volume to emit simultaneously while avoiding PSF overlap, but a relatively small z-range, close to that of the standard PSF. On the other hand, the DH-PSF has a larger z-range, over which it exhibits superior and uniform precision (smaller CRLB) than astigmatism,(135) and the saddle-point/Tetrapod PSFs(130, 131) have an even larger applicable z-range at the cost of potentially larger footprint. Figure 6 shows various different PSFs along with their applicable z-ranges, and Figure 8A–C shows the phase patterns for the astigmatic, DH-PSF, and Tetrapod PSFs.

Figure 8.

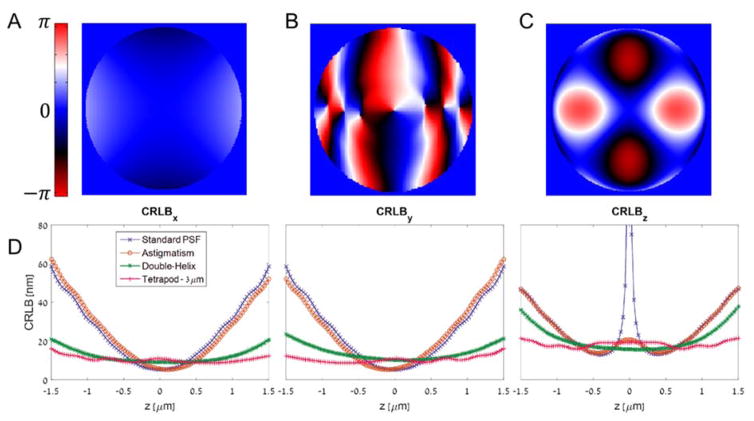
Selected PSF phase patterns and Cramér-Rao Lower Bound calculations. (A) The astigmatic PSF. (B) The DH-PSF. (C) The Tetrapod PSF for 3 μm range. (D) The CRLB for estimating x,y, and z is plotted for the standard PSF and the three 3D PSFs above. Low CRLB means a good potential precision. The calculation assumes 1000 detected signal photons, a background of 2 photons per 160 nm pixel, using a 100X oil immersion objective with a NA of 1.4.

As mentioned earlier, Fisher information is a useful measure to assess the attainable precision of an imaging system, and can be used to compare different PSF designs.(135) Such a comparison is shown in Figure 8D, displaying the calculated CRLB of four PSFs – the standard PSF, astigmatism, Double-Helix, and a 3 μm range Tetrapod. The CRLB bounds the attainable variance, and hence lower CRLB is indicative of superior (smaller) precision. Key observations from Figure 8D include: 1) The standard PSF contains very little information about the axial (z) position of an emitter near the focal plane (z = 0), and only maintains good lateral (x,y) localization performance over a < 1 μm z range. Clearly, a standard PSF is a poor choice for 3D localization. 2) For all PSFs, axial precision is worse than lateral precision. 3) The Tetrapod PSF exhibits the best mean CRLB in 3 dimensions over the 3 μm range. This is because it was algorithmically designed to maximize Fisher information, and therefore to be optimally precise under the conditions simulated.(130) It is worth noting that the design algorithm assumed uniform Poisson background; in certain situations (such as in cells) this may be hard to achieve.

When selecting a PSF for 3D localization, a major consideration is its applicable z-range, which is the axial region where the CRLB is low. Figure 9 shows a comparison between a Tetrapod PSF designed for a 3 μm z-range and a Tetrapod PSF designed for a 6 μm z-range.(131) It is evident that the 6 μm Tetrapod exhibits a larger applicable z-range, albeit at the cost of poorer precision in the shorter (3 μm) z-range. This trade-off in performance means that the experimenter should pick a PSF with a range appropriate to the sample under consideration. If imaging time and drifts are not issues, a short-range PSF can be successively translated again and again in z to build up an image.(101)

Figure 9.

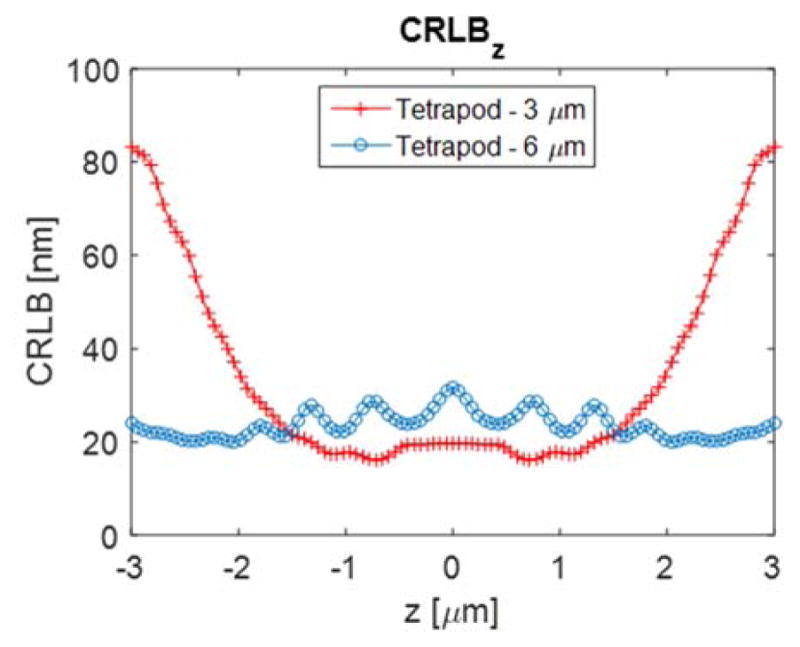
Cramér-Rao Lower Bound calculation comparing the 3 μm z-range Tetrapod PSF with the 6 μm z-range Tetrapod, in terms of precision bound on axial position estimation. The trade-off between precision and z-range is evident in this comparison. Simulation parameters are the same as in Figure 8.

While the focus of this review is on 3D localization, the type of information that one can encode in a PSF is not limited to depth. PSF engineering has been used to encode the 3D orientation of an emitter(136, 137) and even its emission wavelength,(138, 139) adding new ways to extract information about a molecule’s identity and local environment while simultaneously obtaining a nanoscale position estimate.

3.3 Intensity, Interfaces, and Interference

The methods described so far all extract axial position by measuring the shape of the PSF in the far field. However, this is not the only information available from an emitter. Several methods have emerged that perform axial localization using properties such as the intensity gradient of the excitation field, the near-field coupling of the emission to the coverslip, or the phase information of the emitted light. While these are not directly related, the three examples we discuss below highlight the power of carefully considering the physical process in which light couples to and from the emitter, without relying on information from the shape of the standard PSF.

The first class of methods uses the profile of excitation light. If the fluorescence quantum yield and absorption cross-section of an emitter are constant, the fluorescence intensity from a single molecule will depend only on the excitation irradiance. Assuming this, relative axial position can be inferred from fluorescence intensity in the presence of a well-defined axial intensity gradient. One early example made use of the exponentially-decaying evanescent wave produced at the coverslip/sample interface by TIRF microscopy.(74, 140) The lateral position of fluorophores in a polyacrylamide dye was measured as in a standard 2D microscope, while changes in detected fluorescence intensity specified relative axial position. Given the decrease in intensity and thus localization precision away from the coverslip, 3D measurement using TIRF is limited by a short effective detection range. This has been employed indirectly to allow axial “sectioning” of 2D SR data using sequential imaging at different penetration depths.(141) The steep intensity gradient of a confocal illumination volume can be employed in an analogous fashion to that of the TIR illumination profile. While not a wide-field detection method, this has been used to track the motion of single nanoparticles, one at a time, by using a xyz translation stage in closed-loop operation, permitting the observation of complex cellular transport processes with a large range and high resolution both spatially and temporally.(142–145)

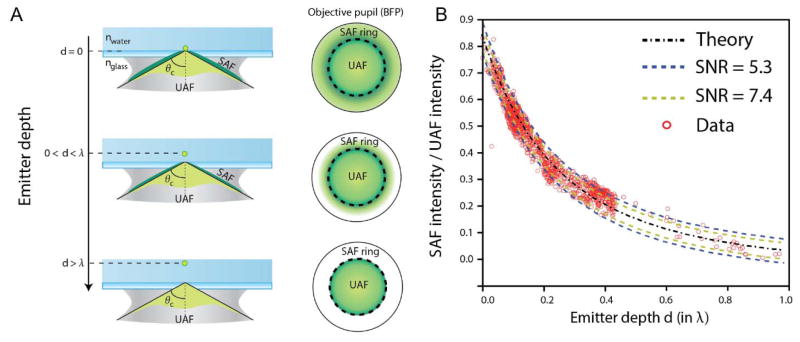
A second related set of methods uses the effects of the sample-coverslip interface on emission, rather than excitation, to extract relative axial position. This can be done with the refractive index mismatch between sample and coverslip, measuring the coupling of emitted light into the coverslip rather than the evanescent excitation profile of TIR. For emitters more than ~λ distant from the coverslip, any light emitted at more than the critical angle (θ_c~61° relative to vertical for a water/glass interface) will be totally internally reflected back into the sample. However, as the emitter gets closer to the surface, “supercritical” light above this angle will be coupled into the coverslip and can be collected with a high-NA objective; the axial dependence of the coupling efficiency is comparable to that of TIR excitation with highly inclined illumination (Figure 10A).(146) (This supercritical, or “forbidden,” light was used to sense the position of a near-field pumping source near a single molecule in the early days of single-molecule spectroscopy.(147)) The supercritical and “undercritical” components of the fluorescence can be discriminated by placing an annular filter in the back focal plane, and comparison of the total fluorescence relative to the undercritical-only fluorescence allows determination of axial position without a large loss in signal as in the TIRF case (Figure 10B). This method has been demonstrated for in vitro experiments with 3D origami nanostructures and for single-molecule imaging very near the interface in cells.(76, 77)

Figure 10.

(A) Coupling of emitters close to the coverslip allows the collection of supercritical angle fluorescence (SAF) in addition to “undercritical” fluorescence (UAF), as can be detected in the back focal plane (BFP). (B) The ratio of supercritical to undercritical light sharply decays away from the coverslip, allowing axial position estimation. Results shown for the ideal case, for simulations with varying signal to noise ratios, and for experimental data with 20 nm beads embedded in 3% agarose gel (n = 1.33 ≈ n_water), with depths confirmed using astigmatism. Adapted by permission from Macmillan Publishers Ltd: Nature Photonics, ref. (77), copyright 2015.

A distinct interface-based axial localization method has been demonstrated that uses a coverslip coated in a thin gold film.(148) Fluorophores close to the film (< 100 nm separation) exhibit lowered fluorescence lifetimes due to coupling to surface plasmons, and the lifetime changes steeply and monotonically with distance from the film.(149) While the quenching lowers the total number of photons detected before photobleaching, lowering lateral precision, it is possible to achieve axial precisions of a few nanometers with standard fluorescent dyes by measuring single-molecule fluorescence lifetimes using confocal detection and a single-photon-counting detector.(148)

A third approach uses the phase of the single-molecule fluorescence, rather than intensity, to interferometrically estimate axial position. While this class of methods can be more experimentally demanding than others discussed in this review, it has high potential precision. Since the light emitted from a single molecule is self-coherent, it can be interfered with itself to sense the relative phase delay between different imaging paths. For a microscope, this can be accomplished using opposed parfocal objectives to collect light from above and below the sample (Figure 11A). A displacement of the emitter δ along the optical axis in a sample of refractive index n will advance the phase of light in one path and delay the other by approximately 2πnδ/λ = δk, causing a total phase shift of 2δk. Interfering the two paths adds axial interference fringes to the PSF: while a given x–y slice of the interfered PSF has roughly the same shape as it would in a conventional microscope (Figure 3), the total intensities of the PSF slices vary sinusoidally with z position, with period ~2π/2k = λ/2n. Before being applied to single-molecule studies, this effect was used in bulk fluorescence microscopies using confocal scanning (4Pi)(150) and wide-field (I⁵M/I⁵S)(151, 152) illumination. By axially scanning the sample and deconvolving the interferometric PSF, an image is produced with ≥5x improved axial resolution relative to standard confocal or wide-field microscopy.(153)

Figure 11.

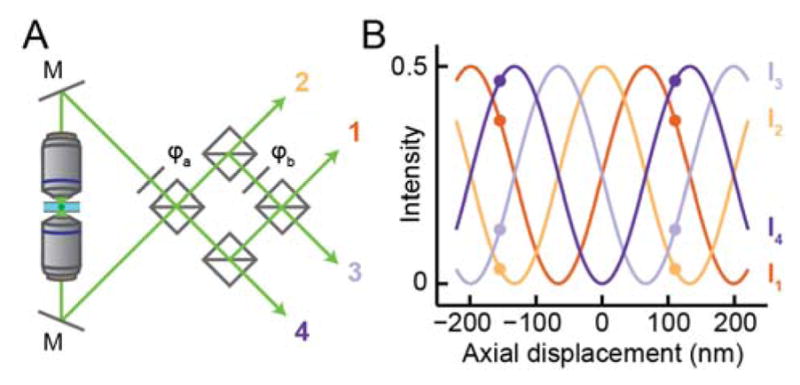
Interference microscopy captures high-resolution axial information with dual-objective detection. (A) Schematic of a four-channel interference microscope, based on the example of (156). M, mirror; φ_a,b phase delay elements, squares, 50:50 beamsplitters. The first beamsplitter combines the light from the two objectives, producing two beams with relative phase delay π. These are recombined to produce two more channels with phase delays π/2 and 3π/2. Not shown: each interfered detection paths is focused and imaged separately, either on different parts of a camera or on separate cameras. The phase delays increase by π/2 between channels, owing to the choice of φ_b= −π/2 and the π/2 delay of reflected vs. transmitted beams. (B) The fraction of total signal intensity in each detection path of (A) as a function of the emitter’s axial displacement from the focal plane. The delay model is as described in ((75, 156)) assuming an aqueous environment, NA 1.4, and fluorescence at 600 nm. As shown by the colored dots, axial position can be read out precisely from a point measurement of the detected intensity in each channel, but is not uniquely determined beyond a period of ~λ/2n.

As discussed in Section 3.1, scanning is not generally feasible for dynamic single-molecule measurements, and as with multifocal microscopy, it is preferable to simultaneously sample several channels that mimic axial displacement of the sample. In the case of interference-based microscopy, this amounts to a different relative phase from the top and bottom objective. Rather than scanning the sample to create an interferogram, different effective displacements are sampled in each channel i by introducing a relative phase delay φ_i between the light from the two objectives. In the limiting case of low-NA collection, the total intensities detected from the molecule in each channel, I_i, have the relationship

$$I_i\propto 1+cos(2kz+{\phi }_i)$$ (13)

for z the axial position relative to focus. (High NA lowers the effective value of k.(75, 154, 155)) A two channel interferometric setup, i ∈ (1, 2), with relative phase delays φ = (0, π) can be generated using a single 50:50 beamsplitter to recombine signal from both objectives due to the π/2 phase retardation upon reflection (Figure 11). From eq. (13),

$$z=\frac{1}{2k}{cos}^{-1}\left(\frac{I_1-I_2}{I_1+I_2}\right)$$ (14)

letting us extract the molecule’s position z from its measured intensity in the channels I₁, I₂. As the range of cos⁻¹ is [0, π], eq. (14) demonstrates that phase aliasing limits the z values that can be detected in a two-channel interferometric microscope to a range of π/2k = λ/4n ≈ 120 nm. The Fisher information vanishes when the two beams perfectly interfere (at phase delays of 0 and π/2), as the cosine response of (13) reaches a point of zero derivative simultaneously for both channels, further limiting the practical range of such a microscope.

Sampling more than two phase delays resolves ambiguity to achieve an axial range of λ/2n and provides more uniformly high Fisher information. Multiple names including “iPALM”(75) and “4Pi-SMS” (156) have been used for setups that use three or four detection paths with relative phase delays multiples of 2π/3 or π/2, respectively. These paths are created using a specially-designed beamsplitter or combination of beamsplitters and phase-shifting elements, respectively, with an approach generating four channels sketched in Figure 11A. The intensities in each detection path are analyzed following eq. (13) to extract z information: as shown in Figure 11B, the four detected intensities change in a well-defined fashion with z, repeating with period ~λ/2n. It was shown early on both by theoretical studies of the CRLB(156) and by experimental measurement(75) that such approaches provide high precision laterally (due to the increased number of photons from two objectives) and even better precision axially, on the order of σ_xy < 10 nm, σ_z < 5 nm for photon counts typical of fluorescent proteins when imaged using TIRF.

While effective for 3D SR imaging near the cell membrane, the first studies using single-molecule interference microscopy could not go beyond the λ/2n limit imposed by phase wrapping. Later implementations used additional features of the image to break this symmetry. For example, for high-NA optics and sufficiently high SNR, the phase oscillation is measurably different at the edges of the PSF, allowing fringes to be disambiguated by spatial filtering.(155) Alternatively, a feature such as astigmatism can be added to the PSF to coarsely localize the molecule to one of the fringes before extracting the precise “intra-fringe” position.(157) By avoiding phase aliasing, these methods achieve an axial range of interference localization microscopy limited primarily by the focal range of the PSF, ~700–1000 nm for the standard or astigmatic PSFs.

The high precision afforded by interference methods comes with practical drawbacks. One is complexity of alignment and maintenance. Since any difference in the path length between the two imaging arms is directly reflected in the measurement, these must be stabilized to nanoscale tolerances over a path length on the order of a meter. Such stabilization can performed with additional interferometric feedback systems.(151, 158) Alternatively, by placing a mirror directly above the sample to collect both paths through the same objective and recombining them using an SLM, it is possible to reduce the amount of stabilization needed, with a trade-off of somewhat poorer localization precision.(159) A separate difficulty arises when imaging thick samples, due to the phase aberrations produced by a heterogeneous refractive index. In a comprehensive study, it was recently demonstrated that by using adaptive optics, it is possible to compensate for both the aberrations of thick cells and the impact of sample drift to achieve accurate imaging at multiple positions within thick cells.(158) While this did not extend the range of the PSF beyond the limit of its focal range, the stability of the setup allowed whole-cell interferometric imaging over a total range of up to 10 μm by combining multiple sequentially acquired axial sections, where aberrations within each section were separately corrected.

Taken together, the multiple new methods for 3D localization described in this section give the experimenter many choices. Since the goal in all such studies is optimal utilization of the available emitted photons from single molecules, it continues to be essential to balance complexity and performance as needed for the application.

4. Challenges and New Developments in 3D Localization

As we have seen, there exist a wide variety of optical enhancements of the standard wide-field fluorescence microscope that significantly improve the precision of 3D localization, enabling otherwise impossible measurements. Along with new possibilities, this advance brings with it new challenges to overcome. Systematic errors can be introduced in 3D imaging by optical aberrations and by dipole emission effects. Similarly, the need to accurately preserve 3D information between imaging channels (such as in multicolor imaging or polarization imaging) requires a careful approach to registration. And in general, adding a new dimension can affect the resolution, sampling rate, and field of view of localization microscopy.

In this section, we highlight some technical implications of moving to 3D imaging and the approaches that have been developed to improve its accuracy and spatiotemporal resolution. This description of possible errors is not exhaustive, and other errors such as those induced by sample drift over the course of acquisition(106, 160–162) are also necessary to correct in quantitative single-molecule microscopy. (In the case of drift, correction can be achieved using fiducial markers, interferometry, or cross-correlation with post-processing or active feedback.) We close by offering a general prospectus of methodological improvements that have either just begun to be made, or that would be a desirable future addition to the field.

4.1 Spatially Dependent Optical Aberrations and Multichannel Registration

Nonidealities of the imaging system that would be minor for a diffraction-limited microscope can cause errors that overwhelm the much finer resolution of a single-molecule microscope if not corrected. Such aberrations can be considered as an additional undesirable phase pattern added to the system, i.e. to the function P(x′,y′) of eq. (11). Since this changes the 3D PSF and alters the expected phase of the emitter, these potential errors are relevant for most 3D microscopy methods. Careful optical alignment is the first step in minimizing aberrations, but even a perfectly aligned setup with index-matched media will have imperfect optics and deviate from the paraxial ideal.(163, 164) As long as the microscope PSF is spatially invariant across the transverse field of the image and at any depth within the sample, minor aberrations can be accounted for with a simple calibration, such as an axial scan of a fluorescent bead adhered to the coverslip. Such calibrations are used in all categories of 3D localization methods,(75, 101, 123, 126) and can be used to extract the exact wavefront aberration using phase retrieval.(165) However, several classes of aberrations undermine the assumption that there is a single PSF over the entire 3D volume, and require more comprehensive consideration and correction. These can be categorized as either depth-dependent or field-dependent aberrations.

Depth-dependent aberrations are due to a refractive index mismatch between the sample and immersion medium, as is common for biological samples (with index close to water, n = 1.33) imaged with high NA oil immersion (n = 1.51) objectives. In addition to axial distortions of the PSF due to spherical aberration, index mismatch induces a well-known rescaling of the effective focal plane depth (~30% for an oil-water mismatch).(68, 166, 167) Index mismatch can be greatly reduced by switching to water immersion objectives (and carefully aligning the sample and correction collar),(168) but due to the need for high NA in 3D single-molecule microscopy, the reduced NA when using low-index media such as water may be undesirable. Two alternative solutions include calibration, and correction via adaptive optics.

Calibrations of depth-dependent errors require a different approach than a simple axial translation of the sample, as this does not actually change the depth of the fiducial (which is typically adhered to the coverslip and does not suffer significant index mismatch effects). One powerful approach, demonstrated for the astigmatic PSF, is to move fiducials through a range of well-defined axial positions within the sample using an optical trap while keeping the focal plane fixed.(169) While it does not require any specific PSF, this approach has not been applied more generally, perhaps owing to its relative complexity. An alternative method computationally synthesizes the 3D PSF at different depths by adding appropriate amounts of aberration to the empirical phase retrieved from a standard calibration. This has been shown to be effective for multifocal(170) and astigmatic(171) localization microscopy.

Adaptive optics (AO) is a powerful means to correct aberrations, and works by measuring or otherwise inferring the aberration phase, then using a programmable modulator to cancel it out.(172, 173) The aberration phase is typically defined and corrected in a plane conjugate to the back focal plane (also referred to as the pupil plane for AO applications), and is modulated by a programmable SLM or DM in this conjugate plane. This is accomplished similar to the 4f system described in Section 3.2, and most AO modulation schemes are straightforward to combine with other PSF engineering methods. Such a geometry is chosen in order to add the same correction to all points within the field of view. Multiple approaches have been reported to determine the appropriate correction phase for a given focal plane depth within the sample. Applications of AO to confocal and 2-photon microscopy often use a bright fluorescent point source or “guide star” to measure the 3D PSF in situ. The aberration phase can be explicitly detected, such as with a Shack-Hartman wavefront sensor conjugate to the back focal plane,(174) or inferred (as is useful for scattering samples and/or thick tissue) indirectly from image-based readouts such as pupil segmentation.(175) In the context of single-molecule imaging, aberration correction has been informed by direct wavefront measurement as well as iterative image optimization with guide stars.(132) Another approach iteratively optimizing the PSFs detected from single molecules observed in the first frames of the SR acquisition.(176) These methods result in improved 3D SR reconstructions in cells, and have permitted 2D SR imaging in tissue at depths of 50 μm.(177) AO was also recently introduced for super-resolution interference microscopy by using one DM in each imaging arm, where system aberrations were corrected by iteratively optimizing the PSF for a guide star at the coverslip.(158)

Aberrations can also depend on position within the sample, such as for cells or tissue with heterogeneous index, as well as for several classes of system aberrations. For many experiments near the coverslip, sample-induced aberrations may not cause a problem, but for precise imaging deep into a biological sample, they should be addressed. For confocal and other scanning microscopies, specimen-induced field-dependent aberrations are relatively tractable, and can be accounted for by performing separate interferometry measurements and AO correction at each pixel of the image. For diffraction-limited confocal imaging, field-dependent system aberrations are often not necessary (and are more complicated) to correct.(178) Field-dependent AO becomes more difficult for wide-field single-molecule techniques both in the measurement (pupil phase is contributed equally from across the field of view) and in correction (phase induced at the pupil alters the whole PSF). It is possible to perform AO corrections conjugate to planes other than the back focal plane, such as at the sample plane.(179) While such corrections could potentially address field-dependent aberrations in single-molecule imaging, this has not been demonstrated.

The high precision of single-molecule methods makes them more susceptible to any system imperfections. Since it is difficult to sense or correct the wavefront of wide-field microscopes in a field-dependent manner, it is expedient to instead directly measure and correct the effect of these aberrations by field-dependent PSF calibration. Such calibrations can be performed by using regularly-spaced point emitters such as subdiffraction apertures (nanoholes) in a metal film filled with fluorescent dye (Figure 12A).(180) Both double-helix and astigmatic PSFs have been tested in this manner by calibrating the PSF over a 30 μm field of view (Figure 12B), and both the rate of change of the PSF, and apparent focal position were observed to vary over the field of view relative to any arbitrary reference calibration. This work showed that using a single calibration could potentially lead to errors in 3D measurements of 20% or more over the field of view (Figure 12C). The observed errors depended on the choice of engineered PSF phase pattern, with the DH-PSF showing less error than astigmatism. (In this case, both PSFs were induced at the back focal plane; it can be expected that inducing astigmatism by placing a cylindrical lens in an intermediate plane would couple field and Fourier space, resulting in worse field-dependent errors.) Using a spatially varying calibration function derived from all the nanoholes, axial localization errors of ~50–100 nm were reduced to less than 25 nm (including random localization error) over a ~25 μm × 25 μm × 1.4 μm volume. Given that errors increased away from the reference calibration, larger fields of view are likely to be more susceptible to such errors if not calibrated by local sampling of the 3D PSF. The high NA objective is one likely contributor to these aberrations, as supported by recent studies of (global) aberrations in orientational imaging(181) and comparative modeling of Fourier microscopy configurations.(182)

Figure 12.

The systemic field-dependent variation in a microscope’s point spread function. (A) A nanohole array samples the double helix PSF at many positions over the lateral field of view. (B) The measured rate of change and apparent focal plane of nanoholes fit with a reference calibration of the DH-PSF (dotted line) varies greatly at different lateral positions despite being measured in the same axial scan. (C) The error in the observed displacements during an axial scan of a nanohole array imaged with the DH-PSF displays a spatial dependence relative to the nanohole used for a reference calibration (white dot; error interpolated between nanoholes). Adapted with permission from ref. (180). Copyright 2015 the Optical Society.

Channel registration can be seen as a special case of compensating for field-dependent aberrations. When images of the same molecule in multiple channels are used together to generate a localization (e.g., for multifocal, interferometic, and some PSF engineering methods, as well as polarization imaging) the different field-dependent aberrations, translations, and magnifications of each channel contribute to the final reconstruction in a complicated fashion. In multicolor imaging, where different molecules appear in each channel, mismatched aberrations or poor channel alignment are even more problematic, and can introduce a false displacement between two labels of different colors. In this case, channels must be registered together to an accuracy at least as good as the image resolution to avoid artifacts in measurements of colocalization or correlation between different labels. (In this case, “channels” may refer to imaging paths that impinge on different cameras or regions on the same camera, or simply to the differences due to chromatic aberrations and/or filters that vary between labels.)

A powerful way to register localizations within the same coordinate system is to derive a transformation function from control points (CP), i.e. localizations of fiducials visible in both channels. Registration accuracy depends on the number of CP sampled and the type of transformation used.(183) For example, an affine transformation (rotation, translation, scaling, and/or reflection) in 2D requires only three CP pairs, while finer distortions require commensurate increases in control point sampling density. When discussing registration accuracy, it is important to clarify the multiple error metrics that have been used, including the Fiducial Registration Error (FRE) and Target Registration Error (TRE): the FRE is defined for CP pairs that were used when generating the transformation function, while the TRE is defined for a set of CP pairs that were set aside and did not contribute to the transformation. (183) The FRE is a useful measure of CP localization errors, but can give extremely overoptimistic estimates of registration accuracy over the field of view. For example, a 2D affine transformation estimated from three CP pairs will overlay the CPs perfectly and give a FRE of zero, yet this clearly does not mean that all aberrations within the field of view have been corrected! The TRE, on the other hand, reports the registration accuracy at intermediate positions not used in constructing the transformation, and is therefore a more representative measure of the error added during registration.

It is common to use ~10 CPs scattered throughout the field of view to generate an affine or low-order global polynomial transformation function for multicolor 3D SR microscopy.(111, 155, 184, 185) This is typically sufficient for registration in applications that do not require fine correlative measurements. However, it was recognized early in 2D colocalization studies that much finer sampling and more flexible local transformation functions were necessary for accuracy on the order of 10 nm.(186, 187) This approach has been extended to 3D SR using a locally weighted transformation function capable of achieving < 10 nm registration accuracy and accurately overlaying super-resolved 3D structures in bacteria using many fluorescent beads sequentially scanned through the 3D imaging volume as control points.(62) As shown in Figure 13, the same protocol can be applied using nanohole arrays. By localizing thousands of control points in both color channels throughout the 3D volume, a high sampling density is achieved, giving a mean TRE < 8 nm. While CP localization precision can contribute slightly to registration errors, this accuracy is still primarily limited by spatial sampling, and it was shown that mean 3D TREs below 6 nm can be achieved by imaging > 25 CPs/μm³.(62) More fundamental limits such as the pixel-to-pixel-nonuniformity of the detector camera have been described for 2D imaging,(188) which should be possible to calibrate in the same manner for 3D imaging.

Figure 13.

(A) The fine variation of 3D imaging channels must also be calibrated in order to obtain accurate multicolor registration. By sequentially localizing many fiducials that appear simultaneously in both spectral windows, it is possible to generate a large set of control points in both color channels with subdiffraction sampling (a subset is shown here). These control point pairs are used to generate a transformation mapping the green and red channels. (B) Locally weighted transformation functions reliably achieve < 10 nm target registration error. Results are shown for 5000 localizations from a nanohole array, acquired and analyzed after the fashion of ref. (62).

4.2 Dipole Effects Which Can Lead to Localization Bias

One specific feature of single-molecule localization microscopy arises from the fact that individual molecules are not isotropic emitters: the dipole nature of the emission from a single fluorophore can be non-negligible, and even informative.(189–194) A practical implication of the dipole nature of fluorophore emission is that the emitter’s orientation may need to be taken into account when localizing single molecules in microscope images. Ignoring this effect can lead to localization errors: out-of-focus molecules can appear to be shifted in the lateral (x–y) plane, simply due to their non-isotropic emission profile.(133, 195, 196) This localization error can be appreciable (~100 nm or more) for molecules far from the nominal focal plane of the microscope. Since this is the regime of interest for 3D imaging, the potential x–y localization bias must be considered.

The x–y localization bias would not occur if the emitters were highly rotationally mobile, because then any anisotropy from the dipole emission pattern would be removed in a time average. To quantify this effect, Lew and Backlund et al. considered the situation for fluorophore labels whose rotational flexibility follows the well-known “wobble in a cone” model.(197) This model assumes that the tip of the emission dipole moves randomly in a 3D cone with half-angle α, and the results of this simulation are shown in Figure 14A. The tilted ellipsoids show the effective intensity distribution near the detector in an x–z projection: the recorded image will be the intersection of this ellipsoid with the x–y oriented camera. As shown in the narrow panels, molecules at different z positions in the sample will produce laterally shifted images. The two cases (A) and (B) refer to α = 15° (a small cone angle indicative of relatively fixed dipoles) and α = 60° (a highly mobile dipole orientation). The conclusion of this modeling study was that the lateral error can be bounded to less than ~20 nm for the larger cone angle, on the order of the localization precision. Notably, for fluorophores attached to an antibody with a floppy saturated carbon linker, this situation is likely to be realized for most emitters. Polarized measurements with a bisected-pupil PSF confirmed that the rotational flexibility is high in this situation(137). Nevertheless, not all attachment strategies or fluorescent labels allow free emitter rotation, requiring a different solution.

Figure 14.

Three strategies to address dipole-induced shift errors. (A) Floppy labels. The panels show the intensity distribution near the camera plane modeled for dipoles with different cone angles of rotational motion. On the left, a small cone angle of 15° produces a large tilt of the detection ellipsoid (i.e. the effective 3D PSF) as shown in x–z projection. The x–y projections show the images on the camera for molecules at different defocus. On the right, a larger cone angle of 60° produces a smaller tilt of the PSF, and a correspondingly small shift of the camera images. Adapted with permission from ref. (197). Copyright 2013 American Chemical Society. (B) Empirically measuring orientation and z with correction by calculation. The left six panels show x and y polarized DH-PSF images of the same molecule at different z, illustrating the changes in lobe asymmetry. The green panels on the right show histograms of x–y localizations of the same single molecule at many different z. Without correction (u), the lateral position shifts dramatically, while with the correction (c), the lateral spread is primarily from photon-limited localization precision. Adapted with permission from ref. (200). Copyright 2013 National Academy of Sciences. (C) Azimuthal emission filtering. The left panel shows the simulated image of a fixed dipole at polar angle 45°, where the shift of the image from the actual location (white spot) is clear. If only azimuthally polarized light is allowed through the back focal plane, the resulting image is centrosymmetric and centered on the correct position. Adapted with permission from ref. (201). Copyright 2014 American Chemical Society.

A brute-force approach to handling dipole-induced localization bias is to measure the 3D orientation of a fluorophore, and later correct for the localization error by post processing. The orientation can be determined by a variety of methods, ranging from the use of polarization optics(190, 191, 198) to analysis of the defocused emitter’s image.(192, 199) One method to determine orientation combines polarization microscopy with PSF engineering, which has the advantage of being simple, precise, and robust to minor defocus errors.(86) This can be achieved, for example, by using the DH-PSF,(133) or by PSFs with a quadrated pupil,(136) or by a bisected pupil.(137) To directly show that orientation measurements can be performed simultaneously with 3D localization microscopy, Backlund and Lew et al. took advantage of the fact that polarized DH-PSF images show varying degrees of lobe asymmetry depending upon z position (Figure 14B, left three columns) (200). By measuring lobe asymmetry, linear dichroism, and the z position of each emitter, the shift error can be estimated from a model and removed from the final determination of the x–y position of the emitter. This approach was illustrated for the case of relatively photostable single molecules immobilized in a polymer, and the right column of Figure 14B shows the x–y localizations found as one single molecule is translated in z, both without (u) and with (c) the correction.

In some experiments, it is quite useful to measure orientations of single molecules along with positions,(202) but this extra step requires more detected photons. Alternatively, there is a direct, purely optical solution to the mislocalization problem, proposed recently by Lew et al. (201) and illustrated in Figure 14C. This solution recognizes that the asymmetry giving rise to the shifted spot on the detector arises only from the radially polarized light in the back focal plane, and so utilizes an azimuthal polarizer to give unbiased lateral localization determination. To demonstrate this experimentally, Backlund et al. used a “y-phi” nanopost mask which converts the azimuthally (i.e. φ) polarized light into y-polarized light,(203) so that the addition of a polarizer to reject x-polarized light restores a final centrosymmetric image on the detector. Analyzing the final image with a centrosymmetric estimator extracts the molecular position without any dipole shift bias. Thus with the analyses and experimental demonstrations in this section, the problem of localization biases in 3D localization microscopy has been addressed in several ways.

4.3 Precision, Sampling Density, and Resolution

As in 2D microscopy, the concept of resolution of an image is very important in the 3D case. As a starting place, many investigators work to quantify the precision of the localizations, and use this as an estimate of resolution. The process of assessing precision can be done in several ways, with increasing degrees of accuracy and sophistication. As described in Section 2.2, eq. (6) provides an analytical expression for the localization precision, σ, in 2D for least-squares fitting of the standard PSF.(85, 88) Similarly, the attainable precision of 3D estimation methods can be calculated with the CRLB,(82, 135, 156) but this may be overoptimistic. Not every estimator will reach the CRLB, and CRLB analysis can be blind to experimental imperfections including aberrations and uneven background. An empirical solution is to localize the same stationary emitter many times,(204) using the standard deviation of the position estimates in all three dimensions as an estimate of the localization precision. To go further, in a study by Gahlmann et al. using the DH-PSF,(62) a fluorescent bead was localized in 3D for many frames, while the detected signal and background were varied by changing the pumping power and illuminating the sample with small amounts of white light. The resulting calibration surface for precision was used to define the precision of each localization based on the observed number of detected photons and background.

However, the true resolution of an image depends upon the ability to distinguish two objects close together, which can be different from simply knowing the localization precision of one isolated object. An estimation-theoretic approach to the case of discriminating the distance between two single emitters was presented by Ram et al.(205, 206), carefully treating the difference between simultaneous and sequential localization. In all cases, the best-case precision for the estimate of distance between two emitters is $\sqrt{2}\sigma$, or the sum in quadrature of the emitters’ localization precisions σ. In order to sample the true resolution of extended structures, and other effects such as label size, it is common to experimentally demonstrate resolution in a SR reconstruction by showing a cross-section of two close-by, well-defined structures such as crossing microtubules.(207)

Regardless of the PSF, the localization precision and fundamental resolution limits for SR scale approximately as the inverse square root of the number of photons detected from each emitter, eq. (7). For this reason, it is important to acquire as many photons as possible. Strategies that improve photon counts include the use of high-yield dyes, high objective NA, and optimizing the experiment to avoid losses. For example, using more focal planes than necessary in multifocal microscopy can result in photons wasted in out-of-focus planes, while using SLMs for PSF engineering can result in a loss of half the signal due to polarization requirements. One of the advantages of interferometric microscopy is the doubled collection efficiency due to using two objectives, and dual-objective setups can benefit other methods as well.(208, 209) Since background worsens localization precision, it must be limited using appropriate filters. Concentrating the PSF using aberration correction can also limit contamination by background by reducing the number of pixels over which the signal is spread.

A critical concern for resolving extended structures is sampling density: if the density of labels on a structure is too low, or if too few labels are detected (e.g. due to emitters prematurely bleaching or not activating), fine structural details can be lost. Early on, the need for Nyquist sampling was clearly noted(210), requiring a density of labels such that at least two molecules are sampled over an interval of the quoted resolution. A more sophisticated approach pursued by two groups defined a Fourier Ring Correlation (FRC) resolution metric for single-molecule imaging, based on similar approaches in cryo-electron microscopy.(211, 212) From a set of localizations, two reconstructed images are generated from disjoint subsets, and the correlation of the two images’ Fourier transforms along a radial coordinate (i.e. rings, or in 3D, shells) gives a FRC (in 3D, FSC) curve. The effective resolution is defined by the support for which the correlation is above a given threshold. This metric effectively senses the degree to which high spatial frequencies in the underlying structure are sampled, taking into account both localization precision and label density. This provides a simple way to gauge approximate resolution and analyze drift correction effectiveness. However, the measured resolution from FRC is sample-dependent: samples (or regions within a given sample) with more high-frequency content will seem to have a higher resolution even if the sampling density and localization precision are the same.(211, 213)

It is worthwhile to realize that the number of fluorophore labels required to sample a space scales with dimension. On the one hand, this can be helpful, as the increased spatial sparsity can help differentiate separate regions, such as in a recent study of target search kinetics of regulatory noncoding RNA.(214) However, if one wishes to image a full 3D object in 3D, the requirements for label density can be extreme. Fortunately, in many real-world cases, structures imaged in 3D have a lower dimensionality (1 for linear structures like microtubules, 2 for sheet-like structures like membranes), and the sampling density requirements are no worse than for 2D SR techniques.

Extracting the position of an emitter from its image becomes more challenging with the existence of neighboring emitters in the ROI. This is because the PSFs of adjacent emitters overlap, which likely degrades the performance of any fitting method. The overlap problem already arises in the case of 2D imaging, limiting the attainable temporal resolution of single-molecule super-resolution imaging methods by forcing a low emitter density per frame. The problem of fitting multiple emitters within the ROI has been tackled by various methods, such as using maximum likelihood estimation to find the most probable number (and position) of emitters,(215, 216) using a prior assumption of sparsity in the ROI (i.e. that only a relatively small number of emitters overlap in each frame),(217) or employing a spatiotemporal statistical model for blinking and overlap.(218, 219)

In the case of 3D imaging, the overlap problem becomes more severe. This is because PSFs designed to encode depth are typically larger than the standard PSF (with some exceptions(127)). Figure 15 illustrates this problem, along with a naïve attempt at a solution.(139). A region of interest consisting of 5 emitters imaged using a 6 μm range Tetrapod PSF is simulated. Each emitter is then fit using MLE, ignoring the other emitters and assuming (wrongly) a spatially constant background with Poisson noise distribution. Once an emitter is fit, its model is subtracted from the ROI, and the next emitter is fit. This basic multiemitter fitting method, while possibly providing reasonable results, is clearly sub-optimal. Indeed, more sophisticated methods have been suggested to overcome the overlapping PSF problem in 3D, such as simultaneous multi-emitter fitting with an astigmatic PSF (220), employing sparsity,(221, 222) combining astigmatism with biplane imaging,(223) or 3D deconvolution based on the alternating direction method of multipliers algorithm.(224)

Figure 15.

A simple method for localizing a high concentration of active emitters relative to the PSF size. The image of five adjacent emitters using a 6 μm range Tetrapod PSF is simulated (a, top). Each emitter is fit using MLE naively ignoring the other emitters, and then its model is subtracted from the image. The top row shows the remaining image after each iteration. The bottom row shows the model PSF of the emitter that is currently being fit. (Scalebar: 5 μm.) Reprinted from ref. (139). Copyright 2016 the authors.

4.4 Future Directions for 3D Localization Microscopy Methods

So far, we have touched on many relatively mature technical developments of 3D localization microscopy, but there is much work left to do. Of course, there are many areas of active development that can be expected to be fruitful for SR and SPT in general, including the design of fluorophores with higher photon yields, less-perturbative labeling techniques, lower-noise detectors, and improved sample buffers. Here, we discuss several research trends specifically pertinent to 3D SR and SPT, highlighting those now beginning to emerge and that we believe will be of increasing importance as these fields develop.

An emerging area for single-molecule and other super-resolution methods has been to address the imaging of large volumes throughout thick, preferably living, cells and tissue. This presents several challenges for 3D localization techniques: thicker cells increase the total amount of background from autofluorescence and out-of-focus emitters, as well as the total number of emitters that must be localized, and the requirement that cells be alive raises concerns about phototoxicity and imaging speed. TIRF is a common method to reduce background by reducing the illumination volume, but is not useful away from the coverslip. Lightsheet microscopy, by contrast, sweeps a ~1–3 μm thick beam through any slice of the sample, sequentially scanning thin volumes within the cell. The development of lightsheet imaging for single-molecule imaging is an area of active research, with only a few current examples of applications to 3D localization.(213, 225, 226) A major source of phototoxicity is DNA damage due to UV or near-UV illumination used in photoactivation or photoswitching. Using lightsheet or two-photon(227)illumination for photoactivation can reduce the total amount of irradiation (and reduce activation of out-of-focus emitters), and engineering dyes that are activatable with relatively red light(228, 229) and/or with higher photoactivation quantum yield(51) can further reduce the need for damaging UV light. Given that imaging a larger volume increases the number of labels that must be imaged for a full reconstruction, acquisition rates will become increasingly important, and it will be necessary to ensure high fluorophore switching rates and image acquisition rates. In part, this may depend on multiemitter fitting algorithms as described above. Since even nominally “dark” or nonemissive labels can still emit some light, it will also be important to ensure the contrast between emissive and nonemissive labels is as high as possible. It will also be necessary to further develop methods for AO, potentially correcting at a plane within the sample to accommodate specimen-induced aberrations.(179)

Another area of interest is quantitative microscopy, including methods that measure molecule stoichiometries and clustering,(230) and that generate particle averages between many identical particles in the sample.(231) 3D localization will improve both of these developing techniques. In clustering studies, adding another dimension helps improve sparsity, allowing better resolution of oligomers or assemblies within the sample.(214) Particle averaging techniques, adapted from those used in cryo-electron microscopy, aim to reconstruct an averaged particle from many presumed-identical particles within the sample. (These techniques can be viewed as an extension of using SR to measure average spatial distributions and distances within a sample, examples of which are described in Section 5.) Particle averaging with single-molecule localization data is capable of reaching Å-scale precision, but has only been applied to a few systems, including the nuclear pore complex.(232, 233) Applying 3D localization will help ensure correct alignment of randomly oriented particles for averaging, and we expect forthcoming developments in registration algorithms for particle averaging in 3D microscopy to enable this technique to be used more broadly.

Finally, as is evident from the many topics within this review, the field of 3D localization faces the organizational challenge of having a large number of details for the experimenter to understand. This makes it difficult for nonspecialists to enter the field and appropriately select between a wide field of options. We anticipate the need for simple and universal selection criteria that apply to all the techniques we have described, ensuring that the correct one can be applied to a given problem. Comparisons of CRLBs have been a useful step in this direction.(130, 135) We believe that the formalism of estimation theory would allow a more comprehensive approach to defining overall imaging resolution available with a given technique, including the conserved product of spatiotemporal bandwidth, field of view and depth of field, and SNR. We are encouraged to see two recent reviews introduce ways to comprehensively describe these quantities in single-molecule microscopy, including a treatment for SR imaging(234) and one for SPT.(34) Along with theoretical comparisons, it will be necessary to characterize how robust various imaging methodologies are to common aberrations, including the effect aberrations have on precision and resolution.(235, 236) Another practical concern is the performance of different localization algorithms, and it will be necessary to continue current efforts to compare existing software packages for SR(237) and SPT(238) as our theoretical understanding and frameworks develop.

5. Selected Applications

The development of single-molecule imaging techniques and their subsequent extension to three dimensions have benefited many domains of cell biology.(27, 63, 239, 240) There is also an interest in applications of single-molecule methods to bottom-up studies in polymer and materials science.(241–243) Here, we present selected studies that demonstrate the utility of accurate and precise 3D single-molecule localization for quantitative structural and dynamical measurements.

5.1 Super-Resolution Imaging

Focal adhesions (FAs) are one of the best-characterized examples of how cells mechanically interact with their external environment, and ~150 known components and hundreds of inter-component interactions of the integrin adhesome have been genetically characterized.(244) FAs of isolated cells are axially aligned, reaching from the cell onto the coverslip. This makes them a particularly attractive system for 3D SR, and difficult to study with other modalities. While measurements with other methods such as electron microscopy and atomic force microscopy showed that FAs form <200 nm thick plaques, researchers had difficulty determining 3D protein organization due to the limitations of specific labeling in those modalities.(245, 246) Early 2D multicolor super-resolution studies revealed that different molecular species were not homogeneously distributed within FAs, but were unable to define any overall organization due to the lack of 3D resolution(210). The need for both molecular specificity and fine axial resolution within the thin FA domain was thus a good fit for early iPALM given its < 10 nm 3D localization precision and < 225 nm range.(75) In a systematic study, Kanchanawong et al. used iPALM to measure the axial distribution of many FA proteins labeled with photoswitchable fluorescent proteins in separate single-color experiments (Figure 16A,B). Because FAs have roughly the same dimensions and are inherently aligned, it was possible to use the plane of the coverslip as a reference position between many separate experiments; this allowed the same label and optical channel to be used to image each protein, avoiding registration errors. Measurements of representative proteins belonging to different functional modules revealed a consistent axial organization of these proteins, such that each could be assigned to distinct multilaminar subdomains within the FA (Figure 16C). Extensions of this work include the addition of FRET sensors to add readout of molecular conformation to 3D SR of FAs.(247) The utility of 2D SPT measurements in FAs(248, 249) suggests a possible place for 3D SPT in future studies, and 3D SR of FAs still has room to expand: for example, it may be possible to image the ≤ 25 nm scale particles at the membrane-cytoskeleton interface that have so far only been observed in EM.(250)

Figure 16.

Interference microscopy reveals molecular organization of focal adhesions in 3D. (A) iPALM measurements of integrin α_v-tdEos show it is positioned in a thin sheet slightly above the height of the plasma membrane (separately measured). (B) By contrast, actin-mEos2 protrudes upwards and away from the cell edge, beginning slightly above the integrin layer. Top: x–y projections, colored by z value; bottom, reconstructions of the z positions within the box. Using measurements of many such proteins, it is possible to build up a complete model of how they are vertically ordered (C), revealing that proteins belonging to separate signaling and structural functions tend to be ordered in axial layers. Adapted by permission from Macmillan Publishers Ltd.: Nature, ref. ((251)) copyright 2010.

The protein organization of chemical synapses is another example of how nanoscale spatial position is coupled to function. The presynaptic active zone (AZ) and postsynaptic density (PSD) of excitatory synapses comprise specialized assortments of proteins that control vesicle release, and receptor organization and signaling, respectively. Electron microscopy is routinely employed to study synapse architecture; in EM, the PSD appears as a clearly-defined electron-dense region with thickness ~30–60 nm, opposite the AZ (itself visible as an electron-dense section of membrane) and separated by the ~20–24 nm synaptic cleft.(252–254) Molecular specificity can be obtained in EM with antibodies conjugated to gold nanoparticles, and such “immunogold” micrographs have shown that key AZ and PSD proteins are concentrated within distinct layers away from the membrane.(255–257) However, immunogold labeling has low labeling density except in certain special situations, limiting throughput.(258)

The specificity and relatively simple sample preparation of super-resolution microscopy complement EM’s limitations, and a study by Dani, Huang et al. demonstrates how 3D multicolor SR can be used for (relatively) high-throughput measurements of synaptic protein organization within mouse brain tissue.(259) The random 3D orientations of synapses within tissue were defined by aligning the protein distributions along the trans-synaptic axis, and without 3D information, it would have been impossible to accurately define this axis. This was achieved with three-color measurements, where the protein of interest was localized relative to the AZ and PSD proteins Bassoon and Homer1 (Figure 17A–D) and placed in absolute coordinates based on EM measurements of Bassoon’s position and the width of the synaptic cleft(257, 260) (Figure 17E). Multicolor labeling was performed using secondary antibodies linked to photoswitchable dye pairs with variable activation wavelengths (Alexa 405, Cy2, and Cy3) and a single emitting species (Alexa 647, a dye with relatively high photon yield). While this labeling scheme produced some activation cross-talk, complicating analysis, it obviated the need for channel registration and ensured high total photon counts in each channel, providing localization precisions of 14 nm laterally and 35 nm axially with an astigmatic PSF. This good precision was obtained in spite of the difficulties of imaging in 10 μm thick cryosections of mouse brain tissue, including autofluorescence, scattering of signal, and fluorescence from labels out of the imaging range; the extra sources of background were reduced in part by using highly inclined illumination, probing only a ~2–3 μm axial section of the sample. The 10 proteins studied could thus be localized to a precision of 5 nm or less (SEM of many synapses), demonstrating different localization patterns (Figure 17E). For example, antibodies labeling membrane receptor subunits (GABA_BR1, NR2B, and GluR1) were observed approximately 10–15 nm from the membrane, roughly consistent with known structural data of AMPA receptors. Bassoon and Piccolo, giant (420 kD and 550 kD) scaffolding proteins of the AZ, were systematically oriented: labels on the N-termini of these two proteins appeared ~30 nm and ~40 nm farther from the membrane than C-terminal labels, respectively, a result later confirmed and extended via EM.(261) Extending such orientational measurements to smaller proteins is limited by localization precision and the size of the label, but as described in earlier sections, both of these areas are constantly being improved.

Figure 17.

Three-color 3D SR microscopy positions proteins along the trans-synaptic axis. (A–D), left: super-resolution reconstructions of multiple protein species labeled with photoswitchable dye pairs. Right: histograms of localizations along the trans-synaptic axis, pooled from several synapses. e, the average positions of proteins localized relative to Bassoon [N] and Homer1 [C], where [N]/[C] refer to the use of antibodies targeting the N- or C-terminal region of a protein. The bar and vertical lines are equal to twice the standard deviation between synapses and the SEM, respectively. Adapted from ref. (259), copyright 2010 with permission from Elsevier.

As evidenced by these studies of focal adhesions and synapses, super-resolution imaging is a powerful tool for understanding the structural organization of domains smaller than the wavelength of light within eukaryotic cells. Yet for prokaryotic organisms such as bacteria that have sizes on the order of the wavelength of light, the entire living cell is such a subdiffraction domain, and super-resolution is critical for quantitative microscopy. SR (and SPT) have been productively applied across bacterial phyla, both to probe universal processes such as DNA transcription and repair in vivo, and to resolve the nanoscale features of prokaryotic anatomy.(27, 262, 263) Here, we show a few examples where extending SR to 3D has been especially useful for studying structural features of bacteria.

As the radius of curvature of almost all bacteria is on the order of the diffraction limit, it is impossible to optically section bacteria. By contrast, 3D SR microscopy can clearly resolve the bacterial cell surface, as demonstrated in a study by Lee et al. that imaged the surface geometry of Caulobacter crescentus, a model organism for developmental biology that exhibits a dimorphic life cycle.(228) Rhodamine spirolactams are typically photoswitchable from a dark to emissive form with UV illumination. Adding highly conjugated substituents to the lactam nitrogen generated new derivatives capable of photoswitching with low-intensity visible light, avoiding the need for potentially phototoxic UV irradiation without significantly changing the photophysics of the emissive form. Adding an N-hydroxysuccinimidyl linker to the dye enabled labeling of surface amines on the proteinaceous surface layer of Caulobacter, while the dye’s positive charge inhibited passage into the cell. The high photon yield of this dye provided localization precisions σ_x,y,z = (15, 13, 17) nm for 3D super-resolution imaging using the double-helix PSF in live cells, and the NHS labeling method provided high and uniform sampling (~4300 localizations per cell), together giving high resolution reconstructions of the Caulobacter surface (Figure 18A). From these data, it was possible to precisely measure features such as the ~100 nm wide (FWHM) stalks present in mature cells, with results consistent with those from earlier electron microscopy, and to clearly resolve geometric details such as the pinching at the division plane in late predivisional cells.

Figure 18.

Applications of 3D super-resolution microscopy to bacterial cell biology. (A) 3D super-resolution reconstructions of the surface of live Caulobacter crescentus cells labeled with a switchable rhodamine spirolactam dye and imaged using the double-helix PSF. The high resolution of this labeling sharply defines the features of cells imaged at different phases of their life cycle (left). This label appeared almost exclusive at the cell surface, as visible in 3D cross-sections (right, yellow localizations correspond to yellow line in white-light image). All scalebars and gridlines are 1 μm. Adapted with permission from ref. (228). Copyright 2014 American Chemical Society. (B) iPALM imaging of constituents of the bacterial divisome (FtsZ, ZapA, ZapB) and an inner membrane marker (MTS) labeled with mEos2 provides anatomical detail in fixed E. coli cells. Two example cells are shown for each labeled strain; the bottom arc of the cell is shown. The dashed box exemplifies where regions were defined for quantitative comparison, averaging ~80–250 cells for each protein. Adapted from ref. (264) under the Creative Commons CC-BY-4.0 license. (C) Multicolor 3D microscopy with the double-helix PSF enables colocalization analysis in live Caulobacter cells. Left: example 3D reconstructions generated as a sum of Gaussian densities centered at each localization with width equal to the localization precision (σ_x,y,z ~40–70 nm). The gray line illustrates the approximate cell shape. Blue grid lines: 500 nm. Middle: reconstruction using a scatterplot of the same localizations. The large spheres and bar mark the centroids of and separation between each distribution. Right: histograms of separations between distributions, defined inward along the cell axis. Adapted from ref. (267). Copyright 2014 the authors.

Bacterial cell division is also difficult to study without 3D resolution, as the bacterial divisome is membrane-associated. By imaging several E. coli divisome components with 3D SR, Buss et al. were able to partially elucidate the radial organization of this multiprotein complex.(264) FtsZ, a central component, forms a ring at the division plane and is necessary to recruit other divisome proteins.(265, 266) Its localization is patchy under wild type conditions, and becomes even more fragmented in the absence of ZapA or ZapB. To understand the organization of this complex, Buss et al. performed separate iPALM measurements for these three proteins and an inner membrane-targeting-sequence (MTS), each labeled with the photoswitchable protein mEos2 (Figure 18B), obtaining localization precisions σ_x,y,z = (21, 23, 17) nm. In these conditions FtsZ and ZapA appeared relatively punctate, while ZapB and the MTS were more uniformly distributed. With 3D measurements, it was possible to compare the axial distributions of proteins using the coverslip as a position reference. To remain within the 225 nm axial range of this iPALM implementation, only the bottommost part of each protein ring was analyzed. FtsZ and ZapA resided in roughly the same layer of the divisome (80±2 and 74±1 nm, away from the coverslip, respectively; ± SEM) slightly offset from the inner membrane (67±1 nm) and distinctly separated from ZapB (117±2 nm). Multicolor imaging in 2D in the same study was used to show that patches of FtsZ and ZapA do not necessarily colocalize despite their similar radial positioning. Altogether, this demonstrated that the divisome is not a simple stoichiometric complex, supporting a model where each protein interacts with other components in a complex manner. Extending the 3D SR approach demonstrated here to multiple colors could add further understanding of divisome organization in future studies.

One example of how multicolor SR measurements can be used to reveal the spatial extent of protein-protein interactions comes from a study of chromosome segregation in Caulobacter. Ptacin et al. examined the localization patterns of PopZ, the “polar organizing protein,” relative to the ParA and ParB chromosome partitioning proteins.(267) ParB attaches to the chromosome, forming an extended complex, while ParA dimers form a distribution along the cell. As the ParB-chromosome complex moves from the old cell pole towards the new cell pole, the ParA dimers it contacts are disassembled, and this interaction creates the motive force for translocation. Ptacin et al. biochemically demonstrated that ParA and ParB molecules specifically bind to PopZ, which was known to form an extended space-filling network at both poles in predivisional Caulobacter cells. To probe the nature of this interaction in vivo, they performed live-cell, two-color 3D SR imaging of PAmCherry-labeled PopZ and of eYFP labeling either ParB or an obligate monomer form of ParA, the ParA_G16V point mutant, which localized only to the poles (Figure 18C). Using a finely sampled registration function to accurately combine the two data channels, it was found that the ParB-centeromere complex at the new pole was consistently displaced from the PopZ region toward the interior of the cell (53.1 ± 4 nm SEM, N = 57) while on average, the ParA_G16V distribution overlaid exactly with that of PopZ (0.0 ± 3 nm, N = 83). This indicated that the centromere was tethered to the edge of the domain filled by PopZ, presumably by ParB binding, and that ParA monomers were recruited within the PopZ region. The recruitment of ParA monomers to a region of high concentration may aid their recycling into dimers, enforcing the polarity of the ParA distribution. In this case, 3D imaging clearly demonstrated that ParA was concentrated within the PopZ network rather than e.g. recruited over its external surface.

5.2 Single-Particle-Tracking

Figure 19 illustrates the results of a recent study which employs PSF engineering to perform 3D SPT with high spatiotemporal resolution to observe dynamical motions present in the nucleus of budding yeast.(268) The goal of the study was to measure the relative motions of the two copies of the GAL locus in diploid cells under activating (galactose as the carbon source) and repressive (dextrose) conditions to quantify the change in correlation between the measured loci as a function of gene activation state. The two chromosomal DNA loci were labeled with two different colors using the LacO/LacI-GFP and the TetO/TetR-mCherry labeling strategies, and imaging was performed on nondividing G1 phase cells with the DH-PSF microscope in two color channels at a frame rate of 10 Hz. The many fluorescent protein copies at each locus provided high signal over track lengths of many seconds, with approximate values of localization precision, σ_x,y,z = (13, 12, 23) nm in the GFP channel and (27, 27, 44) nm in the dimmer mCherry channel. It is worth noting that a previous 3D tracking study of the GAL locus using confocal scanning microscopy (269), while useful, was limited to far lower time resolution (>5 s to acquire a full volume) with significantly poorer localization precision. Figure 19A shows one example of the 3D motion extracted from the DH-PSF data, where the variable of interest chosen is the time-dependent velocity of each locus along all three Cartesian axes. The velocities fluctuate due to thermal excitations, but in addition, this particular pair of loci shows correlations in the velocities, displayed as a velocity cross-correlation in the fourth panel. The findings suggest there is a time lag between the motions of the two loci, possibly arising due to viscoelastic behavior of the chromatin. The two trajectories are shown in space with time coloring of the trajectories in Figure 19B; their apparent motion on a curved surface suggests that these two loci are located near the nuclear periphery. This result was not universal, and as a result of the heterogeneity from cell to cell, correlations were not always observed between pairs of loci.

Figure 19.

(A) Example 3D velocities for a pair of GAL loci in budding yeast. The x, y, and z velocities as a function of time can be extracted from 2-color DH-PSF microscopy. Lower right panel: velocity cross-correlation between the two channels. (B) Spatial trajectories of the two loci with time-coloring. (C) MSD for a single locus imaged in green and red color channels with a mean cross-displacement in black. The inset shows an example trajectory with 1 μm scale bar. (D) Extracted estimates of the anomalous diffusion parameter using the proper expression for the MSD for fractional Brownian motion including static and dynamic errors. (A), (B) reproduced from ref. (268) copyright 2014 the authors, with material under Creative Commons license BY-NC-SA 3.0; (C), (D) reprinted with permission from ref. (270). Copyright 2015 by the American Physical Society.

With quantitative 3D data such as these for many single cells, it was possible to explore the correlations between the two chromosomal loci in considerable detail, providing a clear example of how to quantitatively and simultaneously track two differently colored objects in the same cell.(268) Backlund et al. found that under repressive conditions the GAL loci exhibited significantly higher velocity cross-correlations on average than they did under activating conditions. This relative increase has potentially important biological implications, as it might suggest coupling via shared silencing factors or association with decoupled machinery upon activation. The researchers also found that on the time scale studied (~0.1–30 s), the loci moved subdiffusively, with the time scaling of the mean-squared displacement (MSD) lower than expected for a Brownian diffuser. They reported a higher subdiffusive exponent than previously reported from the less-precise confocal z-slice approach, which has implications for the application of polymer theory to chromatin motion in eukaryotes.

Ensuring the accuracy of these measurements of subdiffusive motion requires careful analysis of the MSD with attention to the effect of measurement errors,(270) including the effect of localization precision (a static error) and of motion blur caused by the motion of the tracked locus during the camera acquisition time (a dynamic error). The GAL locus two-color DH-PSF imaging study included a control that illustrates these errors: in a cell line with only the LacO/LacI-GFP label, removal of a filter in the two-color imaging apparatus allowed light from the same single locus to be imaged in both the green and red imaging channels, but with different signal levels. Figure 19C shows the MSD vs. time on a log-log plot for these two cases in each channel, as well as the “cross-MSD” calculated from the products of displacements in each channel (black). In the error-free case, the MSD scales as τ^α, and would appear linear on a log-log plot. Tellingly, the experimental cases diverge from this ideal. The red channel receives fewer photons, giving it a larger static error than the green channel and causing it to be sharply curved upward in a log-log plot. The cross-MSD averages out static error, but remains sensitive to dynamic error, causing it to curve slightly downward. Finally, the green channel is serendipitously relatively linear, as the errors cancel out. A simple fit assuming τ^α scaling would give completely different results for each case, despite measuring the same underlying motion. Clearly, a more sophisticated approach is needed. For the special case of Brownian motion (α = 1) and continuous illumination, MSD data can be fit to extract a single diffusion coefficient D and correctly account for localization error σ and finite frame acquisition time t_E with the expression(271)

$$\mathit{MSD}(\tau \equiv n{t}_E)=2{\mathit{Dnt}}_E+2{\sigma }^2-\frac{2}{3}D{t}_E$$

An analogous expression was derived by Savin et al. for the case of fractional Brownian motion (271), and Backlund et al. derived appropriate expressions for the velocity cross-correlations.(270) When the correct expression for the MSD is used to extract estimates of the subdiffusive exponent α on different time scales during the trajectory, a single value of α that is independent of time and localization errors is extracted, as shown in Figure 19D. This example highlights how analysis of diffusive motion should always take into account static and dynamic errors, using a model appropriate to the type of diffusion present.

From these studies of chromatin dynamics, we can see that correlative tracking of two mobile objects is a useful approach. Correlating single-particle trajectories with super-resolved structures provides a similar advantage. Bálint and coworkers used such a two-color SPT/SR measurement to study the transport of lysosomes along microtubules (MTs) and at MT intersections.(272) Kinesin and dynein motors act to generate directed motion of cargos on MTs. Previous in vitro SPT studies showed that crossed MTs can result in cargo dissociation, switching, or simply passing at the point of intersection, while in vivo measurements demonstrated track switching, but did not super-resolve the MT network. The focus of this study was to measure the functional impact of MT intersection geometry in vivo using SPT of stained lysosomes in live cells followed by in situ fixation, immunolabeling, and SR of MTs using Alexa Fluor 405/647 dye pairs. Because of the fast (~seconds) timescale of MT network rearrangement in vivo and the relatively slow (< 1 μm/s) speed of motor transport, it was necessary to stabilize the MT network so that it did not move between the beginning of the tracking measurement and the onset of cell fixation. This could be achieved by maintaining reduced temperatures and treatment with drugs inhibiting turnover of actin polymers, with only slight effects on observed behavior.

Given the large size of lysosomes (~600 nm diameter), it is inappropriate to treat them as point emitters, and they were localized and tracked in 2D using a centroid estimator. After tracking and fixation, MTs were imaged in 3D using astigmatic imaging, achieving an axial resolution of ~100 nm. The sample drift, differential aberrations between channels, and distortion from the fixation process were accounted for using a 2D global transformation between fiducial beads imaged during the SPT and SR experiments, which was sufficiently accurate given the desired resolution. Localization in 3D was necessary to quantify the spacing between MTs in intersections, as most MTs are oriented roughly in the xy plane, and crossed MTs are primarily separated in z. This structural information was then correlated with observed lysosome pausing, switching, and reversal events. Figure 20 shows overlaid SR reconstructions with a single lysosome track, highlighting pausing events. Lysosomes were only seen to pause for MT separations less than 200 nm, demonstrating that close proximity is necessary to create a substantial obstruction. However, passing or pause-then-pass events were still observed for small separations, implying that lysosomes are able to rotate, squeeze, or otherwise move past close-by MTs at intersections. Future studies that extend this approach to achieve 3D tracking of lysosomes or other cargo in the context of 3D SR measurements remain an exciting possibility for discriminating between the possible mechanisms for cargo passage and switching at intersections.

Figure 20.

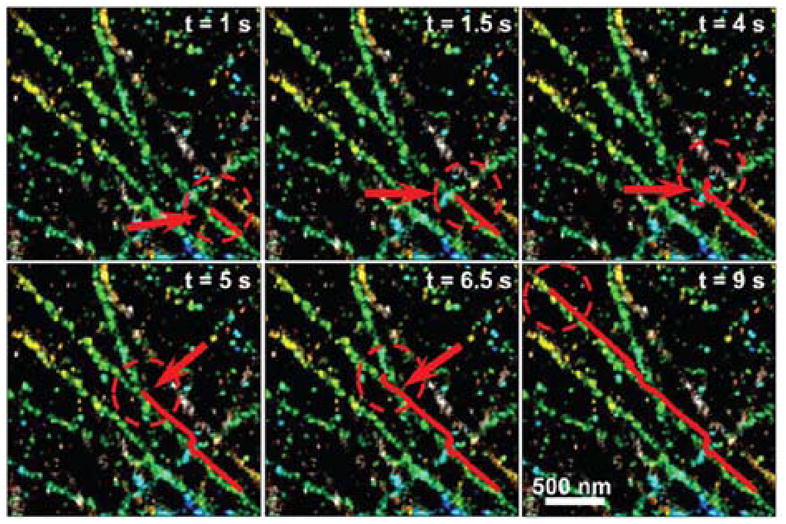
The combination of 3D SR imaging with tracking data allows the contextualization of tracks. In this example, the tracked lysosome (red line) moves through three microtubule intersections (red circles), respectively passing without pausing, pausing for 2.5 s, and pausing for 1.5 s before moving onward. (Axial separations between microtubules: 250, 130, < 100 nm.) Reprinted from Ref. (272). Copyright 2013 the authors.

While most of the applications discussed in this review are biologically oriented, there are many additional uses for 3D localization. One example is flow profiling in microfluidic channels. Specifically, 3D micro particle image velocimetry (μPIV(273–275)) is a technique in which emitters that are flowing in a microfluidic channel are localized as they flow, and the flow profile is then obtained by analyzing their trajectories. Figure 21 shows such an experiment where the long-range capability of PSF engineering leads to fast, precise, and scan-free 3D tracking. Fluorescent beads 200 nm in diameter are imaged using a 20 μm z-range Tetrapod as they flow in a ~20 μm deep microfluidic channel, and consequently localized in 3D(131). The laminar flow profile in the channel can then be obtained by analyzing the trajectories of many beads.

Figure 21.

Microfluidic flow profiling in 3D using a Tetrapod PSF. (A) Example raw frame, showing three emitters at different x,y,z positions, flowing in the x direction. (B) Experimentally derived two-dimensional mean x-velocity map, averaged over x (y–z cross-section). (C),(D) One-dimensional slices from (B), showing mean x, y and z velocities. As predicted by a laminar flow model, the mean x velocity (black) has a parabolic profile, whereas the y and z velocities (blue, red) are negligible by comparison. Adapted with permission from ref. (131). Copyright 2015 American Chemical Society.

6. Conclusions

With the emergence of methods capable of acquiring imaging data with resolution far below the diffraction limit and obtaining trajectories of single particles with sub-second sampling and nanoscale precision, a new and highly quantitative view of the nanoscale structures and dynamic behavior within biological cells and other complex systems is now becoming available. The extension of super-resolution and single-particle-tracking to 3D reveals the true geometry of these systems, and in many ways, the limitations of optical fluorescence microscopy in terms of resolution, dimensionality, and imaging speed are being removed. It is tempting and understandable for the experimenter to rush out and buy a complex machine to enjoy this new regime of nanoscale science. However, as illustrated multiple times in this review, exciting new levels of quantitation must be accompanied by intense attention to both the precision and the accuracy of the imaging methods that enable that quantitation. In addition, the various methods for 3D imaging have a range of trade-offs, advantages and disadvantages. Given the intricacies of single-molecule experiments, data analysis, and interpretation, especially when extended into three dimensions, we cannot emphasize the need for scrutiny enough when validating new results. In addition, as spatial resolution improves beyond the diffraction limit, it becomes important to test for artifacts on ever-smaller scales, and to perform comprehensive controls of the labels, imaging method, and analysis algorithms used.

One can expect to see newer imaging modalities appear, to add to the variables already being extracted from precise and accurate measurements on single molecules. The molecular orientation of labels can be used to infer information about local environments,(202, 276, 277) and such measurements can be combined with 3D measurements to powerful effect. Additional well-known local single-molecule variables such as lifetime, energy transfer, spectra, etc. can certainly be imaged in 3D. Fluorescent probes are improving in both photon yield and small size, and the emergence of other imaging approaches based on scattering may alleviate the need for fluorescent labeling altogether.(278) Without question, the future of 3D imaging on the nanoscale is bright.

Biographies

Alex von Diezmann received his B.A. in Chemistry from Reed College in 2011. His Ph.D. research in the Moerner lab has focused on developing 3D single-molecule imaging techniques to measure the spatial organization and dynamics of proteins within biological structures in vivo. He is fascinated by how quantitative single-molecule experiments can bridge molecular and cellular size scales in our understanding of cellular anatomy and signaling. His current work examines how subcellularly localized protein microdomains generate polarity in the model organism Caulobacter crescentus.

Yoav Shechtman received his B. Sc. degree in electrical engineering and physics in 2007, and his Ph.D. degree in physics in 2013, all from the Technion–Israel Institute of Technology, Haifa, Israel. In 2013 Yoav became a Postdoctoral Fellow in the Department of Chemistry at Stanford University, and in 2016 he joined the Department of Biomedical Engineering in the Technion, as an assistant professor. Yoav is interested in applying signal processing methods to practical biological/physical optical imaging challenges.

W. E. (William Esco) Moerner, the Harry S. Mosher Professor of Chemistry and Professor, by courtesy, of Applied Physics, at Stanford University, has conducted research in the areas of physical chemistry and biophysics of single molecules, development of 2D and 3D super-resolution imaging and tracking for cell biology, nanophotonics, photorefractive polymers, and trapping of single biomolecules in solution.