Stimulated Raman Scattering: From Bulk to Nano

Abstract

Stimulated Raman scattering (SRS) describes a family of techniques first discovered and developed in the 1960s. Whereas the nascent history of the technique is parallel to that of laser light sources, recent advances have spurred a resurgence in its use and development that has spanned across scientific fields and spatial scales. SRS is a nonlinear technique that probes the same vibrational modes of molecules that are seen in spontaneous Raman scattering. While spontaneous Raman scattering is an incoherent technique, SRS is a coherent process, and this fact provides several advantages over conventional Raman techniques, among which are much stronger signals and the ability to time-resolve the vibrational motions. Technological improvements in pulse generation and detection strategies have allowed SRS to probe increasingly smaller volumes and shorter time scales. This has enabled SRS research to move from its original domain, of probing bulk media, to imaging biological tissues and single cells at the micro scale, and, ultimately, to characterizing samples with subdiffraction resolution at the nanoscale. In this Review, we give an overview of the history of the technique, outline its basic properties, and present historical and current uses at multiple length scales to underline the utility of SRS to the molecular sciences.

Graphical abstract

1. INTRODUCTION

The moniker stimulated Raman scattering (SRS) encompasses a collection of optical techniques that share in common a light–matter interaction in which two light fields induce a Raman-active transition in the material. Since the 1960s, these techniques have been used extensively to study the vibrational properties of gases, liquids, and solids. A nonlinear optical technique, SRS is sensitive to the same molecular vibrations that are probed in spontaneous Raman scattering.¹ These vibrational modes include vibrational motions of individual chemical bonds and chemical groups, and thus form a means to not only identify molecules but also study their structural dynamics and probe their intra- and intermolecular interactions. Although SRS and spontaneous Raman scattering are fundamentally related, there are important differences between the two techniques. As compared to spontaneous Raman scattering, in which the light-induced molecular motions in the sample are incoherent, in SRS the vibrational modes are prepared in a coherent fashion. With all modes oscillating in unison, forming a coherent polarization in the sample, the subsequent radiation derived from the polarization is also coherent. The resulting SRS radiation is highly directional and strong, offering signal detection efficiencies that are many orders of magnitude higher than in spontaneous Raman scattering. In addition, SRS techniques enable the direct observation of the coherent molecular motions at ultrafast time scales, following their evolution and dephasing as a function of time. This allows a time-ordered view of processes and molecular dynamics that cannot always be directly inferred from an analysis of the Raman spectrum alone. These two advantages, the strong Raman-sensitive signals and the ability to time-resolve molecular motions, have defined SRS as an important tool in chemistry, biophysics, and biomolecular imaging.

The impact of SRS in the molecular sciences has changed over time, and is still changing today. The development of the technique is intimately linked to the evolution of laser light sources, as we will briefly review below. With the steady advances in laser pulse generation and light detection technologies, the sensitivity of SRS has improved markedly over the years, allowing the registration of molecules at lower concentrations and in smaller sample volumes. Whereas earlier applications of SRS focused on the study of pure liquids or highly concentrated molecular targets, improvements in sensitivity are driving applications into the direction of heterogeneous microstructured samples, individual nanoscopic objects, and, ultimately, single molecules. In this Review, we describe how developments in SRS have enabled the transition from bulk samples to nanostructured samples of chemical relevance. We discuss the properties of SRS in the context of these developments and highlight the impact that the technique has had in various fields of research.

1.1. Raman Shifters and Molecular Vibrations

The years after the first demonstration of a working laser² in 1960 were exciting times for nonlinear optics, as the intense radiation produced by the laser made it possible, for the first time, to induce optical signals in materials that scaled nonlinearly with the light intensity. Within a year of the introduction of the laser, second harmonic generation (SHG) in crystal quartz was discovered,³ followed by third harmonic generation (THG) in 1962.⁴ These new phenomena were observed by focusing the light from a ruby laser into transparent crystals and, sometimes rather fortuitously, detecting light of different colors at the crystal’s output. The discovery of the phenomenon that we call stimulated Raman scattering was perhaps even more fortuitous.

In 1962, a group of researchers from Hughes Aircraft Co. and Research Laboratories headed by Woodbury noticed that the output of their ruby laser was accompanied by an extra line that could not be attributed to the ruby gain medium itself.^5,6 They traced the origin of the line to the cell containing liquid nitrobenzene, which had been placed in the laser cavity to act as a Kerr shutter, a common technique at the time to achieve pulsed laser operation. The line was shifted by an energy corresponding to the symmetric stretching vibration of the NO₂ group of nitrobenzene, indicating that a Raman transition might be responsible for the observed effect. This notion was confirmed when the liquid in the cell was replaced with other organic compounds, producing lines with spectral shifts that coincided with the energy of prominent Raman modes of the liquids.⁶ Recognizing the similarity of the process responsible for the extra emission with the process of stimulated emission in the laser cavity, they labeled the effect as stimulated Raman scattering (SRS), a name that has withstood the test of time.

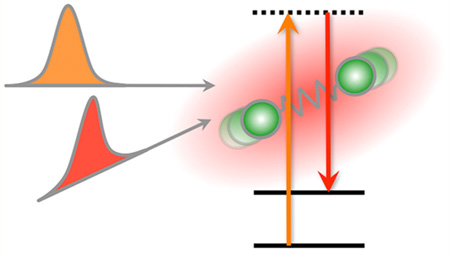
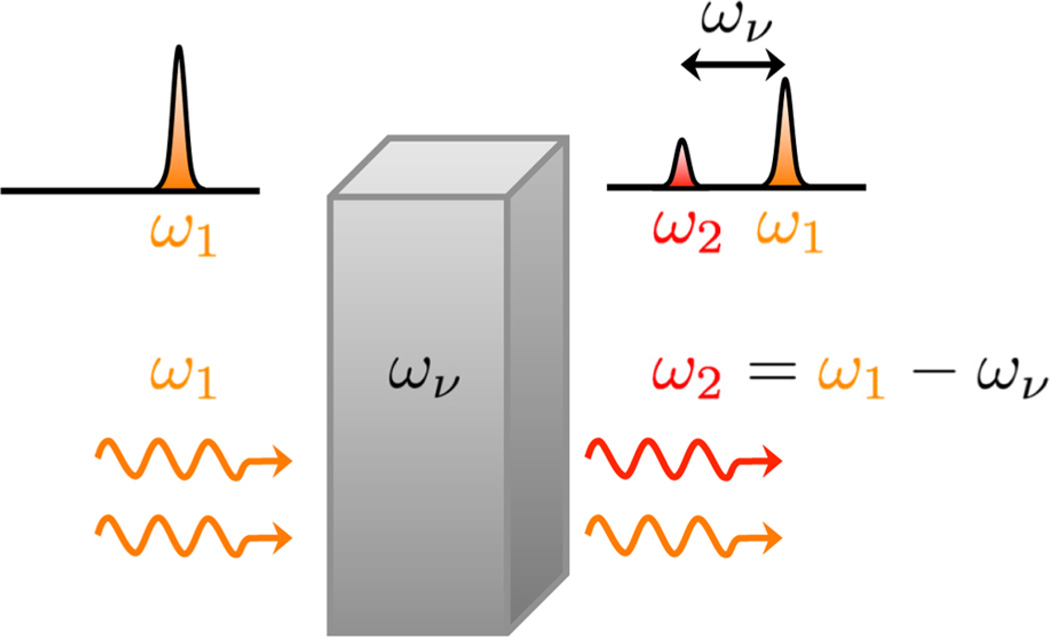
Immediately after the experimental observation of SRS, the physical origin of the effect was explained theoretically, both in terms of polarizability-induced amplitude changes of classical waves^7,8 as well as in terms of quantized fields.⁹ With a general theory of four-wave mixing already in place,¹⁰ a semiclassical theory of SRS was soon to follow.^11,12 By then, the picture of SRS in the laser cavity was clear:¹³ The fundamental laser beam at frequency ω_p produces red-shifted radiation of frequency ω_s (Stokes) through spontaneous Raman scattering. Some of the Raman-shifted light returns to the medium upon traversing the cavity, now stimulating the generation of Stokes photons through the Raman process, eventually producing a coherent beam at the frequency ω_s. This process shares similarity with fluorescence-based stimulated emission in the cavity, with the important difference that no energy is stored in an electronically excited state. Effectively, the Raman transition mediates the energy transfer from the fundamental laser beam to the new, red-shifted optical frequency, as depicted in Figure 1. The photon number of ω_p decreases, while the number of photons of ω_s increases by the same amount. The residual energy ℏω_ν = ℏ(ω_p − ω_s) is absorbed by the Raman active medium through excitation of the vibrational mode at frequency ω_ν. In addition to radiation at ω_s, subsequent experiments also revealed emission at ω_p + ω_ν, the anti-Stokes frequency (ω_as), in the laser cavity.^14,15 Shortly after, these experiments were repeated outside the cavity by sending two coherent light beams at ω_p and ω_s into various crystals and organic liquids,¹⁶ confirming the generation of what became to be known as coherent anti-Stokes Raman scattering (CARS).

Figure 1.

Frequency shifting with SRS. A coherent light beam of frequency ω₁ is incident on a material with a strong Raman resonance at ω_ν. Coherent driving of the Raman mode produces radiation at a new (Stokes-shifted) frequency ω₂ = ω₁ − ω_ν that is also coherent. The SRS process transfers energy from the ω₁ mode to the ω₂ mode. The energy difference ℏ(ω₁ − ω₂) is absorbed through a Raman transition in the material.

It was quickly recognized that the SRS process was useful for shifting laser lines to different wavelengths. By placing the Raman active medium outside the cavity of the laser source, the SRS process can be used as an external Raman shifter, as was first shown for transparent solids.¹⁷ Common Raman shifters include the hydrogen cell^15,18 and inorganic solids such as nitrate-based crystals¹⁹ and potassium gadolinium tungstate (KGd(WO₄)₂),²⁰ used both inside and outside of the laser cavities. Perhaps the most widely used application of SRS as a Raman shifter is found in silica fibers, where the broad Raman spectrum of Si–O modes around 440 cm⁻¹ (13 THz) is used to shift input light toward longer wavelengths.^21,22 The SRS process in fibers is the basis for broadband Raman amplifiers²³ and fiber Raman lasers,²⁴ both of which have had a major impact on today’s fiber-based communication technology.

Although many early applications of SRS focused on the efficient generation of coherent radiation,^25–27 other studies shifted their attention from the light fields toward the response of the material. The analogy with spontaneous Raman scattering was quickly established, although in the early years of SRS its use as a nonlinear spectroscopic tool was not yet fully appreciated: “The spectroscopic information that may be obtained from the stimulated process is very restricted compared to the results from spontaneous scattering,” according to Bloembergen in a review article from 1967.¹³ Nonetheless, coherent radiation implies coherent motions in the material, and several groups realized that the SRS effect can be used to study the dephasing dynamics of the Raman active states in the material. The development of short laser pulses in the picosecond range,^28–30 which had temporal widths shorter than the dephasing times of Raman lines, made it possible to coherently excite vibrational motions in the sample and then follow the ensuing free induction decay of the Raman excitation. The potential of the stimulated Raman effect to study coherently driven vibrations was recognized as early as 1966,³¹ and the first experimental time-resolved measurements of the dephasing dynamics of molecular vibrations^32,33 and phonon modes³⁴ were published in 1971. Propelled by continuous improvements in picosecond pulse generation, the 1970s saw a wave of time-resolved coherent Raman studies of ground-state vibrations in gases, liquids, and solids. Even though it was well understood that the Raman free induction decay of transparent materials measured in the time-domain is directly related to the width of the Raman line in the spectral domain, the ability to drive selective portions of an inhomogeneously broadened band held promise to disentangle several dephasing mechanisms that contribute to the Raman line width.³⁵

1.2. Impulsive and Femtosecond Stimulated Raman Scattering

Many applications of SRS for the purpose of studying dephasing dynamics targeted molecular vibrations in the 200–3000 cm⁻¹ range. To drive these excitations, often one picosecond laser beam at frequency ω_p was used, which was propagated through a sample of up to several centimeters to generate the Stokes-shifted pulse at frequency ω_s. For the probing of the molecular vibrations, however, the anti-Stokes signal at 2ω_p − ω_s or the coherent Stokes signal at 2ω_s − ω_p often proved easier to detect. Surpassed by CARS and CSRS in the late 1970s and early 1980s, the SRS technique had only a limited impact on the field of ultrafast molecular spectroscopy. Things started to change with the advent of femtosecond laser sources, such as the colliding pulse mode-locked laser,³⁶ which brought the pulse duration well into the 100 fs regime. Inspired by stimulated Brillouin scattering of acoustic waves in liquids and solids,^37,38 femtosecond pulses were used to coherently excite optic phonons in crystals, using a spectral bandwidth wide enough to support both the ω_p and the ω_s frequencies to drive the phonon at ω_p − ω_s.³⁹ Because the temporal width of the laser pulse is shorter than the period of the vibrational mode, the technique was dubbed impulsive stimulated Raman scattering (ISRS). Applications of ISRS to crystals were quickly followed by studies of low energy molecular vibrations in liquids.^40,41

ISRS can access low energy modes below 200 cm⁻¹, such as molecular orientational modes and intermolecular vibrations in liquids that are difficult to probe with CARS or CSRS, rendering the SRS method a unique approach for studying the dynamics of molecular motions in this regime. The ISRS technique made it possible for the first time to fully time-resolve the actual vibrational motion of molecules, to see the excited modes evolve and dephase as a function of time. The ISRS technique re-established SRS as a spectroscopic tool, effectively initiating a second wave of SRS applications in the chemical sciences (see Figure 2). Since its introduction in the 1980s, the ISRS approach has been used extensively to interrogate lattice dynamics in solids and intra- and intermolecular vibrations in liquids.⁴² Initial ISRS experiments were conducted on transparent materials, in which the scientific focus was on vibrational modes in the ground state. Yet ISRS can also be used to study electronically resonant samples, allowing a direct inspection of vibrational modes in the excited state, as well as a combined view of electronic and vibrational coherences. In addition, electronic excitation enhances the Raman response, and thus boosts the sensitivity of the measurement, allowing detection of molecules at lower concentrations. Electronically resonant ISRS enables the study of the vibrational dynamics of chromophores in solution, including biologically relevant molecules and complexes. Some applications of ISRS are discussed in sections 3.2 and 4.2.

Figure 2.

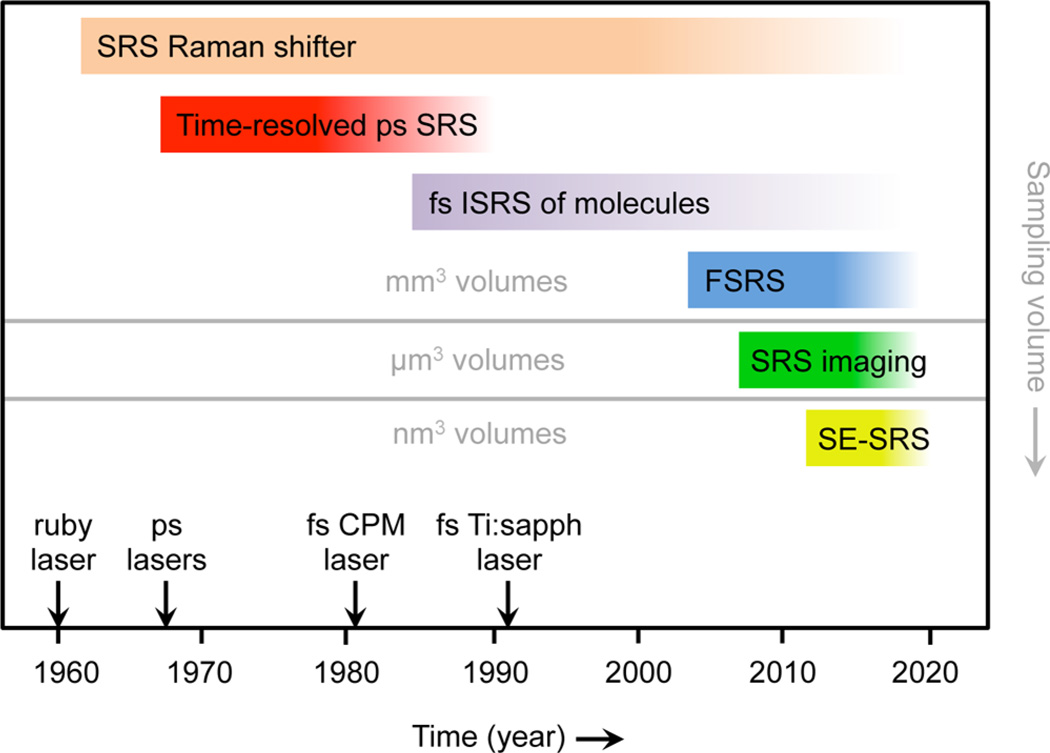
Timeline of several key developments in SRS technology and spectroscopy. The evolution toward smaller sampling volumes is mapped onto the vertical axis. Important advances in laser light sources are indicated as well.

Aided by the versatility of mode-locked femtosecond Ti:sapphire lasers and the ease of generating pulses of desired temporal and spectral properties, an important version of time-resolved SRS spectroscopy of electronically resonant molecules was introduced in the early 2000s. Named after the achievable time-resolution of the experiment, femtosecond stimulated Raman scattering (FSRS) uses a short (actinic) pulse to prepare a wavepacket on an excited-state potential energy surface.^43,44 The structural motion and interactions of the excited molecule are then followed through the lens of Raman active vibrations in the excited state. The SRS process for monitoring the vibrational modes uses a narrowband picosecond pump pulse (ω_p) and a broadband femtosecond Stokes pulse (ω_s).⁴⁵ Using this pulse combination, it is possible to track the vibrational motions as the molecule evolves in the excited state with femtosecond time resolution. The FSRS method has been used to unravel structural dynamics of chromophores such as β-carotene and retinal.⁴⁴ Some examples of FSRS are highlighted in sections 3.2 and 4.2.

1.3. Toward Smaller Probing Volumes

Developments in laser technology have led to light sources with ever improving stability and lower intensity fluctuations. Such output characteristics translate immediately into more sensitive SRS measurements. In combination with modulation techniques and lock-in detection, sensitivity levels can be pushed to the shot noise limit, allowing measurements of smaller sample volumes and ensembles of fewer SRS active molecules. Traditionally, SRS experiments were performed by focusing laser beams with lenses of relatively long focal length into the sample, resulting in interaction lengths that range from a tenth of a millimeter to several millimeters. Improved sensitivity cleared the way for smaller interaction volumes, such as can be obtained with high numerical aperture lenses, in which case the focal length is on the order of a micrometer and sample volumes are on the order of a femtoliter (fL). The earliest demonstration of coherent Raman scattering radiation generated from a fL volume formed by a high numerical aperture lens came in 1999, in the form of CARS.⁴⁶ This study was quickly followed by subsequent technical advances, turning CARS microscopy into a reliable tool for biological imaging.^47–49

Translating SRS techniques to the realm of microscopy proved, however, more challenging. The use of high NA lenses favors a collinear excitation scheme, which makes spatial separation of signal beams impractical. Unlike CARS, which benefits from a signal at the anti-Stokes shifted frequency that is spectrally distinct from the input fields, the SRS response cannot be isolated with spectral filters alone. Instead, modulation techniques and other methods must be implemented to discriminate the SRS signal from the incident laser fields. In an early example of ISRS generated in fL volumes, amplitude modulation in combination with polarization sensitive detection was used, enabling the time-resolved detection of orientational modes of water in living cells.⁵⁰ SRS of higher energy modes, using a broadband SRS approach, was demonstrated for microscopic volumes in 2007,⁵¹ followed by rapid SRS imaging with a pair of narrowband picosecond pump and Stokes pulses.⁵² The exquisite detection sensitivity in SRS imaging was accomplished by implementing a high frequency modulation method. Making use of the fact that laser noise manifests itself predominantly at lower frequencies, detecting a modulated signal at frequencies beyond 1 MHz minimizes the effect of laser noise and boosts the sensitivity significantly.^53–55 Detection levels of ~100 µM or ~10⁴ molecules in focus can be reached in this fashion.^56,57 A discussion of SRS from microscopic volumes and its applications is provided in sections 4.1 and 4.3.

Improvements in laser performance and signal detection techniques have helped reach very high sensitivities, but they do not fundamentally overcome the low Raman cross sections of molecular systems. Because the probability of a Raman scattered photon is low, sizable ensembles of molecules (>10³) or long integration times (>1 ms) are needed to generate a Raman derived signal that rises above the noise. To detect the SRS response from molecules at very low concentrations, additional mechanisms are needed that boost the intrinsic response of the sample to the incident light fields. One approach is the involvement of electronic excitations, as mentioned above for ISRS. Electronic resonances increase the nonlinear susceptibility of molecules, which can raise the number of photons that report on the vibrational motions of the system.⁵⁸ Another route to enlarge the response from the molecule is to increase the amplitude of the driving fields. Yet, simply raising the laser power is not always a desired strategy. Instead, the molecules can be equipped with plasmonic antennas, which enable a much more efficient coupling between the freely propagating excitation fields and the molecule by condensing the electric field to nanoscopic volumes. In addition, the antenna also improves the radiative properties of the molecule by efficiently coupling the near-field molecular response to a far-field photodetector. The use of plasmonic antennas for Raman applications has been popularized through surface-enhanced Raman scattering (SERS),^59,60 which has made it possible to collect spontaneous Raman spectra from single molecules.^61–63 Surface-enhanced SRS (SE-SRS) is the stimulated analogue of SERS, and the feasibility of using plasmonic antennas to enhance SRS was recently demonstrated.⁶⁴ A more thorough discussion on SE-SRS is given in section 4.5.

2. THE STIMULATED RAMAN PROCESS

In this section, we briefly review the nature of the SRS light–matter interaction. We will first consider the process from the perspective of the light fields, which undergo amplitude changes due to the SRS interaction. We will next connect the observed changes in the light fields to vibrational motions in the material. For this purpose, we will qualitatively discuss the material response in both the classical picture as well as the quantum mechanical picture. In particular, we will highlight the use of the density matrix formalism that is commonly used to interpret time-resolved SRS experiments.

2.1. Field Picture

In the following, we will assume two incident light fields E_i with frequency ω_i, where i = 1,2 and ω₁ > ω₂. We will call E₁ the pump field and E₂ the Stokes field. These fields are typically delivered by a laser source. The intensity of each beam is directly proportional to |E_i|², or can quantum mechanically be expressed as n_iℏω_i, where n_i is the number of photons in the mode ω_i. In a typical SRS experiment, both beams are incident on the sample, where they interact with the material. After passing through the sample, the intensity of either the pump or the Stokes beam is measured with a photodetector. The measurement thus reveals changes in the intensity of the pump and Stokes beams. Any changes in the material have to be inferred from the intensity changes of the light beams, as we only measure the molecular response indirectly through the fields. Although it does not explain the nature of the photoinduced response in the material, the field perspective of the SRS process is intuitive and very helpful in recognizing the flow of energy between the light fields and the material.

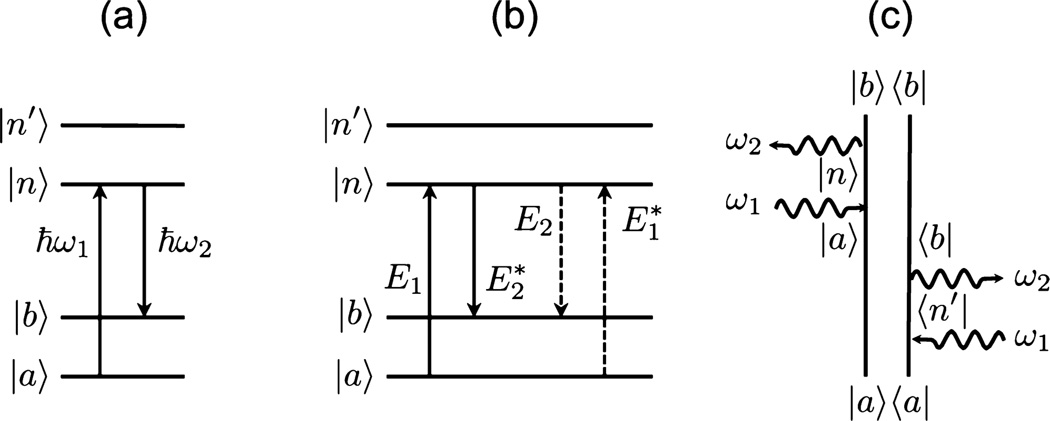
Figure 3a shows the well-known Jablonski diagram of the SRS process. This diagram shows the SRS interaction in terms of the beam intensities. Quantum mechanically, the interpretation is straightforward: upon interacting with the material, a ω₁ photon is absorbed (annihilated) and a ω₂ photon is emitted (created). The difference in photon energies, ℏ(ω₁ − ω₂), is absorbed by the material. The SRS interaction can thus be measured by probing the loss of photons in the pump beam or by detecting the gain of photons in the Stokes channel. The first detection method is called stimulated Raman loss (SRL), and the latter is called stimulated Raman gain (SRG). Note that both detection methods result from the same light–matter interaction; that is, the Raman information detected in SRL and SRG is identical.

Figure 3.

Schematic of the SRS light–matter interaction. (a) Energy level diagram in the intensity representation showing the absorption of an ω₁ photon and the emission of a ω₂ photon. (b) Energy level diagram in the field representation showing the interaction of the fields E₁ and E₂ with the quantum mechanical states of the material. Note that the arrows are not time-ordered. (c) Double sided Feynman diagram of one of the SRS pathways, showing how the field interactions affect the density matrix of the material. This diagram also represents the spontaneous Raman scattering process, with ω₂ a photon mode provided by the vacuum field.

The Jablonski diagram for the spontaneous Raman process is the same as shown in Figure 3a, as the diagram does not explicitly show the occupation numbers of the photon modes. In spontaneous Raman scattering, the ω₁ mode is occupied with a high number of photons, n₁ ≫ 1, whereas the ω₂ mode is initially empty, that is, n₂ = 0. The Raman interaction changes the occupation numbers to n₁ − 1 for the ω₁ mode and to n₂ + 1 for the ω₂ mode, where the new ω₂ photon is created from the vacuum field. The same is true for SRS, with the important difference that the initial occupation number of ω₂ is high (n₂ ≫ 1). In SRS, the rate of photon generation in the ω₂ channel, W_stim, is proportional to both the n₁ and the n₂ occupation numbers, that is, n₁(n₂ + 1).⁹ On the other hand, for spontaneous Raman scattering, the rate of emission, W_spon, is proportional to n₁, because n₂ = 0. The effect of the stimulating field is thus to increase the rate of ω₂ emission:^65,66

$$\frac{W_{\text{stim}}}{W_{\text{spon}}}\propto n_2+1$$ (1)

Because the number of photons in the stimulating beam is high, the increase of the emission rate in ω₂ is significant. This implies that information about the Raman transition can be retrieved much faster in SRS than in spontaneous Raman scattering by many orders of magnitude. This increase in signal acquisition speed is the key advantage of SRS microscopy over spontaneous Raman scattering microscopy.⁶⁷ In practice, the useful information is not determined solely by the number of ω₂ photons, but rather by the signal-to-noise (S/N) ratio. Both spontaneous Raman and SRS are ultimately limited by the shot noise limit, which states that the signal needs to exceed the photon shot noise of $\sqrt{n_i}$, where n_i is the total number of photons in the detection mode ω_i. Because the SRS signal is detected against a background of n₂ of incident photons, nominally the signal needs to be higher than the shot noise limit set by the background, that is, $\sqrt{n_2}$. This implies that the gain in SRS must be sufficient to reach the shot noise limit and to fundamentally outperform spontaneous Raman scattering. Empirically, for a given Raman line, the increase in the signal acquisition rate from a microscopic probing volume typically exceeds 10⁵. In this limit, SRS offers clear benefits. For instance, if a spontaneous Raman measurement of a particular vibrational mode takes 100 ms, SRS can provide the same information with comparable S/N in only 1 μs.

The intensity diagram in 3a also reveals that annihilation of a ω₁ photon and the creation of a ω₂ photon is accompanied by a Raman transition in the material. The molecule has absorbed the residual energy from the light fields and is left in a vibrationally excited state. However, this representation does not provide detailed information about the vibrational motions in the molecule or the Raman coherence in the material. In Figure 3b, the SRS interaction is depicted in terms of fields rather than intensities. As is clear from the diagram, the SRS interaction involves four fields, which classifies SRS as a four-wave mixing technique. As discussed in section 2.3, keeping track of the field interactions with the material is a much more useful way for analyzing the material response in terms of vibrational coherences. For this purpose, it is convenient to describe the material response in terms of the density matrix. Before discussing the SRS signal in the context of the density matrix, which involves a quantum mechanical treatment of the molecule, we will briefly describe the material response in a classical fashion.

2.2. Classical Vibrational Motions

The classical description of the stimulated Raman process provides a very intuitive picture of molecular motions driven by two external fields ω₁ and ω₂.^68–70 Unlike the field picture discussed above, the classical SRS model explicitly takes the vibrational motions of the material into account. The model aims to determine the magnitude of the polarization in the material, due to the presence of vibrational oscillators that are actively driven by the incident fields. The frequency of the incident radiation is typically in the visible to near-infrared range (~10³ THz), whereas the frequencies of the nuclear vibrational motions in molecules are of much lower frequencies (1–100 THz). Therefore, the nuclei cannot follow the incident fields adiabatically. Instead, the molecules couple to the fields through their electrons, which can follow the rapid oscillations of the driving fields. In case there is coupling between the electron motions and the nuclear modes, the resultant electron oscillation contains information about the nuclear vibrations as well. Raman processes thus probe nuclear motions in the molecule indirectly through the motion of electrons.

The response of the electrons to an optical field, E(t) = Ae^−iωt + c.c., is classically modeled by the electronic polarizability α. This quantity is a tensor, but to simplify the discussion we will consider it here as a scalar. The time-dependent molecular polarization μ(t) induced by the optical field is then written as μ(t) = α(t)E(t). In the absence of nuclear modes or any nonlinearities, α can be considered a constant (α₀), and the molecular polarization depends linearly on the field. In the presence of a nuclear mode, written as Q(t), which describes the displacement of the nuclei along the generalized nuclear coordinate Q, the electron motion can be distorted in case α is dependent on the nuclear positions. In this scenario, there is a change in α if there is a change in Q, or in other words (∂α/∂Q)₀ ≠ 0.⁷¹ Vice versa, this coupling between electronic and nuclear motions implies that the nuclear displacements may be affected when the electrons are set in motion. In the presence of the driving fields E₁(t) and E₂(t), the nuclear mode can experience a driving force F(t) at the difference frequency Ω = ω₁ − ω₂:

$$F(t)={\left(\frac{\partial \alpha }{\partial Q}\right)}_0[A_1{A}_2^{*}{\mathrm{e}}^{-i\mathrm{\Omega }t}+\mathrm{c}.\mathrm{c}.]$$ (2)

Note that the magnitude of the force depends explicitly on the coupling term (∂α/∂Q)₀, which acts as a nonlinearity because it drives a material motion in response to two incoming fields. The time-varying nuclear displacement Q(t) in the presence of the force in eq 2 can be modeled with an equation of motion for a damped harmonic oscillator.⁷ The solution of the equation is Q(t) = Q(Ω)e^−iΩt + c.c., which describes a harmonic motion of the nuclear mode with the amplitude:^68,70

$$Q(\mathrm{\Omega })=\frac{1}{m}{\left(\frac{\partial \alpha }{\partial Q}\right)}_0\frac{A_1{A}_2^{*}}{{\omega }_{\nu }^2-{\mathrm{\Omega }}^2-2i\mathrm{\Omega }\gamma }$$ (3)

where m is the reduced mass of the nuclear oscillator, γ is the damping constant, and ω_ν is the resonance frequency of the harmonic nuclear mode. Equation 3 shows that the nuclear motion is significant when the electronic–nuclear coupling is high, underlining that the (∂α/∂Q)₀ term plays a central role in (stimulated) Raman scattering. The amplitude also scales linearly in both driving fields E₁ and E₂. In addition, the amplitude grows when the frequency difference Ω coincides with the resonance frequency of the nuclear mode, that is, when Ω = ω_ν.

In general, the induced polarization of the sample is given by P(t) = Nα(t)E(t), where N is the number of molecules in the interaction volume and E(t) is the total applied field. In the presence of Raman active modes, the electronic polarizability is no longer a constant, as the electron oscillation is affected by the mobility of the nuclei. The electronic polarizability can be expanded in a Taylor series to include the effect of the nuclear modes to lowest order as:⁷¹

$$\alpha ={\alpha }_0+{\left(\frac{\partial \alpha }{\partial Q}\right)}_{0}Q(t)+\dots$$ (4)

Given that the total electric field in the material is E(t) = E₁(t) + E₂(t), the induced polarization in the interaction volume can be written as:

$$P(t)=N[{\alpha }_0+{\left(\frac{\partial \alpha }{\partial Q}\right)}_{0}Q(t)]\{E_1(t)+E_2(t)\}$$ (5)

The terms in the polarization that depend on (∂α/∂Q)₀ include the contribution of three field interactions: two interactions to drive Q(t) and one final interaction with either E₁ or E₂. These three interactions of two frequencies (ω₁,ω₂) produce polarization components at four distinct frequency combinations in the material: ω_cs = 2ω₂ − ω₁ (coherent Stokes frequency), ω_SRG = ω₂ − ω₁ + ω₁ (Stokes frequency), ω_SRL = ω₁ − ω₂ + ω₂ (pump frequency), and ω_as = 2ω₁ − ω₂ (anti-Stokes frequency). The amplitudes of the SRS polarization components are found at ω_SRG and ω_SRL, and are given as:

$$P({\omega }_{\mathrm{S}\mathrm{R}\mathrm{G}})=6{\epsilon }_0{\chi }_{\mathrm{N}\mathrm{L}}^{*}(\mathrm{\Omega }){|A_1|}^2{A}_2$$ (6)

$$P({\omega }_{\mathrm{S}\mathrm{R}\mathrm{L}})=6{\epsilon }_0{\chi }_{\mathrm{N}\mathrm{L}}(\mathrm{\Omega }){|A_2|}^2{A}_1$$ (7)

where ε₀ is the vacuum permittivity and χ_NL is the Raman-dependent nonlinear susceptibility of the material, which is written as:

$${\chi }_{\mathrm{N}\mathrm{L}}(\mathrm{\Omega })=\frac{N}{6m{\epsilon }_0}{\left(\frac{\partial \alpha }{\partial Q}\right)}_0^2\frac{1}{{\omega }_{\nu }^2-{\mathrm{\Omega }}^2-2i\mathrm{\Omega }\gamma }$$ (8)

The nonlinear susceptibility is a material quantity, as it describes the frequency-dependent response of the material to the incoming fields. Equation 8 shows that the Raman-related material response scales with the square of the (∂α/∂Q)₀ coupling term. The material also becomes more responsive when the frequency difference Ω coincides with the resonance frequency of the nuclear mode.

Using this classical model, we see that the SRS process induces oscillating polarization components at the pump and Stokes frequencies in the material, as indicated by eqs 6 and 7. Using this formalism, we can also relate the material response to the measured optical signal by the photodetector. Both the P(ω_SRG) and the P(ω_SRL) components depend on the same Raman nonlinear susceptibility. They exhibit similar amplitudes but oscillate with different phases. Consequently, as the nonlinear polarization radiates, it produces the field components E_SRG(ω₂) and E_SRL(ω₁), which arrive in the far-field detector with distinct phases. If the signal is detected in a phase-matched direction that is different from the direction of the probing fields, the signal is proportional to |P|². On the other hand, if the signal is detected in the phase-matched direction that coincides with the probe field, the induced field components interfere with the incident fields components E₁ and E₂, respectively. For instance, at the Stokes frequency, the measured intensity is I(ω₂) = ε₀c/2|E_SRG + E₂|². The interference term between the signal fields and the incident fields constitutes the SRS signal in the ω₁ and ω₂ channels:

$$S_{\mathrm{S}\mathrm{R}\mathrm{G}}({\omega }_2)\propto {|A_1|}^2{|A_2|}^2\text{Im}\{{\chi }_{\mathrm{N}\mathrm{L}}(\mathrm{\Omega })\}$$ (9)

$$S_{\mathrm{S}\mathrm{R}\mathrm{L}}({\omega }_1)\propto -{|A_1|}^2{|A_2|}^2\text{Im}\{{\chi }_{\mathrm{N}\mathrm{L}}(\mathrm{\Omega })\}$$ (10)

The SRG and SRL signals both scale linearly with the intensity of the pump and Stokes laser beams, and both signals probe the imaginary part of the nonlinear susceptibility, which describes the dissipative part of the material response. Similar to the quantized field picture, the classical description of SRS predicts a gain in the ω₂ channel and a loss in the ω₁ channel. Both models thus arrive at the same conclusion regarding the energy transfer between the field modes, albeit in different ways. Although intuitive, the descriptions thus far do not provide a lot of insight in the material coherences nor take full account of the various quantum mechanical states of the material that partake in the SRS process. The density matrix approach provides a deeper understanding of the material response in terms of quantum coherences, which is discussed in the next section.

2.3. Quantum Mechanical Description: Density Matrix

The semiclassical model of nonlinear optical spectroscopy describes the electromagnetic fields as classical waves but treats the material quantum mechanically. In the quantum mechanical picture, the state of the material is described by molecular wave functions, which are written as a superposition of the molecular eigenstates ψ_n:

$$\mathbf{\Psi }(r,t)=\sum _n{c}_n{\psi }_n(r,t)$$ (11)

where c_n are the amplitude coefficients of the wave function for each of the eigenstates. In the bra and ket notation, the eigenstates of the material ψ_n are indicated by their ket notation as |n〉. The operator Ĥ₀ is the unperturbed Hamiltonian, which, upon acting on the wave function, produces an eigenvalue that corresponds to the energy of the system. In the presence of light, the state of the material can be altered due to light–matter interactions. In the dipole limit, light–matter interactions are described by the interaction Hamiltonian V̂(t) = μ̂·E(t), where μ̂ is the dipole operator, which tracks the motion of charged particles (electrons and nuclei) in response to the optical field E(t). The interaction Hamiltonian perturbs the system and changes the state of the material by enabling transitions between material eigenstates. The probability that the system is in a certain eigenstate |n〉 and the mutual coherence between the eigenstates after the interaction is conveniently captured by the density matrix operator:

$$\hat{\rho }(t)\equiv |\mathbf{\Psi }(t)\rangle \langle \mathbf{\Psi }(t)|=\sum _{nm}{\rho }_{nm}(t)|n\rangle \langle m|$$ (12)

Here, ρ_nm are the matrix elements 〈n|ρ̂|m〉 in bra-ket notation. The diagonal elements (n = m) of the density matrix correspond to the probability that the system is in eigenstate |n〉. In this case, the operator in eq 12 takes on the form |n〉 〈n|, which represents the population of the molecular eigenstate ψ_n. The off-diagonal elements, ρ_nm with n ≠ m, are associated with the operator |n〉 〈m|, which is called the coherence between eigenstates ψ_m and ψ_n. Following the time-dependent density matrix after a light–matter interaction thus reveals information about the population and coherence dynamics in the material.

In section 2.2, it was clear that in the SRS process, a nonlinear polarization is induced in the material through three interactions between the matter and the incident fields. The induced polarization then radiates to produce a fourth field. This process can be described in the density matrix formalism by monitoring the time-dependent evolution of ρ̂(t) following three interactions with the light fields. Generally, ρ̂(t) evolves in the Schrödinger picture as:

$$\frac{\mathrm{d}\hat{\rho }}{\mathrm{d}t}=-\frac{i}{\hslash }[Ĥ,\hat{\rho }]$$ (13)

where the total Hamiltonian includes both Ĥ₀ and V̂. The evolution of ρ̂ in the SRS process is commonly modeled through third-order perturbation theory, where the density operator is calculated to the third order in the electric field.^10,72 In evaluating the density matrix contribution that is third order in the field, ρ̂⁽³⁾(t), many pathways for the material evolution are found. Double-sided Feynman diagrams are a convenient tool for analyzing such pathways. An example is shown in Figure 3c, which shows one pathway that contributes to the overall SRS response. The diagram can be interpreted as follows. The system starts out in the ground state, indicated by the |a〉 〈a| population at the bottom of the diagram. The first light–matter interaction is with the field of frequency ω₁, which changes the bra from 〈a| to 〈n′|. The states indicated by n and n′ can be either real or virtual states. For ground-state SRS, these electronic states are virtual states and the n,n′ labels are dummy indices. The second field interaction on the bra side generates the coherence |a〉 〈b|. This is the Raman coherence in the material, which, in the absence of fields, evolves according to the unperturbed Hamiltonian Ĥ₀. The density matrix ρ_ab is said to propagate during this period, tracking the time-dependent material response to the light-induced superposition of the ground state and the vibrationally excited states. The density matrix is then interacting with fields ω₁ and ω₂ on the ket side, generating the population |b〉 〈b|. Effectively, in this diagram, the SRS interaction has moved population from the ground state to the first vibrationally excited state.

It should be noted that the diagram shown in Figure 3c also denotes the quantum pathway of the spontaneous Raman process, with the important difference that the ω₂ field is provided by the vacuum field. This does not mean, however, that all possible pathways probed in SRS are necessarily accessible through the spontaneous Raman process. This is related to the fact that the photon occupation numbers n₁ and n₂ in SRS and spontaneous Raman scattering are different. The field interactions with ω₂ in the spontaneous Raman process are restricted as they must change the occupation number from zero to one, which limits the freedom of arranging the field interactions in the Feynman diagrams. This restriction is not present for SRS, in which case both n₁ and n₂ are high, allowing more permutations of the field interactions, and thus producing more permissible quantum pathways.⁷² Another important difference between SRS and spontaneous Raman is that SRS offers the possibility to time-resolve the evolution of the Raman coherence |a〉 〈b|, by preparing the coherence with a pump and Stokes pulse pair and probing its propagation by a time-delayed probe pulse.

The third-order polarization in the sample can be obtained from the expectation value of the dipole operator, which can be obtained within the density matrix formalism as

$$P^{(3)}(t)=N\text{tr}[\hat{\mu }{\hat{\rho }}^{(3)}(t)]$$ (14)

where tr indicates the trace over the matrix elements of the operator product between the brackets. Once the nonlinear polarization of the material is known, the signal can be calculated in the same manner as in the classical model. The exact time-dependence of the polarization depends on the evolution of the density matrix, which depends, in turn, on the details of the material Hamiltonian. Predictions of the SRS signal thus rely on proper knowledge of Hamiltonian-dictated dynamics in the system. The simplest model assumes a general dephasing rate γ_nm for the |n〉 〈m| coherence, and the population relaxation rate γ_nn for describing the energy relaxation between material states.¹⁰

In this scenario and assuming that the Raman line is only homogeneously broadened, a typical time-resolved SRS experiment with ultrashort laser pulses can then be understood as follows. The molecule is subjected to pulsed fields at frequencies ω₁ and ω₂, which induce a vibrational coherence |a〉 〈b| in the sample. In Figure 3c, this corresponds to the first two field interactions. The duration of the laser pulses is generally much shorter than the dephasing rate γ_ab. After preparation, the Raman coherence will decay with a rate γ_ab = γ_bb/2 + γ̂_ab, where γ̂_ab is usually referred to as the pure dephasing rate. After a time delay τ, a second pulse with the frequencies ω₁ and ω₂ is incident on the sample to probe the Raman coherence. The probe pulse transfers information about the τ-dependence of the Raman coherence to the ω₁ and ω₂ frequency channels, which are detected by a photodetector. The time-dependence of the resulting third-order polarization, which is encoded in the detection fields, depends on the details of the experiment.

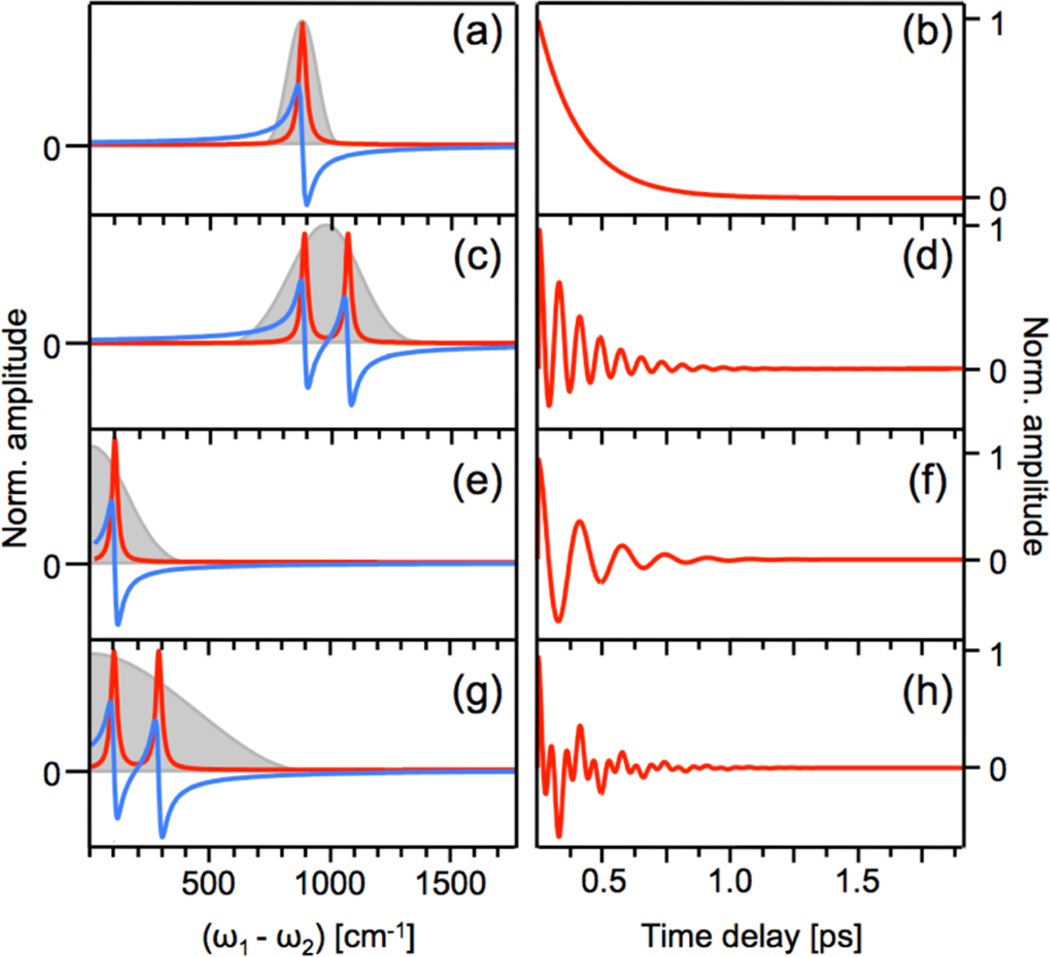
Figure 4 depicts the material response in terms of the frequency- and time-dependent third-order polarization under several different experimental conditions. The frequency-dependent responses, on the left panels, display the real (red) and imaginary (blue) components of the nonlinear polarization. The gray shaded areas represent the driving field (ω₁ − ω₂), which in all examples overlaps with the material resonance(s). The panels on the right depict the time-dependent response of the third-order polarization. In panels (a) and (b), a single mode is driven by two narrowband laser fields, and the polarization decays with a dephasing time of several hundred femtoseconds, corresponding to the frequency-domain line width. No oscillatory pattern is observed in the time-domain as the experimental setup does not have sufficient time resolution to resolve the carrier frequency. In panel (c), the system has two Raman-active modes, which are driven by two broadband laser fields. The beat pattern between the two modes is visible in the time-dependent response in panel (d). Panels (e) and (f) depict a system with one low frequency Raman active mode, which is driven by a single broadband pulse. The temporal response shows a single oscillatory feature corresponding to the vibrational period. In panels (g) and (h), a single broadband pulse drives two low frequency Raman active vibrations. The time-dependent response shows oscillatory features from each of the modes as well as their beat frequency.

Figure 4.

Frequency (a,c,e,g) and time (b,d,f,h) dependence of the third-order polarization as probed under different experimental conditions. (a) Amplitude of the real (red) and imaginary (blue) parts of the nonlinear polarization due to the presence of a single high-frequency Raman resonance. The Raman coherence is driven at (ω₁ − ω₂), where E₁ and E₂ are narrowband fields of ps duration. Gray shaded region indicates the spectral profile of the effective driving field (ω₁ − ω₂). (b) Amplitude of the third-order polarization as a function of time delay τ, corresponding to the situation in (a). (c) Driving two high-frequency Raman resonances with two broadband laser fields, such that the spectrum of the effective driving field (ω₁ − ω₂) overlaps with both resonances. (d) Temporal response corresponding to the situation in (c). (e) Driving one low-frequency Raman resonance with one broadband laser field. (f) Temporal response corresponding to the situation in (e). (g) Driving two low-frequency Raman resonances with one broadband laser field. (h) Temporal response corresponding to the situation in (g).

Similar to the classical model, once the nonlinear polarization is known, the frequency-dependent nonlinear susceptibility of the material can be determined. Within the simple dephasing model discussed above, the contribution χ⁽³⁾(−ω₂;ω₁,ω₂,−ω₁) to χ⁽³⁾ from the pathway shown in Figure 3c is:⁷²

$$\frac{N}{6{\hslash }^3{\epsilon }_0}\sum _{ab,nn\prime }{\rho }_{aa}^{(0)}\times \left({\mu }_{bn}{\mu }_{na}{\mu }_{an\prime }{\mu }_{n\prime b}\right)/([{\omega }_{bn}+{\omega }_2+i{\gamma }_{nb}][{\omega }_{ba}-({\omega }_1-{\omega }_2)+i{\gamma }_{ab}][{\omega }_{n\prime a}-{\omega }_1+i{\gamma }_{an\prime }])$$ (15)

where ω_nm denotes the difference frequency ω_n − ω_m, and μ_mn indicates the transition dipole moment for |n〉 → |m〉. The second term in the denominator in eq 15 contains the information on the density matrix propagator of the Raman coherence |a〉 〈b|. Similar to the classical form of the nonlinear susceptibility (eq 8), the contribution to χ⁽³⁾ shown above grows large when the frequency difference ω₁ − ω₂ approaches a Raman resonance at ω_ba. The spectral dependence of the Raman resonant χ⁽³⁾ contributions follows a Lorentzian line shape with a width directly proportional to γ_ab. Note that the χ⁽³⁾(−ω₂;ω₁,ω₂,−ω₁) contribution contains more resonances, such as the resonance at ω₁ = ω_n′a, which occurs when ω₁ is resonant with an electronic transition in the material. Because the diagram in Figure 3c is also a good representation of the spontaneous Raman scattering process,⁷² we may relate the measured Raman spectrum to this χ⁽³⁾ contribution as follows:

$$S_{\text{Raman}}\approx \text{Im}\{{\chi }^{(3)}(-{\omega }_2;{\omega }_1,{\omega }_2,-{\omega }_1)\}$$ (16)

The approximate sign is present because in spontaneous Raman scattering the field interactions with ω₁ and ω₂, including their independent polarization orientations, cannot be arbitrarily chosen, as discussed above. For ground-state SRS with linear and parallel polarized fields, far from electronic resonances, the diagram in Figure 3c is a dominant contributor to the overall SRS response, and the expression in eq 16 is generally true. This implies that for ground-state vibrational Raman excitations, the dephasing parameters γ_ab extracted from a time-resolved SRS experiment are identical to the dephasing parameters derived from the Raman line width. This is no longer true when electronic excitations are involved, in which case specific time-consecutive processes in the excited state can be resolved in time-domain SRS that cannot always be reconstructed in a time-ordered fashion from the spectral Raman response.

2.4. Magnitude of the Raman Response

From eq 1 it is clear that the rate of SRS emission is much higher than the rate of spontaneous Raman emission. When a Raman active material is illuminated with the ω₁ mode, the number of photons scattered into the ω₂ mode is very small, emphasizing that spontaneous Raman scattering is a very weak effect. The rate of photon emission in spontaneous Raman scattering, measured in all directions, for a transparent sample of length z with an incident light intensity of I(ω₁) (in W/cm²), can be written as

$$W_{\text{spon}}({\omega }_2)=N_{\mathrm{d}}Az\sigma ({\omega }_2)I({\omega }_1)$$ (17)

where N_d is the molecular number density, A is the illuminated area, and σ(ω₂) is the Raman cross section (in cm²). The most important material characteristic is σ, which is a measure for the responsiveness of a given material. It is useful to define the rate of photon emission in a particular direction defined by the solid angle element dΩ. In this case, the material response is defined through the Raman differential cross section dσ/dΩ. The differential cross section can be related to the material properties in the previous sections, that is, $\mathrm{d}\sigma /\mathrm{d}\mathrm{\Omega }\propto {(\partial \alpha /\partial Q)}_0^2\propto \text{Im}\{{\chi }^{(3)}\}$. The differential cross sections of various materials are listed in Table 1. For example, the differential cross section for the O–H stretching mode is 8 × 10⁻³⁰ cm²/molecule·sr when excited at 488 nm. This roughly translates into about three Raman scattered photons out of 10⁷ incident photons when propagating through 1 mL of liquid. Given that 1 mL of liquid contains 3.3 × 10²² of water molecules, the Raman scattering efficiency per molecule is indeed very small. Other modes, such as the ring breathing mode at 992 cm⁻¹ in benzene, exhibit higher polarizabilities, resulting in slightly stronger Raman signals. Even so, for smaller volumes, the number of Raman scattered photons remains low. For microscopic volumes of 1 fL, roughly 2 out of 10¹¹ incident photons are Raman scattered off of the 992 cm⁻¹ mode of benzene.

Table 1.

Absolute Raman Differential Scattering Cross Sections (in cm²/molecule·sr) for Various Compounds

compound	mode (cm−1)	λex (nm)	cross section cm2/molecule·sr)	ref
water	3400	488	8 × 10−30	73,74
cyclohexane	802	514	8.29 × 10−30	75
ethanol	2880	488	1.7 × 10−29	76
benzene	992	488	3.65 × 10−29	77
β-carotene	1520	514	2.04 × 10−24	78
rhodamine 6G	604	532	4.1 × 10−23	79

Clearly, enhancing the photon emission rate as provided through the SRS process offers an attractive strategy to overcome the small Raman signals from fewer molecules and smaller volumes. We have also seen that the Raman reponse of the material can be directly enhanced when the pump beam is tuned close to an electronic resonance (eq 15). The compounds β-carotene and rhodamine 6G listed in Table 1 have electronic resonances in the visible range, resulting in differential Raman cross sections that are several orders of magnitude higher than for materials that are transparent in this range.

2.5. SRS versus CARS

In sections 1.2 and 1.3, some attributes of SRS were contrasted with the properties of CARS. The CARS technique has its own history and application niches, which are not the focus of this Review. Nonetheless, because the comparison between these two coherent Raman techniques is a topic that is frequently discussed in the literature, we will briefly touch on it here as well. It is important to underline that both techniques rely on the same Raman coherences in the sample, driven at ω₁ − ω₂, for generating a detectable signal. The main difference between SRS and CARS is the way in which the amplitude and phase of the excited Raman coherence are translated into a measurable change in the light fields. In terms of the dual color excitation configuration discussed in section 2.2, in the CARS experiment the information about the Raman coherence is probed in the ω_as = 2ω₁ − ω₂ signal channel, whereas in SRL it is detected in the ω₂ channel. The difference is strictly in the detection mode: from the material’s point of view, it does not matter whether the ω₁ − ω₂ vibrational motion is probed in either the ω_as channel or the ω₂ channel. However, the choice of detection channel does have experimental implications, and the preference for either SRS or CARS is largely driven by practical factors that determine how easy the information about the Raman vibration can be extracted from the experimentally measured signal.

One important difference between the two techniques is the fact that SRS, detected in the phase-matched direction of the probe, is dictated by the interference term between the signal field and the incident probe field, and CARS is not. This intrinsic interference of the SRS signal, which is sometimes called the self-heterodyning of the signal, gives rise to signals proportional to the nonlinear polarization P. The resulting signal is thus linearly dependent on the nonlinear susceptibility, and is in-phase with its imaginary component; see eqs 9 and 10. Because Im χ⁽³⁾ is proportional to the Raman cross section, the SRS signal exhibits the same spectral lineshapes as probed in spontaneous Raman scattering. For the same reason, the SRS signal scales linearly with the number of Raman scatterers in the probing volume. The CARS signal, on the other hand, is commonly detected in a homodyne manner. This implies that it is not (self-)heterodyned, and that the signal is instead proportional to the absolute square of the induced nonlinear polarization, |P|².⁷⁰ As a result, the CARS signal scales as |χ⁽³⁾|², giving rise to a spectral response that is not directly proportional to the spectral lineshapes measured in spontaneous Raman scattering. Furthermore, the CARS signal displays a nonlinear dependence on the concentration of Raman scatterers. Additionally, the CARS signal carries purely electronic contributions to the nonlinear susceptibility, which gives rise to a background that is not easily separated from the vibrationally resonant contributions. These attributes make SRS a better choice for certain frequency-domain experiments, especially when the concentration of the target Raman scatterers in heterogeneous samples is relatively low as compared to other sample constituents, in which case the electronic background contributions in CARS can be overwhelming. This limit is relevant for coherent Raman microscopy, and explains why SRS is sometimes advertised as being superior to CARS microscopy.

For time-domain coherent Raman experiments, the specific advantages of SRS mentioned above are less relevant. In fact, for molecular vibrations of higher energy (>200 cm⁻¹), the CARS experiment is often less complicated because of the ease of detecting the signal in a new frequency channel (ω_as). Experimentally, the frequency shift between the incident light and the signal is sufficient for isolating the CARS photons with modern spectral filters. In SRS, spectral filtering cannot be applied, and instead some type of modulation is needed to separate the coherent Raman signal from the incident beam, which can complicate the experiment. The spectral filtering advantage of CARS, however, disappears for low frequency vibrations (<200 cm⁻¹), which produce Raman signals that are too close in frequency to the incident frequencies to easily spectrally separate them. Here, time-domain SRS is preferred. As highlighted in section 1.2, the ISRS technique provides access to such low energy vibrations and offers a mechanism to fully time-solve their coherent motions.

3. FREQUENCY-DOMAIN AND TIME-DOMAIN SRS

In the previous section, we summarized the basics of the SRS process in terms of light–matter interactions. In this section, we highlight several experimental approaches that have been commonly used to interrogate Raman coherences with SRS. Specifically, we discuss frequency-domain SRS methods and the merits of time-resolved SRS.

3.1. Frequency-Domain: Narrowband versus Broadband

In frequency-domain SRS, the main purpose is to resolve the Raman response of the material in a spectral manner. In practice, this typically implies the generation of a vibrational (Raman) spectrum. There are several advantages of recording a vibrational spectrum with SRS as opposed to simply taking a spontaneous Raman spectrum. For instance, spectrally resolved information can be obtained with SRS much faster than with spontaneous Raman scattering. This is the main reason why SRS is used in microscopic imaging. In addition, transient Raman spectra following a trigger pulse can be captured, allowing, for example, the recording of excited-state Raman vibrations.

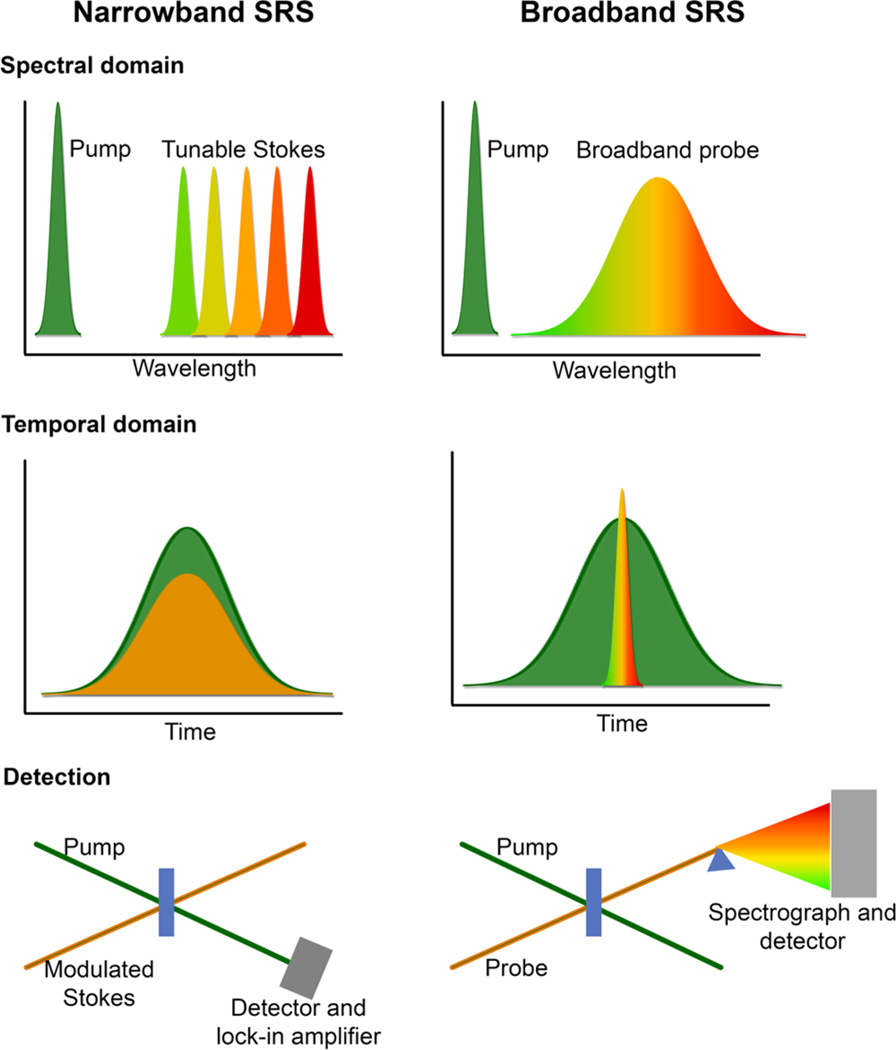
In performing frequency-domain SRS measurements, a primary experimental consideration is determining which combination of narrowband and/or broadband pulses will be used to provide spectral signal generation. This choice is critical in that it dictates detector options and the fundamental time resolution of a given experiment. However, regardless of the pulse spectral conditions, the mechanism of signal generation and information content of the experiment follow the descriptions provided in section 2. In general, most SRS experiments in the frequency-domain can be classified as either narrowband, in which all pulses used have a pulse width of typically less than 20 cm⁻¹, or broadband, in which one or more pulses has a spectral line width of typically more than 100 cm⁻¹.

Narrowband SRS experiments generally consist of two narrowband pulses: one pulse is fixed in frequency, and the other pulse is scanned across the wavelength of interest, as depicted in Figure 5. The pump pulse serves as the ω₁ field, and the Stokes pulse as the ω₂ field, as described in section 2. Pulse generation is typically achieved through the use of picosecond laser systems, with optical parametric oscillators (OPOs) or optical parametric amplifiers (OPAs) providing the necessary tunability.^67,80

Figure 5.

Common experimental implementations of narrowband and broadband SRS. In narrowband SRS, a pump beam of fixed wavelength interacts in the sample with a tunable Stokes beam, which is scanned across the region of interest. Because of the narrowband frequency resolution, the pulses are broad in time. Lock-in amplification is typically used for narrowband SRS detection. In broadband SRS, the tunable probe pulse is replaced with a broadband pulse containing all frequencies of interest. This pulse is by definition short in time, and detection is typically performed with a spectrograph and detector.

The key advantage to a narrowband SRS experiment is the ability to easily use lock-in amplification methods in detection, as the detected gain or loss signal is inherently single channel. Depending on the noise characteristics of the laser system and the speed of the detection electronics, lock-in amplification can provide an estimated 10⁴–10⁶ improvement in the signal-to-noise of the detected peak. Narrowband SRS microscopy is particularly well suited for lock-in amplification, as it is easy to modulate the amplitude of either the pump or the Stokes beam, the signal is intrinsically heterodyned, and the detection is single channel, and it is thus possible to make use of state-of-the-art lock-in amplifiers.

A disadvantage of a narrowband SRS measurement is that one must scan a number of Stokes beam wavelengths to build up a complete vibrational spectrum. Depending on the experiment, this may not be a significant problem as there may be only a few key vibrational markers needed, and the short acquisition times afforded by lock-in amplification detection⁸¹ allow for rapid experiments. However, if the vibrational frequencies of interest are not known a priori, or the signals are weak or broadened by the experiment, the time it takes to scan frequencies may become a significant drawback. An alternative approach is to perform a broadband SRS measurement.

In broadband SRS experiments, a femtosecond broadband pulse is used in place of a wavelength-scanned narrowband pulse. The FSRS technique is a widely utilized form of broadband SRS. FSRS utilizes a picosecond Raman pump pulse at ω₁ and a femtosecond Raman probe pulse, which provides frequencies in the range ω₂ ± Δω, where Δω is a measure of the spectral bandwidth of the pulse. In the frequency-domain picture, shown in Figure 5, the pump frequency can form a pump-Stokes pair with any of the frequencies provided by the broadband probe beam, resulting in the driving of Raman coherences in the range ω₁ − ω₂ ± Δω. The third field interaction in the four-wave mixing SRS process is provided by the same pump pulse, which is long in duration and thus may interact at any point in the vibrational dephasing time. In FSRS, the spectral resolution is normally dictated by the spectral width of the narrowband Raman pump pulse, manifested as narrowband vibrational peaks (gain) on the detected probe beam. The stimulated Raman signal is thus coherently generated in the phase-matched fashion of the probe, and is intrinsically self-heterodyned with the probe field, as in eq 6. FSRS is a convenient method for measuring ground-state vibrational spectra in rapid fashion.

A crucial advantage of broadband SRS is the ability to collect an entire vibrational spectrum, spanning low frequency torsional and phonon modes, through the fingerprint regions, and to the hydrogen stretching region, all in a single acquisition. As the broadband pulse can provide all necessary frequencies to stimulate Raman gain or loss simultaneously, signal is generated and can be detected for all Raman active vibrations. However, the broadband signal generation does put constraints on possible detection schemes for broadband SRS. As multichannel lock-in technology has not yet sufficiently advanced to the point of widespread use, broadband SRS experiments typically utilize CCD or photodiode arrays. Key detector characteristics include a large well depth to accommodate the probe pulse signal, rapid readout times to take advantage of high laser repetition rates, and low noise levels.

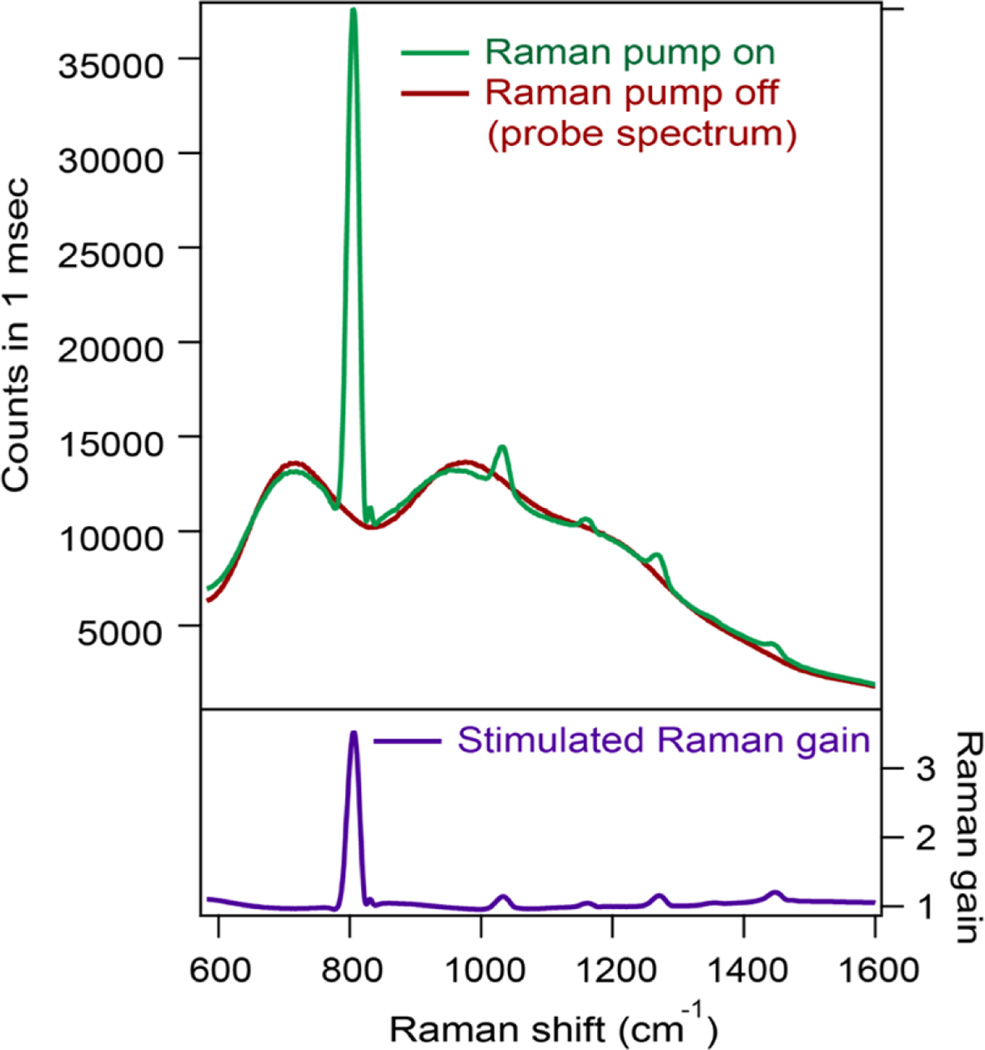
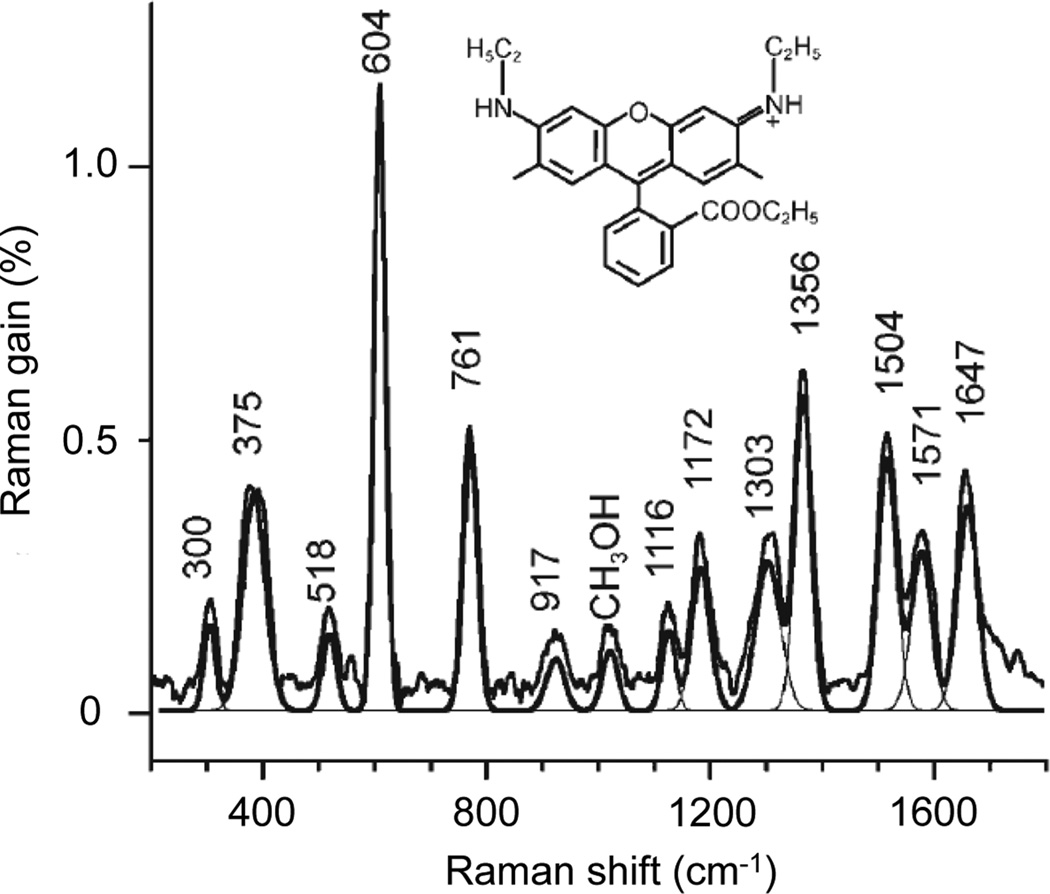
Figure 6 displays an example of rapid broadband SRS signal detection, shown here for a cyclohexane calibration standard. In red is the broadband probe spectrum, and in green is the probe and Raman gain spectrum when the pump pulse is also interacting with the sample. Both spectra were acquired in one laser pulse, corresponding to a millisecond acquisition at the laser repetition rate of 1 kHz. The high signal-to-noise and rapid acquisition time across a wide region of the vibrational spectrum are evident. In this experiment, the Raman gain exceeds 350% for the 801 cm⁻¹ ring breathing mode of neat cyclohexane. The pump-on spectrum can be divided by the pump-off spectrum to provide a background-free SRS spectrum.

Figure 6.

Single shot broadband SRS.

As compared to narrowband SRS, broadband SRS methodologies have several limitations. The need to combine both femtosecond and picosecond duration pulses in a single experiment typically means generating a picosecond pulse from a femtosecond laser system, which is inherently inefficient. Fortunately, numerous methods for tunable and fixed-frequency picosecond pulse generation have been developed.^82–87 Additionally, the broadband signal generation makes detection with lock-in amplification difficult to implement. Broadband lock-in amplification schemes include wavelength-scanning with single channel detection, or the recent development of multichannel lock-in amplifiers⁸⁸ and demodulators.⁸⁹

3.2. Time-Resolved Stimulated Raman Spectroscopy

Time-resolved stimulated Raman spectroscopy is a class of powerful techniques, which enable ultrafast monitoring of the evolution of vibrational coherences in real time. When time-resolved SRS is performed on reactive potential energy surfaces, one is able to experimentally map out the reaction coordinate of a structurally evolving system, by directly observing changes in vibrational spectra and thus molecular structure. This enables acquisition of molecular-level snapshots of a reacting system, allowing mechanisms of bond-breaking and bond-making processes to be determined in real-time. The structural sensitivity of SRS methods over ultrafast electronic absorption and emission measurements, coupled with the experimental convenience of using visible laser pulses, provide a powerful tool for determining reaction mechanisms of ultrafast photo-driven process. Time-resolved SRS techniques can be broadly classified as either time-domain or frequency-domain, depending on the means of detection.

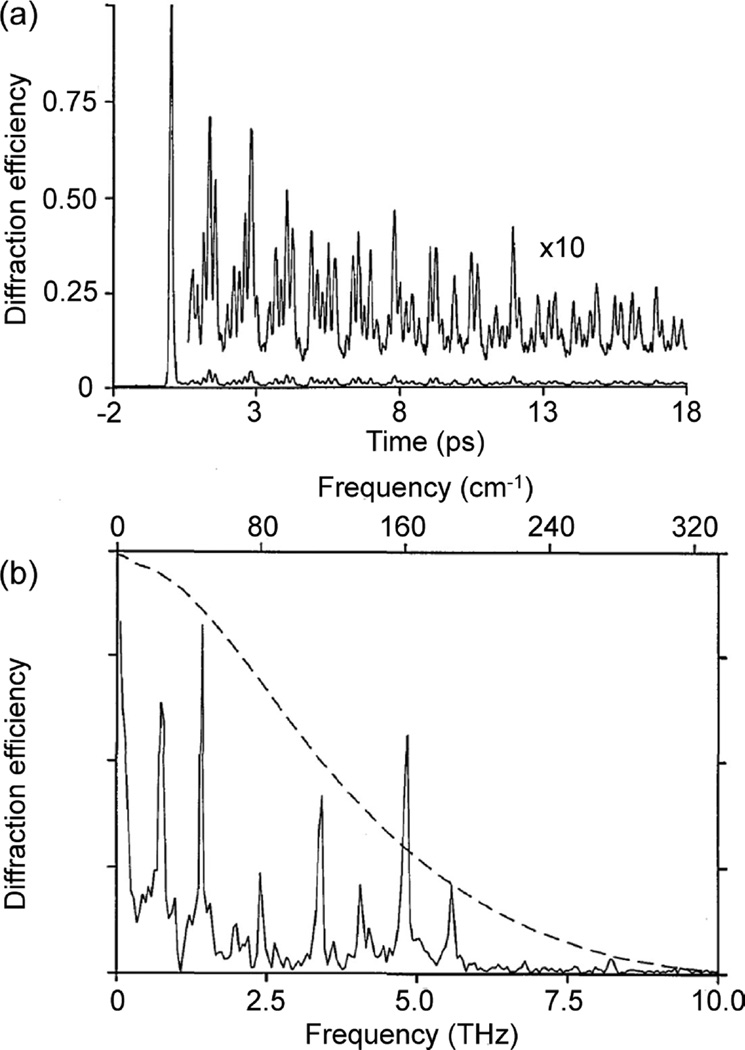
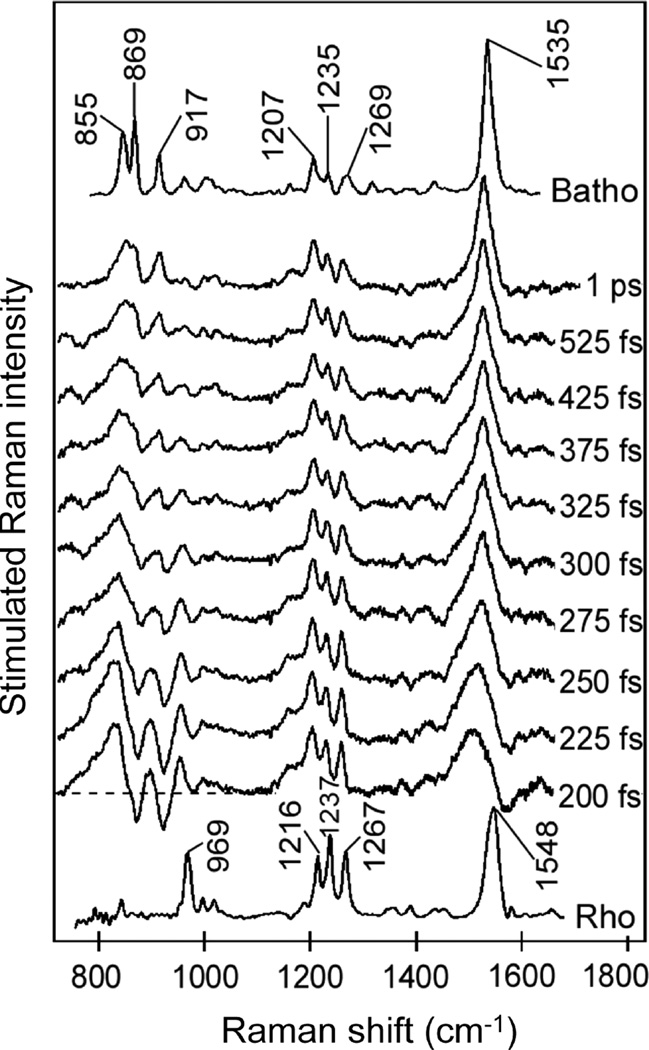
Time-domain SRS techniques were developed by Nelson et al. in the 1980s in the form of ISRS.^40–42 As was briefly mentioned in section 1.2, ISRS uses a short pulse to impulsively excite vibrational coherences in a sample, provided that the pulse bandwidth is sufficient to span one or more vibrational energy levels. This impulsive excitation can be thought of as the initiation of vibrational coherences in the ensemble at the same time and with the same phase. This in turn imprints a macroscopic polarization into the bulk sample (see also Figure 4), and subsequent probe pulses passing through the sample will be modulated by the coherent oscillation. Initial ISRS measurements were used to examine ground-state potential energy surfaces, investigating mode-specific coupling and potential energy surface structure.^39,90,91 Figure 7 shows an example of an early ISRS measurement on perylene crystals. The time-domain response shown in part a is the measured ISRS, which can be Fourier-transformed to give the frequency-domain spectrum shown in part b.⁹² ISRS measurements are particularly effective at observing low frequency modes, such as the various phonon modes observed here for perylene. The dashed line in part b represents the frequency response signal of the measurement, as determined by the finite pulse temporal width.

Figure 7.

ISRS of a perylene crystal in the time (a) and frequency (b) domains. Adapted with permission from ref 92. Copyright 1991 Optical Society of America.

When ISRS is combined with electronic enhancement, SRS signals from chromophores dissolved in solution can be attained. Time-resolved ISRS experiments provide access to ground-state and/or excited-state low frequency modes of the chromophore system. After Fourier transformation of the temporal traces, Raman spectra can be retrieved of modes that, because of their low frequencies (<200 cm⁻¹), are not always easily accessible with spontaneous Raman scattering.

More recently, researchers have taken advantage of the facile creation of stable <10 fs pulses to perform time-domain SRS across the entire vibrational spectrum. Work by Tahara, Kukura, Ruhman, and other groups have provided remarkable insight into the reaction coordinates of a number of evolving systems when the pulse bandwidth is sufficiently broad to impulsively excite vibrational motion from low frequency torsional modes up to the vibrational fingerprint region.^93–95 Techniques to manipulate populations of various excited states have been developed,^94,96 and, taking advantage of the enhancement of the SRS response due to electronic enhancement, these approaches have been used to monitor reaction dynamics in a number of biological systems, such as photoactive yellow protein,⁹⁷ rhodopsins and channelrhodopsins,^98,99 and others.^93,100

Another approach for time-resolved SRS is to detect signals in the frequency-domain. The most commonly utilized technique for such experiments is FSRS, in which the short actinic pulse is used to initiate a given photochemical process, followed by probing with broadband SRS as described above. FSRS is similar to pump–probe transient absorption measurements, but with SRS rather than electronic absorption for probing it is capable of following structural evolution on the femtosecond time scale. Recent reviews of FSRS can be found in refs 101–103. As compared to time-domain methods, a significant disadvantage of frequency-domain ultrafast Raman techniques is background subtraction, which can include transient absorption signals as well as signatures from other four-wave mixing processes.^104,105

In FSRS, as in all time-resolved SRS measurements, the fastest time resolution achievable is dictated by the molecular system. The dephasing time of the vibrational coherences sets a fundamental limit on the line width of the observed vibrational features. Thus, if the dephasing time is quite rapid, the vibrational features may be too broad to be observable. However, if the dephasing time is long, the features can be well-resolved, and transient structural evolution can be monitored. In some cases, dynamics on the sub-50 fs time scale can be extracted from FSRS measurements through analysis of the spectral lineshapes, which may be dispersive, such as the transient measurements of the primary event in vision in the rhodopsin protein shown in Figure 8,¹⁰⁶ or temporally oscillatory.¹⁰⁷

Figure 8.

FSRS spectroscopy of the ultrafast isomerization of the retinal chromophore in the rhodopsin protein. Dispersive lineshapes show the rapid structural evolution during the chemical change. Reproduced with persmission from ref 106. Copyright 2005 AAAS.

A critical advantage of time-domain ultrafast SRS methods as compared to frequency-domain methods is that there are typically fewer issues with background subtraction. In frequency-domain methods, the use of temporally overlapped pulses for SRS signal generation can also lead to signal generation through other four-wave mixing pathways.^104,105,108 However, disadvantages include the fact that impulsively excited mode frequencies are limited to the pulse bandwidth, meaning that to examine the relevant vibrational fingerprint region, laser systems with sub-10 fs pulses must be used, adding experimental complexity. Additionally, the choice of windowing in Fourier transformations for time-domain SRS methods may affect the frequency-domain line width, and depending on the material response may modify the line shape. Additional discussion on variants of ultrafast SRS methods can be found in ref 109.

Interestingly, time-domain and frequency-domain ultrafast SRS measurements on identical systems do not always provide the same information. One recent example includes studies on rhodopsin, a light-sensitive protein found in the retina responsible for vision. FSRS studies on the cis to trans isomerization of the retinal chromophore rhodopsin observed structural evolution of the hydrogen out-of-plane vibrational modes on the sub-50 fs time scale. Fitting to the observed dispersive lineshapes shown in Figure 8 determined that the frequencies of these modes rapidly increased during the photoreaction, proving the importance of these hydrogen motions in driving the isomerization.¹⁰⁶ Two-pulse ISRS measurements on the same system showed weak activity in the hydrogen out-of-plane modes, and no significant transient changes in mode frequency were observed.^98,110 These variations, while not inherently contradictory, have yet to be conclusively explained, but may result from differences in the detection and data analysis processes in the two versions of the time-resolved SRS experiment.

4. BULK ENSEMBLES TO SINGLE MOLECULES

As summarized in Figure 2, SRS techniques have become more sensitive, fostering a trend to measure SRS signals from smaller sample volumes. In this section, we will first highlight some general considerations about reducing the size of the probing volume. We will then discuss several applications of SRS applied to bulk samples, followed by an overview of applications at the microscopic scale, and an effort to retrieve SRS information from subdiffraction limited volumes. Finally, we will consider some early work in the direction of nanoscopic SRS in the form of surface-enhanced nonlinear Raman techniques.

4.1. Reducing Sample Volumes: General Considerations

In section 2, we illuminated the SRS technique from the perspective of light–matter interactions. However, another important aspect, the spatial details of signal generation, was not discussed. To include the spatial dependence of the excitation and signal emission processes, the spatial phase of the participating fields and the spatial variation in the sample polarizability have to be taken into consideration. As we will briefly discuss below, reducing the interaction volume implies that spatial amplitude and phase variations grow in importance and affect the way in which Raman information from the sample is attained.

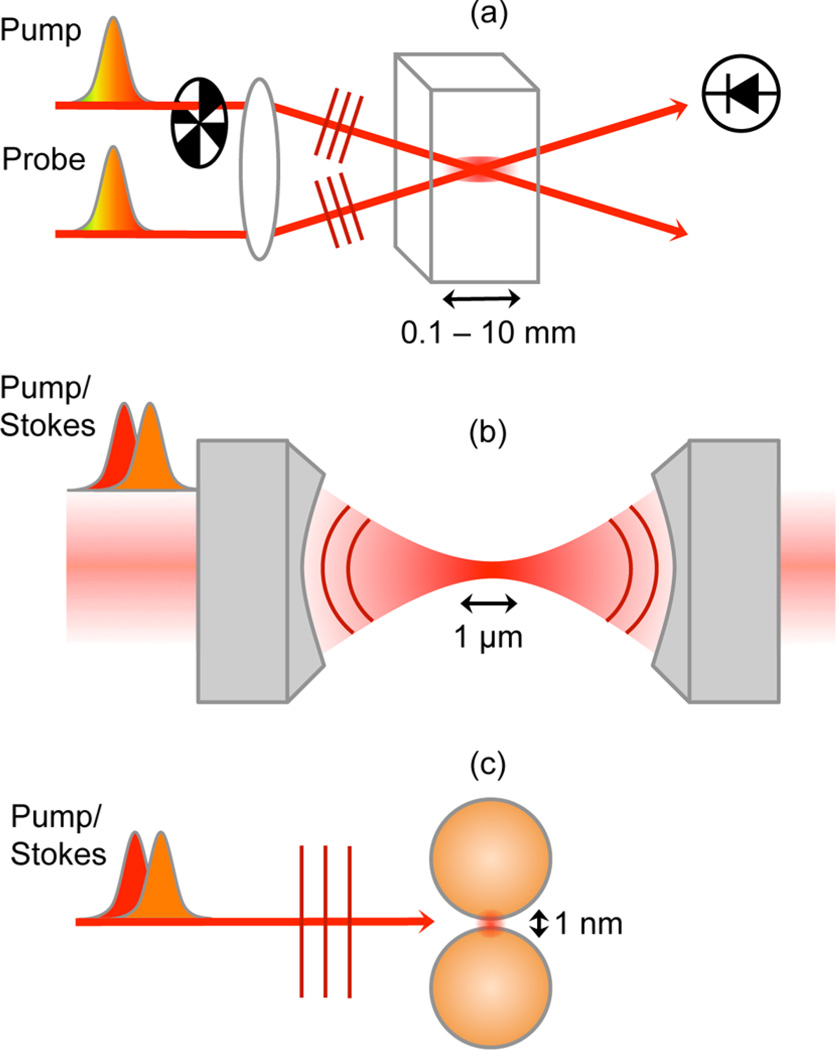
The size of the sample volume is commonly associated with a specific experimental configuration of the SRS measurement. Figure 9 shows the three representative geometries of sample illumination used in SRS spectroscopy. In Figure 9a, an experimental arrangement is shown that has been used for conducting time-resolved ISRS experiments, including optical Kerr effect measurements.^42,111 In this so-called pump–probe arrangement, the pump and probe are spatially offset and focused by a lens to a common interaction volume formed by the intersecting foci. The pump is typically modulated, and the pump-induced changes on the probe are detected by a far-field photodiode. The length of the interaction volume is in the 0.1–10 mm range. For measurements on liquid samples, a jet is commonly used, which brings the interaction length in the 0.1 mm range. In this regime, the beams can be modeled as plane waves with a uniform transverse field distribution. The generation of the nonlinear optical signal is conveniently modeled with the one-dimensional nonlinear wave equation.^68,112 Because the interaction volume is orders of magnitude larger than the optical wavelength, the spatial phase of the nonlinear polarization gives rise to a well-defined direction in which the radiated field propagates. For pump–probe-type SRS, the phase matched-direction of the radiation is typically in the direction of the probe beam, as shown in Figure 9a.

Figure 9.

Different experimental SRS configurations give access to different probing volumes. (a) Typical configuration for ISRS where the interaction volume of length 0.1–10 mm is formed by the intersecting pump and probe beams. (b) Microscope configuration where the incident beams are focused in collinear fashion with a high numerical aperture lens to a diffraction-limited interaction volume (~1 µm³). (c) Use of a nanoantenna to concentrate the incoming field to a nanoscopic volume (~1 nm³).

In this limit, spatial phase considerations are typically discussed in the context of wavevector mismatch. Note that each field component carries a spatial phase ϕ_j = k_j·r, where k_j is the wavevector associated with the wave of frequency ω_j. For an SRG experiment, the induced nonlinear polarization carries a spatial phase of (k₁ + k₂ − k₁)·r, whereas the generated radiation needs a spatial phase of k₂·r to propagate to the far-field. The phase difference ΔΦ between the induced polarization and the propagating signal wave is (k₁ + k₂ − k₁)·L − k₂·L = Δk · L, where Δk is called the wavevector mismatch and L is the interaction length. If ΔΦ is much larger than π, the polarization cannot radiate in the direction of k₂, and the signal is phase mismatched. In the case of SRS, we see that Δk = 0 and thus ΔΦ is zero in the direction of k₂. In other words, the signal is fully phase matched in the forward propagation direction of k₂ (but not in the backward direction!). In homogeneous samples and long interaction volumes, the distance L is large, and thus ΔΦ is small only when Δk is small. This is why the condition of Δk ≈ 0 is so important in nonlinear optical spectroscopy experiments. However, for smaller interaction volumes, L can become small as well, implying that ΔΦ < π can be achieved even when Δk ≠ 0. The latter notion becomes relevant in SRS from microscopic volumes.

In Figure 9b, an SRS experiment is shown where the incident beams are focused to a microscopic probing volume with the aid of a high numerical aperture lens. In this geometry, sketched here for an experiment with narrowband pump and Stokes fields, both beams are focused collinearly. This implies that the incident beams and the signal are not spatially separated. The interaction volume has a length of only ~1 µm, which is on the order of an optical wavelength. In this limit, the condition ΔΦ < π can be fulfilled even if Δk ≠ 0. For the forward propagating direction in SRS, we have Δk = 0, so the signal is phase-matched in this direction regardless. In the backward direction, Δk is much larger than zero, and on the basis of this argument, we may expect that no signal components can reach a detector set up in the epi-direction. However, if the interaction volume contains very small objects, the interaction distance L can be so small that ΔΦ < π is still fulfilled for radiation components emitted in the backward direction.^113,114 This situation is very different from the bulk measurements shown in Figure 9a, where the backward propagating signal is fully phase-mismatched. We thus see that in microscopic focusing, the quantity Δk alone is often not enough for understanding the radiation direction of the signal. Instead, because the interaction volume is short and the sample may not be homogeneous, a full account of the actual three-dimensional phase mismatch is required.

There are other important differences between the plane wave-excitation in Figure 9a and the tightly focused light in Figure 9b. Because the tightly focused fields span a wide range of angular components, the wavefront is not necessarily flat throughout the interaction volume. This means that the plane wave approximation is inadequate and the signal generation can no longer be predicted with the aid of the one-dimensional wave equation. In addition, using incident beams linearly polarized along the transverse x-axis, the microscopic focus contains non-negligible field components in the y and z polarization directions as well.¹¹⁵ Moreover, in microscopic focusing, the Gouy phase shift manifests itself over a distance similar to an optical wavelength, introducing new effects that have no analogue in macroscopic focusing.^116–118 Given the very different nature of how the signal is generated spatially, theoretical models developed for large volume SRS experiments may not be very useful for microscopic SRS. Instead, it has proven much more intuitive to model the microscopic coherent Raman signals by considering the sample as a collection of dipole emitters driven nonlinearly by the incoming fields. The radiation from the point dipoles is then collected in the far-field, and the magnitude of the signal is thus computed.^70,113 This approach for modeling coherent Raman signals in microscopy has been very successful in explaining signal magnitude and direction as a function of size, shape, position, and material properties of objects in focus.^113,118

The use of high numerical aperture lenses can reduce the sampling volume to about a fL. Although such a volume is much smaller by many orders of magnitude as compared to volumes encountered under macroscopic focusing conditions, it is still far removed from the molecular scale. For example, 1 fL of water contains no less than 10¹⁰ water molecules. To reduce the size of the probing volume even more, advanced SRS microscopy techniques can be used, as discussed in section 4.4, which can reduce the probing spot beyond the diffraction limit. For even smaller sampling volumes, freely propagating light is no longer useful, as free space waves cannot be compressed to nanoscopic volumes. However, freely propagating light can be coupled to objects that redirect the electric field distributions in an evanescent manner. Such surface bound fields are manifest only in the near-field but can be focused to nanoscopic “hotspots”. Prominent examples of such objects are plasmonic nanoantennas, which couple efficiently between highly localized near-fields and the far-field. An example is shown in Figure 9c, where two closely spaced gold nanospheres enable the refocusing of propagating plane waves to localized evanescent fields in the interparticle junction. The hotspot thus created constitutes the sampling volume, which is now of nanoscopic dimensions and thus approaches the molecular scale. The field strength in this probing volume can be substantial, due to the surface plasmonic resonance of the metal nanoantenna, with field enhancements relative to the field strength of the incident wave by several orders of magnitude. If a molecule is placed in such a probing spot, it can be optically driven in a very efficient manner in the near-field, while the antenna ensures that such information can be transmitted to the far-field. This principle is used in SERS, and some versions of the nanoantenna approach have also found their way in SRS spectroscopy studies, some of which are discussed in section 4.5. Note that the strongly localized fields may exhibit steep amplitude and phase variations on the nanometer scale, and that field gradients can be substantial. This implies that a simple dipolar model for the light–matter interactions may not be sufficient for understanding the material response in the hotspot, as higher-order multipolar contributions (magnetic dipole, electric quadrupole, etc.) become important as well.¹¹⁹ Hence, the reduction of the sample volume from freely propagating plane waves (Figure 9a) to highly confined near-fields (Figure 9c) is accompanied by a much more complex signal generation mechanism, and requires the development of more advanced models for interpreting the signal.

4.2. Solvents and Solutes

In this section, we provide a brief overview of some of the most significant areas of inquiry for ensemble-averaged SRS, as they lay an important foundation for potential applications in few or single-molecule SRS.

Stimulated Raman spectroscopy is commonly used for chemical structural identification, particularly for systems in which IR or spontaneous Raman spectroscopies are challenging. Applications for bulk measurements span a wide variety of fields, including nanomaterial structural investigation, pharmaceutical characterization, and protein structure determination. As compared to spontaneous Raman measurements, bulk SRS measurements are advantageous in that the signal is both amplified and generated coherently. This can be particularly important when investigating highly fluorescent samples.

SRS has been used in the determination of resonance Raman cross sections of highly fluorescent molecules such as Rhodamine 6G,⁷⁹ for which the spontaneous Raman spectrum is completely dominated by fluorescence. As SRS is a coherent technique, all Raman gain or loss signal is generated in a phase-matched direction. As opposed to spontaneous Raman scattering and fluorescence for which signal is generated in all directions, the coherent SRS signal can be detected using a very small solid angle for collection. The number of fluorescent photons emitted and collected in this solid angle is typically quite small, making SRS relatively free from background fluorescence due to geometric arguments.

Determination of cross sections of highly fluorescent molecules is particularly useful for SERS enhancement factor calculations. In SERS, the spontaneous Raman signal can be enhanced by up to a factor of 10¹² due to electromagnetic field enhancements from proximal plasmonic materials. A key metric in SERS is the determination of the enhancement factor (EF), which is the amount by which the plasmonic material boosts the Raman signal magnitude. Fluorescent molecules are frequently used for SERS EF calculations as they provide tremendous SERS signal when resonant frequency excitation is used, and the fluorescence is quenched when in proximity to a plasmonic surface. However, measurements of the resonance Raman cross section, needed for the EF calculation, are not possible with spontaneous Raman due to the overwhelming fluorescent background. Fortunately, SRS methods have been able to readily determine these cross sections for several of the resonant molecules used in SERS, such as that for Rhodamine 6G as shown in Figure 10.^79,120 In the case of Rhodamine 6G, the inherently strong resonance Raman signal was determined to be several orders of magnitude higher than what had been previously thought, thus providing much more accurate estimates for SERS EFs for a number of plasmonic substrates.

Figure 10.

Broadband stimulated resonance Raman spectrum of Rhodamine 6G, showing the utility of SRS techniques in obtaining Raman spectra from highly fluorescence samples. Reproduced with permission from ref 79. Copyright 2008 John Wiley & Sons.

Another particularly active area in the ensemble averaged SRS research field has been the application of time-resolved SRS techniques, such as ISRS and FSRS, to the study of low frequency coherent motions in molecular systems. SRS approaches hold a significant advantage over spontaneous Raman measurements in assessing low frequency modes, which are often buried in the Rayleigh wing. In the form of ISRS, this advantage has enabled researchers to study, for instance, low frequency coherent motions in the ground and excited states of organic chromophores,^121,122 fluorescent proteins,¹⁰⁰ and metalloprotein complexes.¹²³

If a material exhibits reactive dynamics in the excited state, then the ISRS and FSRS approaches offer a means to study ultrafast molecular motions as the system evolves along the reactive coordinate. Examples of research in which these SRS techniques are employed include studies of polymeric photovoltaic systems,^124–126 charge transfer complexes,^127–129 DNA base pairs,¹³⁰ and other photoactive proteins.^131–133

In all applications mentioned in this section, experiments were performed on bulk samples, typically consisting of solutions at high concentration with large Raman cross sections. On average, roughly 10¹⁰–10¹⁴ molecules are interrogated in each acquisition, leading to significant ensemble averaging of the molecular structure and/or dynamics. Bulk SRS measurements are usually performed with spot sizes well above the optical diffraction limit, with spatial resolution on the 10 µm length scale. However, in a number of biological and materials systems, there is significant variability in chemical content and structure at length scales below these values. Fortunately, advances in stimulated Raman spectroscopy on the micrometer and nanometer length scales have significantly improved both the spatial resolution and the limit of detection, enabling measurements on micrometer, nanometer, and even single-molecule length scales.

4.3. SRS at the Micro Scale

Focusing down from bulk ensembles, we cross into the realm of the microscopic. Here, stimulated Raman scattering plays an important role in imaging biological samples. The chemical selectivity of the technique has been used to study biological processes often tag-free and without the concern of photo-bleaching or altering biological activity. Within the biological domain, it is a multifaceted tool capable of imaging tissues, cellular ensembles, and molecular distributions within single cells. For recent reviews on SRS microscopy and its applications to biology and biomedicine, we also refer to refs 134–137.

The usefulness of SRS in the microscopic domain stems from several important properties of what is known as the tight-focusing limit.⁷⁰ This is the regime that is readily accessed through the use of high numerical aperture objectives, as shown in Figure 9b. The lateral dimension of the nonlinear interaction volume is typically about 0.3 µm and the axial extent about 1 µm. The creation of images in SRS microscopy is achieved by raster-scanning this small interaction volume across the sample. By tuning the Raman shift, ω₁ − ω₂, to match a certain molecular vibrational frequency ω_ν, chemical selectivity is achieved, and contrast is generated in the image as only those species containing the band of interest will amplify the signal.⁵² This allows for many cellular structures to be identified as anything off-resonance will not show up in the image. In addition, the SRS process only occurs in the focal volume, thus allowing for 3D sectioning.

Signal generation in the tight-focusing limit is efficient enough to enable video rate monitoring of biological samples, that is, 30 frames per second.⁸¹ This corresponds to a pixel dwell time of around 100 ns. Even at such high frame rates, the subcellular resolution in SRS microscopy is maintained.⁵² By combining multiple images, SRS can be used to produce tissue maps that can cover up to several centimeters in lateral dimensions.^138,139 Through the use of hyperspectral and/or multiplex acquisition and analysis, detailed maps of chemically distinct structures can be produced and quantitative measurements made, for example, protein to lipid ratios.^140,141 Advances in SRS detection for materials samples include SRS imaging of polystyrene beads with 0.1 ms pixel dwell times using high-speed multichannel detection.¹⁴²

Since the first demonstration of SRS microscopy, several compounds have become common mainstays for imaging.^52,143 Among those first identified for imaging contrast are the 3015 cm⁻¹ band associated with C=C–H stretching modes in unsaturated fatty acids and the CH₂ stretching mode of lipids at 2845 cm⁻¹. These bands were used to image omega-3 fatty acids in living human lung cancer cells and the myelin sheaths of mouse neurons, respectively. Additionally, myelination in tadpoles has been followed in vivo using SRS.¹⁴⁴ Because of the absence of lipids in the nuclei of cells, they are often used to provide cellular contrast. The usefulness of lipids as a contrast mechanism and the ability to show localization and dynamics of specific lipid species have been shown repeatedly.^81,145–148 In addition to lipids, it is possible to distinguish nucleic and amino acids,^140,149,150 which opens opportunities to visualize protein distributions and cell nuclei in a label-free manner. Furthermore, it has been shown that it is possible to follow the percolation of various drugs in skin that are topically applied, especially when the drug exhibits a Raman line that is distinct from the Raman response of endogenous compounds.¹⁵¹ It has also been noted that the technique is well suited to studying lignin and cellulose in plant biomass.¹⁵² An silicarich precipitate produced by plants, which may contain organic matter in small quantities (~0.1% of carbon). Hyperspectral SRS imaging in combination with vertex component analysis helped identify that the organic matter in the phytolith is mainly composed of carbohydrate materials, which are distributed throughout the entire particle.¹⁵³

Recent advances in technique and application have grown the field and use of SRS microscopy. It has been suggested and demonstrated, in principle, that SRS could be a viable tool for in situ differentiation of brain tumor tissue from healthy tissue.^154–158 In addition, the SRS imaging technique has been shown to be capable of following the uptake of kinase inhibitors into living cells.¹⁵⁹ SRS microscopy has also been used to characterize cholesterol and lipids in atherosclerotic plaques.^57,67,160 Combined with two-photon photothermal lensing microscopy, the SRS imaging platform also enables imaging vascular structure.¹⁶¹ Several groups have demonstrated the use of SRS as a tool to study disease progression in a number of different tissues including the eye, teeth, liver, and gastric tract.^{140,162–167}

The use of deuterium and other isotope labeling in SRS has enabled scientists to track lipogenesis from glucose, protein metabolism, and shows further promise as a Raman-based marker with little to no biological effect.^168–173 These markers are especially promising as the Raman band is shifted into a region that does not contain Raman lines from endogenous compounds in biological systems.^174,175 An example is given in Figure 12, where a hyperspectral SRS image is shown of cells that have been cultured with deuterated glucose (d-glucose). Under certain conditions, the cells metabolize the d-glucose and form lipids, resulting in lipid droplets rich in C–D moieties. The SRS image identifies that some droplet-like objects are rich in protein, some rich in neutral lipid, and others rich in lipids with C–D groups. The ability to identify the chemical nature of the lipid reservoirs is helpful in monitoring carbon flow in healthy and diseased cells under various conditions.

Figure 12.

Hyperspectral SRS imaging of cells cultured with d-glucose. (a) SRS spectral component map of cells after vertex component analysis. Red indicates pixels with a spectrum shown in (b), which are lipid-rich, and green indicates pixels with a spectrum shown in (c), which are protein-rich. Blue corresponds to the spectrum of water-rich areas. Purple indicates pixels with a lipid spectrum rich in C−D stretching vibrations (2100 cm⁻¹), indicated by the arrow, showing that d-glucose has been metabolized to lipids by the cells. Scale bar is 20 µm.

In addition to isotope labels, alkyne-tagged molecules have been used in live cells as Raman labels.¹⁷⁶ The latter category of labels is generally bioorthogonal and exhibits a large Raman cross-section, which facilitates their detection in SRS microscopy.^{56,168,177–179} Unlike bulky fluorescent molecules, alkyne tags rely only on the presence of the C≡C bond. The high polarizability of this bond’s stretching mode leads to a well-defined Raman peak around 2125 cm⁻¹, a region that is spectrally silent in biological systems. Additionally, Wei and colleagues reported that the peaks of alkyne tags are up to 40 times more intense than those produced by carbon-deuterium labels. By attaching single alkyne groups to biomolecules such as amino acids, choline, glucose, and nucleosides, it is possible to follow de novo synthesis of new compounds after cellular uptake.^180,181 Moreover, drugs that intrinsically contain alkynes, such as erlotinib, can be imaged to examine their localization and flow in tissue.¹⁷⁹ The alkyne tags provide one of the brightest Raman handles, but other chemical groups, such as nitriles (–C≡N),¹⁸² isonitriles (–N≡C),¹⁸³ azides (–N₃), and the carbon fluoride bond (C–F),¹⁸⁴ have found applications in Raman¹⁸⁵ and SRS imaging¹³⁵ as well. Similarly, larger Raman labels, such as specifically designed reporter molecules,^186–188 have shown their promise in spontaneous Raman microscopy and may find selected applications in future SRS imaging experiments.

4.4. SRS Imaging beyond the Diffraction Limit

The utility of SRS for biological imaging has lead researchers to pursue avenues to achieve significantly better spatial resolution. Several schemes for implementing subdiffraction SRS microscopy have been suggested and attempted.^189–191 Initial attempts to optimize the spatial resolution in nonlinear Raman microscopies proved that resolution just below the diffraction limit is achievable due to the coherent nature of the four-wave mixing process under the tight focusing regime. Previous experiments have achieved experimental resolution below 300 nm using high numerical aperture objectives. However, most implementations of SRS microscopy attain resolution values at or above the diffraction limit, and additional approaches must be utilized to achieve significantly improved resolution.

One approach to breaking the diffraction limit in nonlinear Raman microscopy involves the use of structured illumination methods. In this class of techniques, beams with well-defined patterns are overlapped, providing one or more engineered focal spots in the sample. Because of the nonlinear nature of the coherent Raman process, signal is generated from subdiffraction regions centered at the maximum amplitudes of the spatially shaped beams. Calculations of structured illumination techniques have proven that these techniques can significantly improve the spatial resolution in CARS^192,193 and have been used experimentally to achieve resolution of 130 nm.¹⁹⁴ To date, these methods have not been used with SRS microscopy, but the principles are identical. However, these approaches to focal spot engineering can provide at most a 2–3-fold increase in the resolution.

Other theoretical approaches to subdiffraction SRS microscopy involve population control through ground-state depletion¹⁹⁵ or saturation of the Raman transitions.^190,196,197 In work by Gong et al.,¹⁹⁷ the authors propose a three-pulse scheme in which an additional doughnut-shaped Stokes beam is used to saturate the SRS signal at the edges of the pump beam. This approach is similar to stimulated emission depletion microscopy (STED),¹⁹⁸ a fluorescence-based superresolution microscopy technique, which makes use of a doughnut-shaped beam to saturate an electronic stimulated emission signal. Such an approach was shown to be successful in improving the resolution in electronic pump–probe microscopy,¹⁹⁹ which is experimentally very similar to vibrational pump–probe measurements such as SRS. The work by Gong et al. proposes that by saturating the Raman transitions at the edge of the focal spot, subsequent addition of another Stokes beam will generate signal only from the subdiffraction region in the center of the pump beam. As depicted in Figure 13, their calculations demonstrated significant improvement in the lateral spatial resolution, but the authors cautioned that sample damage may be significant due to the peak powers required in their scheme.

Figure 13.

Theoretical resolution limits for the subdiffraction SRS method proposed by Gong et al. Reproduced with permission from ref 190. Copyright 2014 American Physical Society.

Recent experimental work by Silva et al. provides a route toward achieving super-resolution SRS imaging of biological samples, and has been successful in beating the diffraction limit.¹⁹¹ This work applies similar principles to the theoretical approaches described above, but uses a different combination of beams to achieve near complete saturation of the SRS transition in certain spatially defined regions. As shown in Figure 14a, subdiffraction SRS imaging is achieved through the use of three laser beams. The picosecond pump and femtosecond probe beam are identical to those used in FSRS. These beams are used to generate the vibrational coherences, which would normally lead to SRS signal generation. However, the addition of a third toroidal-shaped beam, termed the depletion beam, interacts with these vibrational coherences and drives the system into a different four-wave mixing pathway. This effectively turns off the SRS signal generation from the edges of the focal spot. Thus, any remaining SRS signal comes from the center of the doughnut hole. Just as in STED, increasing the power of the doughnut-shaped beam will increase the probability of saturating the transition, and will thus dramatically improve the spatial resolution of the experiment.

Figure 14.

Experimental demonstration of one approach to subdiffraction SRS imaging. (a) Similar to fluorescence-based super-resolution techniques, the use of the doughnut-shaped pulse to eliminate SRS signal from the edges of the focal spot, providing signal from a subdiffraction region in the center of the focus. (b) Proof of resolution improvement with this approach, showing the Raman signal intensity while scanning across the sharp interface of a diamond plate. The addition of the depletion beam significantly improves the spatial resolution. Adapted with permission from ref 191. Copyright 2016 American Chemical Society.

Figure 14b shows the improvement in spatial resolution when the approach proposed by Silva et al. is employed. Here, the authors are scanning across the sharp edge of a diamond plate, and the Raman signal intensity of the diamond is plotted as a function of the position of the beams. The addition of the depletion beam significantly improves the spatial resolution of the instrument, as defined by the steep transition in Raman signal across the interface. Saturation of the Raman transition is a plausible mechanism for depleting the SRS coherence pathway in this approach. With this approach, the authors were able to achieve subdiffraction SRS imaging. However, the high peak power laser system used for these experiments can cause significant sample damage to biological samples under these conditions, and optimization using lower peak powers is necessary to achieve super-resolution imaging of biological systems.

4.5. SRS from Nanoscopic Volumes

Plasmonic nanoantennas have proven extraordinarily successful in boosting the effective photon yield in spontaneous Raman scattering. Applications of SERS abound in the literature. The field concentration enabled by the antenna can be described by the field enhancement factor β(ω₁), which enhances the effect of the excitation pump field. In addition, the antenna also enhances the rate of emission by β²(ω₂)σ_s, where σ_s is the Raman cross section of the Stokes-shifted emission. The SERS emission rate can thus be summarized as:

$$R_{\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{S}}\propto ({\beta }^2({\omega }_1){|E({\omega }_1)|}^2)({\beta }^2({\omega }_2){\sigma }_{\mathrm{s}})$$ (18)

We may expect that the enhancement provided by plasmonic antennas can be exploited to enhance the SRS effect in a similar fashion. Because in SRS the emission field is amplified by the Stokes beam, we may write:

$$R_{\mathrm{S}\mathrm{E}-\mathrm{S}\mathrm{R}\mathrm{S}}\propto ({\beta }^2({\omega }_1){|E({\omega }_1)|}^2)({\beta }^2({\omega }_2){|E({\omega }_2)|}^2{\sigma }_{\mathrm{s}})$$ (19)

Like SERS, the SE-SRS is expected to scale approximately as β⁴. Unlike SERS, the SE-SRS signal is actively stimulated by the E(ω₂) field, thus providing an additional mechanism of boosting the signal. SE-SRS was first proposed⁵³ and experimentally implemented²⁰⁰ in 1979 by researchers at Bell Laboratories. In this work, Heritage and co-workers measured Raman gain signals of cyanide monolayers on silver substrates. In these pioneering studies, the debate over the surface enhancement mechanism and experimental difficulties precluded the use of SE-SRS as a routine technique. However, now that the theory of SERS field enhancements is well-accepted and stable ultrafast lasers are commonplace, SE-SRS has advanced significantly in recent years.

In more recent experiments, SE-SRS signals as suggested by eq 19 have been confirmed in a tip-enhanced Raman scattering (TERS) configuration to which a cw stimulating beam was added.²⁰¹ Under these conditions, a Raman gain of up to 10⁹ was observed due to the presence of the stimulated beam. These experiments suggest that SERS-type platforms can be readily used for SE-SRS experiments as well. For pulsed SRS applications, however, the heating kinetics of the antenna system are more dramatic than for cw illumination, which has complicated the design of ultrafast SRS experiments with surface enhancement. Using pulsed lasers, fields strengths on the order of 1 V/nm are easily achieved in a plasmonic hotspot, a limit in which morphological changes to the region of the hotspot may occur and plasmon-induced chemical changes to the molecule have been observed.⁶⁶ Peak intensities higher than 10¹² W/cm² at optical frequencies close to the plasmon resonance have been shown to be detrimental. In addition, such high peak intensities not only affect the antenna system, but can intrinsically lead to Raman saturation effects, in which case the stimulated emission rate no longer scales as eq 19. This discussion emphasizes that pulsed SE-SRS measurements are more complex than their linear SERS analogues.

Nonetheless, under optimized conditions, reproducible surface-enhanced SRS signals with femtosecond pulses have been obtained. The first measurements were reported in 2011,⁶⁴ and are reproduced in Figure 15. Here, the plasmonic antenna is composed of two proximal gold nanospheres, forming a nanoscopic junction that supports a high field enhancement. trans-1,2-Bis(4-pyridyl)-ethylene (BPE) molecules are adhered to the surface of the antenna, and the whole system is encapsulated in a ~90 nm thick silica shell. As in SERS, the strongest molecular signals are expected from the junction, thus generating a nanoscopic probing volume. The experiment is conducted with a narrowband (ps) pump pulse and broadband (fs) probe pulse, to probe the stimulated Raman gain on the basis of the ground-state vibrational states of the BPE molecular target. The measured FSRS spectrum is depicted in Figure 15b, which displays clear molecular signatures, confirming that the measurement registered a Raman response from the molecule. The lineshapes are, however, dispersive, reminiscent of the lineshapes observed in surface-enhanced infrared absorption spectroscopy (SEIRA).^202,203 In the simple far-field interference description of the SRS signal discussed in eqs 9 and 10, Lorentzian-like dissipative lineshapes are predicted, resulting from a relative phase shift of ±π between the induced field and the incident field at the detector. As compared to nonplasmonic SRS signals, the occurrence of dispersive lineshapes thus implies that the SRS field emitted from the metal–molecule system carries a different phase, and that the plasmonic metal plays an important role in the coherent emission process. The exact nature of the mechanism that underpins the lineshapes in SE-SRS is currently a topic of study.^{108,204–206}

Figure 15.

Surface-enhanced SRS on nanoantennas containing trans-1,2-bis(4-pyridyl)-ethylene molecular reporters. Adapted with permission from ref 64. Copyright 2011 American Chemical Society.

The introduction of metal particles inevitably introduces additional scattering contributions, which can produce interference effects at the location of the far-field detector. Because of the role of the metal in SE-SRS, the far-field detection method does not necessarily provide a direct reading of the near-field response of the molecule. In this regard, near-field detection of the molecular response can avoid artifacts introduced by the radiating antenna. One realization of this idea is shown in Figure 16, where a molecular Raman transition is probed with a sharp atomic tip.²⁰⁷ In this experiment, the tip–molecule junction is illuminated by cw pump and Stokes fields that drive the Raman-dependent nonlinear polarization in the molecule. Here, the polarization is probed directly in the nearfield by registering the electromagnetic force between the tip and the molecule. Hence, instead of detecting the field radiated by the polarization, the molecular response is probed nonoptically by monitoring the forces in the tip–sample junction mechanically. The effective volume of the optically induced force is very small, with a lateral dimension smaller than 10 nm and an axial dimension of a few nanometers, thus approaching the regime of single molecules. As shown in Figure 16, the force induced by the stimulated Raman transition is large enough to be detected, even though the interaction volume is on the nm scale. Similar observations have been reported for SRS force measurements with fs pulses.²⁰⁸ In terms of imaging, these photoinduced force measurements currently provide the highest resolution SRS maps under ambient conditions. Table 2 summarizes the various subdiffraction limited SRS imaging techniques discussed above.

Figure 16.

SRS transitions in molecules detected through changes in the local optically induced force. (a) Schematic of Raman force measurement. An atomically sharp tip is brought into the focal volume formed by the tightly focused pump and Stokes fields. The dipole–dipole interaction between tip and molecule is affected by the Raman transition, resulting in a small change in the local force. Drawing is not to scale. (b) Raman force image of nanoclusters of Coomassie Blue when the energy difference between pump and Stokes is tuned on resonance with the 1625 cm⁻¹ vibrational mode. (c) Raman force image if the energy difference is tuned off resonance. Adapted with permission from ref 207. Copyright 2011 AIP Publishing.

Table 2.

Imaging Properties of Various Subdiffraction Limited SRS Approaches

technique	resolution (nm)	notes	ref
structured illumination	>100	minor resolution   improvement
doughnut depletion   beam	<100	limited by photodamaging	191
tip-based force   detection	~10	limited to surfaces	207

The two examples discussed above, SE-SRS and force detection of SRS, demonstrate that stimulated Raman transitions in nanoscopic volumes can be induced and detected. These experimental demonstrations suggest that SRS measurements in the single-molecule limit are within reach, mimicking recent successes in CARS spectroscopy.^66,209,210 Research in this area is still in its infancy, and it is not clear how the sensitivity of SRS measurements in this limit compares with CARS experiments. In some molecular systems equipped with plasmonic antennas, strong vibrationally resonant CARS has been observed, while the electronic signal from the metal antenna was relatively low.⁶⁶ The common advantages of SRS over CARS, such as its sensitivity to the imaginary nonlinear susceptibility of the system (see section 2.5), are not necessarily evident when the molecule is adhered to strongly absorbing plasmonic nano antennas. Future research in this area will define the role that SRS can play in the investigation of single molecules.

5. CONCLUSION

In this Review, we have examined the SRS process with an emphasis on its use for molecular spectroscopic measurements. Even though the SRS mechanism was fully characterized and understood within only a few years after the birth of the laser, the application of the SRS process as a tool for conducting meaningful measurements of molecular systems took several more decades to mature. At present, it is clear that although the SRS technique probes the same molecular modes accessible with conventional spontaneous Raman scattering, there are important advantages to SRS, which open the door to additional pieces of information on vibrational modes beyond what can be assessed with linear Raman techniques. The first clear benefit of SRS is the ability to directly time-resolve the molecular motion. When such molecular motions evolve in the excited state, a clear, time-ordered picture of the ensuing dynamics emerges, information that cannot always be retrieved from spectral line shape analysis alone. A second advantage is the ability of time-domain SRS techniques to access low frequency modes that are otherwise buried in the Rayleigh wing in spectral domain measurements. Another attribute that we have discussed here is the capability of SRS to determine Raman differential cross sections of highly fluorescent molecules. A final important property of SRS is the enormous gain in the photon emission rate over spontaneous Raman scattering, which enables data acquisition rates that are up to a million-fold higher while maintaining good signal-to-noise ratios.

Technological developments in SRS, both on the excitation and on the detection side, have made it possible to leverage the advantages of the technique in examining samples with smaller volumes and fewer molecules. Whereas SRS experiments were previously limited to bulk sample measurements, interrogation of microscopic sample volumes is now well within the realm of experimental capabilities, triggered in part by the recent advances in SRS microscopy. At these reduced spatial scales, precise SRS studies of microstructured samples become possible, moving the applications of the SRS technology from the domain of homogeneous samples to the area of more complex and heterogeneous specimens. This latter capability has fueled the field of SRS microscopy, a rapidly expanding area of research with a significant impact in the biological and material sciences. The trend of reducing sample volume continues into the present with recent attempts focusing on reliable SRS measurements from nanoscopic volumes. Aided by surface-enhancement at plasmonic substrates, SRS signals have already been generated from sample volumes that approach the size of individual molecules.

The quest to push SRS measurements from bulk samples to nanosized volumes is accompanied by new scientific possibilities and challenges. Some of the challenges include the development of a clear picture of SRS signal generation with confined near-fields in the presence of nanoscopic objects such as plasmonic antennas. Given that plasmonic metals exhibit high optical nonlinearities as well as complex heat kinetics, a better understanding of the response of the antenna itself under SRS illumination conditions is required. In addition, the role of optically driven surface plasmon electrons in altering the molecular response or, even more dramatically, inducing chemical changes to the molecular target, needs to be substantiated. Nonetheless, with a better understanding of SRS generation in such nanoscale geometries, the ability to conduct reliable stimulated Raman measurements on single molecules emerges as a plausible avenue. Such a feat would bring the advantages of SRS, which were previously deployed so successfully to examine Raman coherences in bulk ensembles, to the level of individual molecules and vibrational modes. Evidently, single-molecule SRS experiments would represent the culmination of years of advances in this field, likely to open new areas of experimental and theoretical research activities in quantum chemistry and quantum optics.

Figure 11.

Hyperspectral SRS imaging of carbohydrate content in phytoliths. (a) SRS spectral component image of a single phytolith. Brighter pixels exhibit a higher weight of the spectrum displayed in (b). The inset shows an electromicrograph of the same phytolith. Scale bar is 10 µm. (b) Carbohydrate SRS component spectrum after a vertex component analysis (blue ●), superimposed onto the spontaneous Raman spectrum (black line). Adapted with permission from ref 153. Copyright 2015 Gallagher, Alfonso-Garcia, Sanchez, Potma, and Santos.

Biographies

Richard C. Prince is a graduate student in the department of Biomedical Engineering at the University of California, Irvine. Under the direction of Professor Eric O. Potma, his work focuses on the development and applications of molecular tags to stimulated Raman scattering. Richard received his B.A. in College Scholars, science policy emphasis, and academic physics from the University of Tennessee, Knoxville, in 2015.

Renee R. Frontiera is an Assistant Professor of Chemistry at the University of Minnesota, with a graduate appointment in Chemical Physics. Her research group focuses on developing and applying Raman spectroscopic techniques to probe chemical reaction dynamics on nanometer length scales and femtosecond time scales.

Eric O. Potma is a Professor in the Department of Chemistry and the Department of Electrical Engineering & Computer Science at the University of California, Irvine (UCI). He holds an adjunct position at the Beckman Laser Institute at UCI. His research group is active in developing nonlinear optical imaging techniques for the purpose of interrogating biological tissues, nanostructured materials, and single molecules.