Successive relaxation cycles during long-time cell aggregate rounding after uni-axial compression

Abstract

The mean features of cell surface rearrangement during cell aggregate rounding after uni-axial compression between parallel plates are considered. This is based on long-time rheological modeling approaches in order to shed further light on collective cell migration. Many aspects of cell migration at the supra-cellular level, such as the coordination between surrounding migrating cell groups that leads to uncorrelated motility, have remained unclear. Aggregate shape changes during rounding are considered depending on the size and homogeneity of 2-D and 3-D cell aggregates. Cell aggregate shape changes that are taking place during successive relaxation cycles have various relaxation rates per cycle. Every relaxation rate is related to the corresponding cell migrating state. If most of the cells migrate per cycle, the relaxation rate is maximal. If most of the cells are in a resting state per cycle, the relaxation rate is nearing zero. If some cell groups migrate while the others, at the same time, stay in a resting state, the relaxation rate is lower than that obtained for the migrating cells. The relaxation rates per cycles are not random, but they have a tendency to gather around two or three values indicating an organized cell migrating pattern. Such behavior suggests that uncorrelated motility during collective cell migration in one cycle induces a decrease of the relaxation rate in the next cycle caused by an accumulation of cells in the resting state. However, cells have the ability to overcome these perturbations and re-establish an ordered migrating trend in the next cycle. These perturbations of the cell migrating state are more pronounced for: (1) more mobile cells, (2) a heterogeneous cell population, and (3) a larger cell population under the same experimental conditions.

Introduction

Cell surface rearrangement under various loading conditions represents a complex multi-scale dynamical process. This rearrangement influences the viscoelasticity of the multicellular surface. The viscoelasticity can be considered within three time regimes: (1) short-time regime for a milliseconds to seconds time scale that corresponds to a sub-cellular level; (2) middle-time regime for a several tens of seconds to several minutes time scale that corresponds to the cellular level; and (3) a long-time regime for a several tens of minutes to several hours time scale that corresponds to the supra-cellular level. The resting to migrating cell state transition within a crowded cell ensemble is a complex multi-scale process that includes contributions of adhesion complexes, the membrane, microtubules and the cell organizing centrosome [1]. Mechanical relaxation of cell adhesion complexes [2] and the membrane structural changes under its fluctuations [3–5] have been considered during the short-time regime. The milliseconds scale corresponds to protein inter-chain interactions, while the seconds scale corresponds to protein intra-chain interactions during: (1) an adhesion complex formation, (2) cortex-bilayer coupling [5] and (3) binding relaxation of the bilayer [6]. Bruinsma [2] reported that the mechanical relaxation time of adhesion complexes is in the range of 1–10 s. A scale of several tens of seconds corresponds to cell shape relaxation [6]. A scale of minutes corresponds to single cell migration time [7], cell polarization [8], cell signaling [9] as well as the cadherin turnover time [10]. This scale accounts for the cumulative effects of cell structural changes at the sub-cellular level. Cell signaling has an important role in ensuring an ordered trend in cell transport through narrow channels between surrounding cells and prevents uncorrelated motility [9]. The hours scale corresponds to collective cell migration considered at the supra-cellular level. This scale accounts for cumulative effects of cell adhesion, polarization and signaling through changes of the dynamic surface tension.

The main features of collective cell migration related to energy transfer and dissipation during cell rearrangement under various loading conditions are important for the optimization of various biological processes. Brown et al. [11] considered dermal fibroblast rearrangement and reported that increased external loading was followed immediately by a reduction in cell mediated contraction as well as cell migration. Sackmann [1] described this coarse consequence relation at a molecular level. Tse et al. [12] reported that compressive stress stimulates collective migration of mammary carcinoma cells. The mechanical and biochemical responses of multicellular systems depend on cell type and loading conditions [9]. Although the biological processes such as embryogenesis, tumorigenesis and wound healing are more complex than the process of cell aggregate rounding after uni-axial compression considered here, some mechanical aspects of cell surface rearrangement under various in vitro or in vivo conditions could be compared in the context of rheological constitutive equations. Lee and Wolgemuth [10] and Notbohm et al. [13] proposed the Maxwell model for describing long-time surface rearrangement during wound closing. Marmottant et al. [14] formulated an Eyring type rheological model while Beysins et al. [15] formulated a modified Burgers model for describing stress relaxation during cell aggregate compression within the middle viscoelasticity regime (for a several tens of seconds to several minutes time scale). The aim of this work is to formulate a constitutive model for describing long-time surface rearrangement during aggregate rounding after uni-axial compression. Rheological models relate energy transfer and energy dissipation during cell surface rearrangement by accounting for cumulative effects of cell adhesion and polarization. Depending on the ratio of energy dissipation to energy storage, the multicellular surface is treated either as a viscoelastic liquid or viscoelastic solid by accounting for the jamming transition. Pegoraro et al. [13] considered cell-cell adhesion and cell-cell jamming in collective cellular migration. They reported cell system jamming when adhesive energy was smaller than the contractile energy. The viscoelastic liquid did not exhibit strain relaxation under constant stress conditions due to intensive energy dissipation, while the viscoelastic solid exhibited strain relaxation under the same conditions. We consider the long-time dynamics of aggregate surface strain relaxation (rounding) after compression. Strain relaxation is estimated by measuring the aggregate aspect ratio. Marmottant et al. [14], Mombach et al. [16] and Schotz et al. [17] investigated the exponential decrease of the aggregate aspect ratio with intensive fluctuations during aggregate rounding. These fluctuations are caused by perturbations of the velocity fronts. This exponential trend of long-time surface relaxation indicates that the Kelvin-Voigt model equation is suitable. Perturbation of velocity fronts leads to uncorrelated motility [18]. The uncorrelated motility induces inhomogeneity in propagated velocity fronts within multi cellular systems [19]. The fronts collide [20] and their collision leads to the formation of stagnant zones that are unstable. They exist for certain periods of time at some locations and then disappear. Cells within stagnant zones cannot migrate. Notbahm et al. [13] considered the velocity pattern during collective cell migration within the cell mono layer for Madin-Darby canine kidney cells. They reported on oscillating waves of cellular motion. The average cell velocity vector simultaneously changes direction at the same location. Cell migration in one direction corresponds to 3–5 h. Then, the velocity drops to zero for 0.5-1 h. After that, cells migrate in the opposite direction for 3–5 h. During cell migration in the same direction, two velocity domains labeled lighter and darker are observed based on a kymograph of velocity. A rough analysis of the velocity pattern points to three states of cell parts: (1) a state with maximal average velocity v ₁ (labeled darker), (2) a state with velocity v ₂ such that v ₂ ≺ v ₁ (labeled lighter) and (3) a state with velocity v ₃ ≈ 0 (labeled black). These cell states represent the consequence of uncorrelated motility that leads to energy perturbations.

It would be interesting to consider the aggregates ability to overcome this local inhomogeneity in propagated cell velocity fronts. Consequently, there are several possible scenarios for the long-time aggregate shape relaxation after compression: (1) most of the cells migrate all the time, (2) some cell groups migrate while the others (at the same time) stay in a resting state, and (3) cells have successive migrating and resting periods in which most of the cells firstly migrate and then stay in a resting state. The second and third scenarios represent the consequence of inhomogeneity in propagated cell velocity fronts that lead to an accumulation of cells in the resting state. The third scenario also indicates the cells ability to overcome the perturbations of the migrating pattern and to re-establish the migrating state from cycle to cycle. A deeper insight into the long-time rheological response of the cell aggregate may be useful for understanding energetically perturbed cell states.

The distribution of migrating cells under various loading conditions influences the cell aggregate viscoelasticity. Migrating cells are stiffer than resting ones. Lange and Fabry [21] reported that muscle cells can change their elastic modulus by over two orders in magnitude from 10 kPa in a relaxed (resting) state to around 200 kPa in a fully activated (migrating) state. This stiffness increase represents the consequence of stress-fibers polarization and alignment [8, 22]. Adhesion-induced stress influences the dynamics of stress fibers orientation and, consequently, cell contraction. Dynamics of cell contraction as well as single cell migration correspond to the minutes time scale. We are interested in the cumulative effects of these processes that influence collective cell migration considered on a several hours time scale. Consequently, the ordered trend of collective cell migration at the supra-cellular level is estimated rheologically under a simplified condition in vitro such as cell aggregate rounding after uni-axial compression between parallel plates.

Marmottant et al. [14] considered cell aggregate uni-axial compression within a middle viscosity regime and a long-time regime. They measured: (1) stress relaxation under constant strain conditions on a several tens of seconds time scale (middle regime) and (2) aggregate shape relaxation (rounding) after compression on an hours time scale (long-time regime). They treated cell rearrangement within the middle-time regime as a T1 process by formulating the mechanical energy barrier. The mechanical energy barrier is caused by cell migration through narrow channels between surrounding cells. Marmottant et al. [14] proposed the Eyring model for describing stress relaxation. The Eyring model has been applied to describe the rheological response of various viscoelastic systems by accounting for the activation energy necessary for their structural changes [23]. We formulated the Eyring model for describing the long-time relaxation of the multicellular surface.

Here, we are considering the main features of long-time cell surface rearrangement from experimental data sets from Mombach et al. [16] and Schotz et al. [17]. These fluctuations clearly point to an ordered relaxation trend in the form of successive relaxation cycles. The constitutive model equation for the corresponding aggregate rheological response is formulated.

Cell aggregate relaxation after compression – constitutive modeling

Surface effects of long-time cell rearrangement are considered theoretically during relaxation after uni-axial compression for various 2-D and 3-D cell aggregates made by different cell types and aggregate sizes at the hour time scale. During relaxation, the aggregate is treated thermodynamically as a closed system under an isothermal condition and statistically as a canonical ensemble. This cell rearrangement during aggregate rounding is driven by dynamic surface tension. Dynamic surface tension takes into account cumulative effects of cell adhesion, polarization and signaling. Cell surface rearrangement driven by dynamic surface tension leads to an increase of the cell aggregate surface elasticity. The aggregate rounding is quantified by an aspect ratio. Marmottant et al. [14], Mombach et al. [16] and Schotz et al. [17] analyzed exponential changes of the aggregate aspect ratio with intensive fluctuations. Consequently, we consider the long-time surface dilatational effects of the aggregate under uni-axial compression based on the Kelvin-Voigt model equation. Dilatation effects are modeled by correlating the dynamic surface tension difference Δγ(t) = γ(t) − γ ₀ (where γ(t) is the dynamic surface tension and γ ₀ = γ(t _eq) is the equilibrium value of the surface tension) with the dilatational surface strain ε _d(t) = ΔA(t)/A(0) (where ΔA(t) is the aggregate surface perturbation and A(0) is the initial aggregate surface) [24]. We modified this model by correlating the dynamic surface tension with the aggregate aspect ratio expressed as the so-called ‘deformation parameter’ instead of the dilatational surface strain. Mombach et al. [16] expressed the aggregate shape changes as a function of the aspect ratio in the form of the deformation parameter as:

$$\epsilon \left(t\right)=AR\left(t\right)-1$$ 1

where AR(t) is the aggregate aspect ratio equal to $AR\left(t\right)=\frac{d_1\left(t\right)}{d_2\left(t\right)},d_1\left(t\right)$, is the higher aggregate diameter and d ₂(t) is the lower aggregate diameter. Dynamic surface tension includes the contribution of an active (migrating) cell subpopulation and a passive (resting) cell subpopulation near the aggregate surface. Consequently, the dynamic surface tension difference is expressed as:

$$\Delta \gamma \left(t\right)=\Delta {\gamma }_r\left(t\right)+\Delta {\gamma }_m\left(t\right)$$ 2

where Δγ _m(t) is the dynamic surface tension contribution of migrating cells and Δγ _r(t) is the dynamic surface tension contribution of resting cells. The contribution of resting cells is primarily reversible (elastic) and equal to Δγ _r(t) = E _sapp ε(t) (where E _sapp is the apparent surface elasticity modulus), while the contribution of migrating cells is primarily irreversible (viscous) and equal to $\Delta {\gamma }_m\left(t\right)={\eta }_{\mathit{sapp}}\frac{d\epsilon \left(t\right)}{dt}$ (where η _sapp is the apparent surface viscosity). This irreversible part of the dynamic surface tension accounts for energetic perturbations of crowded cell assemblies. The formulated constitutive model equation is:

$$\Delta \gamma \left(t\right)=E_{\mathit{sapp}}\epsilon \left(t\right)+{\eta }_{\mathit{sapp}}\frac{d\epsilon \left(t\right)}{dt}.$$ 3

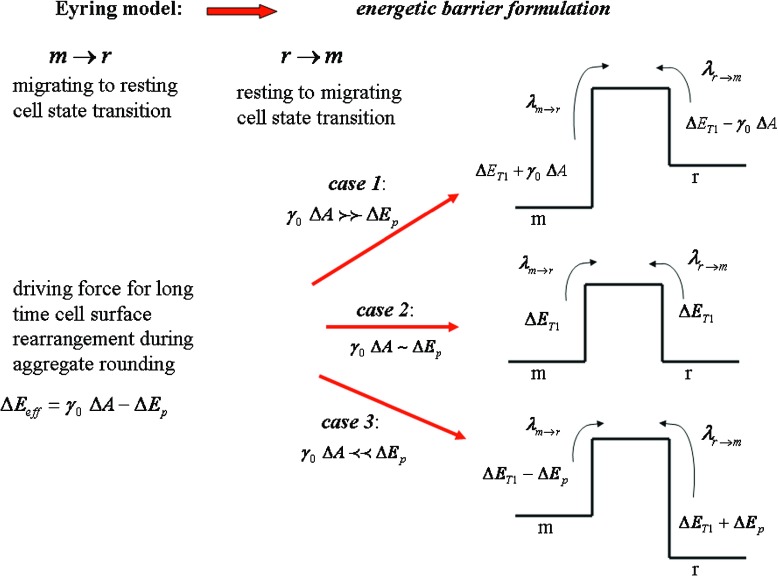
Cell rearrangement was treated as a T1 process by introducing the energy barrier ΔE _T1 in the form of the Eyring model proposed by Marmottant et al. [14]. The energy barrier influences the cell state transition from resting to migrating r → m and vice versa m → r. For describing the surface effects of the cell aggregate rearrangement, we propose the Eyring model in the form:

$$\frac{d\Delta {\gamma }_r\left(t\right)}{dt}=-{\lambda }_{r\to m}\Delta {\gamma }_r\left(t\right)+{\lambda }_{m\to r}\Delta {\gamma }_m\left(t\right)$$ 4

where ${\lambda }_{r\to m}=\lambda e^{-\frac{\Delta E_{T1}-\Delta E_{\mathit{eff}}}{kT}}$ is the probability of the resting to migrating cell state transition, λ is the characteristic frequency, k is the Boltzmann constant, T is the temperature, ΔE _T1 is the energetic barrier for cell rearrangement, ΔE _eff is the effective driving energy and ${\lambda }_{m\to r}=\lambda e^{-\frac{\Delta E_{T1}+\Delta E_{\mathit{eff}}}{kT}}$ is the probability of the migrating to resting cell state transition. The ratio $\frac{{\lambda }_{r\to m}}{{\lambda }_{m\to r}}$ is equal to $\frac{{\lambda }_{r\to m}}{{\lambda }_{m\to r}}=e^{\frac{2\Delta E_{\mathit{eff}}}{kT}}$. The resting to migrating cell state transition within the aggregate surface is driven by the surface tension. However, energy perturbations ΔE _p caused by uncorrelated cell motility act locally during an unpredictable period of time. Perturbations slow down or even reduce the resting to migrating cell state transition. Consequently, the effective driving energy is equal to ΔE _eff = γ ₀ ΔA − ΔE _p (where ΔA is the aggregate surface change during cell rearrangement). Three causes are established depending on the energy perturbation intensity ΔE _p: (1) γ ₀ ΔA ≻ ≻ ΔE _p that corresponds to ${\lambda }_{r\to m}={\lambda }_{m\to r}{e}^{\frac{2{\gamma }_0\Delta A}{kT}}$; (2) γ ₀ ΔA ∼ ΔE _p that corresponds to λ _r → m ∼ λ _m → r; and (3) γ ₀ ΔA ≺ ≺ ΔE _p that corresponds to λ _r → m ≺ ≺ λ _m → r. Changes of the deformation parameter with time are expressed by introducing Eq. 3 into Eq. 4:

$$\frac{d\epsilon \left(t\right)}{dt}+k\epsilon \left(t\right)=0$$ 5

where $k=\frac{{\lambda }_{r\to m}{E}_{\mathit{sapp}}}{E_{\mathit{sapp}}-{\lambda }_{m\to r}{\eta }_{\mathit{sapp}}}$ is the aggregate shape relaxation rate.

The relaxation rate is equal to:

1. $k_m=\frac{{\lambda }_{m\to r}{e}^{\frac{2{\gamma }_0\Delta A}{kT}}{E}_{\mathit{sapp}}}{E_{\mathit{sapp}}-{\lambda }_{m\to r}{\eta }_{\mathit{sapp}}}$ for case 1,

2. $k_t=k_m{e}^{-\frac{2{\gamma }_0\Delta A}{kT}}$ for case 2

   and

3. k _r → 0 for case 3 as schematically presented in Fig. 1.

Fig. 1.

Schematic representation of the cell migrating state changes during long-time shape relaxation of the aggregate after uni-axial compression

Experimental data for the aggregate shape relaxation after uni-axial compression, considered here, show the important feature obtained from the data fluctuations. These fluctuations clearly point to an ordered relaxation trend in the form of successive relaxation cycles. Accordingly, the aggregate shape relaxation after compression for the j ^th cycle is expressed as:

$$\epsilon {\left(t\right)}^j={{\epsilon }^j}_0{e}^{-k^{j}t}$$ 6

where ε(t)^j is the deformation parameter during the j^th relaxation cycle for t ∈ [0, Δt ^j], ε ^j ₀ is the initial value for the deformation parameter and k ^j is the relaxation rate for the j ^th cycle. The relaxation rate per cycle is related to the migration state of cells within the aggregate surface region. The single experimental data suggest the presence of 7–15 successive relaxation cycles with constant values of the relaxation rate per cycle.

Consequently, the relaxation rate for passive (resting) cells is approximately equal to k _r ≈ 0. The cell state described by k _t (such that k _m ≻ k _t ≻ k _r) corresponds to ‘the mixing state’. The mixing state is understood as some cell groups migrate while the others (at the same time) stay in the resting state. These perturbations of the ordered migrating trend lead to an accumulation of cells in the resting state. When approximately half of the cell population migrates and the other half stays in a resting state, then k _t ≈ k _m/2.

The average relaxation rate from Eq. 1 is expressed as:

$$〈k〉={\displaystyle \sum _i{y}_i{k}_i}$$ 7

where i = m, r, t is the corresponding state of cell population, k _i quantifies the i ^th state and $y_i=\frac{{\displaystyle \sum _{j=1}^{N_i}\Delta t_{ij}}}{t_T}$ is the time fraction for the i ^th state, t _T is the total experimental time of observation and N _i is the number of the relaxation cycles for the i ^th state. Three cell states are included within the modeling considerations: (1) cell migrating state quantified by the relaxation rate k _m, (2) cell resting state quantified by the relaxation rate k _r ≈ 0 and (3) cell mixing state (when some cell groups migrate while the others, at the same time, stay in a resting state) quantified by the relaxation rate k _t. The total number of relaxation cycles varies from seven to 15 depending on the single cycle duration.

The relaxation rates per single cycle k ^j are calculated with the following steps: (1) experimental curves are presented in the form of log ε(t) vs. t; (2) the curves are divided into successive parts with constant slopes; (3) the curve parts consist in two to five data points; (4) experimental data for the corresponding curve parts in the form of ε ^j(t) vs. t are compared with the model prediction calculated using Eq. 6; (5) the model values are fitted with the experimental data by minimizing the squared magnitude of the residuals of the deformation parameter ε(t); (6) the optimal values of the slopes per cycle obtained by this fitting procedure enable the best comparison with the experimental data; and (7) corresponding values of the relaxation rate are obtained from the slopes as: k ^j = slope ^j/log(e).

Results and discussion

Cell aggregate long-time shape changes during relaxation after uni-axial compression were considered for various aggregate sizes, cell types and population homogeneity. Experimental data in the form log ε(t) vs. t suggest an ordered relaxation trend in the form of successive relaxation cycles. The relaxation rates per cycle were calculated based on the above described procedure. We presented the relaxation rate vs. cycle together with corresponding log ε(t) vs. t plot for the experimental data from Mombach et al. [16] and Schotz et al. [17]. The log ε(t) vs. t plot with variously colored slopes for corresponding cell migrating states provide a deeper insight into the cell state distribution along experimental curves and cycles duration and the time fraction of the i ^th migrating state. The relaxation rates k ^j = slope ^j/log(e) per cycles are not random, but they have a tendency to gather around two or three values, i.e., k ^j ∈ [k _m, k _r, k _t] indicating an organized cell migrating pattern. Statistical analysis of the experimental slopes indicates that: (1) the value of k _m = slope _m/log(e) is maximal, (2) the value of k _r ≈ 0 (where k _r = slope _r/log(e)) and (3) $\frac{k_m}{k_t}=2-5$ (where k _t = slope _t/log(e)). The standard deviations for the slopes are up to ∼15%.

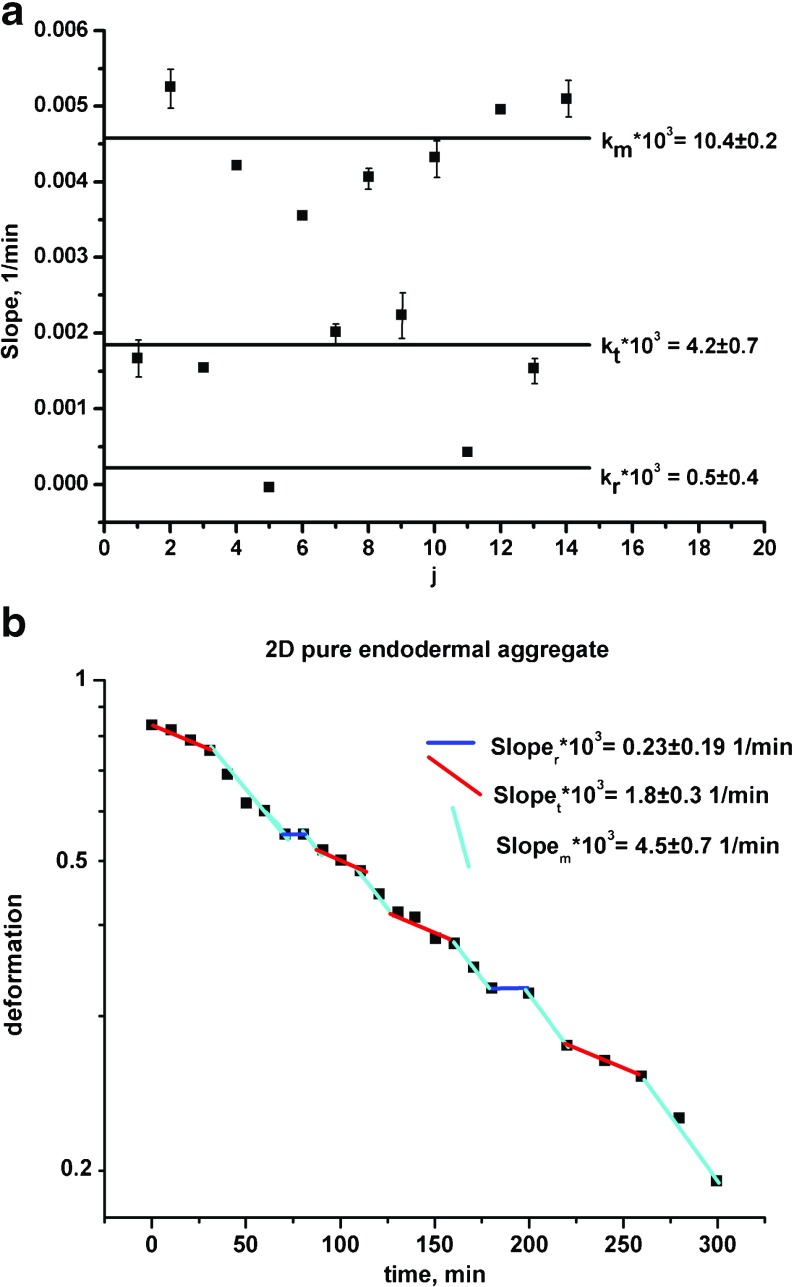
The results suggest that uncorrelated motility leads to an accumulation of cells in a resting state. Consequently, the maximal relaxation rate k _m obtained in one relaxation cycle usually drops to k _t or sometimes to k _r ≈ 0 in the next cycle (where the migrating states are formulated as: (1) ‘m’ – most of the cells migrate, (2) ‘r’ – most of the cells stay in the resting state and (3) ‘t’ – some cell groups migrate while others, at the same time, stay in a resting state). Stagnant zones made by resting cell groups are unstable and disappear after some time. Cell aggregates can re-establish the migrating state again in the next cycle. The uncorrelated motility during collective cell migration under the same experimental conditions depends on cell type, population size and its homogeneity. Mombach et al. [16] considered the influence of various cell types on the aggregate rounding. They examined 2-D hydra aggregates: (1) pure endodermal aggregate, (2) inhomogeneous ectodermal/endodermal aggregate and (3) pure ectodermal aggregate after compression. Experimental data and model prediction for the pure endodermal aggregate are shown in Fig. 2 a,b. Figure 2a represents the relaxation rate vs. cycle while Fig. 2b represents corresponding log ε(t) vs. t plot. The rest of the experimental data for 2-D aggregates showed a similar trend. Optimal values of the model parameters per experimental system are shown in Table 1. The average relaxation rate for cell migrating state k _m is 2.4 times higher for ectodermal cells compared to endodermal cells. Rieu et al. [7] reported that ectodermal cells are more mobile than endodermal cells. The diffusion coefficient for collective migration is $D_c=0.45\pm 0.2\frac{\mu m^2}{min}$ for endodermal cells and $D_c=1.05\pm 0.4\frac{\mu m^2}{min}$ for ectodermal cells. These results are very close to ours since $\frac{D_{\mathit{cectodermal}}}{D_{\mathit{cendodermal}}}\sim \frac{k_{\mathit{mectodermal}}}{k_{\mathit{mendodermal}}}$. Uncorrelated motility is prominent for more mobile cells. For endodermal cells the uncorrelated motility induces a drop in the relaxation rate k _m → k _t more frequently than k _m → k _r. However, for more mobile ectodermal cells the relaxation rate k _m drops to k _r more frequently than to k _t. The time fraction that corresponds to the resting state for ectodermal cells is y _r = 0.53, while for endodermal cells, it is only y _r = 0.10. Less migrating, endodermal cells spent a lot of time in the migrating state, which is quantified by the maximal value of the time fraction y _m = 0.50. In the case of the ectodermal/endodermal cell aggregate, the ectodermal cells become more mobile than in the pure ectodermal aggregate. The average relaxation rate k _m is 1.54 times higher for the ectodermal/endodermal cell aggregate compared to the ectodermal aggregate. It represents the consequence of cell sorting tendency in an inhomogeneous cell population.

Fig. 2.

a The relaxation rate vs. cycle; b log ε(t) vs. t plot for the 2D pure endodermal aggregate from Mombach et al. [16]

Table 1.

The model parameters

model par.	2-D endod. aggregate Mombash et al. [16]	2-D ectod./ endod. aggregate Mombash et al. [16]	2-D ectod. aggregate Mombash et al. [16]	3-D chicken aggregate R = 143μm Mombash et al. [16]	3-D chicken aggregate R = 87μm Mombash et al. [16]	3-Dchicken aggregate R = 65μm Mombash et al. [16]	3-D zebrafish ectod. aggregate Schotz et al. [17]
k r x103	0.5 ± 0.4(min− 1)	0.14 ± 0.2(min− 1)	0.12 ± 0.02(min− 1)	0.5 ± 0.8(h − 1)	6.1 ± 0.2(h − 1)	7.1 ± 2.1(h − 1)	1.5 ± 0.2(min− 1)
k t x103	4.2 ± 0.7(min− 1)	8.4 ± 0.1(min− 1)	12.1 ± 0.5(min− 1)	40.3 ± 4.7(h − 1)	45.5 ± 5.7(h − 1)	85.8 ± 9.9(h − 1)	7.1 ± 0.9(min− 1)
k m x103	10.4 ± 0.2(min− 1)	40.4 ± 8.5(min− 1)	25.0 ± 2.5(min− 1)	–	104.4 ± 14.1(h − 1)	157.3 ± 14.1(h − 1)	13.8 ± 2.4(min− 1)
y r(−)	0.10	0.38	0.53	0.59	0.35	0.52	0.33
y t(−)	0.40	0.41	0.29	0.41	0.33	0.17	0.44
y m(−)	0.50	0.21	0.18	–	0.32	0.31	0.23
〈Δt r〉	15 ± 5(min)	22 ± 13(min)	21 ± 15(min)	1.35 ± 0.23(h)	1.63 ± 0.57(h)	1.71 ± 1.13(h)	22.5 ± 4.3(min)
〈Δt t〉	30 ± 7(min)	10 ± 0(min)	22.5 ± 0.5(min)	0.95 ± 0.21(h)	1.2 ± 0.96(h)	1.33 ± 0.92(h)	60 ± 50(min)
〈Δt m〉	25 ± 11(min)	120 ± 0(min)	14.5 ± 0.5(min)	–	3.0 ± 2.0(h)	1.4 ± 0.51(h)	15 ± 8.7(min)

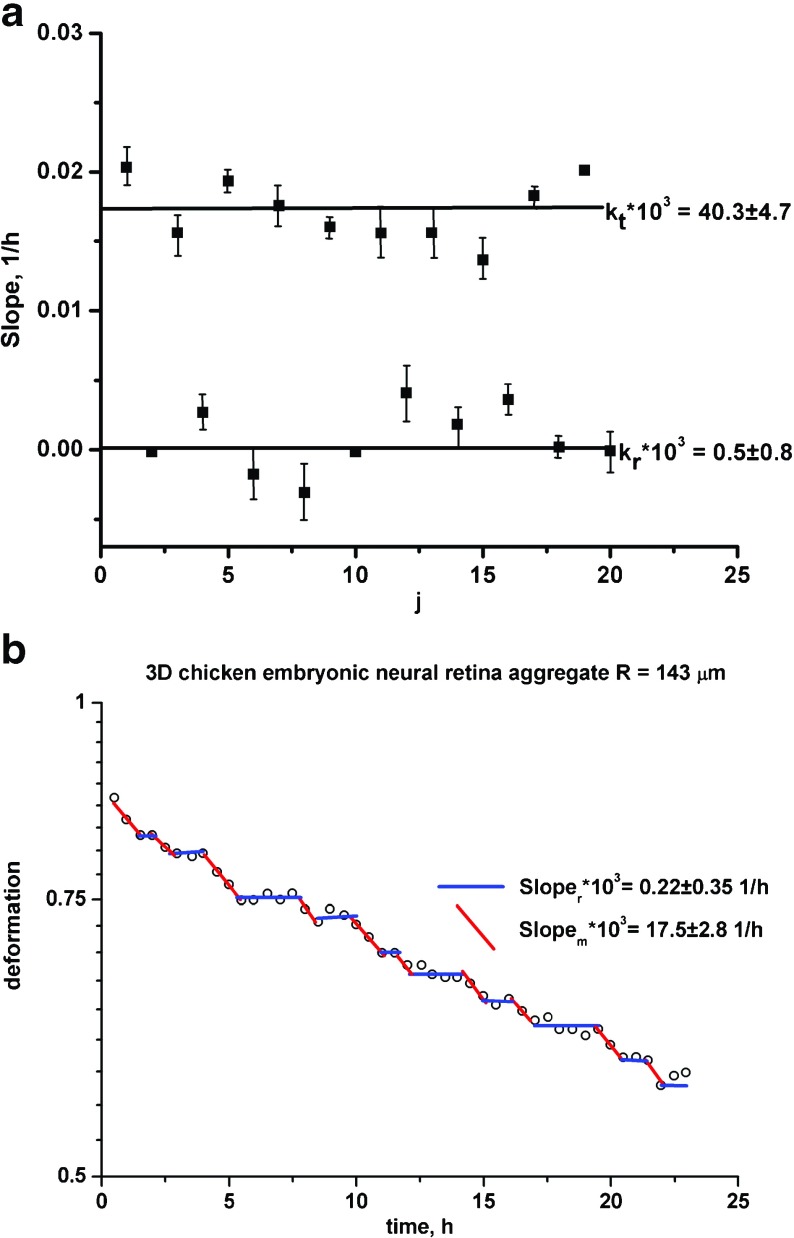
Mombach et al. [16] considered the influence of aggregate size on its rounding. They examined 3-D chicken embryonic neural retina aggregates with various radii: (1) R = 143μm, (2) R = 87μm and (3) R = 65μm. Experimental data and model prediction for aggregates with radius R = 143μm are shown in Fig. 3 a,b. Figure 3a represents the relaxation rate vs. cycle while Fig. 3b represents the corresponding log ε(t) vs. t plot. The rest of the experimental data for 3-D aggregates showed a similar trend. Optimal values of the model parameters per experimental system are shown in Table 1. Experimental sets are described by three slopes except for the largest aggregate. In that case, the experimental curve in the form log ε(t) vs. t is described by two slopes. The smallest cell aggregate shows the highest value of the relaxation rate for the cell migrating state k _m. Cell aggregate size increase induces intensive perturbations of cell velocity fronts during collective cell migration, which result in an accumulation of cells in the resting state. These perturbations of the migrating pattern lead to a decrease of the relaxation rate k _m. For the largest aggregate, we obtained k _m ≈ k _t (where k _t is the relaxation rate for the cell mixing state). Cells are able to overcome uncorrelated motility by two mechanisms: resting-to-migrating cell state transition and mixing-to-migrating cell state transition.

Fig. 3.

a The relaxation rate vs. cycle; b log ε(t) vs. t plot for the 3-D chicken embryonic neural retina aggregate with radius R = 143 μm from Mombach et al. [16]

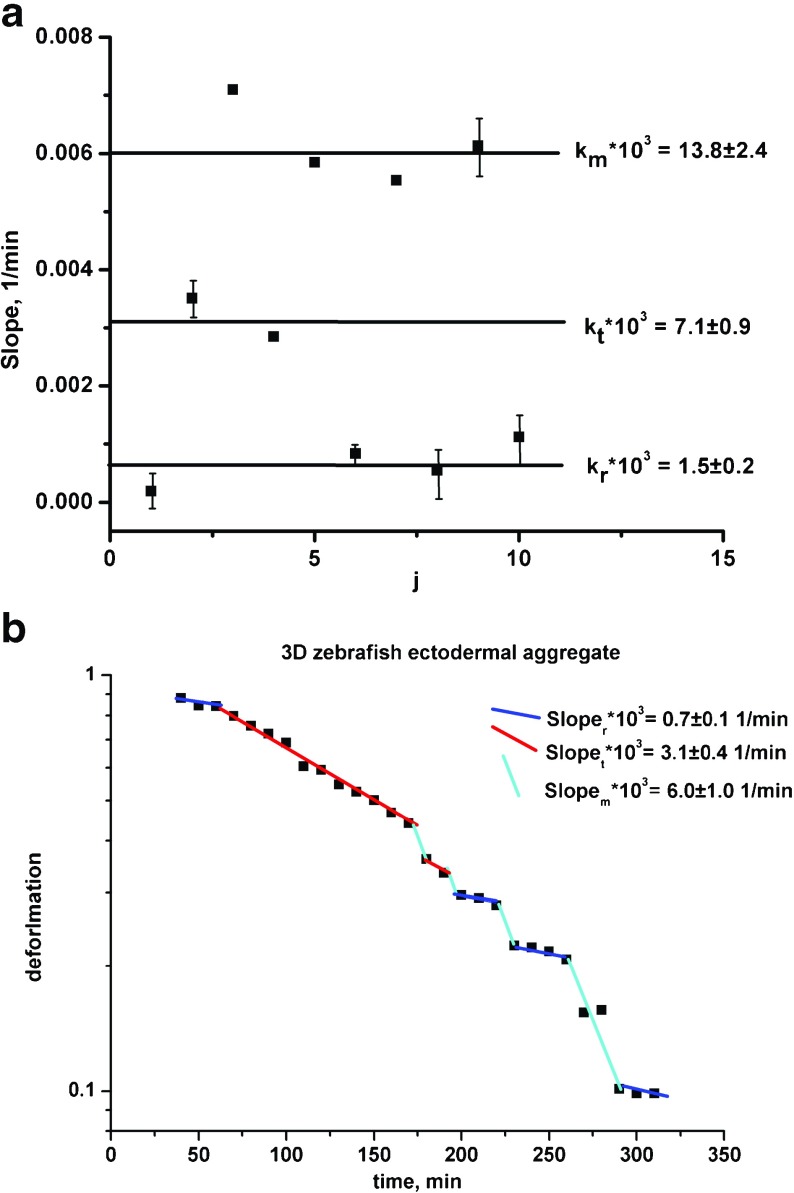
Schotz et al. [17] considered rounding of the zebrafish ectodermal aggregate. Experimental data and model predictions for the relaxation rate vs. cycle together with corresponding log ε(t) vs. t plot are shown in Fig. 4a,b. Optimal values of the model parameters for the determined population states per experimental data set are shown in Table 1. The results indicate that uncorrelated motility induces the relaxation rate change: k _m → k _t more frequently than k _m → k _r. Consequently, the cell mixing state ‘t’ is more prominent compared to the other states.

Fig. 4.

a The relaxation rate vs. cycle; b log ε(t) vs. t plot for the 3-D zebrafish ectodermal aggregate from Schotz et al. [17]

Conclusions

The influence of uncorrelated motility on long-time cell surface rearrangement was estimated from simple rheological experiments of cell aggregate rounding after uni-axial compression for various cell types, population homogeneity and aggregate sizes. This local inhomogeneity of a cell velocity front induces perturbations of cell states that lead to an accumulation of cells in a resting state. The aggregate surface relaxation (its rounding) clearly indicates the presence of successive relaxation cycles described by constant relaxation rates per cycle. The relaxation rates depend on: surface elasticity modulus, surface viscosity, probability of resting to migrating cell state transition and probability of migrating to resting cell state transition. The resting to migrating cell state transition is driven by surface tension. However, energetic perturbations generated during collective cell migration reduce this cell state transition. The relaxation rates are not random but grouped around two or three values indicating an organized cell migrating pattern: (1) k _m – most of the cells migrate, (2) k _r ≈ 0 – most of the cells stay in the resting state and (3) k _t – some cell groups migrate while the others, at the same time, stay in a resting state. Duration of the time periods for the corresponding cycle as well as the number of cycles varied depending on the aggregate characteristics.

The results indicate that uncorrelated motility during collective cell migration in one cycle induces cell state transition (migrating-to-mixing state transition k _m → k _t or migrating-to-resting state transition k _m → k _r) in the next cycle caused by an accumulation of cells in the resting state. However, cells have the ability to overcome these perturbations and re-establish an ordered migrating trend in the next cycle. These perturbations of the cell migrating state are prominent for: (1) more mobile cells, (2) a heterogeneous cell population and (3) a larger cell population under the same experimental conditions.

For practical purposes, it would be interesting to examine the influence of the loading conditions (stress intensity and loading time) on long-time aggregate shape relaxation. It may represent a useful tool for analyzing the collective phenomena of cell rearrangement under stress at a supra-cellular level.

Compliance with ethical standards

Conflict of interest

The authors report no conflict of interest.

Informed consent

Informed consent was obtained from all individual participants included in the study.