Abstract
Comparisons of diagnostic tests on test accuracy alone can be inconclusive. For example, a test may have better sensitivity than another test yet worse specificity. Benefit-risk comparisons of tests may be more conclusive because they also consider clinical consequences of diagnostic error. For benefit-risk evaluation, we propose diagnostic yield, the expected distribution of subjects with true positive, false positive, true negative and false negative test results in a hypothetical population. We construct a table of diagnostic yield that includes the number of false positive subjects experiencing adverse consequences from unnecessary work-up. We then develop a decision theory for evaluating tests. The theory provides additional interpretation to quantities in the diagnostic yield table. It also indicates that the expected utility of a test relative to a perfect test is an average of sensitivity and specificity accuracies weighted for prevalence and relative importance of false positive and false negative testing errors, also interpretable as the cost-benefit ratio of treating non-diseased and diseased subjects. We propose plots of diagnostic yield, weighted accuracy, and relative net benefit of tests as functions of prevalence or cost-benefit ratio. Concepts are illustrated with hypothetical screening tests for colorectal cancer with test positive subjects being referred to colonoscopy.
Keywords: diagnostic yield, weighted accuracy, relative net benefit, clinical utility, decision theory, cost/benefit ratio, risk threshold
1. Introduction
Benefit-risk evaluation of a diagnostic test involves not just the accuracy of the test but the clinical consequences of diagnostic error. Evaluations of the clinical consequences of false positive and false negative test errors depend on the clinical setting, the intended use of the test, and the population on whom it will be used. Sometimes, the test itself has clinical consequences, for example, if it involves an invasive procedure (e.g., biopsy) or introduces energy into the body such as radiation (e.g., X-ray computed tomography (CT) scan). A health economics analysis may also consider the cost of testing and downstream costs of working up test positive subjects (Tsalik et al 2016).
For diagnostic tests that classify subjects as either positive or negative for a clinical condition (e.g., disease absence or presence) or predict a future binary state (e.g., susceptibility or resistance of a microbe to an antimicrobial drug), diagnostic accuracy is commonly evaluated in a clinical performance study for its classification accuracy (e.g., specificity, sensitivity, negative and positive likelihood ratio) or its predictive accuracy (e.g., negative and positive predictive value – NPV, PPV). However, these evaluations can sometimes be insufficient for examining the clinical consequences of the test relative to other tests. For example, a test may have better sensitivity than another test yet worse specificity, or better NPV yet worse PPV. Thus based on such accuracy measures alone, a determination of whether a test has better, worse or about the same clinically utility as another test can be equivocal.
The receiver operating characteristic (ROC) plot plays a fundamental role in the evaluation of the overall intrinsic ability of a quantitative measurement or continuous score to discriminate a binary clinical state. For an excellent and influential overview, see Zweig and Campbell (1983). Yet in an evaluation of the clinical consequences of a test providing a continuous result, overall intrinsic discrimination as measured by the area under the ROC plot (AUC) can be insufficient for evaluating how the test will be used in medical decision making. Sometimes a difference in AUC between tests is small, yet at a commonly used operating point (a cut-off in the continuous test result to define subjects at test positive or negative), differences in NPV and PPV are actually large and clinically significant (Pepe 2004; Cook 2007). Because AUC weights equally a test’s performance at all operating points, it includes some operating points that are irrelevant to decision making in the clinical context in which the test will be used. Comparing tests on the ROC plot itself is more informative than just considering its AUC, yet small deviations in the plot between the tests at particular operating points and crossing of the plots in multiple places can still be difficult to interpret clinically.
To evaluate the clinical consequences of the test, a clinical utility study could be conducted to evaluate if clinical outcomes can be improved when the test is used to influence subject management. However, clinical utility studies could be expensive to conduct, require lengthy follow-up on subjects, and be difficult to design. In fact, a poorly designed clinical utility study can be inefficient and may not even permit an evaluation of a test’s effect on clinical outcome (Bossuyt, Lijmer, and Mol 2000; Simon 2010; Hoering, Leblanc, and Crowley 2008). Moreover, such clinical utility data are usually not available to a regulatory agency when it is deciding whether or not to grant approval of a test for market.
In this paper, we describe methods for evaluating the benefit-risk of a binary diagnostic test based on its diagnostic accuracy from a clinical performance study together with external information on clinical consequences. We describe a simple table in which two tests are compared on their diagnostic yield, i.e., the joint distribution of the test result and disease state, in a hypothetical population of subjects undergoing testing. This joint distribution of true and false positive results and true and false negative results and selected summary quantities can reveal insights into the clinical consequences of the two tests. In the table, clinical consequences are explored assuming a subject testing positive would be referred to an additional procedure that puts them at risk for adverse events. Specifically, we consider two hypothetical screening tests for colorectal cancer with test positive subjects referred to colonoscopy.
We also compare tests on benefit-risk in a decision-theoretic framework, assigning losses to test misclassifications (false positive and false negative), or equivalently, utilities to correct classifications (true positive and true negative). The theory provides additional interpretations to quantities in the diagnostic yield table. The theory also indicates that a weighted accuracy measure proposed previously (Evans, 2016) can be interpreted as a relative utility measure, the expected utility of the test relative to that for a perfect test (sensitivity = specificity = 1). We also describe the concepts of expected benefit from testing and net benefit relative to a perfect test, which are similar to expected benefit measures proposed for risk prediction models (Gail and Pfeiffer 2005; Vickers and Elkin 2006; Baker et al 2009a, 2009b, 2012a, 2012b) and binary diagnostic tests (Pepe et al 2016). For all of these evaluations, we construct plots to compare the benefit-risk of two or more tests over a range in the false positive to false negative relative loss ratio or the prevalence of the clinical condition. To illustrate, we use throughout the example of two hypothetical colon screening tests.
2. Test Accuracy
Consider a new diagnostic test that indicates subjects as test negative or positive for a clinical condition, e.g., disease. The test is evaluated for its diagnostic accuracy by comparing test negative and positive results (T = 0,1) for agreement with absence and presence of the clinical condition (D = 0,1), as determined by a clinical reference standard or best available method. Consider comparing the new test with a standard test for indicating subjects as test negative or positive (S = 0,1).
For concreteness, suppose the new test is used to screen for colorectal cancer (CRC). Test positive subjects are referred to colonoscopy for final diagnosis of CRC (and to remove any pre-cancerous advanced adenomas that are found). In the screening population, assume CRC prevalence is π1 = 0.007. Suppose the new test has false and true positive fractions τ0 = 0.15 and τ0 = 0.90. i.e., specificity Sp = 0.85 and sensitivity Se = 0.90. Consider comparing the new test with a standard fecal immunochemical test (FIT) having false and true positive fractions ξ0 = 0.05 and ξ1 = 0.75, i.e, Sp = 0.95 and Sp = 0.75.
The new test has better sensitivity (0.90 vs. 0.75), but worse specificity (0.85 vs. 0.95). However, one of the tests could still be declared better than the other if its negative and positive predictive values (NPV,PPV) are both better. PPV is monotone increasing in the positive diagnostic likelihood ratio PLR = Se/(1−Sp) = τ1/τ0 (in the notation of the new test). NPV is monotone decreasing in the negative diagnostic likelihood ratio NLR = (1 − Se)/Sp = (1 − τ1)/(1 − τ0). Thus for the same prevalence the new test would have better NPV and PPV than the standard test if its NLR were smaller and its PLR were larger. In this case, the new test has smaller NLR (0.1176 < 0.2632), but also smaller PLR (6 < 15), indicating that it has better NPV but worse PPV than the standard test.
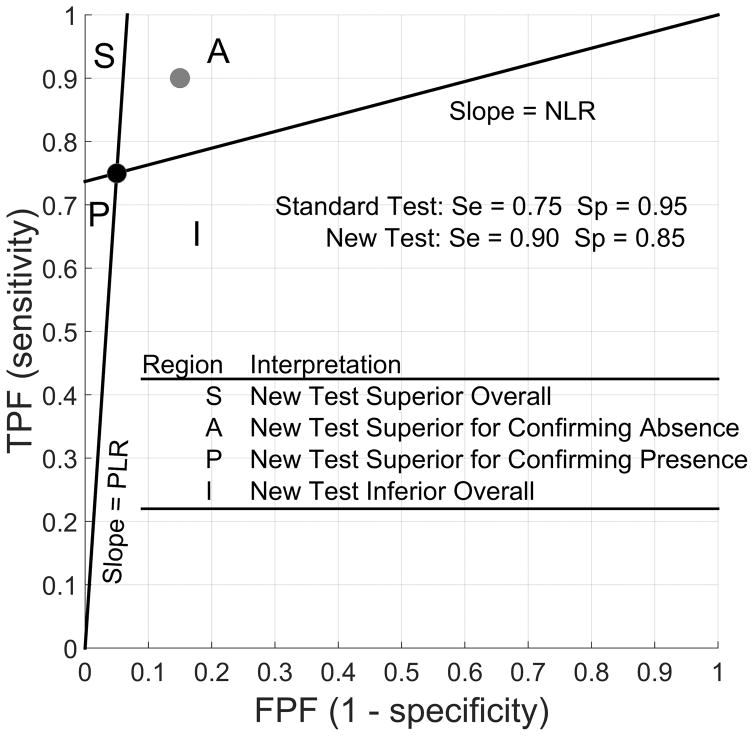
We illustrate these results with the likelihood ratio graph (Figure 1), a useful display proposed by Biggerstaff (2000). The graph has the same axes as the ROC plot. In the graph, the coordinate of the true and false positive fractions of the standard test is plotted, with two lines drawn through it to the points (0,0) and (1, 1). The slope of the lines through (0,0) and (1,1) are PLR and NLR, respectively. The two lines define four regions in which the coordinate of the new test could lie. In this case, the new test falls in region A, indicating that it is better at detecting absence of CRC than the standard test but worse at detecting its presence because, respectively, its PLR is worse (smaller) but its NLR is better (smaller). In sum, the evaluation as to which test is better based on test accuracy alone is equivocal.
Figure 1.
Likelihood Ratio Graph: Regions of Comparison
3. Diagnostic Yield
The diagnostic accuracy measures just described are all based conditional probabilities. Measures of classification accuracy (Se,Sp,NLR,PLR) are based on probabilities of test result conditional on disease status, while measures of predictive accuracy (NPV,PPV) are based on probabilities of disease status conditional on test result.
Alternatively, in a comparison of the two tests on benefit-risk, we consider their diagnostic yield, the distribution of false negative (FN), true positive (TP), true negative (TN), and false positive (FP) results in the screening population. This distribution is given not by conditional probabilities but by joint probabilities of disease status and test result.
Comparing the diagnostic yield of the two tests reveals several insights (Table 1). Consider the left part of the table of test positive counts by disease status. In a population of 100,000 subjects, the new test is expected to detect 105 more subjects with CRC than the standard test (105 more TP test results), but at the expense of falsely detecting 9930 non-CRC subjects as having CRC (9930 more FP test results). The (fractional) number of FP test results for CRC for every TP detection is 23.6 for the new test compared with just 9.5 for the standard test, a 2.5-fold increase. For every extra CRC the new test detects that the standard test does not, an additional 94.6 non-CRC subjects are expected to be falsely detected has having CRC.
Table 1.
Diagnostic Yield of New Screening Test T Compared with Standard Test S for Colorectal Cancer (CRC), 100,000 Subjects.
| Disease | Test Positives | Test Negatives | ||||
|---|---|---|---|---|---|---|
| Status | S+ | T+ | Δ+ | S− | T− | Δ − |
| Absent | 4965 | 14895 | 9930 | 94335 | 84405 | −9930 |
| Presenta | 525 | 630 | 105 | 175 | 70 | −105 |
|
| ||||||
| Ratio | 9.5 | 23.6 | 94.6 | 539.1 | 1205.8 | 94.6 |
| FP AEsb | 33.8 | 101.3 | 67.5 | |||
| ΔFP AEs/ΔTP | 0.64 | |||||
|
|
||||||
Prevalence of disease (CRC) is assumed to be 0.7%, or 700 per 100,000 subjects.
Risk of an adverse event during colonoscopy is assumed to be 0.68% (Rutter et al, 2012, Table 2). All subjects falsely testing positive are assumed to be referred to colonoscopy and undergo the procedure.
Because test positive subjects are referred to colonoscopy, assume that the risk of an adverse event (e.g., bleeding or perforation of the colon) during that procedure is α = 0.0068 (Rutter et al, 2012). Among FP subjects, the (fractional) number who suffer an adverse event during colonoscopy is expected to be 101.3 for the new test and 33.8 for the standard test, a difference of 67.5 subjects (assuming all FP subjects on either test actually undergo the procedure). Thus for every extra true CRC detected by the new test, a fractional 0.64 (= 67.7/105) of FP subjects are expected to suffer an adverse event during an unnecessary colonoscopy.
By comparison, consider the diagnostic yield of a trivial test A that is always positive (Table 2). The (fractional) number of false positive test results for CRC for every true positive detection is 141.9, compared with 23.6 and 9.5 for the new and standard tests (Table 1). For every extra CRC the trivial test detects that the standard test does not, an additional 539.1 non-CRC subjects will be falsely detected as positive for CRC compared with 94.6 for the new test. For every extra true CRC detected by the trivial test that is not detected by the standard test, 3.67 (641.5/175) FP subjects are expected to suffer an adverse event during an unnecessary colonoscopy, a trade-off that is by all accounts unacceptable. By comparison, the figure is 0.64 for the new test, which could be considered a plausible trade-off to some clinicians.
Table 2.
Diagnostic Yield of “Always Positive” Testc A Compared with Standard Test S for Colorectal Cancer (CRC), 100,000 Subjects.
| Disease | Test Positives | Test Negatives | ||||
|---|---|---|---|---|---|---|
| Status | S+ | A+ | Δ+ | S− | A− | Δ− |
| Absent | 4965 | 99300 | 94335 | 94335 | 0 | −94335 |
| Presenta | 525 | 700 | 175 | 175 | 0 | −175 |
|
| ||||||
| Ratio | 9.5 | 141.9 | 539.1 | 539.1 | NaN | 539.1 |
| FP AEsb | 33.8 | 675.2 | 641.5 | |||
| ΔFP AEs/ΔTP | 3.67 | |||||
|
|
||||||
Prevalence of disease (CRC) is assumed to be 0.7%, or 700 per 100,000 subjects.
Risk of an adverse event during colonoscopy is assumed to be 0.68% (Rutter et al, 2012, Table 2). All subjects falsely testing positive are assumed to be referred to colonoscopy and undergo the procedure.
A trivial test that classifies everyone as test positive for CRC.
In addition to the number of FP subjects harmed from unnecessary additional work-up involving an invasive procedure (e.g., colonoscopy), the number of FN subjects harmed by lack of additional work-up can be quantified. The right-hand part of Tables 1–2 lists the expected number of true and false negative subjects of the two tests. The FN and TN counts are actually determined by the FP and TP counts in the left part of the table and the number of diseased subjects and thus provide some redundant information. The standard test is expected to correctly rule out CRC in 9930 more non-CRC subjects than the new test (9930 more TN results), but falsely rule out CRC in 105 more CRC subjects (105 more FN results). The (fractional) number of TN subjects per FN subject is 539.1 for the standard test and 1205.8 for the new test. For every extra CRC falsely ruled out by the standard test but detected by the new test, CRC will be correctly ruled out in an additional 94.6 non-CRC subjects by the standard test.
The harms associated with a FN result include not receiving necessary treatment for a disease that may progress unattended. In some settings, disease is typically aggressive and all FN subjects are harmed by lack of detection. In other settings, disease is typically slowly progressing and harm from delay in detection may be weighed against competing risks (e.g., early stage prostate cancer in older age men who may die of other causes).
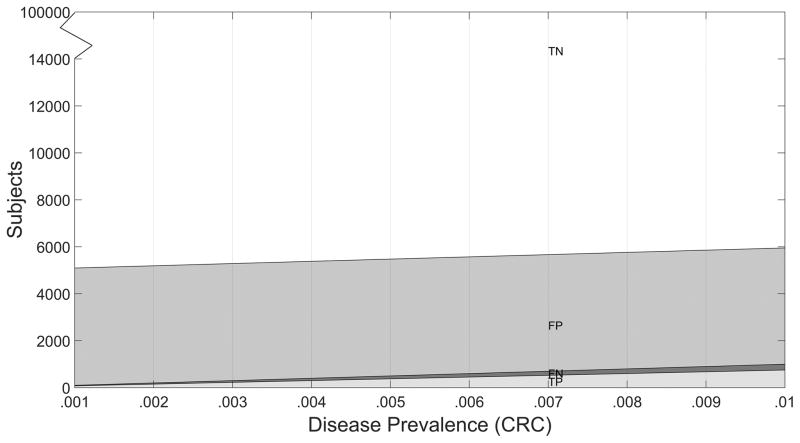
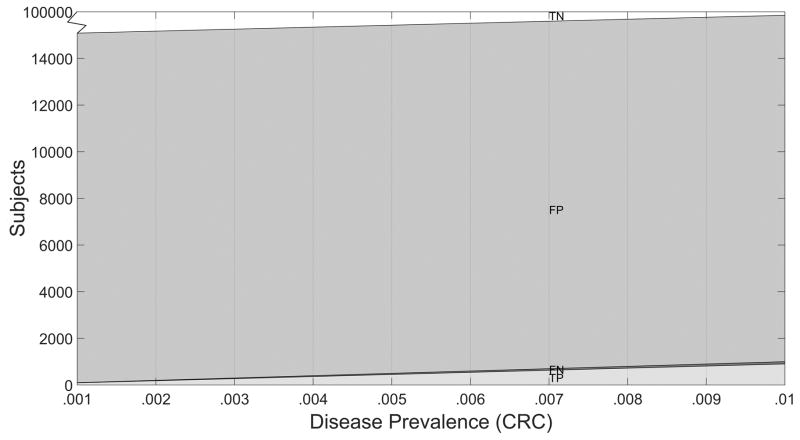
The diagnostic yield table depends on the disease prevalence assumed. In lieu of assuming a single prevalence value, the expected diagnostic yield may be displayed as a function of prevalence (Figures 2–3). These diagnostic yield plots can be useful to inspect, as prevalence can vary temporally, geographically, by population, and by clinical setting,
Figure 2.
Diagnostic Yield Plot for Standard Test S, N = 100,000 Subjects.
Figure 3.
Diagnostic Yield Plot for New Test T, N = 100,000 Subjects.
In sum, the new CRC screening test is certainly better than the trivial always-positive test, which in particular leads to too many adverse events from unnecessary colonoscopy procedures per extra CRC it would detect. Based on test accuracy alone, the new test can appear attractive relative to the standard test because of its superior sensitivity to detect CRC (0.90 vs. 0.75). Yet its inferior specificity (0.85 vs. 0.95) has clinical consequences to many subjects in the intended use population who will falsely test positive. The diagnostic yield table facilitates a quantitative discussion of these consequences.
4. Decision Theoretic Evaluation
The diagnostic yield table and plots (Table 1) can inform on the clinical significance of test results. Yet they also directly relate to formal decision-theoretic evaluations of benefit-risk.
4.1 Expected Loss
For the new test, a count in the diagnostic yield table is just product of disease probability pd = P(D = d), test positive classification probability τd = P(T = 1|D = d), and population size N (= 100,000), where disease status d = 0 or 1 (Table 3). Likewise, for the standard test, the counts involve TP and FP classification probabilities ξd = P(S = 1|D = d).
Table 3.
Parameters of the Diagnostic Yield Table.
| Disease Status | + | + | Δ+ | − | − | Δ− | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Absent | p0ξ0 | p0τ0 | p0(τ0 − ξ0) | p0(1 − ξ0) | p0(1 − ξ0) | −p0(τ0 − ξ0) | ||||
| Present | p1ξ1 | p1τ1 | p1(τ1 − ξ1) | p1(1 − ξ1) | p1(1 − τ1) | −p1(τ1 − ξ1) | ||||
| Ratio |
|
θ1−1 |
|
|
θ0−1 |
|
| Adverse events among subjects falsely testing positive†: | ||||
| FP AEs | αp0ξ0 | αp0τ0 | αp0(τ0 − ξ0) | |
| ΔFP AEs/ΔTP |
|
|||
pd = Pr(D = d)
τd = Pr(T = 1|D = d)
ξd = Pr(S = 1|D = d)
, s = 0,1
Pt = Pr(D = 1|T = t); θt = Pt/(1 − Pt) = odds of disease given T= t, t = 0,1
re = p1(τ1 − ξ1)/p0(τ0 − ξ0) = ratio of relative importance FP:FN or cost benefit C:B at which tests S and T have the same expected utility.
α = Pr(AE|Treat) = risk of adverse event during subsequent management of a test positive subject.
In a decision-theoretic evaluation, consider ascribing a loss rtd to the binary test result T = t on a subject with disease state D = d for values of t,d = 0.1 (Table 4, left-hand table). This loss function for binary test classifications of disease states is fully general, provided that testing itself causes no harm to a subject (i.e., loss ascribed to testing is 0). Without loss of generality (Appendix 1), an equivalent loss function (Table 4, middle table) depends only on B = r01 − r11 and C = r01 − r00. Yet another equivalent loss function (Table 4, right-hand table) depends only on the ratio r = C/B, which can be regarded as the relative importance (or loss ratio) of test result FP to test result FN modulo the losses for test results TN and TP, which are set to 0 in that table. Under this decision-theoretic framework, tests may be compared on expected loss.
Table 4.
Equivalent Loss and Utility Functions (Loss due to the act of testing is assumed to be 0).
| Loss Functions | ||||||||
|---|---|---|---|---|---|---|---|---|
| Test | D = 0 | D = 1 | Test | D = 0 | D = 1 | Test | D = 0 | D = 1 |
| T = 0 | r00 | r01 | T = 0 | 0 | B | T = 0 | 0 | 1 |
| T = 1 | r10 | r11 | T = 1 | C | 0 | T = 1 | r | 0 |
| Utility Functions | ||||||||
|---|---|---|---|---|---|---|---|---|
| Test | D = 0 | D = 1 | Test | D = 0 | D = 1 | Test | D = 0 | D = 1 |
| T = 0 | −r00 | −r01 | T = 0 | C | 0 | T = 0 | r | 0 |
| T = 1 | −r10 | −r11 | T = 1 | 0 | B | T = 1 | 0 | 1 |
C = r10 − r00 = net cost (harm) of treating subject without disease
B = r01 − r11 = net benefit of treating subject with disease
r = C/B = FP:FN loss ratio = TN:TP utility ratio
4.2 Expected Utility
In decision theory, the problem of evaluating expected loss can be equivalently defined as a problem of evaluating expected utility (Appendix 1). Most simply, utilities are set to the negatives of the losses to define utility functions corresponding to the three equivalent loss functions (Table 4). Upon examination of the utility and loss tables, respectively, B and C have been interpreted as the overall net benefit and net cost of treating test positive subjects with and without disease, respectively (Pauker and Kassirer, 1975; Vickers and Elkin 2006, Baker 2012a, Pepe et al 2016). Upon examination of the utility tables, r may be interpreted as the TN: TP utility ratio as well as the FP:FN loss ratio.
Under the utility function, the expected utility for the new test is
a weighted sum of specificity 1 − τ0 and sensitivity τ1 (Appendix 1).
If the test were perfect (τ0 = 0, τ1 = 1), the expected utility would be
A weighted accuracy measure (Evans et al., 2016) is the ratio of expected utility to perfect utility
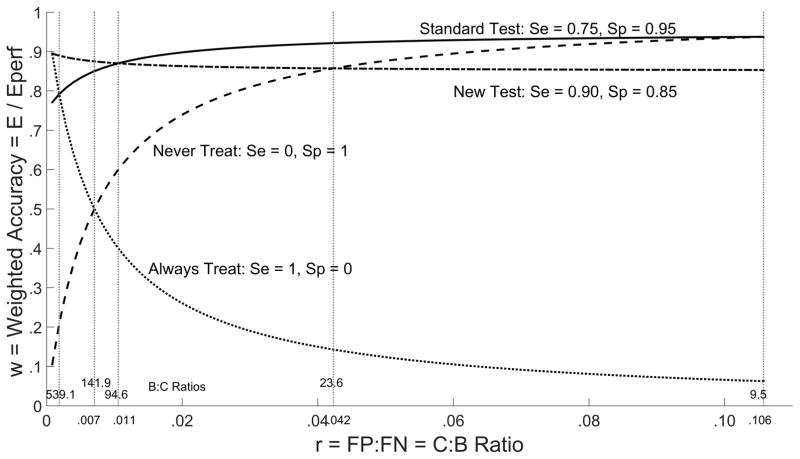
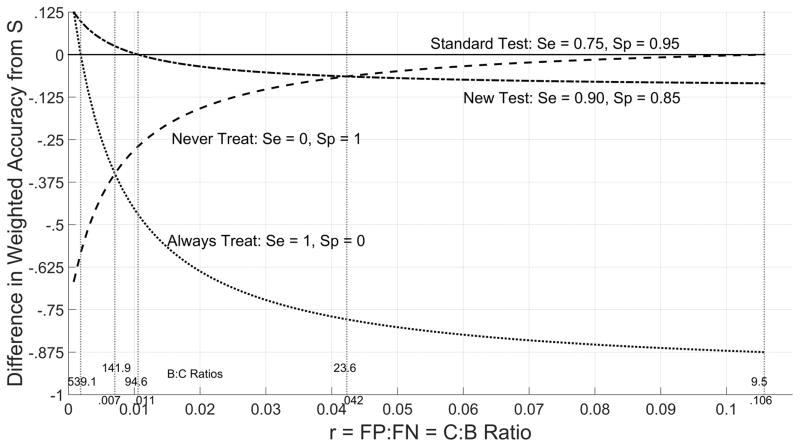
which averages specificity 1 − τ0 and sensitivity τ1 according to weights p0r and p1. For an overall assessment, weighted accuracy is plotted as a function of r for the new and standard tests as well as the trivial test τ0 = τ0 = 0 that always provides a positive test result (and therefore always recommends treatment) and the trivial test τ0 = τ1 = 0 that always provides a test negative result (always recommends no treatment) (Figure 4). The difference in weighted accuracy from the standard test is also plotted for the new and trivial tests as a function of r (Figure 5).
Figure 4.
Weighted Accuracy w by Cost/Benefit Ratio r
Figure 5.
Difference in Weighted Accuracy from Standard Test S by Cost/Benefit Ratio
From Table 1, among the valid choices of r ∈ (0.007,0.0423) for the new test (see next section), for lower limit r = 0.007 weighted accuracy is greater for the new test (0.875) than the standard test (0.850), but for upper limit r = 0.0423 weighted accuracy is smaller for the new test (0.857) than for the standard test (0.921).
4.3Valid Choices for r
At a minimum, the expected utility of the new test should be greater than the expected utility of any non-informative test that renders a test positive result at random with probability τ (0 ≤ τ ≤ 1). The difference in expected utility of a test compared with a random test is called net benefit. The test has positive net benefit compared with any random test if the FP:FN relative importance ratio
where Pt = P(D = 1|T = t) is the predictive value of test result T = t for disease (Appendix 1). In other words, the test is valid (better than any random test) only for choices of r < θ1.
Note θ1 = p1τ1/( p0τ0), the reciprocal of the FP to TP ratio given in third row of the diagnostic yield parameter Table 3. Thus the table gives information on choices of r that are acceptable for the test. Equivalently,
where θ = p1/p0 is the pre-test odds of disease. Noting that a test is informative only if the ratio of its true to false positive fraction τ1/τ0 < 1, we find that r > θ is an additional constraint on valid choices of r. Thus in terms of reducing expected loss relative to the trivial test, the new test is valid only for FP:FN loss ratios
Note θ1 = p1τ1/(p0τ0) is the reciprocal of the FP to TP ratio given in the diagnostic yield table (Table 1). Also θ is the reciprocal of the FP to TP ratio for a trivial test that classifies everyone as test positive, which is gleaned from diagnostic yield table for the always positive test (Table 2).
To illustrate, from Table 1 the range of acceptable choices for r is (1/141.9, 1/23.6) = (0.007, 0.0423 for the new test for CRC and (1/141.9,1/9.5) = 0.007,0.1057 for the standard FIT test. Equivalently, the acceptable range for the ratio of the benefit B to cost C of treating test positive subjects with and without disease is (θ1, θ) = (23.6,141.9) for the new test and (9.5,141.9) for the standard test. The larger range for the standard test suggests that it is applicable to a wider variety of settings over which the relative loss r may vary (e.g., r may be selected higher for a low risk population than a high risk population).
To interpret, the new test has no benefit if the benefit to cost B:C ratio is 23.6 or lower, that is, 23.6 FP or fewer subjects can be traded for 1 TP subject. Another interpretation is that for the new test to beneficial, the risk threshold at which one is indifferent to undergoing colonoscopy should be less than its positive predictive value P1 = (1 + 1/θ1)−1 = (1 + 23.6)−1 0.0406 (Pauker and Kassirer, 1975; Vickers and Elkin 2006, Baker 2012a). In contrast, for the standard test to be beneficial, the risk threshold for undergoing colonoscopy should be less than its positive predictive value .
From the expression of U above, the value for r at which the two tests have the same expected utility is
the reciprocal of the ratio of the extra false positives per extra true positive given in the third row and third column diagnostic yield Tables 1–3. From Table 1, re = 1/94.6 = 0.0106, at which the new and standard tests have the same weighted accuracy value 0.870. That is, the two tests have equivalent utility if 94.6 FP subjects can be traded for 1 TP subject, or the risk threshold at which one expresses indifference to undergoing colonoscopy is (1 + 94.6)−1 = 0.0105.
4.4 Net Benefit
The net benefit of a test compared with a random test with test positive probability τ is defined as
the difference in expected utility between the test (E) and the random test (Eτ). The net benefit from never treating a subject is defined as NB0, the difference in expected utility from the always negative test. The net benefit from always treating a subject is defined as NB1, the difference in expected utility from the always positive test. Relative net benefit of a test is defined as
which scales its net benefit to have a maximum of 1 relative to the net benefit of a perfect test.
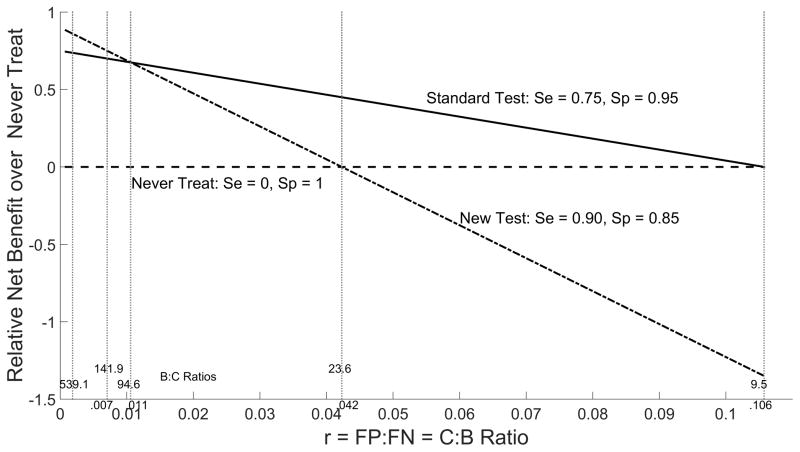
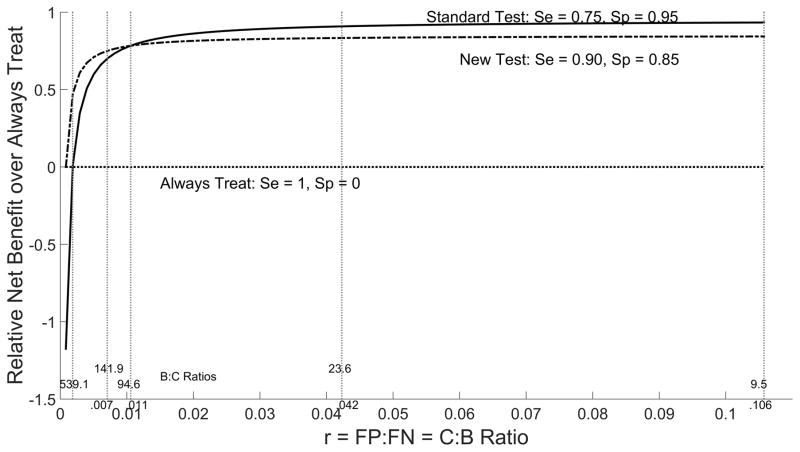
Relative net benefit from never treat and always treat policies can be plotted as a function of relative importance ratio r to provide an overall comparison of the new and standard tests (Figures 6–7). These plots indicate that relative net benefit over the never treat policy is noticeably worse for the new test than the standard over a large range of r values. In contrast, the relative net benefit over the always treat policy is only slightly worse than the standard test over a large range of r values and thus the two tests can be considered comparable in settings where prophylactic treatment is practiced in lieu of testing.
Figure 6.
Relative Net Benefit over Never Treat by Cost/Benefit Ratio r
Figure 7.
Relative Net Benefit over Always Treat by Cost/Benefit Ratio r
4.5 Choosing r
Decision-theoretic benefit-risk comparisons of a new test with a standard test need not be an exercise in sensitivity analysis to the choice of FP: FN ratio r. Suppose the binary value of the new test is t = φ(x) = I(x > c) = 1 or 0 according to whether or not an underlying continuous measurement x exceeds threshold c. Then, threshold c implies loss ratio r =r0 at which c is the optimal operating point in the sense of minimizing expected loss (Appendix 2).
Because r0 is the FP: FN loss ratio implied by the new test, the new and standard tests are best compared on expected utility at loss ratio r0. If the binary value of the standard test is also based on thresholding an underlying continuous value, then its threshold should be moved such that expected loss is minimized with respect to r0 before it is compared with the new test. Otherwise, the two tests are operating at points that attribute a different trade-off between FP and FN errors.
5. Summary
The benefit-risk of a new test is best evaluated in comparison with another test having the same intended use. We have proposed a descriptive diagnostic yield table to compare a new test with a standard test used in practice. A diagnostic yield plot displays the diagnostic yield of a test over a range of disease prevalence.
Quantities of interest displayed in the diagnostic yield table such as the number of false positive subjects per true positive subject have been used before to compare tests informally. As we have shown, such quantities relate directly to formal decision-theoretic measures of expected utility, or equivalently, expected loss under a loss function defined by an assumed false positive to false negative (FP:FN) relative importance or loss ratio r. Values of r that are permissable for the tests are those at which the test has positive net benefit (greater expected utility) compared with a random test. Overall comparisons of the utility of tests can be made by plotting the measures of weighted accuracy and relative net benefit as functions of r.
Our comparisons of binary valued tests on benefit-risk are similar to recent work in the evaluation of new markers for risk prediction (Gail and Pfeiffer 2005; Vickers and Elkin 2006; Baker et al 2009a, 2009b, 2012a, 2012b) and diagnosis (Pepe et al 2016). For example the relative utility curve (Baker 2009a) is the fraction of the expected net benefit of perfect prediction that is achieved by a risk prediction model. Likewise, weighted accuracy is the fraction of the expected utility of a perfect diagnostic test that is achieved by an investigational diagnostic test.
The plots of weighted accuracy and relative net benefit presented can appear to provide a lot of information. However, they are generated solely from binary test accuracy, disease prevalence, and varying r. More information is available if the binary value of the new test (test negative or positive) is based on thresholding an underlying continuous measurement or score. The value of r at which the threshold for the new test minimizes expected loss (maximizes expected utility) can be used to compare the two tests. In this approach, the threshold for the standard test is moved such that expected loss is minimized for the same r value at which the new test expected loss is minimized. Then, binary performance of the new test is compared with the standard test at its modified threshold value. This new approach can be a subject of future research. A brief discussion on determining the optimal threshold from ROC sample data is provided in Appendix 2.
For many tests, the possible test result may be not only negative or positive but also equivocal, defined as a non-missing, non-erroneous result that is neither positive nor negative (El Mubarek et al, 2016). For some tests, equivocal zones are defined by two thresholds in an underlying continuous value. To make decision theoretic comparisons of tests with equivocal results, the three-decision problem can be described by two separate component problems, the problem of deciding between calling a subject a test positive or not, and the problem of deciding between calling a subject test negative or not. If the subject is called neither test positive or test negative, then by definition the test result is equivocal. These two problems may be considered separately. For the test positive problem, the loss of a false positive relative to not calling a true positive (FP:~TP) is considered. Likewise, for the test negative problem, the loss of a false negative relative to not calling a true negative (FN:~TN) is considered. The two thresholds at which the new test operates defines these two loss ratios. The thresholds for the standard test are moved such that it is optimal under these thresholds. The two tests are then compared on expected utility. Additional research is needed to develop this idea from a general outline to specific benefit-risk comparisons of tests permitting equivocal test results.
Acknowledgments
Research reported in this publication was supported by the National Institute Of Allergy And Infectious Diseases of the National Institutes of Health under Award Number UM1AI104681. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Appendix 1
1.1. Loss
Let d = 0,1 indicate disease absence, presence, and t = 0,1 indicate the binary test results (negative, positive). The “loss” of a test can be expressed as
| (1) |
where L0(d) and L1(d) are the losses ascribed to negative and positive test results, respectively.
1.2. Equivalent Re-Expressions of Loss
For the general loss function (Table 4, left-hand table),
Thus from (1)
| (2) |
| (3) |
In expression (2) the loss depends on test result t only through C and B. One can argue that comparative evaluations of tests on expected loss should be invariant to constant terms in the loss function, i.e., those terms independent of test result. In expression (3), the loss function is proportional to one which depends on test result t only through r. One can argue that comparative evaluations of tests on expected loss should be invariant to the scale of the loss function. Taken together, (2) and (3) imply that the left-hand, middle, and right-hand loss functions given in Table 4 are all equivalent for any comparisons of tests that are invariant to the location and scale of the loss function.
1.3. Utility
In lieu of defining losses L0(d) and L1(d) due to incorrect binary test classifications (false negative, false positive), consider utilities U0(d) and U1(d) credited to correct test classifications (true negative, true positive). The “utility” of the test can be expressed as
| (4) |
Because t only appears in the right-hand terms of (1) and (4), then modulo a constant expected loss is the negative expected utility iff
This equality occurs if for instance U1(d) = L0(d) = d and U0(d) = L1(d) = (1 − d)r (using right-hand loss function of Table 4). Thus, r is interpretable not only as the relative loss ratio of false positive to false negative tests results, but also as the relative utility ratio of true negative to true positive test results.
Under these utility functions,
which has expectation
| (5) |
1.4. Valid Choices for r
From (5), for a random test with probability of testing positive τ0 = τ1 = τ, expected utility is
Relative to this random test, the test has positive net benefit if
i.e.,
This inequality imposes a constraint on r that depends on the ordering of τ,τ0, and τ1:
| (6) |
| (7) |
| (8) |
The upper bound constraint imposed on r by (6) is smallest when τ is chosen to minimize
which is minimized at τ = 0, always negative (“never treat”) random test. Thus one need only consider this trivial test to determine valid choices of r for which the test has positive net benefit relative to all random tests. For τ = 0, the constraint is
The lower bound constraint imposed on r by (6) is largest when τ is chosen to maximize
which is maximized at τ = 1, the always positive (“always treat”) test. For τ = 1, the constraint is
This poses no additional constraint for informative tests τ1 > τ0, because then θ0 < p1/p0. We already require r > p1/p0 = the pre-test odds of disease to eliminate random tests from consideration.
The inequality in (8) is not a constraint on r because the right-hand side is negative.
Appendix 2
Considering the ROC plot of (τ0(c), τ1(c)) = (s, ROC(s)) for every cut-off c in x, expected loss may be re-expressed as
Zweig and Campbell (1993) convey a well-known result about the operating point on the plot at which expected loss is minimized. Setting to zero the derivative of expected loss with respect to false positive fraction s, we find it is minimized when
That is, expected loss is minimized at the operating point s on the ROC plot at which the derivative (slope of tangent line) is r/θ. Reversing this process, the loss ratio r at which the operating point s is optimal (minimizes expected loss) is
For sample data, Zweig and Campbell note that “the nonparametric ROC plot for continuous data with no ties is a “staircase” of line segments having alternating slopes of zero and infinity. The operating point can be determined by the point where a line (with the above calculated slope), moving down from above and to the left, intersects the ROC plot”. An algorithm for determining the optimal operating point in ROC sample data is given in Baker and Kramer (2012, Appendix A). Deneef and Kent (1993) consider such thresholding with application to testing for streptococcal pharyngitis.
Contributor Information
Gene Pennello, Center for Devices and Radiological Health, Food and Drug Administration, Silver Spring, MD, USA.
Norberto Pantoja-Galicia, Center for Devices and Radiological Health, Food and Drug Administration, Silver Spring, MD, USA.
Scott Evans, Center for Biostatistics in AIDS Research and the Department of Biostatistics, Harvard T. H. Chan School of Public Health, 651 Huntington Ave, Boston, MA 02115.
References
- 1.Baker SG. Putting risk into perspective: relative utility curves. J Natl Cancer Inst. 2009a;101:1538–1542. doi: 10.1093/jnci/djp353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Baker SG, Van Calster B, Steyerberg EW. Evaluating a New Marker for Risk Prediction Using the Test Tradeoff: An Update. Internat J Biostatistics. 2012a;8(1) doi: 10.1515/1557-4679.1395. Article 5. [DOI] [PubMed] [Google Scholar]
- 3.Baker SG, Kramer BS. Evaluating a new marker for risk prediction: decision analysis to the rescue. Discovery Medicine. 2012b;14(76):181–188. [PubMed] [Google Scholar]
- 4.Baker SG, Cook NR, Andrew Vickers A, Kramer BS. Using relative utility curves to evaluate risk prediction. J R Statist Soc A. 2009b;172(4):729–748. doi: 10.1111/j.1467-985X.2009.00592.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Biggerstaff BJ. Comparing diagnostic tests: a simple graphic using likelihood ratios. Statist Med. 2000;19:649–663. doi: 10.1002/(sici)1097-0258(20000315)19:5<649::aid-sim371>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 6.Bossuyt PM, Lijmer JG, Mol BW. Randomised comparisons of medical tests: sometimes invalid, not always efficient. Lancet. 2000;356:1844–1847. doi: 10.1016/S0140-6736(00)03246-3. [DOI] [PubMed] [Google Scholar]
- 7.Cook NR. Use and misuse of the receiver operating characteristics curve in risk prediction. Circulation. 2007;115(7):928–935. doi: 10.1161/CIRCULATIONAHA.106.672402. [DOI] [PubMed] [Google Scholar]
- 8.Deneef P, Kent D. Using Treatment-tradeoff Preferences to Select Diagnostic Strategies: Linking the ROC Curve to Threshold Analysis. Med Decis Making. 1993;13:126–132. doi: 10.1177/0272989X9301300206. [DOI] [PubMed] [Google Scholar]
- 9.El Mubarak HS, Petrides V, Kondratovich MV, Ye J, Akselrod S, Charnot-Katsikas A, Gawel SH, Simon K, Meier K. Equivocal results in in vitro diagnostic tests. submitted. [Google Scholar]
- 10.Evans SR, Pennello G, Pantoja-Galicia N, Jiang H, Hujer AM, Hujer KM, Manca C, Hill C, Jacobs MR, Chen L, Patel R, Kreiswirth BN, Bonomo RA The Antibacterial Resistance Leadership Group (ARLG) Benefit-Risk Evaluation for Diagnostics: A Framework (BED-FRAME) Clinical Infectious Diseases. 2016 doi: 10.1093/cid/ciw329. Published online May 18, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gail MH, Pfeiffer RM. On criteria for evaluating models of absolute risk. Biostatistics. 2005;6:227–239. doi: 10.1093/biostatistics/kxi005. [DOI] [PubMed] [Google Scholar]
- 12.Hoering A, Leblanc M, Crowley J. Randomized Phase III clinical trial designs for targeted agents. Clin Cancer Res. 2008;14(14):4358–4367. doi: 10.1158/1078-0432.CCR-08-0288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McIntosh MW, Pepe MS. Combining several screening tests: optimality of the risk score. Biometrics. 2002;58:657–664. doi: 10.1111/j.0006-341x.2002.00657.x. [DOI] [PubMed] [Google Scholar]
- 14.Metz CE. Basic principles of ROC analysis. Semin Nucl Med. 1978;8(4):283–298. doi: 10.1016/s0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]
- 15.Pauker SG, Kassirer JP. Therapeutic decision making: a cost-benefit analysis. N Engl J Med. 1975;293:229–34. doi: 10.1056/NEJM197507312930505. [DOI] [PubMed] [Google Scholar]
- 16.Pepe MS, Janes H, Li CI, Bossuyt PM, Feng Z, Hilden J. Early-Phase Studies of Biomarkers: What Target Sensitivity and Specificity Values Might Confer Clinical Utility? Clin Chem. 2016;62:737–42. doi: 10.1373/clinchem.2015.252163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pepe MS, Janes H, Longton G, Leisenring W, Newcomb P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. Am J Epidemiol. 2004;159(9):882–890. doi: 10.1093/aje/kwh101. [DOI] [PubMed] [Google Scholar]
- 18.Simon R. Clinical trial designs for evaluating the medical utility of prognostic and predictive biomarkers in oncology. Per Med. 2010;7(1):33–47. doi: 10.2217/pme.09.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tsalik EL, Li Y, Hudson LL, Chu VH, Himmel T, Limkakeng AT, Katz JN, Glickman SW, McClain MT, Welty-Wolf KE, Fowler VG, Ginsburg GS, Woods CW, Reed SD. Potential Cost-effectiveness of Early Identification of Hospital-acquired Infection in Critically Ill Patients. Annals of the American Thoracic Society. 2016;13(3):401–413. doi: 10.1513/AnnalsATS.201504-205OC. [DOI] [PubMed] [Google Scholar]
- 20.Rutter CM, Johnson E, Miglioretti DL, Mandelson MT, Inadomi J, Buist DSM. Adverse events after screening and follow-up colonoscopy. Cancer Causes Control. 2012;23:289–296. doi: 10.1007/s10552-011-9878-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vickers AJ, Elkin EB. Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making. 2006;26:565–574. doi: 10.1177/0272989X06295361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zweig MH, Campbell G. Receiver-Operating Characteristic (ROC) Plots: A Fundamental Evaluation Tool in Clinical Medicine. Clin Chem. 1993;39(4):561–577. [PubMed] [Google Scholar]