The Processing-Speed Impairment in Psychosis Is More Than Just Accelerated Aging

Abstract

Processing speed is impaired in patients with psychosis, and deteriorates as a function of normal aging. These observations, in combination with other lines of research, suggest that psychosis may be a syndrome of accelerated aging. But do patients with psychosis perform poorly on tasks of processing speed for the same reasons as older adults? Fifty-one patients with psychotic illnesses and 90 controls with similar mean IQ (aged 19–69 years, all African American) completed a computerized processing-speed task, reminiscent of the classic digit–symbol coding task. The data were analyzed using the drift-diffusion model (DDM), and Bayesian inference was used to determine whether psychosis and aging had similar or divergent effects on the DDM parameters. Psychosis and aging were both associated with poor performance, but had divergent effects on the DDM parameters. Patients had lower information-processing efficiency (“drift rate”) and longer nondecision time than controls, and psychosis per se did not influence response caution. By contrast, the primary effect of aging was to increase response caution, and had inconsistent effects on drift rate and nondecision time across patients and controls. The results reveal that psychosis and aging influenced performance in different ways, suggesting that the processing-speed impairment in psychosis is more than just accelerated aging. This study also demonstrates the potential utility of computational models and Bayesian inference for finely mapping the contributions of cognitive functions on simple neurocognitive tests.

Introduction

Cognitive deficits are a core feature of disorders involving psychosis, including schizophrenia^1–4 and bipolar disorder with psychotic symptoms.^5,6 Meta-analyses have shown that, out of all cognitive measures, digit–symbol coding tasks yield the largest differences between patients with psychosis and controls.^7,8 These tasks require subjects to match digits and symbols as quickly as possible, and the dependent variable is usually the number of correct responses made within a time limit (eg, ref.⁹). Traditionally, they have been considered relatively pure measures of “processing speed,”¹⁰ commonly defined as the speed with which an individual can perform any cognitive operation.¹¹

In healthy individuals, performance on processing-speed tasks declines as a function of age, with measurable differences appearing as early as 30 years old (eg, refs.^12,13). Thus, as famously noted by Kraeplin,¹⁴ the pattern of cognitive deficits associated with psychosis appears to mirror the pattern of decline seen in normal aging. This observation was the first to lead to the conceptualization of psychosis as a syndrome of accelerated aging.^15,16 Although originally posed in regard to cognition, it has developed into a general biological hypothesis. Indeed, patients with psychosis exhibit other physical symptoms, such as structural brain abnormalities, that are reminiscent of those seen in older adults.^17,18 Patients with psychosis also have dramatically decreased life expectancy compared to the general population, some—but not all—of which may be explained by increased rates of suicide, accidental death, and lifestyle risk factors.¹⁹

There is an important problem with the interpretation of the processing-speed impairment as evidence for the accelerated-aging hypothesis. Even relatively “pure” measures of processing speed, such as digit–symbol coding, rely on a far more complex set of cognitive functions than traditionally assumed,^20,21 and deficits in various subsets of these functions may cause poor performance.^22,23 Thus, it is quite possible for patients with psychosis and older adults to perform poorly on such tasks for completely different reasons—if so, this would imply that the processing-speed impairment in psychosis is more than just the result of accelerated aging.

One approach to understanding the roles of different cognitive functions on a task is to model the dynamics of performance.^24–26 The drift-diffusion model (DDM) is a popular model of this kind.²⁷ The DDM explains performance in terms of latent parameters with distinct interpretations, including the “drift rate,” which reflects efficiency of information processing, response caution, and “nondecision time,” which incorporates factors such as sensory encoding, motor preparation, and motor execution. The DDM has proven extremely popular in basic science due to its ability to explain accuracy and reaction-time distributions across a vast range of experimental designs,²⁸ the validity of the interpretations of its parameters,²⁹ and its ability to provide insights into the effects of experimental manipulations and subject characteristics on performance. For example, prior work has shown that, across tasks, normal aging is associated with increased response caution, but that the association between aging and drift rate is weaker (eg, ref.³⁰).

Here, patients with psychosis and controls completed a computerized, two-alternative forced-choice variant of the digit–symbol coding task. Our task differed from traditional pen-and-paper versions in several ways, most notably in terms of its reduced motor demands. However, despite these qualitative differences, this variant of the task has been shown to produce similar differences between patients with psychosis and controls,^31,32 and demonstrates similar changes with advancing age,³³ as traditional versions. Crucially, the forced-choice version had the key advantage that it allowed us to record trial-level accuracy and reaction times, and thus fit the DDM to the data. We compared the effects of psychosis and aging on subjects’ DDM parameters to determine if they influenced performance in similar or divergent ways. Based on previous work (eg, ref.³⁰), we expected aging to strongly influence response caution, and to weakly influence drift rate. If psychosis impairs processing speed in a similar way to aging, it should influence response caution more strongly than drift rate. On the other hand, if psychosis and aging impair processing speed differently, psychosis may influence drift rate more strongly than response caution.

Methods

Subjects

Data from 51 patients with psychosis and 90 unaffected individuals from the same community were included in the analysis. All subjects were African Americans. The patient group included subjects with various diagnoses including substantial psychotic features, namely schizophrenia (n = 25), schizoaffective disorder (n = 11), psychotic bipolar disorder (n = 6), psychotic major depression (n = 3), and psychosis not otherwise specified (n = 6). DSM-IV diagnoses were confirmed through structured clinical interviews³⁴ and a consensus process. Neither patients nor controls were excluded for having nonpsychotic psychiatric disorders or substance dependencies, and as a consequence of this liberal strategy, patients and controls had similar full-scale IQ (FSIQ) scores, obtained from the Wechsler Abbreviated Scale of Intelligence (WASI³⁵). Subjects were excluded for a history of major nonpsychiatric medical disorders or FSIQ <70. Table 1 provides additional subject information.

Table 1.

Demographic and Clinical Sample Characteristics

	Patients	Controls	Total	P value
N	51	90	141
Female (%)	25 (49.0)	42 (46.7)	67 (47.5)	.672a
Right handed (%)	47 (92.2)	87 (96.6)	126 (89.3)	.306a
Age (range)	36 (19–69)	43 (19–62)	39 (19–69)	.138b
High school diploma or GED (%)	36 (70.6)	61 (67.8)	97 (68.8)	.440a
Bachelors or higher (%)	4 (7.84)	19 (21.1)	23 (16.3)	.031a,c
WASI FSIQ (range; SD)	90 (70–124; 12.3)	91 (70–124; 11.9)	91 (70–124; 12.0)	.346b
Mean duration of psychotic illness in years (range)	11 (1–40)	—	—	—
Prescribed antipsychotics (%)	38 (74.5)	1 (1.11)	39 (27.7)	.000a,c
Prescribed mood stabilizers (%)	5 (9.80)	0 (0)	5 (3.54)	.005a,c
Prescribed antidepressants (%)	25 (49.0)	2 (2.22)	27 (19.1)	.000a,c
Prescribed benzodiazepines/ barbiturates (%)	6 (11.8)	2 (2.22)	8 (5.67)	.027a,c
Prescribed lithium (%)	1 (1.96)	0 (0)	1 (0.709)	.362a
Prescribed stimulants (%)	0 (0)	1 (1.11)	1 (0.709)	.638a

Note: GED, general educational development; WASI FSIQ, Wechsler Abbreviated Scale of Intelligence full-scale IQ; SD, standard deviation.

^aFisher’s exact test.

^bWelch’s t-test.

^cNominally significant at the 0.05 level.

Digit–Symbol Coding Task

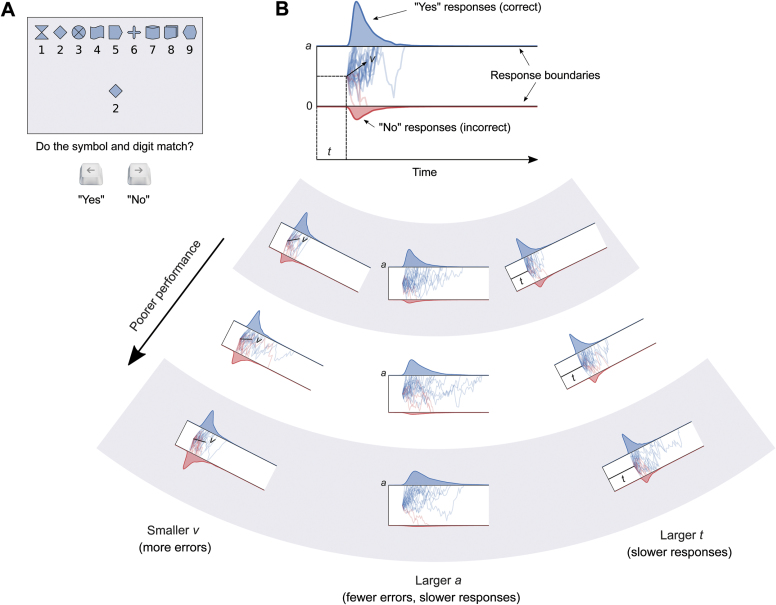
The task, illustrated in figure 1A, was similar to those from previous studies (eg, refs.^5,31,32,36). On each trial, subjects saw a key comprising the digits 1–9 and 9 symbols. They also saw a digit–symbol combination in the middle of the screen, and indicated whether the digit and symbol matched according to the key. Responses were made using the left and right arrow keys. Subjects were instructed to make as many correct responses as possible within 90 s. The task was administered as part of our publically available test battery, “Charlie”.³⁷

Fig. 1.

(A) Example trial and task instructions. This is a “match” trial, so the correct response is “yes.” (B) The top part shows a schematic of the drift-diffusion model. It is valid only for match trials. The blue shaded region at the top is the reaction-time distribution for “yes” (correct) responses, and the red shaded region at the bottom is the reaction-time distribution for “no” (incorrect) responses. The blue and red traces are example diffusion patterns (ie, different trials in the experiment). Note that the corresponding schematic for nonmatch trials would be flipped, and “no” responses would be correct. The bottom part of the panel illustrates how changes in v, a, and t independently influence accuracy and response-time distributions. Smaller v causes more errors, indicated by the increasing height of the error distributions. Greater a causes fewer errors, but also causes the correct distribution to become more rightward-skewed, leading to slower responses on average. Greater t causes both the distributions to be shifted rightward, leading to slower responses. Any one or combination of these effects would lead to poorer performance on the task.

Conventional Analysis

In addition to our DDM analysis, we analyzed the data conventionally with two analyses of covariance (ANCOVAs). The first ANCOVA included diagnostic group, sex, and age in years as independent variables, and the number of correct trials as the dependent variable. The second ANCOVA was the same except that the dependent variable was the proportion of correct responses. We also performed a number of Welch’s independent-samples t-tests to determine whether medication influenced performance in the patient group.

Description of the DDM

The DDM assumes that decisions in two-choice tasks are based on a latent decision variable that represents the evidence for the possible responses. The initial value of this variable sits between two boundaries, and is updated stochastically. When the decision variable crosses a boundary, the corresponding response is executed. As illustrated in the top part of figure 1B, the DDM predicts response probabilities (ie, accuracy) and the shapes of both reaction-time distributions. For a detailed explanation of the DDM and a comparison to other models, see ref.²⁴ For a more accessible introduction, see ref.³⁸

The “basic” DDM contains four parameters. Drift rate (v) reflects the quality of evidence extracted from the stimulus, or information-processing efficiency. It can be considered roughly analogous to sensitivity (d′) from signal detection theory.³⁹ Smaller v leads to more error responses. Boundary separation (a) reflects the amount of information required before making a response (ie, response caution). Although larger a leads to fewer errors, it also causes slower responses, and thus poorer performance on time-sensitive tasks. Nondecision time (t) accounts for factors that are not directly related to the decision process, such as sensory-encoding time, motor preparation, and motor execution. Larger t leads to slower responses. The final parameter in the basic DDM is the starting point (z), reflecting response bias. The “full” DDM includes three additional parameters that reflect trial-by-trial fluctuations in drift rate (s_v), starting point (s_z), and nondecision time (s_t). It is also common to allow v to differ between the different categories of trials presented during the experiment (eg, ref.⁴⁰).

Model Design

We constructed a Bayesian DDM using the HDDM software package.⁴¹ Here, “Bayesian” refers a method of statistical inference that uses Bayes’ theorem to update beliefs about model parameters given the observed data, which is sharply contrasted with traditional frequentist inference (see ref.⁴²). Bayesian inference has numerous advantages over frequentist inference,⁴³ including more efficient parameter recovery through the use of priors, and the propagation of uncertainty throughout all levels of the analysis. The latter advantage is particularly relevant here. Since we had a small amount of data per individual, the DDM parameter values associated with a particular subject had quite high uncertainty. A conventional frequentist analysis such as an ANOVA would ignore this uncertainty, treating the most likely individual parameter values as “point estimates.” Bayesian analysis does not do this, and therefore can be considered fairer.⁴⁴

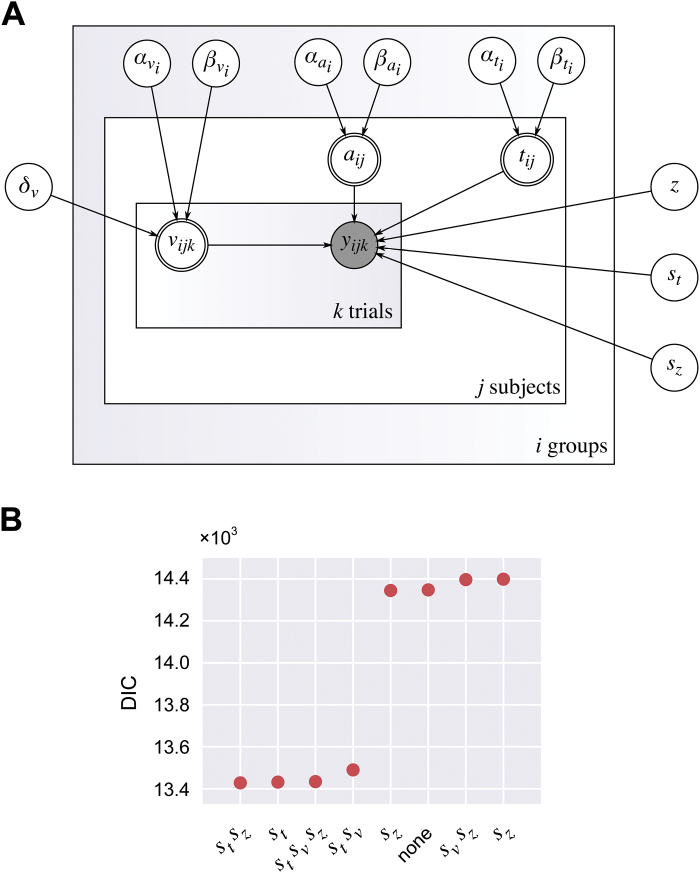
The design of the model is illustrated in figure 2A. Under the model, the value of v for a given subject on a given trial was linearly determined by the subject’s diagnostic group, age, and the type of trial (match or nonmatch). Formally, this can be expressed as v_ijk= α_vi+ β_vix_ij+ δ_vp_ijk, where i indexes the group, j indexes the subject, k indexes the trial, α_v, β_v, and δ_v are covariates, x is the subject’s age in decades minus 1.8, and p is the trial type (coded as a categorical variable with 0 indicating a match trial and 1 indicating a nonmatch trial). Thus, comparing the variables α_v0 and α_v1 reveals the average difference in drift rate between a hypothetical 18-year-old patient and a hypothetical 18-year-old control. This construction allowed us to examine the effects of psychosis independently of the effects of age, which are minimal at 18 years and begin soon after. The variables β_v0 and β_v1 represent the average decline in drift rate per decade for patients and controls, respectively. The variable δ_v represents the average difference in drift rate between match and nonmatch trials. Similar linear models, without effects of trial type, were placed on a and t; these can be expressed as a_ijk= α_ai+ β_aix_ij and t_ijk= α_ti+ β_tix_ij, respectively. A single, group-level z variable was also estimated in the model.

Fig. 2.

(A) Directed acyclic graph showing the probabilistic relationships between all the variables in the final model. Unfilled single-lined circles represent stochastic random variables, double-lined circles represent deterministic variables, and the shaded circle represents the observed data, consisting of reaction times and choices. (B) DIC values of the 8 candidate models.

To determine whether any of the trial-by-trial variables from the full DDM should be included in the model, 8 candidate models, reflecting the power set of combinations of these variables, were fitted to the data separately. We assumed a single value of these parameters for all subjects. Figure 2B shows the deviance information criterion (DIC⁴⁵) values for these models. The model containing s_t and s_z had the smallest (best) DIC score, and was chosen as the final model. However, it turned out that the choice of model made little difference to our conclusions (see “Results” section).

Bayesian Parameter Estimation

All random variables in the model were assigned vague prior distributions, which were updated using the data to produce posterior distributions. Posterior distributions were sampled using the Metropolis-within-Gibbs Markov chain Monte Carlo (MCMC) algorithm,⁴⁶ implemented in PyMC.⁴⁷ Four independent MCMC chains were initialized with random starting values. Each chain comprised 8000 posterior samples, and the first 1000 samples per chain were discarded.

Model Checking

To check whether the model captured important patterns within the data, we performed a posterior predictive check (PPC). PPCs are used to assess, in a qualitative sense, the goodness of fit of Bayesian models.⁴⁸ They involve simulating replicated data from the posterior predictive distribution of the fitted model, and then comparing these to the observed data. Two hundred fifty data sets were simulated in total. Initially, each simulation contained twice as many trials per subject as in the original data set, and trials were dropped when the cumulative reaction time for the subject exceeded 90 s. These simulated data sets were then compared to real data set in various ways (see Results).

Results

Results of the Conventional Analysis

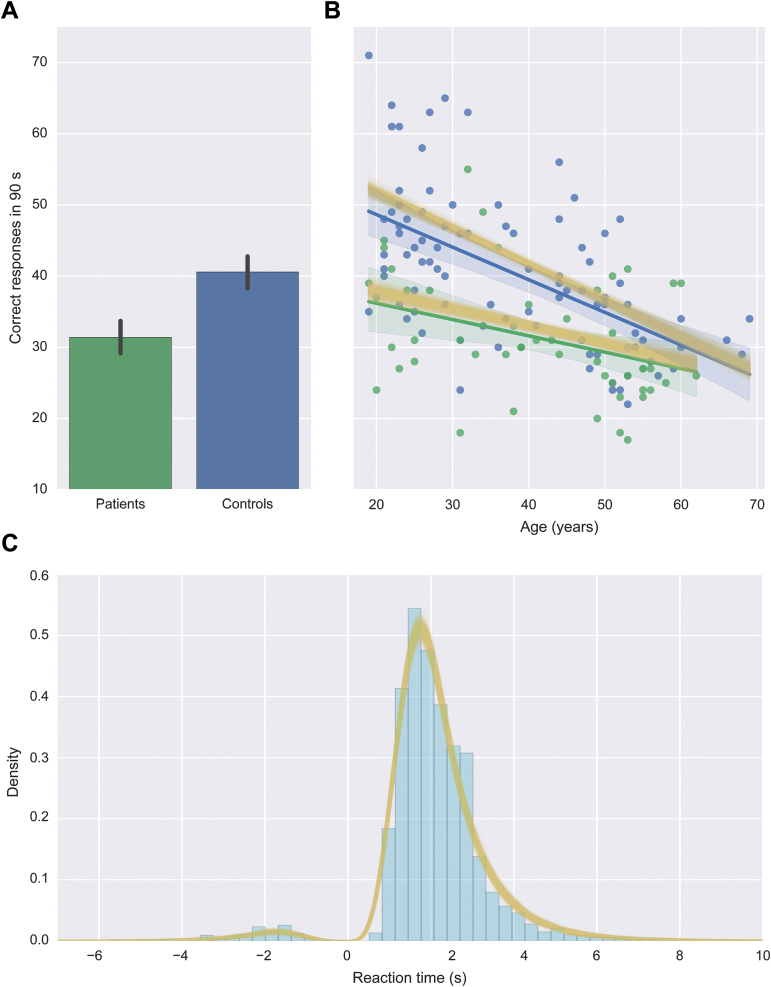
The first ANCOVA revealed main effects of diagnostic group [F(1, 133) = 24.0; P = 2.77 × 10⁻⁶] and age [F(1, 133) = 47.7; P = 1.89 × 10⁻¹⁰] on the number of correct responses, with patients and older adults performing more poorly (figure 3). There was also a significant interaction between group and age [F(1, 133) = 4.24; P = .00414], indicating that aging was less deleterious to performance in patients than in controls. Neither the main effect of sex nor any interaction term involving sex was significant (F ≤ 0.175; P ≥ .0677). The second ANCOVA did not yield any significant main effects or interactions (F ≤ 1.82; P ≥ .180), probably because accuracy was very high overall (mean 96% correct in both groups). While these results point to psychosis- and age-related impairments in processing speed, they cannot be used to assess whether the nature of these impairments are similar or divergent without the use of a model such as the DDM.

Fig. 3.

(A) Mean number of correct responses per group (with 95% confidence intervals). (B) Number of correct responses for all subjects as a function of age. Solid green and blue lines show linear regression lines for the patient and control groups, respectively, and shaded regions are 95% confidence intervals around the regression coefficient. Yellow lines are the results of the PPC (see text for explanation). (C) Distribution of reaction times collapsed across all subjects. Reaction times for error responses are plotted as negative values. Yellow lines are kernel-density estimates of the data simulated via the PPC.

To determine whether antipsychotic medication influenced performance, the patient group was divided into two subgroups based on whether they were taking antipsychotics. A Welch’s t-test revealed a significant difference in performance (number of correct trials) between the subgroup of patients with psychosis taking antipsychotic medication (n = 38) and the unmedicated subgroup (n = 13; t19.022 = 2.27, P = .0035). Despite this significant difference, the unmedicated subgroup was too small to reliably investigate the influence of antipsychotics on the DDM parameters. Similar tests were performed for mood stabilizers, antidepressants, and benzodiazepines/barbiturates, none of which yielded significant differences between the subgroups (t ≤ 0.869, P ≥ .418).

PPC Results

Accuracy and reaction times within the simulated data sets were very similar to those in the real data, and exhibited effects of psychosis and aging that were similar in magnitude to those observed in the real data (figure 3). Thus, the model successfully captured the important features of the real data.

Effects of Psychosis on the DDM Parameters

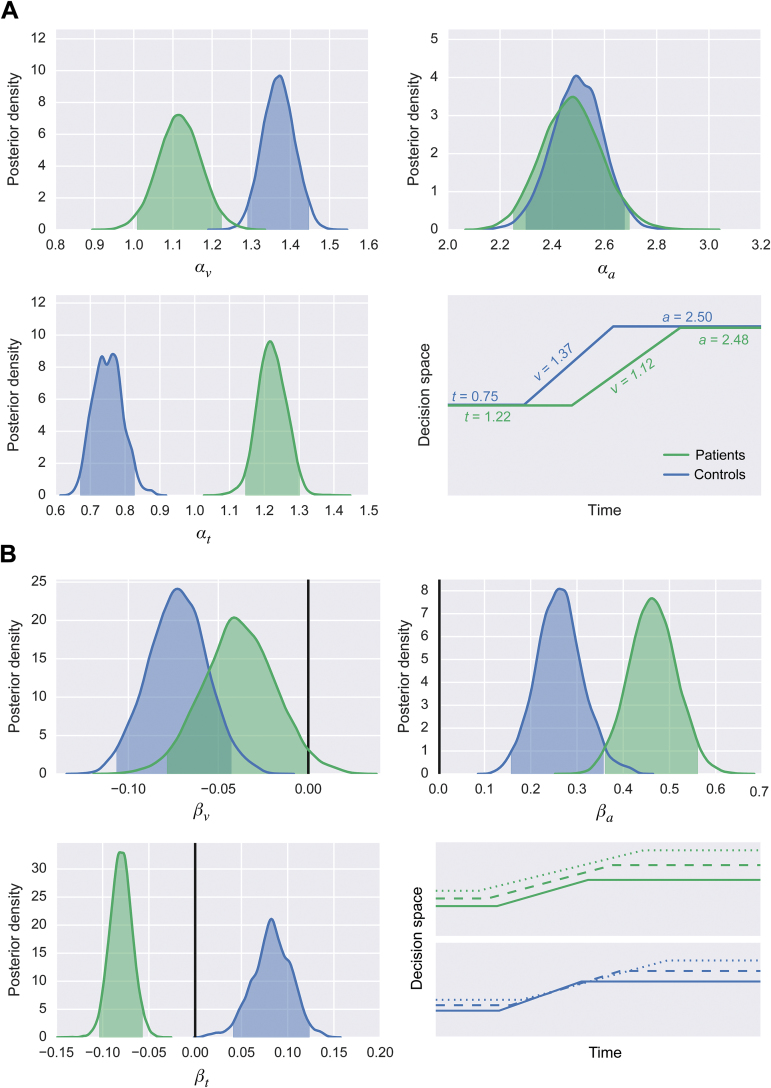
Figure 4A shows the effects of psychosis on drift rate, response caution, and nondecision time. The posterior mean of α_v was smaller for patients (1.12) than controls (1.37). In other words, for an average 18 year-old subject, psychosis conferred a decrease in drift rate of 0.25. Since the 95% highest-density regions (HDRs) of these 2 random variables did not overlap (patients: 1.01–1.23; controls: 1.29–1.45), this difference is considered credibly nonzero. The posterior means of α_a were almost the same for both groups (patients: 2.48; controls: 2.50), and the 95% HDRs overlapped (patients: 2.25–2.70; controls: 2.30–2.69). Thus, psychosis alone did not appear to influence response caution. There was a large difference in the posterior means of α_t between the groups (patients: 1.22; controls: 0.75), and the 95% HDRs did not overlap (patients: 1.15–1.30; controls: 0.67–0.83). For an average 18 year-old subject, psychosis conferred an increase in nondecision time of 0.47 s.

Fig. 4.

(A) Posterior densities reflecting the effects of psychosis on drift rate (top left), response caution (top right), and nondecision time (bottom left), with shaded areas representing 95% HDRs. The bottom-right schematic shows the predicted (posterior mean) values of drift rate, response caution, and nondecision time for the average 18-year-old patient and 18-year-old control. (B) Posterior densities reflecting the effects of psychosis on drift rate (top left), response caution (top right), and nondecision time (bottom left), with shaded areas representing 95% HDRs. Solid vertical lines represent a value of 0, reflecting no effect of aging. The bottom-right schematic shows the predicted (posterior mean) values of drift rate, response caution, and nondecision time for the average 20 (solid lines), 40 (dashed lines), and 60 (dotted lines) year-old patient and control.

Effects of Aging on DDM Parameters

Figure 4B shows the effects of aging on drift rate, response caution, and nondecision time in the patient group and control group. For controls, the 95% HDR of β_v was below zero (mean: −0.07; 95% HDR: −0.11 to −0.04). However, for the patients, the 95% HDR of β_v included zero (mean: −0.04; 95% HDR: −0.08 to 0.001). In other words, aging was likely to have affected drift rate only for the control group. By contrast, β_a did not overlap with zero for either patients (mean: 0.46; 95% HDR: 0.36–0.56) or controls (mean: 0.26; 95% HDR: 0.16–0.36); indicating a likely effect of aging across all subjects. On average, aging by one decade conferred a 0.26–0.46 increase in response caution. Finally, the effect of aging on nondecision time was inconsistent across groups: aging decreased nondecision time for patients (mean: −0.08; 95% HDR: −0.10 to −0.06) but increased it for controls (mean: 0.08; 95% HDR: 0.04–0.12).

Remaining Parameters and Alternative Models

Summary statistics for all parameters in the model are provided in Supplementary Material 1. To determine whether our choice of model affected the results, we re-analyzed the data using the simplest candidate model (containing no trial-to-trial parameters) and the most complex one (containing all the trial-to-trial parameters); the results are shown in Supplementary Material 2 and Supplementary Material 3, respectively. The results from all three models were consistent with the notion of divergent effects of psychosis and aging on the DDM parameters.

Discussion

We tested whether the processing-speed impairment in psychosis is similar to the decline observed in normal aging. This question could not be answered by conventional analyses, but using the DDM,²⁷ we uncovered divergent influences of psychosis and aging. Patients had lower drift rates and larger nondecision times than controls, and psychosis per se did not influence response caution. By contrast, the primary effect of aging was to increase response caution. Aging had inconsistent effects on drift rate and nondecision time across patients and controls: drift rate increased with age in controls only, whereas nondecision time increased with age in controls but decreased with age in patients. The results suggest that the processing-speed impairment in psychosis is not simply the result of accelerated aging.

Accelerated aging in psychosis is a general biological hypothesis, and other features of psychosis support this idea.^17,18,49 In our view, the present findings should not be used to argue against the hypothesis generally. Instead, we suggest that although accelerated aging may contribute to the observed impairments, additional factors, such as differences in task strategy between patients and controls, also play an important role. This suggestion dovetails with evidence of impoverished “executive functioning” or “cognitive control” in patients with psychosis.^50,51 Consider, for example, the work by Knowles et al.^22,23 Using structural equation modeling, they examined the relationships between pen-and-paper digit–symbol coding and other tasks in patients with schizophrenia and controls. Put simply, they found that patients with psychosis and controls approach processing-speed tasks differently (see also ref.⁵²). This difference could have driven the substantial differences in the DDM parameters between the groups in the present study.

Although our results are consistent with the idea of a difference in task strategy, it is difficult to be specific about the nature of this difference. The DDM has been used primarily in basic science, with little application to psychiatry: to our knowledge, only one previous study has applied the DDM to data from patients with psychosis.⁵³ Little is known about how executive functioning or cognitive control influence DDM parameters in processing-speed tasks, especially in patients with psychosis. A promising direction for future research is to combine the DDM approach with structural equation modeling in an attempt to understand these influences (eg, refs.^22,23). The DDM could also be combined with functional neuroimaging—for example, perhaps the reduction in drift rate in patients with psychosis is associated with inadequate recruitment of the dorsolateral prefrontal cortex.^54,55

A limitation of the present study is that the sample was relatively young. Although the maximum age was 69 years, there were few subjects older than 60. Deterioration in performance on processing-speed tasks begins much earlier than on other tasks,^12,13 so a younger sample is appropriate for measuring the influences of psychosis and normal aging on processing speed. However, cognitive decline accelerates after 60 in normal adults,⁵⁶ and impairments in patients with psychosis are usually broader and more severe in later life, especially in those with a history of chronic institutional stay.^57–60 Furthermore, although the observation that aging was associated with increased response caution is highly consistent with previous DDM studies (eg, refs.^30,61–63), the older subjects in those studies tended to be over 60 years old. Thus, an important concern, which could be addressed in future studies, is whether the present results generalize to samples of even older subjects.

All of the subjects in the present study were African Americans. Like other minority groups, African Americans are underserved by psychiatric research, and we specifically chose to study them for this reason. However, focusing on one specific group necessarily raises the question of generalizability. Previous work has revealed race effects on the traditional pen-and-paper version of the digit–symbol coding task, with Black subjects performing worse than White subjects on average (eg, ref.⁶⁴). Such effects are notoriously difficult to understand.⁶⁵ Crucially, however, the rate at which digit–symbol coding performance declines with age does not appear to differ between racial groups.⁶⁶ In or view, this result suggests that the underlying cognitive functions are largely the same across groups, and therefore that the present results would generalize beyond African American subjects.

It is widely recognized that patients with psychosis experience a general cognitive deficit.² Consequently, when a difference in performance is observed between patients with psychosis and controls on a given task, it is often unclear how much of this difference is specific to the task, and how much is a reflection of the general deficit. One way to address this question is to have subjects complete a comprehensive battery of tests, and then estimate the general and task-specific deficits simultaneously (eg, ref.⁶⁷). However, given that digit–symbol coding performance correlates strongly with composite measures of general intellectual ability (eg, ref.⁶⁸), and that patients with psychosis experience the greatest deficits on digit–symbol coding tasks,^7,8 it could be argued that the processing-speed deficit and the general deficit might be one and the same. If this were true, it would not be meaningful to estimate the processing-speed deficit in the context of a general deficit. Models such as the DDM might provide a way to shed more light on this issue in future studies. For instance, an index of general cognition (eg, IQ or g) could be included as a predictor in a DDM, which could reveal whether psychosis and general intellectual ability have similar or divergent effects on DDM parameters.

The present study demonstrates the utility of combining computational modeling and Bayesian inference in future psychiatric research. Using traditional techniques, very many trials per subject are usually needed to obtain meaningful parameter estimates from models like the DDM.⁶⁹ This is problematic for psychiatric research because it is often not possible to collect this many data from individuals with mental illness. Bayesian methods meliorate this limitation by recovering parameters more efficiently than traditional approaches.^41,70 Here, we show that Bayesian methods allow computational models to be applied to data from brief neurocognitive tests, where previously it was infeasible to do so.

Supplementary Material

Supplementary data are available at Schizophrenia Bulletin online.

Funding

National Institute of Mental Health (R01MH106324-01 awarded to Glahn, Poldrack, and Blangero).