A General Approach to Testing for Pleiotropy with Rare and Common Variants

Abstract

Through genome-wide association studies, numerous genes have been shown to be associated with multiple phenotypes. To determine the overlap of genetic susceptibility of correlated phenotypes, one can apply multivariate regression or dimension reduction techniques, such as principal components analysis, and test for the association with the principal components of the phenotypes rather than the individual phenotypes. However, as these approaches test whether there is a genetic effect for at least one of the phenotypes, a significant test result does not necessarily imply pleiotropy. Recently, a method called Pleiotropy Estimation and Test Bootstrap (PET-B) has been proposed to specifically test for pleiotropy, (i.e. that 2 normally distributed phenotypes are both associated with the single nucleotide polymorphism (SNP) of interest). While the method examines the genetic overlap between the 2 quantitative phenotypes, the extension to binary phenotypes, 3 or more phenotypes, and rare variants is not straightforward. We provide two approaches to formally test this pleiotropic relationship in multiple scenarios. These approaches depend on permuting the phenotypes of interest and comparing the set of observed p-values to the set of permuted p-values in relation to the origin (e.g. a vector of zeros) either using the Hausdorff metric or a cut-off based approach. These approaches are appropriate for categorical and quantitative phenotypes, more than 2 phenotypes, common variants and rare variants. We evaluate these approaches under various simulation scenarios and apply them to the COPDGene study, a case-control study of Chronic Obstructive Pulmonary Disease (COPD) in current and former smokers.

Introduction

As genome-wide association studies (GWAS) have become a commonly used research tool over the last decade, genetic associations of the same locus with multiple phenotypes (e.g pleiotropy) have been observed for several phenotypes and disease groups. For example, multiple GWAS have found significant signals in the chromosome 15q25 region for clinical outcomes such as lung cancer [Chen et al., 2015], Chronic Obstructive Lung Disease (COPD) [Cho et al, 2014], emphysema [Cho et al., 2015] and cigarette smoking [Hancock et al., 2015]. Often, the associated phenotypes are correlated, and it is not straight forward to see whether the joint associations with multiple phenotypes are attributable to environmental correlation of the phenotypes or, indeed, by shared genetic components between phenotypes. As the research questions of genetic overlap between diseases becomes more and more the focus of substantive research, statistical methods are needed to formally address this important question and test for pleiotropy.

A variety of multiple phenotype analysis methods have been proposed [Suo et al., 2013] for both case-control and family based genetic association studies. Multiple phenotype analysis methods for unrelated subjects include the canonical correlation analysis (CCA) [Ferreira et al., 2009], extended generalized estimating equation method (EGEE) [Liu et al., 2009], and parameterized multiple phenotype mixed model (MTMM) [Korte et al., 2012]. Family based multiple phenotype analysis methods include principal components based methods [Bensen et al., 2003], [Lange et al, 2004], and FBAT-GEE [Lange et al., 2003]. Multiple phenotype analysis methods that are applicable for both unrelated and related subjects include principal components based methods [Klei et al., 2008], combined multivariate (CMV) analysis [Medland at al., 2010], univariate-statistic combined test [Yang et al., 2010], pleiotropic region identification method (PRIMe) [Huang et al., 2011], and correlated meta-analysis (CMA) [Province et al., 2013]. These methods primarily test whether there is a genetic effect for at least one of the phenotypes, but do not formally test for pleiotropy. While approaches have been suggested to estimate the genetic overlap between phenotypes at a genome-level or chromosomal level [Stoney et al., 2015], only a handful methods are available to characterize pleiotropy at locus level.

Recently, a method has been proposed to specifically test for pleiotropy, (i.e. that 2 normally distributed phenotypes are both associated with the SNP of interest). [Zhang et al., 2014] This method, called Pleiotropy Estimation and Test- Bootstrap (PET-B), estimates the pleiotropy of two normally distributed phenotypes as the ratio of the genetic effect sizes of both phenotypes times the genetic variance over the standard deviation of both phenotypes. [Zhang et al., 2014] While this method examines the genetic overlap between the 2 quantitative phenotypes, extensions to binary phenotypes, 3 or more phenotypes, and rare variants are not straightforward. In practice, an ad hoc approach is to simply observe whether the p-value of each phenotype is less than some alpha level cut-off (e.g. 0.05 or 5e – 8) or that the maximum p-value of the set is less than this cut-off, but this approach does not provide a formal way to test for pleiotropy of these phenotypes and it is not clear how to pick the alpha level cut-off.

Here, we provide two methods to formally test whether the data are consistent with a pleiotropic relationship between 2 or more phenotypes at one locus. These approaches depend on permuting the phenotypes of interest and comparing the set of observed p-values to the set of permuted p-values in relation to the origin either using a cut-off based approach (Approach 1) or the Hausdorff metric (Approach 2). Theses approaches work for binary, categorical, and continuous phenotypes, more than 2 phenotypes, common variants, and rare variants. We evaluate these approaches under various simulation scenarios and apply the approaches to the COPDGene study, a case- control study of COPD in current and former smokers.

Methods

Let the variables Y₁..Y_k denote k vectors of phenotypes where k ≥ 2 for n subjects and let X denote the genetic region or variant where X is a vector for the SNP of interest for the n subjects when considering common variants or X is a matrix of several rare variants in a region when considering rare variant associations. For instance, the variable Y₁ could be COPD affection status, Y₂ could be percent emphysema, Y₃ could be pack-years of smoking history, and X could be rs16969968, a common coding variant in the CHRNA5 gene on chromosome 15q25. The proposed method consists of the following steps.

Step 1

For each set of phenotypes Y₁..Y_k, the corresponding p-values are calculated for genetic association with the particular locus, e.g. SNP, or, if rare variant data is analyzed, with the genetic region of interest X. For instance, for common variants and a quantitative, normally distributed phenotype, the observed p-value is the result of a linear regression of the phenotype Y_i on the SNP X for i = 1..k. For common variants and a binary phenotype, the observed p-value is the result of a logistic regression of the phenotype Y_i on the SNP X for i = 1...k. For rare variants, instead of using a linear or logistic regression to calculate the p-value for each phenotype with the SNP of interest, a variance or burden approach such as SKAT [Wu et al., 2011] can be used to obtain a p-value for the association with the phenotype Y_i and X where X is a matrix of the rare variants in a region for i = 1..k.

Step 2

Once observed p-values are calculated for the association with each observed phenotype Y₁,...Y_k and the genetic variant or region X, the phenotypes are then permuted to form permuted phenotypes Ỹ_si for phenotypes i = 1,..k and permutation set s = 1, ..,N_perm where N_perm is the number of permutations. A set of permuted p-values are calculated for each permuted phenotype Ỹ_s1,.. Ỹ_sk with the genetic variant or region X. For common variants, the SNP is permuted and for rare variants, the collection of rare variants are permuted across subjects in order to maintain the structure of the region.

A reasonable choice for N_perm is 10,000 or 50,000. Although, the choice of the number of required permutations, N_perm, may need to be increased as it depends on the pre-specified overall significance level and the bound on the error of the p-values in order to achieve overall-significance. For instance, a permutation-based method that uses an alpha level of 10⁻⁸ would require at least 10⁸ permutations in order for the p-value estimate to achieve genome-wide significance. This number of permutations would have to be increased even further, if one wants to assure that the bounds on the error of the p-value estimate are sufficiently small.

Step 3a

For the first approach, we propose a method that mirrors the ad hoc approach that simply checks if the p-value of each phenotype is less than 0.05 or the appropriate alpha level. Instead of this ad hoc approach, we propose an approach that compares the observed p-value to the permuted p-value for each phenotype. For the proposed approach, the p-value to test the pleiotropy for phenotypes Y₁,..., Y_k with the genetic variant or region X is the following:

$$1-\left\{\frac{{\displaystyle \sum _{s=1}^{N_{\mathit{perm}}}}I[(p_{{\mathit{observed}}_1}<p_{\mathit{perm}{\mathit{uted}}_{s1}})\&\dots \&(p_{{\mathit{observed}}_k}<p_{\mathit{perm}{\mathit{uted}}_{sk}})]}{N_{\mathit{perm}}}\right\}$$ (1)

where p_observedi is the p-value for the association with the observed phenotype Y_i with the genetic region or variant X and p_permutedsi is the p-value for the association with the permuted phenotype Ỹ_si for phenotype i = 1,.., k and s = 1,..,N_perm with the genetic region or variant X. I [(p_observed1 < p_permuteds1)&...&(p_observedk < p_permutedsk)] is an indicator function that each of the observed p-values are less than the permuted p-values for all k phenotypes for permutation set s.

Consider one of the most extreme situations where none of the k phenotypes are associated with the genetic variant or region X (e.g. p_observedj = 1 for j = 1,.., k). When the observed p-values for all k phenotypes are 1 then I [(p_observed1 < p_permuteds1)&...&(p_observedk < p_permutedsk)] = 0 for all s permutations and the resulting p-value for the proposed approach is 1.

Consider the other most extreme situation where all of the k phenotypes are associated with the genetic variant or region X with p-values of 0. Then, assuming none of the permuted p-values perfectly equal 0, the I [(p_observed1 < p_permuteds1)&...&(p_observedk < p_permutedsk)] = 1 for all s permutations and the resulting p-value for the proposed approach is 0.

Step 3b

An alternative approach for calculating the p-value for pleiotropy is to use a distance measure between the observed and permuted p-values. To compare the set of observed p-values to the set of permuted p-values, we consider the Hausdorff metric, which is the greatest of all the distances from a point in one set to the closest point in the other set. Two sets are close in the Hausdorff distance if every point of one set is close to some point of the other set. Consider two non-empty sets P_o and P_p with elements p_o and p_p respectively and the manhattan distance for the distance metric d. Then Hausdorff Metric is the following:

$$D_{\mathit{Hausdorff}}(P_o,P_p):=\mathit{max}\{{\mathit{sup}}_{p_o\in P_o}{\mathit{inf}}_{p_p\in P_p}d(p_o,p_p),{\mathit{sup}}_{p_p\in P_p}{\mathit{inf}}_{p_o\in P_o}d(p_o,p_p)\}$$ (2)

To calculate the p-value to test the pleiotropy between the genetic region or variant X and phenotypes Y₁,..Y_k, consider the following:

$$(k^k+2)\left\{\frac{{\displaystyle \sum _{s=1}^{N_{\mathit{perm}}}}I[D_{\mathit{Hausdorff}}(p_{\mathit{observed}},0)>D_{\mathit{Hausdorff}}(p_{\mathit{observed}},p_{{\mathit{permutation}}_s})]}{N_{\mathit{perm}}}\right\}$$ (3)

where I [D_Hausdorff (p_observed, 0) > D_Hausdorff (p_observed, p_permutaions)] is an indicator function that the hausdorff metric for the observed p-values for the k phenotypes with the set of 0 (i.e. the origin) is greater than the hausdorff metric for the observed p-values for the k phenotypes with the permuted p-values for the k phenotypes for permutation set s for s = 1,...,N_perm. The quantity (k^k + 2) in the above p-value is multiple comparison correction for the dimensionality of the space and the multiple comparisons the Hausdorff metric makes between the 2 sets.

Both of the proposed methods (i.e. Step 3a: cut-off threshold based on permutation and Step 3b: Hausdorff metric) can also accommodate covariate adjustment. Since the genotype is permuted rather than the phenotype, the covariates can be regressed on the phenotypes and the residuals used for these methods as long as the covariates are not associated with the genotype (i.e. age, gender, etc.). [Freedman and Lane, 1983], [Wagner et al., 2008], [Abney, 2015] Since many forms of population structure can cause confounding that can invalidate a permutation test, careful consideration needs to be given when adjusting for genetic ancestry in permutation based tests. [Abney, 2015] When a limited number of principal components can adjust for the background genetic confounding (e.g. a simple population stratification scenario), it is possible to formulate a valid permutation test [Epstein et al., 2012]. However, in more complicated scenarios of population substructure, other methods are needed such as a parametric bootstrap or MVNpermute, a method designed for permutation testing in the presence of polygenic variation. [Abney, 2015]

Comparison Methods for 2 Quantitative Phenotypes

PET-B, CCA, and CMA

For the simulations when considering two continuous, normally distributed phenotypes, we compare the proposed approaches to PET-B [Zhang et al., 2014] since this method formally tests for pleiotropy. In the PET-B manuscript, the authors compare the PET-B approach to the canonical correlation analysis (CCA) [Ferreira et al., 2009] and correlated meta-analysis (CMA) [Province et al., 2013] approaches. For consistency, we have compared our approaches to the CCA and CMA methods for the simulations studies with two continuous, normally distributed phenotypes. A brief description of these methods is given here. The Pleiotropy Estimation and Test- Bootstrap (PET-B) method [Zhang et al., 2014] firsts fits 2 separate linear models for normally distributed phenotypes Y₁ and Y₂ and estimates the pleiotropy correlation coefficient (PCC) as $\rho =\frac{{\beta }_1{\beta }_2{\sigma }_X^2}{{\sigma }_1{\sigma }_2}$ where ${\sigma }_X^2$ is the variance of X, β_i is the genetic effect size for phenotype i, and σ_i is the standard deviation of Y_i where i = 1, 2. The pleiotropy correlation ρ coefficient is estimated using a bootstrap approach. Note that if either β_i = 0, then the PCC will be 0. CCA is a multivariate approach for analyzing correlation between two groups of variables. [Ferreira et al., 2009] CCA tests the overall association between a variant and two phenotypes by calculating Wilks statistic through an eigen analysis of raw data and obtaining a p-value based on a simplified F-approximation. CMA is a meta-analysis approach that takes between-phenotype correlation into account. [Province et al., 2013] CMA combines statistics from individual phenotypes into a summarized statistic and tests its significance through a correlated multivariate normal distribution.

Simulations

Common variants

The SNP is generated from a binomial distribution with minor allele frequency = 20% for n = 1000 subjects. Binary phenotypes are generated such that

$$\mathit{logit}(p_{jk})={\beta }_0+{\beta }_k{X}_j$$ (4)

for subject j = 1,..., n, genotype X_j, and phenotype Y_k for k = 1,.. where p_jk = Prob(Y_jk = 1). Normally distributed phenotypes are generated such that

$$E[Y_{jk}]={\beta }_0+{\beta }_k{X}_j$$ (5)

for subject j = 1,..., n & phenotype k = 1,... For simplicity, we vary β₁ from 0 to 0.5 by 0.1 for each simulation and fix β_m = 0.2 for m ≥ 2; other values for β_m when m ≥ 2 produced similar results. When at least one β_k = 0 (i.e. β₁ = 0), then this is the null distribution of no pleiotropic effect. For each scenario, we generated 6 sets of 10,000 simulated datasets and ran the proposed approaches for 50,000 permutations each. We evaluated the proposed approaches in the following 6 scenarios for a various number of phenotypes associated with a common variant. In Figure 1, we evaluated the type 1 error rate and power of the proposed methods via simulation studies for 2 normally distributed phenotypes. In the supplemental figures, we evaluated the power and type 1 error rate for the following 5 scenarios: 1 normally distributed phenotype and 1 binary phenotype (Supplemental Figure 1), 2 binary phenotypes (Supplemental Figure 2), 3 normally distributed phenotypes (Supplemental Figure 3), 4 normally distributed phenotypes (Supplemental Figure 4), and 5 normally distributed phenotypes (Supplemental Figure 5).

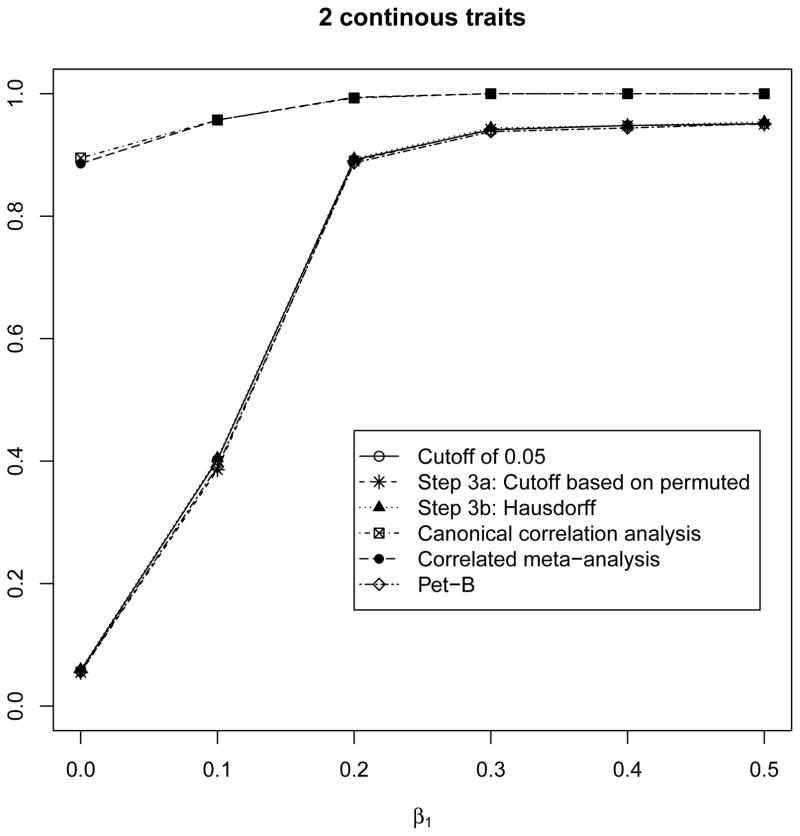
Figure 1.

For 2 normally distributed phenotypes, β₂ = 0.2 and β₁ varies from 0 to 0.5. For β₁ = 0 (e.g. the null hypotheses of no pleiotropic effect), the PET-B, ad-hoc method (e.g. checking if each phenotype has a p-value less than 0.05 for the association with the SNP), and the 2 proposed approaches all maintain the type 1 error rate. The CCA and CMA approaches do not maintain the type 1 error rate since they are testing that at least one phenotype is associated with the SNP, which is true since β₂ = 0.2. For β₁ > 0, all 4 methods (PET-B, the ad-hoc method and the 2 proposed methods) have similar power.

Rare Variants

The rare variant data was generated using SKAT for a 3kb region where 10% of the markers with MAF< 0.001 are causal for n = 5000 subjects. Binary phenotypes are generated such that

$$\mathit{logit}(p_{jk})={\beta }_0+{\beta }_k{I}_j$$ (6)

for subject j = 1,..., n and phenotype Y_k for k = 1,.. where p_jk = Prob(Y_jk = 1) and I_j is an indicator that subject j has any causal variants in the region. Normally distributed phenotypes are generated such that

$$E[Y_{jk}]={\beta }_0+{\beta }_k{I}_j$$ (7)

for subject j = 1,..., n and phenotype k = 1,... Similar to the common variant scenario, we vary β₁ from 0 to 5 by 0.5 for each simulation and fix β₂ = 2. To determine the p-value of phenotype k with the rare variants in the region, we used the SKAT-O test statistic [Wu et al., 2011]. SKAT-O is an extension of the SKAT method that allows for a combined burden and variance based test of rare variants. While we used this method for the simulations, other rare variant methods could have been easily used.

For each scenario, we generated 11 sets of 10,000 simulated datasets and ran the proposed approaches for 10,000 permutations each. In the supplemental Figures 6–8, we evaluated the power and type 1 error rate for the following 3 scenarios: 2 normally distributed phenotypes (Supplemental Figure 6), 1 normally distributed phenotype and 1 binary phenotype (Supplemental Figure 7), and 2 binary phenotypes (Supplemental Figure 8).

Results

Common Variant Simulations

As seen in Figure 1 for 2 normally distributed phenotypes, we compare the approaches to the standard method (PET-B) [Zhang et al., 2014], canonical correlation analysis (CCA) [Province et al., 2013] and correlated meta-analysis (CMA) [Province et al., 2013]. Both CCA and CMA have an inflated type-1 error rate as shown in the PET-B paper [Zhang et al., 2014] and in Figure 1. For all 6 scenarios (Figure 1 and Supplemental Figures 1–5), we compare the two proposed approaches to the ad-hoc approach where pleiotropy is achieved if each of the observed p-values is less than the α cut-off (i.e. α = 0.05) since existing methods are not applicable. The type-1 error rate is maintained for all methods across all scenarios, except CCA and CMA. When various combinations of β_m = 0 for m ≥ 1, both proposed methods maintain the type 1 error rate. The power is also comparable for the 2 proposed approaches, PET-B (for 2 normally distributed phenotypes), and the ad-hoc approach of using a cut-off of 0.05. While the ad-hoc approach does not formally test for pleiotropy (e.g. provide a p-value), the 2 proposed approaches (i.e. Step 3a: cut-off threshold based on permutation and Step 3b: Hausdorff metric) allow to formally test for the pleiotropy, perform well in all of the simulation scenarios, and work for various phenotypes.

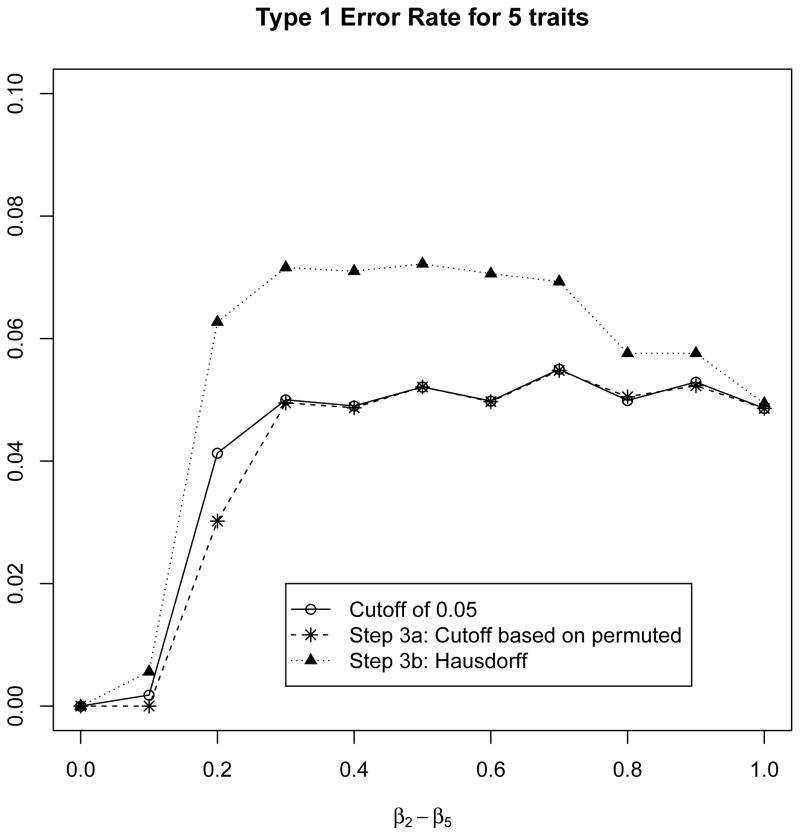
In Figure 2, we also evaluated the type 1 error rate of the 2 proposed approaches when 1 normally distributed phenotype is not associated with the SNP of interest, but the other 4 normally distributed phenotypes are strongly associated with the SNP. For this scenario, we fixed β₁ = 0 and β₂ = β₃ = β₄ = β₅ vary from 0 to 1 by 0.1. Note that the ad hoc approach and the cut-off based permutation approaches both maintain the type 1 error rate, but the Hausdorff based approach has a slightly inflated type 1 error rate of 0.06 to 0.07. Therefore, if several phenotypes are strongly associated with the SNP of interest, then we recommend using the cut-off based permutation approach instead of the Hausdorff based approach.

Figure 2.

For 5 normally distributed phenotypes, we evaluated the type-1 error rate of the proposed approaches when one phenotype is not associated with the SNP, but the other 4 phenotypes are strongly associated with the SNP. We fixed β₁ = 0 and β₂ = β₃ = β₄ = β₅ vary from 0 to 1 by 0.1. Note that the ad hoc approach and the cut-off based permutation approaches both maintain the type 1 error rate, but the Hausdorff based approach has a slightly inflated type 1 error rate of 0.06 to 0.07.

Rare Variant Simulations

The results for the rare variant simulations are similar to those of the common variant scenarios. For all 3 scenarios as seen in Supplemental Figures 6–8, the 2 proposed approached and the ad hoc approach maintain the type 1 error rate and achieve similar power.

Data Analysis

We applied these methods to the Genetic Epidemiology of COPD (COPDGene) Study which is a multi-center case-control study designed to identify genetic determinant of COPD and COPD-related phenotypes. [Regan et al., 2010] The study recruited COPD cases and controls who were non-Hispanic Whites and African Americans ages 45 to 80 all with at least 10 pack-years of smoking history. Among non-Hispanic Whites COPDGene subjects, we considered rs16969968 on chromosome 15 [CHRNA5], which is associated with FEV₁ (p-value=1.38e-08), the log of pack-years of smoking history (p-value=2.30e-9), COPD affection status (p-value=6.36e-06), and the log of percent emphysema (p-value=7.88e-11). However, rs16969968 is not associated with height (p-value=0.43). Table 1 shows that the SNP has a pleiotropic effect for various combinations of FEV₁, pack-years of smoking history, COPD affection status, and emphysema. However, when height is considered, the 2 proposed methods and PET-B do not find a pleiotropic effect as expected. Among non-Hispanic Whites COPDGene subjects, we also considered 40 rare variants (MAF< 0.01) from 78729773 bp to 79027837 bp [CHRNA3/5, CHRNB4, IREB2, AGHPD1]. Using SKAT-O, the region is not significantly associated with any of the phenotypes: FEV₁ (p-value=0.48), the log of pack-years of smoking history (p-value=0.04), COPD affection status (p-value=0.51), the log of percent emphysema (p-value=0.14), and height (p-value=0.09). As expected, Table 1 shows that this region has no pleiotropic effect for any of the various combinations of FEV₁, pack-years of smoking history, COPD affection status, emphysema, and height. This analysis shows that while the common variant rs16969968 has a pleiotropic effect on FEV₁, pack-years of smoking history, COPD affection status, and emphysema, the rare variants in the 15q25 region do not have a pleiotropic effect on these phenotypes.

Table 1.

In the COPDGene study, we tested for pleiotropy for various combinations of the following phenotypes using the PET-B method and the 2 proposed approaches for the common variant rs16969968 on chromosome 15 [CHRNA5/3], and 40 rare variants on chromosome 15q25 [CHRNA5/3, CHRNB4, IREB2, AGHPD1]. For the p-values listed below, note that the SNP rs16969968 has a pleiotropic effect for various combinations of FEV₁, pack-years of smoking history, COPD affection status, and emphysema. However, when height is considered, the 2 proposed methods and PET-B do not find a pleiotropic effect as expected. NAs are given for the PET-B method when any of the phenotypes considered are not normally distributed (e.g. COPD) or there are more than 2 phenotypes. While the common variant rs16969968 has a pleiotropic effect on FEV₁, pack-years of smoking history, COPD affection status, and emphysema, the rare variants in the 15q25 region do not have a pleiotropic effect on these phenotypes.

	Common PET-B	Variant 3a: Cutoff	rs16969968 3b: Hausdorff	Rare 3a: Cutoff	Variants 3b: Hausdorff
FEV1 & Pack-years	0	1.1e-7	1.0e-7	0.35	1.00
FEV1 & COPD	NA	1.6e-7	1.5e-7	0.43	1.00
FEV1 & Emphysema	0	1.0e-8	1.0e-8	0.36	1.00
FEV1 & Height	0.43	0.30	0.861	0.30	0.96
Pack-years & COPD	NA	2.7e-7	2.5e-7	0.33	1.00
Pack-years & Emphysema	0	1.2e-7	1.1e-7	0.21	0.36
FEV1, Pack-years, COPD, & Emphysema	NA	2.8e-7	2.7e-7	0.80	0.94
FEV1, Pack-years, COPD, Emphysema, & Height	NA	0.30	0.987	0.84	0.99

Discussion

The successful applications of GWAS to numerous complex diseases established a large number of robust genetic associations. As many of these associations are for the same locus or region, it also triggered the old question of genetic overlap between diseases, as a further step to better understand the underlying mechanisms of complex diseases. At a genome-wide level/chromosomal level, approaches have been developed that quantify the genetic overlap between phenotypes/diseases in terms of variance, but they cannot identify the causal genomic areas that are shared between the phenotypes. As the question of genetic overlap has moved to the forefront of standard substantive research, locus-specific approaches are required. Here, we provide such approaches that provide a formal statistical test for pleiotropy that is generally applicable to most genetic association studies, as it can handle any type of genetic data, ( e.g. GWAS, sequencing data, etc), and different types of phenotypic variables, (e.g. affection status, quantitative phenotypes). It is computationally fast and easy to implement. The simulations studies and the data analysis show that both of the proposed approaches perform well under various scenarios. The code for the proposed approaches is available upon request.

As examined in Figure 2, while the cut-off based permutation approach maintains the type 1 error rate when 4 phenotypes are strongly associated with the SNP of interest and 1 phenotype is not associated with the SNP of interest, there is a decrease in power when more phenotypes are tested for a pleiotropic relationship. For instance, the power shown in Figure 1 when 2 normally distributed phenotypes are considered is much higher then the power shown in Supplemental Figures 3–5 which consider 3, 4, and 5 normally distributed phenotypes, respectively. Therefore, care needs to be given to the number of phenotypes that are tested for a pleiotropic relationship with common or rare variants. For instance, if several phenotypes are highly correlated such as FEV₁, FEV₆, and FEV₁ percent predicated, then it would be prudent to include only one of these phenotypes (e.g FEV₁) instead of all 3 phenotypes.

Additionally, the null hypothesis will fail to be rejected if only a proportion of the traits are pleiotropic. For example, if four traits are pleiotropic and the fifth trait is not associated with the gene or SNP of interest, then the method will fail to reject the null hypothesis since the SNP does not have a pleiotropic relationship with all five traits. This scenario was demonstrated in the Data Analysis Section when both of the proposed methods rejected the null hypothesis that rs16969968 on chromosome 15 [CHRNA5] was not jointly associated with FEV₁, pack-years of smoking history, COPD affection status, and percent emphysema. However, when height was considered with this set of four traits, the proposed methods failed to reject the null hypothesis since height is not associated with rs16969968 on chromosome 15 [CHRNA5]. Thus, careful consideration is needed to select the traits to test for a pleiotropic relationship with the SNP or gene of interest. A literature review can be used to help identify which subset of traits most likely contribute to the pleiotropic effects.

While the proposed approaches are able to determine if a gene is associated with multiple phenotypes, it is unclear if the joint associations with multiple phenotypes are attributable to environmental correlation of the phenotypes or, indeed, by shared genetic components between phenotypes. It is possible that the phenotypes are associated with the same genetic region due to ascertainment bias. In case-control genetic association studies, the subjects are ascertained based on case-control status which may be correlated with any additional secondary phenotypes that are collected. As a result, analyzing secondary phenotypes that are correlated with case-control status may produce a spurious genetic association. For instance, in the COPDGene study, a gene could be associated with emphysema strictly because (a) that gene is associated with COPD, (b) the subjects were ascertained based on COPD status, and (c) COPD is correlated with emphysema. However, the proposed approaches can be adjusted for this case-control sampling by using an adjusted score test that properly reflects the case-control sampling when the p-values are calculated. [Lin et al., 2009], [Lutz et al., 2014] A similar adjustment can also be used to determine if the pleiotropic effect is the result of correlated (environmental) secondary phenotypes.

While the proposed approaches can determine if a gene is associated with multiple phenotypes, these methods do not determine how the gene is associated with multiple phenotypes. Mediation analysis and causal inference can be used to determine the path from gene to disease once this pleiotropy is established. [Lutz et al., 2014b], [Vansteelandt et al., 2009]