GPU-powered Shotgun Stochastic Search for Dirichlet process mixtures of Gaussian Graphical Models

Abstract

Gaussian graphical models are popular for modeling high-dimensional multivariate data with sparse conditional dependencies. A mixture of Gaussian graphical models extends this model to the more realistic scenario where observations come from a heterogenous population composed of a small number of homogeneous sub-groups. In this paper we present a novel stochastic search algorithm for finding the posterior mode of high-dimensional Dirichlet process mixtures of decomposable Gaussian graphical models. Further, we investigate how to harness the massive thread-parallelization capabilities of graphical processing units to accelerate computation. The computational advantages of our algorithms are demonstrated with various simulated data examples in which we compare our stochastic search with a Markov chain Monte Carlo algorithm in moderate dimensional data examples. These experiments show that our stochastic search largely outperforms the Markov chain Monte Carlo algorithm in terms of computing-times and in terms of the quality of the posterior mode discovered. Finally, we analyze a gene expression dataset in which Markov chain Monte Carlo algorithms are too slow to be practically useful.

1 Introduction

Gaussian graphical models (GGMs) are widely used as a framework for sparse estimation of precision matrices in high dimensional problems (e.g., see Wong et al., 2003; Jones et al., 2005; Scott & Carvalho, 2008). GGMs assume that the joint distribution of a high-dimensional random variable X = (X₁, …, X_p)^T follows a normal distribution whose precision (inverse of the covariance) matrix has non-diagonal zero entries encoded by the absent edges of a p-dimensional graph.

One shortcoming of standard GGMs is that they assume that observations are independent and identically distributed. However, real datasets often exhibit heterogeneity, which can be accommodated through the use of mixtures of Gaussian graphical models that allow for different conditional independence patterns on each cluster (Rodriguez et al., 2011). To illustrate this idea, consider modelling gene expression data, where entry X_j is associated with the expression level of gene j. GGMs have been widely used in this context to identify pathways and define metagenes (e.g., see Dobra et al., 2004; Jones et al., 2005; Peña, 2008). However, recent studies suggest that in applications such as cancer genetics, the population can be more effectively described as a mixture of a small number of components, with each component presenting differentially expressed genes as well as different expression pathways (The Cancer Genome Atlas Network, 2012).

Existing Bayesian procedures for estimating mixtures of GGMs rely on Markov chain Monte Carlo (MCMC) algorithms. However, these algorithms scale poorly as the number of variables p grows. This issue is well known in the literature on Gaussian graphical models (Jones et al., 2005; Scott & Carvalho, 2008), but it is further compounded in the case of mixtures of GGMs because of the need to jointly explore the space of partitions and the space of graphs associated with each element of the partition. The first contribution of this paper is a novel algorithm for stochastic search in mixtures of GGMs. Unlike MCMC methods, stochastic search methods dispense with the goal of converging to a stationary distribution in favor of identifying the mode(s) of the posterior distribution. Stochastic search algorithms for Gaussian graphical models have been discussed in Dobra & West, 2004; Jones et al., 2005; Scott & Carvalho, 2008; Moghaddam et al., 2009; Lenkoski & Dobra, 2011, and have also been applied to other high-dimensional problems such as model selection (Berger & Molina, 2005; Hans et al., 2007; Bottolo & Richardson, 2010; Heaton & Scott, 2010; Kwon et al., 2011), sparse factor analysis models (Carvalho et al., 2008; Yoshida &West, 2010), and dynamic graphical models (Wang et al., 2011). To explore the space of graphs, our algorithm uses a shotgun stochastic search similar to the one discussed in Jones et al., 2005 to quickly explore vast regions of graph spaces and aggressively move towards high-probability models. In addition, in the spirit of Scott & Carvalho (2008), our approach uses estimates of the edge-inclusion probabilities based on its earlier explorations to guide global moves.

The second contribution of this work is a discussion of a massively parallel implementation of the stochastic search algorithm using graphical processing units (GPUs). GPUs are dedicated manycore numerical processors capable of performing massive parallel computational tasks. Originally designed for fast three-dimensional computer graphics rendering, GPUs caught the attention of the scientific community early on (e.g., Larsen & McAllister, 2001; Krüger & Westermann, 2003; Bolz et al., 2003; Agarwal et al., 2003; Charalambous et al., 2005). Owens et al., 2007 provides an excellent survey of early GPU applications. As GPU architectures have evolved to include single program multiple data (SPMD) capabilities, faster double-precision arithmetic capability and rich programming environments, the number of scientific domains in which they have been used has increased dramatically. Examples include applications in bioinformatics (Horn et al., 2005; Liu et al., 2006; Manavski & Valle, 2008; Jiang et al., 2009; Sinnott-Armstrong et al., 2009), finance (Tse, 2012; Oancea et al., 2012; Cai et al., 2013), systems biology (Dematté & Prandi, 2010), data-mining (Takizawa & Kobayashi, 2006; Che et al., 2008; Pangborn, 2010; Heinecke et al., 2012), numerical optimization (Zhou et al., 2010) and molecular dynamics simulation (Yang et al., 2007; Anderson et al., 2008; van Meel et al., 2008).

Over the last few years, GPU computation has started to permeate the statistics literature. Substantial gains have been reported in applications with easily parallelizable components, such as sequential Monte Carlo (SMC) algorithms (Jacob et al., 2011; Fulop & Duan, 2011; Murray et al., 2012; McAlinn et al., 2012; Lee et al., 2012; Murray et al., 2013), approximate Bayesian computation (Liepe et al., 2010; Aune et al., 2013), and parallel-tempering MCMC (Mingas & Bouganis, 2012). GPU parallelization has also been employed for distributing large-scale likelihood computations in spatial modelling and statistical phylogenetics (Eidsvik et al., 2013; Suchard & Rambaut, 2009; Ayres et al., 2012), to accelerate specific calculations involved in fitting generalized linear models (Suchard et al., 2012), and to speedup independent Metropolis-Hastings and multivariate slice-sampling steps within larger MCMC algorithms (Jacob et al., 2011; Tibbits et al., 2011). Most relevant to our work, Suchard et al. (2010) and Cron & West (2011) explored GPU implementations of low-dimensional mixture models with large number of components in massive datasets. However, we are not aware of any application of GPU parallelization in the contexts of structure learning for Gaussian graphical models or mixture models for high-dimensional data. Indeed, unlike previous attempts to parallelize mixtures using GPUs, the model and applications we consider here involve a relatively small number of high-dimensional observations. Implementation of these type of models involves unique challenges including the need to deal with uneven memory requirements across individual tasks and with large numbers of logical operations.

The rest of the paper is organized as follows: We begin by reviewing Bayesian inference for Dirichlet process mixtures of Gaussian graphical models in section 2. Section 3 discusses existing MCMC algorithms for Dirichlet process mixtures of Gaussian graphical models and presents a novel stochastic search algorithm for finding the maximum a-posteriori estimate of relevant model parameters. In section 4 we discuss strategies for the implementation of these algorithms on GPU systems. Computational and inferential usefulness of our algorithm is illustrated in section 5 with synthetic and real data examples. Finally, section 6 concludes with a discussion of future research directions.

2 Mixtures of Gaussian graphical models

2.1 Gaussian graphical models

Let G = (V, E) be an undirected graph with index set V = {1, …, p} and edge-set E. A vector-valued random variable X = (X₁, …, X_p)^T ∈ ℝ^p is said to follow a Gaussian graphical model with mean μ and precision matrix K with respect to the graph G, denoted X | μ, K, G ~ N_G(X | μ, K⁻¹), if X follows a joint p-variate normal distribution mean vector μ and precision matrix K such that K_ij = K_ji = 0 for all (i, j) ∉ E. The random variable X is Markov with respect to the graph G under this model, implying that X_i and X_j are conditionally independent given all other variables in the model, i.e., X_i ⫫ X_j | X_V\{i,j} for all (i, j) ∉ E.

In this paper we focus our attention on the class ${𝒢}_V^D$ of decomposable graphs on V (Lauritzen, 1996). Decomposable graphs may be defined inductively though a decomposition of V into nonempty subsets C₁, C₂ and S such that C₁ ∪ C₂ ∪ S = V, C₁ ∩ C₂ = S, S is completely connected (i.e., any two vertices in S are connected by an edge), and every path connecting a vertex in C₁ to a vertex in C₂ goes through S. Applying this process sequentially leads to a decomposition of V into a collection of k prime components 𝒞(G) = {C₁, …, C_k} that cannot be further decomposed, and a collection of k − 1 separators 𝒮(G) = {S₂, …, S_k}. A graph that admits such a decomposition where each prime component is completely connected is called a decomposable graph.

If G is a decomposable graph, the probability density of a Gaussian graphical model factorizes as (Dawid & Lauritzen, 1993)

$${\mathrm{N}}_G(X|\mu ,K^{-1})=\frac{{\prod }_{C\in 𝒞(G)}\mathrm{N}(X_C|{\mu }_C,K_C^{-1})}{{\prod }_{S\in 𝒮(G)}\mathrm{N}(X_S|{\mu }_S,K_S^{-1})},$$ (1)

where μ_P is the sub-vector of μ corresponding to the indices in P ⊂ V and $K_P^{-1}={(K^{-1})}_P$ is the precision matrix associated with the marginal distribution of the vertices that belong to P. Note that we have slightly abused notation by using N_G(X | μ, K⁻¹) to denote both the law of the graphical Gaussian variable as well as the associated density (and similarly for N(X | μ, K⁻¹)).

2.2 Priors for Gaussian graphical models

Bayesian inference for GGMs requires the specification of priors for the unknown parameters μ, K and G. Conditionally on G, we characterize uncertainties in (μ, K) using a normal/G-Wishart prior of the form μ, K | G ~ N (μ | μ₀, {n₀K}⁻¹) W_G (K | δ₀, D₀). The G-Wishart distribution with parameters δ₀, D₀ and G extends the well known Wishart distribution to the cone of symmetric positive-definite matrices P_G such that K_ij = 0 for all (i, j) ∉ E. Indeed, when G is complete the G-Wishart distribution W_G(K | δ₀, D₀) is identical to the Wishart distribution W(K | δ₀, D₀). The density of the G-Wishart distribution with respect to the Lebesgue measure on P_G has the form (Roverato, 2002; Atay-Kayis & Massam, 2005; Letac & Massam, 2007)

$$p(K|{\delta }_0,D_0,G)=\frac{1}{I_G({\delta }_0,D_0)}{(\text{det }K)}^{({\delta }_0-2)/2}\text{exp}\{-\frac{1}{2}\text{tr}(K{D}_0)\},$$ (2)

where the normalizing constant I_G(δ₀, D₀) is finite if δ₀ > 2 and $D_0^{-1}\in P_G$ (Diaconis & Ylvisaker, 1979). In particular, when G is decomposable, Dawid & Lauritzen (1993) show that the G-Wishart distribution can be factorized into Wishart distributions for the cliques and the separators of G as

$$p(K|{\delta }_0,D_0,G)=\frac{{\prod }_{C\in 𝒞(G)}\mathrm{W}[K_C|{\delta }_0,{(D_0)}_C]}{{\prod }_{S\in 𝒮(G)}\mathrm{W}[K_S|{\delta }_0,{(D_0)}_S]},$$ (3)

where (D₀)_P is the symmetric positive-definite diagonal sub-block of D₀ with indices in P ⊂ V. Hence, for decomposable G, the normalizing constant I_G(δ₀, D₀) in (2) factorizes as (Roverato, 2002)

$$I_G({\delta }_0,D_0)=\frac{{\prod }_{C\in 𝒞(G)}{I}_{G_C}[{\delta }_0,{(D_0)}_C]}{{\prod }_{S\in 𝒮(G)}{I}_{G_S}[{\delta }_0,{(D_0)}_S]}.$$

In the previous expression, I_GP [δ₀, (D₀)_P] is the normalizing constant of the corresponding Wishart distribution, I_GP [δ₀, (D₀)_P] = 2^{(δ₀+|P|−1)|P|/2} Γ_p{(δ₀ + |P| − 1)/2} {det (D₀)_P}^{−(δ₀+|P|−1)/2}, where |P| is the size of P ⊂ V, and ${\mathrm{\Gamma }}_p(x)={\pi }^{p(p-1)/4}{\prod }_{i=0}^{p-1}\mathrm{\Gamma }(x-i/2)$ for x > (p − 1)/2 (Muirhead, 1982).

The model is completed by eliciting a prior for G. Most of the discussion that follows assumes that G is uniformly distributed on ${𝒢}_V^D$ a priori, $G~\text{Uni }({𝒢}_V^D)$, which slightly simplifies the form of the scoring functions used to select graphs. However, one potential drawback of this choice is that a uniform prior on the space of graphs tends to favor graphs of medium size. Alternatively, the algorithms we discuss in this paper can be extended to accommodate alternative priors that alleviate this issue. For example, the algorithm can be extended to accommodate the size-biased prior proposed by Armstrong et al. (2009), in which a uniform prior is assigned to the size (number of edges) of the graph and, conditional on the size, all graphs of the same number of edges are assigned a uniform prior probability.

2.3 Scoring Gaussian graphical model

Let x^(1:n) = (x⁽¹⁾, …, x⁽ⁿ⁾) be an independent and identically distributed sample with x⁽ⁱ⁾ | μ, K, G ~ N_G (μ, K⁻¹). One advantage of decomposable graphs is that computing the marginal posterior distribution for G is relatively straight-forward. Firstly, since we employ a uniform prior on the space of graphs we have

$$p(G|x^{(1:n)})=\frac{p(x^{(1:n)}|G)p(G)}{{\sum }_{G\prime \in {𝒢}_V^D}p(x^{(1:n)}|G\prime )p(G\prime )}\propto p(x^{(1:n)}|G).$$ (4)

Secondly, because the normalizing constant of the G-Wishart distribution is available in closed form for decomposable graphs, we have

$$p(x^{(1:n)}|G)={(2\pi )}^{np/2}{\left(\frac{n_0}{n+n_0}\right)}^{p/2}\frac{{\prod }_{C\in 𝒞(G)}{I}_{G_C}[{\delta }_0+n,{(D_0+U+A)}_C]/I_{G_C}[{\delta }_0,{(D_0)}_C]}{{\prod }_{S\in 𝒮(G)}{I}_{G_S}[{\delta }_0+n,{(D_0+U+A)}_S]/I_{G_S}[{\delta }_0,{(D_0)}_S]},$$ (5)

where $\overline{x}={\sum }_{i=1}^n{x}^{(i)}/n$, μ̄ = (nx̄ + n₀μ₀)/(n + n₀), $U={\sum }_{i=1}^n(x^{(i)}-\overline{x}){(x^{(i)}-\overline{x})}^T$, and $A=-(n+n_0)\overline{\mu }{\overline{\mu }}^T+n\overline{x}{\overline{x}}^T+n_0{\mu }_0{\mu }_0^T$ (see Rodriguez et al., 2011).

Although (5) is easy to compute for any graph G, the sheer size of the space of graphs prevents us from directly sampling from (4). For that reason, most computational approaches for Bayesian inference on GGMs usually explore (4) using random walk proposals that attempt to change a small number of edges at a time (Giudici & Green, 1999; Wong et al., 2003; Scott & Carvalho, 2008). Alternatively, stochastic search algorithms such as those described in Jones et al. (2005) and Lenkoski & Dobra (2011) are used to greedily explore the space of graphs When G is assumed to be decomposable, both types of algorithms often rely on the notion of decomposable local neighborhood to devise a search strategy. The (first order) decomposable local neighborhood of a graph G is composed of all decomposable graphs that differ from G by at most one edge (note that there are at most p(p − 1)/2 + 1 such graphs in this neighborhood, including the current G).

2.4 Dirichlet process mixtures of Gaussian graphical models

Consider now a new random sample x^(1:n) = (x⁽¹⁾, …, x⁽ⁿ⁾) distributed according to a mixture of Gaussian graphical models

$$p(x^{(i)}|w_{1:L}^{*},{\mu }_{1:L}^{*},K_{1:L}^{*},G_{1:L}^{*})=\sum _{l=1}^L{w}_l^{*}{\mathrm{N}}_{G_l^{*}}(x^{(i)}|{\mu }_l^{*},{\{K_l^{*}\}}^{-1}),$$

where $w_1^{*}+\dots +w_L^{*}=1$. A random observation x⁽ⁱ⁾ from this distribution comes from one of the L Gaussian graphical models that have potentially different means, precision matrices and conditional dependence graphs. Consequently, the mixture model adds additional flexibility over regular Gaussian graphical models by allowing a heterogeneous population to be divided into homogeneous groups.

A fully Bayesian specification of the model requires that we elicit prior distributions for the parameters $w_{1:L}^{*},{\mu }_{1:L}^{*},K_{1:L}^{*}$, and $G_{1:L}^{*}$. In this paper we work with the Dirichlet process mixture (DPM) of Gaussian graphical models (Ferguson, 1973; Sethuraman, 1994; Escobar & West, 1995; Rodriguez et al., 2011),

$$p(x^{(i)}|H)=\int {\mathrm{N}}_G(x^{(i)}|\mu ,K^{-1})H(d\mu ,dK,dG),\hspace{1em}H(·)=\sum _{l=1}^{\infty }{w}_l^{*}{\delta }_{({\mu }_l^{*},K_l^{*},G_l^{*})}(·),$$ (6)

where δ_a(·) denotes the degenerate probability measure with all its mass on a, $w_l^{*}=u_l{\prod }_{j<l}(1-u_j)$ with u₁, u₂, … being an independent and identically distributed sequence with u_l ~ Beta(1, α), and $(u_1^{*},K_1^{*},G_1^{*}),(u_2^{*},K_2^{*},G_2^{*}),\dots$ being another independent and identically distributed sequence such that

$$G_l^{*}~\text{Uni}({𝒢}_V^D),\hspace{1em}\hspace{1em}\hspace{1em}{K}_l^{*}|G_l^{*}~{\mathrm{W}}_{G_l^{*}}({\delta }_0,D_0),\hspace{1em}\hspace{1em}\hspace{1em}{\mu }_l^{*}|K_l^{*},G_l^{*}~\mathrm{N}({\mu }_0,{\{n_0{K}_l^{*}\}}^{-1}).$$

It is often useful to rewrite the Dirichlet process mixture model by introducing independent mixture indicators ξ₁, …, ξ_n such that ξ_i = l if and only if x⁽ⁱ⁾ is generated from the l-th component of the mixture. Conditional on these indicators, (6) can be written as

$$x^{(i)}|{\xi }_i=l,{\mu }_{1:\infty }^{*},K_{1:\infty }^{*}~{\mathrm{N}}_{G_l^{*}}(x^{(i)}|{\mu }_l^{*},{\{K_l^{*}\}}^{-1}),\hspace{1em}\hspace{1em}\hspace{1em}\text{Pr}({\xi }_i=l|w_{1:\infty }^{*})=w_l^{*}.$$

Integrating over the prior for the random probabilities $w_1^{*},w_2^{*},\dots$ we can obtain the joint distribution of the vector of indicators ξ_1:n = (ξ₁, …, ξ_n) (Antoniak, 1974)

$$p({\xi }_{1:n}|\alpha )=p(L^{*},m_1,\dots ,m_{L^{*}}|\alpha )=\frac{\mathrm{\Gamma }(\alpha )}{\mathrm{\Gamma }(\alpha +n)}{\alpha }^{L^{*}}\prod _{l=1}^{L^{*}}\mathrm{\Gamma }(m_l),$$ (7)

where L* ∈ {1, …, n} represents the number of distinct values among ξ₁, …, ξ_n (the number of active components) and m_l is the sample-size of l-th component in a sample of size n (note that, without lack of generality, we assume that components are labeled continuously between 1 and L*).

There are strong connections between finite mixtures and Dirichlet Process mixture models. For example, a finite mixture model in which the component weights are assigned a symmetric Dirichlet distribution, $({\omega }_1^{*},\dots ,{\omega }_L^{*})~\text{Dir}(\alpha /L,\dots ,\alpha /L)$ provides an approximation to a Dirichlet process mixture model, in the sense that the marginal distribution for ξ_1:n induced by the symmetric Dirichlet, $p_{SM}({\xi }_{1:n}|\alpha )=\frac{\mathrm{\Gamma }(\alpha )}{\mathrm{\Gamma }(\alpha +n){\{\mathrm{\Gamma }(\alpha /L)\}}^L}{\prod }_{l=1,m_l>0}^L\mathrm{\Gamma }(\alpha /L+m_l)$, converges to (7) as L → ∞ (Ishwaran & Zarepour, 2002). From a computational perspective, one advantage of working with a Dirichlet process in this context is that only components that instantiate observations need to be tracked. However, (7) tends to favor a priori partitions of the data with very uneven sizes (for a more detailed discussion see for example Green & Richardson, 2001).

From (7) it is clear that the value of α plays a critical role in controlling the prior probability over partitions of the data into clusters. More specifically, smaller values of α favor a small number of active components L*, and vice versa. Because of this critical role on the prior configurations we specify a (proper) marginal Jeffrey’s prior on α, $\pi (\alpha )\propto \sqrt{\frac{1}{\alpha }{\sum }_{j=1}^{n-1}\frac{j}{{(\alpha +j)}^2}}$ for α > 0 (Rodriguez, 2013). Under this hyperprior, the marginal prior distribution has the form $p({\xi }_{1:n})\propto \psi (n,L^{*}){\prod }_{l=1}^{L^{*}}\mathrm{\Gamma }(m_l)$, where $\psi (n,L^{*})={\int }_0^{\infty }\frac{\mathrm{\Gamma }(\alpha )}{\mathrm{\Gamma }(\alpha +n)}{\alpha }^{L^{*}-1/2}\sqrt{{\sum }_{j=1}^{n-1}\frac{j}{{(\alpha +j)}^2}}\mathrm{d}\alpha$. Although the integral involved in the definition of ψ(n, L*) cannot be solved in closed form, it can be easily computed using numerical algorithms. In particular, we recommend using the Gauss-Kronrod 21-point integration rule after mapping the integrand onto (0, 1] with the transformation α = (1 − t)/t. Also, note that since the definition of ψ(n, L*) only involves n and L* (but not the actual size of each component). Hence, only a maximum of n such integrals need to be computed, either as a preprocessing step or on the fly, with results for values of L* that had not been observed in the past being stored for possible later reuse.

2.5 Scoring mixtures of Gaussian graphical models

As with standard Gaussian graphical models, we can score a given mixture model for the sample x⁽¹⁾, …, x⁽ⁿ⁾ (which is defined through the number of clusters L*, cluster memberships indicators ξ₁, …, ξ_n, and cluster-specific graphs $G_1^{*},\dots ,G_L^{*}$) using the posterior distribution

$$p(L^{*},{\xi }_{1:n},G_{1:n}^{*}|x^{(1:n)})\propto \psi (n,L^{*})\prod _{l=1}^{L^{*}}\mathrm{\Gamma }(m_l)[{\left(\frac{n_0}{n_0+m_l}\right)}^{p/2}\frac{{\prod }_{C\in 𝒞(G_l^{*})}{I}_{{G_l^{*}}_C}[{\delta }_0+m_l,{(D_0+U_l+A_l)}_C]/I_{{G_l^{*}}_C}[{\delta }_0,{(D_0)}_C]}{{\prod }_{S\in 𝒮(G_l^{*})}{I}_{{G_l^{*}}_S}[{\delta }_0+m_l,{(D_0+U_l+A_l)}_S]/I_{{G_l^{*}}_S}[{\delta }_0,{(D_0)}_S]}]$$ (8)

where x̄_l = ∑_i∈Pl x⁽ⁱ⁾/m_l, μ̄_l = (n₀μ₀ + m_lx̄_l)/(n₀ + m_l), U_l = ∑_i:ξi=l(x⁽ⁱ⁾ − x̄_l)(x⁽ⁱ⁾ − x̄_l)^T, and $A_l=-(n_0+m_l){\overline{\mu }}_l{\overline{\mu }}_l^T+m_l{\overline{x}}_l{\overline{x}}_l^T+n_0{\mu }_0{\mu }_0^T$. In our experience, this score function is comparatively flatter on the graph space associated with $G_{1:n}^{*}$ than in the direction of the clustering parameters (L*, ξ_1:n). This fact will influence the design of the algorithm described in the next section.

3 Computation for Dirichlet process mixtures of Gaussian Graphical models

Even though in (8) the parameters of interest, $(L^{*},{\xi }_{1:n},G_{1:n}^{*})$ lie in a finite set, enumerating all possible models is practically impossible even for relatively small values of n and p. Hence, practical implementation of these models requires the development of algorithms that can efficiently explore the parameter space without enumerating all possible models. We start by reviewing the use of Makov chain Monte Carlo algorithms and then move on to describe a novel shotgun stochastic search algorithm.

3.1 Markov chain Monte Carlo

A Markov chain Monte Carlo algorithm for sampling from (8) that is based on ideas from Neal (2000) was presented in Rodriguez et al. (2011). Their MCMC sampler alternates between updating the configuration vector ξ_1:n and updating the graphs G₁, …, G_L associated with each mixture component. In our numerical evaluations we consider a slightly modified version of the algorithm that uses the non-informative prior on the precision parameter for the Dirichlet process described in Rodriguez (2013). The resulting full conditional distributions for the membership indicators reduces to

$$\text{Pr}({\xi }^{(j)}=l|{\xi }_{-j},x^{(1:n)},G_{1:L^{*,-j}}^{*})\propto \{\begin{array}{cc}\frac{m_l^{-j}A(n,n,L^{*,-j})}{A(n-1,n,L^{*,-j})}\hfill & l\le L^{*,-j}\hfill \\ \frac{A(n,n,L^{*,-j}+1)}{A(n-1,n,L^{*,-j})}\hfill & l=L^{*,-j}+1\hfill \end{array},$$

where L^*,−j is the number of non-empty clusters in the sample after excluding x^(j), $m_l^{-j}$ is the size of the l-th cluster in the sample excluding x^(j), $G_{1:L^{*,-j}}^{*}$ is the collection of component specific graphs associated with non-empty clusters after excluding x^(j), and

$$A(n,m,k)=\frac{{\int }_0^{\infty }{\alpha }^{k-\frac{1}{2}}\frac{\mathrm{\Gamma }(\beta )}{\mathrm{\Gamma }(\beta +n)}\sqrt{{\sum }_{j=1}^{m-1}\frac{j}{{(\alpha +j)}^2}}\mathrm{d}\alpha }{{\int }_0^{\infty }\sqrt{\frac{1}{\alpha }{\sum }_{j=1}^{m-1}\frac{j}{{(\alpha +j)}^2}}\mathrm{d}\alpha }.$$

Note that these quantities can be precomputed before running the MCMC algorithm, and that the denominator of A(n, m, k) cancels out when computing the full conditional distributions, so that $\frac{A(n,n,L)}{A(n-1,n,L)}=\frac{\mathrm{\Psi }(n,L)}{\mathrm{\Psi }(n-1,L)}$ and $\frac{A(n,n,L+1)}{A(n-1,n,L)}=\frac{\mathrm{\Psi }(n,L+1)}{\mathrm{\Psi }(n-1,L)}$. On the other hand, we explore the space of component-specific graphs using a random-walk Metropolis-Hastings sampler in which proposals for the graph $G_l^{*}$ are generated from among its decomposable neighbors with probability proportional to their posterior probability.

3.2 Shotgun stochastic search

Although the previous algorithm works well for relatively low dimensional responses (say, p ≤ 50 or so), it becomes prohibitively slow for a larger number of nodes. As an alternative, we investigate a novel stochastic search algorithm for finding the posterior mode(s) of a Dirichlet process mixture of Gaussian Graphical models. This stochastic search algorithm explores the space of parameters in part using local moves that are similar to those discussed in 3.1, but we now drop the need to maintain reversibility of the moves implied by Markov chain Monte Carlo algorithm and focus instead on a greedy approach to model exploration. Furthermore, we supplement the local moves with mid- and long-range moves that borrow ideas from more sophisticated MCMC algorithms for Dirichlet process mixture models (e.g., Dahl, 2003; Jain & Neal, 2004), as well as shotgun stochastic search (SSS) (Jones et al., 2005) and feature-inclusion selection algorithms (Scott & Carvalho, 2008) for Gaussian graphical models. These mid- and long-range moves are meant to address multimodalities in the posterior distribution. More specifically we consider the following moves:

1. Local shotgun move for $G_{1:L}^{*}$: Recall that the decomposable local neighborhood of $G_l^{*}$ is composed of all decomposable graphs that differ from $G_l^{*}$ by at most one edge (note that there are at most p(p − 1)/2 + 1 such graphs in this neighborhood, including the current $G_l^{*}$). We move to a randomly selected neighbor of $G_l^{*}$ with probability proportional to its score computed according to (4). This step is repeated for each l = 1, …, L*. Note that this is similar to the approach used in section 3.1 for exploring the space of graphs.

2. Local move for ξ_1:n: For a given i, define the local i-neighborhood of ξ_1:n as the set configurations that arises by reallocating ξ_i to one of the clusters. As before, we move to a randomly selected neighbor of ξ_1:n with probability proportional to its score. This step is repeated for every i = 1, …, n. Again, this step is in the same spirit to our approach to exploring graphs from section 3.1.

3. Split move for ξ_1:n: We generate a neighborhood of Q new configurations by randomly selecting and splitting the non-singleton components. Subsequently we move to one of the proposals or retain the current configuration according to their scores. Each proposed configuration is generated by first splitting the selected non-singleton component into two non-empty components uniformly at random, both of which are assigned the same parent graph. Then, for t iterations we perform f local shotgun updates on each of the two graphs and local updates for each of the indexes associated with the component that was split.

4. Merge move for ξ_1:n: If L* = 1 we do nothing. Otherwise, we generate $(\begin{array}{c}\hfill L^{*}\hfill \\ \hfill 2\hfill \end{array})$ proposed configurations by considering all pairwise component merges. We initially assign each merged component the graph associated with the largest of the two components being merged, and then we perform f local shotgun updating for that graph.

5. Mode-break move for $G_l^{*}$: We perform B local shotgun updating moves on $G_l^{*}$, but we disregard the top D high-probability neighbors in each random selection phase so that the search can climb down in the posterior probability surface away from the local mode.

6. Global jump move for $G_l^{*}$: Denote last M distinct graphs selected for the component of observation i by $G_i^{[1]},\dots ,G_i^{[M]}$, where $G_i^{[m]}=(V,E_i^{[m]})$. We generate a random graph with the following marginal edge-inclusion probabilities:

   $$q_l(j,k)=\frac{1}{M{m}_l}\sum _{m=1}^M\sum _{i:{\xi }_i=l}1[(j,k)\in E_i^{[m]}],\hspace{1em}j,k\in \{1,\dots ,p\},$$

   and set $G_l^{*}$ to the minimal decomposable supergraph of the sampled graph.

The different moves described above are organized hierarchically and executed at different frequencies (see algorithm 1). Because the posterior distribution tends to be comparatively flat on the space of graphs, local shotgun updates for the graphs are used most frequently. Every g local shotgun updates we insert a local update on ξ_1:n and a local merge update. Finally, every g × h iterations we insert a local split move. If the previous scheme fails to improve the model posterior for C consecutive iterations, we say that the search is trapped in a local mode. At this point mode-break moves are performed on all components with B = 1 and another C iterations of local shotgun moves are performed. If the new model posterior surpasses the modal posterior then the local-mode is broken. Otherwise, we repeat another set of mode-break moves with B ← B + 1 so that the search climbs further down the posterior surface before it climbs up again. This process is repeated at-most R times, after which the local mode is forcefully broken by a global jump move on a randomly selected component graph. We stop the overall search when no improvement is seen on the posterior probability for S consecutive iterations, where typically S ≫ C. We suggest selecting the threshold parameters C and S on the basis of the dimension of the problem to reflect that the search naturally wanders for longer in higher-dimensional models. In our illustrations we used C = (n + p) and S = 20(n + p). In our experience, a small number of local updates for the component-specific graphs and membership indicators in the split and merge moves is enough to improve the quality of the proposal configurations; in our illustrations we set Q = 1, f = 5 and t = 2 with good empirical results. We also suggest mixing the local shotgun moves on $G_{1:L}^{*}$ with the local updating moves on ξ_1:n in ratio of their respective parameter dimensions. We accomplish this in our implementation by setting g = Lp(p − 1)/2n. Since computation of the minimal triangulation supergraph in the global graph jump move is prohibitively slow with time-complexity of 𝒪(p³) (Berry et al., 2004), several mode-break moves should be attempted before a global graph jump move is called. In our illustration we set R = 10. Finally, we arbitrarily specify D = 10 and h = 10 for all of our mode-break moves.

Total execution time can be greatly reduced if good initial values for the algorithm are chosen. Indeed, in some of our tests the amount of time required to arrive at a meaningful region of the parameter space when a random initial configuration was used was prohibitive. We suggest using either known categorical covariates (as we do in section 5.3) or hierarchical clustering to identify multiple reasonable initial clustering configurations, while constructing component-specific graphs by thresholding the corresponding matrix of partial correlations. In addition, we strongly suggest running multiple search-chains starting at multiple reasonable starting points to more thoroughly explore the posterior distribution. Given I user-specified initial configurations and N search-chains, our algorithm initiates the first I search-chains respectively from the I specified configurations, and each of the subsequent (N − I) chains from one of the initial configurations that is randomly selected with probability proportional to their stopping-time score.

4 Parallel implementation using graphical processing units

4.1 Graphical processing units for parallel, high-performance computing

Graphical processing units (GPUs) are inexpensive manycore processors that can yield tremendous computational power for data-parallel problems. We use NVIDIA GPUs with CUDA 4.0 (NVIDIA CUDA C Programming Guide, Version 4.0, 2011) as our development environment. The NVIDIA GPU architecture is built around a scalable array of multi-threaded streaming multiprocessors (SMs), where each SM consists of a number of computing units (the CUDA cores), and a fast-access memory pool of the order of few kilobytes (the shared memory). Additionally, NVIDIA GPUs have a large, high-latency memory pool of the order of few gigabytes (the global memory).

CUDA is an extension of C where parallel jobs are programmed with special functions called kernels. Copies of a kernel running on the GPU are called threads. The CUDA programming model organizes threads in equal-sized blocks of threads and executes every thread in a thread-block on one SM during runtime. Each thread-block solves a coarse-grained parallel task with individual threads cooperatively performing finer-grained parallel operations. To use a GPU, data accessed by a kernel first need to be transferred to its global memory. Subsequently, a kernel call is executed by parallel execution of multiple threads-blocks on available SMs. After the kernel execution is finished all results need to be written to the global memory and copied back to the CPU.

Compared to other architectures for high-performance computing, GPUs offer the promise of fast computation at a very low cost. However, realizing the full potential of GPUs can be difficult because of the constraints imposed by the architecture. One of such constraint derives from the fact that SMs operate on the thread blocks in single instruction, multiple threads (SIMT) paradigm. Under SIMT, threads are run simultaneously on different pieces of data by different CUDA cores. When threads that are being run simultaneously diverge via data-dependent conditional branching, each branch path is serially executed while other threads are disabled. Parallel processing is restarted when all divergent paths have been completed. Hence substantial performance improvements usually require that the number of logical branching operations in each coarse-grained parallel task be minimized.

Algorithm 1.

Stochastic search for MAP estimation of DPM-GGM parameters

	Input: Initial parameter configurations ${(L,{\xi }_{1:n},G_{1:L}^{*})}_{[1]},\dots ,{(L,{\xi }_{1:n},G_{1:L}^{*})}_{[I]}$.
	Input: # chains N, # follow-up moves C, max # of iterations without score increment before stopping S.
	Input: Max # consecutive mode-break moves R, # top modes disregarded in move-break moves D.
	Input: Split and merge move parameters Q, f, t.
	Input: Mixing ratios: local shotgun graph moves to local ξ-moves g, local ξ-moves to split moves h.
1
2	for i ← 1 to N do
3		% Select the initial configuration for the i-th search chain
4		if i ≤ I then
5			$(L,{\xi }_{1:n},G_{1:L}^{*})\leftarrow {(L,{\xi }_{1:n},G_{1:L}^{*})}_{[i]}$
6		else
7			d ~ Multinomial(1, exp(last_best_score[1:I]))
8			$(L,{\xi }_{1:n},G_{1:L}^{*})\leftarrow {(L,{\xi }_{1:n},G_{1:L}^{*})}_{[d]}$
9
10		% Start the i-th run of stochastic search
11		k ← 0, c ← 0, last_best_score[i] ← −∞
12		while c < S do
13			% Local moves
14			while c < C do
15				if g * k is an integer then
16					Perform local update moves on ξ1, …, ξn
17					Perform the merge move with tuning parameters (f, t)
18					if g * h * k is an integer then
19						Perform the split move with tuning parameters (f, t)
20				else
21					Perform local shotgun update moves on $G_1^{*},\dots ,G_L^{*}$
22
23				if score > last_best_score then c ← 0
24				else c ← c + 1
25
26			% Move break moves
27			r ← 1, B ← 1
28			while c ≥ C and r ≤ R do
29				Perform a mode break move with tuning parameters (B, D)
30				for j ← 1 to C do
31					Perform local shotgun update moves on $G_1^{*},\dots ,G_L^{*}$
32
33				if score > last_best_score then c ← 0
34				else c ← c + C, r ← r + 1, B ← B + 1
35
36			% Global graph jump move
37			if r > R then
38				l ~ uniform{1, …, L}
39				Perform a global jump move on $G_l^{*}$
40				c ← 0
41
42			k ← k + 1
43			if score > last_best_score[i] then last_best_score[i] = score, ${(L,{\xi }_{1:n},G_{1:L}^{*})}_{[i]}^{*}\leftarrow (L,{\xi }_{1:n},G_{1:L}^{*})$
44
45	return ${(L,{\xi }_{1:n},G_{1:L}^{*})}_{[1:N]}^{*}$

Another issue with GPUs is memory organization. A kernel can allocate memory for a coarse-grained task either on the shared memory or on the global memory. The number of active thread-blocks on an SM during runtime is determined by the shared-memory requirement of the kernel. Trading fast-access shared memory allocations with slower global memory ones allows for more thread-blocks to be run simultaneously, but will slow down execution of each individual thread-block. Hence, the memory allocation is an important design choice that needs be optimized for overall GPU performance. Furthermore, when performing global memory read/writes, consecutive positions should be accessed in parallel threads for best performance.

Scaling up the number of GPUs can bring further computational speedups for massive-scale parallel problems (e.g., see section 5.1). Multi-GPU systems are particularly useful for kernels with total global memory requirement exceeding any single GPU’s memory pool. Indeed, kernels that allocate large global memory buffer for the thread-blocks may exhaust the global memory pool on a single GPU quite quickly. In this situations, it may take more than one kernel call to get the whole parallel job done. If one has multiple GPUs at its disposal, the total task may often be split into parts that can be fit into separate GPU global memory pools and executed simultaneously. In this situation, a thorough understanding of the system architecture (hardware configuration) and its impact on CPU-GPU and GPU-GPU memory throughputs is essential to achieve optimal computational performance (see Micikevicius, 2011 for additional details).

4.2 Speeding up model search using graphical processing units

Since shotgun updates for the component-specific graphs are by far the most frequent moves in our algorithm, we focus most of our attention on them. Shotgun updates involve two computationally demanding tasks, namely, testing decomposability of the p(p − 1)/2 neighbors of a given component-specific graph, and computing the score associated with each of those neighbors. GPU parallelization of these tasks is not trivial, as they involve numerous conditional statements which would normally be treated as conditional divergences in GPU thread-parallelization. To deal with this issue, we define 32-thread thread-blocks and treat each graph-decomposition test or score computation as a coarse-level problem solved by a thread-block. This strategy avoids most serial executions of conditional divergences and allows us to properly accommodate the shared memory requirement of each task.

Consider first the parallel implementation of the decomposability tests. Generally speaking, testing the decomposability of a p-vertex graph via maximal cardinality search has a time-complexity of 𝒪(p³) (Rose et al., 1976). However, since adding/deleting one edge to/from a decomposable graph affects at most two cliques and one separator, the decomposability test and marginal probability computations can be performed much more efficiently for local shotgun neighbors following the algorithm of Giudici & Green (1999). The condition for decomposability after an edge-deletion to a graph G = (V, E) verifies whether the edge is contained in exactly one clique of G. The condition for decomposability after adding an edge between vertices a and b examines (i) if a and b belong to different connected components in the parent graph, or (ii) if there exists R, T ⊂ V such that a ∪ R and b ∪ T are cliques of G, and S = R ∩ T is a separator on the path between a ∪ R and b ∪ T in the junction-tree of G.

We set up two kernels, CanDeleteEdge() and CanAddEdge(), to distribute the p(p − 1)/2 decomposability tests associated with the different neighbors to multiple GPUs simultaneously. In addition to implementing these kernels using a thread-block of 32 parallel threads, we reduce the memory requirements and data-transfer times by using a 2-byte short integer type throughout our implementation. Since the decomposability test implemented in CanDeleteEdge() requires single access to each clique, we store them on the global memory rather than the shared memory, and use only 8 bytes of shared memory for inter-thread communications. On the other hand, the test for edge-added neighbors requires multiple accesses to the cliques, separators and the junction tree. The kernel for this test loads the set S, the whole junction tree T, and one clique/separator of G at a time onto the shared memory. The shared memory requirement is (86+2p+4|T|) bytes, where p is the number of vertices in G and |T| is the number of edges in the junction tree. Both kernel-implementations reduce memory-latency by reading from/writing to the global memory pool in parallel threads. Initial data transfers to some GPUs are overlapped with the first kernel call in other GPUs to improve efficiency. Furthermore, transfer of results from the first kernel call is also overlapped with the second kernel execution. Finally, results from the second kernel call are copied back to the CPU, asynchronously, overlapping with the subsequent computations on the CPU.

In terms of parallelizing the computation of the score function, we note that because we are adding or removing a single edge at a time, this step again involves evaluating inverse-Wishart normalizing constants only for two cliques and one separator for each decomposable neighbor. As before, we implement a CUDA kernel GGScore() to evaluate the score of a given neighboring graph with a thread-block of 32 parallel threads. The program starts by copying D₀ and D₀ + U + A to the GPU global memory. Subsequently, the kernel extracts (D₀)_P and (D₀ + U + A)_P for each relevant clique and separator P, then computes det((D₀)_P) and det((D₀ + U + A)_P) by computing their Cholesky factorizations in parallel threads. We reduce memory latency by storing P, (D₀)_P and (D₀ + U + A)_P in $(60+4p_m+2p_m^2)$ bytes of the shared memory buffer, where p_m is the size of the largest clique for which we need to compute the inverse-Wisart normalizing constant. This rather large shared memory requirement constrains the size of cliques and separators that can be accommodated on the GPU. Furthermore, since CUDA allows only a single size dynamic shared memory allocation for a given kernel call, it is too wasteful to evaluate all neighboring graphs in a single kernel call as the shared memory requirement varies widely for different graphs. Hence, to improve GPU performance in this step we divide the decomposable neighbors into bins of comparable shared memory requirement, and evaluate large bins on the GPUs in separate kernel calls, while smaller bins are evaluated on the CPU simultaneously. Results from all GPU kernel calls are copied back to the CPU asynchronously, overlapping with other CPU computations.

4.3 Speeding up MCMC algorithms using graphical processing units

The GPU kernels discussed in Section 4.2 can also be used to accelerate computation for MCMC algorithms. In particular, the decomposability tests associated with the component-specific graph proposals discussed in section 3.1 can be parallelized using the CanDeleteEdge() and CanAddEdge() kernels introduced in section 4.2. Similarly, the GGScore() kernel can potentially be used to accelerate the calculation of the posterior distributions required for the different steps of the algorithm. However, although the use of GPU-enabled versions of the MCMC algorithm do tend to provide speedups when compared with their CPU-based counterparts, the execution times are still much longer than those of our novel stochastic search algorithms (see Section 5).

5 Illustrations and evaluation

We evaluate the performance of our proposed stochastic search algorithm using simulated datasets (sections 5.1 and 5.2) and real gene expressions (section 5.3). All computations were carried out on a system consisting of a AVA Direct Custom CrossFireX workstation with Intel Core i7-975 Extreme Quad-Core processor (clock speed: 3.33 Ghz) and three graphics cards: one Tesla C1060 (30 SMs with clock speed 1.30 Ghz) and two GeForce GTX 285 (30 SMs with clock speed 1.48 Ghz). All graphics cards are architecturally similar, consisting of SMs with 8 CUDA cores and 16 KB shared memory. Although the system has multiple CPU cores available, all of our implementations and tests (both CPU and hybrid CPU/GPU) involve a single core. Furthermore, the same initial random seed is used for both executions so that all implementations yield identical output.

5.1 Performance analyses of GPU kernels

We start by investigating the performance of our GPU kernels with synthetic data experiments that involve both small and large graphs. The performance of our GPU kernels CanDeleteEdge(), CanAddEdge() and GGScore() is compared against that of single-thread, CPU-versions of themselves. We use the insights gained from these performance evaluations to tune the stochastic search algorithm for our other illustrations.

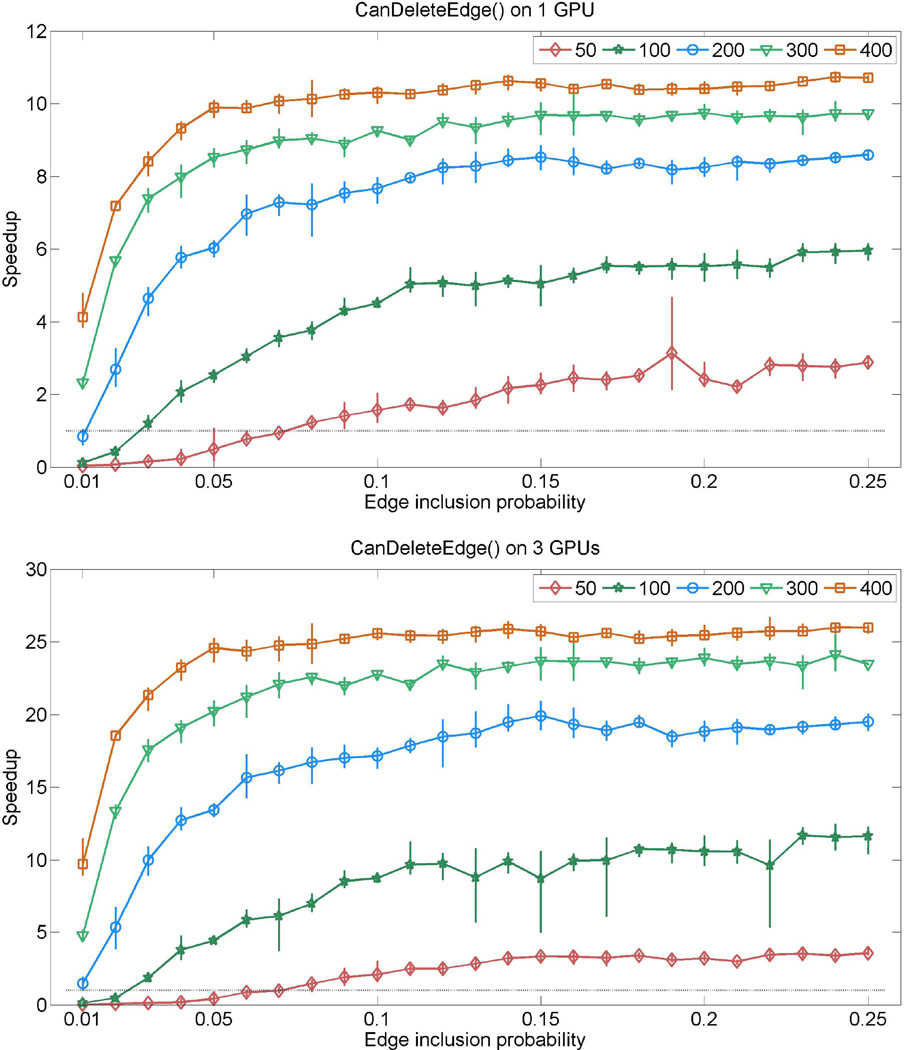
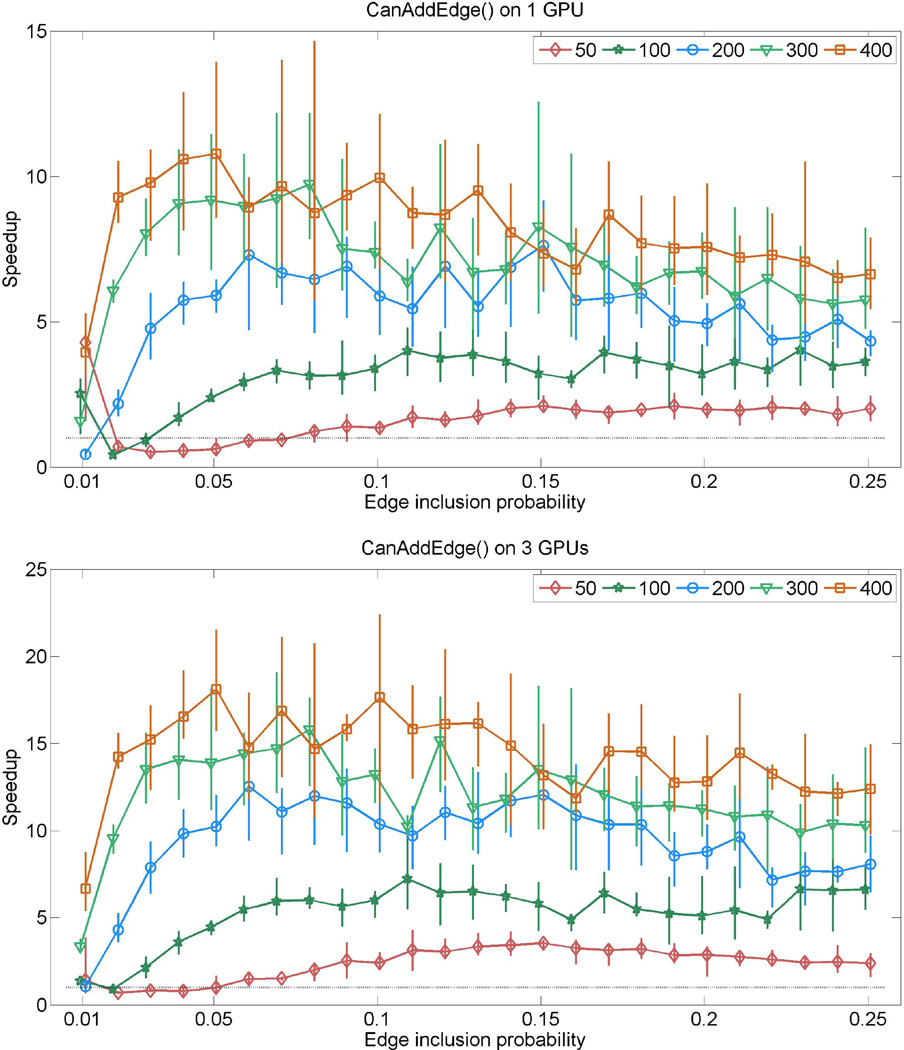
Consider first the evaluation of the CanDeleteEdge() and CanAddEdge(). Our synthetic experiments involve graphs with p = 50, 100, 200, 300, 400 vertices. For each selected graph-dimension, graphs are simulated with edge-inclusion probabilities 0.01, 0.02, …, 0.25. For each of these edge-inclusion probabilities we simulate 5 random graphs and compute a minimal triangulation supergraph of the sampled graph. The resulting graphs are decomposable and range from very sparse to quite dense graphs of that relevant dimension. For each of the graphs we test the decomposability of all neighboring graphs with kernel calls to CanDeleteEdge() and CanAddEdge(), and measure the total execution time for both kernels. Speedups are reported in figures 1 and 2, which present the one-GPU and three-GPU performances in separate panels, where the average speedup for each graph dimension is plotted as different curves. The vertical bars show the range of fluctuation in speedup for the given edge-inclusion probability.

Figure 1.

Relative speedups (runtime on CPU/runtime on GPUs) attained by CanDeleteEdge() for random graphs sampled with various edge-inclusion probabilities. The top panel shows results from using one GeForce GTX 285 GPU, where the bottom panel shows results from using all three GPUs described in sec. 5.1. The five curves in each panel respectively correspond to graphs with 50, 100, 200, 300 and 400 nodes. Each curve shows average speedup for a given dimension, where the associated vertical bars represent the range of speedup (min to max) observed for the given edge-inclusion probability.

Figure 2.

Relative speedups (runtime on CPU/runtime on GPUs) attained by CanAddEdge() for random graphs sampled with various edge-inclusion probabilities. The top panel shows results from using one GeForce GTX 285 GPU, where the bottom panel shows results from using all three GPUs described in sec. 5.1. The five curves in each panel respectively correspond to graphs with 50, 100, 200, 300 and 400 nodes. Each curve shows average speedup for a given dimension, where the associated vertical bars represent the range of speedup (min to max) observed for the given edge-inclusion probability.

Figure 1 shows the results for CanDeleteEdge(), where we observe substantial speedups with increasing graph dimension. This is possible since the Giudici & Green (1999) test for decomposability for edge-deleted neighbors does not require many logical branching operations for implementation. This GPU-kernel is also implemented with a small shared memory requirement. The relatively small ranges of fluctuation come from the fact that the algorithm has very similar computational load for graphs with same dimension and density. Although we observe poor GPU performance for sparse graphs in small dimensions (which can be attributed to not having enough number of tasks to parallelize), as graphs become larger and denser, the one-GPU and three-GPU performances improve dramatically. In particular, we observe up to 25-fold speedup on 3 GPUs for some graphs with 400 vertices. This motivates us to use the 3 GPU implementation in the stochastic search for our real data application.

The GPU-kernel CanAddEdge() requires complex operations involving multiple passes through the cliques and separators of the graph, numerous logical branching, and a large amount of shared memory allocation. Even then, the computational speedups are significant, especially using 3 GPUs, as shown in figure 2. Interestingly, we do not observe an increasing relationship between average speedups and graph density. Also, large ranges of fluctuations in the speedup are seen across all graph dimensions and graph densities. This arises from the fact that the computational load of this kernel is largely dependent on the size of the junction tree, and the cliques and separators of the graph. Peak performance is achieved when the GPU core occupancies are optimal. However, the average speedup is satisfactory in general, with the possible exception of small, sparse graphs.

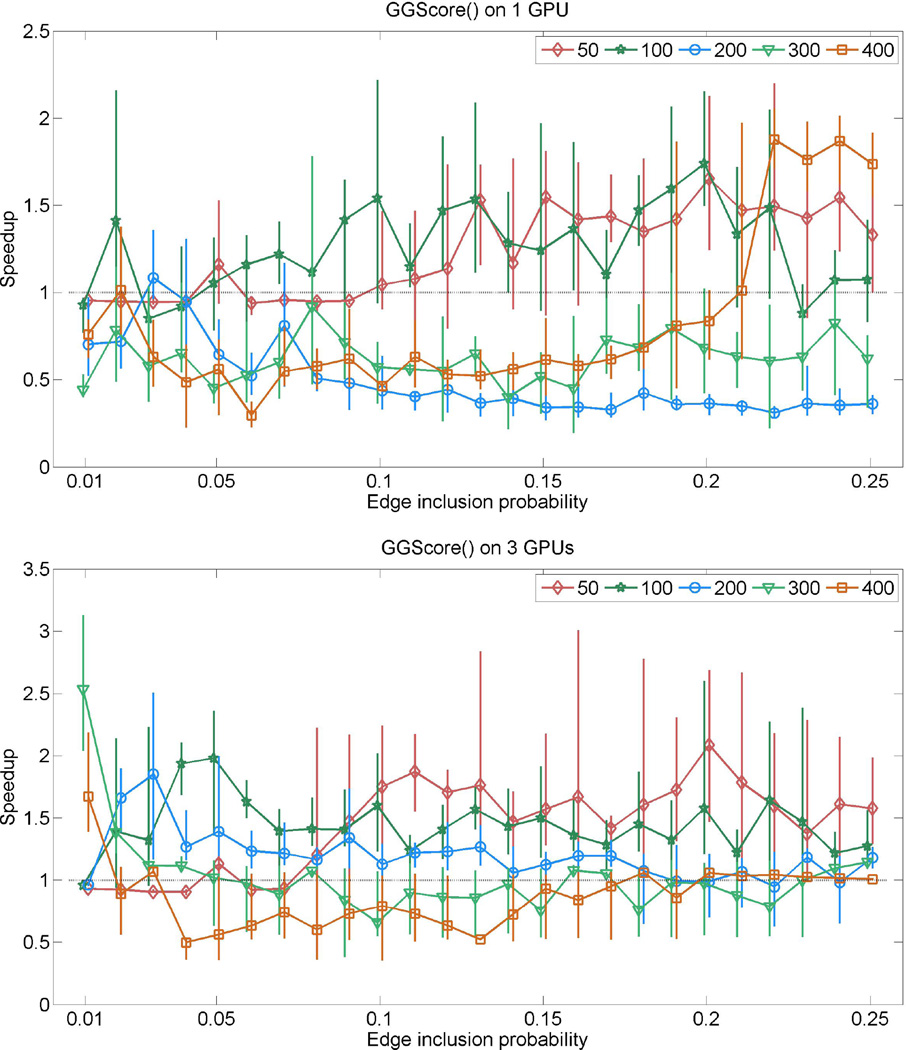
To evaluate the GGScore() kernel we follow a similar procedure, but for each one of the graphs we first simulate a covariance matrix according to a G-Wishart prior with p + 1 degrees of freedom and identity scale matrix, and then generate a sample of 148 observations from a Gaussian distribution with mean zero and the covariance matrix just sampled. Figure 3 plots the GPU performance for the score computation kernel GGScore(). The speedups are often less than 1, and when the GPU-kernel performs better than the CPU-kernel, speedups are not as impressive as for the other two kernels. Interestingly, GGScore() tends to perform better for graphs with 50 and 100 vertices on the GPU. This is because for smaller graphs we can GPU-parallelize score computations of most shotgun neighbors using the shared memory of our GPUs. For large graphs most of the shotgun neighbors are computed using the CPU, where the cost of large CPU-GPU data transfers increase runtime. As a consequence of these results we do not use this GPU-kernel in our current search algorithm. However, we note that current releases of NVIDIA GPUs have much higher amounts of shared memory on each SMs that will allow GPU-parallelization of more shotgun neighbors on the GPUs. Additionally, newer GPU architectures allow for concurrent kernel execution, which facilitate simultaneous score computation of all bins of decomposable neighbors under the shared memory cap. These hold promise for potential usage of our GPU-kernel in score computations of large dimensional graph search as the hardware improves.

Figure 3.

Relative speedups (runtime on CPU/runtime on GPUs) attained by GGScore() for random graphs sampled with various edge-inclusion probabilities. The top panel shows results from using one GeForce GTX 285 GPU, where the bottom panel shows results from using all three GPUs described in sec. 5.1. The five curves in each panel respectively correspond to graphs with 50, 100, 200, 300 and 400 nodes. Each curve shows average speedup for a given dimension, where the associated vertical bars represent the range of speedup (min to max) observed for the given edge-inclusion probability.

5.2 Synthetic data

In this section we analyze a synthetic dataset to demonstrate effectiveness of our stochastic search as a Bayesian learning tool for Dirichlet process mixtures of Gaussian graphical models vis-à-vis Markov chain Monte Carlo algorithms. Our synthetic example deals with a dataset with a relatively small-dimension, n = 150 and p = 50. The data is generated from a three-component mixture with equal weights, where the distribution for the l-th component follows a $\mathrm{N}(0,K_l^{-1})$. To generate the precision matrix K₁, K₂ and K₃ we first simulate three random decomposable graphs G₁, G₂ and G₃ with respective edge-inclusion proportions of 2.53%, 10.12% and 14.94%. Subsequently, the precision matrices are sampled from G-Wishart distributions, K_i ~ W_Gi (d, (d − 2)S) for i = 1, 2, 3, where d = 5000 and S = 0.1I_p + 0.9J_p. Here I_p denotes the p × p identity matrix and J_p denotes the p × p matrix of ones. The parameters of the baseline measure are specified as n₀ = 0.01, δ₀ = 3, D₀ = I_p.

First, we used the stochastic search using the Algorithm 1 to obtain an estimate of the posterior mode of the model. In this example we use three random initial configurations (N = I = 3 in Algorithm 1). In addition, we used a version of the MCMC algorithm discussed in section 3.1 that incorporates single-core CPU versions of the kernels CanDeleteEdge() and CanAddEdge(). For this MCMC algorithm we run a total of three chains (one starting from one of the three initial random configurations used for the stochastic search-chains described below), with each chain generating 100, 000 samples after a burn-in period of 20, 000 iterations. Both the stochastic search and the MCMC algorithm were run first using only the CPU of the AVA Direct Custom CrossFireX desktop computer, and then again using the GPU accelerated versions of the algorithm that simultaneously use all three available GPUs. The seed for the random seed generator is set to the same values for each pair of GPU/CPU runs so that differences in execution times reflect only differences in the implementation.

Table 1 presents a comparison of the performance of the MCMC algorithm with the performance of the stochastic search. We report results for the model with the highest posterior probability under our algorithm (denoted by MAP-SS) and for the model with the highest posterior probability visited by the Markov chain (denoted by MAP-MCMC), as well as the score associated with the true model used to generate the data. Note that the stochastic search algorithm is significantly faster than the MCMC algorithm, and that the computing times of the MCMC chains are prohibitively large even in this relatively low-dimensional dataset. This is true even if the MCMC algorithm is accelerated using massive GPU parallelization. Furthermore, Table 1 suggests that the stochastic search algorithm is able to identify higher probability models than the more standard MCMC algorithm. Another interesting observation is that the score associated with the MAP model is better than the score associated with the true model.

Table 1.

Comparison of the stochastic search with MCMC for the synthetic dataset with n = 150 and p = 50.

	Logscore	# Misclassified observations	Time to MAP (sec) CPU	Total runtime (sec) CPU	Time to MAP (sec) 3 GPU	Total runtime (sec) 3 GPU
Truth	−5721.34	–	–	–	–	–
MAP-SS	−5662.99	1	206.60	264.37	134.16	171.67
MAP-MCMC	−5865.08	1	270389.69	374253.64	177, 887.95	246, 219.50

Some additional insight on the behavior of the algorithms can be gained by exploring the structure of both modes. Both MAP-SS and MAP-MCMC imply the same grouping of observations (both correctly identify the presence of three clusters and misclassify one observation), so the modes differ essentially in terms of the quality of the component-specific graphs they identify. Table 2 shows the error rates (total density, false positive and false negative rates) for each component graph for each of the two algorithms. Note that, although both modes overestimate the total number of edges in all three graphs, MAP-SS is consistently better than MAP-MCMC in all error categories for all component graphs.

Table 2.

Comparison of the stochastic search with MCMC in graph learning for the synthetic dataset with n = 150 and p = 50. The true and false positive discovery rates are the fractions of edges of a component graph that are respectively present or absent in the ‘true’ component graph. Similarly, the true and false negative discovery rates are the fractions of absent edges in a component graph that are respectively absent or present in the ‘true’ component graph.

Learning Method	Graph	% edges (% total +ves)	True +ve discovery rate (%)	False +ve discovery rate (%)	True −ve discovery rate (%)	False −ve discovery rate (%)
	G1	5.88	22.22	77.78	99.22	0.78
MAP-SS	G2	15.84	50.00	50.00	99.03	0.97
	G3	19.67	64.32	35.68	98.88	1.12
	G1	7.10	12.64	87.36	98.76	1.24
MAP-MCMC	G2	25.14	22.40	77.60	95.86	4.14
	G3	32.16	31.47	68.53	94.95	5.05

5.3 Analysis of a gene-expression dataset

As a final illustration, we demonstrate the performance of the GPU-powered stochastic search by analyzing gene expression data of human breast cancers. The original dataset contains gene-expressions of 4512 genes from an Affymatrix HU95aV2 oligonucleotide microarray for 148 breast tumor samples. Each tumor in the dataset has additional classification tags according to its estrogen receptivity (ER+/ER−) and presence of cancer metastasis in neighboring auxiliary lymph-nodes (LN+/LN−). Parts of this dataset have been previously analyzed in West et al. (2001), Huang et al. (2003a), Huang et al. (2003b), Nevins et al. (2003), Pittman et al. (2004) and Hans et al. (2007) using models that assume homogeneity in the underlying population. In contrast, we employ the Dirichlet process mixtures of GGMs to assess whether different genetic-pathways are present in the data.

We created five datasets by first reordering the genes in descending order of their correlation with the binary encoded ER status, and then selecting the first 50, 100, 200, 300 and 400 genes from the reordered list. Within each dataset, gene expression values were standardized by subtracting their mean and then dividing by their marginal standard deviations. In all cases the baseline measure was specified so that n₀ = 0.01, δ₀ = 3 and D₀ = I_p, where I_p is the p × p identity matrix. Three initial configurations for the search were used (i.e., I = 3 in Algorithm 1) in each dataset. These initial configurations correspond to: (i) a single component model, (ii) a two-component model where the sample is split according ER status, and (iii) a four-component model where the sample is split according to all combinations of ER and LN status. Initial graphs for each component are obtained by putting edges between variables that have corresponding within-cluster partial correlation greater than 0.5. We run 9 search-chains (i.e. N = 9 in Algorithm 1) for each dataset. The stochastic search was run twice for each dataset, once using all 3 GPUs, and once using the single-core CPU implementation. Table 3 reports computing times for the CPU- and the three-GPU implementations for all five gene-sets, as well as the relative speedups attained. Observe the increasing speedup as the number of genes increase. In particular, the near 10-times speedup for dimension 400 is encouraging for DPM-GGM applications in high-dimensional problems.

Table 3.

Aggregate runtime (in seconds) of 9 search-chains on CPU and on 3 GPUs for all five gene-sets. Relative speedup for the multi-GPU implementation is presented alongside.

Gene-set size	50	100	200	300	400
CPU time (sec)	230.79	1772.64	18222.92	156940.54	812791.15
3 GPU time (sec)	152.84	757.54	4031.62	21122.55	84754.03
GPU Speedup	1.51	2.34	4.52	7.43	9.59

We consider now in more detail the MAP estimate for the dataset containing 400 genes. This estimate involves two clusters, which roughly match ER status (see Table. 4). This partition is also somewhat similar to the one obtained by first reducing the dimensionality of the responses by computing the first 30 principal components of the data and then using a mixture of Gaussians with equal variance and the Bayesian Information Criteria as implemented in the R package mclust (Fraley & Raftery, 2003) to identify the clusters. (However, we note that the partitions generated by this simple two-stage approach are not robust to changes in the number of principal components used to reduce the dimensionality of the problem, that the structure of the principal components themselves is very sensitive to removal/addition of even a very small number of observations, and that the amount of variability captured by the principal components decreases very slowly). These graphs have very different densities (1.62% of the possible edges are included in the first cluster, while 7.72% are included in the second), with only 24% of the edges present in the first cluster being also present in the second one. This suggests that gene pathways associated with the two groups are significantly different.

Table 4.

Number of matches and mismatches of the DPM-GGM based classification of tumor samples with the ER-status in the 400 gene-expressions dataset.

	ER+	ER−	Total
Cluster 1	96	17	113
Cluster 2	1	34	35
Total	97	51	148

We also compared the results from our stochastic search algorithm for the dataset containing 50 genes with those generated by the MCMC described in section 5.2. The comparison is based on three MCMC chains consisting of 100, 000 samples obtained after a burn-in period of 20, 000 iterations each. Each one of these chains was started from one of the three initial configurations for the stochastic search described before. Table 6 presents the scores associated with the MAP estimate, along with total execution times and the time required by the algorithms to reach the MAP estimate. As with the simulated data, the stochastic search is significantly faster than the MCMC algorithm. Indeed, the computing times of the MCMC chains are prohibitively large, and the quality of the response (as measured by the score of the best model visited in each case) is much lower.

Table 6.

Comparison of the stochastic search with MCMC for the dataset with 50 genes.

	Max log-posterior probability	Time to reach the MAP estimate (sec)	Total runtime (sec)
SS on 3 GPUs	−7052.69	137.57	152.84
SS on CPU	−7052.69	208.13	230.79
MCMC chain 1 on CPU	−7191.95	318314.06	368082.13
MCMC chain 2 on CPU	−7175.45	256305.86	402676.77
MCMC chain 3 on CPU	−7294.68	25418.33	424634.15

6 Discussion

Our stochastic search algorithm relies on a mixture of local and global moves to explore the space of possible models. However, the relative efficiency of these moves varies. In particular, the posterior distribution appears to be much flatter in the direction of the component-specific graphs than in the direction of the partitions. As a consequence, the space of partitions is explored relatively quickly using local moves. The split-merge moves for the partitions, although helpful in terms of allowing the algorithm to quickly move away from local modes, appears to contribute comparatively less to improving the solution. In that regard, it is also worth noting that when we started this work we also considered mid-range moves in which a small number of observations (between two and five) where simultaneously reallocated using their joint full conditional distribution, but these moves proved to be computationally expensive while providing little improvement over reallocating a single observation at time. On the other hand, in the case of of the component specific graphs the mode-break move and the global jump moves appear to play a key role that is as important as that of the local moves.

The use of GPU computation in the context of mixtures of Gaussian graphical models was particularly challenging because of the “large p, small n” nature of the problem at hand. Although we successfully thread-parallelized the graph decomposability tests for moderate numbers of variables (a notable achievement, given the fact that they lack desirable arithmetic intensity due to numerous conditional branching in the tests), we were less successful in achieving speedups in the computation of score functions or the decomposability tests for large graphs involving thousands or tens of thousands of nodes. The main reason for this is the scarcity of shared memory on the GPUs cards and the need to sequentially launch kernel calls. One way to deal with this limitation that we did not pursue in this paper is to use multiple GPU accelerators and load partial tasks on each unit. Furthermore, as new generations of graphical cards become available, these constraints will become less important. Indeed, current releases of NVIDIA GPU cards feature faster clock speeds, lower memory latency at all levels, larger amounts of shared memory on each streaming multiprocessor, and allow for concurrent kernel execution capabilities. In the context of the GGScore kernel, these features would allow us to move away from a fixed specification of the shared memory resource for cliques and separators of various sizes, while in the case of CanAddEdge()and CanDeleteEdge() the additional memory would allow for larger graphs to be considered.

An important limitation of our approach is the restriction to component-specific graphs that are decomposable. Generally speaking, designing an algorithms for mixtures of Gaussian graphical models with non-decomposable graphs has been historically challenging because a formula for the score function is not available in closed form, requiring the use of Laplace approximations or Monte Carlo integration. If Monte Carlo integration is used to approximate the value of the score, GPUs could potentially be used to dramatically speed-up this computation. Alternatively, Uhler et al. (2014) have recently proposed closed-form formulas.

Table 5.

Percentage of exclusive edges and percentage of common edges in component graphs of the maximum a-posteriori DPM-GGM model for the gene-expressions dataset with 400 genes.

% edges in G1 \ G2	% edges in G1 ∩ G2	% edges in G2 \ G1
1.23	0.39	7.33