Abstract
Association and dissociation of particles are elementary steps in many natural and technological relevant processes. For many such processes, the presence of multiple binding sites is essential. For instance, protein complexes and regular structures such as virus shells are formed from elementary building blocks with multiple binding sites. Here we address a fundamental question concerning the role of multivalency of binding sites in the association kinetics of such complexes. Using single replica transition interface sampling simulations, we investigate the influence of the multivalency on the binding kinetics and the association mechanism of patchy particles that form polyhedral clusters. When the individual bond strength is fixed, the kinetics naturally is very dependent on the multivalency, with dissociation rate constants exponentially decreasing with the number of bonds. In contrast, we find that when the total bond energy per particle is kept constant, association and dissociation rate constants turn out rather independent of multivalency, although of course still very dependent on the total energy. The association and dissociation mechanisms, however, depend on the presence and nature of the intermediate states. For instance, pathways that visit intermediate states are less prevalent for particles with five binding sites compared to the case of particles with only three bonds. The presence of intermediate states can lead to kinetic trapping and malformed aggregates. We discuss implications for natural forming complexes such as virus shells and for the design of artificial colloidal patchy particles.
I. INTRODUCTION
Particles with multiple binding sites are ubiquitous in natural and synthetic systems. Proteins naturally form complexes by binding via multiple sites, virus shells are assembled from capsid proteins with multiple interactions,1,2 and nano-structures can be built from multivalent patchy particles.3,4 Indeed, breakthroughs in colloid synthesis enable colloids to bind anisotropically via multiple binding sites or patches.5–10 Such multivalent patchy colloids can form not only crystal phases but also lead to chains, lamellar structures, colloidal micellar structures, and even colloidal hollow shells that are reminiscent of viral shells.3,4,11–14 Patchy particle models have been used also to study protein complex formation, such as clathrin cages,15–17 and protein association dynamics.18 When complex structures are self-assembling from elementary building blocks, their ground state structure should be both thermodynamically stable and at the same time kinetically accessible.14,19–22 When many building blocks are involved, the self-assembly usually occurs via multiple intermediate states before reaching the final ground state. Such intermediate structures can be short-lived, but also very long-lived. Long-lived intermediates occur typically when non-native bonds are formed, yielding a frustrated intermediate, that can only reach the ground state by breaking those frustrated bonds again. Clearly, such frustrated states can restrict the formation of the ground-state cluster within a viable time-frame, also because such malformed bonds can lead to larger kinetically trapped random aggregates. It is therefore, in fact, rather surprising that in nature certain self-assembly processes are so successful, e.g., virus assembly. Indeed, previous studies have shown that the conditions for a successful self-assembly of multivalent particles rely on a fine-tuning of interaction parameters such as the bonding strength or bonding volume.6,14,21,22 When the interaction strength is too weak, there is no binding at all, and when it is too large, the system becomes frustrated. When the bonding volume (patch width) is too narrow, there is no binding, and when it is too wide, the system forms random aggregates.20–22 Moreover, there is an important role for non-specific binding interactions, which allows the particles to bind weakly first, before finding the final correct target configuration.23–25 For instance, in Ref. 24 experiments on lock and key colloids indicate that non-specific binding can enhance association significantly, something that also occurs for protein binding. These findings are universal self-assembly principles that can lead to rational design rules for artificial molecular or colloidal superstructures.
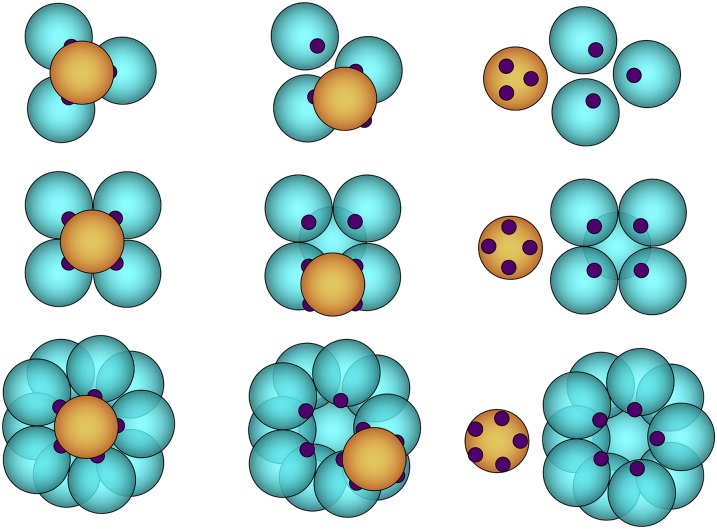
The question we would like to address here is what role multivalency plays in association and dissociation processes and what influence it has on the kinetics and mechanism of these processes. Multivalent particles can form multiple bonds with other particles or previously formed complexes, yielding a correctly formed structure, or possibly a malformed intermediate state. How does the association mechanism and kinetics of correctly formed structures depend on the number of bonds the particles can form? To address this question we study a simple model system of spherical particles with multiple binding sites or patches. In previous work, we studied the formation of a tetramer from its four constituent particles with three binding sites.26 Here, we systematically extend this study to particles with four and five binding sites. Such particles can form symmetrical octahedrons and icosahedrons. Since the number of intermediates rises combinatorially with the number of constituent building blocks, we will investigate as a first step the final assembly process, the association/dissociation of the last particle, which is a uniquely defined step in the assembly as it leads to and from the fully formed symmetric polyhedral cluster. As such, all other particles already in the cluster are constrained. We study three different types of clusters: a tetrahedron, an octahedron, and an icosahedron where each particle forms three, four, or five bonds, respectively (see Fig. 1 for a schematic representation of the clusters). For each of these clusters, three conformations are defined: a fully bound state (B), an unbound state (U), and a partially bound cluster (I) where certain bonds result in a rotationally frustrated state.
FIG. 1.
Cartoon image of the three polyhedrons considered in this work where the orange particle is the motile particle and the patches are depicted in purple. From top to bottom: tetrahedron, octahedron, and icosahedron. From left to right are the three different states: the ground state B, a realization of a frustrated intermediate state I, and the unbound state U.
While previous work focused mostly on the thermodynamic stability as well as the kinetic accessibility,14,20,23,27 here we are more concerned with the actual kinetics, the rate constants of assembly and disassembly, and the reactive pathways of association and disassociation. Due to the high binding energies necessary to obtain stable clustered structures from patchy particles, the transition rate constants are low, and obtaining reactive pathways in a statistically meaningful way by brute force molecular dynamics is extremely inefficient. Recently, path sampling techniques have been developed to solve this problem by biasing the generation of reactive pathways without altering the underlying dynamics. We apply the Single Replica Transition Interface Sampling (SRTIS) framework to study rare association/dissociation events involved in the final steps toward the fully formed polyhedron.28,29
By analyzing the rate matrix obtained from SRTIS, all kinetic information on the overall association dissociation process can be retrieved. A convenient framework is transition path theory (TPT), which gives insight in relevant quantities such as commitment probabilities and the net flux through intermediate states.30,31 The multivalency has a trivial way of influencing the thermodynamics of binding and the associated kinetics: for a fixed patch binding interaction, the binding equilibrium constant increases exponentially with the number of bonds. When the bond strength is fixed, the kinetics also is very dependent of the multivalency, with dissociation rate constants exponentially decreasing with the number of bonds. This makes it hard to study the influence of just the number of binding sites. Therefore, we compare not the individual patch strength but the total binding strength per particle upon complete binding. Remarkably, when the total bond energy is kept constant, the association and dissociation rate constants are rather independent of multivalency. Of course, the kinetics is very dependent on the total binding energy of all particles. The association and dissociation mechanisms, however, depend on the presence and nature of the intermediate states. Pathways that visit the intermediate states are less prevalent for higher five-fold multivalent particles, compared to particles with only three bonds. Such intermediate states can lead to kinetic trapping and malformed aggregates. We discuss implications for natural forming complexes such as virus shells.
In addition, we show that the intermediates have an effect on the overall association or dissociation process and as such the mechanism. A difference is found between the frequency of visiting intermediate states given by TPT and the actual residence time in the intermediate state given by the time-evolution of the populations.
The remainder of the paper is as follows. In Sec. II we introduce the patchy particle model, briefly explain dynamic Monte Carlo, review the SRTIS methods, and end with a small summary of TPT and steady state analysis. In Sec. III we present the main results of the paper. We then end with a discussion.
II. METHODS AND SIMULATION DETAILS
A. Patchy particle model
Similarly to the study of Wilber et al.,20 we use a simple patchy particle model. The potential between particles is defined as
where rij is the inter-particle vector and are the orientations of the particles, stored in the quaternion form. The isotropic repulsive potential is given by
| (1) |
where r = |rij| is the distance between particles and σ determines the size of the particle. The anisotropic patchy interaction is, for distances r below the cutoff rc,
| (2) |
and zero otherwise, where defines the strength of the interaction. We model the interaction between the particles and the patches based on a 24-12 Lennard-Jones (LJ) potential. This potential is of shorter range than the standard 12-6 LJ potential. As such the phase behavior exhibits a metastable liquid vapor coexistence line with respect to the gas solid coexistence,32 similar to protein solutions. The continuous patch function gives a penalty for misalignment,
| (3) |
where δ defines the patch-width and is the minimum angle between the interparticle vector rij and any of the patch vectors pi on particle i. Therefore, only the patches on each particle that are most aligned to rij interact. We consider particles with narrow patches () such that every bond is well defined and there are no multiple overlaps between patches. A small patch-width as used here was shown to reproduce the gas-liquid curves of protein solutions such as -crystallin and lysozyme quite well,33 albeit with more patches.
B. Dynamics
Over-damped Langevin (Brownian) dynamics are typically used to propagate protein or colloidal systems in time.17,34–36 However, due to the constraint on the immobile particles, the force calculation is rather difficult. Therefore, we use dynamic Monte Carlo (DMC) because of the ease of implementation without losing the necessary dynamical information.37 Each DMC cycle consist of a translation and rotation trial move of the motile particle. A translation move consists of translating the motile particle by a randomly chosen shift between [] for each Cartesian axis. A rotation move is done by choosing a random unit vector and rotating the orientation over a randomly chosen angle between []. The main disadvantage of DMC is the fact that the collective motion of clusters is suppressed.38,39 However, the collective motion is not important for this system as we only consider one particle to move freely. The rotational and translational step sizes are fixed following the Stokes-Einstein relation, and .
Taking a colloidal suspension in water, with colloids with a size of , and using the Stokes-Einstein relation to compute the translational diffusion, , we can estimate the actual time step via , so every MC cycle corresponds roughly to . For proteins, which are roughly a hundred times smaller, this time becomes ns. The average acceptance ratios and are always higher than 0.7. It has been demonstrated that this regime leads to proper diffusive dynamics.27,37
C. Single replica transition interface sampling
Single replica transition interface sampling (SRTIS) is used to sample path space and thus obtain the rate matrix.28,29 A path is defined as , a series of L time frames or slices. Each frame is a point in configuration space , with r and Ω the coordinates and orientation (in quaternion representation) of each particle in the N-particle system (note the difference between this definition and previous definitions,28,29,40,41 as here we do not carry the momenta, due to the use of DMC, but we do carry the orientation of the particles).
Three states are defined: the fully bound state (B), the unbound state (U), and an intermediate state (I), where two bonds are formed, and the system is frustrated such that the remaining unbound patches are unable to form bonds via barrier-less rotation (see Fig. 1). While there are states in which 3 or 4 bonds are formed in the octahedron and icosahedron systems, these states are not stable and not even metastable but quickly form the remaining bonds to end in the fully bound stable state B. When the mobile particle is at least rU away from the centre of the polyhedron, the system is in the unbound state, where rU is chosen such that when in U, the mobile particle is at least away from any particle. The other two states are defined by the correct topology and when the energy of the system is lower than , where nb is the number of bonds that defines the state.
For each state α, we define a set of m non-intersecting interfaces based on an order parameter λ (i.e., distance or potential energy). For clarity of notation, we use the convention here that for all interface and indicator functions a superscript refers to the interface index, while a subscript denotes the state the interface belongs to. This might sometimes conflict with the previous literature, e.g., Refs. 28 and 29, but we think this more clearly. Note that while each set of interfaces belonging to a state α is non-intersecting, interfaces belonging to different states are allowed to intersect.
The interfaces around each state are defined by the energy of the system minus the ground state energy. For B and I, the interfaces are equally spaced from the state boundary by 1.5kBT until the maximum possible energy is reached. The interfaces for the unbound state should be defined carefully. If one defines the interfaces based on the same energy spacing as for the bound states, particles could become stuck in a region where there is little binding energy and the system is subsequently not pushed towards the bound states as the transition is mostly entropic in nature. Therefore, we choose to define many interfaces close to the unbound state: [10−6, 10−5, 10−4, 10−3, 10−2, 10−1, 0.4, 1.0]. This choice of interfaces will guide towards to bound states.
In SRTIS a single replica performs a random walk along the interfaces while simultaneously sampling path space by using five different path moves. The primary move is the interface-constrained one-way shooting move.41 From the time slice at which the path first crosses the current interface, a new (partial) path is generated either in the forward or backward direction, and accepted if this (partial) path ends in a stable state, irrespective of the path length (of course, one needs to define a hard-coded maximum path length, to prevent memory overflow). The remainder of the full trajectory is taken from the old path.41 Note that the acceptance criterion becomes very simple because all generated paths already cross the interface, and acceptance ratios can be very high, close to unity. Due to the stochastic nature of the dynamics, the newly generated path will sample a different part of path space. In order to achieve further decorrelation between pathways, we use the time-reversal move where the pathway is reversed in time, by reversing the order of the slices,40 and an inversion of the momenta for each time slice (not needed for Brownian dynamics or DMC). Additionally, replica swap and state-swap moves are employed. A replica swap attempts to change the current interface to a neighbouring interface, with the condition that the path still crosses the new interface. In order to sample uniformly between all interfaces of a state, we perform Wang-Landau (WL) sampling, with the following acceptance criterion for a replica swap between interfaces i and j:
| (4) |
where the min function returns the smaller of its arguments and is a trajectory indicator function that is unity only if the path starts in α, crosses interface , and ends in any stable state (including ). The Wang-Landau bias is imposed via the density of paths which upon visiting is updated by multiplying with a Wang-Landau factor . At the start of the simulation, the densities of paths are set to and fWL = 0.01. Once all replicas have been sampled uniformly within a certain threshold, the WL factor fWL is halved until the scale factor has converged to a sufficiently low number ().28
A state swap attempts to change the current initial state to a different state which is only possible when the path is of type with . This swap requires a path reversal, so that a path of type becomes of type . After the state swap, the set of replicas belonging to the new initial state is used. The acceptance probability for the state swap is
| (5) |
where the arrow to the left in denotes the reverse order of the trial path, the factor is unity if a state swap is only performed between the outermost interfaces, or only between interfaces and with identical indices k, and is the ratio of the number of replicas of states α and β if one allows swaps between all interfaces. When states are nested within interfaces, it can be advantageous to allow all-interface state swaps.
Finally, to randomize within the stable states, we also employ the so-called “minus move,”41,42 sampling an additional first interface ensemble,43 which lets the path evolve (backwards or forward in time) within a state until it exits the state and crosses the first interface. The minus interface ensemble can always exchange with the first (regular) interface ensemble via a replica exchange move.
In principle, just performing (unconstrained) shooting moves and minus moves would be sufficient to sample path space provided each replica is sampled individually. However, the combination of all five different moves together allows a much more efficient sampling of the path space. Convergence is reached when for each state α the WL density of paths is (up to a scaling factor) equal to , the conditional crossing probability to reach from .28,29 We check this condition for all our simulations.
D. Rate constant calculation
The rate between two states α and β is given by
| (6) |
where is the flux out of the state α through the innermost interface and is the conditional crossing probability to reach the state from , with the state definition of . The flux is calculated as , where is the average dwell time in the stable state α, before crossing , which can be calculated directly from the length of the pathways generated by the minus move. Correspondingly, is the average time it takes from the first interface back to the stable state α and follows directly from the length of the pathways sampled in the first interface replica. is calculated by joining all obtained crossing probabilities for every replica of a state via the weighted histogram analysis method (WHAM).44,45 As we sample all association and dissociation transitions, we obtain the full rate matrix K (i.e., the matrix form of ). Note that the obtained rate expression is exact under the assumption of rare event (exponential) kinetics between the states.
In a multiple state system, where states can be nested in between interfaces of other states, Eq. (6) is not valid anymore as it assumes that transitions only can occur when the outermost interface has been reached, which is not necessarily the case for systems which are nested in between interfaces of other states. If Eq. (6) is used naively, many transitions would be missed in the rate calculation. One can circumvent this problem by calculating the rate via the path-type numbers introduced in Ref. 29. A path-type number is defined as , which in words is the number of paths in replica i joining states α and β that have crossed at maximum interface (and by the definition of course also all interfaces below k). The superscript i indicates that the paths should obey the condition of replica i in the ensemble. Because we have set the maximum interface, we can reweight these numbers with the WHAM weights obtained from reweighting of the crossing probability as follows:
| (7) |
with , where are the optimized WHAM weights for paths that have crossed interface at maximum (note that these should be the same as the weights obtained via the crossing probability). Now we have the correctly reweighted number of paths joining the state with the state that have at maximum have crossed interface . Subsequently summing over all interface k gives the reweighted number of paths coming from the state and ending in the state ,
| (8) |
Because the Wang-Landau scheme biases the simulation to sample all states equally via the state-swap bias, the path numbers for each state need to be corrected for this bias. In an unbiased ensemble, each path is as likely as the reversed path. Therefore, we split the obtained path-type matrix, , into M matrices and symmetrize the αth matrix: and setting all other entries of the αth matrix to zero, resulting in M different matrices with only a nonzero αth row and a nonzero βth column. Subsequently, all M matrices are joined via WHAM giving the individual weights for each state. This leads to a transition path type number matrix, . Normalizing the matrix with the total numbers of paths going out of a state yields
| (9) |
This normalized transition probability matrix can be directly used in Eq. (6).
E. TPT analysis
Although the full rate matrix K gives all kinetic information, the overall rate from B to U including the direct and indirect pathway via I can be calculated via TPT.30,31 In the TPT analysis, the commitment probability is calculated from the transition matrix, , where is the transition probability between α and β within a certain lag time τ. If we consider the dissociation process, the committor is the probability the final state U is reached from the state α before returning to the state B and can be obtained in general by solving the linear set of equations,30
| (10) |
with and . However, as there is only one intermediate state, the calculation becomes very simple and the committor probability for state I is given by
| (11) |
From the committor probability, we can calculate two interesting properties. First, the overall rate for the dissociation process, the effective rate constant, can be calculated,
| (12) |
where is the equilibrium probability of state I and is the backward-committor probability, . The effective association rate can be computed likewise,
| (13) |
Second, we can compute the effective fluxes for the dissociation and association. We distinguish direct and indirect fluxes. The direct dissociation flux fBU gives the probability of a reactive pathway directly from B to U, whereas fBIU denote the probability to go indirectly B to U via the intermediate state I. In general, the flux between states and , contributing to the dissociation transition, can be calculated via30
| (14) |
Association fluxes can be computed likewise. The direct dissociation flux for our simple system is thus and the direct association flux is . Since we consider only one intermediate state, there are no recrossings and we do not have to consider the net flux.30 In fact, the net flux is equal to the effective flux. It follows that the indirect dissociation flux is , and the indirect association flux is , where . Note that in equilibrium the association and dissociation fluxes are identical, due to detailed balance.
F. Steady state approximation
We can also approximate the overall rate constant analytically by performing an analysis of the master equation and assume a steady state approximation . This leads to an overall dissociation rate constant,
| (15) |
which is very similar to Eq. (12) if we use , except for the term in the denominator of Eq. (12) which drops out due to the assumption of a steady state where it is considered that (or, for the equilibrium populations, ).
G. Simulation details
SRTIS simulations were performed with DMC in a periodic box of size 2rU. A production cycle of SRTIS cycles was performed after the scale factor for the Wang-Landau biasing was sufficiently low (), where every cycle consisted of 10 shooting, reversal, replica swap, and state swap moves. Averages for the crossing probability and path densities were sampled after each move.
III. RESULTS
A. Rate matrix and effective rate constants
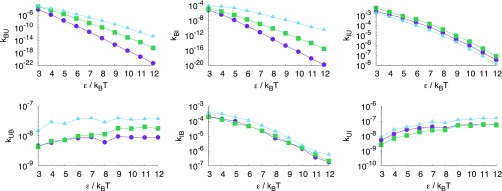
We consider particles with narrow patches (°) such that every bond is well defined and there are no multiple overlaps between patches. A small patch-width as used here was shown to reproduce the gas-liquid curves of protein solutions such as -crystallin and lysozyme quite well,33 albeit with more patches. From SRTIS we obtain the full rate matrix, K, for each polyhedron which we show in Fig. 2 as a function of the patch-patch attraction, . Rate constants kBU, kIU, kBI, and kIB show clear Arrhenius behavior, i.e., , especially at high , where is the activation energy of the transition from α to β, kB is Boltzmann’s constant, and T the temperature. For low rate matrix elements kBI and kIB flatten off slightly because these processes become more diffusion limited at these low values of . Naturally, the rate constant kBU out of the bound state to the unbound state is lowest for the icosahedron as it has the highest number of bonds (note that we compare here the situation for constant fixed patch interaction ). For each polyhedron, the intermediate state has two bonds, and therefore each rate constant out of the state α is very similar. Rate constants kUB and kUI do not show Arrhenius behavior at all. Clearly, the rate limiting step in these types of transitions is the alignment of patches which is mostly a diffusive process. Note that the kUB curves look less smooth because they are plotted on much smaller scales compared to the other rate constants. The variation in these curves is likely due to statistical noise. Unexpectedly, the association rate constants kUB and kUI of the tetrahedron are slightly higher than that of the octahedron and icosahedron. While this could partly be due to slightly different volumes available to the unbound state, the difference is probably caused by geometrical factors, e.g., the orientation dependence of the potential. In the tetramer system, the rather narrow attractive patch potential is pointing outwards with a steeper angle with respect to the basal plane formed by the fixed particles with the free binding sides, compared to the corresponding lower angles in the octahedron and icosahedron systems. The potential therefore extends further out from the fixed cluster, thus increasing the association rate constant for the tetrahedron. Moreover, as can be inferred from Fig. 1, due to the odd-even symmetry, in the octahedron system the narrow potential is relatively more shielded by the particle opposite in the square fixed cluster, compared to the icosahedron system, where the narrow potential points between two particles in the 5-ring. This will then again mitigate the effect of orientation for the icosahedron, so that the rates are roughly similar. In fact, even considering these small differences we would like to stress that all association rates are remarkably similar and independent on .
FIG. 2.
Rate constant matrix, K, for tetrahedron (light blue triangles), octahedron (green squares), and icosahedron (purple circles) plotted as a function of ; the rate constant from bound to unbound, kBU (left top), the rate constant from unbound to bound, kUB (left bottom), the rate constant from bound to intermediate, kBI (center top), the rate constant from intermediate to bound, kIB (center bottom), the rate constant from intermediate to unbound, kIU (right top), and the rate constant from unbound to intermediate, kUI (right bottom).
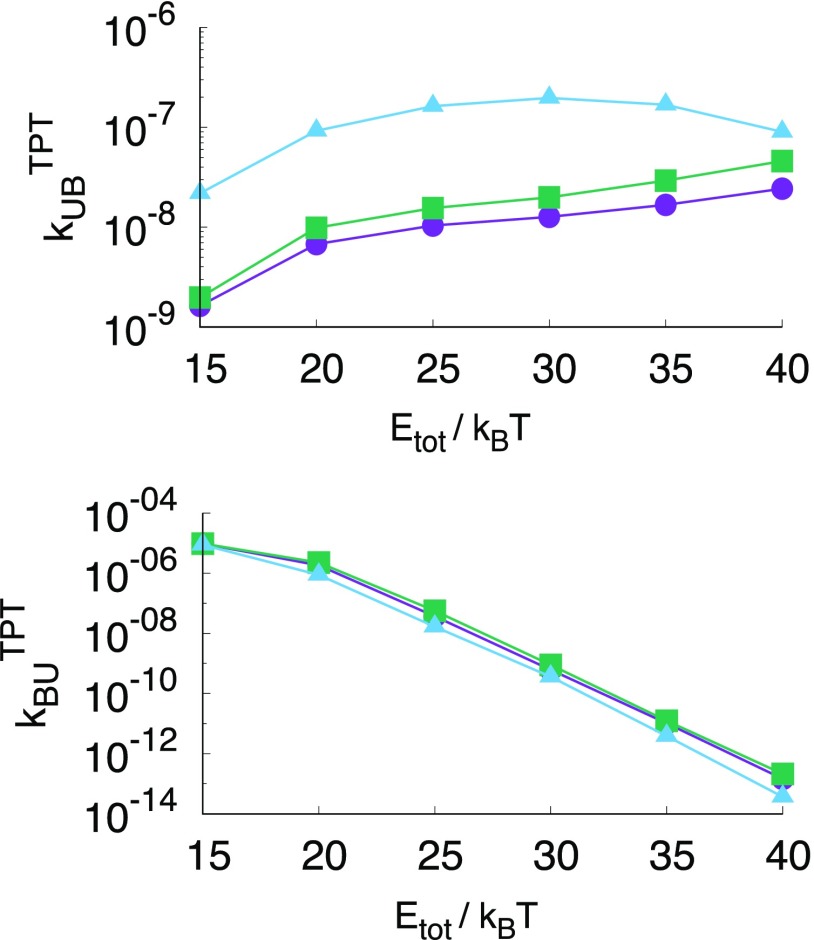
Although the individual rate constants describe in principle the full association process, they are not intuitive. A more interesting quantity for self-assembling systems is the effective rate constant which in part is responsible for the overall polyhedron yield. In Fig. 3 we show the overall association and dissociation rate constants as a function of total energy to compare for equi-energetic clusters where we see that the overall rate constants are similar and there is only a small difference between different polyhedra. The TPT association rate constant of the tetrahedron differs from that of the octahedron and icosahedron, most likely due to the geometry of the system, as discussed above.
FIG. 3.
Effective association (top) and dissociation (bottom) rate constants calculated via TPT for the tetrahedron (blue triangles), octahedron (green squares), and icosahedron (purple circles) as a function of the total energy (in units of kBT). The effective association rate constants do not vary dramatically with the total energy. Differences can be attributed to the volume available to the unbound state and the actual geometry of the cluster. Effective dissociation rate constants do depend on the total energy following roughly the Arrhenius law (except at low binding energy) and do not differ much between polyhedra for the same total energy.
Clearly, the dissociation rate constant depends mostly on the total energy and is less dependent on the number of bonds or the intermediate states. This can be understood if we assume that two pathways contribute to the dissociation: direct dissociation from B to U and indirect dissociation via the intermediate state, as derived via the steady state approximation in Eq. (15). The direct dissociation rate constant should be proportional to , where nb is the number of bonds of the system. The indirect dissociation could be approximated by the steady state solution . Based on simple fits to the Arrhenius relation from Fig. 2, the following relations should approximately hold , , and . The steady state solution then becomes
| (16) |
if we further approximate that which is valid for high , the dissociation rate constant for every polyhedron becomes . Therefore, as shown by Fig. 3 the total dissociation rate constant, , is mostly exponentially dependent on the total energy given by . Vibrational and rotational entropies, while naturally also playing a role, seem less significant, especially at high patch attraction. Apparently the number of bonds a particle can make does not make a difference for the dissociation when comparing for the same total energy. Note that this result remains the same if the state I would have a different number of bonds.
B. Flux ratio of direct and indirect mechanisms
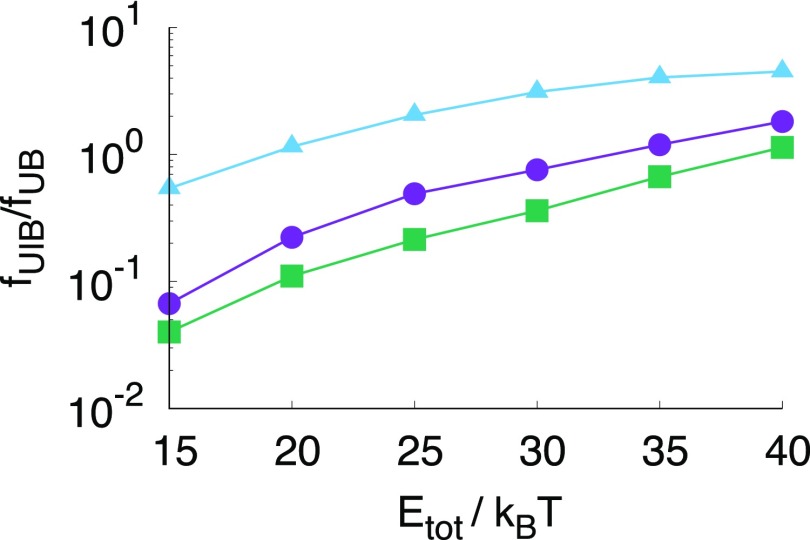
While the rate constants are not very sensitive to the particle’s valency, the mechanism of assembly or disassembly can be different, which in turn impacts the overall assembly. If a system resides longer in the intermediate state, frustrated dangling bonds can lead to kinetically trapped states, when other particles from the bulk attach to a growing structure. Moreover, if during assembly intermediate states are frequently visited, the probability of trapping naturally also increases. More information about the mechanism can be distilled from the TPT analysis. For comparison we plot the ratio fUIB/fUB in Fig. 4. This ratio demonstrates whether the direct or the indirect pathway is dominant in the equilibrium association process. An interesting observation is that the octahedron has the lowest flux via the intermediate state and the tetrahedron the highest. Despite the lower individual patch strength, the intermediate state of the icosahedron is visited more often than the octahedron, possibly because there exist many more distinct but identical intermediate states for the icosahedron (Nint = 50) than for the octahedron (Nint = 16), which increases the accessibility of the intermediate state for the icosahedron, and therefore also the frequency of visiting the intermediate state.
FIG. 4.
Ratio of the flux from the unbound state indirectly via the intermediate state to the bound state over the flux directly to the bound state for the tetrahedron (blue triangles), octahedron (green squares), and icosahedron (purple circles), indicating, surprisingly, that the octahedron visits the intermediate state least frequently. Energy is in units of kBT.
C. Population relaxation
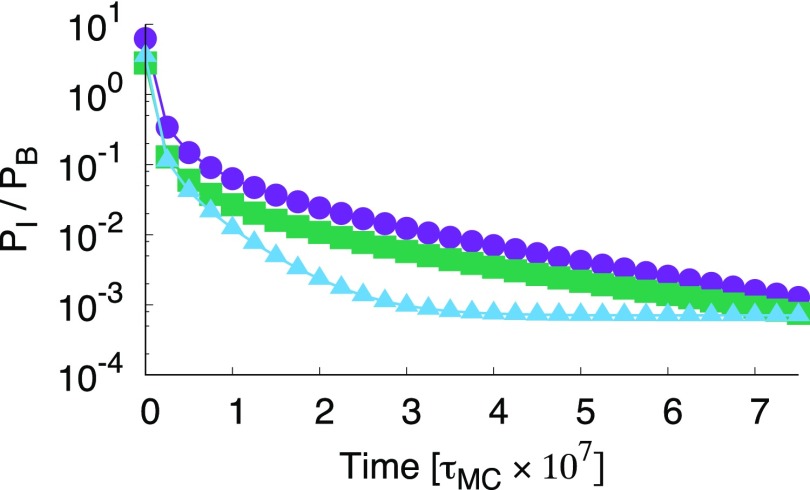
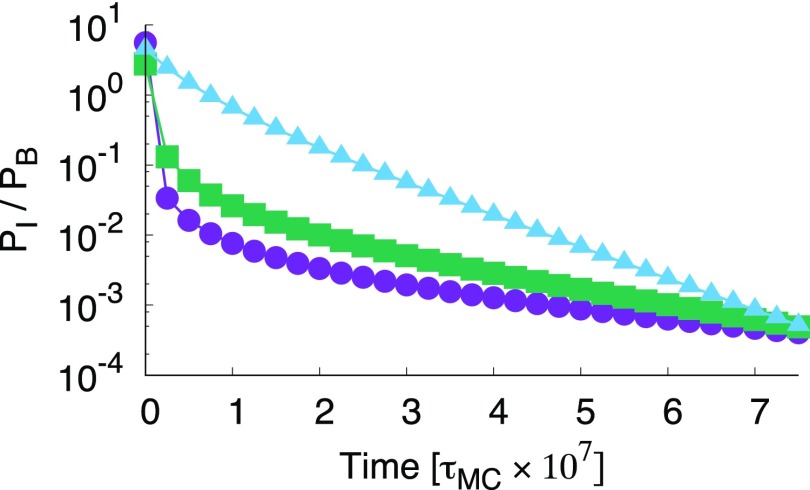
Another way of analyzing the rate matrix is by monitoring the relaxation of the populations towards equilibrium, which reflects the residence time in intermediate states. In Fig. 5 the relaxation of the population ratio PI/PB is shown for on a logarithmic scale. This value of was chosen such that for every polyhedron the bound structure B is the most stable (). Lower binding strength would lead to less frustration of assembly by the intermediate state, lower barriers between states, and hence a speed up of overall kinetics. Nevertheless, the qualitative features, e.g., the order of the curves, are not likely to change. From the plot it is clear that the relative intermediate state population is always highest for the icosahedron and lowest for the tetrahedron system. Therefore, if we compare with equal patch strength, the icosahedron resides the longest in the intermediate state. However, again it makes for a better comparison if the systems are not compared via equal patch strength, but equal total energy. Fig. 6 shows the relaxation of the population ratio PI/PB for Etot = −40 kBT on a logarithmic scale. When the systems are compared with equal total energy, the tetrahedron system has the highest population in the intermediate state during its relaxation to the bound state. Note that for all three systems the equilibrium population of the bound state is almost unity. Also, note that the full relaxation is not shown. Again, lowering the total energy will not qualitatively change the figure but will speed up the kinetics. The ordering in the curves is different compared to that of fUIB/fUB shown in Fig. 4, demonstrating that there is a difference between the equilibrium net flux and the out-of-equilibrium relaxation pathways. Moreover, there is a clear difference between the frequency of visiting intermediate states, as predicted by the TPT analysis, and the dwell time in the intermediate state, which is important for the population dynamics.
FIG. 5.
Ratio of the intermediate population over the bound state relaxing from the unbound state for the tetrahedron (blue triangles), octahedron (green squares), and icosahedron (purple circles) for a fixed bond strength demonstrating that the icosahedron is relatively the longest in the intermediate state. Note that the order is different than for fUIB/fUB shown in Fig. 4, demonstrating that there is a difference between the equilibrium net-flux and the out-of-equilibrium relaxation pathways.
FIG. 6.
Ratio of the intermediate population over the bound state relaxing from the unbound state for Etot = −40 kBT demonstrating that the tetrahedron stays the longest time in the intermediate state, due to the fact that it is harder to break a bond in the tetramer than in the octahedron or icosahedron.
D. Path density for dissociation
From the SRTIS path ensemble, we can also extract the mechanism of association and dissociation by projecting reactive pathways on collective variables. Here, we focus on the dissociation pathways from the bound state B. The reactive path density is defined as43,46
| (17) |
where is an integral over all pathways, is the (correctly reweighted) path probability of a reactive pathway out of the state B (to either I or U), and q(xk) denote the collective variable(s) of choice. The indicator function hq(xL) is unity if a path visits point q, and zero otherwise.
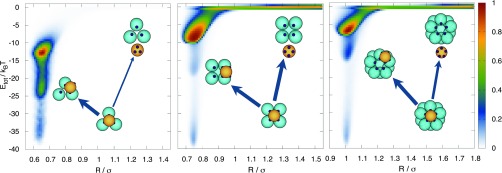
In Fig. 7 we show the reactive path density for dissociation from the state B mapped onto the distance of the motile particle to the polyhedral cluster, R and total energy, Etot. Note that due to microscopic reversibility, this analysis also holds for assembly, rather than disassembly. In case of the tetrahedron reactive, pathways from B are dominated by the transition. This is also reflected in Fig. 4, which shows that the intermediate frustrated state is frequented more often during the (dis)assembly of a tetrahedron complex. In contrast, the intermediate state is avoided more for the octahedron and the icosahedron, as the barrier towards the intermediate state is higher. In these cases, the direct transition has a higher path probability relative to the disassembly of the tetrahedron complex. Note also that the path probability for is slightly higher for the icosahedron than for the octahedron, as is also apparent from Fig. 4. As discussed above, this possibly is caused by the number of available I states for the icosahedron. For lower total energy, the intermediate states would probably be less frustrated due to lower barriers for all three systems.
FIG. 7.
Reactive path density obtained from the reweighted path ensemble, representing the dissociation mechanism starting from a correctly bound state B. The path density is mapped onto the distance between the motile particle center of mass and the center of the perfectly formed polyhedron, R, and the binding total energy, Etot (in units of kBT). The thickness of the arrows indicates the relative path probability for the direct and indirect dissociation. For the tetrahedron (left), the most dominant escape from the bound state (located at Etot = −40 kBT) ends up, via diffusion in the one-bond state (located for the tetrahedron at Etot = −13.3 kBT) in state I (located at Etot = −26 kBT). Clearly, direct dissociation to the unbound state is not very probable. In contrast, escape from B for the octahedron (middle) and icosahedron (right) clearly does end up in U and not only in the frustrated state I. Moreover, the icosahedron has a higher reactive path probability to the I state than the octahedron, which is also reflected in the flux ratio fUIB/fUB in Fig. 4.
IV. DISCUSSION AND CONCLUSIONS
We studied the effect of multivalency on the kinetics and mechanism of elementary steps in the self-assembly of patchy particles forming polyhedral clusters. By using SRTIS, we were able to obtain the complete rate matrix and thus the full kinetic picture of these simple patchy particle systems. No difference in kinetics is found when the total energy of the ground-state is fixed, which corroborates with a simple steady state analysis. In contrast, the mechanism of self-assembly does depend on the properties of the intermediate state. All studied multivalent particles system can associate into a metastable intermediate state, in which two bonds are formed, and the others are not. From this intermediate state, the system can relax into the correctly formed fully bound state. Pathways that visit these intermediate states are less prevalent for five-fold multivalent particles compared to particles with only three bonds. Instead, the association pathways are more likely to navigate directly from unbound to bound without visiting the intermediate states. Long sojourns in the intermediate state can lead to kinetic trapping and malformed aggregates. It is therefore kinetically favorable for self-assembling systems to have a ground state where particles form many bonds which stabilize the ground state instead of only a few which would result in strongly frustrated intermediate states.
Furthermore, we found a difference between the equilibrium net-flux and the out-of-equilibrium relaxation pathways. In the net flux analysis, long sojourns in intermediate states are not taken into account, simply only the number of times a certain state is visited along (dis)assembly. The number of times a state is visited of course does not necessarily depend on the stability of this state, but on the kinetic accessibility of the state which also depends on the number of microstates a macrostate entails. The icosahedron has more microstates in I (50) than the octahedron (16). This difference is also reflected in the net flux ratio. While our evidence is restricted to the symmetric cases that we used here (tetrahedron, octahedron, and icosahedron), we speculate that other symmetries also show similar features.
The studied systems are too simple to represent real proteins or even colloidal particles, but some general observations about self-assembly of complexes can be made. The generic conclusion that particles with many weak bonds in the ground state are able to self-assemble in a more defect-free way than particles with a few strong bonds might be interesting for the experimental design of colloidal particles to form desired structures.6,9
This conclusion is also found in previous studies, albeit often implicitly. Wilber et al.20–22 focus on the thermodynamic and large-scale dynamical pathways and found that tetrahedrons, octahedron, and icosahedrons form relatively easily. However, particles with only three bonds, which should form cubic and dodecahedral cluster with a more open structure, were prone to formed misaligned structures that would not anneal at the required low temperature (strong bonding) conditions. This corresponds to our finding that higher valence results fewer pathways visiting metastable intermediates, and hence less chance of aggregation. Wilber et al. also showed that at relatively high temperature, the correct cluster formation was limited by thermodynamics, i.e., a transition to the monomer gas, where at low temperature it was limited by kinetics, i.e., getting trapped in malformed structures. As we have employed a similar model, with parameter settings that correspond to the edge of their optimal region, we can directly compare. Indeed in our work we see that at low binding energy (corresponding to high temperature) dissociation is dominant, while at high binding energy (low temperature) dissociation is unlikely. At these high binding strengths, we indeed expect malformed states to occur. Wilber et al. did not investigate the possible association pathways, and hence they did not observe the difference in microscopic pathways. Recently, Colón-Meléndez et al.24 performed experiments followed by extensive simulations47 on microscopic association and dissociation kinetics of lock and key colloidal particles, which are essentially patchy particles. They investigated the effect of nonspecific interaction on the kinetics, something that we discuss elsewhere.25 However, these experiments unfortunately did not address the role of multivalency.
The general conclusion mentioned above implies also that natural occurring systems that spontaneously form complex structures with high fidelity from multivalent particles, such as virus capsids, would show a tendency to have more rather less binding sites. Many studies have been devoted to virus assembly modeling.1,2,14,48–51 For instance, Hagan et al.14,50,51 carried out an extensive simulation of virus assembly and encapsulation and found that kinetic trapping can indeed play a role, especially at strong binding sites. Again, the result is that the capsid binding must be sufficiently weak to be able to form proper virus shells. In Ref. 14 it is found that only the capsomere with 5 binding sites grows by the addition of individual sub-units. Nguyen et al.1 investigate the virus capsid formation using coarse grained capsomere models with multiple binding sites and found it to be a downhill process at sufficiently low temperature (strong attraction), except for the rate limiting addition of the last capsomere. Adding this last capsomere is the reminiscent of the process hat we study here: the addition of a single multivalent particle to an existing cluster. The authors conclude that the cause of the rate limitation is a loss of entropy, both translation and orientation entropies of the last capsomere as well as vibrational entropy of the entire capsid. We note that we did not consider any vibrational entropy contribution in our model, as the cluster is held fixed. In future work, it would be interesting to see what the effect of vibrational entropy is on the association dissociation kinetics.
Naturally, it would be even more informative to study the full unrestricted dynamics of particles for these different types of clusters, i.e., to investigate the assembly pathways tarting from 12 unbound particles in the case of the icosahedron. However, with increasing motility also come an exponentially increasing number of intermediate states which might become intractable. In future work, an adaptive scheme can be considered to automatically find only the important intermediate states, such as adaptive SRTIS,28 or Markov state modeling.31
ACKNOWLEDGMENTS
This work is part of the research programme of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO).
REFERENCES
- 1.Nguyen H. D., Reddy V. S., and Brooks C. L., Nano Lett. 7, 338 (2007). 10.1021/nl062449h [DOI] [PubMed] [Google Scholar]
- 2.May E. R., Feng J., and Brooks C. L., Biophys. J. 102, 606 (2012). 10.1016/j.bpj.2011.12.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang Z., Keys A. S., Chen T., and Glotzer S. C., Langmuir 21, 11547 (2005). 10.1021/la0513611 [DOI] [PubMed] [Google Scholar]
- 4.Glotzer S. C. and Solomon M. J., Nat. Mater. 6, 557 (2007). 10.1038/nmat1949 [DOI] [PubMed] [Google Scholar]
- 5.Chen Q., Bae S. C., and Granick S., Nature 469, 381 (2011). 10.1038/nature09713 [DOI] [PubMed] [Google Scholar]
- 6.Kraft D. J., Ni R., Smallenburg F., Hermes M., Yoon K., Weitz D. A., van Blaaderen A., Groenewold J., Dijkstra M., and Kegel W. K., Proc. Natl. Acad. Sci. U. S. A. 109, 10787 (2012). 10.1073/pnas.1116820109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang Y., Wang Y., Breed D. R., Manoharan V. N., Feng L., Hollingsworth A. D., Weck M., and Pine D. J., Nature 491, 51 (2012). 10.1038/nature11564 [DOI] [PubMed] [Google Scholar]
- 8.Chen Q., Whitmer J. K., Jiang S., Bae S. C., Luijten E., and Granick S., Science 331, 199 (2011). 10.1126/science.1197451 [DOI] [PubMed] [Google Scholar]
- 9.Yi G.-R., Pine D. J., and Sacanna S., J. Phys.: Condens. Matter 25, 193101 (2013). 10.1088/0953-8984/25/19/193101 [DOI] [PubMed] [Google Scholar]
- 10.Duguet É., Hubert C., Chomette C., Perro A., and Ravaine S., C. R. Chim. 19, 173 (2016). 10.1016/j.crci.2015.11.013 [DOI] [Google Scholar]
- 11.Bianchi E., Largo J., Tartaglia P., Zaccarelli E., and Sciortino F., Phys. Rev. Lett. 97, 168301 (2006). 10.1103/physrevlett.97.168301 [DOI] [PubMed] [Google Scholar]
- 12.Bianchi E., Capone B., Kahl G., and Likos C. N., Faraday Discuss. 181, 123 (2015). 10.1039/c4fd00271g [DOI] [PubMed] [Google Scholar]
- 13.Bianchi E., Doppelbauer G., Filion L., Dijkstra M., and Kahl G., J. Chem. Phys. 136, 214102 (2012). 10.1063/1.4722477 [DOI] [PubMed] [Google Scholar]
- 14.Hagan M. F. and Chandler D., Biophys. J. 91, 42 (2006). 10.1529/biophysj.105.076851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.den Otter W. K., Renes M. R., and Briels W. J., J. Phys.: Condens. Matter 22, 104103 (2010). 10.1088/0953-8984/22/10/104103 [DOI] [PubMed] [Google Scholar]
- 16.Matthews R. and Likos C. N., Soft Matter 9, 5794 (2013). 10.1039/c3sm50737h [DOI] [Google Scholar]
- 17.Ilie I. M., den Otter W. K., and Briels W. J., J. Chem. Phys. 141, 065101 (2014). 10.1063/1.4891306 [DOI] [PubMed] [Google Scholar]
- 18.Klein H. C. R. and Schwarz U. S., J. Chem. Phys. 140, 184112 (2014). 10.1063/1.4873708 [DOI] [PubMed] [Google Scholar]
- 19.Rapaport D., Phys. Rev. Lett. 101, 186101 (2008). 10.1103/physrevlett.101.186101 [DOI] [PubMed] [Google Scholar]
- 20.Wilber A. W., Doye J. P., Louis A. A., Noya E. G., Miller M. A., and Wong P., J. Chem. Phys. 127, 085106 (2007). 10.1063/1.2759922 [DOI] [PubMed] [Google Scholar]
- 21.Wilber A. W., Doye J. P., and Louis A. A., J. Chem. Phys. 131, 175101 (2009). 10.1063/1.3243580 [DOI] [PubMed] [Google Scholar]
- 22.Wilber A. W., Doye J. P. K., Louis A. A., and Lewis A. C. F., J. Chem. Phys. 131, 175102 (2009). 10.1063/1.3243581 [DOI] [PubMed] [Google Scholar]
- 23.Whitelam S., Phys. Rev. Lett. 105, 088102 (2010). 10.1103/physrevlett.105.088102 [DOI] [PubMed] [Google Scholar]
- 24.Colón-Meléndez L., Beltran-Villegas D. J., van Anders G., Liu J., Spellings M., Sacanna S., Pine D. J., Glotzer S. C., Larson R. G., and Solomon M. J., J. Chem. Phys. 142, 174909 (2015). 10.1063/1.4919299 [DOI] [PubMed] [Google Scholar]
- 25.Newton A. C., Kools R., Swenson D. W. H., and Bolhuis P. G., “The opposing effects of isotropic and anisotropic attraction on association kinetics of proteins and colloids,”J. Chem. Phys. (submitted). [DOI] [PubMed]
- 26.Newton A. C., Groenewold J., Kegel W. K., and Bolhuis P. G., Proc. Natl. Acad. Sci. U. S. A. 112, 15308 (2015). 10.1073/pnas.1513210112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Williamson A. J., Wilber A. W., Doye J. P., and Louis A. A., Soft Matter 7, 3423 (2011). 10.1039/c0sm01377c [DOI] [Google Scholar]
- 28.Du W.-N. and Bolhuis P. G., J. Chem. Phys. 139, 044105 (2013). 10.1063/1.4813777 [DOI] [PubMed] [Google Scholar]
- 29.Du W. and Bolhuis P. G., J. Chem. Phys. 140, 195102 (2014). 10.1063/1.4874299 [DOI] [PubMed] [Google Scholar]
- 30.Noé F., Schütte C., Vanden-Eijnden E., Reich L., and Weikl T. R., Proc. Natl. Acad. Sci. U. S. A. 106, 19011 (2009). 10.1073/pnas.0905466106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Perkett M. R. and Hagan M. F., J. Chem. Phys. 140, 214101 (2014). 10.1063/1.4878494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nayhouse M., Heng V. R., Amlani A. M., and Orkoulas G., J. Phys.: Condens. Matter 24, 375105 (2012). 10.1088/0953-8984/24/37/375105 [DOI] [PubMed] [Google Scholar]
- 33.Liu H., Kumar S. K., and Sciortino F., J. Chem. Phys. 127, 084902 (2007). 10.1063/1.2768056 [DOI] [PubMed] [Google Scholar]
- 34.Northrup S. H. and Erickson H. P., Proc. Natl. Acad. Sci. U. S. A. 89, 3338 (1992). 10.1073/pnas.89.8.3338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gabdoulline R. R. and Wade R.C., Biophys. J. 72, 1917 (1997). 10.1016/S0006-3495(97)78838-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vijaykumar A., Ouldridge T. E., ten Wolde P. R., and Bolhuis P. G., J. Chem. Phys. 146, 114106 (2017). 10.1063/1.4977515 [DOI] [PubMed] [Google Scholar]
- 37.Romano F., De Michele C., Marenduzzo D., and Sanz E., J. Chem. Phys. 135, 124106 (2011). 10.1063/1.3629452 [DOI] [PubMed] [Google Scholar]
- 38.Whitelam S., Mol. Simul. 37, 606 (2011). 10.1080/08927022.2011.565758 [DOI] [Google Scholar]
- 39.Whitelam S. and Geissler P. L., J. Chem. Phys. 127, 154101 (2007). 10.1063/1.2790421 [DOI] [PubMed] [Google Scholar]
- 40.Dellago C., Bolhuis P. G., and Geissler P. L., Adv. Chem. Phys. 123, 1 (2002). 10.1002/0471231509.ch1 [DOI] [Google Scholar]
- 41.Bolhuis P. G., J. Chem. Phys. 129, 114108 (2008). 10.1063/1.2976011 [DOI] [PubMed] [Google Scholar]
- 42.van Erp T. S., Phys. Rev. Lett. 98, 268301 (2007). 10.1103/physrevlett.98.268301 [DOI] [PubMed] [Google Scholar]
- 43.Bolhuis P. G. and Lechner W., J. Stat. Phys. 145, 841 (2011). 10.1007/s10955-011-0324-6 [DOI] [Google Scholar]
- 44.Ferrenberg A. M. and Swendsen R. H., Phys. Rev. Lett. 63, 1195 (1989). 10.1103/physrevlett.63.1195 [DOI] [PubMed] [Google Scholar]
- 45.Kumar S., Bouzida D., Swendsen R. H., Kollman P. A., and Rosenberg J. M., J. Comput. Chem. 13, 1011 (1992). 10.1002/jcc.540130812 [DOI] [Google Scholar]
- 46.Rogal J., Lechner W., Juraszek J., Ensing B., and Bolhuis P. G., J. Chem. Phys. 133, 174109 (2010). 10.1063/1.3491817 [DOI] [PubMed] [Google Scholar]
- 47.Beltran-Villegas D. J., Colón-Meléndez L., Solomon M. J., and Larson R. G., J. Colloid Interface Sci. 463, 242 (2016). 10.1016/j.jcis.2015.10.062 [DOI] [PubMed] [Google Scholar]
- 48.Endres D. and Zlotnick A., Biophys. J. 83, 1217 (2002). 10.1016/s0006-3495(02)75245-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.van der Schoot P. and Zandi R., Phys. Biol. 4, 296 (2007). 10.1088/1478-3975/4/4/006 [DOI] [PubMed] [Google Scholar]
- 50.Hagan M. F., Elrad O. M., and Jack R. L., J. Chem. Phys. 135, 104115 (2011). 10.1063/1.3635775 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Perlmutter J. D., Mohajerani F., and Hagan M. F., eLife 5, e14078 (2016). 10.7554/elife.14078 [DOI] [PMC free article] [PubMed] [Google Scholar]