Static vs. dynamic decoding algorithms in a non-invasive body-machine interface

Abstract

In this study, we consider a non-invasive body-machine interface that captures body motions still available to people with spinal cord injury (SCI) and maps them into a set of signals for controlling a computer user interface while engaging in a sustained level of mobility and exercise. We compare the effectiveness of two decoding algorithms that transform a high-dimensional body-signal vector into a lower dimensional control vector on 6 subjects with high-level SCI and 8 controls. One algorithm is based on a static map from current body signals to the current value of the control vector set through principal component analysis (PCA), the other on dynamic mapping a segment of body signals to the value and the temporal derivatives of the control vector set through a Kalman filter. SCI and control participants performed straighter and smoother cursor movements with the Kalman algorithm during center-out reaching, but their movements were faster and more precise when using PCA. All participants were able to use the BMI’s continuous, two-dimensional control to type on a virtual keyboard and play pong, and performance with both algorithms was comparable. However, seven of eight control participants preferred PCA as their method of virtual wheelchair control. The unsupervised PCA algorithm was easier to train and seemed sufficient to achieve a higher degree of learnability and perceived ease of use.

I. INTRODUCTION

Spinal cord injury (SCI) can lead to severe motor impairments, and currently there is no ‘cure’ for paralysis after SCI. The annual number of SCI cases in the US is estimated to be approximately 12,000, with 50% of these cases occurring at one of the spinal cord’s cervical segments (C1-C7) [1]. Injuries at this level often result in tetraplegia: weakness or total loss of movement that affects all limbs [1]. People with SCI face long-lasting effects such as loss of motor and sensory functions, weakness, altered reflexes, and muscular and cortical atrophy [2]. Furthermore, these patients often lack motivation for exercising their residual motion, have depression and decreased self-confidence [3], and have difficulty controlling their assistive devices [4], [5].

The current commercially available assistive devices for people with tetraplegia – like the sip- and-puff and the head arrays – have a small vocabulary of commands, restrict head movement, and place the burden of learning device operation entirely on the user. One of the challenges for people with paralysis is to preserve their mobility as much as possible. However, current assistive devices, being focused on minimizing body motions, fail to keep an active body and to promote the use of the neural and muscular resources that survived the injury, which could be critical for people with tetraplegia to avoid collateral effects of paralysis and to recover some of the lost mobility [6]–[9]. In fact, even when the injuries occur at a high level of the spinal cord, some residual motor and sensory capacities remain available [4]. These functions could potentially serve as the means to control assistive devices such as robotic arms, computers, and wheelchairs, without requiring invasive interventions [4], [5]. Therefore, it is essential to develop control interfaces that provide a stimulating framework for exercising and practicing motor skills while providing an advanced level of control. Every SCI is different, and the residual abilities vary across people. To overcome current limitations, novel assistive devices for people with high tetraplegia cannot follow a ‘one-size fits all’ approach; instead, they should be user-based [4]. The new generation of assistive devices should have the ability to adapt to each user’s residual ability and be continuously modified according to their evolving skills.

For this purpose, our team has developed new methods for human-machine interfaces, which we call body-machine interfaces (BMI's), harnessing the overabundant number of signals from the cache of body movements that SCI users are still capable of executing. Infrared video cameras and inertial measurement unit (IMU)-based BMIs have allowed unimpaired and SCI participants to use their upper-body movements to engage in exercises that require different operational functions such as controlling a keyboard for typing, playing a videogame, driving a simulated wheelchair in a virtual reality (VR) environment, and performing a center-out reaching task. Two main algorithms have been used to develop a body-to-cursor map, principal component analysis (PCA), and Kalman. In PCA, body-motion signals are recorded during a one-minute calibration ‘dance’ phase, where participants executed self-paced and self-directed motions with the upper-body. Then a static body-to-cursor map is derived from the first two principal eigenvectors, as explained in [10], [11]. In the Kalman experimental setup, analogous to brain-machine interfaces [12]–[15], unimpaired participants generated the body-to cursor map enacting upper body motions as if they were controlling the image of a 2D moving cursor presented to them on a computer monitor. Results from both approaches demonstrated the potential of non-invasive IMU-based BMIs as an alternative or complement to brain-machine interfaces for accomplishing cursor control in 2D space.

Body-machine interfaces based on PCA have been adapted for remote control of a robotic arm [16], to control powered wheelchairs [17], and as a tool for neuromotor rehabilitation after stroke [18] and SCI [19]. The Kalman filter approach has been widely used in the brain-machine interface field [20]–[23], and by unimpaired participants in a BMI to perform center-out reaching tasks and driving a VR wheelchair on a computer screen [24]. PCA and Kalman mapping algorithms transform a high-dimensional body-signal vector into a lower dimensional control vector, and each algorithm offers specific benefits. The PCA ‘dance’ allows capturing each person’s unique residual ability over the high dimensional residual movement space, and using the two first principal components extracted from their movement as the 2D control signals. However, the motions that a user has to make in order to move the cursor horizontally or vertically are not always clear or intuitive. In comparison, the Kalman filter allows participants to explicitly choose two movements they want to use to control horizontally and vertically.

The current exponential decrease in IMU technology cost and size [25] could make the IMU-based BMI an affordable platform for people with tetraplegia to control assistive devices such as powered wheelchairs. However, although the effectiveness of both PCA and Kalman algorithms has been demonstrated independently, a direct comparison between both algorithms has not been performed yet.

II. METHODS

A. Experimental Setup

Six participants with a cervical-level injury to the spinal cord (characteristics in Table 1) and eight healthy participants (4 female, 31±4 years old) gave their informed and signed consent to participate in this study, which was approved by Northwestern University’s Institutional Review Board. Participants sat in front of a computer monitor wearing a vest with Velcro® patches on the shoulder areas. Four IMUs (MTx, Xsens Technologies B.V., Enschede, Netherlands) were attached to the shoulders as shown in Fig. 1A. The IMUs were connected to a CPU via a digital data bus system. The combination of the sensors’ 3D gyroscopes and accelerometers allowed us to capture shoulder and upper-body motions. Data from the IMUs were sampled in real-time (Simulink, Mathwoks, Inc., Massachusetts, United States) at a sampling frequency of 50Hz.

Table 1.

SCI Participant Characteristics

SUBJECT ID	GENDER	AGE	LEVEL OF INJURY	TIME AFTER INJURY	MAP
S003	Female	59	C6	2 years	PCA
S005	Female	41	C6	8 years	PCA
S006	Male	30	C5	10 years	PCA
S301	Male	36	C5-C6	13 years	Kalman
S302	Male	42	C5	16 years	Kalman
S304	Male	55	C6	15 years	Kalman

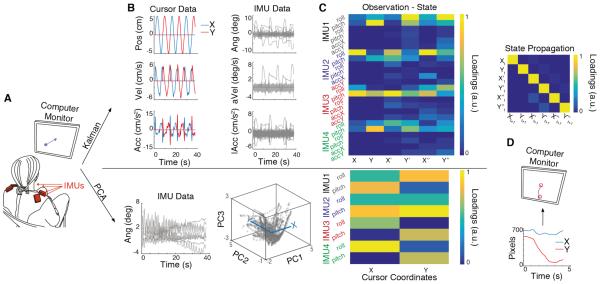
Fig. 1. Mapping algorithms to transform a high-dimensional body-signal vector into a lower dimensional control vector.

(A) Participants sat in front of a computer monitor wearing four IMUs on the shoulder area. (B) The Kalman algorithm (top) required participants to follow a moving cursor on the screen as if they were controlling it with their shoulders while we recorded cursor and body kinematics. The PCA algorithm (bottom) required participants to move freely and randomly with their shoulders. A PCA on the high-dimensional body movement vector resulted in a low-dimensional representation of the body postures that explained most of the variance. (C) A mapping matrix was used to transform body signals into cursor kinematics. The Kalman observation matrix mapped position, velocity, and acceleration of the shoulders into kinematics of the 2D cursor. The state propagation matrix mapped the cursor kinematics at one time step to the cursor kinematics at the future time step. The PCA matrix mapped position of each sensor into the 2D cursor vector. Each column’s loadings are normalized by its maximum value. (D) The position output of both algorithms was projected into the X and Y coordinates of a computer cursor. Participants were able to see the feedback of cursor position and move their body accordingly to perform the required tasks.

B. Calibration

The main purpose of the BMI was to map the high-dimensional body-signal vector of upper-body movements, measured by the IMUs, into a lower dimensional (2D) control vector. We compared the effectiveness of two decoding algorithms that allowed participants to perform center-out reaching and virtual wheelchair driving (VR) tasks.

One algorithm was based on a static mapping from current body position signals to the current value of the control vector, the other was based on dynamically mapping a segment of body signals to the value and the temporal derivatives of the control vector. The dynamic mapping was set by a Kalman Filter [26] as applied by [14] in their brain-machine interface. In analogy with brain-machine interfaces, where the map was based on estimating the desired cursor movement from spike trains, our IMU map was based on explicit information on position, velocity, and acceleration [24], [27]. In contrast, the static mapping was set by Principal Component Analysis (PCA) [28] as applied by [10], [11].

Kalman Calibration

Participants were presented with a cursor on the computer monitor that moved with a pre-determined path. They were instructed to move their shoulders with the cursor as if they were already controlling it with their chosen movements. Participants were instructed to control horizontal cursor movements by moving their left shoulder up (elevation) and down (depression) respectively, and to control vertical cursor movements by moving their right shoulder up and down respectively.

The 2 cm diameter cursor moved with a minimum-jerk velocity profile that resembles commonly observed human point-to-point movement [29]–[31]. The cursor’s position history while moving from the center towards the right and back was governed by the function:

$$x\left(t\right)=x_0+(x_0-x_f)(15{\tau }^4-6{\tau }^5-10{\tau }^3)$$ (1)

$$y\left(t\right)=y_0+(y_0-y_f)(15{\tau }^4-6{\tau }^5-10{\tau }^3)$$ (2)

where τ = t/t_t, s₀, y₀ are the initial cursor position coordinates at t = 0 and x_f and y_f are the final cursor position coordinates at t = t_f [31]. The profile of cursor position, velocity, and acceleration history during training is shown in Fig. 1B, top. The trajectory is a straight line between the center and final positions with a bell-shaped unimodal velocity profile. The total duration of each movement to the right and back lasted 4 sec. A 6×6 cm box delimited the cursor’s movement range so that participants knew where the cursor would stop moving and come back to the center, and plan to move their shoulders accordingly. The cursor moved to each of the four directions (up, down, right, left) six times for a total calibration time of 96 sec.

While participants followed the cursor as if they were controlling it with their shoulders during the calibration phase, we logged body motion and cursor data. The IMU’s Euler angles, angular velocities, and linear accelerations [Fig. 1B] were recorded at each time step k (every 20ms) as the body observation in a 24-dimensional (2 angles, 2 velocities, 2 accelerations * 4 sensors) vector Z_k. The position, velocity, and acceleration of the cursor were recorded at each time step k as the cursor’s state S_k. Both data were fed into a Kalman state estimator to learn the matrices that relate body motions to cursor kinematics.

The purpose of the Kalman filter is to estimate the cursor’s state at every instant in time, based on the body observations. The Kalman model assumes the state to be linearly related to the future state (next time step) by a stochastic linear function:

$${\mathit{s}}_{\mathit{k}+1}=A_k{\mathit{s}}_{\mathit{k}}+w_k$$ (3)

where k = 1,2,…,M, A_k ∈ R^6×6 is the matrix that linearly relates the cursor’s kinematics between successive time steps, w_k represents the process noise term, which we assumed to have zero mean and to be normally distributed, i.e. w_k ~ N(0,W_k), W_k ∈ R^6×6, and M is the total number of time steps.

The Kalman model also assumes that the observation is linearly related to the state at each time step by the stochastic linear function:

$${\mathit{z}}_{\mathit{k}}=H_k{\mathit{s}}_{\mathit{k}}+q_k$$ (4)

where z_k ∈ R ^24×1 is the vector containing the IMUs’ observation at each time step k. H_k ∈ R^24×6 is the coefficient matrix that linearly relates the cursor’s state to the body motion, and q_k is the measurement noise term, i.e. q_k ~ N(0,Q_k), Q_k ∈ R^24×24 .

Through these two assumptions, we can use the calibration data from the cursor and the IMUs to estimate the model’s matrices via least squares (for details, see [14], [24], [27]). After the model’s parameters have been estimated, the model encodes the body observation and cursor propagation [Fig.1C, top], and participants can move their shoulders to control the 2D cursor on the screen [Fig. 1D].

PCA Calibration

During the PCA Calibration phase, participants were asked to perform a “free body dance” where they were instructed to move their shoulders as freely and randomly as possible for 1 minute. Participants were told to make shoulder movements within a comfortable range of motion and to avoid extreme or uncomfortable movements.

As participants performed the “free body dance”, we recorded body motion from the IMUs Euler angles [Fig. 1B, bottom] as the calibration data. Principal component analysis was then performed on the calibration data to rearrange the IMU signals into eight principal components ordered by decreasing variance. The calibration data projected onto the first three principal components is shown in Fig. 1B, bottom. We then used the first two principal components (the ones that accounted for the highest percentage of variance) to determine a forward map (8x2) between the 8-dimensional body vector to the 2-dimensional cursor vector [Fig. 1C, bottom] as demonstrated before in [17]. This method allows the users to exploit the redundancy of their body positions to control the 2D cursor on the screen [Fig. 1D].

Familiarization

After the calibration phase, participants were allowed to familiarize with the control of the body-machine interface before beginning the experiment. There were no specific instructions or goals during the familiarization phase. Participants were told to try different body movements and see how they affected the cursor’s position. They were asked to try to move the cursor up, down, left, right, and to make sure that they could reach all edges and corners of the screen. If the participants could not comfortably reach an edge of the screen, the gain between body motions and cursor coordinates was manually adjusted. If participants had trouble controlling the map, or if they did not feel comfortable with it, the calibration procedure was repeated.

C. Protocol

Once participants were able to comfortably control the 2D cursor using their shoulder motions, they performed a variety of computer tasks that allowed us to chart an explicit learning curve for different performance measures. The first three SCI participants used body-machine interface with the PCA algorithm to complete the tasks. The last three SCI participants used Kalman. In contrast, healthy participants used both maps in random order to complete the same tasks.

Protocol for SCI Participants

Six participants with high-level SCI performed 12 sessions of BMI training. Each session consisted of four blocks. The blocks consisted of: reaching, typing, playing pong, and another reaching block. There was a 1-minute resting period between blocks. Participants performed 24 trials per reaching block, with random target order comprised of exactly three trials in each direction.

Once participants familiarized themselves with the map in the beginning of each session, they controlled a computer arrow cursor to reach eight peripheral 2.2cm diameter targets appearing in pseudorandom order on the screen. Participants had to hold the cursor inside the center target for 1sec in order for one peripheral target to appear in the screen. Participants were instructed to reach the targets as smoothly and accurately as possible, but they were not given any specific time constraints.

During the typing task, participants were asked to type the common pangram “The quick brown fox jumps over the lazy dog”. They moved the 2D cursor over a virtual Keyboard (Click-N-Type) that would click if the cursor hovered over a key for more than 500 milliseconds. During the pong task, they were asked to hit a moving ball as many times as possible. The ball moved in a 45deg angle along the screen with a constant velocity. When participants hit the ball with the paddle, the ball’s vertical velocity component changed sign.

Protocol for Control Participants

Eight non-impaired subjects performed one session of BMI training. The session consisted of four blocks of reaching and one block of virtual driving with a 1-minute resting period between blocks using one of the two maps. The reaching blocks were identical to the ones performed by SCI participants. After the virtual driving block, control participants repeated all five blocks with the other map. The order in which participants tried the maps was determined at random, and there was a 5-minute resting period between maps.

After the fourth block of reaching, participants were placed in a virtual environment developed by our laboratory using a commercial-grade, 3D gaming engine (Unity®, Unity Technologies, San Francisco, CA, USA). The virtual environment provided a safe system for controlling a powered wheelchair without the risk of collisions or accidents. The simulator was adapted so that the 2D cursor output from the decoders was transformed into the virtual wheelchair’s joystick input; by moving the cursor up, the simulated wheelchair moved forward, and so on. The simulated environment reproduced a series of tasks features that a wheelchair user would have to perform in a real wheelchair. The tasks included: a) driving in a straight line, b) turning 90° and 45° clockwise, and c) turning 90° and 45° counter-clockwise [Fig. 7A].

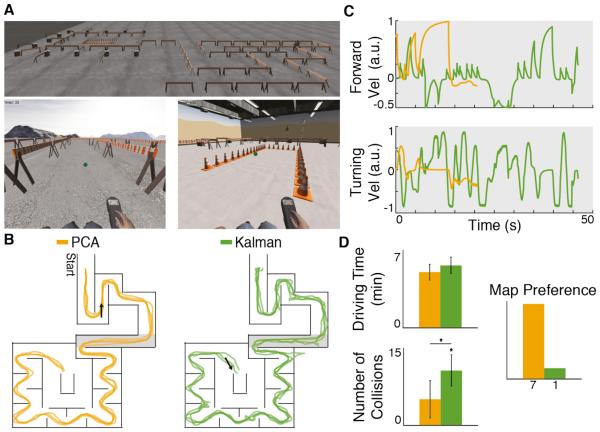
Fig. 7. Virtual wheelchair driving using a body-machine interface based on inertial sensors.

(A) Three-dimensional rendering of the virtual environment used by participants during control of a simulated wheelchair. Participants drive the wheelchair by controlling the position of the green circle that represents the wheelchair’s joystick. (B) Example wheelchair trajectories for four participants are overlaid on the top-view of the VR navigation map. Trajectories are shown in amber of PCA participants and green for Kalman participants. White lines represent walls and obstacles, the black arrows indicate the position and orientation of the camera screenshots in (A), and the shaded area indicates the location for the data in (C). (C) Example wheelchair forward (top) and turning (bottom) velocities during a straight path in the navigation task (shaded area in B). (D) The number of collisions and total driving time is shown for each map. Data are means ± SEM (bars).

D. Analysis

Performance Measures

Performance was quantified by four performance measures. For each center-out trial, jerk, path length, error after 1 sec, and movement time were computed. Jerk was computed as the time derivative of acceleration normalized by movement amplitude, duration, and mean speed. This dimensionless measure of jerk has been shown to properly quantify common deviations from smooth, coordinated movement [32]. A small jerk value would indicate a smooth, well-coordinated movement. Path length was computed as the sum of the Euclidean distance between consecutive cursor positions along each center-out reach trajectory, normalized by the straight-line distance between the starting and ending cursor positions. Path length quantifies movement “straightness” and “effectiveness”. A path length value of 1 would indicate the participant moved in a perfectly straight line from the center target to the peripheral target. Error after 1 sec was defined as the Euclidean distance between the cursor and target positions 1sec after movement initiation. Movement initiation was determined as the instant when the cursor’s velocity was above 10% of the velocity peak for that trial. Movement time was computed as the time between the target appearing on the screen, and 1sec before the participant completed the trial (target had to be held for one second). The movement time measure indicates the time that it took participants to complete the trial.

All performance measures were averaged over all trials to obtain one value per session or block for each participant. This resulted in a total of 12 values for SCI participants (12 sessions, averaged 1^st and 2^nd reaching blocks) and 8 values for control participants (4 blocks, 2 maps) for the whole experiment. Together, these performance measures allowed us to measure differences in cursor control proficiency for each participant, within a map, and between the four different maps (SCI-Kalman, SCI-PCA, Control-Kalman, Control-PCA). Other performance measures were also computed (straight-line distance and aspect ratio), but they were highly correlated to these four, so these four were enough to characterize movement performance during the center-out reaching task. An additional analysis on movement velocity was performed for control participants. Cursor and IMU peak tangential velocities were computed for each center out reach in order to investigate movement speed differences between maps. The tangential velocity at each point in time was calculated as the square root of the sum of the squared instantaneous speeds along each dimension (2 dimensions for cursor, 8 dimensions for IMU).

Typing performance was quantified by the total time it took to type the sentence. A words-per-minute (WPM) metric was computed by dividing the number of characters in the pangram (43) by the total typing time and then again by 5 (making the common assumption that the English language has on average 5 characters per word). Pong performance was quantified by the number of times the participant was able to hit the ball with the paddle.

Virtual wheelchair driving performance was quantified by two metrics. For each driving block, the time to completion, and the number of collisions were recorded. This resulted on a total of 2 values for each performance measure for each control participant (1 for each map).

At the end of the experiment, we asked each control participant to choose the map that they liked the best (Kalman or PCA). Specifically, we asked each participant “What map would you choose to stay with in the future? The one that you calibrated with the dance, or the one were you followed the cursor?”

In order to determine whether we could predict task performance based on calibration data, we tested the correlation between the reconstruction of the training data for Kalman and the performance in the first block. For the Kalman algorithm, we tested each participant’s map on a testing set that consisted of the body-movement observations for the calibration data. We ‘fed’ those observations into the map in order to make a prediction of the state. We then calculated a correlation coefficient between the reconstructed state and the actual state. We averaged the reconstruction correlation coefficients for the first two dimensions of the state (x, y). For each participant, we plotted their reconstruction correlation against each of the performance measures at the first block. This analysis allows us to determine if we can predict what each participant’s performance will be before they begin the experiment, based on their calibration data.

Statistics

A two-way mixed model analysis of variance (ANOVA) was performed on each center-out reaching performance measure. SESSION (1vs12 for SCI or 1vs4 for Controls) was set as the within-participant factor and MAP (PCA vs. Kalman) as the between-participant factor, with a Greenhouse-Geisser correction for violations of sphericity. In order to determine if participants using one map were better than participants using the other map at the end of training, a post-hoc comparison was performed to test the null-hypothesis that the mean between two maps at the last block was the same. In order to test for a learning effect, we performed a post-hoc paired t-test for each map. We tested the null hypothesis that the mean difference between paired observations of the first vs. the last blocks was zero. All statistical tests were repeated for each performance measure and allowed us to reject the null hypothesis at p < 0.05.

A one-sample t-test was performed on the collision VR measure to test the null hypothesis that the mean number of collisions for each map was equal to zero. Additionally, a two-sample t-test was performed on both collision and time measures to test the null-hypothesis that the mean difference between both maps was zero. We rejected the null hypothesis at p < 0.05.

III. RESULTS

A. Qualitative results show that SCI and Control participants perform straighter and smoother cursor movements with Kalman than with PCA

All participants were able to perform the center-out reaching task regardless of the mapping algorithm they were assigned. Center-out cursor trajectories for representative participants in each map group are shown in Figure 2A. Performing the task was somewhat difficult for all participants in the first block of reaching. Cursor trajectories were all over the task space, especially for SCI participants. Participants had trouble moving in the correct direction towards the target, and there were a lot of changes in movement direction while performing each trial. In the first block of reaching, participants in all map groups tended to overshoot and undershoot the target locations. This required participants to either come back to the target, or make another movement that would get them closer to the target. Interestingly, control participants using the Kalman filter appeared to move somewhat straight from the first block, and overshoots appear to be less drastic than for PCA.

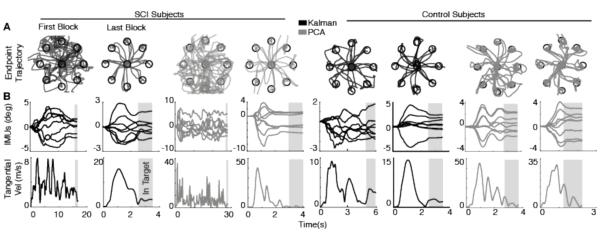
Fig. 2. Qualitative performance for SCI and control participants using the Kalman and PCA algorithms in a body-machine interface during center-out reaching.

(A) Center-out cursor trajectories to eight targets during the first (left) and last (right) blocks of training. Each color represents a participant from a different map group. (B) Representative example of IMU orientation signals time history during one center-out reach. The shaded area indicates the time while the cursor was inside the target. (Bottom) Cursor tangential velocity history during the same center-out reach as the IMU signals above.

Body and cursor movements did not reflect proficient cursor control in the first block. IMU angle signals and cursor tangential velocity time histories for a representative trial for each block are shown in Figure 2B. In the beginning of BMI training, participants moved their bodies in different ways as if they were exploring the space to perform the task. There were many peaks in the velocity profile of the cursor movement, and each trial could take between 20-30 sec for SCI participants and 4-6 sec for controls.

After training, participants in all map groups were moving with what appeared to be proficient cursor control. Participants moved the cursor in the correct direction towards the target, almost in a straight line [Fig. 2A]. There were less target overshoots and less changes in movement direction. Interestingly, cursor movements for control participants using the PCA appeared to be less straight than other maps. In the last block, participants’ cursor movement resembled a smooth, bell-shaped velocity profile (Fig. 2B). There appeared to be one main movement, with a low-speed correction towards the end of the reach and inside the target. By the end, each trial could take between 4-6 sec for SCI participants and 3-4 sec for controls. Trials that showed a representative velocity profile for each map where chosen for the figure.

B. Quantitative results show that both SCI and control participants perform smoother and straighter movements with Kalman decoding but are more precise with PCA

All participants were able to operate the BMI using both algorithms. Calculating performance measures for each trial allowed us to take a deeper look into the details of cursor movement. These measures provide insight into the specific characteristics of cursor movement that would make one map better than the other. Performance for each participant and mean map performance at each block are shown for SCI and control participants in Fig. 3A and Fig. 4A respectively. There was an overall improvement in performance after 12 sessions of BMI practice. However, the level of improvement was not consistent across maps or performance measures. Participants generally moved the cursor in a straight line with a smooth velocity profile while using the Kalman algorithm, and they moved more precisely while using the PCA algorithm.

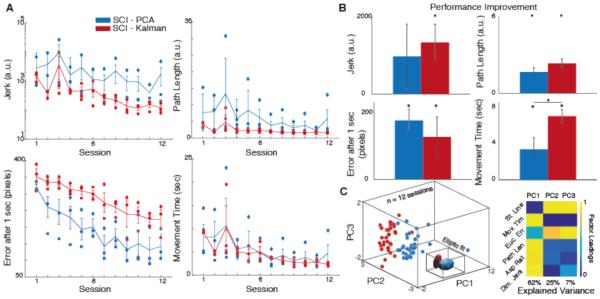
Fig. 3. Spinal cord injured participant performance for 12 sessions of BMI training.

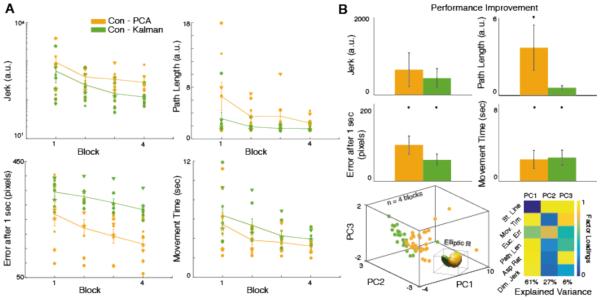
(A) Participants performance at each session is shown for PCA (blue) and Kalman (red) SCI participants. Each marker type denotes a different participant’s mean performance at that session. The lines represent the map averages (n = 3 participants, 48 trials per session). (B) Improvement in performance (first – last) is shown for each map. (C) PCA was applied on 4 performance measures for all participants calculated over 12 successive sessions. Least-square elliptic fits are drawn to emphasize map differences in PC space. The matrix reports the normalized score of each performance measure along each PC. Data are means ± SEM (bars). a.u., arbitrary units.

Fig. 4. Control participant performance for 4 blocks of BMI training.

(A) Participants performance at each block is shown for PCA (amber) and Kalman (green) control participants. Each marker type denotes a different participant’s mean performance at that block. The lines represent the map averages (n = 8 participants, 24 trials per session). (B) Improvement in performance (first – last) is shown for each map. (C) PCA was applied on 4 performance measures for all participants calculated over 4 successive blocks. Least-square elliptic fits are drawn to emphasize map differences in PC space. The matrix reports the normalized score for each performance measure along each PC. Data are means ± SEM (bars). a.u., arbitrary units.

A reduction in jerk after 12 sessions was apparent for most SCI participants in both maps, however only participants using the Kalman algorithm showed a significant effect [Fig. 3A,B, Fig. 4A,B]. This indicated that, with practice, Kalman SCI participants were able to use coordinated shoulder movements to increase the movement smoothness of the controlled 2D cursor. The session effect on jerk was not significant for SCI participants, but was for controls (Table 3). Additionally, map differences did not depend on session, and there was no significant difference in jerk between maps at the end of training (Table 3).

Table 3.

Statistical analysis results for learning and difference at last block (t-statistic, p-value)

	Learning Effect Paired t-test				Difference at last block Two sample t-test
	SCI		CONROL		SCI	CONTROL
Measure	PCA	KAL	PCA	KAL
Jerk (a.u.)	2.01, 0.091	4.92, 0.020*	1.50, 0.088	1.72, 0.064	1.09, 0.391	2.02, 0.083
Error after 1 sec (a.u.)	9.08, 0.006*	3.68, 0.033*	4.02, 0.002*	3.68, 0.004*	4.92, 0.039*	4.64, 0.002*
Path Length (a.u.)	5.01, 0.018*	6.49, 0.011*	2.12, 0.036*	1.73, 0.063	1.17, 0.363	2.41, 0.047*
Movement Time (sec)	4.43, 0.024*	16.44, 0.002*	2.38, 0.024*	3.17, 0.007*	0.997, 0.425	2.35, 0.051

Velocity statistical results for ANOVA (F-statistic, p-values) and t-test (t-statistic, p-value)

	ANOVA			Learning Effect		Difference at last block
	Repeated Measures			Paired t-test		Two sample t-test
Measure	Block	Interaction (Block*Map)	Map	PCA	KAL
Cursor Velocity (m/s)	1.11, 0.355	0.663, 0.580	14.63, 0.002*	1.32, 0.115	1.10, 0.154	4.62, 0.002*
IMU Velocity (deg/sec)	1.44, 0.244	1.08, 0.370	5.30, 0.037*	1.52, 0.087	0.04, 0.190	2.15, 0.068

When a new target appeared, participants had unlimited time to plan and start their center-out movement. However, as they became more familiar with the BMI, the Euclidean distance between the cursor and the target 1 second after movement initiation decreased with both maps (Fig. 3A,B, Fig. 4A,B, and Table 2). This indicated that, with practice participants moved more accurately towards the target location. There was a session and block effect on Euclidean error after 1 sec for SCI and control participants respectively. However, map differences did not depend on session (Table 2). Overall, SCI participants using the PCA algorithm moved more accurately than participants using the Kalman algorithm. There was a significant difference in Euclidean error after 1 sec between the PCA and Kalman maps at the end of training for both SCI and controls (Table 3).

Table 2.

Repeated measures ANOVA statistical results (F-statistic, p-value)

		ANOVA Repeated measures
	SCI			CONTROL
Measure	Session	Interaction (Session*Map)	Map	Block	Interaction (Block*Ma p)	Map
Jerk (a.u.)	1.90, 0.066	0.389, 0.949	0.811, 0.419	4.17, 0.011*	0.20 0.895	1.52, 0.237
Error after 1 sec (a.u.)	21.16, < 0.001*	1.15, 0.347	7.72, 0.049*	19.98, < 0.001*	1.51, 0.227	12.34, 0.003*
Path Length (a.u.)	2.62, 0.011*	0.929, 0.522	1.76, 0.255	5.61, 0.003*	1.05, 0.383	3.45, 0.084
Movement Time (sec)	5.05, < 0.001*	0.341, 0.971	0.11, 0.756	12.42, < 0.001*	0.431, .732	1.37, 0.262

Participants were not instructed to move in a specific manner. However, participants with both maps gravitated towards a straight trajectory from target to target. This was reflected in a reduction in path length for both SCI maps and PCA controls. There was a session effect on path length. However, map differences did not depend on session (Table 2). There was no significant difference in path length between SCI maps at the end of training (Table 3). In contrast, control participants had a shorter path length in the last block while working with the Kalman map. It is important to notice that most control participants had a path length close to 1 while working with the Kalman map, so there was not much room for improvement in their performance, and there exists the possibility of a floor effect.

As participants became proficient using the BMI, both maps showed a reduction in movement time with practice. There was a session and block effect on movement time for SCI and control participants respectively. However, map differences did not depend on session or block (Table 2). Additionally, there was no significant difference in movement time between SCI maps at the end of training (Table 3). Although control participants appeared to move faster by the end of training using the Kalman algorithm, the difference between both maps was not statistically significant (Table 3, p = 0.051).

To characterize map differences and identify the most relevant features reflecting proficient cursor control, we computed 6 performance measures that provided a comprehensive description of the cursor movement quality. We subjected these combined parameters to a PC analysis. Map differences for SCI participants were differentiated along PC1 and PC2, which explained 62% and 25% respectively of the total variance in the data sets for SCI participants and 61% and 27% respectively for controls (Fig. 3C and Fig. 4C). Analysis of factor loadings on PC1 revealed that movement time, path length, aspect ratio, and jerk were the most robust variables (SCI factor loadings, 0.50, 0.49, 0.47, 0.48; Controls factor loadings 0.47, 0.49, 0.46, 0.48 respectively) to capture map differences along PC1. In contrast, straight-line distance and Euclidean error after 1 sec were more robust in capturing differences along PC2 (SCI factor loadings, 0.72 and 0.62; Controls factor loadings, 0.72 and 0.56 respectively). Factor loadings in Fig. 3C and Fig. 4C were normalized by the maximum value in each column for illustration purposes.

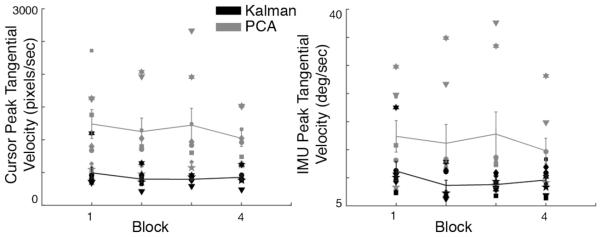
Participants using PCA seemed to be moving at a higher peak velocity in Fig. 2B and, even though PCA participants had a smaller distance between the cursor and the target 1 s after movement initiation, the final movement time did not differ between maps. The additional analysis of movement speed highlights differences between maps. The average block cursor peak velocity and IMU peak velocity for each participant are shown in Fig. 5. Participants moved the cursor and their body with a higher velocity when using the PCA map, compared to Kalman [Fig.5]. Peak velocity for cursor and IMU was not dependent on block, and there was no learning effect after training. Both maps were significantly different at the last block (Table 3).

Fig. 5. Control participant peak velocity of cursor and IMU at each block.

(A) Participants’ mean cursor (left) and IMU (right) peak tangential velocity at each block is shown for PCA (amber) and Kalman (green) control participants. Each marker type denotes a different participant’s mean performance at that block. The lines represent the map averages ± SEM bars (n = 8 participants, 24 trials per session).

C. SCI participants can use the BMI to type on a virtual keyboard and play pong

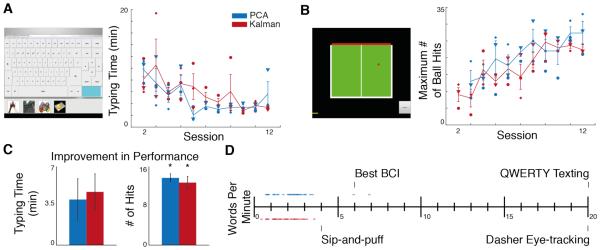
All SCI participants were able to type using the virtual keyboard and play a pong-like game using the BMI. There was no difference between maps in typing or pong performance [Fig. 6A,B]. Although there was no significant improvement in typing time for PCA but there was for Kalman, (Fig. 6C, PCA learning effect t = 2.19, p = 0.080, Kalman learning effect t = 2.93, p = 0.049) performance improvement was evident in the pong task for both maps (Fig. 6C, PCA learning effect t = −16.25, p = 0.002, Kalman learning effect t = −6.14, p = 0.013). The average typing task achieved by most participants at the end was around 3.5 WPM. However, two participants using the PCA map were able to achieve typing speeds of up to 6 and 7 WPM.

Fig. 6. SCI participant performance during typing and pong.

(A) Screenshot of the typing interface (left) and participant performance at each typing session (right) is shown for PCA (blue) and Kalman (red) SCI participants. Each marker type denotes a different participant’s mean performance at that session. The lines represent the participant averages (n = 3 participants, one trial per session). (B) Screenshot of the pong game (left) and participant performance at each pong session (right) is shown for PCA and Kalman participants. PCA participants began playing pong until the 3^rd session. (C) Improvement in performance is shown for each task. Data are means ± SEM (bars). (D) Typing speed in words per minute for each SCI participant overlaid over a scale showing typing speeds for other devices (adapted from [38]).

D. Control participants using PCA outperform participants using Kalman during virtual wheelchair navigation

For the majority of control participants, driving with the PCA algorithm was significantly easier than driving with the Kalman algorithm. Wheelchair trajectories in the VR navigation map, wheelchair forward and turning velocities during a straight hallway, and wheelchair driving performance measures are shown in Figure 6. Participants had straighter and smoother wheelchair trajectories using PCA than using the Kalman algorithm. There was more consistency across participants’ trajectories with PCA, while Kalman trajectories showed sharper turns, many changes in direction, and even instances where the wheelchair went across a wall (that wall was a visual limit, but could be crossed) [Fig. 7B].

Participants were able to drive at a high velocity for a long time while using the PCA map [Fig. 7C]. There were few spikes in the forward velocity profile, and the turning velocity time history for PCA driving showed an almost flat turning velocity, indicating that participants were able to maintain a constant direction while driving with PCA. In contrast, there were many spikes in the velocity time history for Kalman driving. Participants were not able to drive at a high velocity for long periods of time, and a lot of corrections in velocity were needed. Kalman driving required participants to move in reverse several times. Moreover, the turning velocity time history for Kalman driving showed a lot of high-speed changes. This indicates participants constantly corrected the wheelchair’s direction, overshot their correction, and had to adjust in the opposite direction. Participants had trouble moving forward with a constant speed while using the Kalman algorithm.

Even though the time it took participants to complete the navigation task was comparable for both maps (Fig. 7D, two-sample t-test t = 0.586, p = 0.586), the number of collisions was significantly lower when participants were using the PCA algorithm (paired t-test t = 2.31, p = 0.027). The number of collisions for participants using the Kalman map was, in fact, significant (one-sample t-test t = 3.50, p = 0.010). When asked what map participants would prefer keeping for future hypothetical experiments, an overwhelming majority chose the PCA map (7 vs. 1).

Subjects with SCI performed the VR wheelchair task with either the PCA or the Kalman algorithm. Moreover, the VR environment and the driving courses that they used were different. Therefore, performance between algorithms in VR driving for SCI subjects was not directly comparable. We included the results for each individual group in Supplementary Fig. 1.

E. Kalman training can predict reaching performance on the first block

The Kalman state reconstruction coefficient for the training data could moderately predict participant performance in the first block. The initial participant performance dependency on Kalman training data is shown in Fig. 8A. As the reconstruction coefficient between the predicted state and the actual state of the training data became larger, performance in the first block improved. In contrast, we were not able to find a characteristic of the PCA map that could predict participant performance in the first block [Supplementary Fig. 2].

Fig. 8. Initial performance dependency on Kalman training data.

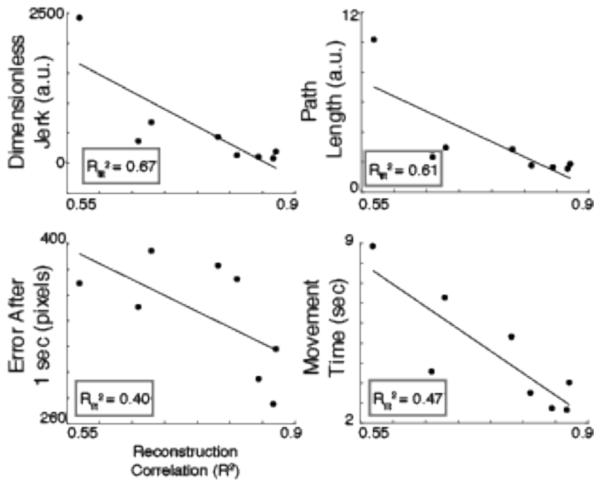
The correlation coefficient for the reconstruction of the Kalman training state based on the training observation is plotted against the first block performance. Each circle represents an individual unimpaired participant. The black line illustrates the linear regression on the map data. The regressions’ r-square values (R^2fitt) are enclosed in the gray box.

IV. DISCUSSION

A. The body-machine interface as an assistive device

Our results confirm the ability of PCA and Kalman methods as decoding algorithms for BMIs used as assistive devices. These results are in agreement with observations of the ability of the motor control system to reorganize motor coordination by exploiting available motor redundancy [33], [34]. Other EEG-based brain-machine interfaces have been proposed for cases where all mobility has been lost –like in locked-in syndrome or advanced multiple sclerosis [35], [36]. Compared to the simplicity of PCA and Kalman, these methods have a low bandwidth, have longer training and familiarization periods, are computationally expensive, and demand high concentration from the user. In contrast, our training and familiarization protocols lasted for 1 minute each, the computation of the matrices is extremely fast, and SCI participants were able to maintain conversations while driving the VR wheelchair. Although the performance of the BMI has been shown to improve with increased calibration duration, there is no noticeable improvement in performance after 48sec of calibration [24].

B. Qualitative and Quantitative differences between PCA and Kalman in center-out reaching

Qualitative reaching differences between PCA and Kalman maps were most apparent in smoothness and straightness of cursor movement. Participants controlling the cursor with the Kalman filter had a generally straighter movement to the target with a smooth cursor and IMU velocity profiles. Even though the task was more difficult for SCI participants, participants in all maps were able to straighten their movements after practice, with little to no overshoot, and a smoother, ‘bell-shaped’ velocity profile. These results are in agreement with observations in studies of coordination of voluntary human arm and cursor movement, where participants performing planar, multi-joint movements, control the endpoint with a unique straight trajectory that can be described with a minimum jerk model [30], [31]. Moreover, movement smoothness has been shown to improve during stroke [37] and SCI recovery [10].

Performance differences between PCA and Kalman during reaching were reflected in measures of smoothness, straightness, and accuracy. SCI participants moved more smoothly with Kalman but were more precise with PCA. Control participants moved straighter with Kalman and more precise with PCA. Control participants did not show a learning effect in smoothness or straightness using Kalman. However, this result could indicate a floor effect, where participants were proficient in those measures from the first block. There appeared to be a slight difference in performance improvement trends between SCI and control subjects. A possible reason is that performance improvement for control subjects was calculated between blocks, within the same session, whereas performance improvement for SCI subjects was computed between their first and their twelfth session.

When the performance measures were represented in a new ‘denoised’ space created by PC1-3, data points associated with each experimental condition clustered in a well-defined location, indicating that participants exhibited map-specific reaching patterns. Typically, PC1 differentiated measures of smoothness, straightness, and timing, while PC2 captured differences in movement accuracy.

Even though control participants were closer to the target 1 second after movement onset while using the PCA map, movement time was not different between maps. An analysis of cursor velocity revealed that participants were in fact moving faster with the cursor with PCA, thus approaching the target in less time than Kalman. However, participants spent more time making small corrections towards the correct target location with PCA than with Kalman. In order to determine if the cursor movement speed difference could be attributed to the map’s kinematics, we also computed the IMU tangential velocity peaks for each reach. The IMU velocity peaks revealed that participants were moving their shoulders with a higher speed while using PCA.

We speculate that the higher effectiveness of the Kalman-based map to induce smooth and rectilinear movements is likely to derive from the very structure of the Kalman filter and from its calibration procedure. To set up the Kalman parameters the participants were explicitly asked to relate their body motions to the observed movements of the cursor, as it was moving along a set of rectilinear paths. Through this approach, the Euclidean structure of the task space (i.e. the computer monitor) was directly associated to the body motions in the calibration procedure, whereas this was not the case for the PCA map. To set up the PCA map, subjects were asked to perform free body motions without any reference to cursor control. Nevertheless, the direct mapping of the dimensions of greater body mobility over the task space by the PCA method resulted in a higher level of accuracy.

C. Generalization tasks using the body-machine interface

Participants with SCI were able to generalize their experience in center-out reaching to other tasks like typing and playing video games. Participants had to use different shoulder combinations, with different movement amplitudes and different timing requirements to complete these tasks. These results are in agreement with studies suggesting the formation of an internal model between the body and the cursor. There was no significant difference in generalization of task performance between both algorithms. Two participants typing with the PCA achieved a typing speed of 6 & 7WPM. In comparison, the sip-and-puff system has reported top speeds of 4WPM, while the best brain-computer interface has achieved a typing speed of 6WPM [38]. Although the typing speed of the BMI is still well below common QWERTY texting (20 WPM), it can serve as a replacement or complement to the majority of current brain-computer interface users that revealed they would only be satisfied by over 90% accuracy and by performance at least 3 times faster than current standard speeds [39].

Participants driving with PCA were able to keep a straight trajectory with small changes in direction, and the number of collisions was not significantly different from zero. In contrast, driving the VR wheelchair was more challenging for participants while using Kalman. The wheelchair path with Kalman was not straight, there was less consistency between participants, and the number of collisions was significantly different than zero. The static properties of the PCA map offer an advantage in collisions avoidance during driving. When participants were about to collide with an object or wall, the urgency of the situation caused them to make fast corrective shoulder movements. With PCA, participants knew exactly where the cursor was going to move to, regardless of how fast they corrected their movement. In contrast, the dynamic properties of the Kalman map caused participants to overshoot in their correction, as the fast acceleration of their shoulders moved the cursor to the edge of the screen, even when the movement amplitude was small. To solve this problem in the future, the Kalman BMI’s gains for position or velocity could be adapted during driving. Alternatively, an asymmetric map could be developed where moving forward and backward is easier than moving right and left. Another alternative would be to make the Kalman algorithm be static by using only the angles of the sensors as the observation to implement a position-to-position map. However, a previous study analyzing the role of sensor signal redundancy on cursor kinematics revealed taking advantage of the numerous available signals from the IMUs improved overall performance [24]. At the end of the experiment, an overwhelming majority of participants preferred PCA as their algorithm of choice.

While reaching performance was comparable with both algorithms, VR driving elicited the largest differences between maps. We believe this difference arises from the differences in cursor movement requirements from both tasks. VR driving had timing requirements for the participants to move the cursor with a high velocity. In contrast, reaching did not have a time constraint, and participants could take as much time as needed in order to move the cursor to the required location. Without a time constraint, participants perhaps concentrated on moving the cursor more smoothly and precisely towards the target. It remains to be investigated whether adding a time constraint on the reaching task would elicit higher differences between the Kalman and PCA decoding algorithms. Moreover, the difference in results between VR and reaching highlights the importance of testing control interfaces in tasks that more closely resemble the desired application, since differences in control abilities might not be reflected by the chosen performance metrics of center-out reaching.

D. Predicting performance from training data

Reaching performance in the first block could be predicted by training data in Kalman. Participants followed a cursor moving with a predetermined trajectory on the screen using their shoulders. When we used the shoulder movements and the learned Kalman map to try to predict the cursor’s predetermined trajectory, we could calculate the accuracy of the reconstruction. As the accuracy of the reconstruction increased, performance during the reaching task in the first block was higher. These results can be used in a Kalman filter approach to develop and test new algorithms before training, and predict what their effect will be during the reaching task. Moreover, this knowledge can serve as a means to test the effectiveness of adaptive algorithms that are adjusted on-line based on participant performance (supervised learning) or the statistics of each participant’s movement (unsupervised learning).

Kalman training required participants to meet certain constraints in order for them to have good performance. For example, participants had to properly follow instructions, they had to be consistent in doing a similar movement every time the cursor moved in the same direction, and participants couldn’t get distracted or make mistakes (moving one way when they intended to move another) during training. In contrast, PCA has no explicit instructions so there is no ‘mistake’ for participants to make. We were not able to find a meaningful relation between the features of the PCA dance (symmetry, planarity, or ‘dance’ reconstruction) and the performance metrics, but this is currently being investigated.

E. Limitations

Our BMI requires more effort from the user compared to current available devices such as joysticks, sip-and-puff, and head and chin arrays. In future studies, we will include a questionnaire that can evaluate whether people with high-level SCI would prefer control interfaces that require more effort. We believe that there will be a tradeoff between required effort and level of control. When participants require more effort to use the BMI than their current interface, such as a joystick, and there is no added control benefit, it would be unlikely that subjects prefer the BMI. However, if the BMI offers a higher level of control that their current interface, for example 360°, continuous, proportional control, the likelihood of participants preferring the BMI would be higher. Studies in healthy subjects suggest that the degree of performance improvement in motor learning is dependent on the amount of practice [40], and that retention of motor learning is best accomplished with variable training schedules [41]. Our BMI can provide an enjoyable environment in which people with neuromuscular disabilities can sustain the motivation to practice for extended periods of time In fact, if properly directed, physical effort may be a therapeutic resource. A recent related study with our BMI [42] has highlighted the potential rehabilitative benefits that derive from exercising the residual mobility while performing functional and/or recreational activities. In fact, the BMI provides patients and therapists with the means to modify the body-to-device mapping so as to target specific rehabilitation objectives.

Measuring the range of motion of SCI and control subjects would give a better idea of each subject’s mobility. However, the IMU system was not sufficient to measure range of motion. The IMU sensors were not placed on the exact same shoulder location on all subjects, and subjects differed in body size. These two factors would result in differences in IMU angle measurement magnitudes, and comparisons between movement amplitudes measured by IMUs would not be appropriate. For a fair comparison of movement amplitude between shoulders, we would need an additional evaluation of shoulder range of motion such as motion tracking my infrared optical markers or by a goniometer.

V. CONCLUSION

Participants using the BMI were able to produce satisfactory performance using the PCA and Kalman algorithms. This study highlights differences and advantages of the different algorithms for SCI participants and controls. Most importantly we have observed an accuracy/smoothness tradeoff between the Kalman and the PCA approaches. While the former establishes an explicit relation between the intended motions of the cursor and the movements of the body, the latter "constructs" the task space by matching the highest mobility of the body with the coordinate system for the cursor. The PCA approach is effectively completely unsupervised as it is only based on the statistics of body motions. This seems sufficient to achieve a higher degree of learnability in terms of efficiency and of perceived ease of use. Future studies will be directed at exploring how the two approaches may be combined to capture the advantages of both.

Learning to use their remaining functions to perform complex motor tasks and adapt to an ever-changing environment is a fundamental component of SCI survivors’ lives. Understanding the benefits deriving from each decoding algorithm is crucial to develop and enhance BMIs used for physical rehabilitation paradigms that improve functional outcomes and facilitate the learning process related to assistive devices used by impaired individuals. Furthermore, this knowledge can be used to continuously modify the BMI in order to a) increase or decrease the level of effort required from the user for rehabilitation or assistive purposes respectively and b) move the sensors over body locations with regained mobility, which may address current problems of control difficulty [43], [44].

IMU-based BMIs using a PCA decoding map have already been developed to control a powered wheelchair using the shoulders [17]. However, these results highlight the importance of long-term VR practice with Kalman before participants drive a real wheelchair. This BMI allows for proportional, continuous, 360° control of their wheelchairs. Moreover, unlike current sip-and-puff and head-and-chin switches to control wheelchairs, the BMI is non-obstructive to the head or the mouth. This system can be used during long-term training to investigate the rehabilitative effects of practicing upper-body control in people with SCI.