A systematic approach to determining the identifiability of multistage carcinogenesis models

Abstract

Multistage clonal expansion (MSCE) models of carcinogenesis are continuous-time Markov process models often used to relate cancer incidence to biological mechanism. Identifiability analysis determines what model parameter combinations can, theoretically, be estimated from given data. We use a systematic approach, based on differential algebra methods traditionally used for deterministic ODE models, to determine identifiable combinations for a generalized subclass of MSCE models with any number of pre-initation stages and one clonal expansion. Additionally, we determine the identifiable combinations of the generalized MSCE model with up to four clonal expansion stages, and conjecture the results for any number of clonal expansion stages. The results improve upon previous work in a number of ways and provide a framework to find the identifiable combinations for further variations on the MSCE models. Finally, our approach, which takes advantage of the Kolmogorov backward equations for the probability generating functions of the Markov process, demonstrates that identifiability methods used in engineering and mathematics for systems of ODES can be applied to continuous-time Markov processes.

1 Introduction

The two-stage clonal expansion (TSCE) model is a continuous-time Markov process proposed by Moolgavkar, Venzon, and Knudson [1, 2] to capture the initiation–promotion–progression hypothesis of carcinogenesis, wherein normal cells undergo a genetic transformation that causes clonal expansion, followed by progression to malignancy. The initiation–promotion–progression paradigm allows one to consider carcinogenic factors as initiators or promoters given their mechanism of action and their differential effects at different stages of life. The TSCE model formulation may be extended to three or more stages or other more complex variations, which are collectively called multistage clonal expansion (MSCE) models. Parameter estimation with multistage clonal expansion models has proven a valuable approach, and MSCE models have been successfully used to analyze and fit data from pancreatic, colorectal, esophageal, and oral cancer, among others [3–16].

Consideration of identifiability is the first step in estimation of model parameters from data. A model is said to be identifiable if all model parameters may be uniquely determined from given observed data [17-19]. Identifiability is a key step in ensuring successful parameter estimation and is often considered in two forms: structural identifiability, which considers the best-case scenario of noise-free, continuously measured data in order to uncover identifiability issues inherent in the model structure, and practical identifiability, which addresses issues such as noise, bias, and frequency of sampling [20]. While the best-case scenario is unrealistic, structural identifiability is necessary for practical identifiability and can often lead to useful insights for model reparameterization and data collection strategies.

For deterministic models, one often frames the identifiability problem as testing the injectivity of the map from the parameters to the output trajectories (implicitly defined by the corresponding ordinary differential equations (ODE) system) [21]. There are a wide range of approaches to answering questions of identifiability for such systems, including Laplace transformation, Taylor series, similarity transformation, and differential algebra [19, 21-28].

The identifiability of certain individual clonal expansion models, which are stochastic rather than deterministic, has been addressed primarily on a case-by-case basis and in no systematic way. Heidenreich et al. [29] determined the identifiability of the TSCE model with constant and piecewise-constant parameters when fitted to incidence data through derivation of closed form solutions of the corresponding hazard function. Luebeck and Moolgavkar [5] similarly analyzed the identifiability of MSCE models with multiple pre-initiation stages and constant parameters. Little et al. [30] developed bounds for the number of identifiable combinations for a class of stochastic cancer models with genomic instability—which includes MSCE models—through observing parameter combinations in the form of the cancer hazard in the model and numerical evaluations of the Fisher information matrix.

Here, we present a derivation of the identifiability of a generalized subclass of MSCE models with multiple pre-initiation steps when fitting to age-specific cancer incidence data, as is typical. We use a differential algebra approach that was developed for deterministic ODE models and which has not previously been brought to bear on this class of models [21, 26, 27, 31, 32]. We do this by leveraging the Kolmogorov backward equations for continuous-time Markov processes, which can be reduced to a system of differential equations. This approach has many advantages: it is analytical and systematic, returns explicit identifiable combinations rather than bounds, and is a global result over the parameter space. We additionally demonstrate the identifiability of the fully general case with multiple clonal expansions for models with up to four clonal expansion stages and conjecture that our framework could be extended to any number of stages. Our work demonstrates that approaches for identifiability in deterministic dynamical systems can be used in Markov branching processes and, more generally, continuous-time Markov processes.

2 Methods

2.1 Derivation of the MSCE model

Although the mathematics of multistage clonal expansion models has been detailed elsewhere [1-3, 11, 29, 33-39], we provide a sketch of the derivation in order to provide a basis for using the differential algebra method of identifiability with other continuous-time Markov processes. The n-stage clonal expansion model (Figure 1a) is characterized by a set of conditional probability generating functions, where Y_k(t), 1 ≤ k ≤ n − 2, and Z(t) are as in Table I, and τ is a fixed time such that 0 ≤ τ ≤ t. If we define

$$\mathrm{\Omega }(t)=y_1^{Y_1(t)}\dots y_{n-1}^{Y_{n-1}(t)}{z}^{Z(t)},$$ (1)

for some dummy variables y₁, ⋯ , y_n−1, and z, then the conditional probability generation functions are as follows:

$$\begin{array}{cc}\hfill \mathrm{\Psi }(y_1,\dots ,y_{n-1},z,\tau ,t)& =E[\mathrm{\Omega }(t)\mid Y_1(\tau )=0,\dots ,Y_{n-1}(\tau )=0,Z(\tau )=0],\hfill \\ \hfill {\mathrm{\Phi }}_1(y_1,\dots ,y_{n-1},z,\tau ,t)& =E[\mathrm{\Omega }(t)\mid Y_1(\tau )=1,Y_2(\tau )=0,\dots ,Y_{n-1}(\tau )=0,Z(\tau )=0],\hfill \\ & ⋮\hfill \\ \hfill {\mathrm{\Phi }}_i(y_1,\dots ,y_{n-1},z,\tau ,t)& =E[\mathrm{\Omega }(t)\mid Y_1(\tau )=0,\dots ,Y_i(\tau )=1,Y_{i+1}(\tau )=0,\dots Y_{n-1}(\tau )=0,Z(\tau )=0],\hfill \\ & ⋮\hfill \\ \hfill {\mathrm{\Phi }}_{n-1}(y_1,\dots ,y_{n-1},z,\tau ,t)& =E[\mathrm{\Omega }(t)\mid Y_1(\tau )=0,\dots ,Y_{n-1}(\tau )=1,Z(\tau )=0],\hfill \\ \hfill \mathrm{\Theta }(y_1,\dots ,y_{n-1},z,\tau ,t)& =E[\mathrm{\Omega }(t)\mid Y_1(\tau )=0,\dots ,Y_{n-1}(\tau )=0,Z(\tau )=1].\hfill \end{array}$$ (2)

Figure 1.

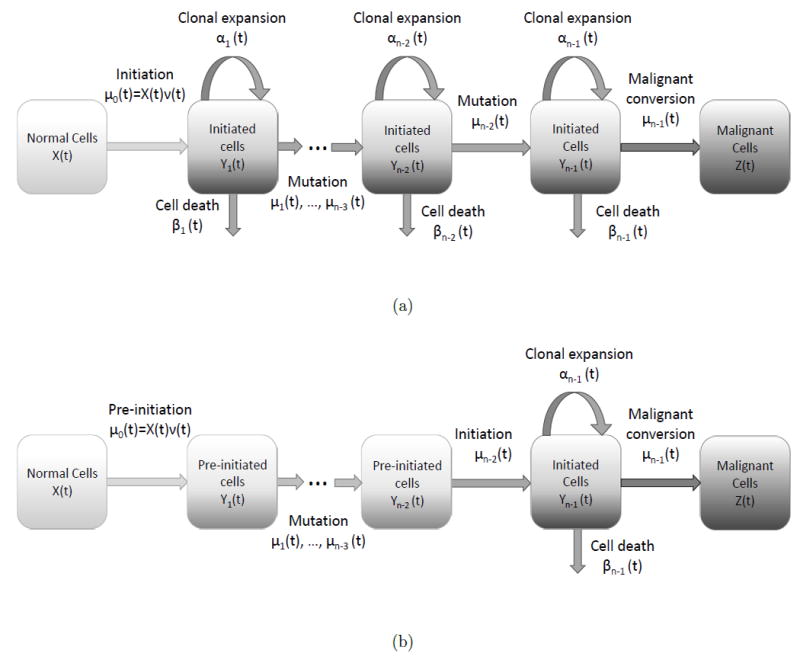
Generalized MSCE models. (a) The fully generalized model with clonal expansion at each pre-malignant step. (b) The standard model with several pre-initiation steps and one clonal expansion.

Table I.

Variables and parameters of the generalized multistage clonal expansion (MSCE) model

Variables
X(t)	Number of normal cells, treated deterministically or set to be constant X(t) = X
Yk(t)	Number of cells in initiated stage k
Z(t)	Number of malignant cells
Parameters
ν(t)	Per cell mutation rate for normal cells (asymmetric division)
μ0(t)	:= ν(t)X(t), a notational convenience
μk(t)	Mutation rate at the kth stage (asymmetric division)
αk(t)	Clonal expansion rate at the kth stage (symmetric division)
βk(t)	Cell death rate at the kth stage

These probability functions satisfy the Kolmogorov backward equations. Here, we assume that the parameters, which are listed in Table I, are constant in time (age). These equations are

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \tau }\mathrm{\Psi }& ={\mu }_0\mathrm{\Psi }(1-{\mathrm{\Phi }}_1),\hfill \\ \hfill \frac{\partial }{\partial \tau }{\mathrm{\Phi }}_1& =({\alpha }_1+{\beta }_1+{\mu }_1){\mathrm{\Phi }}_1-{\beta }_1-{\alpha }_1{\mathrm{\Phi }}_1^2-{\mu }_1{\mathrm{\Phi }}_1{\mathrm{\Phi }}_2,\hfill \\ & ⋮\hfill \\ \hfill \frac{\partial }{\partial \tau }{\mathrm{\Phi }}_{n-2}& =({\alpha }_{n-2}+{\beta }_{n-2}+{\mu }_{n-2}){\mathrm{\Phi }}_{n-2}-{\beta }_{n-2}-{\alpha }_{n-2}{\mathrm{\Phi }}_{n-2}^2-{\mu }_{n-2}{\mathrm{\Phi }}_{n-2}{\mathrm{\Phi }}_{n-1},\hfill \\ \hfill \frac{\partial }{\partial \tau }{\mathrm{\Phi }}_{n-1}& =({\alpha }_{n-1}+{\beta }_{n-1}+{\mu }_{n-1}){\mathrm{\Phi }}_{n-1}-{\beta }_{n-1}-{\alpha }_{n-1}{\mathrm{\Phi }}_{n-1}^2,\hfill \\ \hfill \frac{\partial }{\partial \tau }\mathrm{\Theta }& =0\hfill \end{array}$$ (3)

with initial conditions

$$\begin{array}{cc}\hfill \mathrm{\Psi }(y_1,\dots ,y_{n-1},z,t,t)& =1,\hfill \\ \hfill {\mathrm{\Phi }}_1(y_1,\dots ,y_{n-1},z,t,t)& =y1,\hfill \\ & ⋮\hfill \\ \hfill {\mathrm{\Phi }}_{n-1}(y_1,\dots ,y_{n-1},z,t,t)& =y_{n-1},\hfill \\ \hfill \mathrm{\Theta }(y_1,\dots ,y_{n-1},z,t,t)& =z.\hfill \end{array}$$ (4)

The usual data in this context are age-specific incidence curves (e.g. as are available in the Surveillance, Epidemiology and End Results (SEER) cancer registries). The age-specific incidence curve corresponds to a model hazard. The hazard and survival contain equivalent information $(h(t)=-\frac{d}{dt}\log S(t),S(0)=1,h(0)=0)$, so, for simplicity of analysis, we consider the survival to be known. For this model, the survival can be related to Ψ in the following way:

$$\begin{array}{cc}\hfill S(t)& =\sum _{(i_1,\dots ,i_{n-1},0)}P[Y_1(t)=i_1,\dots ,Y_{n-1}(t)=i_{n-1},Z(t)=0\mid Y_1(0)=0,\dots ,Y_{n-1}(0)=0,Z(0)=0],\hfill \\ & =\sum _{(i_1,\dots ,i_{n-1},j)}P[Y_1(t)=i_1,\dots ,Y_{n-1}(t)=i_{n-1},Z(t)=j\mid Y_1(0)=0,\dots ,Y_{n-1}(0)=0,Z(0)=0]1^{i_1}\cdots 1^{i_{n-1}}{0}^j,\hfill \\ & =\mathrm{\Psi }(y_1=1,\dots ,y_{n-1}=1,z=0,\tau =0,t=t).\hfill \end{array}$$ (5)

Let s = t − τ and define x(s) = Ψ (1, ⋯ , 1, 1, t − s, t), x₁(s) = Φ₁(1, ⋯ , 1, 1, t − s, t), ⋯ , x_n−1(s) = Φ_n−1(1, ⋯ , 1, 1, t − s, t). Then x(t) = S(t). Let ẋ_k denote derivative of x_k with respect to s. Then the following set of differential equations, 1 ≤ k ≤ n − 2, governs the survival:

$$\begin{array}{cc}\hfill \dot{x}& =-{\mu }_{0}x(1-x_1),\hfill \\ \hfill {\dot{x}}_k& =-({\alpha }_k+{\beta }_k+{\mu }_k)x_k+{\beta }_k+{\alpha }_k{x}_k^2+{\mu }_k{x}_k{x}_{k+1},\hfill \\ \hfill {\dot{x}}_{n-1}& =-({\alpha }_{n-1}+{\beta }_{n-1}+{\mu }_{n-1})x_{n-1}+{\beta }_{n-1}+{\alpha }_{n-1}{x}_{n-1}^2,\hfill \end{array}$$ (6)

with initial conditions x(0) = 1, x_k(0) = 1, and x_n−1(0) = 1.

2.2 Differential algebra approach to identifiability

As noted earlier, structural identifiability focuses on examining the inherent, structural estimation properties of a given model and data, assuming a best-case scenario in which the model output (i.e. the observed variable(s)) is perfectly observed and the model is correctly specified. While this is unrealistic for real data, structural identifiability is a necessary condition for practical estimation from real-world data that many times goes unchecked, and in fact many mathematical models used in practice turn out to be structurally unidentifiable. Structural identifiability allows us to resolve these issues and can help in designing data collection or estimation strategies.

Here we give an overview of structural identifiability definitions and the differential algebra approach for deterministic dynamical systems. For more details, the reader is referred to Saccomani et al. [21] and Audoly et al. [26]. For simplicity, here we consider the case where we have only one measured variable υ and one input function u, although the same definitions and approach can be used for multiple inputs and outputs as well. Consider a vector of states x(t) (unobserved), vector of parameters to be estimated ρ, and observed (known) input u(t) and output υ(t) in the ODE model

$$\begin{array}{c}\dot{\mathit{x}}(t)=f(\mathit{x}(t),u(t),\mathit{\rho }),\\ \upsilon (t)=g(\mathit{x}(t),\mathit{\rho }).\end{array}$$ (7)

Structural identifiability analysis addresses the following question: given the model, states x, known input u, and known output υ, is it possible to uniquely identify the model parameters ρ? This can be framed as an injectivity question: is the map (implicitly defined by f and g) from parameter values (ρ) to output trajectories (υ) injective? [21]. Structural identifiability is a global property, but, because there may be some degenerate parameters or initial conditions for which an otherwise identifiable model may be unidentifiable (e.g. if all initial conditions or parameters are zero), it is typically defined almost everywhere over parameter and initial-condition space.

Definition 1

Parameter ρ_i in the model given in Eq. (7) is uniquely structurally identifiable if, for almost all values ${\rho }_i^{\ast }$ and initial conditions, the observation of an output trajectory (υ(t) = υ* (t)) uniquely determines the parameter value ${\rho }_i({\rho }_i={\rho }_i^{\ast })$, i.e. if only one value of ρ_i could have resulted in the observed output.

Definition 2

The model given in Eq. (7) is structurally identifiable if each ρ_i is structurally identifiable.

If a model is not structurally identifiable, it is said to be unidentifiable, and there exists a set of identifiable combinations of parameters that represents the parametric information available in the data (except in degenerate cases where the model is reducible or has insensitive parameters). Such a set is not unique; any set of combinations that generate the same field is an equivalent set of identifiable combinations, e.g. {ab, c/b} and {ab, ac} are equivalent sets of identifiable combinations.

We must emphasize that identifiability is an assessment that is dependent on both what quantities are observed (i.e. the data u(t) and υ(t)) and on the parameterization of the model. A model is unidentifiable if even one parameter cannot be uniquely determined from the available data. An unidentifiable model can sometimes be rendered identifiable by reparameterization (i.e. in terms of identifiable combinations) or by changing what data are measured.

Differential algebra offers one approach for evaluating the structural identifiability of rational-function differential-equation models. Technical details of the differential algebra approach to identifiability may be found elsewhere [21, 32], but this method is built on the idea of treating the differential equations as elements of a differential polynomial ring, that is, a polynomial ring in the variables and their derivatives, with an additional derivative operation. Once framed in this algebraic perspective, reduction techniques such as characteristic sets or Gröbner bases can be used to reduce the model to a form in which the identifiability properties can be determined, called the input–output equation [26, 40].

The input–output equation is central to the differential algebra technique [41]. It is a monic differential polynomial only in terms of u and υ, their derivatives, and the parameters ρ. In the case of multiple outputs, there will be as many of these monic differential polynomials—input–output equations—as there are observed output variables. The solutions of the input–output equation are precisely the possible input-output pairs for the system; in other words, the input–output equation is an equivalent differential equation where the unobserved variables have been eliminated, so that every solution trajectory for the model (in terms of x, u, υ) corresponds to a solution for the input–output equation (in terms of only u and υ), though we note that multiple model trajectories may correspond to the same input–output solution. The coefficients of the input–output equation are a complete, though typically not minimal (redundancies are usual), set of identifiable combinations, and testing for structural identifiability can thus be reduced to testing the injectivity of the map from the parameters to the identifiable combinations. We illustrate the differential algebra technique and the input–utput equation for a simple example in Appendix A.

The input–output equation must be monic—the choice of variable ranking is arbitrary, though u < u̇ < ü < ⋯ < υ < υ̇ < ϋ < ⋯ is traditional [26]—or the set of identifiable combinations may not be uniquely determined. For example, the following are equivalent differential polynomials,

$$\begin{array}{l}0=\frac{1}{a}\dot{\upsilon }+b\upsilon +cu,\\ 0=\dot{\upsilon }+ab\upsilon +acu,\end{array}$$

but the map from {a, b, c} to $\{\frac{1}{a},b,c\}$ is injective while that to {1, ab, ac} is not. The input–output equation is required to be monic to identify the correct set of identifiable combinations.

Finally, we note that, in the notation of this section, the MSCE model (Eq. 6) has states x = (x(t), x₁(t), … , x_n−1(t)), output (data) υ(t) = x(t), and has no input u(t).

3 Results

3.1 Two-stage clonal expansion (TSCE) model

Although the identifiability of the TSCE model is well-known [29], this model provides a tractable test-case for the differential algebra approach to identifiability in this context.

Theorem 1

If cancer survival (or, equivalently, age-specific incidence) is perfectly measured, the two-stage clonal expansion model with constant parameters (ν, X, α, β, μ₁) is unidentifiable but has three identifiable parameter combinations, which may be represented as μ₀μ₁, α₁μ₁, and α₁ − β₁ − μ1, where μ₀ = ν X.

Proof

From Eqs. (6), the following equations contain all information of the the two-stage clonal expansion model:

$$\begin{array}{cc}\hfill \dot{x}& =-{\mu }_{0}x(1-x_1)\hfill \\ \hfill {\dot{x}}_1& =-({\alpha }_1+{\beta }_1+{\mu }_1)x_1+{\beta }_1+{\alpha }_1{x}_1^2\hfill \end{array}$$ (8)

We assume that the survival function x is perfectly measured. The goal here is to determine the identifiable parameter combinations from the input–output equation for the system, which will be a monic polynomial of the observed output x and its derivatives.

We solve for x₁ in terms of x and its derivatives,

$$x_1=\frac{x+\frac{\dot{x}}{{\mu }_0}}{x}.$$ (9)

Plug this in to the ẋ₁ equation,

$${\left(\frac{x+\frac{\dot{x}}{{\mu }_0}}{x}\right)}^{\prime }=-({\alpha }_1+{\beta }_1+{\mu }_1)\left(\frac{x+\frac{\dot{x}}{{\mu }_0}}{x}\right)+{\beta }_1+{\alpha }_1{\left(\frac{x+\frac{\dot{x}}{{\mu }_0}}{x}\right)}^2,$$ (10)

simplifying to

$$0=\ddot{x}x+({\mu }_0{\mu }_1)x^2-({\alpha }_1-{\beta }_1-{\mu }_1)\ddot{x}x-(\frac{{\alpha }_1{\mu }_1}{{\mu }_0{\mu }_1}+1){\dot{x}}^2.$$ (11)

This last equation is a monic polynomial of x and its derivatives, is equivalent to the original differential equations, and is thus an input–output equation. We can read a set of identifiable parameter combinations from the equation coefficients: μ₀μ₁,α₁ − β₁ − μ₁, and α₁μ₁.

Remark

The two-stage clonal expansion is often parameterized [5] as

$$\begin{array}{l}r={\mu }_0/\alpha ,\\ p=\frac{1}{2}((-\alpha +\beta +{\mu }_1)-\sqrt{{(\alpha -\beta -{\mu }_1)}^2+4\alpha {\mu }_1}),\\ q=\frac{1}{2}((-\alpha +\beta +{\mu }_1)-\sqrt{{(\alpha -\beta -{\mu }_1)}^2+4\alpha {\mu }_1}).\end{array}$$ (12)

It is easy to see that {r, p, q} is an equivalent set of identifiable parameter combinations.

Remark

Although the initial conditions can, generally, provide additional identifiable combinations, they do not in this case. At the initial conditions, x(0) = 1 and x₁(0) = 1,

$$\begin{array}{cc}\hfill \dot{x}(0)& =-{\mu }_{0}x(0)(1-x_1(0))=0,\hfill \\ \hfill {\dot{x}}_1(0)& =-({\alpha }_1+{\beta }_1+{\mu }_1)x_1(0)+{\beta }_1+{\alpha }_1{x}_1^2(0)=-{\mu }_1\hfill \end{array}$$ (13)

As the data is x, we can identify ẋ(0), which, in this case, is identically equal to 0 and thus does not provide any additional parametric information. We do not observe x₁, so ẋ₁(0) = −μ₁ is not observed.

3.2 Generalized MSCE model with multiple pre-initiation steps

We extend the result and method for the two-stage model to an n-stage model in which only the final non-malignant compartment has clonal expansion (Figure 1b). This model, unlike the fully generalized MSCE model, is often used in the literature to model cancer progression (e.g. [5, 9, 11]). The differential equations defining the survival x—and implicitly the hazard—of this model may be found by setting each of α₁, … , α_n−2, β₁, … , β_n−2 to zero in Eqs. (6):

$$\begin{array}{cc}\hfill \dot{x}& =-{\mu }_{0}x(1-x_1),\hfill \\ \hfill {\dot{x}}_k& =-{\mu }_k{x}_k(1-x_{k+1}),\hfill \\ \hfill {\dot{x}}_{n-1}& =-({\alpha }_{n-1}+{\beta }_{n-1}+{\mu }_{n-1})x_{n-1}+{\beta }_{n-1}+{\alpha }_{n-1}{x}_{n-1}^2,\hfill \end{array}$$ (14)

for 1 ≤ k ≤ n − 2 and with initial conditions x(0) = 1, x_k(0) = 1, and x_n−1(0) = 1.

Theorem 2

If cancer survival (or, equivalently, age-specific incidence) is perfectly measured, the n-stage (n ≥ 3) multistage clonal expansion (MSCE) model with only one, final clonal expansion and n + 3 constant parameters (ν, X, α, β, μ₁, ⋯ , μ_n−1) is unidentifiable but has n identifiable parameter combinations, which may be represented by μ₀, … , μ_n−3, μ_n−1μ_n−2, α_n−1μ_n−1, α_n−1 − β_n−1 − μ_n−1, where μ₀ = νX.

In order to highlight the result and its implications without the distraction of technical details, we leave the proof to Appendix B. This is a global result over parameter space, and there are no degenerate parameter values of interest: when μ_k = 0, the problem is no longer of biological interest, and, when excluding those cases, α_k = 0 and β_k = 0 are not degenerate values for the theorem.

3.3 Generalized MSCE model with multiple clonal expansions

Here, we consider the full model (Eqs. (6), Figure 1a), allowing clonal expansion to occur at each pre-malignant stage.

Proposition 1

If cancer survival (or, equivalently, age-specific incidence) is perfectly measured, the n-stage (n ≥ 3) multistage clonal expansion (MSCE) model with 3n − 1 constant parameters (ν, X, α₁, … , α_n−1, β₁, … , β_n−1, μ₁, … , μ_n−1) is unidentifiable.

As above, we leave the proof to Appendix B.

Conjecture 1

If cancer survival (or, equivalently, age-specific incidence) is perfectly measured, the n-stage (n ≥ 3) multistage clonal expansion (MSCE) model with 3n − 1 constant parameters has 3n − 3 identifiable parameter combinations, which may be represented as α₁, … , α_n−2, β₁, … , β _n−2, μ₀, … , μ_n−3, μ_n−1μ_n−2, α_n−1μ_n−1, α_n−1 − β_n−1 − μ_n−1, where μ₀ = νX.

The conjecture is true for n ≤ 5; the proof, left to Appendix B, is an extension of that of Proposition 1. We believe that the method developed in the proof of Theorem 1 could be used to prove this conjecture in general, though additional combinatorial results will likely be needed to deal with the added complexity.

In Figure 2, we plot the hazards for the full model with four to eight stages using two different sets of parameters. For each model with n stages, the plotted points are generated using parameter values μ_k−1 = 10⁻², α_k = 3, β_k = 2.8 for k = 1, … , n− 2 and μ_n−2 = 10⁻³, α_n−1 = 3, β_n−1 = 2.5 + 10⁻⁶, and μ_n−1 = 10⁻⁶. The corresponding lines use the parameters μ_k−1 = 10⁻², α_k = 3, β_k= 2.8 for k = 1, … , n − 2 and μ_n−2 = 10⁻², α_n−1 = 30, β_n−1 = 29.5 + 10⁻⁷, and μ_n−1 = 10⁻⁷. The indistinguishability of the hazards generated with each of the two parameters sets is consistent with the conjecture.

Figure 2.

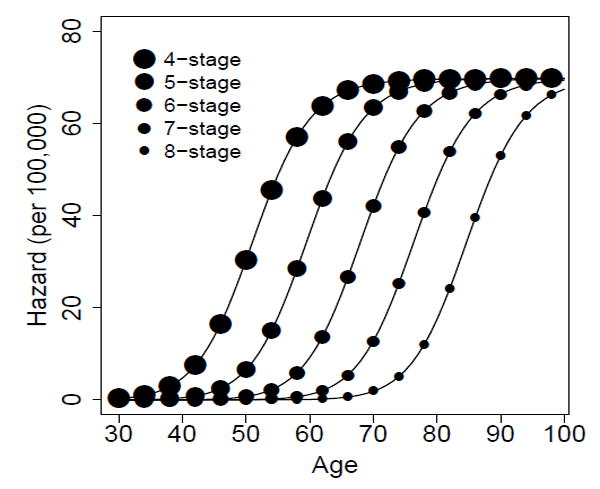
Hazards of multistage clonal expansion models with four to eight stages under two different parameter sets each (points vs. lines). See text for parameter details.

4 Discussion

Structural identifiability analysis is necessary for accurate estimation of model parameters from data, a fact that merits wider appreciation. Failure to verify the identifiable combinations in one’s model given one’s data may result in specious parameter estimates. Conversely, knowing the identifiable combinations can lead to insight and helpful model reparameterizations (e.g. [42]). This is true for the two-stage clonal expansion model. Using the r, p, q parameterization (Eqs. (12)), the survival and hazard can be expressed succinctly, and, observing that r = μ₀/α, p ≈ −(α − β) and $q\approx {\mu }_1/\left(1-\frac{\beta }{\alpha }\right)$ [43], one can identify multiplicative effects (e.g. temporal effects) on initiation, promotion (net cell proliferation), and malignant conversion respectively, as in Brouwer et al. [16].

The identifiability of MSCE models has been previously considered by Heidenreich et al. [29] (two stage model), Luebeck and Moolgavkar [5] (MSCE models with up to three pre-initiation steps), and Little et al. [30] (bounds on the maximum number of identifiable combinations in a generalized class of models that includes the MSCE model with any number of clonal expansion steps). Some of these previous results have relied on the form of the hazard function, which can only bound the identifiable combinations, or numerical evaluations of the rank of the Fisher information matrix, which, although strong evidence of local identifiability, is not formal proof. We offer an analytical proof of the exact identifiable combinations for MSCE models with any number of pre-initiation steps and one clonal expansion. This is a global result over the parameter space. Additionally, we provide a framework and conjecture for considering the exact identifiable combinations for the model with any number of clonal expansion stages, which we prove for n ≤ 5. For practical purposes, parsimonious carcinogenesis models are unlikely to need this many clonal expansion stages, let alone more. Moreover, this framework extends easily to variations of MSCE models that future work may consider, such as those incorporating disease precursors, e.g. gastroesophageal reflux disease (GERD) for esophageal cancer [15] or human papillomavirus (HPV) infection for anogenital or oral cancer [39].

Our methods and results are important in a larger context as well. We expand the differential algebra approach for structural identifiability, which has been primarily been used in the field of biological, deterministic ODE models (though is of course applicable to models in other fields), into the realm of stochastic branching processes and, more generally, continuous-time Markov processes. Once one is able to write a continuous-time Markov process as a system of differential equations of probability generating functions, a variety of identifiability techniques become available (e.g. Taylor series expansion [24] or similarity transform [23]). Of course, use of these techniques requires that one’s data relate to the probability generating functions in some way, so it is as of yet unclear exactly how widely applicable this framework will be. However, our approach to identifiability is applicable to at least one broad class of continuous-time Markov chain models, those that relate data to survival methods (i.e. time-to-event processes), which is true of many carcinogenesis and other health-outcome models.

This work sets the stage for several important problems. We have considered constant parameters, but time varying and piecewise-constant parameters are of great interest in the context of time-varying exposures [44-47]. The results given here address the piecewise constant case in part, since the problem can be expressed as multiple instances of the case with constant parameters, although additional analysis of initial conditions will be needed. Further, as data for each constant-parameter model will be limited (a full trajectory for each constant-parameter model is not observed), practical identifiability considerations arise. For more general time-varying parameters additional analysis is needed, though if the functional forms of the time varying parameters are known and if they are rational functions or approximable as such, then a similar approach as used here could be taken. Future work may also be able to see the conjecture given in this work proved beyond n = 5 using the differential algebra framework, but strong combinatorial tools may be necessary to disentangle the complexity of the coefficients of the input–output equation of the full model. Additionally, as mentioned above, future work that considers variations of the MSCE model will greatly benefit from this adaptable framework.

Finally, another important consideration is that of practical identifiability. In the context of real data, this structural identifiability analysis provides upper bounds on the number of identifiable parameter combinations, but there may be less parametric information available in real data. Such problems have been identified for MSCE models [11], but further analysis will be needed to address these issues more broadly.

Appendix A

To illustrate these differential algebra approach to identifiability, we consider the classic example of a linear two-compartment model, commonly used in pharmacokinetics; the unidentifiability of this model is well-established through a range of methods [17, 26]. The model equations are given by

$$\begin{array}{cc}\hfill {\dot{x}}_1& =k_{12}{x}_2-(k_{21}+k_{01})x_1+u,\hfill \\ \hfill {\dot{x}}_2& =k_{21}{x}_1-(k_{12}+K_{02})x_2,\hfill \\ \hfill \upsilon & =x_1/\psi ,\hfill \end{array}$$ (15)

where x₁(t) and x₂(t) are the masses of a drug/substance in the plasma and tissue respectively, u(t) is a known input function (e.g. an intravenous injection or constant infusion at a known dose), the κ_ij are unknown parameters to be estimated, and the output equation υ(t) is the plasma concentration, where ψ is the plasma volume (another unknown parameter to be estimated). Then our input–output equation should be a differential equation in terms of the parameters, input u, output υ, and their derivatives. This can be generated as follows—we substitute x₁ = ψυ into the ẋ₁ equation above, and solve for x₂ to give

$$x_2=\frac{\psi \dot{\upsilon }+(k_{21}+k_{01})\psi \upsilon -u}{k_{12}}.$$ (16)

Plugging this in to the ẋ₂ equation yields the following (taking a derivative of Eq. (16) to substitute for ẋ₂),

$$\frac{\psi \ddot{\upsilon }+(k_{21}+k_{01})\psi \dot{\upsilon }-\dot{u}}{k_{12}}=k_{21}\psi \upsilon -(k_{12}+k_{02})\left(\frac{\psi \dot{\upsilon }+(k_{21}+k_{01})\psi \upsilon -u}{k_{12}}\right).$$ (17)

Clearing denominators and combining terms yields

$$\psi \ddot{\upsilon }+(k_{21}+k_{01}+k_{12}+k_{02})\psi \dot{\upsilon }-\dot{u}-(k_{12}{k}_{21}+(k_{12}+k_{02})(k_{21}+k_{01}))\psi \upsilon -(k_{12}+k_{02})u=0.$$ (18)

This differential polynomial is monic and thus an input-output equation for the system under a ranking of the variables that places u as higher ranked than υ. However, the ranking u < u̇ < ü < ⋯ < υ < υ̇ < ϋ < ⋯ is traditional [26], so we take

$$\ddot{\upsilon }+(k_{21}+k_{01}+k_{12}+k_{02})\dot{\upsilon }-\frac{1}{\psi }\dot{u}-(k_{12}{k}_{21}+(k_{12}+k_{02})(k_{21}+k_{01}))\upsilon -\frac{1}{\psi }(k_{12}+k_{02})u=0$$ (19)

as our input-output equation. The coefficients of Eq. (19) are the set of identifiable combinations for the model. The importance of making the input-output equation monic (or otherwise clearing the coefficient of one of the terms) can be seen here—if we did not include such a restriction, we could multiply Eq. (19) by an arbitrary parameter combination, which would then be the coefficient of the ϋ term and appear to be identifiable. From these coefficients, we can see immediately that the model is unidentifiable—there are only four identifiable combinations, but there are five parameters. Moreover, we can see from the coefficient of u̇ that the parameter ψ is identifiable (since if 1/ψ is known, then ψ is known).

More broadly, testing for identifiability is usually accomplished by testing injectivity of the map from the parameters to the coefficients, i.e. evaluating each coefficient at two (symbolic) points, setting the two equal (e.g. $k_{21}+k_{01}+k_{12}+k_{02}=k_{21}^{\ast }+k_{01}^{\ast }+k_{12}^{\ast }+k_{02}^{\ast }$), and then testing whether it is possible to solve the resulting equations for each parameter in the form $k_{\mathit{ij}}=k_{\mathit{ij}}^{\ast }$. In this case, it is apparent that the parameters are not identifiable. However we can find simpler representations of the identifiable combinations than the coefficients of Eq. (19): by noting that ψ is identifiable, we see that the coefficient for u shows that (κ₁₂+κ₀₂) is also identifiable (since both ψ and (κ₁₂+κ₀₂)/ψ are). Continuing in this fashion yields a simplified set of identifiable combinations: ψ, (κ₁₂ + κ₀₂), κ₂₁ + κ₀₁, and κ₁₂κ₂₁. Further examination shows that we can reparameterize the model in terms of the identifiable combinations by rescaling x̃₂ = κ₁₂x₂, resolving the identifiability problem for the model (discussed further in [26]).

This example is simple enough to permit by-hand computation of the input–output equations and identifiable combinations. However, many models (even relatively simple nonlinear models) can result in extremely lengthy input output equations (e.g. terms numbering in the hundreds) or complicated combination structures which are not feasible to calculate by hand [27, 31]. Thus, it is common to use computational algebra techniques such as characteristic sets or Gröbner bases for many of the above steps [26, 27, 48], such as elimination of the unobserved variables x to generate an input–output equation or calculation of the identifiability results from the coefficients of the input–output equation. These approaches typically reduce a given set of polynomials/differential polynomials using some sort of ranking of the variables, typically ranking u < υ < x typically [26].

Appendix B

To prove Theorem 2, we begin with a series of lemmas.

Lemma 1

For 1 ≤ k < n − 1, x_k is a rational function of x and its derivatives and may be written in the form $\frac{q_k+u_k}{qk}$, where q_k and u_k are polynomials of x and its derivatives and q_k is monic.

Proof

We proceed by induction. Observe that

$$x_1=\frac{x+\frac{\dot{x}}{{\mu }_0}}{x}$$ (20)

Next, assume that x_k, for some 1 ≤ k < n − 2, may be written in the form $\frac{q_k+u_k}{q_k}$, where q_k and u_k are polynomials of x and its derivatives and q_k is monic. Then, from the ẋ_k equation, we find

$$\begin{array}{cc}\hfill x_{k+1}& =\frac{x_k+\frac{1}{{\mu }_k}{\dot{x}}_k}{x_k}\hfill \\ & =\frac{(\frac{q_k+u_k}{q_k})+\frac{1}{{\mu }_k}\frac{d}{dt}(\frac{q_k+u_k}{q_k})}{(\frac{q_k+u_k}{q_k})}\hfill \\ & =\frac{(q_k+u_k)q_k+\frac{1}{{\mu }_k}(({\dot{q}}_k+{\dot{u}}_k)q_k-(q_k+u_k){\dot{q}}_k)}{(q_k+u_k)q_k}\hfill \\ & =\frac{q_{k+1}+u_{k+1}}{q_{k+1}}\hfill \end{array}$$ (21)

where

$$u_{k+1}=\frac{1}{{\mu }_k}({\dot{u}}_k{q}_k-u_k{\dot{q}}_k)$$ (22)

$$q_{k+1}=(q_k+u_k)q_k$$ (23)

Because q_k is monic, $q_{k+1}=q_k^2+q_k{u}_k$ is also monic. Further, q_k and u_k are clearly polynomials in x and its derivatives. Hence the result.

Lemma 2

The highest power of x in the polynomial q_k is 2^k−1, and the highest order derivative of x is k − 1. In particular, q_k contains the term x^2k−1, which is the only term with this power of x. The only terms in q_k of with the power 2^k−1 − 1 of x are, for 0 ≤ m ≤ k − 1,

$$\frac{2^{k-m-1}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^{k-1}-1}{x}^{(m)}.$$

The highest power of x in the polynomial u_k is 2^k−1 −1 and the highest order derivative is k. In particular, u_k contains the term

$$\frac{1}{{\mu }_0\cdots {\mu }_{k-1}}{x}^{2^{k-1}-1}{x}^{(k)},$$

which is the only term in u_k with this power of x.

Proof

The relevant terms in q_k and u_k for the first few k are written out in Table II for convenience. We have q₁ = x and $u_1=\frac{1}{\mu 0}\dot{x}$, so the base case is—partly vacuously—true. Now, suppose that the hypotheses are true. Let q_k+1 = (q_k + u_k)q_k. Then, its term with the highest power of x is ${\left(x^{2^{k-1}}\right)}^2=x^{2^k}$. Since q_k contains the terms $\frac{2^{k-m-1}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^{k-1}-1}{x}^{(m)}$, 1 ≤ m ≤ k − 1, and x^2k−1 , $q_k^2$ contains the terms, for 1 ≤ m ≤ k − 1,

$$2\cdot x^{2^{k-1}}\cdot \frac{2^{k-m-1}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^{k-1}-1}{x}^{(m)}=\frac{2^{k-m}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^k-1}{x}^{(m)}.$$

Table II.

Relevant terms in q_k and u_k for k ≤ 4

k	Relevant terms in qk	Relevant term in uk
1	x	$\frac{1}{{\mu }_0}\dot{x}$
2	$x^2,\frac{1}{{\mu }_0}x\dot{x}$	$\frac{1}{{\mu }_0{\mu }_1}x\ddot{x}$
3	$x^4,\frac{2}{{\mu }_0}{x}^3\dot{x},\frac{1}{{\mu }_0{\mu }_1}{x}^3\ddot{x}$	$\frac{1}{{\mu }_0{\mu }_1{\mu }_2}{x}^3{x}^{\left(3\right)}$
4	$$x^8,\frac{4}{{\mu }_0}{x}^7\dot{x},\frac{2}{{\mu }_0{\mu }_1}{x}^7\ddot{x},\frac{1}{{\mu }_0{\mu }_1{\mu }_2}{x}^7{x}^{\left(3\right)}$$	$\frac{1}{{\mu }_0{\mu }_1{\mu }_2{\mu }_3}{x}^7{x}^{\left(4\right)}$

Since we have identified all of the terms with a power on x of 2^k−1 and 2^k−1 − 1 in q_k, we have identified all of terms of power 2^k−1 − 1 in $q_k^2$. Additionally, there can be only one such term from q_ku_k: since q_k contains x^2k−1 and u_k contains $\frac{1}{X{\mu }_0\cdots {\mu }_{k-1}}{x}^{2^{k-1}-1}{x}^{(k)}$, q_ku_k contains $\frac{1}{X{\mu }_0\cdots {\mu }_{k-1}}{x}^{2^k-1}{x}^{(k)}$. Hence q_k+1 contains the terms, for 1 ≤ m ≤ k,

$$\frac{2^{k-m}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^k-1}{x}^{(m)}.$$

Further, since the highest order derivative of x in u_k is x^(k), the term in u_k+1 of order k + 1 must come from $\frac{1}{{\mu }_k}{\dot{u}}_k{q}_k$. In particular, u̇_k contains $\frac{1}{{\mu }_0\cdots {\mu }_{k-1}}{x}^{2^{k-1}-1}{x}^{(k+1)}$. Then, $\frac{1}{{\mu }_k}{\dot{u}}_k{q}_k$, u_k+1 contains the term

$$\frac{1}{{\mu }_k}\cdot \frac{1}{{\mu }_0\cdots {\mu }_{k-1}}{x}^{2^{k-1}-1}{x}^{(k+1)}·x^{2^{k-1}}=\frac{1}{{\mu }_0\cdots {\mu }_k}{x}^{2^k-1}{x}^{(k+1)}.$$

Hence the result.

Now, we prove Theorem 2.

Proof

For ease of notation, let q :=q_n−1 and u :=u_n−1. Now, we replace x_n−1 with $\frac{q+u}{q}$ in the ẋ_n−1 equation to find an input–output equation.

$${\dot{x}}_{n-1}=-({\alpha }_{n-1}+{\beta }_{n-1}+{\mu }_{n-1})x_{n-1}+{\beta }_{n-1}+{\alpha }_{n-1}{x}_{n-1}^2$$ (24)

$$\frac{(\dot{q}+\dot{u})q-(q+u)\dot{q}}{q^2}=-({\alpha }_{n-1}+{\beta }_{n-1}+{\mu }_{n-1})\frac{q+u}{q}+{\beta }_{n-1}+{\alpha }_{n-1}{(\frac{q+u}{q})}^2$$ (25)

$$\dot{u}q-\dot{u}q=-({\alpha }_{n-1}+{\beta }_{n-1}+{\mu }_{n-1})(q^2+qu)+{\beta }_{n-1}{q}^2+{\alpha }_{n-1}(q^2+2\mathit{qu}+u^2)$$ (26)

$$0=\dot{u}q-u\dot{q}+{\mu }_{n-1}{q}^2-({\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1})\mathit{qu}-{\alpha }_{n-1}{u}^2$$ (27)

$$0=\frac{1}{{\mu }_{n-1}}(\dot{u}q-u\dot{q})+q^2-\left(\frac{{\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1}}{{\mu }_{n-1}}\right)\mathit{qu}-\frac{{\alpha }_{n-1}}{{\mu }_{n-1}}{u}^2$$ (28)

Viewed as a function of x, this last equation is an input–output equation. Under an appropriate ranking, it is monic because of the x²ⁿ⁻¹ term in q². As in the proof of the previous lemma, q² also contains the terms, for 1 ≤ m ≤ n − 2,

$$2\cdot x^{2^{n-2}}\cdot \frac{2^{n-m-2}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^{n-2}-1}{x}^{(m)}=\frac{2^{n-m-1}}{{\mu }_0\cdots {\mu }_{m-1}}{x}^{2^{n-1}-1}{x}^{(m)}.$$

From the $-(\frac{{\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1}}{{\mu }_{n-1}})$ qu term, we get

$$-\left(\frac{{\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1}}{{\mu }_{n-1}}\right)\cdot x^{2^{n-2}}\cdot \frac{1}{X{\mu }_0\cdots {\mu }_{n-2}}{x}^{2^{n-2}-1}{x}^{(n-1)}=-\frac{{\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1}}{X{\mu }_0\cdots {\mu }_{n-1}}{x}^{2^{n-1}-1}{x}^{(n-1)}.$$

Next, from $\frac{1}{{\mu }_{n-1}}\dot{u}q$, as in the proof of the lemma, we get

$$\frac{1}{{\mu }_{n-1}}.\frac{1}{{\mu }_0\cdots {\mu }_{n-2}}{x}^{2^{n-2}-1}{x}^{(n)}\cdot x^{2^{n-2}}=\frac{1}{{\mu }_0\cdots {\mu }_{n-1}}{x}^{2^{n-1}-1}{x}^{(n)}.$$

From $-\frac{{\alpha }_{n-1}}{{\mu }_{n-1}}{u}^2$, we get

$$-\frac{{\alpha }_{n-1}}{{\mu }_{n-1}}{\left(\frac{1}{{\mu }_0\cdots {\mu }_{n-2}}{x}^{2^{n-2}-1}{x}^{(n-1)}\right)}^2=-\frac{{\alpha }_{n-1}{\mu }_{n-1}}{{({\mu }_0\cdots {\mu }_{n-1})}^2}{x}^{2^{n-2}-2}{(x^{(n-1)})}^2$$

A term of the same kind arrives from $-\frac{1}{{\mu }_{n-1}}u\dot{q}$. Noting that the derivative of $\frac{1}{{\mu }_0\cdots {\mu }_{n-3}}{x}^{2^{n-2}-1}{x}^{(n-2)}$ contains $\frac{1}{{\mu }_0\cdots {\mu }_{n-3}}{x}^{2^{n-2}-1}{x}^{(n-1)}$,

$$-\frac{1}{{\mu }_{n-1}}\cdot \frac{1}{{\mu }_0\cdots {\mu }_{n-2}}{x}^{2^{n-2}-1}{x}^{(n-1)}\cdot \frac{1}{{\mu }_0\cdots {\mu }_{n-3}}{x}^{2^{n-2}-1}{x}^{(n-1)}=-\frac{{\mu }_{n-2}{\mu }_{n-1}}{{({\mu }_0\cdots {\mu }_{n-1})}^2}{x}^{2^{n-2}-2}{(x^{(n-1)})}^2.$$

We have identified n + 1 coefficients in the input–output equation. They are, for 1 ≤ m ≤ n − 2,

$$\frac{2^{n-m-1}}{{\mu }_0\cdots {\mu }_{m-1}},$$

$$-\frac{{\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1}}{{\mu }_0\cdots {\mu }_{n-1}},$$

$$\frac{1}{{\mu }_0\cdots {\mu }_{n-1}},$$

and

$$-\frac{{\alpha }_{n-1}{\mu }_{n-1}+{\mu }_{n-2}{\mu }_{n-1}}{{({\mu }_0\cdots {\mu }_{n-1})}^2}.$$

Thus, we can identify μ₀, μ₁, … , μ_n−3 (n > 3), μ_n−2μ_n−1, α_n−1μ_n−1, α_n−1 − β_n−1 − μ_n−1.

However, there may be additional terms in the input–output equations. Thus, a priori, it is possible that smaller combinations making up these terms could be identifiable (or even that the model itself might be). So, we must show that the overall model is unidentifiable, and, moreover, that none of these combinations can be broken down into smaller identifiable pieces. To this end, we find a model equivalent to the original model (Eq. (14)) that can be parameterized using only the above identifiable combinations. To do so, solve ẋ_n−2 for $x_{n-1}:x_{n-1}=1+\frac{1}{{\mu }_{n_2}}\frac{{\dot{x}}_{n-2}}{x_{n-2}}$, and plug this into the ẋ_n−1 equation to arrive at the following set of equations:

$$\begin{array}{cc}\hfill \dot{x}& =-{\mu }_{0}x(1-x_1),\hfill \\ {\dot{x}}_k& =-{\mu }_k{x}_k(1-x_{k+1}),\hfill \\ \hfill 0& ={\ddot{x}}_{n-2}{x}_{n-2}+({\mu }_{n-2}{\mu }_{n-1})x_{n-2}^2-({\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1}){\dot{x}}_{n-2}{x}_{n-2}-(\frac{{\alpha }_{n-1}{\mu }_{n-1}}{{\mu }_{n-2}{\mu }_{n-1}}+1){\dot{x}}_{n-2}^2,\hfill \end{array}$$ (29)

for 1 ≤ k ≤ n − 3 and with initial conditions x(0) = 1, x_k(0) = 1, x_n−2(0) = 1, and ẋ_n−2(0) = 0. Because the parameters μ_n−2, μ_n−1, α_n−1, and β_n−1 appear only in the combinations μ_n−2μ_n−1, α_n−1μ_n−1, and α_n−1 − β_n−1 − μ_n−1 in the model equations, specifying values for these parameter combinations fully describes the model. Because a product is the smallest unit in a combination, it is clear that μ_n−2, μ_n−1, and α_n−1 are not individually identifiable. Because β_n−1 appears only in a sum with α_n−1 and μ_n−1, it too is unidentifiable.

Hence, the result.

Next, we prove Proposition 1.

Proof

That the full model is unidentifiable, generally, can be seen as follows. The model below is equivalent to that in described by Eqs. (6).

$$\begin{array}{cc}\hfill \dot{x}& =-{\mu }_{0}x(1-x_1),\hfill \\ {\dot{x}}_k& =-({\alpha }_k+{\beta }_k+{\mu }_k)x_k+{\beta }_k+{\alpha }_k{x}_k^2+{\mu }_k{x}_k{x}_{k+1},\hfill \\ \hfill 0& ={\ddot{x}}_{n-2}{x}_{n-2}-\frac{{\alpha }_{n-2}^2({\alpha }_{n-1}{\mu }_{n-1})}{{\mu }_{n-2}{\mu }_{n-1}}{x}_{n-2}^4+2{\alpha }_{n-2}(\frac{{\alpha }_{n-1}{\mu }_{n-1}}{{\mu }_{n-2}{\mu }_{n-1}}-1)x_{n-2}^2{\dot{x}}_{n-2}\hfill \\ & -(({\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1})+\frac{2({\alpha }_{n-2}+{\beta }_{n-2})({\alpha }_{n-1}{\mu }_{n-1})}{{\mu }_{n-2}{\mu }_{n-1}})x_{n-2}{\dot{x}}_{n-2}\hfill \\ & +{\beta }_{n-2}(({\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1})+\frac{2({\alpha }_{n-2}+{\beta }_{n-2})({\alpha }_{n-1}{\mu }_{n-1})}{{\mu }_{n-2}{\mu }_{n-1}})x_{n-2}\hfill \\ & -(({\alpha }_{n-2}+{\beta }_{n-2})({\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1})-{\mu }_{n-2}{\mu }_{n-1}+\frac{({\alpha }_{n-1}{\mu }_{n-1})({\alpha }_{n-2}^2+4{\alpha }_{n-2}{\beta }_{n-2}+{\beta }_{n-2}^2)}{{\mu }_{n-2}{\mu }_{n-1}})x_{n-2}^2\hfill \\ & +{\alpha }_{n-2}(({\alpha }_{n-1}-{\beta }_{n-1}-{\mu }_{n-1})+\frac{2({\alpha }_{n-1}{\mu }_{n-1})({\alpha }_{n-2}+{\beta }_{n-2})}{{\mu }_{n-2}{\mu }_{n-1}})x_{n-2}^3\hfill \\ & -(\frac{{\alpha }_{n-1}{\mu }_{n-1}}{{\mu }_{n-2}{\mu }_{n-1}}+1){\dot{x}}_{n-2}^2+2{\beta }_{n-2}(\frac{{\alpha }_{n-1}{\mu }_{n-1}}{{\mu }_{n-2}{\mu }_{n-1}}+1){\dot{x}}_{n-2}-\frac{{\beta }_{n-2}^2({\alpha }_{n-1}{\mu }_{n-1})}{{\mu }_{n-2}{\mu }_{n-1}}\hfill \end{array}$$ (30)

for 1 ≤ k ≤ n − 3 with initial conditions x(0) = 1, x_k(0) = 1 , and x_n−3(0) = 1, x_n−2(0) = 1, and ẋ_n−2(0) = 0. As in the previous proof, parameters μ_n−2, μ_n−1, α_n−1, and β_n−1 appear only in the combinations μ_n−2μ_n−1, α_n–1 μ_n−1, and α_n−1 − β_n−1 − μ_n−1 in Eqs. (30). So, the full model is indeed unidentifiable.

Finally, we sketch the proof of Conjecture 1 for n ≤ 5. Calculations were carried out in Mathematica 10.2.

Proof

Solve the ẋ equation for x₁. Take a derivative to find ẋ₁. We now have x₁ and ẋ₁ as a function of x and its derivatives. Plug these into the ẋ₁ equation so that it becomes an equation of x₃, x, and derivatives of x. Solve for x₂ as a function of x and its derivatives, and compute ẋ₂. Continue in this manner until we have x_n as a function of x and its derivatives. Substitute x_n and ẋ_n into the final equation. We now have a single equation of x and its derivatives that contains all of the information of the system. Divide the equation by ${\prod }_{k=0}^{n-1}{\mu }_k^{2^{n-1-k}}$, which makes the equation monic under the appropriate ranking. This is an input–output equation. The equation has the following number of coefficients: 11 for n = 3, 48 for n = 4, 365 for n = 5. Determine the identifiable combinations from the list of coefficients by setting the coefficients equal to copies of themselves with placeholder parameter values and finding a Gröbner basis.