Abstract
Brain-machine interfaces (BMIs) are a rapidly progressing technology with the potential to restore function to victims of severe paralysis via neural control of robotic systems. Great strides have been made in directly mapping a user's cortical activity to control of the individual degrees of freedom of robotic end-effectors. While BMIs have yet to achieve the level of reliability desired for widespread clinical use, environmental sensors (e.g. RGB-D cameras for object detection) and prior knowledge of common movement trajectories hold great potential for improving system performance. Here we present a novel sensor fusion paradigm for BMIs that capitalizes on information able to be extracted from the environment to greatly improve the performance of control. This was accomplished by using dynamic movement primitives to model the 3D endpoint trajectories of manipulating various objects. We then used a switching unscented Kalman filter to continuously arbitrate between the 3D endpoint kinematics predicted by the dynamic movement primitives and control derived from neural signals. We experimentally validated our system by decoding 3D endpoint trajectories executed by a non-human primate manipulating four different objects at various locations. Performance using our system showed a dramatic improvement over using neural signals alone, with median distance between actual and decoded trajectories decreasing from 31.1 cm to 9.9 cm, and mean correlation increasing from 0.80 to 0.98. Our results indicate that our sensor fusion framework can dramatically increase the fidelity of neural prosthetic trajectory decoding.
Index Terms: Brain Machine Interface, Cognitive Human-Robot Interaction, Physically Assistive Devices
I. Introduction
NEURAL control over robotic systems may soon enable victims of severe paralysis to regain the autonomy necessary to perform many essential activities of daily living. By directly tapping into patients' cortical signals, brain-machine interfaces (BMI) can deliver a basic level of control of prosthetic devices to quadriplegic users [1]. However, many daily tasks, such as using utensils or retrieving an object from a cluttered workspace, require complex trajectories with a degree of precision that has yet to be obtained from direct neural control. To achieve the level of robust neural control needed for widespread clinical use, it is likely that BMIs will need to incorporate shared control strategies that intelligently capitalize on information obtained from environmental sensors.
Environmental sensors (e.g. RGB-D cameras) and intelligent robotics have been shown to improve system performance in teleoperated robotics [2]. Augmenting tele-operation with shared control can be separated into two core components: prediction of the user's intent, and arbitration between system autonomy and direct user control. Prediction often focuses on inference of a goal location and/or trajectory prediction [3]. It can also involve segmentation of user inputs with a hidden Markov model (HMM) [4] in order to draw from a library of movement primitives that aid in task completion [5], [6]. Arbitration between the system predictions and user commands in teleoperated robotics is often accomplished with a continuous linear blending of user inputs with system predictions [3], [7], [8], which has been used to deliver shared control of a BMI [9]. Intelligent arbitration is paramount to user satisfaction [3] with teleoperated robotics, and is integral for the success of shared control with BMIs [10].
Probabilistic BMI control strategies have been employed with and without information about the user's goal, which can potentially be obtained from external sensors. Most commonly, recursive Bayesian estimation is employed with a state transition matrix built from a large corpus of kinematic data [11] or set manually according to system assumptions [12], [13]. Performance with recursive Bayesian estimation can be increased by including information about potential goals [14]–[17]. Static canonical trajectories have been created for the goal locations and traversed through with neural data [18]. HMMs have been used to segment primates' cognitive states during reaching tasks [19], [20], and switching Kalman filters have been used to improve results [21], [22]. Combining cortical signals with eye-tracking and/or computer vision can further improve system performance [16], [23]–[25]. However, these systems have all relied on simple linear models of motion that are incapable of reproducing the complex movements necessary for many tasks.
Here we present a probabilistic robotics framework for arbitrating between direct neural control and non-linear predictions of user intent, allowing for robust movement decoding of complex trajectories to novel locations. The type of task the user is engaged in (e.g. resting or pushing a button) is predicted through a hidden Markov model. The inferred task is then used to inform a non-linear prediction of the user's desired kinematics using dynamic movement primitives (DMPs) [26]. This prediction is fused with neural sensor measurements via unscented Kalman filtering in order to localize the user's intended position. We demonstrate the utility of this framework by reconstructing the complex trajectories taken by a non-human primate performing four different actions on objects placed in various locations. By intelligently leveraging information from our motion models and potential environmental sensors, we dramatically improve offline 3D trajectory decoding over using neural signals alone.
II. Motion Planning Architecture
A. System Overview
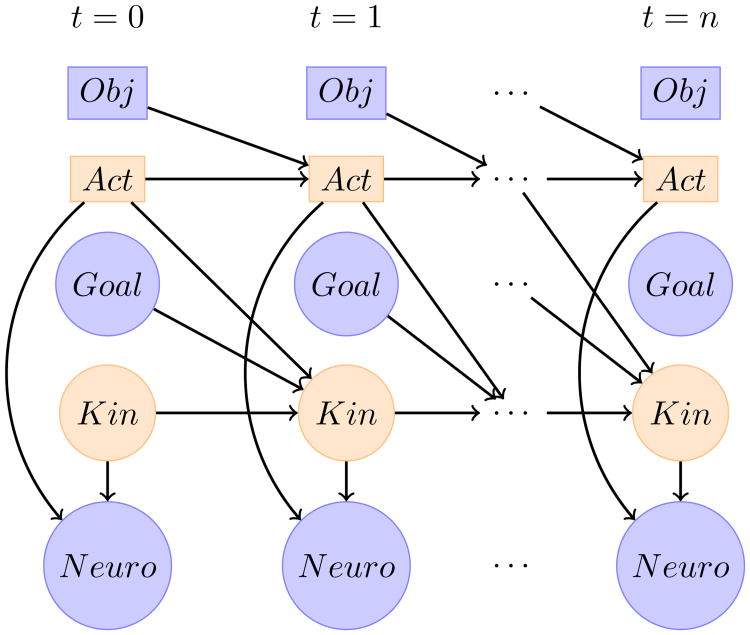
We formalize the problem of tracking the user's desired movements by using a dynamic Bayesian network (DBN), shown in Figure 1. We observe features extracted from the neural signals (Neuro). We also assume we observe the type (Obj) and location (Goal) the user intends to reach to. This can be accomplished with eye-tracking and computer vision [23]. The continuous kinematics variable, Kin, is a 9-dimensional vector tracking the position, velocity, and acceleration of the user's desired 3D endpoint. Kin is assumed to have Gaussian noise and follows switching Kalman filter dynamics [27]. The switching variable, Act, represents the category/state of the current action the user wants to take. Act is a discrete-valued latent variable with first-order Markov properties.
Figure 1.
Dynamic Bayesian network of motion prediction using computer vision and neural signals. Rectangles represent categorical (discrete) variables, circles are continuous. Blue is observed, and orange is inferred at each time step. Obj represents the type of selected object (possibly none), Act is the desired action to execute (e.g. rest or drink), Goal is the 3D endpoint the user is trying to reach, Kin is the current 3D position, velocity, and acceleration, and Neuro is the feature vector extracted from the neurological signals. Arrows denote conditional dependencies between variables.
In general, the value of Act can represent simple subcomponent of a movement (e.g. moving to the object) or sophisticated sequences of movements (e.g. moving to then turning a handle). The transitions of Act represent the onset/offset of movements, which determine when the DMPs start/stop their predictions. The value of Act can also determine the type of DMP selected (e.g. a DMP for a drinking motion vs. a pushing motion). Within this study, however, we make the simplifying assumption that each object has only one possible sequence of actions. During our global system evaluation, the estimated value of Act is only used for detecting the onset and offset of movement, and the type of DMP used for motion prediction is determined by the object type.
The value of Kint is predicted from Kint−1 using the current DMP. The parameters of the DMP are determined by the values of Actt−1 (the movement type) and Goalt−1 (the location of the object). Details of the DMP updates are outlined in section II-B. Actt is predicted from Actt−1 using an Obj dependent state transition matrix. For example, if the identified object is a cup, Act is more likely to transition from rest to drinking than from rest to poking.
After Actt and Kint are predicted from the previous time step, they are updated using the measurement of Neurot. The value of Actt is updated using the HMM forward algorithm, and Kint is updated using the Kalman filter update. The 3D position estimate from Kint is then used as the system output. Table I describes each of the tracked variables.
Table I. Variable Descriptions.
| Variable | Type | Values in this Study | Observed |
|---|---|---|---|
|
| |||
| Obj | Discrete | Sphere, Push Button, Handle, Mallet | Yes |
| Act | Discrete | Rest, and Two Movement States Per Object | No |
| Goal | Continuous | 8 possible locations | Yes |
| Kin | Continuous | Position, Velocity, Acceleration | No |
| Neuro | Continuous | Spike Rate (Hz) of the Neurons | Yes |
B. Dynamic Movement Primitives
BMIs often improve predictions of kinematics by combining a neural observation model with a state transition model with recursive Bayesian estimation. When modeling a user's kinematics with BMIs, previous efforts have typically assumed the user's kinematics evolve linearly over time [12] [21]. However, linear models are often unable to capture many of the dynamics associated with more sophisticated trajectories. We therefore used dynamic movement primitives [26] to develop a library of motion models capable of capturing the nonlinearities involved in complex movements without sacrificing the flexibility needed for navigating dynamic environments. We used these models to predict the kinematic state transitions during Kalman filtering (see section II-E).
When modeling the non-rhythmic movement of a variable y to a goal location g, DMPs combine a simple point attractor system (a damped spring model) with a nonlinear forcing function f:
where τ is a time constant, and αy and βy are positive constants. The point attractor dynamics ensure that the system will end at g, while the forcing function f allows arbitrary trajectories to be taken while approaching g. The forcing function is composed of N weighted Gaussian kernels ψi indexed by a variable x that exponentially decays to zero over time:
where wi is the weight of kernel i and y0 is the initial position. As x decays, it causes f(x) to go to zero, leaving only the stable point attractor that approaches the goal. Readers are referred to [28] for a comprehensive overview.
C. HMM Temporal Update
To track the state of our switching variable, we apply a hidden Markov model approach. At every time step, the probability distribution over actions, Act, is first estimated using the estimate of Act from the previous time step and a state-transition model. We make a first-order Markov assumption that Actt is conditionally independent of everything in the past given Actt−1 and Objt−1. To construct an initial estimate the state distribution, we multiply the posterior estimate of state from the previous time step by the object-dependent state transition matrix. The possible combinations of prior states and transitions are combined by marginalizing over the estimate of Act from the previous time step:
where the action state transition probabilities, P(Actt|Actt−1,Objt−1), can either be learned from example data or intelligently set by an operator.
D. HMM Measurement Update
After obtaining P(Actt|Objt−1), we update our estimates of the action by using the most recent observations of the neural signals. The action is updated following the forward algorithm under the naive assumption that each neural feature is independent:
| i |
| ii |
| iii |
| iv |
| v |
where is the Gaussian distribution of the ith neural feature given current action, with a mean and covariance estimated from training data. Equation v assumes Neurot is conditionally independent of Objt−1 given Actt. Equation v also incorporates the naive assumption of conditional independence of the neural features. The denominator of equation iii is a normalization constant, because P(Neurot|Objt−1) is not influenced by the Actt being estimated.
The estimated probabilities of the actions being performed over time can be used to inform the predictions of the continuous dynamics. However, tracking every possible sequence of trajectories with a switching dynamical system is intractable [27]. In our experimental validation, we make the simplifying assumption that each object has only one possible sequence of actions associated with it (rest, movement state 1, and movement state 2), which is consistent with the experiment performed. For example, when manipulating the mallet, the movement began at rest (Rest), moved to the mallet (Mallet 1), transitioned to holding the mallet in a constant position (Mallet 2), then rested at that position (Rest). We update the predictions of the kinematics using only the most likely action at any given time.
E. UKF Temporal Update
The Kalman filter is a recursive Bayesian method for alternating between predicting the continuously valued state of a series, and updating the prediction with a noisy measurement of the true value. At each time step, both the estimate and the certainty (i.e. the covariance) of the value are tracked. Whenever a prediction is made, noise is introduced and the certainty decreases. Every time a measurement is made, the certainty of the estimate increases. When measurements have higher certainty, they correct the predictions more heavily.
To make a prediction with the standard Kalman filter, a linear model with zero mean offset is assumed. This can be represented with a matrix, F. The mean and covariance of the tracked state X can then be updated as follows:
where Q is the covariance of the noise introduced by the prediction. However, in this study, the predictions are performed using nonlinear DMP functions that can not be represented with a linear matrix multiplication.
Two methods are commonly employed with Kalman filters to account for the impact of a nonlinear transformation on the distribution of the random variable being tracked. The extended Kalman filter uses a first order, local linear approximation of the nonlinear transform. This linear approximation can then be used to update the estimates of the expected value and covariance. However, in situations where there is a large degree of uncertainty in the estimates, this local approximation can have an undesirable degree of inaccuracy that accumulates over time.
The other common method for utilizing a nonlinear function within the Kalman filter is to employ the unscented transform [29]. The unscented transform is a method of approximating the mean and covariance of a random variable after a nonlinear transformation. This is accomplished by propagating samples called sigma vectors through the nonlinear function. The first sigma vector is set to the mean of the distribution, and the rest of the sigma vectors are offset along the main axes of the random variable's covariance. After the nonlinear function is applied to the sigma vectors, they are used to calculate an empirical estimate of the new mean and covariance. Readers are referred to [29] for an in-depth analysis of the method.
In this study, the random variable undergoing a nonlinear transformation is Kin, the 3D position, velocity, and acceleration. The nonlinear functions applied to Kin are the DMPs. The unscented transform is used to calculate and Pt|t−1, the a priori estimates of the mean and covariance of Kint after the DMP is applied to the previous timestep. The a priori estimates are then updated with the measurements from the neural signals to get the a posteriori estimates, denoted as and Pt|t respectively.
F. Kalman Filter Measurement Update
While the prediction step is nonlinear, the mapping between Kin and Neuro, represented with a matrix H, can be represented as a set of linear equations [1]. This enables the standard Kalman filter measurement update to be employed:
Measurement Residual:
Residual Covariance: St = HPt|t−1HT + R
Kalman Gain:
A Posteriori State Estimate:
A Posteriori Cov Estimate: Pt|t = (I − KtH)Pt|t−1
The residual covariance, St, dictates how much weight to place on the measurement. As the certainty of the measurement decreases and R goes to infinity, K will go to 0 and the weight will all be placed on the a priori estimate. As the measurement certainty increases and R goes to 0, the Kalman gain will approach H−1, thereby fully correcting the a priori estimate with the measurement residual, resulting in all the weight being placed on the measurement at every timestep.
III. Experimental Validation
A. Experimental Details
A male rhesus monkey was trained to perform a center-out reach, grasp, and manipulate task. All procedures were approved by the University Committee on Animal Resources at the University of Rochester. The monkey was implanted with floating microelectrode arrays (FMAs) containing 16 microelectrodes each. Eight FMAs were implanted in the left motor and premotor areas. Signals were sorted into spike trains using software from Plexon (Plexon, Dallas, TX). We excluded neurons with low mean firing rates, leaving 80 units of 104 recorded.
A detailed description of the experimental setup can be found in [30]. In brief, the monkey was seated in front of an experimental apparatus consisting of a central home object, a sphere, push button, coaxial cylinder (pull), and perpendicular cylinder (mallet). The objects were spaced with 45° intervals in a circular arc centered on the home object with radius of 13 cm. Target objects were indicated by an LED shortly after the monkey pulled on the home object. The monkey then rotated the sphere, pulled one of the two cylinders, or pressed the button. The final hold state was then maintained for one second for the monkey to get a reward. The apparatus was pseudo-randomly rotated in 22.5° intervals after the monkey performed a block of trials to an object/location pair. This resulted in eight potential locations for the four objects. The reaching kinematics of the monkey's wrist were recorded with a Vicon optical motion capture system (Vicon Motion Systems, Oxford, UK), shown in Figure 2.
Figure 2.
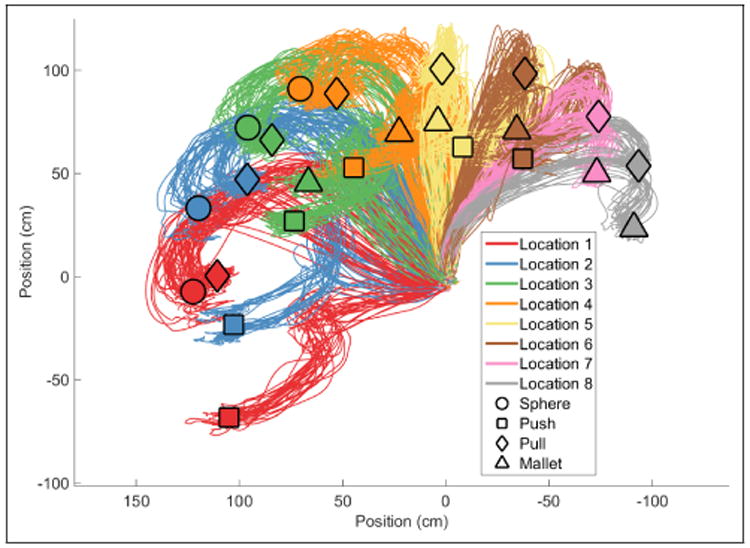
Reach trajectories performed by the non-human primate recorded via optical tracking of the monkey's wrist. The origin corresponds to the home location. Line colors correspond to the location of the target object. Shapes are centered where the monkey completed its trajectory.
B. Neural Modeling
We modeled the smoothed multi-unit firing rates as a function of the kinematics and the action being taken. Firing rate was calculated by convolving spike times with a truncated exponential with a time constant of 20 ms, then smoothing with a moving average filter of 100 ms. We used these features with additional tap delays of 0, 20, and 60 ms to allow for transduction delays from cortical activity to arm kinematics (consistent with previous works [11]). All firing rates and kinematics were standardized using the mean and standard deviation from the training data.
The mapping, H, between the neural features and the kinematics was modeled using ordinary least squares (OLS) regression, and the error covariance was estimated from the residuals. The neural only decoding model was likewise built using OLS. When performing decoding using neural signals alone, we decoded the trajectory continuously without the HMM. Cross-validation was performed by creating a hold-out set of all trials for a particular object/location pair and training on all remaining trials. The fitted model was then evaluated on the hold-out set. This process was repeated for all object/location pairs.
C. Action Prediction Fitting
The switching dynamics of the actions were used to predict the onset and offset of movement. Trials were segmented into rest, movement, and hold periods by thresholding the movement speed of the monkey's hand. An HMM with nine states was built to track the value of Act: one for rest, and two for each of the object/action types (push, pull, mallet, sphere). Two movement states were established for each movement type due to a substantial shift in neural activity as the monkey transitioned from moving towards the object to a constant grasp of the object. The Act variable tracked this shift in activity to provide an estimate of when the end effector should maintain its current position. Transition probabilities between the movement states for different actions were set to zero. The neural features were modeled as conditionally independent Gaussians given Act. For simplicity, we performed supervised learning of the HMM parameters. To do so, the early movement state was defined as the first 200 ms of the movement (the movement to/initial manipulation of the object), and the second state was the transition to hold. Knowledge of the duration of the states was not included in the testing phase. The HMM was assumed to start at rest, then progress to movement state 1, movement state 2, then rest again. The transition from rest to movement state 1 marked movement onset, the beginning of the continuous decoding of the trajectory.
D. Dynamic Movement Primitive Fitting
The DMPs were fit on the unnormalized kinematics using locally weighted regression [28] with 35 Gaussian kernels. It was noted that the monkey's movement strategy could substantially change in different regions of space. This indicated the need for a mixture of DMPs with a dependency on object location, similar to [31]. For each object-location pair, we trained one DMP on all the trajectories taken to the object-location pair to the left, and another DMP on all the trajectories taken to the object-location pair to the right. The weights for these two DMPs were then averaged together. For example, to predict the trajectory taken for the sphere at location 3, we fit a DMP on all the trials to sphere location 2 and averaged it with a DMP fit on all trials to sphere location 4. To help ensure generalization to novel locations, we did not use any of the trajectories taken to the object-location pair in the test set when training the DMPs. Object locations that did not have examples to both the left and the right of the target location were excluded from testing to avoid the need for extrapolation, leaving 408 trials total across our testing sets.
We also noted that the final endpoint of the hold position ended at an offset from the object locations. The final goal location of the monkey's wrist was not the center of the object being manipulated. The offset from the center of the object was dependent on the object type, because different objects are grasped in different locations. We therefore averaged the offset from the two adjacent locations within the training set to approximate the desired offset at the test location.
The error covariance for the DMP models was estimated from the error when predicting Kint based on Kint−1.
E. Action Prediction Results
Prediction of movement transitions based on the neural signals was highly reliable, and is shown in Figure 3. There was one trial where a prediction occurred 289 ms after movement. In the rest of the 408 trials, the predictions occurred between 94 ms before movement onset and 55 ms after movement onset. Predictions occurred a median of 14 ms before movement onset, with a standard deviation of 26 ms. There were 13 false positives (ie predictions during the rest or hold periods) across the 20.8 minutes of data used in the testing sets. The hold period was detected in all the trials within 398 ms, with a median offset of 43.5 ms before hold onset, and a standard deviation of 77.6 ms. There were six false positives incurred by transitioning from state 1 to state 2 then back to state 1. Transitions to state 2 directly from rest were ignored.
Figure 3.
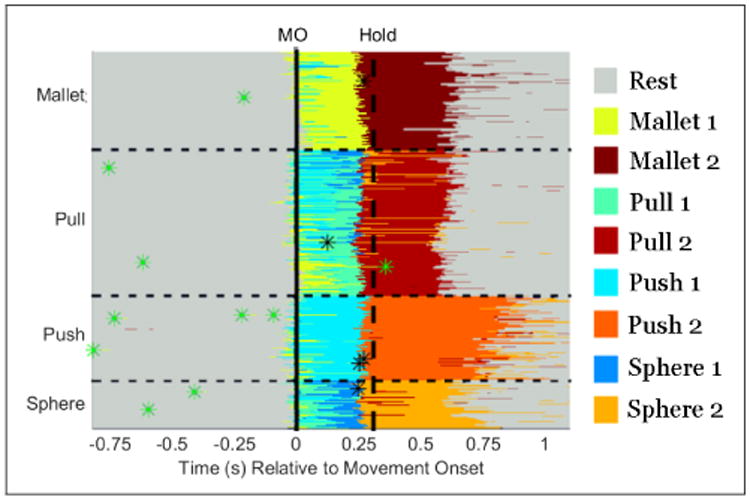
Prediction of rest (grey), movement/object manipulation (light blue/green), and hold (orange/red) from neural data. Each row corresponds to a single trial (sorted by action type). Trials were aligned to movement onset (MO, solid line), and the median onset of the object hold period is shown with a vertical dashed line. Probabilities across action types (i.e. all blue/green and all red/orange labels) were subsequently summed together because each object only had one associated action. Green asterisks denote the 13 false positives transitioning from rest state to the first movement state, and black asterisks mark the 6 false positives transitioning from movement state 1 to 2, then back to state 1.
While the predictions of movement onset and offset were highly reliable, the HMM was relatively unreliable in determining which object manipulation was being performed. Although the transition probabilities between actions were set to 0, the action with the highest probability over time would often switch. This was due to the states all having nonzero probabilities, and measurements indicating different states being the most likely over time. The correct object manipulation was predicted an average of 64% and 94% of the time respectively when the first and second movement states were being predicted.
F. Trajectory Prediction Results
We first evaluated results of using the DMPs to augment motion prediction from neural signals assuming the correct movement (Act). This was done to test the accuracy of the trajectory decoding without any errors induced by the HMM. We excluded the initial and final hold periods of each trial, and assumed the movement onset time was known. Table II shows the median distance between the actual and predicted trajectories, the mean correlation across the three dimensions (i.e. the average correlation for the lateral, vertical, and forward dimensions), and the dynamic time warping (DTW) distance (to test for trajectory shape ignoring time). We compared performance using the neural signals alone, DMPs alone, and the unscented Kalman filter (UKF) combining the two.
Table II. Movement Trajectory Decoding Performance.
| Correlation | Distance | DTW | |
|---|---|---|---|
| Neural Alone | 0.80 | 31.1 | 27.7 |
| DMP | 0.98 | 9.7 | 6.5 |
| UKF | 0.98 | 9.9 | 6.4 |
G. Global System Evaluation Details
The global performance (i.e. including the rest and hold periods) was evaluated by using the HMM dynamics to detect movement onsets for the DMPs (DMP-HMM) and UKF (UKF-HMM) algorithms. The DMP-HMM relies only on the DMP for continuous decoding of the kinematics after the HMM has detected the movement from the neural signals. In contrast, the UKF-HMM fuses the DMP predictions of the kinematics with the neural measurements, as outlined in the Section II-E and II-F.
Figure 4 depicts the flow diagram used for system evaluation. At rest, the DMP-HMM and UKF-HMM both remained at the home location. Because the object type was known and every object was manipulated in only one way, we added up the HMM probabilities across all possible object types for movement state 1 and movement state 2 during global system evaluation. We then used the Act with the highest probability to determine whether the monkey was at rest, in movement state 1, or in movement state 2. When a movement transitioned from rest to movement state 1, the DMP-HMM and UKF-HMM began decoding the continuous trajectory. If the predicted Act with the highest probability reverted back to rest from movement state 1, a point attractor pulled the position back to the home location and the DMPs were reset. If the Act predicted with the highest probability transitioned from movement state 1 to movement state 2, then the predicted hand position was held constant after a 300 ms delay. This delay is used to allow the monkey's hand to settle into its final hold position.
Figure 4.
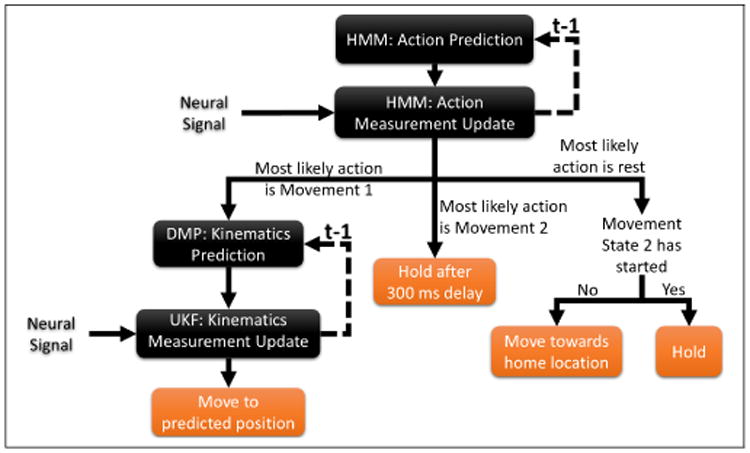
Flow diagram of the UKF-HMM algorithm. A prediction of the current action is first made based on the previous estimate of the action probabilities. This is then updated with the measurement of the neural signals, and the output is used to decide whether to move using the UKF, hold position, or rest. Dashed lines represent inputs from the previous time step.
When movement onset was predicted by the HMM, the DMP corresponding to the object being manipulated began decoding the continuous trajectory. The beginning of the second movement state marked a transition to hold, when the DMP was stopped and the predicted position was held constant (after a 300 ms delay to allow the monkey's hand to stabilize).
H. Global Performance Results
The average resulting traces are shown in Figure 5. Quantitative results are outlined in Table III. The use of the DMP with cortical signals predicting onset and offset of movement substantially improved results. Using the UKF-HMM, however, did not improve over using the DMP-HMM. The supplemental video shows the decoded trajectories at each object/location combination used for testing.
Figure 5.
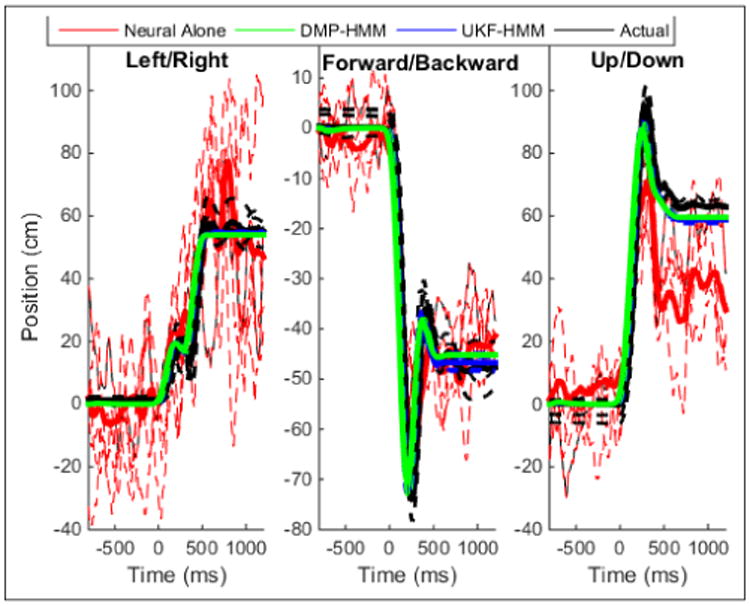
Example trajectories (position relative to home location) for an example object-location pair (push). Line color corresponds to the three dimensions being decoded. The dashed lines are single trials, and thick solid lines are the averaged across all trials for that object-location pair.
Table III. Global Decoding Performance.
| Correlation | Distance | DTW | |
|---|---|---|---|
| Neural Alone | 0.80 | 31.1 | 29.5 |
| DMP-HMM | 0.99 | 6.4 | 6.4 |
| UKF-HMM | 0.99 | 7.0 | 6.7 |
IV. Discussion
Here we show that complex movement trajectories can be reconstructed from the Bayesian fusion of neural measurements and movement primitives by leveraging information attainable from environmental sensors. By only testing on object-location pairs not seen in the training data, we demonstrate that our strategy has the ability to generalize to new locations. In spite of the difficulty of decoding the non-linear kinematics with multiple points of inflection present in the monkey's movements, our system is able to maintain high performance.
The neural signals were essential for estimating the HMM movement state. The UKF-HMM also enabled the neural signals to continuously alter the DMP trajectories with performance comparable to the DMP-HMM. While the UKF-HMM did not improve performance over the DMP-HMM in this study, the quality of neural control dramatically improves with closed loop practice [32]. Re-evaluation of model covariances would allow users to gain more autonomy as their neural control improves. Better cortical coverage would further improve decoding performance. Finally, it may be worth a small degradation in performance to enable users to continuously alter the automated trajectories via the UKF-HMM.
Upon detecting movements from the neural signals, the DMPs displayed remarkable performance in predicting the trajectories taken by the monkey. This may be in part due to the highly trained monkey performing very stereotyped movements across trials. Humans may move with more variability between trials, causing the deterministic DMPs to degrade in performance. The input of neural signals would be essential for enabling the system to account for inter-trial variability of the movements.
While the system was highly accurate in predicting movement onset and offset (rest, phase 1, and phase 2 of the movements), the prediction of the specific object manipulation being performed (e.g. push vs pull) was unstable and often incorrect. In this study, this was resolved by limiting objects to only one possible sequence of actions. During global evaluation, the HMM predicted onset and offset of movement and the object type determined the type of manipulation being performed. However, in general, a single object can be manipulated in multiple ways. Future work will investigate how many actions performed on a single object can be reliably decoded with high accuracy. Techniques such as interacting multiple models (IMM) [33] can be employed to simultaneously track the most likely sequences of actions by employing parallel Kalman filters. The kinematics associated with multiple possible actions could also be tracked using particle filters [34], which can often improve accuracy. However, particle filters can quickly become computationally prohibitive to implement in an online setting.
The immense utility of incorporating continuous shared control with environmental sensors has been shown online with human subjects [9], [24]. By using environmental sensors for object localization, the subjects in [9] were able to complete tasks consistently that could not be completed as well with neural control alone. Here we built on this by incorporating DMPs with Bayesian inference to track the user's current action and handle the challenge of arbitration between user commands and the nonlinear dynamics of autonomous robot control.
V. Conclusion
The probabilistic robotics framework formalized here establishes a novel approach to arbitrate between system automation and neural control of prosthetics for individuals with severe motor impairment. Our system allows for cortical signals to determine a user's desired action, and uses DMPs to assist with the neural control over the end effector's movement trajectories. Our experimental validation demonstrates the system's potential to allow BMI users to gain robust control of the movement of neuroprosthetics, enabling them to achieve an unprecedented level of autonomy.
Supplementary Material
Footnotes
*Supported by National Institutes of Health (NIH) R01 NS079664
References
- 1.Wodlinger B, Downey JE, Tyler-Kabara EC, Schwartz AB, Boninger ML, Collinger JL. Ten-dimensional anthropomorphic arm control in a human brain-machine interface: difficulties, solutions, and limitations. Journal of Neural Engineering. 2015 Feb;12:016011. doi: 10.1088/1741-2560/12/1/016011. [DOI] [PubMed] [Google Scholar]
- 2.Crandall J, Goodrich M. Characterizing efficiency of human robot interaction: a case study of shared-control teleoperation. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 2002;2:1290–1295. vol.2. [Google Scholar]
- 3.Dragan AD, Srinivasa SS. A Policy-blending Formalism for Shared Control. Int J Rob Res. 2013 Jun;32:790–805. [Google Scholar]
- 4.Castellani A, Botturi D, Bicego M, Fiorini P. Hybrid HMM/SVM model for the analysis and segmentation of teleoperation tasks. IEEE Conference on Robotics and Automation, (ICRA) 2004 Apr;3:2918–2923. Vol.3. [Google Scholar]
- 5.Kragic D, Marayong P, Li M, Okamura AM, Hager GD. Human-Machine Collaborative Systems for Microsurgical Applications. The International Journal of Robotics Research. 2005 Sep;24:731–741. [Google Scholar]
- 6.Yu W, Alqasemi R, Dubey R, Pernalete N. Telemanipulation Assistance Based on Motion Intention Recognition. IEEE Conference on Robotics and Automation, (ICRA) 2005 Apr;:1121–1126. [Google Scholar]
- 7.Anderson S, Peters S, Iagnemma K, Overholt J. Semi-Autonomous Stability Control and Hazard Avoidance for Manned and Unmanned Ground Vehicles. The 27th Army Science Conference. 2010:1–8. [Google Scholar]
- 8.Weber C, Nitsch V, Unterhinninghofen U, Farber B, Buss M. Position and force augmentation in a telepresence system and their effects on perceived realism. EuroHaptics conference, 2009 and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems World Haptics 2009 Third Joint. 2009 Mar;:226–231. [Google Scholar]
- 9.Muelling K, Venkatraman A, Valois JS, Downey J, Weiss J, Javdani S, Hebert M, Schwartz AB, Collinger JL, Bagnell JA. Autonomy Infused Teleoperation with Application to BCI Manipulation. arXiv:1503.05451 [cs] 2015 Mar; arXiv: 1503.05451. [Google Scholar]
- 10.Kim DJ, Hazlett-Knudsen R, Culver-Godfrey H, Rucks G, Cunningham T, Portee D, Bricout J, Wang Z, Behal A. How Autonomy Impacts Performance and Satisfaction: Results From a Study With Spinal Cord Injured Subjects Using an Assistive Robot. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans. 2012 Jan;42:2–14. [Google Scholar]
- 11.Wu W, Gao Y, Bienenstock E, Donoghue JP, Black MJ. Bayesian Population Decoding of Motor Cortical Activity Using a Kalman Filter. Neural Computation. 2006 Jan;18:80–118. doi: 10.1162/089976606774841585. [DOI] [PubMed] [Google Scholar]
- 12.Gilja V, Nuyujukian P, Chestek CA, Cunningham JP, Yu BM, Fan JM, Churchland MM, Kaufman MT, Kao JC, Ryu SI, Shenoy KV. A high-performance neural prosthesis enabled by control algorithm design. Nature Neuroscience. 2012 Dec;15:1752–1757. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Golub MD, Yu BM, Schwartz AB, Chase SM. Motor cortical control of movement speed with implications for brain-machine interface control. Journal of Neurophysiology. 2014 Apr; doi: 10.1152/jn.00391.2013. jn.00391.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yu BM, Kemere C, Santhanam G, Afshar A, Ryu SI, Meng TH, Sahani M, Shenoy KV. Mixture of Trajectory Models for Neural Decoding of Goal-Directed Movements. Journal of Neurophysiology. 2007 May;97:3763–3780. doi: 10.1152/jn.00482.2006. [DOI] [PubMed] [Google Scholar]
- 15.Shanechi MM, Williams ZM, Wornell GW, Hu RC, Powers M, Brown EN. A Real-Time Brain-Machine Interface Combining Motor Target and Trajectory Intent Using an Optimal Feedback Control Design. PLoS ONE. 2013 Apr;8:e59049. doi: 10.1371/journal.pone.0059049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Corbett EA, Perreault EJ, Kording KP. Decoding with limited neural data: a mixture of time-warped trajectory models for directional reaches. Journal of neural engineering. 2012 Jun;9:036002. doi: 10.1088/1741-2560/9/3/036002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Srinivasan L, Eden UT, Willsky AS, Brown EN. A State-Space Analysis for Reconstruction of Goal-Directed Movements Using Neural Signals. Neural Computation. 2006 Aug;18:2465–2494. doi: 10.1162/neco.2006.18.10.2465. [DOI] [PubMed] [Google Scholar]
- 18.Kemere C, Shenoy K, Meng T. Model-based neural decoding of reaching movements: a maximum likelihood approach. IEEE Transactions on Biomedical Engineering. 2004 Jun;51:925–932. doi: 10.1109/TBME.2004.826675. [DOI] [PubMed] [Google Scholar]
- 19.Kang X, Sarma S, Santaniello S, Schieber M, Thakor N. Task-Independent Cognitive State Transition Detection From Cortical Neurons During 3-D Reach-to-Grasp Movements. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2015 Jul;23:676–682. doi: 10.1109/TNSRE.2015.2396495. [DOI] [PubMed] [Google Scholar]
- 20.Kemere C, Santhanam G, Yu BM, Afshar A, Ryu SI, Meng TH, Shenoy KV. Detecting Neural-State Transitions Using Hidden Markov Models for Motor Cortical Prostheses. Journal of Neurophysiology. 2008 Oct;100:2441–2452. doi: 10.1152/jn.00924.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu W, Black M, Mumford D, Gao Y, Bienenstock E, Donoghue J. Modeling and decoding motor cortical activity using a switching Kalman filter. IEEE Transactions on Biomedical Engineering. 2004 Jun;51:933–942. doi: 10.1109/TBME.2004.826666. [DOI] [PubMed] [Google Scholar]
- 22.Aggarwal V, Mollazadeh M, Davidson AG, Schieber MH, Thakor NV. State-based decoding of hand and finger kinematics using neuronal ensemble and LFP activity during dexterous reach-to-grasp movements. Journal of Neurophysiology. 2013 Jun;109:3067–3081. doi: 10.1152/jn.01038.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McMullen D, Hotson G, Katyal K, Wester B, Fifer M, McGee T, Harris A, Johannes M, Vogelstein R, Ravitz A, Anderson W, Thakor N, Crone N. Demonstration of a Semi-Autonomous Hybrid Brain-Machine Interface using Human Intracranial EEG, Eye Tracking, and Computer Vision to Control a Robotic Upper Limb Prosthetic. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2014 doi: 10.1109/TNSRE.2013.2294685. vol Early Access Online. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Katyal K, Johannes M, Kellis S, Aflalo T, Klaes C, McGee T, Para M, Shi Y, Lee B, Pejsa K, Liu C, Wester B, Tenore F, Beaty J, Ravitz A, Andersen R, McLoughlin M. A collaborative BCI approach to autonomous control of a prosthetic limb system. 2014 IEEE International Conference on Systems, Man and Cybernetics (SMC) 2014 Oct;:1479–1482. [Google Scholar]
- 25.Kim H, Biggs J, Schloerb DW, Carmena J, Lebedev M, Nicolelis M, Srinivasan M. Continuous shared control for stabilizing reaching and grasping with brain-machine interfaces. IEEE Transactions on Biomedical Engineering. 2006;53(6):1164–1173. doi: 10.1109/TBME.2006.870235. [DOI] [PubMed] [Google Scholar]
- 26.Ijspeert A, Nakanishi J, Schaal S. Movement imitation with nonlinear dynamical systems in humanoid robots. IEEE Conference on Robotics and Automation, (ICRA) 2002;2:1398–1403. [Google Scholar]
- 27.Murphy KP. tech rep. Compaq Cambridge Research Laboratory; Cambridge, MA: 1998. Switching Kalman Filters. [Google Scholar]
- 28.Ijspeert AJ, Nakanishi J, Hoffmann H, Pastor P, Schaal S. Dynamical Movement Primitives: Learning Attractor Models for Motor Behaviors. Neural Computation. 2012 Nov;25:328–373. doi: 10.1162/NECO_a_00393. [DOI] [PubMed] [Google Scholar]
- 29.Wan E, Van Der Merwe R. The unscented Kalman filter for nonlinear estimation. Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000 ASSPCC The IEEE 2000. 2000:153–158. [Google Scholar]
- 30.Rouse AG, Schieber MH. Spatiotemporal distribution of location and object effects in reach-to-grasp kinematics. Journal of Neurophysiology. 2015 Oct; doi: 10.1152/jn.00686.2015. jn.00686.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Muelling K, Kober J, Kroemer O, Peters J. Learning to select and generalize striking movements in robot table tennis. The International Journal of Robotics Research. 2013 Mar;32:263–279. [Google Scholar]
- 32.Taylor DM, Tillery SIH, Schwartz AB. Direct Cortical Control of 3d Neuroprosthetic Devices. Science. 2002 Jun;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- 33.Mazor E, Averbuch A, Bar-Shalom Y, Dayan J. Interacting multiple model methods in target tracking: a survey. IEEE Transactions on Aerospace and Electronic Systems. 1998 Jan;34:103–123. [Google Scholar]
- 34.Doucet A, Freitas ND, Gordon NJ. Sequential Monte Carlo Methods in Practice Series Statistics For Engineering and Information Science. 2001 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.