Generation and analysis of clinically relevant breast imaging x‐ray spectra

Abstract

Purpose

The purpose of this work was to develop and make available x‐ray spectra for some of the most widely used digital mammography (DM), breast tomosynthesis (BT), and breast CT (bCT) systems in North America.

Methods

The Monte Carlo code MCNP6 was used to simulate minimally filtered (only beryllium) x‐ray spectra at 8 tube potentials from 20 to 49 kV for DM/BT, and 9 tube potentials from 35 to 70 kV for bCT. Vendor‐specific anode compositions, effective anode angles, focal spot sizes, source‐to‐detector distances, and beryllium filtration were simulated. For each 0.5 keV energy bin in all simulated spectra, the fluence was interpolated using cubic splines across the range of simulated tube potentials to produce spectra in 1 kV increments from 20 to 49 kV for DM/BT and from 35 to 70 kV for bCT. The HVL of simulated spectra with conventional filtration (at 35 kV for DM/BT and 49 kV for bCT) was used to assess spectral differences resulting from variations in: (a) focal spot size (0.1 and 0.3 mm IEC), (b) solid angle at the detector (i.e., small and large FOV size), and (c) geometrical specifications for vendors that employ the same anode composition.

Results

Averaged across all DM/BT vendors, variations in focal spot and FOV size resulted in HVL differences of 2.2% and 0.9%, respectively. Comparing anode compositions separately, the HVL differences for Mo (GE, Siemens) and W (Hologic, Philips, and Siemens) spectra were 0.3% and 0.6%, respectively. Both the commercial Koning and prototype “Doheny” (UC Davis) bCT systems utilize W anodes with a 0.3 mm focal spot. Averaged across both bCT systems, variations in FOV size resulted in a 2.2% difference in HVL. In addition, the Koning spectrum was slightly harder than Doheny with a 4.2% difference in HVL. Therefore to reduce redundancy, a generic DM/BT system and a generic bCT system were used to generate the new spectra reported herein. The spectral models for application to DM/BT were dubbed the Molybdenum, Rhodium, and Tungsten Anode Spectral Models using Interpolating Cubic Splines (MASMICS_{M ‐T}, RASMICS_M‐T , and TASMICS_M‐T ; subscript “M‐T” indicating mammography and tomosynthesis). When compared against reference models (MASMIP_M , RASMIP_M , and TASMIP_M ; subscript “M” indicating mammography), the new spectral models were in close agreement with mean differences of 1.3%, −1.3%, and −3.3%, respectively, across tube potential comparisons of 20, 30, and 40 kV with conventional filtration. TASMICS _{b CT} ‐generated bCT spectra were also in close agreement with the reference TASMIP model with a mean difference of −0.8%, across tube potential comparisons of 35, 49, and 70 kV with 1.5 mm Al filtration.

Conclusions

The Mo, Rh, and W anode spectra for application in DM and BT (MASMICS_M‐T , RASMICS_M‐T , and TASMICS_M‐T ) and the W anode spectra for bCT (TASMICS_bCT ) as described in this study should be useful for individuals interested in modeling the performance of modern breast x‐ray imaging systems including dual‐energy mammography which extends to 49 kV. These new spectra are tabulated in spreadsheet form and are made available to any interested party.

1. Introduction

Tabulated or computer‐generated x‐ray spectra are useful for computer simulations pertaining to modeling of beam shaping filter performance,^{1, 2} imaging performance modeling,^{3, 4, 5, 6} validation of x‐ray spectral measurements,^{7, 8, 9} radiation dose,^{10, 11} modeling of photon counting spectral/dual‐energy imaging systems,^{8, 12, 13, 14} and many other applications. Recently, a tungsten anode spectral model using interpolating cubic splines (TASMICS¹⁵) was proposed to update the previous tungsten anode spectral model using interpolating polynomials (TASMIP¹⁶). While the TASMIP model was based upon experimentally measured x‐ray spectra for a CT x‐ray tube, the TASMICS spectral model was generated from Monte Carlo‐based calculations of x‐ray spectra using a conventional CT x‐ray tube design and acquisition geometry. TASMICS is capable of producing essentially unfiltered spectra with 0.5 keV energy resolution, and significantly extends the range of tube potentials for available spectra — overcoming the limitations of the TASMIP model.

Although tungsten (W) has become the anode material of choice for most modern breast imaging applications, molybdenum (Mo) and rhodium (Rh) anodes are still used as well. The Hologic Selenia Dimensions combined digital mammography (DM) and breast tomosynthesis (BT) system uses only a W anode with 50 μm Rh or 50 μm silver (Ag) filtration in mammography acquisition mode and 700 μm aluminum (Al) filtration in BT mode. The Philips MicroDose multislit scanning DM system also uses a W anode, but with 500 μm Al filtration. In comparison, the GE Senographe DM system uses both a Mo and Rh anode with 30 μm Mo or 25 μm Rh as the filtration materials. The Siemens Mammomat Inspiration combined DM/BT system uses a W anode with 50 μm Rh or a Mo anode with 30 μm Mo or 25 μm Rh filtration in DM acquisition mode and only W/Rh (50 μm) in BT mode. The specifications regarding target/filter combinations were obtained directly from the vendors via personal communication for the purpose of this work.

In addition to the DM and BT x‐ray imaging modalities, dedicated cone‐beam breast computed tomography (bCT) is an emerging technology in breast cancer detection most importantly because it overcomes the issue of tissue superposition found in DM and BT. The FDA recently approved a bCT system for diagnostic imaging (Koning Corporation, Rochester, NY, USA) that utilizes a W anode with Al filtration. A prototype bCT scanner “Doheny” developed at UC Davis also utilizes a W anode, and in addition to Cu filtration a few other filter strategies are currently in development.

Over the years many different methods for x‐ray spectra estimations have been presented.^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26} To the best of our knowledge, only two of these previously reported methods are focused specifically on mammography x‐ray spectra and offer both a range of tube potentials and different target/filter combinations. IPEM report no. 78 which is based on a semiempirical model provides mammographic spectra from 25 kV to 32 kV for Mo and Rh anodes, but the spectra are provided for specific target/filter combinations.¹⁷ The report also provides unattenuated W anode spectra, but for a minimum tube potential of 30 kV for application specifically in diagnostic radiology. Previous work from our group led to the development of the tungsten, molybdenum, and rhodium anode spectral models for mammography using interpolating polynomials²¹ (TASMIP_M, MASMIP_M, and RASMIP_M, respectively; subscript “M” indicating application to mammography); these models used measured spectra from mammography x‐ray tubes of the past and addressed tube potentials from 20 to 42 kV. New applications in breast imaging utilize tube potentials up to 49 kV with exotic filtration — primarily for dual‐energy contrast‐enhanced imaging applications.^{27, 28, 29, 30}

The two aforementioned mammographic spectral models do not address these higher tube potentials and modern target/filter combinations. In addition, no x‐ray spectral model currently exists specifically for bCT. Given the recent FDA approval for the Koning Corp. bCT scanner, a spectral model which addresses this new modality is needed. bCT scanners operate at higher tube potentials up to 49 kV for the Koning scanner and up to 70 kV for Doheny, because the x rays must travel through greater tissue thicknesses than in DM or BT, therefore requiring higher beam energy to maintain high SNR^{31, 32} at low‐dose levels.

X‐ray spectra based upon the most widely used breast imaging systems in North America were simulated using Monte Carlo techniques for a subset of tube potentials and interpolated to produce x‐ray spectra over the entire range of tube potentials spanning from 20 to 49 kV (in 1 kV increments) for DM/BT, and spanning from 35 to 70 kV (in 1 kV increments) for bCT. The methodology behind the previously reported cubic spline interpolation techniques (i.e., TASMICS¹⁵) was used to extend the raw breast imaging x‐ray spectra to a greater range of tube potentials.

2. Methods

2.A. Monte Carlo simulation geometry for breast x‐ray imaging systems

The Monte Carlo N‐Particle radiation transport code (MCNP6) was used to generate x‐ray spectra for four commercial digital mammography (DM) systems, two commercial digital breast tomosynthesis systems (BT), and both commercial and prototype cone‐beam breast CT (bCT) systems. The prototype Doheny bCT scanner was used in this work for comparing the estimated x‐ray spectra against the commercial Koning system. The effective anode angle, inherent beryllium filtration, source‐to‐detector distance (SDD), orientation of anode–cathode axis, and focal spot size for each vendor's imaging system were incorporated into the simulations. These technical specifications — some of which are proprietary information — were obtained directly from the vendors via personal communication for the purpose of this work.

A detailed description of the simulation geometry and physics is provided in Reference ¹. Only differences between the present simulations and those previously published will be mentioned here. Commercially available DM/BT systems use large (0.3 mm IEC) and small (0.1 mm IEC) x‐ray tube focal spot sizes complying with the International Electrotechnical Commission (IEC) 60336 safety standards. The bCT systems investigated in this work use only a 0.3 mm focal spot size. These focal spot size specifications were used to define the electron source geometry in the Monte Carlo simulations performed for this study.

Consistent with all DM/BT applications, the detector panel was oriented in the simulations with the short dimension parallel to the anode–cathode axis and the projected focal spot coincided with the cathode‐edge of the panel — centered in the long dimension.³³ This geometry results in lower x‐ray intensity on the anode side of the x‐ray field (heel effect) near the nipple of the breast and farthest away from the central ray in order to improve uniformity of the transmitted x rays through the breast. A similar x‐ray tube anode–cathode orientation with respect to the breast anatomy was used in the bCT simulations for the Koning scanner. In order to improve chest wall coverage, the Doheny bCT scanner utilizes an x‐ray tube that has reduced spacing between the focal spot on the anode and the tube housing end wall³⁴ (M‐1500, Varian Medical Systems, Salt Lake City, UT). This anode–cathode orientation allows for the x‐ray tube to be positioned closer to the chest wall of the patient and consequently results in very little heel effect present toward the nipple of the breast.

The breast does not cover the entire field‐of‐view (FOV) of the detector panels used in DM/BT and bCT systems. To assess the spectra incident upon the area of the detector panel typically covered by the breast during DM/BT acquisition, 45 cranial–caudal (CC) mammograms were converted to binary images, and the boundary of the compressed breast was outlined for each mammogram. These 45 CC mammograms were grouped into the largest 10% (N = 5) and smallest 10% (N = 5), with the remaining outlines (N = 35) defining the average breast shape (i.e., the trimmed mean). The measured outlines were then averaged within each group and the resulting rectangular areas were 18 cm × 12 cm, 25 cm × 14 cm, and 27 cm × 19 cm for the small, medium, and large breast sizes, respectively. To assess the spectra incident upon the area of the detector panel typically covered by the breast during bCT acquisition, the shape of the breast was approximated as 10, 14, and 18 cm diameter cylindrical phantoms with the breast length equal to 1.5 times the radius.³⁵ Using the known magnification factors of both the Koning and Doheny bCT scanners, the small, medium, and large detector FOVs covered by the breast were determined for the 10, 14, and 18 cm diameter phantoms, respectively. These FOV sizes were used to define the scoring plane in the Monte Carlo simulations.

2.B. Monte Carlo simulation of x‐ray spectra in MCNP6

The fluence in units of photons/cm²/source electron was tallied in MCNP6 and then converted to photons/mm²/mAs. Fluence tallies were simulated within the small, medium, and large detector FOVs for all breast x‐ray imaging systems of interest in this work. Energy bins were defined with a 0.5 keV energy width, starting at 1 keV, and centered at 1.25 keV, 1.75 keV, etc. The highest energy bin was held at the maximum electron energy for the corresponding spectrum (e.g., 29.5–30.0 keV for a 30 kV spectrum). For ease of discussion in this manuscript, each 0.5 keV energy bin is termed as the upper boundary of that particular energy bin (e.g., the lowest energy bin centered at 1.25 keV, spanning from 1.0 keV to 1.5 keV, is referred to as 1.5 keV).

Monte Carlo simulations of x‐ray spectra were run for tube potentials of 20, 25, 30, 35, 40, 45, 47, and 49 kV for the DM/BT system geometries and 35, 40, 45, 50, 55, 60, 64, 67, and 70 kV for the bCT system geometries. The number of simulated source electrons was increased until each energy bin, containing photon fluence values above 5% of the peak bremsstrahlung fluence, produced a relative error < 1.0%. The eprdata12 photoatomic library was used in MCNP6 by specifying the cross‐section identifier .12p on the material card of the input file. This new library in MCNP6 allows for a complete description of photon‐induced atomic relaxation — addressing the full detailed relaxation cascade and not just the average K‐shell and L‐shell transitions as was the case with MCNPX and previous versions of MCNP.³⁶ It is well understood that MCNP inaccurately simulates electron‐induced characteristic x‐ray emission using condensed history (CH) electron transport physics, which is the default mode when the electron energy is above 1 keV.^{37, 38, 39} The CH method breaks down the electron's path into many small steps that are long enough to include many collisions in order for multiple scattering theories to be valid, but short enough so that for each step the mean energy loss is small. This ensures that the approximations introduced in the multiple scattering theories are also fulfilled.^{36, 40, 41, 42, 43, 44} The most recent version of MCNP (MCNP6) allows for the user to set an alternative method for electron transport physics known as the single‐event (SE) method, which simulates every electron collision separately and therefore is more accurate than the CH method at the cost of an increase in computation.^{36, 39} With this in mind, the present simulations in MCNP6 employ the single‐event method for electron transport physics at all simulated electron energies.

2.C. Spectral modeling using interpolating cubic splines

As described previously¹⁵, cubic splines were employed in this work to produce piecewise third‐order polynomial functions that could be used to fit the photon fluence values per energy bin as a function of tube potential. A built‐in MATLAB function spline was used to fit cubic splines for each simulated tube potential interval (e.g., 20–25 kV). All 96 cubic splines (i.e., 1 keV to 49 keV in 0.5 keV intervals) for the DM/BT simulations were evaluated at 1 kV tube potential intervals to produce a database of x‐ray spectra from 20 kV to 49 kV with 0.5 keV energy bin spacing. The three new spectral models were dubbed the Molybdenum, Rhodium, and Tungsten Anode Spectral Models using Interpolating Cubic Splines for mammography and tomosynthesis (MASMICS_M‐T, RASMICS_M‐T, and TASMICS_M‐T; subscript “M‐T” indicating application to mammography and tomosynthesis). In addition, 138 cubic splines (i.e., 1 keV to 70 keV in 0.5 keV intervals) for the bCT simulations were evaluated at 1 kV tube potential intervals to produce a database of x‐ray spectra from 35 kV to 70 kV with 0.5 keV energy resolution. This new spectral model was dubbed the Tungsten Anode Spectral Models using Interpolating Cubic Splines for breast CT (TASMICS_bCT; subscript “bCT” indicating application to breast CT). The acronym subscripts were used for these new spectral models to alleviate any confusion with the previously reported TASMICS model that was designed to generate generic x‐ray spectra from 20 to 640 kV.¹⁵

2.D. Comparison of clinically relevant breast imaging x‐ray spectra

For a fixed vendor and anode composition, both the FOV size and the choice of x‐ray tube focal spot size could potentially affect spectral shape as described in section 2.A. The mean difference (or mean overall difference as defined in previous work¹⁵) in half‐value layer (HVL) was used to assess differences in spectral quality resulting from differences in FOV size (small vs. large) and focal spot size (0.1 mm vs. 0.3 mm IEC). A tube potential of 35 kV was used for comparisons of DM/BT systems, and 49 kV was used for comparisons of bCT systems. A positive difference would indicate a higher HVL (in units of mm Al) for either the large FOV or the 0.1 mm focal spot size. The mean difference was also used to compare the HVL for different vendors that employ the same anode composition.

2.E. X‐ray spectra comparisons to previous studies

The photon fluence per energy bin for spectra generated using MASMICS_M‐T, RASMICS_M‐T, and TASMICS_M‐T was compared against previously reported Mo, Rh, and W anode spectral models (MASMIP_M, RASMIP_M, and TASMIP_M) which addressed tube potentials from 20 to 42 kV.²¹ The raw x‐ray spectra used in these reference models were physically measured using x‐ray tubes with approximately 0.5 mm of Be in the x‐ray tube port, but no other added filtration was used. A high‐purity germanium detector was used for those measurements and calibrated with 100 eV energy bins. All spectra were then rebinned into 0.5 keV intervals. MASMIP_M and TASMIP_M energy bins started at 0.5 keV and were centered at 0.5, 1.0, 1.5,…, 42 keV. RASMIP_M energy bins started at 0.2 keV and were centered at 0.2, 0.7, 1.2,…, 41.7 keV in order to best highlight the characteristic x‐ray emission lines from the respective anode materials. Both choices of energy binning are different than the present MC simulations and direct comparison using a simple linear interpolation may introduce systematic bias. To make fair comparisons between the MC simulated and reference DM / BT x‐ray spectra, the MC simulations were repeated for tube potentials of 20, 30, and 40 kV and all three anode compositions with energy binning that matched the reference models. This was done only for comparison and was not used to generate the new spectral model described in section 2.B. /BT comparisons with the reference models, the reference spectra were mathematically filtered with 3 mm polycarbonate to account for the compression paddle and with the vendor‐specified amount of added filtration for that specific target/filter combination. The DM/BT simulated spectra were also mathematically filtered with 3 mm polycarbonate, but the amount of added filtration was adjusted to match the calculated HVL of the corresponding reference spectrum. This method for comparison was used to match beam quality to the extent possible which is common practice in modeling x‐ray spectra for a specific clinical system or experimental setup.

For comparison of the bCT x‐ray spectra simulations presented in this work, the CT version of TASMIP was used which was derived from measured x‐ray spectra of a CT x‐ray tube and addresses tube potentials from 30 kV to 140 kV with ~1.6 mm Al of inherent filtration.¹⁶ These TASMIP x‐ray spectra were tabulated in 1 keV energy bins from 10 keV to 140 keV and the bins were centered at 10, 11,…, 140 keV. To again alleviate potential systematic bias introduced by interpolation of the energy bins, MC simulations were repeated — matching the energy binning of TASMIP for the 35, 49, and 70 kV x‐ray spectra. For the simulated bCT comparisons with the reference model (TASMIP), TASMIP‐generated spectra — which already contain ~1.6 mm of Al filtration — were first mathematically unfiltered with 0.1 mm of Al to provide an equivalent added filtration of 1.5 mm Al (specified for the Koning system) and then filtered with 2 mm polycarbonate to account for the protective cup on the Koning system. The bCT‐simulated spectra were also mathematically filtered with 2 mm polycarbonate, but the amount of added Al filtration was adjusted to match the calculated HVL of the corresponding TASMIP spectrum. This method for comparison was again used to match beam quality to the extent possible.

The mathematical filtration performed throughout this study used x‐ray mass attenuation coefficients from the NIST XCOM: Photon Cross Sections Database.⁴⁵ All spectra used for comparisons were also normalized to unity air kerma to match beam quantity as described in previous work.¹⁵ To quantify the comparisons described above, the mean difference in photon fluence per energy bin was calculated over the energy bins containing fluence values above 2% of the peak fluence in each simulated spectrum. This approach reduces the impact of quantum noise in the difference measures where the discrepancies may be large as defined by percent difference but the actual error is small in terms of absolute fluence. The mean difference across all energy bins was reported for each kV comparison, and as an aggregate for all compared kV permutations for each model comparison. X‐ray spectra shown in the present work are plotted using the stairstep graph function in MATLAB, which allows for a more accurate representation of the 0.5 keV energy bin widths relative to the absolute fluence values in each simulated spectrum. For x‐ray spectra that contain relatively large characteristic emission lines in the tube potential range of interest in this work, comparisons were plotted with a log scale on the photon fluence axis in order to more easily visualize the spectral comparisons.

Polyenergetic normalized mean glandular dose coefficients (pDgNs) were also calculated by spectrally weighting previously reported monoenergetic DgN coefficients “DgN(E)” for mammography¹¹ and breast CT³⁵ to evaluate spectrum‐related differences in glandular dose coefficient calculations. The simulated and reference spectra used for spectral comparisons, with equivalent HVL as described above, were also used for producing these pDgN coefficients. A breast phantom with a 6 cm compressed thickness and composed of a homogeneous mixture of 50% fibroglandular glandular tissue was used for the DM/BT spectral comparisons. A 14 cm cylindrical breast composed of a homogeneous mixture of 50% fibroglandular glandular tissue was used for the bCT spectral comparisons.

In addition to direct spectral comparisons, the HVL and relative fluence through 8 cm (DM/BT) and 18 cm (bCT) of 17% glandular breast tissue was also compared between the simulated and reference spectra. However, for these comparisons, both the reference and simulated spectra were filtered with polycarbonate (3 mm for DM/BT and 2 mm for bCT) and the exact amount of vendor‐specified filtration for that specific target/filter combination. This method for comparison is notably different then the direct spectral comparisons described above which were normalized to equivalent HVL and would therefore force agreement when comparing HVL and relative fluence. The calculated HVLs were compared between the simulated and reference spectra and were also compared against measured HVLs for the DM/BT, and bCT systems described in this work. Measured HVLs were either obtained via personal correspondence with the manufacturers or taken from previously measured values at our institution.³³

3. Results

3.A. Comparison of clinically relevant breast imaging x‐ray spectra

The Hologic, GE, and Siemens mammography systems have the option of a small (0.1 mm IEC) or large (0.3 mm IEC) focal spot size. Figure 1(a) qualitatively demonstrates that with only minimal filtration (1.0 mm Be), the difference in HVL for the Siemens W anode spectrum for a small and large focal spot size is minimal (1.1%). The Siemens system uses the same effective anode angle for the large and small focal spot sizes — justifying this negligible difference. In comparison, the GE system uses an effective anode angle that is 9° greater for the large focal spot size compared to the small focal spot size. This difference in anode angle generates a harder x‐ray spectrum for the small focal spot size — a consequence of the anode heel effect — as shown by the GE minimally filtered Rh spectrum at 35 kV in Fig. 1(c) with a difference in HVL of 19.7%. However, after applying the vendor‐specified filtration (25 μm Rh), the HVL for the small focal spot is only 3.8% greater than for the large focal spot (Fig. 1(d)). Similar results were seen for the Mo/Mo (30 μm) spectrum at 35 kV on the GE system (2.9% difference in HVL after Mo filtration was applied) because it has a dual‐track anode and therefore only the source‐to‐detector distances are slightly different for the different anode compositions. The Hologic system also uses a larger effective anode angle for the large focal spot size, but it is only 6° greater relative to the 9° difference utilized on the GE system. This is reflected in the 3.3% difference in HVL when comparing focal spot sizes for the Hologic W spectrum at 35 kV with 50 μm of Ag filtration. For a fixed anode composition and medium FOV size at the detector, the HVL for the small focal spot size is 2.2% higher than the large focal spot size averaged across all vendors after vendor‐specified filtration was applied.

Figure 1.

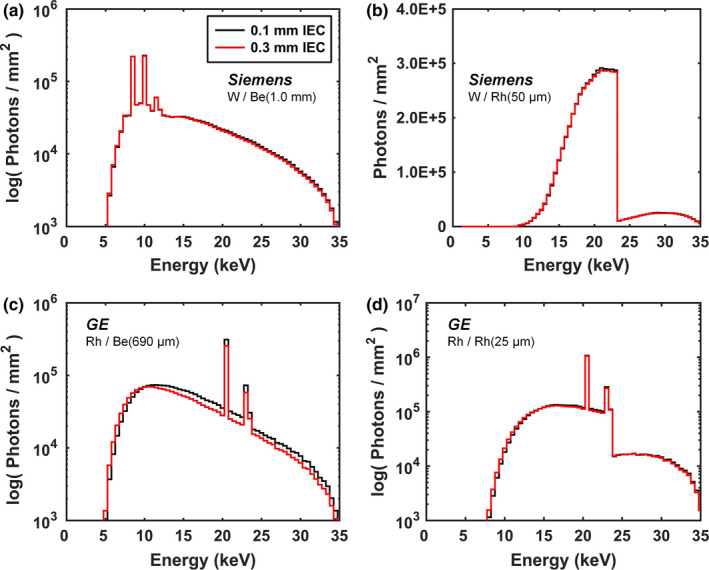
Example comparisons of Monte Carlo simulation results for the small (0.1 mm IEC) and large (0.3 mm IEC) focal spot sizes. Siemens W spectra at 35 kV (a) minimally filtered, and (b) filtered with 50 μm Rh are shown. GE Rh spectra at 35 kV (c) minimally filtered, and (d) filtered with 25 μm Rh are also shown. All comparisons clearly demonstrate that differences in the focal spot size have no significant impact on the resulting spectral shape once conventional filtration is applied. The medium‐sized FOV at the detector was used for all focal spot size comparisons and all spectra are normalized to unity air kerma. A log scale is used for the photon fluence axis when characteristic emission lines are present (a), (c), and (d) in order to more easily depict spectral comparisons. [Color figure can be viewed at wileyonlinelibrary.com]

Example spectral comparisons of the small and large FOV at the detector for the GE Mo anode and Koning W anode spectra are shown in Fig. 2 for a large focal spot size. The large FOV results in slightly harder x‐ray spectra when the spectra are left minimally filtered. The HVL for the large FOV is 3.7% and 1.6% higher than the small FOV for the GE (Fig. 2(a)) and Koning (Fig. 2(c)) comparison, respectively — a consequence of the anode heel effect. Similar results were seen for the GE Rh anode, Siemens Mo and W anodes, Hologic W anode, Philips W anode, and Doheny W anode, with differences of 3.9%, 3.8%, 1.2%, 1.1%, 1.1%, and −1.4%, respectively. The lower HVL for the large FOV relative to the small FOV on Doheny is a result of relatively minimal heel effect present for the x‐ray tube design and orientation used in this bCT system as described in section 2.A. After applying conventional filtration, the differences in HVL are minimal (< 2.4% across all comparisons) as shown for example in Figs. 2(b) and 2(d).

Figure 2.

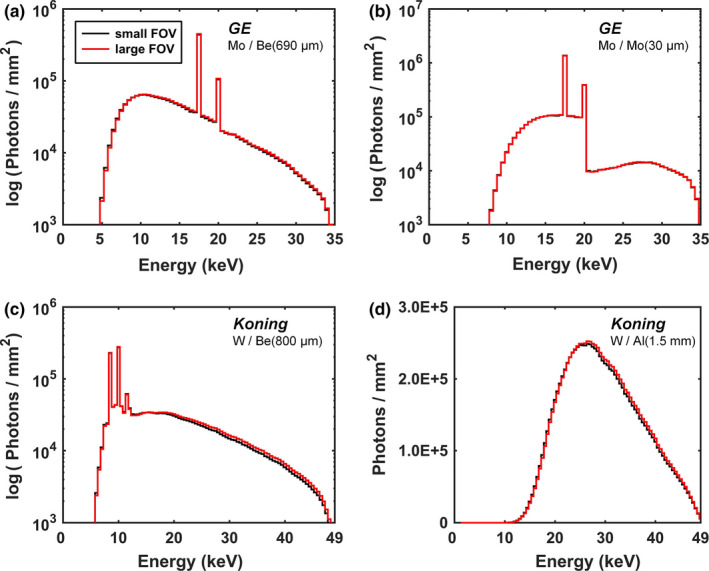
Example comparisons of Monte Carlo simulation results for differences in the solid angle at the detector for a large and small breast size. GE Mo spectra at 35 kV (a) minimally filtered, and (b) filtered with 30 μm Mo are shown. Koning W spectra for bCT at 49 kV (c) minimally filtered, and (d) filtered with 1.5 mm Al are also shown. All comparisons clearly demonstrate that differences in the solid angle at the detector for a large and small breast size has no significant impact on the resulting spectral shape after conventional filtration is applied. The large focal spot size was used for all FOV comparisons and all spectra are normalized to unity air kerma. A log scale is used for the y‐axis when characteristic emission lines are present (a–c) in order to more easily depict spectral comparisons. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 3 shows spectral comparisons from different vendors with the same anode composition. With only minimal filtration (Fig. 3(a)), the HVL for the Siemens system is 4.2% higher when compared to the GE system for the Mo anode. In addition, the HVL for the most penetrating W anode spectrum (Siemens) is 1.9% higher than the least penetrating W anode spectrum (Hologic) as shown in Fig. 3(c). The HVL for the Koning bCT system is 8.1% higher compared to the Doheny with minimal filtration at 49 kV. After applying vendor‐specified filtration to the Mo and W anode DM/BT spectra the HVLs were nearly equivalent with a difference of 0.3% and 0.6%, respectively, as shown qualitatively in Figs. 3(b) and 3(d). The HVL for the Koning system remained slightly higher than Doheny with a difference of 4.2% after conventional filtration was applied (Fig. 3(f)). This is a result of the two systems having opposite anode–cathode orientations. Only the GE system uses a Rh anode so no comparison was needed for this anode composition.

Figure 3.

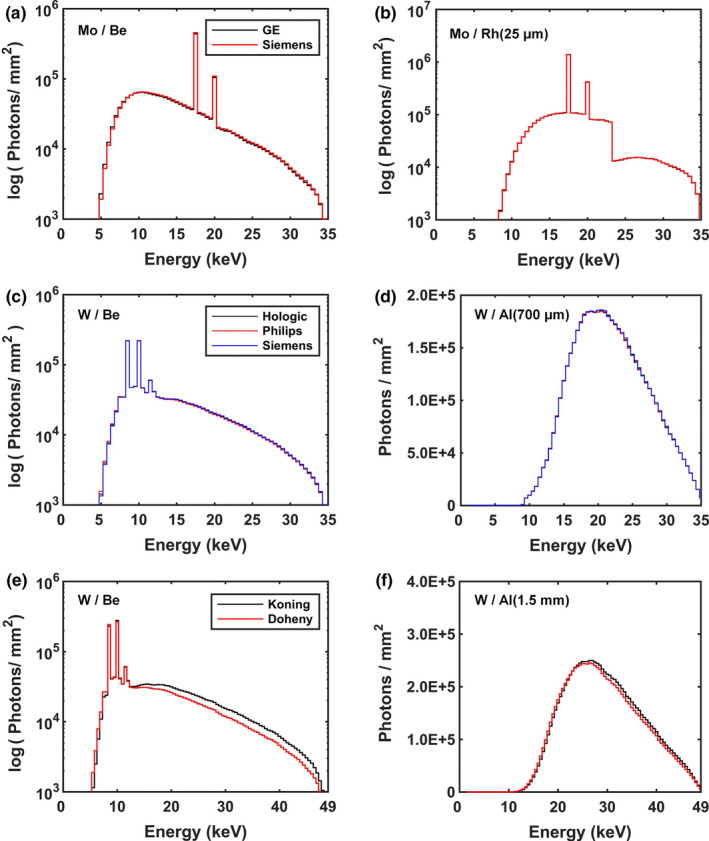
Example comparisons of Monte Carlo simulation results for different vendors employing the same target anode compositions. Mo spectra at 35 kV (a) minimally filtered, and (b) with 25 μm Rh for the Siemens and GE systems. W spectra at 35 kV (c) minimally filtered, and (d) filtered with 700 μm Al for the Hologic, Philips, and Siemens DM/BT systems. W spectra at 49 kV (e) minimally filtered, and (f) filtered with 1.5 mm Al for the Doheny and Koning bCT systems. The large focal spot and medium‐sized FOV at the detector was used for all comparisons and all spectra are normalized to unity air kerma. A log scale is used for the y‐axis when characteristic emission lines are present (a–c), (e) in order to more easily depict spectral comparisons. [Color figure can be viewed at wileyonlinelibrary.com]

Given the minimal differences in HVL resulting from different focal spot sizes (Fig. 1) and differences in the solid angle at the detector for a large and small breast size (Fig. 2) — after vendor‐specified filtration was applied — only the medium‐sized FOV at the detector and large focal spot size were used for the Monte Carlo simulations reported in the present work. In addition, the minimal difference in HVL across vendors that employ the same anode material (see Fig. 3) suggests that simplification is in order. To prevent superfluous x‐ray spectra tabulation and unnecessary complexity, a generic DM/BT system geometry with a large focal spot size and medium FOV at the detector was used in the Monte Carlo simulations necessary to generate the new spectral model for mammography and tomosynthesis (MASMICS_M‐T, RASMICS_M‐T, and TASMICS_M‐T). The system specifications are outlined in Table 1 and generally speaking represent the average across all vendor specifications. Similarly, the Koning system geometry with a large focal spot and medium FOV size was used in the Monte Carlo simulations necessary to generate the new spectral model for breast CT (TASMICS_bCT) as outlined in Table 1.

Table 1.

Digital mammography (DM), breast tomosynthesis (BT), and breast CT (bCT) system specifications used in the MCNP6 simulations for generation of the new spectral models

Modality	DM/DBT	bCT
Spectral model(s)	MASMICSM‐T RASMICSM‐T TASMICSM‐T	TASMICSbCT
Target composition(s)	M, Rh, W	W
Effective anode angle	22.4°	16.0°
Inherent filtration (mm Be)	0.77	0.80
Source‐to‐detector distance (mm)	668	923
Focal spot (mm IEC 60336)	0.3	0.3

3.B. X‐ray spectra comparisons to previous studies

Figure 4 displays the x‐ray spectra generated using the Monte Carlo methods described in this work in comparison to the reference spectra which were derived from measurements of mammography and CT x‐ray tubes of the past. The comparisons demonstrated satisfactory agreement with differences of < 7.6% across all models and several permutations of tube potentials. Table 2 outlines the comparisons for all spectral models. The simulated spectra required additional filtration beyond the filtration indicated in Fig. 4 that was applied to the reference spectra. These amounts are indicated in the fourth column of Table 2. A difference in location of the characteristic emission lines are observed in both the Mo and Rh anode comparisons shown in Figs. 4(a) and 4(b). For example, the K _α2 (17.37 keV) and K _α1 (17.48 keV) Mo anode characteristic emission lines would ideally fall within the energy bin spanning from 17.25–17.75 keV, centered at 17.5 keV. Figure 4(a) demonstrates that for the Monte Carlo‐based MASMICS_M‐T spectrum this is the result; however, for the MASMIP_M spectrum, the finite energy resolution of the physical detector system used to measure those spectra resulted in spectral broadening and therefore the K _α2 and K _α1 emission lines do not fall within a single energy bin. A similar result is seen for the Rh anode characteristic emission lines in Fig. 4(b). This phenomenon is a likely justification for why additional filtration (column 4 of Table 2) is needed to match the HVL of the simulated spectra with the references models. This additional filtration is also likely the reason why there is a disagreement in the spectra above the k‐edge of the filtration material as seen in Figs. 4(a) and 4(b). Despite these differences, the glandular dose (reported in pDgN) were observed to be in excellent agreement with differences < 3.3% across all models and kV permutations compared as shown in the last column of Table 2.

Figure 4.

Example comparisons of 30 kV x‐ray spectra generated using (a) MASMICS_M‐T, (b) RASMICS_M‐T, and (c) TASMICS_M‐T in comparison to reference spectra. (d) A 49 kV spectrum generated using TASMICS_bCT in comparison to the reference spectrum. All spectra were filtered with polycarbonate (3 mm for DM/BT and 2 mm for bCT). The reference spectra were also filtered with the exact amount of indicated filtration, and the simulated spectra were filtered with additional filtration to match the HVL of the corresponding reference spectra. The amount of additional filtration is indicated in Table 2. All spectra shown in figure are normalized to unity air kerma. A log scale is used for the y‐axis when characteristic emission lines are present (a) and (b) in order to more easily depict spectral comparisons. [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

X‐ray spectra comparison results with reference models: mean difference in photon fluence, additional filtration needed to match present spectra with reference models, and mean difference in glandular dose

Reference model target/filter	kV Compared	% Difference	Additional filtration (μm)	pDgN: % difference
MASMIPM Mo/Mo (30 μm)	20	7.2	4.3	1.5
	30	−4.3	7.1	−1.5
	40	−7.0	9.2	−3.3
	20, 30, 40	1.3	6.9	−1.1
RASMIPM Rh/Rh (25 μm)	20	1.2	3.6	0.2
	30	−1.6	6.1	−0.8
	40	−3.4	5.7	−1.2
	20, 30, 40	−1.3	5.1	−0.6
TASMIPM W/Al (700 μm)	20	−5.7	74.7	−1.4
	30	−0.9	129.5	−1.3
	40	−4.0	190.2	−1.6
	20, 30, 40	−3.3	131.5	−1.5
TASMIP W/Al (1.5 mm)	35	7.6	282.3	−1.8
	49	−1.7	429.0	−0.7
	70	−4.9	515.3	0.3
	35, 49, 70	−0.8	408.9	−0.7

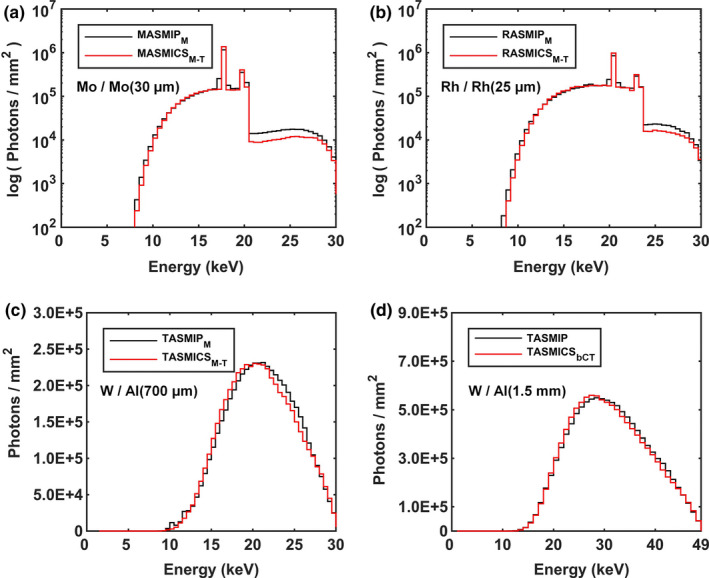
Figure 5 displays HVL comparisons as a function of tube potential for MASMICS_M‐T, RASMICS_M‐T, and TASMICS_M‐T relative to the reference spectral models with 3 mm polycarbonate and the exact amount of vendor‐specified filtration. The mean differences in HVL for MASMICS_M‐T‐generated spectra compared to the reference MASMIP_M model were −4.8%, −6.0%, and −5.4%, respectively, for the 20, 30, and 40 kV comparisons as shown in Fig. 5(a). A difference of −2.4% and 3.5% was observed when comparing the HVL calculated using MASMICS_M‐T and MASMIP_M, respectively, with the measured HVL at 30 kV. Calculated HVLs for RASMICS_M‐T generated spectra compared to the reference RASMIP_M model demonstrated mean differences of −5.1%, −9.0%, and −6.6%, respectively, for the 20, 30, and 40 kV comparisons as shown in Fig. 5(b). At 30 kV, the mean difference in HVL calculated using RASMICS_M‐T and RASMIP_M in comparison with measured values was −5.2% and 3.8%, respectively. The mean differences in HVL for TASMICS_M‐T generated spectra compared to the reference TASMIP_M model were −4.3%, −9.1%, and −13.7%, respectively, for the 20, 30, and 40 kV comparisons as shown in Fig. 5(c). Lastly, a difference of −2.4% and 6.9% was observed when comparing the HVL calculated using TASMICS_M‐T and TASMIP_M, respectively, with the measured HVL at 30 kV. The less penetrating simulated spectra require additional filtration to match the calculated HVL for the reference spectra as shown in column 4 of Table 2. Furthermore, HVLs calculated using the simulated 30 kV spectra are slightly lower than measured values with a mean difference of 5.0%, averaged across all model comparisons, and the HVLs calculated using the reference spectral models are slightly higher than measured values with a mean difference of 3.1%. In addition to HVL comparisons for spectra with identical filtration, comparisons of the fluence attenuation as the x‐ray spectra propagate through 17% glandular breast tissue are shown in Fig. 6. The difference in relative fluence monotonically increases with increasing breast thickness, and the largest discrepancies were observed for the W anode comparisons. Theses finding are consistent with the HVL results described above where the largest difference in HVL was observed for the TASMICS_M‐T comparisons. Together these results provide a detailed understanding of the comparisons between the simulated DM/BT spectra with reference spectra for identical filtration. However, it is common practice in the medical physics community to model spectra for a specific clinical system or experimental setup by matching beam quality (i.e., measured HVL) and therefore these HVL and relative fluence differences would become negligible.

Figure 5.

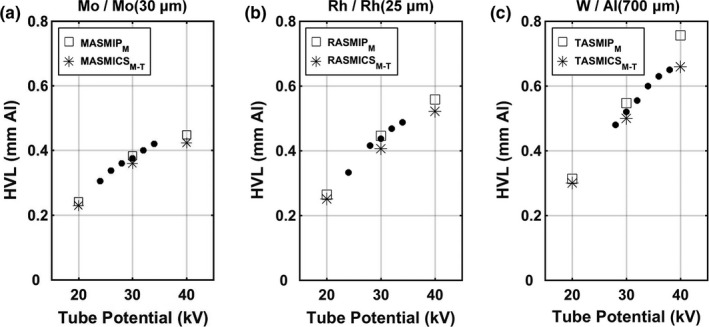
Half‐value layer (HVL) as a function of tube potential for comparisons of (a) MASMICS_M‐T, (b) RASMICS_M‐T, and (c) TASMICS_M‐T with reference spectra. Measured HVLs (solid black circle) are also shown for comparison. All spectra used for the HVL calculations are mathematically filtered with a 3 mm thick polycarbonate compression paddle and the exact indicated added filtration. The Mo and W anode HVL measurements represent an average of several evaluations on various mammography systems at the UC Davis Health System and are generally within ± 0.05 mm of the values shown.³³ The Rh anode HVL measurements were obtained via personal correspondence.

Figure 6.

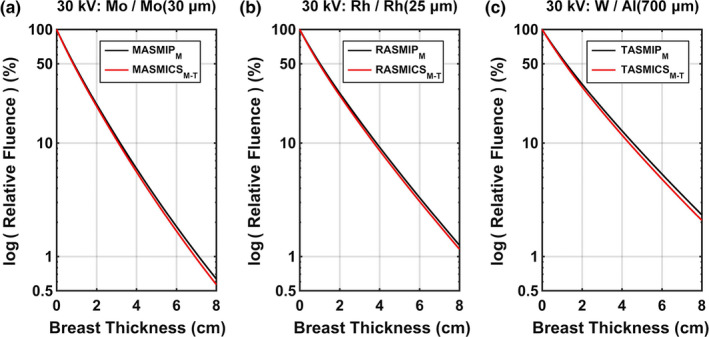
Comparison of transmission curves on a log scale as a function of thickness through 17% glandular breast tissue for the 30 kV spectra. MASMICS_M‐T, RASMICS_M‐T, and TASMICS_M‐T comparisons demonstrated differences in relative fluence at 2 cm breast thickness of −4.3%, −5.0%, and −5.8%, respectively. These differences increased to −11.4%, −8.0%, and −11.2%, respectively, at 8 cm breast thickness. All spectra are mathematically filtered with a 3 mm thick polycarbonate compression paddle and the exact amount of indicated filtration. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 7(a) displays HVL comparisons as a function of tube potential for TASMICS_bCT and the reference TASMIP model with 2 mm polycarbonate to compensate for the protective cup and 1.5 mm Al filtration. HVL measurements for several bCT systems are also shown using solid markers for the commercial Koning system (obtained via personal communication), a clinical prototype similar to the Koning system (Sechopoulos et al.⁴⁶), and a clinical prototype at UC Davis “Doheny”. HVL measurements for the commercial and prototype Koning systems were reported to contain the attenuation from 2 mm polycarbonate for the protective cup and 1.5 mm Al filtration. For comparison, the HVL measurements for the Doheny scanner also contain 2 mm polycarbonate and 1.5 mm Al filtration. Mean differences in HVL for TASMICS_bCT‐generated spectra compared to the reference TASMIP model were −8.8%, −12.7%, and −16.3%, respectively, for the 35, 49, and 70 kV comparisons. In addition, a difference of −19.3% and −8.4% was observed when comparing the HVL calculated using TASMICS_bCT and TASMIP, respectively, with the measured HVL on the commercial Koning system at 49 kV. When comparing against HVL measurements at 49 kV on the prototype Koning system from Sechopoulos⁴⁶, differences of −9.5% and 2.8% were observed for TASMICS_bCT and TASMIP comparisons, respectively. Sechopoulos et al. reported that the known thickness of the actual aluminum filter installed in their bCT system was within 1.5% of the modeled aluminum filter thickness of 1.576 mm. If the simulated and reference spectra compared in the present work were filtered with this amount of Al, the HVL differences would be −7.0% and 5.3%, respectively, relative to the measurements of Sechopoulos et al.⁴⁶ Therefore, care must be taken when interpreting these results given the known uncertainty in the actual filter thickness.

Figure 7.

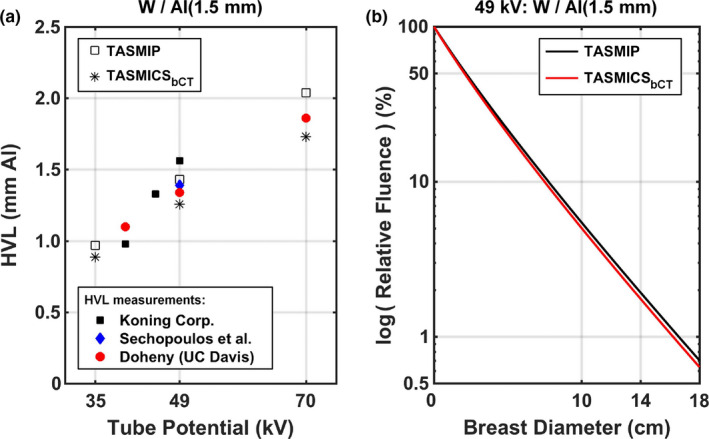
Spectral characteristics for TASMICS_bCT in comparison to the reference TASMIP spectral model. (a) HVL comparisons as a function of tube potential. All TASMIP and TASMICS_bCT spectra were mathematically filtered with 2 mm polycarbonate to compensate for the protective cup and exactly 1.5 mm Al as reported for the Koning system. Measured values from Koning Corp. (personal communication), Sechopoulos et al. (prototype Koning system), and a prototype bCT scanner “Doheny” from UC Davis are also shown using solid markers. (B) Comparison of relative fluence curves on a log scale as a function of diameter through 17% glandular breast tissue for the 49 kV spectrum with the same amount of filtration as in Fig. 7(a). [Color figure can be viewed at wileyonlinelibrary.com]

Lastly, compared against the HVL measurements at 49 kV on the prototype Doheny bCT system, differences of −6.1% and 6.7% were observed for TASMICS_bCT and TASMIP comparisons, respectively. Figure 7(b) demonstrates relative fluence curve comparisons as function of breast diameter through 17% glandular breast tissue at 49 kV. Consistent with the HVL results shown in Fig. 7(a), x‐ray spectra generated using the reference TASMIP model results in a more penetrating x‐ray beam than x‐ray spectra generated using TASMICS_bCT. The differences in relative fluence were −8.4% and −9.9% for breast diameters of 10 and 18 cm, respectively.

4. Discussion

Although there are some discrepancies in raw (minimally filtered) x‐ray spectra, especially in the low energy range of the x‐ray spectrum (< 10 keV), when clinically realistic added filtration is included the spectra tend to converge. The charge of American Association of Physicists in Medicine (AAPM) Task Group 195 was to create reference MC‐based databases for comparison and validation of MC results between different users.³⁷ In this report they noted a relatively large discrepancy in MC codes at low photon energies (< 3 keV for the Mo spectrum and < 12 keV for the W spectrum) due to the high sensitivity of differences in electron interaction physics models between the codes.³⁷ All commercially available breast x‐ray imaging systems are designed such that they fully attenuate L‐shell characteristic x‐rays so these differences do not have a significant impact on breast imaging research. Furthermore, the more detailed electron transport physics in MCNP (i.e., the “single‐event” method) was utilized in the present MC simulations to alleviate the known inaccuracies in MCNP using the default “condensed history” electron transport physics method.

Significant differences exist in the deployment of x‐ray sources by various vendors, even for the same anode material. These differences include the effect of anode angle, orientation of the cathode–anode axis, and the composition and thickness of added filtration materials. Figures 3(a), 3(c), and 3(e) illustrate these differences for the minimally filtered spectra. However, when realistic clinical levels of added filtration are added to the raw spectra for the same tube potential and target/filter combination, the differences in spectra produced by different vendor's systems becomes minimal (e.g., Figures 3(b), 3(d), and 3(f)). This is a fortunate situation for mammography dosimetry, because it means that tables of air kerma to MGD conversion factors (pDgN coefficients) do not have to be produced for each manufacturer's mammography, tomosynthesis, and breast CT systems.

Furthermore, calculated HVLs for the new DM/BT simulated spectra presented in this work which contain the exact amount of vendor‐specified filtration were shown to be in good agreement with measured values and within the ± 0.05 mm uncertainty in HVL reported when averaging evaluations on various mammography systems.³³ Given the 10% thickness tolerance for the added filtration employed in modern mammography systems, and the experimental error associated with HVL measurements in general, these results clearly demonstrate the accuracy of the present simulations.

Calculated HVLs for the new bCT‐simulated spectra presented in this work with exactly 1.5 mm of Al filtration were found to be within 0.08 mm of the range of measured HVLs for the bCT systems compared in this study. Given the known uncertainty in the reported and actual thickness of aluminum filtration used for these systems and the type of Al used for the HVL measurements, these results demonstrate the accuracy of the bCT x‐ray spectra simulations reported in this work.

In this investigation, it was also shown that the differences in x‐ray spectra produced by the large and small focal spot are trivial — validating the use of the same conversion tables for both large and small focal spots in the mammography and tomosynthesis applications. In addition, the influence of the field‐of‐view subtended by the x‐ray spectrum from the smallest breasts to the largest breasts was found to be negligible as well. Again, this demonstrates that dose conversion tables likely do not need to be specific to the planar extent of the breast.

The shape of an x‐ray spectrum, when the characteristic x‐ray peaks are included, can vary significantly depending upon the energy resolution and binning levels used to produce the x‐ray spectrum. Systematic bias potentially introduced by differences in energy binning was addressed in the present work by providing direct comparisons of MC simulated x‐ray spectra with identical energy binning as the reference spectra. Interestingly, the energy resolution of the x‐ray spectrum also has an impact on how it is used in conjunction with monoenergetic DgN coefficients, DgN(E). Because DgN coefficients include mass energy attenuation coefficients for air, they are nonlinear as a function of energy. What this means is that when a polyenergetic “pDgN” coefficient is produced from a DgN(E) function through spectral weighting, the energy binning used to produce the DgN(E) function should be the same as that for the spectrum used in weighting. While this issue is largely moot for the continuous bremsstrahlung spectrum, it has some importance when characteristic x‐ray peaks are prominent in a given spectrum.

Based on this work, a set of tables in spreadsheet format containing all the breast imaging x‐ray spectra described herein can be found in Tables [Link], [Link], [Link], [Link] on the Supplemental Information tab. Separate spreadsheets compatible with both Windows and Mac operating systems (Microsoft Excel, Redmond, WA, USA) are available for MASMICS_M‐T, RASMICS_M‐T, TASMICS_M‐T, and TASMICS_bCT. The spreadsheet layout and simple user interface are identical to the description provided in previous work.¹⁵

5. Conclusion

Monte Carlo modeling and cubic spline interpolation techniques were utilized to generate x‐ray spectra using molybdenum, rhodium, and tungsten anodes pertinent to digital mammography (DM) and breast tomosynthesis (BT) systems. Eight raw DM/BT spectra, produced using MCNP6, were interpolated using cubic spline interpolation methods, to produce the 30 x‐ray spectra spanning from 20 kV to 49 kV at 1 kV intervals. In addition, the same techniques were used to generate W anode x‐ray spectra for breast CT (bCT) systems. Nine raw bCT spectra, produced using MCNP6, were interpolated using cubic spline interpolation methods, to produce the 36 x‐ray spectra spanning from 35 kV to 70 kV in 1 kV intervals.

The present spectral models (MASMICS_M‐T, RASMICS_M‐T, TASMICS_M‐T, and TASMICS_bCT) represent a more comprehensive collection of spectra specific to breast x‐ray imaging, in terms of x‐ray tube potential and minimal filtration (only beryllium) than previously reported MASMIP_M, RASMIP_M, TASMIP_M, and TASMIP x‐ray spectra. In addition, they represent x‐ray spectra produced using the geometrical and x‐ray tube configurations found in commercially available mammography, breast tomosynthesis, and breast CT systems.

Conflicts of interest

John M. Boone has U.S. patents (pending and issued) pertaining to breast CT, HVL measurement, and x‐ray tube design.

Supporting information

Table S1: MASMICS_M‐T.

Table S2: RASMICS_M‐T.

Table S3: TASMICS_M‐T.

Table S4: TASMICS_bCT.