Abstract
In a large-scale genetic association study, the number of phenotyped individuals available for sequencing may, in some cases, be greater than the study’s sequencing budget will allow. In that case, it can be important to prioritize individuals for sequencing in a way that optimizes power for association with the trait. Suppose a cohort of phenotyped individuals is available, with some subset of them possibly already sequenced, and one wants to choose an additional fixed-size subset of individuals to sequence in such a way that the power to detect association is maximized. When the phenotyped sample includes related individuals, power for association can be gained by including partial information, such as phenotype data of ungenotyped relatives, in the analysis, and this should be taken into account when assessing whom to sequence. We propose G-STRATEGY, which uses simulated annealing to choose a subset of individuals for sequencing that maximizes the expected power for association. In simulations, G-STRATEGY performs extremely well for a range of complex disease models and outperforms other strategies with, in many cases, relative power increases of 20–40% over the next best strategy, while maintaining correct type 1 error. G-STRATEGY is computationally feasible even for large datasets and complex pedigrees. We apply G-STRATEGY to data on HDL and LDL from the AGES-Reykjavik and REFINE-Reykjavik studies, in which G-STRATEGY is able to closely-approximate the power of sequencing the full sample by selecting for sequencing a only small subset of the individuals.
Keywords: family data, simulated annealing, sequence, association mapping, selective genotyping
Introduction
Genetic association mapping has been widely used to identify genetic variants associated with a particular trait. For best results, association studies usually require large numbers of individuals to be both genotyped and phenotyped for the trait of interest. In practice, however, sequencing or genotyping all individuals can be a costly endeavor, and in some cases, the sequencing budget might be limited. When phenotyping is considered less expensive than sequencing or genotyping (which is the case in many studies), selective genotyping [Emond et al., 2012; Wheeler et al., 2013; Lee et al., 2014], in which a subset of individuals are selected for sequencing or genotyping based on their phenotypes, can be a cost-saving strategy.
When the sample consists of related individuals, determining an optimal subset of individuals to genotype poses a challenge because of the dependence among individuals’ genotypes and among their phenotypes. For example, selection based only on each individual’s own phenotype will generally not be optimal, because phenotypes of the individual’s relatives also provide information on whether or not the individual is likely to carry alleles predisposing to, e.g., higher values of the trait (the “enrichment principle” [Thornton and McPeek, 2007; Sham and Purcell, 2014]). Selection of an optimal subset of individuals to genotype is also complicated by the fact that genotyped individuals provide varying levels of information on the genotypes of their ungenotyped relatives, which can increase the power of the analysis, depending on how they are chosen. These considerations suggest the need to develop statistically sound and computationally feasible methods for selection of individuals to genotype for subsequent association analysis.
Existing tools that implement selection of individuals for sequencing or genotyping, taking into account relatedness, are limited. One possibility is to choose an unrelated set of individuals, e.g., founders, based on the pedigree information. Although this approach has simplicity, when the study sample is composed of moderate to large pedigrees, there may not be enough unrelated individuals to choose from. A variation on this approach[Housen et al., 1994; Ott et al., 2015] is to select a set of distantly related individuals whose estimated pairwise identity-by-descent (IBD) probabilities do not exceed a pre-specified threshold of relatedness. PRIMUS [Staples et al., 2013] is a method implementing this using network theory. Another well-known selection strategy is extreme phenotype selection [Emond et al., 2012; Lee et al., 2014; Sham and Purcell, 2014], in which the individuals with the highest and lowest phenotype values are preferentially selected for genotyping or sequencing. For a sample of unrelated individuals, it has been shown [Darvasi and Soller, 1992] that by genotyping approximately the most extreme one-quarter of individuals from each end of the phenotype distribution (for a total of half the full sample size), most of the power of association in the full sample is retained. However, when the sample consists of relatives, it is unclear how to prioritize individuals based on available phenotype information. GIGI-Pick [Cheung et al., 2014] is a recently proposed method to prioritize individuals for sequencing in pedigrees. It aims to select the subset of individuals that optimizes the subsequent sequence imputation at either a specific locus or a random locus in the genome. However, there is no guarantee that such a selection strategy will maximize the power in subsequent association studies. Furthermore, the computational burden makes GIGI-Pick infeasible as a tool for selecting a subset of individuals to genotype in, for example, the Icelandic Heart Association (IHA) cohorts.
We propose a novel method, G-STRATEGY, to optimally select individuals for sequencing or genotyping, based on available phenotype, covariate and pedigree information. G-STRATEGY uses simulated annealing to maximize the noncentrality parameter of the MQLS test [Thornton and McPeek, 2007] (in the case of a binary trait without covariates) or the MASTOR test [Jakobsdottir and McPeek, 2013] (in the case of a binary trait with covariates or a quantitative trait). This approach allows G-STRATEGY to optimize power while taking into account not only phenotype information and dependence among relatives, but also the fact that the individuals selected for sequencing or genotyping can provide partial genotype information on ungenotyped relatives, where this contributes power for association. G-STRATEGY allows the user to specify (1) an initial subset of individuals who are already sequenced or genotyped and (2) a subset of ungenotyped individuals available to be selected for sequencing or genotyping, and it optimizes the selection of additional individuals for genotyping within these constraints. To show the power and wide applicability of G-STRATEGY, we perform simulations in a range of scenarios in which the simple modeling assumptions of G-STRATEGY do not hold, and we compare G-STRATEGY with other methods. Finally, we apply G-STRATEGY to data on high-density lipoprotein (HDL) and low-density lipoprotein (LDL) from the IHA cohorts.
Methods
We consider a situation in which genetic association analysis of a trait is to be performed in a sample of individuals among whom only a subset (or perhaps none at all) are currently sequenced or genotyped. The genetic association analysis is permitted to include covariates in addition to genotypes and phenotypes. We assume that budget constraints limit the amount of additional sequencing or genotyping that can be performed. The goal is to select from the sample an additional fixed-size subset of individuals to sequence or genotype in order to maximize power for the subsequent association test.
More specifically, consider a set, D, of sampled individuals, some of whom may be related, with relationships specified by known pedigrees. Let d = |D| be the number of individuals in set D. Assume that data on phenotype and any relevant covariates are available for at least some of the sampled individuals, where missing data are allowed. Let P, “the phenotyped set,” denote the subset of individuals in D who have non-missing values for both the phenotype and the covariates, if any, that will be included in a genetic association analysis of the trait.
We assume that some subset, N0, of the individuals in D have previously been sequenced or genotyped, where we allow for the possibility that N0 = ∅, i.e., that no one in D has yet been genotyped. We call N0 “the initially genotyped set,” and it could include, for example, individuals taken from a generic control panel or individuals who were already sequenced or genotyped for the current or a previous study. Let n0 = |N0| ≥ 0 be the number of individuals in the set N0. Let S be the subset of individuals in D who are not yet genotyped but are available to be selected for additional sequencing or genotyping, for example, those still living. We assume that budget constraints limit us to sequencing or genotyping na additional individuals from among those in S. Then we will employ some selection strategy to choose Na, a subset of S, consisting of na additional individuals selected for genotyping. Let N = N0 ∪ Na, which we call “the extended genotyped set,” with n = |N| = na + n0. Note that the phenotyped set, P, and the extended genotyped set, N, would usually differ. Therefore, even after the additional genotyping, there are likely to be some individuals with partial information, e.g., phenotyped individuals who are not genotyped, and/or genotyped individuals who are not phenotyped. In this context, power for association can typically be gained by making use of the dependence of genotypes among related individuals and the dependence of phenotypes among related individuals in order to incorporate the partial information. We will take this into account in assessing which individuals to genotype.
We consider an analysis in which the genetic variants are tested, one at a time, for association with the trait. For simplicity, we assume that the variant being tested is an autosomal binary variant (e.g., a SNP) with alleles labeled “0” and “1”. For a given variant and a given choice of extended genotyped set, N, let G = (G1, G2, . . . , Gn)T denote the length-n genotype vector, where Gi takes values in {0,.5,1}, according to whether the ith individual in N has 0, 1, or 2 copies of allele 1 at the variant. Let Y = (Y1, Y2, . . ., Yp)T denote the length-p phenotype vector, where p = |P|, and, for a binary trait, Yi = 1 if the ith individual in P is affected and Yi = 0 if the ith individual in P is unaffected. For a quantitative trait, we let Yi be the trait measurement, possibly after suitable transformation. Furthermore, let W be the p × (w + 1) matrix of covariates with (i, j)th entry, Wij, equal to the value of the jth covariate for the ith individual in set P. We assume that W always includes an intercept (i.e., column of 1’s) and therefore has w + 1 columns, where w ≥ 0 is the number of covariates to be included in the analysis in addition to the intercept.
We allow the study sample, D, to include arbitrarily related individuals. For example, study individuals can be sampled from a single complex inbred pedigree or several small outbred families, and unrelated individuals can be included as well. We define the kinship matrix, Φ, for the individuals in set D, to be
| (1) |
where ϕij is the kinship coefficient between individuals i and j, and hi is the inbreeding coefficient of individual i. For a given choice of the extended genotyped set, N, we let ΦN be the n × n sub-matrix of Φ obtained by considering only the individuals in N, we let ΦN P be the n × p sub-matrix obtained by extracting the rows and columns of Φ corresponding to individuals in N and P, respectively, and we set . Note: the main notation used in the paper is summarized in Table 1.
Table 1.
Main Notation
| D | Set of sampled individuals |
| P | Phenotyped set |
| N0 | Initially genotyped set |
| n0 | Number of individuals in the set N0 |
| S | Subset of individuals in D who are available to be selected for genotyping |
| Na | Set of additional individuals selected for genotyping (subset of S) |
| na | Number of individuals in the set Na |
| N = N0 ∪ Na | Extended genotyped set |
| G = (G1, G2, …, Gn)T | Genotype vector, where n = |N| = n0 + na |
| Y = (Y1, Y2, …, Yp)T | Phenotype vector, where p = |P| |
| w ≥ 0 | Number of covariates included in the analysis, in addition to the intercept |
| W | [p × (w + 1)] matrix of covariates for the individuals in P |
| Φ | [d × d] kinship matrix for the individuals in D, where d = |D| |
| ΦN | [n × n] kinship matrix for the individuals in N |
| ΦN P | [n × p] cross-kinship matrix between the individuals in N and P |
We propose a selection method, called G-STRATEGY, to optimally choose the extended genotyped set, N, conditional on the phenotype, covariate and pedigree information and conditional on which individuals are in the initially genotyped set, N0, but not conditional on their actual genotype values. The idea of G-STRATEGY is to maximize the noncentrality parameter of the MQLS test [Thornton and McPeek, 2007] or the MASTOR test [Jakobsdottir and McPeek, 2013], using a simulated annealing algorithm. Both MQLS and MASTOR are association tests that allow samples with related individuals and incomplete data. Both tests increase power by incorporating partial information such as phenotype information on ungenotyped relatives. Before we elaborate on how G-STRATEGY selects the individuals, we first give a brief review of the MQLS and MASTOR tests. More details can be found elsewhere [Thornton and McPeek, 2007; Jakobsdottir and McPeek, 2013].
A Brief Review of MQLS and MASTOR
Both the MQLS and MASTOR methods are χ2 tests of the null hypothesis of no association and no linkage. Both methods are based on a retrospective approach, i.e., we condition on phenotype, Y, (and on covariates, W, in the case of MASTOR), while treating genotype, G, as random.
MQLS was proposed in the context of association testing of a binary trait when some sampled individuals are related, with known relationship. It does not use covariates. MQLS can be constructed as a quasi-likelihood score test of the null hypothesis H0 : γ = 0 vs. HA : γ ≠ 0 based on the following modeling assumptions:
| (2) |
| (3) |
where 0 < f < 1 is an unknown parameter representing the frequency of allele 1 in the population from which the sample is drawn, k is a fixed, known estimate of the population prevalence of the binary trait, γ is an unknown association parameter, 1n denotes a vector of length n with every element equal to 1, and 1p is similar but of length p. Equation (3) models the conditional variance of the genotype vector under the null hypothesis, γ = 0, where is an unknown parameter representing the null genotypic variance of an outbred individual. For example, if the pedigree founders were drawn from a population in Hardy-Weinberg equilibrium (HWE) for the given genetic variant, this null variance would be given by . To make the approach more robust to deviation from HWE, we typically use an estimator [Thornton and McPeek, 2010] for that does not assume HWE, namely,
| (4) |
The resulting MQLS test statistic is given by
| (5) |
Under the null hypothesis of no linkage and no association between the tested variant and trait, the MQLS statistic is asymptotically . In the special case of complete data and independence (i.e., ΦN = I), and when Equation (4) is used for , then the MQLS statistic is equivalent to the Armitage trend test statistic (except for a factor of 1 − 1/n, which is negligible in large samples).
MASTOR can be viewed as an extension, to quantitative traits, of the MQLS method for binary traits. MASTOR differs from MQLS in that it includes covariates and random additive polygenic effects in the trait model. MASTOR can be applied to binary traits as well as to quantitative traits. In analogy to the model in equations (2) and (3), MASTOR can be derived as the quasi-likelihood score test for the null hypothesis H0 : γ = 0 vs. HA : γ ≠ 0 in the following retrospective model,
| (6) |
| (7) |
where (βˆ, Σˆ) is the MLE of (β, Σ) in the following prospective, polygenic, null model
| (8) |
where and are the additive polygenic and environmental variance components, respectively, and Ip is the p × p identity matrix. The resulting formula for MASTOR is
| (9) |
where is chosen to be a consistent estimator of . A previous work [Jakobsdottir and McPeek, 2013] suggests using either , where is given in equation (4), or
| (10) |
with
| (11) |
where Q is defined to be the set of individuals with both genotype and covariate information, who may or may not have known phenotype (N ∩ P ⊆ Q ⊆ N), with q = |Q|; GQ is the sub-vector of length q of G that is obtained by extracting the elements of G that correspond to individuals in Q; ΦQ is the q × q kinship matrix for individuals in Q; and WQ is the q × (w + 1) sub-matrix of W that is obtained by extracting the q rows of W that correspond to individuals in Q. The use of the estimator, , in equation (10) can increase the power of MASTOR by accounting for possible dependence between genotype and covariates. The MASTOR test statistic of equation (9) has a asymptotic null distribution, under assumptions that are somewhat more general [Jakobsdottir and McPeek, 2013] than those given in equations (6) and (7). In the special case of complete data and independence (i.e., when ξ is set to 0), and when Equation (10) is used for , MASTOR is the same as the classical score test for the prospective normal linear regression trait model.
Both MQLS and MASTOR are based on a retrospective approach, rather than a prospective approach. One advantage of the retrospective approach is that it provides a natural way to incorporate individuals with missing genotype, by using the known dependence among relatives’ genotypes under the null hypothesis. A less obvious advantage is that the statistical validity (i.e., correct type 1 error) of the retrospective approach is insensitive to phenotype-based ascertainment and is robust to misspecified trait distribution.
We note that the MQLS and MASTOR χ2 test statistics can be thought of as having the common form
| (12) |
where is taken to be some consistent estimator of , which will not be needed for G-STRATEGY, and where V is a function of Y (and of W, in the case of MASTOR), but not of G, so that, in the retrospective analysis, V is fixed, not random. Specifically,
| (13) |
We call R the “transformed phenotypic residual.”
G-STRATEGY: Selection of Extended Genotyped Set
Our proposed method, G-STRATEGY, works as follows. It selects the additional na individuals to genotype by maximizing the noncentrality parameter, λ, of the MASTOR or MQLS test, where
| (14) |
and where we have used E(VT G|W, Y) = VT E(G|W, Y), with equation (2) or equation (6) used to obtain E(G|W, Y) for the case of MQLS or MASTOR, respectively. If we define the vector of “enrichment values,” E, by E = ΦN P R, then the optimal N chosen by G-STRATEGY is the argmax of the objective function, h(N), where
| (15) |
which is equal to λ up to a scale factor, and where N is a candidate extended genotyped set satisfying
| (16) |
Then the set of additional individuals to be genotyped would correspond to Na = N\N0.
There are several technical points worth mentioning. First, G-STRATEGY selects Na, the set of additional individuals to be genotyped, based on the phenotype, covariate and pedigree information, and based on the set, N0, of individuals already genotyped, but not based on any observed genotype data. Therefore, one would expect the type 1 error to be correct for any subsequent genetic association analysis on the extended genotyped set. This is particularly obvious if the follow-up association test to be performed is MQLS or MASTOR, because both methods are retrospective. (Though the justification may be less obvious, the type 1 error would also be expected to be correct for typical prospective association analyses as well.) Correct type 1 error of G-STRATEGY is confirmed in the Simulation Studies subsection of Results.
Second, in equation (15), the objective function for G-STRATEGY is a function of the enrichment vector, E, and the kinship matrix, ΦN. In particular, h(N) is numerically equal to the residual sum of squares from the generalized least squares regression of E on the intercept vector, 1n, with Cov(E) ∝ ΦN. One can think of the enrichment value, Ei, of individual i, as being a weighted sum of the transformed phenotypic residuals of i and i’s relatives, with weight 2ϕij given to Rj. Thus, for example, in a case-control study, an individual with multiple affected (unaffected) relatives would have a higher (lower) enrichment value than an individual without affected (unaffected) relatives. In binary trait mapping, the idea of the enrichment principle [Thornton and McPeek, 2007] is that in a wide range of genetic models, individuals with extremely high (extremely low) enrichment values are more likely to be carrying predisposing (protective) genetic variants for the trait. The idea for quantitative traits is similar. Thus, intuitively, it would seem to make sense as a selection strategy to prioritize individuals with extreme enrichment values. This strategy, which we call the “Enrichment” strategy, is defined in the next subsection. We compare the performance of the Enrichment strategy to that of G-STRATEGY in simulations in which the underlying true model is not the same as the one assumed by G-STRATEGY.
Third, when G-STRATEGY is implemented using the MASTOR noncentrality parameter, G-STRATEGY requires estimation of the null MLE, (Σ̂, β̂), from the prospective model in equation (8). In G-STRATEGY, we calculate the null MLE, (Σ̂, β̂), based on data from all individuals in P. In contrast, in MASTOR, when some individuals in P are not genotyped, then (Σ̂, β̂) is calculated based on a subset of P, where, for example, phenotyped individuals who are not in the same pedigree with any genotyped individuals are excluded. Our strategy of including data on all individuals in P in the calculation of (Σ̂, β̂) allows us to avoid re-estimating the null MLE of (Σ̂, β̂) for each choice of N.
We conclude this section by giving a computationally useful form for the G-STRATEGY objective function in the case when the sampled individuals belong to F independent families. We make use of the block diagonal structure of the kinship matrix to define three family-specific components:
| (17) |
for 1 ≤ i ≤ F, where mi is the number of extended genotyped individuals in family i, Mi is the set of extended genotyped individuals in family i, EMi is the sub-vector of enrichment values for the individuals in Mi, and ΦMi is the kinship sub-matrix for the individuals in Mi. The selection of the extended genotyped set can then be expressed as finding the argmax of h(N), where
| (18) |
This formulation is computationally convenient for use in the simulated annealing algorithm described in the next subsection.
G-STRATEGY: Search via Simulated Annealing
G-STRATEGY is formulated as an optimization problem in which the domain is a large discrete space with a natural neighborhood structure (described below). In this context, a simulated annealing approach [Kirkpatrick et al., 1983], [Černỳ, 1985], [Press et al., 1992] to optimization has the potential to work much better than, for example, a forward stepwise approach as in GIGI-Pick [Cheung et al., 2014], because simulated annealing typically does a better job of exploring the full search space at a still relatively low computational cost. In what follows, we present the simulated annealing algorithm used by G-STRATEGY when searching for an optimal or nearly optimal subset of additional individuals to genotype.
The search space consists of all possible extended genotyped sets in the collection
Each element of 𝒩 is a candidate for the extended genotyped set. We create a neighborhood structure on 𝒩 by defining candidate sets N1, N2 ∈ 𝒩 to be neighbors if they differ by exactly one element, i.e., if |N1\N2| = 1 = |N2\N1|. In that case, N2 can be obtained from N1 by taking out one individual from N1\N0 and replacing him or her by another individual in S\N1, and N1 can be obtained from N2 similarly.
The simulated annealing algorithm moves through a sequence of steps. At step i, the algorithm proposes a move from the current set Ni to a set Ni+1 chosen uniformly at random from among the neighbors of Ni. The proposal is then accepted with probability
which depends on the change in objective function between Ni and Ni+1, and on a time-varying parameter T called temperature. If the proposal is accepted, we call it a successful move. The temperature schedule describes the change in the value of T over successive steps of the algorithm. At the first step of the algorithm, T is set to a high value, t1, and it is decreased by a multiplicative factor α after every s steps of the algorithm, where 0 < α < 1 and s is some positive integer. Thus, the temperature takes value αct1 for steps cs + 1, . . . , (c + 1)s of the algorithm, for c = 0, 1, . . . until the algorithm is stopped. This temperature schedule requires specification of tuning constants t1, α, and s. To set t1, we draw 500 pairs of neighboring candidate sets, (N1, N2), independently and uniformly from the set of all possibilities, and we set t1 to be the maximum observed value of |h(N1) − h(N2)| in this sample. We use α = 0.95 and s = 5000. We terminate the algorithm when either (1) the temperature decreases below a given threshold, which we set to 1.0e − 5, or (2) no successful moves are found after s steps at any given temperature stage, whichever occurs first.
After obtaining a “best-so-far” candidate, which has the highest value of the objective function found during the simulated annealing, we perform a post-processing procedure, in which we run a small, locally hill-climbing algorithm based on that candidate until no better neighboring candidates are found. The resulting set is the one output by G-STRATEGY.
The probabilistic acceptance and temperature schedule of the simulated annealing algorithm allow it to escape local maxima by not only accepting every new candidate that increases the objective function, but also accepting some new candidates that decrease the objective function. The high initial temperature allows the algorithm to better explore the entire search space. As the temperature decreases so does the chance of accepting worse candidates, so the search will be in a more focused region in which, one hopes, a close-to-global maximum can be found. Furthermore, the algorithm keeps computation and memory costs low by focusing only on candidate sets that are neighbors of the current set. From equations (17) and (18), it is clear that one need only recalculate a few family-specific components at each step, because at each step, the proposed set will differ from the current set in at most two families.
When the number of additional individuals to be genotyped, na, is reasonably large, there will typically be many close-to-optimal choices of N, with negligible differences between their values of the objective function. In that case, it is of little interest to identify a true global maximizer, N, because many other choices will be almost equally good. This is especially true considering that the true trait model is unknown, so the noncentrality parameter used by G-STRATEGY serves as only an approximate guide to power. Therefore, in G-STRATEGY, we use simulated annealing to try to obtain a close-to-optimal choice of N without trying to establish that it is a true global maximizer. Furthermore, because of the probabilistic nature of the algorithm, running G-STRATEGY multiple times on a large data set will typically produce multiple different choices of N that are expected to be approximately equal in power. This can be useful if there are other considerations (such as cost or convenience) that can arise in the choice of whom to genotype, because one can then take into account these other considerations in choosing from among multiple roughly equivalent options for N.
Simulation Studies
We perform simulation studies for both binary and quantitative traits to (1) assess the impact of G-STRATEGY on the type 1 error for various association tests; (2) evaluate the robustness of G-STRATEGY to model misspecification; and (3) compare the empirical power of association tests when G-STRATEGY is applied vs. when other competing strategies are applied to select individuals for genotyping. To do this, we simulate data that include related individuals, under a variety of trait models, as we now describe.
Trait Models
The trait models we simulate are complex and do not satisfy the simple assumptions used in the derivation of G-STRATEGY. This aspect of the simulation is intended to reflect the reality that we do not know the true underlying model, and it allows us to assess the robustness of G-STRATEGY to model misspecification.
For a binary trait, we consider three different classes of multigene trait model which have been described previously [Sun et al., 2002]. Model 1 has two unlinked causal SNPs, with epistasis between them and both of them acting dominantly. In model 1, the frequencies of allele 1 at SNPs 1 and 2 are p1 and p2, respectively. Individuals with at least one copy of allele 1 at SNP 1 and at least one copy of allele 1 at SNP 2 have a penetrance of f1. All other individuals have a penetrance of f2 < f1. We consider two different parameter settings for model 1, which are listed as models 1a and 1b in Supplementary Table S1.
Model 2 also consists of two unlinked causal SNPs with epistasis between them, with SNP 1 acting recessively and SNP 2 following a general two-allele model. There are four penetrance parameters for this model, with f1 > f2 > f3 > f4. Individuals with two copies of allele 1 at SNP 1 and two copies of allele 1 at SNP 2 have a penetrance of f1. Individuals with two copies of allele 1 at SNP 1 and one copy of allele 1 at SNP 2 have a penetrance of f2. Individuals with two copies of allele 1 at SNP1 and no copies of allele 1 at SNP 2 have a penetrance of f3. All other individuals have a penetrance of f4. We consider two parameter settings for this class of model, which are listed as models 2a and 2b in Supplementary Table S1.
Model 3 has three unlinked causal SNPs with epistasis between them and with each SNP acting dominantly. Individuals with both at least one copy of allele 1 at SNP 1 and at least one copy of allele 1 at either SNP 2 or SNP 3 have a penetrance of f1. All other individuals have a penetrance of f2 < f1. We consider two different parameter settings for this class of model, which are listed as models 3a and 3b in Supplementary Table S1.
Supplementary Table S1 contains the allele frequencies and penetrance parameters for each model, as well as the resulting population prevalence, Kp, the prevalence conditional on having an affected sibling, Ks, and the sibling risk ratio, λs = Ks/Kp, where Kp, Ks and λs are calculated in outbred individuals.
For a quantitative trait, we consider three different classes of multigene trait model, which we call models 4, 5 and 6. All three of these model classes have 4 unlinked causal SNPs, three of which interact, with an additional additive polygenic effect, and they all have sex as a covariate. In addition, Model 5 has heavy-tailed noise, and Model 6 has a dominance polygenic effect. Model 4 is given by
| (19) |
where 1female is a vector whose ith element = 1 if individual i is female and = 0 if individual i is male; 1 is a vector all of whose entries = 1; and are specified scalars; f (X1, X2, X3) is a vector with ith element equal to f (X1i, X2i, X3i) and g(X4) is a vector with ith element equal to g(X4i), where X1i, X2i, X3i and X4i are the genotype values of individual i at unlinked, causal SNPs 1, 2, 3, and 4, respectively; f(x1, x2, x3), (x1, x2, x3) ∈ {0, .5, 1}3, is a specified function representing the joint effects (including interaction) of SNPs 1, 2, and 3; and g(x4), x4 ∈ {0, .5, 1}, is a specified function representing the effect of SNP 4. We consider two different parameter settings for model 4, which we call models 4a and 4b. Supplementary Table S2 specifies the allele frequencies, covariate effects (β0, β1), variance component parameters ( ), and function g(x4) for models 4a and 4b, while Supplementary Table S3 specifies the function f(x1, x2, x3) used in those models.
Model 5 is a heavy-tailed polygenic model that satisfies a version of equation (19) in which we redefine ε = e + η, where e and η are independent, and the ηi’s are i.i.d. draws from a Laplace distribution with location parameter 0 and scale parameter 2. We consider one parameter setting for model 5, for which the function f (x1, x2, x3) is specified in Supplementary Table S3 and all other model parameters are specified in Supplementary Table S2.
Model 6 is a polygenic model with both additive and dominance components of variance. The model is given by equation (19) where we redefine , with and , and where Δ7 is the matrix with (i, j)th entry equal to Δ7[i, j], the seventh condensed identity coefficient between individuals i and j, which is the probability that, at any given locus, i and j share two alleles IBD, with neither one homozygous by descent. If the individuals are outbred, then Δ7[i, i] = 1 and, for i ≠ j, Δ7[i, j] is the probability that i and j share two alleles IBD. We consider one parameter setting for model 6, for which the function f(x1, x2, x3) is specified in Supplementary Table S3 and all other model parameters are specified in Supplementary Table S2.
Study Design for Simulations
We consider a study sample with 60 ascertained families each consisting of 16 outbred individuals in a three-generation pedigree, related as in Figure S1. The simulated phenotypes for the individuals in each family vary randomly according to one of the trait models described in the previous subsection. In each sampled pedigree, phenotypes of all individuals are observed. When a binary trait is simulated, pedigrees are sampled conditional on obtaining exactly 20 pedigrees with 4 affected individuals, 20 pedigrees with 5 affected individuals, and 20 pedigrees with 6 affected individuals. When a quantitative trait is simulated, pedigrees are randomly sampled from the population, without additional ascertainment conditions.
The problem addressed in the simulations is to select n = 300 individuals to genotype from among the 960 individuals in the study sample. No individuals are initially genotyped, and all individuals are assumed to be available to be selected. Selection of individuals to be genotyped is based only on the phenotype, covariate and kinship information.
Comparison with Other Selection Strategies
In addition to G-STRATEGY we consider five other selection strategies. The first is the “Maximally-Unrelated” strategy[Staples et al., 2013], in which the largest possible subset of individuals whose estimated pairwise IBD sharing is below a specified threshold is selected. Note that in the simulations, the number of founder individuals in the study sample is 300, which is equal to the number of individuals to be selected for genotyping. Thus, in the context of the simulations, the Maximally-Unrelated strategy can be implemented, with an IBD threshold of 0, by selecting the set of pedigree founders as the subset of individuals to be genotyped.
In the case of a binary trait, we also consider a modified version of the Maximally-Unrelated strategy, which we call the “Rebalanced Founder” strategy, in which we replace some founders by randomly-chosen non-founders in order to obtain equal numbers of cases and controls in the genotyped subset. For example, if there were 200 controls and 100 cases among the founders, then in the Rebalanced Founder strategy, we would randomly select 50 founder controls to be excluded from the set N of individuals to be genotyped and replace them by 50 randomly-chosen non-founder cases, to obtain a final sample of 150 founder controls, 100 founder cases, and 50 non-founder cases.
The third strategy is a novel one we propose called the “Enrichment” strategy, in which individuals are selected based on their enrichment values, where E = ΦN P R is the vector of enrichment values. This strategy is based on the enrichment principle, which is a consequence of biologically plausible assumptions on disease models [Thornton and McPeek, 2007]. In this case, we select the 150 individuals with the highest enrichment values and the 150 with the lowest enrichment values. More generally, the Enrichment strategy is defined as follows: for the case when N0 = ∅, i.e., when there are no individuals already genotyped, select the individuals with the highest enrichment values, and the individuals with the lowest enrichment values, from among the individuals in set S. (When N0 ≠ ∅, i.e., when some individuals are already genotyped, we modify the Enrichment strategy so that the result is that there is some partition of N0 into N0 = B ∪ C, with B ∩ C = ∅ and |B| = b, such that the set Na ∪ B consists of the individuals with the highest enrichment values and the individuals with the lowest enrichment values, from among the individuals in S ∪ N0.) The Enrichment strategy is similar in spirit to classical selective genotyping[Lebowitz et al., 1987; Lander and Botstein, 1989; Darvasi and Soller, 1992], except that individuals are selected based on their enrichment values rather than their original trait values or trait residuals.
The fourth strategy we consider is GIGI-Pick [Cheung et al., 2014], a previously proposed method designed for sequencing studies in pedigrees. GIGI-Pick defines a metric called (either local or genome-wide) “coverage” to relate pedigree-based genotype imputation to individual selection, and it uses inferred inheritance vectors to measure genotype-imputation ability. In our case, we use the “genome-wide” version of GIGI-Pick, which requires only pedigree structure as input and optimizes genotype imputation at a random locus in the genome. We set GIGI-Pick to select five individuals from each pedigree, and we set the two tuning parameters, referred to as λ and α in GIGI-Pick [Cheung et al., 2014], to be 10 and 0.3, respectively.
Finally, in the data analysis, we also consider the “Random” strategy, in which individuals are chosen at random for genotyping.
Data from the AGES and REFINE Studies
We analyze data from two population-based studies conducted by the IHA: the Age, Gene/Environment Susceptibility (AGES) study and the Risk Evaluation for Infarct Estimates (REFINE) study. The AGES study, which has been described previously [Harris et al., 2007], was initiated in 2002 and consists of 5,764 individuals, from a population-based cohort, who were born between 1907 and 1935. The REFINE study was initiated in 2005 and consists of 8,266 inhabitants of the greater Reykjavik area who were born between 1935 and 1985. Information on relatedness of individuals both within and between the AGES and REFINE cohorts is currently in the process of being collected. We include in our analysis only individuals whose pedigree information is available. The resulting combined AGES-REFINE dataset has 8,030 individuals, and it includes unrelated individuals as well as individuals from multigeneration pedigrees. Of the 8,030 sampled individuals, 3,134 have previously been genotyped on the Illumina 370K whole-genome SNP array. The remaining 4,896 individuals are not yet genotyped. All subjects in these cohorts provided informed consent for this research, and procedures followed were in accordance with ethical standards.
We consider two phenotypes: high-density lipoprotein cholesterol levels (HDL) and low-density lipoprotein cholesterol levels (LDL). Both HDL and LDL are quantitative traits, and we adjust each for sex, age, age2 and statin use. In the AGES-REFINE sample, all 3,134 genotyped individuals have complete phenotype and covariate data for HDL, while 2 of the 3,134 individuals have missing LDL. Among the remaining 4,896 ungenotyped individuals, 15 individuals are missing HDL or one or more of the covariates, and 36 individuals are missing LDL or one or more of the covariates.
We approach the problem of selecting a subset of individuals to be genotyped in the AGES-REFINE data in two different ways. In the “masked genotype” analysis, the study sample, D, is taken to include all 8,030 individuals in the data set. The subset, N0, of previously genotyped individuals is taken to be ∅, i.e., we assume no one is previously genotyped. We mask the genotypes of the 3,134 genotyped individuals and treat them as the subset, S, of individuals available to be selected for genotyping. The remaining 4,896 individuals in D are assumed to be unavailable for genotyping, although they are included in the association analysis if they have phenotype and covariate information and at least one genotyped relative. Then, for each trait, using each of four selection methods (G-STRATEGY, Enrichment strategy, Maximally-Unrelated strategy, and Random strategy), we select a subset of size n = 250, 500, 1,000 or 2,000 individuals for genotyping from among the 3,134 individuals in S. We then unmask the genotypes of the selected individuals, while unselected individuals are assumed to have missing genotypes. Then the resulting data are analyzed using MASTOR. We were not able to include GIGI-Pick in this comparison because we were not able to obtain results from GIGI-Pick for the AGES-REFINE data set in a reasonable amount of time.
In addition to the masked genotype analysis, we also perform an additional real-world analysis in which we again let D consist of all 8,030 individuals in the AGES-REFINE data set, with the n0 = 3, 134 previously genotyped individuals put into the set N0, and with the remaining 4,896 ungenotyped individuals assumed to be available for genotyping. For the HDL phenotype, we use G-STRATEGY to choose an additional subset of size na = 500 or 1,000 individuals for genotyping from among the 4,896 ungenotyped individuals. For this real-world analysis, we do not yet have the genotypes on the selected individuals, so we cannot run association tests. However, we can estimate run times and memory usage for G-STRATEGY, and we can examine the features of the subset that is selected.
Results
Impact of G-STRATEGY on Type 1 Error
In the Methods section, we argue on theoretical grounds that G-STRATEGY should maintain correct type 1 error in subsequent association analyses. Using simulations, we provide further verification for both prospective and retrospective association tests. For 960 individuals in 60 ascertained families, we simulate binary and quantitative phenotypes under models 1a and 4a, respectively, we randomly select n0 = 0 or 100 individuals who are assumed to be previously genotyped, and we run G-STRATEGY to select 300 − n0 additional individuals to be genotyped in each scenario, so as to obtained a total of 300 genotyped individuals in each scenario. We then test for association with an unlinked, unassociated SNP with minor allele frequency (MAF) .05, .2 or .4. Association is tested using either MQLS or MASTOR, depending on whether the phenotype is binary or quantitative. For both tests, the default setting is to include in the analysis not only the 300 genotyped individuals, but also their phenotyped relatives who may or may not be genotyped. In the case of a quantitative phenotype, in addition to MASTOR, we also perform the prospective test GTAM [Abney et al., 2002] test, which includes only the 300 genotyped individuals in the analysis. In Table 2, we compare the empirical type 1 error based on 5,000 simulated replicates to the nominal level of .01 or .05. As expected, the empirical type 1 error for all three association tests based on G-STRATEGY samples is well controlled. None of the empirical p-values is significantly different from the nominal level, based on a z-test with significance threshold .05.
Table 2.
Impact of G-STRATEGY on Type 1 Error for Various Association Tests
| Empirical Type 1 Error (SE) with Nominal Type 1 Error of | ||||||
|---|---|---|---|---|---|---|
| .05
|
.01
|
|||||
| Association Test | Trait Model | MAF | n0 = 0 | n0 = 100 | n0 = 0 | n0 = 100 |
| MQLS | 1a | .4 | .046(.003) | .053(.003) | .008(.001) | .007(.001) |
| MQLS | 1a | .2 | .053(.003) | .048(.003) | .011(.002) | .008(.001) |
| MQLS | 1a | .05 | .054(.003) | .051(.003) | .010(.001) | .011(.001) |
| MASTOR | 4a | .4 | .051(.003) | .050(.003) | .009(.001) | .008(.001) |
| MASTOR | 4a | .2 | .051(.003) | .053(.003) | .009(.001) | .011(.001) |
| MASTOR | 4a | .05 | .050(.003) | .048(.003) | .009(.001) | .010(.001) |
| GTAM | 4a | .4 | .049(.003) | .052(.003) | .011(.002) | .010(.001) |
| GTAM | 4a | .2 | .049(.003) | .049(.003) | .009(.001) | .009(.001) |
| GTAM | 4a | .05 | .051(.003) | .047(.003) | .008(.001) | .009(.001) |
Note: In each case, the empirical type 1 error is based on 5,000 simulated replicates. None of the empirical type 1 error values is significantly different (p < .05) from the nominal level based on a z-test. Among the 960 sampled individuals, n0 = 0 or 100 randomly selected individuals are assumed to be previously genotyped. In each case, we implement G-STRATEGY to select 300 − n0 additional individuals to be genotyped, so as to obtain a total of 300 genotyped individuals. Association is tested on an unlinked, unassociated, binary variant using various test statistics.
Power Studies
To compare the power for association of different selection strategies, we perform simulations using the trait models described in the Trait Models subsection of Methods. In any given scenario, each of the selection strategies (Maximally-Unrelated, Enrichment, GIGI-Pick, G-STRATEGY and, in the case of a binary trait, Rebalanced Founder strategy) is implemented to select n = 300 individuals to be genotyped from among the 960 individuals. For the binary trait models 1a, 1b, 2a, 2b, 3a and 3b, we test for association at SNP 2 using MQLS. For the quantitative trait models 4a, 4b, 5 and 6, we test for association at SNP 3 using MASTOR. Although only a subset of individuals are selected for genotyping, it is important to keep in mind that available phenotype and covariate information on their relatives also provides information on association and is included in the association analysis, regardless of whether or not these relatives are selected for genotyping. In each case, empirical power is assessed based on 1,000 simulated replicates, with significance level set to .01.
Figures 1 and 2 compare the power for association based on different selection strategies. In all simulation scenarios, G-STRATEGY outperforms the other strategies. In many cases, the increase in power using G-STRATEGY is substantial. In particular, the relative power increase using G-STRATEGY over the next best approach, which in every case is the Enrichment strategy, is over 30% for models 3a, 3b, and 5, and 20% for models 1a, 1b, 4b and 6. In contrast, neither the Maximally-Unrelated strategy nor GIGI-Pick performs well in terms of power. Presumably, this is due to the fact that neither of them takes into account phenotype information. We note that the GIGI-Pick algorithm provides some flexibility between selecting closely related individuals vs. selecting distantly related individuals via its tuning parameter, α ∈ [0, 0.5]. We have tried repeating GIGI-Pick using different α’s over a grid of 10 equally-spaced points in [0, 0.5]. The empirical power changes very little (results not shown). When α is set to 0, GIGI-Pick selects all 300 founder individuals, which is the same as the Maximally-Unrelated strategy. Our simulations cover a reasonably broad range of disease models in which the modeling assumptions are not met. The results demonstrate that G-STRATEGY performs well across a range of settings and is robust to deviations from modeling assumptions. This makes G-STRATEGY appealing in practice because one usually does not know in advance the true underlying model.
Figure 1. Power Comparison for Selection Strategies in the Case of a Binary Trait.
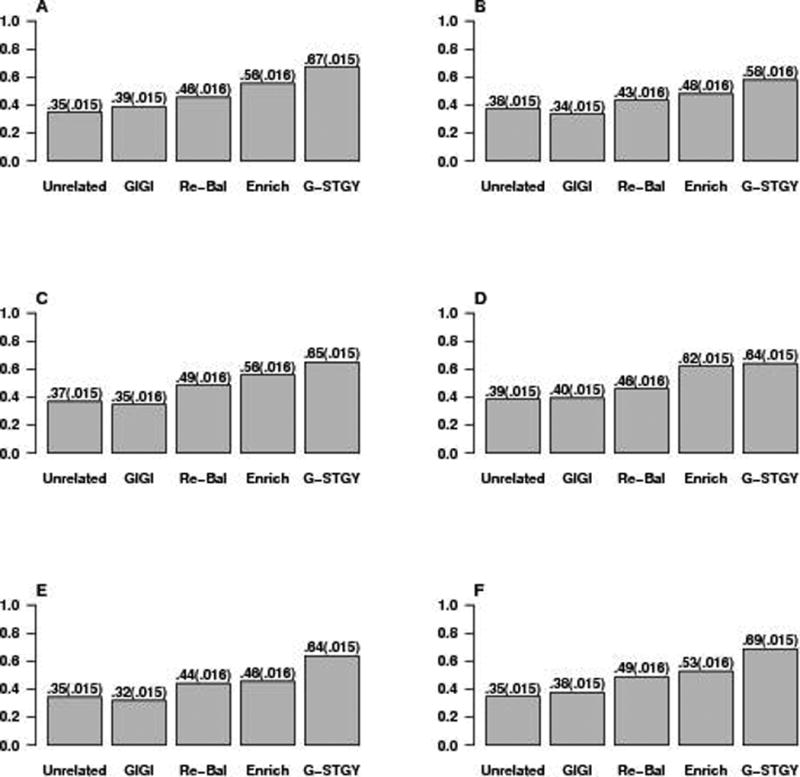
Panels (A), (B), (C), (D), (E), and (F) plot the power for association under binary trait models 1a, 1b, 2a, 2b, 3a, and 3b, respectively (described in the text and in supplementary Table S1). “Unrelated” denotes the Maximally-Unrelated strategy, “GIGI” denotes GIGI-Pick, “Re-Bal” denotes the Rebalanced Founder strategy, “Enrich” denotes the Enrichment strategy, and “G-STGY” denotes G-STRATEGY. Each of the five selection methods is implemented to select n = 300 individuals to be genotyped from among the 960 individuals in the sample. Empirical power for each model is based on 1,000 replicates with analysis performed using MQLS. Standard errors are given in parentheses.
Figure 2. Power Comparison for Selection Strategies in the Case of a Quantitative Trait.
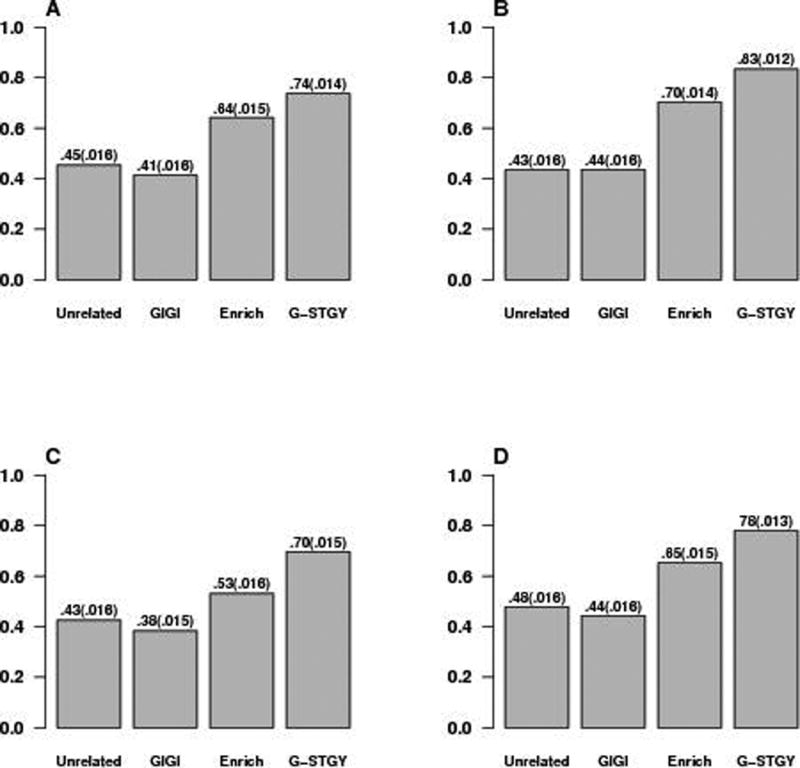
Panels (A), (B), (C), and (D) plot the power for association under quantitative trait models 4a, 4b, 5, and 6, respectively (described in the text and in supplementary Tables S2 and S3). “Unrelated” denotes the Maximally-Unrelated strategy, “GIGI” denotes GIGI-Pick, “Enrich” denotes the Enrichment strategy, and “G-STGY” denotes G-STRATEGY. Each of the four selection methods is implemented to select n = 300 individuals to be genotyped from among the 960 individuals in the sample. Empirical power for each model is based on 1,000 replicates with analysis performed using MASTOR. Standard errors are given in parentheses.
Application of G-STRATEGY to the AGES-REFINE Data
To assess the performance of G-STRATEGY on real data, we conduct association studies of HDL and LDL using the AGES-REFINE data. For each trait, we first conduct a genome-wide association study (GWAS) and then proceed to fine mapping on candidate loci. The GWAS is based on the Illumina 370K SNP array, and the fine mapping is based on a dense set of SNPs imputed from HapMap using MaCH/minimac [Li et al., 2010; Howie et al., 2012]. We consider the following candidate loci that were previously reported by Teslovich et al. (2010) [Teslovich et al., 2010]: (1) HDL loci: LIPC, LIPG, APO1-APOA5, CETP, LPL, ABCA1, LCAT, APOB, PLTP, FADS1-FADS3, GALNT2, TRIB1, LRP4-NR1H3; (2) LDL loci: APOE, LDLR, ABCG8, PCSK9. Both GWAS and fine mapping are performed using “masked genotype” analysis, i.e., individuals who are not selected into the subset for genotyping will have their genotypes masked so that they are missing in the analysis. In the fine mapping, only SNPs with imputation quality Rsq > 0.6 and MAF > 0.5% (evaluated in the subset of individuals selected for genotyping) are used in the analysis.
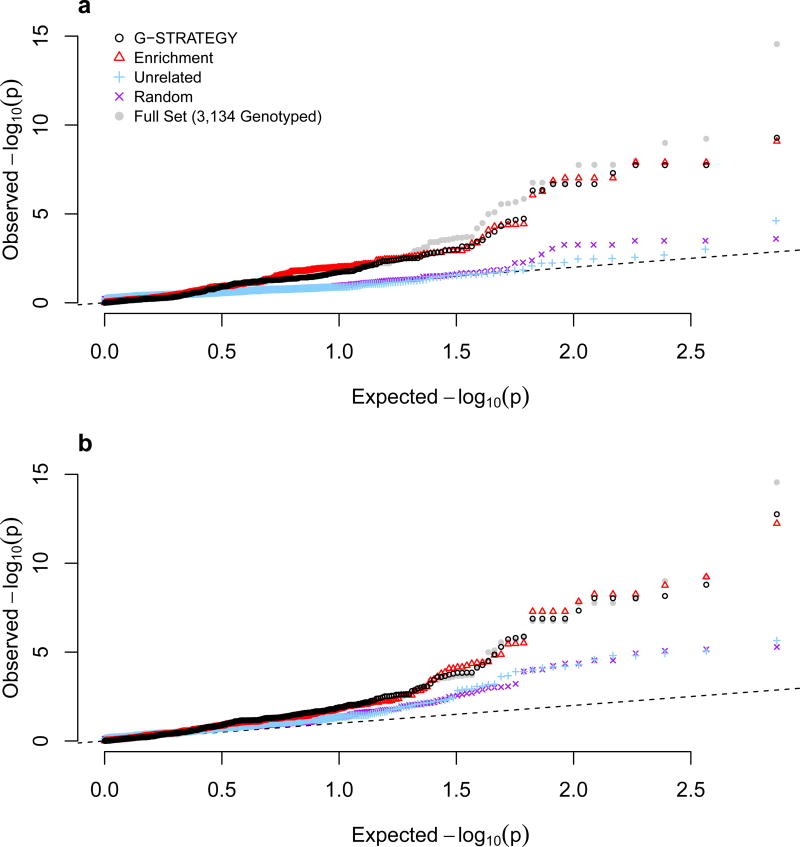
Figure 3 shows the Q-Q plots and genomic control factors of GWAS for HDL, based on G-STRATEGY subsets of size n = 250, 500, 1,000 and 2,000, selected from among the 3,134 previously genotyped individuals using the “masked genotypes” approach. As a benchmark, we also consider the “full set” scenario, in which all 3,134 previously genotyped individuals are assumed to be selected for genotyping. All genomic control factors are close to 1 and similar to that from the benchmark scenario (λ = 1.043), reflecting the fact that use of G-STRATEGY does not affect the type 1 error rate. The results confirm that G-STRATEGY retains the calibration of the association tests on a genome-wide scale.
Figure 3. Q-Q Plots with Genomic Control Coefficients from GWAS for HDL, Based on G-STRATEGY Subsets of Different Sizes.
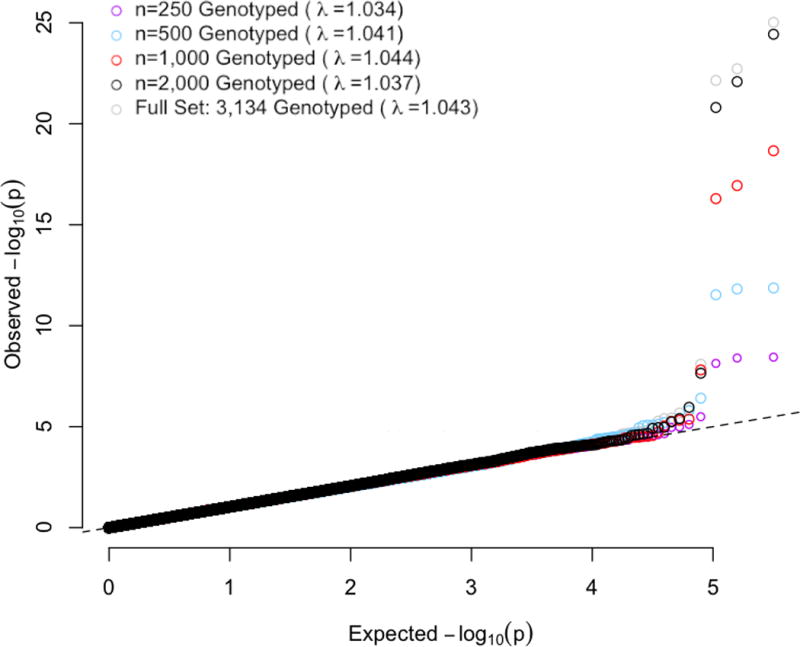
G-STRATEGY is implemented to select a subset of size n = 250, 500, 1,000 or 2,000 individuals to be genotyped from among the 3,134 individuals. The dashed line represents the values expected under the null hypothesis. The gray circles represent the benchmark in which all 3,134 genotyped individuals are selected. GWAS analysis is performed using MASTOR based on each resulting sample.
Figures 4 and 5 show the Q-Q plots for fine mapping of candidate loci for HDL and LDL, respectively, based on different selection strategies. Because some selection strategies (such as the Maximally-Unrelated strategy, random strategy and G-STRATEGY) will typically output different subsets for genotyping in different runs, we repeat each of these selection strategies 20 times and report the geometric average of the corresponding p-values at each SNP over the 20 runs. We do not consider GIGI-Pick in the comparison, because GIGI-Pick is computationally infeasible to run on such a large dataset. (An attempt to apply GIGI-Pick to the HDL data set was stopped after 4 days of running.) As we would expect, all Q-Q plots show clear deviation from the null (because only candidate loci are included). In particular, both G-STRATEGY and the Enrichment strategy give a substantially larger excess of association signals, suggesting the power advantage both G-STRATEGY and the Enrichment strategy can provide over other methods.
Figure 4. Q-Q Plots of HDL p-values for SNPs in Candidate Genes, Based on Different Selection Methods.
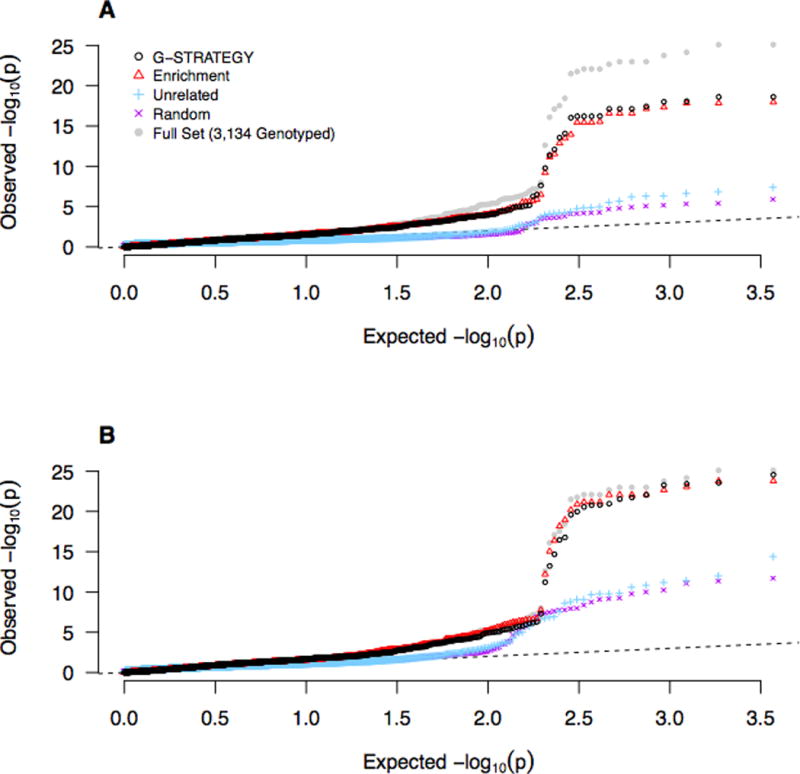
We test for association at ~3,700 SNPs that are located with within 13 candidate loci (comprising 19 candidate genes) for HDL. For each of the four selection methods, the reported p-value is the geometric mean of the corresponding p-values at each SNP over 20 runs. The p-values in Panel (A) are based on selection of n = 1,000 individuals to be genotyped, and the p-values in Panel (B) are based on selection of n = 2,000 individuals to be genotyped. The dashed line represents the values expected under the null hypothesis. The gray dots represent the benchmark in which all 3,134 genotyped individuals are selected.
Figure 5. Q-Q Plots of LDL p-values for SNPs in Candidate Genes, Based on Different Selection Methods.
We test for association at ~740 SNPs that are located within 4 candidate genes for LDL. For each of the four selection methods, the reported p-value is the geometric mean of the corresponding p-values at each SNP over 20 runs. The p-values in Panel (A) are based on selection of n = 1,000 individuals to be genotyped, and the p-values in Panel (B) are based on selection of n = 2,000 individuals to be genotyped. The dashed line represents the values expected under the null hypothesis. The gray dots represent the benchmark in which all 3,134 genotyped individuals are selected.
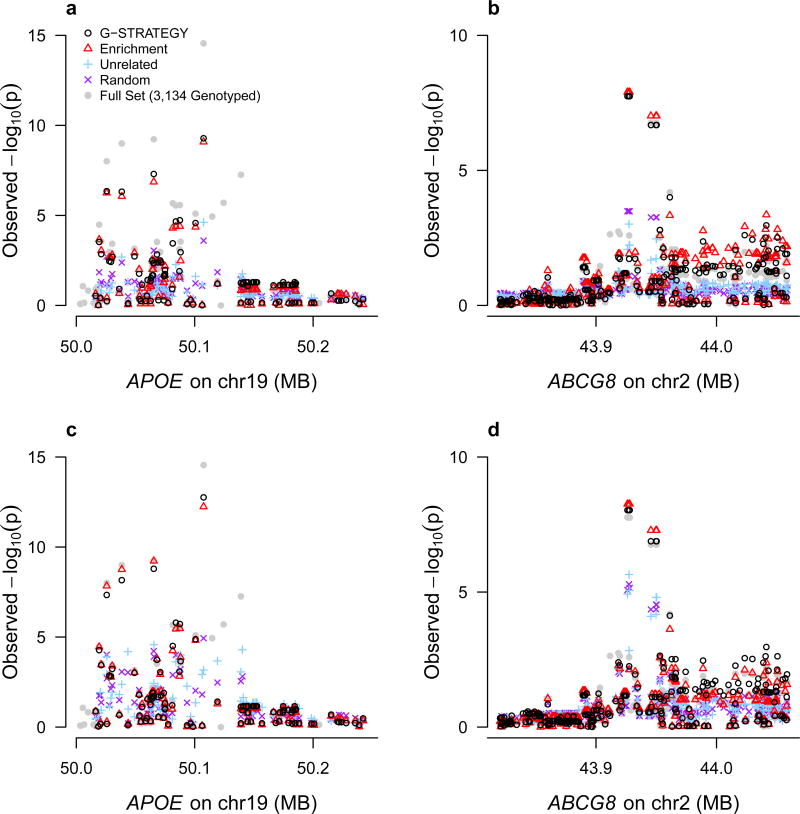
Figures 6 and 7, for HDL and LDL, respectively, compare the regional Manhattan plots for fine mapping within candidate loci, based on different selection strategies. We find that both G-STRATEGY and the Enrichment strategy capture association signals well and yield much higher association peaks than other methods. For association with the HDL gene, CETP, based on n = 1, 000 individuals selected for genotyping, minimum p-values of 2.4 × 10−19 and 1.1 × 10−18 are obtained using G-STRATEGY and the Enrichment strategy, respectively, while the smallest p-value using the Maximally-Unrelated strategy is 4.1 × 10−8. With n = 2, 000 individuals, the corresponding p-values are 2.8 × 10−25, 1.7 × 10−24, and 4.1 × 10−15 using G-STRATEGY, the Enrichment strategy and the Maximally-Unrelated strategy, respectively. The regional Manhattan plots within other top genes, such as LIPC (for HDL), and APOE and ABCG8 (for LDL), reveal similar results.
Figure 6. Manhattan Plots for HDL for Regions within CETP and LIPC, Based on Different Selection Methods.
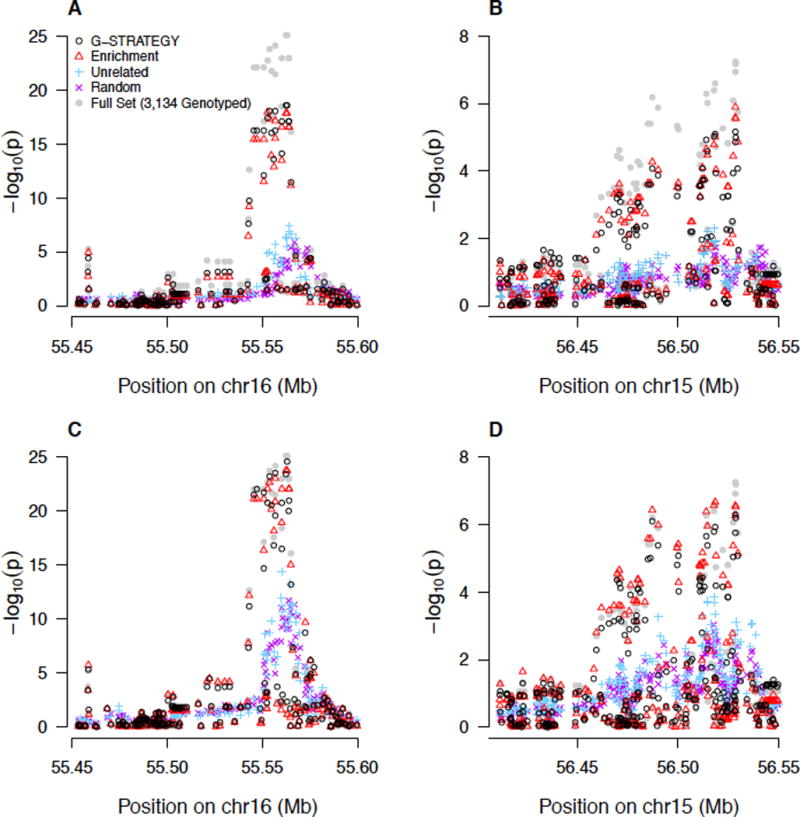
For each of the four selection methods, the reported p-value is the geometric mean of the corresponding p-values at each SNP over 20 runs. The p-values in Panels (A) and (B) are based on selection of n = 1,000 individuals to be genotyped; the p-values in Panels (C) and (D) are based on selection of n = 2,000 individuals to be genotyped. Panels (A) and (C) represent a chromosomal region within CETP; Panels (B) and (D) represent a chromosomal region within LIPC. The gray dots represent the benchmark in which all 3,134 genotyped individuals are selected.
Figure 7. Manhattan Plots for LDL for Regions within APOE and ABCG8, Based on Different Selection Methods.
For each of the four selection methods, the reported p-value is the geometric mean of the corresponding p-values at each SNP over 20 runs. The p-values in Panels (A) and (B) are based on selection of n = 1,000 individuals to be genotyped; the p-values in Panels (C) and (D) are based on selection of n = 2,000 individuals to be genotyped. Panels (A) and (C) represent a chromosomal region within APOE; Panels (B) and (D) represent a chromosomal region within ABCG8. The gray dots represent the benchmark in which all 3,134 genotyped individuals are selected.
In addition to the power evaluation, we perform a real-world example to assess the computational speed of G-STRATEGY. We run G-STRATEGY to select an additional subset of size na = 500 or 1,000 individuals from the AGES-REFINE sample to genotype for the association study with HDL. The HDL dataset consists of 8,030 individuals, among whom n0 = 3, 134 have been previously genotyped. The remaining 4,896 individuals are not yet genotyped, and we assume that they are all available to be selected for genotyping. The run times and memory usage are evaluated using a single processor on an iMac (Mac OS X Lion 10.7.3) desktop with Intel Core i5 (64 bit) 2.5 GHz CPU and 16 GB RAM. Table 3 shows that the memory usage is modest (<700 Mb) and so are the run times (<10 minutes). As G-STRATEGY uses a stochastic algorithm to search for the optimal subset, the actual computing time will be affected by the choice of starting point, the number of iterations, etc. We do not undertake a comprehensive evaluation of how to optimally set tuning parameters in the HDL data application. Instead, we assess the trajectory plot of the G-STRATEGY objective function that is output in the default setting. The trajectory plot in Figure S2 exhibits a smooth transition to a plausible convergence value in reasonable number of steps. The results indicate that the implementation of G-STRATEGY in large-scale studies such as the AGES-REFINE study is computationally feasible.
Table 3.
Run Times and Memory Usage of G-STRATEGY when Applied to the AGES-REFINE HDL Data
| # Individuals to Select for Additional Genotyping (na) |
Memory (Mb) |
Run times (min) |
|---|---|---|
| 500 | 593 | 7.4 |
| 1,000 | 634 | 9.5 |
Note: The AGES-REFINE sample consists of 8,030 individuals, among whom n0 = 3,134 have been previously genotyped. The remaining 4,896 individuals are not yet genotyped, but are all assumed to be available for genotyping.
To illustrate the features of the subset selected by G-STRATEGY, we give as examples two real pedigrees from the AGES-REFINE study. For the family depicted in Figures S3 and S4, we can see that the first individual from that family selected by G-STRATEGY has both the smallest phenotype value and the most extreme enrichment value of the available individuals. When two more individuals are selected (Figure S4), they are the ones with the second smallest and largest phenotype values, who also have the second and third most extreme enrichment values, respectively. This illustrates that G-STRATEGY can often behave similarly to the Enrichment and extreme phenotype selection strategies. However, for the family depicted in Figures S5 and S6, the available individual with the second-highest phenotype value and second most extreme enrichment value is selected by G-STRATEGY in preference to the available individual with the highest phenotype value and most extreme enrichment value, who is selected second. This difference results from the fact that G-STRATEGY also takes into account the correlation among relatives selected for genotyping, which results in a preference for an individual who, in this case, is less closely related to another individual who is already genotyped.
Discussion
When there is a limited sequencing budget, it is of practical importance to prioritize individuals for sequencing, with a view toward maximizing the power of the subsequent association test. We propose G-STRATEGY, a method to optimally choose a fixed-size subset of individuals to sequence or genotype from a sample that includes related individuals. We also propose the closely-related Enrichment strategy.
G-STRATEGY can be thought of as an extension of the classical “selective genotyping” strategy, in which a selected portion of the phenotyped individuals are genotyped. In the context of association testing in a sample that includes related individuals, one way to extend the selective genotyping strategy is to consider an “enrichment value” for each individual rather than a phenotype or phenotypic residual, where the enrichment value of an individual takes into account the phenotypes of the individual’s relatives and his or her kinship coefficient with those relatives. Intuitively, this can be justified by the “enrichment principle”[ Thornton and McPeek, 2007] that says, for example, that in a case-control study, affected (unaffected) individuals with multiple affected (unaffected) relatives tend to be more informative in the association analysis because they are more likely to carry risk (protective) alleles. We have proposed the Enrichment strategy which selects individuals based on extreme enrichment values. G-STRATEGY takes the Enrichment strategy one step further, and in prioritizing individuals for genotyping, it also accounts for the effects, on the association test, of the dependence among relatives’ data.
We have compared G-STRATEGY to other selection strategies, based on both simulations and analysis of HDL and LDL data from the AGES-REFINE study. Our results indicate that the strategies that make use of the enrichment principle (G-STRATEGY and the Enrichment strategy) consistently outperform other strategies that either do not take into account phenotype information on an individual’s relatives (e.g., Rebalanced Founder strategy) or do not take into account phenotype information at all (Maximally-Unrelated strategy and GIGI-Pick). As expected, G-STRATEGY typically outperforms the Enrichment strategy, though the differences can be small, which suggests that most of the advantage of G-STRATEGY comes from the consideration of the individual’s and relatives’ phenotypes, rather than from further taking into account the effect of dependence among individuals on the association test. We implement both G-STRATEGY and the Enrichment strategy in the freely-available G-STRATEGY software. The methods should be helpful for investigators planning sequencing resource allocation and association studies.
G-STRATEGY is applicable to samples containing completely general combinations of related and unrelated individuals, including complex pedigrees with multiple inbreeding loops. The search algorithm is based on simulated annealing and is computationally feasible even for large, complex pedigrees. When the size of the problem is large, there will typically be many close-to-optimal solutions, with negligible differences between their values of the objective function. In that case, it is of little interest to identify the true global maximizer, because many other choices will be almost equally good, especially considering that the true trait model is unknown. The simulated annealing approach in G-STRATEGY lends itself well to this situation. The algorithm is stochastic in nature and can yield a good approximation to the global maximizer. Multiple runs of G-STRATEGY can provide multiple choices of subset to be genotyped that are expected to provide approximately equal power. This can be useful if there are other considerations (such as cost or convenience) that can arise in the choice of whom to genotype, because one can then take into account these other considerations in choosing from among multiple rough equivalent choices of subset of individuals to genotype.
In G-STRATEGY, we condition on phenotypes, covariates, pedigree information, and the information of who is already genotyped, but not on their genotype values, in selecting an additional subset of individuals for genotyping. Another approach[Chen and Abecasis, 2007; Fingerlin et al., 2004; Li et al., 2006] conditions on both pedigree information and genotype information from a non-dense marker panel for all individuals, but not on phenotype information, in choosing a subset of individuals for high-density genotyping or sequencing. The G-STRATEGY approach would be particularly well-suited to situations in which power for an association test with a given phenotype is a priority. It would also be well-suited to the situation in which low-density genotype information is not necessarily available on all individuals. In contrast, the approaches that ignore phenotype information would be well-suited to situations in which power for association with a particular phenotype is not the main goal and all individuals have low-density genotype information available. Note that if one had both phenotype information and non-dense genotype information on all individuals, then use of both pieces of information simultaneously, for choosing a subset of individuals for dense genotyping, could lead to incorrect type 1 error of the subsequent association test.
Supplementary Material
Acknowledgments
This study was supported by National Institutes of Health (NIH) grant R01 HG001645 (to M.S.M.) and by the Icelandic Research Fund grant 130726 (to J.J.). The AGES study is supported by NIH contract N01-AG-1-2100 and the NIA Intramural Research Program. Both the AGES and REFINE studies are also supported by Hjartavernd (the Icelandic Heart Association) and the Althingi (the Icelandic Parliament).
Footnotes
Web Resources
G-STRATEGY source code will be available at http://www.stat.uchicago.edu/~mcpeek/software/
References
- Abney M, Ober C, McPeek MS. Quantitative-trait homozygosity and association mapping and empirical genomewide significance in large, complex pedigrees: fasting serum-insulin level in the hutterites. American Journal of Human Genetics. 2002;70:920–934. doi: 10.1086/339705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Černỳ V. Thermodynamical approach to the traveling salesman problem: An efficient simu-lation algorithm. Journal of Optimization Theory and Applications. 1985;45:41–51. [Google Scholar]
- Chen WM, Abecasis GR. Family-based association tests for genomewide association scans. American Journal of Human Genetics. 2007;81:913–926. doi: 10.1086/521580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung CY, Marchani Blue E, Wijsman EM. A statistical framework to guide sequencing choices in pedigrees. American Journal of Human Genetics. 2014;94:257–267. doi: 10.1016/j.ajhg.2014.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darvasi A, Soller M. Selective genotyping for determination of linkage between a marker locus and a quantitative trait locus. Theoretical and Applied Genetics. 1992;85:353–359. doi: 10.1007/BF00222881. [DOI] [PubMed] [Google Scholar]
- Emond M, Louie T, Emerson J, Zhao W, Mathias R, Knowles M, Wright F, et al. Exome sequencing of extreme phenotypes identifies dctn4 as a modifier of chronic pseudomonas aeruginosa infection in cystic fibrosis. Nature Genetics. 2012;44:886–889. doi: 10.1038/ng.2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fingerlin TE, Boehnke M, Abecasis GR. Increasing the power and efficiency of disease-marker case-control association studies through use of allele-sharing information. American Journal of Human Genetics. 2004;74:432–443. doi: 10.1086/381652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris TB, Launer LJ, Eiriksdottir G, Kjartansson O, Jonsson PV, Sigurdsson G, Thorgeirsson G, et al. Age, gene/environment susceptibility-reykjavik study: multidisciplinary applied phenomics. American Journal of Epidemiology. 2007;165:1076–1087. doi: 10.1093/aje/kwk115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Housen R, Baharloo S, Blankenship K, Raeymaekers P, Juyn J, Sandkuilj L, Freimer N. Genome screening by searching for shared segments: mapping a gene for benign recurrent intrahepatic cholestasis. Nature Genetics. 1994;8:380–386. doi: 10.1038/ng1294-380. [DOI] [PubMed] [Google Scholar]
- Howie B, Fuchsberger C, Stephens M, Marchini J, Abecasis GR. Fast and accurate genotype imputation in genome-wide association studies through pre-phasing. Nature Genetics. 2012;44:955–959. doi: 10.1038/ng.2354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsdottir J, McPeek MS. MASTOR: Mixed-model association mapping of quantitative traits in samples with related individuals. American Journal of Human Genetics. 2013;92:625–666. doi: 10.1016/j.ajhg.2013.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simmulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Lander ES, Botstein D. Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 1989;121:185–199. doi: 10.1093/genetics/121.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebowitz R, Soller M, Beckmann J. Trait-based analyses for the detection of linkage between marker loci and quantitative trait loci in crosses between inbred lines. Theoretical and Applied Genetics. 1987;73:556–562. doi: 10.1007/BF00289194. [DOI] [PubMed] [Google Scholar]
- Lee S, Abecasis G, Boehnke M, Lin X. Rare-variant association analysis: study designs and statistical tests. American Journal of Human Genetics. 2014;95:5–23. doi: 10.1016/j.ajhg.2014.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Boehnke M, Abecasis GR. Efficient study designs for test of genetic association using sibship data and unrelated cases and controls. American Journal of Human Genetics. 2006;78:778–792. doi: 10.1086/503711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR. MaCH: using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genetic Epidemiology. 2010;34:816–834. doi: 10.1002/gepi.20533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ott J, Wang J, Leal S. Genetic linkage analysis in the age of whole-genome sequencing. Nature Reviews Genetics. 2015;16:275–284. doi: 10.1038/nrg3908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in C: the art of scientific computing. New York: Cambrigde University Press; 1992. [Google Scholar]
- Sham P, Purcell S. Statistical power and significance testing in large-scale genetic studies. Nature Reviews Genetics. 2014;15:335–346. doi: 10.1038/nrg3706. [DOI] [PubMed] [Google Scholar]
- Staples J, Nickerson DA, Below JE. Utilizing graph theory to select the largest set of unrelated individuals for genetic analysis. Genetic Epidemiology. 2013;37:136–141. doi: 10.1002/gepi.21684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun L, Cox NJ, McPeek MS. A statistical method for identification of polymorphisms that explain a linkage result. American Journal of Human Genetics. 2002;70:399–411. doi: 10.1086/338660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teslovich TM, Musunuru K, Smith AV, Edmondson AC, Stylianou IM, Koseki M, Pirruccello JP, et al. Biological, clinical and population relevance of 95 loci for blood lipids. Nature. 2010;466:707–713. doi: 10.1038/nature09270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton T, McPeek MS. Case-control association testing with related individuals: A more powerful quasi-likelihood score test. American Journal of Human Genetics. 2007;81:321–337. doi: 10.1086/519497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton T, McPeek MS. ROADTRIPS: Case-control association testing with partially or completely unknown population and pedigree structure. American Journal of Human Genetics. 2010;86:172–184. doi: 10.1016/j.ajhg.2010.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler H, Maitland M, Dolan M, Cox N, Ratain M. Cancer pharmacogenomics: strategies and challenges. Nature Reviews Genetics. 2013;14:23–34. doi: 10.1038/nrg3352. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.