Comparing the Performance of Improved Classify-Analyze Approaches For Distal Outcomes in Latent Profile Analysis

Abstract

Several approaches are available for estimating the relationship of latent class membership to distal outcomes in latent profile analysis (LPA). A three-step approach is commonly used, but has problems with estimation bias and confidence interval coverage. Proposed improvements include the correction method of Bolck, Croon, and Hagenaars (BCH; 2004), Vermunt’s (2010) maximum likelihood (ML) approach, and the inclusive three-step approach of Bray, Lanza, & Tan (2015). These methods have been studied in the related case of latent class analysis (LCA) with categorical indicators, but not as well studied for LPA with continuous indicators. We investigated the performance of these approaches in LPA with normally distributed indicators, under different conditions of distal outcome distribution, class measurement quality, relative latent class size, and strength of association between latent class and the distal outcome. The modified BCH implemented in Latent GOLD had excellent performance. The maximum likelihood and inclusive approaches were not robust to violations of distributional assumptions. These findings broadly agree with and extend the results presented by Bakk and Vermunt (2016) in the context of LCA with categorical indicators.

Introduction

Latent profile analysis (LPA; Gibson, 1959; Lazarsfeld & Henry, 1968) and latent class analysis (LCA; Clogg & Goodman, 1984) are model-based tools for identifying qualitatively distinct subgroups in a population, on the basis of multiple observed indicator variables. LPA and LCA are similar in that they assume a categorical latent variable (called a latent class variable). However, LPA uses normally distributed observed indicator variables to measure the latent variable, whereas LCA uses discrete observed indicator variables. Because LPA uses continuous indicators, it can be used with sums, indices, or factor scores. LPA has been used in many studies in the behavioral sciences, classifying people by, for example, personality traits (Merz & Roesch, 2011; Zhang, Bray, Zhang & Lanza, 2015), psychopathology symptoms (Herman, Bi, Borden & Reinke, 2012), drinking behaviors (Chung, Anthony, & Schafer, 2011), or eating disorder symptoms (Krug et al., 2011). The latent categories in LPA are sometimes called profiles, but we call them classes for comparability with LCA.

The predictive relationship of latent class membership with a distal (i.e., future) outcome is often of interest. For example, Ayer and colleagues (2011) showed that classes found in an LPA of personality variables among adolescents differed in later quantity of alcohol use. The latent class variable is sometimes intended to parsimoniously summarize many predictor variables (Lanza & Rhoades, 2013; Merz & Roesch, 2011). In other cases, the latent classes themselves (i.e., the structure of the relationships among the indicators) are of primary theoretical interest, and questions about their associations with distal outcomes are investigated later (Vermunt, 2010), perhaps to assess the latent class variable’s predictive validity (Collins, 2001). Finally, a latent class variable can be used in a more complex multivariate analysis, such as determining whether class membership moderates the link between treatment condition and outcomes (Herman, Ostrander, Walkup, Silva, & March, 2007). Regardless, methods to estimate accurately the relationship between a latent class variable and observed distal outcome are critical. Such methods have been extensively studied in the context of LCA (Asparouhov & Muthén, 2014; Bakk, Oberski & Vermunt, 2016; Bray, Lanza & Tan, 2015; Lanza, Tan & Bray, 2013). However, they have not been studied in the context of LPA (except for Gudicha & Vermunt, 2013, who studied the related case of LPA with covariates but not distal outcomes specifically). Therefore, this paper will compare methods for linking latent class membership to an observed distal outcome in LPA.

Three-Step vs. One-Step Approaches

Several methods for analysis of distal outcomes in LCA or LPA are available. Classify-analyze, also known as the standard three-step approach, is straightforward: (1) fit the LCA; (2) assign each individual to the latent class with the modal posterior probability for that individual; and (3) estimate the relationship between assigned class membership and the distal outcome. Assigned class membership is treated as if observed and certain. This approach ignores classification error, produces an attenuated estimate (biased towards zero) of the association (Bakk, Tekle, & Vermunt, 2013; Bray et al., 2015; Gudicha & Vermunt, 2013; Vermunt, 2010), and may produce invalid confidence intervals and tests. Because of these concerns, several alternatives have been proposed.

The one-step approach (in the terminology of Bandeen-Roche, Miglioretti, Zeger & Rathouz, 1997) combines the LPA or LCA and the distal outcome in a single model. In this “inclusive” model, the distal outcome is essentially treated as if it were a covariate or additional indicator. This may seem counterintuitive because something later in time (the distal outcome) is used to predict something earlier in time (the latent class membership). However, this distinction is not vital because the goal is to understand an association, not to claim causal precedence. A larger concern is that the inclusion of the distal outcome can influence the LPA measurement model, potentially changing the substantive meaning of the latent classes. In contrast, a three-step approach may seem more natural because it first defines the classes and then compares outcomes across classes (Bakk & Vermunt, 2016; Vermunt, 2010). If the form of the relationship between latent class membership and distal outcome is misspecified in the inclusive model, the estimated distribution of the distal outcome within each class may be affected. This often occurs when a numerical distal outcome is heteroskedastic across classes (Bakk & Vermunt, 2016; Bakk, Oberski, & Vermunt, 2014, 2016). Thus, the one-step approach is not a fully satisfactory replacement for three-step. New methods have been proposed to improve the three-step approach by removing some bias while maintaining its basic structure.

Improved posterior probability estimates

The inclusive classify-analyze approach proposed by Bray, Lanza, and Tan (2015) includes the distal outcome as a covariate in Step 1. Bray et al. (2015) showed that the inclusive classify-analyze approach was less biased than the standard, non-inclusive three-step approach, when model assumptions were met. However, when model assumptions are violated, this method may have the same non-robustness as the one-step method (Bakk & Vermunt, 2016).

In this paper we do not directly address the Lanza, Tan, and Bray (2013) or LTB method, a slightly different approach based on Bayes’ theorem and not directly supported in Latent GOLD. The LTB method is closely related to the inclusive classify-analyze approach with proportional assignment (see Bakk & Vermunt, 2016, p. 22). The LTB method is further discussed by Bakk, Oberski, and Vermunt (2014, 2016).

Improved methods of classification

Both the standard three-step approach and that of Bray, Lanza and Tan (2015) use modal assignment (in the terminology of Vermunt, 2010): when estimating the relation between latent class membership and distal outcome, each individual is considered to belong to her most likely class, ignoring other possibilities. Alternatively, one can perform multiple assignments of class membership using the posterior probabilities; this is referred to as pseudo-class draws. In this method, individuals are randomly assigned to classes according to their posterior probabilities, and then the association between assigned class and distal outcome is estimated. This procedure for class assignment and the subsequent estimation is repeated multiple (e.g., 20) times, and results are combined across draws. However, Peterson, Bandeen-Roche, Budtz-Jørgensen and Jarsen (2012) and Bray, Lanza and Tan (2015) found that using multiple pseudo-class draws in the three-step method produced estimates which were as biased as using modal assignment, or more biased.

A related method, proportional assignment, is a simpler alternative to multiple pseudo-class draws. Proportional assignment treats each individual as belonging partly to each latent class, with weights given by posterior probabilities. Instead of doing multiple imputations for the membership of each individual, with probabilities given by the posterior probabilities (e.g., participant 1 might have a 50% chance of being in Class 1, 30% in Class 2, and 20% in Class 3), a single weighted imputation is constructed (e.g., participant 1 would contribute to the distal mean estimates for Class 1, Class 2, and Class 3, but with weights of .50, .30 and .20). Bray, Lanza, and Tan (2015) conjectured that the bias found in both these methods is due to a mismatch between the imputation model in Steps 1-2 (which omits the distal outcome) and the analysis model in Step 3 (which includes it), and suggested that an inclusive model be used throughout.

Classification error correction

The BCH approach (Bolck, Croon & Hagenaars, 2004) corrects the standard three-step approach by accounting for classification error. It uses the idea that the joint probability distribution of the distal outcome Y and the assigned class variable W is a linear combination of the joint probability distribution of Y and the true latent class variable C, weighted by classification error probabilities. Specifically,

$$P(Y=y,W=w)=\sum _{c=1}^{n_c}P(C=c,Y=y)P(W=w\mid C=c),$$

where n_c is the number of latent classes. Therefore, given the estimated classification probabilities P(W=w|C=c), the probabilities P(Y=y,W=w) can be found by matrix algebra (Bakk et al., 2013; Bolck et al., 2004; Vermunt, 2010). This provides an improved estimate of the association between Y and C, relative to the standard approach which ignores the possibility that W ≠ C.

The BCH approach originally could only be used with categorical distal outcomes, but was later adapted for continuous outcomes (see Bakk, Tekle & Vermunt, 2013; Gudicha & Vermunt, 2013; Vermunt 2010). Previous implementations of BCH sometimes gave uninterpretable negative probability estimates (Bakk, Tekle & Vermunt 2013), but these seem to be avoided in recent versions of Latent GOLD (Vermunt & Magidson, 2015) software; we did not observe any in our simulations. In this paper we consider the improved, not the original, BCH approach. It is possible that if we had considered very small sample sizes, or very poor measurement, these problems might have had a larger chance of occurring (Bakk, Tekle & Vermunt, 2013; Bakk & Vermunt, 2016).

Vermunt (2010) also suggested an alternative correction approach, using maximum likelihood (ML) estimation. In this approach, one builds a new latent class model in Step 3, with the assigned class variable and distal outcome as indicators, and with fixed classification error probabilities calculated from the conditional probabilities of assigned class given true class as estimated in Step 1.

Inclusive classify-analyze, the BCH correction, and the ML correction are each intended to offer better accuracy than the standard three-step approach. However, the conditions under which they succeed or fail require further study. These methods were studied by Asparouhov and Muthén (2014), Bakk and Vermunt (2016), and Bray, Lanza and Tan (2015) for distal outcomes in LCA, but they have not yet been studied for distal outcomes in LPA. In the LCA context, uncorrected approaches were found to be somewhat biased. Inclusive and ML approaches were less biased, except when their assumptions were not met, as in the case of heteroskedasticity; in this case they became much more biased. The BCH approach usually performed well.

It would be reasonable to hypothesize that these findings might also hold in LPA, because LCA and LPA differ only in the nature of their indicator variables and not in the relation of the latent class variable to an external variable. However, to our knowledge, the only currently published investigation of the use of these methods with external variables in LPA was by Gudicha and Vermunt (2013), but they treated the external variables as covariates (predictors of class membership) rather than distal outcomes (predicted by class membership). They found that BCH and ML methods worked well, although they did not investigate situations in which assumptions were violated. In light of these remaining gaps, it is interesting to investigate LPA further with distal outcomes specifically.

Therefore, we conducted a simulation study in Latent GOLD 5.1 to investigate the performance in LPA of the standard three-step approach, the inclusive classify-analyze approach, and the two corrected three-step approaches. We attempted to determine what factors influence the relative performance of these approaches in this context. Also, because distal outcomes in previous simulation investigations were generally either binary or normally distributed, we consider not only binary and normally distributed but also skewed distal outcomes.

Method

A factorial simulation experiment was performed to quantify the effects of distribution shape, measurement quality, relative class size, and effect size on the bias, square root mean squared error (RMSE), and confidence interval (CI) coverage of the methods described above, for estimating within-class means of a distal outcome variable for a three-class LPA. Each method was implemented with modal assignment and with proportional assignment.

Design of the Simulation Experiment

Latent class model

The data-generating model assumes three classes, designated high, medium, and low. The high class has mean +1 on each of five locally (within-class) independent, normally distributed items. The medium and low classes have means of 0 and −1 on each variable, respectively. The within-class error variance of each item is 0.50 for high measurement quality, or 0.75 for low measurement quality. The population proportions of the three classes are set to be equal (proportions 1/3, 1/3, and 1/3), or unequal (proportions .1, .3, .6 for high, medium, and low classes). For poor measurement quality, the scaled entropy (Ramaswamy, DeSarbo, Reibstein, & Robinson, 1993) was approximately .7 to .75. For good measurement quality, Ramaswamy entropy was approximately .8 to .85.

Distal outcome distributions

The data-generating model specifies that people in the high, medium, and low classes (as defined by the indicator variables) also tended to have high, medium, and low distal outcomes. The distribution of the outcome was binary, homoskedastic normal, heteroskedastic normal, or skewed. Table 1 shows the parameters used for each. Bakk and Vermunt (2016) simulated binary and normal but not skewed outcomes.

Table 1.

Distal Outcome Distribution Scenarios Used in Simulations

True Response Probability P(Y=1|C) in Binary Outcome Scenario
Effect Size	High Class	Medium Class	Low Class
Large	0.800	0.500	0.200
Small	0.550	0.500	0.450
True Response Mean E(Y|C) and Standard Deviation in Homoskedastic Normal Outcome Scenario
Effect Size	High Class	Medium Class	Low Class
Large	0.30 (1.00)	0.00 (1.00)	−0.30 (1.00)
Small	0.10 (1.00)	0.00 (1.00)	−0.10 (1.00)
True Response Mean E(Y|C) and Standard Deviation in Heteroskedastic Normal Outcome Scenario
Effect Size	High Class	Medium Class	Low Class
Large	0.60 (3.00)	0.00 (1.00)	−0.60 (1.00)
Small	0.20 (3.00)	0.00 (1.00)	−0.20 (1.00)
True Response Mean E(Y|C) and Standard Deviation in Exponential Skewed Outcome Scenario
Effect Size	High Class	Medium Class	Low Class
Large	1.80 (1.80)	1.40 (1.40)	1.00 (1.00)
Small	1.20 (1.20)	1.10 (1.10)	1.00 (1.00)

For the binary distribution, the response proportions were chosen so that, had class membership been observable, the contingency table of class membership and distal outcome would have Cohen’s w effect size of approximately .5 (large), .3 (medium) or .1 (small) for the χ² test of independence (Cohen, 1988) under the equal class sizes scenario. Similarly, for the homoskedastic normal distribution, the response means were chosen for Cohen’s f of approximately .4 (large), .3 (medium), or.1 (small). The differences in means were doubled in the heteroskedastic condition because the pooled variance was ((3²+1+1)/3)^1/2≈1.9 rather than ((1+1+1)/3)^1/2=1.

The skewed distribution chosen was the single-parameter exponential distribution, used in simple models of survival times; it has density f(y|μ)=μ⁻¹e^y/μ, mean μ, and variance μ². It is inherently right-skewed. The mean values were chosen to give small, medium and large f.

Analysis Procedure for Simulated Data

For each scenario, we generated 1000 replicate datasets with a sample size of 1000 simulated participants each. The data were simulated in R 3.2.1 (R Core Team, 2015), and the LPA (including ML or BCH corrections) was performed in Latent GOLD 5.1 (Vermunt & Magidson, 2015). To save space, results for “medium” effect sizes are available, along with simulation and analysis code, in an online appendix at https://github.com/dziakj1/LpaSims.

LPA parameter estimation

Three alternative LPA models were fit to each dataset. Equal standard deviations for indicators across classes were assumed. The first LPA model was a non-inclusive model (ignoring the outcome variable). The second LPA model included the distal outcome as a covariate, for use with the inclusive approach. In the continuous outcome conditions, a third LPA model included both the distal outcome and its square. This quadratic model is more robust than the usual inclusive model to heteroskedasticity of the outcome across classes (Bakk, Oberki & Vermunt, 2016).

Estimation of class-specific outcome probabilities (binary case) or means (continuous case)

The class-specific response distribution was estimated using the following methods.

1. Standard (unadjusted) three-step, based on the non-inclusive model

2. ML-adjusted three-step, based on the non-inclusive model

3. BCH-adjusted three-step, based on the non-inclusive model

4. Unadjusted three-step, based on the inclusive model

5. Unadjusted three-step, based on the quadratic model

Each of the methods above was performed with modal and with proportional assignment. The quadratic model was omitted for binary data, because 0 and 1 equal their squares. Finally, we defined an “oracle” method (a term from Fan & Li, 2001), by directly computing the average of the simulated participants belonging to each true class. An oracle method is impossible with real data (latent class membership is unobserved by definition) but useful for comparison.

Assessment of accuracy for each method

The accuracy of the estimated class-specific mean of the distal outcome was assessed in terms of bias and RMSE averaged across the three classes in each dataset. Coverage of nominal 95% confidence intervals was also assessed. Label switching was handled by finding the permutation of estimated classes for each dataset that provides a set of item response means as close as possible to the data-generating model. This generally meant labeling the class with the highest average item mean as Class 1, the second highest as Class 2, the lowest as Class 3. After reordering the parameters to have consistent class labels, the bias, RMSE, and coverage were calculated.

Results

The procedures practically always converged. The only failures were for proportional ML in misspecified cases (heteroskedastic or exponential skewed), which still converged more than 99% of the time. Results for selected scenarios are discussed below. For example, results are only shown for the poor measurement (low class separation) scenarios, which provide a more challenging test of performance and robustness. More complete results are available in the online appendix.

Binary Outcome

Bias

The bias in estimating the class-specific response probabilities was generally small. The ML-corrected and BCH-corrected estimates were essentially unbiased. The inclusive three-step estimate had tiny bias (less than. 01, for a parameter on the order of 1). The unadjusted estimate had noticeable but small bias. Bias was greater when measurement quality was low and when effect size was large. Unadjusted proportional assignment had slightly higher bias than unadjusted modal assignment.

The differences in bias by class among the unadjusted and adjusted methods are shown in Table 2. The bias for the standard method is conservative: it attenuates differences between classes. The bias for the inclusive method, although extremely small, is anticonservative: it slightly exaggerates differences between classes. The inclusive bias may come from the distal outcome acting as part of the measurement model, perhaps without the user’s intent. This additional model flexibility can sometimes cause overfitting.

Table 2.

Bias by Class for Binary Outcome Probabilities in Selected Conditions

	Class 1	Class 2	Class 3
True P(Y|C)	0.800	0.500	0.200
Bias in Estimated P(Y|C) under Poor Measurement Quality
Unadjusted (Modal)	−0.029	−0.002	0.030
(Proportional)	−0.043	−0.001	0.043
ML (Modal)	−0.001	−0.002	0.002
(Proportional)	−0.001	−0.001	0.001
BCH (Modal)	−0.001	−0.002	0.001
(Proportional)	0.000	−0.001	0.001
Inclusive (Modal)	0.010	−0.002	−0.010
(Proportional)	0.001	−0.002	0.000

Note. This table contains results only for scenarios with large effect size. For ML and BCH, only modal assignment is shown, because the modal and proportional assignment options provided very similar results.

Estimation error

Table 3 shows the RMSE for the outcome probability within each class, averaged across classes. In general, it is small and similar for all of the methods. When the true effect size is small, the unadjusted methods sometimes outperform the corrected methods. The unadjusted methods are so simple that they have relatively little sampling variance, and if the effect size is small, the attenuation is also small in an absolute sense, so there is not much bias either.

Table 3.

Root Mean Squared Error Across Classes for Binary Outcome Probabilities

Root Mean Squared Error
Class Proportions:	Even		Uneven
Effect Size:	Small	Large	Small	Large
Unadjusted (Modal)	0.028	0.036	0.036	0.048
(Proportional)	0.026	0.043	0.032	0.060
ML (Modal)	0.033	0.031	0.043	0.041
(Proportional)	0.032	0.030	0.041	0.039
BCH (Modal)	0.033	0.031	0.043	0.041
(Proportional)	0.032	0.030	0.041	0.039
Inclusive (Modal)	0.035	0.033	0.047	0.044
(Proportional)	0.032	0.030	0.042	0.039
Oracle	0.027	0.024	0.036	0.030

Note. This table contains results only for scenarios with large effect size and poor measurement.

Coverage

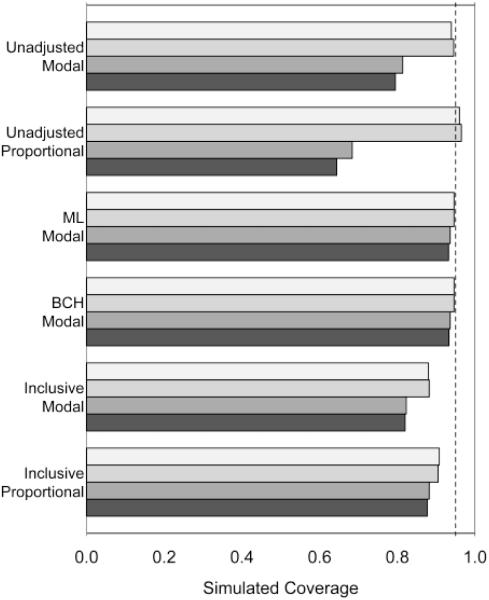
Figure 1 shows the simulated CI coverage obtained for nominal 95% confidence intervals for class-specific outcome probabilities. The unadjusted methods perform poorly, but ML and BCH perform well. The inclusive approaches have rather poor coverage, perhaps because the standard errors are underestimated due to slight overfitting. Among unadjusted methods, proportional assignment has poorer coverage than modal assignment.

Figure 1.

Simulated coverage for 95% confidence intervals of selected methods in low measurement quality scenarios with binary outcomes. The four bars for each method, in order from top (light) to bottom (dark), represent coverage for the following four conditions: small effect size, even class sizes; small, uneven; large, even, large, uneven. Results for high measurement quality were similar. Larger effect sizes and uneven class sizes resulted in poorer coverage for uncorrected techniques. The BCH and ML methods with proportional assignment are omitted here as their coverage was very close to that of the corresponding method with modal assignment.

Continuous Outcomes

For brevity, we describe the homoskedastic normal, heteroskedastic normal, and exponential skewed results together. In these scenarios, the inclusive methods implicitly assumed homoskedastic normality of the distal outcome; the latter two scenarios therefore served to assess robustness.

Bias

Table 4 shows the absolute bias, averaged across conditions, under the various methods. In the homoskedastic scenario, no method had large bias, although the unadjusted methods had slight bias. However, in the heteroskedastic scenario, the ML and non-quadratic inclusive methods had extremely high bias. The BCH and quadratic methods had little or no bias.

Table 4.

Mean Absolute Bias Across Classes for Outcome Means E(Y|C) of Continuous Distal Outcomes

Distribution:	Homoskedastic		Heteroskedastic		Exponential
Classes:	Even	Uneven	Even	Uneven	Even	Uneven
Unadjusted (Modal)	0.020	0.029	0.040	0.059	0.028	0.040
(Proportional)	0.029	0.047	0.057	0.093	0.039	0.063
ML (Modal)	0.001	0.003	0.367	0.338	0.044	0.329
(Proportional)	0.001	0.003	0.307	0.724	0.077	0.767
BCH	0.001	0.003	0.001	0.008	0.003	0.008
Inclusive (Modal)	0.008	0.015	0.487	0.153	0.009	0.018
(Proportional)	0.001	0.001	0.475	0.134	0.003	0.006
Quadratic (Modal)	0.008	0.015	0.015	0.027	0.008	0.019
(Proportional)	0.001	0.001	0.002	0.002	0.002	0.006
Oracle	0.001	0.001	0.002	0.003	0.002	0.003

Note. This table contains results only for scenarios with large effect size and poor measurement. For BCH, only modal assignment is shown, because modal and proportional assignment were found to give identical results in LatentGOLD for continuous distal outcomes.

In the skewed scenario, the ML approach sometimes failed due to misspecification, but the other methods did not fail; in particular, the BCH method had practically no bias. One might ask why the inclusive method performed adequately despite non-normality. Possibly, because a single parameter controls both mean and variance in the exponential distribution, only one regression parameter per class was needed. Thus, a quadratic term was unnecessary for this distribution, but might be needed for others.

Table 5 shows the direction of biases for each class, analogous to Table 2. In the heteroskedastic scenario, the ML method cannot distinguish between classes on the distal outcome, whereas the inclusive method actually reversed the order of Classes 1 and 2. The unadjusted method is biased in a conservative direction, whereas the quadratic inclusive method is slightly anticonservative.

Table 5.

Bias by Class for Estimation of Outcome Means E(Y|C) in Selected Conditions

Homoskedastic Normal True Distribution
	Class 1	Class 2	Class 3
True E(Y|C)	0.300	0.000	−0.300
Unadjusted	−0.031	−0.001	0.030
ML	−0.002	−0.001	0.001
BCH	−0.002	−0.001	0.001
Inclusive	0.011	−0.002	−0.011
Quadratic	0.011	−0.001	−0.011
Heteroskedastic Normal True Distribution
	Class 1	Class 2	Class 3
True E(Y|C)	0.600	0.000	−0.600
Unadjusted	−0.059	0.000	0.060
ML	−0.513	−0.039	0.550
BCH	−0.002	0.000	0.003
Inclusive	−0.969	0.370	0.122
Quadratic	0.014	0.012	−0.018
Exponential True Distribution
	Class 1	Class 2	Class 3
True E(Y|C)	1.800	1.400	1.000
Unadjusted	−0.039	−0.002	0.044
ML	0.032	−0.064	0.037
BCH	0.000	−0.004	0.006
Inclusive	0.016	−0.003	−0.009
Quadratic	0.014	−0.002	−0.008

Note. In order to conserve space, this table contains only results for high effect size scenario, poor measurement quality, even class size scenario, and modal assignment method.

Estimation Error

Table 6 shows the RMSE under the different methods, again averaging across classes. Under the homoskedastic condition, all methods had low error. Under heteroskedasticity, the ML and non-quadratic inclusive approaches had extremely high error, but the BCH and quadratic inclusive approaches had fairly little error. Under the skewed condition, the ML approach (which had assumed normality) had high error, but the other approaches did fairly well. These results for RMSE largely agree with those for absolute bias in Table 4. One surprise was that, in terms of RMSE, the unadjusted methods often outperformed the adjusted methods and sometimes even performed comparably to the oracle. This is explainable as a bias-variance tradeoff, similar to that of ridge regression versus ordinary least squares regression (see Hastie, Tibshirani & Friedman, 2013). Their slight attenuation bias helped control unusual estimates that sometimes occurred for the other methods due to random noise.

Table 6.

Root Mean Squared Error Across Classes for Outcome Means E(Y|C) of Continuous Distal Outcomes

	Homoskedastic		Heteroskedastic		Exponential
	Even	Uneven	Even	Uneven	Even	Uneven
Unadjusted (Modal)	0.060	0.081	0.120	0.190	0.088	0.127
(Proportional)	0.061	0.082	0.123	0.184	0.087	0.123
ML (Modal)	0.064	0.088	0.519	0.595	0.105	0.841
(Proportional)	0.062	0.085	0.392	1.118	0.121	1.413
BCH (Modal)	0.064	0.088	0.126	0.210	0.096	0.141
Inclusive (Modal)	0.068	0.097	1.600	1.041	0.098	0.154
(Proportional)	0.062	0.086	1.524	0.970	0.091	0.136
Quadratic (Modal)	0.068	0.097	0.119	0.209	0.098	0.152
(Proportional)	0.063	0.086	0.115	0.193	0.092	0.136
Oracle	0.054	0.071	0.109	0.183	0.077	0.117

Note: Only the results for low measurement quality and modal assignment are shown. For BCH, only modal assignment is shown, because modal and proportional assignment were found to give identical results in LatentGOLD for continuous distal outcomes.

Confidence interval coverage

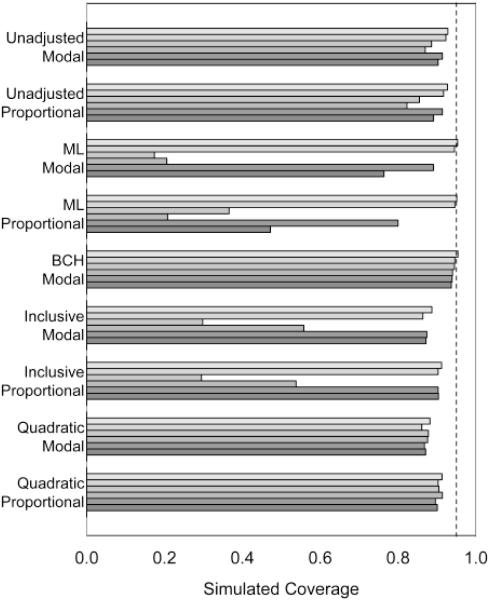
Figure 2 shows the simulated CI coverage for nominal 95% confidence intervals. In the homoskedastic scenario, the methods that have bias (unadjusted, inclusive and quadratic) have poorer coverage. Confidence intervals typically account for random variability but not for systematic bias; bias will cause them to overstate confidence (to mistake precision for accuracy).

Figure 2.

Simulated coverage for 95% confidence intervals of selected methods in low measurement quality, high effect size scenarios with continuous outcomes. The six bars for each method, in order from top (light) to bottom (dark), represent coverage for the following six conditions: homoskedastic distribution with even class sizes, homoskedastic with uneven class sizes, heteroskedastic with even, heteroskedastic with uneven, exponential skewed with even, and exponential skewed with uneven. Class proportions have relatively little effect on coverage, but distribution shape has a large effect on coverage, with the ML and inclusive methods having very poor coverage for the heteroskedastic distribution. The BCH proportional method was omitted as its coverage was identical with BCH modal.

In the heteroskedastic condition, the ML and non-quadratic inclusive methods did poorly because of large bias. The unadjusted methods did well for small effect sizes but poorly for large ones; this is because their bias increases with effect size. In the skewed condition, the ML method sometimes has very poor coverage, although the inclusive method does not do as badly.

Discussion

The inclusive approach (i.e., using the distal outcome as a covariate) was non-robust to violations of an implicit assumption pointed out by Bakk and Vermunt (2016) and Bakk, Oberski, and Vermunt (2016), that the distribution of a normally distributed distal outcome has the same variance in each class. This assumption is relatively implausible. It is not directly testable, because the estimated variances of the classes in an inclusive approach, which assumes homoskedasticity, will be biased towards homoskedasticity even if this alters the class definitions. Thus, inclusive methods for relating latent classes to distal outcomes should be used only when either the outcome is binary or at least a quadratic term is included.

Similarly, the ML correction, at least as currently implemented in Latent GOLD, fails in the presence of heteroskedasticity or unmodeled non-normality. This is apparently recognized by the Latent GOLD developers; the current graphical interface presents a warning if the ML correction is requested with a continuous outcome, and recommends BCH.

The BCH approach may be the best readily available solution for including a distal outcome in an LPA. This agrees with the findings of Bakk and Vermunt (2016) for LCA. Further research is warranted, however, because it is unknown whether there are situations that might cause the BCH approach to fail. Future study is also needed on the performance of inclusive approaches or BCH in more complex models with moderators or mediators (Bray et al., 2015).

Limitations of the Current Study

This study did not consider the least square class approach (Peterson et al., 2012), another recently proposed alternative. This method requires interpreting multidimensional latent scores, and does not seem to be as widely supported in current software.

Generally there was no advantage to proportional over modal assignment. It is possible that somewhat higher coverage could have been obtained by using random pseudo-class draws instead of proportional weights, if the uncertainty of the results in each draw had been combined as in multiple imputation (see Schafer, 1999), simply because this would have made the estimated standard errors larger. This method does not appear to be currently available in Latent GOLD. However, making the estimated standard errors larger would only provide a possible improvement in coverage, not estimation performance, relative to proportional assignment. Importantly, Asparouhov and Muthen (2014) and Bray, Lanza and Tan (2015) found that pseudo-class draws could be noticeably more biased than modal assignment. Therefore, in general pseudo-class draws are not an ideal solution. It is also possible that for some methods and scenarios, confidence interval coverage could have been improved using bootstrapping as in Bakk, Oberski, and Vermunt (2016), but we have not explored this here.

Finally, although we have explored the consequences of violating distributional assumptions about the outcome variables (for example, the effects of heteroskedasticity or skew), we did not explore the consequences of breaking distributional assumptions about indicator variables. The latter issue is important but beyond the scope of this paper.

Conclusion

We investigated the relative performance of three recently proposed improvements to the standard three-step approach (inclusive model, BCH correction, and ML correction) in the context of LPA with a binary or continuous outcome variable. Various scenarios were considered, involving different levels of measurement quality, relative latent class size, and strength of association between latent class and distal outcome. Results agreed with Bakk and Vermunt (2016) that Latent GOLD’s modified implementation of the BCH approach has excellent and robust performance.