Collagen Organization in Facet Capsular Ligaments Varies With Spinal Region and With Ligament Deformation

Abstract

The spinal facet capsular ligament (FCL) is primarily comprised of heterogeneous arrangements of collagen fibers. This complex fibrous structure and its evolution under loading play a critical role in determining the mechanical behavior of the FCL. A lack of analytical tools to characterize the spatial anisotropy and heterogeneity of the FCL's microstructure has limited the current understanding of its structure–function relationships. Here, the collagen organization was characterized using spatial correlation analysis of the FCL's optically obtained fiber orientation field. FCLs from the cervical and lumbar spinal regions were characterized in terms of their structure, as was the reorganization of collagen in stretched cervical FCLs. Higher degrees of intra- and intersample heterogeneity were found in cervical FCLs than in lumbar specimens. In the cervical FCLs, heterogeneity was manifested in the form of curvy patterns formed by collections of collagen fibers or fiber bundles. Tensile stretch, a common injury mechanism for the cervical FCL, significantly increased the spatial correlation length in the stretch direction, indicating an elongation of the observed structural features. Finally, an affine estimation for the change of correlation length under loading was performed which gave predictions very similar to the actual values. These findings provide structural insights for multiscale mechanical analyses of the FCLs from various spinal regions and also suggest methods for quantitative characterization of complex tissue patterns.

1. Introduction

The spinal facet joints are complex intervertebral anatomical structures whose injury can lead to pain [1–6]. The facet joints are positioned bilaterally and symmetrically on the posterolateral aspects of each spinal motion segment and provide the articulation of the lateral mass of adjacent vertebrae (Fig. 1). Like the other synovial joints, the spinal facet joint is fully enclosed by a capsular ligament. The FCL provides mechanical support, and couples and resists motions to help to guide the relative movement between the articular facets. The FCL is mainly composed of dense collagen fiber bundles and elastin fibers that withstand the tensile and shear loading [1,6,7], such as that which occurs during the spinal loading and motion [8–10]. Differences in the loading demands for the cervical and lumbar FCLs are attributable to many factors: varied spinal motions, distinctive ligament geometry, and distinctive vertebral anatomy in different regions across the spine [1,9,11]. For example, the orientation angles of the cervical facet articulation are 70–96 deg with respect to the sagittal plane and 20–78 deg with respect to the axial plane [12,13]. In contrast, the lumbar facets are oriented 15–70 deg relative to the sagittal plane and 82–86 deg relative to the axial plane [1,14]. In addition to their macroscopic differences, the FCLs in the cervical and lumbar regions may have dissimilar microscopic architectures that affect and adapt to tissue loading. To the best our knowledge, however, there has been no microstructural comparison between the cervical and the lumbar FCL, limiting our understanding of the structure–function relationships of this ligament.

Fig. 1.

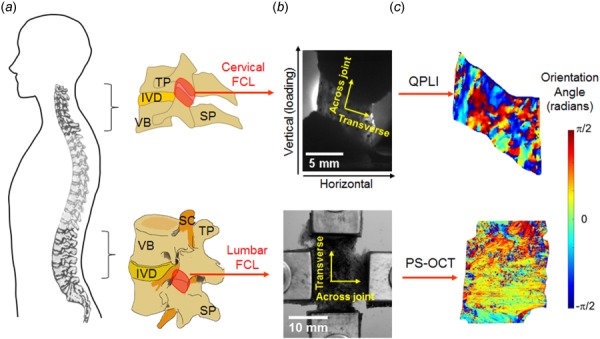
Anatomy and imaging of FCLs in the cervical and lumbar spinal regions. (a) Schematics showing the lateral view of the spine and vertebrae to demonstrate the overall anatomy of the cervical and lumbar facet joints and the location of the FCL in each spinal region. (b) The relevant anatomical and loading directions are labeled on the grayscale images of isolated cervical and lumbar FCLs positioned on the mechanical testing devices. (c) Orientation angles showing collagen alignment measurements using the quantitative polarized light imaging (QPLI) and polarization-sensitive optical coherence tomography (PS-OCT) for cervical and lumbar FCLs, respectively. TP: transverse process; SP: spinous process; IVD: intervertebral disk; VB: vertebral body; and SC: spinal cord.

With the advent of new biomedical imaging tools, especially polarized-light-based tools, it has become possible to study the FCL microstructure, which has enabled studies to define the relationships between microstructure and mechanical functions [15–19]. Since collagen fibers constitute the major component of the FCL, collagen fiber orientation3 has been suggested by numerous previous ex vivo and in vitro studies to play a key role in FCL mechanics [6,16,19]. Although there are histological studies showing that both the cervical and lumbar FCLs contain regions with parallel and unaligned fibers [4,6], evidence of the anisotropy and heterogeneity in collagen organization for an entire ligament and across FCLs from different spinal levels is very limited. This information is critical in understanding, and possibly explaining, the mechanical behavior of the FCL, especially the nonuniform capsule strains of the human cervical and lumbar facets under flexion, extension, bending, and rotation [1,8,11,20].

Beyond its mechanical function, the sensory function of the FCL may also be affected by its fibrous microstructure. The FCL has been increasingly recognized as a sensory organ due to its innervation by mechanoreceptors and nociceptors [2,4,21,22]. Indeed, it has been identified as a common source of posttraumatic neck pain and chronic lower back pain [1,2,23]. Nerve fibers that innervate regions of the FCL with irregular or highly organized collagen fibers may be injured to different extents when the FCL undergoes large, heterogeneous deformations. The previous ex vivo and in vitro studies have provided evidence for the dependence of nociceptive signaling on the orientation of collagen fibers surrounding the neurons [17,24]. Specifically, local collagen disorganization has been observed during loading of the cervical FCLs at strains that induce pain in vivo [16,25,26], and stretch-induced collagen realignment affects the nociceptor activation in in vitro neuron–collagen constructs [24]. To begin to understand the relationships between collagen fiber kinematics and possible neurophysiological effects, and to identify injury-prone regions in the FCL for potential treatment and/or protection, the fibrous structure of the FCL and its response to loading must be characterized. Thus, two hypotheses were evaluated in this work: (1) that the tissue-level heterogeneity of the collagen fiber network in the FCL varies between the cervical and lumbar regions, and (2) that structural differences become more pronounced when the tissue is stretched.

2. Materials and Methods

2.1. Quantitative Polarized Light Imaging of Cervical Facet Capsular Ligaments.

The fiber orientation in cervical FCLs at rest in a prestressed unstretched configuration and during loading were obtained previously using a QPLI system [15,16]. This system was integrated with a tensile testing machine (Instron, Norwood, MA) and acquired real-time pixelwise collagen alignment maps during loading, based on the linear birefringence of collagen fibers [16,27]. Briefly, FCL specimens from the C4/C5 joints (n = 7; age 63 ± 15 yr; two females) were prestressed to 5 kPa (Fig. 1(b)). Polarized light images were acquired at 12.5 pixel/mm resolution in the preloaded reference position and during continuous tensile loading until ligament failure occurred. The measured light intensity was fit to a harmonic equation; the average fiber orientation direction and the strength of the fiber alignment in the mean alignment direction (measured as the retardation) at each pixel were determined based on the phase and amplitude of the harmonic responses [25,27]. Fiber alignment maps (Fig. 1(c)) were created at increments of 1 mm displacement (approximately 1.18 stretch ratio) until ligament failure at approximately 1.55 stretch ratio; detailed mechanical information for each specimen is provided in Table 1. Spatial maps of collagen fiber orientation before and during tensile loading were analyzed via autocorrelation analysis as described below.

Table 1.

Sample information of cervical and lumbar FCLs

Cervical FCLsa				Lumbar FCLsa
Sample ID	Widthb (mm)	Lengthb (mm)	Rupture displacement (mm)	Sample ID	Widthb (mm)	Lengthb (mm)
C1	6.12	6.09	2.28	L1	12	23.16
C2	7.24	5.47	3.81	L2	13	20
C3	8.74	6.38	2.58	L3	12.16	19.16
C4	5.77	4.43	3.22	L4	14	19.16
C5	6.58	4.94	1.69	L5	18.16	18.16
C6	7.52	5.37	4.53	L5	10	21
C7	8.37	6.60	3.64
Avg	7.19	5.61	3.11	Avg	13.22	20.11
SD	1.11	0.79	0.98	SD	2.76	1.77

^aThe average thickness for cervical FCLs is 0.42 ± 0.07 mm; the average thickness for lumbar samples is 2.65 ± 0.30 mm [37].

^bWidth and length correspond to the medial–lateral and superior–inferior directions, respectively.

2.2. Optical Coherence Tomography of Lumbar Facet Capsular Ligaments.

Because the lumbar FCL is roughly five times thicker than the cervical FCL (Table 1) and less transparent, QPLI is not a viable imaging tool for measuring the collagen matrix organization in the lumbar FCL. However, the polarization-sensitive optical coherence tomography (PS-OCT) can be effective for structural characterization of the lumbar FCL [28]. As such, PS-OCT was used to image lumbar FCL samples in a prestressed resting state [19]. Briefly, lumbar L4/L5 FCL specimens (n = 6; 51 ± 12 yr; one female) were clamped biaxially and pulled with ∼1 N force on each side to make them as flat as possible (Fig. 1(b)). Samples were then imaged using the PS-OCT system (resolution of ∼250 pixel/mm), with multiple images being tiled together to produce a single image of fiber orientation over the entire lumbar FCL sample (Fig. 1(c)). The phase retardance and optic axis quantified the strength of the alignment of fibers and aggregated in-plane collagen fiber orientation, respectively.

2.3. Spatial Autocorrelation Calculation.

The orientation imaging provides the fiber direction $(\mathit{x})$ at each point located at $\mathit{x}$ in the two-dimensional region being imaged. For simplicity, we used cosine of the orientation angles to study the correlation in the orientation fields. The autocorrelation [29] of the orientation angle's cosine at a distance $\delta$ can be defined as follows (Fig. 2):

Fig. 2.

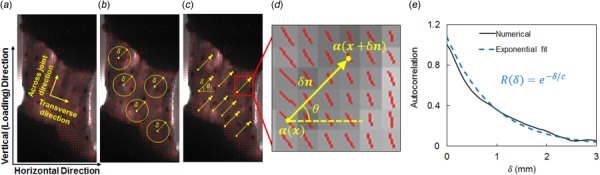
Image-based spatial correlation analysis of collagen orientation in the facet capsular ligaments. (a) A representative vector plot showing the derived spatial collagen alignment from polarized light images (orientation and length of lines indicate the direction and strength of alignment) and relevant anatomical and loading directions for the spatial correlation calculation. (b) Isotropic (angle averaged) and ((c) and (d)) directional (along θ) correlations of orientation α were evaluated by averaging over pairs of points separated by δ. (e) Correlation length, c, was extracted by fitting an exponential function to the calculated autocorrelation.

$$R(\delta )=\frac{E\left[c^{\prime }\left(\mathit{x}\right)c^{\prime }\left(\mathit{x}+\delta \mathit{n}(\theta )\right)\right]}{{\sigma }_c^2}$$ (1)

where E is the expected value operator, which averages over all values of θ and vectors $\mathit{x}$ in the domain. The vector $\mathit{n}$ is of unit length and points in the direction given by $\theta ,$ that is, the vector $[\text{cos}\hspace{0.17em}\theta ,\hspace{0.17em}\text{sin}\hspace{0.17em}\theta ]$. So, $E[c^{\prime }(\mathit{x})c^{\prime }(\mathit{x}+\delta \mathit{n}(\theta ))]$ is the average of the product of $c^{\prime }$ values for all possible pairs of pixels located at a distance $\delta$. The function $c^{\prime }$ measures the deviation of an orientation from the average value, i.e., $c^{\prime }(\mathit{x})=\text{cos}\hspace{0.17em}(\alpha (\mathit{x}))-E[\text{cos}\hspace{0.17em}(\alpha (\mathit{x}))]$. The expression $E[\text{cos}\hspace{0.17em}(\alpha (\mathit{x}))]$ gives the average of the cosine of all orientation values in an orientation map, so $E[c^{\prime }(\mathit{x})]=0$, and $R(\delta )$ is greater than zero if the fiber orientation angles at points a distance δ apart are positively correlated. $R$ is normalized by ${\sigma }_c^2,$ the variance of $\text{cos}\hspace{0.17em}(\alpha (\mathit{x}))$ over the problem domain, so $R=1$ for perfectly correlated orientations.

The autocorrelation function defined in Eq. (1) includes averaging over all possible directions of the unit vector $\mathit{n}$, i.e., over $\theta \in (0,\pi )$. To numerically calculate $R(\delta )$, the expected value, $E$, was evaluated by starting from a point inside the sample, located at $\mathit{x}$, and calculating $c^{\prime }(\mathit{x})c^{\prime }(\mathit{x}+\delta \mathit{n}(\theta ))$ for every pixel located at a distance $\delta$. Then, $\mathit{x}$ was changed to a new pixel, and the calculation was repeated (Fig. 2(b)). After trying all possible pixels for $\mathit{x}$, the expected value was found by averaging all evaluated values $c^{\prime }(\mathit{x})c^{\prime }(\mathit{x}+\delta \mathit{n}(\theta ))$.

In some cases, one is particularly interested in a specific direction, such as the bone-to-bone direction or the loading direction. In this case, the autocorrelation measure for a specific direction ${\theta }_i$, $R(\delta ,{\theta }_i)$, becomes

$$R\left(\delta ,{\theta }_i\right)=\frac{E\left[c^{\prime }\left(\mathit{x}\right)c^{\prime }\left(\mathit{x}+\delta \mathit{n}\left({\theta }_i\right)\right)\right]}{{\sigma }_c^2}$$ (2)

In Eq. (2), the expected value was calculated by starting from a point at $\mathit{x}$, finding another point at distance $\delta$ and orientation ${\theta }_i$ (with respect to the horizontal direction) and evaluating $c^{\prime }(\mathit{x})c^{\prime }(\mathit{x}+\delta \mathit{n}({\theta }_i))$. Then, all possible pixels for $\mathit{x}$ were tried to repeat the previous step for all possible pairs of pixels (Figs. 2(c) and 2(d)). The expected value is the average of all calculated values $c^{\prime }(\mathit{x})c^{\prime }(\mathit{x}+\delta \mathit{n}({\theta }_i))$. To compare structural differences between cervical and lumbar FCLs in the prestressed, unstretched configuration, the autocorrelation was calculated using Eq. (1), averaging over all orientations in the plane (Eq. (1)), as well as in the across-joint and transverse directions, using Eq. (2) (Fig. 2). For cervical FCLs, the transverse direction was defined by connecting the midpoints of the medial and lateral boundaries of the ligament, and the across-joint direction was constructed orthogonal to the transverse direction (Fig. 1). For the lumbar samples, the across-joint and transverse directions were defined as the medial–lateral and superior–inferior directions and were aligned with the grips that held the samples in place when the images were taken (Fig. 1).

In addition to comparing cervical and lumbar samples, structural changes in the cervical FCL under stretch were also evaluated. Specifically, the autocorrelation function was computed for images taken during uniaxial tensile loading of the cervical FCLs. As above, the isotropic autocorrelation function, as well as direction-specific autocorrelations for the loading (vertical) and cross-loading (horizontal) directions, was calculated (Fig. 2).

2.4. Structural Analysis Using Autocorrelation.

Autocorrelation functions express the way a stochastic field fluctuates in space and can be approximated with exponential, stretched exponential, or power functions. If the autocorrelation follows an exponential decay, $R(\delta )\sim \hspace{0.17em}\text{exp}(-\delta /c)$, constant c is called the correlation length [30,31], which provides a measure of the size of subdomains over which the respective field is close to being constant. The autocorrelation function for the cervical FCL can be approximated using an exponential function (Fig. 2(e)). Therefore, the correlation length was evaluated directly by fitting an exponential function to the measured autocorrelation for each sample and loading state (Fig. 2(e)). In the case of the FCL, the correlation length represents the size of the ligament subdomains over which the collagen orientation is approximately identical. The correlation length was calculated separately for the cervical and lumbar FCLs at the unstretched resting state to assess regional differences in FCL's microstructure. A two-way analysis of variance compared differences in correlation length with the spinal region and alignment direction being the two factors. For the cervical FCL extension tests, the correlation length was calculated at 1 mm increments in displacement (1.18 stretch ratio on average) until the tissue damage was detected. Four of the seven samples sustained no tissue rupture before 3 mm displacement (Table 1). The correlation lengths of these four samples at 0–3 mm displacements in the horizontal, vertical, and average directions were compared using a two-way repeated measures analysis of variance with post hoc Tukey test. To evaluate the relationships between the correlation length and the imposed regional strain, the mean maximum principal strain across each four-node elements was computed by tracking the position of the fiduciary markers (Fig. 1(b)) during ligament loading.

2.5. Correlation Length in Affine Deformation.

In uniaxial stretch of a material, if strain at each point inside the sample equals the externally applied strain, the deformation is affine. Deviations from the applied strain at each point in the material are nonaffine strains [32,33]. Autocorrelations were calculated by computationally imposing an affine uniaxial stretch on each of the samples and comparing the resulting correlations against the actual autocorrelations to study the degree of deformation nonaffinity.

An affine estimation of the orientation maps under tensile loading was calculated using the orientation maps at the prestressed resting state, the applied stretch ratio in the vertical direction, and an estimation of the average stretch ratio in the horizontal direction. The stretch ratio in the lateral direction was calculated by dividing the sample's relative change of area by the vertical stretch ratio. The affine estimation was evaluated by resizing the height and width of each pixel by the FCL vertical and horizontal stretch ratios, respectively, while accounting for the rotation of the pixel's orientation. For example, if a hypothetical square pixel had dimensions 0.1 mm and an orientation value of $\pi /4$ rad before deformation, and if the sample was stretched to twice its size in the vertical direction without contracting in the lateral direction, the pixel would deform into a rectangle 0.1 mm in width and 0.2 mm in height. The pixel's orientation would be transformed affinely to 1.11 rad. We repeated this procedure for all pixels to calculate an affinely transformed orientation map. We evaluated the autocorrelation functions using these maps and calculated affine estimations of the correlation lengths.

3. Results

3.1. Anatomic Regional Dependence of Collagen Architecture.

FCLs from the cervical and lumbar spines exhibit different collagen fiber organization; high intra- and intersample variability was observed in the cervical FCLs (Fig. 3). Each cervical FCL contains regions with heterogeneous fiber orientation and areas comprising parallel collagen bundles with strong alignment as inferred from QPLI-based orientation maps (Fig. 3). The strongly aligned collagen fiber collections have different orientations in different regions of the FCL, and some of them together form curvy patterns (Figs. 3(b)–3(d)). In contrast, although local heterogeneity in collagen orientation is also observed in lumbar samples, the majority of the fibers in lumbar FCLs align in the across-joint direction, with alignment strength more uniform than that observed in cervical samples (Fig. 4). Among the six lumbar samples examined, five have probability density functions of the PS-OCT preferred angle peaking near 0 deg, which corresponds to the medial–lateral direction (Fig. 4(a)). In contrast, the cervical FCLs show no consistency in their collagen orientation probability density functions (Fig. 3(a)).

Fig. 3.

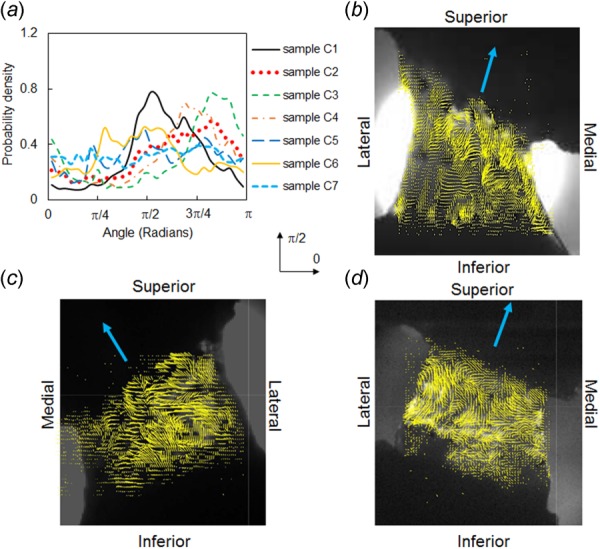
Collagen fiber orientation in cervical FCLs. (a) Fiber orientation distribution and representative fiber alignment maps (from samples (b) C1, (c) C2, and (d) C7) demonstrate highly heterogeneous structures and large variability between different specimens. The single line arrows indicate directions across the joint. The orientation distribution functions in (a) were computed relative to the horizontal direction marked by 0.

Fig. 4.

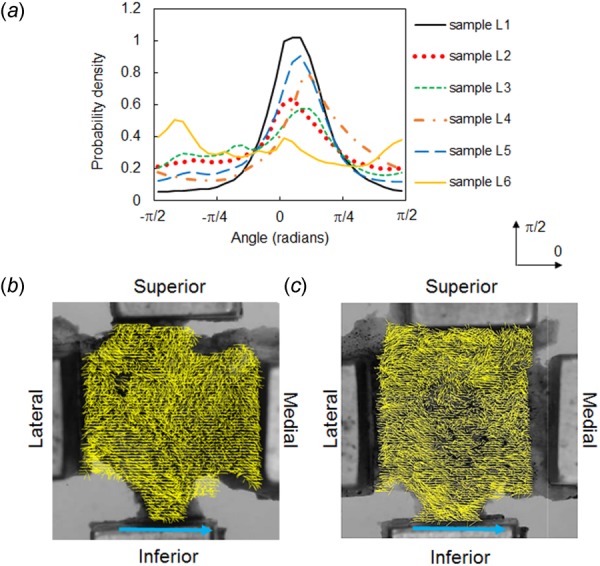
Collagen fiber orientation in lumbar FCLs. Fiber orientation distribution (a) and representative fiber alignment maps (for samples L2 (b) and L5 (c)) show that the dominant fiber alignment is along the medial–lateral direction with varied local orientations. The single line arrows indicate the across-joint direction. The orientation distribution functions in (a) were computed relative to the horizontal direction marked by 0.

Differences in collagen architecture between cervical and lumbar FCLs are captured quantitatively by the computed spatial autocorrelation of the orientation field. In the cervical FCLs, preferentially aligned collagen fibers are observed at the local scale, but no global alignment is observed at the scale of the samples. Therefore, as distance, $\delta$, increases from 0 to 2 mm (approximately 1/3 to 1/4 of the sample size), the normalized autocorrelation decays from 1 and vanishes in most cases, indicating weak or no correlation between orientation of two points that are 2 mm apart (Fig. 5(a); Table 1). In contrast, the spatial correlation of the lumbar samples does not vanish within 2 mm (Fig. 5(b)). As the distance $\delta$ increases, the autocorrelation decays quickly and reaches a relatively steady level above zero (Fig. 5(b)), signifying that collagen is preferentially aligned at the scale of the ligament in the lumbar FCL case. There is an overall significant difference (p = 0.037) in the correlation length between the cervical and lumbar FCLs along different alignment directions, and the difference in spinal region is the main factor contributing to this difference (p < 0.002 by t-test) (Fig. 5(c)). Comparing the correlation length in each direction between the cervical and lumbar regions using separate t-tests, significantly smaller correlation lengths are found in the cervical FCLs along the transverse direction (p = 0.020) and averaged across all directions (p = 0.022) (Fig. 5(c)). The smaller correlation length and more randomness in spatial autocorrelation on the scale larger than the correlation length in the cervical region relative to the lumbar region suggest greater isotropy of fiber orientation on the scale of the ligament in the cervical FCL case.

Fig. 5.

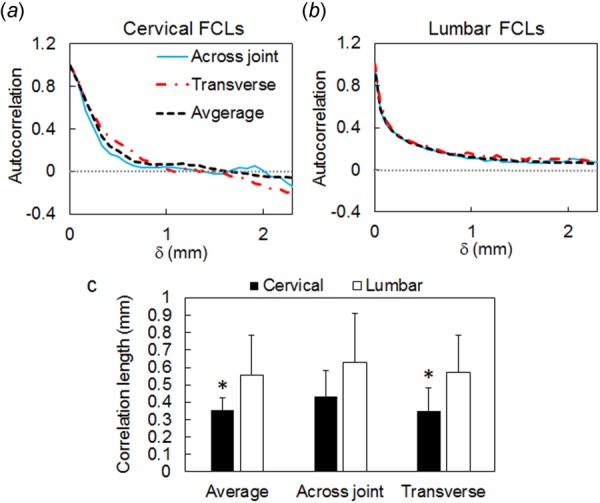
Spatial correlation of orientation in cervical and lumbar FCLs in the prestressed resting configuration. Representative autocorrelation curves are shown for (a) a cervical FCL (sample C2) and (b) a lumbar FCL (sample L3) in the across-joint direction, in the transverse direction, and averaged over all directions. Spatial correlation in both cervical and lumbar FCLs exhibits an initial drop within 1 mm. In the cervical region, correlations vanish beyond this distance, while in the lumbar samples correlations are longer ranged. (c) Comparison between correlation length, c, shows an overall significant difference due to anatomical region of the FCLs (p = 0.037). The correlation length in the cervical FCL is significantly smaller than that in the lumbar region in the average and transverse directions (*p < 0.022), indicating higher heterogeneity in the cervical FCLs compared with lumbar FCLs. Error bars indicate standard deviations.

3.2. Deformation Dependence of Collagen Architecture.

Real-time measurements of fiber alignment in cervical FCLs reveal complex collagen re-orientation patterns during loading. As expected, tensile stretch induces collagen fiber realignment toward the loading (vertical) direction in subregions of the ligaments, resulting in increased spatial correlations in the vertical direction with increasing ligament deformation (Fig. 6). However, not all fibers reorient vertically; as suggested by spatial alignment maps derived from QPLI, a few subregions display fiber realignment perpendicular to loading with increasing ligament stretch (Fig. 6(a)). The tensile loading results in minor perturbations of the horizontal autocorrelation in individual ligaments (Fig. 6(b)) and to a slight increase of the autocorrelation range in the vertical, loading direction. This indicates that collagen reorientation takes place across the sample, although with different intensities in various subdomains. The initial heterogeneity of the cervical ligament orientation persists during loading, which is demonstrated by the clear strain invariance of the θ-averaged autocorrelation (labeled isotropic in Fig. 6(b)).

Fig. 6.

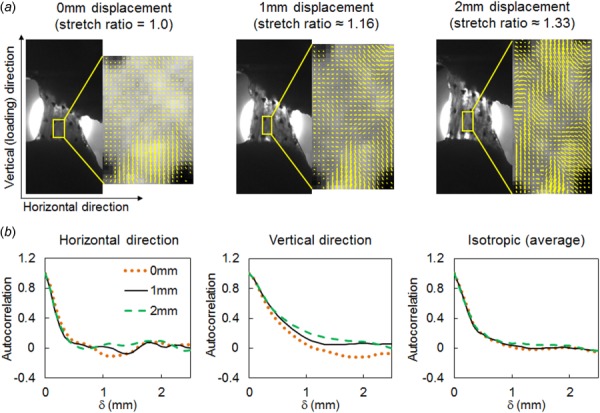
Representative collagen fiber reorganization in a cervical FCL sample (C1) under uniaxial tension (applied in the vertical direction in this figure). (a) Representative regional fiber alignment maps show nonuniform fiber realignment with increasing deformation and a preferred re-orientation direction along the applied loading. (b) Representative correlation curves show more reorganization during stretch along the loading direction as compared to the horizontal direction or isotropic measurements.

These trends can be described more quantitatively using the correlation length which provides a measure of the size of the subdomain over which collagen orientation is approximately identical. For the four cervical ligaments that were not damaged before 3 mm of the stretch (Table 1), the vertical feature size measured at 3 mm displacement is significantly larger (p < 0.050) than that of the prestressed unstretched configuration and greater (p < 0.006) than the horizontal feature size at 3 mm stretch (Fig. 7(a)). The correlation length in the horizontal direction slightly decreases with increasing deformation, but this change is not statistically significant (Fig. 7(a)). Decreases in the horizontal feature size with increasing strain are only observed in four of the seven samples (Fig. 7(b)). In contrast, all samples exhibit a trend of increasing vertical feature size with increasing maximum principal strain (Fig. 7(c)).

Fig. 7.

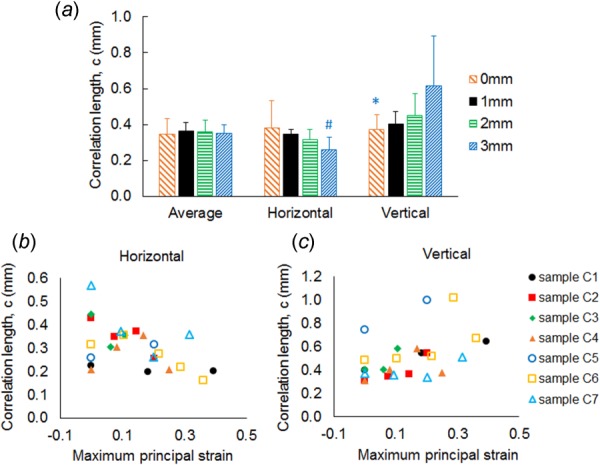
Evolution of correlation lengths with the deformation of cervical FCLs. (a) Correlation length in the vertical direction at 3 mm displacement (1.55 stretch ratio on average) is significantly higher than both the vertical correlation length in the prestressed resting configuration (*p < 0.050) and horizontal correlation length of the deformed sample at same strain (#p < 0.006). Error bars indicate standard deviations. (b) Correlation length in the horizontal direction shows high sample-to-sample variability and no definite trend as the applied strain increases, whereas (c) vertical correlation length of all samples tends to increase with increasing macroscopic strain.

3.3. Nonaffinity in Ligament Deformation.

In a uniaxial stretch test, fibrous networks deform in a highly nonaffine manner [32,33], marked by deviations from the externally applied strain at each point in the sample. This motivated a comparison between the measured correlation lengths against values calculated based on hypothetical affinely deformed samples. Like the actual correlation lengths, the affinely calculated correlation lengths increase in the loading direction. However, they do not follow the small decreasing trend observed in the correlation length in the lateral direction. Overall, the affinely deformed maps result in correlation lengths that are close to the actual values (Fig. 8).

Fig. 8.

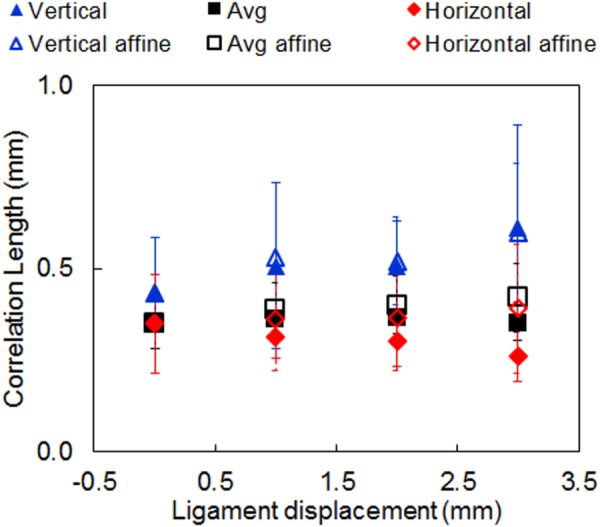
Comparison of the experimental correlation length with the prediction of the affine deformation model. The affine model assumes that the strains at each point inside the sample are identical to the macroscale, applied strains. The local reorientation was computed based on this assumption. A good agreement is observed with the measured data in the vertical direction. Error bars indicate standard deviations.

4. Discussion

Tissue microstructure, such as collagen organization in ligaments, plays an important role in mediating mechanics and physiology of the tissue [16,17,19,24,25,34–36]. In this study, we utilized analytical tools common in the analysis of random functions to investigate tissue patterns, collagen architecture in particular, in the facet capsular ligament. The FCL plays an important role in the biomechanics of the facet joint and is a common source of neck and lower back pain from excessive capsule stretch [1,2]. Uniaxial tension at supraphysiologic strains can induce abnormal collagen reorganization in subregions of the cervical FCL and concurrent activation of nociceptors embedded in the impaired fibrous networks [2,16,17,26]. Equibiaxial loading of lumbar FCL has shown to produce normal and shear forces [37]. The lumbar FCL undergoes extension and shear due to physiological loadings such as spinal torsion (primarily extension), lateral bending (primarily shear), and flexion/extension (primarily shear). To capture the spatial heterogeneity of the fibrous structure in the FCL, collagen fiber alignment maps were generated using specialized optical imaging techniques, namely, QPLI and PS-OCT for cervical and lumbar FCLs, respectively. The spatial correlation analysis was performed to compare collagen organization in FCLs in cervical and lumbar regions quantitatively and to evaluate collagen reorganization during tensile loading of cervical FCLs.

Each of the different spinal FCLs displays distinct collagen organization patterns based on their anatomic region. High spatial heterogeneity and curvy substructures are observed in cervical FCLs (Fig. 3). In contrast, collagen orientation in lumbar FCLs is more homogeneous with the majority of the fibers aligning along the direction across the joint (Fig. 4). This structural difference likely associates with the different mechanical properties of FCLs in these two spinal regions. For example, the maximum principal strains, including those produced by bending, flexion, and extension, are generally larger in the cervical than in the lumbar FCL [3,38,39]. The mean failure strains during tensile loading of FCLs in the cervical spine range from 100% to 150% [3,16,40]; whereas for the lumbar FCL, the extensibility to failure is 0.65 and 0.60 in the direction parallel and perpendicular to the collagen fiber orientation, respectively [20].

Cervical FCLs can accommodate larger macroscopic deformation maybe due to differently oriented collagen fiber or fiber bundles, as suggested by the curvy subsubstructure observed in orientation maps derived from the QPLI data (Fig. 3). Collagen fibers or fiber bundles with spatial orientations different from the loading direction can first rotate toward the loading direction before getting stretched, a process analogous to the straightening of a single wavy fiber. Of note, the current study did not measure the waviness of the collagen fibers, because the orientation obtained here is the optical anisotropy viewed by polarized light, which indicates, but is not the same as, the collagen fiber direction, and the images suggest the average fiber alignment at each pixel rather than fiber-level orientations.

On the other hand, the predominant lateral–medial fiber orientation in the lumbar FCL provides it with the mechanical strength and stiffness necessary to bear the large extension and shear loads required for daily activity. During torsion or lateral bending, the lumbar FCL experiences extension along the joint direction (lateral–medial), and thus, the lateral–medial fiber orientation stiffens their structure in a functionally relevant direction. During extension or flexion, the lumbar FCL also undergoes substantial shear, transverse to joint direction [37,38,41,42]. Fiber alignment in the joint direction also provides resistance in tissue shear since fibers resist more when sheared transverse to their direction, as compared to when sheared along their axis of orientation.

It has been shown that fiber orientation in the lumbar FCL affects the tissue's stress–strain behavior in tension, and different mathematical models have been used to describe facet capsules loaded in directions parallel and perpendicular to the collagen fibers [19,20]. Similar to the lumbar region, inhomogeneous collagen organization in the cervical FCL also likely results in varied mechanical behaviors under loading in different directions and requires future mathematical descriptions that can account for the spatial variability in collagen organization. Although this study demonstrates spinal region-dependent microstructure that potentially relates to FCL mechanical function, it remains unclear whether these structural characteristics are inherent or result from adaptation during maturation and aging. Thus, the causal relation ships of the structure–function coupling need to be further elucidated.

The fiber orientation autocorrelation along different directions of the cervical and lumbar FCLs both exhibit rapid decay within 1 mm, with a mean isotropic (average direction) correlation length of 0.35 mm for cervical FCL and 0.56 mm for lumbar FCL, which corresponds to approximately 5% and 3% of the size of the cervical and lumbar samples, respectively (Fig. 5; Table 1). The correlation for the cervical FCL samples vanishes within 2 mm of distance, but the lumbar correlation drops by about 70% within 1 mm and remains relatively stable with a long tail above 0 between 1 mm and 3 mm (Fig. 5). This lack of spatial correlation of inferred collagen orientation in the cervical FCL on the scale larger than the correlation length suggests lack of periodicity in the observed microstructural patterns, more randomness, and higher structural isotropy at the ligament scale. These findings are consistent with the spatial variation of collagen alignment observed in the cervical FCLs (Figs. 3 and 4).

In addition to intrasample heterogeneity, cervical FCLs also exhibit high interspecimen variability. No two cervical samples show identical fiber orientation distributions (Fig. 3). In contrast, five of the six lumbar samples display an orientation distribution with a peak in the joint direction (Fig. 4). These results suggest that sample-specific computational models may be needed to correctly represent the structure of cervical FCLs. Since collagen fiber alignment may affect the mechanical behavior of tissues [16,19,35,36], it is important to incorporate fiber orientation into computational models of the FCLs, especially cervical FCLs.

Spatial alignment maps derived from polarized light images of the cervical FCL during loading suggest complex collagen reorganization patterns, with collagen within some subdomains realigning toward the loading direction, while that in other subdomains rotating in the direction perpendicular to the direction of average maximum principal stretch (Fig. 6). In addition to heterogeneous reorganization within each individual sample, different FCLs show different realignment responses. These observed behaviors are likely due to varied initial orientation and slightly different FCL geometries, and they may contribute to the inhomogeneous strain field and different failure locations observed during tensile loading of FCL specimens [16,25]. Besides the shape and structure of the FCL itself, surrounding muscles may also contribute to the heterogeneity of this ligament. For example, the cervical facet capsule has nonuniformly distributed muscle insertions that cover approximately 23% of the capsule [43], which also locally alter the stress and strain responses in the different and overall regions of that capsule and also across different specimens. Further characterizing these and other physiological and anatomic inputs to the FCL would go a long way in better understanding the mechanical function of this ligament.

Structural reconfiguration of collagen during loading of the cervical FCL was quantified by extracting a correlation length, representing a characteristic feature size, from the autocorrelation data. At large (vertical) displacement, the cervical FCLs show significantly greater correlation lengths in the vertical direction than in the horizontal direction and in the prestressed resting configuration (Fig. 7(a)). This finding is consistent with multiple previous observations that tensile loading realigns collagen fibers in soft tissues in the principal strain direction [27,36]. The mean vertical feature size exhibits a 75% increase, while the samples undergo on average 55% stretch (i.e., 1.55 stretch ratio; Fig. 7(a) and Table 1), suggesting that the substructure size changes more rapidly than the imposed deformation of the ligament. All seven samples have increased vertical feature size as the applied strain increases (Fig. 7(b)); however, changes in the horizontal correlation length are unexpectedly variable (Fig. 7(c)). The small change in feature size in the horizontal direction is accompanied by small lateral contractions observed in these experiments. This may be explained by the bone constraining the induced deformation and minimizing lateral contraction during extension of these samples (apparent Poisson's ratio = 0.08 ± 0.26).

The affine model predicts vertical correlation lengths that are in very good agreement with our experimental measurements, indicating substantial homogenous stretches in this direction (Fig. 8). However, the large variability in stretch ratio in the horizontal direction and the difficulty in its estimation cause uncertainties in predicting the correlation length in the horizontal direction. The tissue damage prior to failure might also contribute to the observed discrepancies between the actual correlation lengths and predictions from the affine model.

Understanding the structural variation and stretch-induced reconfiguration in the FCLs may be confounded by limitations of the imaging methods used in this study. QPLI and PS-OCT are the two distinct imaging modalities with inherent differences, such as the imaging depth and level of depolarization. To evaluate the depth-dependent collagen orientation in the cervical FCL and ensure accurate comparison of the fibrous structure between lumbar and cervical FCLs, collagen fiber alignment in the cervical specimens may be remeasured using the PS-OCT system in future studies. Furthermore, other imaging techniques are needed to assess noncollagenous components, such as elastic fibers, in the FCL. Previous histological studies investigating the morphology of facet capsules in microscopic domains have demonstrated that lumbar FCLs contain densely packed parallel collagen bundles, but irregularly organized elastic fibers [6]. Different organization and properties of collagen and elastic fibers may differentially modulate the mechanical responses of the FCL, which need to be evaluated in the future using appropriate imaging approaches.

There are several methodological considerations associated with this work in addition to technical limitations related to using polarized-light-based imaging tools to measure collagen orientation. First, the interpretation of the results of any image-based study is dependent on the imaging resolution. New features might be revealed under finer resolution, while the currently characterized features might be neglected when using a coarser resolution. Nevertheless, like any other microstructural characterization method, the presented results may inform coarser scale models about microstructural features and phenomena related to them at a finer scale. For example, in a homogenization multiscale analysis, measurements at the representative volume element can provide adequate information required by the coarser scale model, shaping a model at the larger scale that takes microstructural details into account. Second, in this work, fiber alignment strength (retardation) was not considered in the correlation analysis. Both alignment angle and strength are needed to characterize the fiber organization fully. Future studies could incorporate fiber alignment strength by methods that include filtering or weighting the fiber orientation using retardation, but such manipulation could bias the computed spatial autocorrelations. Despite potential limitations pertinent to this work, our study demonstrated that the spatial correlation analysis can be applied to the complex fibrous structure of the FCL. This approach, along with fiber alignment visualization, reveals the dependence of the collagen organization in FCLs on spinal region and on the tissue deformation state. The application of spatial correlation analysis can be coupled with other imaging techniques at different length scales, such as confocal microscopy and scanning electron microscopy [30,44], and it may be extended to characterizing structural anisotropy of other tissues or tissue analogs at rest and in response to loading.