How geometric frustration shapes twisted fibres, inside and out: competing morphologies of chiral filament assembly

Abstract

Chirality frustrates and shapes the assembly of flexible filaments in rope-like, twisted bundles and fibres by introducing gradients of both filament shape (i.e. curvature) and packing throughout the structure. Previous models of chiral filament bundle formation have shown that this frustration gives rise to several distinct morphological responses, including self-limiting bundle widths, anisotropic domain (tape-like) formation and topological defects in the lateral inter-filament order. In this paper, we employ a combination of continuum elasticity theory and discrete filament bundle simulations to explore how these distinct morphological responses compete in the broader phase diagram of chiral filament assembly. We show that the most generic model of bundle formation exhibits at least four classes of equilibrium structure—finite-width, twisted bundles with isotropic and anisotropic shapes, with and without topological defects, as well as bulk phases of untwisted, columnar assembly (i.e. ‘frustration escape’). These competing equilibrium morphologies are selected by only a relatively small number of parameters describing filament assembly: bundle surface energy, preferred chiral twist and stiffness of chiral filament interactions, and mechanical stiffness of filaments and their lateral interactions. Discrete filament bundle simulations test and verify continuum theory predictions for dependence of bundle structure (shape, size and packing defects of two-dimensional cross section) on these key parameters.

1. Introduction

Assemblies of chiral building blocks often inherit the lack of mirror symmetry at the mesoscale from the microscopic scale of those subunits [1]. This effect is well known in the context of chiral mesophases of liquid crystals [2,3], in which the lack of inversion symmetry of rod-like molecules leads to self-organized, twisted textures. One such state is the cholesteric phase, where the molecular axis adopts a handed twist throughout the sample. In a second class of systems, membranes formed by chiral molecules (e.g. surfactants), the local two-dimensional packing of chiral elements ultimately leads to mesoscopically handed morphologies, including helicoidal and spiral ribbons [4–6]. In biological assemblies, where protein building blocks are universally chiral at the molecular scale, the effect of chirality to template morphology at a super-molecular length scale is well known [7–9].

In this paper, we consider the influence of chirality to shape rope-like assemblies of one-dimensional filamentous elements, a common materials architecture. Chiral bundles and fibres form in a diverse range of systems, from supramolecular polymers, organogels and columnar fibres [10–14], to protein fibres, both functional (collagen [15,16], cellulose [17], fibrin [18]) and pathological (amyloids [19], sickle haemoglobin [20]). While these systems are clearly diverse in terms of both their structure and interactions at the molecular scale, they share a common geometrical template, with filaments or columnar molecular stacks winding helically along the long axis of the bundle or fibre (figure 1a). This basic geometry leads to generic, yet non-trivial, consequences for the resulting structures and thermodynamics of assembly, owing to the geometrical frustration of long-range order by chiral textures in self-organized bundles.

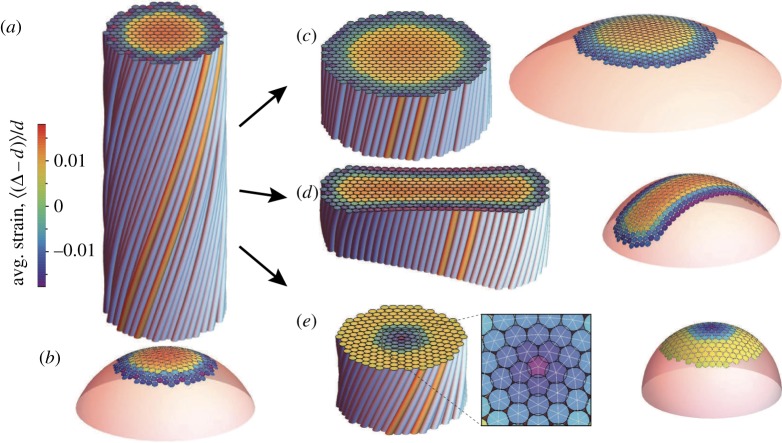
Figure 1.

Competing morphologies of self-assembled chiral filaments. Compression at the perimeter is due to geometric frustration of twisted textures. We show equivalent bundle cross section (a) and curved crystal structure (b) using the previously derived mapping. At the top, elements are shaded according to local strain of inter-filament distance Δ, relative to ideal separation d. In (c), unwinding preferred chiral twist (or equivalently decreasing spherical curvature) allows a larger assembly with reduced compression. In (d), excess free surface of anistropic, tape-like bundles leads to compression that grows only with thinner cross-section dimension. In (e), the introduction of a fivefold defect in the inter-filament order relaxes hoop compression.

Geometric frustration refers to the incompatibility of preferred patterns of local order and global constraints, which prevents the propagation of distortion-free order in assemblies [21–23]. In rope-like twisted bundles, frustration arises from two geometric mechanisms. The first, orientational frustration, results from the tendency of chirality to promote non-parallel textures of filament backbone orientation throughout the assembly [24]. Lateral gradients of filament bending introduced by chiral ordering give rise to important size-dependent assembly costs that can establish the equilibrium (self-limiting) finite size of bundles [25–28]. The second mechanism is metric frustration, where the non-parallel, twisted textures of filaments favoured by chirality make uniform inter-filament spacing impossible [29]. It has been shown that this metric frustration in twisted bundles can be mapped onto the metric frustration of packing elements on a positively curved two-dimensional surface [30,31]. Specifically, the distance of closest approach between filaments in a twisted bundle corresponds one-to-one to the geodesic distance between equivalent points on the ‘dual surface’, whose curvature radius is proportional to the helical pitch of bundle twist (figure 1b). This ‘dual problem’ has received broad interest in diverse contexts ranging from the long-standing Thomson problem [32] to the structure of particle assemblies at liquid droplet interfaces [33]. Previous studies have shown that metric frustration in both bundles and curved crystals leads to intrinsic gradients of stress in the assembly that in turn may trigger a rich set of morphological responses [23], including self-limiting domains [25,26], defective bulk order [32,34–37] and anisotropic surface shapes [38–41].

In this paper, we explore the principles that select among the multiple competing morphologies stabilized by geometric frustration in chiral filament bundles. These distinct morphological responses are illustrated in figure 1, associated with bundle geometry along the bundle (figure 1c), bundle surface geometry (figure 1d) and symmetries of inter-filament order in the bulk (figure 1e). While chiral filament interactions select a preferred amount of bundle twist, the cost of both intra- and inter-filament strains may be relaxed via an untwisting of skewed filament packing (figure 1c), which corresponds to a geometric ‘flattening’ of the dual metric surface as lateral bundle area grows and allows bundles to reach a larger diameter than possible for fixed twist. Indeed, when chiral interactions are sufficiently ‘soft’, bundle assemblies may ‘escape’ frustration by untwisting completely, and consequently grow to unbounded domains. Alternatively, a second mechanism to relax frustration cost is possible if surface energies (associated with fewer cohesive bonds at the bundle exterior) are sufficiently small compared with the cost to deform inter-filament bonds, so that the bundle cross section becomes highly anisotropic as shown in the tape-like morphology in figure 1d. Analogous to the elastic instability for growing crystalline domains on spherical surfaces described below, this morphology is driven by a tendency to lower the overall growth of inter-filament strains with increasing filament number in the bundle. Finally, figure 1e shows that for sufficiently high overall twist in the assembly, it becomes advantageous to adopt (fivefold) disclination defects in the two-dimensional bundle cross section to lower the cost of geometric frustration of inter-filament spacing, a phenomenon well studied for the assembly of crystalline arrays of positively curved surfaces.

Several previous studies [24,26,30,31,36,37,41] have investigated how each of these ‘morphological responses’ may effectively lower the cost of geometric frustration imposed by chiral order in bundles. Here, we address how these distinct responses compete in the broader phase space of chiral filament assembly. Specifically, we use a combination of continuum elasticity theory and discrete-filament bundle simulations to show that equilibrium morphology is selected by a combination of key thermodynamic (bundle surface energy), geometric (preferred chiral twist) and mechanical (stiffness of filaments and their interactions) properties of filament assemblies. In §2, we present a generic continuum model of defect-free twisted bundle assemblies, which allows us to compare the structure and thermodynamics of finite width bundle assemblies (possessing both isotropic and anisotropic cross sections) to the cost of unwinding chiral interactions to allow bulk order to grow without frustration. We show that the possibility of ‘escaping frustration’ is governed by the ratio of stiffness of chiral filament interactions to the combined surface energy and mechanical costs of forming finite width twisted domains. Above a critical chiral interaction stiffness, bundles exhibit both distinct isotropic (cylinder) and anisotropic (tape-like) morphologies, while below this critical stiffness, finite-diameter bundles are favoured only within a narrow range of weakly cohesive surface energies, above which equilibrium bundle growth causes assemblies to untwist to the parallel, unfrustrated state. In §3, we present discrete filament bundle simulations that compare the relative stability of bundles with anisotropic lateral dimensions to bundles which possess topological defects in their interior order. We find that the optimal morphological response (boundary shape or bulk defects) is determined by the filament number N, the bundle twist and the ductility of inter-filament bonds. For small-N and ductile inter-filament interactions, bundles pass directly from defect-free cylinders (i.e. isotropic boundary shape) to defective cylinders with increasing twist, while for large-N and brittle interactions, the defective cylinder phase is preempted by an intermediate phase of defect-free anisotropic (tape-like) bundles. We argue that the stability window of anisotropic tapes can be modelled via continuum theory estimates for the relative costs of straining inter-filament bonds (by geometric frustration) compared with the surface energy cost of introducing excess (anisotropic) boundary. We conclude with a discussion of these results in the context of outstanding questions regarding the role of geometric frustration in shaping the assembly of chiral filament bundles.

2. Escaping frustration to bulk assembly: continuum model of morphology selection

In this section, we present a continuum elastic theory for the formation of twisted bundles of chiral filaments that relates the free energy of assembly to bundle morphology, specifically the equilibrium twist and lateral dimensions of the cross section. We begin by introducing the model and its application to the thermodynamics of assembly with isotropic versus anisotropic bundle cross sections, and then analyse the possibility of bundle assemblies to ‘escape frustration’ by relaxing inter-filament twist with increasing size.

2.1. Model

We describe the assembly of twisted bundles as finite domains of filaments with two-dimensional columnar order and preference for chiral textures of filament backbones [37]. A columnar bundle is described by the shape of its two-dimensional cross section normal to the mean orientation of filaments (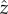 axis), a local two-dimensional displacement u(x) (⊥ to 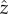) of local filament positions away from a parallel and equally spaced (e.g. hexagonal) reference configuration, and the unit vector orientation field of filament backbones 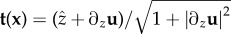. Given the shape and geometry of the bundle (described by u(x) and t(x)) the following free energy describes bundle formation:

2.1

Here,

2.2

represents the bulk and surface terms for a bundle of length L, cross-sectional area and perimeter, A and P, respectively, and areal filament density, ρ₀. The net per filament gain of inter-filament cohesion (minus entropic loss) to add filaments to a bundle is −μ, while fewer cohesive interactions at the lateral surface of the bundle leads to a positive surface energy Σ.¹ The elastic energy has the form

2.3

where the first term represents the cost for intra-filament, bending deformation, with B and κ(x) = |∂_zt|, the filament stiffness and curvature, respectively. The second term describes the continuum elastic cost of deforming lateral inter-filament order (spacing and symmetry) where σ_ij and u_ij are the respective in-plane stress and strain tensors (with components in the plane of lattice order, ⊥ to ). We assume an isotropic, linear elasticity appropriate for hexagonal inter-filament order u_ij = Y⁻¹[(1 + ν)σ_ij − νδ_ijσ_kk], where Y and ν are the respective Young's modulus and Poisson's ratio of the two-dimensional filament array. The geometric coupling between positional and orientational degrees of freedom is built into the form of the nonlinear columnar strain [42],

2.4

The nonlinear contribution from tilt is necessary to preserve rotational invariance of the theory, and more intuitively, represents the fact that distance of closest approach between filaments will be reduced when filaments tilt relative to 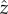(i.e. t_i ≠ 0) without changing their positions in that plane (i.e. ∂_iu_j = 0). The final contribution to F derives from orientation dependent interactions between chiral, rod-like elements, and hence has the form of the twist-elastic contribution to the Frank energy of nematic phases [43],

2.5

where K is the twist elastic constant (often written as K₂₂) and q₀ ≠ 0 parametrizes the drive of chiral filaments to adopt a twisted texture with t · (∇ × t) =−q₀.²

In simple chiral nematics (which lack positional order) q₀≠0 leads to a uniaxial cholesteric ground-state texture, with nematic director rotating along a direction orthogonal to the nematic axis with a pitch 2π/q₀. Owing to the two-dimensional positional order, uniaxial cholesteric textures require constant longitudinal gradients of in-plane shears [44], and hence are suppressed as L → ∞. Hence, for finite chiral columnar domains such as bundles, chirality favours an alternative ‘double twist’ texture [45], in which filament orientations wind helically around a central axis, and filament positions are simply rigidly rotated (shear-free to linear order) from one transverse section to the next along the bundle. Parametrizing this texture by the twist Ω of filaments around the axis, the backbone texture is

2.6

where (r, ϕ) are polar coordinates with respect to the twist axis. In this geometry, (i) each filament adopts a helical shape and possesses a single pitch P = 2π/Ω and (ii) neighbour filaments spaced δr along the radial direction adopt a nearly constant inter-filament skew angle δθ ≃ Ωδr (figure 2). Because t · (∇ × t) ≃ 2Ω ∝ δθ for this texture, the preference for double-twist in the bundle can therefore be linked to microscopic interactions between chiral filaments which favour a fixed inter-filament skew between neighbours δθ₀ ∝ q₀ and generate an inter-backbone torque ∝K(δθ − δθ₀) for deviations from this preferred local packing for which F_chiral/V ≃ 2K(Ω − Ω₀)², where Ω₀≡−q₀/2 is the rate of bundle twist preferred by chiral interactions [24,26].

Figure 2.

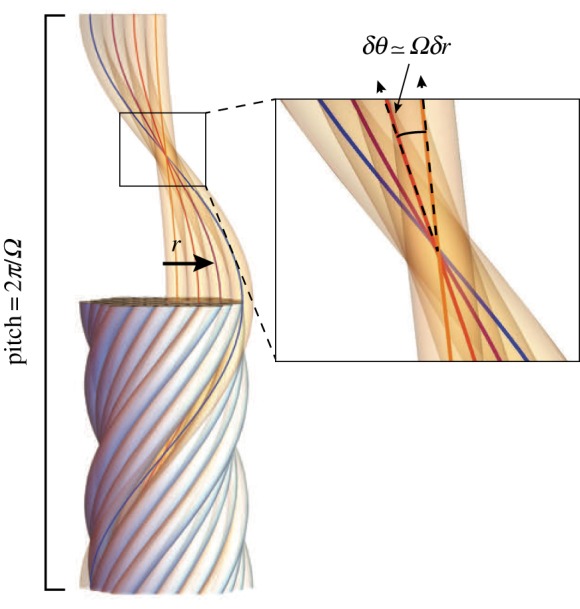
The double-twist geometry is characterized by twist rate Ω, related to the helical pitch of filaments and the inter-filament skew angle, δθ. Here, r describes the radial distance from the central axis.

Given this double twist texture, these elastic costs for intra-filament and inter-filament deformations may be derived for a given two-dimensional cross section. For example, as filament curvature grows linearly with distance from the bundle axis κ(x) ≃ Ω²r, the bending energy (per unit volume) takes the simple form F_bend/V = Bρ₀Ω⁴〈r²〉/2, where 〈r²〉 is the moment of inertia of the cross section. Calculation of the inter-filament elastic energy requires solution of the mechanical equilibrium equations, which are the Euler–Lagrange equations for u(x), ∂_iσ_ij = 0 combined with a compatibility condition that relates in-plane gradients of inter-filament stresses to in-plane gradients of filament tilt t_⊥ (in-plane components of t)

2.7

where K_eff ≃∇_⊥ × [t_⊥(∇_⊥ × t_⊥) − (t_⊥ × ∇_⊥)t_⊥]/2 and plays a role equivalent to the Gaussian curvature in two-dimensional elastic membranes, connecting gradients of out-of-plane tilt to gradients of in-plane stress. For the double-twist texture in equation (2.6) K_eff = +3Ω², where the small-tilt approximation assumes sufficiently large helical pitch such that (Ωr) ≪ 1, the frustration of inter-filament spacing is equivalent to crystalline order on a sphere of radius 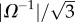[29].

In this model, consider two limiting classes of bundle cross-sectional shape: cylindrical and tape-like twisted bundles. Cylindrical bundles possess an isotropic (circular) cross section, which would be optimal from the point of view of surface energy. For a cylindrical bundle of radius R the inter-filament elastic pressure has the form σ_ii = 3YΩ²(R² − 2r²)/8, illustrating the tendency of compression to increase with distance from the bundle centre, analogous to the geometric compression of a (flat) two-dimensional membrane confined to the spherical surface. From this stress distribution and the second moment of the cross section, 〈r²〉 = R²/2, we have

2.8

In the second morphology, the helical tape, we assume the cross section has a rectangular shape with one lateral dimension, the width w, much larger than its transverse thickness t. We approximate the stress distribution by taking the w ≫ t limit, where introducing Cartesian coordinates (x, y) along the respective width and thickness axes, stresses will be independent of x (away from distant ends at x = ±w/2). In this case, mechanical equilibrium and vanishing normal stress along the wide edges require σ_yy ≃ σ_xy ≃ 0. Combining compatibility with the condition of zero average stresses along 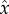direction, we find σ_xx ≃ YΩ²(t² − 12y²)/16. Notably, this solution shows that compression increases away from the line y = 0, leading to stress growth only along the thin dimension of the cross section (as opposed to w). This illustrates the effect of introducing additional free surface to the frustrated assembly. Compatibility requires a non-zero stress drop across that bundle cross section, and the introduction of free surface allows that stress drop to take place along the narrow dimension of the domain through unconstrained displacement of the boundary, thereby lowering the elastic cost of frustration (at the expense of breaking cohesive bonds and raising the surface energy). Integrating the elastic stress through the section and using 〈r²〉 = (w² + t²)/12, we have

2.9

This shows the key result that elastic costs (per unit volume) of extrinsic (i.e. bending) geometry of anisotropic bundles are most sensitive to the wide dimension (growing as ∼w²) when compared with costs of intrinsic (i.e. metric) geometry which are controlled by the narrow dimension (growing as ∼t⁴).

To analyse the free energy density of competing morphologies, it is useful to introduce two material dependent length scales

2.10

where the first length scale, the elasto-cohesive length, effectively characterizes the ratio of cohesive depth and elastic stiffness of inter-filament bonds, and the second, called the bend penetration depth in the context of columnar order [43], characterizes the relative cost of intra-filament bending in comparison with inter-filament bond stretching. Further by introducing the dimensionless length scales

2.11

and energy scales

2.12

we arrive at dimensionless free energies for cylindrical bundles

2.13

and tape-like bundles

2.14

where we neglect the τ² contribution to bending in the w ≫ t limit and we have dropped the constant contribution from the bulk chemical potential.

2.2. Cylindrical bundles: finite diameter versus frustration escape

First, we analyse the equilibrium conditions for bundles assumed to form cylindrical morphologies. Specifically, we analyse the role played by the strength of chiral inter-filament interactions, as parametrized by k, to control the ability to unwind the helical twist of the bundle (i.e. ω < 1) and allow the bundle to reach larger equilibrium sizes than possible for fixed twist, ω = 1. Here, we consider the canonical ensemble and assume conditions (e.g. saturated filament solutions) where all but a negligible fraction of filaments are condensed into bundles. In this case, assuming bundles adopt a mean radius ρ (with negligible size fluctuations), the preferred size and twist of bundles follow from minimization of f_cyl with respect to ρ and ω yielding the equations of state, respectively

2.15

and

2.16

Solving the latter cubic equation for equilibrium twist, we find

2.17

where 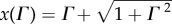and

2.18

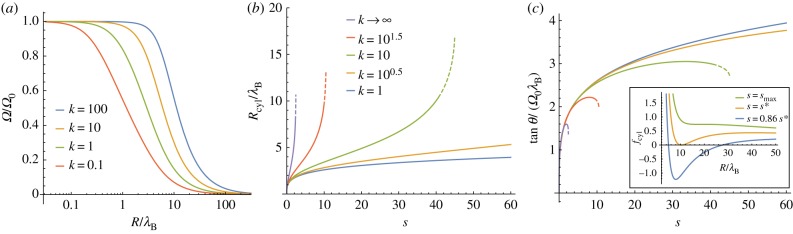
Figure 3a shows the radius dependence of equilibrium twist. Small bundles adopt preferred twist, ω_cyl ≃ 1, while large bundles untwist as ω_cyl ∼ (k/ρ⁴)^1/3 as ρ → ∞ due to the size dependent elastic costs of twist frustration. The crossover between ‘twist-locked’ and ‘mechanically untwisted’ bundles can be associated by the ‘half-twist size’ ρ_1/2 defined by 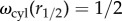in equation (2.17). For weak chiral interactions (k ≪ 1) ρ_1/2 ∼ k^1/2 indicating that bundles prefer to untwist upon reaching only a small radius, while for stiff chiral interactions (k ≫ 1) ρ_1/2 ∼ k^1/4 indicating that in the limit of clamped chirality (k → ∞) bundles retain preferred twist at all sizes.

Figure 3.

In (a), plotting equilibrium twist of cylindrical bundles Ω (relative to value preferred by chirality, Ω₀) as a function of outer bundle radius, for a range of reduced chiral stiffness, k = K/(YΩ²₀λ⁴_B), shows untwisting radius (defined by Ω = Ω₀/2) increases with k. In (b), we show the selection of equilibrium cylinder size, R_cyl, as a function of reduced surface energy s = Σ/(YΩ⁴₀λ⁵_B), for a range of reduced chiral stiffness k. In (c), the outer filament twist angle tanθ = ΩR_cyl of equilibrium cylinders shows a generic non-monotonic dependence on surface energy. The inset in (c) shows the radius dependence of twisted cylinders near to the transition from finite-diameter bundles and bulk, untwisted assembly at s = s* for k = 10. In (b) and (c), dashed curves show metastable branches (for 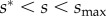) where finite cylinders are separated from (equilibrium) bulk assembly by a finite free energy barrier.

Inserting the size-dependent twist, equation (2.17), into equation (2.15) yields the relation between surface energy and equilibrium bundle size ρ_cyl. In the limit of s ≪ 1, bundles are driven by relatively weak cohesive interactions and retain preferred twist (ω_cyl ≃ 1), reaching only a narrow size ρ_cyl ∼ s^1/3 ≪ 1 limited by intra-filament bending. The growth of bundles with increasing s is highly dependent on the stiffness of chiral interactions, k (figure 3b). In the k → ∞ limit of ‘twist-locked’ interactions, bundles cross over from s ≪ 1 to size limited by geometrically induced inter-filament stress at large surface energy, ρ_cyl ∼ s^1/5 ≫ 1. For finite k, the reduction of equilibrium twist (shown in figure 3a) leads to larger bundle sizes for a given s, relative to the ‘twist-locked’ limit, due to the untwisting of bundles with increasing size. This leads to a maximal s beyond which surface energy drives the bundle to completely untwist and reach infinite size. Thus, assembly can escape the costs of geometric frustration provided that the cohesive drive (as quantified by s) is sufficiently strong to untwist assembly to the parallel state. This follows from the fact that beyond r_1/2 bundle twist falls rapidly, and consequently the size-dependent mechanical costs fall (proportional to ω⁴_cyl) allowing bundles to grow to much larger sizes, peeling away from the k → ∞ behaviour and ultimately exhibiting a singular divergence at a critical surface value s_max. The k-dependence of this maximal s_max can be estimated by using half-twist condition (ρ_1/2 and 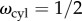) in the equation of state, equation (2.15), yielding 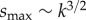for k ≪ 1 and for k ≫ 1. Thus, the stable range of self-limiting chiral filament bundle assembly vanishes as k → 0, and conversely, extends at all s for infinitely stiff chiral interactions.

Before considering the effect of ‘frustration escape’ on the competition between cylindrical and tape-like bundles, we point out two features of the untwisting transition. Figure 3c shows the non-monotonic evolution of the twist angle 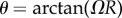as a function of s for a range of chiral stiffness, k. For weakly cohesive assembly, θ generically increases with s due to the increasing radius and roughly constant pitch, while for sufficiently large s, bundles untwist substantially (say for s near the half-twist condition) leading to a maximum θ beyond which twist angle begins to decrease before a singular drop at s_max. A second feature is illustrated in the inset of figure 3c, showing plots of the free energy versus bundle radius near to s_max, where f_cyl is plotted relative to the bulk, untwisted (ω → 0, ρ → ∞) state. As surface energy approaches this value from below, the depth of the finite-ρ minimum increases until it reaches a critical value 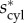where finite cylinder assembly is in equilibrium with bulk, untwisted assembly. For 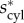finite diameter bundles remain metastable in the regime of equilibrium bulk order (depicted as dashed curves in figure 3), while for 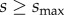the barrier associated with untwisting to the parallel, unfrustrated state is removed. While bundle metastability is a generic feature for finite k assembly, the range of metastable s is relatively narrow, because s*_cyl exhibits the same scaling dependence on stiffness of chiral interactions as s_max.

2.3. Twisted cylinders versus helical tapes versus bulk, untwisted assembly

We now revisit a previous prediction for morphology transition between twisted cylindrical bundles and twisted tapes, which assumed fixed twist (i.e. fixed Ω) as a opposed to fixed chiral interactions (i.e. variable Ω for fixed K and Ω₀). Previously [41], we showed that for fixed Ω, as Σ increases, the rapidly growing cost of inter-filament frustration drives a morphology transition to highly anisotropic tapes. In this case, frustration by chirality is assumed to be fixed, so that while tapes reach lateral dimensions (widths) that are larger than would be possible for cylindrical morphologies, they remain finite for all Σ due to the non-vanishing cost of finite twist. Hence, in the present model (fixed chiral interactions) chirality acts as a ‘soft frustration’ mechanism, which can be overcome for sufficiently strong cohesive assembly drives by untwisting from the preferred chiral twist to parallel assembly.

Based on the continuum model, we consider the competition between three phases: cylindrical bundles (finite R and Ω), tape-like bundles (finite t,w and Ω), and untwisted bulk assembly (R → ∞ and Ω → 0). Along with the equations of state for cylindrical bundles, the free energy of tape-like bundles is determined via the solution for the equations of state of lateral bundle dimensions and twist (minimization of f_tape with respect to τ, υ and ω):

2.19

and

2.20

The first two conditions are easily solved for a given twist υ = (24s/ω⁴)^1/3 and τ = (80s/ω⁴)^1/5. When s ≫ ω⁴, due to the weaker growth of the bending energy (∼υ²) compared with the cost of inter-filament frustration (∼τ⁴), large cohesive energies cause tapes to grow increasingly more anisotropic, leading to w/t ≫ 1.

Solving the additional condition for twist equilibrium, we find a qualitatively similar trend as described above for isotropic cylinders: tape dimensions increase with approximately constant ω_tape ≃ 1 for small s, and at a critical size range equilibrium tapes rapidly unwind leading to a singular increase in tape size at critical s, the value of which increases with k. Indeed, because the thickness of tapes scales in the same way as cylinder radius for large s, the escape to bulk untwisted assembly (ω_tape → 0) occurs at comparable, if somewhat larger, values of surface energy for tapes relative to cylindrical bundles.

The boundary between equilibrium cylinders and tapes is found by solving the condition f_cyl = f_tape for equilibrium structures, while the transition to bulk (untwisted) assembly is determined by comparing free energies of bundle morphologies to f_bulk = 2k. For the k → ∞ limit of stiff chirality, we find that reduced inter-filament frustration, at the expense of excess surface energy, in tapes leads to a transition from cylinders to tapes at s_c/t(k → ∞) ≃ 3860, as previously reported in [41]. For finite k, soft chiral interactions allow bundles, both tapes and cylinders, to untwist to bulk parallel assembly above a critical surface energy, as estimated by s_max above. Whether this untwisting transition occurs from a cylinder phase or tape phase of bundles can crudely be determined by comparing the k dependence of s_max to s_c/t. This crude estimate suggests a critical range of k ≈ 100, above which stiff chiral interactions allow bundles to grow to sufficient size that inter-filament frustration drives a morphology transition to equilibrium tapes at large s. For ‘soft’ chiral interactions (k ≲ 100), frustration escape proceeds at sufficiently low s to prevent a broad range of stable equilibrium tapes before the bulk phase is reached at high s.

This crude picture is consistent with the three-phase assembly phase diagram computed from exact solution of the equations of state above, as shown in figure 4. We note, however, that even in the regime of ‘soft’ chiral interactions (k ≲ 100) a narrow window of equilibrium persists between cylindrical bundles and bulk assembly due to the fact that bundle sizes grow dramatically with s near to the untwisting transition, generically accompanied by a sufficient rise in inter-filament frustration costs to drive a transition to tapes, albeit tapes which are also very close to the point of frustration escape via untwisting. A narrowing window of tapes persists down to a triple point at s_tri = 6.65 and k_tri = 2.4, below which very soft chiral interactions permit weak surface energy to drive finite cylinders directly to bulk, untwisted filament arrays.

Figure 4.

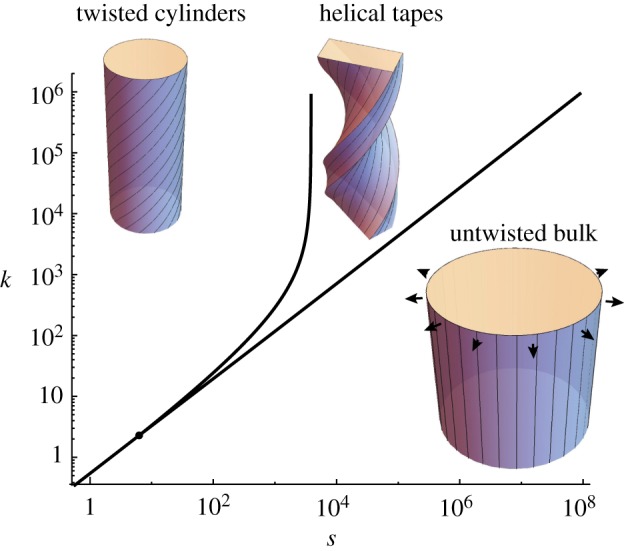
Equilibrium morphology phase diagram for condensed chiral filaments (canonical ensemble) according to stiffness of chiral interaction k = K/(YΩ²₀λ⁴_B) versus surface energy s = Σ/(YΩ⁴₀λ⁵_B). Filled circle indicates a triple point at s_tri = 6.65 and k_trip = 2.4, where finite cylinders, tapes and bulk, untwisted assemblies coexist.

3. Reshaping the boundary versus reorganizing the inter-filament order: discrete-filament model of morphology

In this section, we investigate how frustrated chiral bundle assemblies select between two fundamentally distinct morphologies: defect-free bundles with anisotropic shapes (tapes) and bundles possessing topological defects in the interior, but with otherwise isotropic cross sections. Previous studies have investigated these distinct morphologies as independent structural responses to frustration in chiral bundles.

Disclinations are point-like locations in a two-dimensional quasi-hexagonal packing where sixfold inter-filament bond order breaks down. As shown schematically in figure 1e, fivefold disclinations allow partial relaxation of the frustration-induced compression along the azimuthal direction in twisted bundles [29,36], akin to how they relax hoop compression in spherically curved crystals [46]. Defect configurations are characterized by their net topological charge Q, which is the sum of total deficit in coordination (e.g. assigning value +1/−1 to fivefold/sevenfold disclinations). Previous theory [36] and simulation studies [30,31] of twisted bundles with quasi-cylindrical boundary shapes show that the stability of excess disclinations in the ground state packing is controlled by the product ΩR≡tanθ, which corresponds to the area integral of Gaussian curvature of packings mapped onto the dual surface [29]. For bundles 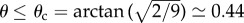, cylindrical bundles favour Q = 0 packings (largely defect free), while for θ > θ_c ground states possess excess fivefold disclinations, Q > 0 with a number that increases from +1 to a maximum of +6 for highly twisted bundles (θ → π/2).

In a parallel study, Hall and co-workers [41] investigated the possibility for bundles to relax frustration without defects, through a reorganization of boundary shape. As described above, surface energy drives bundles to form larger diameters, which in turn increases the costs of frustration-induced elastic energy. Because the cost of metric frustration grows rapidly with the area of isotropic bundle cross sections A, growing as ∼A², relatively stiff inter-filament bonds ultimately lead to an elastic instability of boundary shape that drives cross sections to adopt anisotropic shapes (i.e. tape-like morphologies). This instability, which parallels the behaviour of defect free crystal growth on spherical surfaces [38,40,47], lowers the elastic cost of inter-filament frustration by limiting the narrow dimension of the structure, at the expansion of increased surface energy and intra-filament bending cost. In this previous study, which considered the (fixed twist) canonical ensemble, we showed that this bundle to tape transition occurred at the critical value of surface energy, s_c ≃ 3860 (simulation results showed a lower threshold, s_c ≈ 20–60).

Here, we employ a discrete filament bundle simulation model to compare the relative stability of these competing morphological responses. For simplicity, we focus this study on the fixed twist and fixed filament number (microcanonical) ensembles. In contrast with previous studies, we compare numerically simulated bundle cross sections that alternately optimize boundary shape and inter-filament order, and investigate the conditions that select between boundary shape versus defect-mediated morphology response.

3.1. Discrete filament bundle model and simulation methods

We consider a discrete filament model of chiral filament bundles. Bundles are described by a fixed number of filaments N and fixed (post-equilibrium) value of twist Ω. The energy of bundle assembly is modelled by the energy of a cross-sectional slice of height Δz, whose energy ΔE is described by

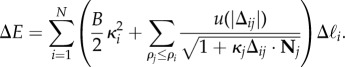3.1

The first term describes bending energy of filaments with κ_i = Ω²ρ_i/[1 + (Ωρ_i)²] with ρ_i the radial distance of the ith filament from the twist axis. The second term describes the cohesive interaction of filament i with filament j (by definition at an inner radial distance, ρ_j ≤ ρ_i), which can be captured by the distance of closest approach Δ_ij between centre lines of the filaments. Owing to the three-dimensional geometry of filament backbones, the closest contact between curves of i and j is generically out of the plane of the cross section, depending not only on distance between points in the cross section, but also on their distance from the central axis and the bundle twist Ω (see equations (B 8) and (B 9) in appendix B.1). Here, we choose the same class of cohesive potentials as in [41]:

3.2

where ε is the cohesive energy per unit length of filaments separated at an equilibrium distance d (e.g. their diameter). We choose a ‘5–11’ potential as the form follows directly from the integration of a pair-wise Lennard-Jones potential between a point on i and a (locally straight) section of j, Δ_ij away, where the factor of (1 + κ_jΔ_ij · N_j)^−1/2 corrects for the curvature of j (with N_j, its normal). Here, σ sets the ductility of pairwise bonds: σ ≪ d results in brittle inter-filament bonds and σ ≫ d results in ductile bonds. In equation (3.1), is the length element of i in the cross section. From the energy per slice, we define the (intensive) energy per filament length,

3.3

where 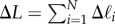is the total filament length per cross-sectional slice. We focus simulations on the case of negligible bending energy content, and choose only a minimal non-zero value of B = 10εd², so as to provide a slight inward force on filaments towards the bundle centre.

To determine equilibrium morphologies for a given N, Ω, bending stiffness and inter-filament potential, we minimize 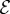with respect to in-plane filament coordinates x_i. As the energy landscape of this optimization problem is rough due to the underlying frustration, resulting equilibria are highly dependent on both initial configurations and sampling protocol. Rather than seek a rigourous ground state (say via advanced sampling), here we aim to identify candidate ground state structures which are assumed to closely parallel the true ground state in terms of energy and structure. As the structural competitors of ground states fall into at least two morphologically very distinct states (presumably separated by multiple large energy barriers) for each set of simulated bundle parameters we use a combination of the following methods.

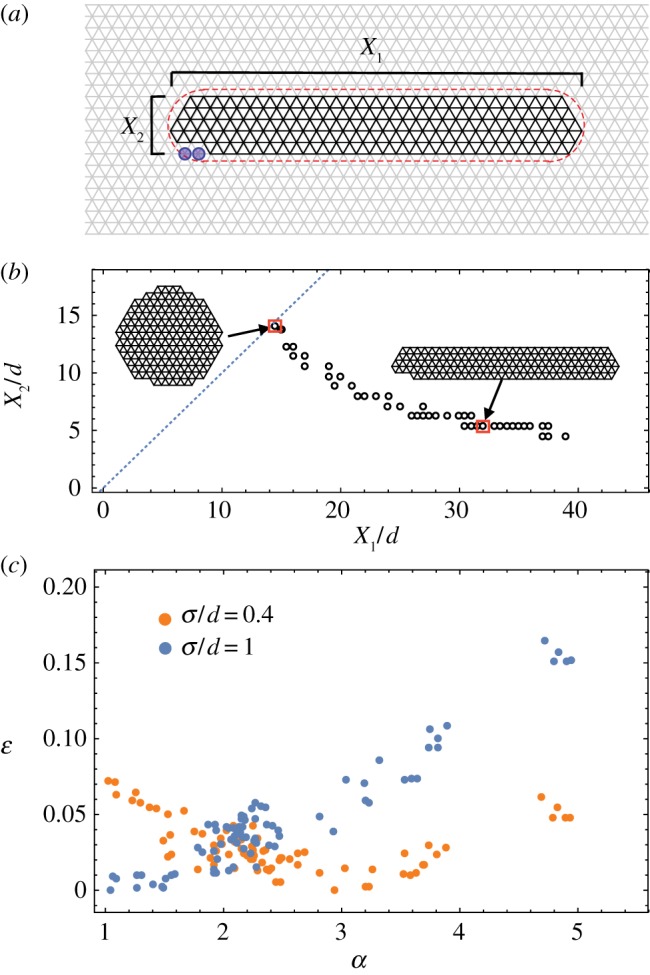
3.1.1. Method A

This method considers filament positions which are initially defect-free and templated from a hexagonal lattice of spacing d, but fall within a cross-sectional ‘stencil’ of variable anisotropic structures. The stencil is described by a stadium curve with lateral inner dimensions, X₁ and X₂, such that narrower ends of the stencil are capped by hemicircular arcs of radius |X₁ − X₂|/2. The stencil dimensions and boundary filaments are adjusted such that the total number of enclosed filaments is N (see appendix B.2), producing a distinct initial configuration that varies from nearly isotropic cylinders (X₁ ≈ X₂) to highly anisotropic, tape-like bundles (X₁ ≫ X₂). From each of these distinct initial configurations, filament positions are first relaxed to avoid overlaps with Δ_ij < d (see appendix B.2), and following this, filament positions are relaxed according to conjugate gradient minimization of 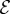, and the lowest energy (per length) is selected as the defect-free ground state candidate.

3.1.2. Method B

This method makes no assumption of initial triangular order and instead allows bundles to form with uncontrolled defect types, numbers and locations in the bundle cross sections. Bundle initial positions are generated by random placement of filament positions within a distance of 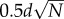from the bundle axis, followed by a post-initialization relaxation to remove overlaps (see appendix B.2). From random initial configurations, filament positions are relaxed according to conjugate gradient minimization of 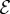. For each set of bundle parameters, at least 3000 random initial configurations are generated, and the lowest final energy is selected as the ground state candidate.

For both methods, the initial relaxation step accounts for overlaps according to the filament geometry prescribed by the system's twist Ωd, but is purposely chosen to use a repulsive potential that does not reflect the system's interaction stiffness σ/d, and produces smaller energy gradients compared with the second relaxation. As a result, this preconditioning step enables the larger displacements necessary to produce structures with more uniform density.

Following application of both relaxation methods, ground state competitors are characterized according to lateral aspect ratio, α, defined by the dimensions of the rectangle with minimal area that encloses the cross section, including filament volumes. Additionally, the inter-filament packing is triangulated, making use of the conformal projection from the dual curved surface to the two-dimensional plane [31], bulk disclination defects are identified as positions of non-sixfold coordination not lying along the outer edge of the bundle, and the net topological charge Q is computed as the sum of total deficit in coordination (relative to sixfold) from that set of defects.

3.2. Simulation results and discussion

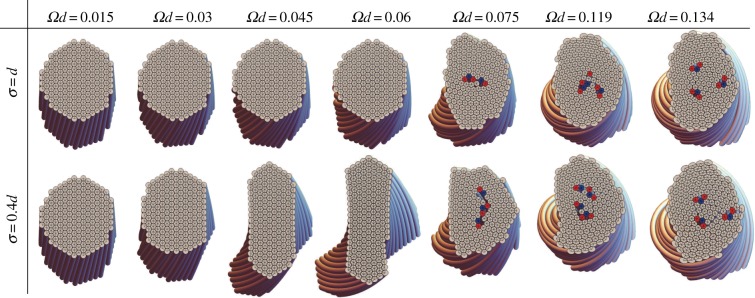
Results of minimal energy morphologies for N = 181 filaments are shown in figure 5 for two different interaction ranges and a sequence of increasing twist, between Ωd = 0.015 and 0.134. For the relatively ductile potential σ = d, we find that bundle cross sections remain roughly circular, but adopt excess fivefold disclinations above a critical twist (Q ≥+1 for Ωd ≥ 0.075), and increasing topological charge with further twist, consistent with the results for the same potential in [30]. By contrast, for the shorter-range, or relatively brittle, potential σ = 0.4d, at relatively low twist, before the onset of defects, optimal bundles become anisotropic. At Ωd = 0.03 the cross section becomes weakly anisotropic α ≃ 1.49 (compared with the zero twist value of α = 1.04) and becomes increasing tapered as twist is raised to Ωd = 0.06, where α ≃ 2.94. For larger twist, optimal bundles return to relatively circular boundary shapes (defined according to α < 1.5), and punctuated with the same excess of fivefold disclinations as the ductile potential states. Thus, for sufficiently brittle inter-filament potentials, anisotropic, defect-free bundles appear intermediate to defect-free cylinders at low twist and defective cylinders at high twist.

Figure 5.

Simulated ground states of discrete-filament model of chiral bundles at fixed N = 181, for increasing values of reduced twist Ωd, where d is equilibrium centre-to-centre filament spacing, or diameter. Top row shows a relatively ductile case where cohesive interaction range σ is equal to d, showing a transition from (approximately) cylindrical defect-free bundles to defective, cylindrical packings possessing excess fivefold disclinations, i.e. Q = +1, +2 and +3. Red (blue) filaments label sites of interior fivefold (sevenfold) disclinations. The bottom row shows a relatively ductile case, where low-twist, defect-free cylinders transition to intermediate-twist anistropic ‘tape-like’ bundles, followed by a re-entrant cylindrical morphology (with excess defects) at high twist.

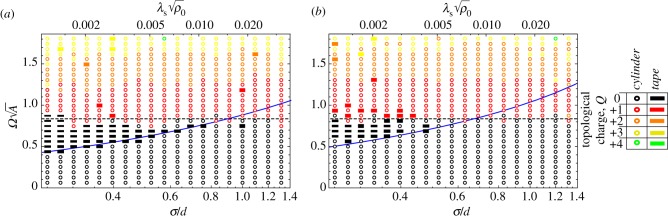
In figure 6a, we present the morphology phase diagram of N = 181 bundles spanned by ductility σ/d (ranging from 0.253 to 1.318) and reduced twist 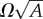where A≡Nρ⁻¹₀ with 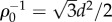the area per filament in a uniform hexagonal packing. Consistent with the above, we observe that stable defect-free, anisotropic tapes are generally confined to a range of twist intermediate to defect-free and defective cylinders below a critical value of ductility, (σ/d)_c ≃ 1.0, beyond which the boundary between cylinders and tapes shifts to lower twist with increasingly brittle interactions. In this range of potentials, the transition from defect-free bundles (either cylinders or tapes) to defective cylinders appears largely independent of ductility, occurring at a critical twist of roughly 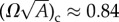. Assuming a circular symmetry, A = πR², this critical twist is consistent with the previous prediction and simulation result for threshold twist at which the relaxation of geometric frustration per fivefold defect is sufficient to overcome the elastic self-energy for defect formation in isotropic bundles [36,37]. We note that transitions to higher topological charge packings (Q = +2, +3, +4) also appear to be relatively independent of ductility, occurring at roughly the same reduced twist for all values of σ/d.

Figure 6.

Morphology phase diagrams from discrete filament simulations for N = 181 (a) and N = 59 (b), where a threshold value of aspect ratio α = 1.5 is used to distinguish cylinders from tapes and apparent aspect ratios of bars highlight optimal energy aspect ratios. Dashed line is drawn from predicted threshold for critical twist to stabilize fivefolds in cylindrical bundles and solid blue line is determined by continuum theory prediction for fixed N (and λ_B = 0) transition between defect-free cylinders and tapes (as discussed in the text).

In figure 6b, we show the morphology phase diagram for a smaller bundle, with N = 59, which shows the same generic trends as the larger bundle discussed above. While the threshold reduced twists for stabilizing defective bundles are not observed to change significantly from the N = 181 case, the range of stable tapes shifts to relatively lower values of σ/d (more brittle interactions) with defect-free tapes stable only below (σ/d)_c ≃ 0.48 for N = 59. We observe the same basic trends in the phase diagram (not shown) for bundles at intermediate (N = 101) and larger (N = 440 and N = 1540) filament number, with defect-free cylinders for low-twist/ductile interactions, defect-free tapes for intermediate-twist/brittle interactions and defective cylinders at high twist, above 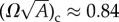. Moreover, we observe the critical ductility (σ/d)_c, above which anisotropic cylinders do not form and pass directly from low-twist defect-free cylinders to high-twist defective cylinders, to increase with N, as shown in figure 7.

Figure 7.

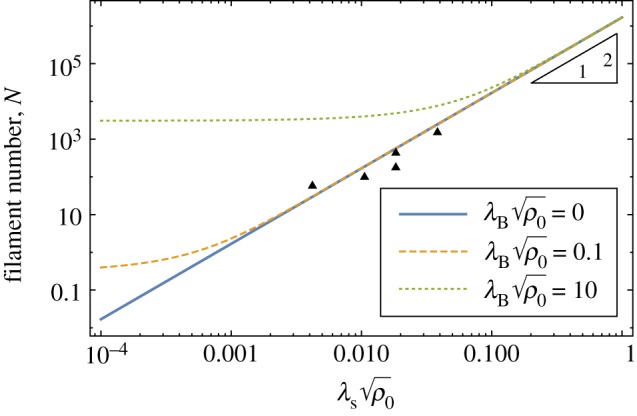
Triple point relation between filament number N = Aρ₀ and maximum 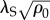for which tapes are stable. The black triangles indicate results from N = 59, 101, 181, 440 and 1540 simulations where triple point 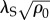was taken as the highest σ/d value at which a defect-free tape structure was found. Curves are predicted from continuum model where the defect-free cylinder/tape boundary (appendix A) crosses the critical threshold for fivefold defect stability in cylinders, .

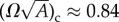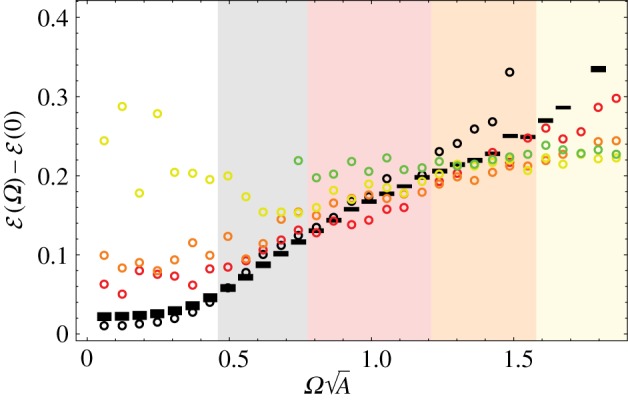
To understand the observed morphology transitions, in figure 8 we analyse the energetics of ground state bundles for a sequence of increasing twist at fixed σ/d = 0.3 and N = 181 (i.e. sufficiently brittle to form tapes) and compare to continuum theory predictions at fixed N and B = λ_B = 0 (see appendix A). Specifically, we analyse the cohesive energy (relative to the Ω = 0 state), decomposed in the two pieces, E_bulk and E_surf, the energy of interior and surface filaments, respectively (see appendix B.3). The energy of defect-free cylinders increases with small twist (both in the bulk and at boundary), in accordance with the elastic penalty due to frustration, ≈YA²Ω⁴, from equation (2.8). For the fixed-N case, the transition to tapes can be estimated by the point at which the the inter-filament elastic energy of cylindrical bundles grows in excess of the surface energy cost, or 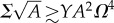, indicating that it is advantageous to create additional surface in order to relax bulk frustration. A more careful analysis (see appendix A) gives a reduced twist for the cylinder–tape transition 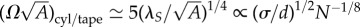, where we used Y ≈ ε/σ², Σ ≈ ε/d and hence λ_S ≈ σ²/d. These values of reduced twist are shown as blue curves in the phase diagrams in figure 6, and agree well with the defect-free cylinder-to-tape transition twist, and more significantly, its tendency to decrease with N and increase with σ/d, depending on the relative cost of inter-filament strain in comparison to bundle surface.

Figure 8.

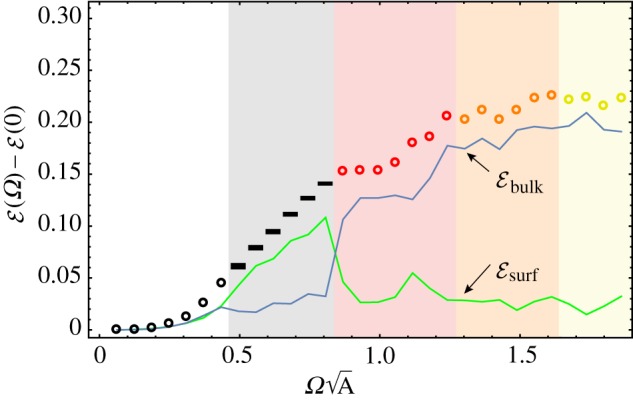
Surface, bulk and total cohesive energy density of simulated ground states (relative to Ω = 0 value), for N = 181 and σ/d = 0.30. Points show total energy , with morphology indicated as in figure 6 legend. The green and blue lines show surface (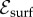) and bulk (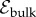) filament contributions, where 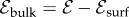and 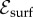is the cohesive energy of surface filaments relative to unstrained sixfold order, i.e. equation (B 12). Shaded vertical regions highlight transitions between stable morphology.

As shown in figure 8, at an intermediate range of reduced twist 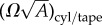, anisotropic bundle shapes become favourable. From the continuum model (see appendix A), the equilibrium aspect ratio (for α ≫ 1) is determined by a balance of excess surface energy, growing with narrow dimension 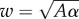as 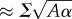, and inter-filament strain growing with thin dimension 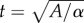as ≈ YΩ⁴(A/α)², yielding an equilibrium α* ≈ A(Ω⁴/λ_S)^2/5 that increases with filament number, twist and brittleness of inter-filament bonds. This power-law trend for tape aspect ratio is compared with simulated bundles in figure 9. Because equilibrium anisotropy increases with twist Ω, the surface energy E_surf of tapes increases rapidly with twist, while E_bulk remains relatively constant with Ω due to the mitigation of inter-filament strain by the narrow bundle thickness, as shown for stable tapes at intermediate-twist in figure 8.

Figure 9.

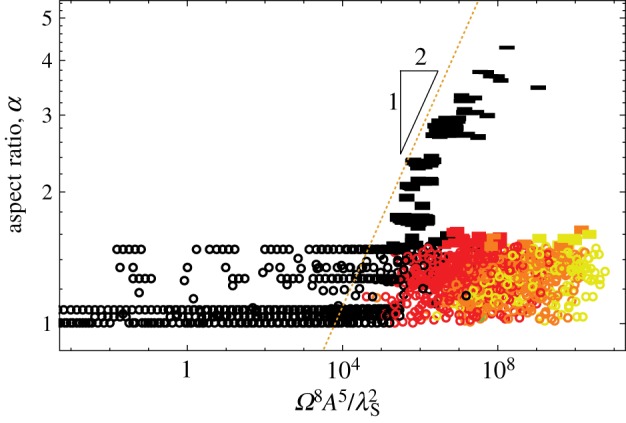
Optimal aspect ratio, α, for simulation bundle ground states plotted versus a dimensionless ratio of predicted bulk-frustration to surface energy penalty for cylinders, A^5/2Ω⁴/λ_S, for values of N = 59, 101 and 181. The dashed line shows large-α power law predicted from fixed-N continuum model, with morphology indicated as in figure 6 legend. Note that defective morphologies fall below α ≃ 1.5, the threshold we use to discriminate tapes from cylinders.

At high twist (above 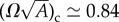), defective cylinders become stable, leading to a drop of surface energy due to the fewer number of boundary filaments in the circular cross section. For high twist, E_bulk > E_surf due to the straining of inter-filament bonds by the combined effect of frustration and topological defects. As reported previously in [31] the steady increase of Q with Ω leads to a nominal plateau of energy density at high twist as interior defects effectively mediate the cost of increased frustration by twist. This generic flattening of the bulk frustration energy due to one or more excess fivefold disclinations is responsible for the generic crossover from stable intermediate twist tapes, with energies that grow modestly with twist (f_tape∼Ω^4/5 when compared with f_cyl ∼ Ω⁴ for cylinders), to defective cylinders, which approach a relatively constant, if somewhat cuspy energy density due to the fixed circular boundary and neutralizing effect of fivefold disclinations.

We use the predictions of the continuum model to present an overview of the fixed-N morphology selection in figure 10, here as a phase diagram spanned by the axes Ω²A and Ωλ_S. The intersection of the cylinder–tape boundary Ω²A ≃ 13.2Ωλ_S with the critical condition for stabilizing fivefold defects in cylinders Ω²A ≃ 0.71 yields the triple point where defect-free cylinder, defect-free tape and defective cylinder phases meet, giving also the prediction for the dependence of the critical ductility (σ/d)_c on N, shown in figure 7. Here, we also show the effect of non-zero bending stiffness or Ωλ_B ≠ 0. The effect of bending stiffness in this morphology phase diagram is to penalize tape morphologies (which possess a larger second moment of cross-sectional area 〈r²〉) relative to cylinders, shifting the cylinder–tape boundary to larger values of Ω²A as shown in figure 10, particularly at low values of Ωλ_S where brittle interactions otherwise favour very wide tapes. This analysis shows that above a critical stiffness value, for 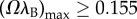, the window of intermediate twist tapes is shifted above the threshold for stable defects (which are insensitive to bending stiffness) and we therefore expect tape-like bundles to be preempted entirely by defective cylinders when filaments exceed this critical stiffness .

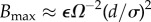Figure 10.

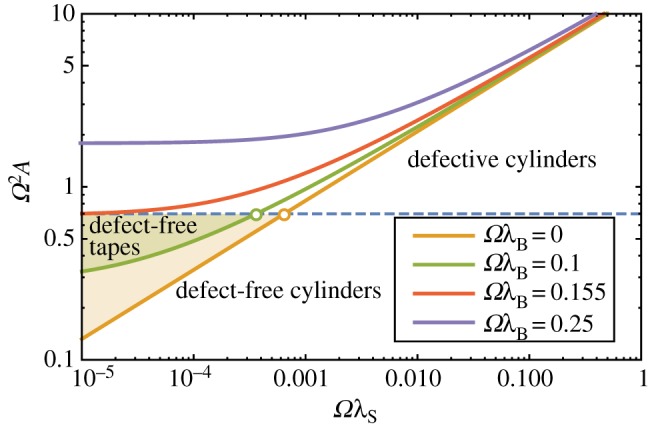
Continuum theory (fixed-N/fixed-Ω) phase diagrams for morphology selection of twisted bundles for a range of values of Ωλ_B. Solid lines are predicted transition lines between defect-free cylinders and tapes, and dashed line is threshold stability for fivefold disclinations in cylinders. Equilibrium tapes are predicted in the shaded regions between the solid boundaries and dashed lines, with triple points indicated as empty circles. For Ωλ_B ≥ 0.155, tape morphologies are not stable.

4. Conclusion

In this paper, we investigate two models of morphology competition for self-assembled chiral filament bundles. The first considers the ability to ‘escape’ frustration by untwisting chiral inter-filament skew and its effect on the otherwise self-limiting assembly of bundles. We find that finite stiffness of inter-filament chiral interactions, K, puts an upper limit on the (cohesive) surface energy 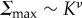at which finite, frustration-limiting bundles form where 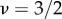for K ≪ K_c and for K ≫ K_c, where K_c = Ω²₀(ρ₀B)²/Y. When chiral interactions are sufficiently stiff (K ≳ 100K_c) equilibrium assembly includes windows of both cylindrical (small Σ) and tape-like bundles (intermediate Σ) as well as bulk, untwisted assembly (large Σ), while in the opposite limit of ‘soft’ chiral interactions, the window of tapes narrows dramatically and ultimately vanishes, leading to direct transition from twisted cylinders to bulk assembly for even weakly cohesive bundles. The second model investigates the interplay between competing morphological responses to inter-filament frustration: bulk defects versus boundary anisotropy. We found that when inter-filament bonds are sufficiently brittle, tape-like bundles are stable as an intermediate-twist phase between defect-free cylinder (low twist) and defective cylinder (high twist) morphologies, and that the selection of the energetically favourable morphology was controlled by the relative cost of straining inter-filament bonds in the bulk (as required to form large isotropic domains and topological defects) compared with the cohesive cost of creating excess free bundle surface, which has the critical effect of lowering frustration costs through low-energy boundary deformation.

The results demonstrate surprising and generally overlooked properties of geometrically frustrated assemblies [23]. Preferred chiral ordering makes uniform order, both intra- and inter-filament, impossible, leading to a competing set of heterogeneous, and morphologically distinct, local free energy minima. Thus, a proper understanding of even the equilibrium behaviour of these systems is a far greater challenge than canonical, unfrustrated systems, requiring an analysis of all classes of metastable equilibrium, each of which is governed by a distinct set of thermodynamic or microscopic parameters describing assembly. In the context of this work, an outstanding challenge still remains to compare and understand the competition of all four classes of morphological responses at once: self-limiting width, untwisting of chiral interactions, formation anisotropic boundary shape or topological defect in the interior.

Furthermore, a much broader challenge will remain to understand how the principles of morphology selection analysed here also control non-equilibrium assembly. For example, in [41] we analysed the tape-like and cylindrical morphologies of twisted amyloid protein bundles in terms of the equilibrium (fixed twist) model of domain shape selection, and we find that tapes form at a degree of bundle twist, where based on the present study, we would expect equilibrium morphologies to relax frustration via one or more fivefold interior defects while retaining a cylindrical shape. The observation of tapes in this regime suggests a kinetically limited assembly pathway, where the bundles are kinetically free to relax frustration upon reaching a critical size through anisotropic domain growth, but may be subject to very large barriers that inhibit the global reorganization of defect-free tapes into defective cylinders.

We note recent development of numerical techniques, including basin-hopping to more completely identify energy-minimizing structures and discrete path sampling to characterize the minima in geometrically frustrated assemblies [48–51]. These methods hold promise to map out the proximity and connectivity of structurally distinct local minima (e.g. those with and without defects) within the energy landscape of frustrated bundles. A systematic study of the thermodynamically and kinetically accessible pathways between distinct morphologies of chiral filament bundles, or geometrically frustrated assemblies more broadly, remains a critical and unresolved aspect of the anomalous behaviour of these systems.

Appendix A. Continuum theory of fixed-area bundles

Here, we describe the continuum model prediction for coexistence between cylindrical and tape morphologies, restricted to fixed twist rate Ω and fixed area A, equivalent to fixed filament number, N ≃ Aρ₀. In this case, cylinder radius R and tape width w and thickness t satisfy A = πR² = wt. Defining dimensionless area , elasto-cohesive length 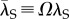, and bend penetration depth 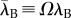, we rewrite equations (2.8) and (2.9) (neglecting the contribution from twist elasticity for fixed-twist ensemble and re-casting energy density f ≡ F/YV):

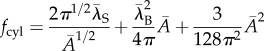A 1

and

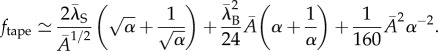A 2

The equilibrium value of aspect ratio α* is determined by the condition

A 3

where we consider only the stable solutions where aspect ratio α* > 1, as the inter-filament elastic energy fails to hold for α ≲ 1. For example, if we consider the limit of α ≫ 1 and λ_B = 0 (as discussed in the text), we may neglect the bending terms and the surface contribution from the narrow ends of the tape section (∝α^−1/2 ≪ 1), relative to the large contribution from the wide dimension (∝α^1/2 ≫ 1). From this limit of (A 3) we find equilibrium tape dimensions and energy,

A 4

Coexistence is determined by the solution to f_cyl(α*) = f_tape.

Exact numerical solution of equilibrium conditions for λ_B = 0 gives coexistence between cylinders and tapes along the line

A 5

With increasing bending cost, tapes become less stable due to the distribution of filaments to larger radial distances from the twist axis, and therefore higher curvature. Notably, for Ωλ_B > 0.155, tapes are unstable for all Ω²A below the threshold 2π/9 which defines coexistence of the defect-free cylindrical morphology with defective cylindrical morphology with (+1) topological charge (equivalent to 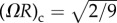derived in [36]). The triple point where defective structures coexist with both defect-free tapes and cylinders is found according to the above conditions for coexistence, subject to the constraint (Ω²A)_c = 2π/9 ≃ 0.7.

Appendix B. Simulation methods

B.1. Inter-filament potential

Here, we describe formulae used to model the inter-filament cohesive interactions. Similar descriptions appeared previously in [30,31,41].

We assume the form of the pairwise interaction potential defined by u(Δ) and ΔE in equations (3.2) and (3.1) derives from the superposition of pairwise interaction V(r) between material points along two filaments, as described before in [31]. Parametrizing centrelines of i and j filaments by X_i(s_i) and X_j(s_j) (s_i and s_j are arc length coordinates), then the total energy is simply

B 1

Taking X_i(s_i) as the outer filament (such that ρ_i ≥ ρ_j), we define Δ_ij as the separation that connects X_i(s_i) with the closest point on i at X_j(s*_j (s_i)). That is X_j(s*_j (s_i)) − X_i(s_i) = Δ_ij, such that (d/ds_j)|X_i(s_i) − X_j(s_j)|²|_s*j(si) = 0. Defining δs_j ≡ s_j − s*_j (s_i) as the arc-distance from the closest contact on j to i, we have

B 2

where Δ_ij · N_j is the projection of the inter-filament separation along the normal direction of the inner filament. For sufficiently short-range potential V(r) with respect to filament curvature and constant filament curvatures

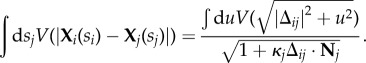B 3

Defining

B 4

and for outer filament length ℓ_i

B 5

Thus, the total energy depends on the length of the outer filament and the second-order deflection of j near to close contact with i, accounting for the factor of (1 + κ_jΔ_ij · N_j)^−1/2. Taking Δℓ_i as the discrete approximation for ds_i, we arrive at the formula for ΔE_ij used in equation (3.1).

When the interaction has the form of a Lennard-Jones potential, V(r) = V₀[(σ₀/r)¹² − 2(σ₀/r)⁶], then u(Δ) = (ε/6)[5(σ/Δ]¹¹ − 11(σ/Δ)⁵] with preferred filament spacing d = σ = 0.947σ₀ and minimum energy ε = 1.686V₀σ₀ [31]. Hence the range (and curvature) of the cohesive potential is locked to the equilibrium spacing for this particular model of cohesive ‘threads’. Here, we use a broader class of inter-filament potentials, u(Δ), that allow for independent adjustment of equilibrium spacing, d, and range, σ, of attractive well:

B 6

At the minimum Δ = d, the curvature, or stiffness, of the potential is a function of σ only,

B 7

The above form of this potential at the minimum controls the coarse-grained modulus of the inter-filament array (see [31,41]), 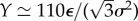, while the filament diameter controls the surface energy Σ ≃ ε/d, allowing for a broadly tunable range of elasto-cohesive length λ_S = Σ/Y.

The inter-filament spacing Δ is computed according to an approximation previously established [30]. In short, for filaments with centerlines intersecting the cross section at positions x_i and x_j, the exact expression for inter-filament distance comes from minimization with respect to the vertical component of separation z of the following:

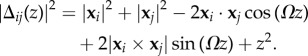B 8

To approximate the contact separation z_*, we use the following interpolation:

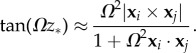B 9

This form interpolates between the exact solutions to (d/dz)|Δ_ij(z)|² = 0, in the limits of small and large Ω²ρ_iρ_j and has been shown to be sufficiently accurate for potentials whose range is smaller than their thickness, a limit well satisfied by simulations here.

B.2. Simulation details

B.2.1. Method A, lattice sampling

Initial configurations were generated with filament positions on a triangular lattice with spacing d, at points within a stadium perimeter (connecting two half-circles with straight lines as in figure 11a). The stadium aspect ratios were taken ranging from 1.0 to 7.5 in increments of 0.2, and taken with centre on a lattice point, lattice edge and the centre of of a triangular plaquette. For aspect ratio larger than 1, the longer dimension (tape width) was oriented along the close-packed lattice direction. Stadium dimensions were chosen to be the smallest so that each choice of aspect ratio and stadium centre enclosed the desired number of filaments. When this produced a structure with excess filaments (i.e. close to, but more than predetermined N), additional points were omitted from the last close-packed row, starting from the end. This filament ‘pruning’ is illustrated in figure 11a, where two outer points are omitted to produce the structure with 181 filaments. Figure 11b shows the dimensions, and two limiting example structures, of lattice initialized configurations sampled for N = 181 filaments. Corresponding relaxed energies for each lattice structure sampled are shown in figure 11c for twisted bundles at two sample values of ductility σ/d (brittle/ductile).

Figure 11.

In (a), starting configurations are sampled with filament centreline positions arranged on a hexagonal lattice. Structures of varying aspect ratio are taken by selecting points within a stadium boundary with varying dimensions. Lattice vertices circled blue correspond to ‘pruned’ filament positions removed to maintain target N. In (b), the dimensions of the lattice configurations sampled for N = 181 filaments are shown, corresponding to sampling with stadium boundary aspect ratios α = 1−7.5, with example configurations shown as highlighted. In (c), the energy densities of relaxed lattice configurations are shown at twist 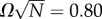, for two values of ductility σ/d. For brittle case, σ/d = 0.4, α ≃ 3 tapes are favoured, while for the relative ductile case, σ/d = 1.0, roughly cylindrical bundles (α ≃ 1) are optimal.

B.2.2. Method B, random sampling

Random initial configurations were generated by uniformly distributing filament positions within a circular boundary of radius , such that the starting configuration always had slight compression. In figure 12, we show how these randomly seeded configurations lead to competing energy minima with a range of Q for given bundle parameter values. For the purposes of this study, we chose to exhaustively sample the defective configurations for N = 59 and N = 181, and sample defect configurations in N = 101 and N = 440 bundles more sparsely, only to confirm the transition from defect-free cylinders/tapes to defective packings at the critical twist. Accordingly, the number of randomly initial configurations n_init per set of bundle parameters (Ω and σ/d) was varied with N: n_init = 6000 for N = 59; n_init = 3000 for N = 101; n_init = 60 000 for N = 181; and n_init = 3000 for N = 440. For N = 1540, no attempt was made to sample random initial structures, due to the prohibitive computational cost for bundles at this size.

Figure 12.

Lowest-energy states of competing morphologies, for N = 181, σ/d = 0.40, plotted according to cohesive energy density (relative to Ω = 0 value). Here, we show lowest energy obtained with each morphological class, with morphology indicated as in figure 6 legend: defect-free cylinders or tapes and defective cylinders for each non-zero Q value. Shaded vertical regions highlight transitions between stable morphology.

For each value of filament number N, simulations were run with twist 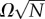ranging from 0 to 2.0 with 30 equally incremented values. The range of ductility σ/d varied with filament number N, and values of σ/d were spaced logarithmically with successive ratio 1.096:

no. filaments N	ductility σ/d	no. random samples
59	0.253–1.318	6000
101	0.253–1.318	3000
181	0.253–1.318	60 000
440	0.253–1.738	3000
1540	0.253–1.738	n.a.

B.2.3. Structure relaxation

From each set of initial filament positions, a local equilibrium was found by steepest descent according to the defined energy density, stopping when the largest component of the gradient (parametrized by filament coordinates) had magnitude less than 10⁻⁴ε/d. In areas of low twist, the best structures were generated by slight relaxation of configurations generated from a triangular lattice. Larger rearrangements were required in regions of high twist, and randomly generated starting configurations consistently produced more favourable structures. In order to allow larger rearrangements even with brittle systems and to remove overlaps with filament ‘cores’ (Δ < d − σ), initial structures were first (before steepest descent) preconditioned by relaxation via steepest descent according to a soft repulsive potential,

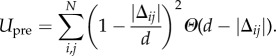B 10

B.3 Simulation analysis

B.3.1. Morphology characterization

The lowest-energy structure at each point on the phase diagram was analysed, taking both the aspect ratio and net topological charge of the interior. The aspect ratio was taken from the lateral dimension of the minimum-area rectangle that encloses the cross section. The minimal-area rectangle is found from considering all rectangles enclosing the structure's convex hull where one edge of the rectangle must coincide with an edge of the convex hull.

The net topological charge was computed by Delaunay triangulation of the transformed cross-sectional positions. As the true distances between filaments are properly encoded in the dual metric surface, we triangulate based on a conformal map of filament positions from the dual surface to the two-dimensional plane. This map is performed by radial dilation of filament position, 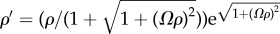for a filament with cross-sectional radial position ρ. This mapping results in the angles between filament separations reflecting the true inter-filament bond angles when measuring filament distances according to the geodesic distance on the dual surface [30]. The conformal map allows regular Delaunay triangulation, subdividing the convex hull of the packing into triangles connecting filament positions, so that the minimum inter-bond angle of the triangulation is maximized.

The perimeter of the bundle was constructed by starting with the convex hull, then successively removing exterior bonds with large distance of closest approach, |(Δ_ij/d)| > 1.4, and adding the interior point that shared a triangular plaquette according to the Delaunay triangulation. The net topological charge of the interior was then taken by totalling the excess coordination for each filament not belonging to the set of boundary filaments.

B.3.2. Surface and bulk cohesive energies

Here we decompose the cohesive contribution from pair-wise interactions,

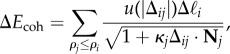B 11

into energies associated with surface formation and bulk inter-filament deformation. The surface energy is taken to be the deficit of exterior filament contact from a reference state with total cohesive energy 3ε. The surface energy is then

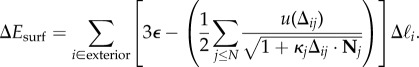B 12

The bulk energy is taken as the difference, ΔE_bulk = ΔE_coh − ΔE_surf.

Authors' contributions

G.M.G. developed continuum theory analysis for the predictions of frustration escape to bulk assembly. D.M.H. and G.M.G. designed numerical simulations for the competition between anisotropic and defect morphology responses. D.M.H. and G.M.G. conducted and analysed simulation results. D.M.H. and G.M.G. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by the NSF through grant no. DMR 16-08862 and by the Donors of the American Chemical Society Petroleum Research Fund through ACS PRF grant no. 54513-ND.