Abstract
In genetic transcription, molecular dynamic details and energetics of NTP binding to the active site of RNA polymerase (RNAP) are poorly understood. In this article, we investigated the NTP binding process in T7 RNAP using all-atom MD simulation combined with the umbrella sampling technique. Based on our simulations, a two-step mechanism was proposed to explain NTP binding: first, substrate NTP in aqueous solution, which carries a magnesium ion, diffuses through a secondary channel of RNAP to attain a pore region, where it undergoes conformational changes to give a correct orientation; next, the NTP establishes initial basepairing contacts with the template nucleoside (TN). Our free-energy calculations suggest that both steps are spontaneous. This mechanism can easily explain the problem of NTP binding with different orientations. Moreover, it is found that the nascent NTP:TN basepair is fragile and easily broken by thermal disturbance. Therefore, we speculate that the fingers domain will be triggered to close, so as to create a steady environment for the next chemical step. The observations from the work provide valuable information for comprehensively understanding the mechanism of the basic step in genetic transcription.
Introduction
Genetic transcription serves as a bridge to transfer genetic information from template DNA to protein so as to realize gene expression. Information encoded in DNA is copied to RNA by the cellular machinery RNA polymerase (RNAP), where RNA transcript is synthesized through consecutive nucleotide addition cycles (NACs). Experiments have provided abundant high-resolution x-ray crystal structures in NAC. For example, Steitz et al. (1) captured crystal structures of T7 RNAP complex in the post-translocation, insertion, and product states; meanwhile Temiakov et al. (2) obtained the one in the pre-insertion state. These crystal structures make up an almost complete NAC and bring people’s knowledge of transcription to atomic resolution. The NTP-addition reaction occurs at the catalytic active site of RNAPs, where a steady environment is needed to shield intense thermal oscillation. To explain the substrate binding mode in RNAP, Temiakov et al. (2) revealed that NTP’s triphosphate moiety is mainly fixed through hydrogen bonds with three O-helix residues, R627, K631, and R632, and two additional residues, K472 and Y571, in the substrate complex (2). Additionally, Huang et al. (3) proposed a three-component (hydrophobic contact, base stacking, and basepairing) mechanism to describe how NTP’s base is correctly positioned in the active site. However, how does NTP diffuse into the active site and basepair with template nucleoside (TN)? If an NTP comes in with a wrong orientation, how does it correct the conformation? Which residues have participated in NTP conformational correction? These questions also seem interesting, and they are important for comprehensively understanding the mechanism of RNAP efficient operation. NTPs, which are negatively charged molecules with a high affinity to metal ions, mostly exist in the form of (Mg-NTP)2− complex in cells (4). Batada et al. (5) investigated theoretically NTP diffusing in yeast RNA polymerase II (pol II) and found that the funnel and pore of pol II reduced NTP diffusion rate. However, the (Mg-NTP)2− complex was treated as a negatively charged sphere, and detailed information at molecular level was completely lost. As NTP binding occurs at nanometer length scale and hundreds-of-microseconds timescale, it is not easy to investigate by conventional experimental methods. Computer simulations can complement experimental approaches by providing information inaccessible to experiments and helping address many important questions (6, 7). Molecular dynamics (MD) simulation, a powerful computer simulation tool, can reproduce dynamic behaviors of biomolecules at atomistic resolution, offering the potential to gain new insight into functional mechanisms of biomolecules (8). However, conventional MD simulations are capable of simulating biological activities occurring at a timescale of tens to hundreds of nanoseconds, far from the biologically relevant timescales of microseconds or even longer (9). Therefore, other methods have been employed to bridge the time gap between conventional MD simulations and biological activities. Coarse-grained methods can greatly increase the simulation timescale, whereas atomistic details are also lost (10, 11). Recently, Huang et al. (7, 12) successfully applied Markov state models to elucidate the transcription mechanism. However, the resultant free-energy landscapes are unconvincing on account of insufficient sampling in the conformational space. In this study, all-atom MD simulation combined with the umbrella sampling (US) method was used to estimate free energies for NTP binding. T7 RNAP, a single-subunit RNA polymerase that can carry out all steps of the transcription process without extra protein components (13), was used as a model enzyme to investigate NTP binding in this work. We performed three rounds of MD simulations. The first two were US simulations, exploring the energetics and molecular mechanism of NTP binding. The third round elucidated the basepairing contacts in the nascent NTP:TN basepair. Based on our simulations, NTP binding process was proposed to consist of two steps: first, NTP diffuses through a secondary channel in T7 RNAP to attain the active site, where it undergoes conformational changes to give a correct orientation; next the NTP establishes initial basepairing contacts with the TN. The resulting free-energy profiles suggest that both steps are spontaneous processes. We believe this work may shed light on the molecular mechanism of the basic step in genetic transcription.
Materials and Methods
Model construction
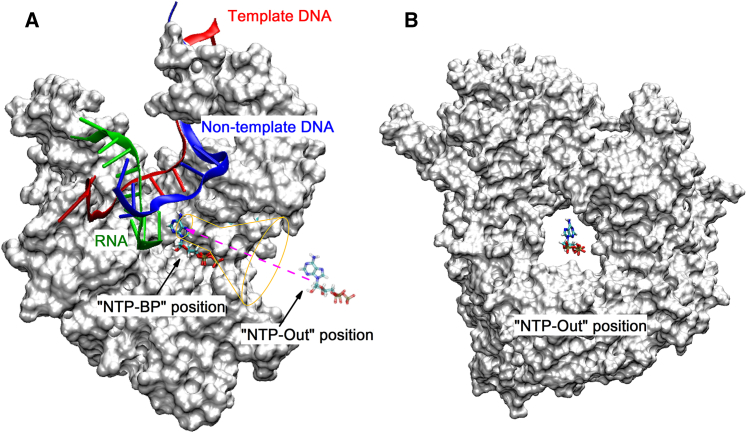
In each NAC, the substrate NTP should diffuse through a secondary channel (a funnel-shaped opening that narrows to a pore) before binding to the active site of RNAP. To investigate the NTP binding process in RNAP, two configurations were defined as shown in Fig. 1. When an NTP in bulk solution gets close to the secondary-channel entrance, we term this configuration the “NTP-Out” state, and the NTP position is denoted as the “NTP-Out” position; when the NTP binds to the active site and establishes initial Watson-Crick basepairing contacts with the TN, we term this the NTP basepairing (NTP-BP) state and the NTP position is denoted as the “NTP-BP” position. Experiments have provided abundant x-ray crystal structures for the transcription system, which can be used as a structural basis to construct our model systems. The “NTP-BP” structure was derived from the pre-insertion complex (PDB: 1S0V), where the bound ATP analog was modified to an ATP molecule. The “NTP-Out” structure was generated by moving the (Mg-ATP)2− complex to the middle position of the secondary channel entrance, as shown in Fig. 1, A and B.
Figure 1.
Schematic diagram of the NTP binding pathway. (A) Cross section of the T7 RNAP-ATP complex. NTP diffuses through a secondary channel of T7 RNAP before binding to the active site. The purple dashed arrow denotes the pathway of NTP binding defined in this work, which connects the “NTP-Out” and “NTP-BP” positions. (B) Front view of the funnel region in the “NTP-Out” state. The (Mg-ATP)2− complex is placed in the middle position of the secondary-channel entrance. To see this figure in color, go online.
Simulation details
All simulations in this work were carried out using all-atom MD simulation in explicit water. GROMACS, one of the fastest and most popular simulation software packages (14, 15, 16), was used to perform MD simulations. The AMBER99SB force field with ParmBSC0 nucleic acid parameters (17) was used to describe protein, DNA, RNA, and metal ions. The AMBER parameters for ATP were developed by Meagher et al. (18). The initial T7 RNAP complex was placed in a rectangular box of 106.37 × 101.80 × 102.02 Å, where the distance from box surfaces to the closest atoms of the complex is ∼10 Å, which is large enough to prevent T7 RNAP complex from contacting with its periodic images. Then, ∼16,200 three-point transferable intermolecular potential (TIP3P) water molecules (19) were added to solvate the complex, and 71 Na+ and 51 Cl− ions were added to neutralize the system at an ionic concentration of 0.15 mol·L−1. The final size of the system reached ∼110,000 atoms. The cutoff distances for van der Waals (vdW) and short-range electrostatic interactions were set as 10.0 Å. Long-range electrostatic interactions were treated with the particle-mesh Ewald method (20, 21). Pressure and temperature were controlled at 1 bar and 310 K by Berendsen barostat (22) and velocity rescaling thermostat (23), respectively. The LINCS algorithm was applied to constrain all bonds involving hydrogen atoms (24). Motion equations were numerically solved with a time step of 2 fs and the neighbor list was updated every 10 steps. Each solvated complex was subjected first to a thorough energy minimization using steepest-descent minimization, and then to a 200 ps MD simulation with position restraints on heavy atoms. The final configuration was used for product simulation. Trajectories were saved at 2 ps intervals. Conformation characterization and energetic analysis were performed using built-in tools of GROMACS. The protein structures were visualized using VMD software (25).
US simulation
The US method was employed to estimate the potential of mean force (PMF) profiles for NTP binding. We performed two rounds of US simulations, the first to investigate the overall NTP binding process and the second to focus specifically on NTP basepairing with TN. In the first round, the distance between the two centers of mass of ATP and TN was chosen as the reactive coordinate for PMF calculation, referred to as ζ1. To conduct US simulation, a series of configurations along the NTP binding pathway should be prepared as seed configurations. The steered MD (SMD) technique was used to generate the initial pathway. As NTP binding to the active site is a delicate process that is not easy to reproduce directly, an NTP dissociation trajectory was generated by SMD and then reversed as the initial pathway for NTP binding. Forty frames were extracted from the SMD trajectory and used as seed configurations for US simulations. In the second round, since basepairing occurs only between the two bases of ATP and the TN, the distance between the two bases was chosen as the reactive coordinate (denoted as ζ2) for PMF calculation. To generate the seed configurations, the two bases were separated to a series of specified distance values using a strong spring force (k = 10,000 kJ·mol−1·nm−2). After equilibration for 500 ps, the resulting configurations were used for seed configurations in the second US simulation. Using this approach, 40 other seed configurations were prepared. Each US window was simulated for 10 ns with a force constant of k = 1000 kJ·mol−1·nm−2 (26). The later 8 ns trajectory was sampled at a frequency of 2 ps for PMF calculations. PMF profiles were generated using the GROMACS tool g_wham (27). Error was estimated through 200 rounds of bootstrapping analysis.
Results and Discussion
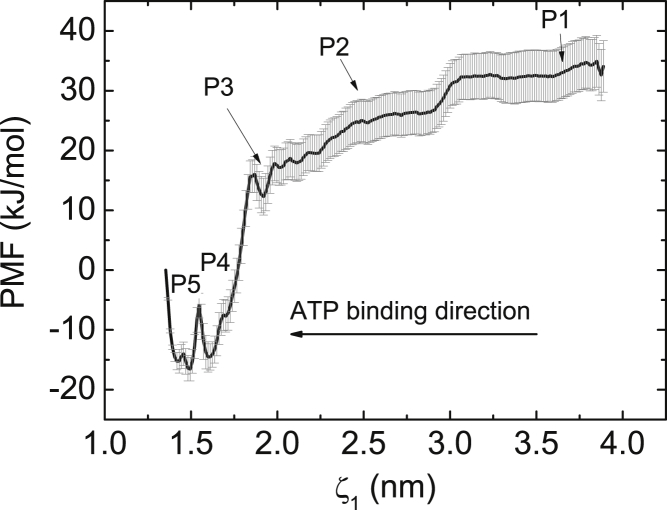
To study the energetics and molecular mechanism of NTP binding, we have attempted several pathways in different directions while similar free energy results were obtained. Fig. 2 displays a representative free-energy profile as a function of ζ1. The pathway covers the entire process of ATP binding from bulk solution to active site. Based on the PMF profile, five representative points, P1∼P5, were chosen to characterize the ATP binding process in T7 RNAP, as shown in Fig. 2. To gain a comprehensive understanding of the NTP binding process, we conducted residue-level analysis at the five representative points. By determining the vdW (EvdW) and electrostatic (Eelec) interactions between ATP and each amino acid residue of T7 RNAP, we were able to identify the critical contacts contributing to free-energy changes. Fig. 3, A–E, displays the snapshots in the active site at the five representative points, as well as their corresponding EvdW and Eelec profiles.
Figure 2.
One-dimensional PMF profile of ATP binding in T7 RNAP. The distance ζ1 between two centers of mass of ATP and TN was chosen as the reactive coordinate. The P1 and P5 sites correspond to the “NTP-Out” and “NTP-BP” states in Fig. 1, respectively.
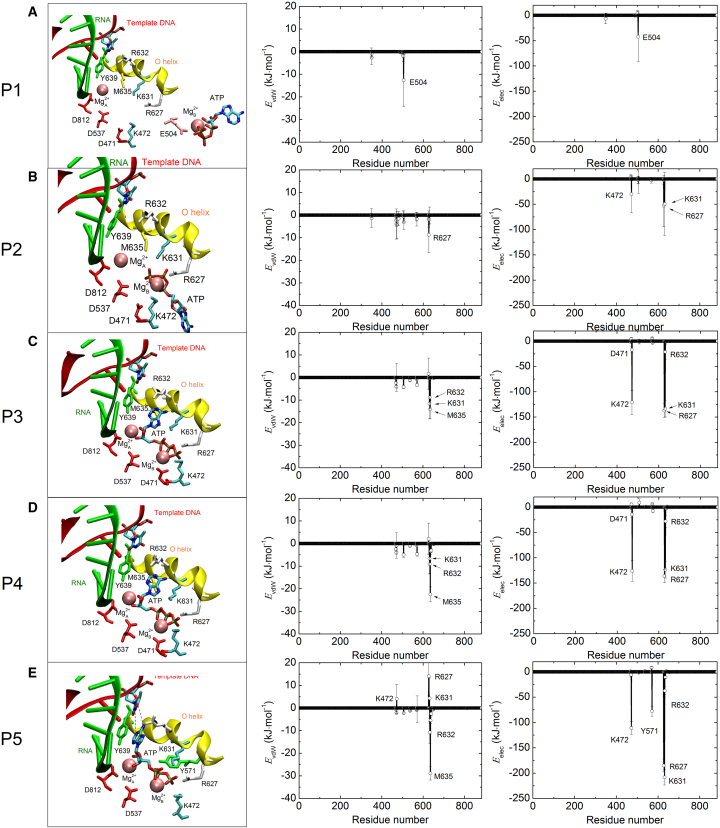
Figure 3.
(A–E) Residue-level analysis of protein-ATP contacts at the five representative points, respectively. The left column displays snapshots in the active site at the five points; the middle and right columns show vdW and electrostatic interactions between ATP and each amino acid residue of T7 RNAP, respectively. To see this figure in color, go online.
At the initial stage of each NAC, the fingers domain of T7 RNAP is in the open conformation. When an (ATP-Mg)2− complex approaches the secondary channel entrance, it would be attracted by these polar or charged residues on the entrance wall. As shown in Fig. 3 A, a negatively charged residue, E504, has formed initial contacts with the (ATP-Mg)2− complex in the entrance. Although these interactions are weak (Evdw = ∼−13 kJ/mol, Eelec = ∼−42 kJ/mol), they are important for RNAP to capture NTPs from the solution. Subsequently, the (ATP-Mg)2− complex is induced to diffuse toward the active site. After diffusing through the funnel region, the (ATP-Mg)2− complex reaches the pore region (P2 site), where the number of groups in contact with the (ATP-Mg)2− complex is significantly increased. R627, K631, and K472 are observed to establish contacts with the (ATP-Mg)2− complex through salt-bridge interactions. Between the P2 and P3 sites, the ATP is undergoing conformational changes, and a pronounced flip movement is observed. After the conformational changes, the (ATP-Mg)2− complex obtains a correct orientation for basepairing at the P3 site, as shown in Fig. 3 C. At the P4 site, the (ATP-Mg)2− complex strengthens its contacts with surrounding groups (Fig. 3 D). Non-bonded energy analysis reveals that four positively charged residues, R627, K631, K472, and R632, form strong electrostatic contacts with the ATP from one side while three negatively charged groups, D812, D537, and D471, establish firm contacts with the ATP through two Mg2+ ions as bridges from the other side; furthermore, M635 and R632 form relatively weak vdW contacts with the ATP. As a result, these interactions contribute to a deep valley on the PMF curve at the P4 site (Fig. 2), suggesting that the correct orientation of ATP is energetically favorable in the active site. Therefore, the (ATP-Mg)2− complex is firmly stabilized at the pore region. Many experimental works have confirmed that mutations of these conserved residues will result in moderate to drastic reductions in T7 RNAP transcriptional activity (28, 29). At last, the ATP establishes initial Watson-Crick basepairing contacts with the TN at the P5 site, as shown in Fig. 3 E. From the above analysis, it is clear that these charged and polar groups in the pore region capture the ATP by the triphosphate moiety firmly, guaranteeing a reasonable distance between the ATP and TN for basepairing. Since the ATP base is not constrained by any factors, it is free to align the conformation to basepair with the TN.
According to the “two-metal ion mechanism” (30, 31), two magnesium ions are involved in substrate recognition and catalytic specificity. In this study, two Mg2+ ions are observed to play important roles in positioning and stabilizing NTP during its binding. These residues with negative charges make contact with NTP’s triphosphate moiety through the two ions, which act as bridges. D537 and D812 are metal ion-binding sites. The Mg2+A ion, which stays permanently in the active site and facilitates the nucleophilic attack of the 3′-oxygen from the RNA terminal nucleotide on the α-phosphate of the substrate NTP, is mainly bound to D812 and D537. Osumi-Davis et al. (32) have shown that the mutants D537N and D812N are totally inactive. The Mg2+B ion is bound to D471 (see Fig. 3, B–D). K472 is a positively charged residue adjacent to D471. Its presence will significantly weaken the contacts between D471 and the (Mg-ATP)2− complex. As a result, D471 forms a weaker contact with the (Mg-ATP)2− complex compared to D537. On the other hand, in the insertion state (PDB: 1S76), both the two ions are trapped in the gap between D812 and D537 so as to catalyze the SN2 chemical reaction. Therefore, we speculate that when the fingers domain is closing, D471 may function as a hop site to deliver the Mg2+B ion to the gap between D812 and D537.
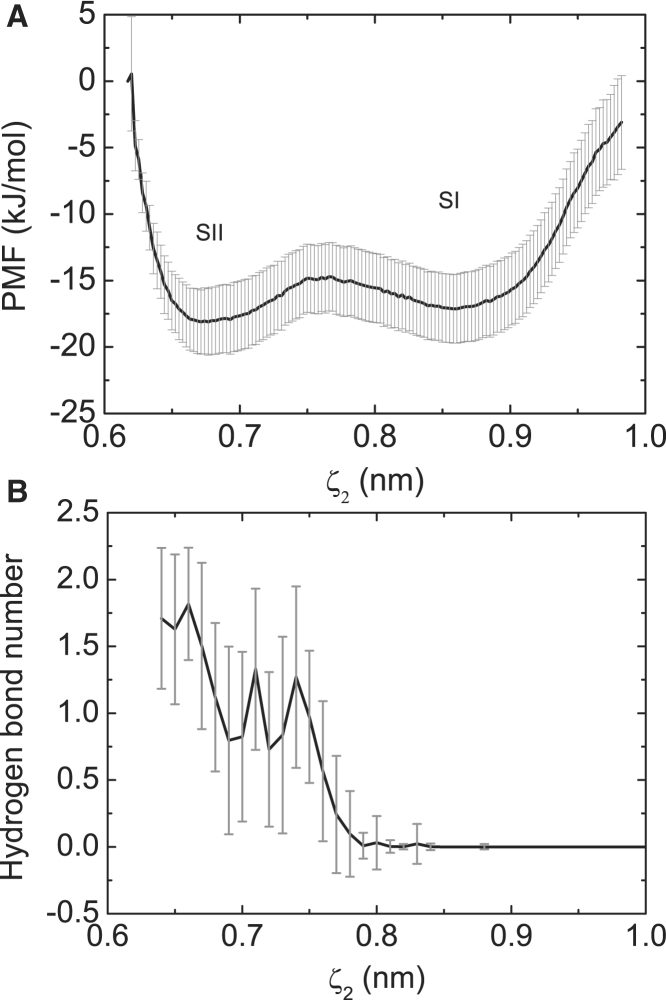
Basepairing is a delicate process between NTP and TN. Although the ATP has established initial basepairing contacts with the TN in the P5 site, we have not obtained many molecular details about NTP/TN pairing. Thus, we performed the second US simulation focusing on the basepairing process, where the distance between the two bases of ATP and TN was chosen as the reactive coordinate ζ2. Fig. 4 A shows the resulting PMF profile for ATP:TN basepairing. Two minima are observed, representing two metastable states during basepairing. For convenience, they are referred to as states SI and SII. Fig. 4 B shows the changes in the number of hydrogen bonds in the ATP/TN pairing, which are closely correlated to free-energy changes. In the SI state, the two bases are not close enough (ζ2 = ∼0.86 nm), so no hydrogen bonds are formed. As ζ2 decreases, the average number of hydrogen bonds increases rapidly in the range ζ2 = 0.6–0.8 nm. In the SII state (ζ2 = ∼0.67 nm), an average of ∼1.7 hydrogen bonds are formed between the ATP and TN, suggesting that the ATP has established initial basepairing contacts with the TN. It is clear that the two local minima correspond to the two metastable states before and after ATP:TN basepairing (33). Furthermore, a careful examination reveals that the SII site is slightly lower than the SI site by ∼1 kJ/mol, suggesting that the SII state is more energetically favorable than the SI state and that the basepairing is a spontaneous process. Nevertheless, the small energy barrier (∼6 kJ/mol) between them denotes that the basepairing contacts are not robust, and are thus easily damaged by thermal disturbance. Our previous work has suggested that for a normal dA:dT basepair in the DNA duplex, the average distance between the two bases is ∼0.64 nm (33). Under the conditions presented here, the nascent basepair is formed between a pre-inserted ATP and the TN (see Fig. 5, A and B), and the favorable value of ζ2 is ∼0.67 nm (Fig. 4 A). The small increment may imply that the nascent ATP:TN basepair is not as stable as a normal dA:dT basepair in the DNA duplex.
Figure 4.
(A) PMF profile for ATP:TN basepairing. (B) Hydrogen bond number evolution during ATP:TN basepairing.
Figure 5.
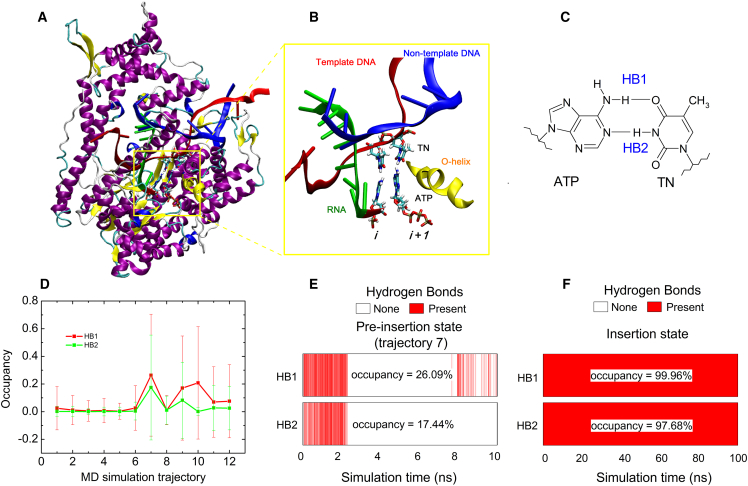
(A) Cartoon representation of the pre-insertion complex of T7 RNAP. The yellow box denotes the location of the active site. (B) Enlarged drawing of the active site, where ATP has established initial basepairing contacts with the TN while the O-helix is in open conformation. (C) Structure of an ATP:TN basepair, in which the two hydrogen bonds referred to as HB1 and HB2, respectively. (D) Hydrogen-bond occupancies for the two hydrogen bonds in 12 un-biased MD trajectories. (E and F) Hydrogen-bond existence maps for HB1 and HB2 in the seventh trajectory and another 100 ns MD simulation with the insertion complex as the starting configuration respectively. To see this figure in color, go online.
To examine the robustness of the ATP:TN basepair, we performed a third round of MD simulations, in which 12 short (10-ns) unbiased MD simulations were launched with the pre-insertion complex (the open active site, PDB: 1S0V) as the starting configuration. As a comparison, another long (100-ns) unbiased MD simulation was carried out using the insertion complex (the closed active site, PDB: 1S76) as the starting configuration. A detailed analysis of H-bonding was conducted to examine the robustness of the ATP:TN basepair. The two hydrogen bonds in the basepair are referred to as HB1 and HB2, as shown in Fig. 5 C. A hydrogen bond is considered to be formed if the donor-acceptor distance is <3.5 Å and the hydrogen-donor-acceptor angle is <30°. If a hydrogen bond survives >90% of the trajectory time, we consider it to be a stable bond (34). Fig. 5 D displays the H-bond occupancy for the two hydrogen bonds in the 12 trajectories. It can be seen that both hydrogen bonds have very low occupancy values in most of the trajectories. Both hydrogen bonds have the highest hydrogen-bond occupancy in the seventh trajectory. However, both hydrogen bonds are disconnected at the time t = ∼2.4 ns. Although HB1 was later re-formed, the H-bond occupancies were <30% for both hydrogen bonds (Fig.5 E), far less than the stability criterion of 90%. This result indicates that the ATP has established initial basepairing contacts with the TN in the pre-insertion state, but the contacts are very fragile and easily broken by thermal disturbance. It is obvious that the weak basepairing contacts are unfavorable to the chemical step that follows. Considering the fact that the active site is in the open conformation in the pre-insertion state, we speculate that the closure of the fingers domain will enhance the robustness of the nascent ATP:TN basepair. Fig.5 F displays the H-bond map for the ATP:TN basepair in the insertion state, where the active site of T7 RNAP has been closed. It is observed that both hydrogen bonds are very robust, with high occupancy values (>90%). Therefore, we deduce that once the substrate NTP has established initial pairing contacts with TN, the fingers domain will be triggered to close, so as to protect the nascent NTP:TN basepair. Fortunately, Wang et al. (35) have demonstrated that the trigger loop (corresponding to the O-helix in T7 RNAP) will close spontaneously with a cognate active-site NTP, creating a steady environment for the chemistry that follows.
Conclusion
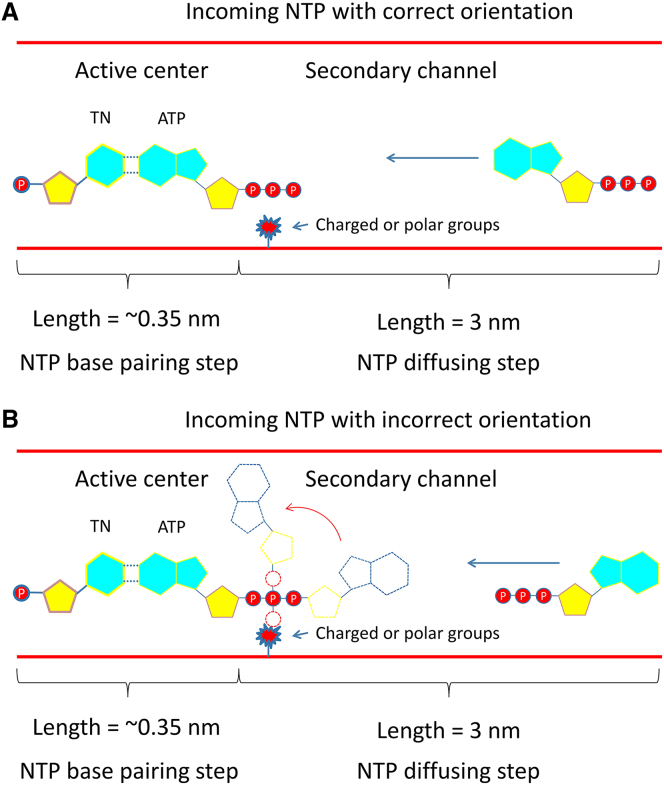
In this work, we investigated the mechanism of NTP binding to the active site of T7 RNAP from the perspective of free energy. Our model systems were derived from high-resolution crystal structures of the T7 RNAP complex, which were solvated in explicit solvent (0.15 mol/L sodium chloride solution) to mimic a real physiological environment. All-atom MD simulation combined with the US method was employed to estimate the free energies for NTP binding. On the basis of our observations, we proposed a two-step mechanism to explain the NTP binding process: first, NTP in aqueous solution diffuses through a secondary channel to reach the active site of RNAP (the NTP diffusing step); second, the NTP establishes the initial basepairing contacts with TN (the NTP basepairing step). The free-energy results indicate that both steps are spontaneous processes. In more detail, when a substrate NTP in bulk solution approaches the entrance of the secondary channel, it will be attracted by these charged or polar amino acid residues on the wall of the entrance. These groups induce the NTP to diffuse toward the energetically preferable active site. In the pore region, some O-helix residues with positive charges hold the NTP by the triphosphate moiety from one side while the other side is firmly constrained by several negatively charged residues through two magnesium ions that serve as bridges. As a result, the triphosphate moiety of the NTP is tightly trapped in the pore region, giving a reasonable distance between the NTP and TN for basepairing. On the other hand, due to the lesser constraint, the NTP base can freely adjust its conformation to obtain a correct orientation. Then, the NTP establishes initial basepairing contacts with the TN. This mechanism can easily address the problem of NTP binding with different orientations. As shown in Fig. 6 A, when an NTP diffuses into the active site in the correct orientation, it can smoothly basepair with the TN; when the NTP diffuses into the active site with an incorrect orientation, its phosphate moiety will be firmly grasped by the pore region, resulting in the conformational changes of the base part to obtain a correct orientation for basepairing (as shown in Fig.6 B). Therefore, when a matched NTP diffuses into the active site, no matter what orientation it adopts, it will eventually complete basepairing.
Figure 6.
Schematic diagram of NTP binding to the active site of T7 RNAP with correct (A) or incorrect (B) orientations. To see this figure in color, go online.
Moreover, we investigated the NTP/TN basepairing process and found that the basepairing step is also a spontaneous process. The resulting PMF curve exhibits two minima corresponding to two metastable states before and after ATP:TN basepairing. The small energy barrier indicates that although NTP has established initial basepairing contacts with the TN in the pre-insertion state, the contacts are very fragile and easy to break by thermal disturbance. The further unbiased MD simulation with the insertion complex reveals that a closed active site can effectively protect the newly formed basepair and create a steady environment for the next chemistry. Our study offers insight into the energetics and molecular details of NTP binding, providing valuable information for comprehensively understanding the mechanism of the basic step in genetic transcription.
Author Contributions
S.W. designed the research. S.W., L.L., and Q.L. performed the research. S.W., L.L., and Q.L. analyzed the data. S.W., L.L., and Q.L. wrote the article.
Acknowledgments
The authors thank Prof. Hualin Shi of the Institute of Theoretical Physics, Chinese Academy of Sciences, Prof. Jin Yu of the Beijing Computational Science Research Center, and Prof. Yi Wang of the Chinese University of Hong Kong for helpful advices.
This work was supported by the National Natural Science Foundation of China (No. 11405113) and the Science and Technology Plan of Sichuan Province, China (No. 2010JY0122).
Editor: Tamar Schlick.
References
- 1.Yin Y.W., Steitz T.A. The structural mechanism of translocation and helicase activity in T7 RNA polymerase. Cell. 2004;116:393–404. doi: 10.1016/s0092-8674(04)00120-5. [DOI] [PubMed] [Google Scholar]
- 2.Temiakov D., Patlan V., Vassylyev D.G. Structural basis for substrate selection by t7 RNA polymerase. Cell. 2004;116:381–391. doi: 10.1016/s0092-8674(04)00059-5. [DOI] [PubMed] [Google Scholar]
- 3.Huang X., Wang D., Levitt M. RNA polymerase II trigger loop residues stabilize and position the incoming nucleotide triphosphate in transcription. Proc. Natl. Acad. Sci. USA. 2010;107:15745–15750. doi: 10.1073/pnas.1009898107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Storer A.C., Cornish-Bowden A. Concentration of MgATP2- and other ions in solution. Calculation of the true concentrations of species present in mixtures of associating ions. Biochem. J. 1976;159:1–5. doi: 10.1042/bj1590001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Batada N.N., Westover K.D., Kornberg R.D. Diffusion of nucleoside triphosphates and role of the entry site to the RNA polymerase II active center. Proc. Natl. Acad. Sci. USA. 2004;101:17361–17364. doi: 10.1073/pnas.0408168101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Da L.T., Pardo-Avila F., Huang X. Bridge helix bending promotes RNA polymerase II backtracking through a critical and conserved threonine residue. Nat. Commun. 2016;7:11244. doi: 10.1038/ncomms11244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Silva D.A., Weiss D.R., Huang X. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proc. Natl. Acad. Sci. USA. 2014;111:7665–7670. doi: 10.1073/pnas.1315751111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Da L.-T., Pardo Avila F., Huang X. A two-state model for the dynamics of the pyrophosphate ion release in bacterial RNA polymerase. PLOS Comput. Biol. 2013;9:e1003020. doi: 10.1371/journal.pcbi.1003020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yamamoto S., Maruyama Y., Hyodo S. Dissipative particle dynamics study of spontaneous vesicle formation of amphiphilic molecules. J. Chem. Phys. 2002;116:5842–5849. [Google Scholar]
- 11.Shelley J.C., Shelley M.Y., Klein M.L. Simulations of phospholipids using a coarse grain model. J. Phys. Chem. B. 2001;105:9785–9792. [Google Scholar]
- 12.Jiang H., Sheong F.K., Huang X. Markov state models reveal a two-step mechanism of miRNA loading into the human argonaute protein: selective binding followed by structural re-arrangement. PLOS Comput. Biol. 2015;11:e1004404. doi: 10.1371/journal.pcbi.1004404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Woo H.J., Liu Y., Sousa R. Molecular dynamics studies of the energetics of translocation in model T7 RNA polymerase elongation complexes. Proteins. 2008;73:1021–1036. doi: 10.1002/prot.22134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kutzner C., van der Spoel D., Grubmüller H. Speeding up parallel GROMACS on high-latency networks. J. Comput. Chem. 2007;28:2075–2084. doi: 10.1002/jcc.20703. [DOI] [PubMed] [Google Scholar]
- 15.Pronk S., Páll S., Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 17.Pérez A., Marchán I., Orozco M. Refinement of the AMBER force field for nucleic acids: improving the description of alpha/gamma conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Meagher K.L., Redman L.T., Carlson H.A. Development of polyphosphate parameters for use with the AMBER force field. J. Comput. Chem. 2003;24:1016–1025. doi: 10.1002/jcc.10262. [DOI] [PubMed] [Google Scholar]
- 19.Miyamoto S., Kollman P.A. Settle: an analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992;13:952–962. [Google Scholar]
- 20.Essmann U., Perera L., Pedersen L.G. A smooth particle mesh ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 21.Darden T., York D., Pedersen L. Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 22.Berendsen H.J., Postma J.P.M., Haak J. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 23.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 24.Hess B., Bekker H., Fraaije J.G. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- 25.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 26.Lemkul J.A., Bevan D.R. Assessing the stability of Alzheimer’s amyloid protofibrils using molecular dynamics. J. Phys. Chem. B. 2010;114:1652–1660. doi: 10.1021/jp9110794. [DOI] [PubMed] [Google Scholar]
- 27.Hub J.S., De Groot B.L., Van Der Spoel D. g_wham—A free weighted histogram analysis implementation including robust error and autocorrelation estimates. J. Chem. Theory Comput. 2010;6:3713–3720. [Google Scholar]
- 28.Osumi-Davis P.A., Sreerama N., Woody A.Y. Bacteriophage T7 RNA polymerase and its active-site mutants. Kinetic, spectroscopic and calorimetric characterization. J. Mol. Biol. 1994;237:5–19. doi: 10.1006/jmbi.1994.1205. [DOI] [PubMed] [Google Scholar]
- 29.Bonner G., Patra D., Sousa R. Mutations in T7 RNA polymerase that support the proposal for a common polymerase active site structure. EMBO J. 1992;11:3767–3775. doi: 10.1002/j.1460-2075.1992.tb05462.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sosunov V., Sosunova E., Goldfarb A. Unified two-metal mechanism of RNA synthesis and degradation by RNA polymerase. EMBO J. 2003;22:2234–2244. doi: 10.1093/emboj/cdg193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yang W., Lee J.Y., Nowotny M. Making and breaking nucleic acids: two-Mg2+-ion catalysis and substrate specificity. Mol. Cell. 2006;22:5–13. doi: 10.1016/j.molcel.2006.03.013. [DOI] [PubMed] [Google Scholar]
- 32.Osumi-Davis P.A., de Aguilera M.C., Woody A.Y. Asp537, Asp812 are essential and Lys631, His811 are catalytically significant in bacteriophage T7 RNA polymerase activity. J. Mol. Biol. 1992;226:37–45. doi: 10.1016/0022-2836(92)90122-z. [DOI] [PubMed] [Google Scholar]
- 33.Wu S., Feng D. Free energy calculation for base pair dissociation in a DNA duplex simulation. Acta Phys.-Chim. Sinica. 2016;32:1282–1288. [Google Scholar]
- 34.Zhang L.Y., Xiao X.C., Pu X.M. Probing immobilization mechanism of α-chymotrypsin onto carbon nanotube in organic media by molecular dynamics simulation. Sci. Rep. 2015;5:9297. doi: 10.1038/srep09297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang B., Predeus A.V., Feig M. Energetic and structural details of the trigger-loop closing transition in RNA polymerase II. Biophys. J. 2013;105:767–775. doi: 10.1016/j.bpj.2013.05.060. [DOI] [PMC free article] [PubMed] [Google Scholar]