Hidden role of intermolecular proton transfer in the anomalously diffuse vibrational spectrum of a trapped hydronium ion

Significance

Understanding the origin of the extremely diffuse vibrational spectrum of an excess proton in water presents a grand challenge for contemporary physical chemistry. Here, we report the key observation that such diffuse bands occur even when the hydronium ion is held in the binding pocket of a rigid crown ether scaffold at 10 K. The broadening is traced to the zero-point vibrational displacements of the ion in the crown. The diffuse spectra are therefore an intrinsic property of the system and mimic the action of thermal fluctuations at elevated temperatures. We treat the mechanics underlying this phenomenon with a vibrationally adiabatic ansatz, from which emerges a qualitative picture that emphasizes the hidden role of vibrationally driven, intermolecular proton transfer.

Abstract

We report the vibrational spectra of the hydronium and methyl-ammonium ions captured in the C_3v binding pocket of the 18-crown-6 ether ionophore. Although the NH stretching bands of the CH₃NH₃⁺ ion are consistent with harmonic expectations, the OH stretching bands of H₃O⁺ are surprisingly broad, appearing as a diffuse background absorption with little intensity modulation over 800 cm⁻¹ with an onset ∼400 cm⁻¹ below the harmonic prediction. This structure persists even when only a single OH group is present in the HD₂O⁺ isotopologue, while the OD stretching region displays a regular progression involving a soft mode at about 85 cm⁻¹. These results are rationalized in a vibrationally adiabatic (VA) model in which the motion of the H₃O⁺ ion in the crown pocket is strongly coupled with its OH stretches. In this picture, H₃O⁺ resides in the center of the crown in the vibrational zero-point level, while the minima in the VA potentials associated with the excited OH vibrational states are shifted away from the symmetrical configuration displayed by the ground state. Infrared excitation between these strongly H/D isotope-dependent VA potentials then accounts for most of the broadening in the OH stretching manifold. Specifically, low-frequency motions involving concerted motions of the crown scaffold and the H₃O⁺ ion are driven by a Franck–Condon-like mechanism. In essence, vibrational spectroscopy of these systems can be viewed from the perspective of photochemical interconversion between transient, isomeric forms of the complexes corresponding to the initial stage of intermolecular proton transfer.

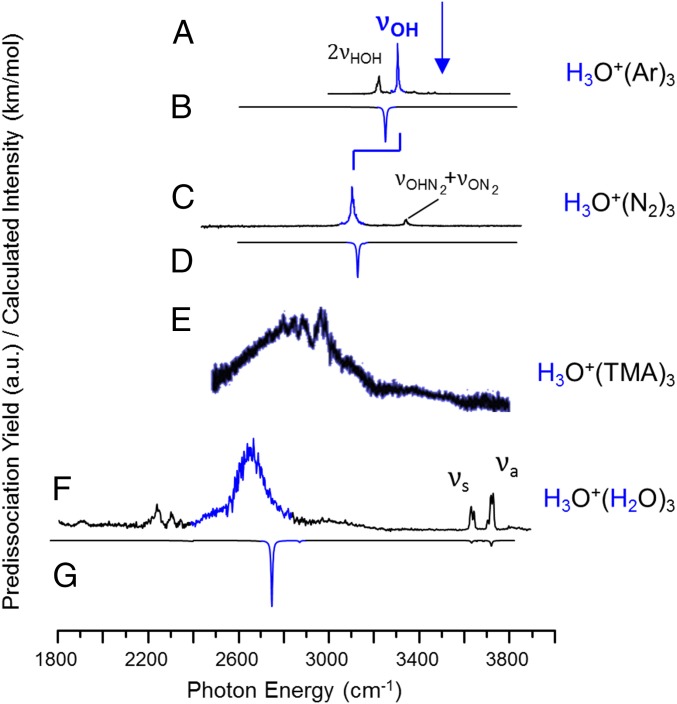
Understanding the molecular-level nature of the hydrated proton remains a major puzzle in aqueous chemistry, despite decades of experimental and theoretical work (1–6). One of the reasons this is so challenging is that vibrational spectroscopy, which is often a reliable tool in the analysis of strongly hydrogen-bonded systems, is severely compromised by the extreme broadening that can occur even when isolated, size-selected H⁺(H₂O)_n clusters are cooled close to their vibrational zero-point energies (7). One expects that the spectrum of H₃O⁺ embedded in a tricoordinated ligand environment will be dominated by the nearly degenerate OH stretching bands that red-shift relative to the bare ion with increasing H-bond strength to the ligand. For weakly bound species such as Ar and N₂, this expectation is borne out experimentally as evidenced by the spectra reported earlier, which are reproduced in Fig. 1 A and C, respectively (8). Sharp features are observed along with weaker nearby transitions that are readily explained as overtones or combination bands (8). Complexation of the H₃O⁺ with three water molecules yields the Eigen cation with the structure indicated in Fig. 2A, and its vibrational spectrum (reproduced from ref. 8 in Fig. 1F) displays diffuse band structure that extends over 400 cm⁻¹. In addition, it exhibits more distinct features than can be accounted for by the expected fundamentals, as illustrated by comparison with the harmonic spectrum displayed inverted in Fig. 1G. The assignments of these features has proven challenging (9–11), even raising the question (11) of whether other locally stable isomers contribute to the observed pattern of complex bands. The formation of the Eigen structure has been confirmed, however, by analysis of the much simpler spectrum displayed by the D₃O⁺(D₂O)₃ isotopologue (9). This suggests that strong nuclear quantum effects act to broaden the spectrum of the light isotopologue as well as introduce extra features arising from overtones and combination bands (12). In this context, the behavior of the closely related H₃O⁺(TMA)₃ [trimethylammonium (TMA) = N(CH₃)₃] cluster reported by Fujii and coworkers (13) (reproduced in Fig. 1E) is particularly interesting, as it displays a remarkably diffuse, bell-shaped absorption in the OH stretching region that extends over 700 cm⁻¹ with very little modulation. Those authors rationalized this behavior by considering the contribution of multiple isomers, and in particular noted the role of low-lying structures featuring an intracluster, proton transfer configuration.

Fig. 1.

Vibrational predissociation spectra of the H₃O⁺ ion in several tricoordinated environments including (A) Ar₃, (C) (N₂)₃ (reproduced from ref. 8), (E) (TMA)₃ (TMA, trimethylammonium; reproduced from ref. 13), and (F) (H₂O)₃ (reproduced from ref. 9). Harmonic predictions [B3LYP/6-311++G(2d,2p) scaled by 0.99556 below 2,700 cm⁻¹ and by 0.95732 above 2,700 cm⁻¹] are included as inverted traces for (B) Ar₃, (D) (N₂)₃, and (G) (H₂O)₃.

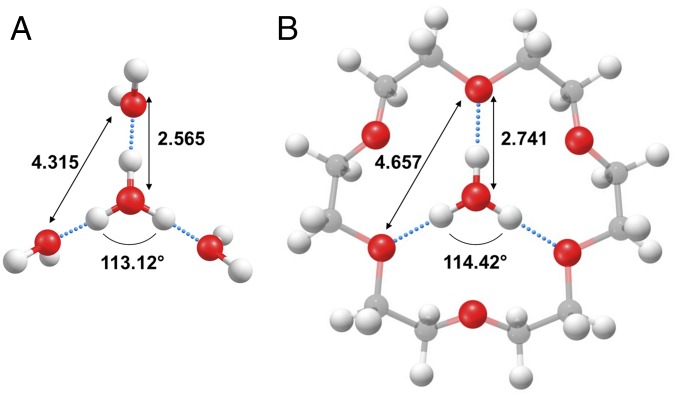
Fig. 2.

Structures, selected bond lengths, and angles for the hydronium ion embedded in two tricoordinated environments: (A) H₃O⁺(H₂O)₃ and (B) H₃O⁺(18C6). Calculations were performed at the B3LP/6-311++G(2d,2p) level of theory.

Here, we are concerned with the origin of this broadening in the OH stretching spectrum of the hydronium ion, H₃O⁺, embedded in a symmetrical, tricoordinate environment through three strong H bonds. We specifically focus on the complex with the relatively rigid 18-crown-6 ether (18C6) scaffold with the calculated structure displayed in Fig. 2B. The H₃O⁺(18C6) structure, featuring three quasilinear H bonds to oxygen atoms in the ring, has been verified through analysis of the vibrational bands associated with the ether moiety over the range 500–1,900 cm⁻¹ (14–16). We therefore extended this study to the OH stretching region to determine the behavior of H₃O⁺ embedded in the crown. Instead of simplifying the spectrum displayed by the more floppy Eigen ion, however, we will show that the OH stretching manifold of H₃O⁺(18C6) is, in fact, even more diffuse with continuous absorption over 800 cm⁻¹ in the OH stretching region. We follow the evolution of this diffuse absorption with H/D isotopic substitution to reveal that its envelope is a property of a single OH oscillator. The dramatic simplification of the spectra in the OD stretching region of the deuterated isotopologues indicates that strong nuclear quantum effects are at play in this system, which are not evident when CH₃NH₃⁺ is placed in the crown pocket. We consider these effects in the context of similar behavior reported previously on the formate monohydrate binary complex along with new results for the partially and fully deuterated complex (17, 18). In that case, very strong anharmonic coupling between the OH stretch and a soft intermolecular mode is treated in the context of vibrationally adiabatic (VA) potential energy surfaces. These potential surfaces allow us to quantify the changes in the intermolecular geometries with increasing levels of excitation in the OH stretching degree of freedom. In the case of hydronium trapped in 18C6, this approach yields a simple qualitative picture for the origin of the extreme spectral broadening as a consequence of photoinduced structural deformations toward the intermolecular proton transfer asymptote.

Results and Discussion

Vibrational Spectra of the K⁺, CH₃NH₃⁺, and H₃O⁺ Complexes with 18C6.

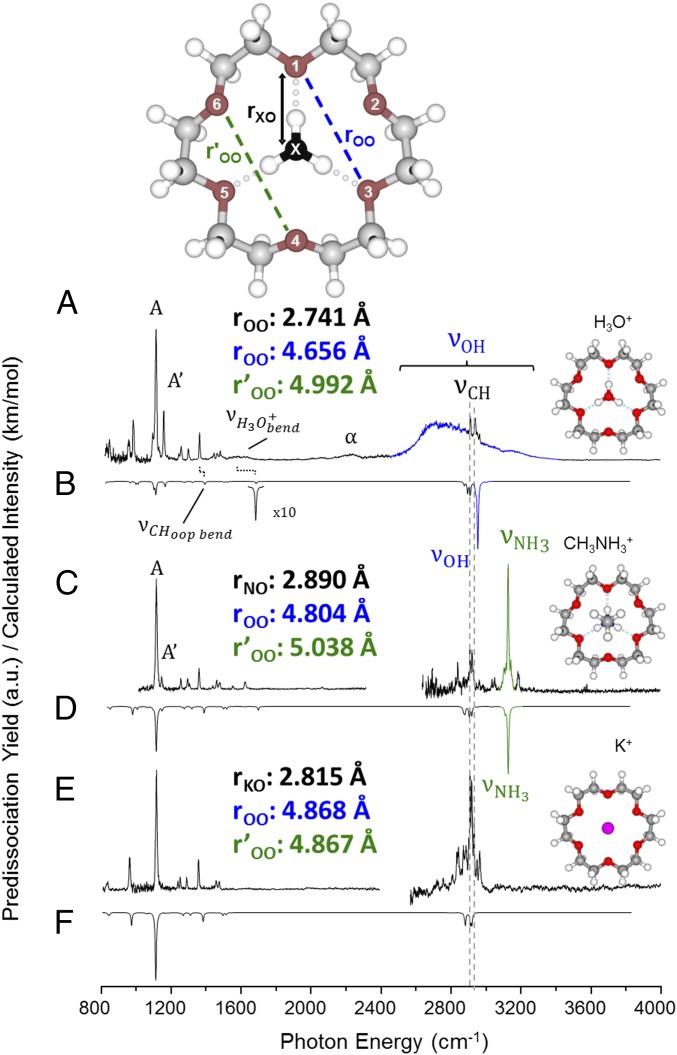
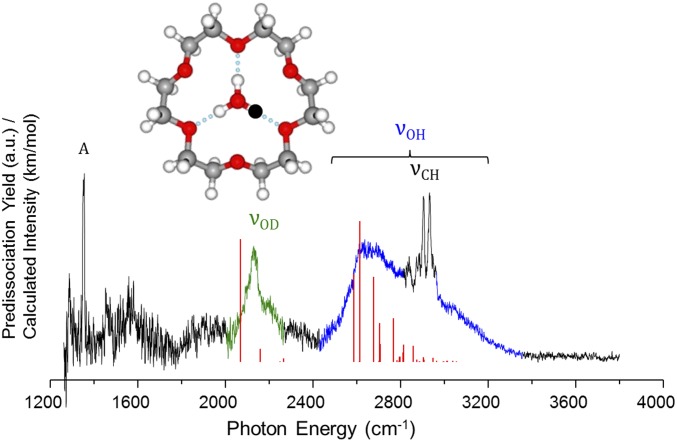
Fig. 3 compares the vibrational predissociation spectra of the K⁺, CH₃NH₃⁺, and H₃O⁺ ions in the 18C6 binding pocket. The low-frequency region is dominated by the CO stretch near 1,100 cm⁻¹ (labeled A), which appears with a higher energy shoulder (denoted A′) that indicates increasing distortion of the ring scaffold in going from K⁺ to CH₃NH₃⁺ to H₃O⁺, as reported earlier by Oomens and coworkers (14, 19). This is consistent with the calculated bond lengths highlighted in Fig. 3, with a more complete list collected in SI Appendix, Table S1. In the higher energy region, all spectra contain sharp features associated with the CH stretches near 2,900 cm⁻¹, which are again weakly dependent on the guest ion as illustrated by the expanded spectra in SI Appendix, Fig. S1. Of primary concern here are the dramatic differences in the breadth of the NH and OH stretches in the CH₃NH₃⁺ and H₃O⁺ complexes.

Fig. 3.

D₂ vibrational predissociation spectra of (A) H₃O⁺, (C) CH₃NH₃⁺, and (E) K⁺ embedded in 18C6. Corresponding harmonic predictions [B3LYP/6–311++G(2d,2p) scaled by 0.99556 below 2,700 cm⁻¹ and by 0.95732 above 2,700 cm⁻¹] for each species are included as inverted traces in B, D, and F. The bond lengths in traces A, C, and E correspond to the distances, calculated at the same level of theory, described in the Inset at the Top of the figure.

The antisymmetric NH₃ stretching fundamental (${\nu }_{\mathrm{N}{\mathrm{H}}_3}$, green) in the CH₃NH₃⁺(18C6) spectrum (Fig. 3C) is readily identified as a very sharp, strong feature at 3,126 cm⁻¹, which occurs quite close to the scaled harmonic prediction (inverted trace in Fig. 3D). The H₃O⁺(18C6) spectrum (Fig. 3A), on the other hand, is surprising. It displays continuous absorption with an asymmetrical, bell-shaped envelope over the range 2,600–3,300 cm⁻¹, with the sharp CH stretching bands appearing on top of this broad band near 2,900 cm⁻¹. The OH stretching band in the H₃O⁺(18C6) spectrum is even broader than that of H₃O⁺(H₂O)₃ (Fig. 1F) (7, 20), and its maximum is shifted by ∼100 cm⁻¹ to higher energy with a similar onset at around 2,600 cm⁻¹. This behavior is independent of the number of D₂ tag molecules (one vs. three) (SI Appendix, Fig. S2). Moreover, the calculated pattern at the harmonic level (inverted trace in Fig. 3B), which accurately recovers the behavior of the ammonium-based complex, predicts a single dominant transition at 2,950 cm⁻¹ (blue, Fig. 3B) due to the degenerate (in C_3v symmetry) antisymmetric OH (${\nu }_{\mathrm{OH}}$) stretching fundamental. This band is calculated to occur almost 400 cm⁻¹ above the observed onset of the diffuse absorption in the H₃O⁺(18C6) spectrum.

We note that diffuse bands very similar to those displayed by H₃O⁺(18C6) were reported for the H₃O⁺(TMA)₃ cluster (Fig. 1E) by Fujii and coworkers (13), who rationalized this behavior on the basis of a large number of isomers in the ion ensemble. The rigid crown scaffold, however, cannot support such isomers. The H₃O⁺(18C6) platform is calculated to have two low-lying structures that differ according to which three oxygen atoms of the ring are bound to hydronium. The two sets of three atoms are distinct and are calculated to be separated by a large (∼1,500 cm⁻¹) barrier with respect to interconversion through rotation of H₃O⁺ by 60° about its symmetry axis. The harmonic spectra of the two isomers are calculated to be almost identical (14). To address this issue of spectral heterogeneity more explicitly, we carried out a series of photodepletion experiments to establish that the feature is indeed homogenous by observing complete photofragmentation upon excitation at many representative photon energies throughout the spectrum.

Isotope Effects in the OH and OD Stretching Regions.

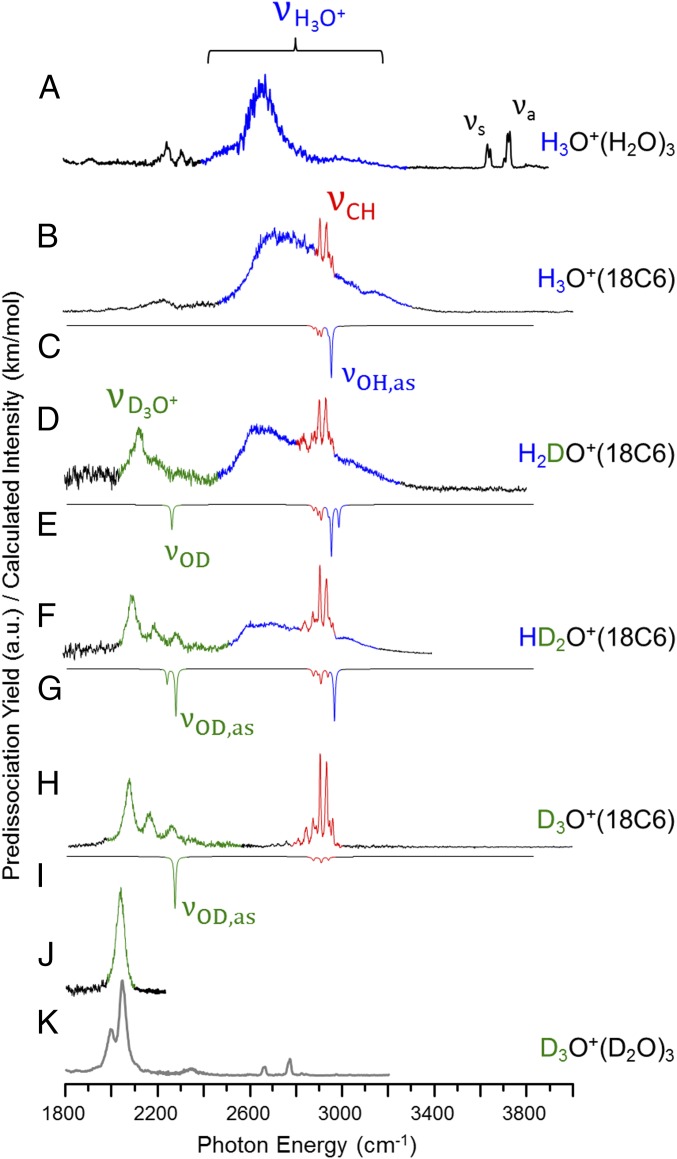
The observation of very diffuse bands arising from the OH stretching degree of freedom in the H₃O⁺(H₂O)₃ and H₃O⁺(TMA)₃ configurations suggests that this behavior is an intrinsic property of strong H bonds in this arrangement. In the case of the H₃O⁺(H₂O)₃ cluster, it has been very recently reported that the OH stretching features sharpen dramatically upon deuteration to reveal a closely spaced doublet (Fig. 4K) readily assigned to a small splitting of the symmetric and antisymmetric OD stretches of the embedded D₃O⁺ group, calculated to result from the perturbation induced by the D₂ tag (9). In the course of this work, this interpretation was confirmed by recording the spectrum of the bare molecule by using an IR–IR double-resonance technique (described in SI Appendix) (Fig. 4J), which reveals a single peak from the quasi-degenerate OD stretches.

Fig. 4.

Evolution of the D₂-tagged vibrational predissociation spectra of H₃O⁺(18C6) upon sequential deuteration of the embedded H₃O⁺ core are given in traces B, D, F, and H. Note that the OD stretching features (green) in the D₃O⁺(18C6) spectrum (H) occur close to that of D₃O⁺(D₂O)₃ (K). Additionally, the green trace in J shows the D₃O⁺ peak without the splitting due to the tag effect. This was accomplished using a two-color, IR–IR double-resonance scheme (46) described in SI Appendix. Trace A displays the H₃O⁺(H₂O)₃ spectrum for comparison (reproduced from ref. 9). Harmonic spectra [B3LYP/6–311++G(2d,2p) are scaled by 0.99556 below 2,700 cm⁻¹ and by 0.95732 above 2,700 cm⁻¹] and are included as inverted traces in C, E, G, and I.

Fig. 4 also includes the spectra of the H₃O⁺(18C6) isotopologues in which one of the hydronium H atoms is incrementally replaced by D. As in the case of the Eigen cation, the D₃O⁺(18C6) spectrum (Fig. 4H) sharpens dramatically, but now the breadth is resolved into a progression of at least three nearly equally spaced peaks with a separation of 85 cm⁻¹. What is more remarkable, however, is the fact that the breadth in the OH region of the spectrum is maintained with only a single OH in the HD₂O⁺(18C6) isotopomer spectrum (highlighted blue in Fig. 4F). The diffuse spectrum is thus revealed to be a property of an isolated OH group. The progression displayed by D₃O⁺(18C6) in the OD stretching region (Fig. 4H) is also clearly maintained in the HD₂O⁺ isotopologue (Fig. 4F), but is more diffuse in the H₂DO⁺ spectrum (Fig. 4D). The predicted harmonic OD stretching fundamentals are included (inverted under each spectrum) in Fig. 4, and the dominant OD stretching feature occurs about 200 cm⁻¹ below the harmonic prediction. Note that the OD stretching bands in the perdeuterated Eigen cation (Fig. 4 J and K) and D₃O⁺(18C6) (Fig. 4H) complex are quite similar, with the Eigen band falling only 33 cm⁻¹ below the dominant peak in the crown progression. The very strong isotope dependence of the spectral breadth displayed by the H₃O⁺ complexes suggests that the underlying cause is anharmonic coupling between the OH stretching frequency and the soft modes of the cluster (21, 22). The relevant calculated soft modes at the harmonic level are included in SI Appendix, Table S2B, and the two likely candidates for anharmonic coupling are the frustrated translation of the ion in the cage and the associated deformation of the ring scaffold. The former is calculated to occur at a scaled value of 205 cm⁻¹, however, which is a factor of 2 higher than the observed splittings, whereas the asymmetric ring deformation (93 cm⁻¹ scaled) is quite close to this spacing.

Second-order vibrational perturbation theory (VPT2) is a widely used theoretical treatment for handling anharmonic coupling in which cubic and quartic terms in the potential energy surface are included in the context of perturbation theory. We have carried out such calculations using the implementation of the method in Gaussian 09 (23), with the results for H₃O⁺(18C6) included in SI Appendix, Fig. S8. Although some broadening is recovered in the OH stretching region, the extent is much smaller than the experimentally observed feature. Moreover, the calculated anharmonic peak falls close to that of the harmonic origin, whereas the observed strong absorption appears about 200 cm⁻¹ below it. As such, the observed behavior clearly falls well beyond the limitations of the VPT2 approach. To clarify the type of anharmonic behavior that can account for the large deviations from harmonic and VPT2 expectations, we next revisit a related class of ion hydration systems that exhibit many similar features to those encountered here in the spectra of the H₃O⁺(18C6) isotopologues. In particular, the spectra of the monohydrates of molecular anions with triatomic domains (24–26) also display a soft-mode progression built on the OH stretching manifold with onsets that occur far below the harmonic predictions.

Strong Anharmonic Coupling in Ionic H Bonds to Water and the VA Treatment of Nuclear Quantum Effects

Quantifying Isotope Effects in Soft-Mode Progressions: Revisiting the Archetypal HCO₂⁻H₂O System.

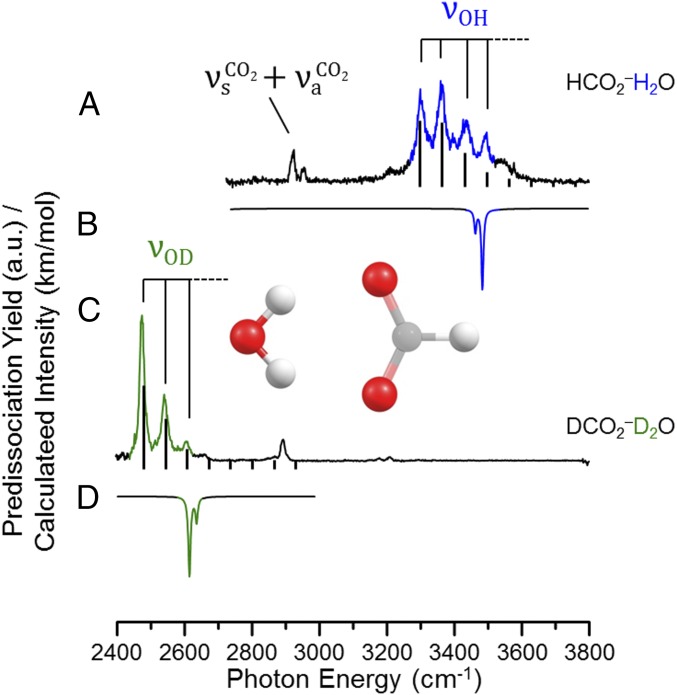
The dramatic difference in the OD and OH stretching features associated with the isotopologues of the H₃O⁺(18C6) complex is unusual, especially in the occurrence of a clear progression involving soft-mode excitation in the OD stretching region. This raises the question of whether the diffuse band in the OH stretching region is associated with a more extended progression, but is broadened so as to obscure the modulations that are clear in the OD region. We therefore turn our attention to a known system where an extended progression is observed in the OH stretching region due to strong anharmonic coupling with a soft mode: the formate monohydrate binary ion–molecule cluster with the structure displayed as an Inset in Fig. 5. The observed progression evolves from an origin about 300 cm⁻¹ below the predicted harmonic fundamentals (inverted trace in Fig. 5B). Although the mechanics that drive this behavior are well established as we discuss further below, the isotope dependence of the effect has not been established experimentally. We therefore obtained the predissociation spectrum of the DCO₂⁻D₂O isotopologue, with the result displayed in Fig. 5C. Indeed, like the situation observed in the H₃O⁺(18C6) system (Fig. 4), the progression is dramatically suppressed upon deuteration, while displaying a similar spacing in both cases (64 cm⁻¹ for HCO₂⁻H₂O vs. 67 cm⁻¹ for DCO₂⁻D₂O).

Fig. 5.

2H₂ vibrational predissociation spectra of (A) HCO₂⁻H₂O and its perdeuterated analog (given in C). Harmonic calculations [B3LYP/6–311++G(2d,2p) scaled by 0.99556 below 2,700 cm⁻¹ and by 0.95732 above 2,700 cm⁻¹] are included as inverted traces in B and D for each vibrational spectrum. The Inset in the Center shows the structure of HCO₂⁻H₂O at its equilibrium position. Stick spectra included in traces A and C were calculated using the VA treatment described in SI Appendix.

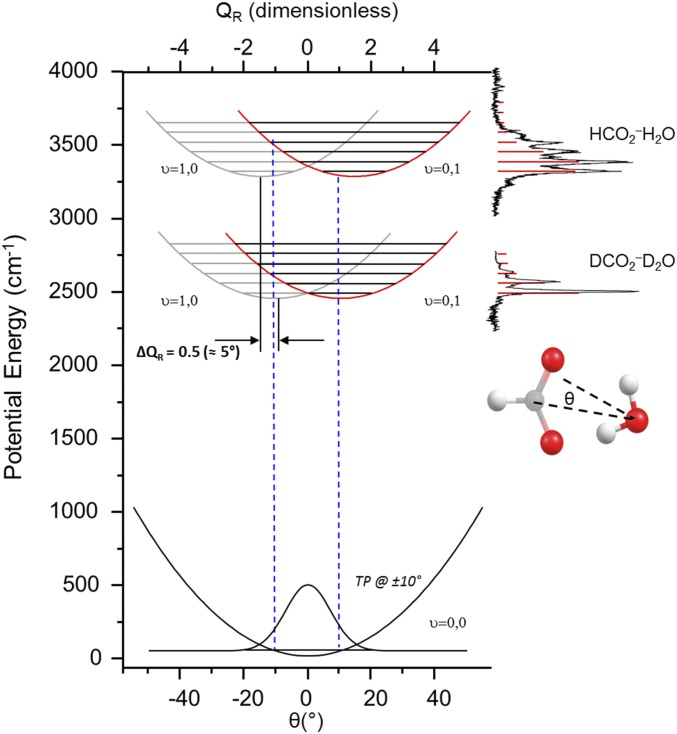
Because the formate monohydrate spectra display such a clear manifestation of isotope effects in anharmonic behavior, it is valuable to review the key features of the theoretical models that accurately predicted its behavior, and then apply these methods to the more complex H₃O⁺(18C6) system. There is consensus (18, 25) that this progression is due to combination bands arising from excitation of the OH stretch fundamental along with several quanta of the low-frequency (∼70 cm⁻¹) water rocking mode (angle θ as defined in Fig. 6), which acts to break the strong H bond of one of the OH groups while strengthening the other. When this occurs, the frequencies of the two OH stretches, which are nearly degenerate at θ = 0°, dramatically split apart with increasing θ, with one of them evolving toward the OH stretch position in isolated water while the other red-shifts by hundreds of wavenumbers (18, 24, 26). The spectroscopic consequences of this strong anharmonic coupling in the HCO₂⁻H₂O ion have been treated in detail by Sibert and coworkers (25) in 2003, and then more recently by Stock and Hamm (18), in the context of a VA model involving a separation between the OH stretching degree of freedom and the displacements associated with the rocking mode. This treatment invokes the VA potential energy curves displayed in Fig. 6, each of which corresponds to the degree of excitation in one of the OH oscillators. The specific details involved in applying this approach to the anharmonic potentials for both isotopologues of the formate–water complex are described in the supplementary computational details, SI Appendix, section SII, and presented in SI Appendix, Figs. S10 and S11. These potentials then define the quantum levels associated with the rocking mode for each OH stretching quantum level, and within this simple model of the VA mechanics (25), they form a set of displaced harmonic oscillators. Optical excitation between these curves nominally corresponds to the excitation of the OH stretching fundamentals. In extreme cases, ground [OH(v = 0)] state potentials can also distort such that the observed structure at 0 K is isotope dependent, which is usually referred to as a “geometric isotope effect” (27–29).

Fig. 6.

Adiabatic rock potential energy curves for both HCO₂⁻H₂O (Top) and DCO₂⁻D₂O (Middle) that each has one quantum of OH stretch. Blue lines map from the classical turning points of the ground-state Gaussian (Bottom) to each potential curve.

When the transition moment for local excitation of the OH stretch is only weakly dependent on θ, the vibrational spectrum in the OH stretching region displays a progression in the rocking mode with an intensity profile governed by the vibrational overlap (i.e., Franck–Condon factor) between rocking wavefunctions. This is in exact analogy to the usual situation in electronic spectroscopy when promotion of an electron involves an orbital that causes a change in the equilibrium geometry in the excited electronic state.

The degree of displacement in the intermolecular potentials extracted from the VA approach should be strongly dependent on the isotopic composition of the water molecule (1, 30–32) according to the $\sim 1/\sqrt{2}$ reduction in the OH stretch frequency at each value of Q_R upon deuteration. A comparison of the VA potential curves for the DCO₂⁻(D₂O) and HCO₂⁻(H₂O) isotopologues is presented in Fig. 6 to illustrate this effect. Because this prediction has not been challenged experimentally, we next extend the study to the deuterated isotopologues of the formate monohydrate complex. The 2H₂-tagged DCO₂⁻(D₂O) spectrum is included in Fig. 5C, along with the stick spectra calculated from the VA curves in Fig. 6. This model indeed accounts for the reduction of the extent of the progression, and the quanta comprising it are approximately the same for both isotopologues.

The extent of the soft-mode progression is thus revealed to be a consequence of the overlap of the ground-state Gaussian wavefunction in the rocking mode with the displaced wavefunctions for the levels of the VA excited states. In effect, the zero-point displacement plays a similar role in distorting the scaffold as does thermal excitation in a classical system, leading the system to explore a range of OH stretching frequencies (21, 22). Like the well-known “reflection principle” in electronic spectroscopy, when the displacements in VA curves are large, the envelope of the vibrational excitation profile can be viewed as a mirror of the ground-state vibrational wavefunction (33, 34). In Heller’s semiclassical picture of vibrational wave packets in electronic spectroscopy (35), the width of the vibrational manifold reflects the time evolution of the ground-state wavefunction launched on the excited-state potential energy surface. In the present context, the breadth of the vibrational oscillator strength thus encodes the ultrafast vibrational dynamics corresponding to the lifetime of the ground-state shape in the OH(v = 1) adiabatic potential surface.

Application of the VA Model to the H₃O⁺(18C6) System.

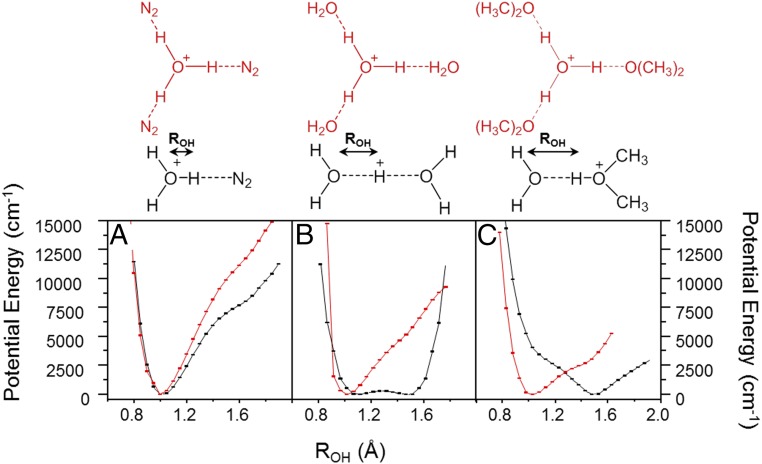
Given the strong similarities in the isotopic behavior of the spectra from the formate monohydrate system and the hydronium ion embedded in the crown, we next consider the behavior of H₃O⁺(18C6) in the context of the VA model. We anticipate that the important soft modes coupled to the OH stretches are those that would act to strengthen a local OH hydrogen bond to one of the oxygen atoms in the crown. By analogy with the formate monohydrate case, a promising candidate is therefore the symmetry breaking, largely translational motion of the hydronium along the ${\text{O}}_{18\text{C}6}-{\text{O}}_{{\text{H}}_3{\text{O}}^{+}}$ axis of one of the linear H bonds. An important consideration related to this distortion involves the extent to which the global minimum, tricoordinated structure differs from that adopted by the isolated binary complexes held at the same distance between the heavy atoms. To illustrate this point, Fig. 7 presents the potential curves as a function of the distance between the bridging hydrogen and the hydronium oxygen, R_OH, in three binary complexes featuring ligands with increasingly strong interactions to H₃O⁺: N₂, H₂O, and dimethyl ether. In the case of N₂, the proton is well localized on the hydronium oxygen in both the binary complex and the H₃O⁺(N₂)₃ cluster, and the resulting spectrum (Fig. 1C) is sharp and readily explained at the harmonic level. We note that there is a point of inflection in both curves at an OH distance of around 1.4 Å. This feature occurs in many ionic H-bonded systems (10) and generally occurs due to the endothermic, intermolecular proton transfer, in this case to N₂. Turning to the case of H₂O, the H₃O⁺H₂O binary complex corresponds to the Zundel ion, and the potential curve for H-atom displacement with the OO distance of the two water molecules fixed at the equilibrium position for H₃O⁺(H₂O)₃ appears as a double minimum with a small barrier. Upon addition of two more water molecules to form the Eigen cation, however, the scan of the OH distance between oxygen atoms (Fig. 7B, red curve) now appears with a much more pronounced shelf feature. The much larger difference in the behavior of the binary complex relative to the tricoordinated cluster is a manifestation of the anticooperative nature of multiple strong H bonds to the same center. Because the crown presents the tricoordinate arrangement in the context of an intact scaffold, we evaluate the differences in 1 vs. 3 coordination using dimethyl ether as a proxy. Fig. 7C compares the potentials for the binary H₃O⁺(CH₃)₂O and the H₃O⁺((CH₃)₂O)₃ complexes with the O–O distance fixed at the equilibrium distance in the tricoordinated cluster. Here, the difference in the two potentials is dramatic. Specifically, the binary complex behaves as a hydrated, protonated ether (see black structure above Fig. 7C) with a high energy minimum at roughly 1 Å corresponding to intermolecular proton transfer back to the water molecule to form H₃O⁺. Upon addition of two more ether molecules, however, the relative energies of the two minima are reversed such that now the proton resides closer to the water, reforming the hydronium ion at the center of the structure. The anticooperativity effect thus completely changes the intrinsic character of the binary interactions. We note that the CH₃NH₃⁺(18C6) complex, which displayed a simple, sharp NH stretching band close to the scaled harmonic prediction in Fig. 3C, behaves very similarly in this context to the H₃O⁺(N₂)₃ case shown in Fig. 7A, except this time the proton is closest to the N atom in both the binary and tricoordinated systems.

Fig. 7.

Potential energy scans of the bridging proton displacement between heavy atoms involved in the H bond of the binary (black) and tricoordinated (red) complexes of H₃O⁺ with the following: (A) N₂, (B) H₂O, and (C) (CH₃)₂O. The binary compounds are held at the OX (X = N, O) distances of the tricoordinated complexes, while all other coordinates are allowed to relax. Calculations were carried out at the B3LYP/6-311++G(2d,2p) level of theory.

These considerations suggest that the extreme broadening is correlated to the difference in the intrinsic behavior of the binary interaction between H₃O⁺ and a single H-bond acceptor and that in play when H₃O⁺ engages with three H bonds. The larger this difference, the more extreme the anticooperative action that is required for the intact H₃O⁺ molecular ion to reside at the center of the ring. Any motion away from the symmetrical geometry of this global minimum will push the oxygen atom in H₃O⁺ and the proton acceptor closer together, breaking the anticooperative interactions required to maintain the equilibrium structure. This effect is amplified because the quasirigid crown forces the O–O distances (2.741 Å) to be rather large compared with the binary complex (2.515 Å) or the fully coordinated variation of this system, H₃O⁺((CH₃)₂O)₃ where R_OO = 2.524 Å. As a result, the forces on the hydronium at the symmetrical geometry are rather soft in the more open coordination environments, creating a scenario where the distortions in the VA curves caused by the position-dependent OH stretching frequencies act against a flatter Born–Oppenheimer (B.O.) potential for more frustrated translation in the H₃O⁺(18C6) than those at play in the Eigen complex.

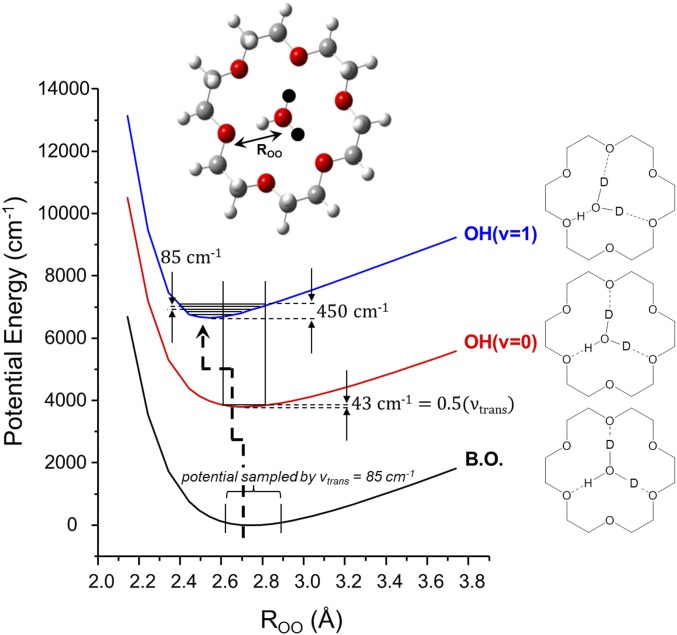
To gauge whether anharmonic coupling between the OH stretches and the frustrated translation of the hydronium is sufficiently strong to qualitatively account for the observed behavior of the isotopologues, we calculated the B.O. potential for displacement of the hydronium oxygen toward one of the ring oxygen atoms, with the result presented in the black trace (B.O.) in Fig. 8. This features a minimum at ∼2.7 Å, which corresponds to the center of the ring. We further restrict our attention to the HD₂O⁺ isotopologue because the breadth of the OH stretching feature is retained in its spectrum (Fig. 4F), and it simplifies the problem by focusing on the properties of a single, uncoupled OH oscillator. We then calculated the local OH stretch and two OD frequencies as a functions of the OO distance, R_OO, and used these values to construct VA surfaces displayed in Fig. 8 for both the OH(v = 0) (red) and OH(v = 1) (blue) levels. The upper [OH(v = 1)] curve is displaced by 0.157 Å in the direction of a contraction in the R_OO distance for the oxygen atoms that share the OH group. Like the case in the formate monohydrate complex, the spatial extent of the zero-point wavefunction for one-dimensional displacement in this potential [indicated by vertical bars on the B.O. curve (black) in Fig. 8] would provide overlap with the OH(v = 1) curve in the repulsive region over the range of the v_trans = 1–5 levels, accounting for redistribution of the OH oscillator strength over about 450 cm⁻¹. An analogous calculation for the OD stretching region based on the D₃O⁺ isotopologue is included in SI Appendix, Fig. S5, which indeed predicts a smaller displacement (0.151 Å) and hence a less extended range of the soft-mode progression.

Fig. 8.

VA curves for HD₂O⁺(18C6) were generated by first calculating the Born–Oppenheimer (B.O.) potential energy (black curve) as the distance between the oxygen of the central hydronium and the oxygen of the crown ether was scanned while allowing all other degrees of freedom to relax so as to minimize the total energy subject to this single constraint. The v = 0 (red) and v = 1 (blue) curves were then obtained by adding the harmonic energies of the OH stretch at each position along the B.O. curve. These curves were calculated at the B3LYP/6-311++G(2d,2p) level of theory. The black balls (Top Inset) indicate deuterons. The schematics on the Right indicate the distortion of the H₃O⁺ within the crown upon the addition of one quantum of the OH stretch corresponding to the proton closest to the crown.

Qualitatively, the deformations of the excited-state curves correspond to the partial proton transfer to one of the oxygen atoms in the crown, as illustrated schematically by the structures at the Right of Fig. 8. As such, the Franck–Condon driven progressions appear formally similar to those common in electronic excitation between states with different geometries (36–41). In the present IR analog, the states involved are based on entrance channel intermediates in the intermolecular proton transfer reaction (H₃O⁺ + B → H₂O + HB⁺) where the reactant is suspended by anticooperative H bonding to lie in the center of the ring. Although we have concentrated on the VA curves for the simpler D₂HO⁺ system, we note that, in the case of H₃O⁺, the same considerations imply that the potential surface corresponding to one quantum of OH stretching excitation should display three equivalent minima corresponding to displacement of the H₃O⁺ ion toward one of the three oxygen atoms in the crown that accept H bonds. This type of distortion is analogous to that found in strong Jahn–Teller distortions arising from vibronic interactions between different electronic states, as discussed early on by Lippincott, Witkowski, and coworkers (42, 43). This feature of the surface is included in an approximate interpolation of the behavior along each of the three OHO directions displayed in SI Appendix, Fig. S12.

We remark that the intermolecular proton-transfer process underlying the breadth in the crown complex could also be in play in the spectrum of the related H₃O⁺(TMA)₃ system, where locally stable, intermolecular proton transfer arrangements were invoked to understand the extreme breadth displayed by that system in the OH/NH stretching region (13). Challenging this suggestion would appear to be a fruitful direction for further theoretical work on these effects, as the hidden role of intermolecular proton transfer may indeed emerge as an important new paradigm in the spectroscopic exploration of proton defects in a wide range of systems.

It is clear that proper treatment of anharmonicity in the local OH stretch frequencies and explicit quantum treatment of the hydronium motion in the soft VA wells will act to increase the magnitude of the effect. Nonetheless, although qualitative, these results indicate that the VA mechanism can play a significant role in the spectroscopic behavior of the H₃O⁺(18C6) system. Finally, we remark that applying a similar treatment to the CH₃NH₃⁺(18C6) complex (with the curves presented in SI Appendix, Fig. S6) does not display the shifts exhibited by the hydronium system, consistent with the observation that the NH stretching bands in that system can be explained at the harmonic level.

One way to more quantitatively estimate the magnitudes of the anharmonic couplings underlying the VA curves presented in Fig. 8 is to explicitly diagonalize the vibrational Hamiltonian by including the cubic couplings that are included in a perturbation expansion in the VPT2 method mentioned earlier. The computational demands for such a calculation that includes all vibrational degrees of freedom in the H₃O⁺(18C6) complex are beyond the scope of this work. We, therefore, carried out a more limited model treatment that included seven modes [the v = 1 states of the three OH stretches and a large basis in each of the four low-frequency modes that involve significant displacements of the OO distances. These motions involve either translation of the H₃O⁺ or ring breathing (SI Appendix, Table S2 A and B)] in the anharmonic basis functions. The OH stretch diagonal frequencies were taken from the VPT2 calculation (computational details are included in SI Appendix). Following the approach taken for the formate monohydrate system, the only off-diagonal terms that are considered are the cubic terms that are quadratic in the OH stretch modes and linear in the low-frequency modes. This highlights the extent of soft-mode progressions anticipated by the calculated coupling terms, with the results for the H₂DO⁺(18C6) complex in the OH(D) stretch region presented in Fig. 9, along with the observed spectrum. Note that the spacing between the progression in the OD stretching region closely matches that observed in the OD series (Fig. 4) (∼85 cm⁻¹), whereas the extent of the band envelope is indeed much broader in the OH region, which interestingly occurs with a different spacing in this case, unlike the situation in formate monohydrate.

Fig. 9.

D₂-tagged vibrational predissociation spectra of H₂DO⁺(18C6) with calculations of the seven-mode coupling of the low-frequency modes and the OH stretches of the H₂DO⁺(18C6) displayed as red bands underneath the experimental spectra.

Conclusions

We report the observation of surprisingly diffuse vibrational spectra associated with the OH stretching region of the hydronium ion embedded in the pocket of the 18-crown-6 ionophore. This diffuse band evolves into a progression of distinct peaks in the OD stretching region of the deuterated isotopologues with a spacing of about 85 cm⁻¹, indicative of strong anharmonic coupling to a soft mode of the complex. A similar progression was reported earlier in the symmetrical monohydrates of carboxylates and analogous species with triatomic anionic domains, which represent an extreme case of anharmonic coupling between the OH stretch in water and the rocking motion of the water molecule. This motion breaks the C_2v symmetry as the OH groups bounce from one oxygen atom in the carboxylate anion to the other. The problem was treated with a VA approach in which OH stretching excitation leads to an unusual situation where different OH(v) vibrational levels occur with strong structural distortions in the intermolecular VA potentials that drive the rocking mode. We verified the strong nuclear quantum effects predicted by this model in a study of the H₂O and D₂O isotopologues of the formate monohydrate binary complex, and then applied a similar model to the H₃O⁺(18C6) complex. A key feature that emerges from this study is the hidden role that intracluster proton transfer plays in the vibrational spectrum of the H₃O⁺ ion held in the tricoordinated H-bonding environment offered by the crown. Large changes in the local OH stretching frequency are calculated to occur as H₃O⁺ is displaced away from the center of the 18C6 pocket. This yields a nested set of offset VA potential energy surfaces for each OH stretching vibrational level. These potentials become increasingly distorted for higher levels of OH excitation such that, although the ground state occurs with accommodation of the hydronium at the center of the ring, the excited states develop threefold minima, with each corresponding to the onset of an intracluster proton transfer process to one of the ether oxygen atoms [e.g., H₂O∙∙H⁺O(CH₃)₂]. This leads to vibrational level-dependent symmetry breaking in the cluster structure that is reminiscent of Jahn–Teller distortions (42, 43) that result from displacement induced mixing between electronic states. As such, vibrational spectroscopy in this unusual regime can be best considered in the ansatz traditionally applied to understand energy transfer and band structure in electronic spectroscopy.

Materials and Methods

Ions were extracted from solution (preparations described in SI Appendix) by electrospray ionization and injected into the source region of the custom tandem time-of-flight photofragmentation mass spectrometer previously described (44, 45). The ions then travel through radiofrequency octopole ion guides through several stages of differential pumping until they are turned 90° by a DC ion bender and then guided into a 3D Paul trap (Jordan) that is mounted to the second stage of a 4 K helium cryostat where they are accumulated for 95 ms. During this time, they are cooled to about 10 K by a pulsed helium buffer gas containing 10% D₂ resulting in D₂-tagged ions. The tagged clusters are then pulsed out of the Paul trap and into the acceleration region of the tandem time-of-flight photodissociation mass spectrometer where they are later mass-selected by a pulsed deflector. The ions are then intersected by a tunable OPO/OPA IR laser (LaserVision) to photoevaporate the D₂ tag and yield a vibrational spectrum.

All calculations were performed at the B3LYP/6-311++G(2d,2p) level of theory using the Bernie algorithm within the Gaussian G09 software package. Additional information is given in SI Appendix.