Bacteria exploit a polymorphic instability of the flagellar filament to escape from traps

Significance

It has long been established that flagella provide an efficient means of movement for bacteria in planktonic environments (free swimming) or across surfaces (swarming). However, rather little is known about bacterial motility in structured environments. In this study, we demonstrate that polarly flagellated bacteria can exploit a polymorphic instability of the flagellar filament for a third type of flagella-mediated movement in which the flagellum wraps around the cell body and the cells back out from narrow passages in a screw-like motion.

Abstract

Many bacterial species swim by rotating single polar helical flagella. Depending on the direction of rotation, they can swim forward or backward and change directions to move along chemical gradients but also to navigate their obstructed natural environment in soils, sediments, or mucus. When they get stuck, they naturally try to back out, but they can also resort to a radically different flagellar mode, which we discovered here. Using high-speed microscopy, we monitored the swimming behavior of the monopolarly flagellated species Shewanella putrefaciens with fluorescently labeled flagellar filaments at an agarose–glass interface. We show that, when a cell gets stuck, the polar flagellar filament executes a polymorphic change into a spiral-like form that wraps around the cell body in a spiral-like fashion and enables the cell to escape by a screw-like backward motion. Microscopy and modeling suggest that this propagation mode is triggered by an instability of the flagellum under reversal of the rotation and the applied torque. The switch is reversible and bacteria that have escaped the trap can return to their normal swimming mode by another reversal of motor direction. The screw-type flagellar arrangement enables a unique mode of propagation and, given the large number of polarly flagellated bacteria, we expect it to be a common and widespread escape or motility mode in complex and structured environments.

Motility is an important element of bacterial life in a range of different environments (1–5) and a driving factor in processes as diverse as the spreading of diseases and degradation of biomaterial (6, 7). For active movement, many bacteria rely on flagella, long helical proteinaceous filaments extending from the cell’s surface, which they rotate at the filament’s base by a membrane-embedded motor and which allow effective swimming through liquid environments or swarming across surfaces (8). The prominent helical flagellar filament is composed of 11 protofilaments consisting of the filament’s building block, the protein flagellin. Any number of these 11 protofilaments may adopt a certain conformation (“L” or “R”) that produces bending and a helical twist, resulting in an overall helical configuration of the filament (9, 10). Different ratios of L to R protofilaments enable the formation of 12 different polymorphic states of the filament, 2 of which are straight (L or R only), 3 of which are left-handed, and 7 of which are right-handed (11–13). External perturbations, such as increasing force or torque, may lead to switches between the filament’s polymorphic forms (14–17). This important property of the flagellum is exploited by bacteria to adjust their swimming behavior.

Most flagellar motors are bidirectional and allow counterclockwise (CCW) and clockwise (CW) rotation (as seen from the tip of the flagellum looking toward the motor) (18, 19). The paradigmatic example Escherichia coli has five or six flagellar filaments arranged in a peritrichous pattern around the cell body. CCW rotation leads to association of the flagella into a left-handed bundle driving smooth swimming of the cell (“run”). Upon switching one or several motors to CW rotation, the corresponding flagella will transform into a right-handed helix, which leaves the flagellar bundle and leads to cellular realignments (“tumble”). Upon resuming CCW rotation, the bundle is reestablished, and the cell runs smoothly into a new direction (20, 21). By adjusting the run lengths between tumbles, the cells can move along signal gradients in a biased random walk toward preferred environmental niches (22). In contrast to the run-and-tumble movement of bacteria with peritrichous flagellation, cells of many bacterial genera with polar flagella (such as Vibrio, Pseudomonas, Aeromonas, and Shewanella, to name just a few) navigate by “run–reverse–flick” patterns. Although CCW rotation of a left-handed helix drives the cells forward, motor reversal to CW rotation does not transform flagellar helicity into a right-handed shape as in E. coli. Instead, the flagellum remains left-handed, and the cells are pulled backward (23). Upon resuming CCW rotation, the filament is compressed and the cell is reoriented as a consequence of buckling of the flagellum in the hook region, the flexible structure joining flagellar filament and motor (24, 25). However, other bacteria, such as Rhodobacter sphaeroides, navigate by “run–stop–run” cycles. In this species, a single right-handed flagellum is rotated in a CW fashion to drive the cells forward. During periodic stops of the motor, cellular reorientation occurs through conversion of the flagellar filament from a helical to a relaxed coiled form (26). These examples illustrate how bacteria take advantage of the flagellar polymorphism and rigidity to effectively modulate their swimming behavior.

Studies on movement of single bacteria and the behavior and position of the flagellar filaments are almost entirely restricted to free-swimming cells. However, many motile bacterial species reside in soil, sediments, and other porous environments with pore sizes of only a few micrometers or less (27), and other bacteria, including many pathogens, have to move through diverse structured environments such as mucus layers, tissues, or biofilm matrices. It has been shown that E. coli or Bacillus subtilis strains can efficiently move through pores with diameters that exceed the diameter of the cells only slightly (28). When entering wedge-shaped narrow passages, bacteria have been observed to back up, either by reversing their motor or by a flip of their flagellar bundle (29). In these cases, the flagellum or the flagellar bundle points away from the cell body. In this study, we performed single-cell tracking of the sediment isolate Shewanella putrefaciens CN-32 to explore flagella-mediated movement of a polarly flagellated species within structured environments.

Results and Discussion

Trapped Cells Show an Unusual Behavior of the Flagellar Filament.

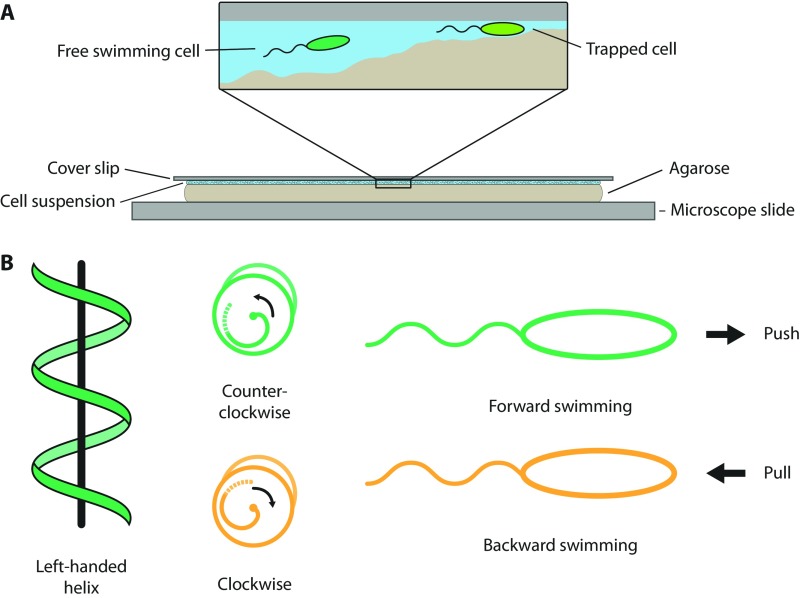
S. putrefaciens CN-32 is a bacterium with a primary single polar flagellum and additional lateral flagella that are implicated in realignment of the cells during swimming (30, 31). To concentrate on the role of the main polar flagellum, we used an S. putrefaciens CN-32 strain, which we genetically engineered to not produce the lateral flagellum by deleting the corresponding flagellin-encoding genes. To visualize flagellar filaments by fluorescence microscopy, we genetically introduced threonine-to-cysteine substitutions into the environment-exposed surface of the two flagellins, the building blocks of the filament, which were then used for the ligation of maleimide-ligated fluorescent dyes. Details of the strain constructions are given in SI Materials and Methods. To create a suitable structured environment that enables microscopic recordings of swimming cells, we used an agarose surface that was overlaid with a sample of medium containing an appropriate dilution of cells with fluorescently labeled flagella. A coverslip was added on top so that the liquid-covered uneven surface of the agarose provided a structured environment with varying distances between agarose and the glass surface (Fig. S1).

Fig. S1.

(A) Experimental setup: Bacteria move in the small liquid pockets between the agarose and the coverslip where they can be monitored with a microscope from above. (B) Illustration of the regular swimming mechanism of S. putrefaciens. Changing the rotation of their flagellum while maintaining the handedness of the helix can switch the directional motion of the bacteria. CCW rotation (viewed from behind the cell) results in forward swimming, and CW rotation in backward swimming.

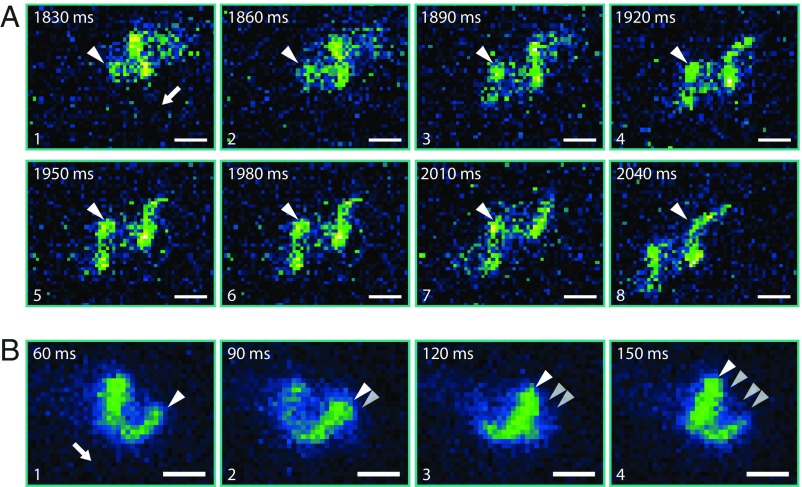
Fluorescence imaging revealed that the polar flagellum of S. putrefaciens CN-32 is on average ∼6.5 µm in length and exhibits a left-handed helical structure (diameter, 0.6 µm; pitch, 1.9 µm), which mediates forward and backward swimming upon CCW and CW rotation, respectively. Free-swimming cells displayed the expected “run–reverse–flick” motility patterns (30), whereas cells that got stuck between the glass coverslip and the agarose surface showed flagellar rotation without spatial propagation. In an effort to escape the trap, cells alternated between CCW and CW rotation of the motors. In cases where these changes in flagellar rotation did not suffice to free the cell, we frequently noticed that the flagellar filament eventually wrapped around the cell body, forming a spiral- or screw-like large helix (Fig. 1, Movie S1, and Dataset S1). This behavior was often accompanied by a backward translation of the cell body in a screw-like motion for up to several seconds. Notably, during this backward maneuver, the general orientation of the flagellar helix relative to the substratum did not change while the cell moved through the spiral formed by the flagellum (Fig. 2A and Movie S2). Once the cells had escaped the narrow passage, the motor reversed direction and the filament unwound the spiral to resume its normal helicity and position behind the cell, which then continued moving by normal forward swimming. Some cells could not escape by this mechanism and alternated between the two positions of the filament without moving the cell (Movie S3).

Fig. 1.

Approach, trapping, and escape of a bacterium between agarose and cover slide. (From Left to Right and Top to Bottom) The bright structures in the microscope image result from the fluorescently labeled flagellum. The cell body is indicated by a dotted ellipsoid. The yellow dashed line marks the position of the flagellated cell pole when the cell got stuck and maintained in subsequent frames to display the backward motion of the cell. The cartoon on the right summarizes the sequence of events and highlights the switch from counterclockwise (CCW) rotation of the motor (green frames) to clockwise (CW) rotation (orange frames; viewed from behind the cell). The cell approaches from the Lower Left (frame 1), moves upward, and then gets stuck (frames 2 and 3). While still pushing forward, the flagellum wiggles circularly in an instability known to occur for stronger applied torque. It then switches direction of rotation to CW (frame 4), and the flagellum wraps around the cell (frames 5 and 6). The strong forces during screw formation caused the cell to move, as indicated by the reorientation of the cell body between frames 5 and 6. The cell continues to the Lower Left, as indicated in frames 7–9. Exposure time was 30 ms; the number in the upper left corner of each micrograph displays the time each still image was taken from the movie (Movie S1 and Dataset S2). (Scale bars: 2 µm.) The freely rotating flagellum (frames 1–5) appears blurry because the rotation of the helical filament in normal medium is faster than the exposure time.

Fig. 2.

Screw-like propagation relies on interaction between the flagellar filament and asperities on the surface. The white arrow indicates the orientation of the cell body (flagellated pole). The white triangles indicate one peak of the flagellar waveform. (A) Still images taken from Movie S2 showing screw-like propagation of a cell that is stuck between agarose medium and the coverslip surface while the waveform of the flagellar helix does not move relative to the surrounding medium. (B) Still images taken from Movie S4 showing screw-like propagation of a free swimming cell (at least 50 µm away from the coverslip). Here, the flagellar helix waveform is moving relative to the surrounding medium, as indicated. (Image exposure time, 30 ms; scale bars, 1 µm.)

Efficient Backward Screwing Requires Surface Contact.

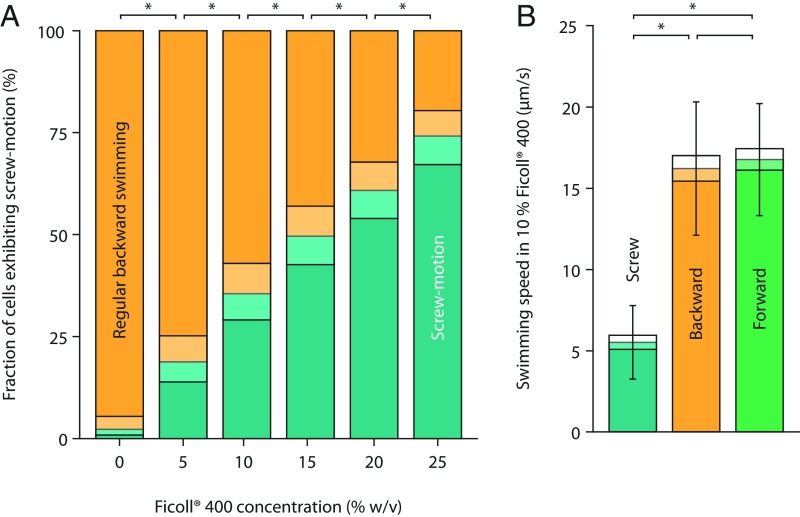
Because immobilizing the cell body increases the forces acting on the flagellar filament (32), we explored the possibility to trigger the transition also during free swimming by increasing the viscosity and hence the drag on the cell. To this end, we monitored cellular movement and position of the flagellar filament of free-swimming cells in media supplemented with increasing amounts of Ficoll to enhance the viscosity (33). In Ficoll-free media, we observed almost no cells with filaments wrapped around the cell body (Fig. 3). However, with increasing Ficoll concentrations, the number of cells displaying screw formation increased significantly to more than 74% of the population for Ficoll concentrations up to 25% (Fig. 3). The flagellum wrapped around the cell body rotated in CW direction. This suggests that the forces on the cell and the flagellar filament induce the formation of the spiral around the cell. At 10% Ficoll, the cells with the filament wrapped around the cell body moved slowly at about 5 µm/s, which is barely above the general background diffusion of immobile cells caused by Brownian motion and general drift (∼3 µm/s), but significantly slower than cells that were still pushed or pulled by the flagellar filament (both at ∼16 µm/s). Moreover, the flagellum moved around the cell body without efficient translation (Fig. 2B and Movie S4). In contrast, for cells near surfaces, the flagellar helix maintained a fixed location relative to the surroundings and the cell (Fig. 2A and Movie S2). We therefore propose that the propagation relies on an interaction between the flagellum and asperities on a surface, while continuous rotation of the flagellum around its molecular axis by the motor prevents strong binding. Thus, the screw-like state allows a backward movement of cells across surfaces or through appropriately structured environments but is not effective under free-swimming conditions with increased viscosity.

Fig. 3.

Inducing the transition to screw mode in media with higher viscosity (Left) and differences in swimming speed (Right). (A) Adding Ficoll 400 increases the viscosity and causes a larger torque when the cells switch from CCW to CW rotation. The fraction of cells in the “screw” state increases with Ficoll concentration (determined far away from surfaces). The viscosities are ∼2, 5, 10, 18, and 33 cP for 5%, 10%, 15%, 20%, and 25% Ficoll 400, respectively. Bars with an asterisk indicate that the differences are significant (Fisher’s exact test of independence; P ≤ 0.05, Bonferroni corrected). The exact P values from 0 to 25% Ficoll are 1.36 × 10⁻¹², 2.90 × 10⁻⁶, 3.96 × 10⁻⁴, 4.27 × 10⁻³, and 3.67 × 10⁻⁴, respectively. The number of counted backward swimming events are 309, 316, 313, 317, 324, and 313, respectively. Shaded boxes display 95% confidence intervals. (B) Measurements of the swimming speed show that, although forward and backward swimming have very similar speeds, the motion in the screw state is reduced. Bars with an asterisk indicate that the differences are significant (two-sample t test; P ≤ 0.01, Bonferroni corrected). The exact P values are <2.20 × 10⁻¹⁶ for screw vs. backward and screw vs. forward and 0.3 for backward vs. forward. For each swimming mode, 105 cell tracks were analyzed. Error bars represent SD; shaded boxes display 95% confidence intervals.

Screw Formation Is Triggered by a Polymorphic Filament Instability at CW Rotation.

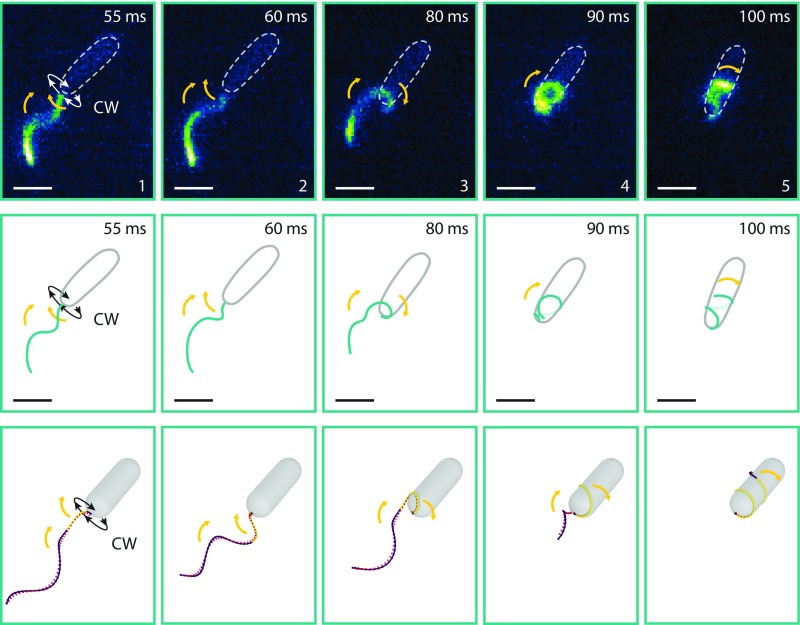
The effects of Ficoll are to slow down the motion of the flagellum and to increase the drag forces (32, 34). We therefore used Ficoll-supplemented medium on agarose surfaces to reduce the speed of the rotating flagellar filament, allowing us to obtain sufficient temporal resolution to monitor its motion and morphology during formation and release of the large helix around the cell body (Fig. 4, Fig. S2, Movie S5, and Dataset S2). Flagella of stuck cells rotating in CCW direction generally maintained the left-handed helical shape; however, diameter and pitch varied dynamically, indicative of flagellar filament polymorphism. When the rotational direction switched to CW, the flagellar helix quickly became unstable.

Fig. 4.

Comparison between observed and simulated flagellar states during screw formation. The upper panel shows flagellar states taken from Movie S5. These images are inverted horizontally to match the correct handedness of the flagellar helix (SI Materials and Methods). The flagellar filament was fluorescently labeled, and the medium was supplemented with 20% Ficoll 400 to slow down flagellar rotation (exposure, 5 ms; scale bars, 2 µm). The cell body is indicated by a dotted ellipsoid. Yellow arrows indicate the movement of the flagellar filament. The same states are depicted as cartoons in the middle panel. The lower panel displays the corresponding images from the simulation of screw formation (Movie S6). The stretched helix configuration is color-coded in purple, whereas the coiled state is marked in yellow. Details of the numerical simulation are described in SI Materials and Methods. Both imaging and simulations show that CW rotation results in an instability at the base of the flagellar filament, leading to a pull of the filament toward the cell body and, eventually, wrapping of the flagellum around the cell.

Fig. S2.

Fluorescence microscopy (Upper) and cartoon (Lower) showing the formation of the screw with high temporal resolution. Screw formation begins with the unwinding of the left-handed flagellar helix, which drives polymorphic transitions and leads to a movement of the filament toward the cell body. Ultimately, the filament is wrapped around the cell body and continues its CW rotation, now pushing instead of pulling the cell backward. The bright structures in the microscope image result from the fluorescently labeled flagellum. The cell body is indicated by a dotted ellipsoid. Yellow arrows indicate the movement of the flagellar filament. Still images were taken from Movie S5. These images are inverted horizontally to match the correct handedness of the flagellar helix (Materials and Methods). (Image exposure time, 5 ms; scale bars, 2 µm.)

To gain more insight into the origin and the dynamics of the transition, we implemented an established model for the flagellum as an elastic rod coupled to the fluid through resistive force theory (35, 36). The elastic forces acting on the filament come from changes in the shape of the filament, from the interaction between segments of the filament and between filament and cell body. They are represented by free energies and local interaction potentials. Different polymorphisms of the flagellum can be implemented by switches in the equilibrium parameters and the requirement that the local minimum of the free energy is chosen, as shown for E. coli in refs. 37 and 38. The crystal structure of the S. putrefaciens CN-32 flagellar filament will be different from that of well-studied organisms like E. coli. However, we anticipate that its general mechanical properties and the different polymorphisms will not differ significantly, as the S. putrefaciens sequence and deduced structure is very similar to that of Salmonella in all five α-helices that constitute the polymorphic structural part of the filament (Fig. S3A). From our observations, we can deduce at least two equilibria, one for a stretched-helix flagellum typical during normal swimming, and one for the coiled state when the flagellum is wrapped around the cell body. For the frictional forces, we use resistive force theory, which characterizes the forces on the segments by three local friction coefficients, one each for motion perpendicular to the flagellums centerline, for motion along the centerline, and for rotations around the centerline. No measurements of the various parameters have been reported thus far, so we adopted values obtained for E. coli. Although some uncertainty about the precise values for the elastic constants and the presence of other morphologies during the transition remain, numerical simulations for several different parameter choices show that the qualitative features of the flagellar dynamics are insensitive to the details of the parameter choice. The full set of equations and the complete list of parameters values are given in SI Materials and Methods.

Fig. S3.

Substitution of serine or threonine to cysteine in the variable domain of the polar flagellin monomers does not impair the swimming motility of S. putrefaciens. (A) Predicted structure of the polar flagellin FlaA1 of Shewanella putrefaciens CN-32 (calculated by Phyre V 2.0; illustration created with PyMOL 1.3). The threonine 174-to-cysteine substitution site is indicated by a blue sphere. The approximate corresponding substitution sites (T166C and S174C) are indicated by gray arrows. Thus, all substitution sites in both flagellins are located in the variable domain (approximately amino acids 163–183), which is exposed to the surrounding medium in the assembled flagellar filament. (B) Radial extension of FlaAB1-cys mutants and ∆flaAB2 as background strain (control) in 0.25% soft agar. The strains are labeled accordingly. The substitutions do not reduce the extension radius. (C) Swim speed and time between reversals for FlaAB1-cys are highly similar to its background strain ∆flaAB2 (control). For each strain, 598 cell tracks were evaluated (TrackMate plugin for ImageJ). The differences are not significant (two-sample t test; P = 0.087 and 0.891, respectively). Time between reversals was measured over the whole population, so the sample size is only three. Error bars represent SD; shaded boxes represent 95% confidence intervals. (D) FlaA1 and FlaB1 immunostaining subsequent to separation of the protein crude extract by SDS/PAGE and Western transfer to a membrane. Substitution of serine or threonine to cysteine does not cause a mass shift of the flagellins. This would only occur if glycosylation sites were substituted to cysteine.

Close to the cell body we have to take the driving and the increased flexibility of the filament in the hook region into account. Because the hook region itself is not resolved in the numerical simulations, we model its properties by the boundary conditions. The flagellum’s rotation is driven by a constant motor torque. The angle under which the filament leaves the cell surface is not prescribed, accounting for the fact that the bacterial hook is much more flexible than the flagellum (24). The torque applied by the motor is split into a component parallel to the axis of the motor, and one parallel to the filament, with a parameter that controls the relative contributions. Formation of the screw was reliably observed when 10–50% of the torque acted along the centerline of the filament.

The motion of the flagellum with two different morphologies is shown in Movies S5 and S6, and the snapshots in Fig. 4. Both model and observations show that, when initiated with a left-handed spiral rotating CCW, the flagellum pushes the bacterium along. When increasing the torque on the cell, the flagellum begins to move sideways, as also observed in Movie S1 and in Fig. 1 (frames 2 and 3). Upon switching to CW rotation, the flagellum begins to pull on the bacterium. As the forces on the filament increase, the first loop of the helix above the motor is stretched and bends around toward a right-handed helix. In elastic filaments, such transitions in helicity under stress are known as “perversions” (39). Here, however, the formation of the perversion is not completed. Instead, the flagellum switches to another equilibrium shape reminiscent to the left-handed coiled forms observed for the E. coli flagellum (11, 13). The orientation of the filament, deduced from the direction of the tangent along filament, which initially points away from the cell, locally changes direction and points toward the cell. This induces a force on the upper part of the flagellum that pulls it toward the cell and the flagellum begins to wrap around the cell body. Because the formation of the perversion and the transition to a right-handed helix is not completed, the filament remains a left-handed helix.

The instability discovered and described here is different from the buckling instability described by Son et al. (24) and Xie et al. (25). They showed that the hook region buckles when the bacterium switches from a backward pull to a forward push: During the pull, the flagellum is stretched, but during the push, it experiences a strong compression, which, combined with the high flexibility of the hook region, triggers the buckling instability and the directional change. The instability described here occurs during the pulling phase, where the flagellum is stretched, and the motor forces push toward a right-handed helix. During normal swimming, when the cell body is free to rotate, the instability is avoided because the applied torque is reduced by the counterrotation of the cell body (32). When the bacterium is stuck, or the friction on the cell body is enlarged by an increase in viscosity, the full torque of the motor acts on the flagellum and triggers the transition to the screw-like state. The transition might also be assisted by an increase in torque due to the acquisition of additional motor proteins, which has been shown to occur under conditions of high load on the flagellum (40, 41).

SI Materials and Methods

Bacterial Strains, Growth Conditions, and Media.

All strains used in this study are listed in Table S1. Escherichia coli strains DH5α-λpir and WM3064 and Shewanella putrefaciens CN-32 were grown in LB medium at 37 and 30 °C, respectively. Cultures of the 2,6-diaminoheptanedioic acid (DAP)-auxotroph E. coli WM 3064 were supplemented with DAP at a final concentration of 300 µM. To solidify media, LB agar was prepared using 1.5% (wt/vol) agar. For soft-agar plates, 0.2–0.3% (wt/vol) agar was used. Whenever necessary, media were supplemented with 50 mg/mL kanamycin, 50 µM phenamil, and/or 10% (wt/vol) sucrose. Agarose pads for microscopy were prepared by solidifying LM100 medium [10 mM Hepes, pH 7.3; 100 mM NaCl; 100 mM KCl; 0.02% (wt/vol) yeast extract; 0.01% (wt/vol) peptone; 15 mM lactate] with 1% (wt/vol) agarose.

Table S1.

Bacterial strains used in this study

Strain	Genotype	Purpose	Source
Escherichia coli
DH5αλpir	ϕ80dlacZ ∆M15 ∆(lacZYA-argF)U169 recA1 hsdR17 deoR thi-l supE44 gyrA96 relA1/λpir	Cloning strain	Ref. 56
WM3064	thrB1004 pro thi rpsL hsdS lacZ ∆M15 RP4-1360 ∆(araBAD) 567∆dapA 1341::[erm pir(wt)]	Conjugation strain	W. Metcalf, University of Illinois at Urbana–Champaign, Champaign, IL
Shewanella putrefaciens
S271	CN-32	Wild type
S2576	∆flaAB2; ∆Sputcn32 3455–56	Markerless deletion of both lateral flagellin genes	Ref. 31
S3807	∆flaA1-ext; ∆Sputcn32 2586	Markerless deletion of polar minor flagellin gene	This study
S3810	∆flaB1-ext; ∆Sputcn32 2585	Markerless deletion of polar major flagellin gene	This study
S4152	flaA1-T174C - ∆flaAB2	Markerless insertion of cysteine-labeled flaA1 gene into ∆flaA1-ext and deletion of lateral flagellin genes	This study
S4143	flaB1-T166C	Markerless insertion of cysteine labeled flaB1 gene into ∆flaB1-ext	This study
S4154	flaB1-T166C - ∆flaAB2	Markerless insertion of cysteine labeled flaB1 gene into ∆flaB1-ext and in-frame deletion of lateral flagellin genes	This study
S4156	flaB1-S174C - ∆flaAB2	Markerless insertion of cysteine labeled flaB1 gene into ∆flaB1-ext and deletion of lateral flagellin genes	This study
S4147	flaB1-S174C	Markerless insertion of cysteine labeled flaB1 gene into ∆flaB1-ext	This study
S4401	∆flaAB2 flaA1T174C flaB1-T166C	Markerless insertion of cysteine labeled flaB1 gene into ∆flaB1-ext and cysteine labeled flaA1 gene into ∆flaA1-ext and deletion of lateral flagellin genes	This study

Strains and Vector Constructions.

All genetic manipulations of S. putrefaciens CN-32 were introduced into the chromosome by sequential double homologous recombination using the suicide vector pNPTS138-R6K essentially as described previously (44). Plasmids and corresponding oligonucleotides are summarized in Tables S2 and S3, respectively. All kits for preparation and purification of nucleic acids (VWR International) and enzymes (Fermentas) were used according to the manufacturers’ protocols. Plasmids were constructed using standard Gibson assembly protocols (45) and introduced into Shewanella cells by conjugative mating with E. coli WM3064 as donor. In-frame deletions were generated by combining ∼500-bp fragments of the upstream and downstream regions of the gene to generate a deletion leaving only a few codons of the designated gene. Gene versions encoding flagellins bearing threonine-to-cysteine substitutions were reintegrated into those deletion strains in basically the same fashion. The design of these substitutions is described in detail below. As a background strain, we used S. putrefaciens CN-32 S2576 lacking the ability to produce lateral flagella due to deletion in the genes encoding the secondary flagellin subunits (31).

Table S2.

Plasmids used in this study

Name	Insert	Purpose	Source
pNPTS138-R6KT	mobRP4+, ori-R6K, sacB, betagalactosidase fragment alpha, Kmr	Suicide plasmid for in-frame deletions or integrations	Ref. 44
pNPTS138-R6KT-R6KT-flag-clusterII-KO	∆flaAB2 (Sputcn32_3455–56)	In-frame deletion fragment	Ref. 31
pNPTS138-R6KT-flaA1-KO-ext	∆flaB1 (Sputcn32 2586)	In-frame deletion fragment	This study
pNPTS138-R6KT-flaB1-KO-ext	∆flaB1 (Sputcn32 2585)	In-frame deletion fragment	This study
pNPTS138-R6KT-flaA1 - T174C	flaA1-T174C (Sputcn32_2586)	In-frame insertion fragment; threonine 174 substituted with cysteine	This study
pNPTS138-R6KT-flaB1 - T166C	flaB1-T166C (Sputcn32 2585)	In-frame insertion fragment; threonine 166 substituted with cysteine	This study
pNPTS138-R6KT-flaB1 - S174C	flaB1-S174C (Sputcn32 2585)	In-frame insertion fragment; serine 174 substituted with cysteine	This study

Table S3.

Oligonucleotides used in this study

ID	Name	Sequence	Purpose	Source
B 31	BamHI-flagL-fwd	AGG ATC CTG ACA CTG TAT TTA	Construction of in-frame deletion vector pNPTS138R6KT-R6KT-flag-clusterII-KO	Ref. 31
		TGG CGC AGG
B 32	OL-flagL-rev	CAG TAG ACC GTG AAC ACC TAA
		CAT ATT AAT TCT CCA G
B 33	OL-flagL-fwd	GGT GTT CAC GGT CTA CTG CGT
		TAA TCT AGC TC
B 34	PspOMI-flagL-rev	TGT CGG GCC CGT CGC CGT CGC
		ATT TTC GC
B 35	Check-flagL-fwd	GTA TTA GCT TCG ATC GGG ATT	Check primer for flaAB2	Ref. 31
		GG
B 36	Check-flagL-rev	GTT ACC CTT TGG CGC ATC GG
MJK 26	OL flaA1 KO ext rv	GTG ACA GCG CAA TAG CCA TAG	Construction of in-frame deletion vector pNPTS138-	This study
		TAT TTT CCT CTT CTA AG	R6KT-flaA1-KO-ext
MJK 27	OL flaA1 KO ext fw	TAT GGC TAT TGC GCT GTC ACT		This study
		ACT GGG ATA ATT TAC
FR299	EcoRV flaA1 KO fw	GAA TTC GTG GAT CCA GAT GAA		This study
		GTT AAA GTG TCT GGG AAA CCC
FR302	EcoRV flaA1 KO rv	CAA GCT TCT CTG CAG GAT GCA		This study
		TCG CAC CTT CAG AAA TTT GG
MJK 28	OL flaB1 KO ext rv	AGG CCA CTT GGG CCA TGA TCG	Construction of in-frame deletion vector pNPTS138-	This study
		TTT CCT CTG TA	R6KT-flaB1-KO-ext
MJK 29	OL flaB1 KO ext fw	GAT CAT GGC CCA AGT GGC CTT		This study
		ATC ACT GCT GTA ATA G
FR295	EcoRV flaB1_KO fw	GAA TTC GTG GAT CCA GAT ATA		This study
		ACC AAC GTG CAG CGT TAG G
FR298	EcoRV flaB1_KO rv	CAA GCT TCT CTG CAG GAT CAG		This study
		CTA ATG CCA ACG CTT CTT C
B 49	Check-flagP-fwd	AAT TTT GAT GCG ACT ACC CCC G	Check primer for flaAB1	Ref. 31
B 50	Check-flagP-rev	TAT CTA GAC CTG ACC CCA TGC C
MJK 78	FlaA1-T174C-R	TCG TTA AAC AAC TAA CCA TTA	Construction of in-frame insertion vector pNPTS138-	This study
		AAC TCC CCG CAT TAT TGG	R6KT-flaA1-T174C
MJK 79	FlaA1-T174C-F	TGG TTA GTT GTT TAA CGA TTG		This study
		CAA CTT CAG GTG GTC G
MJK 82	FlaB1-T166C-R	CTG ATG CAC AGG TTT TTG ACA	Construction of in-frame insertion vector pNPTS138-	This study
		CAG AAA TCG	R6KT-flaB1-T166C
MJK 83	FlaB1-T166C-F	CAA AAA CCT GTG CAT CAG CAT		This study
		TAA AAG TTG G
MJK 86	FlaB1-S174C-R	ATA TCT AAA CAA CCA ACT TTT	Construction of in-frame insertion vector pNPTS138-	This study
MJK 87	FlaB1-S174C-F	AAT GCT GAT GC	R6KT-flaB1-S174C
		AGT TGG TTG TTT AGA TAT TAA		This study
		AGG CTC TGC

Visualizing Flagellar Filaments.

To visualize the flagellar filaments, maleimide-ligated dyes were coupled to surface-exposed cysteine residues, which were specifically introduced into the flagellins, FlaA and FlaB, of the S. putrefaciens CN-32 polar flagellum. However, the flagellins of the close relative S. oneidensis MR-1 were shown to be modified by O-linked glycosylation via threonine or serine residues. Single substitutions of the corresponding residues resulted in a clearly visible shift in the protein’s position when separated by polyacrylamide electrophoresis (PAGE) due to loss of the modification (49). We therefore performed a similar Western immunoblot analysis on the S. putrefaciens CN-32 flagellins bearing the serine- and threonine-to-cysteine substitutions to rule out that a functionally important modification was lost by the substitution. To determine potential differences in the molecular mass of flagellin protein, lysates from exponentially growing LB cultures were obtained for Western blot analyses by harvesting cells corresponding to an OD₆₀₀ of 10 by centrifugation, resuspending in sample buffer (50), and heating at 95 °C for 5 min. After separation by SDS/PAGE using 15% (wt/vol) polyacrylamide gels, the proteins were transferred to a nitrocellulose Roti-PVDF membrane (Roth) by semidry transfer. For detection of flagellins FlaA1 and FlaB1, polyclonal antibodies were used that were raised against the N-terminal conserved region of Shewanella oneidensis MR-1 FlaB (Eurogentec Deutschland) in the dilution of 1:500. Anti-rabbit IgG-horseradish peroxidase antibody (Thermo Fisher Scientific) was used as secondary antibody at a dilution of 1:20,000. For signal detection, the membranes were incubated with SuperSignalH West Pico Chemiluminescent Substrate (Thermo Scientific) and documented using the CCD System LAS 4000 (Fujifilm). The S. putrefaciens CN-32 flagellins were detected at a position corresponding to a molecular mass of ∼37 kDa (FlaA1) or ∼35 kDa (FlaB1) and thus significantly higher than the estimated molecular mass (∼28.5 kDa for both FlaA1 and FlaB1), strongly indicating that both FlaA1 and FlaB1 are decorated by modifications. No mass shifts were detected for the flagellins harboring the cysteine substitutions, demonstrating that no modified serine or threonine residues were lacking (Fig. S3).

Handedness of the Flagellar Helix and Orientation of the Microscope Images.

Images of the flagellar helix, in regular or in screw mode, show a different pattern depending on the z position of the focal plane (51). An image taken of a left-handed helix appears to be left-handed when the focal plane is above the cell. However, when the focal plane is below the cell, the helix appears right-handed. This is due to the image of the cell body, which always seems to be below the focal plane, although it might be above the focal plane. To determine the handedness properly, the focal plane was slowly shifted through the cell body to reliably localize the cell body and to determine whether the flagellar helix continues upward or downward. In this study, this was done for 115 cells with normal flagellar filament and 108 cells with filaments in screwing mode using cell cultures with fluorescently labeled flagellar filaments (not or slowly rotating). The regular flagellar helix, aligned with the cell axis, was found to be left-handed. The flagellar helix wrapped around the cell body was also found to be left-handed. Because the appearance of the handedness of the flagellar helix depends on the z position of the focal plane and the image from the microscope is inverted technically, the microscopic images and movies were inverted appropriately, as stated in the legends, so that the visible handedness matches the true handedness of the flagellar helix.

Statistics.

Calculations were carried out in R, version 3.3.2, unless stated otherwise. Two-sided testing was used for all tests. The swimming behavior of the double flagellin-labeled strain (S4401) in medium with increased viscosity was investigated by supplementing LM medium with Ficoll 400 and recording multiple videos in bulk medium for each Ficoll 400 concentration from 0 to 25%, corresponding to 2, 5, 10, 18, and 33 cP (52). The experiment was repeated three times with always about 100 counted cells per concentration, resulting in a total of at least 300 counts. Only backward swimming was considered, and we determined whether it was regular backward swimming (flagellar filament behind the cell body aligned with the cell axis) or screw mode (flagellar filament wrapped around the cell body). Significance was tested pairwise using the Fisher’s exact test of independence (P < 0.05, Bonferroni corrected). The 95% confidence intervals were calculated with the exact binomial test.

These videos were also used to measure forward, backward, and screw swimming speed using the MTrackJ, version 1.5.1, plugin in the ImageJ distribution Fiji (48). For each swimming mode, 105 tracks were evaluated. Significance was tested using a two-sample t test (P < 0.01, Bonferroni corrected). Mean, SD, and 95% confidence intervals were calculated in Microsoft Excel 2013.

To determine swimming speeds and time between reversals, nine videos (three biological replicates with three technical replicates each) were recorded for each strain (S2576 and S4401) as described above. Cell tracks were obtained to measure the speed of individual cells as well as the total swim time. For calculating the mean of the swimming speeds, the track data were randomized and excess data were deleted to match the sample size of the comparative strain (598 for each strain). A two-sample t test was used to test significance (P < 0.05). Although both datasets were not perfectly normally distributed but slightly skewed to the left, the test should be reliable as both datasets show very similar distribution. Mean, SD, and 95% confidence intervals were calculated in Microsoft Excel 2013.

Cell tracks were examined manually to count reversals. The average time between reversals was calculated for each biological replicate using the total swim time. Therefore, the sample size is only three, and normal distribution could not be tested. Significance, mean, SD, and 95% confidence intervals were calculated similarly to swim speed calculations.

Numerical Model for the Flagellum.

The numerical simulations are based on equations for an elastic rod and resistive force theory (35, 36), extended to allow for multiple polymorphic equilibrium states (38). The position along the rod is measured by the arclength s and the torsional state of the rod at position s is described by the rotational strain vector Ω(s). The flagellum is assumed to have a circular cross-section and a helical rest state, characterized by a vector ${\mathbf{\Omega }}_{\mathbf{0}}=\left(0,{\kappa }_0,{\tau }_0\right)$. The curvature κ₀ and torsion τ₀ are related to the helix radius R and pitch P by the following:

$$\begin{array}{l}{\tau }_0=\frac{2\pi P}{4{\pi }^2{R}^2+P^2},\\ {\kappa }_0=\frac{4{\pi }^{2}R}{4{\pi }^2{R}^2+P^2}.\end{array}$$ [S1]

Deviations from this rest state give quadratic contributions to the free energy:

$${\mathrm{ℱ}}_K={\displaystyle {\int }_0^L\left(\frac{A}{2}\right)\left[{\left({\mathrm{\Omega }}_1-{\mathrm{\Omega }}_{\mathrm{0,1}}\right)}^2+{\left({\mathrm{\Omega }}_2-{\mathrm{\Omega }}_{\mathrm{0,2}}\right)}^2\right]+\left(\frac{C}{2}\right){\left({\mathrm{\Omega }}_3-{\mathrm{\Omega }}_{\mathrm{0,3}}\right)}^{2}ds},$$ [S2]

where A is the bending and C is the torsional rigidity.

The polymorphic states of the flagellum can be characterized by their equilibrium helical parameters ${\mathrm{\Omega }}_0=\left(0,{\kappa }_0,{\tau }_0\right)$. Transitions between the states are obtained by local minimization of the free energies for the different polymorphic states (38). From the observations, we can unambiguously deduce only two states, one corresponding to the initial helix during swimming, and the other to the state with the flagellum wrapped around the cell. Further states could be added as well, but without independent evidence for their existence and parameters, their addition has an element of arbitrariness. We label the two conformational states S for the stretched rest state and C for the coiled state around the cell. For each state, the curvature ${\kappa }_0^{S,C}$ and torsion ${\tau }_0^{S,C}$ are related to the helix radius $R_{S,C}$ and pitch $P_{S,C}$ by Eq. S1. For the quadratic deviations, we take the same elastic coefficients A and C, because we do not have independent numbers for the different equilibrium states. The flagellum is assumed to relax locally to the configuration with minimal free energy:

$${\mathrm{ℱ}}_K=\underset{0}{\overset{L}{{\displaystyle \int }}}\min \left(f_K^S\left(\mathrm{\Omega }\left(s\right)\right),f_k^C\left(\mathrm{\Omega }\left(s\right)\right)+{\delta }_C\right)ds,$$ [S3]

with ${\delta }_C$ indicating the energy difference between coiled and stretched state.

To control the amount of stretching of the flagellum, a global harmonic spring potential is added:

$${\mathrm{ℱ}}_S=\left(K/2\right)\underset{0}{\overset{L}{{\displaystyle \int }}}{\left(\partial \mathbf{r}/\partial s\right)}^{2}ds,$$ [S4]

with an elastic constant that keeps the variations in length within 0.1%.

The elastic forces follow from variational derivative $\delta \mathrm{ℱ}/\delta r$ of the combined functional ${\mathrm{ℱ}}_K+{\mathrm{ℱ}}_S$. In the numerical representation, the flagellum is divided into N discrete segments that are characterized by a position ri and a local tripod of unit vectors [f⁽ⁱ⁾, v⁽ⁱ⁾, u⁽ⁱ⁾] to keep track of the torsional state of the flagellum. The points are distributed uniformly along the flagellum, so that each segment has a length h = L₀/N, where L₀ is the contour length of the flagellum. The unit vectors u are related to the positions by ${\mathbf{u}}_i=({\mathbf{r}}_{i+1}-{\mathbf{r}}_i)/|{\mathbf{r}}_{i+1}-{\mathbf{r}}_i|$. The vectors fi for the initial helix configuration are obtained from the relation ${\mathbf{f}}_{\mathbf{i}}=({\mathbf{u}}_{i-1}\times {\mathbf{u}}_i)/\text{sin}\left({\theta }_i\right)$, where θi is the angle between segment i − 1 and i. For each time step of the simulation, fi is adjusted following the procedure proposed by Chirico and Langowski (53). The tripod is completed with the vector ${\mathbf{v}}_i={\mathbf{u}}_i\times {\mathbf{f}}_i$.

The local strain Ω for each segment is calculated according to the following:

$$\begin{array}{ccc}{\Omega }_1^i& =& -\frac{{\theta }_i}{\sin {\theta }_i}{\mathbf{v}}_i\cdot {\mathbf{u}}_{i+1},\\ {\Omega }_2^i& =& \frac{{\theta }_i}{\sin {\theta }_i}{\mathbf{f}}_i\cdot {\mathbf{u}}_{i+1},\\ {\Omega }_3^i& =& {\varphi }_i,\end{array}$$ [S5]

where ${\varphi }_i$ is the local twist angle,

$$\text{sin}{\varphi }_i=\text{cos}{\theta }_i\left({\mathbf{v}}_i\cdot {\mathbf{f}}_{i+1}\right)-\left({\mathbf{v}}_i\cdot {\mathbf{u}}_{i+1}\right)\left({\mathbf{u}}_i\cdot {\mathbf{f}}_{i+1}\right)+\frac{\left({\mathbf{f}}_i\cdot {\mathbf{u}}_{i+1}\right)\left({\mathbf{u}}_i\cdot {\mathbf{v}}_{i+1}\right)}{1+\text{cos}{\theta }_i}.$$ [S6]

The derivative of the free energy for the stretching force is obtained analytically, so that, for instance, the force acting on segment i is given by the following:

$${\mathbf{F}}_s^i=-K\left[\left(L_i-L_0\right){\mathbf{u}}_i-\left(L_{i+1}-L_0\right){\mathbf{u}}_{i+1}\right],$$ [S7]

whereas the derivatives of the free energy corresponding to bending and twisting forces are calculated by finite differences.

The flagellum’s rotation is driven by a constant motor torque M₀, applied to the first segment. To account for the effects of the bacterial hook, which is much more flexible than the flagellum (24), this segment is allowed to rotate freely and thereby transmit the torque to the following segments. The dynamics of the motor segment are described by the following:

$${\omega }_0={\mu }_0\left[{\mathbf{M}}_0^z+{\mathbf{M}}_0^u-A\left[\left({\Omega }_1-{\Omega }_{\mathrm{0,1}}\right){\mathbf{f}}_0+\left({\Omega }_2-{\Omega }_{\mathrm{0,2}}\right){\mathbf{v}}_0\right]-C\left({\Omega }_3-{\Omega }_{\mathrm{0,3}}\right){\mathbf{u}}_0\right],$$ [S8]

where the total torque is split between a component parallel the axis of the motor ${\mathbf{M}}_0^z=M_0(\sqrt{1-{\alpha }^2{\text{sin}}^2{\varphi }_m}-\alpha \text{cos}{\varphi }_m){\mathbf{e}}_z$, and one parallel to the first segment, ${\mathbf{M}}_0^u=\alpha M_0{\mathbf{u}}_1$, with the parameter α controlling the relative contributions. ${\varphi }_m$ is the angle between the tangential motor segment u₀ and the first filament segment u₁. Finally, µ₀ is the motor segment’s self-mobility, which depends of the rotational and the translational friction. The boundary conditions on the final segment are that no external torque is applied so that it is torque free.

In addition to the elastic forces, we have to model the interactions with the cell body, and also between segments of the flagellum, because the deformations become very large and parts of the flagellum come into mechanical contact. The cell body is modeled as a cylindrical object of radius R_cell = 0.45 µm that is sufficiently long that the flagellum does not pass underneath it. In the images, a length H_cell = 3 µm is shown. The flagellum is assumed to be 20 nm thick, and distances between approaching segments are computed following a procedure proposed by Adhyapak and Stark (54). In both cases, the repulsion between the segments of the flagellum and other segments or the cell body was modeled with a Lennard-Jones–type potential, truncated at its minimum, so that the forces vary continuously,

$${\mathrm{\Phi }}_c=\{\begin{array}{cc}ϵ\left[{\left(r_m/r\right)}^{12}-2{\left(r_m/r\right)}^6\right],& \text{if}\hspace{0.17em}r\le r_m\\ 0,& \text{otherwise}\end{array}$$ [S9]

where r_m is either the cell radius or the radius of the filament and is the strength of the potential.

For the frictional forces, we use resistive force theory (36). The local motion of the flagellum’s segments is characterized by three local friction coefficients (36) that depend on the geometry of the flagellum:

$${\gamma }_{\perp }=\frac{4\pi \eta }{\text{ln}\left(0.09l/r_f\right)+1/2}$$ [S10]

is the friction coefficient for motion perpendicular to the flagellum’s centerline, where η is the viscosity, $r_f$ is the radius of the filament, and $l=\sqrt{4{\pi }^2{R}^2+P^2}$ is the contour length of one helical turn. The tangential friction coefficient is as follows:

$${\gamma }_{\parallel }=\frac{2\pi \eta }{\ln \left(0.09l/r_f\right)},$$ [S11]

and the friction encountered by the filament during rotation is characterized by the following:

$${\gamma }_r=4\pi \eta r_f^2.$$ [S12]

The friction coefficients and the mobilities µ_t and µ_r that enter in the equations of motion are related by the following:

$${\mu }_t={\mathbf{u}}_i\otimes {\mathbf{u}}_i/{\gamma }_p+\left(1-\hspace{0.17em}{\mathbf{u}}_i\otimes {\mathbf{u}}_i\right)/{\gamma }_n,$$ [S13]

and µ_r = 1/γr. The translational equation of motion for segment i is then obtained from the elastic forces Fel (2, 3) the stretching force Fs (8) and the repulsive forces Fc and Ffl, resulting from filament–cell and filament–filament interactions (10):

$$\frac{\partial {\mathbf{r}}_{\mathbf{i}}}{\partial t}={\mu }_t\left({\mathbf{F}}_{\mathbf{i},\mathbf{e}\mathbf{l}}+{\mathbf{F}}_{\mathbf{i},\mathbf{s}}+{\mathbf{F}}_{\mathbf{i},\mathbf{c}}+{\mathbf{F}}_{\mathbf{i},\mathbf{f}\mathbf{l}}\right).$$ [S14]

The change in the torsion angle ${\varphi }_i$ of segment i depends on the elastic torque Mel only:

$$\frac{\partial {\varphi }_i}{\partial t}={\mu }_r{M}_{i,el}.$$ [S15]

To achieve high accuracy while keeping the computational costs down, the equations of motions were integrated using the Cash–Karp method (55), a high-order Runge–Kutta integrator with embedded error estimation and steps size control. During each partial integration step, the segment positions are updated according to $r_i(t+h_t)=r_i\left(t\right)+h_t{v}_i$, where and h_t is the partial step size. Using the new positions and velocities ${\mathbf{v}}_i=\partial {\mathbf{r}}_i/\partial t$, the attached tripods are aligned in a second step, following the procedure proposed by Chirico and Langowski (53).

As initial conditions for the simulations, we took a left-handed helix with P^S = 1.91 µm and R^S = 0.315 µm in accordance with observations, resulting in τ^S = 1.59/µm and κ^S = 1.64/µm. We adapted the helix parameters of the second state to the parameters of the screw, namely, R^C = 0.473 µm and P^C = 1.44 µm. The contour length of the flagellum was set to Lc = 6 µm, corresponding to two helical turns. The discretization length is h = 0.15 µm, comparable to the values taken by Vogel and Stark (35). For the elastic constants, no direct measurements of A and C have been reported so far. Although the flagellum’s crystal structure differs from that of well-studied organisms like E. coli, we anticipate that its mechanical properties will not differ significantly from that of E. coli, and hence choose the values A = C = 3.5 pN⋅µm² in accordance to values obtained by Darnton and Berg (16). We also explored values between A = C = 2.5 pN⋅µm² and A = C = 4 pN⋅µm² to study the influence of the rigidity on the screw formation, without noting significant differences. The various parameters in the model for the flagellum and their values are summarized in Table S4.

Table S4.

The various parameters in numerical model and their values

Parameter	Description	Values
RS	Helical radius, stretched	0.315 µm
PS	Helical pitch, stretched	1.91 µm
κS	Curvature, stretched	1.64/µm
τS	Torsion, stretched	1.59/µm
RC	Helical radius, coiled	0.473 µm
PC	Helical pitch, coiled	1.44 µm
κC	Curvature, coiled	1.71/µm
τC	Torsion, coiled	0.829/µm
Lc	Contour length	6.5 µm
A	Bending rigidity	3.5 pN⋅µm2
C	Twisting rigidity	3.5 pN⋅µm2
K	Stretching stiffness	10,000 pN/µm
Rcell	Cell radius	0.45 µm
Hcell	Cell height	3.0 µm
γ⊥	Friction coefficient, normal to flagellum	2.85 η
γk	Friction coefficient, parallel to flagellum	1.61 η
γr	Rotational friction coefficient	0.0012 η
h0	Segment length	0.125 µm
$\alpha$	Relative motor contribution along first segment	0.25
$M_0$	Motor torque	7.6 pN⋅μm
δc	Energy difference between states	0.1 pN

To probe the effects of the polymorphic transitions, we also did simulations with a single equilibrium configuration. They also show the formation of the screw, but require stronger torque and need more time to wrap the flagellum around the cell. We anticipate that further polymorphic states will similarly assist the formation of the screw but will not bring about qualitative changes.

Conclusions

Flagella-mediated movement is a common means of locomotion for bacteria and has previously been demonstrated to mediate swimming through liquid environments or swarming across surfaces. We have shown here that, in polarly flagellated species, these organelles of locomotion can, in addition to regular planktonic swimming through liquids or swarming across surfaces, provide a third type of movement, a screwing motion through structured environments. We also show that screwing is an efficient means to release cells that have been trapped in narrow passages. This flagellar behavior is an example of “failure turned into function” (42) by a biological system, and, given the wide range of monopolarly flagellated bacterial species (43), we expect it to be a common mode of escape or movement among bacteria in structured environments.

Materials and Methods

Bacterial Strains.

Bacterial strains and plasmids are summarized in Tables S1 and S2. Construction of plasmids and genetically modified strains of S. putrefaciens CN-32 was essentially carried out as previously described (44, 45). Detailed information on strain construction, growth conditions, and media is provided in SI Materials and Methods.

Visualizing Flagellar Filaments.

To visualize the flagellar filaments, maleimide-ligated dyes were coupled to surface-exposed cysteine residues, which were specifically introduced into the flagellins, FlaA and FlaB, of the S. putrefaciens CN-32 polar flagellum as previously described (46, 47). A number of motility controls ensured that the modification did not negatively affect cell motility (SI Materials and Methods). Cells of an exponentially growing LB culture (OD₆₀₀, 0.6) were harvested by centrifugation (1,200 × g, 5 min, room temperature) and resuspended in 50 µL of PBS. For all cell-handling steps, the tip of the pipette tip was cut to prevent shearing off flagellar filaments. A volume of 0.5–1 µL of Alexa Fluor 488 C5 maleimide fluorescent dye (Thermo Fisher Scientific) was added, and the cell suspension was incubated in the dark for 15 min. Cells were sedimented again and carefully washed once with 1 mL of PBS to remove residual unbound dye. After final resuspension in LM100 medium in an appropriate volume (usually to reach a final OD₆₀₀ of 0.2), the cells were kept shaking in the dark until microscopy, but never longer than 1 h. If necessary, LM100 medium was supplemented with Ficoll 400 for final resuspension. Ficoll 400 was always diluted to the appropriate concentration from a 50% (wt/vol) stock solution in LM. After coupling of the maleimide fluorescent dye, the cells were carefully washed before microscopic analysis.

For microscopy in bulk medium (always about 100 µm away from the glass surface), a 250-µL aliquot was loaded on a swim slide [coverslip fixed on a microscope slide by four silicone droplets (Baysilone; VWR International) to generate a space of about 1 mm]. For microscopy in structured environments, a 1- to 3-µL aliquot was spotted on an agarose slide and topped with a coverslip before the liquid was taken up by the agarose surface. Agarose slides were made by pipetting hot LM100 medium with 1% (wt/vol) agarose between a microscope slide and a coverslip, both separated by two microscope slides as spacers. After solidification, the coverslip and both microscope slide spacers were removed, leaving an uneven surface on the microscopic scale (Fig. S1). Movies were taken at room temperature at a custom microscope setup (Visitron Systems) with a Leica DMI 6000 B inverse microscope (Leica) equipped with a pco.edge sCMOS camera (PCO), a SPECTRA light engine (lumencor), and an HCPL APO 63×/1.4–0.6 objective (Leica) using a custom filter set (T495lpxr, ET525/50m; Chroma Technology). Usually, 200–500 frames were taken with an exposure time of 5 ms as a compromise between temporal resolution and optical contrast. Image processing and analysis were carried out using the ImageJ distribution Fiji (48). Cells were counted using the cell counter plugin, and swimming-speed measurement was done using the TrackMate (semiautomatic) or MTrackJ (manual) plugin. Details on the statistical analysis can be found in SI Materials and Methods.

Numerical Model for the Flagellum.

The equations, potentials, parameters, and method of integration for the numerical simulations are given in SI Materials and Methods.