Influence of Cholesterol on the Oxygen Permeability of Membranes: Insight from Atomistic Simulations

Abstract

Cholesterol is widely known to alter the physical properties and permeability of membranes. Several prior works have implicated cell membrane cholesterol as a barrier to tissue oxygenation, yet a good deal remains to be explained with regard to the mechanism and magnitude of the effect. We use molecular dynamics simulations to provide atomic-resolution insight into the influence of cholesterol on oxygen diffusion across and within the membrane. Our simulations show strong overall agreement with published experimental data, reproducing the shapes of experimental oximetry curves with high accuracy. We calculate the upper-limit transmembrane oxygen permeability of a 1-palmitoyl,2-oleoylphosphatidylcholine phospholipid bilayer to be 52 ± 2 cm/s, close to the permeability of a water layer of the same thickness. With addition of cholesterol, the permeability decreases somewhat, reaching 40 ± 2 cm/s at the near-saturating level of 62.5 mol % cholesterol and 10 ± 2 cm/s in a 100% cholesterol mimic of the experimentally observed noncrystalline cholesterol bilayer domain. These reductions in permeability can only be biologically consequential in contexts where the diffusional path of oxygen is not water dominated. In our simulations, cholesterol reduces the overall solubility of oxygen within the membrane but enhances the oxygen transport parameter (solubility-diffusion product) near the membrane center. Given relatively low barriers to passing from membrane to membrane, our findings support hydrophobic channeling within membranes as a means of cellular and tissue-level oxygen transport. In such a membrane-dominated diffusional scheme, the influence of cholesterol on oxygen permeability is large enough to warrant further attention.

Introduction

Optimal bioavailability of O₂ within tissues is crucial for aerobic metabolism. Timely delivery of sufficient oxygen is essential to maintaining a favorable cellular energy status, yet excessive oxygenation can be toxic (1). The normal oxygen level of tissues varies substantially according to the tissue type (2). Some cells normally occupy low-oxygen niches, notably including embryonic and hematopoietic stem cells (3, 4) as well as fiber cells of the eye lens—which shelter the lens nucleus from oxidative damage and cataracts (5, 6). Aberrant tissue hypoxia contributes significantly to pathological conditions, including heart disease, obesity, diabetes, and cancer (7, 8, 9, 10, 11). Clinical oxygenation of tumors is key to the efficacy of radiation therapy and to the action of many chemotherapeutics (12, 13).

All of the abovementioned pathologies are also linked to hyperabundance of cholesterol (14, 15, 16, 17), which is ubiquitous in animal cell plasma membranes. Most normal tissues have cholesterol content in the range 20–40 mol % (equivalent to percentage by number of molecules), though some have higher levels and may even incorporate “cholesterol bilayer domains” (18, 19, 20). Notably, red blood cell membranes normally contain 50 mol % cholesterol (1:1 ratio with phospholipid), and this level is apparently exceeded in hypercholesterolemia (14, 21).

As a very small, nonpolar molecule, O₂ is generally thought to diffuse readily across cellular membranes, and no other transport mechanism is well established. Whether cellular membranes can limit O₂ diffusional flux under any circumstance is not fully understood. Further knowledge of the influence of membrane composition on oxygen distribution, diffusivity, and permeability will help to clarify whether and to what extent membranes can contribute to cellular hypoxia.

Previous biological, biophysical, and computational work strongly suggests that cholesterol can reduce membrane oxygen permeability (7, 14, 19, 22, 23, 24, 25), but the magnitude, mechanism, and significance of the effect require clarification. One recent computational study implies that cholesterol may not decrease the membrane permeability to gases, even when present at very high levels (26). Extensive simulation work on membrane gas transport has established a strong theoretical and methodological basis for further study (25, 26, 27, 28, 29, 30, 31).

We seek to clarify ambiguities in interpreting the experimental studies and to augment the existing theoretical framework, using all-atom molecular dynamics (MD) simulations conducted without restraints and taking advantage of recent advances in force-field quality as well as accessibility of long simulation times. These simulations offer the benefit of precisely controlled membrane composition, along with atomic resolution insight and the capacity to reproduce experimental observables. We use simplified bilayer models, consisting of cholesterol in combination with 1-palmitoyl,2-oleoylphosphatidylcholine (POPC), a neutral phospholipid found abundantly in eukaryotic membranes (32). Given the availability of electron paramagnetic resonance (EPR) oximetry data for the cholesterol bilayer domain observed in cholesterol-saturated membranes (24), we also mimic this noncrystalline, 100% cholesterol system. We calculate transbilayer permeabilities and free energy profiles as well as estimate oxygen transport parameter curves for comparison with EPR measurements. This study focuses on characterizing transbilayer localization and movement of oxygen but also considers the potential for lateral transport within the plane of the membrane.

Materials and Methods

Simulations

General approach. This work used tensionless MD simulations with the graphics processing unit (GPU)-accelerated/CUDA implementation (single precision fixed point model) of the software Amber14 (33, 34). The featured production simulations used the well validated, all-atom Lipid14 force field and cholesterol extension, along with the TIP3P water model (35, 36, 37). The temperature was maintained at 310 K and the pressure at 1 atm with anisotropic scaling and a 1-ps relaxation time. Bonds to hydrogen were constrained with the SHAKE algorithm, at a tolerance of 10⁻⁶ (38). The simulation timestep was 2 fs. Periodic boundary conditions were applied using particle mesh Ewald to calculate nonbonding interactions (39), with a cutoff distance of 10 Å. Coordinate wrapping was turned on, and the translational center-of-mass motion was removed every 2 ps. Other parameters were set to their default values in Amber, except where noted below. Individual runs were limited to 1 ns, after which Amber restart files were used to initiate subsequent runs.

Initial structures. All systems were constructed with the CHARMM-GUI membrane builder (40). Each included a total of 128 lipids, with 64 lipids in each leaflet and equal distribution of POPC and cholesterol across the leaflets. Further compositional details are given in Table 1.

Table 1.

Composition of Simulation Systems: Number of Molecules

Cholesterol Content %	POPC	Cholesterol	H2O	O2
0	128	0	4445	35
12.5	112	16	4446	34
25	96	32	4447	33
37.5	80	48	4448	32
50	64	64	4449	31
62.5	48	80	4450/4451a	30/29a
100b	0	128	4453/4454a	27/26a

Two independent trajectories were run for each system composition, except where noted.

^aDifferent number of O₂ molecules needed to reach 200 mM, given distinct equilibrated system volumes.

^bFour independent trajectories.

Premixing simulations. Two replicates for every bilayer composition were premixed for 500 ns at 310 K, using the GAFFlipid force field (41) and the cholesterol parameters from Lipid11 (42). These premixing simulations enabled substantial divergence of the duplicate trajectories as well as substantial lateral reorganization of the cholesterol and POPC (confirmed visually). Binary and more complex lipid systems require long mixing times, to allow for slow lateral diffusion of the lipids within the plane of the bilayer (43). During premixing, the Langevin thermostat (44) was used, with a collision frequency of 1.0 ps⁻¹, and a unique pseudorandom number generator seed was assigned for each run.

Oxygen modeling. Force-field parameters for O₂ were developed in our laboratory. As described in Shea et al. (45), the bond length was set to 1.21 Å, with a vibrational force constant of 849.16 kcal/mol·Å² and all other parameters defined the same as the Lipid 11 carbonyl oxygen (oC) atom type, which originated with the General Amber Force Field (GAFF) (46). O₂ molecules were introduced into the simulation systems by replacing water molecules to reach a concentration of 200 mM O₂ for the entire water-lipid system. Whereas the resulting O₂ concentration in the water layer was several hundred times the expected concentration in atmosphere-equilibrated water (∼200 μM), the simulated concentration allows the oxygen molecules to diffuse independently while facilitating rapid sampling of configurational space. We confirmed that the free energy profile was unchanged upon reducing the O₂ level by a factor of 2 in a POPC bilayer simulation. Further reducing the O₂ concentration to a single O₂ molecule in the POPC simulation system gave a similar free energy profile, though less resolved due to insufficient sampling (unpublished data).

Independent trajectories. Every bilayer composition was simulated in duplicate, starting with the final structures of separate premixing simulations (trajectories 1 and 2). Trajectory 1 for 25 mol % cholesterol produced a bilayer with substantial curvature, which confounded the analyses involving bilayer depth (z coordinate). We, thus, initiated a 300-ns production trajectory 2a, which diverged from trajectory 2 at the point of adding oxygen. In the same manner, we ran trajectories 1, 1a, 2, and 2a for 100% cholesterol, generating four separate 300-ns production simulations for improved sampling.

Further equilibration and production. The high-quality Lipid14 force field and associated cholesterol parameters were used for the production simulations (36, 37). The premixed bilayers were further equilibrated for 200 ns, using Langevin temperature control and the Monte Carlo barostat, as implemented in Amber14 (ambermd.org/doc12/Amber14.pdf). Oxygen was introduced, as described above. Then, each system was energy minimized for 20,000 steps, followed by heating from 100 to 310 K with weak restraints on the O₂ molecules. The restraints were released gradually, while equilibrating over 750 ps. For production, we used the Berendsen thermostat (47) and the Monte Carlo barostat; we have confirmed that this thermostat/barostat combination gives free energy curves and permeability coefficients similar to those obtained with Langevin temperature regulation with a collision frequency of 1.0 ps⁻¹ (unpublished data). Each trajectory was run without restraints for 300 ns, writing coordinates every 1 ps.

Permeability and diffusivity

For insight into the kinetics of oxygen diffusion, we estimated oxygen permeability coefficients for the membrane, P_M, using the following equation:

$$P_M=\frac{{\text{Φ}}_{\text{esc}}}{2}\left(\frac{1}{N_w}\right).$$ (1a)

P_M is a membrane attribute that relates the diffusional flux, J, to the difference in the oxygen concentration in water, C_w, on either side of the membrane, where J = −P_M (C_w2 – C_w1). In Eq. 1a, Φ_esc is the escape rate in molecules per second, determined by counting the number of times O₂ molecules cross an escape threshold, ±h/2, on either side of the bilayer, after first crossing the bilayer midplane. At equilibrium, Φ_esc equals the rate of entry into the bilayer center and is twice the rate of full permeation across the membrane. The parameter N_w is the average O₂ population per 1 Å bin along z in the solvent region, expressed as molecules per centimeter. We estimated the uncertainty for P_M by applying common rules of error propagation to the standard deviations for the terms of the equation. Namely, a sample standard deviation was calculated for Φ_esc and N_w over two independent trajectories (or four for 100% cholesterol). (1a), (1b) is a simplified form of the relation

$$P_M={\text{Φ}}_{\text{esc}}\left(\frac{1}{2A_{\text{bil}}}\right)\left(\frac{1}{C_w}\right),$$ (1b)

where 2A_bil is the average interfacial area, equaling twice the bilayer area, and C_w is the average concentration of O₂ in the water. The bilayer area, A_bil, is also used in calculating C_w = N_w/A_bil and, thus, cancels algebraically, giving (1a), (1b). Another research group has used a similar approach to calculating P_M from simulation data (28, 48).

We defined entry and escape thresholds by identifying minima in the free energy profiles near the bilayer center and at the bilayer-water interface. An entry threshold of ±1 Å from the center was used for all bilayers except 100% cholesterol, for which the threshold was ±3 Å. The escape thresholds, along with the observed escape rates, are provided in Table 2, in the Results and Discussion section. At all bilayer cholesterol levels, plots of O₂ molecule escapes versus time are essentially linear throughout the 300 ns (Fig. S1). For pure POPC, the plots of O₂ molecule escapes per time deviate slightly from linearity after 250 ns; thus, we calculated the permeability for both POPC trajectories using the number of O₂ escapes over 250 ns. For all other bilayers, we used the total number of O₂ escapes over 300 ns.

Table 2.

Oxygen Permeability, Partitioning, and Related Data for Bilayers Composed of POPC and/or Cholesterol

Cholesterol Content %	PM (cm/s)	Experimental PM (cm/s)	PM/Pwa	Bilayer Thickness, DHH (Å)	Escape Threshold, ±h/2 (Å)	Escape Rate, Φesc (×10−4 molecules/ps)	O2 Population in Water, Nw (×10−2 molecules/Å)	[O2] in Water, Cw (mM)	Partition Coefficient, KP
0	52 ± 2	157.4b	1.12 ± 0.04	38.0	±28	7.96 ± 0.06	7.60 ± 0.23	30.50 ± 0.93	8.0 ± 0.5
12.5	47 ± 2	—	1.09 ± 0.05	39.8	±30	8.15 ± 0.26	8.65 ± 0.32	39.11 ± 1.46	6.4 ± 0.4
25	48 ± 3	—	1.11 ± 0.06	44.0	±30	7.97 ± 0.09	8.32 ± 0.44	42.64 ± 2.28	6.2 ± 0.1
37.5	46 ± 2	—	1.10 ± 0.05	44.5	±31	8.40 ± 0.00	9.08 ± 0.38	51.58 ± 2.15	5.2 ± 0.1
50	43 ± 3	49.7b	0.99 ± 0.06	45.5	±30	8.12 ± 0.02	9.47 ± 0.58	57.78 ± 3.51	5.0 ± 0.0
62.5	40 ± 2	—	0.92 ± 0.04	45.0	±30	7.03 ± 0.05	8.81 ± 0.38	56.10 ± 2.39	5.1 ± 0.0
100c	10 ± 2	15.9d	0.20 ± 0.04	24.3	±26	1.58 ± 0.28	7.55 ± 0.46	51.41 ± 3.12	6.9 ± 1.1

Simulations at 37°C. Shown are mean values ± SD.

^aP_w calculated using Eq. 4 with the experimental D_w value of 2.60 × 10⁻⁵ cm²/s.

^bProbe-based spin-relaxation EPR experiments at 35°C (19).

^cMetastable mimic of the noncrystalline cholesterol bilayer domain.

^dProbe-based spin-relaxation EPR experiments at 25°C (24).

Equations 1a and 1b enable calculation of permeability directly from unrestrained simulation data. Given sufficient sampling, the P_M values calculated this way should be highly accurate, as they implicitly account for all degrees of freedom that impact the molecular dynamics. A more common method of calculating bilayer permeability applies the “inhomogeneous solubility diffusion model” (27, 30, 49), which describes P_M as directly proportional to the concentration and diffusivity of a solute at a given depth within the bilayer. In this model, P_M is the inverse of the resistance to permeation, R_P, which corresponds with the area under the curve produced by the inverse of the product of the bilayer depth-dependent O₂ concentration and diffusivity curves, C(z) and D_z(z), as follows:

$$P_M=\frac{1}{R_P}={\left(C_w\sum _{-h/2}^{+h/2}\frac{1}{C\left(z\right)D_z\left(z\right)}\Delta z\right)}^{-1}.$$ (2)

D_z(z) is also sometimes called D_⊥(z), as it represents the diffusivity component perpendicular to the bilayer. Whereas C(z) is obtained easily for O₂ from unrestrained simulation data, accurate calculation of D_z(z) is more complex and usually requires restrained simulations (30). Bilayer depth-dependent diffusivity values can differ substantially, even when calculated with state-of-the-art methods (50). The parameter Δz is the length increment used in calculating C(z) and D(z). The values ±h/2 define the boundaries of the bilayer along the z coordinate and correspond with the entry and escape thresholds (Table 2 in Results and Discussion). We find P_M values calculated with this method to be highly dependent on the quality of the D_z(z) curve (unpublished data), which we have not determined with high accuracy.

We estimated the diffusivity from our unrestrained simulation data using the Einstein relation:

$$D=\frac{1}{nt}\langle {\left(r_t-r_0\right)}^2\rangle .$$ (3)

Here, n is the number of dimensions considered; t is the time increment; and 〈(r_t − r₀)²〉 is the mean-squared displacement over the time increment, which was 1 ps in our study. This method has been used frequently but is known to yield low accuracy in the more ordered regions of the membrane (30, 50). We reset the reference value, r₀, every picosecond (following (27)) and calculated D(z) curves from displacements binned according to the mean z position traversed over each picosecond. The extensive sampling achieved with 300,000 time points (300 ns) provides reasonable estimates of D(z), as evidenced by comparison with more accurate curves calculated for dipalmitoylphosphatidylcholine by Gaalswyk et al. (50). For the oxygen transport parameter calculations below, we used diffusivity curves reflecting O₂ displacement in all three dimensions, D_xyz(z), assuming that EPR spin-label probes would not specifically distinguish the direction of O₂ diffusional motion.

To find the permeability of water layers of varying thickness, h, we used the relationship

$$P_w=\frac{D_w}{h}.$$ (4)

We extrapolated the diffusion coefficient for O₂ in pure water at 37°C, D_w = 2.60 × 10⁻⁵ cm²/s, from a set of experimental diffusivity values near this temperature (51). The viscosity of TIP3P water is known to be substantially lower than that of real water, resulting in overestimation of solute diffusivity by a factor of 2–3 (30). Thus, we have used Eq. 4 with the experimental D_w value above for all calculations involving P_w.

Oxygen transport parameter

Widomska et al. (19) and Raguz et al. (24) have published EPR oximetry data for bilayers composed of POPC alone, POPC with 50 mol % cholesterol, and the noncrystalline cholesterol bilayer domain. We conducted a detailed comparison of our simulations with the EPR data. Specifically, we calculated the depth-dependent oxygen transport parameter, which is a quantitative measure of the collision rate of nitroxide spin-label probes with oxygen and reflects the difference between the spin-lattice relaxation times of the probes in the presence and absence of oxygen. The oxygen transport parameter, W(z), is thought to correspond to the product of the depth-dependent oxygen concentration and diffusivity, scaled by a factor, A, as follows:

$$\begin{array}{l}W\left(z\right)=AC\left(z\right)D\left(z\right),\hfill \\ A=8\pi p{r}_0.\hfill \end{array}$$ (5a)

The factor A incorporates the interaction distance, r₀, between oxygen and the nitroxide radical of a given spin label and the probability, p, that a collision of oxygen with the probe will be observable. We assumed the values r₀ = 4.5 Å and p = 1, as in the experimental studies (19, 24, 52). For the simulations, we calculated W(z) curves using the following:

$$W\left(z\right)=A{X}_{p}c\left(z\right)D\left(z\right).$$ (5b)

This equation accounts for the abundance of the EPR spin-label probes, scaling the raw simulation data by the mole fraction of probe, X_p, utilized in the experiments. We used X_p values of 0.010 for the pure POPC bilayer and 0.005 for the 50 mol % cholesterol bilayer—assuming 1 mol % spin label for the POPC lipid fraction (52). For our 100% cholesterol mimic of the cholesterol bilayer domain, we used X_p = 0.005, assuming that the reference experiments used 1 mol % spin label for the cholesterol fraction of lipid mixtures where 75% of the molecules were cholesterol and where ∼67% of the cholesterol and associated spin label was expected to reside in cholesterol-only structures (24). Thus, for 100% cholesterol, X_p = (0.010)(0.75)(0.67) = 0.005. The aforementioned X_p values produce internal consistency in the oxygen transport parameter curves, as the calculated W(z) value in the water layer is approximately equal for the pure POPC, 50 mol % cholesterol, and 100% cholesterol simulation systems (Fig. 3). It should be noted that we have not accounted for the aqueous probe concentration and, thus, do not expect the simulation W(z) values for the water layer to be quantitatively accurate. Equation 5b uses a fractional, depth-dependent O₂ concentration, designated c(z), which is the O₂ population per 1 Å bin, N(z), divided by the total O₂ population, N_total, and the average bilayer area. Namely, c(z) = N(z)/(N_total × A_bil). The resulting W(z) values have units of reciprocal time, μs⁻¹.

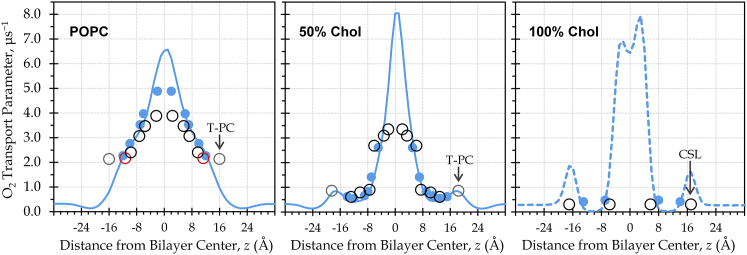
Figure 3.

Calculated oxygen transport parameter curves show strong agreement with EPR measurements and enhanced O₂ transport parameter near the bilayer center. Blue lines show the oxygen transport parameter, W(z), calculated from a single simulation trajectory per bilayer composition, using Eq. 5b. Blue dots represent the oxygen transport parameter as sensed by atoms imitating the spin-label probes used in EPR oximetry; each dot corresponds with a W_i value calculated using Eq. 5c. Open circles represent published experimental EPR oximetry values (19, 24, 52). Red circles highlight the probes near carbon 5 of the POPC oleoyl tail. Gray circles mark the T-PC probes meant to measure oxygen in the headgroup region. T-PC and the cholesterol CSL probe are labeled to indicate possible positional uncertainty. To see this figure in color, go online.

To account for the positioning of the spin-label probes, we calculated depth-dependent positional probability distributions, ρ(z), for carbon atoms at depths roughly corresponding with the assumed positions of the nitroxide probes (Fig. S2). Inspired by an approach used for comparing simulations with nuclear magnetic resonance (NMR) measurements (53), we used the ρ(z) data to localize the calculated oxygen transport parameter values to bilayer depths occupied by probe atoms representing the EPR spin labels, according to the following relationship:

$$W_i=A{X}_p\sum _z{\rho }_i\left(z\right)c\left(z\right)D\left(z\right).$$ (5c)

This equation produces a discrete oxygen transport parameter value for each probe, i. The POPC oleoyl tail carbons 5, 7, 10, 12, and 16 represented corresponding spin-label probes for the pure POPC bilayer, whereas the POPC oleoyl tail carbons 5, 7, 9, 10, 12, and 14 represented probes for the 50 mol % cholesterol bilayer. For 100% cholesterol, we used ρ(z) curves with peaks near the edges of the cholesterol ring region of the bilayer, as delineated in the electron density plot (Fig.1 A, below) to represent the cholestane spin label (CSL) and the androstane spin label (24).

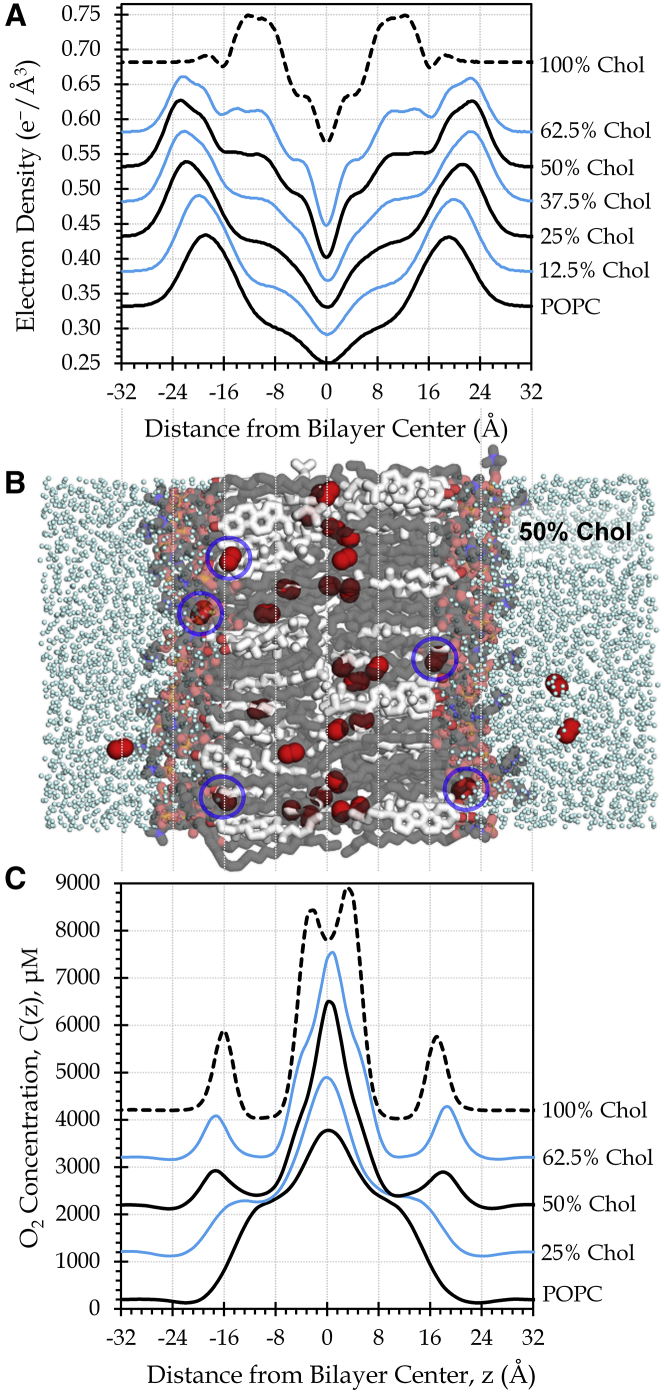
Figure 1.

Membrane cholesterol generates physical barriers and alters the distribution of oxygen. (A) Electron density profiles reflect increasing cholesterol (Chol) content. For clarity, curves are displaced vertically by increments of 0.05 e⁻/ų (or 0.10 e⁻/ų for 100% Chol). (B) This simulation snapshot features a bilayer composed of 50% cholesterol (white carbons) and POPC phospholipid (gray carbons). O₂ is shown as red spheres and water as cyan dots. H atoms are omitted for clarity. PyMOL was used for imaging (83). Blue circles indicate O₂ molecules located in the sub-headgroup surface region. (C) Cholesterol content influences the local O₂ concentration, which has been normalized to 200 μM in the water. Curves are displaced vertically by 1000 μM and smoothed slightly. Data are shown for one simulation trajectory per bilayer composition. To see this figure in color, go online.

Other analyses

Electron density, O₂ concentration, O₂ free energy curves, and histograms of atomic positions were calculated using the AmberTools program CPPTRAJ (54). The free energy was calculated according to the following relation:

$$\Delta G\left(z\right)=-RT\text{ln}\frac{C\left(z\right)}{C_{\text{bulk}}}.$$ (6)

Here, ΔG(z) is the depth-dependent relative free energy for O₂ and is equivalent to the potential of mean force (27), which is often calculated with restraint-based computational methods. R is the ideal gas constant, T is the temperature, and C_bulk is the O₂ concentration in bulk water. With 300-ns production simulations, we obtained well converged free energy profiles using Eq. 6. A partition coefficient, K_P, for each bilayer was calculated as the average over the entire bilayer of the local partition coefficient, K_P(z) = C(z)/C_w. For this calculation, the bilayer boundaries were defined as ±h/2 (values given in Table 2).

Computing resources

This work used the “Maverick” NVIDIA Tesla K40 GPU cluster at the Texas Advanced Computing Center and New Mexico Tech’s “Electra” NVIDIA GeForce GTX-Titan GPU cluster, custom-built by Exxact Corporation (Fremont, CA). Both clusters generally yielded at least 60 ns/day of data for an individual simulation on a single GPU.

Results and Discussion

O₂ accumulation in sub-headgroup surface region

Cholesterol incorporation substantially influences the membrane physical properties. We observe intensified electron density in the range near ±8–16 Å on both sides of the bilayer as the cholesterol content increases (Fig. 1 A). This change reflects close packing of the cholesterol molecules and phospholipid tails along the rigid cholesterol ring system, which generates a physical barrier to oxygen diffusion and alters the local concentration profile of oxygen (Fig. 1 C). Specifically, the oxygen concentration is reduced in the region spanning the cholesterol rings and elevated in the center of the bilayer. This trend is consistent with the findings of prior experimental and simulation studies (22, 26, 55, 56).

The increase of oxygen concentration in the central core of the membrane accompanies reduced electron density in that region, likely due to length mismatch between the flexible cholesterol tails and the tails of the phospholipids (56). Moreover, oxygen accumulates at the surface of the cholesterol-spanning region, beneath the charged headgroups, in mixed POPC-cholesterol bilayers (Fig. 1, C and B, blue circles). A previous simulation study reported positional distribution curves for nitric oxide reflecting similar gas accumulation in the hydrophobic region just below the headgroups (26).

In our study, O₂ accumulation at the sub-headgroup hydrophobic surface corresponds with free energy wells that develop near ±16 Å, on either side of the bilayer center (Fig. 2). The free energy profile of oxygen diffusion is altered more broadly, as new barriers develop in the ring region when cholesterol is present at levels of 50 mol % and above and as these cholesterol-related barriers increase in prominence with greater cholesterol content. The free energy profile shapes and the growth of the barrier in the cholesterol ring region are in agreement with previously reported free energy profiles for nitric oxide (25).

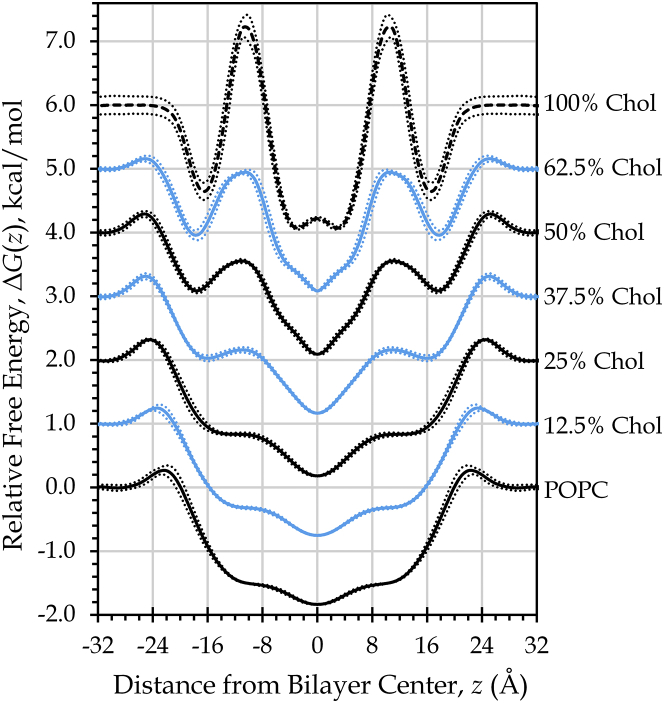
Figure 2.

Internal free energy barriers and wells emerge with rising cholesterol content. Shown are relative depth-dependent free energy profiles for O₂, displaced vertically by 1.0 kcal/mol. Curves show mean ± SD across both bilayer leaflets and two independent simulations (or four for 100% Chol). To see this figure in color, go online.

Oxygen permeability and partitioning

The growth of the cholesterol-related barriers coincides with decreasing permeability, P_M, for bilayers incorporating 50, 62.5, or 100 mol % cholesterol (Table 2). Yet, accumulation of O₂ in the cholesterol-generated hydrophobic surface region seems to compensate for the local loss of oxygen permeability along the cholesterol ring system. A recent permeation study (57) observed that the rate impact of the barrier produced by a local free energy well is essentially canceled by enrichment of the solute concentration at the position of the well. Only the portion of a barrier that rises above the bulk free energy value will tend to reduce the permeability (57). Viewing our free energy curves from this perspective, we expect to see a sizeable change in O₂ permeability only for 100% cholesterol, given that its peak rises substantially above the bulk value in the water (Fig. 2). The calculated P_M values are congruent with this prediction, as we find the permeability of 100% cholesterol to be five times lower than that of pure POPC (Table 2).

We can also predict permeability changes by looking directly at the relative solute concentration. First, consider that the depth-dependent relative free energy is proportional to the natural log of the local solute concentration (Eq. 6). As such, the local concentration will dip below the bulk concentration wherever the free energy peak exceeds the value in bulk water. Equation 2 predicts that the membrane permeability will be directly proportional to C(z)/C_w, the ratio of the O₂ concentration at a given bilayer depth to the concentration in bulk water. Thus, the membrane permeability will tend to be reduced by the occurrence of regions with C(z) values less than C_w, coinciding with local free energy barriers that exceed the bulk water free energy value. Conversely, C(z) values greater than C_w will tend to increase P_M, enhancing the bilayer permeability. From this perspective, the permeability of the 100% cholesterol bilayer declines because C(z) falls below the bulk O₂ concentration throughout the region spanned by the cholesterol rings (Fig. 1 C). In contrast, C(z) does not drop below the bulk value in the cholesterol ring region for the 37.5, 50, and 62.5 mol % cholesterol bilayers, which show much more modest reductions in P_M, compared to pure POPC.

Interestingly, the overall solubility of oxygen in the membrane is reduced with increasing cholesterol-to-POPC ratios, as indicated by the decreasing partition coefficients, K_P, reported in Table 2, which drop from ∼8 for pure POPC to ∼5 for bilayers nearly saturated with cholesterol. This solubility change is also reflected in increased average concentration of O₂ in the water compartment, C_w (Table 2). The reduced partitioning of O₂ into the membrane with rising cholesterol content is consistent with prior simulation work with other solutes, which identified favorable van der Waals contacts among the lipid tails and cholesterol as the major factor governing low solute partitioning within the cholesterol ring-spanning region (25). In accordance with that work and with experimental observations (58, 59), we see increasing POPC tail order (Fig. S3) and bilayer thickness (Table 2) as the membrane cholesterol content rises.

Validation and convergence

The contours and values of our calculated electron density curves (Fig. 1 A) correspond well with experimental curves (59, 60). Likewise, simulation order parameters for POPC with cholesterol (and O₂) closely match solid-state NMR measurements (Fig. S3), and our results are nearly identical to those reported previously for Lipid14 POPC and cholesterol (37, 58). Convergence within and across the simulation trajectories is demonstrated by the linearity of plots of O₂ molecule escapes over time (Fig. S1). Further, symmetry between the two bilayer leaflets in the curves for electron density, O₂ concentration, and free energy signifies ample sampling of the thermodynamic ensemble (Figs. 1, A and C, and 2). Close overlap of curves calculated from the independent simulations indicates convergence to a common result (unpublished data; reflected in the standard deviations shown in Fig. 2). The slower kinetics of O₂ diffusion in 100% cholesterol resulted in less thorough sampling and poorer convergence of the O₂ concentration and free energy curves for this bilayer composition.

Calculation of the oxygen transport parameter, W(z), enables comparison of the simulations with EPR oximetry experiments for pure POPC, 50 mol % cholesterol, and the cholesterol bilayer domain (100% cholesterol) (Fig. 3). The simulation curves (blue lines) were calculated using Eq. 5b, treating W(z) as a scaled product of the depth-dependent O₂ concentration and diffusivity curves. The blue dots represent W_i values calculated according to Eq. 5c, which estimates the O₂ that would be detected by specific probe atoms of POPC or cholesterol at various depths along the bilayer. For POPC, the atoms used for attachment of the doxyl spin-label probes in the EPR experiments were designated to represent the approximate probe positions. It should be noted that the actual EPR probes are somewhat bulky and, thus, are almost certain to deviate from the positions we have approximated. Probability distributions, ρ(z), of the atoms representing the probes are shown in Fig. S2. The designated atoms are meant to represent the EPR spin-label probes, but the actual positions of the experimental probes are not well defined (19). In Fig. 3, published EPR values are shown as open circles located on the z axis at the estimated average probe positions reported in the respective articles (19, 24, 52).

The simulation and experimental oxygen transport parameter values show strong agreement. However, in several cases, our data suggest that the EPR probe positions along the bilayer depth may differ from those approximated in the experimental articles. Notable among these are the cholesterol-derived CSL, as well as the tempocholine (T-PC) probe meant to monitor oxygen in the POPC headgroup region. T-PC is structurally related to the phosphatidylcholine headgroup but is largely nonpolar. For pure POPC, the experimental oxygen transport parameter values are nearly equal for the T-PC probe (gray circles) and the probe placed at carbon 5 (red circles) in the hydrophobic region. Ongoing work will examine the T-PC probe’s behavior by modeling it explicitly. Preliminary simulations indicate that the T-PC probe predominantly samples the nonpolar membrane interior of pure POPC, just below the headgroups (61). This finding is consistent with the observation that the parent TEMPO compound (2,2,6,6-tetramethyl-1-piperidinyloxy) resides relatively near the membrane-water interface in fluid phospholipid membranes (62). For 50 mol % cholesterol bilayers, the close packing of the POPC and cholesterol atoms along the cholesterol ring system may reduce T-PC partitioning into the nonpolar region, providing a more accurate description of the O₂ solubility-diffusion product in the headgroup region. This prediction is supported by evidence that TEMPO experiences reduced partitioning into dipalmitoylphosphatidylcholine membranes at low temperatures (63), where the hydrocarbon tails are ordered and closely packed.

To validate our description of the O₂ concentration in the headgroup region, we pursued the comparison shown in Fig. 4, juxtaposing our POPC concentration curve, C(z), with an experimental O₂ concentration curve generated using ¹³C NMR for another fluid-phase PC phospholipid (53). The shape of the curves is similar in the headgroup region, indicating that the simulation curve accurately represents the O₂ concentration in that vicinity. However, the two curves differ in the water layer O₂ concentration when the maximum peak heights are matched. This difference implies that the oxygen partitioning in our systems is not fully accurate. The bulk water O₂ concentration, C_w, for the simulation system is approximately half that of the experimental system, suggesting that the simulations overestimate partitioning into the bilayer by a factor of 2.

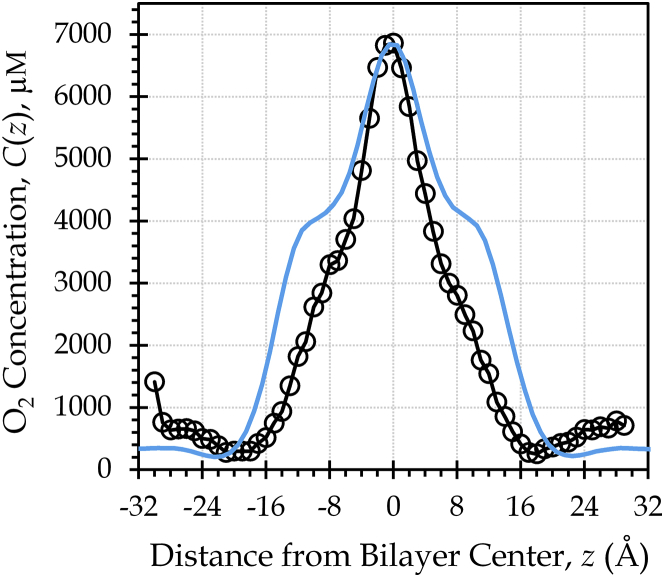
Figure 4.

Comparison with NMR data reveals an accurate O₂ concentration curve shape. A single simulation POPC curve (blue line) is overlaid on an experimental NMR curve for the phospholipid MLMPC at 42°C. Both tails of MLMPC are 14 carbons in length, and one of the tails incorporates a trans double bond (53). The simulation curve is rescaled by matching its maximum peak height to that of the NMR data, to facilitate visual comparison of the curve shapes as well as quantitative comparison of the membrane-water partitioning. To see this figure in color, go online.

Indeed, the oxygen partition coefficient is 8.0 ± 0.5 for the POPC simulation system (Table 2) and 3.3 for the experimental system (calculated from the curve in Fig. 4, by averaging C(z)/C_w in the range −25 to +25 Å). A similar experimental value of 3.9 ± 0.4 was reported for O₂ partitioning between the hydrophobic fraction of egg yolk phosphatidylcholine liposomes and water at 25°C (64). This value is roughly equivalent to a whole-bilayer K_P of 2.9, as the hydrophobic fraction of egg yolk phosphatidylcholine was taken to be 0.75 in the experimental study. Further, we calculate an experimental K_P of 8.2 for hexadecane and water, based on O₂ solubility data at 22°C (65). Given the similarity of hexadecane to phospholipid tails, the hexadecane–water K_P value may be expected to approximate the maximum depth-dependent partitioning in a bilayer system, K_P(z)_max = C(z)_max/C_w. From the concentration data in Fig. 4, K_P(z)_max is 11 for the experimental system (1-myristelaidoyl,2-myristoylphosphatidylcholine (MLMPC)) and 19 for the simulation system (POPC). Altogether, these comparisons suggest that O₂ partitioning into the membrane interior is exaggerated by a factor of 2–3 in our simulations. We expect the membrane permeability to be directly proportional to the ratio C(z)/C_w, as described in Eq. 2. Hence, we infer that the simulation P_M values may be overestimated by a factor of 2–3, due to excess partitioning of O₂ into the hydrophobic interior.

The excess partitioning may arise due to a force-field limitation that manifests as a tendency to overestimate the favorability of O₂ interactions with the phospholipid tails or to underestimate the favorability of O₂–water interactions. A recent study of atomistic O₂ models suggests the need for explicit treatment of electronic polarizability, to describe with quantitative accuracy the thermodynamics of solvating nonpolar species in nonpolar media (66). If the exaggerated partitioning is related to force-field quality or electronic polarizability, we expect that it should influence the cholesterol-containing systems to the same extent as the POPC-only systems. Thus, the relative permeabilities of the bilayers as a function of cholesterol content should be largely unaffected. Future work will address the accuracy of partitioning in both homogeneous and mixed phospholipid/cholesterol systems.

Negligible influence of membrane cholesterol on water-dominated diffusion

We shall now consider our permeability coefficient values, P_M, in comparison with those calculated from depth-dependent EPR resistance to permeation, which is the inverse of the oxygen transport parameter. We calculate a value of 43 ± 3 cm/s for 50 mol % cholesterol at 37°C, similar to the experimental value of 49.7 cm/s at 35°C (19) (Table 2). Our value of 10 ± 2 cm/s for the 100% cholesterol bilayer also agrees reasonably well with the EPR estimate of 15.9 cm/s at 25°C for the noncrystalline cholesterol bilayer domain (24). However, we find a substantially lower permeability for POPC (52 ± 2 cm/s) than expected from EPR (157.4 cm/s at 35°C (19)). We attribute the difference to a possible underestimation of the EPR resistance to permeation, 1/W(z), in the headgroup region for the POPC bilayer because of oversampling of the hydrophobic tail region by the T-PC probe. A value near 52 cm/s would place the oxygen permeability of a POPC bilayer close to that of a water layer of the same thickness, P_w = 46 cm/s at 37°C. Given that our simulations seem to overestimate partitioning into the membrane, the actual P_M value may be somewhat lower than P_w.

The bilayer thickness varies according to cholesterol content, as observed in both the escape threshold values, ±h/2, and the electron density headgroup-to-headgroup peak distances, D_HH (Table 2). To account for the influence of the thickness on the P_M value, we evaluated the ratio of the membrane permeability to the permeability of a water layer of the same thickness, P_M/P_w. Here, we used the experimental value for the diffusivity of oxygen in water, D_w = 2.60 × 10⁻⁵ cm²/s, to calculate P_w according to Eq. 4, using the escape threshold to define the thickness of each bilayer. Table 2 provides the P_M/P_w ratios, from which we observe that bilayers incorporating 0–37.5 mol % cholesterol have equivalent oxygen permeability. At 50 mol % cholesterol and above, the P_M/P_w ratio decreases. The permeability of the 50 mol % cholesterol bilayer is ∼10% below that of pure POPC. The permeability drops a bit more at the near-saturating level of 62.5 mol % cholesterol, to a value roughly 20% below pure POPC. Finally, at 100% cholesterol, the P_M/P_w ratio is about five times lower than POPC.

Biological membranes are thought to be surrounded by a static layer of aqueous fluid, in which diffusional processes govern solute movement. These unstirred layers, or boundary layers, remain stagnant even when the bulk solution is stirred (67, 68). The apparent thickness of unstirred layers has been found to depend inversely on the diffusion coefficient of the solute (69). Given its relatively large diffusion coefficient in water, O₂ should, thus, experience relatively thick unstirred layers, on the order of hundreds of micrometers, as observed for CO (70).

Given the permeabilities we have calculated for POPC, POPC/cholesterol, and even 100% cholesterol membranes, the impact of the membrane on the rate of oxygen transport would decline within tens of nanometers in unstirred water. For instance, unstirred layers as thin as 3.25 nm on either side of the membrane—6.5 nm total—would have a permeability, P_USL, of ∼40 cm/s, equaling the permeability of POPC membranes nearly saturated with cholesterol (62.5 mol %). Modest-sized unstirred layers of 13 nm on either side of the membrane—26 nm total—would have a P_USL of ∼10 cm/s, equaling the permeability of a noncrystalline 100% cholesterol bilayer and greatly diminishing the impact of the membrane cholesterol content on oxygen diffusion. We infer that unstirred water layers much thinner than anticipated for O₂ would be rate limiting for oxygen diffusion, rendering the cholesterol content of the membrane irrelevant for O₂ flux for all the membrane compositions studied here. Therefore, if oxygen is assumed to travel primarily along water dominated diffusional paths, membranes of the compositions we have studied are highly unlikely to be rate limiting for oxygen diffusion.

Favorability of intramembrane transport

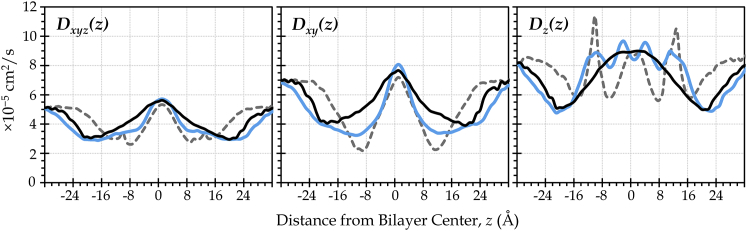
Given the favorable partitioning of O₂ into the membrane interior at all cholesterol levels, it is reasonable to consider whether the membrane core, itself, could serve as a conduit for oxygen diffusion. The depth-dependent oxygen diffusivity, D(z), is also enhanced in the center of the membrane, regardless of the cholesterol content (Fig. 5). Thus, oxygen is not only more soluble in the membrane than in water but is also able to diffuse readily within the plane of the membrane, as evidenced especially by the in-plane diffusivity curve, D_xy(z). We note that the estimated diffusivity curves shown in Fig. 5 are similar to curves reported elsewhere (30, 49, 50, 53).

Figure 5.

Oxygen diffusivity is high near the bilayer center, regardless of cholesterol content. These are representative curves, calculated using Eq. 3. D_xyz(z) reflects displacements in all three dimensions; D_xy(z) reflects displacements parallel to the plane of the bilayer; and D_z(z) reflects displacements perpendicular to the bilayer plane. (Black lines, POPC; blue lines, 50 mol % cholesterol; dashed gray lines, 100% cholesterol.) To see this figure in color, go online.

The oxygen transport parameter curves in Fig. 3 show the combined impact of favorable partitioning and elevated diffusivity in the membrane interior at all cholesterol levels studied. Namely, for membranes composed of POPC and/or cholesterol, the membrane interior provides lower resistance to O₂ diffusional transport than the surrounding water. Whereas the breadth of the oxygen transport parameter peak is reduced due to cholesterol, the peak intensity is enhanced, implying that cholesterol may slightly improve the efficiency—although not the volume—of lateral O₂ transport in the central core region.

Thus, our results suggest that oxygen may preferentially diffuse within the plane of the membrane, rather than traversing aqueous compartments with higher resistance and lower permeability. This mode of diffusion has previously been called “hydrophobic channeling” or “lateral transport” and has been discussed by several researchers as a likely mechanism for cellular- and tissue-level oxygen transport, especially within mitochondrial networks and pulmonary surfactant membranes (19, 71, 72, 73, 74, 75). In pulmonary surfactant, O₂ has been suggested to travel rapidly from membrane to membrane, due to proposed protein-mediated intermembrane contacts (75). Similar contacts at gap junctions are known to hold the cells of nearly all animal tissues in very close proximity, estimated to reach minima of 0.1–0.4 nm (76, 77). Mitochondria, likewise, form physically interconnected networks that visually resemble macroscopic pipelines (72, 78). Virtually all other cellular membranes are stitched together by tethering structures at membrane contact sites—enabling rapid exchange of metabolites and information among the plasma membrane, the endoplasmic reticulum, mitochondria, and other organelles (79).

Our data indicate that the barriers encountered by O₂ in passing between interfaced membranes are small. Namely, compared with the resistance encountered in crossing a sizeable unstirred layer, the barriers to passage from membrane to membrane are negligible. Yet, the magnitude of these barriers increases somewhat in cholesterol-enriched membranes. Near the cholesterol solubility threshold, we see permeability reductions of 10–20%, compared with pure POPC. Such reductions are consistent in magnitude with changes observed in cellular studies where the impact of cholesterol on transmembrane oxygen diffusion was investigated (7, 14, 80). Those studies imply that the modest oxygen permeability reductions we observe might be substantial enough to have biological significance. However, further work is needed to clarify the mechanism of such an effect, especially to determine whether cellular and tissue-level oxygen diffusional pathways are membrane dominated.

Limitations of this work

Although insightful, this work has several limitations. In particular, we have examined a highly simplified model of biological membranes, setting aside heterogeneities due to membrane proteins, minor lipid composition (especially sphingomyelin), lipid rafts, and bilayer leaflet asymmetry. Including membrane proteins in the models will be critical for better understanding the lower limits of gas permeability, as proteins may be negligibly permeable to oxygen and may promote ordering of the surrounding lipids (81, 82). Future work will address the omission of proteins from our current models.

Conclusions

We calculate the permeability of POPC phospholipid to be slightly higher than that of water. Incorporating cholesterol has no effect on the permeability, until it reaches levels near the saturation point for cholesterol in POPC. At 50 mol % cholesterol, the permeability drops 10% below POPC, and at 62.5 mol % cholesterol, it falls 20% below POPC. In the extreme, a 100% cholesterol mimic of the noncrystalline cholesterol bilayer domain is approximately five times less permeable than POPC or a water layer of the same thickness as the cholesterol bilayer. Considering the presence of unstirred water layers thought to flank biological membranes, we conclude that none of the bilayers studied would be rate limiting for oxygen transport, assuming diffusional paths dominated by movement across aqueous compartments. Rather, even unrealistically thin unstirred water layers would present substantially greater resistance than the membrane, regardless of cholesterol content.

However, our data and the work of others indicate that membrane dominated diffusional pathways may be the preferred mode of oxygen transport on the cellular and tissue levels. Specifically, we observe high oxygen solubility and high diffusivity within the central core of the membrane. Incorporation of cholesterol enhances the solubility in this region, likely due to reduced packing density of the lipid molecules near cholesterol’s flexible tail. Further, we find low barriers to direct passage from membrane to membrane, compared with the barrier oxygen would experience upon exiting the hydrophobic membrane milieu and traversing an aqueous compartment. Thus, our work supports the idea of hydrophobic channeling of O₂ through networks of interconnected or proximal membranes.

Cholesterol reduces the overall solubility of oxygen in the bilayer, possibly diminishing the volume of oxygen that can be transmitted laterally within the membrane. However, locally enhanced O₂ solubility in the central core of cholesterol-containing membranes may slightly improve the efficiency of lateral transport. Further experimental and simulation work is needed to clarify the extent to which lateral transport is feasible within compositionally complex biological membranes, as well as the potential influence of cholesterol on the efficiency of hydrophobic channeling.

Author Contributions

R.J.D. performed the permeability-related analyses and contributed substantially to the manuscript preparation. C.R.S. carried out the simulations and preliminary analyses. K.B. wrote code that enabled the permeability calculations. G.A. conducted preliminary oxygen transport parameter analysis and contributed theoretical knowledge. S.C.P. directed the project and wrote the manuscript.

Editor: Georg Pabst.