Focal Adhesion Kinase: The Reversible Molecular Mechanosensor

Abstract

Sensors are the first element of the pathways that control the response of cells to their environment. Protein complexes that produce or enable a chemical signal in response to a mechanical stimulus are called “mechanosensors”. In this work, we develop a theoretical model describing the physical mechanism of a reversible single-molecule stiffness sensor. Although this has the potential for general application, here we apply the model to focal adhesion kinase, which initiates the chemical signal in its active phosphorylated conformation, but can spontaneously return to its closed folded conformation. We find how the rates of conformation changes depend on the substrate stiffness and the pulling force applied from the cell cytoskeleton. We find the sensor is homeostatic, spontaneously self-adjusting to reach a state where its range of maximum sensitivity matches the substrate stiffness. The results compare well with the phenotype observations of cells on different substrates.

Introduction

Cells exist within a complex and varying environment. To function effectively, they must collect information about their surroundings, and then respond appropriately. Cell environment has a profound effect on cell migration, many aspects of metabolism, and the cell fate. It is also a major factor in metastasis of certain cancers (1, 2). Sensing is the first part of the chain of events that constitute the cell response to external stimuli.

By definition, a sensor is a device that detects or measures a physical property (the signal or stimulus) and records, indicates, or otherwise responds to it by generating an output. Fig. 1 illustrates what a typical sensor output should be, in response to an appropriate signal. When the transition between off- and on-states is very sharp, this may be regarded as an on/off relay producing a digital all-or-nothing response. When this transition is diffuse, over a broad range of input, the sensor works in an analog manner providing a proportional response to the input signal in the range of its sensitivity. Outside of this range, the sensor is not responsive to changes in the input signal.

Figure 1.

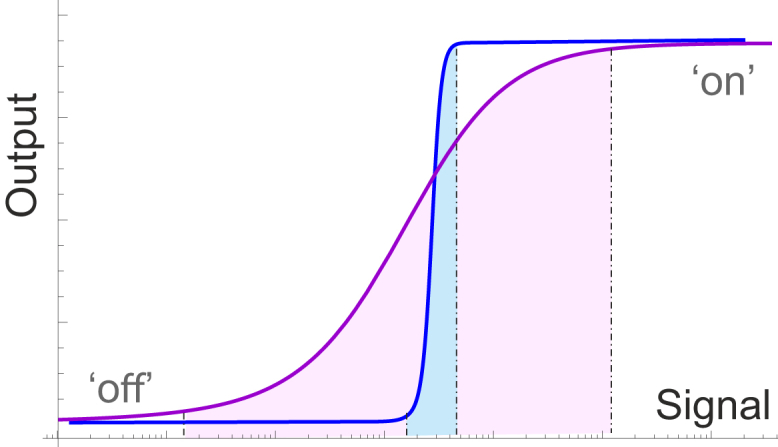
Given here is an illustration of sensor response to an input signal: the output is generated proportionally to the signal, and has a region of maximum sensitivity. This region can be narrow in a digital on-off relay, or continuously spread over a broad range of input values to generate an analog proportional output. To see this figure in color, go online.

Cells respond to a variety of cues; both chemical and mechanical stimuli must be transduced inside the cell. Mechanosensors are protein complexes that produce responses to mechanical inputs (3, 4). There are two distinct types of mechanosensing: reacting to an external force (we call this “mechanosensitivity of the first kind”), or sensing the viscoelastic properties of the cell environment (we call this “mechanosensitivity of the second kind”).

Mechanosensitive ion channels (MSC), such as alamethicin (5), are an example of mechanosensors of the first kind. MSCs exist in all cells and provide a nonspecific response to stress in a bilayer membrane (6, 7). Traditionally, MSC operation is understood as a two-state model, as we will have in our model below, and has the response characterized in Fig. 1, where the input signal is membrane tension and the sensor output is the channel diameter. These two-state systems (open/closed, or bonded/released) with the energy barrier between the states depending on applied force are common in biophysics (8, 9). Rates of transition in these systems are often calculated using the Bell formula (10), which has them increasing exponentially with the force. This is just the classical result of Kramers and Smoluchowski (11, 12), but the application of this formula is problematic in the limit of small barriers.

A mechanosensor of the second kind has a different challenge: to actively measure the response coefficient (stiffness in this case, or matrix viscosity in the case of bacterial flagellar motion). On macroscopic scales (in engineering or rheometry) we can do this with two separate measurements: of force (stress) and of position (strain), or we could contrast two separate points of force application. One could also use inertial effects, such as impact or oscillation, to measure the stiffness or elastic constant of the element. None of these options are available on a molecular scale because of a very high resistance, and of a short-distance cutoff of elasticity. The single sensor complex cannot measure relative displacements in the substrate, and the overdamped dynamics prevents any role of inertia. Cells must come up with novel ways of measurement.

In an earlier study (13), this was examined by developing a physical mechanism with an action similar to the two-spring model of Erdmann and Schwarz (14) and Schwarz et al. (15). That work focused on the latent complex of TGFβ (16, 17, 18), which is an irreversible one-off sensor: after the latent complex is broken and active TGFβ released, the whole construct has to be replaced. Here we apply these ideas to a reversible mechanosensor: protein tyrosine-kinase, now called “focal adhesion kinase” (FAK) (19, 20, 21, 22). As the name suggests, FAK is abundant in the regions of focal adhesions (20), which are developed in the cells on more stiff substrates, often also associated with fibrosis: the development of stress fibers of bundled actin filaments connecting to these focal adhesions and delivering a substantially higher pulling force. FAK is also present in cells on soft substrates despite the lack of any focal adhesions, and also in the lamellipodia during cell motility (21, 23, 24). Phosphorylation of tyrosine residues of FAK is well known as the initial step of at least two signaling pathways of mechanosensing (25), leading to the cell increasing production of smooth muscle actin, and eventually fibrosis, as well as producing and activating more myosin motors in the cytoskeleton.

Mechanosensing at focal adhesions

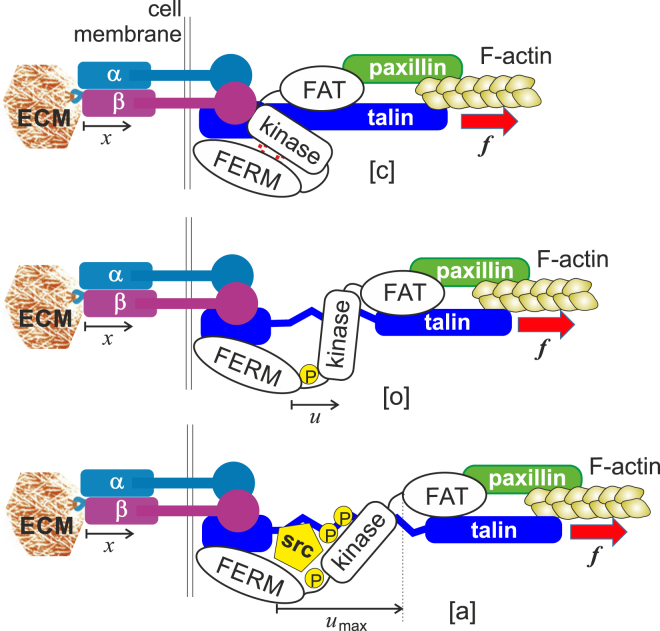
To probe the mechanical modulus of a medium, a force has to be applied to it, either as a local point source, or as distributed stress. In focal adhesions, the source of this force is the actin-myosin activity of the cytoskeleton. Therefore, we need to trace the series of connected devices, from the point of force origin (F-actin) to the point of its application to the ECM. Fig. 2 illustrates this force chain, which has been reproduced in a large number of important publications in this field (26, 27, 28, 29, 30). There are several key players that we should consider: integrins, focal adhesion kinase, talin, paxillin, and the cytoskeleton. How do these components each contribute to the function of the complex?

Figure 2.

Given here is the assumed chain of force transduction from the F-actin of the cytoskeleton, through the activated β-integrin binding to ligands of the deformable ECM. The FERM domain of FAK is associated with the cell membrane, near the integrin-talin head assembly, whereas the FAT domain is associated with actin through its binding to paxillin (30). The pulling force is transmitted through this chain to the FERM-kinase physical bond. In the closed state [c] the kinase domain is inactive and the whole FAK protein is in its native low-energy state. Once the physical bond holding the FERM domain and the kinase together is broken, the protein adopts the open conformation [o]. In the open state, first the Tyr³⁹⁷ site spontaneously phosphorylates, which in turn allows binding of Src and further phosphorylation of the kinase—turning it into the active state [a] (see (45, 70, 71)). To see this figure in color, go online.

The integrin family of transmembrane proteins links the extracellular matrix (ECM) to the intracellular actin cytoskeleton via a variety of protein-tyrosine kinases, one of which is FAK (31). Integrins are aggregated in focal adhesions, and they mediate the cell interaction with ECM (3). Activation of integrins is required for adhesion to the substrate; active integrins acquire ligand affinity and bind to the proteins of the ECM. It is well established that integrin activation and clustering leads to FAK activation and the subsequent signaling chain of mechanosensing and cytoskeletal remodeling; e.g., see the review by Parsons (32). There is a large body of literature on integrins, with definitive reviews by Hynes (33, 34) explicitly stating that integrins are the mechanosensors. It has recently been demonstrated (35, 36) that the integrin bond with fibronectin has catch-bond characteristics, and therefore could have a graded response to force and stiffness.

However, activated integrins possess no further catalytic activity, and so cannot act as a mechanosensor on their own. A good summary by Giancotti (37), although talking about integrin signaling, in fact shows schemes where FAK is the nearest to cytoskeletal actin filaments. The important work by Guan et al. (38) and Guan and Shalloway (39) establishes a clear correlation chain of extracellular fibronectin-transmembrane integrins-intracellular FAK, but offers no reason to assume that integrin is the sensing device on this chain. There is a clear indication that phosphorylation of FAK is a key step in the mechanosensing process (4). Indeed, Schaller et al. (20) state that FAK phosphorylation is the initial step of signaling, and show evidence that cross-linking integrins and ECM (i.e., making the substrate stiffer) leads to an enhanced FAK phosphorylation, although, conversely, damage to integrin is connected with a reduced activation of FAK.

This lack of clarity on the link between integrin engagement and FAK activation during mechanosensing arises from the lack of detailed knowledge at a molecular/physical level of how FAK is activated. One possibility, explored by Erdmann and Schwarz (14) and Schwarz et al. (15), is that clusters of activated integrins always activate FAK and generate the mechanosensing signal that leads to the increasing F-actin pulling force. As some of the integrins are broken off from their ECM attachment, the associated FAK signal reduces, regulating the further force increase—and that is the action of the focal adhesion mechanosensor complex. More recently, these same ideas have incorporated newly discovered catch-bond characteristics of the integrin-ECM links (35). In both cases, the mechanosensing response is an emergent property—you need a collection of coupled mechanosensors of the first kind to generate a stiffness sensing response. We think this work is elegant, and important, but ask the question: are there any other possible mechanisms?

The application of tension in mechanosensing at focal adhesions is now well established (30). A key role in this system is played by talin. There are many articles investigating the correlation of talin (as well as paxillin) with β-integrin and FAK; recent studies clearly show that talin is capable of high stretching by a tensile force (40, 41), implying a function similar to that of titin in muscle cells: acting as an extension-limiter. It is also now clear that the immobile domain at the N-terminal of talin is associated with integrin, and also closely associated with the FERM domain of FAK (40, 41), whereas the C-terminal of talin is associated with paxillin, which in turn may associate (perhaps via vinculin) with the focal adhesion targeting (FAT) domain (C-terminal) of FAK. Both talin and paxillin also bind to cytoskeletal F-actin. These actin filaments exert a pulling force on the C-terminal of talin, making it play a role of a scaffold for other proteins to arrange around. More importantly, this allows the pulling force to be transmitted from the cytoskeleton to the ECM, via the force chain sketched in Fig. 2. This could be used to effect the conformational change in FAK required for its activation. In this model, integrin is merely the bridging element from FAK to the ECM, with the FERM domain localized near the cell membrane and N-terminal of talin. At the opposite end, the FAT domain can be pulled away by the cytoskeletal force transmitted through paxillin/talin. This model is supported by the recent computational analysis (42) showing that the closed and the open states of FAK are reversibly reached by increasing and decreasing of pulling force.

Here, using this idea of FAK conformational change under applied force, we demonstrate that sensing of stiffness may be a distinct single-molecule response, and develop a theoretical model of reversible mechanosensor of the second kind. The underlying physics of our model is applicable to a wide variety of protein complexes, but here we concentrate on the focal adhesion kinase, because FAK occupies a central point in mechanosensing pathways of focal adhesions (25). We posit that the activation of FAK is dependent on cytoskeletal tension and ECM stiffness, and the integrin (along with other members of the force chain in Fig. 2) is playing a role of force transducer. Of course, without the activated integrin there would be no force transduction to ECM, and no mechanosensing. We do not consider the role of clustering. This is clearly an area of further work in this field, because clustering is definitely an important aspect of the process on stiff substrates: allostery of integrins (and associated FAK) must have a role in the signaling process, as it has in chemotaxis (43, 44). This article focuses on the physical model of an individual FAK sensor operation.

Materials and Methods

Our work relies on identifying the conformational transitions associated with FAK’s activation, and how the effective free energy of such a protein must evolve on conformational change. From this information, we can construct the physical model that includes the viscoelastic response of the ECM and the thermally activated response of the protein mechanosensor. It turns out that thermal activation (thermal noise) and the associated viscous damping are essential in both elements of the mechanical chain. We then derive the effective rate of FAK opening and activation (as well as the reverse rate of its autoinhibition) using the methods of stochastic Kramers theory.

Structural model

There are three key conformational states, illustrated in Fig. 2. In the native folded state of FAK, the FERM domain (the N-terminal of the protein) is physically bonded to the catalytic domain (kinase) (22, 45) via a number of weak interactions, such as hydrophobic, van der Waals, and hydrogen bonds; we call this the closed state, [c]. A conformational change occurs, which we shall call a transition to an open state, [o], when this physical bond is disrupted and the kinase separates from the FERM domain. Note that because there is a peptide chain link ([362–411] segment) between the FERM and kinase domains, they remain closely associated even after the conformational change—this is what makes FAK a reversible mechanosensor. The activation of the catalytic domain occurs in two steps: first the Tyr³⁹⁷ residue is phosphorylated, which then allows binding of the Src kinase (46), which in turn promotes phosphorylation of several other sites of the catalytic domain (Tyr⁴⁰⁷, Tyr⁵⁷⁶, Tyr ⁵⁷⁷, Tyr⁸⁶¹, and Tyr⁹²⁵), making FAK fully activated. There is also a process involving p130cas, acting as a kinase substrate, involved in generating the response of activated FAK (47, 48). We identify this state as active, [a], in the subsequent discussion.

Because we shall not consider the cell motility in this article, one has to assume that the FERM domain remains fixed with respect to the ECM/integrin reference frame. That is, if there is a deformation in (soft) ECM, then this point will move accordingly, with the integrin and the local cell membrane all joined together. In our model, to achieve the large displacement associated with the [c] → [o] conformational transition of FAK, in the crowded intracellular environment, a mechanical work is expended. This mechanical energy can only come from the active cytoskeletal forces, delivered via actin filaments.

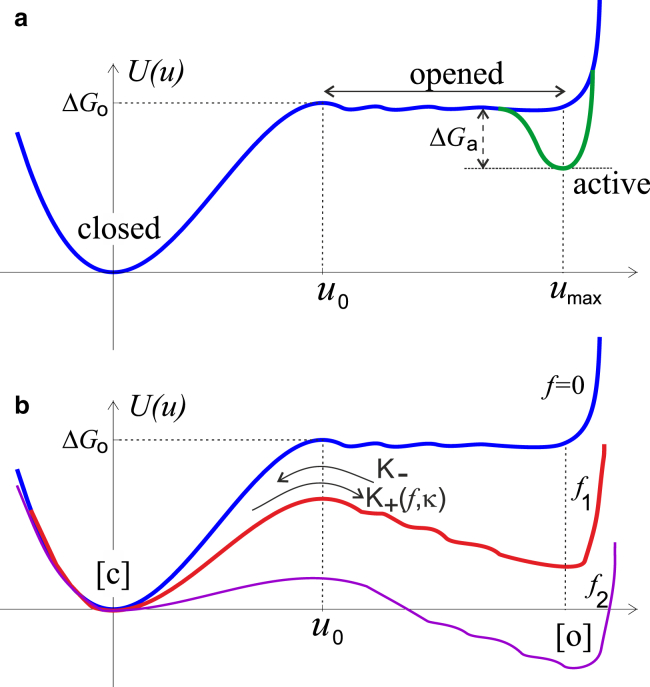
We can now record these conformational changes in the FAK structure in the schematic plot of the unfolding free energy, which will play the role of potential energy U(u) for the subsequent stochastic analysis of the sensor action. This free energy is illustrated in Fig. 3 a in the absence of pulling force. The concept of such unfolding free energy is becoming quite common (49). One identifies an appropriate reaction coordinate and discovers that a deep free energy minimum exists in the native folded state, which is our state [c]. Outside of this global free energy minimum, there is a broad range of intermediate conformations having a ragged, but essentially flat, free energy profile, forming what is commonly known as a funnel for the protein folding/unfolding. In our context, this range represents the open state [o], and the protein will rapidly fold back into its native state [c], unless this refolding is inhibited by, e.g., changing pH, temperature, or in our case—transition to the active state [a]. The subsequent unfolding of protein domains into a random coil of its secondary structure would cause a significant raise of the free energy.

Figure 3.

Shown here is a schematic of potential energy of different FAK conformations. (a) The force-free molecule has its native folded state [c] (compare with Fig. 2). The binding free energy ΔG_o has to be overcome to separate the kinase from the FERM domain, after which there is a range of conformations of where roughly the same energy is achieved by further separating these two domains in the open state [o]. At full separation (distance u_max) the Src binding and kinase phosphorylation lead to the active state [a] of the protein, with the free energy gain ΔG_a. (b) When a pulling force is applied to this system (f₂ > f₁ > 0), the potential energy profile distorts, so that both [o] and [a] states shift down in energy by the same amount of −f × u_max. To see this figure in color, go online.

Fig. 3 a needs to be looked at together with the conformation sketches in Fig. 2: the native state [c] needs a substantial free energy (ΔG_o) to disrupt the physical bonds holding the kinase and FERM domains together. However, once this is achieved, there are only very minor free energy changes due to the small bending of the [362–411] segment (22), when the kinase and FERM domains are gradually pulled apart. This change is measured by the relative distance, which we label u in the sketch and in the plot. If one insists on further separation of the protein ends, past the fully open conformation [o] at u = u_max, the protein will have to further unfold at a great cost to the free energy. Binding of Src and phosphorylation (i.e., converting the [o] state into the [a] state) lowers the free energy of the fully open conformation by an amount ΔG_a. Note that there is no path back to the closed state, once the kinase is activated: one can only achieve autoinhibition (22) via the [a] → [o] → [c] sequence.

If we accept the basic form of the protein potential profile, as shown in Fig. 3 a, the effect of the pulling force f applied to FAK from the actin cytoskeletal filaments is accounted for by the mechanical work −(f × u) added to the original protein free energy. If we take the reference point u = 0 as the closed native conformation [c], then under an external pulling force the opening barrier reduces by ΔG_o − f × u₀. Similarly, the free energy of the fully open state [o] becomes lower by ΔG_o − f × u_max (see Fig. 3 b). This develops the second free energy minimum, and makes the [o] state increasingly more stable. We assume the binding of Src and phosphorylation are not parts of the force chain (ECM-integrin-FAK-cytoskeleton) and so do not depend on the applied force. Therefore the energy level of the active state [a] lowers by the same amount of ΔG_a relative to this [o] state.

Stochastic two-spring model

The two-spring model discussed in detail by Erdmann and Schwarz (14) and Schwarz et al. (15) and often reproduced afterwards (25) is a correct concept, except that it needs to take into account that both the viscoelastic substrate and the sensor, described by the effective potential energy U(u), experience independent thermal excitations. This is inevitable at the molecular level, because we are considering the mechanical damping in the substrate (as we must) and in the sensor (as we will). In the overdamped limit, all forces must balance along the series of connected elements, so the system is always in mechanical equilibrium. Here it is important to distinguish between mechanical equilibrium and chemical equilibrium. The former sets up the free energy profile, which then determines the latter. The mechanical stimulus does not drive the system. Instead, as in the classical rate theory, it is thermal fluctuations that allow the system to evolve. In our case, thermal fluctuations (which are independent in the two elements) can create a relative displacement in the middle of this series (i.e., on the sensor). It is this relative displacement that one needs to measure the stiffness.

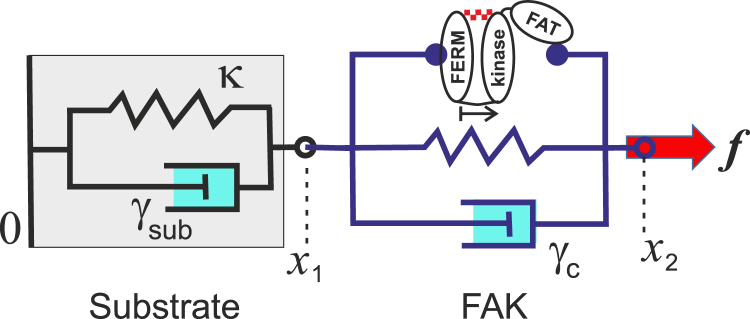
Following the logic outlined in greater detail in earlier work (13), we introduce two independent stochastic variables. The first is x₁ = x, which measures the displacement of the substrate with respect to its undeformed reference state, and therefore also marks the position of the FERM domain (or the origin of the length u). The second is x₂, which measures the displacement of the far end of the kinase domain: the point of application of the pulling force f (see Fig. 4 for an illustration). The approach to chemical equilibrium, in these variables, is described as follows by a pair of coupled overdamped Langevin equations:

$$\begin{array}{l}{\gamma }_{\text{sub}}{\dot{x}}_1=-\kappa x_1+\frac{\text{d}U}{\text{d}\left(x_2-x_1\right)}+\sqrt{2k_{\text{B}}T{\gamma }_{\text{sub}}}{\zeta }_1\left(t\right),\\ {\gamma }_{\text{FAK}}{\dot{x}}_2=-\frac{\text{d}U}{\text{d}\left(x_2-x_1\right)}+f+\sqrt{2k_{\text{B}}T{\gamma }_{\text{FAK}}}{\zeta }_2\left(t\right),\end{array}$$ (1)

where κ is the elastic stiffness, γ_sub is the damping constant of viscoelastic substrate (ECM), and γ_FAK is the (completely independent) damping constant for the conformational changes in FAK structure. The base stochastic processes ζ_1,2(t) are assumed to be Gaussian and normalized to unity, whereas the fluctuation-dissipation theorem determines the magnitude of thermal force in each equation. Note that it is the difference in independent position coordinates u = x₂ – x₁, which affects the sensor potential U(u) plotted in Fig. 3. The problem naturally reduces to a two-dimensional Smoluchowski equation for the variables x(t) = x₁ for the substrate, and u(t) for the FAK conformations, with the corresponding diffusion constants D_i = k_BT/γ_i, and the Cartesian components of diffusion current, as follows:

$$J_i=-\frac{k_{\text{B}}T}{{\gamma }_i}{e}^{-V_{\text{eff}}/k_{\text{B}}T}{\nabla }_i\left(e^{V_{\text{eff}}/k_{\text{B}}T}P\right),$$ (2)

where j = 1, 2, P(x₁, x₂; t) is the probability distribution of the process, and the following expression:

$$\begin{array}{cc}{V}_{\text{eff}}\left(x_1,x_2\right)& =\frac{1}{2}\kappa x_1^2-f{x}_2+U\left(x_2-x_1\right)\\ & =\frac{1}{2}\kappa x^2-fx+U\left(u\right)-fu\end{array}$$ (3)

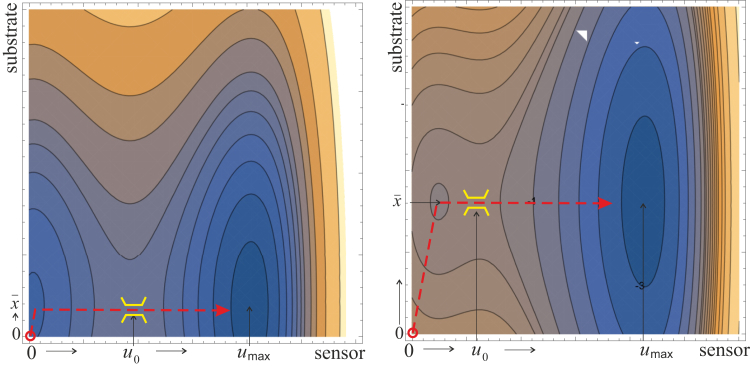
represents the effective potential landscape over which the substrate and the mechanosensor complex move, subject to thermal excitation and the external constant force f. This landscape is illustrated in Fig. 5.

Figure 4.

Here is a scheme of the two-spring model used to produce Eq. 1. The viscoelastic substrate is characterized by its elastic stiffness and stress-relaxation time given by γ_sub/κ. The conformational change of FAK is described by a potential U(u) (see Fig. 3), and the associated relaxation time determined by the damping constant γ_FAK. To see this figure in color, go online.

Figure 5.

Given here is the two-dimensional contour plot of the effective potential V_eff(x,u) at low pulling force (left) and at high pulling force (right). The position of substrate anchoring has moved from x = 0 to $\overline{x}=f/\kappa$, and the depth of the energy well of the [o] state has lowered to ΔG_o − fu_max. The dashed line shows the path of the system evolution that leads to crossing the barrier toward the open state. To see this figure in color, go online.

The effective Kramers problem of escape over the barrier has been solved many times over the years (8, 11, 12, 50, 51). The multidimensional Kramers escape problem, with the potential profile not dissimilar to that in Fig. 5, was also solved many times (52, 53). Unlike many previous approaches, we will not allow unphysical solutions by mistreating the case of very low/vanishing barrier. In the case when the effective potential barrier is not high enough to permit the classical Kramers approach of steepest descent integrals, one of several good general methods is via Laplace transformation of the Smoluchowski equation (12, 54). The compact answer for the mean time of first passage from the closed state [c] to the top of the barrier of height Q a distance Δu away is as follows:

$${\tau }_{+}=\frac{\Delta u^2}{D}\left[{\left(\frac{k_{\text{B}}T}{Q}\right)}^2\left(e^{Q/k_{\text{B}}T}-1\right)-\frac{k_{\text{B}}T}{Q}\right].$$ (4)

This is a key expression, which gives the standard Kramers thermal-activation law when the barrier is high (which is also the regime when the Bell formula (10) is valid), but in the limit of the low barrier, it correctly reduces to the simple diffusion time across the distance Δu.

Estimates of material parameters

We shall find that our model predictions are very sensitive to values of several key parameters, so a careful discussion of their estimates is required.

We start with the strength of the bond holding the FERM and kinase domain in the closed (inhibited) state, labeled as ΔG_o in Fig. 3. The MD simulation study (42) estimated the energy barrier for FAK opening as ΔG_o ≈ 28.5 k_BT, which is 17 kcal/mol at room temperature. This value seems too high, and Zhou et al. (42) also comment on that. It is known that interdomain hydrophobic interaction in such proteins is usually low affinity. For instance, a measurement in a different multidomain protein gives a value for this bonding energy as 7 kcal/mol, or ∼11 k_BT (55). However, this is close to an energy of just 1–2 hydrophobic contacts, and there is more affinity between FERM and kinase domains observed in Zhou et al. (42). In the end, we select an intermediate value between the two limits mentioned above: ΔG_o ≈ 17 k_BT, or 10 kcal/mol, and illustrate how alternative values (stronger and weaker interdomain bond) change our predictions in the Supporting Material.

We take the position of the barrier from the computational study: u₀ = 0.9 nm (42), which is a reasonable value for the protein domain structure. This determines the value of critical force at which the native minimum disappears, and the closed state [c] becomes completely unstable, f_c = 3ΔG_o/2u₀ ≈ 110 pN. This is a very high force that is likely to unfold most proteins, and is also unlikely to be generated by a single actin filament of a cell cytoskeleton. For comparison, studies investigating the force required to disrupt the fibronectin-integrin-cytoskeleton linkage, report the value of only 1–2 pN (56, 57); this is probably too low (an underestimate), because a single myosin motor exerts ∼3 pN of force (58, 59). So we should explore the effect of pulling forces in the range of single to tens of pN.

We now look at substrate stiffness. For reference, the elastic modulus of a typical collagen-rich mammalian tendon is 1.2 GPa (60), of a collagen/elastin ligament is 1.1 MPa (61), and of an aorta wall is 0.8 MPa (62). Synthetic rubber has a modulus at ∼100 kPa (63). Epithelial and glial tissues have a much lower modulus of 100–1 kPa (64, 65); see Supporting Material for an illustration of viscoelastic response of several other soft materials. If a half-space occupied by an elastic medium (e.g., gel substrate or glass plate) with the Young’s modulus Y, and a point force f, is applied along the surface (modeling the pulling of the integrin-ECM junction; see Fig. 2), the response coefficient (spring constant) that we have called the “stiffness” is given by κ = (4/3)πYξ, where ξ is a short-distance elastic cutoff: a length scale analogous to the mesh size of a densely packed (nonfilamentous) substrate. This is a classical relation going as far back as Lord Kelvin (66). In the work of Yeung et al. (67) on comparative cell response on soft substrates, the weakest meaningful substrate had Y = 540 Pa. For a more typical weak gel with Y = 10 kPa, and a characteristic network mesh size ξ = 10 nm, we obtain κ = 4.2 × 10⁻⁴ N/m. On a stiff mineral glass with Y = 10 GPa, we must take the characteristic size to be a cage size (slightly above the size of a monomer), ξ = 1 nm, which gives κ = 42 N/m. A typical stiff plastic has a value ∼10 times smaller. So a large spectrum of stiffnesses κ could be explored by living cells.

Finally, we need estimates of the damping constants. The simulation study (42) determined a very reasonable value for the internal diffusion constant of the FAK complex of D = k_BT/γ_FAK ≈ 6 × 10⁻¹² m² s⁻¹. At room temperature, this gives the damping constant as γ_FAK = 7 × 10⁻¹⁰ kg s⁻¹. Then, the overall scale (i.e., the bare magnitude) of the FAK opening rate K₊ derived below, Eq. 8, is (ΔG_o/u₀²γ_FAK) ≈ 8 × 10⁷ s⁻¹, which means a timescale of ∼12 ns. This bare timescale is compatible with available data and simulations on full and partial protein unfolding (68); naturally, at given bonding energy and low pulling force, the actual rate of FAK opening/activation would be much lower: the plots below suggest tens of microseconds to milliseconds range.

To estimate the damping constant of the viscoelastic substrate, we need the characteristic time of its internal relaxation, which is the ratio γ_sub/κ in our notation. There is an extended discussion of this issue (of substrate viscoelasticity and how to interpret it in our context) in the Supporting Material. It is important to note here that the local time of relaxation of thermal fluctuations must not be confused with the macroscopic stress relaxation time, which can sometimes be very long in rubbers and gels. To our surprise, we note that this fluctuation relaxation time, τ_sub ≫ 0.01 s, appears relatively universal across substrate stiffnesses. Therefore, we take γ_sub = τ_subκ. As such, the ratio between the damping coefficients, γ_FAK = γ_sub, takes a wide range of values, from 10⁻⁶ for soft substrates, to 0.1 for stiffer substrates.

Results and Discussion

We now apply the generic expression for the mean first passage time in Eq. 4 to V_eff(x₁, x₂) to find the rates of [c] → [o] conformational change. We can plot these rates, and test their predictions against what is observed in this biological system.

Rate of [c] → [o] transition: K⁺

There are many complexities regarding choosing an optimal path across the potential landscape V_eff(x,u), some of which are discussed in Langer (52) and Suzuki and Dudko (53), but we are aiming for the quickest way to a qualitatively meaningful answer. As such, we shall assume that the reaction path consists of two legs: from the origin down to the minimum of the potential, which is shifted to $\overline{x}=f/\kappa$ due to the substrate deformation, and then from this minimum straight over the saddle (barrier) into the open state of FAK conformation. The average time along the first leg is given by the Eq. 4 with the distance $\Delta u=\overline{x}$ and the negative elastic energy in this minimum, E = −f²/2κ, with the diffusion constant determined as follows by the damping constant of the substrate:

$${\tau }_{\text{drift}}=\frac{2{\gamma }_{\text{sub}}}{\kappa }+\frac{4{\gamma }_{\text{sub}}{k}_{\text{B}}T}{f^2}\left(e^{-f^2/2\kappa k_{\text{B}}T}-1\right).$$ (5)

Here the ratio γ_sub/κ is the characteristic time of fluctuation relaxation in the viscoelastic substrate (69), which will play a significant role in our results. Naturally, τ_drift = 0 when there is no pulling force and the effective potential minimum is at (x = 0, u = 0).

In the region between the minimum of V_eff and the potential barrier, a number of earlier articles (13, 51, 53) have used the effective cubic potential to model this portion of U(u). In this case, when the pulling force is applied, the barrier height is reducing, as E = ΔG_o(1 – 2 fu₀/3ΔG_o)^3/2. The distance between the minimum [c] and the maximum at the top of the barrier is reducing as well, at Δu = u₀(1 – 2 fu₀/3ΔG_o)^1/2. Substituting these values into Eq. 4, we find the mean passage time over the barrier as follows:

$$\begin{array}{c}{\tau }_{\text{open}}=-\frac{{\gamma }_{\text{FAK}}{u}_0^2}{\Delta G_{\text{o}}{\left(1-\frac{2f{u}_0}{3\Delta G_{\text{o}}}\right)}^{1/2}}\\ +\frac{{\gamma }_{\text{FAK}}{k}_{\text{B}}T{u}_0^2}{\Delta G_{\text{o}}^2{\left(1-\frac{2f{u}_0}{3\Delta G_{\text{o}}}\right)}^2}\left(e^{\Delta G_{\text{o}}{\left(1-\frac{2f{u}_0}{3\Delta G_{\text{o}}}\right)}^{3/2}/k_{\text{B}}T}-1\right).\end{array}$$ (6)

In the limit of high barrier ΔG_o ≫ k_BT, and small pulling force, this expression becomes proportional to $e^{-\left(\Delta G_{\text{o}}-f{u}_0\right)/k_{\text{B}}T}$, i.e., it recovers the Bell formula that people use widely. When the force increases toward the limit f_c = 3ΔG_o/2u₀, this time τ_open reduces dramatically: there is no barrier left to overcome, and the minimum of V_eff shifts to coincide with the entrance to the [o] state.

The overall rate constant of the [c] → [o] transition, K₊, is then determined as the inverse of the total time, as follows:

$$K_{+}=\frac{1}{{\tau }_{\text{drift}}+{\tau }_{\text{open}}}.$$ (7)

From examining Eqs. 5 and 6 it is evident that the rate of FAK opening is a strong function of the pulling force f, but more importantly: it changes dramatically with the substrate stiffness κ. The important exponential factor $e^{f^2/2\kappa k_{\text{B}}T}$ appears in τ_drift; it was discussed at length in Escudé et al. (13), where it has emerged in a very different approach to solving a similar problem, and interpreted as an effective enzyme effect of the system being confined at the bottom of the potential well before jumping over the barrier.

We can scale the rate constant K₊ to convert it into nondimensional values. First, we can identify a characteristic timescale of the FAK conformational change: u₀²γ_FAK/ΔG_o. The two control parameters defining the opening rate K₊ are also made nondimensional by scaling the force by the natural value of the FERM-kinase holding potential, ΔG_o/u₀, and scaling the substrate stiffness by ΔG_o/u₀². After these transformations, and some algebra, we obtain the following:

$$K_{+}=\left(\frac{\Delta G_{\text{o}}}{u_0^2{\gamma }_{\text{FAK}}}\right)\frac{g{\overline{f}}^2{\left(1-2\overline{f}/3\right)}^2\zeta }{4{\left(1-2\overline{f}/3\right)}^2{\text{Ψ}}_1\left[f\right]+{\overline{f}}^2\zeta {\text{Ψ}}_2\left[f\right]},$$ (8)

with shorthand notations as follows:

$$\begin{array}{l}{\text{Ψ}}_1\left[f\right]=\text{exp}\left[-g{\overline{f}}^2/2\overline{\kappa }\right]+g{\overline{f}}^2/2\overline{\kappa }-1,\\ {\text{Ψ}}_2\left[f\right]=\text{exp}\left[g{\left(1-2\overline{f}/3\right)}^{3/2}\right]-g{\left(1-2\overline{f}/3\right)}^{3/2}-1,\end{array}$$

where the nondimensional abbreviations stand for the energy barrier g = ΔG_o/k_BT, the force $\overline{f}=f\times u_0/\Delta G_{\text{o}}$, the substrate stiffness $\overline{\kappa }=\kappa \times u_0^2/\Delta G_{\text{o}}$, and the ratio of damping constants ζ = γ_FAK/γ_sub. There are several key effects predicted by this expression, which we can examine by plotting it.

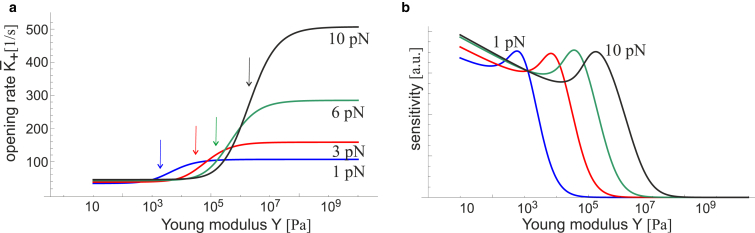
Fig. 6 presents the rate of FAK opening for several values of pulling force, as a function of substrate stiffness. The rate of FAK activation has a characteristic (generic) form of any sensor (as in Fig. 1) in that it undergoes a continuous change between the off- and on-states. The latter is a state of high rate of FAK opening and the subsequent phosphorylation that occurs on stiffer substrates. The force applied to the complex determines its response for a given substrate: the substrate could be too soft, meaning that FAK does not activate at all—and also too stiff, where the rate of activation reaches a plateau and no longer responds to further stiffening. Between these two limits, there is a range of maximum sensitivity where the rate of activation directly reflects the change of substrate stiffness. Note that due to the logarithmic scale, this range is actually as much as one order of magnitude in stiffness—quite broad, and we suspect more than enough to precisely sense local variations in stiffness. Fig. 6 b highlights this by presenting the sensitivity directly as the value of the derivative dK₊/dκ. We see that cells with a higher pulling force (i.e., with high actin-myosin activity and more developed stress fibers) are sensitive to the substrates in the more stiff range. In contrast, cells that exert a low pulling force (i.e., no stress fibers, lower actin-myosin activity) are mostly sensitive to soft substrates. This is in good agreement with broad observations about the cell mechanosensitivity of the second kind, and their response to substrate stiffness.

Figure 6.

(a) The rate constant of the [c] → [o] transition K₊(f,κ) is plotted against the substrate stiffness (on logarithmic scale) for several values of pulling force f. The arrows point at the inflection point on each curve, i.e., the region of maximum sensitivity. (b) Given here is the plot of sensitivity dK₊/dY for the same parameters, illustrating the maximum sensitivity range at each level of pulling force. To see this figure in color, go online.

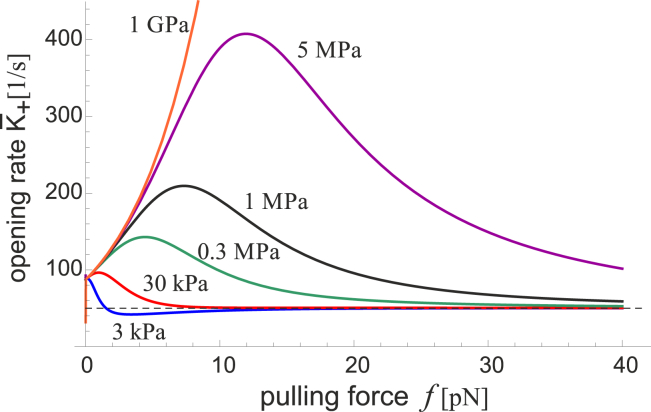
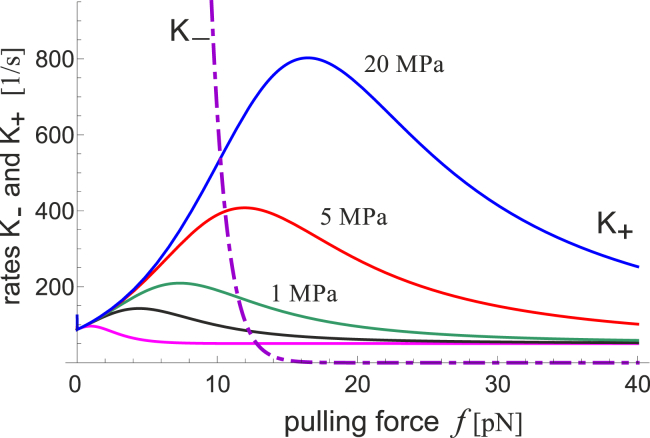
The dependence of the sensor on the force applied by the cytoskeleton is illustrated in Fig. 7. We see a rapid increase in the rate that FAK opens (and its subsequent phosphorylation) on stiffer substrates. For the complex to actively probe the substrate stiffness (mechanosensitivity of the second kind), we posit that the cell remodels itself in response to FAK activation, increasing the pulling force. This further increases the level of FAK activation in a positive feedback manner, until a maximum rate is reached. Any increase in force beyond this point decreases the rate of FAK opening. This would act as a mechanism for negative feedback, which settles the cell tension in homeostasis at the peak of the corresponding curves in Fig. 7. The stiffer the substrate, the higher the rate of FAK activation and, accordingly, the more α-SMA stress fibers one would find in this adjusted cell (leading to morphological changes such as fibroblast-myofibroblast transition, or the fibrosis of smooth muscle cells). On soft substrates with sufficiently small Young’s modulus there is no positive force that gives a maximum in the opening rate. Thus, any pulling force on the FAK-integrin-ECM chain has the effect of further lowering the activation of FAK relative to the tension-free state, and so the cell does not develop any additional tension in the cytoskeleton. This is consistent with the observation that cells do not develop focal adhesions on soft gels.

Figure 7.

The rate constant of FAK opening K₊(f,κ) is plotted as a function of the cytoskeletal pulling force f, for several values of substrate stiffness labeled on the plot. The dashed line marks the rate K_sub = 1/2τ_sub for the opening without any barrier. The homeostatic peaks of activation rate K₊(f), for each given substrate stiffness, roughly correspond to the peak of sensitivity in Fig. 6b at the same level of force. This suggests that the cell self-adjusts the sensor to keep it at the optimal sensitivity on each substrate. To see this figure in color, go online.

Stress relaxation in substrate regulates K₊

There are many indications in the literature that not only the substrate stiffness, but also the degree of viscoelasticity (often measured by the characteristic time of stress relaxation), have an effect on cell mechanosensitivity (69). It is certainly impossible to have a universal model covering the highly diverse viscoelasticity of gels, filament networks, and disordered solids like plastic and glass. In the spirit of our ultimately simplified viscoelastic model expressed in Eq. 1, the single parameter characterizing viscoelasticity could be the characteristic timescale τ_sub = γ_sub/κ: this could be a measure of the actual stress relaxation time of different substrates. Although we have taken τ_sub = 0.01 s up to this point, we now vary this timescale.

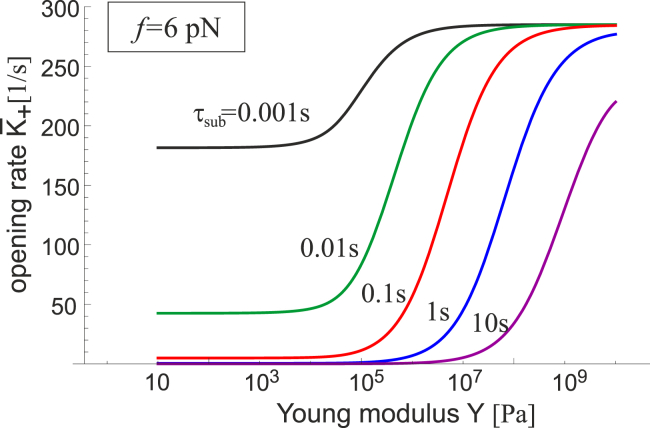
We assume that the damping constant γ_FAK of the FAK complex remains the same. In that case, Fig. 8 shows how changing the damping constant of the substrate τ_sub can regulate the FAK mechanosensor. All curves retain the same topology, but the amplitude varies, and the range of sensitivity shifts in proportion to τ_sub. The green curve for τ_sub = 0.01 s is the same as the green curve for f = 6 pN in both plots in Fig. 6. We find that for substrates with larger relaxation times, i.e., with a greater role of viscous dissipation, the FAK sensor will activate at higher stiffnesses. In other words, stress relaxation suppresses the response of a sensor with respect to a strictly elastic substrate. It is also important to note that the difference in activation rate between the off- and on-states increases with increasing stress relaxation time. If we were to send τ_sub → 0, i.e., place the cell on an ideal purely elastic material, then we would see no sensing response at all. So, the viscoelastic nature of the substrate is important for the sensing behavior of the complex.

Figure 8.

The rate of the [c] → [o] transition K₊(f,κ) is plotted against the substrate stiffness for a fixed (low) value of pulling force and a set of changing stress-relaxation properties of the substrate measured by the internal relaxation time τ_sub (see Eqs. 1 and 8). The range of maximum sensitivity shifts to the effectively stiffer substrate range for materials with longer internal relaxation; in contrast, a purely elastic material with τ_sub → 0 has very little effect on the mechanosensor. To see this figure in color, go online.

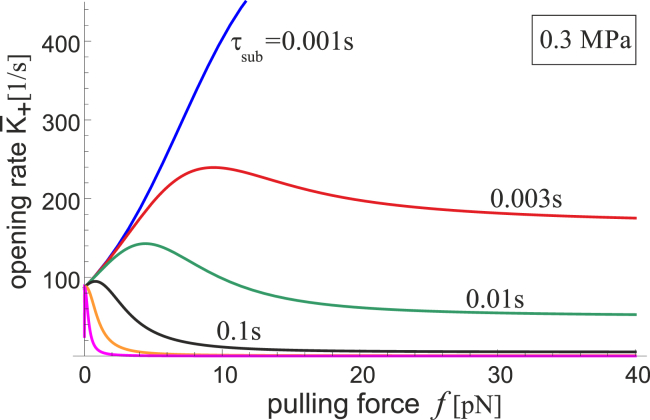
The strong effect of substrate viscoelasticity on the absolute value of rate of FAK activation K₊ is shown in Fig. 9, for an example of a typical rubber with the Young’s modulus of ∼300 MPa. A range of τ_sub is tested, and here we again see how the material with a longer relaxation time has a reduced response at any pulling force. This is essentially analogous to the substrate appearing softer.

Figure 9.

The rate of the [c] → [o] transition K₊(f,κ) is plotted against the pulling force f (in the biologically relevant range of small forces) for a set of values τ_sub labeled on the plot representing the change in stress-relaxation characteristics of the substrate (the last two curves are for τ_sub = 1 and 10 s, respectively). To see this figure in color, go online.

Rate of [o] → [c] autoinhibition: K₋

The free energy profile of the conformation change leading to the [o] →[c] transition (i.e., the spontaneous return of FAK to its native folded conformation, i.e., the autoinhibition) is essentially described by a linear potential (see Fig. 3). From the reference point of [o] state, the energy barrier is E = f(u_max – u₀), and we should assume that the physical distance the FERM domain needs to travel remains constant: it is determined by the extent of the protein structure (22, 70). This process also does not depend on the substrate stiffness. As a result, the rate of the folding transition is the inverse of the mean first-passage time (4) with these parameters, as follows:

$$K_{-}\left(f\right)=\frac{f}{{\gamma }_{\text{FAK}}\Delta u}{\left(\frac{k_{\text{B}}T}{f\Delta u}\left[e^{f\Delta u/k_{\text{B}}T}-1\right]-1\right)}^{-1},$$ (9)

with the shorthand notation Δu = (u_max – u₀). When the force is high, and the [o] state has a deep free-energy minimum generated by this external mechanical work (see Fig. 3 b), this rate reduces exponentially with pulling force: $K_{-}\approx \left(f^2/{\gamma }_{\text{FAK}}{k}_{\text{B}}T\right)e^{-f\Delta u/k_{\text{B}}T}$. This reflects the increasing stability of the [o] state when FAK is pulled with a high force, even before it phosphorylates and further stabilizes in the active state [a]. On the other hand, at vanishing force, f → 0, this rate becomes K₋ ≈ 2k_BT/γ_FAKΔu², which is the free-diffusion time over the distance (u_max – u₀), or the natural time of refolding of the force-free open state.

We must mention several factors that would make the process of autoinhibition more complicated, and its rate K₋ deviates from the simple expression (9). First of all, the [o] state will in most cases be quickly phosphorylated, which means there will be an additional binding energy ΔG_a stabilizing this conformation—making the effective rate of autoinhibition lower than is predicted by Eq. 9. On the other hand, there is an effect of extension-elasticity of talin (40, 41) that would provide an additional returning force acting on the FAK complex: this would make the low/zero force case fold back faster, at a higher rate K₋. Although these are interesting and important questions that need to be investigated, at the moment we will focus on the simplest approximation to understand the universal qualitative features of FAK sensor dynamics.

To be able to compare different expressions, and plot different versions of transition rates, we must identify the nondimensional scaling of K₋. Factoring the same natural timescale as we used for K₊, the expression takes the following form:

$$K_{-}=\left(\frac{\Delta G_{\text{o}}}{u_0^2{\gamma }_{\text{FAK}}}\right)\frac{g{\overline{f}}^2}{\left(e^{g\overline{f}\lambda }-1\right)-g\overline{f}\lambda },$$ (10)

where, as before, the force is scaled as $f=\overline{f}\Delta G_{\text{o}}/u_0$, the opening energy barrier is g = ΔG_o/k_BT, and the ratio of two length scales (in [c] and [o] states) is labeled by the parameter λ = (u_max – u₀)/u₀ (see Fig. 2). We do not have direct structural information about the physical extent of FAK opening. However, taking the structural data on the separate FAK domains from the work of Lietha et al. (22), Cai et al. (70), and Zhao and Guan (71), we make an estimate that u_max ≈ 6.5 nm, essentially determined by the double of the size of folded kinase domain (see Fig. 2). This gives λ ≈ 6 and lets us plot the comparison of the two transition rates, ${\overline{K}}_{+}$ and ${\overline{K}}_{-}$.

Fig. 10 gives the transition rates, K₊(f,κ) and ${\overline{K}}_{-}\left(f\right)$, plotted as a function of increasing pulling force. The rate of closing, ${\overline{K}}_{-}$, does not depend on the substrate parameters and is rapidly increasing when the [c] → [o] range of protein potential energy is flat (see Fig. 3). In this range of parameters, the product $g\overline{f}\lambda$ in the Eq. 10 is large, and the expression decays exponentially as $\text{exp}\left[-g\overline{f}\lambda \right]$. This implies that the transition from the strongly autoinhibited population of FAK sensors to the largely activated sensors is rather sharp. We find that the cross-over force at which K₊ ≈ K_{_} is a relatively universal prediction, giving an estimate for the order-of-magnitude force required to keep the FAK conformation open as f^∗ ≈ 10 pN.

Figure 10.

Given here is a comparison of the opening and closing rates, K₊ and K₋, for several different substrate stiffnesses (the last two K₊ curves are for 0.3 MPa and 30 kPa). When the cytoskeleton pulling force is too low, the rate of autoinhibition rapidly increases and one does not expect strong phosphorylation and positive feedback of mechanosensor. To see this figure in color, go online.

One might be tempted, in the traditional way, to interpret the ratio of the on- and off-rates K₊/K_{_} as an equilibrium concentration of closed and open/activated states. However, we must remember that this process of mechanosensing is inherently nonequilibrium, even though it might be steady state on the timescale of sensor response. Even in the regime of very low pulling forces, when K_{_} ≫ K₊, the few FAK molecules that are spontaneously open would provide the required (low) level of signal to the cell pathways. It is simply an indication of sensor reversibility: Fig. 10 predicts that as soon as the force reduces below f^∗, most of the FAK molecules would fold back and autoinhibit their action.

Conclusions

Figs. 6 and 7 each contain lots of information, but when we link the two we uncover the true nature of this reversible mechanosensor. If we place a cell on a substrate of given stiffness κ_f (or Young’s modulus Y_f), then, if the cytoskeletal tension is initially zero, the mechanosensors will generate a positive feedback loop: FAK activation leads, via the Erk or Rho GTPase pathways (25), to the increased production of actin and activation of myosin. Assembling more F-actin, and using more motors, the cell will increase tension in the cytoskeleton, which will further increase the rate of FAK activation on stiffer substrates. This positive feedback goes until approximately the peak position of the curves in Fig. 7 a, after which the further increase of tension shuts down the FAK activation response. The resulting negative feedback loop returns the cell to its homeostatic level of the cytoskeleton tension f(κ_f), corresponding to the given substrate stiffness. If we look at the stiffness sensitivity of the FAK complex at this fixed level of force, f(κ_f), we find the maximum sensitivity (identified with the peaks in Fig. 6 b) is very close to the actual substrate stiffness, κ_f. So, this physical model describes a naturally adaptive sensor: not only does cytoskeletal tension adjust according to the substrate stiffness, but this remodeling adapts the sensor response so that it remains sensitive to its immediate surroundings—small changes in the substrate stiffness will give large changes in the activation rate of FAK activation once the positive and negative feedback rebalance in homeostasis.

This is desirable behavior in a biological sensor, and it is remarkable that it is produced in our simple model with no prior stipulation. We initially only required that the cell be responsive to changes in the stiffness—how big these changes were, or if they were optimal, was not close to the front of our minds. For such a simple model to predict useful adaptive sensing behavior is exciting to us.

Importantly, on soft substrates (gels or soft tissues), the FAK signaling feedback is always negative and FAK autoinhibition on its own would lead to a very low cytoskeletal tension—no focal adhesions or stress fibers are formed on such substrates. It is likely that other mechanosensors become more relevant on very soft substrates (and in planktonic suspension), such as the TGF-β latent complex (13): after all, the very name of FAK suggests its relation to focal adhesions, which only occur in stiffer environments. This idea corresponds very well with experimental work showing that cells on sufficiently soft substrates do not form stable focal adhesions (72).

Focal adhesions are extremely complex assemblies, and it would be naive of us to suggest that FAK is the only way the cell responds to its mechanical environment. In reality, we feel it is likely that several options for mechanosensing exist at focal adhesions, and not one of them tells the whole story. We feel that there is a role for FAK to play in this story, but perhaps the clustering of integrins is a significant factor—at least on stiff substrates.

Why did we choose to focus on FAK? We could instead (or simultaneously) examine any of the other big molecules with autocatalytic activity involved in the force chain in Fig. 2. The obvious alternative would be talin, which has the confirmed connection between integrin and actin (30) and the large conformational change under applied force (41). However, as already stated, the literature acknowledges the crucial role of focal adhesion kinase in mechanosensing at focal adhesions (4, 20), but does not yet understand how this role takes place. With the context of the simulation study (42), we felt it would be most stimulating to frame our discussion in terms of FAK. It may be that maybe talin and FAK both play the same role—in this case, it feels natural that any modification to the model happens at a higher level, when the kinetic equations of all the mechanosensing processes are written down and analyzed.

We did not attempt to capture any collective effects in this model, and acknowledge that there is significant ground to be gained in expanding our model to one describing the allosteric coupling. As an example of an extension to collective effects within our model, we note that phosphorylated FAK acts on several important signaling molecules, such as Rho and Rac. If these molecules act to increase the tension in actin filaments in the broad vicinity, rather than strictly for filaments attached to active FAK molecules, then there will be a cooperative effect—once a single focal adhesion kinase autophosphorylates, the tension in surrounding filaments will increase, and this increases the probability of a second opening event, and so on.

The dependence of the FAK opening rate on viscoelastic stress relaxation partly explains results obtained in experimental work on cell spreading with different viscoelastic substrates (69). Chaudhuri et al. (69) saw suppression of cell spreading (associated with lower FAK activation) on substrates with significant stress relaxation, compared with purely elastic substrates of nominally the same storage modulus. We should note that we fail to capture the behavior Chaudhuri et al. (69) observed at very low stiffness (1.4 kPa). On such a soft substrate, they saw that the number of cells with stress fibers was actually enhanced on substrates with stress relaxation—the opposite trend to stiffer substrates. This is not surprising; our model deals with mature focal adhesion complexes that would not develop on substrates of ∼kPa stiffness.

In summary, this work develops a theoretical model of the physical mechanism that a reversible mechanosensor of the second kind should use. We focus all our discussion on the focal adhesion kinase, in association with integrin and talin, connecting the force-providing cytoskeletal F-actin and the varying-stiffness ECM. However, the fundamental principles of the model apply to many multidomain protein complexes. The next steps are to link the main result of this work (the rate of opening K₊) with the nonlinear dynamics of one or several signaling pathways that produce the morphological response of the cell to the signal the mechanosensor generates.

Author Contributions

All authors contributed to carrying out research and writing the article.

Editor: Alexander Dunn.