Abstract
Collective cell migration underlies many biological processes, including embryonic development, wound healing, and cancer progression. In the embryo, cells have been observed to move collectively in vortices using a mode of collective migration known as coherent angular motion (CAM). To determine how CAM arises within a population and changes over time, here, we study the motion of mammary epithelial cells within engineered monolayers, in which the cells move collectively about a central axis in the tissue. Using quantitative image analysis, we find that CAM is significantly reduced when mitosis is suppressed. Particle-based simulations recreate the observed trends, suggesting that cell divisions drive the robust emergence of CAM and facilitate switches in the direction of collective rotation. Our simulations predict that the location of a dividing cell, rather than the orientation of the division axis, facilitates the onset of this motion. These predictions agree with experimental observations, thereby providing, to our knowledge, new insight into how cell divisions influence CAM within a tissue. Overall, these findings highlight the dynamic nature of CAM and suggest that regulating cell division is crucial for tuning emergent collective migratory behaviors, such as vortical motions observed in vivo.
Introduction
A fundamental process of animal life, collective cell migration builds organs, heals wounds, and spreads cancer (1, 2, 3, 4). As a “collective” process, the emergent cellular motion is coordinated by chemical or mechanical interactions between cells, in the form of chemotaxis or cell-cell adhesions (2, 5, 6, 7). On one hand, this coordinated behavior can facilitate the transport of many cells across large distances: coordinated exchange of neighboring cells enables the formation of a three-dimensional (3D) body plan during gastrulation (8, 9, 10); collective migration builds complex, branched organs, as in kidney (11) and mammary morphogenesis (12); and multicellular invasion spreads metastatic cancer cells in a manner that depends on the internal fluid mechanics of the tumor (13). On the other hand, coherent cellular motion can occur within a relatively small, confined area: vortices of collectively moving cells form and persist during the development of the primitive streak in gastrulating embryos (14). This latter type of collective motion, termed collective angular motion (CAM), is not well understood, and it is unclear how such cellular vortices may arise, persist, or change over time.
Progress in uncovering quantitative details of CAM has primarily resulted from simulations or experiments using two-dimensional (2D) epithelial tissues (15, 16, 17, 18). In such cases, well-defined tissues are created from cells cultured on a planar microfabricated adhesive template. Over time, the cells move coherently about a central axis within the tissue. Surprisingly, this cellular motion can fluctuate over time, as non-periodic switches in the orthoradial direction of the global velocity distribution indicate changes in the direction of CAM. These fluctuations, however, are thought to arise purely in a stochastic manner. As such, details regarding this “stochasticity” and the concomitant changes in direction of collective rotation remain unclear.
Simulations of epithelial monolayers have revealed that robust CAM occurs when at least a few cells can move persistently with minimal fluctuations in some internal direction of polarization (18). But what might disrupt this cellular persistence and influence fluctuations in the cellular motion? In unbounded monolayers, cell divisions induce active stresses to generate hydrodynamic flow of surrounding cells, with a single division event influencing cells located up to 100 μm (5–10 cell diameters) away (19). Thus, it seems plausible that cell divisions may influence or facilitate the onset of CAM within bounded epithelial tissues. Furthermore, simulations of tissues constrained to annular geometries suggest that synchronous cell divisions, in which all cells within the tissue divide simultaneously, are required to influence patterns of migration (20). However, synchronous divisions are relatively rare in these types of systems (15, 16, 17, 18), and so the extent to which cell division might influence CAM within epithelial tissues remains unclear.
Here, we investigated the effects of cell division on the onset and spatiotemporal dynamics of CAM. Using 2D engineered mammary epithelial tissues, we quantified the onset of collective rotation, as well as switches in its direction. We found that cell divisions, which have been ignored by most previous models, play an important role in collective rotation. Finally, we provide quantitative details that illustrate how perturbations induced by cell divisions dictate the emergence and reemergence of CAM in epithelial tissues. We thus provide quantitative insight into a mode of collective migration that is involved in many biological processes, including establishing a 3D embryo (14) and facilitating multicellular morphogenesis (21).
Materials and Methods
Cell culture and reagents
Functionally normal EpH4 mouse mammary epithelial cells were cultured in 1:1 Dulbecco’s modified Eagle’s medium: Ham’s F12 nutrient mixture (DMEM:F12) (GE Healthcare Life Sciences, Marlborough, MA) supplemented with 2% fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA), 50 μg/mL gentamycin (Gibco, Gaithersburg, MD), and 5 μg/mL insulin (Sigma-Aldrich, St. Louis, MO). To label nuclei, cells were transduced with recombinant adenovirus encoding for histone 2B (H2B)-mCherry at a multiplicity of infection resulting in >99% transduction efficiency. To inhibit cell division, tissues were treated with 5 μg/mL mitomycin C (Santa Cruz Biotechology, Dallas, TX) or 0.1 μg/mL aphidicolin (Sigma-Aldrich) for 1 h, extensively washed with fresh culture medium, and allowed to equilibrate for 30 min before timelapse imaging. Cells were cultured at 37°C in a 5% CO2 atmosphere.
Microfabrication of 2D epithelial tissues
Islands of fibronectin were prepared as described previously (22). Briefly, sterile stamps of polydimethylsiloxane (PDMS; Sylgard 184) were coated with 25 μg/mL fibronectin (BD Biosciences, Franklin Lakes, NJ) in phosphate-buffered saline (PBS) for 2 h and dried under compressed nitrogen. Fibronectin was microcontact-printed onto custom-made, ultraviolet/ozone-treated, PDMS-coated glass-bottom tissue culture dishes, and unstamped regions were blocked with 1% Synperonic F108 (Fluka, Buchs, Germany) in PBS. Cells were seeded and allowed to reach confluence on the resulting islands of fibronectin.
Immunofluorescence analysis
To visualize E-cadherin, tissues were prepared as described above and fixed with 4% paraformaldehyde. Samples were rinsed with PBS supplemented with 0.3% Triton X-100, blocked with 0.1% bovine serum albumin in PBS, and incubated with primary antibody against E-cadherin (Cell Signaling Technology, Danvers, MA). Samples were then rinsed with PBS and incubated with Alexa-conjugated secondary antibodies (Invitrogen, Carlsbad, CA). Nuclei were counterstained with Hoechst 33342 (Invitrogen). Images were acquired with a Plan Fluor 20×/0.45 NA air objective (Nikon, Tokyo, Japan) and captured with a Hamamatsu Photonics (Hamamatsu City, Japan) Orca-1394 camera.
Timelapse imaging
Timelapse imaging was performed using a Nikon Ti-U inverted microscope equipped with a stage-top incubator maintained at 37°C in a 5% CO2, 90% relative humidity atmosphere (Pathology Devices, Westminster, MD). Tissues were imaged every 15 min through a Plan Fluor 20×/0.45 NA air objective (Nikon) using a Hamamatsu Orca-100 camera. Automated stage control enabled the imaging of multiple tissues in a single experiment. Tissues with visibly apoptotic cells were excluded from subsequent analysis.
Quantification of tissue movement
Nuclear positions were tracked from the H2B-mCherry timelapse images using Bitplane Imaris version 7.1.1 or the Manual Tracking plugin in ImageJ. Each cell was tracked until it divided, at which point two new tracks spawned from the positions of the daughter cells’ nuclei. To characterize coherent motion of cells within a tissue, we fit the position vectors of all nuclei present in adjacent time points to a simple mathematical relationship in which all points (i.e., nuclei) are subject to collective rotation or translation, with some deviation. This is represented in Eq. 1:
| (1) |
Here, refers to the rotational transformation tensor and refers to the translation transformation vector, both of which are applied to all cells within the tissue at time t. These transformations are given by the following formulae:
Additionally, refers to the position vector of the ith cell at time t and refers to the position of the ith cell at the next time point, i.e., time t + 1. The deviation of the position of the ith nucleus from the position predicted by a rotational and translational transformation of the previous set of nuclei is given by . This value is equivalent to the displacement between the predicted and the measured positions of the ith cell at time t + 1 and represents deviations from “ideal” tissue movement. Here, ideal tissue movement refers to movement in which cells translate or rotate as a collective without changing positions relative to one other.
The parameters , , and were computed by minimizing the sum-square error of the deviation between the model predictions and the experimental results for N cells at each time t (Eq. 2):
| (2) |
Cells that divided over the period t to t + 1 were excluded from the analysis at time t. At each time step, was computed. The cumulative rotation of the tissue, relative to its original orientation, up to a given time t was determined by summing all prior (Eq. 3):
| (3) |
The rotation of each tissue was automatically evaluated by determining when the tissue persistently rotated with an average outer velocity, , of 15 μm/h:
Here, represents the average angular velocity between t and t + 3 and L represents the edge length of the tissue. This threshold reproducibly corresponded to periods of coherent rotational motion readily identifiable to an unbiased observer. All quantification was performed using custom scripts written in MATLAB (release 2015b; The MathWorks, Natick, MA).
Simulation of tissue movement
A minimalistic model, similar to those used elsewhere (23), was created to capture the essential physics of the underlying cellular motion. In this model, the positions of particles with defined radii, hereafter referred to as “cells,” were updated by a force balance that accounts for repulsion, flocking, persistence, and fluctuations (Fig. S1 in the Supporting Material). In the limit that the effective cellular viscosity dominates inertial terms, this balance reduces to Eq. 4:
| (4) |
Here, represents the position vector of the ith cell within the tissue; the repulsive term, , discourages multiple cells from occupying the same position in space; the flocking term, , accounts for intercellular adhesive interactions that align the trajectories of neighboring cells; the persistence term, , biases the motion of a cell toward its previous trajectory (Fig. S2); and the noise term, , provides for local fluctuations that may influence cellular motion. Normalizing by , the viscous drag coefficient, Eq. 4 reduces to Eq. 5:
| (5) |
In this form, the constants , , , and weight the contribution of cell-cell repulsion, flocking, persistence, and random fluctuations in updating the next position of a given cell, gives a dimensionless vector determined by short-range repulsive interactions with neighboring cells, gives a dimensionless vector determined by flocking interactions, gives the prior velocity of the ith cell, and gives a unit vector with a random angle in the interval . By specifying Hookean repulsion (23, 24), the dimensionless vector associated with cell-cell repulsion, , takes the form of Eq. 6:
| (6) |
Here, ai,t represents the radius of the ith cell at time t, is the initial size of the cells at the start of the simulation, represents the distance between the center points of the ith and jth cells, and H(z) is the Heaviside function. In this form, repulsion occurs only when the center points of two cells come closer than the sum of their radii (Fig. S1 a). Since we estimate the magnitude of repulsion to be proportional to the cell radii (described below), the prefactor scales the repulsive interaction by the size of the cell.
The dimensionless vector arising from flocking interactions accounts for Vicsek-like alignment of particle velocities (25) and is specified by Eq. 7:
| (7) |
Here, gives the prior angular velocity of the jth cell that resides within the distance R of the ith cell. The jth cell was allowed to exert a flocking interaction on all cells separated by < from the jth cell (Fig. S1 b). This requirement corresponds to an interaction radius, R, specified by the form . By specifying the interaction radius in this way, we ensure that a cell’s velocity is only influenced by its immediate neighbors. The prefactor serves to weight the flocking interaction of nearby cells to a greater extent than cells farther away but still within the interaction radius.
At the start of a given simulation, four cells were placed uniformly within a square region corresponding to the boundaries of the engineered tissues that were used experimentally. Hard boundaries were enforced in the simulations such that any cell about to cross an outer edge instead moved along that boundary for the remainder of that time step. To facilitate comparison with the experimental observations, the edge length of the boundary in the simulation was chosen to be 50 units wide so as to provide a 1:1 correspondence with the experimental space. Furthermore, by estimating parameters from experimentally observed cell displacements, we implicitly specified a 1:1 correspondence between simulation and experimental time units. In particular, all cell positions were simultaneously updated according to Eq. 5 based on current positions and prior movements at time intervals corresponding to three experimental minutes. In this way, simulation parameters were appropriately scaled from experimental observations to produce motion that mimicked the dynamics of 50 × 50-μm tissues.
Incorporating cell division into simulations
After the initial placement of cells during the simulation setup, each cell was assigned a random cell division time between simulation time points corresponding to 0 and 15 h. Once a cell divided, its progeny were assigned random, subsequent division times randomly selected between 11.5 and 15 h later. These specifications were chosen to correspond to the experimentally observed doubling time for these cells (Fig. S3 a).
A cell was treated as “actively dividing” for six simulation time points, corresponding to 18 experimental minutes. During this brief time, the cell stopped moving for one time point and then split into two daughter cells spaced a simulation distance equivalent to 15 μm apart for the remainder of the mitotic time, corresponding to experimental observations (Fig. S3 b). For subsequent analyses of simulation data, the time point following birth of daughter cells was chosen as the time index for that division event. The orientation of this cell division was specified to preferentially occur perpendicular to the radial direction within the tissue (Fig. S1 e), matching experimental observations (Figs. S3 c and S4).
Additionally, repulsive interactions were removed from the mitotic cell and a weak attractive force, directed toward an actively dividing cell i, was applied to all nearby non-dividing cells j (Eq. 8):
| (8) |
Here, represents the distance between the jth cell and cell i, the actively dividing cell.
Incorporating produced cell movement that mimicked the experimentally observed motion of cells into regions adjacent to mitotic cells as they retract their membranes, round up, and begin to divide (Fig. S5). Finally, the radii of daughter cells were chosen such that each division conserved cell area.
Estimation of model parameters
In the model used here, the positions of all cells were updated at each time point according to Eq. 5, which contains four free parameters, the constants , , , and . To use physiologically relevant values, each of these constants was approximated from effective cellular material properties and the experimentally observed motion: , where is the effective spring constant, is the initial cell radius, is the viscous drag coefficient, is the effective elastic modulus, and is the effective viscosity of a cell; , where denotes the average cell displacement per time interval; and , where denotes the average error per time interval given in Eq. 1. Since, as observed experimentally, the motion of a given cell is similar to its previous trajectory 10% more often than would be expected if its movement was purely random (Fig. S2), the persistence constant, , was taken to be an order of magnitude less than . Given the observed experimental and literature values, ∼102–103 Pa (26), ∼ 10 μm, ∼ 104 Pa·s (26), ∼ 3 μm/15 min, ∼ 5 μm/15 min, the model used the coefficients ∼ 1–10 μm/min, ∼ 0.1–1 μm/min, and ∼ 0.01–0.1 μm/min. , present only when cells actively divided, was taken to be on the same order of magnitude as . Specific values and terms used in the model are listed in Table S1.
Statistical analysis
Results were analyzed with MATLAB (release 2015b; The MathWorks, Natick, MA). We used a one-tailed Fisher’s exact test to compare the frequencies at which CAM or switches in the direction of rotation occurred in tissues treated with or without cell cycle inhibitors. We evaluated the dependence of the onset of CAM on the position and angle of cell division with a one-tailed Fisher’s exact test and the χ2 goodness-of-fit test comparing the experimental and simulated results to a uniform distribution.
Results
Microfabricated 2D epithelial tissues exhibit CAM
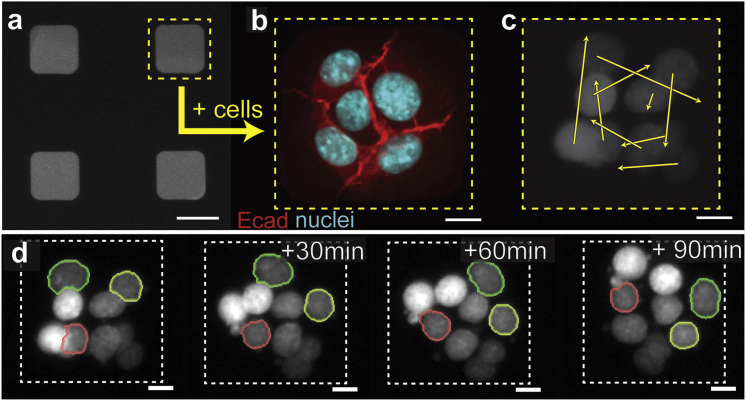
To investigate quantitatively the collective behavior of epithelial tissues, we prepared arrays of well-defined epithelial monolayers. Specifically, we used microcontact printing to produce micrometer-scale islands of fibronectin on a silicone surface (Fig. 1 a). Phenotypically normal mouse mammary epithelial cells that expressed H2B-mCherry as a nuclear marker were seeded on these islands, and they formed bounded epithelial tissues (Fig. 1 b) at initial densities ranging from 1.1 to 2.5 cells/900 μm2. We used the H2B-mCherry signal to track the positions of the cells over time and observed that these tissues exhibited CAM, as evidenced by sequential image frames (Fig. 1 d) and the corresponding displacement maps (Fig. 1 c). This agrees with previous observations of CAM arising in bounded tissues consisting of Madin Darby canine kidney epithelial cells (15, 16, 17) and suggests that CAM is an emergent phenomenon general to cultured epithelial tissues.
Figure 1.
2D microfabricated mammary epithelial tissues exhibit CAM. Epithelial monolayers of defined geometry were produced by (a) microcontact printing micrometer-scale islands of fibronectin onto a silicone surface and seeding phenotypically normal mammary epithelial cells onto these regions, resulting in (b) confluent epithelial tissues. Cells within these tissues exhibit CAM, as observed in (c) the displacement field and (d) image sequence of a representative tissue. Three cells in (d) are outlined to ease visualization of CAM. The scale bars represent (a) 50 μm and (b–d) 10 μm. To see this figure in color, go online.
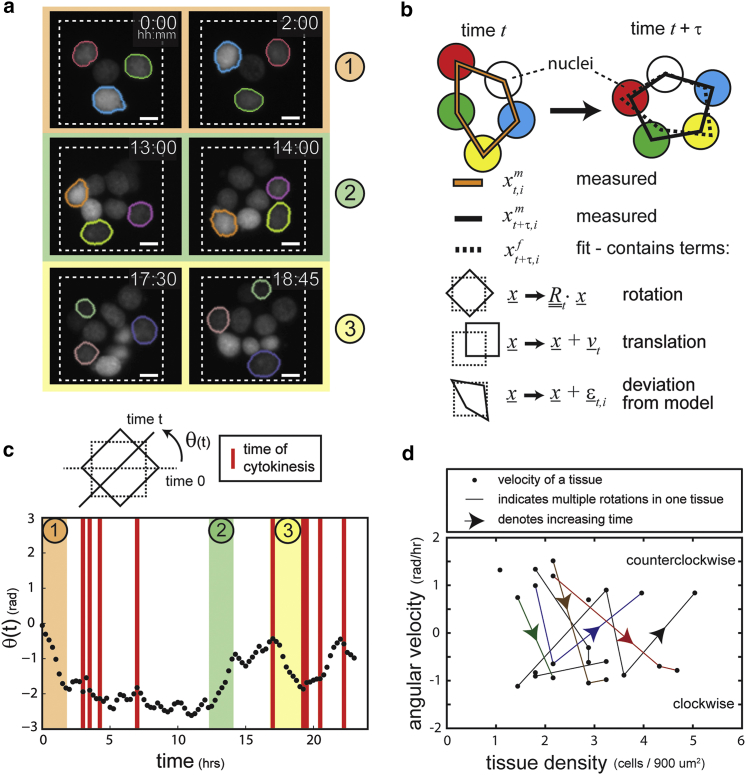
The direction of rotation switches over time
We observed that the direction of rotation often switched over time (Fig. 2 a; Movie S1), consistent with previous observations (16). To describe more precisely the rotational motion of the tissues, we quantified the overall rotation and translation of the cellular collective (Fig. 2 b). This process applied a rotational and translational transformation to the position vectors of all nuclei at a given time point. The parameters of these transformations were calculated by minimizing the deviation between the predicted positions (using the transformations) and the actual positions measured at the next time point. One output of this calculation is a rotational term that describes the best-fit rotational motion of the tissue between two time points. By summing the rotational terms from the initial time point up to the current time point, we obtained , a measure of the extent of tissue rotation over time (Fig. 2 c).
Figure 2.
The direction of rotation switches over time. (a) Three different periods of CAM (orange, green, and yellow) during the observation of a given tissue demonstrate that the direction of CAM can switch over a 24-h period of observation. A subset of nuclei are highlighted to help visualize rotational motion. The scale bars represent 10 μm. (b) The best-fit bulk rotational motion of a tissue, θ(t), is determined by comparing the measured positions of the cells with those predicted if the tissue were subjected to purely rotational or translational motion. See Materials and Methods. (c) Periods of CAM can be observed within a representative tissue as periods of steadily increasing or decreasing θ(t). This representative tissue shows switches in the direction of CAM over the duration of observation. Note that the colored regions correspond to the periods of CAM illustrated in (a). Red bars indicate a cell division event. (d) The rotational velocities of tissues often switch sign, indicating a change in direction, as the tissue density increases because of cell division. The solid lines connect periods of CAM that are observed in a given tissue as time and density increase. To see this figure in color, go online.
When we applied this quantification approach to the timelapse data from multiple tissues, we observed that cell divisions often preceded or coincided with both the onset of CAM and switches in rotational direction (Fig. 2 c). Here, a persistent increase in indicated counterclockwise rotation of the tissue, whereas a persistent decrease in indicated clockwise rotation. Periods of CAM were determined by finding consecutive time points encompassing at least 1 h in which the tissue persistently rotated with an average outer velocity of 15 micrometer/h. Employing this threshold reproducibly yielded periods of CAM that agreed with the coherent tissue movements qualitatively discerned from the timelapse movies (Fig. 2, a and c). Between periods of rotation, the tissues often exhibited cell divisions, cell rearrangements, and disorderly motion. Changes in within these interim periods were therefore treated as noise that did not indicate significant CAM.
The dynamic nature of the rotational motion was further illustrated when monitoring the rotational velocities achieved over the course of timelapse imaging (Fig. 2 d). Rotation occurred in both directions, as indicated by both positive and negative velocities, and switches in the direction of rotation occurred as the tissue density increased after cell divisions. These changes in rotational direction often followed individual cell division events (Fig. 2 c), suggesting that a single cell could influence the rotation of the entire population and that synchronous divisions throughout the population are not required for tissues to change their direction of rotation. Taken together, these results suggest a possible link between cell divisions and the onset and switching of collective motion, features previously attributed to stochastic noise (16).
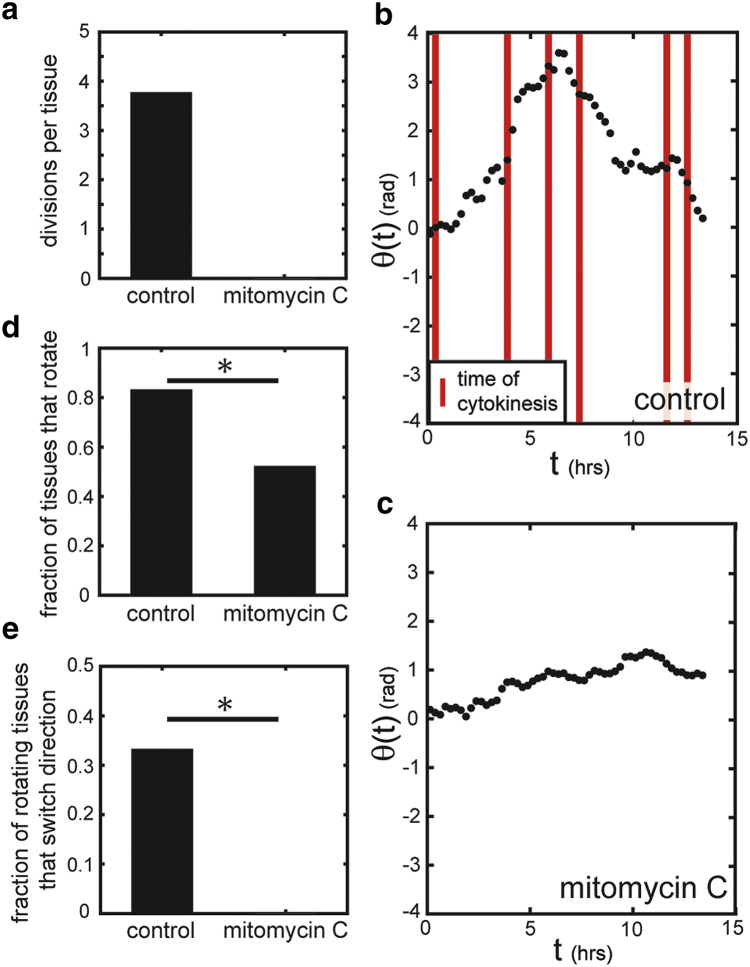
Blocking cell division impairs CAM
Given that changes in the direction of CAM often correlated with cell divisions, we next investigated how blocking proliferation might influence the dynamic behavior of the tissues. We treated tissues with mitomycin C, which impairs cell cycle progression through cross-linking-mediated DNA damage (27). Over a 14-h period of timelapse imaging, cells in mitomycin-C-treated tissues did not divide (Fig. 3 a). Compared to untreated tissues (Fig. 3 b; Movie S2), those treated with mitomycin C exhibited fewer cell rearrangements and impaired CAM (Fig. 3 c; Movie S3). Specifically, eliminating cell divisions significantly reduced the number of tissues that exhibited CAM (Fig. 3 d) and abolished the fraction of rotating tissues that exhibited switches in rotational direction (Fig. 3 e). This was not a result of changes in individual cell motility, as mitomycin C did not affect cell speed (Fig. S6). We observed similar behavior in tissues treated with aphidicolin, another inhibitor of cell cycle progression (Fig. S7). These results suggest that cell divisions promote the dynamic CAM that is observed in epithelial tissues and induce switches in the direction of collective rotation.
Figure 3.
Blocking cell division impairs CAM within tissues. (a) Treatment with mitomycin C abolishes cell divisions over a 14 hr period of observation. (b) Untreated tissues exhibit greater CAM compared to (c) tissues treated with mitomycin C. (d) The fraction of tissues exhibiting at least one period of CAM is significantly reduced in tissues treated with mitomycin C, as compared to untreated tissues. (e) The fraction of rotating tissues that exhibit switches in the direction of CAM is significantly reduced in tissues treated with mitomycin C, as compared to untreated tissues. To generate these plots, rotational motion starting 90 minutes after the beginning of experimental observation was analyzed to ensure that cell division did not immediately precede the period of analysis. ∗p < 0.05. To see this figure in color, go online.
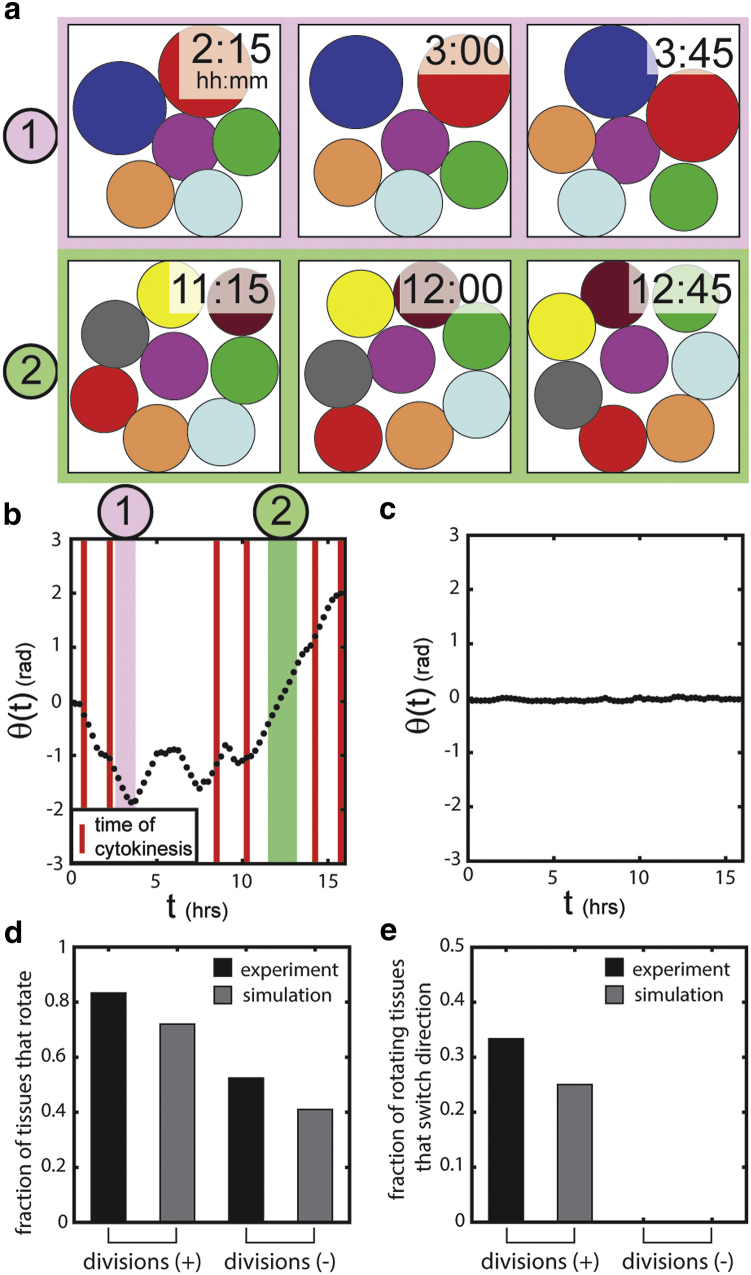
Particle-based simulations recreate cell-division-dependent CAM
The experimental results described above demonstrate that cell divisions are necessary for dynamic CAM. However, it is not clear how a perturbation introduced by a dividing cell eventually contributes to an altered rotational state, as cell divisions have been excluded from previous quantitative models that attempt to describe CAM in bounded tissues (15, 16, 18). We thus created a minimalistic, particle-based model to replicate the observed behavior and make predictions about how dividing cells might facilitate the onset of CAM. As described by Eqs. 4 and 5, cells were treated as 2D particles that experience viscous drag, close-proximity repulsive forces, persistence, and local velocity alignment by the motion of neighboring cells (Fig. S1). The local velocity alignment, often observed in the flocking behavior of birds (28) and locusts (29), was included to mimic the intercellular mechanical interactions expected from epithelial cells. Employing this model revealed that simulated tissues exhibit periods of CAM similar to that observed in the experiments (Fig. 4 a). Simulated tissues in which cells could divide demonstrated dynamic CAM (Fig. 4 b; Movie S4), whereas removing cell division from the simulations often resulted in diminished CAM (Fig. 4 c; Movie S5). These qualitative trends agree with experimental observations (Fig. 3).
Figure 4.
Simulated tissues exhibit dynamic CAM and recreate the experimentally observed trends. (a) Two different periods of CAM observed in a simulated tissue. These simulations occurred within a square region corresponding to the experimental tissue boundaries. See Materials and Methods. Note that the indicated simulation times correspond to analogous experimental times. (b) Dynamic CAM is observed in simulated tissues that include cell division. The colored regions correspond to the periods of CAM illustrated in (a). Red bars indicate a cell division event. (c) Simulated tissues that do not include cell divisions do not exhibit dynamic CAM. (d and e) The model reproduces division-dependent trends that are observed experimentally, namely (d) the fraction of tissues undergoing CAM and (e) the fraction of rotating tissues that switch direction. The experimental data correspond to those depicted in Fig. 3, d and e. To see this figure in color, go online.
To better compare the model to the experimental results, we performed simulations of tissue movement and analyzed the results using the quantification scheme described above (Fig. 2 b). Juxtaposing the analysis of experimental (N = 18) and simulated (N = 200) tissues revealed strikingly similar trends. In both cases, most tissues exhibited CAM when cells could divide, and CAM was reduced when cell division was removed (Fig. 4 d). Similarly, little or no switching of the direction of CAM was observed in the absence of proliferating cells, whereas an increased fraction of tissues switched direction when cells could actively divide (Fig. 4 e). Thus, a minimalistic model incorporating flocking interactions of noisy particles embedded in a viscous medium faithfully reproduced the migratory trends observed experimentally across many tissues in culture.
The position of a dividing cell, rather than its axis of division, correlates with increased incidence of CAM
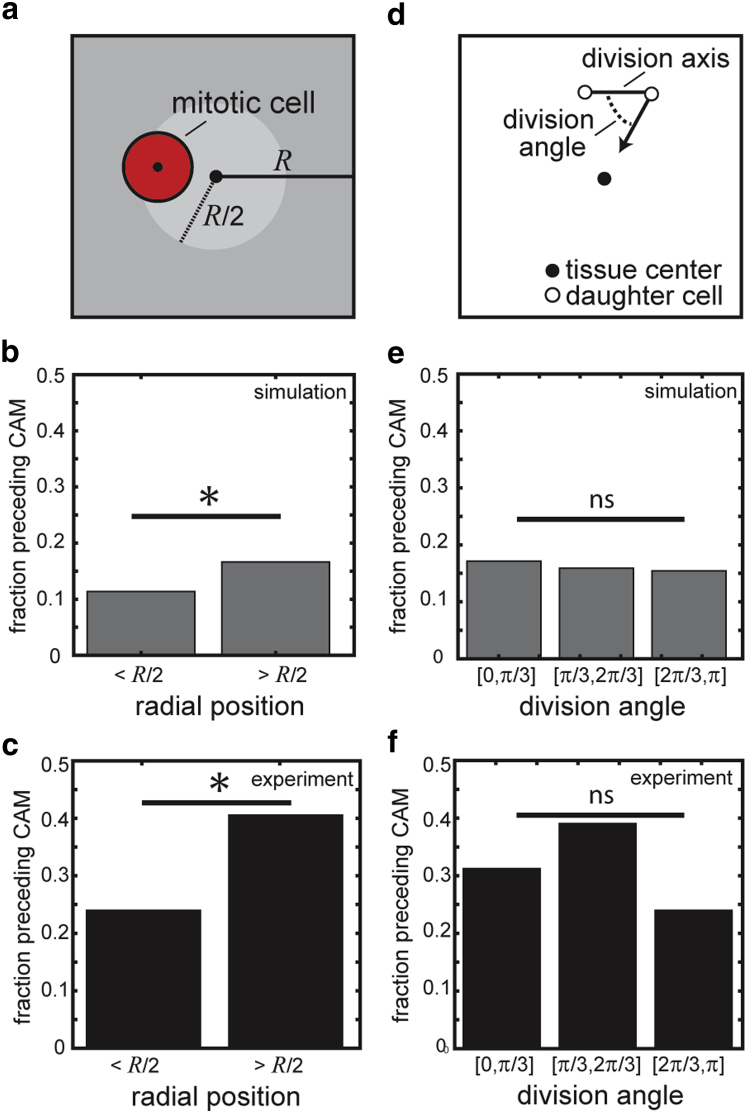
Using this minimalistic model, we sought to predict how particular details of a cell division event might promote the onset of CAM. Specifically, we investigated two factors, the position of the dividing cell within the tissue as it underwent cytokinesis (Fig. 5 a) and the orientation of the axis along which the cell divided (Fig. 5 d). To define how each factor might correlate with the onset of CAM, we simulated 200 tissues, recorded how each cell divided, and isolated periods of time during which the tissue rotated coherently. We then determined which cell divisions occurred between 3 h before the onset of CAM and 1 h before the conclusion of CAM and marked these as likely to promote CAM.
Figure 5.
Simulations and experiments suggest that the location of cell division influences the onset of CAM. (a) To evaluate whether the position of a dividing cell within the tissue might contribute to the onset of CAM, all divisions were binned by radial position. In both (b) simulations and (c) experiments, divisions at the periphery of the tissue more frequently precede a period of CAM than divisions closer to the tissue center. (d) Similarly, cell divisions were binned by the angle along which the cell divides to determine whether this property might contribute to CAM. In this case, (e) simulations and (f) experiments both reveal that the orientation of the division axis does not preferentially promote CAM. ∗p < 0.05. To see this figure in color, go online.
Using the data set of simulated cell divisions, we first investigated whether the position of a dividing cell might contribute to the onset of tissue rotation. Here, division events were segregated according to the radial position of the cell within the tissue immediately before it underwent cytokinesis (Fig. 5 a). The data from the simulations predicted that dividing cells located closer to the tissue periphery more frequently preceded the emergence of CAM (Fig. 5 b). Performing the same analysis with the experimental data revealed a similar dependence: CAM arose more often after division of a cell located near the periphery of the tissue (Fig. 5 c). These findings are consistent with the time courses described above: as 50% and 66% of periods of CAM correlated with peripheral cell divisions in Figs. 2 c and 3 b, respectively, but only 33% correlated with interior cell divisions. Furthermore, we observed a similar correlation between the onset of CAM and the location of cell division in tissues of smaller and larger sizes (Fig. S8).
Given the importance of the position of a cell division, we wondered whether the division orientation might similarly contribute to the onset of CAM. To evaluate this quantitatively, we first determined the line segment defined by the positions of the two daughter cells immediately after cytokinesis and then calculated the angle between this axis and the radial base vector (Fig. 5 d). Binning the simulation data by this orientation value revealed that CAM did not arise with any preference toward the division axis (Fig. 5 e). A similar relationship was again observed in the experimental data: the axis of cell division did not affect the emergence of CAM (Fig. 5 f). Taken together, these results further demonstrate that the minimalistic model faithfully resembles the tissues in culture and suggests that the position of the cells as they divide is an important consideration in the dynamic, coherent motion of cells that arises within a tissue.
Discussion
Cells move coherently within tissues during morphogenetic processes in vivo as well as in engineered systems in culture. Here, we used engineered mammary epithelial monolayers to investigate CAM, one specific mode of collective motion. Our experiments and simulations reveal that dividing cells are necessary for robust emergence of CAM and also cause switches in the direction of rotation. These results are consistent with a recent study that characterized the forces generated by cell division in relation to patterns of cell migration that arise in unbounded epithelial monolayers (19), though specific details of the cell divisions were not investigated in that study. Taken together, our findings highlight the importance of dividing cells within tissues that exhibit complex behavior. Given that coherent motion is ubiquitous in multiparticle systems, from cell biology to ecology to granular mechanics, it will be interesting to determine whether the effects of introducing new particles are broadly generalizable to the internal dynamics of diverse systems.
Although our analysis is unable to distinguish between the influences of cell divisions that occur in quick succession, our results suggest that dividing cells located near the periphery of a tissue favor the onset of CAM. For this reason, it seems possible that the spatial pattern of cell division might be regulated during examples of CAM in vivo. One such instance occurs in the developing chicken embryo, where epiblastic cells rotate collectively before and during the formation of the primitive streak (14, 30). Although the cells within this epithelium divide at a low rate during the process, BrdU incorporation assays have revealed elevated proliferation in the cells located near the boundary of the migrating epithelium (31). Although the functional significance of this patterning has not been previously described, properly regulated cell divisions might be necessary to facilitate the rotational motion and to prevent aberrant switches in the direction of CAM, two requirements for avoiding potentially catastrophic deviations from normal morphogenesis. Experimental observations are consistent with this postulation, as CAM does not occur and gastrulation fails when cell proliferation is pharmacologically inhibited in the developing chicken embryo (30, 31). Disrupted CAM has been associated with a diseased phenotype in other contexts as well (15). Insightful work in the future might help elucidate whether cell division contributes to CAM by altering the profile of stress exerted by cells within a tissue or by acting as a local source of particle velocity alignment that manifests as CAM in a purely probabilistic manner.
Our results also provide insight into a potential source of stochasticity within an active material. Over time, cells migrate and interact mechanically with their neighbors. When a cell divides, it creates a local disturbance that can disrupt the motion of neighboring cells. In the epithelial tissues considered here, the presence of cell divisions leads to the emergence of CAM and potentially a switch in the direction of rotation. Such switches were previously attributed to the noisy movement of the cells (16). Explicitly incorporating cell divisions thus removes a potential confounding variable from this intrinsic noise. Future models of collective cell migration should account for cell divisions, when they are warranted, to provide a more complete description of the biological phenomenon being studied.
Finally, the work described here suggests an intriguing possibility for a feedback loop that specifies the onset of collective cell migration and regions of patterned cell proliferation. Specifically, it is known that patterns of mechanical stress within an epithelial tissue define patterns of cell proliferation (32). It thus seems reasonable that the endogenous mechanics generated by a tissue favor specific locations for cell division, which may induce the onset or switching of CAM, which may in turn generate active stresses within the tissue to again promote cell proliferation. It will be interesting to determine in future work how CAM influences the onset of cell divisions.
Author Contributions
M.J.S. designed research, performed research, and wrote the article; S.M. performed research; I.G.K. designed research; and C.M.N. designed research and wrote the article.
Acknowledgments
This work was supported in part by grants from the National Institutes of Health (GM083997, HL110335, HL118532, HL120142, and CA187692), the National Science Foundation (CMMI-1435853), the David and Lucile Packard Foundation, the Alfred P. Sloan Foundation, the Camille and Henry Dreyfus Foundation, and the Burroughs Wellcome Fund. M.J.S. was supported in part by the National Science Foundation Graduate Research Fellowship Program. C.M.N. was supported in part by a Faculty Scholar Award from the Howard Hughes Medical Institute.
Editor: Sean Sun.
Footnotes
Eight figures and five movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30501-5.
Supporting Material
References
- 1.Siedlik M.J., Nelson C.M. Regulation of tissue morphodynamics: an important role for actomyosin contractility. Curr. Opin. Genet. Dev. 2015;32:80–85. doi: 10.1016/j.gde.2015.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Scarpa E., Mayor R. Collective cell migration in development. J. Cell Biol. 2016;212:143–155. doi: 10.1083/jcb.201508047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Méhes E., Vicsek T. Collective motion of cells: from experiments to models. Integr. Biol. 2014;6:831–854. doi: 10.1039/c4ib00115j. [DOI] [PubMed] [Google Scholar]
- 4.Mayor R., Etienne-Manneville S. The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 2016;17:97–109. doi: 10.1038/nrm.2015.14. [DOI] [PubMed] [Google Scholar]
- 5.Theveneau E., Steventon B., Mayor R. Chase-and-run between adjacent cell populations promotes directional collective migration. Nat. Cell Biol. 2013;15:763–772. doi: 10.1038/ncb2772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tambe D.T., Hardin C.C., Trepat X. Collective cell guidance by cooperative intercellular forces. Nat. Mater. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim J.H., Serra-Picamal X., Fredberg J.J. Propulsion and navigation within the advancing monolayer sheet. Nat. Mater. 2013;12:856–863. doi: 10.1038/nmat3689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Behrndt M., Salbreux G., Heisenberg C.P. Forces driving epithelial spreading in zebrafish gastrulation. Science. 2012;338:257–260. doi: 10.1126/science.1224143. [DOI] [PubMed] [Google Scholar]
- 9.Campinho P., Behrndt M., Heisenberg C.P. Tension-oriented cell divisions limit anisotropic tissue tension in epithelial spreading during zebrafish epiboly. Nat. Cell Biol. 2013;15:1405–1414. doi: 10.1038/ncb2869. [DOI] [PubMed] [Google Scholar]
- 10.Shindo A., Wallingford J.B. PCP and septins compartmentalize cortical actomyosin to direct collective cell movement. Science. 2014;343:649–652. doi: 10.1126/science.1243126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lienkamp S.S., Liu K., Walz G. Vertebrate kidney tubules elongate using a planar cell polarity-dependent, rosette-based mechanism of convergent extension. Nat. Genet. 2012;44:1382–1387. doi: 10.1038/ng.2452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gjorevski N., Nelson C.M. Integrated morphodynamic signalling of the mammary gland. Nat. Rev. Mol. Cell Biol. 2011;12:581–593. doi: 10.1038/nrm3168. [DOI] [PubMed] [Google Scholar]
- 13.Piotrowski-Daspit A.S., Tien J., Nelson C.M. Interstitial fluid pressure regulates collective invasion in engineered human breast tumors via Snail, vimentin, and E-cadherin. Integr. Biol. 2016;8:319–331. doi: 10.1039/c5ib00282f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vasiev B., Balter A., Weijer C.J. Modeling gastrulation in the chick embryo: formation of the primitive streak. PLoS One. 2010;5:e10571. doi: 10.1371/journal.pone.0010571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Doxzen K., Vedula S.R., Lim C.T. Guidance of collective cell migration by substrate geometry. Integr. Biol. 2013;5:1026–1035. doi: 10.1039/c3ib40054a. [DOI] [PubMed] [Google Scholar]
- 16.Deforet M., Hakim V., Silberzan P. Emergence of collective modes and tri-dimensional structures from epithelial confinement. Nat. Commun. 2014;5:3747. doi: 10.1038/ncomms4747. [DOI] [PubMed] [Google Scholar]
- 17.Segerer F.J., Thüroff F., Rädler J.O. Emergence and persistence of collective cell migration on small circular micropatterns. Phys. Rev. Lett. 2015;114:228102. doi: 10.1103/PhysRevLett.114.228102. [DOI] [PubMed] [Google Scholar]
- 18.Li B., Sun S.X. Coherent motions in confluent cell monolayer sheets. Biophys. J. 2014;107:1532–1541. doi: 10.1016/j.bpj.2014.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Doostmohammadi A., Thampi S.P., Yeomans J.M. Celebrating soft matter’s 10th anniversary: cell division: a source of active stress in cellular monolayers. Soft Matter. 2015;11:7328–7336. doi: 10.1039/c5sm01382h. [DOI] [PubMed] [Google Scholar]
- 20.Soumya S.S., Gupta A., Inamdar M.M. Coherent motion of monolayer sheets under confinement and its pathological implications. PLOS Comput. Biol. 2015;11:e1004670. doi: 10.1371/journal.pcbi.1004670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tanner K., Mori H., Bissell M.J. Coherent angular motion in the establishment of multicellular architecture of glandular tissues. Proc. Natl. Acad. Sci. USA. 2012;109:1973–1978. doi: 10.1073/pnas.1119578109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gomez E.W., Chen Q.K., Nelson C.M. Tissue geometry patterns epithelial-mesenchymal transition via intercellular mechanotransduction. J. Cell. Biochem. 2010;110:44–51. doi: 10.1002/jcb.22545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yamao M., Naoki H., Ishii S. Multi-cellular logistics of collective cell migration. PLoS One. 2011;6:e27950. doi: 10.1371/journal.pone.0027950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shinbrot T., Chun Y., Foty R. Cellular morphogenesis in silico. Biophys. J. 2009;97:958–967. doi: 10.1016/j.bpj.2009.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vicsek T., Czirók A., Shochet O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995;75:1226–1229. doi: 10.1103/PhysRevLett.75.1226. [DOI] [PubMed] [Google Scholar]
- 26.Thoumine O., Ott A. Time scale dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J. Cell Sci. 1997;110:2109–2116. doi: 10.1242/jcs.110.17.2109. [DOI] [PubMed] [Google Scholar]
- 27.Zhou Q.M., Wang X.F., Su S.B. Curcumin enhanced antiproliferative effect of mitomycin C in human breast cancer MCF-7 cells in vitro and in vivo. Acta Pharmacol. Sin. 2011;32:1402–1410. doi: 10.1038/aps.2011.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nagy M., Akos Z., Vicsek T. Hierarchical group dynamics in pigeon flocks. Nature. 2010;464:890–893. doi: 10.1038/nature08891. [DOI] [PubMed] [Google Scholar]
- 29.Yates C.A., Erban R., Sumpter D.J. Inherent noise can facilitate coherence in collective swarm motion. Proc. Natl. Acad. Sci. USA. 2009;106:5464–5469. doi: 10.1073/pnas.0811195106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chuai M., Weijer C.J. The mechanisms underlying primitive streak formation in the chick embryo. Curr. Top. Dev. Biol. 2008;81:135–156. doi: 10.1016/S0070-2153(07)81004-0. [DOI] [PubMed] [Google Scholar]
- 31.Cui C., Yang X., Weijer C.J. Analysis of tissue flow patterns during primitive streak formation in the chick embryo. Dev. Biol. 2005;284:37–47. doi: 10.1016/j.ydbio.2005.04.021. [DOI] [PubMed] [Google Scholar]
- 32.Nelson C.M., Jean R.P., Chen C.S. Emergent patterns of growth controlled by multicellular form and mechanics. Proc. Natl. Acad. Sci. USA. 2005;102:11594–11599. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.